1 引言
随着电力变压器空载合闸时,会产生比额定电流高出6~10倍的励磁涌流,且波形畸变严重。高幅值的畸变电流,将使得变压器绕组出现高力学应力[1 ] 、热应力、过电流等现象,直接影响变压器的寿命及可靠性[2 ] ;同时,由于涌流波形中存在大量的非周期分量和谐波分量,容易导致电流互感器(CT)发生饱和,使CT无法线性传变而造成保护误动作,影响系统的可靠运行[3 ] 。在工程应用中,为了有效区分励磁涌流与故障电流,学者们普遍采用基于二次谐波制动原理[4 -5 ] 和间断角原理[6 -7 ] 的辨识方法,但该类单一参量特性监测的辨识方法存在一定的应用局限性,如改进优化后的变压器铁心材料[8 ] 会使涌流的二次谐波占比减小,而CT饱和[9 ] 会使涌流间断角消失。
为了进一步提升励磁涌流辨识的可靠性,国内外学者提出了一些基于波形特征的辨识方法及判据。文献[10 ]采用边界离散小波变换方法,提取电流高频分量作为涌流识别的判据,其识别准确率较高;文献[11 ]研究了励磁涌流下故障分量瞬时功率的相空间轨迹特征,该方法可用于识别故障伴随CT饱和的情况。需要指出的是,该类方法依旧是通过对信号的局部特征或某一分量特征进行提取,在未充分考虑信号整体特性及复杂度的情况下,无法实现复杂扰动下励磁涌流的可靠识别,如CT饱和、匝间短路等场景。文献[12 -13 ]采用Hausdroff距离表征涌流与正弦信号的波形整体相似度,通过判断涌流信号与正弦信号的相似程度来识别涌流,该方法较好地描述了涌流信号的整体特征,但并未充分考虑变压器空载合闸于CT饱和场景下的扰动及可靠性。近年来,许多智能算法也开始应用于励磁涌流的快速识别,如神经网络[14 ] 、深度学习[15 ] 、模糊逻辑算法[16 ] 等,通过对信号分解后提取多个波形特征量组合成输入向量,参与智能算法的模型训练。此类智能算法能够充分考虑涌流信号的整体及局部特征,其识别准确率提高,并且可应用于CT饱和、匝间故障等复杂扰动场景;但是,该类算法需要经过大量的模型训练,所需算力及时间成本较高,不易于工程应用中涌流特性的快速辨识。较为前沿的信号分解算法是变分模态分解(Variational mode decomposition,VMD)[17 ] ,它是一种完全非递归的分解算法,对非线性、不规则性等信号的分解具有较强的准确性。文献[18 ]采用VMD算法对变压器和应涌流进行有效分解并识别,未考虑励磁涌流下VMD的分解情况。文献[19 ]通过采用VMD算法对励磁涌流进行分解,再结合极限学习机对模型进行训练,该算法将VMD与神经网络结合,提高算法辨识准确性,但也增大了时间与算力成本,并且该算法未考虑变压器空载合闸时剩磁的重要性,以及空载合闸于CT饱和、匝间故障等扰动场景下的可靠性。因此,亟需一种既考虑信号的整体特性,又能满足快速计算的多场景复杂扰动下励磁涌流的识别算法。
针对考虑CT饱和、轻微匝间故障等扰动下励磁涌流快速识别困难的问题,本文通过研究正常情况、CT饱和、匝间故障时励磁涌流的波形复杂特性,提出一种基于固有模态分量与样本熵的波形复杂特性表征策略,选定分量的样本熵和值作为励磁涌流识别判据,结合改进的变分模态分解算法,实现励磁涌流的快速可靠辨识。此算法不同于信号波形的单一特征识别,可实现对波形整体复杂特性的快速分析与数值表征,实现励磁涌流的快速识别。
2 励磁涌流的波形复杂特性及表征
2.1 信号的波形复杂特性
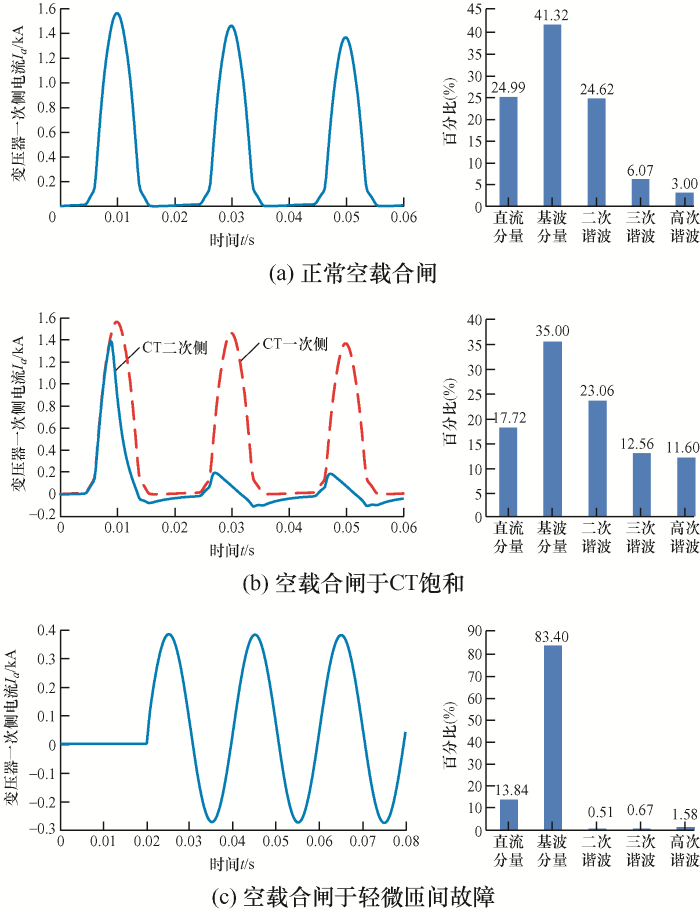
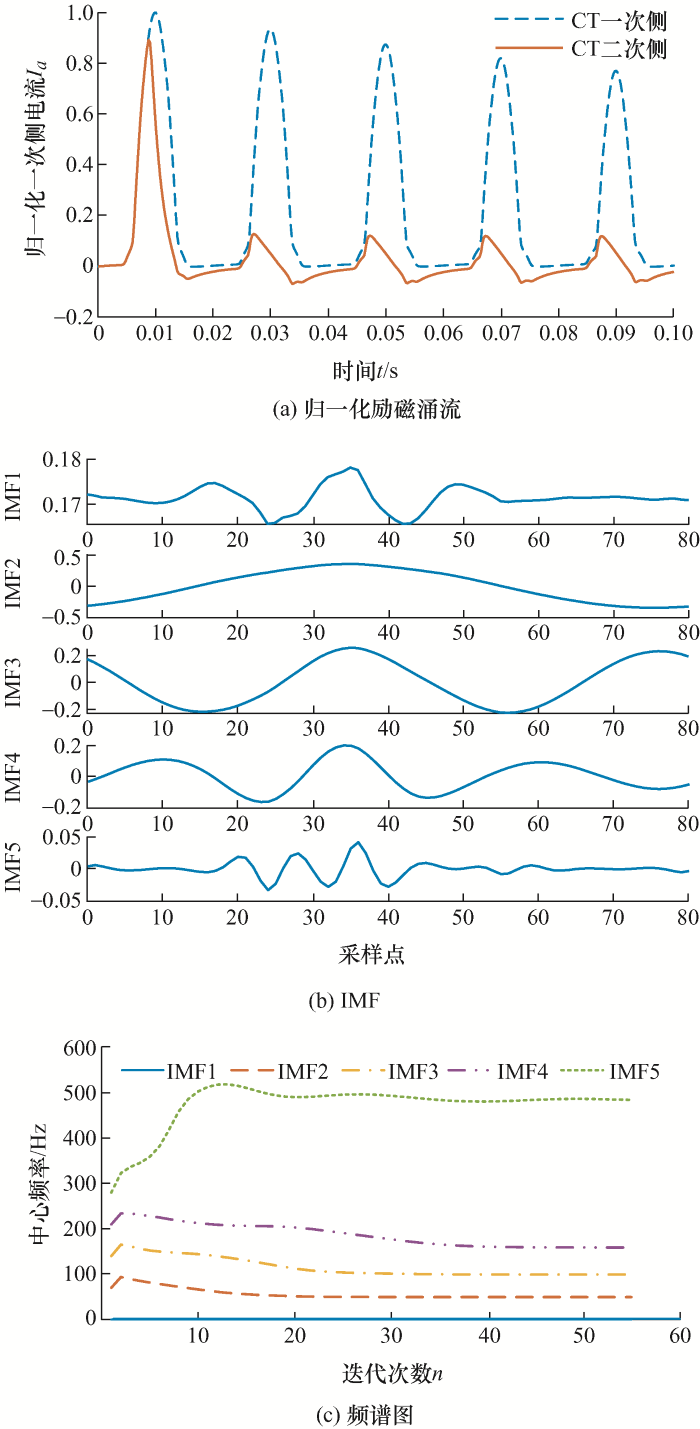
本文借鉴文献[17 ]应用时间序列的非线性与不规则性来表征时间序列复杂程度的定义,采用波形的非周期性与谐波特性来体现波形的复杂特性,非周期和谐波含量与复杂特性成正相关。图1 是变压器空载合闸、合闸于CT饱和、合闸于匝间故障时的涌流波形及信号含有的分量图。
图1
图1
变压器多种合闸情况及信号含有的分量占比柱状图
由图1a 可知,励磁涌流波形的复杂特性体现在其存在大量的非周期直流分量与谐波分量,其中以二次谐波分量为主,波形复杂程度严重。由于涌流含有大量的直流分量与谐波分量,极易引发CT饱和,饱和后的副边电流迅速衰减至零附近,间断角消失并且产生反向电流,电流出现明显的畸变现象,导致CT无法线性传变,如图1b 所示;CT饱和时的励磁涌流基波与直流分量占比有所减小,高次谐波占比增大,仍存在大量直流分量与谐波分量,其波形特性仍然非常复杂,波形复杂程度严重。
当变压器发生轻微匝间故障(故障匝数比5%)时,由于故障电流相对额定电流幅值变化很小,容易躲过整定值使保护未能及时动作。因此,本文进一步分析了变压器合闸于轻微匝间故障时的波形复杂特性,如图1c 所示;合闸于轻微匝间故障时,电流以基波分量为主,非周期性分量和谐波分量显著减少。相比于涌流,其波形复杂程度较轻,波形复杂特性不明显。
鉴于其他故障电流主要以正弦信号为主,周期性强且谐波含量少,其波形复杂特性体现不明显,波形复杂程度较轻,故不再赘述。
2.2 波形复杂特性的数值表征策略
经过初步分析可知,相比于变压器发生区内及内部故障、合闸于轻微匝间故障场景,变压器正常合闸与合闸于CT饱和时的励磁涌流波形复杂特性明显、复杂程度严重。为准确表征不同信号的波形复杂特性,本文对信号采用变分模态分解来获得固有模态分量,再引入样本熵原理,并结合分量与信号的关系,提出波形复杂特性的数值表征策略。
2.2.1 固有模态分量的定义
通过将分析信号进行Hilbert变换、调谐模态中心频率以及解调信号的高斯平滑度处理后,得到下列约束变分方程式(1),再经过迭代搜寻变分模型的最优解,获得信号的固有模态分量(Intrinsic mode function,IMF)集合。
(1) $\left\{ \begin{align} & \underset{\left\{ {{u}_{k}} \right\},\left\{ {{\omega }_{k}} \right\}}{\mathop{\min }}\,\left\{ \underset{k}{\mathop \sum }\,\left\| {{\partial }_{t}}\left[ (\delta (t)+\frac{\text{j}}{\mathrm{ }\!\!\pi\!\!\text{ }t})\ \centerdot \ {{u}_{k}}(t) \right]\exp (-\text{j}{{\omega }_{k}}t) \right\|_{2}^{2} \right\} \\ & \mathrm{s}.\mathrm{t}.\underset{\ \ \ \ k\ }{\mathop \ \ \sum }\,{{u}_{k}}=f \\ \end{align} \right.$.
式中,$\left\{ {{u}_{k}} \right\}$ $\left\{ {{\omega }_{k}} \right\}$ $\sum{{{u}_{k}}}$ f 表示输入信号。
固有模态分量是分析信号经过变分模态分解算法后得到的具有中心频率及有限带宽的调频-调幅信号集合。信号的第k 个IMF表达式为
(2) ${{u}_{k}}\left( t \right)={{A}_{k}}\left( t \right)\cos \left( {{\phi }_{k}}\left( t \right) \right)$
式中,相位${{\phi }_{k}}\left( t \right)$ ${{A}_{k}}\left( t \right)$
2.2.2 基于IMF与样本熵的波形复杂特性表征
样本熵是一种表征时间序列复杂程度的测度方法[20 ] 。样本熵越小,序列自我相似性越高;样本熵越大,序列的非线性与复杂性越高。原理如下所示。
(1) 设序列$X=\left\{ x\left( 1 \right),x\left( 2 \right),\cdots,x\left( N \right) \right\}$ m 维矢量,m =2,即$X\left( i \right)=\left\{ x\left( i \right),x\left( i+1 \right),\cdots,x\left( i+m-1 \right) \right\}$
(2) 定义$d[X(i),X(j)](i\ne j)$ $dr$ N-m 的比值$B_{i}^{m}$ ${{B}^{m}}$
(3) $B_{i}^{m}\left( r \right)=\frac{1}{N-m}num\left\{ d\left[ X\left( i \right),X\left( j \right) \right]<r \right\}$
(4) ${{B}^{m}}\left( r \right)=\frac{1}{N-m+1}\underset{i=1}{\overset{N-m+1}{\mathop \sum }}\,B_{i}^{m}\left( r \right)$
式中,r 为相似容限,r =0.2 std,std为序列标准差。
(3) 将维数m 加1得到${{B}^{m+1}}$
(5) $SampEn\left( X,N,m,r \right)=-\ln \left[ \frac{{{B}^{m+1}}\left( r \right)}{{{B}^{m}}\left( r \right)} \right]$
通过对分解得到的IMF采用样本熵测度方法,获得每个IMF的样本熵值,可实现信号中单一分量的复杂特性数值表征。
励磁涌流的IMF主要是非周期、基频以及其他高频分量,各分量的幅值大且复杂程度严重,故各分量的样本熵值较大,共同影响着原信号的整体波形复杂特性。相比之下,故障电流的IMF主要是非周期和基频分量,这两个分量虽然幅值较大且具有一定的复杂程度,但是余下的多个分量幅值非常小,复杂程度也很弱,以至于余下的分量样本熵值很小并且几乎不影响信号的整体特点,即故障信号的复杂特性主要以非周期分量和基频分量体现。因此,可以认为,励磁涌流的各个IMF复杂程度相似并且熵值较大;而故障电流的各个IMF复杂程度相差较大,仅非周期和基频分量的熵值较大,其余分量的熵值非常小。
进一步地,为实现信号整体的波形复杂特性表征,观察式(1)的约束条件发现,固有模态分量总和应等于原信号,则IMF总和的复杂特性和复杂程度也应与原信号相似,故采用IMF的样本熵和值来表征信号的波形复杂特性,样本熵和值越大,该信号的波形复杂特性越明显,复杂程度越严重。综上,本文提出一种基于IMF与样本熵的波形复杂特性表征策略:首先对IMF的单个分量逐个求解样本熵值,然后将各分量样本熵求和,得到基于IMF集合的样本熵和值,最后以此作为信号波形复杂特性的数值表征。其表达式为
(6) $SumSE=\sum\limits_{k=1}^{K}{SampEn(}{{u}_{k}})$
表1 是多种工况下电流信号的样本熵和值,由于故障电流以正弦信号为主,其非周期分量与谐波含量很少,波性复杂程度较轻,因此样本熵和值较小;而变压器不论是否合闸于CT饱和,涌流都含有大量非周期分量与谐波分量,其IMF是多种不同中心频率的调幅调频信号,其复杂程度将远超故障电流,因此涌流的样本熵和值将大于故障电流。
3 基于复杂特性表征策略的改进识别算法
3.1 改进的变分模态分解
变分模态分解(VMD)通过迭代搜寻变分模型的最优解,将信号分解为多个具有中心频率及有限带宽的IMF。它能够刻画出信号在时域上的局部特性,对励磁涌流、CT饱和等此类突变或非平稳信号的分解效果很好。
VMD通过引入拉格朗日乘数λ 和二次惩罚项α ,将式(1)转换为增广拉格朗日函数来获取非约束变分模型
(7) $L\left( \left\{ {{u}_{k}} \right\},\left\{ {{w}_{k}} \right\},\lambda \right)=\alpha \underset{k}{\mathop \sum }\,\left\| {{\partial }_{t}}\left[ \alpha \left( t \right)+\frac{\mathrm{j}}{\mathrm{ }\!\!\pi\!\!\text{ }t} \right]{{u}_{k}}\left( t \right)\exp (-\mathrm{j}uxt) \right\|_{2}^{2}+\left\| x\left( t \right)-\underset{k}{\mathop \sum }\,{{u}_{k}}\left( t \right) \right\|_{2}^{2}+\left\langle \lambda \left( t \right),x\left( t \right)-\underset{k}{\mathop \sum }\,{{u}_{k}}\left( t \right) \right\rangle $
接着采用交替方向乘子法(Alternating direction method of multipliers,ADMM)对式(7)中的变量进行迭代求解,并直接在傅里叶域中进行优化。即交替更新$u_{k}^{n+1}$ $\omega _{k}^{n+1}$ $\lambda _{k}^{n+1}$
(8) $\hat{u}_{k}^{n+1}\left( \omega \right)=\frac{\hat{f}\left( \omega \right)-\sum\limits_{i\ne k}{{{{\hat{u}}}_{i}}\left( \omega \right)+\hat{\lambda }\left( \omega \right)/2}}{1+2\alpha {{(\omega -{{\omega }_{k}})}^{2}}}$
(9) $\omega _{k}^{n+1}=\frac{\int_{0}^{\infty }{\omega {{\left| \hat{u}_{k}^{n+1}\left( \omega \right) \right|}^{2}}}\mathrm{d}\omega }{\int_{0}^{\infty }{{{\left| \hat{u}_{k}^{n+1}\left( \omega \right) \right|}^{2}}}\mathrm{d}\omega }$
(10) ${{\hat{\lambda }}^{n+1}}\left( \omega \right)={{\hat{\lambda }}^{n}}\left( \omega \right)+\tau \left[ \hat{f}\left( \omega \right)-\underset{k}{\mathop \sum }\,\hat{u}_{k}^{n+1}\left( \omega \right) \right]$
式中,$\{\hat{u}_{k}^{1}\}$ ${{\hat{\lambda }}^{n+1}}$ ${{u}_{k}}$ λ 的傅里叶变换。
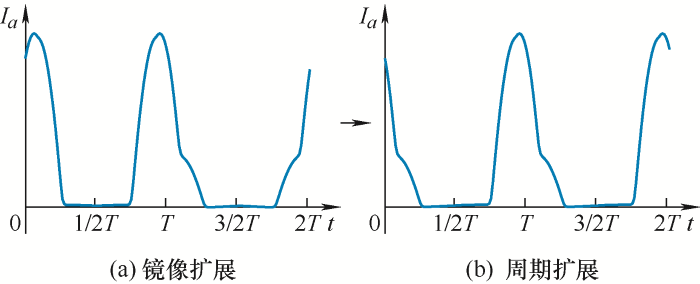
VMD算法为消除端点效应(分解后的IMF首末端点处数据波动幅度较大),采用镜像扩展的预处理,将长度为L 的数据扩展为2L 。经过镜像扩展的信号波形如图2a 所示。结合涌流波形发现,涌流信号类似于衰减的周期信号,使用镜像扩展与原涌流波形差别较大,不能完整地体现涌流波形特点,其分解准确性与端点效应的消除效果一般。
图2
因此,本文采用周期扩展的方法,对VMD算法进行改进,设原数据YL ={y (1),y (2),…,y (n )},t ∈(1/2T ,3/2T ),则经周期扩展后的数据Y 2 L , c 图2b 所示。
(11) ${{Y}_{2L,c}}=\left\{ \begin{matrix} y\left( \frac{L}{2}+1 \right),y\left( \frac{L}{2}+2 \right),\cdots,y(L)\ \ \ 0<i<\frac{L}{2} \\ y(1),y(2),\cdots,y(L) \frac{L}{2}+1<i<\frac{3L}{2} \\ y(1),y(2),\cdots,y(\frac{L}{2}) \frac{3L}{2}+1<i<2L \\\end{matrix} \right.$
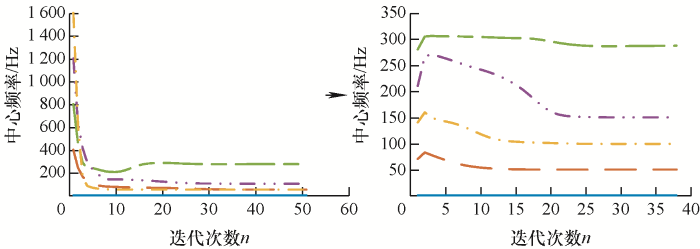
同时,为加快VMD的分解速率,结合励磁涌流的高次谐波特点,将中心频率初始化原按奈奎斯特频率均匀分布,改进为按最大7次谐波的均匀分布。图3 是中心频率初始化改进前后的VMD频谱图,可以看出,在相同参数下,经过频率初始化改进后的算法总迭代次数更少,分解速率更快。
图3
综上,改进变分模态分解算法能够使得扩展信号更符合励磁涌流波形变化趋势,确保IMF准确反映励磁涌流的波形复杂特性,有效消除端点效应;同时,改进的频率初始化使得算法加速完成迭代收敛,大大提升算法的分解速率;即改进后VMD算法的准确性和快速性得到显著提升。
3.2 识别算法的参数整定
3.2.1 VMD的初始参数整定
VMD算法的分解效果主要受预定义的模态分量个数K 和惩罚因子α 影响,现有方案多以经验值选取参数,但不同参数下的分解效果相差甚远。当K 或α 较大时,迭代次数增加,分解速率降低,出现多余的虚假分量,即过分解现象;当K 或α 较小时,则会出现多个分量混叠成一个模态,即欠分解现象。因此,结合励磁涌流各分量特点及已有的经验取值法,采用遍历法对参数K 和α 进行选择。由于采样频率为4 kHz,所以惩罚因子α 取2 000~8 000(以500为步长),分量个数K 取4~8,随机选取励磁涌流总仿真数据的1/2作为遍历法分析样本。考虑励磁涌流是变压器的暂态特性,需要快速识别并使得保护闭锁。因此,以快速性为主,准确性为辅,构建评估VMD算法分解效果的适应度函数为
(12) ${{F}_{s}}={{f}_{n}} \cdot n+{{f}_{e}} \cdot {{E}_{er}}$
式中,n 为分解的总迭代次数;${{E}_{er}}$ ${{f}_{n}}$ ${{f}_{e}}$
研究发现,n 越小,分解速率越快,越快完成收敛,说明此参数越适合此场景;能量差值越小则说明分解效果越准确。因此,在参数遍历过程中,计算每组参数下的Fs ,选择Fs 的最小平均值所对应的参数组合作为分解励磁涌流的最佳参数。
经过仿真验证,改进后的VMD算法能够更好地消除端点效应,更快速地分解出励磁涌流的各分量。结合遍历法搜寻最优参数组合,得出最快完成迭代收敛的最佳参数组合为(K ,α )=(5,2 000)。
3.2.2 识别算法的门槛值整定
由第2节的分析可知,变压器空载合闸、合闸于CT饱和时的涌流样本熵和值皆大于变压器发生故障时的样本熵和值,并且故障与涌流之间的样本熵和值有明显的数值区分。因此,针对这一数值特点,本文通过分析变压器在剩磁、合闸角、CT饱和、故障匝数比、故障类型等多种复杂工况下的励磁涌流与故障电流的样本熵和值分布规律,设定区分涌流的样本熵和门槛值为
(13) ${{S}_{set}}={{K}_{rel}}{{S}_{\max.fault}}$
式中,${{S}_{\max.fault}}$ ${{S}_{\max.fault}}$ ${{K}_{rel}}$ ${{S}_{set}}$
鉴于该门槛值是基于电流波形复杂特性而设定,其特性是通用变压器都具有的特点,与变压器的具体参数相关性不大,因此该门槛值适用于大部分变压器的励磁涌流识别。
3.3 基于改进VMD与样本熵和的涌流识别算法
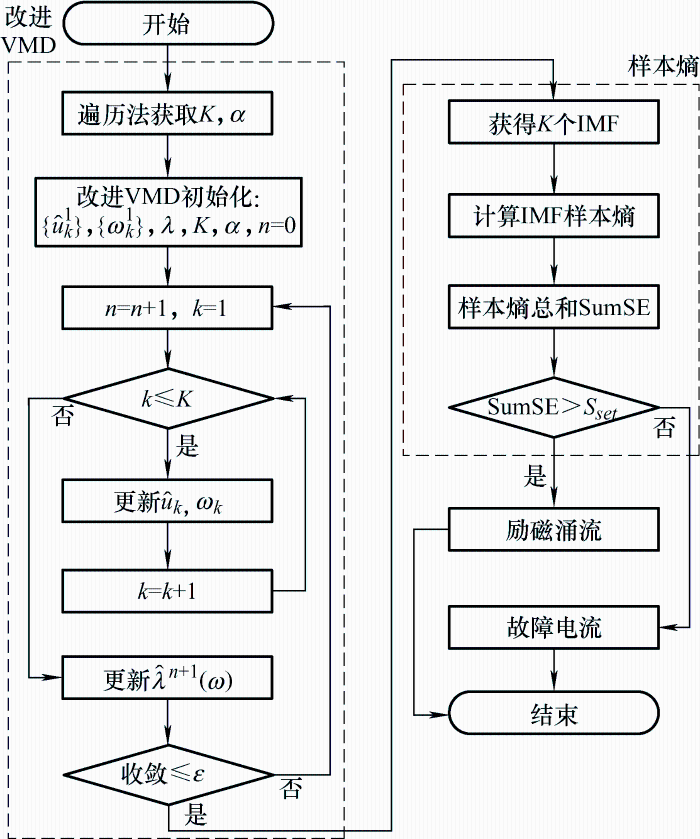
为实现将励磁涌流与故障电流的波形复杂特性存在明显差异的特点作为励磁涌流的识别判据,本文采用改进的变分模态分解算法,将信号快速并准确地分解为多个固有模态分量,再引入表征序列复杂程度的样本熵原理,采用固有模态分量的样本熵和值表示信号的波形复杂程度,实现波形复杂特性的数值表征。最后通过判断电流信号的样本熵和值SumSE与门槛值Sset 的大小,实现在复杂扰动下的励磁涌流快速识别。若SumSE>Sset ,则为励磁涌流,否则为故障电流。算法识别具体流程如图4 所示。
图4
图4
基于改进VMD与样本熵和的励磁涌流识别算法流程
4 仿真验证
为验证所提基于波形复杂特性的励磁涌流快速识别算法的准确性和可靠性,本文采用PSACD仿真搭建了如图5 所示的励磁涌流电路模型。其中,变压器变比为500/220 kV,容量为500 MV·A,连接组别为YNd11,磁滞模型为JA模型。电流互感器为JA模型,变比为5/1 000。本文选择变压器一次侧A相电流作为分析对象,取第一个周期电流作为分析信号,采样频率为4 kHz,即取80个采样点。
图5
变压器运行过程中主要存在两种典型剩磁[21 ] :① 平衡剩磁。由断路器开闭所造成的剩磁,三相剩磁之和为0,表达式为ϕra =-0.5ϕrb =-0.5ϕrc ;② 不平衡剩磁。由直流电阻测试或直流偏磁等导致的剩磁,表达式为ϕra =-ϕrb =-ϕrc ;本文以剩磁ϕr 和合闸角θ 作为影响励磁涌流变化的主要因素,仿真模拟多场景扰动下的励磁涌流,表2 是多场景仿真案例汇总。
4.1 识别算法的基础验证
4.1.1 案例1:空载合闸
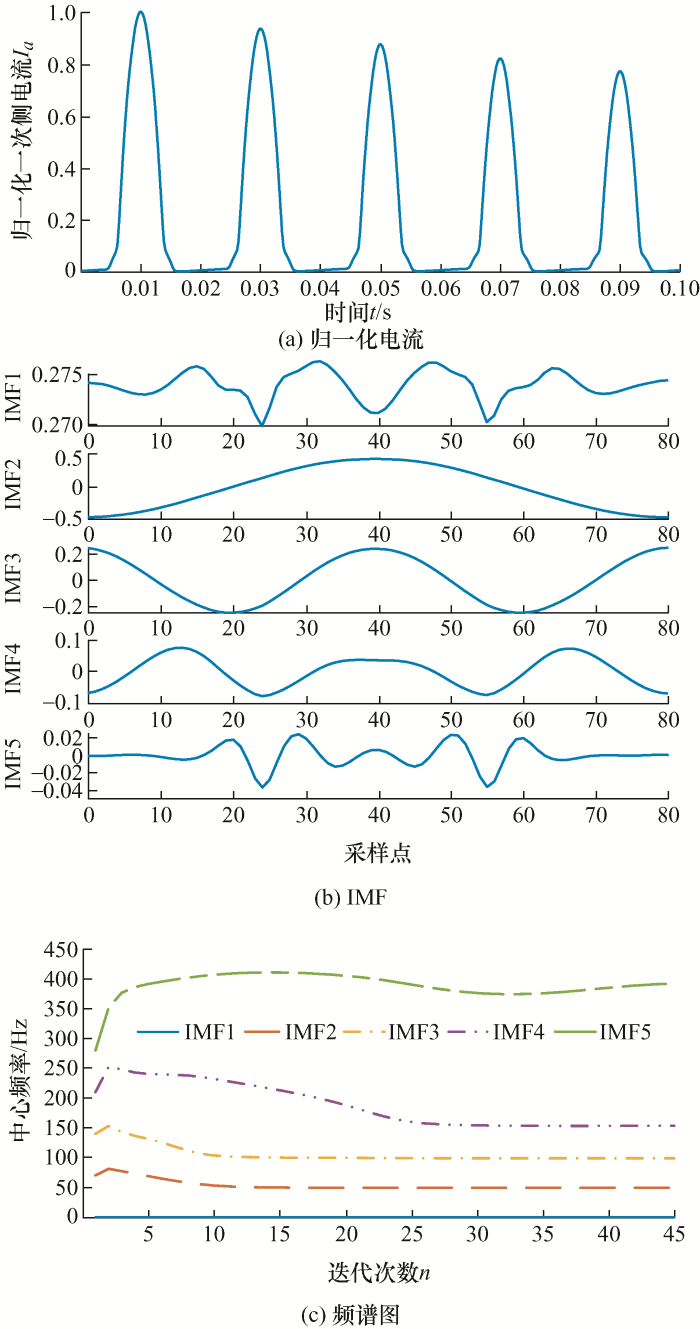
图6 是变压器在θ = 0°且无剩磁下空载合闸的归一化励磁涌流及VMD算法的分量图、频谱图,下面以此工况为例进行简要分析。
图6
由图6 可知,算法完成45次迭代后完整分离出直流、基波及其他分量,说明改进VMD算法能够准确地分解励磁涌流。同时,算法用时23 ms,其快速性得到保证。采集在不同剩磁与合闸角工况下励磁涌流的第一个周波信号,应用本文所提算法计算样本熵和值SumSE,整理所得结果如图7 所示。
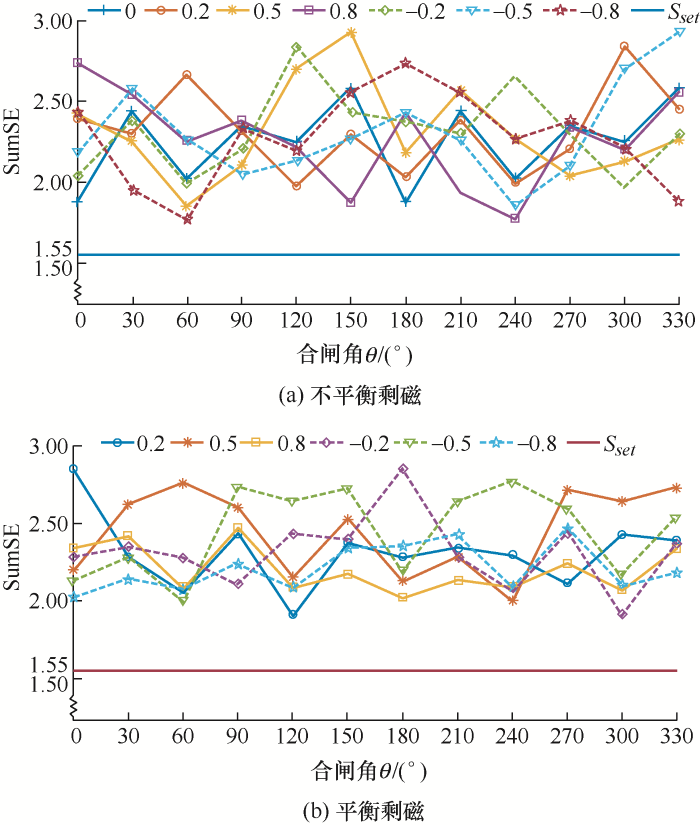
图7
本文所提算法在变压器空载合闸时的分解效果与分解速率都表现出改进VMD的优异性,算法收敛条件表示为IMF总和与原信号的误差,本文取10-6 ,即分解的准确性得到了保证;且经过统计可知,算法的最快识别时间仅需要21 ms,即分解的快速性也得到了保证。由图7 可知,在不同剩磁类型与大小、合闸角工况下,励磁涌流的样本熵和值皆大于门槛值,并且离门槛值有较大的距离,说明该算法在变压器正常空载合闸场景下可快速准确地识别出涌流信号,应用效果最好。
4.1.2 案例2:变压器区内故障
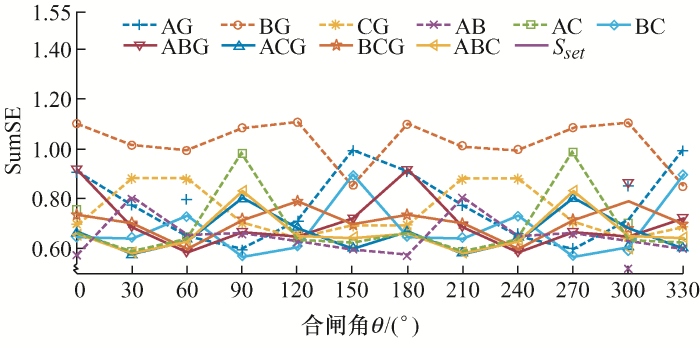
本文讨论的区内故障为变压器出口处发生的单相接地、相间短路、两相接地、三相短路故障。采集在不同故障与故障相位角工况下故障电流的第一个周波信号,应用本文所提算法计算样本熵和值SumSE,整理所得结果如图8 所示,图8 中ABC表示三相,G表示带接地故障。
图8
由图8 可知,区内故障电流的样本熵和值皆小于门槛值1.55,并且距离门槛值有一定的裕度,验证了第2节中故障电流波形复杂度小于励磁涌流的结论,表明该算法能够准确地识别出变压器区内故障电流。
4.1.3 案例3:变压器内部故障
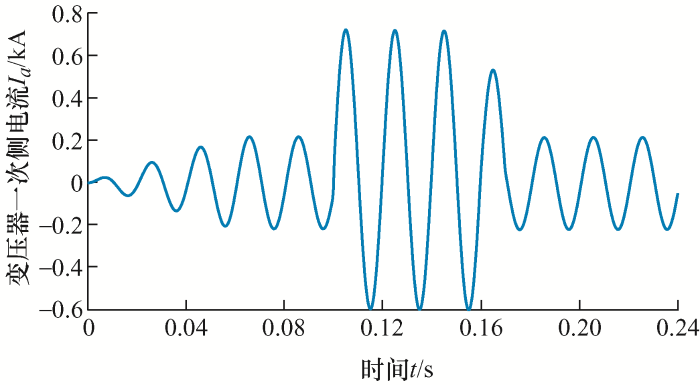
变压器内部故障以匝间故障为主,当发生轻微匝间故障(5%)时,其电流幅值变化很小,如图9 所示,容易躲开保护整定值而使保护无法动作,导致变压器运行在故障状态下。
图9
图9
0.1~0.16 s时A相发生5%匝间短路故障
本文主要讨论变压器二次侧发生匝间短路与匝间接地故障场景。采集不同故障相位角与匝数比工况下故障电流的第一个周波信号,应用本文所提算法计算样本熵和值SumSE,整理所得结果如表3 所示。
由表3 可知,在不同故障相位角与匝数比工况下,变压器内部故障电流的样本熵和值最大为1.134,远小于门槛值1.55,再次验证故障电流波形复杂度小于励磁涌流的结论,表明此方案能够准确识别出变压器内部故障电流。
本文所提算法在变压器发生区内故障与内部故障场景下,考虑了多种故障类型与工况下的仿真验证,结合图8 与表3 可知,算法在不同场景与工况下的样本熵和值都明显小于门槛值,并且距离门槛值有一定的距离,说明该算法可以准确识别出变压器区内故障与内部故障场景,应用效果较好。
4.2 复杂扰动下的识别验证
4.2.1 案例4:合闸于CT饱和
励磁涌流含有的大量直流分量极易引发CT出现饱和现象,造成CT二次侧电流出现畸变,使测量值存在误差,导致保护误动作。本文在与案例1相同仿真参数下进行CT饱和试验,仿真时将CT铁心截面积减小至1 cm2 ,并适当增大变比,使CT更易进入饱和状态。图10 是CT饱和时的归一化励磁涌流波形以及VMD算法的分量图、频谱图。
图10
图10
当θ = 0°且无剩磁时发生CT饱和的励磁涌流
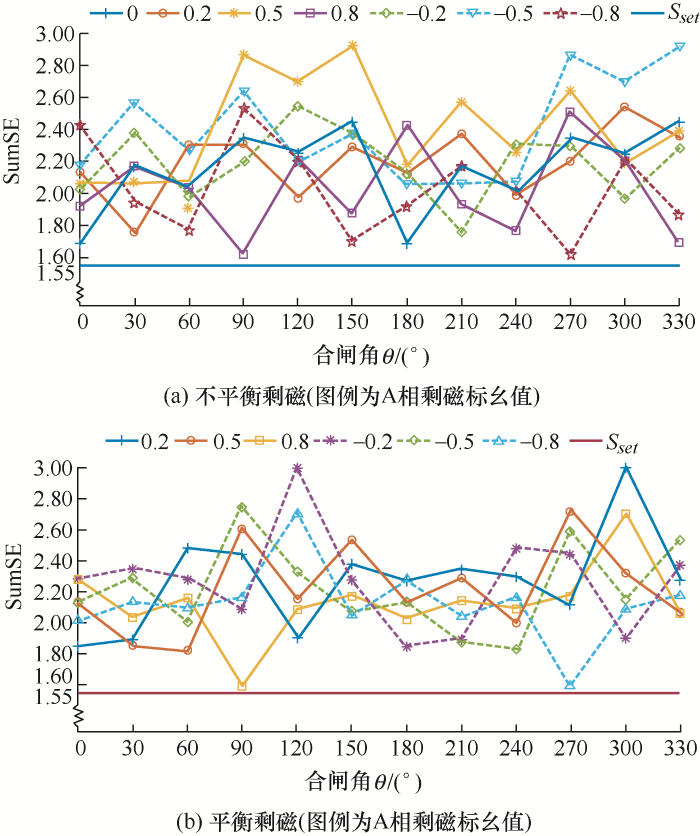
由图10 可知,即使是CT饱和时的励磁涌流,算法也能在完成第55次迭代后准确分解出直流分量与其他分量,并且用时仅30 ms,保证了分解的快速性和准确性。采集在不同剩磁与合闸角工况下CT饱和时涌流的第一个周波信号,应用本文所提算法计算样本熵和值SumSE,整理结果如图11 所示。
图11
由图11 可知,当θ = 90°与270°时,不论剩磁是否平衡,都出现样本熵和接近门槛值的情况。分析发现,此时变压器A相剩磁为±0.8 p.u.,为剩磁最大值场景,一般变压器在合闸前不会存有如此大的剩磁,此为极少数情况。总之,不论在何种剩磁及合闸角工况下,合闸于CT饱和时的励磁涌流样本熵和都大于门槛值1.55,并且经过统计发现,算法识别时间最快只需要25 ms,能够快速准确地识别出合闸于CT饱和时的励磁涌流。
考虑实际情况中,算法应快速准确地识别出CT饱和下的励磁涌流并及时使保护闭锁,因此此处只详细分析第一个周期下的CT饱和时的励磁涌流。仿真验证过程中分析了CT饱和下励磁涌流的后续几个周期的样本熵总和值,皆大于门槛值1.55,符合算法实际应用情况,考虑篇幅问题,未详细展开。
本文所提算法在变压器合闸于CT饱和场景下,算法收敛条件依旧保持在10-6 ,识别时间则在25~30 ms。相比于正常空载合闸场景,算法在CT饱和场景下的分解效果良好,虽然算法在CT饱和且剩磁为最大值时,出现样本熵和值接近门槛值的情况,但统计所有工况下的励磁涌流样本熵和值均大于门槛值,准确性较好,应用效果较好。
4.2.2 案例5:合闸于轻微匝间故障
本案例讨论变压器空载合闸于轻微匝间故障(故障匝数比5%)的场景,分析合闸于匝间短路和匝间接地故障情况,共24组仿真数据。采集在不同故障类型与相位角工况下故障电流的第一个周波信号,应用本文所提算法计算样本熵和值SumSE,所得结果如表4 所示。
由表4 可知,变压器合闸于轻微内部故障时,样本熵和最大值为1.41,低于门槛值1.55,验证了第2节中合闸于轻微匝间故障的波形复杂度小于励磁涌流的结论,表明此算法可用于识别变压器空载合闸于轻微匝间故障情况,使保护及时动作。算法在该场景下应用效果较好。
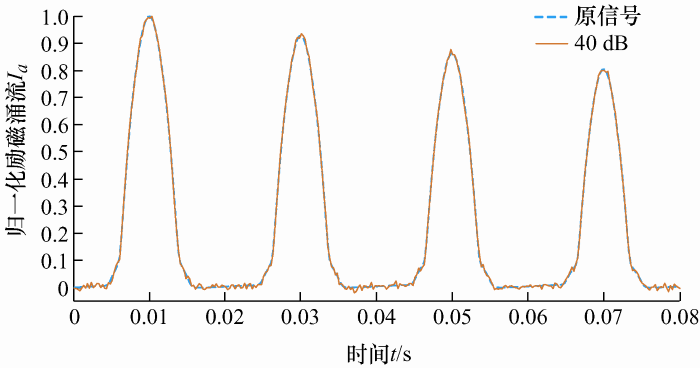
4.2.3 案例6:系统噪声的干扰
电力设备在运行中会互相干扰并产生一定的噪声,根据文献[22 ]可知,电力系统的常见噪声为45 dB。因此,本案例讨论采样信号在受到40~60 dB的高斯白噪声干扰下算法的抗噪性能。往励磁涌流加入40 dB噪声后的波形图如图12 所示。
图12
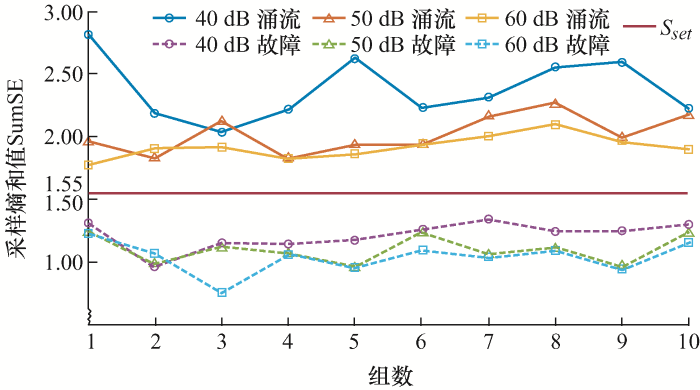
随机选取励磁涌流与故障电流各10组数据,并分别添加40 dB、50 dB、60 dB的高斯白噪声作为检验算法抗噪性能的样本数据,再将所得样本数据分别应用本文所提算法计算得到样本熵和值,整理所得数据如图13 所示。
图13
图13
算法在40~60 dB的干扰噪声下的样本熵和值SumSE
由图13 可知,本文所提算法在40~60 dB的噪声干扰下,仍能准确地识别出励磁涌流与故障电流,表明本文所提算法具有一定的抗噪能力,易于工程实践的应用。
5 结论
针对电力变压器空载合闸于CT饱和与匝间故障时励磁涌流快速识别困难的应用需求,本文研究了变压器空载合闸、CT饱和、匝间故障下励磁涌流的波形复杂特性,得到如下结论。
(1) 提出一种基于固有模态分量与样本熵的波形复杂特性表征策略,选定分量的样本熵和值表征复杂特性并以此作为励磁涌流的识别判据,得出励磁涌流样本熵和值大于故障电流的特点。
(2) 提出改进的变分模态分解算法,提升算法的快速性与准确性;再结合表征策略,可实现第一个周波电流采集下的快速励磁涌流模态分解及辨识。
(3) 所提算法可实现变压器合闸于CT饱和、轻微匝间故障下的励磁涌流可靠辨识。能够满足多场景环境下励磁涌流的快速识别应用,并具有抗40 dB噪声干扰的抗噪性能,多场景扰动下的仿真效果较好且模型应用的可靠性高。
参考文献
View Option
[1]
NI H FANG S LIN H A simplified phase-controlled switching strategy for inrush current reduction
[J]. IEEE Transactions on Power Delivery , 2021 , 36 (1 ):215 -222 .
DOI:10.1109/TPWRD.61
URL
[本文引用: 1]
[2]
SAMET H SHADAEI M TAJDINIAN M et al. Statistical discrimination index founded on rate of change of phase angle for immunization of transformer differential protection against inrush current
[J]. International Journal of Electrical Power & Energy Systems , 2022 ,134:107381.
[本文引用: 1]
[3]
黄景光 , 罗亭然 , 林湘宁 , 等 . 励磁涌流波形密度系数鉴别算法
[J]. 电力系统及其自动化学报 , 2017 , 29 (7 ):34 -40 .
[本文引用: 1]
HUANG Jingguang LUO Tingran LIN Xiangning et al. Identification algorithm for magnetizing inrush current in terms of waveform density coefificient
[J]. Proceedings of the CSU-EPSA , 2017 , 29 (7 ):34 -40 .
[本文引用: 1]
[4]
WU J Fuzzy recognition method and simulation analysis on second harmonic excitation inrush current of transformer
[J]. Applied Mechanics & Materials , 2014 ,484 -485 :1076-1080.
[本文引用: 1]
[5]
张双梓 , 王铮 , 孙世勇 , 等 . 变压器差动保护二次谐波制动方案分析与改进
[J]. 电测与仪表 , 2014 , 51 (23 ):123 -128 .
[本文引用: 1]
ZHANG Shuangzi WANG Zheng SUN Shiyong et al. Analysis and improvement of secondary harmonic restraint strategy for transformer differential protection
[J]. Electrical Measurement & Instrumentation , 2014 , 51 (23 ):123 -128 .
[本文引用: 1]
[6]
卢雪峰 , 王增平 , 徐岩 , 等 . 基于波形间断角原理识别变压器励磁涌流的新方法
[J]. 继电器 , 2007 , 35 (S1 ):1 -4 .
[本文引用: 1]
LU Xuefeng WANG Zengping XU Yan et al. A new method to identify inrush current based on the principle of dead angle
[J]. Power System Protection and Control , 2007 , 35 (S1 ):1 -4 .
[本文引用: 1]
[7]
何奔腾 , 徐习东 . 波形比较法变压器差动保护原理
[J]. 中国电机工程学报 , 1998 (6 ):20 -23 ,29.
[本文引用: 1]
XU Benteng XU Xidong Principle of differential protection of transformer by waveform comparison method
[J]. Proceedings of the CSEE , 1998 (6 ):20 -23 ,29.
[本文引用: 1]
[8]
张员宁 , 黄景光 , 张艳华 , 等 . 利用双重特征量鉴别变压器励磁涌流的高阶统计原理
[J]. 电力系统保护与控制 , 2021 , 49 (24 ):21 -30 .
[本文引用: 1]
ZHANG Yuanning HUANG Jingguang ZHANG Yanhua et al. High order statistical theory for identifying transformer inrush current by using dual characteristics
[J]. Power System Protection and Control , 2021 , 49 (24 ):21 -30 .
[本文引用: 1]
[9]
翁汉琍 , 陈皓 , 万毅 , 等 . 基于巴氏系数的变压器励磁涌流和故障差流识别新判据
[J]. 电力系统保护与控制 , 2020 , 48 (10 ):113 -122 .
[本文引用: 1]
WENG Hanli CHEN Hao WAN Yi et al. A novel criterion to distinguish inrush current from fault current based on the Bhattacharyya coefficient
[J]. Power System Protection and Control , 2020 , 48 (10 ):113 -122 .
[本文引用: 1]
[10]
MEDEIROS R P COSTA F B A wavelet-based transformer differential protection:Internal fault detection during inrush conditions
[J]. IEEE Transactions on Power Delivery , 2018 , PP (6 ):2965 -2977 .
[本文引用: 1]
[11]
戎子睿 , 林湘宁 , 金能 , 等 . 基于相空间轨迹识别和多判据融合的变压器保护新策略
[J]. 中国电机工程学报 , 2020 , 40 (6 ):1924 -1938 .
[本文引用: 1]
RONG Zirui LIN Xiangning JIN Neng et al. A new transformer protection scheme based on the recognition of phase space trajectory and multi-criteria fusion
[J]. Proceedings of the CSEE , 2020 , 40 (6 ):1924 -1938 .
[本文引用: 1]
[12]
翁汉琍 , 刘华 , 林湘宁 , 等 . 基于Hausdorff距离算法的变压器差动保护新判据
[J]. 中国电机工程学报 , 2018 , 38 (2 ):475 -483 ,678.
[本文引用: 1]
WENG Hanli LIU Hua LIN Xiangning et al. A novel criterion of the transformer differential protection based on the Hausdorff distance algorithm
[J]. Proceedings of the CSEE , 2018 , 38 (2 ):475 -483 ,678.
[本文引用: 1]
[13]
WENG H WANG S LIN X et al. A novel criterion applicable to transformer differential protection based on waveform sinusoidal similarity identification
[J]. International Journal of Electrical Power & Energy Systems , 2019 ,105:305 -314 .
[本文引用: 1]
[14]
AFRASIABI S AFRASIABI M PARANG B et al. Integration of accelerated deep neural network into power transformer differential protection
[J]. IEEE Transactions on Industrial Informatics , 2020 , 16 (2 ):865 -876 .
DOI:10.1109/TII.9424
URL
[本文引用: 1]
[15]
AFRASIABI S AFRASIABI M PARANG B et al. Designing a composite deep learning based differential protection scheme of power transformers
[J]. Applied Soft Computing , 2019 ,87.
[本文引用: 1]
[16]
BEJMERT D REBIZANT W SCHIEL L Transformer differential protection with fuzzy logic based inrush stabilization
[J]. International Journal of Electrical Power & Energy Systems , 2014 .
[本文引用: 1]
[17]
DRAGOMIRETSKIY K ZOSSO D Variational mode decomposition
[J]. IEEE Transactions on Signal Processing , 2014 , 62 (3 ):531 -544 .
[本文引用: 2]
[18]
赵学文 , 付泽宇 , 李乐 , 等 . 基于VMD和PSO-SVM模型的和应涌流识别
[J]. 电工技术 , 2021 (19 ):30 -34 .
[本文引用: 1]
ZHAO Xuewen FU Zeyu LI Le et al. Sympathetic inrush current identification based on VMD and PSO-SVM model
[J]. Electric Engineering , 2021 (19 ):30 -34 .
[本文引用: 1]
[19]
井萌 . 基于EO优化ELM的变压器励磁涌流识别方法研究 [D]. 西安 : 西安科技大学 , 2021 .
[本文引用: 1]
JING Meng Research on recognition method of transformer magnetizing inrush current based on EO optimized ELM [D]. Xi’an : Xi’an University of Science and Technology , 2021 .
[本文引用: 1]
[20]
RICHMAN J S RANDALL M J Physiological time-series analysis using approximate entropy and sample entropy
[J]. American Journal of Physiology Heart & Circulatory Physiology , 2000 , 278 (6 ):H2039 .
[本文引用: 1]
[21]
冯宝成 , 田志浩 , 摆世彬 , 等 . 防止超高压备自投诱发线路零序过流保护误动的对策初探
[J]. 电力系统保护与控制 , 2021 , 49 (2 ):98 -106 .
[本文引用: 1]
FENG Baocheng TIAN Zhihao BAI Shibin et al. Study on countermeasures to prevent maloperation of zero-sequence overcurrent protection caused by ultra-high-voltage automatic device transfer
[J]. Power System Protection and Control , 2021 , 49 (2 ):98 -106 .
[本文引用: 1]
[22]
VÁZQUEZ E ANDRADE M A ESPONDA H et al. A new differential protection algorithm for power reactors based on the second central moment
[J]. International Journal of Electrical Power and Energy Systems , 2020 ,118:105795.
[本文引用: 1]
A simplified phase-controlled switching strategy for inrush current reduction
1
2021
... 随着电力变压器空载合闸时,会产生比额定电流高出6~10倍的励磁涌流,且波形畸变严重.高幅值的畸变电流,将使得变压器绕组出现高力学应力[1 ] 、热应力、过电流等现象,直接影响变压器的寿命及可靠性[2 ] ;同时,由于涌流波形中存在大量的非周期分量和谐波分量,容易导致电流互感器(CT)发生饱和,使CT无法线性传变而造成保护误动作,影响系统的可靠运行[3 ] .在工程应用中,为了有效区分励磁涌流与故障电流,学者们普遍采用基于二次谐波制动原理[4 -5 ] 和间断角原理[6 -7 ] 的辨识方法,但该类单一参量特性监测的辨识方法存在一定的应用局限性,如改进优化后的变压器铁心材料[8 ] 会使涌流的二次谐波占比减小,而CT饱和[9 ] 会使涌流间断角消失. ...
Statistical discrimination index founded on rate of change of phase angle for immunization of transformer differential protection against inrush current
1
2022
... 随着电力变压器空载合闸时,会产生比额定电流高出6~10倍的励磁涌流,且波形畸变严重.高幅值的畸变电流,将使得变压器绕组出现高力学应力[1 ] 、热应力、过电流等现象,直接影响变压器的寿命及可靠性[2 ] ;同时,由于涌流波形中存在大量的非周期分量和谐波分量,容易导致电流互感器(CT)发生饱和,使CT无法线性传变而造成保护误动作,影响系统的可靠运行[3 ] .在工程应用中,为了有效区分励磁涌流与故障电流,学者们普遍采用基于二次谐波制动原理[4 -5 ] 和间断角原理[6 -7 ] 的辨识方法,但该类单一参量特性监测的辨识方法存在一定的应用局限性,如改进优化后的变压器铁心材料[8 ] 会使涌流的二次谐波占比减小,而CT饱和[9 ] 会使涌流间断角消失. ...
励磁涌流波形密度系数鉴别算法
1
2017
... 随着电力变压器空载合闸时,会产生比额定电流高出6~10倍的励磁涌流,且波形畸变严重.高幅值的畸变电流,将使得变压器绕组出现高力学应力[1 ] 、热应力、过电流等现象,直接影响变压器的寿命及可靠性[2 ] ;同时,由于涌流波形中存在大量的非周期分量和谐波分量,容易导致电流互感器(CT)发生饱和,使CT无法线性传变而造成保护误动作,影响系统的可靠运行[3 ] .在工程应用中,为了有效区分励磁涌流与故障电流,学者们普遍采用基于二次谐波制动原理[4 -5 ] 和间断角原理[6 -7 ] 的辨识方法,但该类单一参量特性监测的辨识方法存在一定的应用局限性,如改进优化后的变压器铁心材料[8 ] 会使涌流的二次谐波占比减小,而CT饱和[9 ] 会使涌流间断角消失. ...
Identification algorithm for magnetizing inrush current in terms of waveform density coefificient
1
2017
... 随着电力变压器空载合闸时,会产生比额定电流高出6~10倍的励磁涌流,且波形畸变严重.高幅值的畸变电流,将使得变压器绕组出现高力学应力[1 ] 、热应力、过电流等现象,直接影响变压器的寿命及可靠性[2 ] ;同时,由于涌流波形中存在大量的非周期分量和谐波分量,容易导致电流互感器(CT)发生饱和,使CT无法线性传变而造成保护误动作,影响系统的可靠运行[3 ] .在工程应用中,为了有效区分励磁涌流与故障电流,学者们普遍采用基于二次谐波制动原理[4 -5 ] 和间断角原理[6 -7 ] 的辨识方法,但该类单一参量特性监测的辨识方法存在一定的应用局限性,如改进优化后的变压器铁心材料[8 ] 会使涌流的二次谐波占比减小,而CT饱和[9 ] 会使涌流间断角消失. ...
Fuzzy recognition method and simulation analysis on second harmonic excitation inrush current of transformer
1
2014
... 随着电力变压器空载合闸时,会产生比额定电流高出6~10倍的励磁涌流,且波形畸变严重.高幅值的畸变电流,将使得变压器绕组出现高力学应力[1 ] 、热应力、过电流等现象,直接影响变压器的寿命及可靠性[2 ] ;同时,由于涌流波形中存在大量的非周期分量和谐波分量,容易导致电流互感器(CT)发生饱和,使CT无法线性传变而造成保护误动作,影响系统的可靠运行[3 ] .在工程应用中,为了有效区分励磁涌流与故障电流,学者们普遍采用基于二次谐波制动原理[4 -5 ] 和间断角原理[6 -7 ] 的辨识方法,但该类单一参量特性监测的辨识方法存在一定的应用局限性,如改进优化后的变压器铁心材料[8 ] 会使涌流的二次谐波占比减小,而CT饱和[9 ] 会使涌流间断角消失. ...
变压器差动保护二次谐波制动方案分析与改进
1
2014
... 随着电力变压器空载合闸时,会产生比额定电流高出6~10倍的励磁涌流,且波形畸变严重.高幅值的畸变电流,将使得变压器绕组出现高力学应力[1 ] 、热应力、过电流等现象,直接影响变压器的寿命及可靠性[2 ] ;同时,由于涌流波形中存在大量的非周期分量和谐波分量,容易导致电流互感器(CT)发生饱和,使CT无法线性传变而造成保护误动作,影响系统的可靠运行[3 ] .在工程应用中,为了有效区分励磁涌流与故障电流,学者们普遍采用基于二次谐波制动原理[4 -5 ] 和间断角原理[6 -7 ] 的辨识方法,但该类单一参量特性监测的辨识方法存在一定的应用局限性,如改进优化后的变压器铁心材料[8 ] 会使涌流的二次谐波占比减小,而CT饱和[9 ] 会使涌流间断角消失. ...
Analysis and improvement of secondary harmonic restraint strategy for transformer differential protection
1
2014
... 随着电力变压器空载合闸时,会产生比额定电流高出6~10倍的励磁涌流,且波形畸变严重.高幅值的畸变电流,将使得变压器绕组出现高力学应力[1 ] 、热应力、过电流等现象,直接影响变压器的寿命及可靠性[2 ] ;同时,由于涌流波形中存在大量的非周期分量和谐波分量,容易导致电流互感器(CT)发生饱和,使CT无法线性传变而造成保护误动作,影响系统的可靠运行[3 ] .在工程应用中,为了有效区分励磁涌流与故障电流,学者们普遍采用基于二次谐波制动原理[4 -5 ] 和间断角原理[6 -7 ] 的辨识方法,但该类单一参量特性监测的辨识方法存在一定的应用局限性,如改进优化后的变压器铁心材料[8 ] 会使涌流的二次谐波占比减小,而CT饱和[9 ] 会使涌流间断角消失. ...
基于波形间断角原理识别变压器励磁涌流的新方法
1
2007
... 随着电力变压器空载合闸时,会产生比额定电流高出6~10倍的励磁涌流,且波形畸变严重.高幅值的畸变电流,将使得变压器绕组出现高力学应力[1 ] 、热应力、过电流等现象,直接影响变压器的寿命及可靠性[2 ] ;同时,由于涌流波形中存在大量的非周期分量和谐波分量,容易导致电流互感器(CT)发生饱和,使CT无法线性传变而造成保护误动作,影响系统的可靠运行[3 ] .在工程应用中,为了有效区分励磁涌流与故障电流,学者们普遍采用基于二次谐波制动原理[4 -5 ] 和间断角原理[6 -7 ] 的辨识方法,但该类单一参量特性监测的辨识方法存在一定的应用局限性,如改进优化后的变压器铁心材料[8 ] 会使涌流的二次谐波占比减小,而CT饱和[9 ] 会使涌流间断角消失. ...
A new method to identify inrush current based on the principle of dead angle
1
2007
... 随着电力变压器空载合闸时,会产生比额定电流高出6~10倍的励磁涌流,且波形畸变严重.高幅值的畸变电流,将使得变压器绕组出现高力学应力[1 ] 、热应力、过电流等现象,直接影响变压器的寿命及可靠性[2 ] ;同时,由于涌流波形中存在大量的非周期分量和谐波分量,容易导致电流互感器(CT)发生饱和,使CT无法线性传变而造成保护误动作,影响系统的可靠运行[3 ] .在工程应用中,为了有效区分励磁涌流与故障电流,学者们普遍采用基于二次谐波制动原理[4 -5 ] 和间断角原理[6 -7 ] 的辨识方法,但该类单一参量特性监测的辨识方法存在一定的应用局限性,如改进优化后的变压器铁心材料[8 ] 会使涌流的二次谐波占比减小,而CT饱和[9 ] 会使涌流间断角消失. ...
波形比较法变压器差动保护原理
1
1998
... 随着电力变压器空载合闸时,会产生比额定电流高出6~10倍的励磁涌流,且波形畸变严重.高幅值的畸变电流,将使得变压器绕组出现高力学应力[1 ] 、热应力、过电流等现象,直接影响变压器的寿命及可靠性[2 ] ;同时,由于涌流波形中存在大量的非周期分量和谐波分量,容易导致电流互感器(CT)发生饱和,使CT无法线性传变而造成保护误动作,影响系统的可靠运行[3 ] .在工程应用中,为了有效区分励磁涌流与故障电流,学者们普遍采用基于二次谐波制动原理[4 -5 ] 和间断角原理[6 -7 ] 的辨识方法,但该类单一参量特性监测的辨识方法存在一定的应用局限性,如改进优化后的变压器铁心材料[8 ] 会使涌流的二次谐波占比减小,而CT饱和[9 ] 会使涌流间断角消失. ...
Principle of differential protection of transformer by waveform comparison method
1
1998
... 随着电力变压器空载合闸时,会产生比额定电流高出6~10倍的励磁涌流,且波形畸变严重.高幅值的畸变电流,将使得变压器绕组出现高力学应力[1 ] 、热应力、过电流等现象,直接影响变压器的寿命及可靠性[2 ] ;同时,由于涌流波形中存在大量的非周期分量和谐波分量,容易导致电流互感器(CT)发生饱和,使CT无法线性传变而造成保护误动作,影响系统的可靠运行[3 ] .在工程应用中,为了有效区分励磁涌流与故障电流,学者们普遍采用基于二次谐波制动原理[4 -5 ] 和间断角原理[6 -7 ] 的辨识方法,但该类单一参量特性监测的辨识方法存在一定的应用局限性,如改进优化后的变压器铁心材料[8 ] 会使涌流的二次谐波占比减小,而CT饱和[9 ] 会使涌流间断角消失. ...
利用双重特征量鉴别变压器励磁涌流的高阶统计原理
1
2021
... 随着电力变压器空载合闸时,会产生比额定电流高出6~10倍的励磁涌流,且波形畸变严重.高幅值的畸变电流,将使得变压器绕组出现高力学应力[1 ] 、热应力、过电流等现象,直接影响变压器的寿命及可靠性[2 ] ;同时,由于涌流波形中存在大量的非周期分量和谐波分量,容易导致电流互感器(CT)发生饱和,使CT无法线性传变而造成保护误动作,影响系统的可靠运行[3 ] .在工程应用中,为了有效区分励磁涌流与故障电流,学者们普遍采用基于二次谐波制动原理[4 -5 ] 和间断角原理[6 -7 ] 的辨识方法,但该类单一参量特性监测的辨识方法存在一定的应用局限性,如改进优化后的变压器铁心材料[8 ] 会使涌流的二次谐波占比减小,而CT饱和[9 ] 会使涌流间断角消失. ...
High order statistical theory for identifying transformer inrush current by using dual characteristics
1
2021
... 随着电力变压器空载合闸时,会产生比额定电流高出6~10倍的励磁涌流,且波形畸变严重.高幅值的畸变电流,将使得变压器绕组出现高力学应力[1 ] 、热应力、过电流等现象,直接影响变压器的寿命及可靠性[2 ] ;同时,由于涌流波形中存在大量的非周期分量和谐波分量,容易导致电流互感器(CT)发生饱和,使CT无法线性传变而造成保护误动作,影响系统的可靠运行[3 ] .在工程应用中,为了有效区分励磁涌流与故障电流,学者们普遍采用基于二次谐波制动原理[4 -5 ] 和间断角原理[6 -7 ] 的辨识方法,但该类单一参量特性监测的辨识方法存在一定的应用局限性,如改进优化后的变压器铁心材料[8 ] 会使涌流的二次谐波占比减小,而CT饱和[9 ] 会使涌流间断角消失. ...
基于巴氏系数的变压器励磁涌流和故障差流识别新判据
1
2020
... 随着电力变压器空载合闸时,会产生比额定电流高出6~10倍的励磁涌流,且波形畸变严重.高幅值的畸变电流,将使得变压器绕组出现高力学应力[1 ] 、热应力、过电流等现象,直接影响变压器的寿命及可靠性[2 ] ;同时,由于涌流波形中存在大量的非周期分量和谐波分量,容易导致电流互感器(CT)发生饱和,使CT无法线性传变而造成保护误动作,影响系统的可靠运行[3 ] .在工程应用中,为了有效区分励磁涌流与故障电流,学者们普遍采用基于二次谐波制动原理[4 -5 ] 和间断角原理[6 -7 ] 的辨识方法,但该类单一参量特性监测的辨识方法存在一定的应用局限性,如改进优化后的变压器铁心材料[8 ] 会使涌流的二次谐波占比减小,而CT饱和[9 ] 会使涌流间断角消失. ...
A novel criterion to distinguish inrush current from fault current based on the Bhattacharyya coefficient
1
2020
... 随着电力变压器空载合闸时,会产生比额定电流高出6~10倍的励磁涌流,且波形畸变严重.高幅值的畸变电流,将使得变压器绕组出现高力学应力[1 ] 、热应力、过电流等现象,直接影响变压器的寿命及可靠性[2 ] ;同时,由于涌流波形中存在大量的非周期分量和谐波分量,容易导致电流互感器(CT)发生饱和,使CT无法线性传变而造成保护误动作,影响系统的可靠运行[3 ] .在工程应用中,为了有效区分励磁涌流与故障电流,学者们普遍采用基于二次谐波制动原理[4 -5 ] 和间断角原理[6 -7 ] 的辨识方法,但该类单一参量特性监测的辨识方法存在一定的应用局限性,如改进优化后的变压器铁心材料[8 ] 会使涌流的二次谐波占比减小,而CT饱和[9 ] 会使涌流间断角消失. ...
A wavelet-based transformer differential protection:Internal fault detection during inrush conditions
1
2018
... 为了进一步提升励磁涌流辨识的可靠性,国内外学者提出了一些基于波形特征的辨识方法及判据.文献[10 ]采用边界离散小波变换方法,提取电流高频分量作为涌流识别的判据,其识别准确率较高;文献[11 ]研究了励磁涌流下故障分量瞬时功率的相空间轨迹特征,该方法可用于识别故障伴随CT饱和的情况.需要指出的是,该类方法依旧是通过对信号的局部特征或某一分量特征进行提取,在未充分考虑信号整体特性及复杂度的情况下,无法实现复杂扰动下励磁涌流的可靠识别,如CT饱和、匝间短路等场景.文献[12 -13 ]采用Hausdroff距离表征涌流与正弦信号的波形整体相似度,通过判断涌流信号与正弦信号的相似程度来识别涌流,该方法较好地描述了涌流信号的整体特征,但并未充分考虑变压器空载合闸于CT饱和场景下的扰动及可靠性.近年来,许多智能算法也开始应用于励磁涌流的快速识别,如神经网络[14 ] 、深度学习[15 ] 、模糊逻辑算法[16 ] 等,通过对信号分解后提取多个波形特征量组合成输入向量,参与智能算法的模型训练.此类智能算法能够充分考虑涌流信号的整体及局部特征,其识别准确率提高,并且可应用于CT饱和、匝间故障等复杂扰动场景;但是,该类算法需要经过大量的模型训练,所需算力及时间成本较高,不易于工程应用中涌流特性的快速辨识.较为前沿的信号分解算法是变分模态分解(Variational mode decomposition,VMD)[17 ] ,它是一种完全非递归的分解算法,对非线性、不规则性等信号的分解具有较强的准确性.文献[18 ]采用VMD算法对变压器和应涌流进行有效分解并识别,未考虑励磁涌流下VMD的分解情况.文献[19 ]通过采用VMD算法对励磁涌流进行分解,再结合极限学习机对模型进行训练,该算法将VMD与神经网络结合,提高算法辨识准确性,但也增大了时间与算力成本,并且该算法未考虑变压器空载合闸时剩磁的重要性,以及空载合闸于CT饱和、匝间故障等扰动场景下的可靠性.因此,亟需一种既考虑信号的整体特性,又能满足快速计算的多场景复杂扰动下励磁涌流的识别算法. ...
基于相空间轨迹识别和多判据融合的变压器保护新策略
1
2020
... 为了进一步提升励磁涌流辨识的可靠性,国内外学者提出了一些基于波形特征的辨识方法及判据.文献[10 ]采用边界离散小波变换方法,提取电流高频分量作为涌流识别的判据,其识别准确率较高;文献[11 ]研究了励磁涌流下故障分量瞬时功率的相空间轨迹特征,该方法可用于识别故障伴随CT饱和的情况.需要指出的是,该类方法依旧是通过对信号的局部特征或某一分量特征进行提取,在未充分考虑信号整体特性及复杂度的情况下,无法实现复杂扰动下励磁涌流的可靠识别,如CT饱和、匝间短路等场景.文献[12 -13 ]采用Hausdroff距离表征涌流与正弦信号的波形整体相似度,通过判断涌流信号与正弦信号的相似程度来识别涌流,该方法较好地描述了涌流信号的整体特征,但并未充分考虑变压器空载合闸于CT饱和场景下的扰动及可靠性.近年来,许多智能算法也开始应用于励磁涌流的快速识别,如神经网络[14 ] 、深度学习[15 ] 、模糊逻辑算法[16 ] 等,通过对信号分解后提取多个波形特征量组合成输入向量,参与智能算法的模型训练.此类智能算法能够充分考虑涌流信号的整体及局部特征,其识别准确率提高,并且可应用于CT饱和、匝间故障等复杂扰动场景;但是,该类算法需要经过大量的模型训练,所需算力及时间成本较高,不易于工程应用中涌流特性的快速辨识.较为前沿的信号分解算法是变分模态分解(Variational mode decomposition,VMD)[17 ] ,它是一种完全非递归的分解算法,对非线性、不规则性等信号的分解具有较强的准确性.文献[18 ]采用VMD算法对变压器和应涌流进行有效分解并识别,未考虑励磁涌流下VMD的分解情况.文献[19 ]通过采用VMD算法对励磁涌流进行分解,再结合极限学习机对模型进行训练,该算法将VMD与神经网络结合,提高算法辨识准确性,但也增大了时间与算力成本,并且该算法未考虑变压器空载合闸时剩磁的重要性,以及空载合闸于CT饱和、匝间故障等扰动场景下的可靠性.因此,亟需一种既考虑信号的整体特性,又能满足快速计算的多场景复杂扰动下励磁涌流的识别算法. ...
A new transformer protection scheme based on the recognition of phase space trajectory and multi-criteria fusion
1
2020
... 为了进一步提升励磁涌流辨识的可靠性,国内外学者提出了一些基于波形特征的辨识方法及判据.文献[10 ]采用边界离散小波变换方法,提取电流高频分量作为涌流识别的判据,其识别准确率较高;文献[11 ]研究了励磁涌流下故障分量瞬时功率的相空间轨迹特征,该方法可用于识别故障伴随CT饱和的情况.需要指出的是,该类方法依旧是通过对信号的局部特征或某一分量特征进行提取,在未充分考虑信号整体特性及复杂度的情况下,无法实现复杂扰动下励磁涌流的可靠识别,如CT饱和、匝间短路等场景.文献[12 -13 ]采用Hausdroff距离表征涌流与正弦信号的波形整体相似度,通过判断涌流信号与正弦信号的相似程度来识别涌流,该方法较好地描述了涌流信号的整体特征,但并未充分考虑变压器空载合闸于CT饱和场景下的扰动及可靠性.近年来,许多智能算法也开始应用于励磁涌流的快速识别,如神经网络[14 ] 、深度学习[15 ] 、模糊逻辑算法[16 ] 等,通过对信号分解后提取多个波形特征量组合成输入向量,参与智能算法的模型训练.此类智能算法能够充分考虑涌流信号的整体及局部特征,其识别准确率提高,并且可应用于CT饱和、匝间故障等复杂扰动场景;但是,该类算法需要经过大量的模型训练,所需算力及时间成本较高,不易于工程应用中涌流特性的快速辨识.较为前沿的信号分解算法是变分模态分解(Variational mode decomposition,VMD)[17 ] ,它是一种完全非递归的分解算法,对非线性、不规则性等信号的分解具有较强的准确性.文献[18 ]采用VMD算法对变压器和应涌流进行有效分解并识别,未考虑励磁涌流下VMD的分解情况.文献[19 ]通过采用VMD算法对励磁涌流进行分解,再结合极限学习机对模型进行训练,该算法将VMD与神经网络结合,提高算法辨识准确性,但也增大了时间与算力成本,并且该算法未考虑变压器空载合闸时剩磁的重要性,以及空载合闸于CT饱和、匝间故障等扰动场景下的可靠性.因此,亟需一种既考虑信号的整体特性,又能满足快速计算的多场景复杂扰动下励磁涌流的识别算法. ...
基于Hausdorff距离算法的变压器差动保护新判据
1
2018
... 为了进一步提升励磁涌流辨识的可靠性,国内外学者提出了一些基于波形特征的辨识方法及判据.文献[10 ]采用边界离散小波变换方法,提取电流高频分量作为涌流识别的判据,其识别准确率较高;文献[11 ]研究了励磁涌流下故障分量瞬时功率的相空间轨迹特征,该方法可用于识别故障伴随CT饱和的情况.需要指出的是,该类方法依旧是通过对信号的局部特征或某一分量特征进行提取,在未充分考虑信号整体特性及复杂度的情况下,无法实现复杂扰动下励磁涌流的可靠识别,如CT饱和、匝间短路等场景.文献[12 -13 ]采用Hausdroff距离表征涌流与正弦信号的波形整体相似度,通过判断涌流信号与正弦信号的相似程度来识别涌流,该方法较好地描述了涌流信号的整体特征,但并未充分考虑变压器空载合闸于CT饱和场景下的扰动及可靠性.近年来,许多智能算法也开始应用于励磁涌流的快速识别,如神经网络[14 ] 、深度学习[15 ] 、模糊逻辑算法[16 ] 等,通过对信号分解后提取多个波形特征量组合成输入向量,参与智能算法的模型训练.此类智能算法能够充分考虑涌流信号的整体及局部特征,其识别准确率提高,并且可应用于CT饱和、匝间故障等复杂扰动场景;但是,该类算法需要经过大量的模型训练,所需算力及时间成本较高,不易于工程应用中涌流特性的快速辨识.较为前沿的信号分解算法是变分模态分解(Variational mode decomposition,VMD)[17 ] ,它是一种完全非递归的分解算法,对非线性、不规则性等信号的分解具有较强的准确性.文献[18 ]采用VMD算法对变压器和应涌流进行有效分解并识别,未考虑励磁涌流下VMD的分解情况.文献[19 ]通过采用VMD算法对励磁涌流进行分解,再结合极限学习机对模型进行训练,该算法将VMD与神经网络结合,提高算法辨识准确性,但也增大了时间与算力成本,并且该算法未考虑变压器空载合闸时剩磁的重要性,以及空载合闸于CT饱和、匝间故障等扰动场景下的可靠性.因此,亟需一种既考虑信号的整体特性,又能满足快速计算的多场景复杂扰动下励磁涌流的识别算法. ...
A novel criterion of the transformer differential protection based on the Hausdorff distance algorithm
1
2018
... 为了进一步提升励磁涌流辨识的可靠性,国内外学者提出了一些基于波形特征的辨识方法及判据.文献[10 ]采用边界离散小波变换方法,提取电流高频分量作为涌流识别的判据,其识别准确率较高;文献[11 ]研究了励磁涌流下故障分量瞬时功率的相空间轨迹特征,该方法可用于识别故障伴随CT饱和的情况.需要指出的是,该类方法依旧是通过对信号的局部特征或某一分量特征进行提取,在未充分考虑信号整体特性及复杂度的情况下,无法实现复杂扰动下励磁涌流的可靠识别,如CT饱和、匝间短路等场景.文献[12 -13 ]采用Hausdroff距离表征涌流与正弦信号的波形整体相似度,通过判断涌流信号与正弦信号的相似程度来识别涌流,该方法较好地描述了涌流信号的整体特征,但并未充分考虑变压器空载合闸于CT饱和场景下的扰动及可靠性.近年来,许多智能算法也开始应用于励磁涌流的快速识别,如神经网络[14 ] 、深度学习[15 ] 、模糊逻辑算法[16 ] 等,通过对信号分解后提取多个波形特征量组合成输入向量,参与智能算法的模型训练.此类智能算法能够充分考虑涌流信号的整体及局部特征,其识别准确率提高,并且可应用于CT饱和、匝间故障等复杂扰动场景;但是,该类算法需要经过大量的模型训练,所需算力及时间成本较高,不易于工程应用中涌流特性的快速辨识.较为前沿的信号分解算法是变分模态分解(Variational mode decomposition,VMD)[17 ] ,它是一种完全非递归的分解算法,对非线性、不规则性等信号的分解具有较强的准确性.文献[18 ]采用VMD算法对变压器和应涌流进行有效分解并识别,未考虑励磁涌流下VMD的分解情况.文献[19 ]通过采用VMD算法对励磁涌流进行分解,再结合极限学习机对模型进行训练,该算法将VMD与神经网络结合,提高算法辨识准确性,但也增大了时间与算力成本,并且该算法未考虑变压器空载合闸时剩磁的重要性,以及空载合闸于CT饱和、匝间故障等扰动场景下的可靠性.因此,亟需一种既考虑信号的整体特性,又能满足快速计算的多场景复杂扰动下励磁涌流的识别算法. ...
A novel criterion applicable to transformer differential protection based on waveform sinusoidal similarity identification
1
2019
... 为了进一步提升励磁涌流辨识的可靠性,国内外学者提出了一些基于波形特征的辨识方法及判据.文献[10 ]采用边界离散小波变换方法,提取电流高频分量作为涌流识别的判据,其识别准确率较高;文献[11 ]研究了励磁涌流下故障分量瞬时功率的相空间轨迹特征,该方法可用于识别故障伴随CT饱和的情况.需要指出的是,该类方法依旧是通过对信号的局部特征或某一分量特征进行提取,在未充分考虑信号整体特性及复杂度的情况下,无法实现复杂扰动下励磁涌流的可靠识别,如CT饱和、匝间短路等场景.文献[12 -13 ]采用Hausdroff距离表征涌流与正弦信号的波形整体相似度,通过判断涌流信号与正弦信号的相似程度来识别涌流,该方法较好地描述了涌流信号的整体特征,但并未充分考虑变压器空载合闸于CT饱和场景下的扰动及可靠性.近年来,许多智能算法也开始应用于励磁涌流的快速识别,如神经网络[14 ] 、深度学习[15 ] 、模糊逻辑算法[16 ] 等,通过对信号分解后提取多个波形特征量组合成输入向量,参与智能算法的模型训练.此类智能算法能够充分考虑涌流信号的整体及局部特征,其识别准确率提高,并且可应用于CT饱和、匝间故障等复杂扰动场景;但是,该类算法需要经过大量的模型训练,所需算力及时间成本较高,不易于工程应用中涌流特性的快速辨识.较为前沿的信号分解算法是变分模态分解(Variational mode decomposition,VMD)[17 ] ,它是一种完全非递归的分解算法,对非线性、不规则性等信号的分解具有较强的准确性.文献[18 ]采用VMD算法对变压器和应涌流进行有效分解并识别,未考虑励磁涌流下VMD的分解情况.文献[19 ]通过采用VMD算法对励磁涌流进行分解,再结合极限学习机对模型进行训练,该算法将VMD与神经网络结合,提高算法辨识准确性,但也增大了时间与算力成本,并且该算法未考虑变压器空载合闸时剩磁的重要性,以及空载合闸于CT饱和、匝间故障等扰动场景下的可靠性.因此,亟需一种既考虑信号的整体特性,又能满足快速计算的多场景复杂扰动下励磁涌流的识别算法. ...
Integration of accelerated deep neural network into power transformer differential protection
1
2020
... 为了进一步提升励磁涌流辨识的可靠性,国内外学者提出了一些基于波形特征的辨识方法及判据.文献[10 ]采用边界离散小波变换方法,提取电流高频分量作为涌流识别的判据,其识别准确率较高;文献[11 ]研究了励磁涌流下故障分量瞬时功率的相空间轨迹特征,该方法可用于识别故障伴随CT饱和的情况.需要指出的是,该类方法依旧是通过对信号的局部特征或某一分量特征进行提取,在未充分考虑信号整体特性及复杂度的情况下,无法实现复杂扰动下励磁涌流的可靠识别,如CT饱和、匝间短路等场景.文献[12 -13 ]采用Hausdroff距离表征涌流与正弦信号的波形整体相似度,通过判断涌流信号与正弦信号的相似程度来识别涌流,该方法较好地描述了涌流信号的整体特征,但并未充分考虑变压器空载合闸于CT饱和场景下的扰动及可靠性.近年来,许多智能算法也开始应用于励磁涌流的快速识别,如神经网络[14 ] 、深度学习[15 ] 、模糊逻辑算法[16 ] 等,通过对信号分解后提取多个波形特征量组合成输入向量,参与智能算法的模型训练.此类智能算法能够充分考虑涌流信号的整体及局部特征,其识别准确率提高,并且可应用于CT饱和、匝间故障等复杂扰动场景;但是,该类算法需要经过大量的模型训练,所需算力及时间成本较高,不易于工程应用中涌流特性的快速辨识.较为前沿的信号分解算法是变分模态分解(Variational mode decomposition,VMD)[17 ] ,它是一种完全非递归的分解算法,对非线性、不规则性等信号的分解具有较强的准确性.文献[18 ]采用VMD算法对变压器和应涌流进行有效分解并识别,未考虑励磁涌流下VMD的分解情况.文献[19 ]通过采用VMD算法对励磁涌流进行分解,再结合极限学习机对模型进行训练,该算法将VMD与神经网络结合,提高算法辨识准确性,但也增大了时间与算力成本,并且该算法未考虑变压器空载合闸时剩磁的重要性,以及空载合闸于CT饱和、匝间故障等扰动场景下的可靠性.因此,亟需一种既考虑信号的整体特性,又能满足快速计算的多场景复杂扰动下励磁涌流的识别算法. ...
Designing a composite deep learning based differential protection scheme of power transformers
1
2019
... 为了进一步提升励磁涌流辨识的可靠性,国内外学者提出了一些基于波形特征的辨识方法及判据.文献[10 ]采用边界离散小波变换方法,提取电流高频分量作为涌流识别的判据,其识别准确率较高;文献[11 ]研究了励磁涌流下故障分量瞬时功率的相空间轨迹特征,该方法可用于识别故障伴随CT饱和的情况.需要指出的是,该类方法依旧是通过对信号的局部特征或某一分量特征进行提取,在未充分考虑信号整体特性及复杂度的情况下,无法实现复杂扰动下励磁涌流的可靠识别,如CT饱和、匝间短路等场景.文献[12 -13 ]采用Hausdroff距离表征涌流与正弦信号的波形整体相似度,通过判断涌流信号与正弦信号的相似程度来识别涌流,该方法较好地描述了涌流信号的整体特征,但并未充分考虑变压器空载合闸于CT饱和场景下的扰动及可靠性.近年来,许多智能算法也开始应用于励磁涌流的快速识别,如神经网络[14 ] 、深度学习[15 ] 、模糊逻辑算法[16 ] 等,通过对信号分解后提取多个波形特征量组合成输入向量,参与智能算法的模型训练.此类智能算法能够充分考虑涌流信号的整体及局部特征,其识别准确率提高,并且可应用于CT饱和、匝间故障等复杂扰动场景;但是,该类算法需要经过大量的模型训练,所需算力及时间成本较高,不易于工程应用中涌流特性的快速辨识.较为前沿的信号分解算法是变分模态分解(Variational mode decomposition,VMD)[17 ] ,它是一种完全非递归的分解算法,对非线性、不规则性等信号的分解具有较强的准确性.文献[18 ]采用VMD算法对变压器和应涌流进行有效分解并识别,未考虑励磁涌流下VMD的分解情况.文献[19 ]通过采用VMD算法对励磁涌流进行分解,再结合极限学习机对模型进行训练,该算法将VMD与神经网络结合,提高算法辨识准确性,但也增大了时间与算力成本,并且该算法未考虑变压器空载合闸时剩磁的重要性,以及空载合闸于CT饱和、匝间故障等扰动场景下的可靠性.因此,亟需一种既考虑信号的整体特性,又能满足快速计算的多场景复杂扰动下励磁涌流的识别算法. ...
Transformer differential protection with fuzzy logic based inrush stabilization
1
2014
... 为了进一步提升励磁涌流辨识的可靠性,国内外学者提出了一些基于波形特征的辨识方法及判据.文献[10 ]采用边界离散小波变换方法,提取电流高频分量作为涌流识别的判据,其识别准确率较高;文献[11 ]研究了励磁涌流下故障分量瞬时功率的相空间轨迹特征,该方法可用于识别故障伴随CT饱和的情况.需要指出的是,该类方法依旧是通过对信号的局部特征或某一分量特征进行提取,在未充分考虑信号整体特性及复杂度的情况下,无法实现复杂扰动下励磁涌流的可靠识别,如CT饱和、匝间短路等场景.文献[12 -13 ]采用Hausdroff距离表征涌流与正弦信号的波形整体相似度,通过判断涌流信号与正弦信号的相似程度来识别涌流,该方法较好地描述了涌流信号的整体特征,但并未充分考虑变压器空载合闸于CT饱和场景下的扰动及可靠性.近年来,许多智能算法也开始应用于励磁涌流的快速识别,如神经网络[14 ] 、深度学习[15 ] 、模糊逻辑算法[16 ] 等,通过对信号分解后提取多个波形特征量组合成输入向量,参与智能算法的模型训练.此类智能算法能够充分考虑涌流信号的整体及局部特征,其识别准确率提高,并且可应用于CT饱和、匝间故障等复杂扰动场景;但是,该类算法需要经过大量的模型训练,所需算力及时间成本较高,不易于工程应用中涌流特性的快速辨识.较为前沿的信号分解算法是变分模态分解(Variational mode decomposition,VMD)[17 ] ,它是一种完全非递归的分解算法,对非线性、不规则性等信号的分解具有较强的准确性.文献[18 ]采用VMD算法对变压器和应涌流进行有效分解并识别,未考虑励磁涌流下VMD的分解情况.文献[19 ]通过采用VMD算法对励磁涌流进行分解,再结合极限学习机对模型进行训练,该算法将VMD与神经网络结合,提高算法辨识准确性,但也增大了时间与算力成本,并且该算法未考虑变压器空载合闸时剩磁的重要性,以及空载合闸于CT饱和、匝间故障等扰动场景下的可靠性.因此,亟需一种既考虑信号的整体特性,又能满足快速计算的多场景复杂扰动下励磁涌流的识别算法. ...
Variational mode decomposition
2
2014
... 为了进一步提升励磁涌流辨识的可靠性,国内外学者提出了一些基于波形特征的辨识方法及判据.文献[10 ]采用边界离散小波变换方法,提取电流高频分量作为涌流识别的判据,其识别准确率较高;文献[11 ]研究了励磁涌流下故障分量瞬时功率的相空间轨迹特征,该方法可用于识别故障伴随CT饱和的情况.需要指出的是,该类方法依旧是通过对信号的局部特征或某一分量特征进行提取,在未充分考虑信号整体特性及复杂度的情况下,无法实现复杂扰动下励磁涌流的可靠识别,如CT饱和、匝间短路等场景.文献[12 -13 ]采用Hausdroff距离表征涌流与正弦信号的波形整体相似度,通过判断涌流信号与正弦信号的相似程度来识别涌流,该方法较好地描述了涌流信号的整体特征,但并未充分考虑变压器空载合闸于CT饱和场景下的扰动及可靠性.近年来,许多智能算法也开始应用于励磁涌流的快速识别,如神经网络[14 ] 、深度学习[15 ] 、模糊逻辑算法[16 ] 等,通过对信号分解后提取多个波形特征量组合成输入向量,参与智能算法的模型训练.此类智能算法能够充分考虑涌流信号的整体及局部特征,其识别准确率提高,并且可应用于CT饱和、匝间故障等复杂扰动场景;但是,该类算法需要经过大量的模型训练,所需算力及时间成本较高,不易于工程应用中涌流特性的快速辨识.较为前沿的信号分解算法是变分模态分解(Variational mode decomposition,VMD)[17 ] ,它是一种完全非递归的分解算法,对非线性、不规则性等信号的分解具有较强的准确性.文献[18 ]采用VMD算法对变压器和应涌流进行有效分解并识别,未考虑励磁涌流下VMD的分解情况.文献[19 ]通过采用VMD算法对励磁涌流进行分解,再结合极限学习机对模型进行训练,该算法将VMD与神经网络结合,提高算法辨识准确性,但也增大了时间与算力成本,并且该算法未考虑变压器空载合闸时剩磁的重要性,以及空载合闸于CT饱和、匝间故障等扰动场景下的可靠性.因此,亟需一种既考虑信号的整体特性,又能满足快速计算的多场景复杂扰动下励磁涌流的识别算法. ...
... 本文借鉴文献[17 ]应用时间序列的非线性与不规则性来表征时间序列复杂程度的定义,采用波形的非周期性与谐波特性来体现波形的复杂特性,非周期和谐波含量与复杂特性成正相关.图1 是变压器空载合闸、合闸于CT饱和、合闸于匝间故障时的涌流波形及信号含有的分量图. ...
基于VMD和PSO-SVM模型的和应涌流识别
1
2021
... 为了进一步提升励磁涌流辨识的可靠性,国内外学者提出了一些基于波形特征的辨识方法及判据.文献[10 ]采用边界离散小波变换方法,提取电流高频分量作为涌流识别的判据,其识别准确率较高;文献[11 ]研究了励磁涌流下故障分量瞬时功率的相空间轨迹特征,该方法可用于识别故障伴随CT饱和的情况.需要指出的是,该类方法依旧是通过对信号的局部特征或某一分量特征进行提取,在未充分考虑信号整体特性及复杂度的情况下,无法实现复杂扰动下励磁涌流的可靠识别,如CT饱和、匝间短路等场景.文献[12 -13 ]采用Hausdroff距离表征涌流与正弦信号的波形整体相似度,通过判断涌流信号与正弦信号的相似程度来识别涌流,该方法较好地描述了涌流信号的整体特征,但并未充分考虑变压器空载合闸于CT饱和场景下的扰动及可靠性.近年来,许多智能算法也开始应用于励磁涌流的快速识别,如神经网络[14 ] 、深度学习[15 ] 、模糊逻辑算法[16 ] 等,通过对信号分解后提取多个波形特征量组合成输入向量,参与智能算法的模型训练.此类智能算法能够充分考虑涌流信号的整体及局部特征,其识别准确率提高,并且可应用于CT饱和、匝间故障等复杂扰动场景;但是,该类算法需要经过大量的模型训练,所需算力及时间成本较高,不易于工程应用中涌流特性的快速辨识.较为前沿的信号分解算法是变分模态分解(Variational mode decomposition,VMD)[17 ] ,它是一种完全非递归的分解算法,对非线性、不规则性等信号的分解具有较强的准确性.文献[18 ]采用VMD算法对变压器和应涌流进行有效分解并识别,未考虑励磁涌流下VMD的分解情况.文献[19 ]通过采用VMD算法对励磁涌流进行分解,再结合极限学习机对模型进行训练,该算法将VMD与神经网络结合,提高算法辨识准确性,但也增大了时间与算力成本,并且该算法未考虑变压器空载合闸时剩磁的重要性,以及空载合闸于CT饱和、匝间故障等扰动场景下的可靠性.因此,亟需一种既考虑信号的整体特性,又能满足快速计算的多场景复杂扰动下励磁涌流的识别算法. ...
Sympathetic inrush current identification based on VMD and PSO-SVM model
1
2021
... 为了进一步提升励磁涌流辨识的可靠性,国内外学者提出了一些基于波形特征的辨识方法及判据.文献[10 ]采用边界离散小波变换方法,提取电流高频分量作为涌流识别的判据,其识别准确率较高;文献[11 ]研究了励磁涌流下故障分量瞬时功率的相空间轨迹特征,该方法可用于识别故障伴随CT饱和的情况.需要指出的是,该类方法依旧是通过对信号的局部特征或某一分量特征进行提取,在未充分考虑信号整体特性及复杂度的情况下,无法实现复杂扰动下励磁涌流的可靠识别,如CT饱和、匝间短路等场景.文献[12 -13 ]采用Hausdroff距离表征涌流与正弦信号的波形整体相似度,通过判断涌流信号与正弦信号的相似程度来识别涌流,该方法较好地描述了涌流信号的整体特征,但并未充分考虑变压器空载合闸于CT饱和场景下的扰动及可靠性.近年来,许多智能算法也开始应用于励磁涌流的快速识别,如神经网络[14 ] 、深度学习[15 ] 、模糊逻辑算法[16 ] 等,通过对信号分解后提取多个波形特征量组合成输入向量,参与智能算法的模型训练.此类智能算法能够充分考虑涌流信号的整体及局部特征,其识别准确率提高,并且可应用于CT饱和、匝间故障等复杂扰动场景;但是,该类算法需要经过大量的模型训练,所需算力及时间成本较高,不易于工程应用中涌流特性的快速辨识.较为前沿的信号分解算法是变分模态分解(Variational mode decomposition,VMD)[17 ] ,它是一种完全非递归的分解算法,对非线性、不规则性等信号的分解具有较强的准确性.文献[18 ]采用VMD算法对变压器和应涌流进行有效分解并识别,未考虑励磁涌流下VMD的分解情况.文献[19 ]通过采用VMD算法对励磁涌流进行分解,再结合极限学习机对模型进行训练,该算法将VMD与神经网络结合,提高算法辨识准确性,但也增大了时间与算力成本,并且该算法未考虑变压器空载合闸时剩磁的重要性,以及空载合闸于CT饱和、匝间故障等扰动场景下的可靠性.因此,亟需一种既考虑信号的整体特性,又能满足快速计算的多场景复杂扰动下励磁涌流的识别算法. ...
1
2021
... 为了进一步提升励磁涌流辨识的可靠性,国内外学者提出了一些基于波形特征的辨识方法及判据.文献[10 ]采用边界离散小波变换方法,提取电流高频分量作为涌流识别的判据,其识别准确率较高;文献[11 ]研究了励磁涌流下故障分量瞬时功率的相空间轨迹特征,该方法可用于识别故障伴随CT饱和的情况.需要指出的是,该类方法依旧是通过对信号的局部特征或某一分量特征进行提取,在未充分考虑信号整体特性及复杂度的情况下,无法实现复杂扰动下励磁涌流的可靠识别,如CT饱和、匝间短路等场景.文献[12 -13 ]采用Hausdroff距离表征涌流与正弦信号的波形整体相似度,通过判断涌流信号与正弦信号的相似程度来识别涌流,该方法较好地描述了涌流信号的整体特征,但并未充分考虑变压器空载合闸于CT饱和场景下的扰动及可靠性.近年来,许多智能算法也开始应用于励磁涌流的快速识别,如神经网络[14 ] 、深度学习[15 ] 、模糊逻辑算法[16 ] 等,通过对信号分解后提取多个波形特征量组合成输入向量,参与智能算法的模型训练.此类智能算法能够充分考虑涌流信号的整体及局部特征,其识别准确率提高,并且可应用于CT饱和、匝间故障等复杂扰动场景;但是,该类算法需要经过大量的模型训练,所需算力及时间成本较高,不易于工程应用中涌流特性的快速辨识.较为前沿的信号分解算法是变分模态分解(Variational mode decomposition,VMD)[17 ] ,它是一种完全非递归的分解算法,对非线性、不规则性等信号的分解具有较强的准确性.文献[18 ]采用VMD算法对变压器和应涌流进行有效分解并识别,未考虑励磁涌流下VMD的分解情况.文献[19 ]通过采用VMD算法对励磁涌流进行分解,再结合极限学习机对模型进行训练,该算法将VMD与神经网络结合,提高算法辨识准确性,但也增大了时间与算力成本,并且该算法未考虑变压器空载合闸时剩磁的重要性,以及空载合闸于CT饱和、匝间故障等扰动场景下的可靠性.因此,亟需一种既考虑信号的整体特性,又能满足快速计算的多场景复杂扰动下励磁涌流的识别算法. ...
1
2021
... 为了进一步提升励磁涌流辨识的可靠性,国内外学者提出了一些基于波形特征的辨识方法及判据.文献[10 ]采用边界离散小波变换方法,提取电流高频分量作为涌流识别的判据,其识别准确率较高;文献[11 ]研究了励磁涌流下故障分量瞬时功率的相空间轨迹特征,该方法可用于识别故障伴随CT饱和的情况.需要指出的是,该类方法依旧是通过对信号的局部特征或某一分量特征进行提取,在未充分考虑信号整体特性及复杂度的情况下,无法实现复杂扰动下励磁涌流的可靠识别,如CT饱和、匝间短路等场景.文献[12 -13 ]采用Hausdroff距离表征涌流与正弦信号的波形整体相似度,通过判断涌流信号与正弦信号的相似程度来识别涌流,该方法较好地描述了涌流信号的整体特征,但并未充分考虑变压器空载合闸于CT饱和场景下的扰动及可靠性.近年来,许多智能算法也开始应用于励磁涌流的快速识别,如神经网络[14 ] 、深度学习[15 ] 、模糊逻辑算法[16 ] 等,通过对信号分解后提取多个波形特征量组合成输入向量,参与智能算法的模型训练.此类智能算法能够充分考虑涌流信号的整体及局部特征,其识别准确率提高,并且可应用于CT饱和、匝间故障等复杂扰动场景;但是,该类算法需要经过大量的模型训练,所需算力及时间成本较高,不易于工程应用中涌流特性的快速辨识.较为前沿的信号分解算法是变分模态分解(Variational mode decomposition,VMD)[17 ] ,它是一种完全非递归的分解算法,对非线性、不规则性等信号的分解具有较强的准确性.文献[18 ]采用VMD算法对变压器和应涌流进行有效分解并识别,未考虑励磁涌流下VMD的分解情况.文献[19 ]通过采用VMD算法对励磁涌流进行分解,再结合极限学习机对模型进行训练,该算法将VMD与神经网络结合,提高算法辨识准确性,但也增大了时间与算力成本,并且该算法未考虑变压器空载合闸时剩磁的重要性,以及空载合闸于CT饱和、匝间故障等扰动场景下的可靠性.因此,亟需一种既考虑信号的整体特性,又能满足快速计算的多场景复杂扰动下励磁涌流的识别算法. ...
Physiological time-series analysis using approximate entropy and sample entropy
1
2000
... 样本熵是一种表征时间序列复杂程度的测度方法[20 ] .样本熵越小,序列自我相似性越高;样本熵越大,序列的非线性与复杂性越高.原理如下所示. ...
防止超高压备自投诱发线路零序过流保护误动的对策初探
1
2021
... 变压器运行过程中主要存在两种典型剩磁[21 ] :① 平衡剩磁.由断路器开闭所造成的剩磁,三相剩磁之和为0,表达式为ϕra =-0.5ϕrb =-0.5ϕrc ;② 不平衡剩磁.由直流电阻测试或直流偏磁等导致的剩磁,表达式为ϕra =-ϕrb =-ϕrc ;本文以剩磁ϕr 和合闸角θ 作为影响励磁涌流变化的主要因素,仿真模拟多场景扰动下的励磁涌流,表2 是多场景仿真案例汇总. ...
Study on countermeasures to prevent maloperation of zero-sequence overcurrent protection caused by ultra-high-voltage automatic device transfer
1
2021
... 变压器运行过程中主要存在两种典型剩磁[21 ] :① 平衡剩磁.由断路器开闭所造成的剩磁,三相剩磁之和为0,表达式为ϕra =-0.5ϕrb =-0.5ϕrc ;② 不平衡剩磁.由直流电阻测试或直流偏磁等导致的剩磁,表达式为ϕra =-ϕrb =-ϕrc ;本文以剩磁ϕr 和合闸角θ 作为影响励磁涌流变化的主要因素,仿真模拟多场景扰动下的励磁涌流,表2 是多场景仿真案例汇总. ...
A new differential protection algorithm for power reactors based on the second central moment
1
2020
... 电力设备在运行中会互相干扰并产生一定的噪声,根据文献[22 ]可知,电力系统的常见噪声为45 dB.因此,本案例讨论采样信号在受到40~60 dB的高斯白噪声干扰下算法的抗噪性能.往励磁涌流加入40 dB噪声后的波形图如图12 所示. ...