一种无电压尖峰的改进型分裂Δ源逆变器*

doi:10.11985/2024.01.025

一种无电压尖峰的改进型分裂Δ源逆变器^*

房绪鹏^,, 孙翔飞^,, 张胜男, 赵冰冰

山东科技大学电气与自动化工程学院青岛 266590

An Improved Split Δ-source Inverter without Voltage Spikes

FANG Xupeng^,, SUN Xiangfei^,, ZHANG Shengnan, ZHAO Bingbing

College of Electrical Engineering and Automation, Shandong University of Science and Technology, Qingdao 266590

通讯作者: 孙翔飞，男，1995年生，硕士研究生。主要研究方向为电力电子技术及应用。E-mail：965456709@qq.com

收稿日期: 2023-01-22 修回日期: 2023-06-10

基金资助:

山东省重点研发计划资助项目(2019GGX103049)

Received: 2023-01-22 Revised: 2023-06-10

作者简介 About authors

房绪鹏，男，1971年生，博士，教授。主要研究方向为阻抗源变流器及其应用，现代电力电子技术在电力系统、电气传动和新兴能源利用方面的应用等。E-mail：xpfang@sdust.edu.cn

摘要

针对传统Δ源逆变器(Δ-source inverter，DSI)存在着开关管有较大的电压尖峰、高增益下输出电能质量差的问题，在分裂Δ源逆变器(Split Δ-source inverter，SDSI)的基础上，加入电压箝位单元，提出了一种改进型分裂Δ源逆变器(Improved split Δ-source inverter，ISDSI)，研究了它的拓扑结构与工作状态，重点分析了其稳态升压特性与消除电压尖峰过程，并计算了各开关器件的电压应力。新提出的拓扑保留了SDSI升压占空比和调制因数同向调整的优点，这有助于改善高增益下输出电能质量。此外，新拓扑消除了开关管电压尖峰，降低了开关管和二极管的电压应力。Matlab/Simulink软件仿真和样机试验的结果验证了变换器的性能，证明了所提逆变器能够有效解决Δ源逆变器存在的突出问题。

关键词： 逆变器; 电压尖峰; 高电压增益; 电压箝位单元

Abstract

Aiming at the problems of the Δ-source inverter(DSI) of large voltage spike of the switch and poor output power quality under high gain, a voltage clamping cell is added on the basis of the split Δ-source inverter(SDSI), and an improved split Δ-source inverter(ISDSI) is proposed. The topological structure and working state of the inverter are studied, the steady-state voltage boosting characteristics and the process of eliminating voltage spikes are analyzed, and the voltage stress of each switching device is calculated. The proposed topology retains the advantages of SDSI boost duty ratio and modulation factor adjustment in the same direction, which helps to improve the output power quality at high voltage gain. The results of Matlab/Simulink software simulation and prototype experiment verify the performance of the converter, and prove the proposed inverter can effectively solve the outstanding problems existing in Δ-source inverter.

Keywords： Inverter; voltage spike; high voltage gain; voltage-clamp cell

PDF (60923KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

房绪鹏, 孙翔飞, 张胜男, 赵冰冰. 一种无电压尖峰的改进型分裂Δ源逆变器^*[J]. 电气工程学报, 2024, 19(1): 235-242 doi:10.11985/2024.01.025

FANG Xupeng, SUN Xiangfei, ZHANG Shengnan, ZHAO Bingbing. An Improved Split Δ-source Inverter without Voltage Spikes[J]. Chinese Journal of Electrical Engineering, 2024, 19(1): 235-242 doi:10.11985/2024.01.025

1 引言

众所周知，逆变器在电力电子电路中占据着举足轻重的地位。传统的桥式逆变器因其结构简单、调制方便而被广泛使用，但它只有降压能力，即交流输出电压无法超过其直流输入电压^[1]。在一些要求交流输出电压高于直流输入电压的场合，比如燃料电池系统，就需要在桥式逆变器的前/后加入升压级^[2⇓-4]。近些年，具有boost功能的单级DC-AC变流器因体积更小、成本更低，得到了广泛的关注和长足的发展。在此类逆变器中最经典的是Z源逆变器(Z-source inverter，ZSI)^[5]。针对ZSI输入电流不连续、升压能力有限等问题，文献[6 ⇓⇓-9]通过增加电抗元件，实现了提高电压增益、接续输入电流的目的。文献[10 ⇓⇓-13]通过采用双绕组耦合电感作为变流器的主体，进一步提高了升压能力。文献[14-15]分别将Y源阻抗网络和Δ源阻抗网络应用于逆变器中，由这两种耦合电感网络为主体构成的逆变器有着很高的电压增益，但也存在开关管开通瞬间有较大的电压尖峰、高增益下输出电能质量差的缺点。学者们对Y源和Δ源逆变器进行了多方面的改进，但仍没有找到解决其高增益时电能质量差问题的方案^[16-17]。

文献[18]给出了另一种能在单级中实现boost功能的DC-AC变流器—分裂源逆变器(Spilt-source inverter，SSI)。与ZSI相比，SSI的优点是连续的输入电流、采用与电压源型逆变器(Voltage source inverter，VSI)相同的8种状态的标准调制策略以及具有低频分量的恒定逆变器电压。文献[19]将Δ源与分裂源逆变器相结合，构成了分裂Δ源逆变器(Split Δ-source inverter，SDSI)。SDSI相较于SSI电压增益得到了较大的提升，但是也带来了二极管电压应力过大的问题。

针对DSI和SDSI存在的问题，本文提出了一种改进型分裂Δ源逆变器(Improved split Δ-source inverter，ISDSI)，在SDSI的基础上引入了电压箝位单元实现。本文介绍了新型逆变器工作在电流连续模式下的工作原理和稳态特性，给出了状态转换过渡过程的分析。最后，通过仿真和试验证明了理论分析的正确性。

2 电路原理及性能参数

2.1 电路原理分析

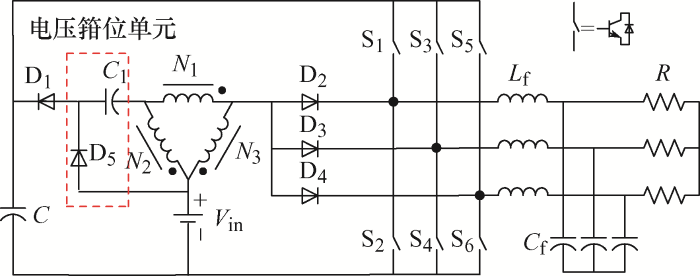
所提改进型分裂Δ源逆变器的电路结构如图1所示。它由直流电源、1个Δ型三绕组耦合电感、2个电容、5个二极管以及逆变桥组成。ISDSI仅使用标准逆变桥，与需要注入直通来达到升压目的的阻抗源逆变器不同，它的控制方式与传统电压型逆变器类似，控制方式在下文详细给出。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 所提ISDSI拓扑

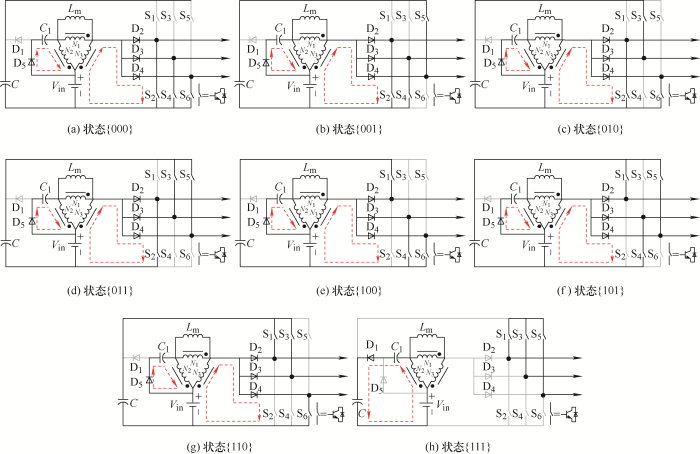
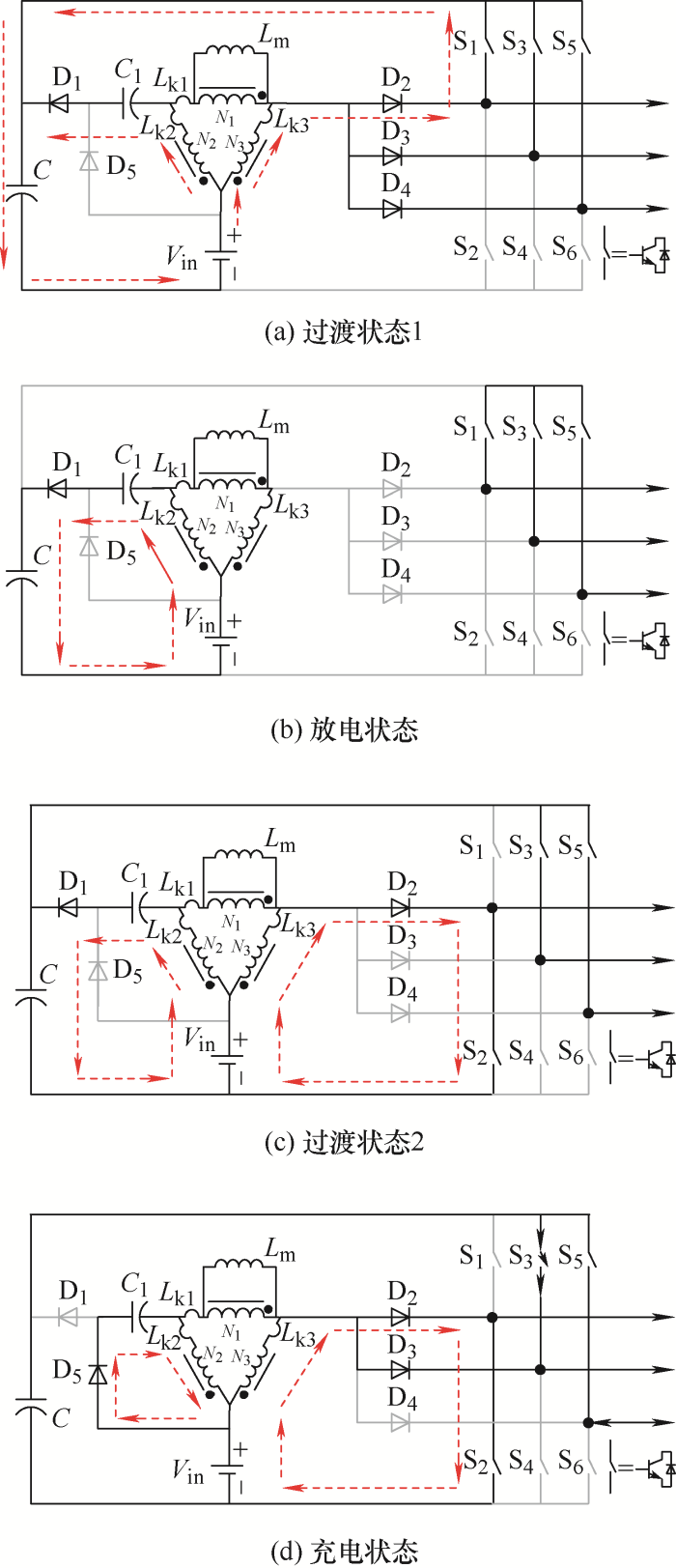
ISDSI的工作状态如图2所示。它有8种不同的开关状态，工作时同一桥臂的一对开关管不能同时导通。将桥臂上开关管导通记为1，桥臂下开关管导通记为0，8种开关状态表示为从{000}到{111}。在每个开关周期内，根据耦合电感的状态，可分为电感充电和电感放电两个阶段。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 ISDSI的状态分解

(1) 感应充电：耦合线圈感应充电阶段的状态如图2a~2g所示。在此阶段，三相逆变桥下半部分的三个开关管(S₂、S₄、S₆)至少有一个处于导通状态，所对应的三个二极管(D₂、D₃、D₄)也至少有一个处于导通状态，直流电源只与耦合线圈形成通路。另外，二极管D₁处于截止状态，D₅处于导通状态。直流电源一方面通过D₂、D₃、D₄对耦合电感充电，另一方面通过D₅对耦合电感和电容C₁充电。负载的能量状况分为两种：在状态{000}时，负载侧与电源侧不连通，负载处于零输入状态，如图2a所示；在状态{001}~{110}时，电容C与三相负载形成通路，并为负载提供能量，如图2b~2g所示。

根据基尔霍夫第二定律可列如下等式

(1)${{V}_{\text{in}}}={{V}_{N3}}={{V}_{\text{Lm}}}\frac{{{N}_{3}}}{{{N}_{1}}}$

(2)${{V}_{C1}}={{V}_{N2}}={{V}_{\text{Lm}}}\frac{{{N}_{2}}}{{{N}_{1}}}$

(2) 感应放电：耦合线圈感应放电阶段的状态如图2h所示。在此阶段，三相逆变桥下半部分的三个开关管(S₂、S₄、S₆)均处于截止状态，而上半部分的三个开关管(S₁、S₃、S₅)均处于导通状态，因此负载侧与输入端断开，负载侧处于零输入状态。二极管D₁导通，D₂、D₃、D₄、D₅均截止。耦合电感与电容C₁共同向电容C充电，从而达到升高直流链电压的目的。

根据基尔霍夫第二定律可列如下等式

(3)${{V}_{\text{in}}}-{{V}_{\text{C}}}={{V}_{\text{L2}}}-{{V}_{\text{C1}}}={{{V}'}_{\text{Lm}}}\frac{{{N}_{2}}}{{{N}_{1}}}-{{V}_{\text{in}}}\frac{{{N}_{2}}}{{{N}_{3}}}$

将式(1)与式(3)重新整理，得到关于V_Lm的表达式，对其使用电感伏秒平衡原理进行分析，可得式(4)

(4)$\frac{{{N}_{1}}}{{{N}_{3}}}{{V}_{\text{in}}}{{T}_{0}}+\frac{{{N}_{1}}}{{{N}_{2}}}\left( \frac{{{N}_{2}}+{{N}_{3}}}{{{N}_{3}}}{{V}_{\text{in}}}-{{V}_{\text{C}}} \right){{T}_{1}}=0$

式中，${{T}_{0}}=DT$为电感充电时间；${{T}_{1}}=(1-D)T$为电感放电时间。

对式(4)进行整理，可得直流链电压V_C和输入电压V_in之间的增益表达式

(5)$B=\frac{{{V}_{\text{C}}}}{{{V}_{\text{in}}}}=\frac{\frac{{{N}_{2}}+{{N}_{3}}}{{{N}_{3}}}-D}{1-D}=1+\frac{\frac{{{N}_{2}}}{{{N}_{3}}}}{1-D}$

由式(5)可知，改进型分裂Δ源逆变器的电压增益B的大小不仅与占空比D有关，而且与耦合电感的匝数比密切相关。考虑理想的三绕组变压器的伏特/匝数关系，即V_N₁/N₁ = V_N₂/N₂= V_N₃/N₃，其中V_N₁、V_N₂和V_N₃分别是三个绕组两端的电压，它们之间的KVL关系为V_N₂ = V_N₁ + V_N₃，由此可以简单地总结出N₁、N₂和N₃之间的关系应满足

(6)${{N}_{2}}={{N}_{1}}+{{N}_{3}}$

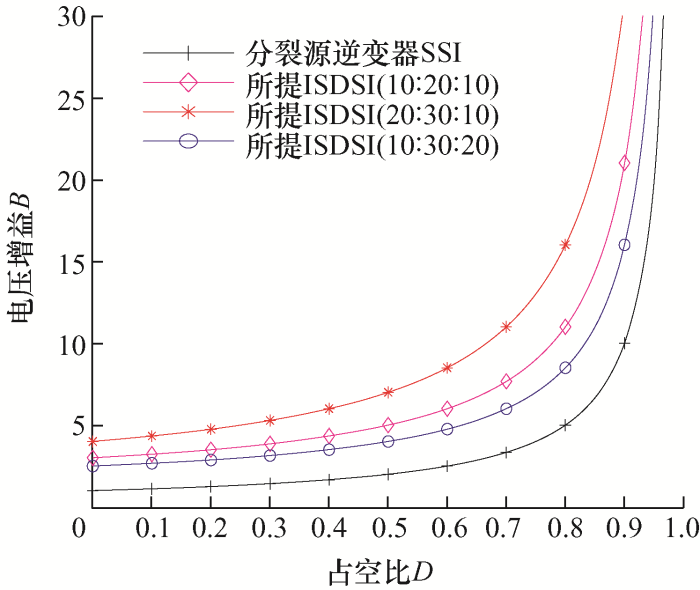
图3描绘了不同绕组系数下电压增益B随感应充电占空比D的变化曲线，清晰地展示了逆变器的升压性能。显然，在占空比相同的条件下，新型分裂源逆变器ISDSI比普通分裂源逆变器SSI的电压增益更高，并且新型分裂源逆变器可以通过增加N₂/N₃比值的方式获得更高的电压增益。通过比较星号线和空心圆形线的图像可以发现，选用相同的拓扑，如果要达到10倍及以上的电压增益，绕组系数取20∶30∶10时，D取0.67即可满足要求，而绕组系数取10∶30∶20时，D需要取到0.8以上才能满足要求。D-B曲线的升压能力差距如此悬殊，而它们的不同之处仅为互换了N₁与N₃的匝数。因此，如果要更好地提高分裂Δ源逆变器的升压能力，在满足N₂= N₁+ N₃的同时，也需要满足N₂>N₁≥N₃。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 电压增益和电感充电占空比的关系

2.2 SPWM控制策略下的交流参数

与传统分裂源逆变器一样，本文提出的ISDSI可以通过三相电压型逆变器调制方案中的任何调制方案进行调制。本文采用了正弦脉宽调制(SPWM)，其感应充电占空比D的公式如式(7)所示。值得注意的是，占空比不固定，并且在采用SPWM调制技术的情况下，占空比变化很大。

(7)$D(\theta )=\frac{1}{2}(1-M\sin \theta )\ \ \ \ \frac{7}{6}\mathrm{ }\!\!\pi\!\!\text{ }\le \theta \le \frac{11}{6}\mathrm{ }\!\!\pi\!\!\text{ }$

式中，M是逆变器的调制系数；充电占空比D为角度θ的函数。

为方便计算交流参数，可将式(7)给出的占空比D与调制系数M之间的非线性关系转换为线性关系，对式(7)在其取值范围内积分，所得的占空比称为平均占空比，即

(8)$D_{\mathrm{av}}=\frac{1}{\frac{2 \pi}{3}} \int_{\frac{7 \pi}{6}}^{\frac{11 \pi}{6}} D(\theta) \mathrm{d} \theta=\frac{1}{2}+\frac{3 \sqrt{3}}{4 \pi} M$

从式(8)可以看出，随着调制系数M的增大，感应充电占空比D也会随之增加。将式(8)代入式(5)，可得

(9)$B=\frac{V_{\mathrm{C}}}{V_{\text {in }}}=1+\frac{4 \pi N_{2}}{2 \pi N_{3}-3 \sqrt{3} N_{3} M}$

则交流输出电压增益为

(10)$\frac{V_{\text {ac }}}{V_{\text {in }}}=\frac{M}{2}+\frac{2 \pi N_{2} M}{2 \pi N_{3}-3 \sqrt{3} N_{3} M}$

式中，${{V}_{\text{ac}}}$是交流输出相电压的幅值。

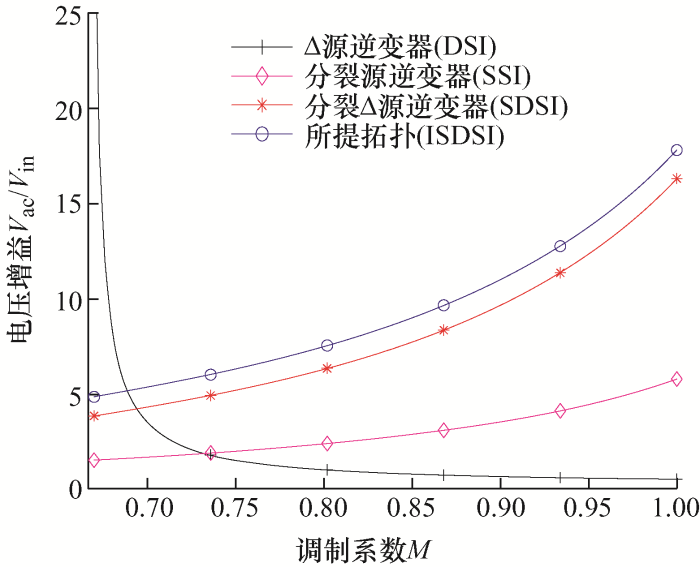
图4给出了四种不同拓扑逆变器的交流输出电压增益与调制系数之间的关系。设定Δ源逆变器耦合电感绕组系数为30∶20∶10，采用简单直通升压调制，其最大直通占空比D为$1-M$。设定其余的分裂源逆变器耦合电感绕组系数均为20∶30∶10，采用SPWM控制技术，占空比D与调制系数M的关系如式(8)所示。由图4可以看出，Δ源逆变器要想获得较大的电压增益，调制系数M的选择范围很窄，这使得其对高增益下M的变化比分裂源逆变器敏感得多，从而降低直流母线的利用率。在同一调制系数M(M >0.69)的条件下，所提ISDSI的交流输出电压增益明显高于SSI与SDSI，这是该拓扑的一大优势。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 交流输出电压增益与调制系数的关系

3 器件电压应力分析

为了给选择器件提供依据，有必要对器件电压应力进行分析。

(1) 电感充电阶段，二极管D₂、D₃、D₄交替导通，故它们在导通时电压为零，不导通时承受的反向电压为V_C，如式(11)所示。二极管D₅一直处于导通状态，故电压为零。二极管D₁承受的反向电压如式(12)所示。

(11)$V_{\mathrm{D} 2}, V_{\mathrm{D} 3}, V_{\mathrm{D} 4}=\left\{\begin{array}{ll}0 & \text { 该二极管导通时 } \\V_{\mathrm{C}} & \text { 该二极管截止时 }\end{array}\right.$

(12)${{V}_{\text{D1}}}={{V}_{C}}-{{V}_{\text{in}}}$

(2) 电感放电阶段，二极管D₁处于导通状态，电压为零。二极管D₂、D₃、D₄在该阶段承受的反向电压如式(13)所示，二极管D₅承受的反向电压如式(14)所示。

(13)${{V}_{\text{D2}}}={{V}_{\text{D3}}}={{V}_{\text{D4}}}=\frac{{{N}_{2}}-{{N}_{3}}}{{{N}_{2}}}{{V}_{\text{C}}}+\frac{{{N}_{3}}}{{{N}_{2}}}{{V}_{\text{in}}}$

(14)${{V}_{\text{D5}}}={{V}_{\text{C}}}-{{V}_{\text{in}}}$

在选择器件时，应以器件在整个周期内承受反向电压的最大值为标准，并保留一定的裕量。比较式(11)与式(13)，在匝数比为20∶30∶10的条件下，前者的电压应力大于后者的电压应力，故二极管D_2-4应根据式(11)来选择。开关管S_1-6在一个周期内承受的最大反向电压为直流链电压V_C。

如表1所示为新型分裂源逆变器与相关现有逆变器拓扑在电压增益、元器件数量、开关管和二极管所承受最大反向电压等方面的比较结果。

表1 改进型分裂Δ源逆变器与相关现有逆变器的比较

名称	改进型分裂Δ源逆变器	分裂Δ源逆变器	Δ源逆变器
电压增益B	$1+\frac{\frac{{{N}_{2}}}{{{N}_{3}}}}{1-D}$	$\frac{1+\frac{{{N}_{1}}}{{{N}_{3}}}}{1-D}$	$\frac{1}{1-\frac{{{N}_{1}}}{{{N}_{3}}}D}$
电容电感数目	1个三绕组耦合电感 2个电容	1个三绕组耦合电感 1个电容	1个三绕组耦合电感 1个电容
开关和二极管数目	6个开关管 5个二极管	6个开关管 4个二极管	6个开关管 1个二极管
绕组间的关系	N₂=N₁+N₃ (N₂>N₁>N₃)	N₂=N₁+N₃ (N₂>N₁>N₃)	N₁=N₂+N₃ (N₁>N₂>N₃)
开关管最大电压	${{V}_{\text{C}}}$	${{V}_{\text{C}}}$	$\frac{{{N}_{1}}}{{{N}_{2}}}{{V}_{\text{C}}}-\frac{{{N}_{3}}}{{{N}_{2}}}{{V}_{\text{in}}}$.
二极管最大电压	${{V}_{\text{C}}}$	${{V}_{\text{C}}}+\frac{{{N}_{2}}-{{N}_{3}}}{{{N}_{3}}}{{V}_{\text{in}}}$	$\frac{{{N}_{1}}}{{{N}_{3}}}{{V}_{\text{C}}}-{{V}_{\text{in}}}$

新窗口打开| 下载CSV

从表1中的各项数据对比中可知，所提新型分裂源逆变器相比于分裂Δ源逆变器多用了1个电容和1个二极管，但它的升压能力更强，并且在二极管所承受的最大电压方面有所降低。以输入直流电压V_in = 24 V，M = 0.6时为例，所提逆变器的电压增益比分裂Δ源逆变器提高了约8.5%，并且二极管电压应力降低了约8%，这些数据证实了上述结论。类似地，所提新型分裂源逆变器相比于Δ源逆变器多用了1个电容和4个二极管，但它在开关管以及二极管所承受的最大电压方面均有所降低。在电压增益相同的情况下，前者在开关管所承受的最大电压方面略有优势，而且在二极管所承受的最大电压方面优势很大，仅为后者的三分之一。这些关键参数的改进使得新型逆变器综合性能更好，并且对于器件的选型也是有利的。

合适的LC滤波参数是输出波形不失真的关键。考虑到三相系统的对称性，可以将三相逆变器的其中一相取出，形成的单相等效电路如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 单相等效电路

借鉴文献[20]中的研究成果，将重点公式罗列如下

(15)$0.1{{f}_{\mathrm{c}}}<{{f}_{\mathrm{L}}}<\text{0}\text{.2}{{f}_{\mathrm{c}}}$

(16)$\omega_{\mathrm{L}}=2 \pi f_{\mathrm{L}}$

(17)${{L}_{\text{f}}}=\sqrt{\frac{\frac{{{\omega }_{1}}U_{\mathrm{o}}^{2}}{\omega _{\mathrm{L}}^{2}}+\frac{{{\omega }_{1}}^{3}U_{\mathrm{o}}^{2}}{\omega _{\mathrm{L}}^{4}}}{{{\omega }_{1}}I_{\mathrm{o}}^{2}}}$

(18)${{C}_{\text{f}}}=\frac{1}{\omega _{\mathrm{L}}^{2}}\sqrt{\frac{{{\omega }_{1}}I_{\mathrm{o}}^{2}}{\frac{{{\omega }_{1}}U_{\mathrm{o}}^{2}}{\omega _{\mathrm{L}}^{2}}+\frac{{{\omega }_{1}}^{3}U_{\mathrm{o}}^{2}}{\omega _{\mathrm{L}}^{4}}}}$

式中，f_c为载波频率，取10 kHz；f_L为LC滤波器的截止频率；ω_L为LC滤波器的截止角频率；ω₁为基波角频率；U_o为输出相电压的有效值；I_o为流过电阻的电流有效值。

对于LC滤波器的截止频率f_L可取中间值，即0.15f_c。将此值代入式(16)可得截止角频率ω_L，根据式(17)、式(18)可分别求得L和C的值。

4 消除电压尖峰分析

为了简化分析难度，通常在建模时认为耦合线圈不存在漏感电流，而在研究逆变器工作状态的转换时，漏感电流所带来的影响就不能忽略。Δ源逆变器的某一开关处于断开状态时，承受的电压为直流链电压，当它从直通状态转换到非直通状态时，在开关管上会出现较大的电压尖峰；对于所提ISDSI拓扑来说，则不会出现这种电压尖峰。

在分析之前，假定充电为状态{001}，L_k1、L_k2和L_k3为线圈漏感。从感应充电状态转换到感应放电状态的过程为如图6a所示的过渡过程1，在此期间流过二极管D₂、D₃、D₄的电流逐渐减小，而流过D₁的电流逐渐增大，它们的电流在任何时刻均等于电源V_in输入的电流。该过程持续到流过电路右侧三个二极管的电流均减小到零时结束，电路进入感应放电状态。类似地，在如图6c所示的过渡过程2中，流过二极管D₁的电流呈减小趋势，流过二极管D₂、D₃、D₄的电流呈增大趋势，直到电路进入感应充电状态。此时，二极管D₁关断，D₅开始导通，漏感能量被储存在中间电容C₁中。由上述分析可知，在充电与放电的相互转换期间，过渡状态能够使要关断的二极管流过的漏感电流平稳下降到零，因此不会出现明显的电压尖峰。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 ISDSI的状态转换

5 仿真与试验验证

5.1 仿真验证

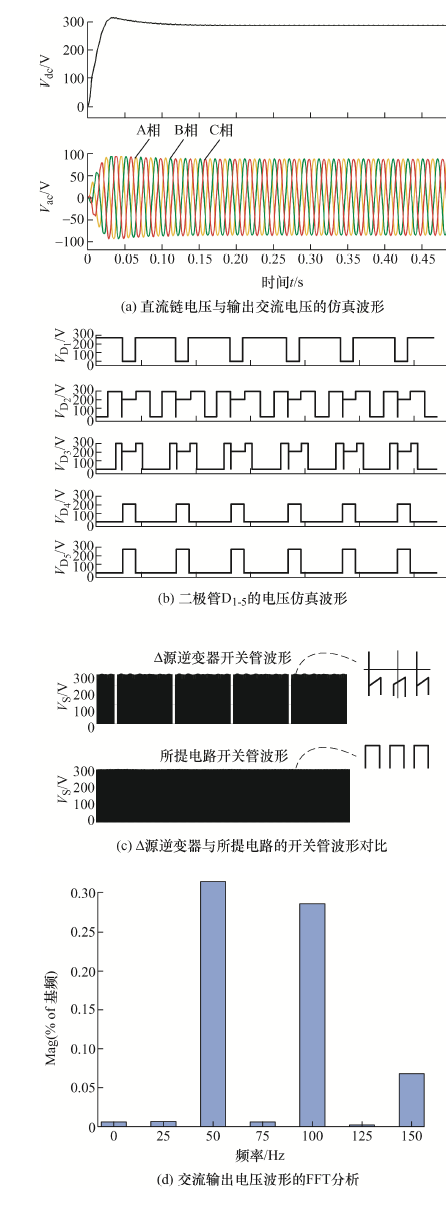
为验证理论分析的正确性，在Matlab/Simulink软件中搭建出电路模型并进行了仿真，具体参数设置如表2所示。仿真结果如图7所示。

表2 仿真参数设置

参数	数值
输入电压V_in/V	24
开关频率f/kHz	10
调制系数M	0.6
耦合电感匝数比电容C、C₁/μF 滤波电容C_f/μF 滤波电感L_f/mH 负载电阻R/Ω	20∶30∶10 470，3.3 22 1 100

新窗口打开| 下载CSV

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 仿真结果

在表2所给出的试验条件下，所提改进型分裂Δ源逆变器的理论值如下：输出直流链电压V_C为309.7 V，交流输出相电压的幅值V_ac为92.9 V。各二极管承受的反向电压分别为：V_D1= V_D5= 285.7 V，V_D2= V_D3= V_D4= 214.5 V。将上述理论数值对比图7a、7b中的数据，误差在可容许范围内，并且逆变器的输出可以很快地稳定在相应的数值上。

由图7b可以发现，二极管D₂、D₃在一个周期内出现了三个不同的电压值，而D₄仅出现了两个不同的电压值，这是由于D₂、D₃、D₄在感应充电状态下交替导通造成的。在稍后的时刻会出现D₂、D₃中的一只管子和D₄出现三个不同电压值，而D₂、D₃中的另一只管子只有两个电压值的情况。对比理论结果与仿真结果，可以发现仿真结果略低于理论结果，这是因为在理论计算中忽略了耦合电感的漏感以及非理想开关管所带来的影响。

图7c为改进型分裂Δ源逆变器(ISDSI)逆变桥端开关管电压V_S的波形。正如前节所述，ISDSI的开关管截止时承受的电压为直流链电压V_C，该逆变器没有出现电压尖峰对开关管产生的消极影响，因此ISDSI的输出电压质量比DSI更好。

图7d为交流输出电压V_ac的FFT分析图。从FFT分析结果来看，二次谐波与三次谐波的总谐波畸变系数为0.36%。其中二次谐波含量相对较大，三次谐波含量已经降至很低的水平。

5.2 试验验证

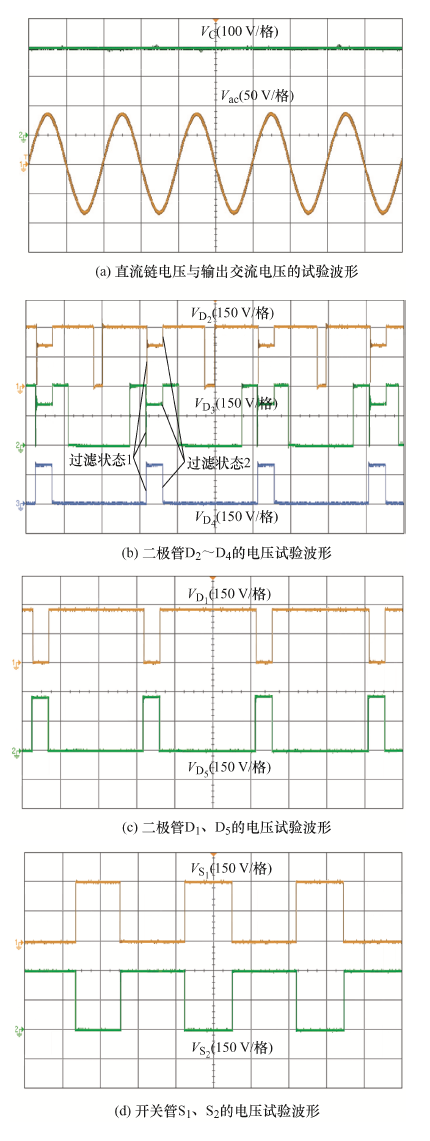
为了进一步验证所提新拓扑的正确性与优越性，根据仿真中的参数搭建了如图8所示的试验电路。采用TI公司生产的TMS320F28335芯片产生逆变器所需的六路触发脉冲，并通过落木源公司生产的DA962D6驱动板将脉冲输出放大，去驱动H25R1203型IGBT。试验结果如图9所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 试验样机

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 试验结果

从图9a可以发现，直流链电压约为300 V，交流输出为幅值90 V、频率50 Hz的三相交流电。图9b的试验波形表明，无论是从电感充电状态转换到电感放电状态，还是从电感放电状态转换到电感充电状态时均有一段短暂的时间，分别对应于图6a的过渡状态1与图6c的过渡状态2。在图9b、9c中，二极管的实测与仿真在波形上别无二致，在数值上也基本吻合，证明了前述分析的正确性。在图9d中，开关管的电压波形不存在电压尖峰，证实了ISDSI具有消除电压尖峰的特性。总体来说，试验结果的各项数值比理论值略小，但在合理的误差范围内，进一步证明了理论分析的可行性。

6 结论

本文提出了一种改进型分裂Δ源逆变器(ISDSI)，分析了所提电路的工作过程，推导了直流与交流的电压增益，并对逆变器充电与放电转换间的过渡过程进行了阐述。仿真和试验结果均验证了理论分析的正确性与可行性。试验结果表明，改进型分裂Δ源逆变器具有以下优点。

(1) 增加少量器件使电压增益得到较大提升，同时降低了二极管上的电压应力。

(2) 漏感能量通过二极管注入中间电容，使能量得到了有效利用，消除了开关电压尖峰。

(3) 调制系数M与升压占空比D是同向增长的关系，这有助于提升输出电能质量。总的来说，新型分裂源逆变器克服了传统Δ源逆变器的突出缺陷，能够在高压场合取代传统Δ源逆变器。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

王兆安, 刘进军.

电力电子技术[M]. 北京: 机械工业出版社, 2009.