1 引言
变压器、电机等电磁设备,普遍采用硅钢片叠片的铁心结构,而铁心的磁滞特性直接影响此类电磁设备的运行性能,如电机的损耗温升问题、变压器的剩磁和励磁涌流问题等。因此,铁心磁滞特性的精准预估一直是学者们研究的难点问题。
在变压器铁心磁滞模型[1 ] 的理论研究方面,形成了包括磁滞Preisach模型[2 -3 ] 、期望损失(Expected shortfall,E&S)模型[4 ] 、磁化(Jiles-Atherton,J-A)模型[5 ] 等理论模型。其中,由于J-A模型具有清晰的物理含义,能够较好地描述B-H 曲线的非线性关系;同时,该模型所需辨识参数相对少,仿真运行时间较短,在现阶段的工程研究及应用中推广较好[6 ] 。
但是,现阶段J-A模型的参数辨识,依旧需要同时实现包含饱和磁化强度M s 、磁畴间耦合的平均场系数α 、无磁滞磁化曲线的形状系数a 、钉扎常数k 、可逆磁化系数c 等参数的有效辨识,在缺乏良好的全局寻优、局部寻优智能算法的情况下,其计算量大,计算精度低,且容易陷入局部最优解[7 ] 。在J-A模型参数辨识的算法研究中,学者们进行了一系列的算法优化探索。文献[8 ]提出改进鲸鱼算法辨识J-A模型参数,并通过仿真验证了该方法的有效性。虽然该方法不易陷入局部最优解,但辨识步骤繁多,导致收敛速度变慢。文献[9 ]对模型的5个参数单独优化,虽然计算简便且结果精度较高,但步骤繁琐且收敛较慢。文献[10 ]采用粒子群优化算法对不同噪声环境下J-A磁滞模型的参数进行了识别,该方法在含噪声情况下仍能得到较高的参数精度,但迭代次数过多,仿真时间过长。
针对传统粒子群优化(Particle swarm optimization,PSO)算法在J-A模型参数辨识中存在的计算量大、辨识精度低等问题,本文提出一种基于收缩因子改进的PSO优化算法。该算法不单独依赖种群信息或个体信息,可以综合考虑所有信息,且取消了粒子飞行速度的限制,有利于提升算法的收敛速度和精度。研究以磁感应强度为输入变量的J-A静态磁滞逆模型的建模方法,提出考虑动态损耗因素下的动态磁滞模型,仿真验证所提基于收缩因子改进PSO算法于J-A磁滞模型参数辨识应用的有效性,评估所提算法的计算精度及准确率。
2 Jiles-Atherton磁滞模型
2.1 静态磁滞模型
J-A静态磁滞模型[11 ] ,主要是忽略了动态损耗因素的影响,其磁化强度M 可分为可逆分量M rev 、不可逆分量M irr ,具体表达式为
(1) $M\text{=}{{M}_{\mathrm{irr}}}+{{M}_{\mathrm{rev}}}$
(2) ${{M}_{\mathrm{rev}}}=c\left( {{M}_{\mathrm{an}}}-{{M}_{\mathrm{irr}}} \right)$
式中,c 为可逆磁化系数;M an 为无磁滞磁化强度。参照J-A模型的建模方法,无磁滞磁化强度M an 可表示为
(3) ${{M}_{an}}={{M}_{\mathrm{s}}}\left( \coth \frac{{{H}_{\mathrm{e}}}}{a}-\frac{a}{{{H}_{\mathrm{e}}}} \right)$
式中,H e =H +αM 。H e 为有效磁场强度,H 和M 分别为磁场强度、磁化强度。
(4) ${{\mu }_{0}}{{\delta }_{\mathrm{M}}}\int{M\text{d}{{H}_{\mathrm{e}}}}={{\mu }_{0}}{{\delta }_{\mathrm{M}}}\int{{{M}_{\mathrm{an}}}\text{d}{{H}_{\mathrm{e}}}-{{\mu }_{0}}k{{\delta }_{\mathrm{H}}}\int{\frac{\text{d}{{M}_{\mathrm{irr}}}}{\text{d}{{H}_{\mathrm{e}}}}}}\text{d}{{H}_{\mathrm{e}}}$
式中,δ M 为防止出现非物理解的系数[12 -13 ] ;δ H 为方向系数,其取值范围为
(5) $\left\{ \begin{align} & sgn \left( \frac{\text{d}H}{\text{d}t} \right)\cdot sgn \left( {{M}_{\mathrm{an}}}-M \right)>0\ \ \ \ {{\delta }_{\mathrm{M}}}=1 \\ & sgn \left( \frac{\text{d}H}{\text{d}t} \right)\cdot sgn \left( {{M}_{\mathrm{an}}}-M \right)<0\ \ \ \ {{\delta }_{\mathrm{M}}}=0 \\ \end{align} \right.$
(6) $\left\{ \begin{align} & {{\delta }_{\mathrm{H}}}=1\ \ \ \ \ \ \ \ \frac{\text{d}H}{\text{d}t}\text{0} \\ & {{\delta }_{\mathrm{H}}}=-1\ \ \ \ \ \frac{\text{d}H}{\text{d}t}\text{0} \\ \end{align} \right.$
通过式(1)~(6)的迭代求解计算,可得出磁化强度M 和磁场强度H 的微分方程,即J-A静态磁滞模型正模型
(7) $\frac{\text{d}M}{\text{d}H}\text{=}\frac{{{\delta }_{M}}\left( 1-c \right)\left( {{M}_{\mathrm{an}}}-M \right)+k\delta c\cdot \frac{\text{d}{{M}_{\mathrm{an}}}}{\text{d}H}}{k{{\delta }_{H}}-\alpha {{\delta }_{M}}\left( 1-c \right)\left( {{M}_{\mathrm{an}}}-M \right)}$
采用J-A正模型进行磁滞曲线的参数辨识,需要以磁场强度H 作为输入变量,由于工程应用中磁场强度H 的直接测试困难,在参数辨识中容易产生较大的辨识误差,甚至出现辨识结果的畸变现象,不利于J-A模型参数辨识的快速寻优。同时,在J-A磁滞模型参数辨识中,选择磁通密度B 作为输入变量具有较大的优势。
(1) 在测量方面,磁通密度B 的试验测试更加直观,有利于保证参数辨识中磁通密度B 的变化为正弦变化。
(2) 在数值计算方面,J-A磁滞模型通常需要跟诸如有限元法等数值计算方法结合,以实现精细化的电磁性能分析,而有限元计算直接能够得到磁通密度B ,因此,选择J-A逆模型更容易和有限元计算相结合。所以,本文选定磁通密度B 作为输入变量,其中,磁化过程中磁通密度B 与磁场强度H 之间的关系,可表示为
(8) $\frac{\text{d}{{H}_{\mathrm{e}}}}{\text{d}B}=\frac{1}{{{\mu }_{0}}}+\left( \alpha -1 \right)\frac{\text{d}{{M}_{\mathrm{an}}}}{\text{d}H}$
将式(8)代入式(4),可得出以磁通密度B 为输入量的J-A静态磁滞模型逆模型
(9) $\begin{matrix} \frac{\text{d}M}{\text{d}B}= \\ \frac{{{\delta }_{\mathrm{M}}}\left( 1-c \right)\left( {{M}_{\mathrm{an}}}-M \right)+k{{\delta }_{\mathrm{B}}}c\cdot \left( \frac{\text{d}{{M}_{\mathrm{an}}}}{\text{d}H} \right)}{{{\mu }_{0}}{{\delta }_{\mathrm{M}}}\left( 1-\alpha \right)\left( 1-c \right)\left( {{M}_{\mathrm{an}}}-M \right)+{{\mu }_{0}}k{{\delta }_{\mathrm{B}}}\left( 1+c \right)\cdot \left( \frac{\text{d}{{M}_{\mathrm{an}}}}{\text{d}H} \right)} \\ \end{matrix}$
(10) $\left\{ \begin{align} & sgn \left( \frac{\text{d}B}{\text{d}t} \right)\cdot sgn \left( {{M}_{\mathrm{an}}}-M \right)>0\ \ \ \ \ {{\delta }_{\mathrm{M}}}=1 \\ & sgn \left( \frac{\text{d}B}{\text{d}t} \right)\cdot sgn \left( {{M}_{\mathrm{an}}}-M \right)<0\ \ \ \ \ {{\delta }_{\mathrm{M}}}=0 \\ \end{align} \right.$
(11) $\left\{ \begin{align} & {{\delta }_{\mathrm{B}}}=1\ \ \ \ \ \ \ \ \ \ \frac{\text{d}B}{\text{d}t}>0 \\ & {{\delta }_{\mathrm{B}}}=-1\ \ \ \ \ \frac{\text{d}B}{\text{d}t}<0 \\ \end{align} \right.$
通过式(10)和式(11),可计算得到不同磁滞过程中系数δ M 和δ B 的取值,通过式(9)进行编程求解,可计算得到以磁通密度为输入量的静态磁滞曲线。
2.2 动态磁滞模型
静态磁滞模型属于一类相对较为理想的数学模型,其简化了动态损耗因素的影响。为了更好地模拟不同工况下的动态磁滞特性,在此需要对静态磁滞模型进行修正[12 ] 。
根据Bertotti提出的铁心损耗分离理论可知,铁心的磁损耗分为静态损耗和动态损耗。其中,动态损耗又由涡流损耗和异常损耗构成,静态损耗即磁滞损耗。一个周期内铁心损耗W 为
(12) $W={{W}_{\mathrm{hys}}}+{{W}_{\mathrm{eddy}}}+{{W}_{\mathrm{anom}}}$
式中,W hys 为一个周期内磁滞损耗;W eddy 为一个周期内涡流损耗;W anom 为一个周期内异常损耗。
(13) ${{W}_{\text{eddy}}}=\int_{0}^{T}{\frac{{{d}^{2}}}{2\rho \beta }}{{\left( \frac{\text{d}B}{\text{d}t} \right)}^{2}}\text{d}t={{k}_{\text{e}}}\int_{0}^{T}{{{\left( \frac{\text{d}B}{\text{d}t} \right)}^{2}}\text{d}t}$
式中,k e 为涡流损耗系数;ρ 为铁心材料电阻率;d 为硅钢片厚度;β 为铁心材料形状系数;T 为一个时间周期。而单位体积内一个周期产生的异常损耗可表示为
(14) ${{W}_{\text{anom}}}={{\int_{0}^{T}{\left( \frac{GS{{V}_{0}}}{\rho } \right)}}^{\frac{1}{2}}}{{\left| \frac{\text{d}B}{\text{d}t} \right|}^{\frac{3}{2}}}\text{d}t={{k}_{\text{a}}}\int_{0}^{T}{{{\left| \frac{\text{d}B}{\text{d}t} \right|}^{\frac{3}{2}}}}\text{d}t$
式中,k a 为异常损耗系数;G 为无量纲常数;S 为电工钢截面积;V 0 为铁心材料形状系数。
在考虑动态损耗的情况下,需要对静态模型进行修正[13 ] 。其中,式(4)的能量守恒方程需要修正为
${{\mu }_{0}}{{\delta }_{\mathrm{M}}}\int{M\text{d}{{H}_{\mathrm{e}}}}={{\mu }_{0}}{{\delta }_{\mathrm{M}}}\int{{{M}_{\mathrm{an}}}\text{d}{{H}_{\mathrm{e}}}}-{{\mu }_{0}}k{{\delta }_{\mathrm{H}}}\int{\frac{\text{d}{{M}_{\mathrm{irr}}}}{\text{d}{{H}_{\mathrm{e}}}}}\text{d}{{H}_{\mathrm{e}}}-$
(15) ${{k}_{\text{e}}}\int{{{\left( \frac{\text{d}B}{\text{d}t} \right)}^{2}}}\text{d}t-{{k}_{\text{a}}}\int{{{\left( \left| \frac{\text{d}B}{\text{d}t} \right| \right)}^{\frac{3}{2}}}\text{d}t}$
式中,右侧第一项和第二项为磁滞损耗因素分量,第三项为涡流损耗因素分量,第四项为异常损耗因素分量。同时,修正磁场强度后的表达式为
(16) ${{H}_{\text{total}}}={{H}_{\text{hys}}}+{{H}_{\text{eddy}}}+{{H}_{\text{anom}}}$
基于铁心损耗分离理论和场分离理论[14 ] ,参照式(16)中磁场强度的数学关系,考虑动态损耗因素下各磁场强度关系式可表示为
(17) ${{H}_{\text{eddy}}}=\frac{\text{d}\int{\frac{\text{d}{{W}_{\text{eddy}}}}{\text{d}t}\text{d}t}}{\text{d}B}={{k}_{\text{e}}}\left( \frac{\text{d}B}{\text{d}t} \right)$
(18) ${{H}_{\text{anom}}}=\frac{\text{d}\int{\frac{\text{d}{{W}_{\text{anom}}}}{\text{d}t}\text{d}t}}{\text{d}B}={{k}_{\text{a}}}{{\delta }_{B}}{{\left| \frac{\text{d}B}{\text{d}t} \right|}^{\frac{1}{2}}}$
式中,H total 为总磁场强度;H hys 为静态磁场强度;H eddy 为涡流损耗磁场强度;H anom 为异常损耗磁场强度。此外,将静态磁滞模型中的有效磁场强度关系:H e =H +αM ,可修正为H e =H hys +αM 。
因此,考虑涡流损耗、异常损耗因素下,以磁通密度B 为输入量的J-A动态磁滞模型逆模型,可表示为
(19) $\frac{\text{d}M}{\text{d}B}=\frac{{{\delta }_{\mathrm{M}}}\left( M-{{M}_{\mathrm{an}}} \right)-k{{\delta }_{\mathrm{B}}}c\frac{\text{d}{{M}_{\mathrm{an}}}}{\text{d}{{H}_{\mathrm{e}}}}+{{P}_{\mathrm{d}}}\left( t \right)}{{{\mu }_{0}}\left( 1-\alpha \right)\left[ {{\delta }_{\mathrm{M}}}\left( M-{{M}_{\mathrm{an}}} \right)-k{{\delta }_{\mathrm{B}}}c\frac{\text{d}{{M}_{\mathrm{an}}}}{\text{d}{{H}_{\mathrm{e}}}} \right]-{{\mu }_{0}}k{{\delta }_{\mathrm{B}}}}$
式中,${{P}_{\mathrm{d}}}\left( t \right)={{k}_{\text{e}}}\left( \frac{\text{d}B}{\text{d}t} \right)+{{k}_{\text{a}}}\sqrt{\left( \frac{\text{d}B}{\text{d}t} \right)}$ ${{k}_{\text{e}}}=\frac{{{d}^{2}}}{2\rho \beta }$ ${{k}_{\text{a}}}=\sqrt{\left( \frac{GS{{V}_{0}}}{\rho } \right)}$
3 参数辨识方法
3.1 经典PSO算法
粒子群优化算法[15 -16 ] ,最初被应用于模拟鸟群的觅食过程,因其具有较好的寻优效果,近年来备受学者们的青睐。
PSO优化算法通过给定一组随机参数生成初始种群,即生成一群随机粒子,其中,每一个粒子表示为求解问题中的一个可能解,通过目标函数确定该粒子的适应度值。以模拟鸟群的觅食过程为例,通过每个粒子模拟鸟的行为,在解空间自由随机移动,移动的方向和位移由粒子的速度决定。通常情况下,每次迭代粒子有两种运动趋势,一是朝当前粒子群中最优粒子的方向运动,二是朝粒子本身寻到的最优位置运动。粒子速度与位置更新可表示为
(20) ${{v}_{ij}}\left( t+1 \right)=\omega {{v}_{ij}}\left( t \right)+{{c}_{1}}{{r}_{1}}\left[ \left( \text{pbes}{{\text{t}}_{ij}}\left( t \right)-{{x}_{ij}}\left( t \right) \right) \right]+{{c}_{2}}{{r}_{2}}\left[ \text{gbes}{{\text{t}}_{gj}}\left( t \right)-{{x}_{ij}}\left( t \right) \right]$
(21) ${{x}_{ij}}\left( t+1 \right)={{x}_{ij}}\left( t \right)+{{v}_{ij}}\left( t+1 \right)$
式中,v 为粒子的速度;i =1,2,3,…,n ,n 为粒子数量;j =1,2,3,…,m ,m 为粒子的维数;t 为当前迭代代数;ω 为惯性因子[17 ] ;pbest为第i 个粒子自身寻到的最优位置;gbest为粒子群中寻到的最优位置;x 为粒子的位置;c 1 、c 2 为认知因子和社会因子;r 1 、r 2 为均匀分布在(0,1)区间的随机数。
采用传统PSO算法应用于J-A模型的参数辨识,因涉及多个磁参量辨识的多目标优化,为了提升计算速度和精度,防止陷入局部最优解,需要对PSO算法进行优化。
3.2 惯性权重PSO算法
惯性权重PSO(Inertia weight particle swarm optimization,IwPSO)算法[18 ] ,是一种改进的PSO智能算法。在引入惯性因子的基础上,采用线性递减权值策略动态调整惯性因子,从而实现快速寻优。该方法可由式(20)~(22)表示
(22) $\omega \left( t \right)=\frac{\left( {{\omega }_{\mathrm{start}}}-{{\omega }_{\mathrm{end}}} \right)\left( {{t}_{\max }}-t \right)}{{{t}_{\max }}}+{{\omega }_{\mathrm{end}}}$
式中,ω (t )当前迭代代数的惯性因子;ω start 为初始迭代代数的惯性因子;ω end 为迭代终止时的惯性因子;t max 为最大迭代代数。在IwPSO算法求解过程中,通过式(22)随迭代次数增加动态调整惯性因子,可随之调整PSO算法的全局与局部寻优能力。惯性因子ω 较大时,全局寻优能力较强,局部寻优能力较弱;而惯性因子ω 较小时,寻优集中在局部小范围以寻得最优解范围内的唯一最优解。为了更好地实现算法的快速寻优,往往需要酌情修正惯性因子ω ,在缺乏精确的修正模型时,寻优能力的提升并不明显。
3.3 基于收缩因子改进的PSO优化算法
经典PSO算法中,粒子有自身与种群两处信息来源,每个粒子根据掌握的信息调整自己的运动方向,并向全局最优位置(最优解)靠近。在此过程中,粒子会渐渐加大依靠种群信息调整轨迹的比例,导致种群多样性丢失,粒子不再对自己局部区域进行搜索,故该算法容易陷入局部最优解。虽然惯性权重PSO算法在一定程度上缓解了PSO信息依赖性过高的缺陷,保证PSO算法在寻优过程中稳定地朝最优解方向移动,最终能够得到较好的寻优效果。但惯性权重PSO算法的寻优能力,过于依赖惯性因子ω 的取值,在惯性因子ω 取值待优化的情况下,存在寻优过程时间长、收敛不够迅速的问题。
本文采用基于收缩因子改进的PSO算法(Constriction factor particle swarm optimization,CFPSO),在有效控制粒子飞行速度的同时,保证了算法在全局与局部寻优平衡,提高算法寻优能力,确保了算法的收敛性,避免了经典PSO算法中出现的“早熟”现象。
由于经典PSO算法和惯性权重PSO算法都对粒子的飞行速度有一定的限制,需要保证飞行速度不会超过设定的最大值,而CFPSO算法通过引入收缩因子$\chi $
(23) ${{v}_{ij}}\left( t+1 \right)=\chi \left( \begin{align} & {{v}_{ij}}\left( t \right)+{{c}_{1}}{{r}_{1}}\left[ \text{pbes}{{\text{t}}_{ij}}\left( t \right)-{{x}_{ij}}\left( t \right) \right]+ \\ & {{c}_{2}}{{r}_{2}}\left[ \text{gbes}{{\text{t}}_{gj}}\left( t \right)-{{x}_{ij}}\left( t \right) \right] \\ \end{align} \right)$
(24) $\chi =\frac{2}{\left| 2-\varphi -\sqrt{{{\varphi }^{2}}-4\varphi } \right|}$
式中,$\varphi $ c 1 +c 2 ,$\varphi $ c 1 =c 2 =2.05,$\varphi $ c 1 +c 2 =4.1,因此收缩因子$\chi $
为了验证所提CFPSO算法的计算准确性,本文采用适应度值优劣判别,来表征J-A模型参数识别的精确度;同时,采用实测磁场强度值与仿真计算磁场强度值的均方根误差作为适应度函数fitness (即适应度值)
(25) $fitness=\sqrt{\frac{\sum\limits_{i=1}^{N}{{{\left( {{H}_{\mathrm{mea}}}\left( i \right)-{{H}_{\mathrm{cal}}}\left( i \right) \right)}^{2}}}}{N}}$
式中,H mea 为理论/实测磁场强度值;H cal 为仿真计算磁场强度值;N 为采样点数。
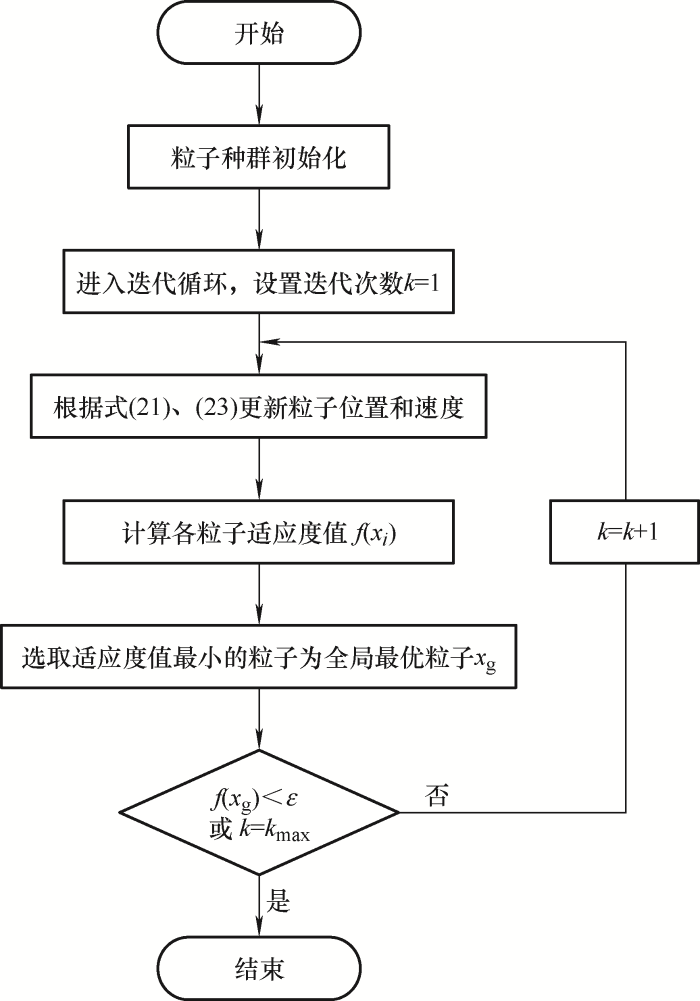
结合上述模型参数及算法理论分析,提出基于收缩因子改进的PSO优化算法,算法流程如图1 所示。其中,适应度值的收敛判据,采用以下两种判定标准。
图1
(1) 在迭代计算过程中预设寻优的适应度值阀值(本文设定阀值ε =1×10-14 ),当迭代求解精度达到设定阀值时,则判定迭代计算收敛完成,不需要再进行迭代计算过程。
(2) 若迭代次数已到设定的上限次数,此时取迭代计算过程完成后的最终寻优参数值作为结果输出。
4 仿真参数辨识
4.1 J-A静态磁滞模型参数辨识
为了验证所提基于收缩因子改进PSO优化算法的有效性,在静态J-A磁滞模型的辨识过程中,参照文献[19 ]给定的一组实测参数,作为静态J-A磁滞模型辨识的样本数据。分别研究经典PSO算法、IwPSO算法、CFPSO优化算法对给定实测磁滞曲线的辨识效果评估,并讨论各算法的准确性及快速性。采用各智能算法辨识得到J-A模型参数结果,如表1 所示(该样本数据的磁场强度H 范围设定为-300~300 A/m)。
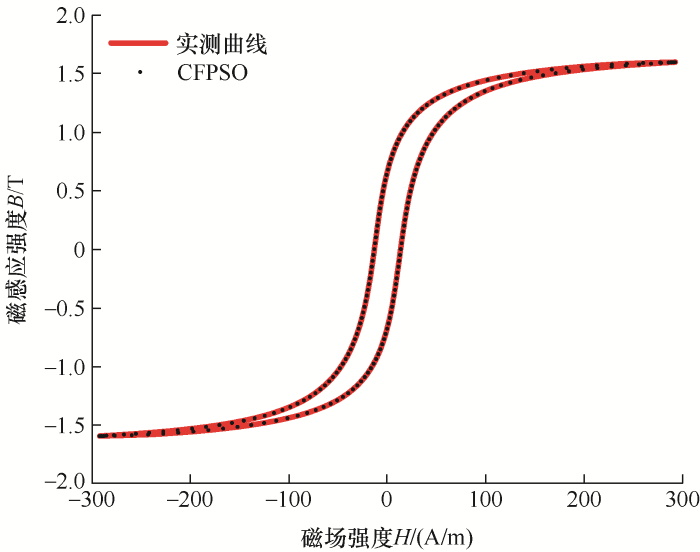
由表1 可知,采用经典PSO算法辨识得到的参数误差最大为25.24%,IwPSO算法辨识结果的误差最大为9.80%,采用CFPSO算法辨识结果的误差最大为8.28%,最小误差为0.36%。因此,在单一参数精度、整体参数误差等方面,CFPSO优化算法均优于其他算法,在J-A磁滞模型参数辨识中优势明显。图2 为采用CFPSO算法辨识得到静态磁滞曲线的跟踪效果,其中,曲线为J-A参数辨识模型的实测曲线,点线为采用CFPSO辨识参数绘制得到的最终跟踪曲线。由图2 可知,采用CFPSO优化算法对实测磁滞曲线的辨识跟踪效果较好。
图2
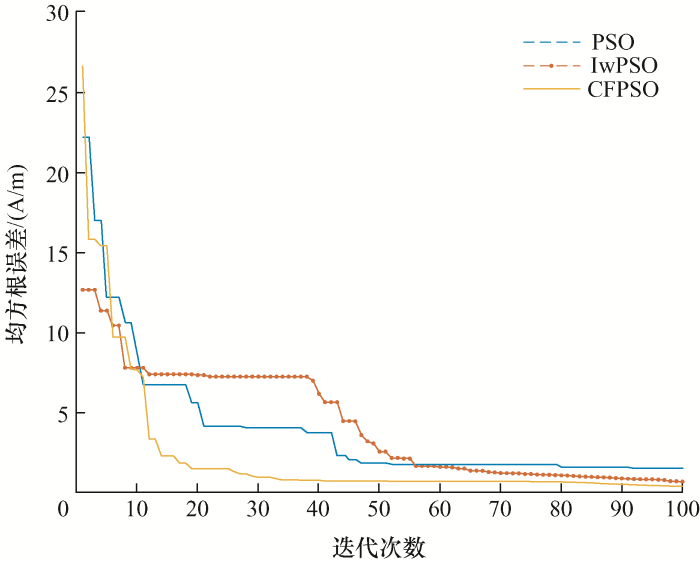
图3 为经典PSO算法、IwPSO算法以及CFPSO优化算法在迭代求解过程中的误差结果对比。从图3 可知,CFPSO优化算法在迭代次数达到10次后,其均方根误差明显小于经典PSO算法和IwPSO算法,验证了本文所提CFPSO优化算法的快速辨识效果。为了进一步分析各算法的迭代收敛速度,表2 给出了三种算法均方根误差随迭代次数的数学关系。
图3
从图3 和表2 的结果对比可知,在计算迭代磁场小于20次的情况下,经典PSO算法和IwPSO算法仍存在较大的计算误差;而CFPSO优化算法因其参数辨识的高精度优势,生成的磁滞回线与实测曲线的吻合度最高,在约10次计算迭代后,均方根误差便可控制在3 A/m以内。同时,经典PSO算法迭代到后期,收敛速度较慢,在迭代到80次后,陷入了局部最优解;IwPSO算法虽然没有陷入局部最优解,但直到最后仍然未停止收敛,因为IwPSO算法要收敛到全局最优解需要较多的迭代次数;CFPSO优化算法在迭代前期收敛速度较快,后期也没有陷入局部最优解,因此适应度值持续降低,最终寻得全局最优解。
综上所述,采用CFPSO优化算法应用于J-A静态磁滞模型的参数辨识,相对误差较小且计算收敛速度快,而经典PSO算法和IwPSO算法存在陷入局部最优解和未完全收敛的问题。
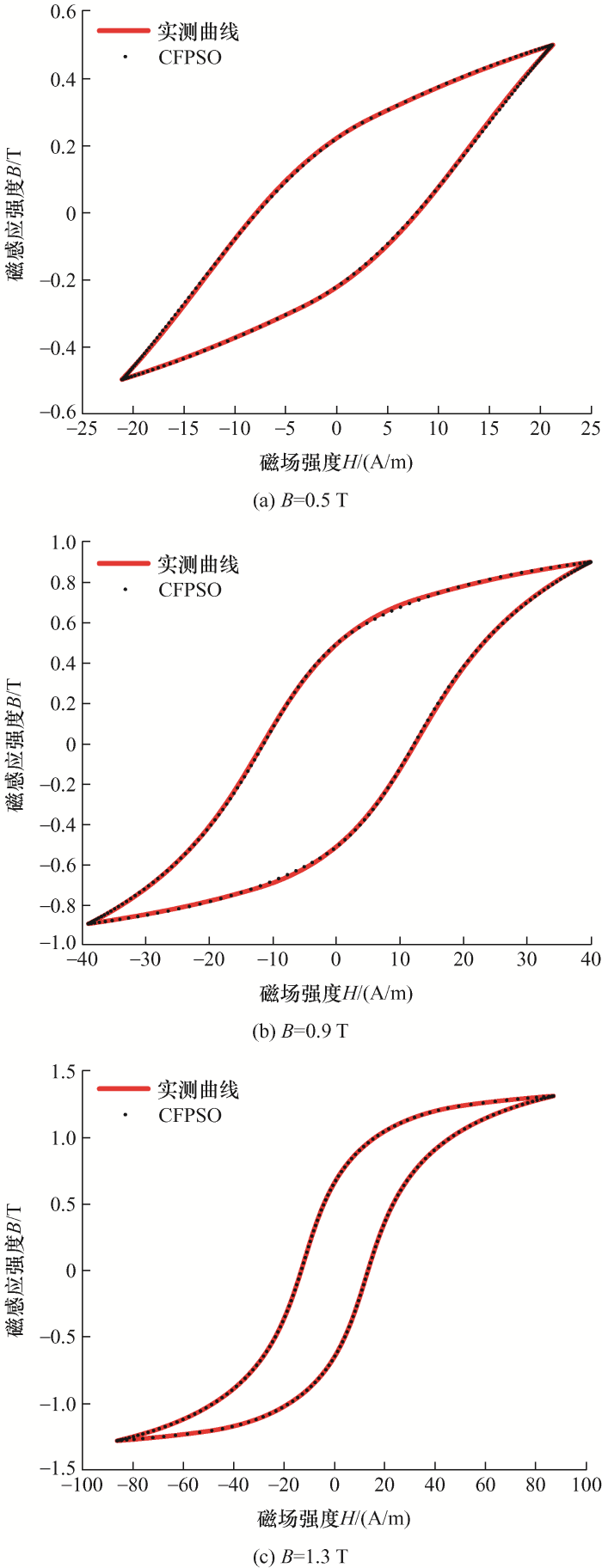
为进一步验证CFPSO算法在不同磁密峰值下的辨识应用效果,图4a 、4b 、4c 给出CFPSO算法分别在0.5 T、0.9 T、1.3 T下的局部磁滞曲线拟合图,采用CFPSO优化方法在各磁密峰值下的局部磁滞曲线跟踪效果依旧较好,误差较小。
图4
4.2 基于CFPSO算法的动态磁滞模型参数辨识
静态磁滞模型通常应用在低频工况环境,往往忽略了涡流损耗、异常损耗等动态损耗。但是由于变压器等电磁设备的铁心往往工作在交变磁场环境,且环境中将包含诸多谐波因素,采用静态磁滞模型进行模拟应用存在一定的应用瓶颈。所以,完全有必要针对工程应用中的动态磁滞模型进行参数辨识。
为了进一步验证CFPSO算法在动态磁滞模型参数辨识中的应用效果,需要结合前文所建立的动态磁滞模型,进行7个关键参量的有效辨识。其中,5个参数为静态磁滞模型的参数,剩余2个参数为动态参数,即动态参数k e 和k a 。k e 、k a 一般利用损耗分离法,可通过大量的试验测试结果来提取获得。在动态磁滞模型的参数辨识中,采用CFPSO优化算法进行7个参数的快速寻优,选定的辨识数据来自文献[20 ],辨识结果如表3 所示(工频50 Hz)。对比表3 结果可知,CFPSO算法在J-A动态磁滞模型参数辨识中的应用效果较好,7个辨识参量(M s 、α 、a 、k 、c 、k e 、k a )的辨识误差相对较小,验证了CFPSO优化算法在J-A动态磁滞模型参数辨识中的有效性。
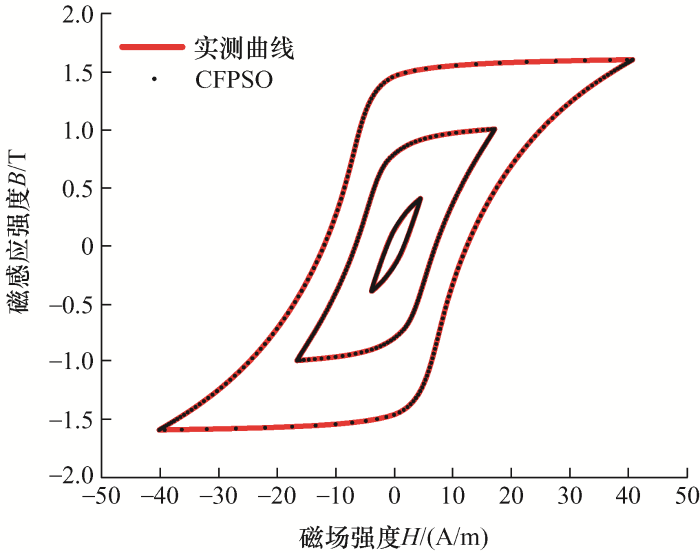
图5 和图6 为采用CFPSO优化算法辨识得到的工频不同磁密峰值下的曲线跟踪效果及其误差结果,其中,辨识结果与实测结果吻合较好。
图5
图5
动态磁滞回线与实测磁滞回线对比(工频50 Hz)
图6
图6
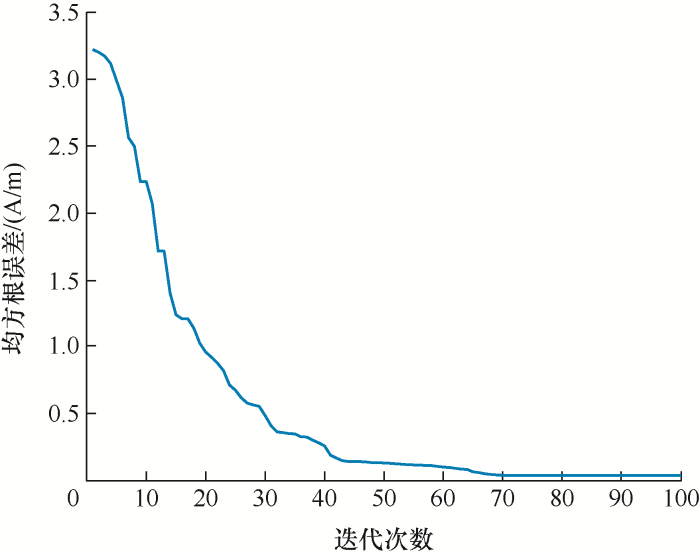
CFPSO优化算法参数寻优中均方根误差随迭代次数变化(B max =1.6 T)
图6 为采用CFPSO优化算法寻优的均方根误差变化趋势,相比于准静态的计算结果,其计算收敛速度稍有下降,这主要是因为动态模型中增加了损耗系数k e 和k a ,迭代收敛的次数将有所增加;同时,动态模型在10~30次迭代后保持较小的均方根误差,体现了动态J-A磁致模型参数辨识的准确性。因此,采用CFPSO优化算法应用于J-A磁滞模型的参数辨识,具有快速计算收敛的优点,且计算精度高,不易陷入局部最优解。
5 结论
针对传统PSO算法于J-A磁滞模型参数辨识应用,存在的辨识准确率低、时间长等问题,提出一种基于收缩因子改进的PSO优化算法,得到如下结论。
(1) 提出改进基于收缩因子的PSO优化算法,不改变惯性因子从而避免减少种群多样性,有利于提升计算收敛速度,防止陷入局部最优解,可实现J-A磁滞模型快速且准确的参数辨识。
(2) 所提算法在静态磁滞、动态磁滞辨识中均具有较好的辨识准确性。同时,在考虑动态损耗因素下的磁滞模型辨识,无需单独求解实际的动态参数,采用增加2个动态参数的辨识方法,可缩短辨识的迭代次数,保证迭代精度。
(3) 相比于静态磁滞模型的辨识,动态磁滞模型的参数辨识,可保证7个参数同时寻优,虽然相比静态辨识结果存在误差增大的现象,但仍然具有足够的计算精准度,且迭代计算次数相对较优。
参考文献
View Option
[1]
王洋 . 变压器铁芯剩磁预测研究 [D]. 济南 : 山东大学 , 2017 .
[本文引用: 1]
WANG Yang Research on residual flux prediction of the transformer [D]. Jinan : Shandong University , 2017 .
[本文引用: 1]
[2]
JIN Shuhan Modeling of one dimensional hysteresis properties based on Preisach model
[J]. IOP Conference Series:Earth and Environmental Science , 2020 , 440 (4 ):042069 .
DOI:10.1088/1755-1315/440/4/042069
[本文引用: 1]
The B-based Preisach model, which employs magnetic induction intensity B as input and magnetic field intensity H as output, is proposed to overcome limitations and imperfections of the classical Preisach model (H-based model). Based on measured data of major hysteresis loop, first order reversal curves were created by numerical method, and Everett function was then established. Thus B-based model can be realized. Finally, the B-based and H-based model is applied to simulate the concentric hysteresis loops of soft magnetic materials and the high order reversal curves of hard magnetic materials, respectively. And the validity and accuracy of B-based Preisach model are verified by comparing with the experimental data measured under DC conditions.
[3]
刘小娜 . 基于Preisach模型的软磁材料磁滞特性模拟研究 [D]. 北京 : 华北电力大学 , 2020 .
[本文引用: 1]
LIU Xiaona Research on the hysteretic modeling of soft magnetic materials based on the Preisach model [D]. Beijing : North China Electric Power University , 2020 .
[本文引用: 1]
[4]
SODA N ENOKIZONO M E&S hysteresis model for two-dimensional magnetic properties
[J]. Journal of Magnetism & Magnetic Materials , 2000 ,215:626 -628 .
[本文引用: 1]
[5]
赵越 . J-A磁滞模型的仿真与实验研究 [D]. 北京 : 华北电力大学 , 2019 .
[本文引用: 1]
ZHAO Yue Simulation and experimental research of J-A hysteresis model [D]. Beijing : North China Electric Power University , 2019 .
[本文引用: 1]
[6]
SCHNEIDER S C GEDNEY D S JOYCE M S et al. Measurement and exponential model of ferromagnetic hysteresis
[J]. Physica B:Physics of Condensed Matter , 2019 ,570:259 -265 .
[本文引用: 1]
[7]
SILVA D CAMPOS D A model for the hysteresis curves of soft magnetic materials
[J]. Materials Science Forum , 2012 ,1994:727 -728 .
[本文引用: 1]
[8]
李宜伦 , 张异殊 , 宋光 . 基于改进鲸鱼算法的电流互感器J-A模型磁滞参数识别
[J]. 中国电力 , 2022 , 55 (2 ):190 -199 .
[本文引用: 1]
LI Yilun ZHANG Yishu SONG Guang Hysteresis parameter identification of J-A model current transformer based on improved whale algorithm
[J]. Electric Power , 2022 , 55 (2 ):190 -199 .
[本文引用: 1]
[9]
李晓萍 , 彭青顺 , 李金保 , 等 . 变压器铁芯磁滞模型参数辨识
[J]. 电网技术 , 2012 , 36 (2 ):200 -205 .
[本文引用: 1]
LI Xiaoping PENG Qingshun LI Jinbao et al. Parameter identification of hysteresis loop model for transformer core
[J]. Power System Technology , 2012 , 36 (2 ):200 -205 .
[本文引用: 1]
[10]
郝晓亮 , 叶美盈 . 基于粒子群优化算法的Jiles-Atherton磁滞模型参数计算
[J]. 浙江师范大学学报 , 2015 , 38 (2 ):133 -141 .
[本文引用: 1]
HAO Xiaoliang YE Meiying Parameter calculation of the Jiles-Atherton hysteresis model using particle swarm optimization algorithm
[J]. Journal of Zhejiang Normal University , 2015 , 38 (2 ):133 -141 .
[本文引用: 1]
[11]
董张卓 , 伍弘 , 尚腾 , 等 . 铁磁元件J-A磁滞模型参数辨识
[J]. 电气应用 , 2017 , 36 (9 ):22 -28 .
[本文引用: 1]
DONG Zhangzhuo WU Hong SHANG Teng et al. Parameter identification of J-A hysteresis model for ferromagnetic elements
[J]. Electrotechnical Application , 2017 , 36 (9 ):22 -28 .
[本文引用: 1]
[12]
CHWASTEK K Modelling of dynamic hysteresis loops using the Jiles-Atherton approach
[J]. Mathematical Modelling of Systems , 2009 , 15 (1 ):95 -105 .
[本文引用: 2]
[13]
BRANKO K IOAN D ALENKA M et al. Harmonic analysis and modelling of magnetisation process in soft ferromagnetic material
[J]. FACTA UNIVERSITATIS Series:Electronics and Energetics , 2017 , 30 (1 ):121 -136 .
DOI:10.2298/FUEE1701121K
URL
[本文引用: 2]
The aim of this paper is to present a research of magnetic hysteresis loops\n of a toroidal ferromagnetic core made of electrical steel. The experimental\n results of induced voltage, magnetic induction and hysteresis loop obtained\n at different frequencies of the sinusoidal excitation magnetic field have\n been presented. The harmonic content of the induced voltage and magnetic\n induction have been calculated using Fast Fourier Transformation. Observed\n variation of higher harmonics with frequency has been correlated to the\n mechanism of magnetic domain walls damping. A variation of harmonics of the\n magnetic induction with the amplitude of the excitation magnetic field has\n been analysed and a proper mathematical model has been proposed. Furthermore,\n the influence of the triangularly shaped excitation magnetic field and the\n distorted shape excitation that produces sinusoidal induction on the shape of\n hysteresis loop and harmonic content of the induced voltage and the magnetic\n induction has been analysed and discussed.
[14]
JILES D C Frequency dependence of hysteresis curves in conducting magnetic materials
[J]. IEEE Transactions on Magnetics , 1994 , 75 (10 ):5511 -5511 .
[本文引用: 1]
[15]
胡康 . 一种改进粒子群算法及其应用 [D]. 北京 : 华北电力大学 , 2019 .
[本文引用: 1]
HU Kang An improved particle swarm optimization algorithm and its application [D]. Beijing : North China Electric Power University , 2019 .
[本文引用: 1]
[16]
鲁欣欣 , 王淮冬 . 遗传算法和粒子群算法的现状及发展策略研究
[J]. 无线互联科技 , 2021 , 18 (21 ):108 -109 .
[本文引用: 1]
LU Xinxin WANG Huaidong Study on the current status and development strategy of genetic algorithm and particle group algorithms
[J]. Wireless Internet Technology , 2021 , 18 (21 ):108 -109 .
[本文引用: 1]
[17]
LIU Z LU J ZHU P Lightweight design of automotive composite bumper system using modified particle swarm optimizer
[J]. Composite Structures , 2016 ,140:630 -643 .
[本文引用: 1]
[18]
王生亮 , 刘根友 . 一种非线性动态自适应惯性权重PSO算法
[J]. 计算机仿真 , 2021 , 38 (4 ):249 -253 ,451.
[本文引用: 1]
WANG Shengliang LIU Genyou A nonlinear dynamic adaptive inertial weight particle swarm optimization
[J]. Computer Simulation , 2021 , 38 (4 ):249 -253 ,451.
[本文引用: 1]
[19]
赵越 , 李琳 , 刘任 . 基于人工鱼群与L-M混合算法的J-A磁滞模型参数提取
[J]. 华北电力大学学报 , 2018 , 45 (6 ):21 -27 ,51.
[本文引用: 1]
ZHAO Yue LI Lin LIU Ren J-A hysteresis model parameter extraction based on artificial fish and L-M hybrid algorithm [D]. Journal of North China Electric Power University , 2018 , 45 (6 ):21 -27 ,51.
[本文引用: 1]
[20]
赵越 , 李琳 , 刘任 , 等 . 基于损耗统计理论的动态J-A磁滞模型
[J]. 电工电能新技术 , 2019 , 38 (5 ):90 -96 .
DOI:10.12067/ATEEE1806077
[本文引用: 1]
针对传统基于损耗分离经验法的动态J-A模型缺乏物理基础、精度较低的问题,通过借鉴磁场强度分离的理念,将损耗统计理论引入原始静态J-A模型,提出了一种基于损耗统计理论的新型动态J-A模型。其中,静态磁场强度分量利用静态J-A模型求解,而涡流及剩余磁场强度分量则根据损耗统计理论推导而得。通过将计算结果与测量结果对比,表明本文所提动态J-A模型相比于传统基于损耗分离经验法的动态J-A模型精度较高,模型参数物理意义更为明确。
ZHAO Yue LI Lin LIU Ren et al. New dynamic hysteresis J-A model based on statistical theory of losses
[J]. Advanced Technology of Electrical Engineering and Energy , 2019 , 38 (5 ):90 -96 .
DOI:10.12067/ATEEE1806077
[本文引用: 1]
The traditional dynamic J-A model based on the empirical method of loss separation lacks physical foundation and has low accuracy. Referring to the idea of magnetic field intensity separation, the statistical theory of losses is introduced into the original static J-A model. Therefore, a new dynamic J-A model based on the statistical theory of losses is proposed. Among them, the static J-A model is used to solve the static magnetic field strength component, and the eddy current and anomalous magnetic field strength components are derived from the statistical theory of losses. Comparing the calculated results with the measured results, the dynamic J-A model proposed in this paper is more accurate than the traditional dynamic J-A model, which is based on the empirical method of loss separation. In terms of physical meaning of the parameters, the dynamic J-A model proposed in this paper is more explicit than the traditional one.
1
2017
... 在变压器铁心磁滞模型[1 ] 的理论研究方面,形成了包括磁滞Preisach模型[2 -3 ] 、期望损失(Expected shortfall,E&S)模型[4 ] 、磁化(Jiles-Atherton,J-A)模型[5 ] 等理论模型.其中,由于J-A模型具有清晰的物理含义,能够较好地描述B-H 曲线的非线性关系;同时,该模型所需辨识参数相对少,仿真运行时间较短,在现阶段的工程研究及应用中推广较好[6 ] . ...
1
2017
... 在变压器铁心磁滞模型[1 ] 的理论研究方面,形成了包括磁滞Preisach模型[2 -3 ] 、期望损失(Expected shortfall,E&S)模型[4 ] 、磁化(Jiles-Atherton,J-A)模型[5 ] 等理论模型.其中,由于J-A模型具有清晰的物理含义,能够较好地描述B-H 曲线的非线性关系;同时,该模型所需辨识参数相对少,仿真运行时间较短,在现阶段的工程研究及应用中推广较好[6 ] . ...
Modeling of one dimensional hysteresis properties based on Preisach model
1
2020
... 在变压器铁心磁滞模型[1 ] 的理论研究方面,形成了包括磁滞Preisach模型[2 -3 ] 、期望损失(Expected shortfall,E&S)模型[4 ] 、磁化(Jiles-Atherton,J-A)模型[5 ] 等理论模型.其中,由于J-A模型具有清晰的物理含义,能够较好地描述B-H 曲线的非线性关系;同时,该模型所需辨识参数相对少,仿真运行时间较短,在现阶段的工程研究及应用中推广较好[6 ] . ...
1
2020
... 在变压器铁心磁滞模型[1 ] 的理论研究方面,形成了包括磁滞Preisach模型[2 -3 ] 、期望损失(Expected shortfall,E&S)模型[4 ] 、磁化(Jiles-Atherton,J-A)模型[5 ] 等理论模型.其中,由于J-A模型具有清晰的物理含义,能够较好地描述B-H 曲线的非线性关系;同时,该模型所需辨识参数相对少,仿真运行时间较短,在现阶段的工程研究及应用中推广较好[6 ] . ...
1
2020
... 在变压器铁心磁滞模型[1 ] 的理论研究方面,形成了包括磁滞Preisach模型[2 -3 ] 、期望损失(Expected shortfall,E&S)模型[4 ] 、磁化(Jiles-Atherton,J-A)模型[5 ] 等理论模型.其中,由于J-A模型具有清晰的物理含义,能够较好地描述B-H 曲线的非线性关系;同时,该模型所需辨识参数相对少,仿真运行时间较短,在现阶段的工程研究及应用中推广较好[6 ] . ...
E&S hysteresis model for two-dimensional magnetic properties
1
2000
... 在变压器铁心磁滞模型[1 ] 的理论研究方面,形成了包括磁滞Preisach模型[2 -3 ] 、期望损失(Expected shortfall,E&S)模型[4 ] 、磁化(Jiles-Atherton,J-A)模型[5 ] 等理论模型.其中,由于J-A模型具有清晰的物理含义,能够较好地描述B-H 曲线的非线性关系;同时,该模型所需辨识参数相对少,仿真运行时间较短,在现阶段的工程研究及应用中推广较好[6 ] . ...
1
2019
... 在变压器铁心磁滞模型[1 ] 的理论研究方面,形成了包括磁滞Preisach模型[2 -3 ] 、期望损失(Expected shortfall,E&S)模型[4 ] 、磁化(Jiles-Atherton,J-A)模型[5 ] 等理论模型.其中,由于J-A模型具有清晰的物理含义,能够较好地描述B-H 曲线的非线性关系;同时,该模型所需辨识参数相对少,仿真运行时间较短,在现阶段的工程研究及应用中推广较好[6 ] . ...
1
2019
... 在变压器铁心磁滞模型[1 ] 的理论研究方面,形成了包括磁滞Preisach模型[2 -3 ] 、期望损失(Expected shortfall,E&S)模型[4 ] 、磁化(Jiles-Atherton,J-A)模型[5 ] 等理论模型.其中,由于J-A模型具有清晰的物理含义,能够较好地描述B-H 曲线的非线性关系;同时,该模型所需辨识参数相对少,仿真运行时间较短,在现阶段的工程研究及应用中推广较好[6 ] . ...
Measurement and exponential model of ferromagnetic hysteresis
1
2019
... 在变压器铁心磁滞模型[1 ] 的理论研究方面,形成了包括磁滞Preisach模型[2 -3 ] 、期望损失(Expected shortfall,E&S)模型[4 ] 、磁化(Jiles-Atherton,J-A)模型[5 ] 等理论模型.其中,由于J-A模型具有清晰的物理含义,能够较好地描述B-H 曲线的非线性关系;同时,该模型所需辨识参数相对少,仿真运行时间较短,在现阶段的工程研究及应用中推广较好[6 ] . ...
A model for the hysteresis curves of soft magnetic materials
1
2012
... 但是,现阶段J-A模型的参数辨识,依旧需要同时实现包含饱和磁化强度M s 、磁畴间耦合的平均场系数α 、无磁滞磁化曲线的形状系数a 、钉扎常数k 、可逆磁化系数c 等参数的有效辨识,在缺乏良好的全局寻优、局部寻优智能算法的情况下,其计算量大,计算精度低,且容易陷入局部最优解[7 ] .在J-A模型参数辨识的算法研究中,学者们进行了一系列的算法优化探索.文献[8 ]提出改进鲸鱼算法辨识J-A模型参数,并通过仿真验证了该方法的有效性.虽然该方法不易陷入局部最优解,但辨识步骤繁多,导致收敛速度变慢.文献[9 ]对模型的5个参数单独优化,虽然计算简便且结果精度较高,但步骤繁琐且收敛较慢.文献[10 ]采用粒子群优化算法对不同噪声环境下J-A磁滞模型的参数进行了识别,该方法在含噪声情况下仍能得到较高的参数精度,但迭代次数过多,仿真时间过长. ...
基于改进鲸鱼算法的电流互感器J-A模型磁滞参数识别
1
2022
... 但是,现阶段J-A模型的参数辨识,依旧需要同时实现包含饱和磁化强度M s 、磁畴间耦合的平均场系数α 、无磁滞磁化曲线的形状系数a 、钉扎常数k 、可逆磁化系数c 等参数的有效辨识,在缺乏良好的全局寻优、局部寻优智能算法的情况下,其计算量大,计算精度低,且容易陷入局部最优解[7 ] .在J-A模型参数辨识的算法研究中,学者们进行了一系列的算法优化探索.文献[8 ]提出改进鲸鱼算法辨识J-A模型参数,并通过仿真验证了该方法的有效性.虽然该方法不易陷入局部最优解,但辨识步骤繁多,导致收敛速度变慢.文献[9 ]对模型的5个参数单独优化,虽然计算简便且结果精度较高,但步骤繁琐且收敛较慢.文献[10 ]采用粒子群优化算法对不同噪声环境下J-A磁滞模型的参数进行了识别,该方法在含噪声情况下仍能得到较高的参数精度,但迭代次数过多,仿真时间过长. ...
Hysteresis parameter identification of J-A model current transformer based on improved whale algorithm
1
2022
... 但是,现阶段J-A模型的参数辨识,依旧需要同时实现包含饱和磁化强度M s 、磁畴间耦合的平均场系数α 、无磁滞磁化曲线的形状系数a 、钉扎常数k 、可逆磁化系数c 等参数的有效辨识,在缺乏良好的全局寻优、局部寻优智能算法的情况下,其计算量大,计算精度低,且容易陷入局部最优解[7 ] .在J-A模型参数辨识的算法研究中,学者们进行了一系列的算法优化探索.文献[8 ]提出改进鲸鱼算法辨识J-A模型参数,并通过仿真验证了该方法的有效性.虽然该方法不易陷入局部最优解,但辨识步骤繁多,导致收敛速度变慢.文献[9 ]对模型的5个参数单独优化,虽然计算简便且结果精度较高,但步骤繁琐且收敛较慢.文献[10 ]采用粒子群优化算法对不同噪声环境下J-A磁滞模型的参数进行了识别,该方法在含噪声情况下仍能得到较高的参数精度,但迭代次数过多,仿真时间过长. ...
变压器铁芯磁滞模型参数辨识
1
2012
... 但是,现阶段J-A模型的参数辨识,依旧需要同时实现包含饱和磁化强度M s 、磁畴间耦合的平均场系数α 、无磁滞磁化曲线的形状系数a 、钉扎常数k 、可逆磁化系数c 等参数的有效辨识,在缺乏良好的全局寻优、局部寻优智能算法的情况下,其计算量大,计算精度低,且容易陷入局部最优解[7 ] .在J-A模型参数辨识的算法研究中,学者们进行了一系列的算法优化探索.文献[8 ]提出改进鲸鱼算法辨识J-A模型参数,并通过仿真验证了该方法的有效性.虽然该方法不易陷入局部最优解,但辨识步骤繁多,导致收敛速度变慢.文献[9 ]对模型的5个参数单独优化,虽然计算简便且结果精度较高,但步骤繁琐且收敛较慢.文献[10 ]采用粒子群优化算法对不同噪声环境下J-A磁滞模型的参数进行了识别,该方法在含噪声情况下仍能得到较高的参数精度,但迭代次数过多,仿真时间过长. ...
Parameter identification of hysteresis loop model for transformer core
1
2012
... 但是,现阶段J-A模型的参数辨识,依旧需要同时实现包含饱和磁化强度M s 、磁畴间耦合的平均场系数α 、无磁滞磁化曲线的形状系数a 、钉扎常数k 、可逆磁化系数c 等参数的有效辨识,在缺乏良好的全局寻优、局部寻优智能算法的情况下,其计算量大,计算精度低,且容易陷入局部最优解[7 ] .在J-A模型参数辨识的算法研究中,学者们进行了一系列的算法优化探索.文献[8 ]提出改进鲸鱼算法辨识J-A模型参数,并通过仿真验证了该方法的有效性.虽然该方法不易陷入局部最优解,但辨识步骤繁多,导致收敛速度变慢.文献[9 ]对模型的5个参数单独优化,虽然计算简便且结果精度较高,但步骤繁琐且收敛较慢.文献[10 ]采用粒子群优化算法对不同噪声环境下J-A磁滞模型的参数进行了识别,该方法在含噪声情况下仍能得到较高的参数精度,但迭代次数过多,仿真时间过长. ...
基于粒子群优化算法的Jiles-Atherton磁滞模型参数计算
1
2015
... 但是,现阶段J-A模型的参数辨识,依旧需要同时实现包含饱和磁化强度M s 、磁畴间耦合的平均场系数α 、无磁滞磁化曲线的形状系数a 、钉扎常数k 、可逆磁化系数c 等参数的有效辨识,在缺乏良好的全局寻优、局部寻优智能算法的情况下,其计算量大,计算精度低,且容易陷入局部最优解[7 ] .在J-A模型参数辨识的算法研究中,学者们进行了一系列的算法优化探索.文献[8 ]提出改进鲸鱼算法辨识J-A模型参数,并通过仿真验证了该方法的有效性.虽然该方法不易陷入局部最优解,但辨识步骤繁多,导致收敛速度变慢.文献[9 ]对模型的5个参数单独优化,虽然计算简便且结果精度较高,但步骤繁琐且收敛较慢.文献[10 ]采用粒子群优化算法对不同噪声环境下J-A磁滞模型的参数进行了识别,该方法在含噪声情况下仍能得到较高的参数精度,但迭代次数过多,仿真时间过长. ...
Parameter calculation of the Jiles-Atherton hysteresis model using particle swarm optimization algorithm
1
2015
... 但是,现阶段J-A模型的参数辨识,依旧需要同时实现包含饱和磁化强度M s 、磁畴间耦合的平均场系数α 、无磁滞磁化曲线的形状系数a 、钉扎常数k 、可逆磁化系数c 等参数的有效辨识,在缺乏良好的全局寻优、局部寻优智能算法的情况下,其计算量大,计算精度低,且容易陷入局部最优解[7 ] .在J-A模型参数辨识的算法研究中,学者们进行了一系列的算法优化探索.文献[8 ]提出改进鲸鱼算法辨识J-A模型参数,并通过仿真验证了该方法的有效性.虽然该方法不易陷入局部最优解,但辨识步骤繁多,导致收敛速度变慢.文献[9 ]对模型的5个参数单独优化,虽然计算简便且结果精度较高,但步骤繁琐且收敛较慢.文献[10 ]采用粒子群优化算法对不同噪声环境下J-A磁滞模型的参数进行了识别,该方法在含噪声情况下仍能得到较高的参数精度,但迭代次数过多,仿真时间过长. ...
铁磁元件J-A磁滞模型参数辨识
1
2017
... J-A静态磁滞模型[11 ] ,主要是忽略了动态损耗因素的影响,其磁化强度M 可分为可逆分量M rev 、不可逆分量M irr ,具体表达式为 ...
Parameter identification of J-A hysteresis model for ferromagnetic elements
1
2017
... J-A静态磁滞模型[11 ] ,主要是忽略了动态损耗因素的影响,其磁化强度M 可分为可逆分量M rev 、不可逆分量M irr ,具体表达式为 ...
Modelling of dynamic hysteresis loops using the Jiles-Atherton approach
2
2009
... 式中,δ M 为防止出现非物理解的系数[12 -13 ] ;δ H 为方向系数,其取值范围为 ...
... 静态磁滞模型属于一类相对较为理想的数学模型,其简化了动态损耗因素的影响.为了更好地模拟不同工况下的动态磁滞特性,在此需要对静态磁滞模型进行修正[12 ] . ...
Harmonic analysis and modelling of magnetisation process in soft ferromagnetic material
2
2017
... 式中,δ M 为防止出现非物理解的系数[12 -13 ] ;δ H 为方向系数,其取值范围为 ...
... 在考虑动态损耗的情况下,需要对静态模型进行修正[13 ] .其中,式(4)的能量守恒方程需要修正为 ...
Frequency dependence of hysteresis curves in conducting magnetic materials
1
1994
... 基于铁心损耗分离理论和场分离理论[14 ] ,参照式(16)中磁场强度的数学关系,考虑动态损耗因素下各磁场强度关系式可表示为 ...
1
2019
... 粒子群优化算法[15 -16 ] ,最初被应用于模拟鸟群的觅食过程,因其具有较好的寻优效果,近年来备受学者们的青睐. ...
1
2019
... 粒子群优化算法[15 -16 ] ,最初被应用于模拟鸟群的觅食过程,因其具有较好的寻优效果,近年来备受学者们的青睐. ...
遗传算法和粒子群算法的现状及发展策略研究
1
2021
... 粒子群优化算法[15 -16 ] ,最初被应用于模拟鸟群的觅食过程,因其具有较好的寻优效果,近年来备受学者们的青睐. ...
Study on the current status and development strategy of genetic algorithm and particle group algorithms
1
2021
... 粒子群优化算法[15 -16 ] ,最初被应用于模拟鸟群的觅食过程,因其具有较好的寻优效果,近年来备受学者们的青睐. ...
Lightweight design of automotive composite bumper system using modified particle swarm optimizer
1
2016
... 式中,v 为粒子的速度;i =1,2,3,…,n ,n 为粒子数量;j =1,2,3,…,m ,m 为粒子的维数;t 为当前迭代代数;ω 为惯性因子[17 ] ;pbest为第i 个粒子自身寻到的最优位置;gbest为粒子群中寻到的最优位置;x 为粒子的位置;c 1 、c 2 为认知因子和社会因子;r 1 、r 2 为均匀分布在(0,1)区间的随机数. ...
一种非线性动态自适应惯性权重PSO算法
1
2021
... 惯性权重PSO(Inertia weight particle swarm optimization,IwPSO)算法[18 ] ,是一种改进的PSO智能算法.在引入惯性因子的基础上,采用线性递减权值策略动态调整惯性因子,从而实现快速寻优.该方法可由式(20)~(22)表示 ...
A nonlinear dynamic adaptive inertial weight particle swarm optimization
1
2021
... 惯性权重PSO(Inertia weight particle swarm optimization,IwPSO)算法[18 ] ,是一种改进的PSO智能算法.在引入惯性因子的基础上,采用线性递减权值策略动态调整惯性因子,从而实现快速寻优.该方法可由式(20)~(22)表示 ...
基于人工鱼群与L-M混合算法的J-A磁滞模型参数提取
1
2018
... 为了验证所提基于收缩因子改进PSO优化算法的有效性,在静态J-A磁滞模型的辨识过程中,参照文献[19 ]给定的一组实测参数,作为静态J-A磁滞模型辨识的样本数据.分别研究经典PSO算法、IwPSO算法、CFPSO优化算法对给定实测磁滞曲线的辨识效果评估,并讨论各算法的准确性及快速性.采用各智能算法辨识得到J-A模型参数结果,如表1 所示(该样本数据的磁场强度H 范围设定为-300~300 A/m). ...
1
2018
... 为了验证所提基于收缩因子改进PSO优化算法的有效性,在静态J-A磁滞模型的辨识过程中,参照文献[19 ]给定的一组实测参数,作为静态J-A磁滞模型辨识的样本数据.分别研究经典PSO算法、IwPSO算法、CFPSO优化算法对给定实测磁滞曲线的辨识效果评估,并讨论各算法的准确性及快速性.采用各智能算法辨识得到J-A模型参数结果,如表1 所示(该样本数据的磁场强度H 范围设定为-300~300 A/m). ...
基于损耗统计理论的动态J-A磁滞模型
1
2019
... 为了进一步验证CFPSO算法在动态磁滞模型参数辨识中的应用效果,需要结合前文所建立的动态磁滞模型,进行7个关键参量的有效辨识.其中,5个参数为静态磁滞模型的参数,剩余2个参数为动态参数,即动态参数k e 和k a .k e 、k a 一般利用损耗分离法,可通过大量的试验测试结果来提取获得.在动态磁滞模型的参数辨识中,采用CFPSO优化算法进行7个参数的快速寻优,选定的辨识数据来自文献[20 ],辨识结果如表3 所示(工频50 Hz).对比表3 结果可知,CFPSO算法在J-A动态磁滞模型参数辨识中的应用效果较好,7个辨识参量(M s 、α 、a 、k 、c 、k e 、k a )的辨识误差相对较小,验证了CFPSO优化算法在J-A动态磁滞模型参数辨识中的有效性. ...
New dynamic hysteresis J-A model based on statistical theory of losses
1
2019
... 为了进一步验证CFPSO算法在动态磁滞模型参数辨识中的应用效果,需要结合前文所建立的动态磁滞模型,进行7个关键参量的有效辨识.其中,5个参数为静态磁滞模型的参数,剩余2个参数为动态参数,即动态参数k e 和k a .k e 、k a 一般利用损耗分离法,可通过大量的试验测试结果来提取获得.在动态磁滞模型的参数辨识中,采用CFPSO优化算法进行7个参数的快速寻优,选定的辨识数据来自文献[20 ],辨识结果如表3 所示(工频50 Hz).对比表3 结果可知,CFPSO算法在J-A动态磁滞模型参数辨识中的应用效果较好,7个辨识参量(M s 、α 、a 、k 、c 、k e 、k a )的辨识误差相对较小,验证了CFPSO优化算法在J-A动态磁滞模型参数辨识中的有效性. ...