1 引言
永磁同步电机(Permanent magnet synchronous motor,PMSM)以其低惯性、高效率、轻量化等优点,在工业领域引起了广泛的关注[1 ⇓ ⇓ -4 ] 。对于永磁同步电机驱动的无传感器矢量控制(Field orientation control,FOC),需要使用转子位置编码器或高精度传感器获取转子的位置和速度。但是传感器的安装成本较高,导致设备复杂性的增加和机械鲁棒性的降低。为了解决以上问题,一种无传感器矢量控制技术被应用于估计转子的位置和速度[5 ⇓ ⇓ -8 ] 。
无传感器矢量控制方法一般可分为两类:利用电机转子凸极效应的高频注入技术和基于观测器的估计方法。常见的估计转子位置和速度的方法有模型参考自适应系统(Model reference adaptive system,MRAS)、非线性观测器和滑模观测器(Sliding model observer,SMO)[9 ⇓ ⇓ -12 ] 。MRAS在低速时具有较好的稳定性,但是需要调节器和滤波器,增加了系统复杂性[13 ] 。滑模控制具有较好的抗干扰性和鲁棒性,且数学模型较为简单,易于构建[14 -15 ] ,被广泛应用于研究领域。
然而,滑模控制的缺点是由算法的高频切换引起的抖振现象。许多学者针对减小或消除抖振现象提出了不同的方法。文献[16 ]提出了一种自适应一阶滑模控制器(Sliding mode controller,SMC),其中包括设计各种趋近律方法、滑动面、高阶SMC和复合SMC。许多SMC的变种已被提出,超螺旋滑模控制(Super twisting sliding mode controller,STSMC)技术引起了广泛关注,特别是对于控制律出现在滑动变量一阶导数中的系统。文献[17 ]提出了一种实时STSMC来控制电机转子磁链和机械转速,并提出了一种一阶SMO来估计磁链和负载转矩,在实现无位置传感器和减少抖振方面发挥了关键的作用。文献[18 ]结合了STSMC和积分SMC方案的属性,提出了一种基于积分超螺旋滑模控制的感应电机无传感器预测电流控制,解决了传统PI控制鲁棒性差的缺点。文献[19 ]以扩展卡尔曼滤波(Extended Kalman filter,EKF)算法为基础,通过EKF得到转子的位置和角速度。该估计算法既不需要机械参数的知识,也不需要转子的初始位置,利用改进滑模控制器取代PI控制器作为电流环调节器,提高了系统性能。
基于以往的研究,本文提出了一种积分超螺旋滑模控制(Integral super twisting SMC,ISTSMC)技术。通过在PMSM矢量控制驱动系统外环用高阶SMC,并结合STSMC PI型曲面的优点,克服一阶滑模控制的缺点,以进一步增强控制系统在外部扰动和故障扰动状况下的鲁棒性和收敛性。在观测器的设计方面,设计了一种分段正弦型的开关函数,极大程度上改善了传统的基于sigmoid函数的滑模观测器系统的抖振缺点,并在滑模观测器上结合扩展卡尔曼滤波器消除高频纹波,对电机转速与位置进行精确在线估计。通过对各种性能指标进行仿真,验证了所提策略的良好稳定性能和跟踪精确性。
2 PMSM数学模型
表贴式PMSM经三相静止-两相静止后,PMSM的定子电压方程为
(1) $\left\{ \begin{align} & {{u}_{\alpha }}={{L}_{s}}\frac{d{{i}_{\alpha }}}{dt}+R{{i}_{\alpha }}+{{e}_{\alpha }} \\ & {{u}_{\beta }}={{L}_{s}}\frac{d{{i}_{\beta }}}{dt}+R{{i}_{\beta }}+{{e}_{\beta }} \\ \end{align} \right.$
式中,uα 、uβ 为αβ 轴电压;iα 、iβ 为αβ 轴电流;L s 为定子电感。
(2) $\left\{ \begin{align} & {{e}_{\alpha }}=-{{\psi }_{f}}{{\omega }_{m}}\sin \theta \\ & {{e}_{\beta }}={{\psi }_{f}}{{\omega }_{m}}\cos \theta \\ \end{align} \right.$
式中,eα 、eβ 为α -β 坐标系下反电动势分量;ψ f 为永磁体磁链;ω m 为电机的机械角速度;θ 为转子位置角。
(3) $\left\{ \begin{align} & {{u}_{d}}=R{{i}_{d}}+{{L}_{s}}\frac{d{{i}_{d}}}{dt}-{{p}_{n}}{{\omega }_{m}}{{L}_{s}}{{i}_{q}} \\ & {{u}_{q}}=R{{i}_{q}}+{{L}_{s}}\frac{d{{i}_{q}}}{dt}-{{p}_{n}}{{\omega }_{m}}{{L}_{s}}{{i}_{d}}+{{p}_{n}}{{\omega }_{m}}{{\psi }_{f}} \\ & J\frac{d{{\omega }_{\mathrm{m}}}}{dt}=\frac{3}{2}{{p}_{n}}{{\psi }_{f}}{{i}_{q}}-{{T}_{L}}-B{{\omega }_{\mathrm{m}}} \\ \end{align} \right.$
式中,p n 为极对数;J 为转动惯量;B 为阻尼系数;T L 为负载转矩。
对于表贴式PMSM,为了获得较好的控制效果,采用id =0的转子磁场定向控制,通过对速度环设计滑模控制器代替传统PI控制器,对式(3)进行改写为
(4) $\left\{ \begin{align} & \frac{d{{i}_{q}}}{dt}=\frac{1}{{{L}_{s}}}(-R{{i}_{q}}-{{p}_{n}}{{\psi }_{f}}{{\omega }_{m}}+{{u}_{q}}) \\ & \frac{d{{\omega }_{m}}}{dt}=\frac{1}{J}(-{{T}_{L}}+\frac{3}{2}{{p}_{n}}{{\psi }_{f}}{{i}_{q}}) \\ \end{align} \right.$
3 滑模控制器设计
3.1 一阶滑模控制(SMC)
(5) $\left\{ \begin{align} & {{x}_{1}}={{\omega }_{ref}}-{{\omega }_{m}} \\ & {{x}_{2}}={{{\dot{x}}}_{1}}=-{{{\dot{\omega }}}_{m}} \\ \end{align} \right.$
(6) $\left\{ \begin{align} & {{{\dot{x}}}_{1}}=-{{{\dot{\omega }}}_{m}}=\frac{1}{J}\left( {{T}_{L}}-\frac{3{{p}_{n}}{{\psi }_{f}}{{i}_{q}}}{2} \right) \\ & {{{\dot{x}}}_{2}}=-{{{\ddot{\omega }}}_{m}}=-\frac{3{{p}_{n}}{{\psi }_{f}}{{{\dot{i}}}_{q}}}{2J} \\ \end{align} \right.$
定义${{u}_{\mathrm{SMC}}}={{\dot{i}}_{\mathrm{qSMC}}}$ D =3p n ψ f /2J ,则式(6)可变为
(7) $\left[\begin{array}{l}\dot{x}_{1} \\\dot{x}_{2}\end{array}\right]=\left[\begin{array}{ll}0 & 1 \\0 & 0\end{array}\right]\left[\begin{array}{l}x_{1} \\x_{2}\end{array}\right]+\left[\begin{array}{c}0 \\-D\end{array}\right] u_{\mathrm{SMC}}$
(8) ${{S}_{1}}=e(t)=c{{x}_{1}}+{{x}_{2}}$
(9) ${{\dot{S}}_{1}}=\dot{e}(t)=c{{\dot{x}}_{1}}+{{\dot{x}}_{2}}=c{{x}_{2}}+{{\dot{x}}_{2}}=c{{x}_{2}}-D{{u}_{\mathrm{SMC}}}$
为了使PMSM具有较好的动态效果,采用指数趋近律,则SMC控制器的表达式为
(10) ${{u}_{SMC}}=\frac{1}{D}[c{{x}_{2}}+\varepsilon sgn (s)+qs]$
(11) ${{i}_{q\mathrm{SMC}}}=\frac{1}{D}\int_{0}^{t}{[c{{x}_{2}}+\varepsilon sgn (s)+qs]d\tau }$
式(11)中的积分项可以消除系统的稳态误差,一定程度上提高了鲁棒性。
3.2 积分滑模控制(ISMC)
SMC系统的运动分为两个阶段:滑动阶段和到达阶段,但系统只有在滑动阶段才具有抵抗参数变化和外界扰动的能力,通过消除滑模控制的到达阶段来改善系统的动态性能。基于ISMC理论可得新滑模面为
(12) ${{S}_{2}}=e(t)-\int_{0}^{t}{\gamma e(\tau )d\tau }$
式中,γ 滑模增益为非零正常数。对式(12)进行求导得
(13) ${{\dot{S}}_{2}}=\dot{e}(t)-\gamma e(t)$
(14) ${{\dot{S}}_{2}}=c{{x}_{2}}-D{{u}_{\mathrm{ISMC}}}-\gamma e(t)$
(15) $\begin{matrix} {{u}_{I\mathrm{SMC}}}=\frac{1}{D}[c{{x}_{2}}-\gamma e(t)+\varepsilon sgn (e(t)-\int_{0}^{t}{\gamma e(\tau )d\tau )}+ \\ q(e(t)-\int_{0}^{t}{\gamma e(\tau )d\tau )]\ \ \ \ \ \varepsilon,q>0} \\ \end{matrix}$
(16) $\begin{matrix} {{i}_{q\mathrm{ISMC}}}=\frac{1}{D}\int_{0}^{t}{[c{{x}_{2}}-\gamma e(t)+\varepsilon sgn (e(t)}-\int_{0}^{t}{\gamma e(\tau )d\tau )}+ \\ q(e(t)-\int_{0}^{t}{\gamma e(\tau )d\tau )]d\tau }\ \ \ \ \varepsilon,q>0 \\ \end{matrix}$
3.3 改进积分超螺旋滑模控制(ISTSMC)
为了使控制系统具有ISMC的抗干扰能力,并减少滑模抖动,提出一种将积分滑模控制与超螺旋算法相结合的控制策略。新的控制律将ISMC的等效控制部分与超螺旋滑模控制的不连续控制部分结合,可表示为
(17) ${{u}_{ref}}={{u}_{eq}}+{{u}_{\mathrm{ST}}}$
式中,u eq 为ISMC控制器去掉干扰项的等效部分,则${{u}_{eq}}=\frac{1}{D}[c{{x}_{2}}-\gamma e(t)]$
(18) $\left\{ \begin{align} & {{u}_{\mathrm{ST}}}=\frac{1}{D}[-{{k}_{1}}\sqrt{\left| {{S}_{2}} \right|}sgn ({{S}_{2}})+{{u}_{1}}] \\ & {{{\dot{u}}}_{1}}=-{{k}_{2}}sgn ({{S}_{2}}) \\ \end{align} \right.$
传统超螺旋滑模控制采用的符号函数受高频切换影响较大,改进超螺旋滑模控制采用饱和函数可以更好地解决抖振问题。改进控制器的表达式为
(19) ${{u}_{\mathrm{ST}}}=\frac{1}{D}[-{{k}_{1}}\sqrt{\left| {{S}_{2}} \right|}\mathrm{sat}({{S}_{2}})-{{k}_{2}}\int_{0}^{t}{\mathrm{sat}({{S}_{2}})d\tau }]$
(20) $\left\{ \begin{align} & {{k}_{2}}>\frac{\varphi }{{{k}_{\mathrm{M}}}} \\ & {{k}_{1}}\ge \frac{4\phi {{k}_{\mathrm{M}}}({{k}_{2}}+\varphi )}{k_{\mathrm{m}}^{3}({{k}_{2}}-\varphi )} \\ \end{align} \right.$
式中,φ 、k m 、k M 均大于0。φ 为函数$\Phi $ k M 、k m 为函数µ 处于滑动曲面二阶导数的上、下正界限。
${{\omega }_{m}}$
(21) ${{\ddot{\hat{\omega }}}_{m}}=\Phi (x,t)+\mu (x,t)\dot{u}$
(22) $\begin{matrix} {{u}_{ref}}={{u}_{eq}}+{{u}_{\mathrm{ST}}}=\frac{1}{D}[c{{x}_{2}}-\gamma e(t)]+ \\ \frac{1}{D}[-{{k}_{1}}\sqrt{\left| {{S}_{2}} \right|}\mathrm{sat}({{S}_{2}})-{{k}_{2}}\int_{\ 0}^{\ t}{\mathrm{sat}({{S}_{2}})d\tau }] \\ \end{matrix}$
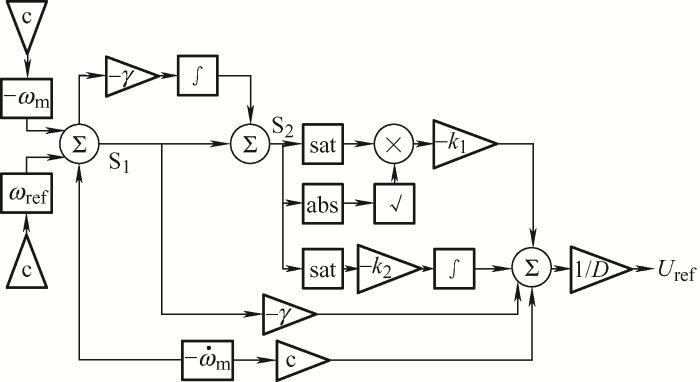
图1
文献[20 ]为超螺旋算法的稳定条件提供了证明。空间向量为
(23) $\left\{ \begin{align} & Z_{\mathrm{ST}}^{\mathrm{T}}=({{Z}_{1}},{{Z}_{2}})=({{k}_{1}}\sqrt{\left| {{S}_{2}} \right|}\mathrm{sat}({{S}_{2}}),{{u}_{1}}) \\ & {{{\dot{Z}}}_{\mathrm{ST}}}=\frac{1}{\sqrt{\left| {{S}_{2}} \right|}}A{{Z}_{\mathrm{ST}}} \\ \end{align} \right.$
(24) $A=\left[ \begin{matrix} -\frac{1}{2}{{k}_{1}} & \frac{1}{2} \\ -{{k}_{2}} & 0 \\\end{matrix} \right]$
为了证明ISTSMC的稳定性,选取V ISTC 作为李雅普诺夫稳定性函数。
(25) ${{V}_{\mathrm{ISTC}}}=Z_{\mathrm{ST}}^{\mathrm{T}}P{{Z}_{\mathrm{ST}}}$
(26) $P=\left[ \begin{matrix} {{p}_{11}} & {{p}_{12}} \\ {{p}_{21}} & {{p}_{22}} \\\end{matrix} \right]$
若使控制器达到稳定,则${{\dot{V}}_{\mathrm{ISTC}}}=\frac{-1}{\sqrt{\left| S \right|}}Z_{\mathrm{ST}}^{\mathrm{T}}Q\dot{Z}_{\mathrm{ST}}^{\mathrm{T}}$
(27) $-{{A}^{\mathrm{T}}}P-PA=Q$
则${{\dot{V}}_{\mathrm{ISTC}}}$
(28) ${{\dot{V}}_{\mathrm{ISTC}}}=\frac{-1}{\sqrt{\left| S \right|}}Z_{\mathrm{ST}}^{\mathrm{T}}[-{{A}^{\mathrm{T}}}P-PA]{{\dot{Z}}_{\mathrm{ST}}}$
(29) ${{A}^{\mathrm{T}}}P+PA<0$
式中,$1/\sqrt{\left| S \right|}\ne 0$ k 1 、k 2 >0,Q P ${{\dot{V}}_{\mathrm{ISTC}}}$
4 改进滑模观测器
4.1 改进滑模观测器数学模型
传统滑模观测器通过计算定子电流估计值与实际值的定子电流误差,分析反电动势与转子估算速度的代数关系,PMSM的滑模观测器数学模型为
(30) $\left\{ \begin{align} & \frac{d{{\widehat{i}}_{\alpha }}}{dt}=-\frac{R}{{{\widehat{L}}_{s}}}{{\widehat{i}}_{\alpha }}+\frac{1}{{{\widehat{L}}_{s}}}{{u}_{\alpha }}-\frac{k sgn ({{\widehat{i}}_{\alpha }}-{{i}_{\alpha }})}{{{\widehat{L}}_{s}}} \\ & \frac{d{{\widehat{i}}_{\beta }}}{dt}=-\frac{R}{{{\widehat{L}}_{s}}}{{\widehat{i}}_{\beta }}+\frac{1}{{{\widehat{L}}_{s}}}{{u}_{\beta }}-\frac{k sgn ({{\widehat{i}}_{\beta }}-{{i}_{\beta }})}{{{\widehat{L}}_{s}}} \\ \end{align} \right.$
式中,${{\widehat{i}}_{\alpha }}{{\widehat{i}}_{\beta }}$ α -β 轴定子电流估计值;k 为观测器开关增益:sgn(s )为开关函数。
由于高频信号的切换,传统的基于sigmoid函数的滑模观测器系统具有很大的抖振缺点,为了改善这一缺点,设计了一种分段正弦型函数。
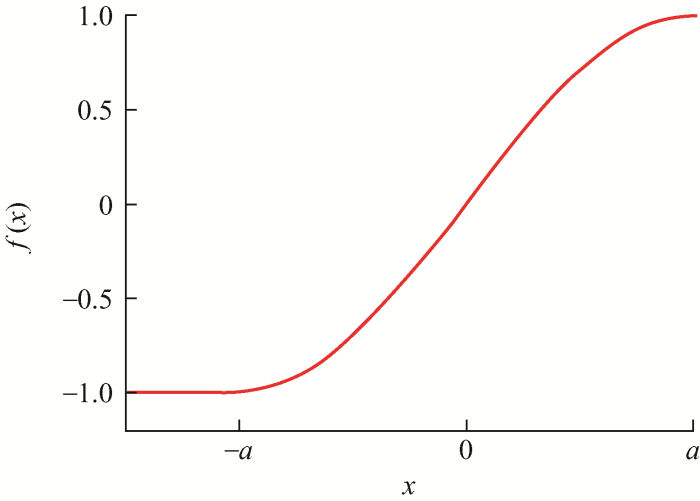
(31) $f(x)=\left\{ \begin{align} & 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x\ge a \\ & \sin \left| \frac{x}{2a} \right|\pi \ \ \ \ \ 0\le x<a \\ & -\sin \left| \frac{x}{2a} \right|\pi \ \ \ -a\le x<0 \\ & -1\ \ \ \ \ \ \ \ \ \ \ \ \ \ x\le -a \\ \end{align} \right.$
式中,a 为边界层厚度;$x\text{=}\left[ \begin{matrix} {{\widehat{i}}_{\alpha }}-i\alpha \\ {{\widehat{i}}_{\beta }}-i\beta \\\end{matrix} \right]$
如图2 所示,当x ≥a 时和x ≤-a 时,电流误差均达到饱和;当0≤x <a 和-a <x <0时,f (x )以正弦函数变化,通过对sgn函数的改进,反电动势的鲁棒性会更强。
图2
(32) $\left\{ \begin{align} & \frac{d{{\widehat{i}}_{\alpha }}}{dt}=-\frac{R}{{{\widehat{L}}_{s}}}{{\widehat{i}}_{\alpha }}+\frac{1}{{{\widehat{L}}_{s}}}{{u}_{\alpha }}-\frac{kf({{\widehat{i}}_{\alpha }}-{{i}_{\alpha }})}{{{\widehat{L}}_{s}}} \\ & \frac{d{{\widehat{i}}_{\beta }}}{dt}=-\frac{R}{{{\widehat{L}}_{s}}}{{\widehat{i}}_{\beta }}+\frac{1}{{{\widehat{L}}_{s}}}{{u}_{\beta }}-\frac{kf({{\widehat{i}}_{\beta }}-{{i}_{\beta }})}{{{\widehat{L}}_{s}}} \\ \end{align} \right.$
(33) $\left\{ \begin{align} & \frac{d{{\widetilde{i}}_{\alpha }}}{dt}=-\frac{R}{{{\widehat{L}}_{s}}}{{\widetilde{i}}_{\alpha }}+\frac{1}{{{\widehat{L}}_{s}}}{{u}_{\alpha }}-\frac{kf({{\widetilde{i}}_{\alpha }})}{{{\widehat{L}}_{s}}} \\ & \frac{d{{\widetilde{i}}_{\beta }}}{dt}=-\frac{R}{{{\widehat{L}}_{s}}}{{\widetilde{i}}_{\beta }}+\frac{1}{{{\widehat{L}}_{s}}}{{u}_{\beta }}-\frac{kf({{\widetilde{i}}_{\beta }})}{{{\widehat{L}}_{s}}} \\ \end{align} \right.$
式中,${{\widetilde{i}}_{\alpha }}\text{=}{{\widehat{i}}_{\alpha }}-{{i}_{\alpha }}\ \ {{\widetilde{i}}_{\beta }}\text{=}{{\widehat{i}}_{\beta }}-{{i}_{\beta }}$ α -β 轴定子电流误差。
(34) $\left\{ \begin{align} & {{e}_{\alpha }}=kf({{\widetilde{i}}_{\alpha }}) \\ & {{e}_{\beta }}=kf({{\widetilde{i}}_{\beta }}) \\ \end{align} \right.$
4.2 基于扩展卡尔曼滤波的改进滑模观测器
由于扩展卡尔曼滤波器(EKF)能够对非线性系统进行状态估计,使测量值和估计值之间的误差最小化。此外,EKF的估计速度具有较低的稳态误差和反电动势纹波,同时还可以滤除系统噪声、测量噪声,不仅显著缩短了计算时间,更增强了系统的鲁棒性。因此,在同步电机的转子位置和转速估计中得到了广泛的应用。EKF状态方程和观测方程为
(35) $\left\{ \begin{align} & x(t+1)=f(x(t))x(t)+Bu(t)+\sigma (t) \\ & y(t)=h(x(t))+w(t) \\ \end{align} \right.$
式中,σ (t )为系统白噪声,w (t )为测量误差,且
(36) $\left\{ \begin{align} & E(\sigma (t))=0 \\ & E(w(t))=0 \\ \end{align} \right.$
由于电机的惯性采样常数比采样的周期高很多,系统会随着时间慢慢收敛至稳定,状态与输出之间存在线性关系,进行线性化处理,将连续系统进行离散化可得
(37) $f(x(t))=\left[ \begin{matrix} -\frac{R}{{{L}_{s}}} & -{{{\hat{\omega }}}_{m}} \\ {{{\hat{\omega }}}_{m}} & -\frac{R}{{{L}_{s}}} \\\end{matrix} \right]$
(38) $B(t)=\left[ \begin{matrix} \frac{R}{{{L}_{s}}} & 0 \\ 0 & \frac{R}{{{L}_{s}}} \\\end{matrix} \right]$
(39) $h(t)=\left[ \begin{matrix} 1 & 0 \\ 0 & 1 \\\end{matrix} \right]$
(40) $\left\{ \begin{align} & x(t)={{\left[ \begin{matrix} {{{\hat{e}}}_{\alpha }} & {{{\hat{e}}}_{\beta }} \\\end{matrix} \right]}^{\mathrm{T}}} \\ & u(t)={{\left[ \begin{matrix} {{e}_{\alpha }} & {{e}_{\beta }} \\\end{matrix} \right]}^{\mathrm{T}}} \\ & y(t)={{\left[ \begin{matrix} {{{\hat{e}}}_{\alpha }} & {{{\hat{e}}}_{\beta }} \\\end{matrix} \right]}^{\mathrm{T}}} \\ \end{align} \right.$
式中,${{\hat{e}}_{\alpha }}$ ${{\hat{e}}_{\beta }}$
(41) $\left\{ \begin{align} & {{{\hat{\omega }}}_{m}}=\frac{\sqrt{\hat{e}_{\alpha }^{2}+\hat{e}_{\beta }^{2}}}{{{\psi }_{\mathrm{f}}}} \\ & \widehat{\theta }=-\arctan \left( \frac{{{{\hat{e}}}_{\alpha }}}{{{{\hat{e}}}_{\beta }}} \right) \\ \end{align} \right.$
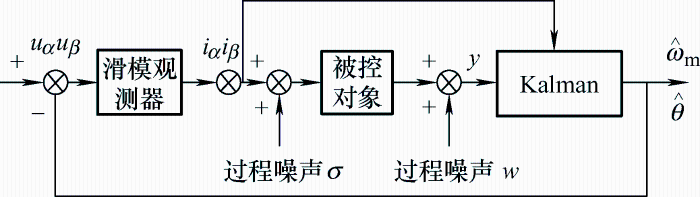
基于扩展卡尔曼滤波器的滑模观测器的控制结构如图3 所示。
图3
5 仿真分析
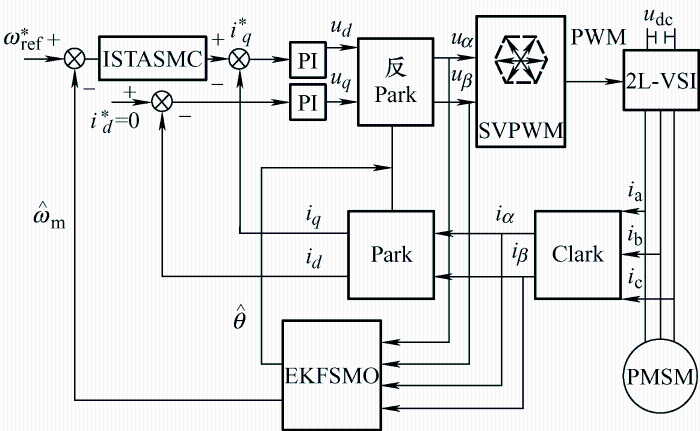
为了验证本文所提的PMSM无传感器矢量控制,通过Matlab和Simulink搭建基于积分超螺旋滑模控制器及改进扩展卡尔曼滤波的滑模观测器的矢量控制仿真模型,为了充分验证该系统的有效性,此次采用方案一(传统PI控制和普通滑模观测器)与方案二(积分超螺旋滑模控制和基于扩展卡尔曼滤波的改进滑模观测器)分别进行负载扰动、速度变化以及电机反转时电机转速、id 、iq 、电机转速与位置的估计仿真。仿真的电机参数设置如表1 所示。所提系统的PMSM矢量控制框图如图4 所示。
图4
5.1 负载扰动对系统性能影响
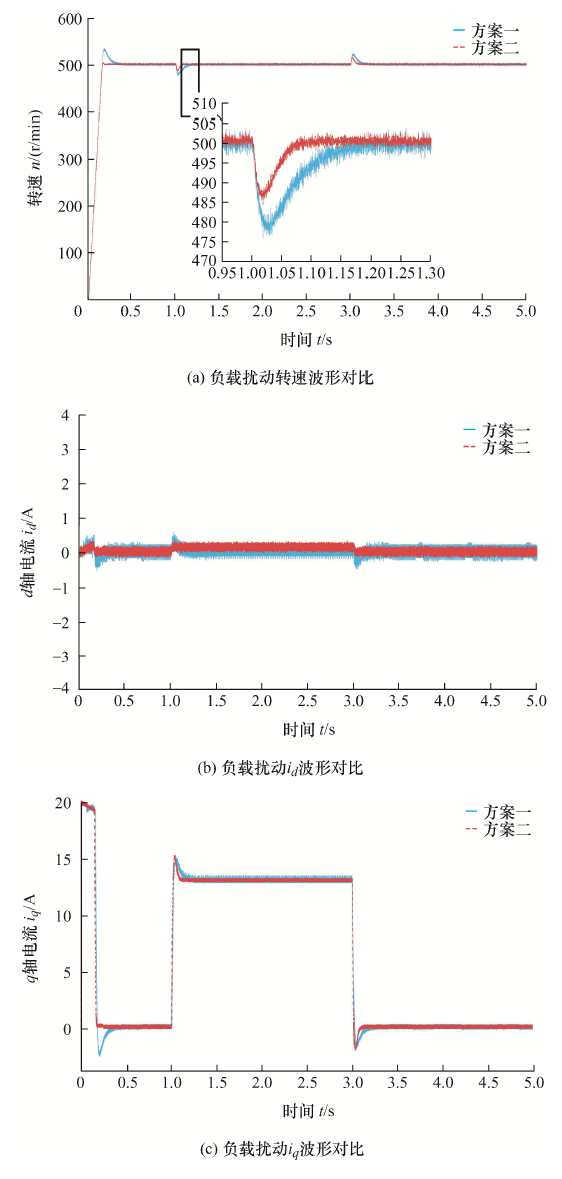
为验证负载扰动对电机性能的影响,在0 s时以500 r/min的恒定速度空载起动。在1 s时对电机施加20 N·m的负载,3 s时将负载降为0,两种方案的仿真结果如图5 所示。
图5
根据图5a ,电机起动时,方案一具有明显的超调现象,在1 s施加负载时,方案一的转速为477 r/min,下降了4.2%,经过了0.2 s转速回到稳态;所提改进方案二起动平缓,并未出现超调,施加负载时,方案二的转速为487 r/min,下降了2.6%,且回到稳态仅用了0.1 s。图5b 给出了负载扰动状况下的id 波形,由图5b 可知,方案一具有明显的电流谐波,方案二在很大程度上改善了方案一的谐波缺陷,并且在施加负载时的响应速度更快。由图5c 可知,在0 s时,相比于方案一的iq ,改进方案起动时更加平缓,具有极好的稳定性能。当出现负载扰动时,响应时间更短,电流跟踪效果更快。
5.2 速度变化对系统性能影响
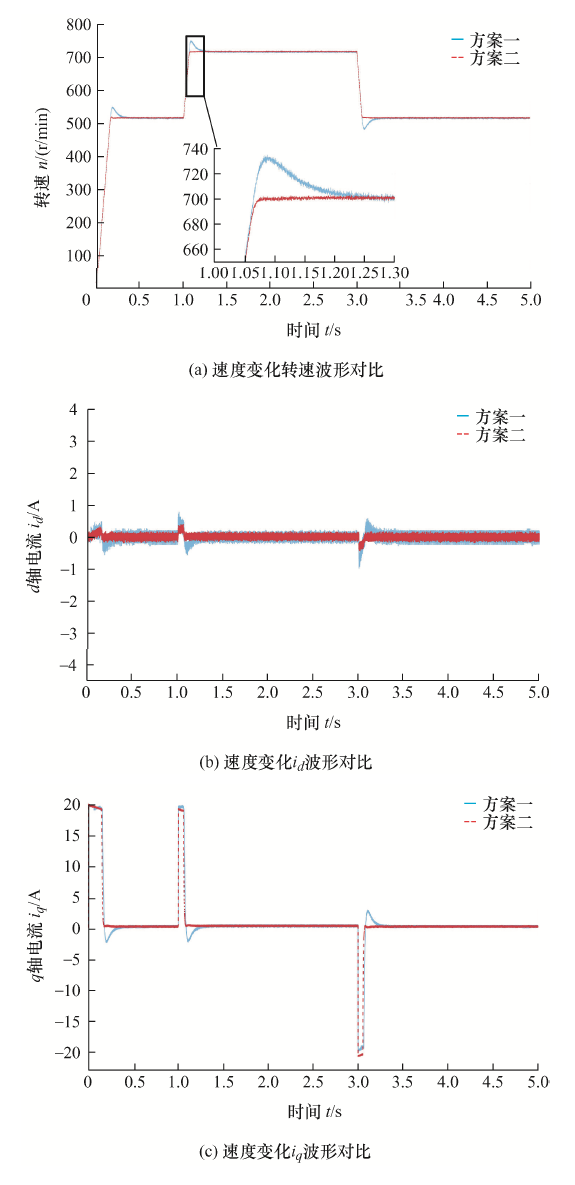
为更好地观察速度变化对系统性能的影响,在0 s起动时转速设置为500 r/min,1 s时速度上升至700 r/min,3 s时将转速恢复至500 r/min,仿真结果如图6 所示。
图6
图6a 给出了两种方案的加减速对比结果,相对于方案一出现的超调现象,改进方案弥补了这一缺点,电机运行后能在0.07 s内达到设定值,比方案一快了约0.23 s,具有完美的速度响应能力。根据图6b 、6c 可知,id 的振荡明显减轻,d -q 轴电流的干扰尖峰脉冲信号变弱,控制效果更好。
5.3 电机反转对系统性能影响
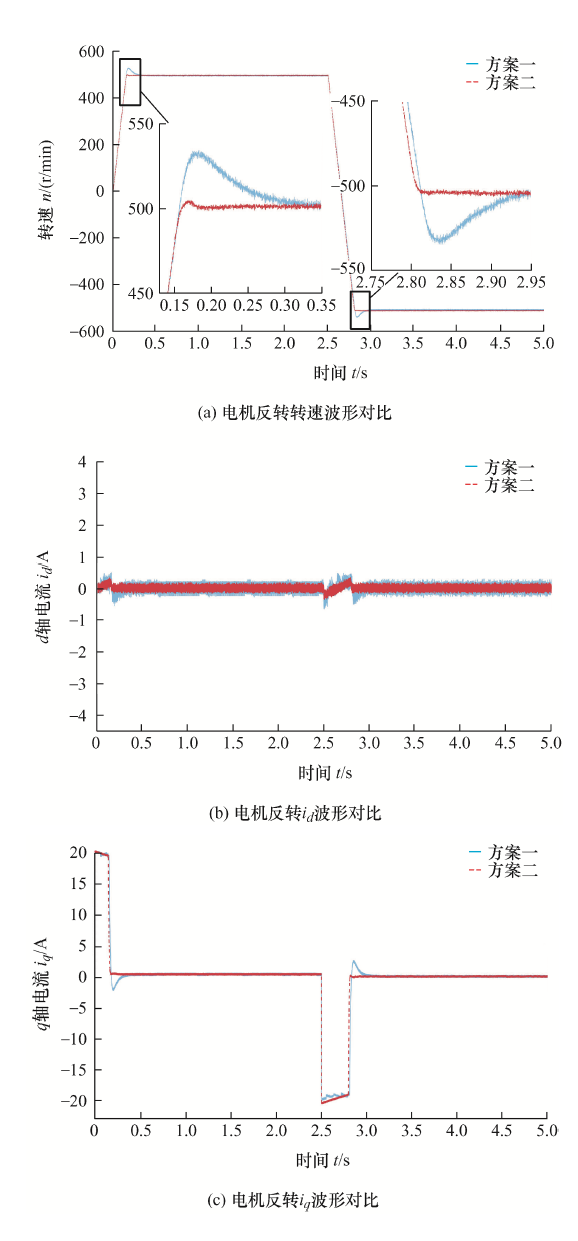
为了探究两种方案应对电机反转时的控制效果,电机初始转速设置为500 r/min,在2.5 s时转速设置为-500 r/min,仿真结果如图7 所示。
图7
根据图7a 可知,电机起动时,方案一转速峰值达到约535 r/min,经过0.35 s达到稳定;方案二无超调产生,且在0.17 s内将转速控制在500 r/min,在应对电机突然反转时也表现出了良好的速度跟踪性能。根据图7b 、7c 可知,改进观测器作用下的电流谐波幅值减小,高频抖动得到改善,具有很好的鲁棒性。
5.4 电机转速与位置的估计
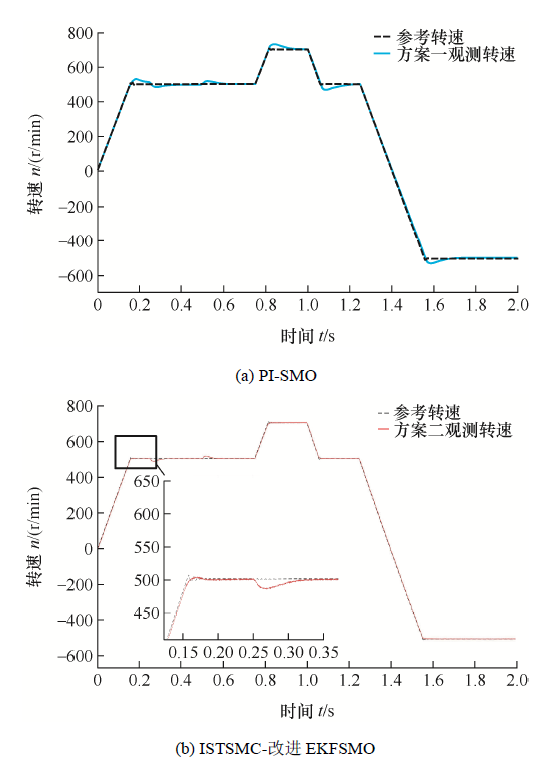
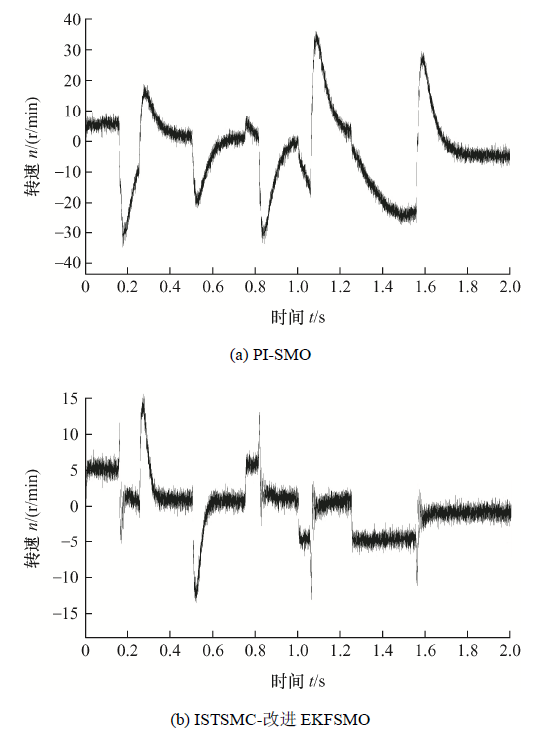
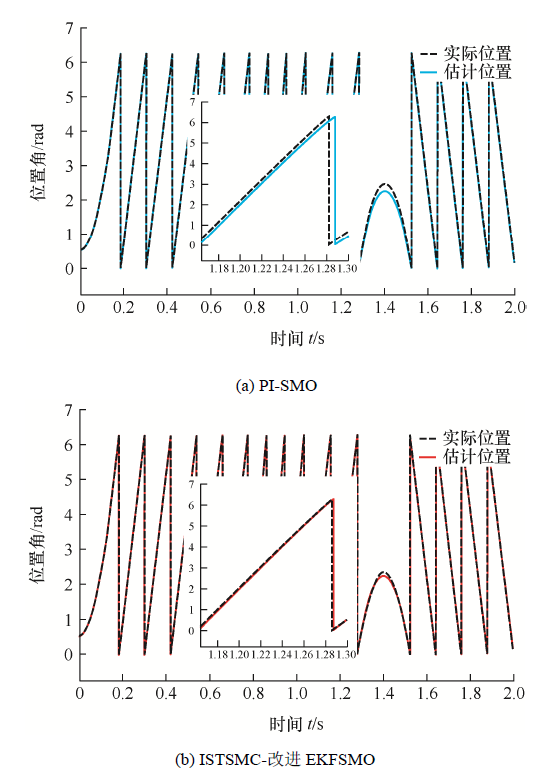
为了验证负载扰动、速度变化时控制系统的鲁棒性以及对转子位置的精确跟踪,在0 s时,给定电机转速500 r/min,0.25 s时给电机施加20 N·m的负载,0.5 s时卸载,0.75 s时将转速升至700 r/min,1 s时恢复500 r/min,1.25 s时电机反转运行,在此工况下,观察电机的转速估计以及转子位置估计波形。
由图8 、9 可知,传统方法的转速突变误差十分明显,而改进方案在负载扰动、转速变化时均具有较好的鲁棒性,只有负载变化时具有微小的抖动,相比传统方法得到很大的改善。转速误差均能以最短的时间恢复至0附近,通过转速估计误差波形的对比,所提改进系统的消抖效果明显。图10 反映了转子位置估计效果,传统方案实际位置与观测位置之间存在显著的位置误差,位置误差的平均值约为12.3°,改进方案的位置误差值约为4.3°。改进方案不仅改善了抖振现象,还提高了对转子位置的估计精度。
图8
图9
图10
6 结论
本文提出了一种基于ISTSMC和EKFSMO的高性能PMSM控制策略,得出以下结论。
(1) 搭建了PMSM数学模型,设计滑模控制器,该控制器将积分SMC和超螺旋算法相结合,不仅解决了抖振问题,而且提高了系统的鲁棒性和稳定性,利用李雅普诺夫稳定性定理对系统稳定性进行了证明。
(2) 设计了一种基于扩展卡尔曼滤波的滑模观测器,实现无位置传感器控制以及电机转速与位置的在线估计,提出了一种分段正弦切换函数代替传统的sgn函数,减少了由于高频切换引起的抖动。仿真结果表明,该方法在负载变化、反转运行和故障扰动影响下,电机控制系统具有良好的响应速度和检测精度,极大增强了系统的稳定性以及消抖效果,结果证实了该策略为高性能永磁同步电机控制提供了很好的方案。
参考文献
View Option
[1]
赵希梅 , 王超 , 金鸿雁 . 基于NDO的永磁同步电动机自适应分数阶滑模控制
[J]. 中国机械工程 , 2023 , 34 (9 ):1093 -1099 ,1119.
[本文引用: 1]
ZHAO Ximei WANG Chao JIN Hongyan Adaptive fractional order sliding mode control for PMSMs based on NDO
[J]. China Mechanical Engineering , 2023 , 34 (9 ):1093 -1099 ,1119.
[本文引用: 1]
[2]
张晓光 , 张亮 , 侯本帅 . 永磁同步电机优化模型预测转矩控制
[J]. 中国电机工程学报 , 2017 , 37 (16 ):4800 -4809 ,4905.
[本文引用: 1]
ZHANG Xiaoguang ZHANG Liang HOU Benshuai Permanent magnet synchronous motor optimization model predictive torque control
[J]. Proceedings of the CSEE , 2017 , 37 (16 ):4800 -4809 ,4905.
[本文引用: 1]
[3]
巫庆辉 , 黄成鑫 , 侯元祥 . 基于高频方波电压注入法和改进龙伯格观测器的永磁同步电机转速估计的研究
[J]. 电气工程学报 , 2021 , 16 (4 ):120 -126 .
[本文引用: 1]
WU Qinghui HUANG Chengxin HOU Yuanxiang Sensorless FOC of PMSM based on high frequency square-wave voltage injection and improved Luenberger position observer
[J]. Journal of Electrical Engineering , 2021 , 16 (4 ):120 -126 .
[本文引用: 1]
[4]
史涔溦 , 马红如 , 陈卓易 , 等 . 永磁同步电机模糊代价函数预测转矩控制
[J]. 电机与控制学报 , 2022 , 26 (1 ):1 -8 .
[本文引用: 1]
SHI Cenwei MA Hongru CHEN Zhuoyi et al. Fuzzy tuning of weight coefficient in model predictive torque control of PMSM
[J]. Electric Machines and Control , 2022 , 26 (1 ):1 -8 .
[本文引用: 1]
[5]
祝新阳 , 曾国辉 , 黄勃 , 等 . 无速度传感器的永磁同步电机矢量控制
[J]. 控制工程 , 2021 , 28 (5 ):898 -904 .
[本文引用: 1]
ZHU Xinyang ZENG Guohui HUANG Bo et al. Speed sensorless vector control of permanent magnet synchronous motor
[J]. Control Engineering , 2021 , 28 (5 ):898 -904 .
[本文引用: 1]
[6]
WEN Yuliang ZHENG Hanfang YANG Fang et al. A novel MTPA and flux weakening method of stator flux oriented control of PMSM
[J]. Transportation Safety and Environment , 2021 , 3 (3 ):tdab008.
[本文引用: 1]
[7]
杨旭东 , 王云冲 , 沈建新 . 同步磁阻电机模型参考自适应法无位置传感器控制
[J]. 电机与控制学报 , 2019 , 23 (11 ):1 -9 .
[本文引用: 1]
YANG Xudong WANG Yunchong SHEN Jianxin MRAS sensorless control for synchronous reluctance motors
[J]. Electric Machines and Control , 2019 , 23 (11 ):1 -9 .
[本文引用: 1]
[8]
LIN Yuzhe HU Hongming CHANG Yuhan et al. Permanent magnet synchronous motor vector control based on BP neural network
[J]. Journal of Physics:Conference Series , 2022 , 2369 (1 ):012068 .
DOI:10.1088/1742-6596/2369/1/012068
[本文引用: 1]
In this paper, the traditional permanent magnet synchronous motor vector control system has problems such as low control precision, low reliability, poor system operation status. To solve these problems, because of the neural network has self-learning and self-adaptive ability to BP algorithm can be applied to parts of speed control system. This paper proposes a PMSM which based on BP neural network algorithm and control systems. Then the system model is established in Simulink environment, and the superiority and feasibility of the strategy are verified by comparing with traditional PID controller.
[9]
ZHANG Yongchang ZHU Jianguo Direct torque control of permanent magnet synchronous motor with reduced torque ripple and commutation frequency
[J]. IEEE Transactions on Power Electronics , 2010 , 26 (1 ):235 -248 .
DOI:10.1109/TPEL.2010.2059047
URL
[本文引用: 1]
[10]
陈有鹏 , 卜文绍 , 张晓峰 , 等 . 无轴承异步电机的无功功率MRAS转速辨识研究
[J]. 控制工程 , 2020 , 27 (7 ):1118 -1124 .
[本文引用: 1]
CHEN Youpeng BU Wenshao ZHANG Xiaofeng et al. Research on reactive power MRAS speed identification of bearingless induction motor
[J]. Control Engineering , 2020 , 27 (7 ):1118 -1124 .
[本文引用: 1]
[11]
曹亚丽 , 曹竣奥 , 宋昕 , 等 . 一种改进滑模观测器的PMSM矢量控制研究
[J]. 电力系统保护与控制 , 2021 , 49 (16 ):104 -111 .
[本文引用: 1]
CAO Yali CAO Junao SONG Xin et al. Research on PMSM vector control based on improved sliding mode observer
[J]. Power System Protection and Control , 2021 , 49 (16 ):104 -111 .
[本文引用: 1]
[12]
GONG Chao HU Yihua GAO Jinqiu et al. An improved delay-suppressed sliding-mode observer for sensorless vector-controlled PMSM
[J]. IEEE Transactions on Industrial Electronics , 2020 , 67 (7 ):5913 -5923 .
DOI:10.1109/TIE.41
URL
[本文引用: 1]
[13]
李争 , 安金峰 , 肖宇 , 等 . 基于自适应观测器的永磁同步直线电机模型预测控制系统设计
[J]. 电工技术学报 , 2021 , 36 (6 ):1190 -1200 .
[本文引用: 1]
LI Zheng AN Jinfeng XIAO Yu et al. Model predictive control system design of permanent magnet synchronous linear motor based on adaptive observer
[J]. Transactions of China Electrotechnical Society , 2021 , 36 (6 ):1190 -1200 .
[本文引用: 1]
[14]
周娟 , 孙啸 , 刘凯 , 等 . 联合扩展卡尔曼滤波的滑模观测器SOC估算算法研究
[J]. 中国电机工程学报 , 2021 , 41 (2 ):692 -703 .
[本文引用: 1]
ZHOU Juan SUN Xiao LIU Kai et al. Research on SOC estimation algorithm of sliding mode observer combined with extended Kalman filter
[J]. Proceedings of the CSEE , 2021 , 41 (2 ):692 -703 .
[本文引用: 1]
[15]
张立伟 , 李行 , 宋佩佩 , 等 . 基于新型滑模观测器的永磁同步电机无传感器矢量控制系统
[J]. 电工技术学报 , 2019 , 34 (S1 ):70 -78 .
[本文引用: 1]
ZHANG Liwei LI Xing SONG Peipei et al. Sensorless vector control system of permanent magnet synchronous motor based on new sliding mode observer
[J]. Transactions of China Electrotechnical Society , 2019 , 34 (S1 ):70 -78 .
[本文引用: 1]
[16]
PLESTAN F SHTESSEL Y BREGEAULT V et al. New methodologies for adaptive sliding mode control
[J]. International Journal of Control , 2010 , 83 (9 ):1907 -1919 .
DOI:10.1080/00207179.2010.501385
URL
[本文引用: 1]
[17]
MORFIN O A VALENZUELA F A BETANCOUR R R et al. Real-time SOSM super-twisting combined with block control for regulating induction motor velocity
[J]. IEEE Access , 2018 ,6:25898 -25907 .
[本文引用: 1]
[18]
SAMI I ULLAH S BASIT A et al. Integral super twisting sliding mode based sensorless predictive torque control of induction motor
[J]. IEEE Access , 2020 ,8:186740 -186755 .
[本文引用: 1]
[19]
苗敬利 , 于俊林 , 马晨浩 , 等 . 基于EKF的PMSM 滑模控制策略研究
[J]. 机械工程与自动化 , 2021 (5 ):1 -3 ,6.
[本文引用: 1]
MIAO Jingli YU Junlin MA Chenhao et al. Research on PMSM sliding mode control strategy based on EKF
[J]. Mechanical Engineering and Automation , 2021 (5 ):1 -3 ,6.
[本文引用: 1]
[20]
MORENO J A OSORIO M Strict Lyapunov functions for the super-twisting algorithm
[J]. IEEE Transactions on Automatic Control , 2012 , 57 (4 ):1035 -1040 .
DOI:10.1109/TAC.2012.2186179
URL
[本文引用: 1]
基于NDO的永磁同步电动机自适应分数阶滑模控制
1
2023
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)以其低惯性、高效率、轻量化等优点,在工业领域引起了广泛的关注[1 ⇓ ⇓ -4 ] .对于永磁同步电机驱动的无传感器矢量控制(Field orientation control,FOC),需要使用转子位置编码器或高精度传感器获取转子的位置和速度.但是传感器的安装成本较高,导致设备复杂性的增加和机械鲁棒性的降低.为了解决以上问题,一种无传感器矢量控制技术被应用于估计转子的位置和速度[5 ⇓ ⇓ -8 ] . ...
Adaptive fractional order sliding mode control for PMSMs based on NDO
1
2023
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)以其低惯性、高效率、轻量化等优点,在工业领域引起了广泛的关注[1 ⇓ ⇓ -4 ] .对于永磁同步电机驱动的无传感器矢量控制(Field orientation control,FOC),需要使用转子位置编码器或高精度传感器获取转子的位置和速度.但是传感器的安装成本较高,导致设备复杂性的增加和机械鲁棒性的降低.为了解决以上问题,一种无传感器矢量控制技术被应用于估计转子的位置和速度[5 ⇓ ⇓ -8 ] . ...
永磁同步电机优化模型预测转矩控制
1
2017
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)以其低惯性、高效率、轻量化等优点,在工业领域引起了广泛的关注[1 ⇓ ⇓ -4 ] .对于永磁同步电机驱动的无传感器矢量控制(Field orientation control,FOC),需要使用转子位置编码器或高精度传感器获取转子的位置和速度.但是传感器的安装成本较高,导致设备复杂性的增加和机械鲁棒性的降低.为了解决以上问题,一种无传感器矢量控制技术被应用于估计转子的位置和速度[5 ⇓ ⇓ -8 ] . ...
Permanent magnet synchronous motor optimization model predictive torque control
1
2017
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)以其低惯性、高效率、轻量化等优点,在工业领域引起了广泛的关注[1 ⇓ ⇓ -4 ] .对于永磁同步电机驱动的无传感器矢量控制(Field orientation control,FOC),需要使用转子位置编码器或高精度传感器获取转子的位置和速度.但是传感器的安装成本较高,导致设备复杂性的增加和机械鲁棒性的降低.为了解决以上问题,一种无传感器矢量控制技术被应用于估计转子的位置和速度[5 ⇓ ⇓ -8 ] . ...
基于高频方波电压注入法和改进龙伯格观测器的永磁同步电机转速估计的研究
1
2021
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)以其低惯性、高效率、轻量化等优点,在工业领域引起了广泛的关注[1 ⇓ ⇓ -4 ] .对于永磁同步电机驱动的无传感器矢量控制(Field orientation control,FOC),需要使用转子位置编码器或高精度传感器获取转子的位置和速度.但是传感器的安装成本较高,导致设备复杂性的增加和机械鲁棒性的降低.为了解决以上问题,一种无传感器矢量控制技术被应用于估计转子的位置和速度[5 ⇓ ⇓ -8 ] . ...
Sensorless FOC of PMSM based on high frequency square-wave voltage injection and improved Luenberger position observer
1
2021
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)以其低惯性、高效率、轻量化等优点,在工业领域引起了广泛的关注[1 ⇓ ⇓ -4 ] .对于永磁同步电机驱动的无传感器矢量控制(Field orientation control,FOC),需要使用转子位置编码器或高精度传感器获取转子的位置和速度.但是传感器的安装成本较高,导致设备复杂性的增加和机械鲁棒性的降低.为了解决以上问题,一种无传感器矢量控制技术被应用于估计转子的位置和速度[5 ⇓ ⇓ -8 ] . ...
永磁同步电机模糊代价函数预测转矩控制
1
2022
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)以其低惯性、高效率、轻量化等优点,在工业领域引起了广泛的关注[1 ⇓ ⇓ -4 ] .对于永磁同步电机驱动的无传感器矢量控制(Field orientation control,FOC),需要使用转子位置编码器或高精度传感器获取转子的位置和速度.但是传感器的安装成本较高,导致设备复杂性的增加和机械鲁棒性的降低.为了解决以上问题,一种无传感器矢量控制技术被应用于估计转子的位置和速度[5 ⇓ ⇓ -8 ] . ...
Fuzzy tuning of weight coefficient in model predictive torque control of PMSM
1
2022
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)以其低惯性、高效率、轻量化等优点,在工业领域引起了广泛的关注[1 ⇓ ⇓ -4 ] .对于永磁同步电机驱动的无传感器矢量控制(Field orientation control,FOC),需要使用转子位置编码器或高精度传感器获取转子的位置和速度.但是传感器的安装成本较高,导致设备复杂性的增加和机械鲁棒性的降低.为了解决以上问题,一种无传感器矢量控制技术被应用于估计转子的位置和速度[5 ⇓ ⇓ -8 ] . ...
无速度传感器的永磁同步电机矢量控制
1
2021
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)以其低惯性、高效率、轻量化等优点,在工业领域引起了广泛的关注[1 ⇓ ⇓ -4 ] .对于永磁同步电机驱动的无传感器矢量控制(Field orientation control,FOC),需要使用转子位置编码器或高精度传感器获取转子的位置和速度.但是传感器的安装成本较高,导致设备复杂性的增加和机械鲁棒性的降低.为了解决以上问题,一种无传感器矢量控制技术被应用于估计转子的位置和速度[5 ⇓ ⇓ -8 ] . ...
Speed sensorless vector control of permanent magnet synchronous motor
1
2021
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)以其低惯性、高效率、轻量化等优点,在工业领域引起了广泛的关注[1 ⇓ ⇓ -4 ] .对于永磁同步电机驱动的无传感器矢量控制(Field orientation control,FOC),需要使用转子位置编码器或高精度传感器获取转子的位置和速度.但是传感器的安装成本较高,导致设备复杂性的增加和机械鲁棒性的降低.为了解决以上问题,一种无传感器矢量控制技术被应用于估计转子的位置和速度[5 ⇓ ⇓ -8 ] . ...
A novel MTPA and flux weakening method of stator flux oriented control of PMSM
1
2021
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)以其低惯性、高效率、轻量化等优点,在工业领域引起了广泛的关注[1 ⇓ ⇓ -4 ] .对于永磁同步电机驱动的无传感器矢量控制(Field orientation control,FOC),需要使用转子位置编码器或高精度传感器获取转子的位置和速度.但是传感器的安装成本较高,导致设备复杂性的增加和机械鲁棒性的降低.为了解决以上问题,一种无传感器矢量控制技术被应用于估计转子的位置和速度[5 ⇓ ⇓ -8 ] . ...
同步磁阻电机模型参考自适应法无位置传感器控制
1
2019
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)以其低惯性、高效率、轻量化等优点,在工业领域引起了广泛的关注[1 ⇓ ⇓ -4 ] .对于永磁同步电机驱动的无传感器矢量控制(Field orientation control,FOC),需要使用转子位置编码器或高精度传感器获取转子的位置和速度.但是传感器的安装成本较高,导致设备复杂性的增加和机械鲁棒性的降低.为了解决以上问题,一种无传感器矢量控制技术被应用于估计转子的位置和速度[5 ⇓ ⇓ -8 ] . ...
MRAS sensorless control for synchronous reluctance motors
1
2019
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)以其低惯性、高效率、轻量化等优点,在工业领域引起了广泛的关注[1 ⇓ ⇓ -4 ] .对于永磁同步电机驱动的无传感器矢量控制(Field orientation control,FOC),需要使用转子位置编码器或高精度传感器获取转子的位置和速度.但是传感器的安装成本较高,导致设备复杂性的增加和机械鲁棒性的降低.为了解决以上问题,一种无传感器矢量控制技术被应用于估计转子的位置和速度[5 ⇓ ⇓ -8 ] . ...
Permanent magnet synchronous motor vector control based on BP neural network
1
2022
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)以其低惯性、高效率、轻量化等优点,在工业领域引起了广泛的关注[1 ⇓ ⇓ -4 ] .对于永磁同步电机驱动的无传感器矢量控制(Field orientation control,FOC),需要使用转子位置编码器或高精度传感器获取转子的位置和速度.但是传感器的安装成本较高,导致设备复杂性的增加和机械鲁棒性的降低.为了解决以上问题,一种无传感器矢量控制技术被应用于估计转子的位置和速度[5 ⇓ ⇓ -8 ] . ...
Direct torque control of permanent magnet synchronous motor with reduced torque ripple and commutation frequency
1
2010
... 无传感器矢量控制方法一般可分为两类:利用电机转子凸极效应的高频注入技术和基于观测器的估计方法.常见的估计转子位置和速度的方法有模型参考自适应系统(Model reference adaptive system,MRAS)、非线性观测器和滑模观测器(Sliding model observer,SMO)[9 ⇓ ⇓ -12 ] .MRAS在低速时具有较好的稳定性,但是需要调节器和滤波器,增加了系统复杂性[13 ] .滑模控制具有较好的抗干扰性和鲁棒性,且数学模型较为简单,易于构建[14 -15 ] ,被广泛应用于研究领域. ...
无轴承异步电机的无功功率MRAS转速辨识研究
1
2020
... 无传感器矢量控制方法一般可分为两类:利用电机转子凸极效应的高频注入技术和基于观测器的估计方法.常见的估计转子位置和速度的方法有模型参考自适应系统(Model reference adaptive system,MRAS)、非线性观测器和滑模观测器(Sliding model observer,SMO)[9 ⇓ ⇓ -12 ] .MRAS在低速时具有较好的稳定性,但是需要调节器和滤波器,增加了系统复杂性[13 ] .滑模控制具有较好的抗干扰性和鲁棒性,且数学模型较为简单,易于构建[14 -15 ] ,被广泛应用于研究领域. ...
Research on reactive power MRAS speed identification of bearingless induction motor
1
2020
... 无传感器矢量控制方法一般可分为两类:利用电机转子凸极效应的高频注入技术和基于观测器的估计方法.常见的估计转子位置和速度的方法有模型参考自适应系统(Model reference adaptive system,MRAS)、非线性观测器和滑模观测器(Sliding model observer,SMO)[9 ⇓ ⇓ -12 ] .MRAS在低速时具有较好的稳定性,但是需要调节器和滤波器,增加了系统复杂性[13 ] .滑模控制具有较好的抗干扰性和鲁棒性,且数学模型较为简单,易于构建[14 -15 ] ,被广泛应用于研究领域. ...
一种改进滑模观测器的PMSM矢量控制研究
1
2021
... 无传感器矢量控制方法一般可分为两类:利用电机转子凸极效应的高频注入技术和基于观测器的估计方法.常见的估计转子位置和速度的方法有模型参考自适应系统(Model reference adaptive system,MRAS)、非线性观测器和滑模观测器(Sliding model observer,SMO)[9 ⇓ ⇓ -12 ] .MRAS在低速时具有较好的稳定性,但是需要调节器和滤波器,增加了系统复杂性[13 ] .滑模控制具有较好的抗干扰性和鲁棒性,且数学模型较为简单,易于构建[14 -15 ] ,被广泛应用于研究领域. ...
Research on PMSM vector control based on improved sliding mode observer
1
2021
... 无传感器矢量控制方法一般可分为两类:利用电机转子凸极效应的高频注入技术和基于观测器的估计方法.常见的估计转子位置和速度的方法有模型参考自适应系统(Model reference adaptive system,MRAS)、非线性观测器和滑模观测器(Sliding model observer,SMO)[9 ⇓ ⇓ -12 ] .MRAS在低速时具有较好的稳定性,但是需要调节器和滤波器,增加了系统复杂性[13 ] .滑模控制具有较好的抗干扰性和鲁棒性,且数学模型较为简单,易于构建[14 -15 ] ,被广泛应用于研究领域. ...
An improved delay-suppressed sliding-mode observer for sensorless vector-controlled PMSM
1
2020
... 无传感器矢量控制方法一般可分为两类:利用电机转子凸极效应的高频注入技术和基于观测器的估计方法.常见的估计转子位置和速度的方法有模型参考自适应系统(Model reference adaptive system,MRAS)、非线性观测器和滑模观测器(Sliding model observer,SMO)[9 ⇓ ⇓ -12 ] .MRAS在低速时具有较好的稳定性,但是需要调节器和滤波器,增加了系统复杂性[13 ] .滑模控制具有较好的抗干扰性和鲁棒性,且数学模型较为简单,易于构建[14 -15 ] ,被广泛应用于研究领域. ...
基于自适应观测器的永磁同步直线电机模型预测控制系统设计
1
2021
... 无传感器矢量控制方法一般可分为两类:利用电机转子凸极效应的高频注入技术和基于观测器的估计方法.常见的估计转子位置和速度的方法有模型参考自适应系统(Model reference adaptive system,MRAS)、非线性观测器和滑模观测器(Sliding model observer,SMO)[9 ⇓ ⇓ -12 ] .MRAS在低速时具有较好的稳定性,但是需要调节器和滤波器,增加了系统复杂性[13 ] .滑模控制具有较好的抗干扰性和鲁棒性,且数学模型较为简单,易于构建[14 -15 ] ,被广泛应用于研究领域. ...
Model predictive control system design of permanent magnet synchronous linear motor based on adaptive observer
1
2021
... 无传感器矢量控制方法一般可分为两类:利用电机转子凸极效应的高频注入技术和基于观测器的估计方法.常见的估计转子位置和速度的方法有模型参考自适应系统(Model reference adaptive system,MRAS)、非线性观测器和滑模观测器(Sliding model observer,SMO)[9 ⇓ ⇓ -12 ] .MRAS在低速时具有较好的稳定性,但是需要调节器和滤波器,增加了系统复杂性[13 ] .滑模控制具有较好的抗干扰性和鲁棒性,且数学模型较为简单,易于构建[14 -15 ] ,被广泛应用于研究领域. ...
联合扩展卡尔曼滤波的滑模观测器SOC估算算法研究
1
2021
... 无传感器矢量控制方法一般可分为两类:利用电机转子凸极效应的高频注入技术和基于观测器的估计方法.常见的估计转子位置和速度的方法有模型参考自适应系统(Model reference adaptive system,MRAS)、非线性观测器和滑模观测器(Sliding model observer,SMO)[9 ⇓ ⇓ -12 ] .MRAS在低速时具有较好的稳定性,但是需要调节器和滤波器,增加了系统复杂性[13 ] .滑模控制具有较好的抗干扰性和鲁棒性,且数学模型较为简单,易于构建[14 -15 ] ,被广泛应用于研究领域. ...
Research on SOC estimation algorithm of sliding mode observer combined with extended Kalman filter
1
2021
... 无传感器矢量控制方法一般可分为两类:利用电机转子凸极效应的高频注入技术和基于观测器的估计方法.常见的估计转子位置和速度的方法有模型参考自适应系统(Model reference adaptive system,MRAS)、非线性观测器和滑模观测器(Sliding model observer,SMO)[9 ⇓ ⇓ -12 ] .MRAS在低速时具有较好的稳定性,但是需要调节器和滤波器,增加了系统复杂性[13 ] .滑模控制具有较好的抗干扰性和鲁棒性,且数学模型较为简单,易于构建[14 -15 ] ,被广泛应用于研究领域. ...
基于新型滑模观测器的永磁同步电机无传感器矢量控制系统
1
2019
... 无传感器矢量控制方法一般可分为两类:利用电机转子凸极效应的高频注入技术和基于观测器的估计方法.常见的估计转子位置和速度的方法有模型参考自适应系统(Model reference adaptive system,MRAS)、非线性观测器和滑模观测器(Sliding model observer,SMO)[9 ⇓ ⇓ -12 ] .MRAS在低速时具有较好的稳定性,但是需要调节器和滤波器,增加了系统复杂性[13 ] .滑模控制具有较好的抗干扰性和鲁棒性,且数学模型较为简单,易于构建[14 -15 ] ,被广泛应用于研究领域. ...
Sensorless vector control system of permanent magnet synchronous motor based on new sliding mode observer
1
2019
... 无传感器矢量控制方法一般可分为两类:利用电机转子凸极效应的高频注入技术和基于观测器的估计方法.常见的估计转子位置和速度的方法有模型参考自适应系统(Model reference adaptive system,MRAS)、非线性观测器和滑模观测器(Sliding model observer,SMO)[9 ⇓ ⇓ -12 ] .MRAS在低速时具有较好的稳定性,但是需要调节器和滤波器,增加了系统复杂性[13 ] .滑模控制具有较好的抗干扰性和鲁棒性,且数学模型较为简单,易于构建[14 -15 ] ,被广泛应用于研究领域. ...
New methodologies for adaptive sliding mode control
1
2010
... 然而,滑模控制的缺点是由算法的高频切换引起的抖振现象.许多学者针对减小或消除抖振现象提出了不同的方法.文献[16 ]提出了一种自适应一阶滑模控制器(Sliding mode controller,SMC),其中包括设计各种趋近律方法、滑动面、高阶SMC和复合SMC.许多SMC的变种已被提出,超螺旋滑模控制(Super twisting sliding mode controller,STSMC)技术引起了广泛关注,特别是对于控制律出现在滑动变量一阶导数中的系统.文献[17 ]提出了一种实时STSMC来控制电机转子磁链和机械转速,并提出了一种一阶SMO来估计磁链和负载转矩,在实现无位置传感器和减少抖振方面发挥了关键的作用.文献[18 ]结合了STSMC和积分SMC方案的属性,提出了一种基于积分超螺旋滑模控制的感应电机无传感器预测电流控制,解决了传统PI控制鲁棒性差的缺点.文献[19 ]以扩展卡尔曼滤波(Extended Kalman filter,EKF)算法为基础,通过EKF得到转子的位置和角速度.该估计算法既不需要机械参数的知识,也不需要转子的初始位置,利用改进滑模控制器取代PI控制器作为电流环调节器,提高了系统性能. ...
Real-time SOSM super-twisting combined with block control for regulating induction motor velocity
1
2018
... 然而,滑模控制的缺点是由算法的高频切换引起的抖振现象.许多学者针对减小或消除抖振现象提出了不同的方法.文献[16 ]提出了一种自适应一阶滑模控制器(Sliding mode controller,SMC),其中包括设计各种趋近律方法、滑动面、高阶SMC和复合SMC.许多SMC的变种已被提出,超螺旋滑模控制(Super twisting sliding mode controller,STSMC)技术引起了广泛关注,特别是对于控制律出现在滑动变量一阶导数中的系统.文献[17 ]提出了一种实时STSMC来控制电机转子磁链和机械转速,并提出了一种一阶SMO来估计磁链和负载转矩,在实现无位置传感器和减少抖振方面发挥了关键的作用.文献[18 ]结合了STSMC和积分SMC方案的属性,提出了一种基于积分超螺旋滑模控制的感应电机无传感器预测电流控制,解决了传统PI控制鲁棒性差的缺点.文献[19 ]以扩展卡尔曼滤波(Extended Kalman filter,EKF)算法为基础,通过EKF得到转子的位置和角速度.该估计算法既不需要机械参数的知识,也不需要转子的初始位置,利用改进滑模控制器取代PI控制器作为电流环调节器,提高了系统性能. ...
Integral super twisting sliding mode based sensorless predictive torque control of induction motor
1
2020
... 然而,滑模控制的缺点是由算法的高频切换引起的抖振现象.许多学者针对减小或消除抖振现象提出了不同的方法.文献[16 ]提出了一种自适应一阶滑模控制器(Sliding mode controller,SMC),其中包括设计各种趋近律方法、滑动面、高阶SMC和复合SMC.许多SMC的变种已被提出,超螺旋滑模控制(Super twisting sliding mode controller,STSMC)技术引起了广泛关注,特别是对于控制律出现在滑动变量一阶导数中的系统.文献[17 ]提出了一种实时STSMC来控制电机转子磁链和机械转速,并提出了一种一阶SMO来估计磁链和负载转矩,在实现无位置传感器和减少抖振方面发挥了关键的作用.文献[18 ]结合了STSMC和积分SMC方案的属性,提出了一种基于积分超螺旋滑模控制的感应电机无传感器预测电流控制,解决了传统PI控制鲁棒性差的缺点.文献[19 ]以扩展卡尔曼滤波(Extended Kalman filter,EKF)算法为基础,通过EKF得到转子的位置和角速度.该估计算法既不需要机械参数的知识,也不需要转子的初始位置,利用改进滑模控制器取代PI控制器作为电流环调节器,提高了系统性能. ...
基于EKF的PMSM 滑模控制策略研究
1
2021
... 然而,滑模控制的缺点是由算法的高频切换引起的抖振现象.许多学者针对减小或消除抖振现象提出了不同的方法.文献[16 ]提出了一种自适应一阶滑模控制器(Sliding mode controller,SMC),其中包括设计各种趋近律方法、滑动面、高阶SMC和复合SMC.许多SMC的变种已被提出,超螺旋滑模控制(Super twisting sliding mode controller,STSMC)技术引起了广泛关注,特别是对于控制律出现在滑动变量一阶导数中的系统.文献[17 ]提出了一种实时STSMC来控制电机转子磁链和机械转速,并提出了一种一阶SMO来估计磁链和负载转矩,在实现无位置传感器和减少抖振方面发挥了关键的作用.文献[18 ]结合了STSMC和积分SMC方案的属性,提出了一种基于积分超螺旋滑模控制的感应电机无传感器预测电流控制,解决了传统PI控制鲁棒性差的缺点.文献[19 ]以扩展卡尔曼滤波(Extended Kalman filter,EKF)算法为基础,通过EKF得到转子的位置和角速度.该估计算法既不需要机械参数的知识,也不需要转子的初始位置,利用改进滑模控制器取代PI控制器作为电流环调节器,提高了系统性能. ...
Research on PMSM sliding mode control strategy based on EKF
1
2021
... 然而,滑模控制的缺点是由算法的高频切换引起的抖振现象.许多学者针对减小或消除抖振现象提出了不同的方法.文献[16 ]提出了一种自适应一阶滑模控制器(Sliding mode controller,SMC),其中包括设计各种趋近律方法、滑动面、高阶SMC和复合SMC.许多SMC的变种已被提出,超螺旋滑模控制(Super twisting sliding mode controller,STSMC)技术引起了广泛关注,特别是对于控制律出现在滑动变量一阶导数中的系统.文献[17 ]提出了一种实时STSMC来控制电机转子磁链和机械转速,并提出了一种一阶SMO来估计磁链和负载转矩,在实现无位置传感器和减少抖振方面发挥了关键的作用.文献[18 ]结合了STSMC和积分SMC方案的属性,提出了一种基于积分超螺旋滑模控制的感应电机无传感器预测电流控制,解决了传统PI控制鲁棒性差的缺点.文献[19 ]以扩展卡尔曼滤波(Extended Kalman filter,EKF)算法为基础,通过EKF得到转子的位置和角速度.该估计算法既不需要机械参数的知识,也不需要转子的初始位置,利用改进滑模控制器取代PI控制器作为电流环调节器,提高了系统性能. ...
Strict Lyapunov functions for the super-twisting algorithm
1
2012
... 文献[20 ]为超螺旋算法的稳定条件提供了证明.空间向量为 ...