非晶合金电机性能分析及铜耗优化

doi:10.11985/2024.01.017

非晶合金电机性能分析及铜耗优化

宋祎轩^,, 吴旭升^,, 高嵬^,

海军工程大学电气工程学院武汉 430033

Performance Analysis and Copper Loss Optimization of Amorphous Alloy Motor

SONG Yixuan^,, WU Xusheng^,, GAO Wei^,

School of Electrical Engineering, Naval University of Engineering, Wuhan 430033

通讯作者: 高嵬，男，1980年生，博士，讲师。主要研究方向为电机与电器及其控制。E-mail：depkin@163.com

收稿日期: 2023-05-12 修回日期: 2023-08-11

Received: 2023-05-12 Revised: 2023-08-11

作者简介 About authors

宋祎轩，男，1996年生，硕士研究生。主要研究方向为电机设计优化。E-mail：syx620@qq.com;

吴旭升，男，1976年生，博士，教授。主要研究方向为电力集成技术。E-mail：wuxusheng0111@163.com

摘要

针对新型软磁材料非晶合金在电机中的应用对电机性能影响的问题，首先测试对比分析了新型软磁材料与普通硅钢材料损耗等性能，验证了其应用于高效电机的可行性，然后对同结构的非晶合金电机和传统硅钢电机进行了初步对比分析，研究表明非晶合金电机铁耗仅为传统硅钢的10%左右，但其铜耗升高28%左右，致使电机效率提升效果不明显。最后针对非晶合金电机铜耗产生机理进行了分析，根据电机铜耗增加的原因，对电机结构有针对性地进行调整优化。对优化前后电机铜耗、铁耗以及效率等电机性能参数进行对比分析，研究结果表明优化后电机本体效率可达到98.14%，相对优化前提升1.012%，比传统硅钢电机效率提高1.54%。

关键词： 新型软磁电机; 电机优化; 电机铜耗; 高效电机; 永磁电机

Abstract

Aiming at the influence of the application of new soft magnetic material amorphous alloy in motor on the performance of motor, firstly, the loss and other properties of the new soft magnetic material and ordinary silicon steel are tested and compared, and the feasibility of its application in high-efficiency motor is verified. Then the comparative analysis of the same structure two motors that the amorphous alloy motors and traditional silicon steel motors is conducted. It shows that the core loss of amorphous alloy motor is only about 10% of that of traditional silicon steel, but its copper loss increases by about 28%, so the effect of improving motor efficiency is not obvious. Finally, the reasons for the increase of copper loss of amorphous alloy motor are analyzed. According to the reasons for the increase of copper loss, the motor structure is adjusted and optimized. The performance parameters of the motor such as copper loss, core loss and efficiency before and after optimization are compared and analyzed. The research results show that the efficiency of the motor body after optimization can reach 98.14%, which is 1.012% higher than that before optimization, and 1.54% higher than that of the traditional silicon steel motor.

Keywords： New soft magnetic motor; motor optimization; copper loss of motor; high efficiency motor; permanent magnet motor

PDF (26427KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

宋祎轩, 吴旭升, 高嵬. 非晶合金电机性能分析及铜耗优化[J]. 电气工程学报, 2024, 19(1): 159-168 doi:10.11985/2024.01.017

SONG Yixuan, WU Xusheng, GAO Wei. Performance Analysis and Copper Loss Optimization of Amorphous Alloy Motor[J]. Chinese Journal of Electrical Engineering, 2024, 19(1): 159-168 doi:10.11985/2024.01.017

1 引言

2021年，“碳达峰”“碳中和”写入政府工作报告，我国力争在2030年前“碳达峰”，在2060年前实现“碳中和”。电机在能源输出和消耗中有着重要的地位，电机系统用电量占我国工业用电量的2/3，约为全国用电量的60%，低损耗高效率的节能电机仍然是未来电机发展的主要方向^[1]。国防军工、特殊工业、高端民用等领域对低噪声、低损耗、高效率、宽调速范围的高效电机的需求十分紧迫。

非晶态软磁材料是一种新型软磁材料，应用兴起于20世纪70年代末，非晶态原子排列短程有序，长程无序，大幅降低了材料的各向异性，在结构上有利于获得高的磁导率和较低的矫顽力，目前常用的非晶合金软磁材料中，铁基非合金与其他材料相比，其磁性更强(饱和磁感应强度达1.4~1.7 T)，磁导率、激磁电流和铁损等软磁性能均优于传统硅钢，且价格便宜，节能效果显著^[2⇓-4]。文献[5]采用水冷铜坩埚感应熔炼或相变致冷等铸造技术铸造出较大尺寸的块体非晶合金铸件，推进了非晶材料在电机领域大规模应用的可能。文献[6-7]采用组合型磁极与Halbach阵列相结合的方法，优化设计了一台36 000 r/min、12 kW的4极表贴式非晶合金高速永磁同步电机，采用1 mm铝合金夹2 mm硅钢的复合夹片将非晶合金定子分4段的结构，优化后电机的最高齿部温度由110 ℃降低到96 ℃。文献[8-9]用非晶合金铁心设计制造了一台2.1 kW径向磁通非晶合金永磁电机和一台7 kW轴向磁通非晶合金永磁电机，研究表明高频非晶合金永磁电机相比于传统硅钢片永磁电机，铁耗优势十分明显。文献[10-11]针对非晶合金永磁电机电磁振动噪声相关问题进行研究，提出一种综合考虑电磁力、磁致伸缩效应和叠片压紧力的电机电磁振动噪声数值计算方法，研究表明，磁通密度每增加0.2 T，不同频率下叠压铁心噪声增加2.8%~11.6%，卷绕铁心噪声增加2.3%~13.8%，频率每增加200 Hz，不同磁通密度下叠压铁心噪声增加1.6%~33.3%。文献[12]研究了非晶合金高速开关磁阻电机的电磁设计以及非晶合金高速开关磁阻电机的振动特性，研究表明，相比传统硅钢铁心的高速开关磁阻电机，非晶合金铁心电机能够降低铁损、提高效率，在额定工作点下，非晶合金方案铁心损耗仅为 B20AT1200硅钢方案铁心损耗的24.5%，非晶合金方案的效率比硅钢方案提高了4%，但是非晶合金电机的振动更为严重。文献[13-14]就非晶合金永磁无刷直流电机进行相关研究，提出了一种轴场永磁无刷直流电机，在额定转速下，非晶合金永磁无刷电机铁心损耗仅为输出功率的6%。文献[15]采用激光测试仪对非晶合金铁心材料的磁致伸缩特性进行测试分析，并建立铁心材料磁致伸缩特性的预估模型，当磁通密度为0.6 T时，最大损耗预测误差由30%降低到7.5%。文献[16]研究了非结构参数对非晶合金高速永磁电机振动噪声的影响，且磁致伸缩系数每增加10 000 nm/m，非晶合金永磁电机的噪声值大约增加2.6%。

非晶合金能够显著地降低损耗，但是目前大多数研究集中于高频高速领域^[17⇓-19]，对于中低频领域的研究相对较为匮乏。因此本文对中低频非晶合金电机进行相关研究，旨在进一步扩大非晶合金应用领域，助力高性能高效电机发展。本文首先根据传统电机设计方法进行相关设计，然后将电机定子材料由普通硅钢20WTG1500替换为铁基非晶合金材料1K101，对两个同结构不同定子材料的电机模型进行仿真分析，研究表明非晶合金电机能够显著地降低电机铁心损耗，但是电机定子铜耗有所上升，要想非晶合金在中低频领域得到应用，解决电机铜耗问题是一个十分重要的问题。因此根据新材料特性，对电机定子铜耗进行解析计算，分析影响电机定子铜耗产生的机理，对电机结构进行优化调整，最后对优化前后的电机模型进行仿真对比分析。研究表明通过铜耗优化，同结构电机，非晶合金电机与传统硅钢电机铜耗相近的情况下，其铁耗仅为传统硅钢电机的10%，电机效率可达98.14%，电机效率得到了有效提升。本文研究从电机本体设计的根本上降低新材料增加的电机定子铜耗，有效地提升了电机效率，也为后续非晶合金电机的应用与研究提供一定的参考。

2 软磁材料及电机性能对比分析

2.1 软磁材料测试分析

本次测试旨在获取非晶合金与普通硅钢在相同环境下各个工作频率段的电磁性能，为后续新型软磁材料电机的相关设计、仿真试验以及对比分析等做铺垫。测试方案及铁心环样尺寸形状均参照《GB/T 3658—2008软磁材料交流磁性能环形试样的测量方法》严格制定。

本次测试选取牌号为1K101的非晶合金和普通低损耗硅钢20WTG1500两种材料进行测试。测试装置使用联众MATS-3000M材料测量装置，如图1所示，该装置原理基于国家标准中要求的伏安法测定，采用集成组合装置，可方便测出相应材料的性能，在相同环境下对两种材料进行测试。测试环样采用内径35 mm，外径42 mm卷绕环样，内外径比为1.2，符合相应国家标准要求，测试环样如图1所示。电机铁心都进行退火处理，因此本文分析均基于退火处理后的材料。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 试验测试装置与测试环样

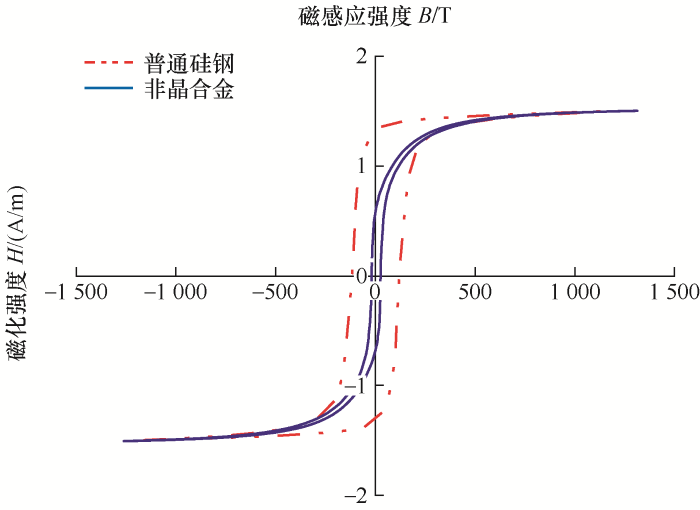
测试所得两种材料在同频率下的磁滞回线如图2所示，横坐标B为材料磁感应强度，纵坐标H为材料磁化强度。对比两种材料磁滞回线可以看出，非晶合金的矫顽力、剩磁和曲线闭合面积均小于普通硅钢材料。因此新型软磁材料非晶合金的软磁性要优于普通硅钢材料，磁滞损耗要远低于普通硅钢材料。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 磁滞回线对比曲线

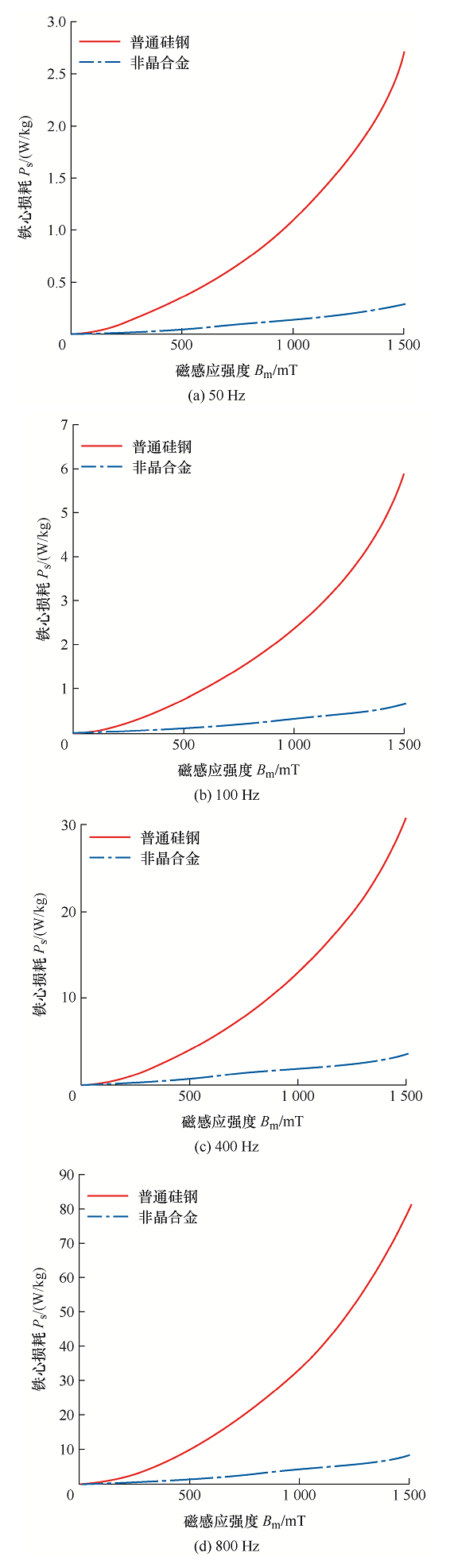
频率为50 Hz、100 Hz、400 Hz、800 Hz时，新型软磁材料非晶合金1K101和普通硅钢材料20WTG1500损耗对比曲线分别如图3a~3d所示，实曲线为普通硅钢材料，划点曲线为非晶合金材料，横坐标B_m为磁感应强度，P_s为材料铁心损耗。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 不同频率下材料损耗对比曲线

对两种材料的损耗曲线进行分析可以明显看出，无论低频还是中高频，新型软磁材料铁心损耗都要远低于普通硅钢材料。通过数据计算分析可得，非晶合金材料铁心损耗相对于普通硅钢情况如下：50 Hz，1.5 T时下降89.45%，1.2 T时下降88.55%；100 Hz，1.5 T时下降88.78%，1.2 T时下降87.4%；400 Hz，1.5 T时下降88.51%，1.2 T时下降87.59%；800 Hz，1.5 T时下降89.97%，1.2 T时下降88.87%。

材料性能的测试初步证明了新型软磁材料相对于普通硅钢在全频率段具有低损耗的优势，将前期测试得到的相应电磁性能数据导入有限元仿真材料库中，进行仿真验证试验，进一步证明非晶合金材料应用于电机进而提升电机效率的可行性。

2.2 电机仿真对比分析

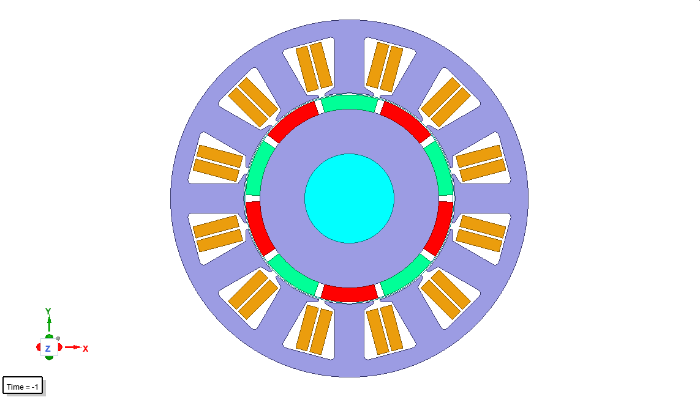
因舰船工作环境特殊性的要求，使得中低速大转矩的调速永磁无刷电机需求较大。但非晶合金电机尺寸设计目前还受带材宽度制约，因此设计过程中要充分考虑带材影响。设计前期经调研可知，目前非晶带材加工定子外径最大为210 mm，超过尺寸的也可采用定子拼接技术，但是拼接定子加工难度大、成本高，同时连接处有空气隙以及连接点等会带来新问题。考虑到舰船用电机的安全稳定性，本次定子外径设计尺寸严格保持在210 mm以内。本次设计首先根据传统硅钢电机设计方法设计一款25 kW、1 700 r/min的正弦波驱动表贴式三相永磁无刷调速电机，永磁体采用平行充磁方式，然后建立定子铁心材料不同的电机模型如图4所示，最后结合有限元仿真分析，对比其工作特性，并根据实际情况对非晶合金电机结构进行适当修正优化。电机初始结构参数如表1所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 电机模型

表1 电机初始主要结构参数

参数	数值
额定功率/kW	25
额定电压/V	380
额定转速/(r/min)	1 700
定子内/外径/mm	145/210
转子内/外径/mm	44/143
定/转子铁心/mm	180/180
每槽导体数	30
极槽配合	10极12槽

新窗口打开| 下载CSV

对电机在1 700 r/min额定工况下进行有限元仿真试验。测得两台电机主要损耗、效率等参数结果进行对比，并以传统硅钢电机性能为基准，对同工况下非晶合金电机运行性能参数进行对比计算，非晶合金电机性能相对于传统硅钢电机变化参数变化情况如表2所示。

表2 电机仿真结果

性能	定子材料			参数变化率(%)
性能	普通硅钢	非晶合金		参数变化率(%)
铁心损耗/W 定子铜耗/W 效率(%)	323.486 557.122 96.598		23.499 715.975 97.128	-92.74
				+28.51
				+0.53

新窗口打开| 下载CSV

通过计算可得，在额定值工况下，电机定子铁耗降低92.74%，效果明显，但是铜耗增加28.51%，致使电机效率仅提升0.53%。因此将电机定子材料直接简单地替换为非晶合金，对于电机能效提升并不明显。需要针对非晶合金材料的特殊性，在普通硅钢电机设计的基础上进行修正、优化调整，得到适合非晶合金材料的电机结构尺寸。

3 非晶合金电机铜耗分析

由第2节可知，非晶合金在低频领域虽然能显著降低铁心损耗，但仿真试验表明，当电机计算电磁功率保持不变时，非晶合金电机定子铜耗有所上升，导致电机效率提升并不明显。因此传统硅钢电机的部分结构参数设计方法并不完全适用于非晶合金。要在低频领域推进非晶合金永磁电机，必须分析其铜耗增加的原因，并针对其增加原因进行结构调整，以求电机铁耗大幅度降低的同时铜耗不能增加过多，从而得到更高的电机效率。

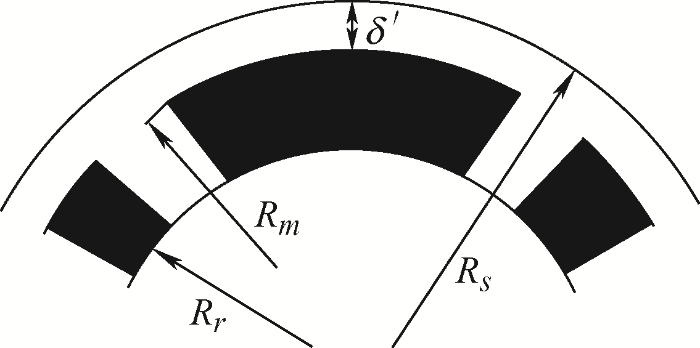
对材料性能分析可知，非晶合金电机相对于普通硅钢电机，其电阻率大于普通硅钢材料且工作磁密与饱和磁密较低，从而会影响电机气隙磁密，直接影响电机电枢绕组感应电动势等相关参数。因此对电机气隙磁密进行径向与切向解析再合成计算，忽略电机铁心齿槽的影响，电机气隙近似均匀。因此电机有效气隙长度为^[18]

(1)$ \delta^{\prime}=k_{\delta} \delta$

式中，$\delta $为气隙长度；${{k}_{\delta }}$为气隙系数；${\delta }'$为有效气隙长度，电机部分磁极与气隙结构示意图如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 电机部分永磁体与气隙结构图

假设铁心磁导率无穷大，设定气隙与永磁体为求解域，则在求解域内

(2)$ \left\{\begin{array}{l}B_{1}=\mu_{0} \boldsymbol{H}_{1} \\B_{2}=\mu_{0} \mu_{r} \boldsymbol{H}_{2}+\mu_{0} \boldsymbol{M}_{0}\end{array}\right.$

式中，B₁为空气域磁密；B₂为永磁体磁密；${{\mu }_{r}}$为相对磁导率；$ \boldsymbol{M}_{0}$为矢量剩磁强度矢量，可表示为

(3)$ \boldsymbol{M}_{0}=M_{r} r+M_{\theta} \theta$

式中，$ \boldsymbol{M}_{r}$表示径向分量；$ M_{\theta}$表示切向分量。

根据电磁场相关原理，用标量磁位$ \varphi$求解，气隙与永磁体满足^[20]

(4)$ \left\{\begin{array}{l}\nabla^{2} \varphi=0(\text { 气隙 }) \\\nabla^{2} \varphi=\frac{\operatorname{div} \boldsymbol{M}_{0}}{\mu_{r}}(\text { 永磁体 })\end{array}\right.$

式中，$\text{div}{{\mathbf{M}}_{0}}=\frac{{{M}_{r}}}{r}+\frac{\partial {{M}_{r}}}{\partial r}+\frac{1}{r}\frac{\partial {{M}_{\theta }}}{\partial \theta }$。

对于平行充磁永磁体，$ M_{r}=M_{0} \cos \theta$，$ M_{\theta}=M_{0} \sin \theta$，因此其径向、切向分量可分别表示为

(5)$ M_{r}=\left\{\begin{array}{ll}-M_{0} \cos \left(\theta+\frac{\pi}{p}\right) & -\frac{\pi}{p} \leqslant \theta \leqslant-\frac{\pi}{p}+\frac{\alpha_{p} \pi}{2 p} \\0 & -\frac{\pi}{p}+\frac{\alpha_{p} \pi}{2 p}<\theta<-\frac{\alpha_{p} \pi}{2 p} \\M_{0} \cos \theta & -\frac{\alpha_{p} \pi}{2 p} \leqslant \theta \leqslant \frac{\alpha_{p} \pi}{2 p} \\0 & \frac{\alpha_{p} \pi}{2 p}<\theta<\frac{\pi}{p}-\frac{\alpha_{p} \pi}{2 p} \\-M_{0} \cos \left(\theta-\frac{\pi}{p}\right) & \frac{\pi}{p}-\frac{\alpha_{p} \pi}{2 p} \leqslant \theta \leqslant \frac{\pi}{p}\end{array}\right.$

(6)$ M_{\theta}=\left\{\begin{array}{ll}M_{0} \sin \left(\theta+\frac{\pi}{p}\right) & -\frac{\pi}{p} \leqslant \theta \leqslant-\frac{\pi}{p}+\frac{\alpha_{p} \pi}{2 p} \\0 & -\frac{\pi}{p}+\frac{\alpha_{p} \pi}{2 p}<\theta<-\frac{\alpha_{p} \pi}{2 p} \\-M_{0} \sin \theta & -\frac{\alpha_{p} \pi}{2 p} \leqslant \theta \leqslant \frac{\alpha_{p} \pi}{2 p} \\0 & \frac{\alpha_{p} \pi}{2 p}<\theta<\frac{\pi}{p}-\frac{\alpha_{p} \pi}{2 p} \\M_{0} \sin \left(\theta-\frac{\pi}{p}\right) & \frac{\pi}{p}-\frac{\alpha_{p} \pi}{2 p} \leqslant \theta \leqslant \frac{\pi}{p}\end{array}\right.$

式中，${{\alpha }_{p}}$为极弧系数。

磁化强度的径向与切向分量可用傅里叶级数展开

(7)$ M_{r}=\sum_{n=1,3,5, \ldots}^{\infty} M_{m} \cos n p \theta$

(8)$ M_{\theta}=\sum_{n=1,3,5, \ldots}^{\infty} M_{\theta n} \sin n p \theta$

(9)$ \left\{\begin{array}{l}M_{m}=\frac{B_{r}}{\mu_{0}} \alpha_{p}\left\{\frac{\sin \left[(n p+1) \frac{\alpha_{p} \pi}{p}\right]}{(n p+1) \frac{\alpha_{p} \pi}{p}}+\frac{\sin \left[(n p-1) \frac{\alpha_{p} \pi}{p}\right]}{(n p-1) \frac{\alpha_{p} \pi}{p}}\right\} \\M_{\theta n}=\frac{B_{r}}{\mu_{0}} \alpha_{p}\left\{\frac{\sin \left[(n p+1) \frac{\alpha_{p} \pi}{p}\right]}{(n p+1) \frac{\alpha_{p} \pi}{p}}-\frac{\sin \left[(n p-1) \frac{\alpha_{p} \pi}{p}\right]}{(n p-1) \frac{\alpha_{p} \pi}{p}}\right\}\end{array}\right\}$

在极坐标系下，标量磁位$\varphi $满足

(10)$ \left\{\begin{array}{l}\frac{\partial^{2} \varphi_{1}}{\partial r^{2}}+\frac{1}{r} \frac{\partial \varphi_{1}}{\partial r}+\frac{1}{r^{2}} \frac{\partial^{2} \varphi_{1}}{\partial \theta^{2}}=0(\text { 空气 }) \\\frac{\partial^{2} \varphi_{2}}{\partial r^{2}}+\frac{1}{r} \frac{\partial \varphi_{2}}{\partial r}+\frac{1}{r^{2}} \frac{\partial^{2} \varphi_{2}}{\partial \theta^{2}}=\frac{M_{r}}{r \mu_{r}}(\text { 永磁体 })\end{array}\right.$

磁位${{\varphi }_{1}}$和${{\varphi }_{2}}$和$H$的关系式为

(11)$ \left\{\begin{array}{l}H_{r}=-\frac{\partial \varphi}{\partial r} \\H_{\theta}=-\frac{1}{r} \frac{\partial \varphi}{\partial r}\end{array}\right.$

其定解条件为

(12)$ \left\{\begin{array}{l}\left.H_{\theta 1}(r, \theta)\right|_{r=R_{s}}=0 \\\left.H_{\theta 2}(r, \theta)\right|_{r=R_{s}}=0 \\\left.B_{r 1}(r, \theta)\right|_{r=R_{m}}=\left.B_{r 2}(r, \theta)\right|_{r=R_{m}} \\\left.H_{\theta 1}(r, \theta)\right|_{r=R_{m}}=\left.H_{\theta 2}(r, \theta)\right|_{r=R_{m}}\end{array}\right.$

由式(1)~(12)可求得求解域内磁场分布表达式。气隙磁密径向、切向分量可分别表示为

(13)$ B_{r1}(r,\theta)=\sum_{n=1,2,3,\cdots}^{\infty}\frac{\mu_{0}M_{n}}{\mu_{r}}\frac{np}{\left(np\right)^{2}-1}\Bigg[\Bigg(\frac{r}{R_{m}}\Bigg)^{np-1}+\Bigg(\frac{R_{s}}{r}\Bigg)^{np+1}\Bigg(\frac{R_{s}}{R_{m}}\Bigg)^{np-1}\Bigg]\times\\\left\{\frac{\left[\left(np-\frac{1}{np}\right)\frac{M_{m}}{M_{n}}+\frac{1}{np}-1\right]+2\left(\frac{R_{r}}{R_{m}}\right)^{np+1}-\left[\left(np-\frac{1}{np}\right)\frac{M_{m}}{M_{n}}+\frac{1}{np}-1\right]\left(\frac{R_{r}}{R_{m}}\right)^{2np}}{\frac{\mu_{r}+1}{\mu_{r}}\Bigg[\left(\frac{R_{s}}{R_{m}}\right)^{2np}-\left(\frac{R_{r}}{R_{m}}\right)^{2np}\Bigg]-\frac{\mu_{r}-1}{\mu_{r}}\Bigg[1-\frac{\left(R_{s}R_{r}\right)^{2np}}{R_{m}^{4np}}\Bigg]}\cos np\theta\right.$

(14)$ \begin{array}{c}B_{\theta 1}(r, \theta)=\sum_{n=1,3,5, \cdots}^{\infty} \frac{\mu_{0} M_{n}}{\mu_{r}} \frac{n p}{(n p)^{2}-1}\left[\left(\frac{r}{R_{m}}\right)^{n p-1}-\left(\frac{R_{s}}{r}\right)^{n p+1}\left(\frac{R_{s}}{R_{m}}\right)^{n p-1}\right] \times \\\left\{\frac{\left[\left(n p-\frac{1}{n p}\right) \frac{M_{m}}{M_{n}}+\frac{1}{n p}-1\right]+2\left(\frac{R_{r}}{R_{m}}\right)^{n p+1}-\left[\left(n p-\frac{1}{n p}\right) \frac{M_{m}}{M_{n}}+\frac{1}{n p}-1\right]\left(\frac{R_{r}}{R_{m}}\right)^{2 n p}}{\frac{\mu_{r}+1}{\mu_{r}}\left[\left(\frac{R_{s}}{R_{m}}\right)^{2 n p}-\left(\frac{R_{r}}{R_{m}}\right)^{2 n p}\right]-\frac{\mu_{r}-1}{\mu_{r}}\left[1-\frac{\left(R_{s} R_{r}\right)^{2 n p}}{R_{m}^{4 n p}}\right]}\right\} \sin n p \theta\end{array}$

代入相关数值经过计算，普通硅钢电机气隙平均磁密为0.755 T，而非晶合金电机气隙平均磁密为0.695 T。

正弦波驱动永磁无刷电机每极磁通为

(15)$ \Phi=B_{\delta a v} \tau l_{e f}$

由式(15)可知，非晶合金电机气隙磁密的降低会使得非晶合金电机每极磁通相对于普通硅钢电机有所下降，同时每极磁通会影响电机感应电电动势，电枢绕组感应电动势为

(16)$ E=4 K_{N m} f N_{0} K_{d p} \Phi$

式中，E为电枢感应电动势；${{K}_{Nm}}$为气隙磁场波形系数；$f$为电流频率；${{N}_{0}}$为电枢绕组每相串联匝数；${{K}_{dp}}$为电枢绕组系数；$\Phi $为每极磁通。

由式(16)可知，每极磁通的降低会降低电机感应电动势。电机电磁计算功率为

(17)$ P^{\prime}=m E I$

式中，${P}'$为计算功率；$m$为电机相数；$I$为电枢绕组相电流。

由式(17)可知，当电机电磁功率不变时，感应电动势的降低必然导致电枢电流的增加。电机绕组有效长度铜耗为

(18)$ P_{c u}=m 2 N R_{c e f} I^{2}$

式中，${{P}_{cu}}$为电机绕组有效长度铜耗；${{R}_{cef}}$为每根导体有效部分电阻。由式(18)可以看出，电枢电流的增加是非晶合金电机铜耗增加的直接原因。

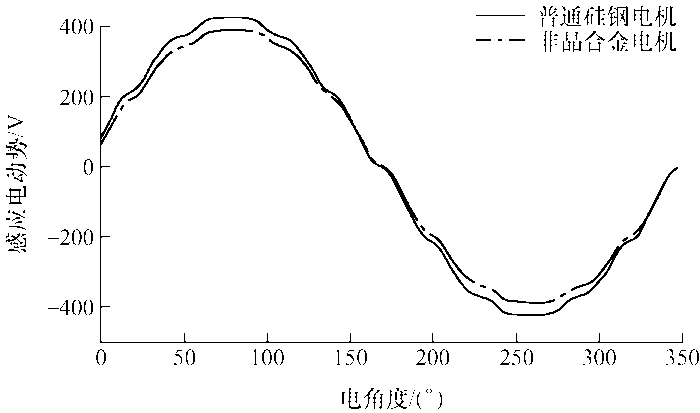
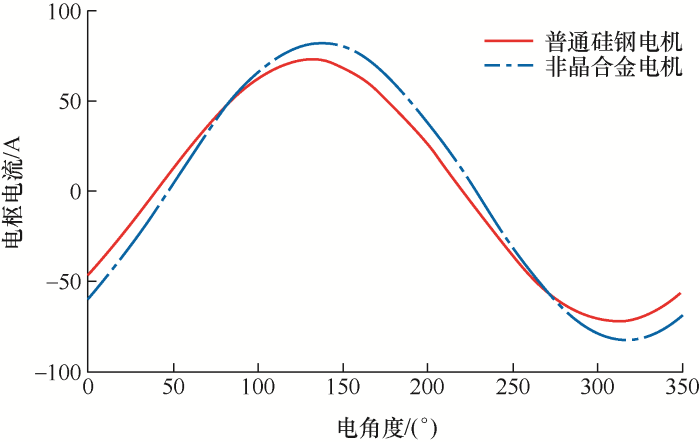
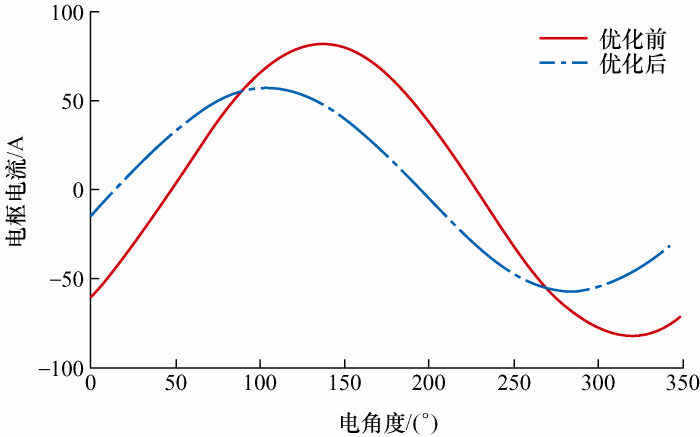
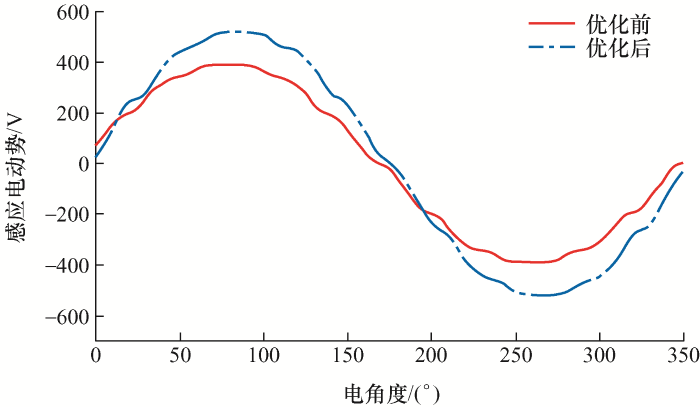
对电机绕组感应电动势和电流进行对比分析，电枢三相电流呈周期分布，为方便对比分析，电枢电流仅选取A相电流进行对比分析。普通硅钢和非晶合金感应电动势对比如图6所示，电枢电流对比如图7所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 电机电枢感应电动势对比图

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 电机电枢电流对比图

由图6、7可以看出，相对于普通硅钢电机，非晶合金电机感应电动势明显降低，而电枢电流有明显增加，仿真结果与上述理论分析保持一致。

由式(18)分析可知要降低电机铜耗，需要降低电机电枢电流，但是电枢电流降低不能降低电机计算电磁功率，根据式(17)分析可知，要在保持电机计算电磁功率不变的情况下降低电机铜耗，需要降低电枢电流，增加电机的感应电动势，因此由式(16)可知，要增加电机感应电动势可通过增加电机磁通来实现，再由式(15)可知，要增加电机磁动势可适当增加电机铁心长度来实现。另一方面降低电枢电流，可从电机设计中进行分析，线负荷A为

(19)$A=\frac{2m{{N}_{0}}I}{\pi D}$

式中，$A$为线负荷，$D$为电枢直径。

由式(19)可得电枢电流为

(20)$I=\frac{\pi DA}{2m{{N}_{0}}}$

由式(20)可知，通过增加电枢绕组每相串联匝数${{N}_{0}}$可降低电枢电流，从而达到降低电枢铜耗的目的，电枢绕组每相串联匝数可通过增加每槽导体数N实现。但电枢长度的增加会增加电枢绕组长度，电枢有效电阻为

(21)$ R_{c e f}=\rho \frac{l}{A_{0}}$

式中，$\rho $为电枢绕组电阻率；$l$为导体有效部分长度；${{A}_{0}}$为导体截面积。

由式(21)可知，电枢长度增加会增加电枢绕组等效电阻，电枢绕组电阻的增加会增加电机铜耗，电枢铁心长度的增加会增加电机铁心损耗，电枢长度增加导致绕组变长，绕组中阻值变大反而会在一定程度上增加电机铜耗，同时每槽导体数的增加也会增加绕组阻值，反而增加电机铜耗。因此，通过增加电枢长度增加感应电动势，增加每槽导体数降低电枢电流、电机铜耗，增加绕组以及每槽导体数导致阻值增加带来铜耗的增加存在一个最优的“平衡点”，且该优化方法仅在特定范围内存在。同时该优化使得电机制造中材料增加，必然使得成本有所增加，因此，该方法可主要应用于高端民用、军事国防等追求电机效率等性能为第一因素，经济成本不是主要考虑因素的场合。

4 非晶合金电机结构优化

对式(15)~(21)分析可知，可采取在一定范围内增加电机铁心长度或增加绕组每槽导体数方式降低非晶合金电机铜耗。考虑到电机制作工艺与通风冷却效率，结合电机设计主要尺寸比进行估算，电机铁心长度L优化范围为160~350 mm。同时每槽导体数N受电机槽满率约束，考虑到下线与散热问题，电机设计要求该电机槽满率不高于70%，经过计算，每槽导体数为30~40时电机槽满率为51.76%~69.02%，符合设计要求，因此，电机每槽导体数优化范围为30~40。

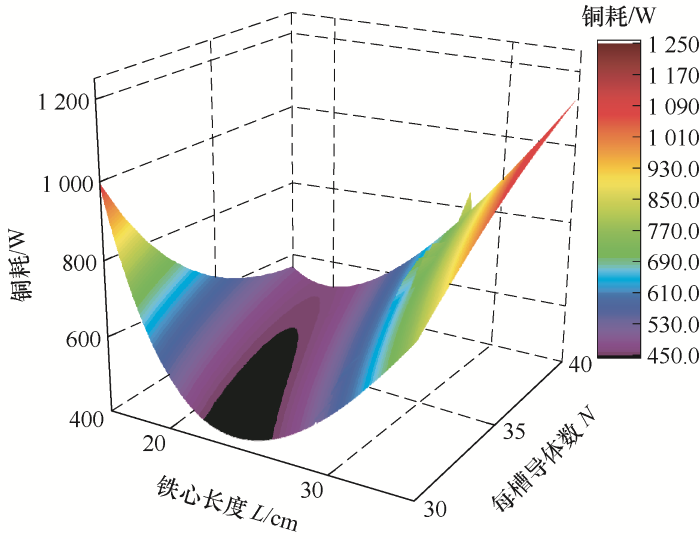
在每槽导体数与电机铁心优化范围内，结合有限元仿真软件对电机各个结构参数逐次排列，进行参数化分析，然后对电机性能的影响进行参数化分析。参数化分析电机铜耗随电机铁心长度与每槽导体数变化结果如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 电机铜耗参数化分析三维图

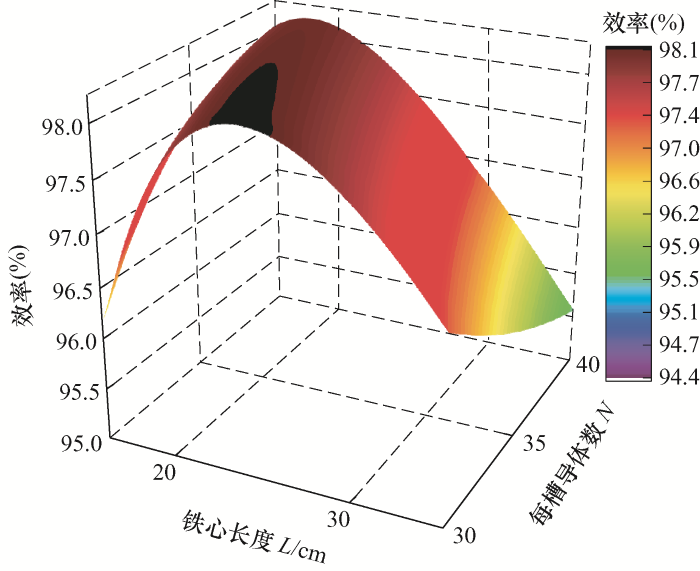
电枢铁心长度的增加还会增加电机铁心损耗，因此，在降低铜耗的同时也要考虑电机铁耗的增加，必须以电机效率最大为最终优化目的。因此，在相同范围内对电机效率也进行参数化优化分析，其分析结果如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 电机效率参数化分析三维图

结合图8、9可以看出，随着每槽导体数和铁心长度的增加，电机铜耗先降低再增加，图8中最低点黑色区域为铜耗最低范围，图9中最高点黑色区域为效率最大点，也是第3节中的“平衡点”区域，同时结合电机制造工艺实际情况，最终选取每槽导体数为36，铁心长度为200 mm为最优尺寸，然后对其进行有限元仿真试验验证分析。

5 电机优化前后性能对比分析

经过分析优化对比，该电机最终铁心长度L选取200 mm，每槽导体数N为36，对其进行有限元仿真验证。

首先对电枢电流进行对比分析，对比如图10所示，可以看出电枢电流有明显下降，经过计算，电枢电流有效值由优化前的58.04 A降低为40.10 A。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 非晶合金电机优化前后电枢电流对比图

由于电机功率保持不变，增加每槽导体数降低电枢电流，必然会导致感应电动势上升，优化前后感应电动势变化如图11所示。经过计算，电枢感应电动势幅值由优化前的389.34 V增加为519.01 V。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 非晶合金电机优化前后电枢电动势对比图

最后对优化前后电机性能进行计算分析，数据分析如表3所示。

表3 电机优化前后性能对比表

参数	优化前	优化后	优化后变化
电流有效值/A	58.06	40.10	-18.5
感应电动势峰值/V	389.34	519.01	+129.67
铁心损耗/W	23.50	26.10	+2.6
定子铜耗/W	715.98	447.87	-268.11
效率(%)	97.128	98.140	+1.012

新窗口打开| 下载CSV

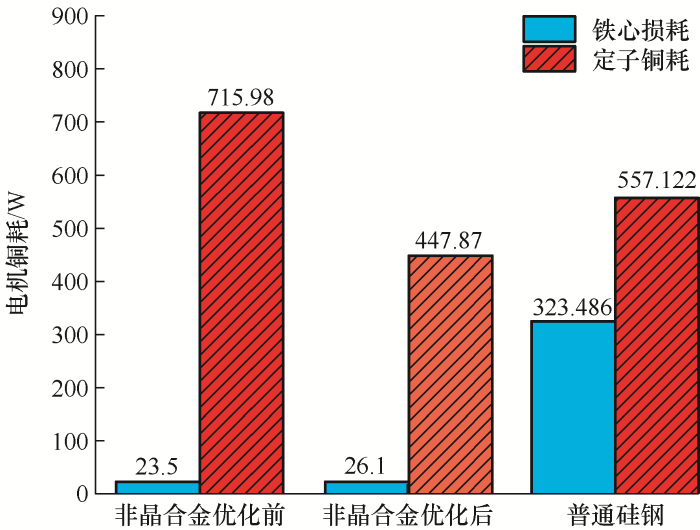
电机优化前后损耗对比如图12所示。由图12分析可得，经过结构优化，非晶合金电机铜耗由715.98 W降低到447.87 W，铜耗显著降低，相对于普通硅钢电机的557.122 W也优势明显，虽然铁耗由23.5 W增加到26.1 W，但电机总损耗仍然得到了有效降低。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 电机优化前后损耗对比图

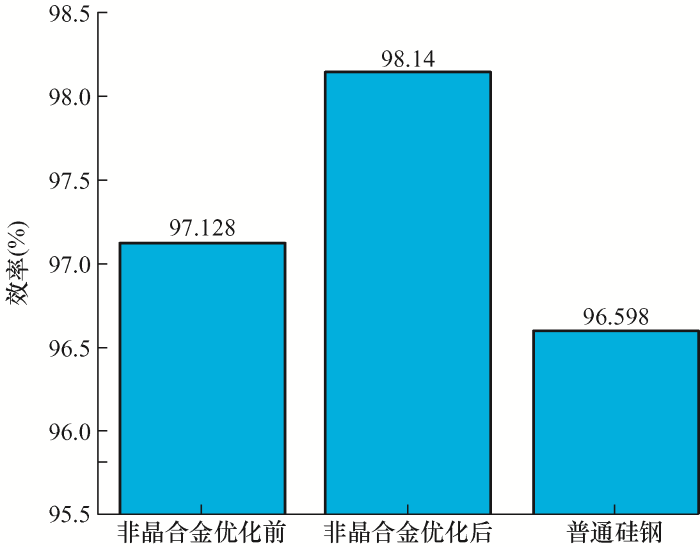
电机优化前后效率对比如图13所示，通过数据计算以及结合图13与表3分析，在忽略变频器等附加损耗的情况下，优化后电机本体效率可达98.14%，比优化前高出1.012%，比普通硅钢提高1.542%。但是不能忽视的是，由于优化增加了电机的铁心长度与每槽导体数，这种优化在效率上有所提升，但是在电机制作成本以及电机重量均会有所增加。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 电机优化前后效率对比图

6 结论

非晶合金的应用能够有效降低电机损耗，提升电机效率，本文找到了适合中低频非晶合金电机的最优结构，将非晶合金材料拓展到中低频电机领域应用，同时得到以下结论。

(1) 非晶合金可以显著降低电机铁耗，但是由于材料属性问题，与普通硅钢电机相比，同结构的非晶合金电机气隙磁密较低，导致电机感应电动势降低，在电机设计中要综合考虑非晶合金材料的优缺点，在合适的应用场合非晶合金材料才能体现出较大优势。

(2) 可通过适当增加电机铁心长度与每槽导体数，来降低电机铜耗。本文中的非晶合金电机经过优化，其电机铜耗显著降低，忽略变频器等附加损耗情况下电机本体效率可达98.14%，相对于传统硅钢电机效率提升1.542%，有效提高了电机效率，因此在效率为第一考虑因素的领域可优先使用非晶合金材料。

(3) 本文研究内容验证了非晶合金在中低频领域应用的可行性，拓展了非晶合金在电机领域的应用范围，顺应全球倡导的节能减排大趋势，可助力我国“双碳”事业的发展。

(4) 非晶合金材料可以有效降低电机铁耗，由此可推断非晶合金电机在温升上也有所优势，同时相关研究也表明其可以有效降低电机温升。本文研究内容有限，后续研究将对非晶合金电机温度场分析，探求非晶合金电机更多的优缺点，判断其更为合适的应用领域。

(5) 本文中电机优化使得其制作成本有所增加，该优化目前仍然存在一定的局限性，仅在特定范围内适用，但对于一般的相关研究可提供一定参考。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

国家发展改革委经济运行调节局,国家电网公司营销部,南方电网公司市场营销部.

电机系统节能技术[M]. 北京: 中国电力出版社, 2013.