1 引言
近年来,潜水电泵在农业排灌、矿产开采、抢险救灾等关系国民经济的重要场景中受到了越来越广泛的关注。维持电泵安全稳定的运行就是对人民财产和生命安全的最大保障。在实际工程中,潜水电机发生故障的概率在整个潜水电泵系统中占比最高,其中,又以局部过热导致绝缘失效,造成匝间短路故障最为常见。风冷和液冷[1]散热系统是两种常用的电机散热系统。其中风冷系统主要分为自然风冷系统和强迫风冷系统[2⇓-4],潜水电机系统通常采用强迫风冷系统,在尾部添加风扇,利用风扇旋转,提升风速流动,从而加强电机与空气的热交换。同时液冷系统在潜水电机中的应用也较为广泛,区别于机壳水冷和定子绕组水冷等通过在电机机壳或定子槽内布置水道对电机进行冷却的方式[5⇓-7],充水式潜水电机腔体内部充满冷却水,并通过叶轮带动冷却水在电机腔体内部循环,对电机进行散热。
文献[12-13]对定子端部的涡流损耗及温升采用有限元法做了仿真分析,并提出了一种以降低端部损耗和温升为目的的定子压板,降低了21.5%的定子压圈涡流损耗。电机的冷却方式、流体的流速及绝缘材料的选择都会对潜水电机的温升产生巨大的影响[14]。文献[15]对深井潜水电机的冷却结构进行了设计和优化,实现了潜水电机运行时的内外水循环,稳定时工作温度在59.7 ℃,避免了局部高温的问题。文献[16]建立了基于分区解耦的全局流体场传热模型,结合计算流体力学和传热学理论得到了电机内部零件的温度分布和流体流动状态,分析了流体流动状态对温度场的影响。文献[17]分析了电机温度场对相关因素的敏感性,定子铜耗及散热翅高度会影响电机整体的温升,其中,定转子温升和定子铜耗近似正比例变化,散热翅高度对电机冷却能力的影响随着高度增加不断减缓,定子绕组浸渍质量则主要对定子温升产生影响。
在电机温度场的计算过程中,定子槽内部分的等效模型直接关系到温度场仿真的精确度。电机的定子槽内包含漆包铜线、浸渍环氧树脂、空气、绝缘衬等,具有种类多、尺寸小的特点。在有限元计算中对上述物体进行单独建模不仅过程繁琐还会导致网格增加,计算时间增长,为了解决这些问题,国内外学者提出了多种等效模型。
目前对于干式潜水电机定子绕组的等效主要采用的是第一种等效模型,与风冷电机不同的是,湿式潜水电机单根导体由多根纯铜导线并绕而成,外部包裹1~3 mm厚的防水绝缘层,电机腔体内充满冷却水,所以传统的等效模型不适用于湿式潜水电机,需要提出新的等效模型。同时现有工作较少考虑充水式潜水电机内部冷却水循环过程以及定子槽内冷却水流动对电机温度场的影响。
本文对充水式潜水电机进行温度场计算,分析了充水式潜水电机的主要换热过程以及充水式潜水电机换热过程的数学模型,对温度场仿真过程中所需要的单值性条件进行了分析和计算,建立了充水式潜水电机包括冷凝器、外部水道及导流罩等组件在内的温度场计算模型。同时,对定子槽内区域进行等效,考虑了内部冷却水从定子槽内流过时对整体温升带来的影响。最后,搭建充水式潜水电机的试验平台,对电机的温升进行了测量。
2 充水式潜水电机结构特点及参数
2.1 充水式潜水电机结构特点
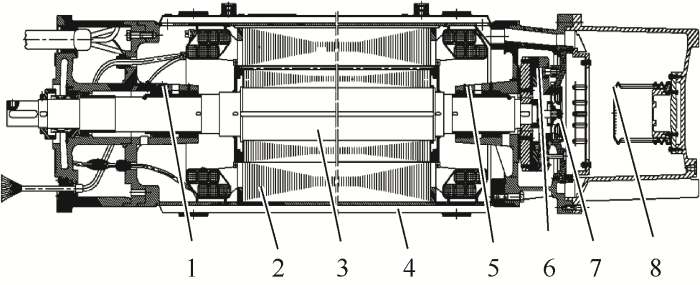
充水式潜水电机本质上就是一种特殊的三相笼型异步感应电动机。充水式潜水电机的整体结构如图1所示。充水式潜水电机腔体内部充满冷却水。因此,电机的定子绕组长时间工作在水中,定子绕组需要采用绝缘耐水线。电机腔体内部的冷却水在电机工作时会产生非常大的粘滞摩擦损耗,而定、转子采用开口槽无疑会加重电机的水摩擦损耗,尤其是转子采用开口槽时。所以在潜水电机的设计过程中,一般情况下定转子均采用闭口槽设计。为了避免绕组的振动,需要采用合适厚度的木制槽楔将耐水线压紧。
图1
2.2 电机参数
本文以一台QKSG500型充水式潜水电机为例,电机参数如表1所示。
3 充水式潜水电机换热过程
3.1 充水式潜水电机冷却结构
电机的散热和冷却是保证电机安全稳定运行的关键因素,随着潜水电机的不断发展,众多学者对潜水电机的冷却系统进行了改进,在考虑经济性和加工复杂程度的前提下最大化电机的冷却能力,设计了如下的冷却结构。
3.1.1 内部冷却过程
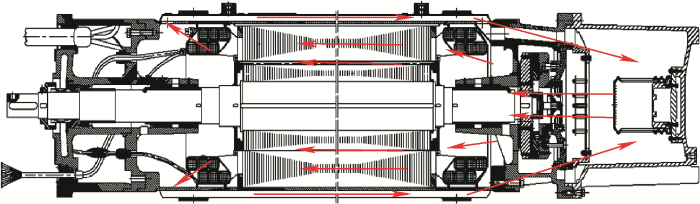
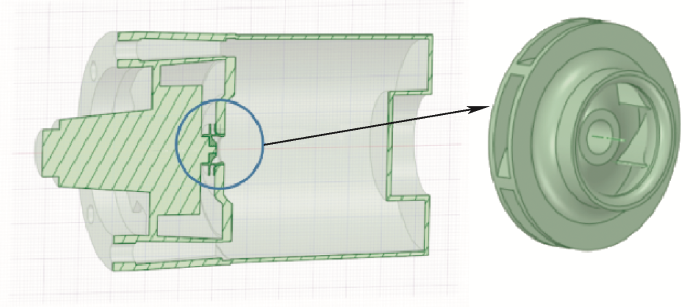
充水潜水电机的内部充满冷却水,电机内外水相互不连通。对于大型高压充水式潜水电机,由于其具有功率等级高、损耗及发热量大的特点,在电机转轴尾部加装一个泵轮来带动电机腔体内部冷却水循环。在叶轮的带动下,电机内部的冷水从尾部冷凝器流经电机端部绕组,进入气隙和定子槽,流至另一侧端部后经电机外部水道流回冷却器,如此往复,形成电机内部的水循环,其循环路径如图2中箭头所示。
图2
3.1.2 外部冷却过程
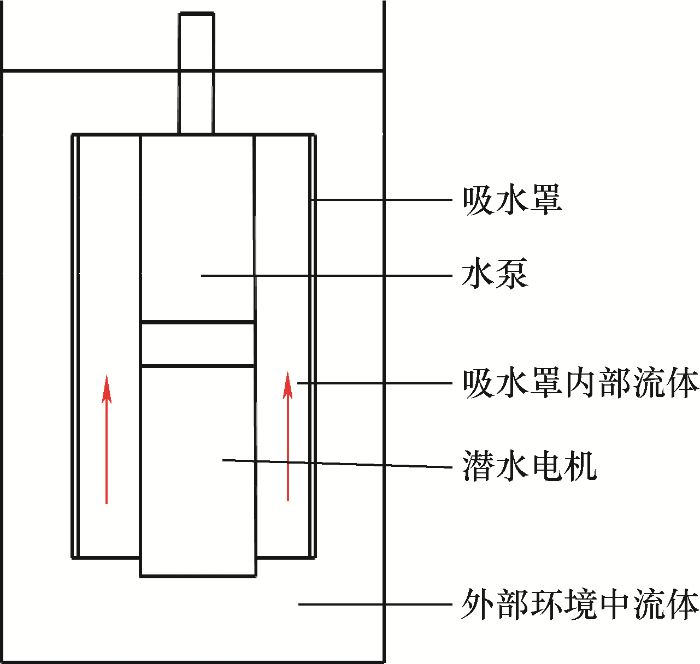
在充水式潜水电机的外部,除了内部冷却水流动的水道,还在电机表面焊有散热筋来加强电机表面的散热。此时,将电机放置在矿井、湖泊、海洋中时,电机表面会发生自然对流散热,电机表面水的流动可以忽略不计。为了进一步提高电机的散热能力,在电机外部加装吸水罩,水泵的入口在吸水罩内部,在潜水电泵运行时,外部水经吸水罩底部的滤网过滤后,在水泵的吸力下进入吸水罩的内部,流经机壳表面,对电机的表面进行冷却,最后被水泵抽出。此时在电机表面的自然对流过程就变为受迫对流过程,大大提高了电机的散热能力。吸水罩的结构以及工作原理如图3所示。
图3
3.2 传热方式
基本的传热方式有热传导、热对流、热辐射。在计算充水式潜水电机温升的过程中,除去上述的基本传热过程,最常见的传热过程是对流换热过程,对流换热过程发生在流体与固体的接触面。通常采用牛顿冷却定律对对流传热过程进行计算
式中,Φ为热流量;q为热流密度;A为传热表面积;h为表面传热系数;tw为近壁面流体温度;tf为远壁面流体温度。
从流体流动的原因分类,对流换热可以分为自然对流换热过程以及强制对流换热过程。在充水式潜水电机的换热过程中,由于电机内部泵轮带动内部冷却水流动,定转子表面和气隙内部的冷却水、绕组端部和冷却水以及外部水道和冷却水之间均是强制对流换热过程。电泵在工作时,水泵将机壳和吸水罩之间的水抽走,所以电机机壳外部也是强制对流换热过程。
4 导热过程中的单值性条件
传热过程中的单值性条件包括几何条件、物理条件、时间条件以及边界条件。在充水式潜水电机的温度场仿真分析中,几何条件对应着电机的几何形状以及各部分的尺寸,也就是充水式潜水电机温度场的计算模型,物理条件是电机所用材料的物性参数以及电机的内热源。本文求解的是充水式潜水电机的稳态导热过程,不考虑时间条件。
4.1 边界条件
第一类边界条件是已知任一瞬间导热体边界上的温度值;第二类边界条件是已知物体边界上热流密度的分布及变化规律;第三类边界条件规定了边界上物体与周围流体间的表面传热系数及周围流体的温度。将电机机壳外壁定义为第三类边界条件,机壳表面的散热系数通过下文模拟。
4.2 物理条件
4.2.1 物性参数
物理条件中的物性参数主要包括各项材料的密度、比热容以及热导率。热导率表征物体的导热能力,除了水,绝大多数金属和液体的热导率与温度成反比。比热容则反映材料的储热能力。本文所述充水式潜水电机中使用的材料物性参数如表2 所示。
表2 充水式潜水电机中材料物性参数
| 材料 | 热导率 λ/[W/(m·℃)] | 比热容 c/[kJ/(kg·℃)] | 密度 ρ/(kg/m3) |
|---|---|---|---|
| 电工用铜 | 394 | 0.385 | 8 930 |
| 绝缘材料 | 0.16 | 1.9 | 940 |
| 水 | 0.6 | 4.18 | 1 000 |
| 结构钢 | 39 | 0.463 | 7 840 |
上述材料均为各项同性材料,除去上述材料,电机中最重要的材料就是用来叠压定转子铁心的硅钢片,硅钢片本身的热导率与其组成成分和加工工艺相关。定、转子铁心由硅钢片叠压而成,为了防止片间短路故障,在硅钢片与硅钢片之间涂有绝缘漆。同时,在叠装硅钢片的过程中,片间还会残余气隙,空气与绝缘介质的导热能力远远小于硅钢片,这也就导致了定、转子铁心径向的导热能力优于轴向的导热能力。计算时为了简化建模及计算过程,将硅钢片以及片间的绝缘层等效成一个导热能力为各向异性的整体进行计算,等效后的铁心叠片在径向的热导率近似为硅钢片的热导率,在叠压方向的等效热导率为
式中,δFe为硅钢片的厚度;δ0为硅钢片间绝缘漆的厚度;KFe为定子铁心叠压系数;λ1为硅钢片的热导率;λ0为片间绝缘的热导率。
4.2.2 电机内热源
在三维温度场仿真中,充水式潜水电机的热源主要来自于机械损耗以及电气损耗,在电机的温度场计算过程中,对发热体施加载荷的方式主要有两种,一种是赋予发热体恒定的温度,另一种是将发热功率赋给发热体。本文采用第二种方法,并分别计算出定子铁心、定子绕组及转子鼠笼等各部分损耗,并根据损耗计算出电机各部分的发热功率加载在充水式潜水电机的温度场计算模型中,发热功率为
式中,Wq为发热体的损耗;V为发热体的体积。
4.3 充水式潜水电机温度场计算模型
4.3.1 基本假设
在建立充水式潜水电机温度场计算模型之前做出如下假设:① 充水式潜水电机表面的对流散热系数恒定,忽略电机中各项材料的物性条件随温度的变化;② 忽略定子绕组的集肤效应;③ 电机的损耗均匀地分布在电机的各个结构;④ 电机的水摩擦损耗作为热源加载在转子上;⑤ 充水式潜水电机的各项损耗全部用来产生热量,作为热源加载在温度场计算模型中。
4.3.2 机壳外部温度场计算模型
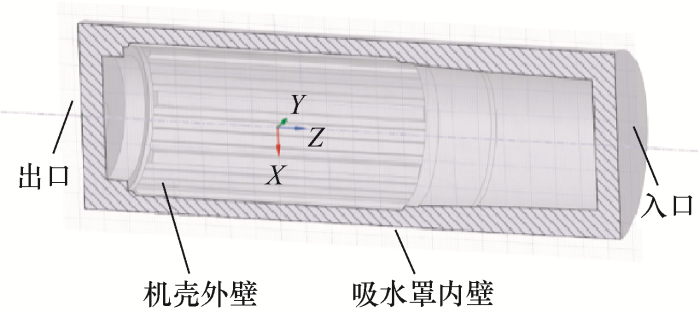
充水式潜水电机的工作方式决定了电机外部环境中流体的温度几乎保持不变,建立充水式电机外部、吸水罩内部流体的温度场计算模型,计算电机表面的对流换热系数,模型如图4所示。
图4
4.3.3 电机内部温度场计算模型
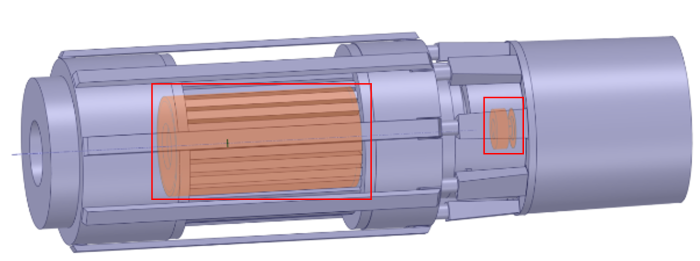
根据电机的尺寸参数,利用SpaceClaim建立电机的三维模型如图5所示,包括电机的端盖、机壳、水道、散热筋、定子、转子、转轴、冷却器等结构。
图5
图6
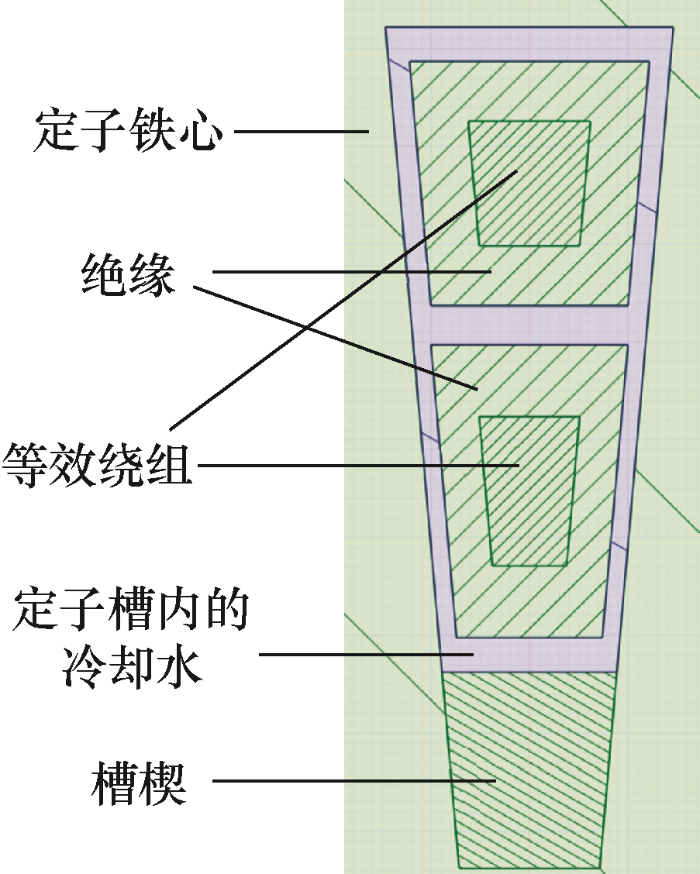
电机的定子槽内部结构等效模型如图7所示,槽楔单独建模放置在定子槽底部,将耐水线绝缘层和铜导体等体积分为两部分,并使绝缘层包裹着导体一上一下放置在槽内,周围则是冷却水。
图7
图8
4.3.4 网格剖分
图9
图10
5 充水式潜水电机稳态温度场的计算与分析
5.1 温度场仿真计算流程
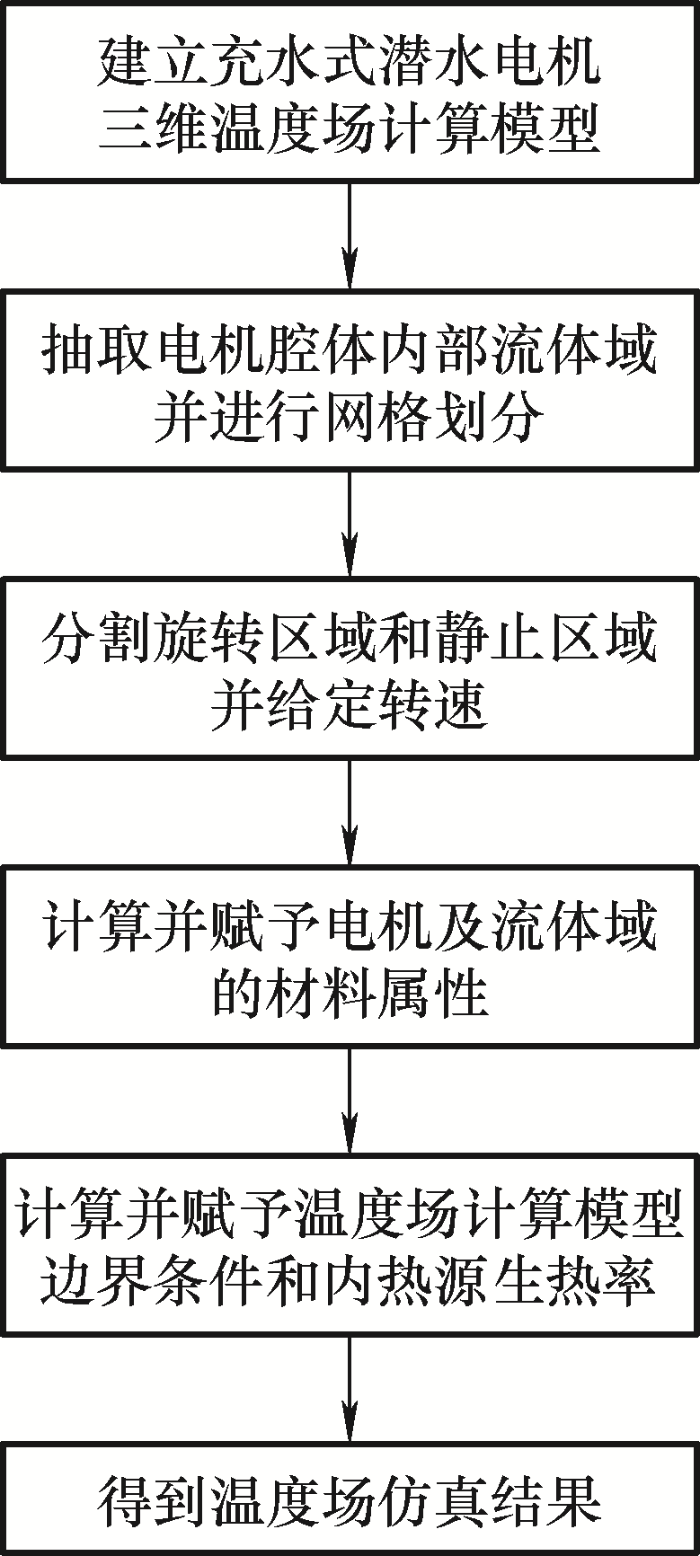
本文采用Fluent对充水式潜水电机进行温度场仿真计算,主要的流程如图11所示。首先,对充水式潜水电机模型执行体积抽取命令,得到电机腔体内部的流体域,同时分割旋转区域和静止区域并给定旋转区域的转速。将流体模型与电机模型同时导入Fluent并进行网格划分,对气隙、绕组等部位进行加密剖分。随后,将材料性质、边界条件、内热源发热量分别赋予计算模型,选择合适的湍流模型进行温度场求解,待仿真结果稳定后,得到充水式潜水电机温度场分布的结果。
图11
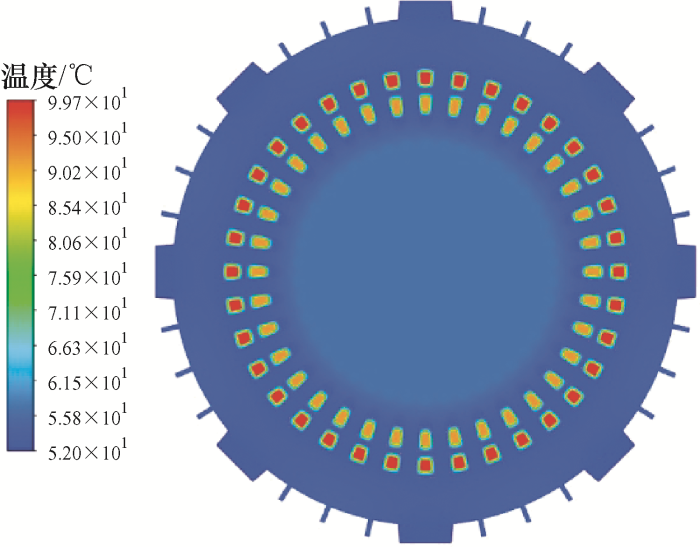
5.2 仿真结果分析
图12
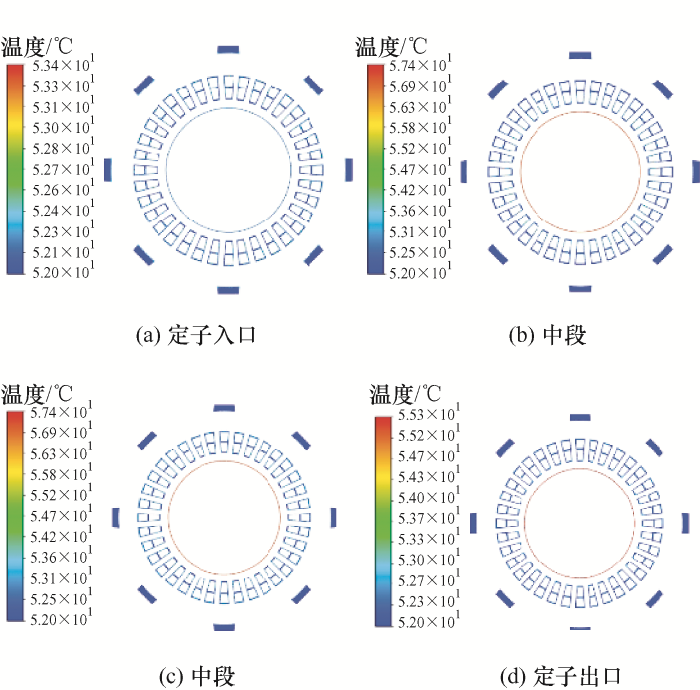
图13绘制了气隙与定子入口、出口以及中段的内部冷却水温度场分布情况,同时对应着外部水道的出口、入口以及水道中段。四个截面等距分布在定子轴向上。图13a为定子入口,图13d为定子出口。可以看到电机气隙中冷却水的温度高于定子槽内水的温升,定子槽入口处的温度最低为52.1 ℃,电机的中段温度最高为53.6 ℃,出口处的温度又有所下降为53 ℃。气隙出口与入口处的冷却水温度分别为53.4 ℃和55.3 ℃,相差1.9 ℃,定子槽内冷却水出口与入口的冷却水温度分别为52.1 ℃和53 ℃,相差0.9 ℃以内。电机气隙内的冷却水最高温度为57.4 ℃,相同位置的定子槽内冷却水温度为53.1 ℃,相差4.3 ℃,说明电机稳定运行时,转子的温升更高,需要进一步改善电机转子的散热条件。
图13
图14
图15
图16
6 试验结果对比分析
图17
表3 充水式潜水电机温升试验数据
| 时间 | 绕组A处温度/℃ | 绕组B处温度/℃ |
|---|---|---|
| 9∶14 | 42.0 | 45.5 |
| 9∶24 | 45.8 | 48.3 |
| 9∶34 | 46.7 | 49.8 |
| 9∶44 | 48.3 | 51.1 |
| 9∶54 | 48.8 | 48.9 |
| 10∶04 | 49.7 | 49.2 |
| 10∶14 | 47.4 | 49.6 |
| 10∶24 | 47.9 | 49.7 |
绕组A处温度为定子槽进口处绕组表面的温度,绕组B处温度为定子槽出口处绕组表面温度。可以看出在电机达到稳定状态后,定子槽进出口温度分别为47.9 ℃和49.7 ℃,二者相差1.8 ℃。在对流换热过程中,固体表面温度与近壁流体温度相同,由图13可以得到稳定后的定子槽进出口的流体温升分别为52.1 ℃和53 ℃,与试验结果中的47.9 ℃和49.7 ℃相差5 ℃以内。同时,仿真结果中的定子槽进出口温度相差0.9 ℃,与试验结果近似,进一步证明了仿真的准确性。
7 结论
本文结合几种传热方式对充水式潜水电机内部换热过程进行了分析,并对计算流体场所需要的数学方程和物性条件进行了分析。建立了充水式潜水电机完整的温度场计算模型,分别对内外冷却过程进行建模分析,并采用pt100对充水式潜水电机进行温度测量,得到如下结论。
(1) 电机的流体场仿真结果显示,流体场的流动状态符合充水式潜水电机的循环过程,流体场模型可以较好地模拟充水时潜水电机内部流体的流动状态。在泵轮出口和转子上部的流体流速相对较大,在电机两侧的端部会形成涡流,这也说明了气隙入口和水道入口处的流阻较大,整体结构还需要进一步改进。
(2) 仿真结果中电机温升达到稳定状态后,电机绝缘表面的流体温度与试验测得的温度最大相差4 ℃,最小相差1 ℃,试验测得的定子两侧温度相差2 ℃左右,仿真得到的定子槽进出口流体温度相差2 ℃左右,证明了本文所建立的充水式潜水电机的温度场仿真模型可以相对准确地模拟电机的稳态温升。
参考文献
Experimental study of oil cooling systems for electric motors
[J].
Fan performance analysis for rotor cooling of axial flux permanent magnet machines
[J].
Effect of air-gap fans on cooling of windings in a large-capacity,high-speed induction motor
[J].
Development of a totally enclosed fan-cooled traction motor
[J].DOI:10.1109/TIA.2013.2256872 URL [本文引用: 1]
Direct liquid cooling method verified with an axialflux permanent-magnet traction machine prototype
[J].DOI:10.1109/TIE.41 URL [本文引用: 1]
Development of a yokeless and segmented armature axial flux machine
[J].
Development and validation of a thermal model for electric induction motors
[J].DOI:10.1109/TIE.2010.2043044 URL [本文引用: 1]
基于流体相似理论和三维有限元法计算大中型异步电动机的定子三维温度场
[J].
Calculation of 3D stator temperature field of large and medium scale asynchronous motor on the basis of theory of fluid similarity and 3D FEM
[J].
大型高压干式潜水电机定子三维温度场有限元分析
[J].
Calculation of stator 3D temperature field for large-size high-voltage dry submersible motor
[J].
基于三维有限元的大型充水式潜水电机端部涡流损耗
[J].
3D finite element method analysis of eddy current losses in the end region of large water filling submersible motor
[J].
Influences of 3D fluid field for submersible permanent magnet motors on thermal field distribution
[C]// 2019 22nd International Conference on Electrical Machines and Systems(ICEMS). IEEE:
The design and experimental research of cooling structure in deep well submersible motor
[J].
Analysis of heat transfer based on fluid network decoupling in submersible motor
[C]// 2015 IEEE International Conference on Applied Superconductivity and Electromagnetic Devices (ASEMD). IEEE,2015:
感应电动机定转子全域温度场数值计算及相关因素敏感性分析
[J].
Stator-rotor coupled thermal field numerical calculation of induction motors and correlated factors sensitivity analysis
[J].
Winding temperature field model considering void ratio and temperature rise of a permanent-magnet synchronous motor with high current density
[J].DOI:10.1109/TIE.2016.2625242 URL [本文引用: 1]
Thrust and thermal characteristics of electromagnetic launcher based on permanent magnet linear synchronous motors
[J].DOI:10.1109/TMAG.2008.2008883 URL [本文引用: 1]
Solving the more difficult aspects of electric motor thermal analysis in small and medium size industrial induction motors
[J].DOI:10.1109/TEC.2005.847979 URL [本文引用: 1]
Equivalent stator slot model of temperature field for high torque-density permanent magnet synchronous in-wheel motor
[C]//