电气工程学报, 2024, 19(1): 133-140 doi: 10.11985/2024.01.014

电机与电器

感应电机模型预测直接速度控制*

张昊男,, 张永昌,, 布佳龙,, 王兴,

华北电力大学电气与电子工程学院 北京 102206

Model Predictive Direct Speed Control of Induction Motor

ZHANG Haonan,, ZHANG Yongchang,, BU Jialong,, WANG Xing,

School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206

通讯作者: 张永昌，男，1982年生，博士，教授。主要研究方向为电力电子并网发电、电机系统及控制。E-mail：zyc@ncepu.edu.cn

收稿日期: 2023-02-16   修回日期: 2023-04-16  

基金资助: 国家自然科学基金资助项目(52077002)

Received: 2023-02-16   Revised: 2023-04-16  

作者简介 About authors

张昊男，男，1996年生，硕士研究生。主要研究方向为感应电机模型预测控制。E-mail：zhanghn@ncepu.edu.cn;

布佳龙，男，1998年生，硕士研究生。主要研究方向为永磁同步电机模型预测控制。E-mail：bjl@ncepu.edu.cn;

王兴，男，1997年生，博士研究生。主要研究方向为感应电机模型预测控制。E-mail：15811464387@163.com

摘要

传统的模型预测转矩控制具有原理简单、动态响应快和控制灵活等优点，在感应电机高性能控制中得到了广泛研究。但是，现有方法一般通过转速外环来得到转矩参考指令，而转矩和磁链跟踪则通过内环的模型预测控制来实现。这种双闭环级联结构虽然保证了系统的稳定性，但存在内外环互相影响、调试参数较多等缺点。针对上述问题，舍去了传统控制方案中的双闭环串联结构，提出一种仅包括单个控制回路的模型预测直接速度控制方法。通过在价值函数中引入定子磁链误差和转子转速误差，实现了对不同时间尺度的转速和磁链的同时控制，具有结构简单、调试参数少等优点。另外，通过引入负载转矩观测器，提高了转速控制的稳态性能。相比传统模型预测转矩控制，提出的模型预测直接速度控制转矩和转速脉动显著减小，另外在全速范围具有更小的电流谐波，其有效性通过试验进行了验证。

关键词： 感应电机; 直接速度控制; 单环控制; 稳态性能

Abstract

The traditional model predictive torque control has the advantages of simple principle, fast dynamic response and flexible control. It has been widely studied in the high-performance control of induction motor. However, the existing methods usually obtain the torque reference command through the outer speed loop, while the torque and flux tracking are realized through the model predictive control of the inner loop. Although the cascaded double-loop structure ensures the stability of the system, it has some disadvantages, such as the interaction between the inner and outer loops, more debugging parameters and so on. To solve the above problems, the cascaded double-loop structure in the traditional control scheme is eliminated, and a model predictive direct speed control method including only a single control loop is proposed. By introducing stator flux linkage error and rotor speed error into the cost function, the simultaneous control of speed and flux linkage with different time scales is realized, which has the advantages of simple structure and few debugging parameters. In addition, the steady-state performance of speed control is improved by introducing load torque observation. Compared with the traditional model predictive torque control, the proposed model predictive direct speed control significantly reduces the torque and speed ripple. In addition, it has lower current harmonics in the full speed range. The effectiveness of the proposed method is verified by experiment results.

Keywords： Induction motor; direct speed control; single control loop; steady-state performance

PDF (20603KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

张昊男, 张永昌, 布佳龙, 王兴. 感应电机模型预测直接速度控制*[J]. 电气工程学报, 2024, 19(1): 133-140 doi:10.11985/2024.01.014

ZHANG Haonan, ZHANG Yongchang, BU Jialong, WANG Xing. Model Predictive Direct Speed Control of Induction Motor[J]. Chinese Journal of Electrical Engineering, 2024, 19(1): 133-140 doi:10.11985/2024.01.014

1 引言

近年来，随着数字信号处理器(Digital signal processor，DSP)性能的提高与成本的降低，模型预测控制(Model predictive control，MPC)被广泛应用于感应电机驱动控制[1-2]。MPC基于电机的动态数学模型，考虑逆变器的离散特性，通过枚举逆变器的开关状态，选择价值函数最小的开关状态作为控制器的最优输出[3⇓⇓-6]，具有原理简单、瞬态响应快、可以处理非线性约束和多个变量的优点。

MPC用于感应电机控制时，通常将电机电磁转矩和定子磁链幅值作为控制目标，这种控制方式被称为模型预测转矩控制(Model predictive torque control，MPTC)。MPTC相对于直接转矩控制(Direct torque control，DTC)的主要优点之一是当电路拓扑发生变化时控制实现的简单性[7-8]，另一个优点是它可以灵活地结合不同的控制目标，例如最小化开关频率[9]、降低共模电压[10]或控制输入无功功率[11-12]。但是由于电磁转矩和定子磁链的幅值和量纲均不一样，因此在价值函数中需要加入一个权重系数来实现二者的平衡控制，增加了调试工作量。针对此问题，文献[13]提出了模型预测磁链控制(Model predictive flux control，MPFC)的思想，通过对感应电机数学模型的推导，将传统方法中对磁链和转矩的同时控制转换为对一个等效定子磁链矢量的控制，从而消除了繁复的权重系数设计问题。

在实际应用中，无论是MPTC还是MPFC，仍采用转速外环控制加模型预测内环控制的双闭环结构。这种级联结构在一定程度上限制了电机的动态响应性能。为避免造成很大的超调，级联线性控制器对带宽具有限制，调速性能将变得适中[14-15]，因此需要对传统模型预测控制方法中的级联结构进行改进。

随着伺服系统应用的范围不断扩大，现代伺服系统的中低速性能要求也越来越高，如高精度数控机床工作台系统、雷达卫星天线自动跟踪系统、工业机器人、光学加工等领域都要求电机在低速运行时有良好的跟随特性和抗干扰性能，即电机能够快速跟随指令值变化，同时在给定转速变化、负载变化的条件下能够低速平稳运行[16-17]。MPC兼具矢量控制(Field oriented control，FOC)稳态性能好和直接转矩控制动态响应快等优点，在伺服系统中的应用具有广阔前景。

模型预测直接速度控制(Model predictive direct speed control，MPDSC)综合了模型预测控制和直接速度控制的优点，实现转速上的高性能控制。文献[18]提出了短预测步长的有限集模型预测速度控制，其消除了比例积分(Proportional integral，PI)控制器，为了保证系统的稳定性，通过在代价函数中加入合适的加权因子来平衡转速误差、定子磁链误差和电流误差，以改善系统的性能，但较多权重系数的使用增加了调试难度。此外，为了解决模型预测转速控制下电机模型设定值可能与实际值不匹配或负载扰动等所引起的非线性扰动现象，文献[19]提出了基于卡尔曼滤波算法与无模型预测控制方法相结合的扰动观测器，通过估计预测量和输出量的扰动项和状态量，来消除模型不匹配和负载扰动等影响。

本文提出的MPDSC采用定子磁链和转子转速作为控制目标，消除了传统MPTC中的级联结构，相比现有方法减少了需要调整参数的个数，试验结果表明所提方法提高了系统的稳态性能。

2 感应电机数学模型

感应电机的数学模型可以用复矢量来表示。在$\alpha \beta $静止坐标系下，选取感应电机定子电流${{i}_{\mathrm{s}}}$和定子磁链${{\mathrm{ }\!\!\psi\!\!\text{ }}_{\text{s}}}$为状态变量，电机的状态方程可表示为[20]

$p\mathrm{x}=\mathrm{Ax}+\mathrm{B}{{\mathrm{u}}_{\text{s}}}$
$\mathrm{x}={{\left( \begin{matrix} {{\mathrm{i}}_{\text{s}}} & {{\mathrm{ }\!\!\psi\!\!\text{ }}_{\text{s}}} \\\end{matrix} \right)}^{\text{T}}}$
$\mathrm{A}=\left( \begin{matrix} \begin{matrix} -\lambda \left( {{R}_{s}}{{L}_{r}}+{{R}_{r}}{{L}_{s}} \right)+\text{j}{{\omega }_{r}} & \lambda \left( {{R}_{r}}-\text{j}{{L}_{r}}{{\omega }_{r}} \right) \\\end{matrix} \\ \begin{matrix} \begin{matrix} \begin{matrix} -{{R}_{s}} & {} & {} \\\end{matrix} & {} & {} \\\end{matrix} & \begin{matrix} {} & 0 \\\end{matrix} \\\end{matrix} \\\end{matrix} \right)$
$\mathrm{B=}\left( \begin{matrix} \lambda {{L}_{r}} \\ 1 \\\end{matrix} \right)$

式中，$\lambda =1/\left( {{L}_{s}}{{L}_{r}}-L_{m}^{2} \right)$；$p$表示微分算子；${{R}_{s}}{{R}_{r}}$、${{L}_{s}}{{L}_{r}}$、${{L}_{\text{m}}}$分别为电机定子电阻、转子电阻、定子电感、转子电感、定转子绕组的互感；${{\omega }_{r}}$为电机转速；${{\mathrm{u}}_{\text{s}}}$为定子电压矢量。

3 模型预测直接速度控制

3.1 基本原理

MPDSC将定子磁链和转子转速作为控制目标，与模型预测转矩控制(MPTC)相比，不需要进行复杂的PI参数整定，不需要转矩指令，舍去了模型预测转矩控制方案中的双闭环串级调速结构，采用新型简洁的单环结构。MPDSC的核心内容如下所示。

(1) 由于感应电机的磁链、转矩等无法直接通过测量得到，利用容易测量得到的转速、电流信息，通过观测器观测或估计需要的状态变量值，如负载转矩，定、转子磁链等。

(2) 根据电机数学模型来预测控制变量(转速、磁链)在基本电压矢量输入下的变化。

(3) 根据控制变量的预测值来计算相应的价值函数值，将所有备选电压矢量分别代入价值函数进行计算，选取使价值函数最小的电压矢量作为最优电压矢量。

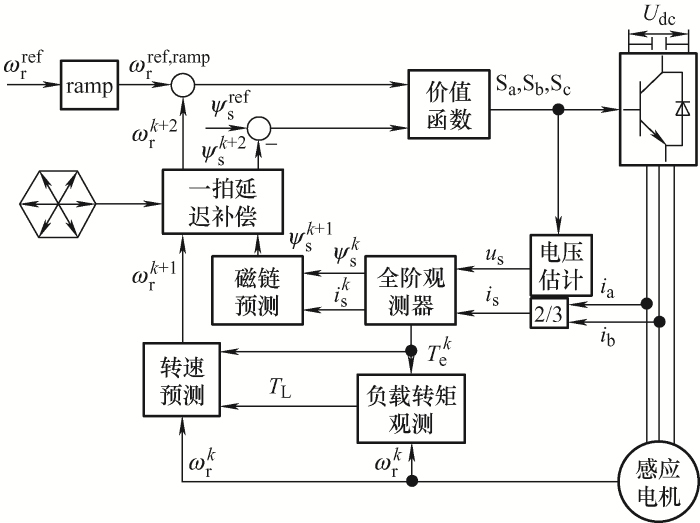
MPDSC的整体控制框图如图1所示。下面将从磁链观测、转矩和磁链预测、负载转矩观测和转速预测、价值函数和矢量选择等四方面对图1做简要说明。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   感应电机模型预测直接速度控制框图


3.2 磁链观测

本文采用全阶观测器来进行磁链观测。传统电流模型在中、高速度域内观测精度有限，为解决此问题，在全阶观测器中加入了电流闭环反馈环节，使得观测器在全速度域内具备良好的预测精度[21]，其数学模型如下

$\left\{ \begin{align} & \mathsf{p}{{{\mathrm{\hat{i}}}}_{\text{s}}}=\left[ -\lambda \left( {{R}_{s}}{{L}_{r}}+{{R}_{r}}{{L}_{s}} \right)+\text{j}{{\omega }_{r}} \right]{{{\mathrm{\hat{i}}}}_{\text{s}}}+ \\ & \lambda \left( {{R}_{r}}-\text{j}{{L}_{r}}{{\omega }_{r}} \right){{{\mathrm{\hat{ }\!\!\psi\!\!\text{ }}}}_{s}}+\lambda {{L}_{r}}{{\mathrm{u}}_{\text{s}}}+{{\mathsf{g}}_{1}}\left( {{\mathrm{i}}_{\text{s}}}-{{{\mathrm{\hat{i}}}}_{\text{s}}} \right) \\ & \mathsf{p}{{{\mathrm{\hat{ }\!\!\psi\!\!\text{ }}}}_{s}}=-{{R}_{s}}{{{\mathrm{\hat{i}}}}_{\text{s}}}+{{\mathrm{u}}_{\text{s}}}+{{\mathsf{g}}_{2}}\left( {{\mathrm{i}}_{\text{s}}}-{{{\mathrm{\hat{i}}}}_{\text{s}}} \right) \\ \end{align} \right.$

式中，g1、g2为电流闭环反馈环节对应的电流误差反馈系数，数值的选取见式(3)，其中b=-40。该观测器的详细介绍可以参见文献[21]。

$\left\{ \begin{align} & {{g}_{1}}=-2b \\ & {{g}_{2}}=-\frac{b}{\lambda {{L}_{m}}} \\ \end{align} \right.$

通过式(2)得到的定子磁链和定子电流，可以计算得到电磁转矩

$T_{e}^{k}=\frac{3}{2}{{N}_{\text{p}}}\mathrm{ }\!\!\psi\!\!\text{ }_{\text{s}}^{k}\otimes \mathrm{i}_{\text{s}}^{k}$

式中，${{N}_{\text{p}}}$为电机极对数，$\otimes $表示叉积。

3.3 磁链预测

将感应电机磁链数学模型进行离散化，可以得到下一时刻的磁链预测值。一阶欧拉公式计算精度有限，影响预测控制效果[22]。在不显著提升计算量的情况下，本文采用计算精度更高的二阶欧拉公式[20]来离散式(1)，可得

$\left\{ \begin{matrix} \mathrm{x}_{\text{p}}^{k\text{+1}}={{\mathrm{x}}^{k}}+{{T}_{sc}}\left( \mathrm{A}{{\mathrm{x}}^{k}}+\mathrm{Bu}_{\text{s}}^{k} \right)\ \ \ \\ {{\mathrm{x}}^{k\text{+1}}}=\mathrm{x}_{\text{p}}^{k\text{+1}}+\frac{{{T}_{sc}}}{2}\mathrm{A}\left( \mathrm{x}_{\text{p}}^{k\text{+1}}-{{\mathrm{x}}^{k}} \right) \\\end{matrix} \right.$

式中，$\mathrm{x}_{\text{p}}^{k\text{+1}}$与${{T}_{sc}}$分别为预测校正变量和控制周期，${{\mathrm{x}}^{k\text{+1}}}={{\left( \begin{matrix} \mathrm{i}_{\text{s}}^{k\text{+1}} & \mathrm{ }\!\!\psi\!\!\text{ }_{\text{s}}^{k\text{+1}} \\\end{matrix} \right)}^{\text{T}}}$为定子电流和定子磁链在(k+1)时刻的预测值。

3.4 负载转矩观测和转速预测

电机在运行过程中，所处的工况不同，除空载状况外，由于MPDSC直接控制电机的转速和磁链，负载转矩的变化会直接影响电机的转速进而影响MPDSC的控制效果，因此对负载转矩观测是必要的。在以往的文献中将负载转矩看成一种输入扰动，提出了几种观测器用于估计负载转矩，例如模型参考自适应系统[23]、龙贝格观测器[24]、卡尔曼滤波器[25]。本文采用龙贝格负载转矩观测器。

选取状态量$\mathrm{x}=\left[ \begin{matrix} {{\omega }_{\text{r}}} \\ {{T}_{L}} \\\end{matrix} \right]$，输入量$u={{T}_{e}}$，输出量$\mathrm{y}={{\mathrm{ }\!\!\omega\!\!\text{ }}_{r}}$。根据电机运动方程$\frac{d{{\omega }_{\text{r}}}}{dt}=\frac{{{N}_{p}}}{J}\left( {{T}_{e}}-{{T}_{L}} \right)$可得

$\left[ \begin{matrix} p{{\omega }_{\text{r}}} \\ p{{T}_{L}} \\\end{matrix} \right]=\left[ \begin{matrix} 0 & -\frac{{{N}_{\text{p}}}}{J} \\ 0 & 0 \\\end{matrix} \right]\left[ \begin{matrix} {{\omega }_{\text{r}}} \\ {{T}_{L}} \\ \end{matrix} \right]+\left[ \begin{matrix} \frac{{{N}_{\text{p}}}}{J} & 0 \\ 0 & 0 \\\end{matrix} \right]\left[ \begin{matrix} {{T}_{e}} \\ 0 \\ \end{matrix} \right]$

令${{\mathrm{A}}_{1}}=\left[ \begin{matrix} 0 & -\frac{{{N}_{\text{p}}}}{J} \\ 0 & 0 \\\end{matrix} \right]$，${{\mathrm{B}}_{1}}=\left[ \begin{matrix} \frac{{{N}_{\text{p}}}}{J} & 0 \\ 0 & 0 \\\end{matrix} \right]$，${{\mathrm{C}}_{1}}=\left[ \begin{matrix} 1 & 0 \\\end{matrix} \right]$，${{\mathrm{D}}_{1}}=0$。可得龙贝格观测器形式

$\left\{ \begin{align} & p\mathbf{\hat{x}}={{\mathrm{A}}_{1}}\mathbf{\hat{x}}+{{\mathrm{B}}_{1}}u+\mathrm{L}\left( \mathbf{y}-\mathbf{\hat{y}} \right) \\ & \mathbf{\hat{y}}={{\mathrm{C}}_{1}}\mathbf{\hat{x}}+{{\mathrm{D}}_{\mathsf{1}}}u \\ \end{align} \right.$

将$\mathrm{\hat{y}}$代入，得$p\mathbf{\hat{x}}=\left( {{\mathrm{A}}_{1}}-\mathrm{L}{{\mathrm{C}}_{1}} \right)\mathbf{\hat{x}}+\left( {{\mathrm{D}}_{1}}-\mathrm{L}{{\mathrm{D}}_{1}} \right)\mathsf{u}+\mathrm{L}\mathbf{y}$，设$\mathrm{L}=\left[ \begin{matrix} {{L}_{1}} \\ {{L}_{2}} \\\end{matrix} \right]$，则有

${{\hat{T}}_{L}}={{L}_{2}}\left( {{\omega }_{\text{r}}}-{{{\hat{\omega }}}_{\text{r}}} \right)$

式中，Np为感应电机极对数，$J$为电机转动惯量，矩阵$\mathrm{L}$为给定的系数，通过求取${{\mathrm{A}}_{1}}-\mathrm{L}{{\mathrm{C}}_{1}}$矩阵特征值，选取合适的期望极点，使得系统保持稳定[26]，本文中${{L}_{2}}$为-30。${{\hat{\omega }}_{\text{r}}}$为观测器观测的转速，${{\hat{T}}_{L}}$为观测到的负载转矩。

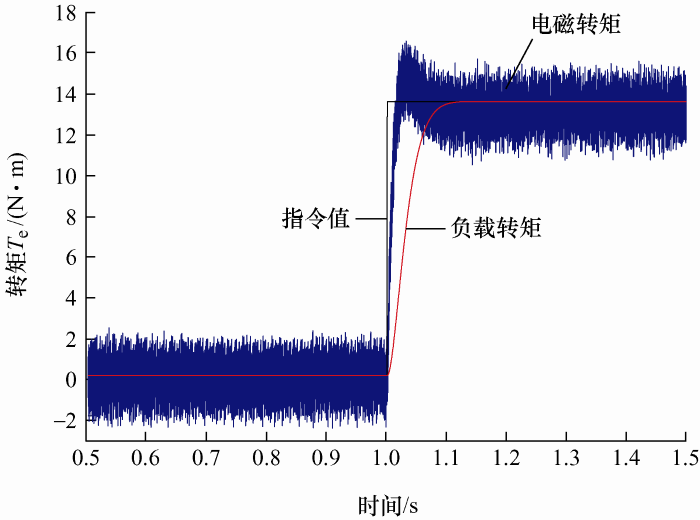
通过仿真对构建的负载转矩观测器进行验证，使用的电机参数如表1所示，在电机稳态运行至1 s时突加额定负载13.5 N·m，仿真结果如图2所示。图2中指令值为所加载的实际转矩，电磁转矩根据定子电流和电子磁链计算获得，负载转矩为负载转矩观测器观测得到的波形。由图2可以看出，观测的负载转矩很快收敛到实际负载转矩且波动较小。与此同时，由于闭环控制的作用，电磁转矩响应迅速，在实际负载变化后迅速增加并与之平衡，使系统达到稳态。

表1   仿真和试验所用感应电机参数

序号参数数值
1Udc/V550
2Pn/Un/fn2.2 kW/380 V/51.7 Hz
3Np2
4J0.02
5Rs/Ω3.365 1
6Rr/Ω1.168 3
7Lm/H0.145 8
8Lls、Llr/mH8.6

新窗口打开| 下载CSV


图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   负载转矩观测器仿真结果


根据式(4)得到的电磁转矩和式(8)观测得到的负载转矩，应用电机运动方程对转速进行预测可以得到

$\omega _{\text{r}}^{k\text{+1}}={{N}_{p}}\left( T_{\text{e}}^{k}-{{T}_{\text{L}}} \right){{T}_{\text{sc}}}/J+\omega _{\text{r}}^{k}$

3.5 价值函数和矢量选择

根据上文得到的磁链预测值$\mathrm{ }\!\!\psi\!\!\text{ }_{s}^{k+1}$和转速预测值$\omega _{\text{r}}^{k+1}$可以构造式(10)所示价值函数。值得注意的是，由于价值函数没有直接控制电流，参考转速给定阶跃指令时会产生过大的电流，所以需要给定参考转速一个斜坡斜率来避免参考转速突增、突减导致的电流过大的问题。MPDSC的价值函数为

$G={{k}_{\psi }}|\mathbf{\psi }_{\text{s}}^{\text{*}}-\mathbf{\psi }_{\text{s}}^{k\text{+1}}|+|\omega _{\text{r}}^{\text{*}}-\omega _{\text{r}}^{k\text{+1}}|$

式中，${{k}_{\psi }}$为磁链幅值的权重系数，通过仿真和试验来确定，其值给定为100。

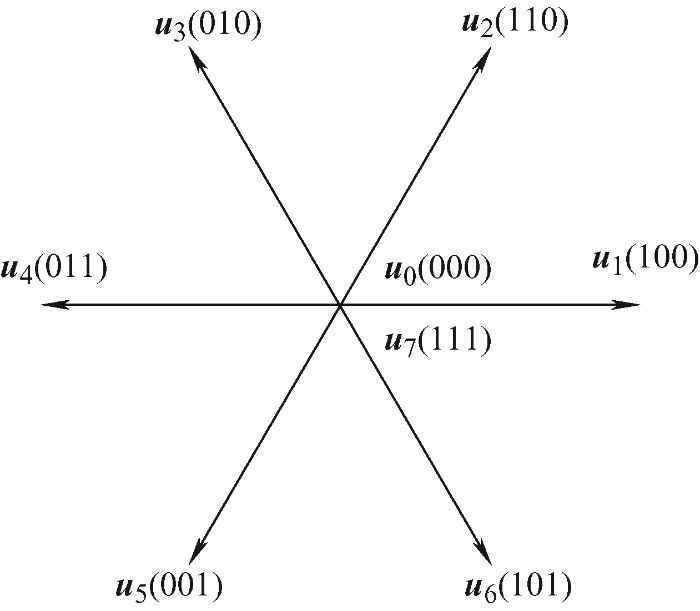
两电平电压源型逆变器一共有7种不同的基本电压矢量，如图3所示。首先，根据式(5)、式(9)对7种电压矢量作用下的定子磁链$\mathbf{\psi }_{si}^{k+1}$和转速$\omega _{\text{r}i}^{k\text{+1}}$进行预测$(i=0,1,\cdot \cdot \cdot,6)$；再根据预测值计算相应的价值函数值；最后，根据最小化价值函数的原则选取最优电压矢量由逆变器输出。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   两电平逆变器的电压矢量


由于数字控制系统在实际应用中存在一拍延迟，本应在当前k时刻作用的电压矢量要到下一时刻(k+1)时刻才会被更新输出。为消除一拍延迟对控制效果的影响，控制器可以采用超前一步确定(k+1)时刻电压矢量的方式对延迟进行补偿。简要总结如下所示。

(1) 设定在k时刻，按照式(2)、式(9)得到$\mathrm{ }\!\!\psi\!\!\text{ }_{\text{s}}^{k}$、$\omega _{\text{r}}^{k}$，通过式(5)的二阶欧拉离散来预测(k+1)时刻的状态变量。

(2) 在得到(k+1)时刻状态变量的基础上，继续对状态变量进行一步预测，得到(k+2)时刻状态变量。

(3) 在(k+2)时刻，根据式(11)将所有备选电压矢量分别计算，按照最小化价值函数的原则，确定(k+1)时刻由逆变器输出的最优电压矢量。经此得到最终价值函数为

$G={{k}_{\psi }}|\mathbf{\psi }_{\text{s}}^{\text{*}}-\mathbf{\psi }_{\text{s}}^{k\text{+2}}|+|\omega _{\text{r}}^{\text{*}}-\omega _{\text{r}}^{k\text{+2}}|$

4 试验结果

为验证所提方法的有效性，本文对MPTC和MPDSC在两电平交流调速试验平台进行了试验验证，并对两种方法所得的试验结果进行了对比，所用到的电机参数如表1所示。试验中所用的2.2 kW感应电机机组、驱动电路和控制电路如图4所示。在试验中通过调节磁粉制动器电流的大小来提供负载转矩，直流母线电压为540 V。采用DSP TMS320F28335来运行核心控制算法部分，试验结果图5~8中所示的四个通道从上到下分别为转子转速、电磁转矩、定子磁链和定子相电流。除定子相电流是直接由电流探头直接测量得到外，其余三个通道均由控制板扩展DA通道输出到DL950录波仪中显示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   两电平逆变器驱动电机试验平台


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   0~150 r/min空载起动波形


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   750 r/min空载运行稳态波形


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   0~1 500 r/min空载起动波形


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   负载转矩变化时的试验波形


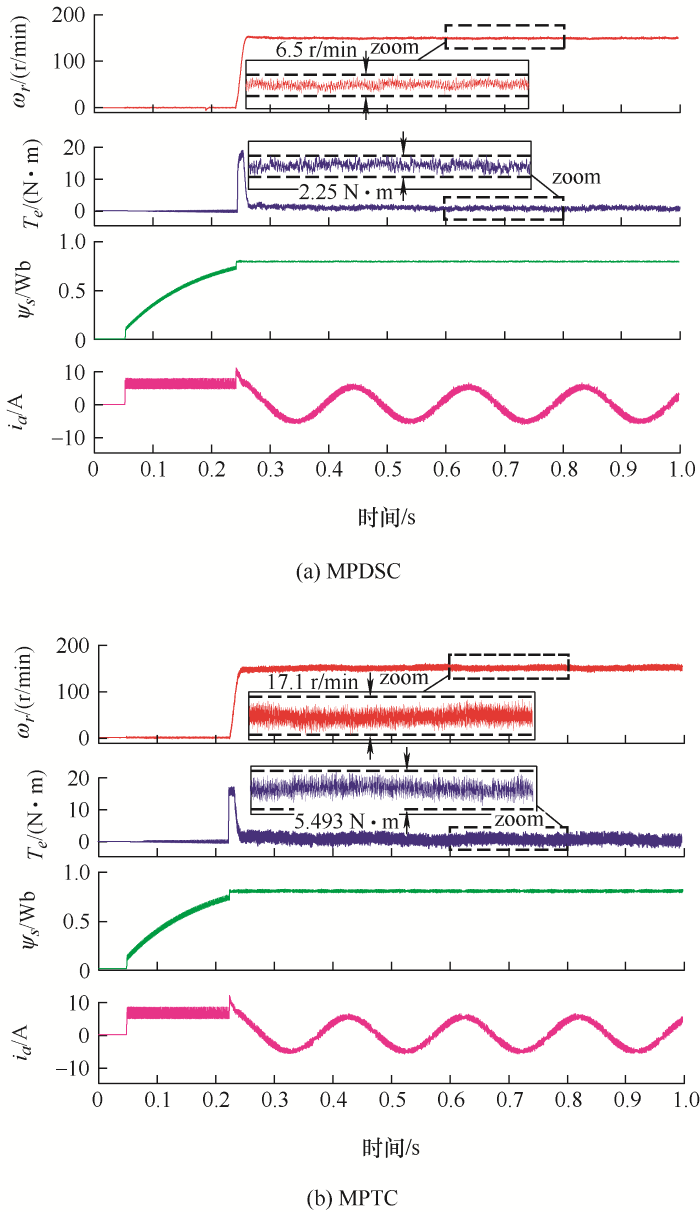
在试验中系统采样频率设定为15 kHz，为避免在启动过程中出现过流现象，本文采用直流预励磁的方法先在电机内部建立起磁通再施加转速指令起动电机。图5为两种方法将电机从静止空载起动至150 r/min时的试验波形。由图5可以看出，两种方法都能够很快达到指定的转速，动态响应相当。但达到稳态时MPDSC的转速、转矩脉动更小。

图6为两种方法控制电机运行在750 r/min时的稳态试验波形，MPDSC的转速脉动为9.6 r/min，MPTC的转速脉动为22.9 r/min，转矩脉动也是MPDSC的较小。因试验设备运行中存在摩擦转矩，所以会出现空载时转矩不完全为0的情况。

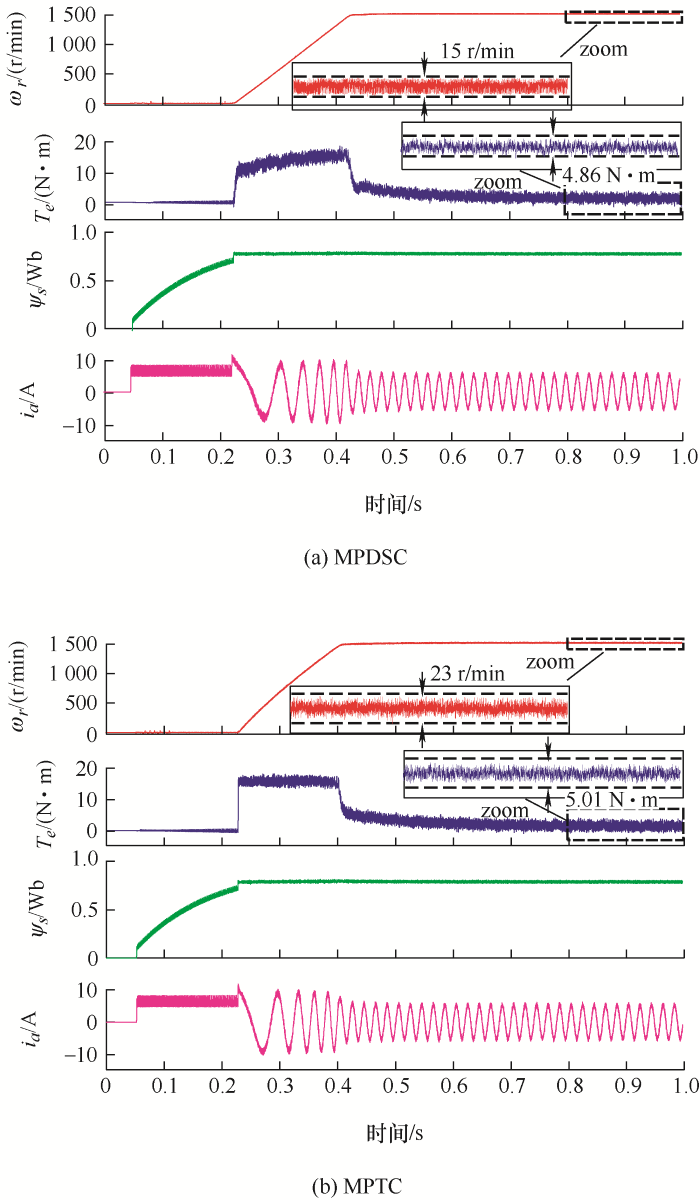
图7为两种方法将电机从静止起动至1 500 r/min时的试验波形，将稳态时电机转速、转矩部分放大后可以看出，MPDSC的转速脉动为15 r/min，MPTC的转速脉动为23 r/min，同时MPDSC的转矩脉动也略好于MPTC。

在三种转速下可以发现MPDSC的转速、转矩脉动均小于MPTC，这是因为MPDSC的价值函数直接对转速进行控制，更加精确。而MPTC的价值函数是对电磁转矩进行控制，电机在运行过程中参数可能会发生变化，由电磁转矩到转速的转化会受到电机参数的影响。同时MPTC要通过调节PI参数获得与MPDSC相同的动态响应，也会导致稳态性能稍差。由此说明了所提MPDSC的有效性。

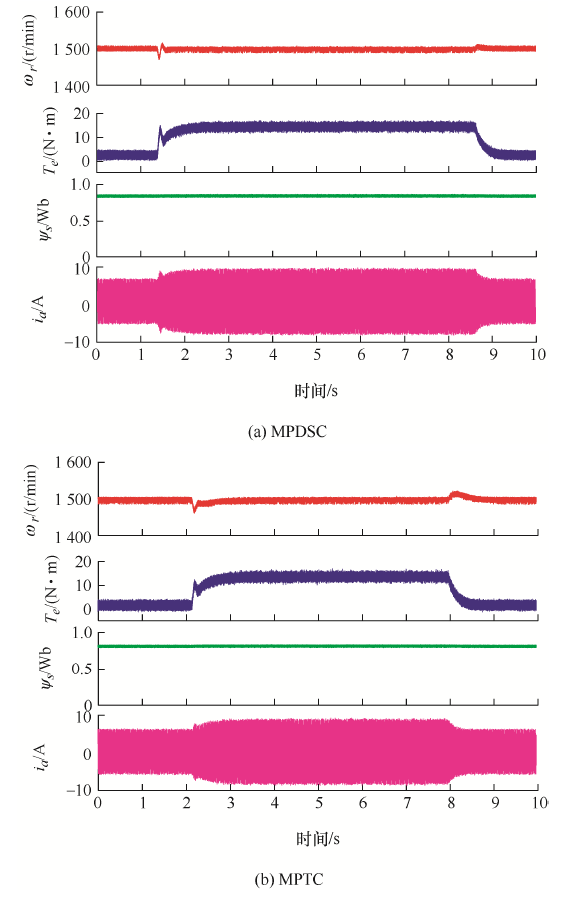
图8为两种方法控制电机运行在1 500 r/min时突加、突减额定负载试验。两种方法在负载转矩变化后电磁转矩也随之迅速变化。由图8可以看出，MPDSC转速脉动小于MPTC，在突加、突减负载后转速也能更快恢复到指令值。

表2为两种方法在全速范围内空载运行的电流THD对比，由表2可以看出，电机运行在150 r/min、750 r/min、1 500 r/min时，MPDSC的电流THD均小于MPTC，说明MPDSC电流谐波含量更低，具有更正弦的电流波形。

表2   不同方法在全速范围的电流THD对比

转速/(r/min)THD(%)
MPDSCMPTC
15011.862 612.085
75010.129 811.026 2
1 5009.979 110.532 7

新窗口打开| 下载CSV


5 结论

本文提出了一种非级联单环模型预测直接速度控制方法，并对其进行了深入的仿真和试验研究，得到以下结论。

(1) 舍去了传统控制方案中的双闭环串级调速结构，采用新的单环结构，简化了系统结构，实现了单控制器对不同时间尺度的速度和磁链的同时控制。

(2) 相对传统MPTC，转速环无需进行复杂的PI参数整定，控制算法简单实用。

(3) 试验结果表明，MPDSC比MPTC的转速和转矩脉动更小，且MPDSC在中低速范围内效果更好，相比MPTC更适用于伺服系统。MPDSC在全速度范围内的稳态电流谐波都小于MPTC。

参考文献

RODRIGUEZ J, GARCIA C, MORA A, et al.

Latest advances of model predictive control in electrical drives—Part I:Basic concepts and advanced strategies

[J]. IEEE Transactions on Power Electronics, 2021, 37(4):3927-3942.

DOI:10.1109/TPEL.2021.3121532      URL     [本文引用: 1]

RODRIGUEZ J, GARCIA C, MORA A, et al.

Latest advances of model predictive control in electrical drives—Part II:Applications and benchmarking with classical control methods

[J]. IEEE Transactions on Power Electronics, 2021, 37(5):5047-5061.

DOI:10.1109/TPEL.2021.3121589      URL     [本文引用: 1]

齐昕, 苏涛, 周珂, 等.

交流电机模型预测控制策略发展概述

[J]. 中国电机工程学报, 2021, 41(18):6408-6419.

[本文引用: 1]

QI Xin, SU Tao, ZHOU Ke, et al.

Development of AC motor model predictive control strategy:An overview

[J]. Proceedings of the CSEE, 2021, 41(18):6408-6419.

[本文引用: 1]

苏光靖, 李红梅, 李争, 等.

永磁同步直线电机无模型电流控制

[J]. 电工技术学报, 2021, 36(15):3182-3190.

[本文引用: 1]

SU Guangjing, LI Hongmei, LI Zheng, et al.

Research on model-free current control of permanent magnet synchronous linear motor

[J]. Transactions of China Electrotechnical Society, 2021, 36(15):3182-3190.

[本文引用: 1]

ZHANG Yongchang, YANG Haitao.

Two-vector-based model predictive torque control without weighting factors for induction motor drives

[J]. IEEE Transactions on Power Electronics, 2016, 31(2):1381-1390.

DOI:10.1109/TPEL.2015.2416207      URL     [本文引用: 1]

於锋, 朱晨光, 吴晓新, 等.

基于矢量分区的永磁同步电机三电平双矢量模型预测磁链控制

[J]. 电工技术学报, 2020, 35(10):2130-2140.

[本文引用: 1]

YU Feng, ZHU Chenguang, WU Xiaoxin, et al.

Two vector based model predictive flux control of three-level based permanent magnet synchronous motor with sector subregion

[J]. Transactions of China Electrotechnical Society, 2020, 35(10):2130-2140.

[本文引用: 1]

ESCALANTE M, VANNIER J C, ARZANDE A.

Flying capacitor multilevel inverters and DTC motor drive applications

[J]. IEEE Transactions on Industrial Electronics, 2002, 49(4):809­815.

[本文引用: 1]

DAN Hanbing, ZENG Peng, XIONG Wenjing, et al.

Model predictive control based direct torque control for matrix converter fed induction motor with reduced torque ripple

[J]. CES Transactions on Electrical Machines and Systems, 2021, 5(2):90­99.

[本文引用: 1]

LEE K B, SONG J H, CHOY I, et al.

Torque ripple reduction in DTC of induction motor driven by three level inverter with low switching frequency

[J]. IEEE Transactions on Power Electronics, 2002, 17(2):255­264.

[本文引用: 1]

VARGAS R, AMMANN U, RODRIGUEZ J, et al.

Predictive strategy to control common-mode voltage in loads fed by matrix converters

[J]. IEEE Transactions on Industrial Electronics, 2008, 55(12):4372­4380.

[本文引用: 1]

VARGAS R, RODRIGUEZ J, AMMANN U, et al.

Predictive current control of an induction machine fed by a matrix converter with reactive power control

[J]. IEEE Transactions on Industrial Electronics, 2008, 55(12):4362­4371.

[本文引用: 1]

VARGAS R, AMMANN U, HUDOFFSKY B, et al.

Predictive torque control of an induction machine fed by a matrix converter with reactive input power control

[J]. IEEE Transactions on Power Electronics, 2010, 25(6):1426­1438.

[本文引用: 1]

张永昌, 杨海涛.

感应电机模型预测磁链控制

[J]. 中国电机工程学报, 2015, 35(3):719-726.

[本文引用: 1]

ZHANG Yongchang, YANG Haitao.

Model predictive flux control for induction motor drives

[J]. Proceedings of the CSEE, 2015, 35(3):719-726.

[本文引用: 1]

GONG Chao, HU Yihua, NI Kai, et al.

SM load torque observer-based FCS-MPDSC with single prediction horizon for high dynamics of surface-mounted PMSM

[J]. IEEE Transactions on Power Electronics, 2019, 35(1):20-24.

DOI:10.1109/TPEL.2019.2929714      URL     [本文引用: 1]

PREINDL M, BOLOGNANI S.

Model predictive direct speed control with finite control set of PMSM drive systems

[J]. IEEE Transactions on Power Electronics, 2012, 28(2):1007-1015.

DOI:10.1109/TPEL.2012.2204277      URL     [本文引用: 1]

纪科辉. 低速交流电机伺服系统的研究与实现[D]. 杭州: 浙江大学, 2013.

[本文引用: 1]

JI Kehui. Study and realization on low speed AC motor servo system[D]. Hangzhou: Zhejiang University, 2013.

[本文引用: 1]

阚京波. 低开关频率下异步电机高性能控制技术研究[D]. 武汉: 华中科技大学, 2017.

[本文引用: 1]

KAN Jingbo. Research on high performance control of induction motor at low switching frequency[D]. Wuhan: Huazhong University of Science and Technology, 2017.

[本文引用: 1]

KAKOSIMOS P, ABU-RUB H.

Predictive speed control with short prediction horizon for permanent magnet synchronous motor drives

[J]. IEEE Transactions on Power Electronics, 2017, 33(3):2740-2750.

DOI:10.1109/TPEL.2017.2697971      URL     [本文引用: 1]

刘凤扬, 康尔良, 崔乃政, 等.

基于扰动观测的永磁同步电机单环预测控制

[J]. 电气传动, 2021, 51(4):13-21.

[本文引用: 1]

LIU Fengyang, KANG Erliang, CUI Naizheng, et al.

Single loop predictive control of permanent magnet synchronous motor based on disturbance observation

[J]. Electric Drive, 2021, 51(4):13-21.

[本文引用: 1]

ZHANG Yongchang, YANG Haitao.

Model predictive torque control of induction motor drives with optimal duty cycle control

[J]. IEEE Transactions on Power Electronics, 2014, 29(12):6593-6603.

DOI:10.1109/TPEL.2014.2302838      URL     [本文引用: 2]

ZHANG Yongchang, ZHU Jianguo, ZHAO Zhengming, et al.

An improved direct torque control for three-level inverter-fed induction motor sensorless drive

[J]. IEEE Transactions on Power Electronics, 2010, 27(3):1502-1513.

DOI:10.1109/TPEL.2010.2043543      URL     [本文引用: 2]

MIRANDA H, CORTES P, YUZ J, et al.

Predictive torque control of induction machines based on state-space models

[J]. IEEE Transactions on Industrial Electronics, 2009, 56(6):1916-1924.

DOI:10.1109/TIE.2009.2014904      URL     [本文引用: 1]

WANG Fengxiang, CHEN Zhe, STOLZE P, et al.

Encoderless finite-state predictive torque control for induction machine with a compensated MRAS

[J]. IEEE Transactions on Industrial Informatics, 2013, 10(2):1097-1106.

DOI:10.1109/TII.2013.2287395      URL     [本文引用: 1]

鲁文其, 胡育文, 梁骄雁, 等.

永磁同步电机伺服系统抗扰动自适应控制

[J]. 中国电机工程学报, 2011, 31(3):75-81.

[本文引用: 1]

LU Wenqi, HU Yuwen, LIANG Jiaoyan, et al.

Anti disturbance adaptive control for permanent magnet synchronous motor servo system

[J]. Proceedings of the CSEE, 2011, 31(3):75-81.

[本文引用: 1]

GARCIA C, RODRIGUEZ J, SILVA C, et al.

Full predictive cascaded speed and current control of an induction machine

[J]. IEEE Transactions on Energy Conversion, 2016, 31(3):1059-1067.

DOI:10.1109/TEC.2016.2559940      URL     [本文引用: 1]

彭颖涛, 陆可.

基于模型预测的PMSM速度环PI自整定控制

[J]. 电机与控制应用, 2021, 48(6):37-43.

[本文引用: 1]

PENG Yingtao, LU Ke.

PI self-tuning control of PMSM speed loop based on model prediction

[J]. Electric Machines & Control Application, 2021, 48(6):37-43.

[本文引用: 1]

/

〈 〉