1 引言
传统燃油车排放的汽车尾气对环境造成很大危害。为了减少稀缺能源的消耗,实现环境友好的可持续发展,新能源汽车应运而生[1 ⇓ -3 ] 。随着新能源汽车保有量的快速增加,对于锂离子电池的需求呈现出爆发式增长的趋势[4 ⇓ -6 ] 。2023年1—10月,全球动力电池装车量达到552.2 GW·h[7 ] 。截止到2023年末,锂离子动力电池的退役量超过58万吨[8 ] 。退役的动力电池仍有约70%的可用容量,工业和信息化部也在《新能源汽车动力蓄电池梯次利用管理办法》中鼓励各机构合作,充分挖掘电池剩余可用价值信息,实现电池合理梯次利用[9 ] 。
动力电池老化机理复杂,性能“每用必衰”,当电池性能不能满足日常使用需求时,需要退役并及时更换。事实上,退役电池仍有较大的使用价值。电池剩余使用价值受多种参数耦合影响,如电池容量、健康状态(State of health, SOH)、剩余寿命(Remaining useful life, RUL)等[10 -11 ] 。退役电池仍然有约70%的容量可供不同场景使用。电池容量衰减率不同会导致后续衰退曲线呈现不同的趋势,即使其退役之前容量衰减相同,电池的剩余价值也会因为容量衰减率不同而不同,导致后续可应用领域有所差别[12 ⇓ -14 ] 。目前在电池的回收估值及再利用领域,尚缺乏有效的剩余使用价值估计方法。如何合理定义剩余价值(Remaining useful value, RUV)且精准客观评估是一项具有挑战性的工作,也是本文要解决的关键科学难题。
国内外学者对电池的剩余价值指标估计进行了研究。文献[15 ]根据电池衰退的不一致性提出了基于衰退速度预测的电池剩余价值优化方法,估算过程较为复杂。文献[16 ]提出了充电曲线分段(Charging curve segmentation, CCS)与离散Arrhenius老化模型(Discrete Arrhenius aging model, DAAM)的融合来估算容量。第一个卡尔曼滤波(Kalman filter, KF)更新了DAAM的模型参数;第二次KF基于修正参数的CCS和DAAM估算聚变能力。然而,经验模型难以跟踪负荷动态特性,且受外部环境因素的干扰,它们的适应性和准确性是有限的。等效电路模型通过KF[17 ] 、粒子滤波PF[18 ] 、递推最小二乘RLS[19 ] 等方法实现SOC和容量的共同估计。文献[20 ]建立了用于SOC和容量估计的多尺度双H无限滤波器(H-infinity filter, HIF)。与单/多尺度双KF相比,该方法具有更好的鲁棒性和更高的估计精度。然而,等效电路模型在等效过程中没有考虑电池内部状态变量的信息,影响了电池估计的准确性。对于其他价值参数SOH、RUL的估计,文献[21 ]提出了一种基于神经网络的新的SOH估计方案,可以利用短时间内的电压和电流数据来估计SOH值,达到减少参考性能测试(Reference performance test, RPT)次数的效果,但是估计耗时较长。文献[22 ]使用混合神经网络来捕获电池数据的层次特征和时间信息,结合贝叶斯优化的神经网络结构来实现电池健康状态(SOH)和剩余使用寿命(RUL)的端到端估计,估计效果泛化性强,但是对于输入数据的要求较高。
综上,目前方法大多都是基于单一指标,如健康状态(SOH)、剩余寿命(RUL)及容量来评估电池剩余价值,忽视了各指标之间的耦合关系,导致电池在回收过程中没有统一的指标衡量其剩余使用价值,评估既不准确也不客观[23 ⇓ ⇓ -26 ] 。
为了解决上述问题,本文提出了一种基于多参量的动力电池剩余使用价值(RUV)定义与评价方法。以电池健康状态(SOH)、剩余寿命(RUL)、容量衰减率等影响电池性能的参数作为指标,根据熵权法计算各指标权值,并通过最大最小法计算各评价指标得分,从而得到剩余使用价值。基于MIT公开数据集上的验证结果表明,本文所提方法能够合理客观地评估电池剩余价值,计算简单,鲁棒性强。
2 动力剩余使用价值评估方法
2.1 评估特征选择
锂离子电池在使用过程中不断老化,电池健康状态(SOH)是用来评估电池性能的参数。它反映了电池当前的健康程度。SOH通常以容量的比值定义,定义公式如下
(1) $\mathrm{SOH}=\frac{{{C}_{\mathrm{c}}}}{{{C}_{0}}}\times 100\%$
式中,C c 表示当前循环最大可用容量;C 0 表示初始循环最大可用容量。
电池的剩余可用寿命(RUL)是指电池在当前状态下预计还能正常工作的时间或循环次数。它是评估电池寿命和性能衰退程度的关键参数,对于电池的后续使用价值起着至关重要的作用。
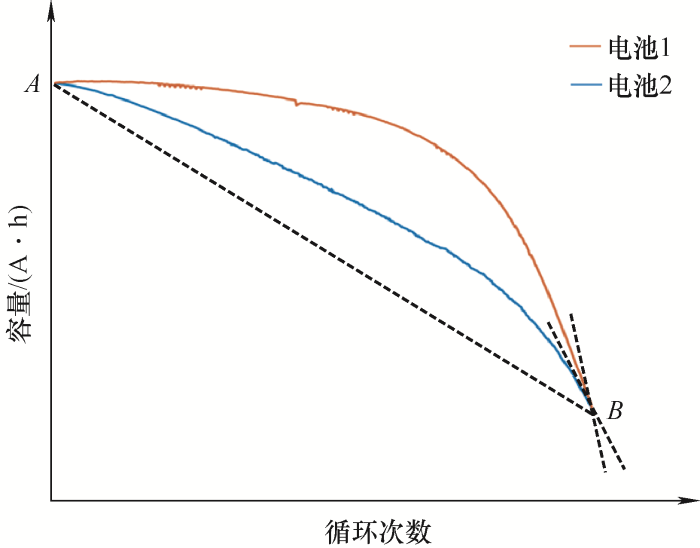
除了上述两个参数,容量衰减率也影响着电池的使用价值,两节相同型号的MIT电池的容量循环曲线如图1 所示。从图1 可以看出,电池1和电池2的容量循环曲线在A 、B 点之间容量变化量相同,SOH变化程度相同。二者为同一种电池,故剩余寿命(RUL)也相同。但两条曲线在B 点的斜率不同,容量衰减率不同,电池1曲线容量比电池2容量曲线下降更快,会更快到达完全报废状态,剩余使用价值更低。所以容量衰减率也是影响电池剩余使用价值的重要参数,故根据SOH、RUL和容量衰减率对电池剩余使用价值(RUV)进行定义合理可行。然而实际车载动力电池在使用时会电池的放电更多取决于驾驶员的驾驶习惯,故需要从电动汽车各循环匀速行驶时的容量数据中获取容量衰减率。
图1
2.2 动力电池剩余使用价值评估框架
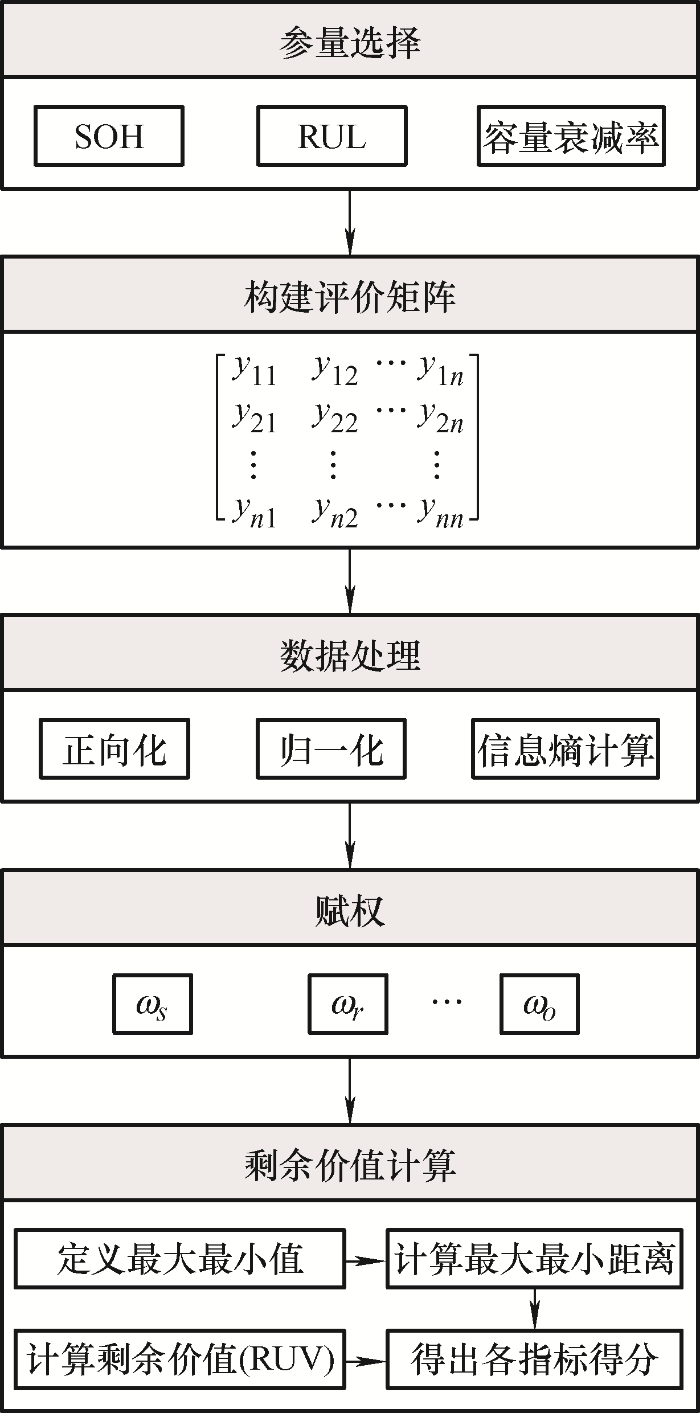
本文提出的基于多参量的动力电池剩余使用价值定义与评价方法整体框架如图2 所示,主要由以下5部分组成:① 参量选择,选择与电池可用性能最密切的SOH、RUL和容量衰减率三个指标作为计算参数,并分析了指标选择的合理性和重要性;② 构建评价矩阵;③ 数据处理,对评价矩阵进行正向化、归一化和信息熵计算;④ 赋权并调配比例,根据各指标对于剩余价值的影响程度为各指标赋最优权重;⑤ 剩余价值计算,包括最大最小值定义、最大最小距离计算、获得得分及计算剩余价值RUV,进一步根据实例验证了电池剩余价值定义的合理性。
图2
2.3 熵权法确定权重
熵权法是一种多准则决策分析方法。通过计算指标之间的信息熵,确定每个指标的权重,从而实现对不同指标在决策中的相对重要性的量化评估。熵权法的优势在于能够充分考虑各指标的信息量和相互关系,避免主观赋权带来的偏差,提高决策的客观性和准确性,相较于层次分析法等主观法具有更好的精确性。
利用熵权法对SOH、RUL和容量衰减率进行权重分配,首先需要确定评价指标,构建评价指标体系构建水平矩阵
(2) $Y=\left[ \begin{matrix} {{y}_{11}} & {{y}_{12}} & \cdots & {{y}_{1m}} \\ {{y}_{21}} & {{y}_{22}} & \cdots & {{y}_{2m}} \\ \vdots & \vdots & {} & \vdots \\ {{y}_{n1}} & {{y}_{n2}} & \cdots & {{y}_{nm}} \\\end{matrix} \right]$
式中,y 11 , y 21 ,…, yn 1 为第一个参量的各项值;y 1 m y 2 m ynm 为第m 个参量的各项值。
对评价矩阵进行标准化处理得到矩阵R
(3) $Z=\left[ \begin{matrix} {{z}_{11}} & {{z}_{12}} & \cdots & {{z}_{1m}} \\ {{z}_{21}} & {{z}_{22}} & \cdots & {{z}_{2m}} \\ \vdots & \vdots & {} & \vdots \\ {{z}_{n1}} & {{z}_{n2}} & \cdots & {{z}_{nm}} \\\end{matrix} \right]$
式中,z 11 , z 12 ,…, znm 为正向化后的指标值。
归一化并计算第j 项指标下第i 个样本值占该指标的比重
(4) ${{q}_{ij}}=\frac{{{z}_{ij}}}{\sum\limits_{i=1}^{m}{{{z}_{ij}}}}$
(5) ${{M}_{j}}=-\frac{1}{\ln m}\sum\limits_{i=1}^{m}{{{q}_{ij}}\ln {{q}_{ij}}}$
式中,qij 为式(3)得到的样本值所占指标比重;m 为指标数。
(6) ${{\omega }_{j}}=\frac{1-{{M}_{j}}}{\sum\limits_{j=1}^{n}{(1-{{M}_{j}})}}$
2.4 动力电池剩余使用价值定义
利用评价方法结合上述权重表达式推导评分表达式。最大最小值法是一种经典的综合评价方法,通过将指标的最大值和最小值进行归一化处理,以消除指标之间的量纲和单位差异,实现不同指标之间的对比。该方法能充分利用原始数据信息,其结果能精确地反映各评价方案之间的差距。
(7) ${{Z}^{+}}=\max (Z_{1}^{+},Z_{2}^{+},\cdots,Z_{m}^{+})$
(8) ${{Z}^{-}}=\min (Z_{1}^{-},Z_{2}^{-},\cdots,Z_{m}^{-})$
定义第i (i =1, 2, …, n )个评价对象与最大值的距离
(9) $D_{i}^{+}=\sqrt{\sum\limits_{j=1}^{m}{{{({{\omega }_{j}}\times Z_{j}^{+}-{{\omega }_{j}}\times {{z}_{ij}})}^{2}}}}$
式中,Z+ j 为式(7)中定义的最大值;ωj 为式(6)所得权重。
定义第i (i =1, 2, …, n )个评价对象与最小值的距离
(10) $D_{i}^{-}=\sqrt{\sum\limits_{j=1}^{m}{{{({{\omega }_{j}}\times Z_{j}^{-}-{{\omega }_{j}}\times {{z}_{ij}})}^{2}}}}$
式中,$Z_{j}^{-}$
(11) ${{T}_{i}}=\frac{D_{i}^{-}}{D_{i}^{+}+D_{i}^{-}}$
(12) ${{T}_{i}}=\frac{\sqrt{\sum\limits_{j=1}^{m}{{{({{\omega }_{j}}\times Z_{j}^{-}-{{\omega }_{j}}\times {{z}_{ij}})}^{2}}}}}{\sqrt{\sum\limits_{j=1}^{m}{{{({{\omega }_{j}}\times Z_{j}^{-}-{{\omega }_{j}}\times {{z}_{ij}})}^{2}}}}+\sqrt{\sum\limits_{j=1}^{m}{{{({{\omega }_{j}}\times Z_{j}^{+}-{{\omega }_{j}}\times {{z}_{ij}})}^{2}}}}}$
根据式(12)的电池评分,得到电池剩余使用价值百分比的计算公式为
(13) $Per={{T}_{i}}\cdot 90%+10%$
式中,性能参数影响的使用价值占价值百分比的90%,电池原料费占价值百分比的10%。
(14) $\mathrm{RUV}=P\cdot Pe{{r}_{i}}$
式中,Peri 为各单体电池评分;P 为单体电池市场价格,电池包的总剩余价值根据各个单体剩余价值耦合计算。
3 试验结果及分析
3.1 数据介绍
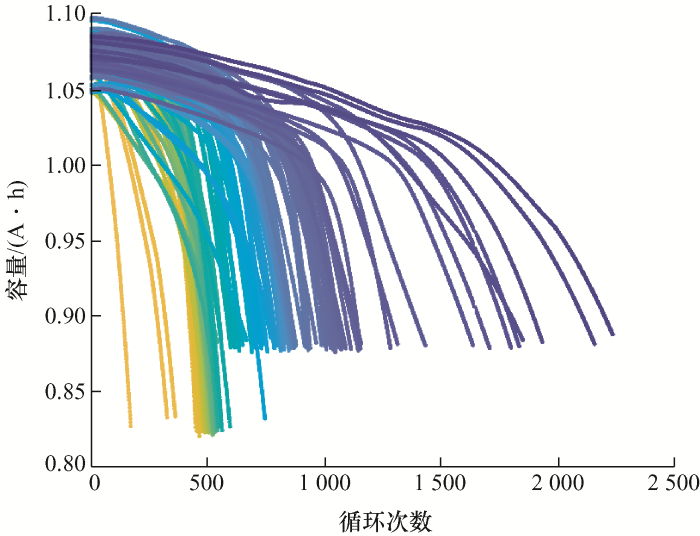
本文采用美国麻省理工学院MIT的数据集验证所提方法的可行性和有效性。数据集由124节标称容量为1.1 A·h的商用LFP/石墨电池在不同循环快充条件下测得。测试温度为恒温30 ℃。电池以3.6C /8C 的电流恒流充电,并都以4C 放电至2.0 V,具体参数如表2 所示。电池放电容量随循环次数变化曲线图如图3 所示。
图3
3.2 动力电池剩余使用价值评估
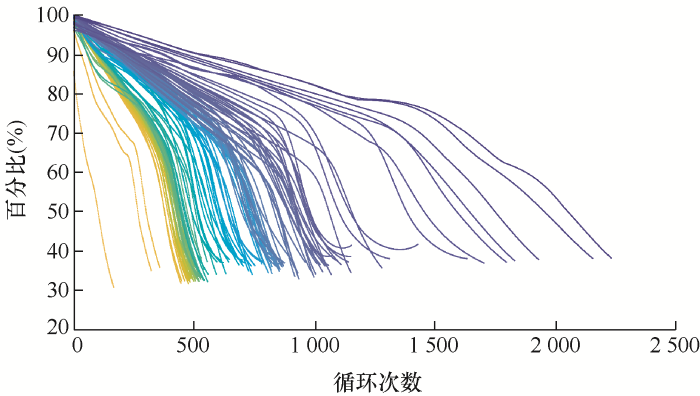
对数据集中的124节电池数据根据所述方法评估电池在各区间的剩余使用价值,选取电池各恒流充电循环的容量数据计算SOH,通过寿命预测方法进行RUL估算,容量衰减率为电池所处循环在容量衰退曲线上的斜率。根据熵权法确定的SOH、RUL及容量衰减率的权值如表3 所示,利用最大最小法得到电池剩余价值百分比图如图4 所示。随机选取10个电池单体中的某一循环,其参量指标值及剩余价值百分比如表4 所示。根据图4 与表4 可以看出,电池SOH越低,RUL越小,容量衰减率越大,电池的后续使用价值较小,剩余价值百分比越低。由表4 中2号电池和65号电池可以看出,两节电池的SOH和RUL基本相同,而65号电池的容量衰减率较大,后续电池容量衰退得较快,可使用时限也因此降低,对应的剩余价值百分比也较低,验证了定义的正确性。
图4
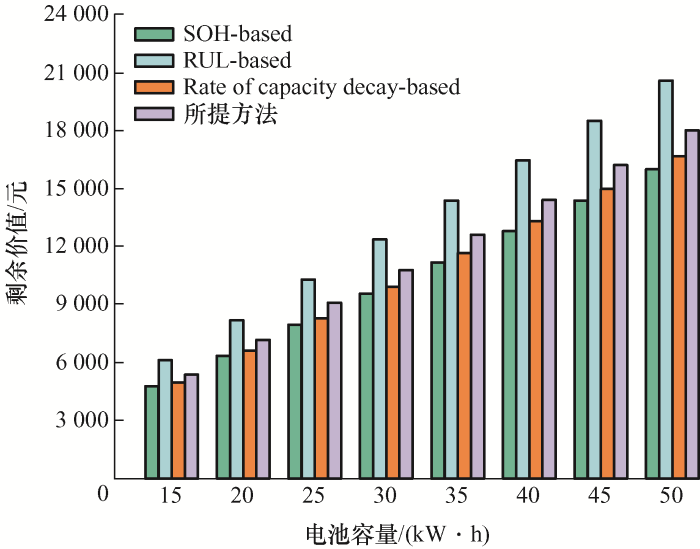
进一步地,对电池剩余价值进行估计,由于各单体的单价及原料价格会随着市场的变化而变化,故选择当下应用最广的18650电池作为实施例,按照850元/(kW·h)计算电池剩余价值。基于不同参量的电池剩余价值估计值如图5 所示。从图5 可以看出,在不同容量的电池中,基于RUL评估的电池剩余价值最高,基于SOH评估的电池价值剩余最低,参量耦合评估的电池剩余价值处于中位。这表明根据多参量耦合对电池剩余价值进行估算是合理的。
图5
4 结论
本文根据SOH、RUL和容量衰减率等多参量通过熵权法以及综合评价方法得出得分并定义电池剩余使用价值,解决了传统方法仅靠单一参量评估造成的评估不准难题,对指导电池回收利用提供了合理有效的评价指标。通过MIT数据集验证了定义的合理性,得出了以下结论。
(1) 所提出的电池剩余使用价值RUV定义与评估方法全面考虑了影响电池价值的因素,并利用最大最小法计算各指标评分,能够实现合理高效的剩余价值评估,结果客观准确。
(2) 提出的RUV计算方法简单高效、鲁棒性强,能够根据电池不同状态计算评估剩余使用价值,有利于优化电池使用寿命及合理回收利用,具有较好的实用效果。
参考文献
View Option
[1]
张茜 . 乘用车和商用车场景下电动汽车与燃油车技术路线对比分析
[J]. 石油石化绿色低碳 , 2022 , 7 (4 ):6 -9 ,53.
[本文引用: 1]
ZHANG Xi Comparative analysis of EV and ICE vehicles in passenger and commercial vehicle scenarios
[J]. Green Petroleum & Petrochemicals , 2022 , 7 (4 ):6 -9 .
[本文引用: 1]
[2]
来鑫 , 陈权威 , 顾黄辉 , 等 . 面向“双碳”战略目标的锂离子电池生命周期评价:框架、方法与进展
[J]. 机械工程学报 , 2022 , 58 (22 ):3 -18 .
DOI:10.3901/JME.2022.22.003
[本文引用: 1]
在国家“双碳”重大战略驱动下,锂离子电池在迎来了重大发展机遇的同时,它的全生命周期碳足迹追踪与环境指标评价成为研究热点,在碳排放计算及减碳措施方面遇到严峻挑战。首先,对全生命周期评价的基本框架、基本方法、评价指标等基础共性问题进行简要概述。然后,从锂离子电池可持续发展出发,提出从“摇篮”到“摇篮”的全生命周期闭环评价路线,对电池全生命周期内(包括电池生产、电池使用、梯次利用、电池回收与再制造等环节)各阶段碳排放计算的研究现状与进展进行详细综述,总结各阶段潜在的研究热点与难点,提出一种“技术-生态-价值”综合评价框架。在此基础上,对锂离子电池生命周期价值评价存在的机遇与挑战进行讨论,对资源风险与供应链风险进行分析与梳理。最后,总结与展望了能源脱碳、体系创新、智能制造、优化管理、材料回收、碳捕集等六大潜在的锂离子电池全生命周期减碳措施。
LAI Xin CHEN Quanwei GU Huanghui et al. Life cycle assessment of lithium-ion batteries for carbon-peaking and carbon-neutrality:Framework,methods,and progress
[J]. Journal of Mechanical Engineering , 2022 , 58 (22 ):3 -18 .
DOI:10.3901/JME.2022.22.003
[本文引用: 1]
Driven by the Carbon-peaking and Carbon-neutrality strategic goals, lithium-ion batteries usher in significant development opportunities. Meanwhile, it has become a research hotspot for tracking the life cycle carbon footprint and environmental indicators assessment and faced severe challenges in carbon emission calculation and reduction measures. First, the basic framework, methods,evaluation indicators, and other common problems of the life cycle assessment are briefly summarized. Then, a whole life cycle closed-loop assessment route from "cradle" to "cradle" is proposed for the sustainable development of lithium-ion batteries. The research progress of carbon emission calculation at all stages of the battery life cycle(including battery production, battery use,echelon utilization, battery recycling, and remanufacture) is summarized in detail, the potential research hotspots and difficulties are generalized, and a comprehensive evaluation framework of "Technology-Ecology-Value" is proposed. The opportunities and challenges in lithium-ion batteries' life cycle value assessment are discussed, and the resource and supply chain risks are analyzed.Finally, six potential carbon reduction measures for the whole life cycle of lithium-ion batteries are summarized and prospected, such as energy decarbonization, system innovation, intelligent manufacturing, optimization management, material recovery, and carbon capture.
[3]
肖曦 , 田培根 , 于璐 , 等 . 动力电池梯次利用储能系统电热安全研究现状及展望
[J]. 电气工程学报 , 2022 , 17 (1 ):206 -224 .
[本文引用: 1]
XIAO Xi TIAN Peigen YU Lu et al. Status and prospect of safety studies of cascade power battery energy storage system
[J]. Journal of Electrical Engineering , 2022 , 17 (1 ):206 -224 .
[本文引用: 1]
[4]
SEVERSON K A ATTIA P M JIN N et al. Data-driven prediction of battery cycle life before capacity degradation
[J]. Nature Energy , 2019 , 4 (5 ):383 -391 .
DOI:10.1038/s41560-019-0356-8
[本文引用: 1]
Accurately predicting the lifetime of complex, nonlinear systems such as lithium-ion batteries is critical for accelerating technology development. However, diverse aging mechanisms, significant device variability and dynamic operating conditions have remained major challenges. We generate a comprehensive dataset consisting of 124 commercial lithium iron phosphate/graphite cells cycled under fast-charging conditions, with widely varying cycle lives ranging from 150 to 2,300 cycles. Using discharge voltage curves from early cycles yet to exhibit capacity degradation, we apply machine-learning tools to both predict and classify cells by cycle life. Our best models achieve 9.1% test error for quantitatively predicting cycle life using the first 100 cycles (exhibiting a median increase of 0.2% from initial capacity) and 4.9% test error using the first 5 cycles for classifying cycle life into two groups. This work highlights the promise of combining deliberate data generation with data-driven modelling to predict the behaviour of complex dynamical systems.
[5]
ZHOU Z LIU Y YOU M et al. Two-stage aging trajectory prediction of LFP lithium-ion battery based on transfer learning with the cycle life prediction
[J]. Green Energy and Intelligent Transportation , 2022 , 1 (1 ):100008 .
DOI:10.1016/j.geits.2022.100008
URL
[本文引用: 1]
[6]
HARIS M HASAN M N QIN S Degradation curve prediction of lithium-ion batteries based on knee point detection algorithm and convolutional neural network
[J]. IEEE Transactions on Instrumentation and Measurement , 2022 ,71:1 -10 .
[本文引用: 1]
[7]
WAAG W FLEISCHER C SAUER D U Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles
[J]. Journal of Power Sources , 2014 , 258 (14 ):321 -339 .
DOI:10.1016/j.jpowsour.2014.02.064
URL
[本文引用: 1]
[8]
LIU Zhenbao SUN Gaoyuan BU Shuhui et al. Particle learning framework for estimating the remaining useful life of lithium-ion batteries
[J]. IEEE Transactions on Instrumentation and Measurement , 2017 , 66 (2 ):280 -293 .
DOI:10.1109/TIM.2016.2622838
URL
[本文引用: 1]
[9]
ZHANG Lijun MU Zhongqiang SUN Changyan Remaining useful life prediction for lithium-ion batteries based on exponential model and particle filter
[J]. IEEE Access , 2018 ,6:17729 -17740 .
[本文引用: 1]
[10]
孙丙香 , 任鹏博 , 陈育哲 , 等 . 锂离子电池在不同区间下的衰退影响因素分析及任意区间的老化趋势预测
[J]. 电工技术学报 , 2021 , 36 (3 ):666 -674 .
[本文引用: 1]
SUN Bingxiang REN Pengbo CHEN Yuzhe et al. Analysis of influencing factors of degradation under different interval stress and prediction of aging trend in any interval for lithium-ion battery
[J]. Transactions of China Electrotechnical Society , 2021 , 36 (3 ):666 -674 .
[本文引用: 1]
[11]
方德宇 , 楚潇 , 刘涛 , 等 . 基于数据-模型驱动的锂离子电池健康状态估计
[J]. 电气工程学报 , 2022 , 17 (4 ):20 -31 .
[本文引用: 1]
FANG Deyu CHU Xiao LIU Tao et al. Research on health assessment method of lithium-ion battery based on bata-model hybrid drive
[J]. Journal of Electrical Engineering , 2022 , 17 (4 ):20 -31 .
[本文引用: 1]
[12]
胡晓亚 , 郭永芳 , 张若可 . 锂离子电池健康状态估计方法研究综述
[J]. 电源学报 , 2022 , 20 (1 ):126 -133 .
[本文引用: 1]
HU Xiaoya GUO Yongfang ZHANG Ruoke Review of state-of-health estimation methods for lithium-ion battery
[J]. Journal of Power Supply , 2022 , 20 (1 ):126 -133 .
DOI:10.13234/j.issn.2095-2805.2022.1.126
[本文引用: 1]
Battery management system is an important guarantee for the efficient and safe operation of lithium-ion batteries, in which the battery state estimation plays an important role. The state-of-health(SOH) is one of the important indicators for the state estimation of lithium-ion batteries. In this paper, the definition and estimation methods for the SOH of lithium-ion batteries are reviewed through the summary of related literatures in recent years, and the existing estimation methods are classified and described. Finally, aimed at the shortcomings of the existing estimation methods, the direction of improvement in the future is put forward.
[13]
LIU Kailong SHANG Yunlong OUYANG Quan et al. A data-driven approach with uncertainty quantification for predicting future capacities and remaining useful life of lithium-ion battery
[J]. IEEE Transactions on Industrial Electronics , 2021 , 68 (4 ):3170 -3180 .
DOI:10.1109/TIE.41
URL
[本文引用: 1]
[14]
贾俊 , 胡晓松 , 邓忠伟 . 数据驱动的锂离子电池健康状态综合评分及异常电池筛选
[J]. 机械工程学报 , 2021 , 57 (14 ):141 -149 ,159.
DOI:10.3901/JME.2021.14.141
[本文引用: 1]
锂离子电池是电动汽车和储能系统最重要的组成部分,其故障预测和健康管理对于运行维护至关重要。数据驱动的方法较基于模型的方法更适合大规模工程应用,针对实际应用中工况复杂和数据质量较差的场景,提出数据驱动的健康状态综合评分及异常筛选算法,具有较强的适应性。首先,针对电池实际运行工况提出一种新的特征提取方案,可适用于非恒流的不稳定工况。开发了基于多维特征和混合聚类算法的健康状态综合评分体系,该方案采用无监督学习的算法框架,对可提取特征的数量和质量要求不高,无需进行事先的模型训练和复杂的超参数调整。然后,在麻省理工学院和斯坦福大学提供的公开数据集进行了算法验证,基于电池生命周期各阶段特征集进行健康度等级预测,并应用于健康度高低分选,均能达到92%以上的准确率。在某用户侧储能电站实现了该算法的应用,采用早期运行数据即可快速筛选异常电池,有利于尽早维护,提高电池系统的安全性和经济性。
JIA Jun HU Xiaosong DENG Zhongwei Data-driven comprehensive evaluation of lithium-ion battery state of health and abnormal battery screening
[J]. Journal of Mechanical Engineering , 2021 , 57 (14 ):141 -149 ,159.
DOI:10.3901/JME.2021.14.141
[本文引用: 1]
Lithium-ion batteries are the most important part of electric vehicles and energy storage systems, and their health management and fault identification are critical to operation and maintenance. The data-driven method is more suitable for large-scale engineering applications than the model-based method. Aiming at scenarios with complex working conditions and poor data quality in practical applications, a data-driven comprehensive evaluation of lithium-ion battery state of health and abnormal battery screening algorithm are proposed. First, a novel feature extraction scheme is proposed for the actual operating conditions of batteries, which can be applied to unstable working conditions with non-constant current. A comprehensive state of health scoring system based on multi-dimensional features and hybrid clustering algorithms is developed. This scheme is an algorithm framework for unsupervised learning, which does not require high quantity and quality of extractable features, without prior model training and complicated hyper parameter adjustment. Then, the algorithm is verified at the public data set of Massachusetts Institute of Technology and Stanford. Based on the feature set of each stage of the battery life cycle, the health level prediction can be achieved, and the accuracy is more than 92% when applied to classify the health level. Finally, the proposed algorithm is implemented in a user-side energy storage power station. Early operation data can be used to quickly screen abnormal batteries, which is beneficial to early maintenance, and improve the safety and economy of the battery system.
[15]
李欣 . 车用锂离子电池全生命周期寿命预测与健康管理方法研究 [D]. 长春 : 吉林大学 , 2022 .
[本文引用: 1]
LI Xin Research on life prognostics and health management of electric vehicles lithium-ion battery in the whole life cycle [D]. Changchun : Jilin University , 2022 .
[本文引用: 1]
[16]
ZHENG Y QIN C LAI X et al. A novel capacity estimation method for lithium-ion batteries using fusion estimation of charging curve sections and discrete Arrhenius aging model
[J]. Applied Energy , 2019 ,251:113327.
[本文引用: 1]
[17]
YAN W ZHANG B ZHAO G et al. A battery management system with a Lebesgue-sampling-based extended Kalman filter
[J]. IEEE Transactions on Industrial Electronics , 2018 , 66 (4 ):3227 -3236 .
DOI:10.1109/TIE.2018.2842782
URL
[本文引用: 1]
[18]
MA Y CHEN Y ZHOU X et al. Remaining useful life prediction of lithium-ion battery based on Gauss-Hermite particle filter
[J]. IEEE Transactions on Control Systems Technology , 2018 , 27 (4 ):1788 -1795 .
DOI:10.1109/TCST.87
URL
[本文引用: 1]
[19]
YU Q XIONG R YANG R et al. Online capacity estimation for lithium-ion batteries through joint estimation method
[J]. Applied Energy , 2019 ,255:113817.
[本文引用: 1]
[20]
CHEN C XIONG R SHEN W A lithium-ion battery-in-the-loop approach to test and validate multiscale dual H infinity filters for state-of-charge and capacity estimation
[J]. IEEE Transactions on Power Electronics , 2017 , 33 (1 ):332 -342 .
DOI:10.1109/TPEL.2017.2670081
URL
[本文引用: 1]
[21]
KIM J CHUN H KIM M et al. Data-driven state of health estimation of Li-ion batteries with RPT-reduced experimental data
[J]. IEEE Access , 2019 ,7:106987 -106997 .
[本文引用: 1]
[22]
HAN T WANG Z MENG H End-to-end capacity estimation of Lithium-ion batteries with an enhanced long short-term memory network considering domain adaptation
[J]. Journal of Power Sources , 2022 ,520:230823.
[本文引用: 1]
[23]
HU X CHE Y LIN X et al. Health prognosis for electric vehicle battery packs:A data-driven approach
[J]. IEEE/ASME Transactions on Mechatronics , 2020 , 25 (6 ):2622 -2632 .
DOI:10.1109/TMECH.3516
URL
[本文引用: 1]
[24]
WANG Z P MA J ZHANG L State-of-health estimation for lithium-ion batteries based on the multi-island genetic algorithm and the Gaussian process regression
[J]. IEEE Access , 2017 ,5:21286 -21295 .
[本文引用: 1]
[25]
KATTERNBORN T LEITLOFF J SCHIEFER F et al. Review on convolutional neural networks (CNN) in vegetation remote sensing
[J]. ISPRS Journal of Photogrammetry and Remote Sensing , 2021 ,173:24 -49 .
[本文引用: 1]
[26]
LI Y LIU K L FOLEY A M et al. Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review
[J]. Renewable and Sustainable Energy Reviews , 2019 ,113:109254.
[本文引用: 1]
乘用车和商用车场景下电动汽车与燃油车技术路线对比分析
1
2022
... 传统燃油车排放的汽车尾气对环境造成很大危害.为了减少稀缺能源的消耗,实现环境友好的可持续发展,新能源汽车应运而生[1 ⇓ -3 ] .随着新能源汽车保有量的快速增加,对于锂离子电池的需求呈现出爆发式增长的趋势[4 ⇓ -6 ] .2023年1—10月,全球动力电池装车量达到552.2 GW·h[7 ] .截止到2023年末,锂离子动力电池的退役量超过58万吨[8 ] .退役的动力电池仍有约70%的可用容量,工业和信息化部也在《新能源汽车动力蓄电池梯次利用管理办法》中鼓励各机构合作,充分挖掘电池剩余可用价值信息,实现电池合理梯次利用[9 ] . ...
Comparative analysis of EV and ICE vehicles in passenger and commercial vehicle scenarios
1
2022
... 传统燃油车排放的汽车尾气对环境造成很大危害.为了减少稀缺能源的消耗,实现环境友好的可持续发展,新能源汽车应运而生[1 ⇓ -3 ] .随着新能源汽车保有量的快速增加,对于锂离子电池的需求呈现出爆发式增长的趋势[4 ⇓ -6 ] .2023年1—10月,全球动力电池装车量达到552.2 GW·h[7 ] .截止到2023年末,锂离子动力电池的退役量超过58万吨[8 ] .退役的动力电池仍有约70%的可用容量,工业和信息化部也在《新能源汽车动力蓄电池梯次利用管理办法》中鼓励各机构合作,充分挖掘电池剩余可用价值信息,实现电池合理梯次利用[9 ] . ...
面向“双碳”战略目标的锂离子电池生命周期评价:框架、方法与进展
1
2022
... 传统燃油车排放的汽车尾气对环境造成很大危害.为了减少稀缺能源的消耗,实现环境友好的可持续发展,新能源汽车应运而生[1 ⇓ -3 ] .随着新能源汽车保有量的快速增加,对于锂离子电池的需求呈现出爆发式增长的趋势[4 ⇓ -6 ] .2023年1—10月,全球动力电池装车量达到552.2 GW·h[7 ] .截止到2023年末,锂离子动力电池的退役量超过58万吨[8 ] .退役的动力电池仍有约70%的可用容量,工业和信息化部也在《新能源汽车动力蓄电池梯次利用管理办法》中鼓励各机构合作,充分挖掘电池剩余可用价值信息,实现电池合理梯次利用[9 ] . ...
Life cycle assessment of lithium-ion batteries for carbon-peaking and carbon-neutrality:Framework,methods,and progress
1
2022
... 传统燃油车排放的汽车尾气对环境造成很大危害.为了减少稀缺能源的消耗,实现环境友好的可持续发展,新能源汽车应运而生[1 ⇓ -3 ] .随着新能源汽车保有量的快速增加,对于锂离子电池的需求呈现出爆发式增长的趋势[4 ⇓ -6 ] .2023年1—10月,全球动力电池装车量达到552.2 GW·h[7 ] .截止到2023年末,锂离子动力电池的退役量超过58万吨[8 ] .退役的动力电池仍有约70%的可用容量,工业和信息化部也在《新能源汽车动力蓄电池梯次利用管理办法》中鼓励各机构合作,充分挖掘电池剩余可用价值信息,实现电池合理梯次利用[9 ] . ...
动力电池梯次利用储能系统电热安全研究现状及展望
1
2022
... 传统燃油车排放的汽车尾气对环境造成很大危害.为了减少稀缺能源的消耗,实现环境友好的可持续发展,新能源汽车应运而生[1 ⇓ -3 ] .随着新能源汽车保有量的快速增加,对于锂离子电池的需求呈现出爆发式增长的趋势[4 ⇓ -6 ] .2023年1—10月,全球动力电池装车量达到552.2 GW·h[7 ] .截止到2023年末,锂离子动力电池的退役量超过58万吨[8 ] .退役的动力电池仍有约70%的可用容量,工业和信息化部也在《新能源汽车动力蓄电池梯次利用管理办法》中鼓励各机构合作,充分挖掘电池剩余可用价值信息,实现电池合理梯次利用[9 ] . ...
Status and prospect of safety studies of cascade power battery energy storage system
1
2022
... 传统燃油车排放的汽车尾气对环境造成很大危害.为了减少稀缺能源的消耗,实现环境友好的可持续发展,新能源汽车应运而生[1 ⇓ -3 ] .随着新能源汽车保有量的快速增加,对于锂离子电池的需求呈现出爆发式增长的趋势[4 ⇓ -6 ] .2023年1—10月,全球动力电池装车量达到552.2 GW·h[7 ] .截止到2023年末,锂离子动力电池的退役量超过58万吨[8 ] .退役的动力电池仍有约70%的可用容量,工业和信息化部也在《新能源汽车动力蓄电池梯次利用管理办法》中鼓励各机构合作,充分挖掘电池剩余可用价值信息,实现电池合理梯次利用[9 ] . ...
Data-driven prediction of battery cycle life before capacity degradation
1
2019
... 传统燃油车排放的汽车尾气对环境造成很大危害.为了减少稀缺能源的消耗,实现环境友好的可持续发展,新能源汽车应运而生[1 ⇓ -3 ] .随着新能源汽车保有量的快速增加,对于锂离子电池的需求呈现出爆发式增长的趋势[4 ⇓ -6 ] .2023年1—10月,全球动力电池装车量达到552.2 GW·h[7 ] .截止到2023年末,锂离子动力电池的退役量超过58万吨[8 ] .退役的动力电池仍有约70%的可用容量,工业和信息化部也在《新能源汽车动力蓄电池梯次利用管理办法》中鼓励各机构合作,充分挖掘电池剩余可用价值信息,实现电池合理梯次利用[9 ] . ...
Two-stage aging trajectory prediction of LFP lithium-ion battery based on transfer learning with the cycle life prediction
1
2022
... 传统燃油车排放的汽车尾气对环境造成很大危害.为了减少稀缺能源的消耗,实现环境友好的可持续发展,新能源汽车应运而生[1 ⇓ -3 ] .随着新能源汽车保有量的快速增加,对于锂离子电池的需求呈现出爆发式增长的趋势[4 ⇓ -6 ] .2023年1—10月,全球动力电池装车量达到552.2 GW·h[7 ] .截止到2023年末,锂离子动力电池的退役量超过58万吨[8 ] .退役的动力电池仍有约70%的可用容量,工业和信息化部也在《新能源汽车动力蓄电池梯次利用管理办法》中鼓励各机构合作,充分挖掘电池剩余可用价值信息,实现电池合理梯次利用[9 ] . ...
Degradation curve prediction of lithium-ion batteries based on knee point detection algorithm and convolutional neural network
1
2022
... 传统燃油车排放的汽车尾气对环境造成很大危害.为了减少稀缺能源的消耗,实现环境友好的可持续发展,新能源汽车应运而生[1 ⇓ -3 ] .随着新能源汽车保有量的快速增加,对于锂离子电池的需求呈现出爆发式增长的趋势[4 ⇓ -6 ] .2023年1—10月,全球动力电池装车量达到552.2 GW·h[7 ] .截止到2023年末,锂离子动力电池的退役量超过58万吨[8 ] .退役的动力电池仍有约70%的可用容量,工业和信息化部也在《新能源汽车动力蓄电池梯次利用管理办法》中鼓励各机构合作,充分挖掘电池剩余可用价值信息,实现电池合理梯次利用[9 ] . ...
Critical review of the methods for monitoring of lithium-ion batteries in electric and hybrid vehicles
1
2014
... 传统燃油车排放的汽车尾气对环境造成很大危害.为了减少稀缺能源的消耗,实现环境友好的可持续发展,新能源汽车应运而生[1 ⇓ -3 ] .随着新能源汽车保有量的快速增加,对于锂离子电池的需求呈现出爆发式增长的趋势[4 ⇓ -6 ] .2023年1—10月,全球动力电池装车量达到552.2 GW·h[7 ] .截止到2023年末,锂离子动力电池的退役量超过58万吨[8 ] .退役的动力电池仍有约70%的可用容量,工业和信息化部也在《新能源汽车动力蓄电池梯次利用管理办法》中鼓励各机构合作,充分挖掘电池剩余可用价值信息,实现电池合理梯次利用[9 ] . ...
Particle learning framework for estimating the remaining useful life of lithium-ion batteries
1
2017
... 传统燃油车排放的汽车尾气对环境造成很大危害.为了减少稀缺能源的消耗,实现环境友好的可持续发展,新能源汽车应运而生[1 ⇓ -3 ] .随着新能源汽车保有量的快速增加,对于锂离子电池的需求呈现出爆发式增长的趋势[4 ⇓ -6 ] .2023年1—10月,全球动力电池装车量达到552.2 GW·h[7 ] .截止到2023年末,锂离子动力电池的退役量超过58万吨[8 ] .退役的动力电池仍有约70%的可用容量,工业和信息化部也在《新能源汽车动力蓄电池梯次利用管理办法》中鼓励各机构合作,充分挖掘电池剩余可用价值信息,实现电池合理梯次利用[9 ] . ...
Remaining useful life prediction for lithium-ion batteries based on exponential model and particle filter
1
2018
... 传统燃油车排放的汽车尾气对环境造成很大危害.为了减少稀缺能源的消耗,实现环境友好的可持续发展,新能源汽车应运而生[1 ⇓ -3 ] .随着新能源汽车保有量的快速增加,对于锂离子电池的需求呈现出爆发式增长的趋势[4 ⇓ -6 ] .2023年1—10月,全球动力电池装车量达到552.2 GW·h[7 ] .截止到2023年末,锂离子动力电池的退役量超过58万吨[8 ] .退役的动力电池仍有约70%的可用容量,工业和信息化部也在《新能源汽车动力蓄电池梯次利用管理办法》中鼓励各机构合作,充分挖掘电池剩余可用价值信息,实现电池合理梯次利用[9 ] . ...
锂离子电池在不同区间下的衰退影响因素分析及任意区间的老化趋势预测
1
2021
... 动力电池老化机理复杂,性能“每用必衰”,当电池性能不能满足日常使用需求时,需要退役并及时更换.事实上,退役电池仍有较大的使用价值.电池剩余使用价值受多种参数耦合影响,如电池容量、健康状态(State of health, SOH)、剩余寿命(Remaining useful life, RUL)等[10 -11 ] .退役电池仍然有约70%的容量可供不同场景使用.电池容量衰减率不同会导致后续衰退曲线呈现不同的趋势,即使其退役之前容量衰减相同,电池的剩余价值也会因为容量衰减率不同而不同,导致后续可应用领域有所差别[12 ⇓ -14 ] .目前在电池的回收估值及再利用领域,尚缺乏有效的剩余使用价值估计方法.如何合理定义剩余价值(Remaining useful value, RUV)且精准客观评估是一项具有挑战性的工作,也是本文要解决的关键科学难题. ...
Analysis of influencing factors of degradation under different interval stress and prediction of aging trend in any interval for lithium-ion battery
1
2021
... 动力电池老化机理复杂,性能“每用必衰”,当电池性能不能满足日常使用需求时,需要退役并及时更换.事实上,退役电池仍有较大的使用价值.电池剩余使用价值受多种参数耦合影响,如电池容量、健康状态(State of health, SOH)、剩余寿命(Remaining useful life, RUL)等[10 -11 ] .退役电池仍然有约70%的容量可供不同场景使用.电池容量衰减率不同会导致后续衰退曲线呈现不同的趋势,即使其退役之前容量衰减相同,电池的剩余价值也会因为容量衰减率不同而不同,导致后续可应用领域有所差别[12 ⇓ -14 ] .目前在电池的回收估值及再利用领域,尚缺乏有效的剩余使用价值估计方法.如何合理定义剩余价值(Remaining useful value, RUV)且精准客观评估是一项具有挑战性的工作,也是本文要解决的关键科学难题. ...
基于数据-模型驱动的锂离子电池健康状态估计
1
2022
... 动力电池老化机理复杂,性能“每用必衰”,当电池性能不能满足日常使用需求时,需要退役并及时更换.事实上,退役电池仍有较大的使用价值.电池剩余使用价值受多种参数耦合影响,如电池容量、健康状态(State of health, SOH)、剩余寿命(Remaining useful life, RUL)等[10 -11 ] .退役电池仍然有约70%的容量可供不同场景使用.电池容量衰减率不同会导致后续衰退曲线呈现不同的趋势,即使其退役之前容量衰减相同,电池的剩余价值也会因为容量衰减率不同而不同,导致后续可应用领域有所差别[12 ⇓ -14 ] .目前在电池的回收估值及再利用领域,尚缺乏有效的剩余使用价值估计方法.如何合理定义剩余价值(Remaining useful value, RUV)且精准客观评估是一项具有挑战性的工作,也是本文要解决的关键科学难题. ...
Research on health assessment method of lithium-ion battery based on bata-model hybrid drive
1
2022
... 动力电池老化机理复杂,性能“每用必衰”,当电池性能不能满足日常使用需求时,需要退役并及时更换.事实上,退役电池仍有较大的使用价值.电池剩余使用价值受多种参数耦合影响,如电池容量、健康状态(State of health, SOH)、剩余寿命(Remaining useful life, RUL)等[10 -11 ] .退役电池仍然有约70%的容量可供不同场景使用.电池容量衰减率不同会导致后续衰退曲线呈现不同的趋势,即使其退役之前容量衰减相同,电池的剩余价值也会因为容量衰减率不同而不同,导致后续可应用领域有所差别[12 ⇓ -14 ] .目前在电池的回收估值及再利用领域,尚缺乏有效的剩余使用价值估计方法.如何合理定义剩余价值(Remaining useful value, RUV)且精准客观评估是一项具有挑战性的工作,也是本文要解决的关键科学难题. ...
锂离子电池健康状态估计方法研究综述
1
2022
... 动力电池老化机理复杂,性能“每用必衰”,当电池性能不能满足日常使用需求时,需要退役并及时更换.事实上,退役电池仍有较大的使用价值.电池剩余使用价值受多种参数耦合影响,如电池容量、健康状态(State of health, SOH)、剩余寿命(Remaining useful life, RUL)等[10 -11 ] .退役电池仍然有约70%的容量可供不同场景使用.电池容量衰减率不同会导致后续衰退曲线呈现不同的趋势,即使其退役之前容量衰减相同,电池的剩余价值也会因为容量衰减率不同而不同,导致后续可应用领域有所差别[12 ⇓ -14 ] .目前在电池的回收估值及再利用领域,尚缺乏有效的剩余使用价值估计方法.如何合理定义剩余价值(Remaining useful value, RUV)且精准客观评估是一项具有挑战性的工作,也是本文要解决的关键科学难题. ...
Review of state-of-health estimation methods for lithium-ion battery
1
2022
... 动力电池老化机理复杂,性能“每用必衰”,当电池性能不能满足日常使用需求时,需要退役并及时更换.事实上,退役电池仍有较大的使用价值.电池剩余使用价值受多种参数耦合影响,如电池容量、健康状态(State of health, SOH)、剩余寿命(Remaining useful life, RUL)等[10 -11 ] .退役电池仍然有约70%的容量可供不同场景使用.电池容量衰减率不同会导致后续衰退曲线呈现不同的趋势,即使其退役之前容量衰减相同,电池的剩余价值也会因为容量衰减率不同而不同,导致后续可应用领域有所差别[12 ⇓ -14 ] .目前在电池的回收估值及再利用领域,尚缺乏有效的剩余使用价值估计方法.如何合理定义剩余价值(Remaining useful value, RUV)且精准客观评估是一项具有挑战性的工作,也是本文要解决的关键科学难题. ...
A data-driven approach with uncertainty quantification for predicting future capacities and remaining useful life of lithium-ion battery
1
2021
... 动力电池老化机理复杂,性能“每用必衰”,当电池性能不能满足日常使用需求时,需要退役并及时更换.事实上,退役电池仍有较大的使用价值.电池剩余使用价值受多种参数耦合影响,如电池容量、健康状态(State of health, SOH)、剩余寿命(Remaining useful life, RUL)等[10 -11 ] .退役电池仍然有约70%的容量可供不同场景使用.电池容量衰减率不同会导致后续衰退曲线呈现不同的趋势,即使其退役之前容量衰减相同,电池的剩余价值也会因为容量衰减率不同而不同,导致后续可应用领域有所差别[12 ⇓ -14 ] .目前在电池的回收估值及再利用领域,尚缺乏有效的剩余使用价值估计方法.如何合理定义剩余价值(Remaining useful value, RUV)且精准客观评估是一项具有挑战性的工作,也是本文要解决的关键科学难题. ...
数据驱动的锂离子电池健康状态综合评分及异常电池筛选
1
2021
... 动力电池老化机理复杂,性能“每用必衰”,当电池性能不能满足日常使用需求时,需要退役并及时更换.事实上,退役电池仍有较大的使用价值.电池剩余使用价值受多种参数耦合影响,如电池容量、健康状态(State of health, SOH)、剩余寿命(Remaining useful life, RUL)等[10 -11 ] .退役电池仍然有约70%的容量可供不同场景使用.电池容量衰减率不同会导致后续衰退曲线呈现不同的趋势,即使其退役之前容量衰减相同,电池的剩余价值也会因为容量衰减率不同而不同,导致后续可应用领域有所差别[12 ⇓ -14 ] .目前在电池的回收估值及再利用领域,尚缺乏有效的剩余使用价值估计方法.如何合理定义剩余价值(Remaining useful value, RUV)且精准客观评估是一项具有挑战性的工作,也是本文要解决的关键科学难题. ...
Data-driven comprehensive evaluation of lithium-ion battery state of health and abnormal battery screening
1
2021
... 动力电池老化机理复杂,性能“每用必衰”,当电池性能不能满足日常使用需求时,需要退役并及时更换.事实上,退役电池仍有较大的使用价值.电池剩余使用价值受多种参数耦合影响,如电池容量、健康状态(State of health, SOH)、剩余寿命(Remaining useful life, RUL)等[10 -11 ] .退役电池仍然有约70%的容量可供不同场景使用.电池容量衰减率不同会导致后续衰退曲线呈现不同的趋势,即使其退役之前容量衰减相同,电池的剩余价值也会因为容量衰减率不同而不同,导致后续可应用领域有所差别[12 ⇓ -14 ] .目前在电池的回收估值及再利用领域,尚缺乏有效的剩余使用价值估计方法.如何合理定义剩余价值(Remaining useful value, RUV)且精准客观评估是一项具有挑战性的工作,也是本文要解决的关键科学难题. ...
1
2022
... 国内外学者对电池的剩余价值指标估计进行了研究.文献[15 ]根据电池衰退的不一致性提出了基于衰退速度预测的电池剩余价值优化方法,估算过程较为复杂.文献[16 ]提出了充电曲线分段(Charging curve segmentation, CCS)与离散Arrhenius老化模型(Discrete Arrhenius aging model, DAAM)的融合来估算容量.第一个卡尔曼滤波(Kalman filter, KF)更新了DAAM的模型参数;第二次KF基于修正参数的CCS和DAAM估算聚变能力.然而,经验模型难以跟踪负荷动态特性,且受外部环境因素的干扰,它们的适应性和准确性是有限的.等效电路模型通过KF[17 ] 、粒子滤波PF[18 ] 、递推最小二乘RLS[19 ] 等方法实现SOC和容量的共同估计.文献[20 ]建立了用于SOC和容量估计的多尺度双H无限滤波器(H-infinity filter, HIF).与单/多尺度双KF相比,该方法具有更好的鲁棒性和更高的估计精度.然而,等效电路模型在等效过程中没有考虑电池内部状态变量的信息,影响了电池估计的准确性.对于其他价值参数SOH、RUL的估计,文献[21 ]提出了一种基于神经网络的新的SOH估计方案,可以利用短时间内的电压和电流数据来估计SOH值,达到减少参考性能测试(Reference performance test, RPT)次数的效果,但是估计耗时较长.文献[22 ]使用混合神经网络来捕获电池数据的层次特征和时间信息,结合贝叶斯优化的神经网络结构来实现电池健康状态(SOH)和剩余使用寿命(RUL)的端到端估计,估计效果泛化性强,但是对于输入数据的要求较高. ...
1
2022
... 国内外学者对电池的剩余价值指标估计进行了研究.文献[15 ]根据电池衰退的不一致性提出了基于衰退速度预测的电池剩余价值优化方法,估算过程较为复杂.文献[16 ]提出了充电曲线分段(Charging curve segmentation, CCS)与离散Arrhenius老化模型(Discrete Arrhenius aging model, DAAM)的融合来估算容量.第一个卡尔曼滤波(Kalman filter, KF)更新了DAAM的模型参数;第二次KF基于修正参数的CCS和DAAM估算聚变能力.然而,经验模型难以跟踪负荷动态特性,且受外部环境因素的干扰,它们的适应性和准确性是有限的.等效电路模型通过KF[17 ] 、粒子滤波PF[18 ] 、递推最小二乘RLS[19 ] 等方法实现SOC和容量的共同估计.文献[20 ]建立了用于SOC和容量估计的多尺度双H无限滤波器(H-infinity filter, HIF).与单/多尺度双KF相比,该方法具有更好的鲁棒性和更高的估计精度.然而,等效电路模型在等效过程中没有考虑电池内部状态变量的信息,影响了电池估计的准确性.对于其他价值参数SOH、RUL的估计,文献[21 ]提出了一种基于神经网络的新的SOH估计方案,可以利用短时间内的电压和电流数据来估计SOH值,达到减少参考性能测试(Reference performance test, RPT)次数的效果,但是估计耗时较长.文献[22 ]使用混合神经网络来捕获电池数据的层次特征和时间信息,结合贝叶斯优化的神经网络结构来实现电池健康状态(SOH)和剩余使用寿命(RUL)的端到端估计,估计效果泛化性强,但是对于输入数据的要求较高. ...
A novel capacity estimation method for lithium-ion batteries using fusion estimation of charging curve sections and discrete Arrhenius aging model
1
2019
... 国内外学者对电池的剩余价值指标估计进行了研究.文献[15 ]根据电池衰退的不一致性提出了基于衰退速度预测的电池剩余价值优化方法,估算过程较为复杂.文献[16 ]提出了充电曲线分段(Charging curve segmentation, CCS)与离散Arrhenius老化模型(Discrete Arrhenius aging model, DAAM)的融合来估算容量.第一个卡尔曼滤波(Kalman filter, KF)更新了DAAM的模型参数;第二次KF基于修正参数的CCS和DAAM估算聚变能力.然而,经验模型难以跟踪负荷动态特性,且受外部环境因素的干扰,它们的适应性和准确性是有限的.等效电路模型通过KF[17 ] 、粒子滤波PF[18 ] 、递推最小二乘RLS[19 ] 等方法实现SOC和容量的共同估计.文献[20 ]建立了用于SOC和容量估计的多尺度双H无限滤波器(H-infinity filter, HIF).与单/多尺度双KF相比,该方法具有更好的鲁棒性和更高的估计精度.然而,等效电路模型在等效过程中没有考虑电池内部状态变量的信息,影响了电池估计的准确性.对于其他价值参数SOH、RUL的估计,文献[21 ]提出了一种基于神经网络的新的SOH估计方案,可以利用短时间内的电压和电流数据来估计SOH值,达到减少参考性能测试(Reference performance test, RPT)次数的效果,但是估计耗时较长.文献[22 ]使用混合神经网络来捕获电池数据的层次特征和时间信息,结合贝叶斯优化的神经网络结构来实现电池健康状态(SOH)和剩余使用寿命(RUL)的端到端估计,估计效果泛化性强,但是对于输入数据的要求较高. ...
A battery management system with a Lebesgue-sampling-based extended Kalman filter
1
2018
... 国内外学者对电池的剩余价值指标估计进行了研究.文献[15 ]根据电池衰退的不一致性提出了基于衰退速度预测的电池剩余价值优化方法,估算过程较为复杂.文献[16 ]提出了充电曲线分段(Charging curve segmentation, CCS)与离散Arrhenius老化模型(Discrete Arrhenius aging model, DAAM)的融合来估算容量.第一个卡尔曼滤波(Kalman filter, KF)更新了DAAM的模型参数;第二次KF基于修正参数的CCS和DAAM估算聚变能力.然而,经验模型难以跟踪负荷动态特性,且受外部环境因素的干扰,它们的适应性和准确性是有限的.等效电路模型通过KF[17 ] 、粒子滤波PF[18 ] 、递推最小二乘RLS[19 ] 等方法实现SOC和容量的共同估计.文献[20 ]建立了用于SOC和容量估计的多尺度双H无限滤波器(H-infinity filter, HIF).与单/多尺度双KF相比,该方法具有更好的鲁棒性和更高的估计精度.然而,等效电路模型在等效过程中没有考虑电池内部状态变量的信息,影响了电池估计的准确性.对于其他价值参数SOH、RUL的估计,文献[21 ]提出了一种基于神经网络的新的SOH估计方案,可以利用短时间内的电压和电流数据来估计SOH值,达到减少参考性能测试(Reference performance test, RPT)次数的效果,但是估计耗时较长.文献[22 ]使用混合神经网络来捕获电池数据的层次特征和时间信息,结合贝叶斯优化的神经网络结构来实现电池健康状态(SOH)和剩余使用寿命(RUL)的端到端估计,估计效果泛化性强,但是对于输入数据的要求较高. ...
Remaining useful life prediction of lithium-ion battery based on Gauss-Hermite particle filter
1
2018
... 国内外学者对电池的剩余价值指标估计进行了研究.文献[15 ]根据电池衰退的不一致性提出了基于衰退速度预测的电池剩余价值优化方法,估算过程较为复杂.文献[16 ]提出了充电曲线分段(Charging curve segmentation, CCS)与离散Arrhenius老化模型(Discrete Arrhenius aging model, DAAM)的融合来估算容量.第一个卡尔曼滤波(Kalman filter, KF)更新了DAAM的模型参数;第二次KF基于修正参数的CCS和DAAM估算聚变能力.然而,经验模型难以跟踪负荷动态特性,且受外部环境因素的干扰,它们的适应性和准确性是有限的.等效电路模型通过KF[17 ] 、粒子滤波PF[18 ] 、递推最小二乘RLS[19 ] 等方法实现SOC和容量的共同估计.文献[20 ]建立了用于SOC和容量估计的多尺度双H无限滤波器(H-infinity filter, HIF).与单/多尺度双KF相比,该方法具有更好的鲁棒性和更高的估计精度.然而,等效电路模型在等效过程中没有考虑电池内部状态变量的信息,影响了电池估计的准确性.对于其他价值参数SOH、RUL的估计,文献[21 ]提出了一种基于神经网络的新的SOH估计方案,可以利用短时间内的电压和电流数据来估计SOH值,达到减少参考性能测试(Reference performance test, RPT)次数的效果,但是估计耗时较长.文献[22 ]使用混合神经网络来捕获电池数据的层次特征和时间信息,结合贝叶斯优化的神经网络结构来实现电池健康状态(SOH)和剩余使用寿命(RUL)的端到端估计,估计效果泛化性强,但是对于输入数据的要求较高. ...
Online capacity estimation for lithium-ion batteries through joint estimation method
1
2019
... 国内外学者对电池的剩余价值指标估计进行了研究.文献[15 ]根据电池衰退的不一致性提出了基于衰退速度预测的电池剩余价值优化方法,估算过程较为复杂.文献[16 ]提出了充电曲线分段(Charging curve segmentation, CCS)与离散Arrhenius老化模型(Discrete Arrhenius aging model, DAAM)的融合来估算容量.第一个卡尔曼滤波(Kalman filter, KF)更新了DAAM的模型参数;第二次KF基于修正参数的CCS和DAAM估算聚变能力.然而,经验模型难以跟踪负荷动态特性,且受外部环境因素的干扰,它们的适应性和准确性是有限的.等效电路模型通过KF[17 ] 、粒子滤波PF[18 ] 、递推最小二乘RLS[19 ] 等方法实现SOC和容量的共同估计.文献[20 ]建立了用于SOC和容量估计的多尺度双H无限滤波器(H-infinity filter, HIF).与单/多尺度双KF相比,该方法具有更好的鲁棒性和更高的估计精度.然而,等效电路模型在等效过程中没有考虑电池内部状态变量的信息,影响了电池估计的准确性.对于其他价值参数SOH、RUL的估计,文献[21 ]提出了一种基于神经网络的新的SOH估计方案,可以利用短时间内的电压和电流数据来估计SOH值,达到减少参考性能测试(Reference performance test, RPT)次数的效果,但是估计耗时较长.文献[22 ]使用混合神经网络来捕获电池数据的层次特征和时间信息,结合贝叶斯优化的神经网络结构来实现电池健康状态(SOH)和剩余使用寿命(RUL)的端到端估计,估计效果泛化性强,但是对于输入数据的要求较高. ...
A lithium-ion battery-in-the-loop approach to test and validate multiscale dual H infinity filters for state-of-charge and capacity estimation
1
2017
... 国内外学者对电池的剩余价值指标估计进行了研究.文献[15 ]根据电池衰退的不一致性提出了基于衰退速度预测的电池剩余价值优化方法,估算过程较为复杂.文献[16 ]提出了充电曲线分段(Charging curve segmentation, CCS)与离散Arrhenius老化模型(Discrete Arrhenius aging model, DAAM)的融合来估算容量.第一个卡尔曼滤波(Kalman filter, KF)更新了DAAM的模型参数;第二次KF基于修正参数的CCS和DAAM估算聚变能力.然而,经验模型难以跟踪负荷动态特性,且受外部环境因素的干扰,它们的适应性和准确性是有限的.等效电路模型通过KF[17 ] 、粒子滤波PF[18 ] 、递推最小二乘RLS[19 ] 等方法实现SOC和容量的共同估计.文献[20 ]建立了用于SOC和容量估计的多尺度双H无限滤波器(H-infinity filter, HIF).与单/多尺度双KF相比,该方法具有更好的鲁棒性和更高的估计精度.然而,等效电路模型在等效过程中没有考虑电池内部状态变量的信息,影响了电池估计的准确性.对于其他价值参数SOH、RUL的估计,文献[21 ]提出了一种基于神经网络的新的SOH估计方案,可以利用短时间内的电压和电流数据来估计SOH值,达到减少参考性能测试(Reference performance test, RPT)次数的效果,但是估计耗时较长.文献[22 ]使用混合神经网络来捕获电池数据的层次特征和时间信息,结合贝叶斯优化的神经网络结构来实现电池健康状态(SOH)和剩余使用寿命(RUL)的端到端估计,估计效果泛化性强,但是对于输入数据的要求较高. ...
Data-driven state of health estimation of Li-ion batteries with RPT-reduced experimental data
1
2019
... 国内外学者对电池的剩余价值指标估计进行了研究.文献[15 ]根据电池衰退的不一致性提出了基于衰退速度预测的电池剩余价值优化方法,估算过程较为复杂.文献[16 ]提出了充电曲线分段(Charging curve segmentation, CCS)与离散Arrhenius老化模型(Discrete Arrhenius aging model, DAAM)的融合来估算容量.第一个卡尔曼滤波(Kalman filter, KF)更新了DAAM的模型参数;第二次KF基于修正参数的CCS和DAAM估算聚变能力.然而,经验模型难以跟踪负荷动态特性,且受外部环境因素的干扰,它们的适应性和准确性是有限的.等效电路模型通过KF[17 ] 、粒子滤波PF[18 ] 、递推最小二乘RLS[19 ] 等方法实现SOC和容量的共同估计.文献[20 ]建立了用于SOC和容量估计的多尺度双H无限滤波器(H-infinity filter, HIF).与单/多尺度双KF相比,该方法具有更好的鲁棒性和更高的估计精度.然而,等效电路模型在等效过程中没有考虑电池内部状态变量的信息,影响了电池估计的准确性.对于其他价值参数SOH、RUL的估计,文献[21 ]提出了一种基于神经网络的新的SOH估计方案,可以利用短时间内的电压和电流数据来估计SOH值,达到减少参考性能测试(Reference performance test, RPT)次数的效果,但是估计耗时较长.文献[22 ]使用混合神经网络来捕获电池数据的层次特征和时间信息,结合贝叶斯优化的神经网络结构来实现电池健康状态(SOH)和剩余使用寿命(RUL)的端到端估计,估计效果泛化性强,但是对于输入数据的要求较高. ...
End-to-end capacity estimation of Lithium-ion batteries with an enhanced long short-term memory network considering domain adaptation
1
2022
... 国内外学者对电池的剩余价值指标估计进行了研究.文献[15 ]根据电池衰退的不一致性提出了基于衰退速度预测的电池剩余价值优化方法,估算过程较为复杂.文献[16 ]提出了充电曲线分段(Charging curve segmentation, CCS)与离散Arrhenius老化模型(Discrete Arrhenius aging model, DAAM)的融合来估算容量.第一个卡尔曼滤波(Kalman filter, KF)更新了DAAM的模型参数;第二次KF基于修正参数的CCS和DAAM估算聚变能力.然而,经验模型难以跟踪负荷动态特性,且受外部环境因素的干扰,它们的适应性和准确性是有限的.等效电路模型通过KF[17 ] 、粒子滤波PF[18 ] 、递推最小二乘RLS[19 ] 等方法实现SOC和容量的共同估计.文献[20 ]建立了用于SOC和容量估计的多尺度双H无限滤波器(H-infinity filter, HIF).与单/多尺度双KF相比,该方法具有更好的鲁棒性和更高的估计精度.然而,等效电路模型在等效过程中没有考虑电池内部状态变量的信息,影响了电池估计的准确性.对于其他价值参数SOH、RUL的估计,文献[21 ]提出了一种基于神经网络的新的SOH估计方案,可以利用短时间内的电压和电流数据来估计SOH值,达到减少参考性能测试(Reference performance test, RPT)次数的效果,但是估计耗时较长.文献[22 ]使用混合神经网络来捕获电池数据的层次特征和时间信息,结合贝叶斯优化的神经网络结构来实现电池健康状态(SOH)和剩余使用寿命(RUL)的端到端估计,估计效果泛化性强,但是对于输入数据的要求较高. ...
Health prognosis for electric vehicle battery packs:A data-driven approach
1
2020
... 综上,目前方法大多都是基于单一指标,如健康状态(SOH)、剩余寿命(RUL)及容量来评估电池剩余价值,忽视了各指标之间的耦合关系,导致电池在回收过程中没有统一的指标衡量其剩余使用价值,评估既不准确也不客观[23 ⇓ ⇓ -26 ] . ...
State-of-health estimation for lithium-ion batteries based on the multi-island genetic algorithm and the Gaussian process regression
1
2017
... 综上,目前方法大多都是基于单一指标,如健康状态(SOH)、剩余寿命(RUL)及容量来评估电池剩余价值,忽视了各指标之间的耦合关系,导致电池在回收过程中没有统一的指标衡量其剩余使用价值,评估既不准确也不客观[23 ⇓ ⇓ -26 ] . ...
Review on convolutional neural networks (CNN) in vegetation remote sensing
1
2021
... 综上,目前方法大多都是基于单一指标,如健康状态(SOH)、剩余寿命(RUL)及容量来评估电池剩余价值,忽视了各指标之间的耦合关系,导致电池在回收过程中没有统一的指标衡量其剩余使用价值,评估既不准确也不客观[23 ⇓ ⇓ -26 ] . ...
Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review
1
2019
... 综上,目前方法大多都是基于单一指标,如健康状态(SOH)、剩余寿命(RUL)及容量来评估电池剩余价值,忽视了各指标之间的耦合关系,导致电池在回收过程中没有统一的指标衡量其剩余使用价值,评估既不准确也不客观[23 ⇓ ⇓ -26 ] . ...