1 引言
无功补偿装置配置优化问题所考虑的重点是目标函数的构建和优化求解方法的设计。文献[12]采用了改进粒子群算法,对考虑系统电压偏移总量与有功损耗最小的无功优化问题进行求解,但未考虑装置的成本。文献[13]基于和声搜索算法实现配网电容器的多目标优化配置,从而在降低网损的同时最小化无功补偿费用。文献[14]引入反向学习对鸡群算法进行改进,从而提升了配电网无功优化模型的整体性能,但该方法耗时较长。文献[15]采用粒子群算法求解城市配电网无功优化配置问题,模型目标函数为运行成本的期望值最小,但未开展安装节点的选取,同时求解耗时较长。文献[16]提出了鲸鱼优化算法对以有功损耗最小为目标的无功配置优化问题进行求解,但目标函数较为单一,易于陷入局部最优。此外未综合考虑关键节点的优先选择。文献[17]将布谷鸟算法中的飞行和淘汰机制引入粒子群算法,对以有功损耗最小为目标的无功优化配置问题进行求解,但目标函数过于单一,所得结果不完全符合配电网实际运行。文献[18]考虑含分布式电源的接入,提出了基于模糊聚类下的混沌优化人工鱼群算法,对以网损最小为目标的无功优化配置问题进行建模求解。文献[19]利用改进教与学算法,实现以有功网损和电压偏离度最小为综合目标的无功优化配置。
上述优化方法可实现无功补偿装置位置与容量的优化配置,但总体而言设计的目标函数较为单一,对关键节点的优选考虑不足,优化求解方法易陷入局部最优。为此,本文提出了计及功率损失指数的配电网两阶段无功补偿多目标优化配置方法。首先利用功率损失指数进行无功补偿装置安装节点的优先选取;其次以有功损耗相应的损失、装置购买费用、安装费用以及运行费用最小化为综合目标函数,引入罚函数并建立了计及功率损失指数的无功补偿装置多目标优化配置模型,应用鮣鱼优化算法进行模型求解,得到不同负荷条件且已有分布式电源接入的配电网无功补偿装置的最佳安装位置和容量,通过在IEEE-34及PG-69节点系统中的算例验证了所提方法的有效性和性能优势。
2 基于功率损失指数的候选节点选取
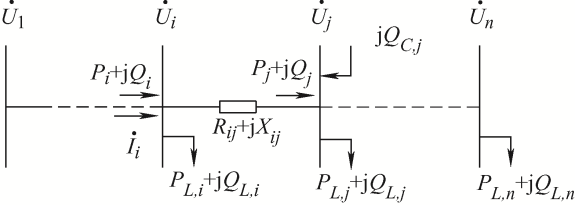
采用图1所示网络模型进行配电网功率损耗的计算。
图1
节点i与下游节点j之间线路的有功损耗∆Pij和无功损耗∆Qij的计算方法为
式中,
在节点j接入无功补偿装置后,线路有功损耗将减少。本文提出基于功率损失指数来初选无功补偿装置的安装位置。该方法对每个母线节点(首端母线节点除外)注入无功功率,并进行潮流计算,对比有功功率损耗的变化,最后选取具有较大功率损失指数的母线节点作为无功补偿装置的优先配置位置。功率损失指数定义为
式中,Pl ( j)为母线节点j处安装无功补偿装置引起的有功损耗减少值;Plmin=min{Pl(j)},Plmax=max{Pl(j)}, j=2,…, n,其中n为配电网节点总数,首节点编号为1。
3 无功补偿装置优化配置模型
3.1 目标函数
无功补偿装置优化配置模型的目标为最小化总成本费用,包括有功损耗相应的电价损失f1、安装费用f2、购置费用f3以及运行费用f4,同时加入对节点电压、总有功损耗越限的罚函数,如式(3)所示
式中,α为电价(元/kW·h);PLoss为总有功损耗;T=8 760 h;β为折旧系数;CI为无功补偿装置的安装费用(元/台);k为装置总安装台数。Ca为电容器的购买费用(元/kVar);QCi为注入的无功功率值(kVar);χ为运行成本(元/台);λ1为电压越限惩罚系数;ΔUi为节点电越限值;Uimin、Uimax分别为节点电压最小值、最大值;λ2为总有功损耗越限惩罚系数;ΔP为总有功损耗越限值。
PLoss计算方法为
式中,Rd、Xd为支路d的电阻、电抗;L为支路总数;Ui、Uj分别为母线i、j的电压。
节点电压越限值的计算方法为
总有功损耗越限值的计算方法为
3.2 约束条件
(1) 无功补偿容量约束。节点安装的无功补偿装置容量应满足
式中,QCmin、QCmax分别为无功补偿装置容量的最小值、最大值。
(2) 潮流约束。系统有功和无功功率需要满足如下平衡约束
式中,PS、QS分别为系统有功功率、无功功率;PLineloss(i)、QLineloss(i)分别为支路i的有功损耗、无功损耗;PLoad(e)、QLoad(e)分别为节点e负荷的有功功率、无功功率;QC(r)为第r台无功补偿装置的容量。
(3) 无功功率约束。总无功补偿装置容量不超过无功负荷的75%
(4) 功率因数约束。电网的功率因数必须满足以下约束
式中,PF(i)为节点i的功率因数值;PFmin、PFmax分别为该节点功率因数的最小值、最大值。
(5) 线路最大容量约束。线路的容量应低于其限值
式中,SLine(i)、SLineR分别为线路i的容量及额定容量。
3.3 鮣鱼优化算法建模分析
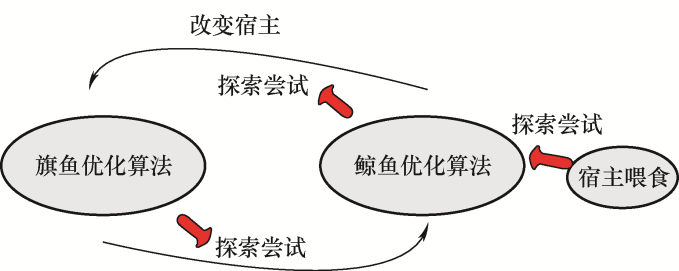
图2
3.3.1 初始化
假设候选解为鮣鱼,其在搜索空间中的位置O是问题变量。鮣鱼的当前位置记为Ox=(Ox1,Ox2,…, Oxm),其中x为䲟鱼的数量,m为其搜索空间的维数,另外,OB=(
3.3.2 全局勘探
当䲟鱼附着在旗鱼上,基于旗鱼优化算法的精英思想,䲟鱼的改进位置更新如式(12)所示
式中,
式(12)既保证了最优个体引导更新,同时又增加䲟鱼的随机选择,保证了搜索空间的探索性。
为了确定䲟鱼更换宿主与否,其必须在宿主附近不断尝试小幅度移动,建模公式如下
式中,
在该步骤之后,还需要进一步判断两个位置的适应度值的大小来决定是否更换宿主。
3.3.3 局部开发
当䲟鱼附着在鲸鱼上时,基于鲸鱼优化算法推导了䲟鱼的位置更新公式如下
式中,G为猎人与猎物之间的距离(当前最优解);δ为[-1,1]的随机数;w在[-2,-1]之间线性下降;T为最大迭代次数。
由于鱼群的聚集性不是时时都很强,所以鮣鱼会在宿主嘴边捡漏,当鮣鱼在宿主旁游行,其数学公式如下
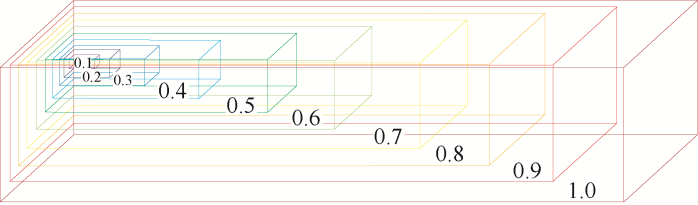
式中,E为与鮣鱼空间维数相关的移动步长;V为鮣鱼因子,表示鮣鱼占据宿主体积的大小,其取值范围一般在[0,0.3]。图3为V=0.1条件下的宿主取食模型。
图3
4 基于鮣鱼优化算法优化模型求解
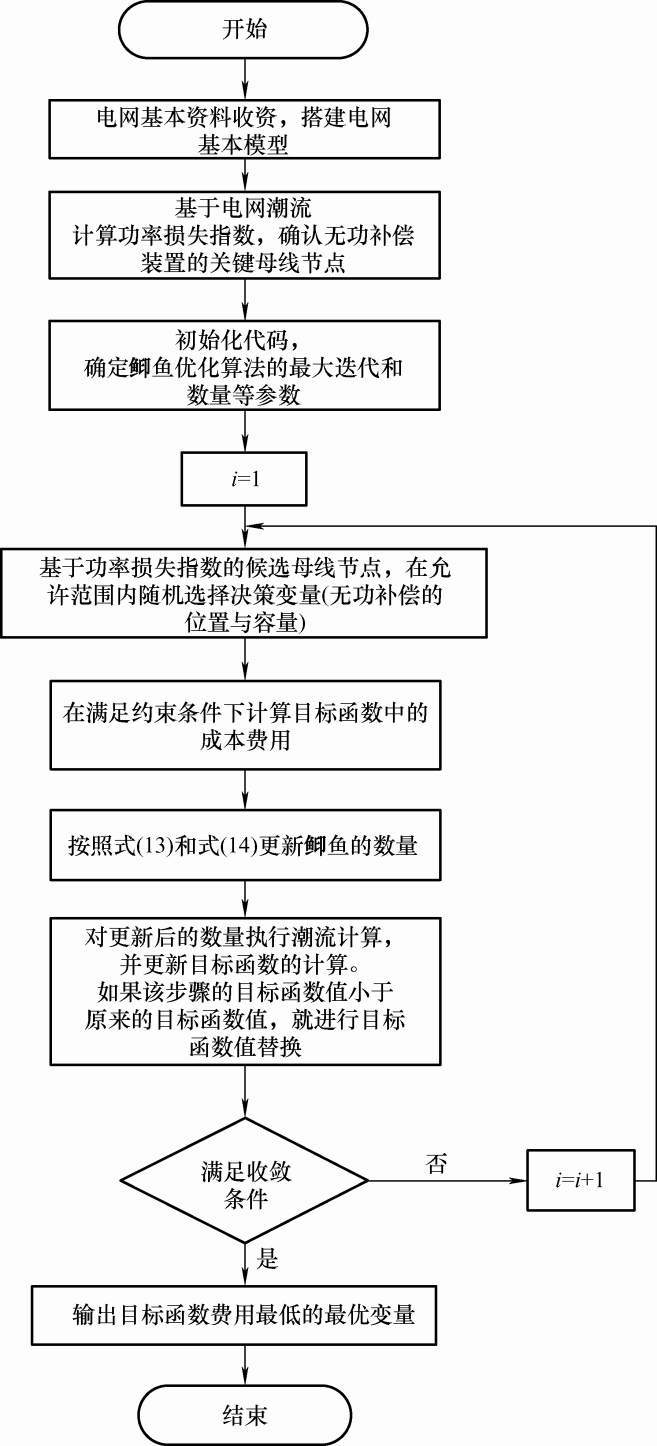
本文设计的计及功率损失指数的电网两阶段无功补偿多目标优化配置方法,流程如图4所示。具体步骤如下所示。
图4
步骤1:进行电网基本资料收资,并搭建电网基本模型。
步骤2:针对电网的初始状态进行潮流计算,并根据式(2)计算功率损失指数,确认无功补偿装置的关键母线节点。
步骤3:将步骤2中的关键母线节点作为无功补偿位置默认值输入到优化代码中,并确定鮣鱼优化算法的最大迭代次数和数量等参数。
步骤4:设定每个䲟鱼在其允许范围内为优化算法中的变量向量X=[位置,容量],在约束条件下由每个鮣鱼(一组优化变量)代入式(3)来计算目标函数的总成本费用。
步骤5:根据式(13)、式(14)更新鮣鱼的数量。
步骤6:对更新后的数量执行潮流计算,并更新目标函数的计算。若该步骤的目标函数值小于步骤4,则将更新后的目标函数计算值替换原来的计算值。
步骤7:若满足收敛条件则执行下一步,输出费用最低的最优变量,否则返回继续执行步骤5。
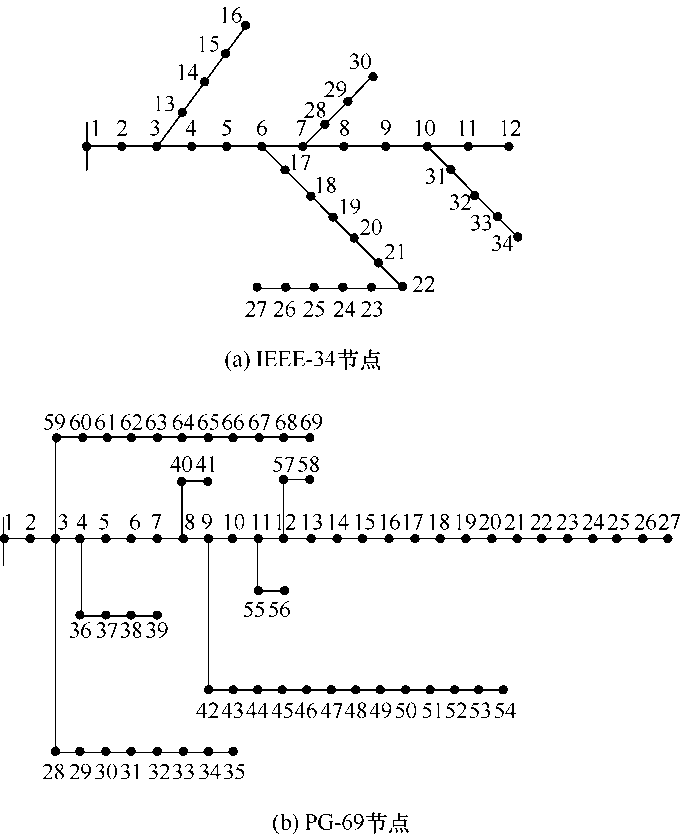
5 算例分析
图5
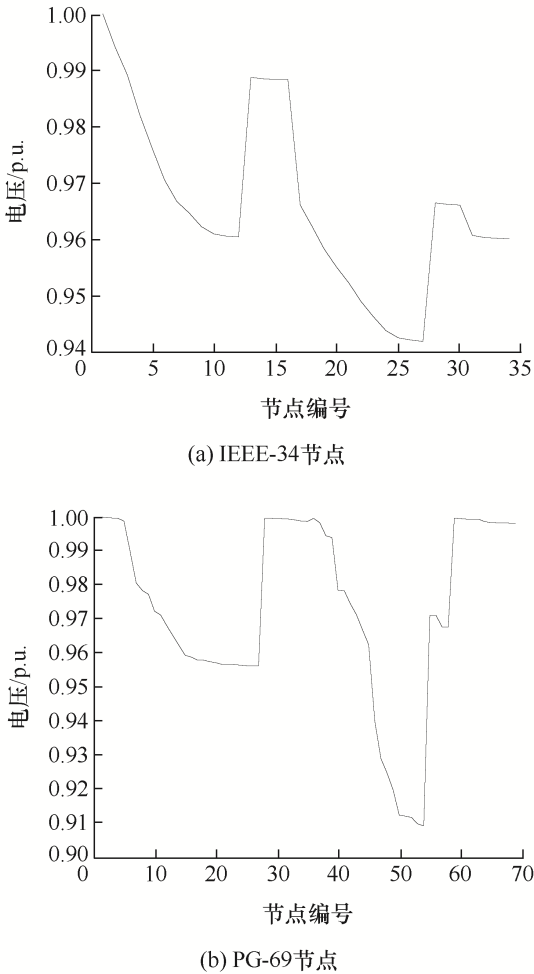
5.1 基础仿真分析
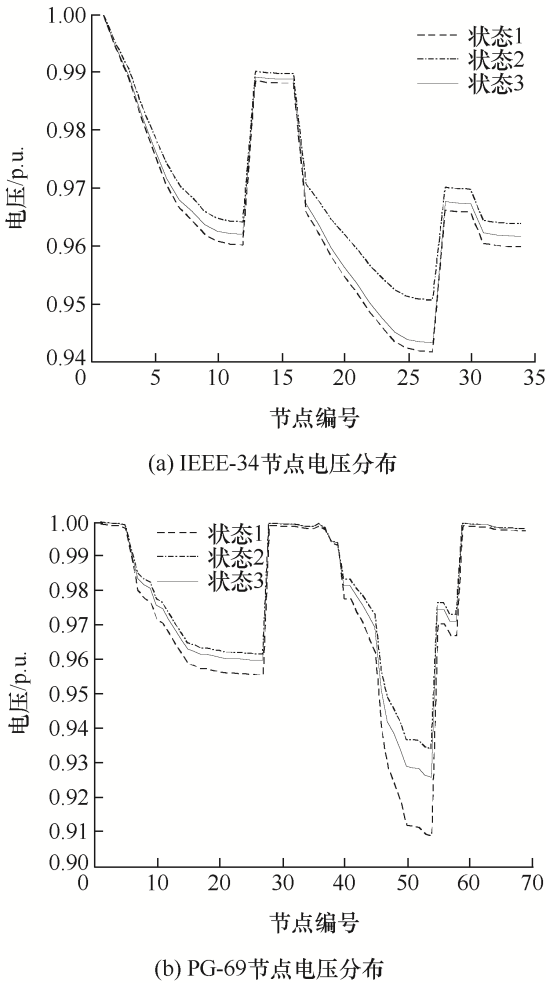
图6
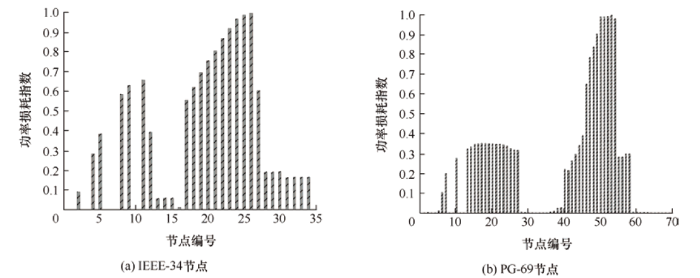
图7
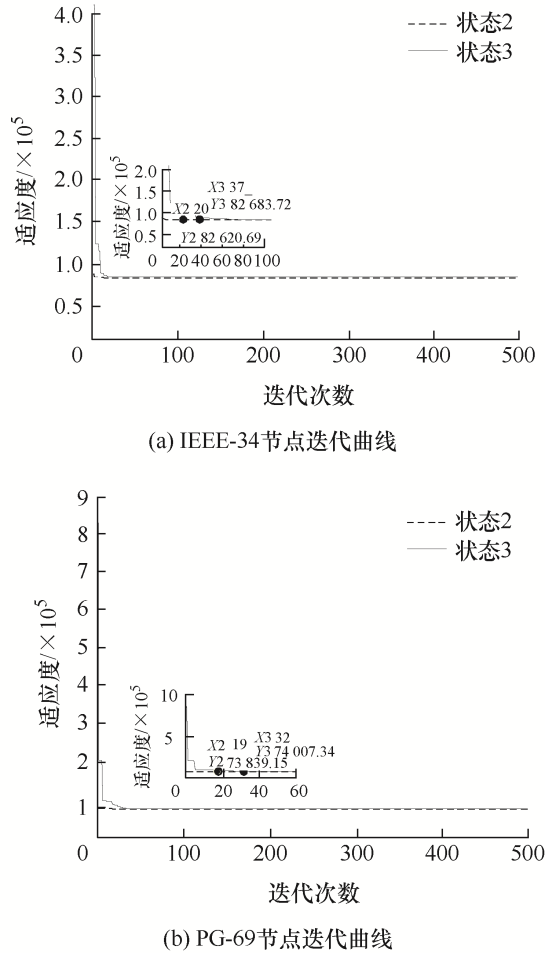
5.2 算法性能分析
表2 三种情况下无功优化配置结果对比
| 对比指标 | IEEE-34节点 | PG-69节点 | ||||
|---|---|---|---|---|---|---|
| 无补偿 | 鮣鱼优化 | 鮣鱼优化+功率损失指数 | 无补偿 | 鮣鱼优化 | 鮣鱼优化+功率损失指数 | |
| 有功损耗/kW | 221.72 | 173.91 | 169.53 | 226.47 | 156.62 | 153.56 |
| 最小电压/p.u. | 0.941 6 | 0.948 3 | 0.950 7 | 0.908 9 | 0.928 2 | 0.932 3 |
| 无功配置(节点/容量kVar) | — | BUS26/817.91 BUS13/636.45 | BUS24/701.86 BUS20/816.25 | — | BUS50/1 000 BUS48/210.61 | BUS51/979.36 BUS49/233.21 |
| 成本费用/元 | 97 113.36 | 82 683.72 | 82 620.69 | 99 193.86 | 74 007.34 | 73 839.15 |
| 电容器费用/元 | — | 7 632.29 | 7 921.49 | — | 6 537.70 | 6 546.56 |
| 优化求解时间/s | — | 2.72 | 1.92 | — | 4.26 | 3.53 |
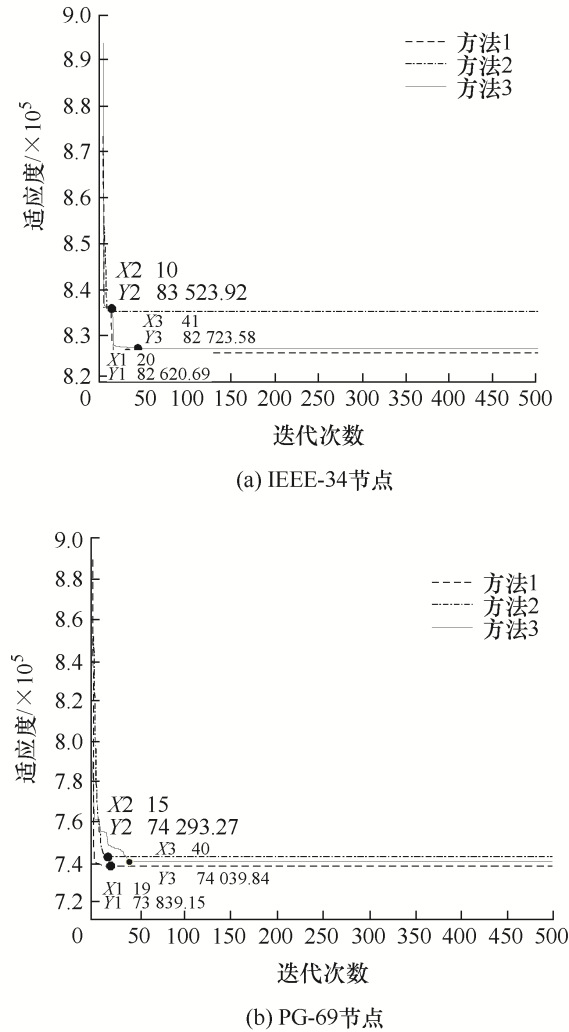
图8
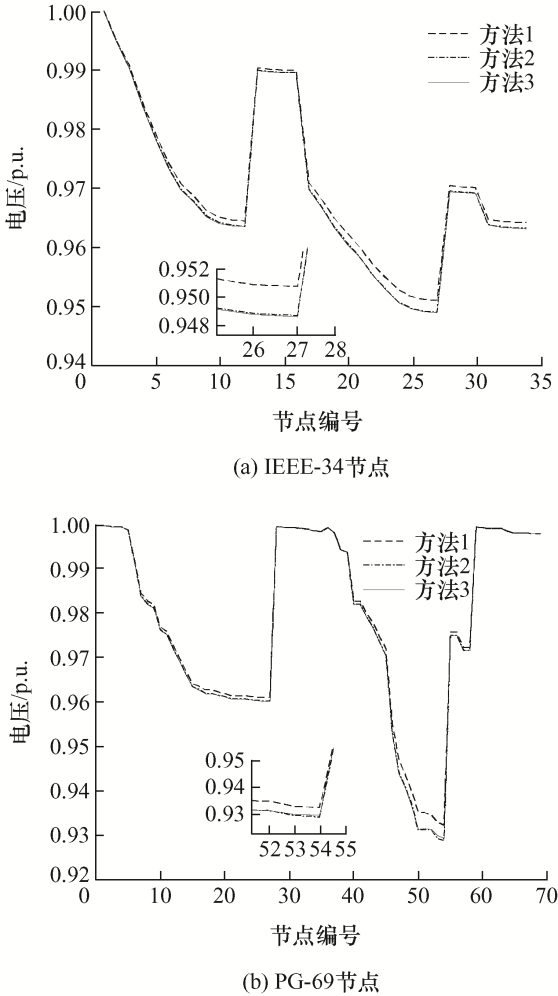
图9
由表2可知,对于IEEE-34节点系统,与未考虑功率损失指数和不进行无功补偿相比,采用本文方法时系统有功损耗分别减小了2.52%和23.54%,最小电压值分别提升了0.25%和0.95%,优化配置成本费用节省了0.07%和14.9%。考虑功率损失指数后,优化求解时间可减少29.05%,但优化结果的电容器费用增加了3.78%。
对于PG-69节点系统,与未考虑功率损失指数和不进行无功补偿相比,采用本文方法时网络有功损耗分别减小了1.95%和32.19%,最小电压值提升了0.44%和2.51%,优化配置成本费用节省了0.22%和25.56%;考虑功率损失指数后,优化求解时间可减少17.08%,电容器费用增加0.13%。
表3 不同优化算法下的无功优化配置结果对比
| 对比指标 | IEEE-34节点 | PG-69节点 | ||||
|---|---|---|---|---|---|---|
| 方法1 | 方法2 | 方法3 | 方法1 | 方法2 | 方法3 | |
| 有功损耗/kW | 169.53 | 170.12 | 171.49 | 153.56 | 154.67 | 154.41 |
| 最小电压/p.u. | 0.950 7 | 0.948 6 | 0.948 6 | 0.932 3 | 0.928 7 | 0.929 3 |
| 无功配置(节点/容量kVar) | BUS24/701.86 BUS20/816.25 | BUS25/370.20 BUS24/276.40 BUS21/298.20 BUS20/573.13 | BUS25/590.03 BUS21/857.36 | BUS51/979.36 BUS49/233.21 | BUS52/825.60 BUS49/387.59 | BUS53/205.25 BUS51/978.38 |
| 成本费用/元 | 82 620.69 | 83 523.92 | 82 723.58 | 73 839.15 | 74 293.27 | 74 038.84 |
| 电容器费用/元 | 7 921.49 | 9 010.75 | 7 606.58 | 6 546.56 | 6 549.36 | 6 416.33 |
| 优化求解时间/s | 1.92 | 1.25 | 2.02 | 3.53 | 2.69 | 3.72 |
| 最差值/元 | 87 361.52 | 85 423.60 | 89 399.04 | 89 962.27 | 85 288.35 | 79 047.01 |
| 均值/元 | 82 649.74 | 83 536.80 | 82 757.93 | 73 875.31 | 74 387.65 | 74 131.33 |
| 方差 | 62 097.48 | 20 465.45 | 105 578.84 | 521 930.11 | 718 890.92 | 166 520.63 |
| 标准差 | 249.19 | 143.06 | 324.92 | 722.44 | 847.87 | 408.07 |
图10
图11
由表3可知,对IEEE-34/PG-69节点系统,方法1所得有功损耗较(方法2、方法3)分别减小了(0.34%、1.15%)/(0.72%、0.55%),最小电压值提升了(0.22%、0.22%)/(0.39%、0.32%)。
对两个配电网,方法1下的优化配置成本费用较(方法2、方法3)节省了(1.09%、0.12%)/(0.61%、0.27%)。而电容器相关费用则是方法3最小,相较于(方法1、方法2)减少(3.97%、15.58%)/(1.98%、2.03%);对比三种方法的优化均值可知,方法1的性能优于方法2及方法3,比后两者分别小了(1.07%、0.13%)/(0.69%、0.35%)。
因此,通过计及功率损失指数并采用鮣鱼优化算法求解多目标无功补偿装置优化配置问题将具有最佳综合性能。
5.3 负荷水平的影响分析
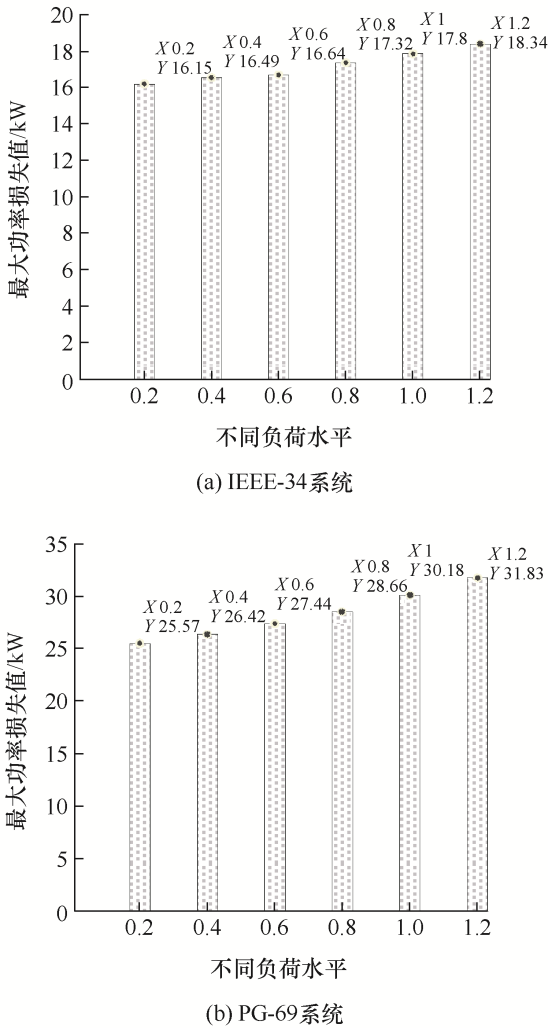
为进一步研究不同负荷条件下本文算法性能,将IEEE-34和PG-69节点系统的有功负荷乘以相应系数以模拟不同负荷条件。图12给出了不同负荷条件下Pl (j)的最大值。
图12
表4 不同负荷条件下的无功优化配置结果
| 对比指标 | IEEE-34节点系统 | PG-69节点系统 | ||||
|---|---|---|---|---|---|---|
| 负荷系数 | 负荷系数 | |||||
| 1 | 0.8 | 0.6 | 1 | 0.8 | 0.6 | |
| 有功损耗/kW | 169.53 | 111.26 | 47.54 | 153.56 | 100.44 | 60.42 |
| 最小电压/p.u. | 0.950 7 | 0.959 5 | 0.977 3 | 0.932 3 | 0.951 9 | 0.954 6 |
| 无功配置(节点/容量kVar) | BUS24/701.86 BUS20/816.25 | BUS24/649.91 BUS21/783.66 | BUS26/549.98 BUS21/870.59 | BUS51/979.36 BUS49/233.21 | BUS52/215.92 BUS50/968.20 | BUS51/1 000 BUS50/32.71 |
| 成本费用/元 | 82 620.69 | 56 952.32 | 28 369.52 | 73 839.15 | 49 774.73 | 31 717.77 |
| 电容器费用/元 | 7 921.49 | 7 541.10 | 7 482.59 | 6 546.56 | 6 417.74 | 5 737.15 |
| 优化求解时间/s | 1.92 | 1.84 | 1.75 | 3.53 | 3.42 | 3.38 |
由表4可知,对不同规模配电网,不同负荷水平对无功补偿装置的选址均将产生影响。负荷水平降低时,有功损耗会减少、功补偿配置容量、成本费用、电容器费用、优化求解时间均减少,而系统最小电压提高。其中,IEEE34/PG-69节点系统在负荷系数(0.6、0.8)下比负荷系数1下的有功损耗减少了(34.37%、71.95%)/(34.59%、60.65%),成本费用减少了(31.07%、65.66%)/(32.59%、57.04%),最小电压值提升了(0.92%、2.79%)/(2.10%、2.39%),电容器费用减少了(4.80%、5.54%)/(1.96%、12.36%),优化时间减少了(4.15%、8.87%)/(3.28%、4.27%),系统负载水平的增加一定程度上将导致无功补偿容量及其相应成本的增加。
5.4 DG接入的影响分析
表5 DG接入信息
| 接入信息 | IEEE-34节点系统 | PG-69节点系统 | ||
|---|---|---|---|---|
| 1 DG | 2 DG | 1 DG | 2 DG | |
| 接入节点 | BUS 26 | BUS 26, 11 | BUS 53 | BUS 53, 17 |
| 容量/kVar | 2 086 | 1 400, 850 | 1 700 | 1 560, 618.78 |
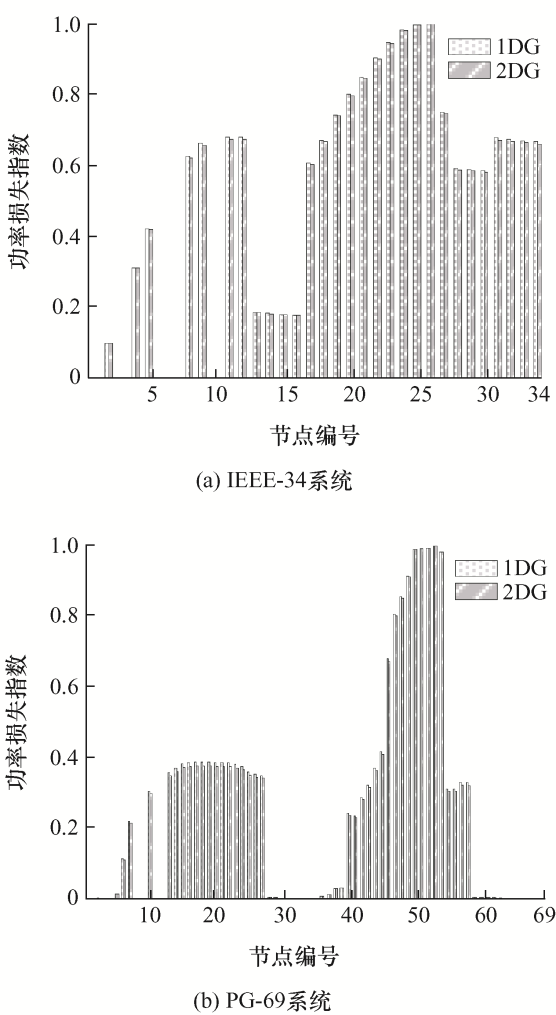
图13
表6 DG接入后的无功优化配置对比
| 对比指标 | IEEE-34节点 | PG-69节点 | ||||
|---|---|---|---|---|---|---|
| 无DG | 1 DG | 2 DG | 无DG | 1 DG | 2 DG | |
| 有功损耗/kW | 169.53 | 61.20 | 48.33 | 153.56 | 46.90 | 34.31 |
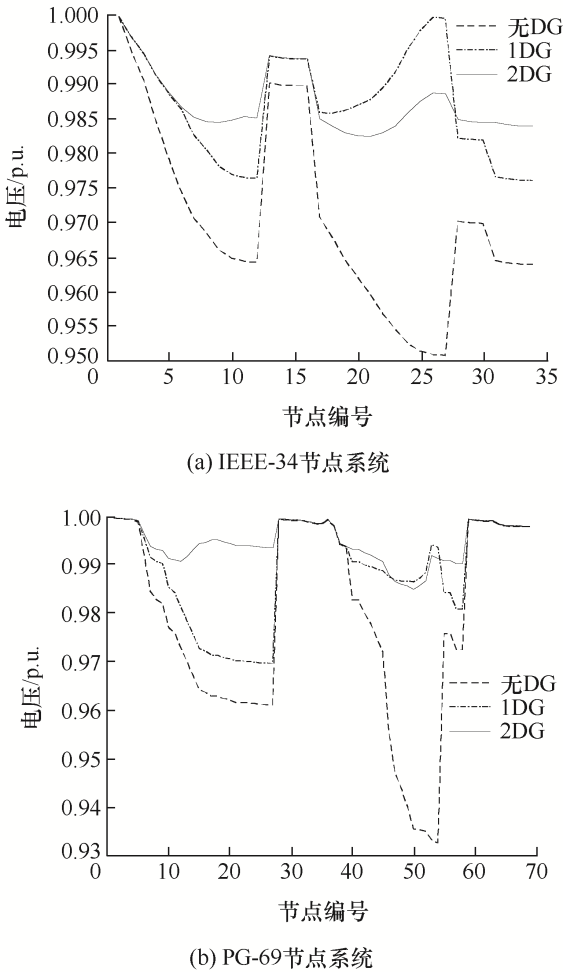
| 最小电压/p.u. | 0.950 7 | 0.976 1 | 0.982 5 | 0.932 3 | 0.969 7 | 0.985 2 |
| 无功配置/(节点/容量kVar) | BUS24/701.86 BUS20/816.25 | BUS26/611.33 BUS20/881.79 | BUS26/119.63 BUS25/623.86 | BUS51/979.36 BUS49/233.21 | BUS50/547.67 | BUS50/473.40 |
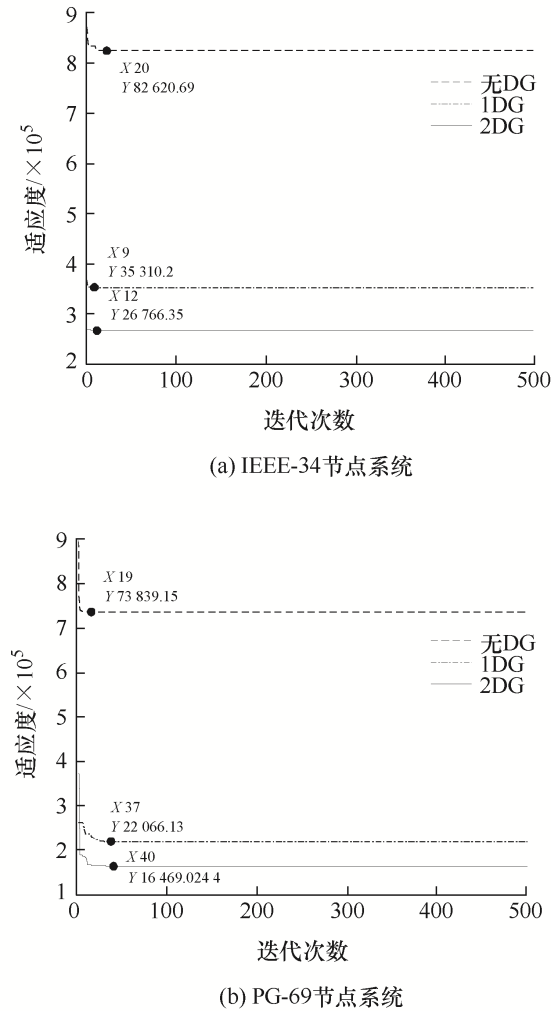
| 成本费用/元 | 82 620.69 | 35 310.13 | 26 766.35 | 73 839.15 | 22 066.13 | 16 469.02 |
| 电容器费用/元 | 7 921.49 | 7 809.10 | 4 435.72 | 6 546.56 | 3 009.53 | 2 675.30 |
| 优化求解时间/s | 1.92 | 1.86 | 1.78 | 3.53 | 3.44 | 3.36 |
图14
图15
由图13可知,DG的接入将对配电网系统的功率损失指数产生一定影响,2个DG接入下的功率损失指数略小于1个DG接入下的情况,但关键节点保持不变:对IEEE-34节点系统为26、25、24、23、22、21、20,对PG-69节点系统为54、53、52、51、50、49、48。
如表6所示,在已有DG接入时IEEE-34/PG-69节点系统所需无功配置容量均减少,且DG接入越多无功配置容量可降低更多,最大可达51.02%/60.95%;接入(1个、2个)DG时,两个配电网有功损耗值减少达(63.90%、71.49%)/(69.45%、77.65%),相应成本费用减少(57.62%、67.60%)/ (70.11%、77.69%),最小电压分别从0.950 7 p.u./ 0.932 3 p.u.升至(0.976 1 p.u.、0.982 5 p.u.)/ (0.969 7 p.u.、0.985 2 p.u.)。
6 结论
本文提出了计及功率损失指数的电网两阶段无功补偿多目标优化配置方法,并通过基于IEEE-34及PG-69节点的算例进行了仿真验证,算例结果表明如下结论。
(1) 计及功率损失指数的方法可优先对候选出的关键节点进行补偿,减少了搜索空间规模,优化配置效果整体优于未考虑功率损失指数的情况。
(2) 计及功率损失指数的鮣鱼优化算法可以更好均衡优化配置的多个目标,相比常规粒子群算法及鲸鱼优化算法,可更好获取多目标优化问题的全局最优解,解决了传统优化算法易陷入局部最优的问题,提高了无功补偿多目标优化配置的准确性及适用性。
(3) 所提方法能够适应负荷水平的变化和分布式电源的接入。充分利用DG的接入开展无功补偿装置的优化配置可进一步提升配电网运行性能,同时节省所需无功补偿装置的相关费用。
参考文献
计及风电与负荷不确定性的电力系统无功随机优化调度
[J].
Stochastic optimal reactive power dispatch in a power system considering wind power and load uncertainty
[J].
考虑DG不确定性的主动配电网两阶段无功机会约束优化方法
[J].
Two-stage reactive power chance-constrained optimization method for an active distribution network considering DG uncertainties
[J].
基于柔性软开关的主动配电网两阶段鲁棒优化运行
[J].
Two-stage robust optimization operation for active distribution network based on soft open point
[J].
基于场景法的配电网有功-无功协调优化
[J].
Coordinated optimization of active power and reactive power in distribution network based on scenario method
[J].
基于负荷曲线分段的配电网无功优化策略
[J].
Reactivepower optimization strategy of distribution network based onsegmental load curve
[J].
数据驱动的无精确建模含源配电网无功运行优化
[J].
Data-driven optimization for reactive power operation in source distribution network without accurate modeling
[J].
考虑风光不确定性的高比例可再生能源电网短期联合优化调度方法
[J].
Short term joint optimal operation method for high proportion renewable energy grid considering wind-solar uncertainty
[J].
主动配电网分布式混合时间尺度无功/电压控制
[J].
Distributed hybrid-timescale voltage var control in active distribution networks
[J].
计及风光出力相关性的配电网多目标无功优化
[J].
Multi-objective reactive power optimization of distribution net-work considering output correlation between wind turbine sand photovoltaic units
[J].
主动配电网分布式有功无功优化调控方法
[J].
Optimization and control method of distributed active and reactive power in active distribution network
[J].
等﹒基于集群划分的高渗透率分布式系统无功优化
[J].
Reactive power optimization of high-penetrati on distributed generation system based on clusters partition
[J].
基于改进粒子群算法的分布式光伏集群划分与无功优化策略
[J].
Distributed photovoltaic cluster partition and reactive power optimization strategy based on improved particle swarm optimization algorithm
[J].
基于和声搜索算法的配电网多目标无功优化
[J].
Multi objective reactive power optimization of distribution network based on harmony search algorithm
[J].
基于改进鸡群算法的无功优化综合分析
[J].
Comprehensive analysis of reactive power optimization based on improved chicken swarm algorithm
[J].
考虑负荷多无功用电场景的城市配电网无功优化配置
[J].
DOI:10.12204/j.issn.1000-7229.2022.08.005
[本文引用: 1]

高比例电力电子设备与高比例分布式光伏的广泛接入以及城市电缆化率的提升,使配电网用户侧的无功特性变得复杂,导致负荷无功用电不确定性增加,不利于配电网安全运行。因此,为了更好地进行无功优化配置,文章采用不同负荷日功率因数变化曲线的组合场景及其概率来反映无功用电的不确定性,以运行成本的期望值最小为目标,建立多无功用电场景的期望值优化配置模型。首先,利用多重一维卷积自编码器(one-dimensional convolutional autoencoders,1D-CAEs)提取不同用户日功率因数数据的低维表征;随后,利用k-means方法进行场景缩减,获得典型日功率因数变化场景,并组合出多用户的场景集;最后,建立期望值无功优化模型,采用粒子群算法求解,确定出最优配置方案。依据上海市某配电网不同类型用户实际的无功用电信息,采用改进的IEEE 33节点系统进行仿真,以验证所提方法的有效性。
Reactive power optimization of urban distribution network considering multiple reactive power scenarios of loads
[J].
DOI:10.12204/j.issn.1000-7229.2022.08.005
[本文引用: 1]

The wide access of the high proportion of power electronic equipment and the high proportion of distributed photovoltaic power, and the improvement of the urban cabling rate make the reactive power characteristics on the user side of the distribution network complicate. The increased uncertainty of the load reactive power consumption is not conducive to the safe operation of distribution network. Therefore, to better optimize reactive power, the combined scenarios and their probabilities of daily power-factor variation curves of different loads are used to reflect the uncertainty of reactive power. Taking the minimum expected value of operation cost as the objective function, an optimal configuration model for the expected value of multiple reactive power scenarios is established. Firstly, multiple one-dimensional convolutional autoencoders (1D-CAEs) is used to extract the low-dimensional representation of the daily power factor data of different users. Then, the k-means method is used for scene reduction to obtain typical daily power-factor variation scenes, and multi-user scenario set is combined. Finally, the expected value reactive power optimization model is established, and the particle swarm algorithm is used to solve it to determine the optimal configuration scheme. According to the reactive power consumption scenarios of users in a distribution network in Shanghai, the modified IEEE 33-node system is taken as an example to verify the effectiveness of the proposed method.
基于鲸鱼优化算法的无功优化调度
[J].
Reactive power optimal dispatching based on whale optimization algorithm
[J].
基于CS-PSO算法的配电网无功优化
[J].
Reactive power optimization of distribution network based on CS-PSO algorithm
[J].
模糊聚类下混沌优化人工鱼群算法的无功优化
[J].
Reactive power optimization of chaotic optimization artificial fish swarm algorithm under fuzzy clustering
[J].
基于改进教与学算法的含电能路由器的电力系统无功优化
[J].
DOI:10.12204/j.issn.1000-7229.2022.06.012
[本文引用: 1]

针对传统智能算法在求解计及电能路由器的电力系统无功优化模型时存在的收敛性和多样性问题,提出一种基于轮盘赌选择和自适应柯西变异策略的改进教与学算法,并应用于含电能路由器的电力系统无功优化。该算法在学习阶段引入轮盘赌选择法,提高群体的学习效率,在教学完成后引入自适应柯西变异策略,增强班级种群的多样性,避免迭代过程陷入局部最优解。然后,建立以有功网损和电压偏离度最小为目标函数的电力系统无功优化模型,并以修改后的IEEE RTS-79标准测试系统为算例进行仿真分析,结果表明改进后的算法兼顾了收敛性和多样性,相比于传统算法具有更好的优化效果。
Reactive power optimization of power system with power router based on improved teaching and learning algorithm
[J].
DOI:10.12204/j.issn.1000-7229.2022.06.012
[本文引用: 1]

In this paper,an improved teaching and learning algorithm based on roulette wheel selection and adaptive Corsi variation strategy is proposed to solve the convergence and diversity problems of the traditional intelligent algorithm and it is applied to the reactive power optimization of power system with electric energy router (EER). The algorithm introduces roulette selection method in the learning phase to improve the learning efficiency of the group, and adopts adaptive Cauchy mutation strategy after the teaching to enhance the diversity of the class population, which avoids falling into local optimal solutions in the iterative process. Then, a reactive power optimization model is established with the objective function of minimizing active network loss and voltage deviation. The modified IEEE RTS-79 standard test system is used as an example for simulation analysis. The results show that the improved algorithm has both convergence and diversity, which has better optimization effect than the traditional algorithm.
Remora optimization algorithm
[J].