基于奇异谱分析的车载电缆局部放电窄带干扰抑制

doi:10.11985/2023.03.005

基于奇异谱分析的车载电缆局部放电窄带干扰抑制

杨思为^,¹, 高国强^,¹, 刘凯¹, 周书圆², 陈奎¹, 唐于京¹, 辛东立¹, 吴广宁¹

1.西南交通大学电气工程学院成都 611756

2.西南交通大学唐山研究院唐山 063000

Narrowband Interference Suppression of Partial Discharge for High-speed Train on Singular Spectrum Analysis

YANG Siwei^,¹, GAO Guoqiang^,¹, LIU Kai¹, ZHOU Shuyuan², CHEN Kui¹, TANG Yujing¹, XIN Dongli¹, WU Guangning¹

1. School of Electrical Engineering, Southwest Jiaotong University, Chengdu 611756

2. Tangshan Research Institute of Southwest Jiaotong University, Tangshan 063000

收稿日期: 2023-07-10 修回日期: 2023-08-23

Received: 2023-07-10 Revised: 2023-08-23

作者简介 About authors

杨思为，男，1999年生，硕士研究生。主要研究方向为车载电缆局部放电信号降噪。E-mail：1375688690@qq.com

高国强，男，1981年生，博士，教授。主要研究方向为高电压与绝缘技术、电力系统及其自动化、电机电器和轨道交通电气工程。E-mail：xnjdggq@163.com

摘要

局部放电检测是评估车载高压电缆绝缘状态的重要方法之一。而窄带干扰作为最常见的干扰之一，会导致局部放电信号淹没在噪声中，从而难以获取准确的局部放电信号，给电缆绝缘状态的评估带来困难。介绍一种基于奇异频谱分析的方法，用于抑制车载高压电缆局部放电信号中的窄带干扰。该方法通过对奇异谱分析(Singular spectrum analysis，SSA)实现对一维信号的分析和预测，从而从时间序列中分解出趋势项、周期项和噪声。为了验证所提方法的有效性，模拟了具有窄带干扰的理想局部放电信号，并应用所提方法对信号进行降噪处理。同时，在实验室内进行了真实局部放电信号的验证试验。降噪结果表明，所提方法能够有效地消除车载高压电缆局部放电信号中的窄带干扰，对于判断车载电缆的绝缘状态具有一定的指导意义。本文研究为车载高压电缆局部放电信号提取提供了一种新的方法，对车载电缆绝缘状态评估具有潜在的工程应用价值。

关键词： 车载电缆; 局部放电; 周期性窄带干扰; 奇异谱分析

Abstract

Partial discharge detection is one of the important methods for assessing the insulation status of vehicle-mounted high-voltage cables. Narrowband interference, as one of the most common interferences, causes the partial discharge signal to be submerged in noise, which makes it difficult to obtain an accurate partial discharge signal and brings difficulties to the assessment of the cable insulation state. A method based on singular spectrum analysis is introduced for suppressing the narrowband interference in the localized discharge signal of vehicle-mounted high-voltage cables. The method realizes the analysis and prediction of one-dimensional signals by singular spectrum analysis(SSA), which decomposes the trend term, period term and noise from the time series. In order to verify the effectiveness of the proposed method, an ideal localized discharge signal with narrow-band interference is simulated, and the proposed method is applied to noise reduction of the signal. At the same time, the validation experiments of real localized discharge signals are carried out in the laboratory. The noise reduction results show that the proposed method can effectively eliminate the narrow-band interference in the partical discharge signal of the vehicle-mounted high-voltage cable, which is of some significance for judging the insulation status of the vehicle-mounted cable. This study provides a new method for localized discharge signal extraction for on-board high-voltage cables, which has potential engineering applications for the assessment of insulation status of on-board cables.

Keywords： Vehicle cable; partial discharge; periodic narrow-band interference; singular spectrum analysis

PDF (25120KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

杨思为, 高国强, 刘凯, 周书圆, 陈奎, 唐于京, 辛东立, 吴广宁. 基于奇异谱分析的车载电缆局部放电窄带干扰抑制[J]. 电气工程学报, 2023, 18(3): 46-53 doi:10.11985/2023.03.005

YANG Siwei, GAO Guoqiang, LIU Kai, ZHOU Shuyuan, CHEN Kui, TANG Yujing, XIN Dongli, WU Guangning. Narrowband Interference Suppression of Partial Discharge for High-speed Train on Singular Spectrum Analysis[J]. Chinese Journal of Electrical Engineering, 2023, 18(3): 46-53 doi:10.11985/2023.03.005

1 引言

高压电缆终端在制作、运输、安装以及运行过程中由于结构和材料缺陷会产生多种形式的绝缘缺陷，包括高压导体尖刺、浮电极、绝缘子表面污染、内部缺陷、自由金属离子等，最终导致绝缘击穿。局部放电检测是评估机载电缆绝缘老化状况的有效手段之一^[1⇓⇓-4]。在实际的信号采集过程中，由于局部放电信号较弱和复杂的环境干扰，被测信号中含有白噪声^[5⇓-7]、窄带干扰^[8-9]、脉冲干扰^[10]等污染信号；其中周期性的窄带干扰具有能量强、持续时间长、数量大的特点，使得局部放电信号严重失真，加大了评估高压电缆绝缘状态的难度，因此研究局部放电信号监测对窄带干扰的抑制策略有着重大意义，国内外学者对抑制窄带干扰技术进行了大量研究工作^[11-12]。

文献[13]采用FFT阈值法根据其频谱特性进行滤波，技术难度大，实现简单，但该方法的窄带干扰在滤波后出现了频谱泄漏和锐边残留；文献[14 ⇓-16]提出小波降噪法抑制窄带干扰，小波变换只对各尺度的低频段进行二值分解，小波包变换在频率分辨率较高时同时对低频和高频段进行分解，小波和小波包去噪都深受放电波形匹配的影响，需要对信号有较高的先验知识，而且小波基函数和分解层数都难以选择。文献[17 ⇓⇓-20]中提出了经验模态分解法(Empirical mode decomposition, EMD)，EMD是一种具有自适应分解信号能力的方法，可以将信号拆解为多个固有模态函数(Intrinsic mode function, IMF)。但EMD也存在一些问题，其中包括端点效应和模态混杂。

本文研究了局部放电信号中窄带干扰抑制方法的问题，并提出了一种新方法，即基于奇异频谱分析(Singular spectrum analysis, SSA)的局部放电窄带干扰抑制方法。该方法通过对原始噪声局部放电信号进行奇异频谱分析，将噪声序列与有效信号进行分离，并通过建立理论上的局部放电染噪模型分析出窄带干扰的奇异频谱特征。通过对理论模型的计算和分析，总结了最优参数选择方法，并提出了适用于干扰信号和有效信号分离的分解和重建方法，从而实现了对窄带干扰噪声的有效滤除。

2 技术原理

奇异频谱分析(SSA)是一种广泛应用于处理一维非线性时间序列数据的方法。它通过将时间序列数据转换为特定的矩阵，并对该矩阵进行奇异值分解，从而实现对信号的分析和预测。SSA可以从时间序列中提取出趋势项、周期项和噪声等信息，从而帮助深入理解信号的特征和规律。SSA主要包括以下四个步骤：嵌入-分解-分组-重构^[21-22]。

SSA作为一种灵活的信号处理方法，可以在不需要假设线性或周期性关系的情况下，对复杂的时间序列数据进行分析和预测。在局部放电窄带干扰抑制中，SSA可以通过对原始噪声局部放电信号进行奇异频谱分析，提取出窄带干扰的特征，并实现对干扰信号和有效信号的分离和重构，从而有效地抑制窄带干扰的影响，提高局部放电信号的质量和可靠性。

2.1 嵌入

奇异谱是用于处理和分析的有限长度的一维时间序列，N是序列的长度，首先将一维时间序列数据转换为二维矩阵。这一步骤通过将时间序列数据按照一定的窗口大小L进行滑动，L选择在(1，N/2)范围内，形成多个子序列，并将这些子序列作为矩阵的行或列进行排列，得到轨迹矩阵

(1)$H=\left[ {{x}_{1}}{{x}_{2}}{{x}_{3}}\cdots {{x}_{K}} \right]=\left[ \begin{matrix} {{x}_{1}} & {{x}_{2}} & \cdots & {{x}_{N-L+1}} \\ {{x}_{2}} & {{x}_{3}} & \cdots & {{x}_{N-L\text{+2}}} \\ \vdots & \vdots & {} & \vdots \\ {{x}_{L}} & {{x}_{L+1}} & \cdots & {{x}_{N}} \\ \end{matrix} \right]$

式中，K=N-L+1，轨迹矩阵H是一个L×K的矩阵。

2.2 奇异值分解

对嵌入矩阵进行奇异值分解(Singular value decomposition, SVD)，得到矩阵的奇异值和奇异向量。奇异值表示矩阵中的能量分布情况，奇异向量则表示矩阵中的主要成分对于任何一个矩阵H，存在一个分解，使得

(2)$A=U*\Lambda *{{V}^{T}}$

式中，A是矩阵的奇异值分解，其中包括左奇异值矩阵${{U}_{m\times m}}$，H矩阵分解后的对角线矩阵${{\Lambda }_{m\times n}}$，右奇异值矩阵$U{{U}^{T}}=E$，矩阵U、V均为单位正交矩阵，满足$U{{U}^{T}}=E$。轨迹矩阵的直接分解较为复杂，可先计算轨迹矩阵的协方差矩阵$S=X{{X}^{T}}$，并进行特征值分解得到奇异谱，矩阵S的特征值分解由其特征值${{\lambda }_{1}}>{{\lambda }_{2}}>{{\lambda }_{3}}>\cdots {{\lambda }_{L}}\ge 0$和相应的特征向量${{U}_{1}},{{U}_{2}},{{U}_{3}}\cdots,{{U}_{L}}$得到，此时$U=[{{U}_{1}},{{U}_{2}},{{U}_{3}}\cdots,{{U}_{L}}]$,${{\lambda }_{1}}>{{\lambda }_{2}}>{{\lambda }_{3}}>\cdots {{\lambda }_{L}}\ge 0$，有$X=\sum\limits_{m=1}^{L}{\sqrt{{{\lambda }_{m}}}{{U}_{m}}V_{m}^{\mathrm{T}}}$，${{V}_{m}}={{X}^{T}}{{U}_{m}}/\sqrt{{{\lambda }_{m}}}$，m=1，2，···，L。特征向量反映时间序列的演化类型，称为时间正交函数(T-EOF)。

2.3 分组

根据奇异值和奇异向量的信息，对分解得到的奇异向量进行聚类，将相似的奇异向量分为一组。这一步骤可以帮助识别出信号中的趋势项、周期项和噪声等不同成分。分组的目的是为了找到一个相对较小的奇异值k，以k为界保留前k个奇异值和相应的奇异向量，其中U的维度从m×n到$m\times k$，V的维度从n×n到$m\times k$，将方阵的维度n×n改为$k\times k$，从而达到降维和去噪的效果。

2.4 重构

将分组得到的奇异向量重新组合成重构矩阵，并通过逆SVD操作将重构矩阵还原为时间序列。这一步骤可以得到去除趋势项和周期项后的噪声信号。首先计算滞后序列对的投影为$a_{i}^{m}={{X}_{i}}{{U}_{m}}=$$\sum\limits_{j=1}^{L}{{{x}_{i+j}}{{U}_{m,j}}}$，其中0≤i≤N-L，表示轨迹矩阵X的第i列，$a_{i}^{m}$是原始序列中反映时间演化类型的权重，记为时间主成分(Time principal component，TPC)，通过时间经验正交函数和时间主成分来进行信号重建，原理公式如下

(3)${{x}_{i}}^{k}=\left\{ \begin{matrix} \frac{1}{i}\sum\limits_{j=1}^{i}{a_{i-j}^{k}{{U}_{k,j}}\ \ \ \ \ \ 1\le i\le L-1}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \frac{1}{L}\sum\limits_{j=1}^{L}{a_{i-j}^{k}{{U}_{k,j}}\ \ \ \ \ \ L\le i\le N-L+1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } \\ \frac{1}{N-i+1}\sum\limits_{j=i-N+L}^{L}{a_{i-j}^{k}{{E}_{k,j}}\ \ \ \ \ \ N-L+2\le i\le N} \\ \end{matrix} \right.$

根据这一原则，重建的序列之和等于原始序列。

2.5 周期性窄带干扰抑制步骤

在经过对奇异值大小分组之后，便能确定代表窄带干扰的奇异值个数，得到滤除窄带干扰步骤如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 SSA方法降噪流程

步骤1：通过原始收集信号构造Hankel矩阵，得到轨迹矩阵通过将一维时间序列进行滞后排列。

步骤2：对步骤1构造出的矩阵进行奇异值分解，得到含噪信号的奇异值，并按降序排列，即${{\lambda }_{1}}>{{\lambda }_{2}}>{{\lambda }_{3}}>\cdots {{\lambda }_{L}}\ge 0$。

步骤3：对奇异值进行分组，定义步骤2中获得的奇异值窄带干扰的边界，该边界之前的奇异值个数即为有效奇异值个数。

步骤4：通过使用分组得到的前n个有效奇异值，对信号进行重构得到一维时间序列。然后，将原始信号减去重构的窄带干扰信号，从而得到降噪后的局部放电(Partial discharge, PD)信号，或使用有效奇异值之后的所有奇异值直接重构出滤除了窄带干扰后的理想PD信号。

3 仿真结果分析

3.1 理想局部放电信号模拟

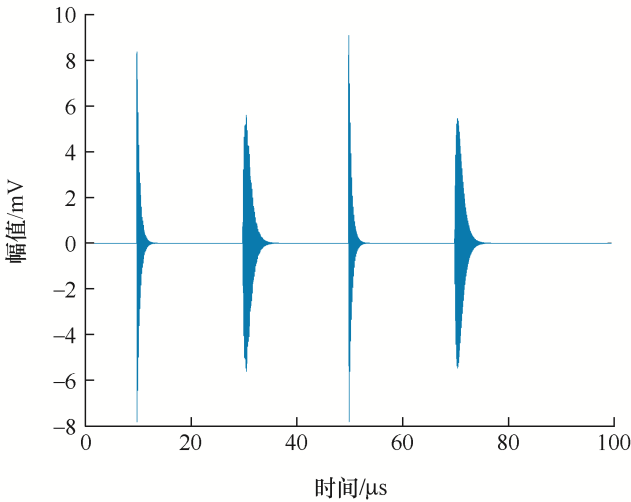
以往的研究指出，局部放电信号通常包含四种类型的脉冲，为了验证本文方法的实际效果，并模拟更真实的局部放电信号，使用了两种脉冲模型，分别为单指数振荡衰减脉冲和双指数振荡衰减脉冲。其表达式分别为

(4)${{Y}_{1}}(t)=A\exp \left( -\frac{t}{\tau } \right)\sin (2\pi {{f}_{c}}t)$

(5)${{Y}_{2}}(t)=A\left[ \exp \left( -\frac{1.3t}{\tau } \right)-\exp \left( -\frac{2.2t}{\tau } \right) \right]\sin (2\pi {{f}_{c}}t)$

式中，A表示信号幅度，$\tau $是衰减时间常数，${{f}_{c}}$是振荡频率，采样频率为50 MHz，设采样时间为100 μs，本文设计参数模拟了四种脉冲信号，具体参数详情如表1所示。

表1 局部放电信号模拟参数

序号	幅值/mV	时间常数/μs	振荡频率/MHz
1	12	0.5	8
2	12	0.5	7
3	30	1	8
4	30	1	10

新窗口打开| 下载CSV

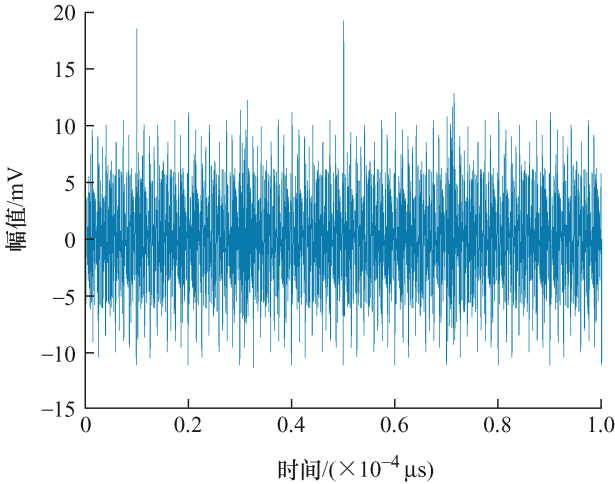
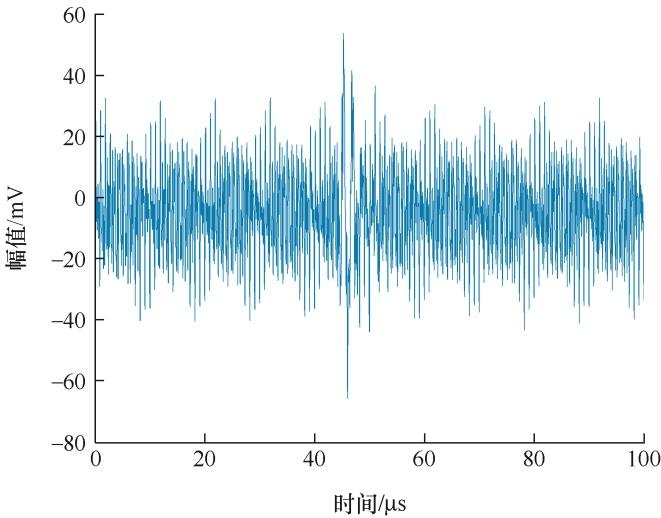
理想的PD信号如图2所示，实际测量中测试环境中会存在谐波、载波和无线电信号等干扰会产生窄带干扰，为了准确模拟现场测试信号，给理想PD信号掺周期性窄带干扰，周期性窄带干扰是一类正弦脉冲信号，表述为

(6)${{Y}_{3}}(t)={{A}_{i}}\sum\limits_{i=1}^{n}{\sin (2\pi {{f}_{i}}t)}$

式中，${{A}_{i}}$是每个周期性窄带干扰的振幅，f_i为干扰信号频率。本文设置窄带干扰幅度分别为3 mV、3.4 mV、2.6 mV、3.8 mV，频率分别设为3 MHz、3.7 MHz、4.5 MHz、5.7 MHz。根据脉冲模型仿真出的PD信号波形如图2所示，加入噪声信号后，理想信号被噪声完全淹没，其信号如图3所示，根据该信号对其进行绝缘状态评估带来了困难，很难找出对研究有用的信号。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 理想局部放电信号

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 含噪局部放电信号

3.2 窄带干扰抑制

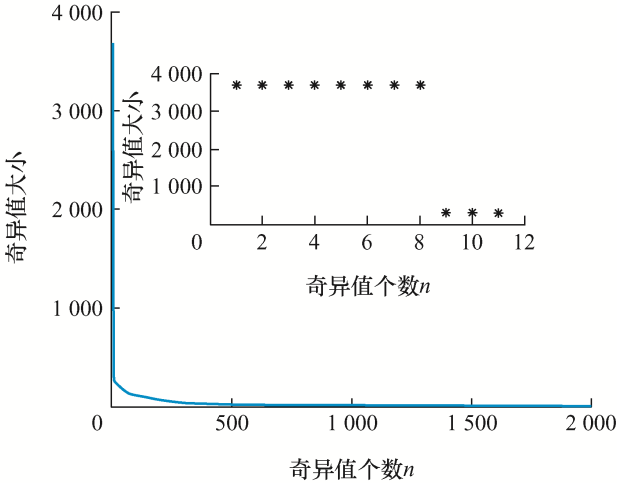
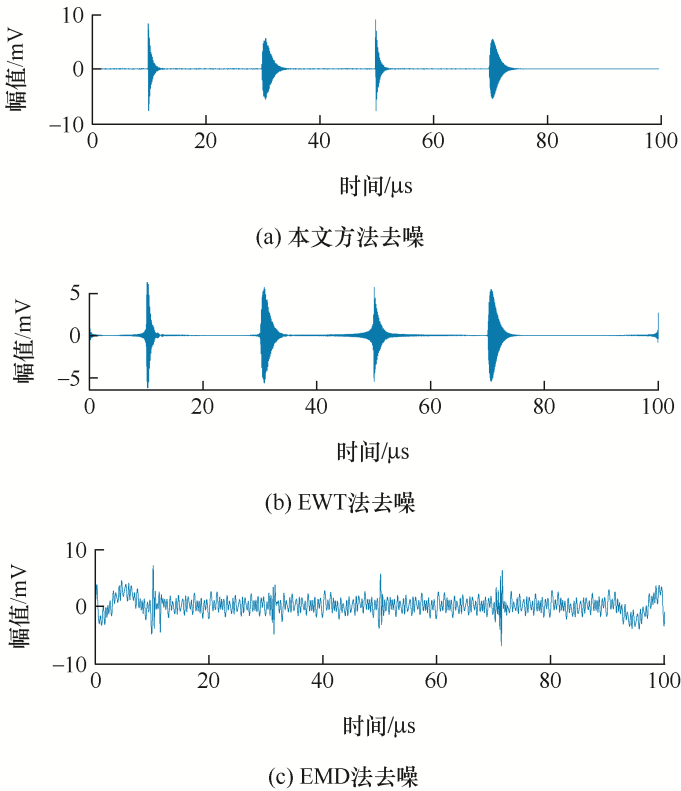
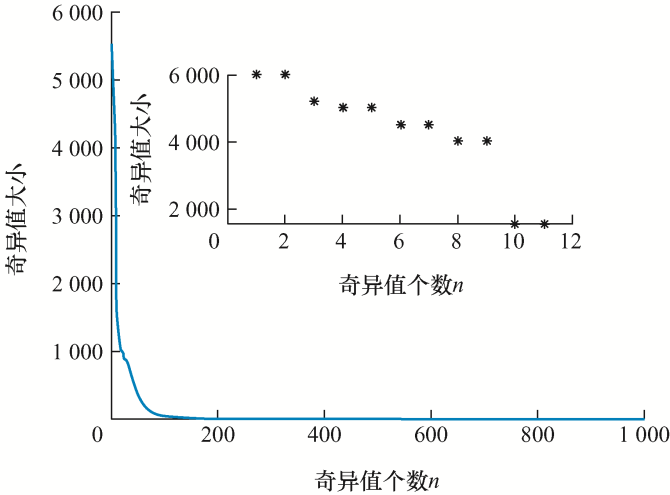
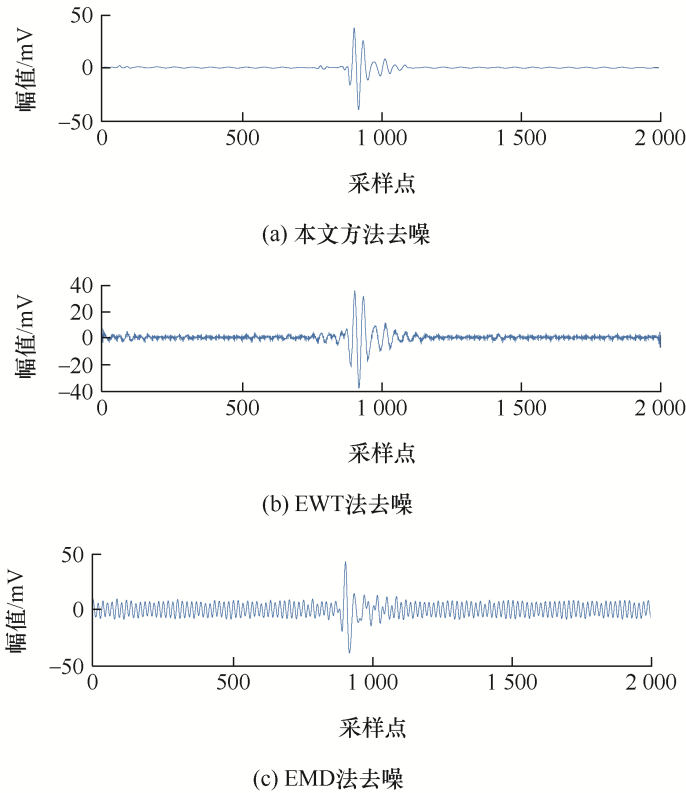
对信号进行SSA分解，对窄带干扰进行去噪。图4展示了奇异值分布，根据斜率变化曲线，可以发现第9个奇异值点是一个突变点，故推断前9个奇异值对应的是周期性的窄带干扰，分组后重建相应的矩阵，得到窄带干扰信号，将其从含噪信号中分离出得到滤除窄带干扰后的PD信号，如图5a所示，经过奇异频谱分析处理后，PD信号较降噪前波形易于识别分析，可用于后续局部放电定位和缺陷程度识别工作。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 奇异值分布特性

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 SSA降噪后的含噪PD信号

为了评价各方法降噪前后的实际效果，本文引用了三个用于评价降噪算法性能指标的参数，即信噪比、波形相似系数(Normalized correlation coefficient, NCC)和均方根误差。信噪比是指理想信号与噪声的比值，通常情况下，信噪比越大，噪声抑制效果较好，波形还原度较高；均方根误差通过计算预测值与实际值的误差平方来评价降噪性能，均方误差值越小，代表降噪信号对原始信号的还原度越高；NCC可以反映去噪前后信号波形的相似度，其取值区间为[-1，1]，越接近于1表示波形越相似。其计算公式如下

(7)$SNR=10\lg \left( \frac{\sum\limits_{i=1}^{n}{x_{i}^{2}}}{\sum\limits_{i=1}^{n}{{{\left( {{x}_{i}}-{{{\tilde{x}}}_{i}} \right)}^{2}}}} \right)$

(8)$MSE=\frac{1}{n}\sum\limits_{i=1}^{n}{{{\left( {{{\tilde{x}}}_{i}}-{{x}_{i}} \right)}^{2}}}$

(9)$NCC=\frac{E[(x-{{\mu }_{x}})(\tilde{x}-{{\mu }_{{\tilde{x}}}})]}{{{\sigma }_{x}}{{\sigma }_{{\tilde{x}}}}}$

式中，${{x}_{i}}$代表信号，${{\tilde{x}}_{i}}$代表降噪后信号。原始信号和降噪信号的标准差分别用${{\sigma }_{x}}$和${{\sigma }_{{\tilde{x}}}}$表示，${{\mu }_{x}}$和${{\mu }_{{\tilde{x}}}}$分别表示预处理和后处理信号的预期。

为了显示本文方法的优越性，引入了EMD和EWT与本文方法进行比较，其降噪后波形效果如图5所示。三种方法的去噪评价参数结果如表2所示，由表2可知，经验模态分解和经验小波变换的窄带干扰抑制效果较差，EMD法降噪的波形中存在较大的残余噪声，抑制窄带干扰能力明显较差，无法有效地提取出PD信号；EWT法降噪后波形出现一定程度的失真，信号幅值存在大幅度衰减，第一和第三个波形失真严重；而本文所提方法在抑制混合噪声干扰方面表现最佳，降噪后波形细节信息得到有效保留，有利于对波形信号的进一步分析。

表2 PD信号降噪评价指数

方法	SNR	MSE	NCC
SSA	20.480 6	0.024 39	0.957 8
EMD法	5.936 0	0.762 6	0.646 6
EWT法	10.520 4	0.054 4	0.892 5

新窗口打开| 下载CSV

4 应用案例

为获得HFCT法应用于高压电缆局部放电测试的局部放电信号，在实验室内部对预制缺陷的高压电缆终端做局部放电测试，通过在电缆终端低压端制作切口并向电缆主绝缘与应控管间插入直径为2 mm的钢钎以构建缺陷。借助钢钎插入不同深度构建不同长度的气隙缺陷。局放试验开始前抽出钢钎，并采用绝缘胶带进行切口密封，缺陷制作细节如图6所示。在实验室内搭建工频试验平台，对实验室内预制气隙缺陷车载电缆进行局部放电测试。接线回路图如图7a所示，实际回路图如图7b所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 缺陷电缆制造流程

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 PD测试接线图

试验方法采用高频电流法测试，HFCT线圈频带范围为3~30 MHz，阻抗为50 Ω；采样比为8 mV∶1 mA。测试时将线圈扣在电缆接地线上，设置采集频率为100 MHz。由于实验室环境为屏蔽室环境，因此收集到的PD信号噪声较小，人为向其中添加了幅值8 mV、12 mV、9 mV、10 mV，频率为1.2 MHz、2.3 MHz、3.5 MHz、4.5 MHz的四组窄带干扰，得到含有窄带干扰的实测PD噪声信号如图8所示，由图8可知，PD信号被噪声掩盖，对后续状态评估工作带来了困难。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 实测含窄带干扰PD信号

通过使用本文所提方法对含噪信号进行分析，得到了其奇异值的排列如图9所示。以第9个奇异值为分界点对信号进行重构，可以判断出含噪信号中的窄带干扰数量为9。为了对比降噪效果，同时使用了EMD法和EWT法对实测的含噪信号进行处理，并得到了如图10所示的结果。可以明显看出，本文提出的方法在降噪性能上优于EMD法和EWT法，降噪后的波形保留了较为完整的波形特征信息。现车测试时环境干扰较多，因此难以获取不含噪声的PD信号，传统的降噪评价指标难以对其降噪性能评估，故本文采用噪声抑制比(Noise rejection ratio, NRR)来评估三种方法的去噪效果。其定义为

(10)${{\rho }_{NRR}}=10\left( \lg {{\sigma }_{1}}^{2}-\lg {{\sigma }_{2}}^{2} \right) $

式中，${{\sigma }_{1}}$、${{\sigma }_{2}}$分别为去噪前和去噪后的信号标准差。噪声抑制比越大代表降噪效果越好。三种降噪方法的降噪性能指标如表3所示。从表3可以看出，对实际测量的PD信号进行降噪时，本文所提方法具有更大的噪声抑制比，有效信号提取效果更好。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 实测PD信号奇异值排列

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 实测PD信号去噪结果对比

表3 不同降噪方法的NRR

降噪方法	标准差
SSA	18.21
EWT法	16.31
EMD法	12.28

新窗口打开| 下载CSV

5 结论

本文提出一种基于奇异谱分析的电缆终端窄带干扰抑制方法，用于处理局部放电信号中存在的窄带干扰问题。该方法利用奇异谱分析技术对信号进行分解，并通过自适应筛选分解后的奇异值，实现了对干扰信号和原始信号的有效分离。其主要优点如下所述。

(1) 在该方法中，首先对电缆终端局部放电信号进行奇异谱分析，将信号分解为一系列奇异值和奇异向量。然后，通过设定一个自适应门限值，对奇异值进行筛选，将干扰信号的奇异值排除，而保留原始信号的奇异值，通过保留的奇异值和对应的奇异向量重构，成功实现了对干扰信号的去除，从而实现了窄带干扰的抑制。

(2) 通过仿真和试验验证，本文所提方法在处理电缆终端局部放电信号中的窄带干扰时表现出较好的效果。相较于传统方法，该方法能够有效地去除干扰信号，提取出有用的PD信号，避免了传统方法中可能出现的信息缺失或信号失真等问题。

(3) 该方法在电缆终端局部放电信号处理中具有较高的实际工程应用价值，可以为高速列车车载电缆绝缘性能评估及缺陷程度识别提供技术支持。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

谢敏, 周凯, 何珉, 等.

史坦无偏估计自适应奇异值分解在局放信号白噪声抑制中的应用

[J]. 电网技术, 2018, 42(12):4153-4159.