基于模型预测的光伏参与电网调频方法研究*

doi:10.11985/2023.03.037

基于模型预测的光伏参与电网调频方法研究^*

吴馥云^,¹, 程卫^,², 李高宁^,², 吕建国^,²

1.三江学院机械与电气工程学院南京 210012

2.南京理工大学自动化学院南京 210094

Research on the Method of Photovoltaic Participation in Grid Frequency Regulation Based on Model Prediction Control

WU Fuyun^,¹, CHENG Wei^,², LI Gaoning^,², LÜ Jianguo^,²

1. School of Mechanical and Electrical Engineering, Sanjiang University, Nanjing 210012

2. School of Automation, Nanjing University of Science and Technology, Nanjing 210094

通讯作者: 程卫，男，1997年生，硕士研究生。主要研究方向为分布式发电与微电网技术。E-mail：1803255993@qq.com

收稿日期: 2022-08-8 修回日期: 2023-05-24

基金资助:

* 江苏省高等学校自然科学研究资助项目(20KJB470029)

Received: 2022-08-8 Revised: 2023-05-24

作者简介 About authors

吴馥云，女，1988年生，讲师。主要研究方向为分布式发电与微电网技术。E-mail：wufuyun0606@163.com

李高宁，男，1998年生，硕士研究生。主要研究方向为分布式发电与微电网技术。E-mail：li15256971761@163.com

吕建国，男，1987年生，博士，副教授。主要研究方向为分布式发电与微电网技术、电力电子变换器控制技术。E-mail：jianguolyu@njust.edu.cn

摘要

针对大规模光伏并网导致电力系统一次调频能力不足的问题，光伏发电主动参与电网频率调节是解决这一问题的重要手段。首先介绍了两级式光伏发电系统的拓扑结构与控制策略，然后考虑到下垂控制对电网频率暂态调节有限，提出了一种模型预测控制与下垂控制相结合的调频控制策略。该控制策略在光伏发电保留一定有功功率的基础上，通过频率差值改变下垂控制的输出增量与频率偏差率改变模型预测控制的输出增量，进而改变光伏发电的有功输出功率，使其参与系统调频。最后在Matlab/Simulink平台上搭建了一套含光伏发电的区域电网仿真模型，通过仿真分析验证了调频控制策略的可行性与有效性。仿真结果表明，该控制策略不仅对电网频率的稳态起到调节作用，还改善了电网频率的暂态与动态效果。

关键词： 两级式光伏发电系统; 频率调节; 下垂控制; 模型预测控制

Abstract

Aiming at the problem of insufficient primary frequency regulation ability of the power system caused by large-scale photovoltaic grid connection, photovoltaics actively participate in grid frequency regulation is an important means to solve this problem. Firstly, the topology structure and control strategy of two-stage photovoltaic power generation system are introduced. Then, considering that droop control has limited effect on frequency transient regulation of power grid, a frequency regulation control strategy combining model predictive control and droop control is proposed. On the basis of active power reserve, the strategy changes the output increment of droop control by frequency difference and the output increment of model predictive control by frequency deviation rate, so as to change the output power of photovoltaic power generation and make it participate in system frequency regulation. Finally, a simulation model of a regional grid with PV power generation is built on Matlab/Simulink platform, the feasibility and effectiveness of the frequency regulation control strategy are verified. The simulation results show that the control strategy not only regulates the steady state of grid frequency, but also improves the transient and dynamic effects of grid frequency.

Keywords： Two-stage photovoltaic power generation system; frequency regulation; droop control; model predictive control

PDF (16596KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

吴馥云, 程卫, 李高宁, 吕建国. 基于模型预测的光伏参与电网调频方法研究^*[J]. 电气工程学报, 2023, 18(3): 348-357 doi:10.11985/2023.03.037

WU Fuyun, CHENG Wei, LI Gaoning, LÜ Jianguo. Research on the Method of Photovoltaic Participation in Grid Frequency Regulation Based on Model Prediction Control[J]. Chinese Journal of Electrical Engineering, 2023, 18(3): 348-357 doi:10.11985/2023.03.037

1 引言

为实现人类社会的可持续发展，风能、太阳能等可再生能源的应用得到了不断扩展。根据国家能源局的统计数据，截至2020年底，中国光伏发电装机容量达到2.23亿kW，较上年新增1 870万kW^[1]，预计到2030年，光伏发电装机容量将达到1 050 GW^[2]。

传统电力系统的频率由同步机的转子转速决定，转子具有较大的旋转惯量，可提供功率支撑，抑制电网频率波动，具有较好的频率响应特性^[3]。但随着光伏发电的逐渐增加，常规发电机组总容量在系统中的占比逐渐减小，降低了电网一次调频资源储备容量，导致传统电力系统转动惯量逐渐减小，削弱了电网调频能力^[4⇓-6]。此外，由于光伏发电系统自身不具备惯性，光伏发电的功率输出并不响应系统频率的变化，不参与系统的一次调频^[7]。由于大规模光伏发电并网挤占了具有转动惯量的同步发电机组空间，会导致电力系统惯量减小与调频能力不足等问题。为此，迫切需要光伏发电主动参与电网频率调节。

目前，国内外学者对光伏参与电网频率调节的研究主要集中在减载控制策略^[8-9]、虚拟同步控制^{[10⇓⇓⇓-14]}、光储联合调频^{[15⇓⇓⇓-19]}等方面，如表1所示。文献[9]从经济性方面表明，通过减载运行比加入储能电池在售电收益中优势明显。文献[20]提出了一种离线最大功率跟踪与变系数下垂控制方法，实现两级式光伏发电系统对电网的频率支撑。文献[21]提出了基于变减载率的减载控制策略，依据电网频率改变光伏发电减载水平，使其主动参与电网频率调节。文献[22]讨论虚拟惯量对电网频率扰动的支撑，但是忽略了光伏电源的动态性能。

表1 调频类型分析

调频类型	优点	缺点
减载控制	不需要额外设备，调频成本较低	一般需要弃光，有能量损失
虚拟同步控制	提供更好的惯性，改善动态特性	通常与储能结合，忽略光伏源端特性
光储联合控制	功率稳定，消除功率波动	储能单元的造价与维护成本昂贵

新窗口打开| 下载CSV

本文在当前现有研究的基础上，以两级式光伏发电系统为研究对象，利用光伏电源的自身特性，提出一种模型预测控制与下垂控制相结合的调频策略。该策略在有功备用的基础上，通过频率差值改变下垂控制的输出增量与频率偏差率改变模型预测控制的输出增量，从而改变光伏发电的输出功率，使其参与系统调频。最后在Matlab/Simulink平台中搭建了含光伏的两区域仿真模型，并通过仿真结果对理论分析和控制策略进行了有效验证。

2 基于有功备用的光伏发电系统拓扑及运行策略

2.1 光伏发电系统拓扑及运行策略

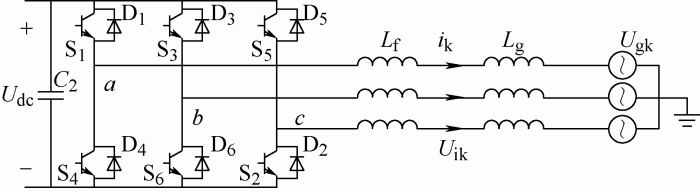
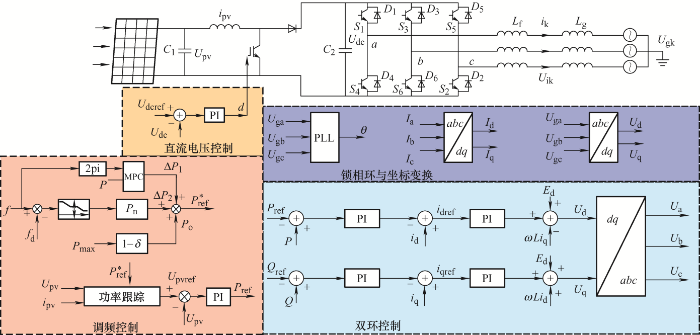
本文所研究的基于有功备用的光伏发电系统如图1所示。图1所示的拓扑结构不含储能部分，其由光伏发电阵列、DC/DC变换器、DC/AC逆变器、变压器、线路、负荷和交流电网构成。图1中C_b1为直流低压侧电容，C_b2为直流高压侧电容，U_pv为光伏发电阵列的输出电压，U_dc为U_pv经过DC/DC变换器斩波后的直流电压，L_f为滤波电感，L_g和R_g为线路阻抗，P_load为线路负载，U₁为并网点电压，U_g为电网电压。DC/DC变换器使用Boost升压变换器；DC/AC逆变器为两电平三相桥式逆变器。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 双级式光伏发电系统拓扑

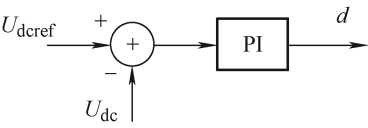
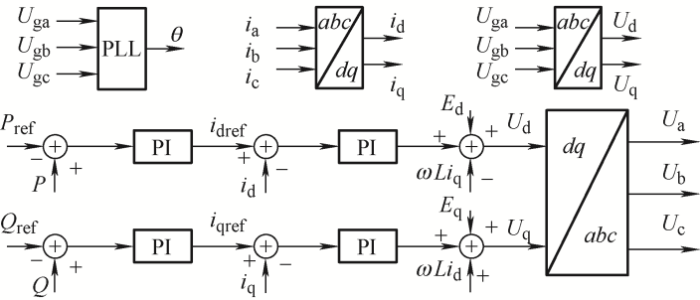
DC/DC变换器采用Boost变换器结构，Boost变换器的控制策略如图2所示，采用直流电压控制策略，直流侧电压参考值U_dcref与U_dc的误差信号经PI控制器后生成占空比d，进而产生驱动信号驱动Boost变换器工作。DC/AC逆变器为两电平三相桥式逆变器，网侧逆变器的拓扑结构如图3所示。网侧逆变器采用基本的恒定功率控制策略，如图4所示。P_ref和P分别为有功功率的参考值和实际值；Q_ref和Q分别为无功功率的参考值和实际值；i_dref和i_qref分别为d轴电流和q轴电流的参考值；i_d和i_q分别为逆变器输出d轴电流和q轴电流；U_d和U_q分别为电流控制器输出的d轴调制电压和q轴调制电压；θ为锁相环输出的相位。功率外环控制根据有功和无功功率的需求分别生成d轴和q轴电流指令值，通过调节d轴和q轴电流值来调节注入电网的有功和无功功率。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 Boost变换器的控制策略

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 网侧逆变器的拓扑结构

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 网侧逆变器控制策略

2.2 基于有功备用的下垂控制策略

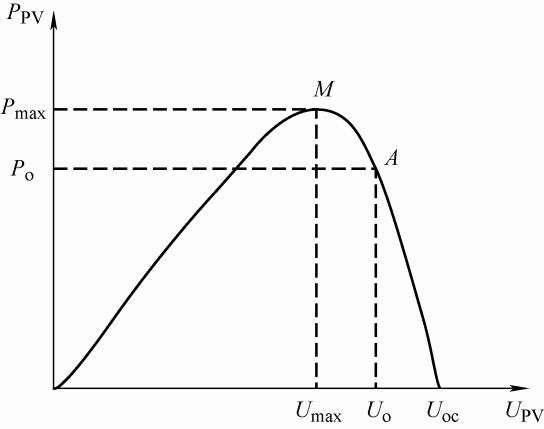
在最大功率运行模式下，功率输出并不响应系统频率的变化，光伏电站不参与系统的一次调频，所以光伏电站若要参与系统一次调频，需要运行在功率差值模式为调频留出一定的有功备用，本文选取光伏功率特性曲线右侧为备用侧，预留20%的备用容量^[8,23]。具体如图5所示，图中M为最大功率点，P_max为最大功率点处功率，U_max为最大功率点处电压；A为有功备用点，P_o为备用点功率，U_o为备用点电压；U_oc为光伏电源得开路电压。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 光伏功率特性曲线

根据有功备用下垂控制策略可知，系统若要参与调频应减载运行，首先需要确定的是有功备用工作点。当系统处于正常运行状态时，即电网频率没有波动时，给定电网同步角速度与网侧实际角速度相等，光伏应运行在有功备用点处P_o。如果网侧频率发生变化，频率-有功环路发生作用，根据网侧频率变化的升降，对原功率指令P_o施加修正量ΔP值进行修正得到功率指令P^*_ref，以此改变光伏的有功出力达到一次调频的效果。总体上当电网频率跌落低于正常运行状态时，光伏发电系统将向外增加输出的有功功率，而当频率上升高于正常运行状态时，光伏发电系统将降低输出的有功功率。

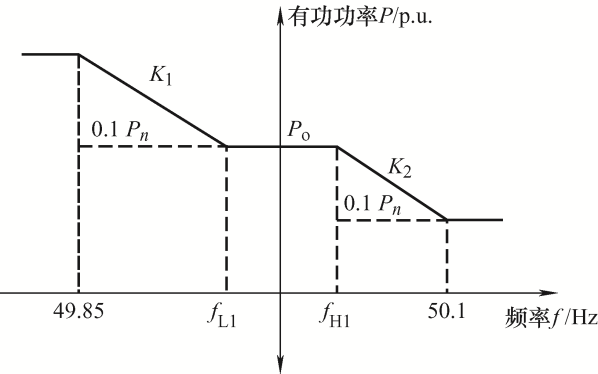
由此可以得到如图6所示的有功频率特性曲线。用式(1)表示如下

(1)

Δ P = \{\begin{cases} K_{1} \cdot (f_{L 1} - f) \cdot P_{n} f < f_{L 1} \\ K_{2} \cdot (f_{H 1} - f) \cdot P_{n} f > f_{H 1} \end{cases}

式中，P_n为光伏发电阵列有功功率额定值；K为调频控制增益，分为上饶值(欠频)K₁和下饶值(过频)K₂；f为当前测量频率，f_L1为系统欠频动作死区阈值，取49.96，f_H1为系统过频动作死区阈值，取50.03。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 有功功率-频率特性下垂曲线

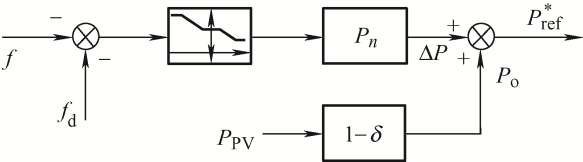
根据式(1)与图6所示的有功频率特性曲线，可以设计基于有功备用的下垂控制策略如图7所示，图中δ为备用系数，f_d为额定电网频率。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 基于有功备用的控制策略框图

3 光伏虚拟转子控制策略

3.1 频率预测模型的建立

逆变器的主电路结构和同步发电机的结构存在着一一对应的关系，因此光伏发电系统的逆变器结构可以等效为同步发电机结构。

由同步发电机的转子运动方程可知

(2)

J ω_{0} \frac{d ω}{d t} = P_{m} - P_{e} - D ω_{0} (ω - ω_{0})

式中，P_m和P_e分别为机械功率和电磁功率；J为转动惯量；D为阻尼系数；ω为电网同步角速度；ω₀为同步发电机的机械角速度。

将式(2)进一步化简可以得到式(3)

(3)

J \frac{d ω^{'}}{d t} = T_{m} - T_{e} - D ω^{'}

(4)

\{\begin{cases} ω^{'} = ω - ω_{0} \\ T_{m} = P_{m} / ω_{0} \\ T_{e} = P_{e} / ω_{0} \end{cases}

式中，T_m为机械转矩；T_e为电磁转矩； $ω^{'}$ 为电网同步角速度与机械角速度之差。

由此可以得到连续状态下的控制模型为

(5)

\{\begin{cases} {\dot{ω}}^{'} (t) = \frac{1}{J} T_{m} (t) - \frac{1}{J} T_{e} (t) - \frac{1}{J} D ω^{'} (t) \\ y (t) = C_{c} ω^{'} (t) \end{cases}

式中，y(t)表示系统输出响应，物理含义为角速度偏差。

3.2 频率预测模型求解

先将连续状态下的控制模型进行离散化处理，即根据式(5)可得到式(6)

(6)

\{\begin{cases} ω^{'} (k + 1) = A_{c} ω^{'} (k) + B_{cu} T_{m} (k) + B_{cd} T_{e} (k) \\ y (k) = C_{c} ω^{'} (k) \end{cases}

(7)

\{\begin{cases} A_{c} = \exp (- \frac{D}{J} T_{s}) \\ B_{cu} = \frac{1}{J} \int_{0}^{T_{s}} \exp d x (- \frac{D}{J} T_{s}) d t \\ B_{cd} = - \frac{1}{J} \int_{0}^{T_{s}} \exp (- \frac{D}{J} T_{s}) d t \\ C_{c} = 1 \end{cases}

式中， $ω^{'} (k)$ 是状态变量，表示k时刻的角频率偏差； $T_{m} (k)$ 是控制输入量，表示k时刻的机械转矩；$y(k)$表示k时刻被控输出量； $T_{e} (k)$ 是可以测量的外部干扰量，表示k时刻的电磁转矩；T_s是系统采样时间。

系统的全部状态都可以测量得到，为了减少静态误差，可以将式(6)改为增量式(8)

(8)

\{\begin{cases} Δ ω^{'} (k + 1) = A_{c} Δ ω^{'} (k) + B_{cu} Δ T_{m} (k) + B_{cd} Δ T_{e} (k) \\ y (k) = C_{c} Δ ω^{'} (k) + y (k - 1) \end{cases}

(9)

Δ ω^{'} (k) = ω^{'} (k) - ω^{'} (k - 1) = Δ ω (k)

式中， $Δ ω^{'} (k)$ 为k时刻的系统角频率变化率。

设定预测时域为p，控制时域为m，且m≤p。控制时域之外，控制量机械转矩 $Δ T_{m}$ 不变^[24]，即

(10)

Δ T_{m} (k + i) = 0 i = m, m + 1, \dots, p - 1

可测干扰量电磁转矩 $Δ T_{e}$ 在k时刻之后就保持不变，即

(11)

Δ T_{e} (k + i) = 0 i = 1, 2, \dots, p - 1

本文取预测时域与控制时域相等且为3，即m=p=3，可以根据式(8)得到输出预测方程为

(12)

Y_{p} (k + 1 | k) = S_{ω} Δ ω^{'} (k) + I y (k) + S_{d} Δ T_{e} (k) + S_{u} Δ U (k)

Y_{p} (k + 1| k) = {[\begin{matrix} y (k + 1) & y (k + 2) & y (k + 3) \end{matrix}]}^{T}

Δ U (k) = {[\begin{matrix} Δ T_{m} (k) & Δ T_{m} (k + 1) & Δ T_{m} (k + 2) \end{matrix}]}^{T}

S_{ω} = {[\begin{matrix} A_{c} & A_{c} + A_{c}^{2} & A_{c} + A_{c}^{2} + A_{c}^{3} \end{matrix}]}^{T}

I = {[\begin{matrix} 1 & 1 & 1 \end{matrix}]}^{T}

S_{d} = {[\begin{matrix} B_{cd} & B_{cd} + B_{cd}^{2} & B_{cd} + B_{cd}^{2} + B_{cd}^{3} \end{matrix}]}^{T}

(13)

S_{u} = [\begin{matrix} B_{cu} & 0 & 0 \\ B_{cu} + A B_{cu} & B_{cu} & 0 \\ B_{cu} + A B_{cu} + A_{cu}^{2} & B_{cu} + A B_{cu} & B_{cu} \end{matrix}]

式中，Y_P(k+1|k)表示对系统未来3步预测的输出量 $Δ ω^{'}$ 矩阵；ΔU(k)表示对系统3步预测的控制输入量 $Δ T_{m}$ 矩阵。

本文控制目标是根据频率变化来改变功率增量，故可以将目标函数定为式(14)

(14)

f = {\sum_{i = 1}^{3} ‖Q y (k + i)‖}^{2} + {\sum_{i = 1}^{3} ‖R Δ U (k + i - 1)‖}^{2}

式中，第一项反映了系统对参考轨迹的跟踪能力，参考轨迹为0，即频率变化率为0，其中Q代表第一项的权重；第二项反映了对控制量变化的控制能力，即对有功功率变化量的控制能力，其中R代表第二项的权重。

其中权重系数Q、R矩阵表达式如下

(15)

\{\begin{cases} Q = d i a g (q, q, q) q > 0 \\ R = d i a g (r, r, r) r > 0 \end{cases}

式中，q、r为权重系数因子。

为了方便计算式(14)，定义辅助变量λ

(16)

λ = [\begin{array}{l} Q Y_{P} (k + 1 | k) \\ R Δ U (k) \end{array}]

则目标函数式(14)可以简化为式(17)

(17)

f = λ^{T} λ

将式(12)代入式(16)化简后可得

(18)

λ = [\begin{array}{l} Q S_{u} \\ R \end{array}] Δ U (k) - [\begin{array}{l} Q E_{p} (k + 1) \\ 0 \end{array}] = A z - b

(19)

\{\begin{cases} A = [\begin{array}{l} Q S_{u} \\ R \end{array}] \\ z = Δ U (k) \\ b = [\begin{array}{l} Q E_{p} (k + 1) \\ 0 \end{array}] \\ E_{p} (k + 1) = - [S_{ω} Δ ω^{'} (k) + I Q + S_{d} Δ T_{e} (k)] \end{cases}

将式(18)、(19)代入式(17)可以求得极值解为

(20)

Z = {(A^{T} A)}^{- 1} A^{T} b

将式(19)代入式(20)可以得到k时刻时最优控制序列解，即最优控制量ΔT_m的序列解为

(21)

Δ U (k) = {(S_{u}^{T} Q^{T} Q S_{u} + R^{T} R)}^{- 1} S_{u}^{T} Q^{T} Q E_{P} (k + 1 | k)

根据上述理论可以得到控制策略流程图如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 控制策略流程图

3.3 控制策略稳定性分析

根据模型预测控制的基本原理，优化解得第一个元素作用于控制系统，即

(22)

Δ u (k) = [1 0 0] Δ U (k) = K_{mpc} E_{p} (k + 1)

(23)

K_{mpc} = {(S_{u}^{T} Q^{T} Q S_{u} + R^{T} R)}^{- 1} S_{u}^{T} Q^{T} Q

考虑到一些不确定因素，将被控系统进一步描述为式(24)所示

(24)

Δ ω^{'} (k + 1) = A_{c} Δ ω^{'} (k) + B_{cu} Δ T_{m} (k) + B_{cd} Δ T_{e} (k) + B_{ξ} Δ ξ (k)

式中，Δξ(k)为不可测量的外部干扰量。

将式(6)和式(19)代入式(22)可以得到闭环系统预测控制的表达式为

(25)

\begin{matrix} Δ u (k) = - K_{mpc} (S_{w} + I C_{c}) Δ ω^{'} (k) - K_{mpc} I C_{c} ω^{'} (k - 1) - \\ K_{mpc} S_{d} Δ T_{e} (k) \end{matrix}

将式(25)代入式(24)可得闭环系统表达式为

(26)

\begin{matrix} Δ ω^{'} (k + 1) = (A_{c} - B_{cu} K_{mpc} (S_{ω} + I C_{c})) Δ ω^{'} (k) + \\ B_{ξ} Δ ξ (k) + (B_{cd} - B_{cu} K_{mpc} S_{d}) Δ T_{e} (k) - \\ B_{cu} K_{mpc} I C_{c} ω^{'} (k - 1) \end{matrix}

定义中间变量η如下

(27)

η = A_{c} - B_{cu} K_{mpc} (S_{ω} + I C_{c})

如果η的所有特征值均在单位圆内，则闭环系统是稳定的。即只要η的绝对值小于1，则频率变化率可收敛至0。

本文中J=0.1 kg·m²，D=10 rad/(N·m)，T_s=1×10^-3 s。根据式(7)、(13)、(15)和式(23)可知

(28)

\{\begin{cases} A_{c} \approx 0.95 \\ B_{cu} K_{mpc} (S_{ω} + I C_{c}) \approx 4.8 \times 10^{- 3} \frac{q}{r} \end{cases}

进而结合式(28)可将式(27)表示为

(29)

η = 0.95 - 4.8 \times 10^{- 3} \frac{q}{r}

根据式(29)可以计算出η的绝对值小于1时，即q/r<406.3时，本文取r=1，q=100，r=100，闭环系统可以稳定。

结合上述章节，本文采用模型预测控制与下垂控制相结合的控制策略。该策略在有功备用的基础上，通过频率差值改变下垂控制的输出增量与通过频率偏差率改变模型预测控制的输出增量，从而改变光伏发电的输出功率，使其参与系统调频。

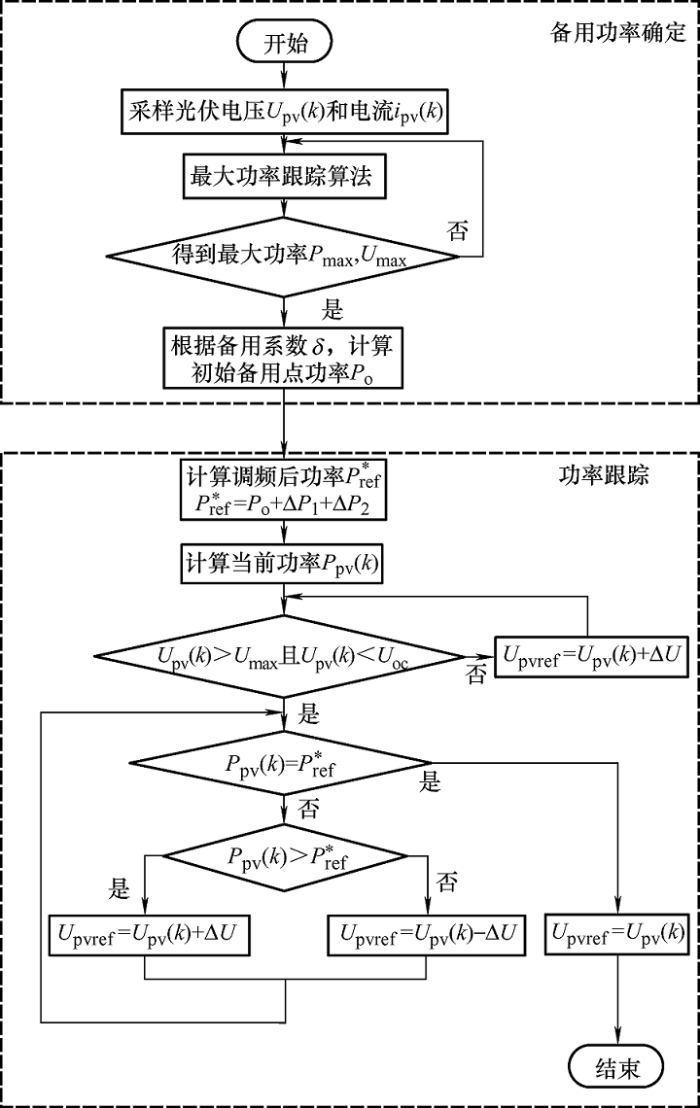
其中基于有功备用的光伏调频功率跟踪算法如图9所示。首先运行最大功率跟踪算法，得到最大功率点的电压U_max、功率P_max，然后根据备用系数得到初始备用点功率P_o。计算光伏参与调频后功率P^*_ref，运行功率跟踪部分，得到参考电压U_pvref，最后经过积分环节得到参考功率P_ref。整体控制策略图如图10所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 基于有功备用的光伏调频功率跟踪算法流程图

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 光伏发电主动参与电网频率调节控制策略图

4 仿真分析

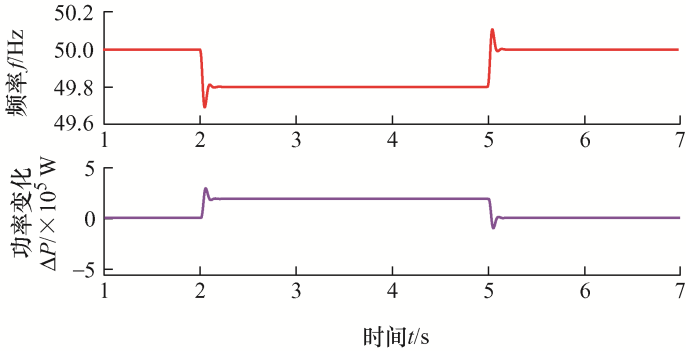
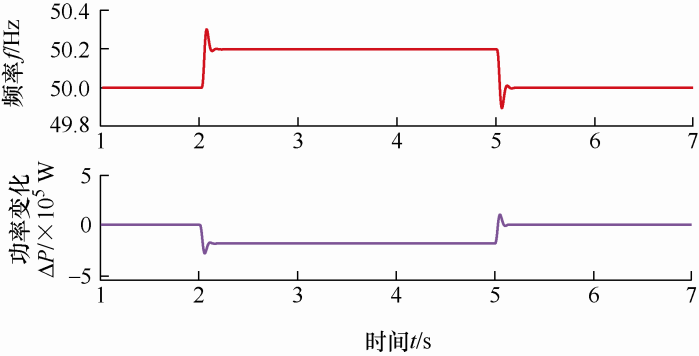
在Matlab/Simulink仿真平台下搭建单台光伏模型，来验证基于转子运动方程的模型预测控制策略的有效性。光伏电站由多台光伏发电单元组成，其中光伏发电单元采用单机等值模型，光伏电站在限功率状态运行容量为20 MW。仿真时通过并网频率的变化来观察基于转子运动方程的模型预测控制策略能否起到一定的调节作用。仿真波形如图11和图12所示。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 频率突降时的功率变化图

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 频率突增时的功率变化图

通过图11可知，当电网频率突减0.2 Hz时，光伏发电增加发出的功率约为200 kW。通过图12可知，当电网频率突增0.2 Hz时，光伏发电减少发出的功率约为200 kW。由此可知，基于同步转子运动方程的模型预测策略可以很好地跟随频率变化并使功率增量做出响应。

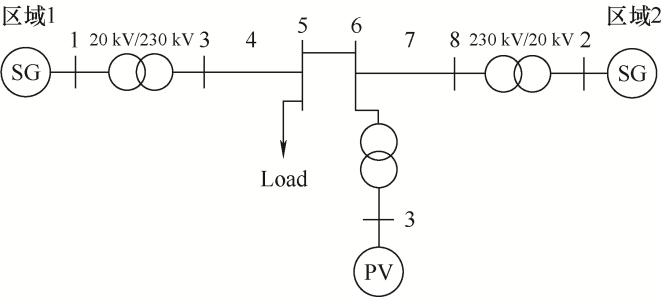
搭建如图13所示的区域电网仿真模型，验证本文最终的控制策略，即模型预测控制与下垂控制相结合的控制策略。其中，光伏电站额定容量为125 MW，有功备用为δ=20%，各同步发电机组容量均为198 MW，负载消耗有功功率为480 MW。仿真参数如表2所示。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 区域电网仿真拓扑

表2 仿真参数

参数	数值
区域1发电机容量/MW	198
区域2发电机容量/MW	198
光伏容量/MW	125
负载消耗有功功率/MW	480
有功备用δ	0.2
转动惯量J	0.1
阻尼系数D	10
Boost 电压环的PI参数	(1, 100)
调频电压环的PI参数	(0.2, 100)
逆变器无功功率外环的PI参数	(7, 800)
逆变器有功功率外环的PI参数	(7, 800)
逆变器有功电流内环的PI参数	(0.3, 20)
逆变器无功电流内环的PI参数	(0.3, 20)
输出量权重系数q	100
控制量权重系数r	1

新窗口打开| 下载CSV

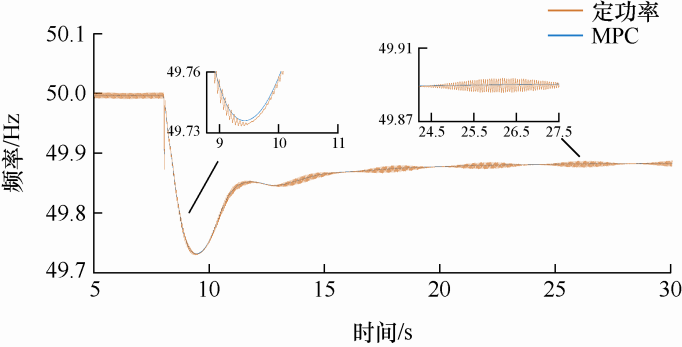
条件一：在短时间内光伏的输出功率保持不变，处于限功率运行状态。在仿真时间t=8 s时，负荷突增100 MW，仿真结果图如图14、图15所示。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 条件一(负荷突增100 MW)，仿真波形1

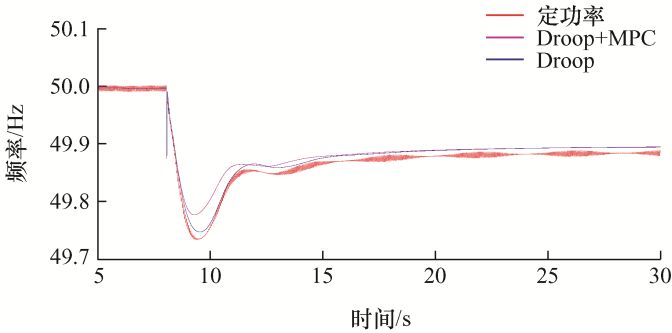
图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 条件一(负荷突增100 MW)，仿真波形2

由图14可知：① 光伏发电采用定功率控制时，当系统增加100 MW负荷时，系统最低频率低于49.75 Hz，危及系统安全稳定运行，且频率有一定的波动；② 当光伏发电采用虚拟转子MPC控制时，暂态过程中瞬间会增发功率来抑制电网频率跌落，起到一定的改善作用；稳态情况下，光伏发电与第一种情况下的稳态值一致。

由图15可知：① 当光伏发电采用基于有功备用下垂控制策略时，频率给定会按照设置的有功-频率曲线来控制光伏发电增加发出的有功功率来参与电网的频率调节，频率向下波动，系统最低频率低于49.77 Hz，经过10 s后频率重新达到稳定，稳定后频率约为49.9 Hz；② 当采用本文所提的控制策略时，系统最低频率低于49.8 Hz，暂态效果更好，经过9 s后频率重新达到稳定，稳态后频率与下垂控制时保持一致。

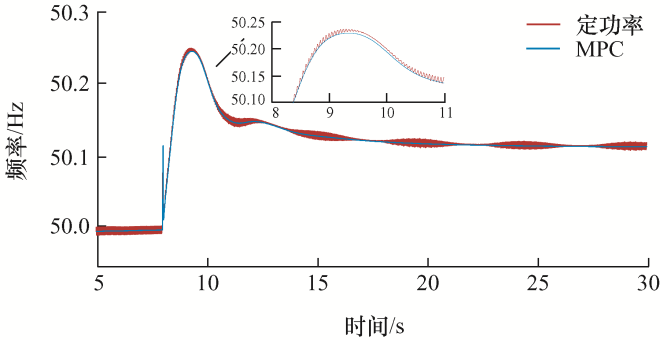
条件二：在短时间内光伏的输出功率保持不变，处于限功率运行状态。在仿真t=8 s时，负荷突减100 MW，仿真结果如图16、图17所示。

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 条件二(负荷突减100 MW)，仿真波形1

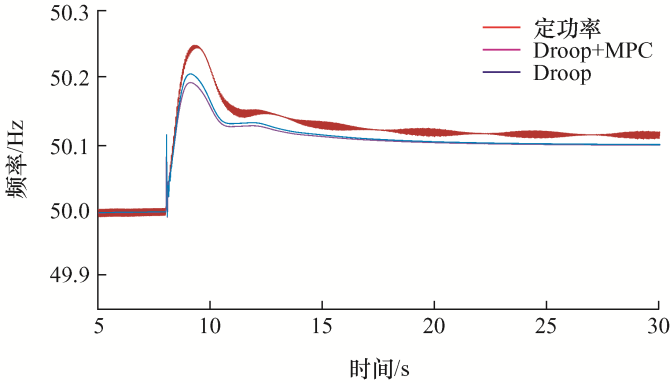
图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 条件二(负荷突减100 MW)，仿真波形2

由图16可知：① 光伏发电采用定功率控制时，当系统减少100 MW负荷时，系统最高频率接近50.25 Hz，危及系统安全稳定运行，且频率有一定的波动；② 当光伏发电采用虚拟转子MPC控制时，暂态效果起到一定的改善作用，而稳态效果则更加平稳。

由图17可知：① 当光伏发电采用基于有功备用下垂控制策略时，负荷突减100 MW，频率向上波动。暂态效果比定功率控制下更好，并且经过15 s后频率重新达到稳定，稳定后频率约为50.1 Hz；② 可以明显看到与下垂控制相比，当采用本文所提的控制策略时，暂态效果更好，并且经过12 s后频率重新达到稳定，稳态后频率与下垂控制时保持一致。

综上，即本文所提控制策略的效果与单独的有功备用下垂控制效果相比，暂态效果有明显的改善，动态调节速度更快。

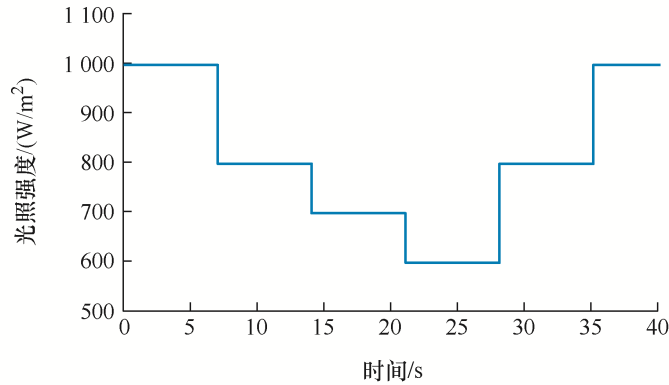
条件三：由于光伏电池输出功率随光照强度变化大而受温度影响较小。因此本文考虑光伏源端特性时，只分析光照强度突变的情景。

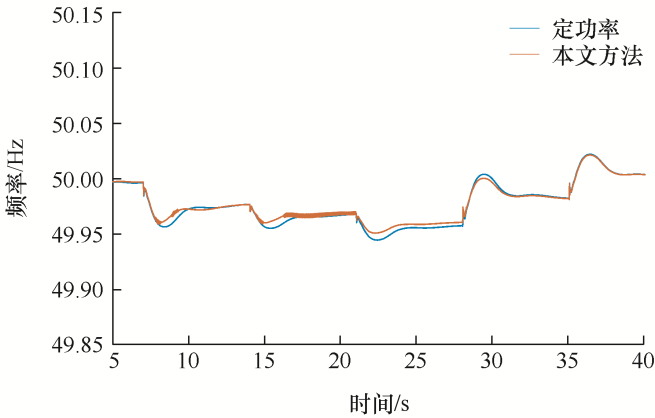
由图18和图19可知，当光照变化的情况时，采用本文所提控制策略得到的频率波形，在频率死区阈值(49.96~50.03 Hz)内，对频率的暂态效果有改善作用，并且动态调节速度更快，稳态值保持不变；在频率死区阈值(49.96~50.03 Hz)外，不仅暂态与动态调节效果得到改善，而且对稳态频率也起到了调节作用。综上所述，在考虑光照强度变化的情况下，本文所提控制策略依然有效。

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18 光照强度变化图

图19

新窗口打开| 下载原图ZIP| 生成PPT

图19 条件三(光照强度变化)，仿真波形

5 结论

本文以两级式光伏发电为例，考虑了实际应用中光伏要留有一定的备用容量，提出一种模型预测控制与下垂控制相结合的调频策略，通过调节光伏发电输出功率，实现了光伏主动参与电网频率调节的支撑。该策略在有功备用的基础上，通过频率差值改变下垂控制的输出增量与频率偏差率改变模型预测控制的输出增量，从而改变光伏发电的输出功率，使其参与系统调频。最后通过Matlab/Simulink平台建立两区域电网仿真模型，进行仿真验证。得到以下结论。

(1) 本文提出了模型预测控制与下垂控制相结合的控制策略，该控制策略能够较好地跟随频率的变化来改变光伏发电的输出功率，使之参与电网的频率调节，不仅对暂态与动态效果起到改善作用，而且对稳态起到调节作用。

(2) 与传统的下垂控制策略相比，本文所提方法对暂态效果有明显的改善作用，动态调节速度更快，而且不影响系统频率的稳态值。

(3) 在考虑光照强度变化的情况下，本文控制策略依然有效。在频率阈值内能够对频率的暂态与动态效果起到调节，在频率阈值外还能够对稳态起到改善作用。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

国家能源局.

2018年可再生能源并网运行情况介绍

[EB/OL]. [2019-01-28]. http://www.nea.gov.cn/2019-01/28/c_137780519.htm.

URL [本文引用: 1]

National Energy Administration.

Introduction to the operation of grid-connected renewable energy in 2018

[EB/OL]. [2019-01-28]. http://www.nea.gov.cn/2019-01/28/c_137780519.htm.

URL [本文引用: 1]

[2]

国家发展和改革委员会能源研究所.

中国2050高比例可再生能源发展情景暨路径研究

[R]. 北京: 国家发展和改革委员会能源研究所, 2015.