基于Stackelberg主从博弈多目标模型的综合能源优化调度*

doi:10.11985/2023.03.036

基于Stackelberg主从博弈多目标模型的综合能源优化调度^*

赵帅^,¹, 撖奥洋², 周生奇², 菅学辉², 张智晟^,¹

1.青岛大学电气工程学院青岛 266071

2.国网山东省电力公司青岛供电公司青岛 266002

Comprehensive Energy Optimal Scheduling Based on Stackelberg Master Slave Game Multi-objective Model

ZHAO Shuai^,¹, HAN Aoyang², ZHOU Shengqi², JIAN Xuehui², ZHANG Zhisheng^,¹

1. College of Electrical Engineering, Qingdao University, Qingdao 266071

2. Qingdao Power Supply Company, State Grid Shandong Electric Power Company, Qingdao 266002

通讯作者: 张智晟，男，1975年生，博士，教授，博士研究生导师。主要研究方向为电力系统短期负荷预测和经济调度。E-mail：slnzzs@126.com

收稿日期: 2022-09-24 修回日期: 2023-02-14

基金资助:

* 国网山东省电力公司科技资助项目(2020A-022)

Received: 2022-09-24 Revised: 2023-02-14

作者简介 About authors

赵帅，男，1995年生，硕士研究生。主要研究方向为综合能源系统经济运行与调度。E-mail：1547484641@qq.com

摘要

为进一步提高综合能源系统的灵活性和经济性，将分布式能源站作为综合能源系统的研究对象，建立了能源站收益模型和用户获能满意度模型，在用户获能满意度模型内部，以用户获取最大综合效能和用户满意度构成多目标函数。在传统博弈模型基础上增加对用户满意度的考虑，将能源站作为决策者，用户作为反应者建立Stackelberg主从博弈模型，并通过天牛须分布式算法对模型进行求解。算例仿真结果表明，Stackelberg博弈在考虑用户满意度和新能源参与下的综合能源系统中有良好的适用性，天牛须分布式算法在对目标优化模型求解具有良好的可行性，最后验证了不同程度新能源接入系统时对系统的影响。

关键词： 综合能源系统优化调度; Stackelberg主从博弈; 多目标模型; 天牛须分布式算法; 分时能源需求

Abstract

In order to further improve the flexibility and economy of the integrated energy system, the distributed energy station is taken as the research object of the integrated energy system, and the revenue model of the energy station and the user satisfaction model are established. In the user satisfaction model, the multi-objective function is composed of the maximum comprehensive efficiency and user satisfaction. Based on the traditional game model, considering the user satisfaction, the Stackelberg master-slave game model is established with the energy station as the decision maker and the user as the responder, and the model is solved by the beetle antenna search distributed algorithm. The simulation results show that the Stackelberg game has good applicability in the integrated energy system considering the user satisfaction and new energy participation, and the beetle antenna search distributed algorithm has good feasibility in solving the multi-objective optimization model. Finally, the influence of different degrees of new energy access to the system is verified.

Keywords： Optimal scheduling of integrated energy system; Stackelberg master slave game; multi-objective model; beetle antenna search distributed algorithm; time sharing energy demand

PDF (6752KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

赵帅, 撖奥洋, 周生奇, 菅学辉, 张智晟. 基于Stackelberg主从博弈多目标模型的综合能源优化调度^*[J]. 电气工程学报, 2023, 18(3): 341-347 doi:10.11985/2023.03.036

ZHAO Shuai, HAN Aoyang, ZHOU Shengqi, JIAN Xuehui, ZHANG Zhisheng. Comprehensive Energy Optimal Scheduling Based on Stackelberg Master Slave Game Multi-objective Model[J]. Chinese Journal of Electrical Engineering, 2023, 18(3): 341-347 doi:10.11985/2023.03.036

1 引言

随着人们对能源需求的不断增加，能源利用率问题已成为当今社会的热点问题，为实现能源的高效利用和多种能源之间的相互耦合，基于电-气-热-冷等多种能源为一体，共同实现能源生产、传输、分配、消费等环节的“综合能源系统”的概念被提出^[1]。分布式能源站作为综合能源系统中的区域综合能源系统，可为用户就近提供电、气、热、冷等能源，很大程度上降低了能量在传输过程中的损耗，相较于传统综合能源系统，具有独立性好、灵活性高、规模小的特点，为能源的灵活调度和控制提供了便利^[2-3]。分布式能源站的发展对于新能源的发展有着重要意义，分布式能源站灵活性高，可建在光伏和风力电站附近，实现小范围内就地上网、自产自销，不仅减少了能源输送过程中的损耗，还减轻了新能源上网对大电网稳定性的影响。

现今，对于综合能源系统优化调度方案的研究是综合能源系统中的热点问题。文献[4]提出基于机会约束目标规划优化调度方案，并将风险备用成本纳入系统成本目标，降低了能源不确定性对系统造成的影响。文献[5]提出了一种基于系统层、网络层、能源中心层、本地层共同组成的多代理系统的优化调度方案，对于每一层均以经济性最优为目标，实现了调度过程中多类任务同时分布式处理，提高了调度的快速性和准确性。文献[6]建立了定额投资下综合能源系统规划模型，解决了定额投资下设备的最优容量配置问题，综合考虑定额投资、设备出力、能量耦合等多种约束，利用帕累托前沿解集实现系统的经济性、环保性。文献[7]以经济和环境为出发点，构建了能量供应和能量转换相结合的综合能源系统，提高了系统的经济性、环保性。文献[8]构建了以系统经济性、环保性、可靠性为目标的多目标优化调度模型，并提出了结合双层优化算法和自适应潮流算法的分布式算法，为多目标的求解提供了新思路。

综合能源系统优化调度中博弈思想的引入，为优化调度问题的研究提供了新方向，近年来不少学者针对博弈做了大量的研究。文献[9]将辅助服务模型和经济运行模型相结合，构建了Stackelberg主从博弈模型，并证明了博弈过程中该模型存在唯一的均衡解，最后通过双层分布式算法对该模型进行求解。文献[10]提出了基于Stackelberg主从博弈模型的区域综合能源系统分布式协同优化调度方案，将综合能源系统的交易方式和数学模型嵌入到博弈理论的框架下，建立了一主多从的非合作博弈，使得系统和用户消费剩余都得到大幅提升。文献[11]在计及需求响应的条件下，构建了能源集线器不可转移支付的双层优化联盟博弈模型，提高了系统能源集线器之间相互协作的经济性和灵活性。

现有研究成果中对于博弈模型已经进行了众多探索，但是对于博弈模型中用户在追求最大获取效能时满意度要求方面鲜有研究。本文在已有Stackelberg博弈的基础上，建立了能源站收益模型和用户获能满意度模型，将能源站作为决策者，用户作为反应者，建立Stackelberg主从博弈模型。在考虑用户获取最大综合效能和系统获取最大净收益的同时，考虑用户满意度对调度进行优化，并通过天牛须分布式算法对模型进行求解。最后通过算例验证所提模型和算法的有效性。

2 综合能源系统博弈框架

本文所研究的综合能源系统是由K个分布式能源站( $T = {1, 2, \dots, K}$ )和N个用户小区( $V = {1, 2, \dots, N}$ )构成，其中各个分布式能源站的电价和热价由市场统一决定。作为能源供应方的能源站追求其自身最大收益，而用户根据自身的电热需求以及自身满意度追求最优效能，构成相互竞争的博弈关系。

2.1 分布式能源站

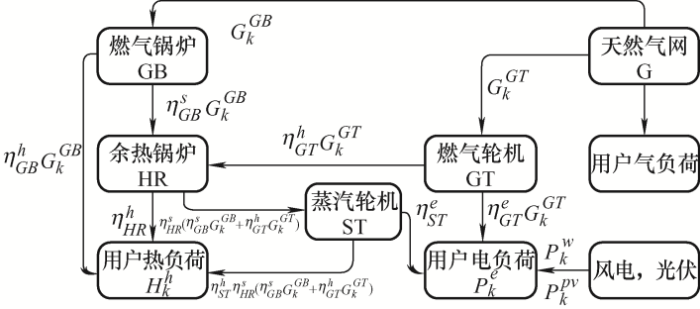
本文所研究的综合能源系统是由分布式能源站组成，其结构示意图如图1所示。其中，天然气网、风力发电和光伏发电作为能量来源，由风力发电、光伏发电、燃气轮机(GT)和蒸汽轮机(ST)为用户提供电能，实现新能源的就地消纳；由燃气锅炉(GB)、余热锅炉(HR)和蒸汽轮机为用户提供热能，余热锅炉的主要热量来源为燃气锅炉和燃气轮机的剩余热量，实现了能量的高效利用。天然气负荷由天然气网直接承担，故本文不考虑其调度。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 分布式能源站示意图

由图1可得系统供能方程为

(1)

\{\begin{matrix} \begin{array}{l} P_{k}^{e} = η_{G T}^{e} G_{k}^{G T} + η_{S T}^{e} η_{H R}^{s} (η_{G B}^{s} G_{k}^{G B} + η_{G T}^{h} G_{k}^{G T}) + \\ P_{k}^{w} + P_{k}^{p v} \end{array} \\ \begin{array}{l} H_{k}^{h} = η_{G B}^{h} G_{k}^{G B} + η_{H R}^{h} (η_{G B}^{s} G_{k}^{G B} + η_{G T}^{h} G_{k}^{G T}) + \\ η_{S T}^{h} η_{H R}^{s} (η_{G B}^{s} G_{k}^{G B} + η_{G T}^{h} G_{k}^{G T}) \end{array} \end{matrix}

式中， $P_{k}^{e}$ 、 $H_{k}^{h}$ 、 $P_{k}^{w}$ 、 $P_{k}^{p v}$ 分别为第k个分布式能源站电功率产量、热功率产量、风电出力、光伏出力； $η_{G T}^{e}$ 、 $η_{S T}^{e}$ 分别为燃气轮机、蒸汽轮机发电效率； $η_{G T}^{h}$ 、 $η_{G B}^{h}$ 、 $η_{H R}^{h}$ 、 $η_{S T}^{h}$ 分别为燃气轮机、燃气锅炉、余热锅炉、蒸汽轮机发热效率； $η_{G B}^{s}$ 、 $η_{H R}^{s}$ 分别为燃气锅炉余热传递效率和余热锅炉蒸汽传递效率； $G_{k}^{G T}$ 、 $G_{k}^{G B}$ 分别为第k个分布式能源站燃气轮机和燃气锅炉消耗天然气功率。为简化计算，本文假设所构建的分布式能源站所有相同设备能量传递效率均相同。

2.2 目标函数

本文所研究的综合能源系统是将分布式能源站看成决策者决定能源出力，将用户看成反应者对能源出力做出反应。博弈过程中分布式能源站最大净收益、用户获得最大综合效能和用户满意度三者构成多目标模型。

(1) 分布式能源站最大净收益。分布能源站作为决策者，会根据给出的电、热价格确定其电、热的产值，作为盈利机构会制定合理处理方案，获得盈利。获得净收益为所获得盈利与温室气体处理成本之差。决策者净收益目标函数为

(2)

L_{k}^{D E S} = f_{1} - f_{2}

式中， $f_{1}$ 为分布式能源站所获盈利； $f_{2}$ 为气体处理成本。

分布式能源站获得盈利 $f_{1}$ 为

(3)

\begin{matrix} f_{1} = \sum_{k = 1}^{T} \{p^{e} P_{k}^{e} + p^{h} H_{k}^{h} - [c_{k} (G_{k}^{G T} + G_{k}^{G B}) + \\ f_{k} + c_{w p} P_{k}^{c u t}]\} \end{matrix}

式中， $p^{e}$ 、 $p^{h}$ 分别为单位电价和单位热价； $c_{k}$ 、 $f_{k}$ 分别为能量转换设备的成本系数和系统固定成本； $c_{w p}$ 、 $P_{k}^{c u t}$ 分别为弃风、弃光惩罚系数和弃风、弃光量。

弃风量 $P_{k}^{c u t}$ 为

(4)$P_{k}^{c u t}=\left\{\begin{array}{ll} 0 & P_{k}^{w}+P_{k}^{p v} \leqslant P_{k}^{e} \\ P_{k}^{w}+P_{k}^{p v}-P_{k}^{e} & P_{k}^{w}+P_{k}^{p v}>P_{k}^{e} \end{array}\right.$

气体处理成本 $f_{2}$ 为

(5)

\begin{array}{l} f_{2} = \sum_{k = 1}^{T} (c_{p}^{G T} G_{k}^{G T} + c_{p}^{G B} G_{k}^{G B} + c_{p}^{H R} G_{k}^{H R}) = \\ \sum_{k = 1}^{T} [(c_{p}^{G T} + c_{p}^{H R} η_{G B}^{s}) G_{k}^{G T} + (c_{p}^{G B} + c_{p}^{H R} η_{G T}^{h}) G_{k}^{G B}] \end{array}

式中， $c_{p}^{G T}$ 、 $c_{p}^{G B}$ 、 $c_{p}^{H R}$ 分别为燃气轮机、燃气锅炉、余热锅炉处理单位气体成本系数。

(2) 用户获取最大综合效能。用户作为反应者，会根据自身对电能、热能的需求和能源价格对所需能量做出合理调整，使获得综合效能最高。用户在购电过程中通过获取综合效用与购能成本之差作为用户的最大获取综合效能，因此作为反应者的目标函数为

(6)

\max W_{n} = f_{3} - (p^{e} d_{n}^{e} + p^{h} d_{n}^{h}) \begin{matrix} \forall n \end{matrix} \in V

式中， $W_{n}$ 为用户获取最大综合效能函数； $f_{3}$ 为用户获得效能。

本文采用的效能函数^[12]为

(7)

f_{3} = [b_{n}^{e} d_{n}^{e} - \frac{a_{n}^{e}}{2} {(d_{n}^{e})}^{2}] + [b_{n}^{h} d_{n}^{e} - \frac{a_{n}^{h}}{2} {(d_{n}^{h})}^{2}]

式中， $a_{n}^{e}$ 、 $b_{n}^{e}$ 、 $a_{n}^{h}$ 、 $b_{n}^{h}$ 为电能、热能的需求系数，反映用户对能源的需求意愿； $d_{n}^{e}$ 、 $d_{n}^{h}$ 为用户电需求量和热需求量。

(3) 用户满意度。用户根据电价调整需求量，会一定程度上降低其满意度，通过牺牲满意度来获取效能最大，其满意度函数为

(8)

W_{m}^{k} = 1 - \frac{\sum_{t = 1}^{24} (|P_{l o a d, t}^{e} - d_{n, t}^{e}| + |P_{l o a d, t}^{h} - d_{n, t}^{h}|)}{\sum_{t = 1}^{24} (P_{l o a d, t}^{e} + P_{l o a d, t}^{h})}

式中， $W_{m}^{k}$ 为用户满意度函数； $P_{l o a d, t}^{e}$ 、 $P_{l o a d, t}^{h}$ 分别为不参加博弈时t时用户电和热负荷量。

由式(8)可知，当用户需求量 $d_{n}^{e}$ 、 $d_{n}^{h}$ 越接近电、热负荷量 $P_{l o a d, t}^{e}$ 、 $P_{l o a d, t}^{h}$ 时，用户满意度越高，用户幸福指数越高。

2.3 约束条件

分布式能源站所产生的电、热量与用户所需求电、热量相等，其等式约束为

(9)

\{\begin{matrix} \sum_{k = 1}^{K} P_{k}^{e} = (1 + α^{e}) \sum_{n = 1}^{N} d_{n}^{e} \\ \sum_{k = 1}^{K} H_{k}^{h} = (1 + α^{h}) \sum_{n = 1}^{N} d_{n}^{h} \end{matrix}

式中， $α^{e}$ 、 $α^{h}$ 分别为电、热传输网损系数。

电价、热价、电需求量、热需求量应始终为正值以及各设备应满足出力上下限约束，其不等式约束为

(10)

\{\begin{matrix} p^{e} \geq 0 \\ p^{h} \geq 0 \\ \begin{matrix} d_{n}^{e} \geq 0 \\ d_{n}^{h} \geq 0 \end{matrix} \\ 0 \leq G_{k}^{G T} \leq G_{\max}^{G T} \\ \begin{matrix} 0 \leq G_{k}^{G B} \leq G_{\max}^{G B} \\ 0 \leq G_{k}^{HR} \leq G_{\max}^{HR} \end{matrix} \end{matrix}

式中， $G_{\max}^{G T}$ 、 $G_{\max}^{G B}$ 、 $G_{\max}^{HR}$ 分别为燃气轮机、燃气锅炉和余热锅炉出力上限。

3 Stackelberg博弈

根据分布式能源站与用户之间的相互竞争关系建立主从博弈模型。两层主从博弈模型最初由Stackelberg以微分的形式提出并研究，因此又称为Stackelberg博弈^[13-14]。因为在竞争的过程中分布式能源站与用户之间没有信息的交流，因此属于非合作Stackelberg主从博弈。其中能源站作为决策者，用户作为反应者。博弈过程中，上层决策者以获得自身最大净收益为目标制定各能源价格，下层反应者会综合考虑获取最大综合效能以及自身满意度来制定合适的能量需求方案。

当所有反应者对决策者策略做出最优响应并且决策者接受了这个响应时，博弈达到Stackelberg均衡^[15⇓-17]。若要实现能源交易过程中的Stackelberg均衡，需要满足以下条件

(11)

\{\begin{matrix} L_{k}^{D E S} (ρ^{*}, δ^{*}) \geq L_{k}^{D E S} (ρ_{k}, ρ_{- k}^{*}, δ^{*}) \\ W_{n} (ρ^{*}, δ^{*}) \geq W_{n} (ρ^{*}, δ_{n}, δ_{- n}^{*}) \\ \forall ρ_{k} \in S_{k} \\ \forall k \in T \\ \forall δ_{n} \in s_{n} \\ \forall n \in V \end{matrix}

式中， $ρ^{*}$ 为所有能源站的均衡策略向量； $δ^{*}$ 表示所有用户的最优响应策略向量； $ρ_{- k}^{*}$ 、 $δ_{- n}^{*}$ 分别为除了能源站、用户以外的其他均衡策略； $ρ_{k}$ 为能源站策略向量， $δ_{n}$ 为用户策略向量； $S_{k}$ 、 $s_{n}$ 分别为分布式能源站和用户策略集。每一个参与博弈的策略集在达到Stackelberg均衡时，都无法通过单独改变自身策略实现更大程度的优化。

3.1 博弈的求解过程

本文采用天牛须分布式算法对博弈过程进行求解。对于上层决策者，将通过莱维飞行策略下的天牛须算法对燃气轮机和燃气锅炉消耗天然气 $G_{k}^{G T}$ 、 $G_{k}^{G B}$ 进行寻优求解，再将p^e、p^h、 $G_{k}^{G T}$ 、 $G_{k}^{G B}$ 代入式(1)可得出分布式能源站电能和热能出力方案。

分析式(6)、(7)可以看出，用户目标函数要严格满足凸函数，因此对式(7)求关于 $d_{n}^{e}$ 、 $d_{n}^{h}$ 的一阶偏导，可得出当函数取最大值时 $d_{n}^{e}$ 、 $d_{n}^{h}$ 应满足

(12)

\{\begin{matrix} d_{n}^{e} = \frac{b_{n}^{e}}{a_{n}^{e}} - \frac{1}{a_{n}^{e}} p^{e} \begin{matrix} \forall n \in V \end{matrix} \\ d_{n}^{h} = \frac{b_{n}^{h}}{a_{n}^{h}} - \frac{1}{a_{n}^{h}} p^{h} \begin{matrix} \forall n \in V \end{matrix} \end{matrix}

为了保证用户需求量非负，单位电价和单位热价应满足 $p^{e} \leq \min (b_{n}^{e})$ 和 $p^{h} \leq \min (b_{n}^{h})$ 。

通过式(6)、式(12)分析可知，用户会根据能源价格制定合适的能源需求方案 $d_{n}^{e}$ 、 $d_{n}^{h}$ 。此时，判断能源站出力和用户用能方案的能量是否吻合，若吻合则该方案就是博弈所取得的最优方案；反之则根据式(13)对价格进行调整。

(13)

\{\begin{matrix} p_{i + 1}^{e} = p_{i}^{e} + τ_{i} [(1 + α^{e}) \sum_{n = 1}^{N} d_{n, i}^{e}^{'} - \sum_{k = 1}^{K} P_{k, i}^{e}] \\ p_{i + 1}^{h} = p_{i}^{h} + τ_{i} [(1 + α^{h}) \sum_{n = 1}^{N} d_{n, i}^{h}^{'} - \sum_{k = 1}^{K} P_{k, i}^{h}] \end{matrix}

式中，i为迭代次数； $τ_{i}$ 为单位电价和单位热价的调整系数，为加快调整速度提高收敛精度，将调整系数设置为

(14)

τ_{i} = 0.1 - \frac{\lg (1 + i)}{10 n}

其中， $d_{n, i}^{e}^{'}$ 、 $d_{n, i}^{h}^{'}$ 分别为

(15)

\{\begin{matrix} d_{n, i}^{e}^{'} = ω_{1} P_{l o a d}^{e} + ω_{2} d_{n, i}^{e} \\ d_{n, i}^{h}^{'} = ω_{1} P_{l o a d}^{h} + ω_{2} d_{n, i}^{h} \end{matrix}

式中， $ω_{1}$ 、 $ω_{2}$ 分别为用户电热负荷和实际需求量权重系数，直接影响用户满意度； $ω_{1} + ω_{2} = 1$ 。

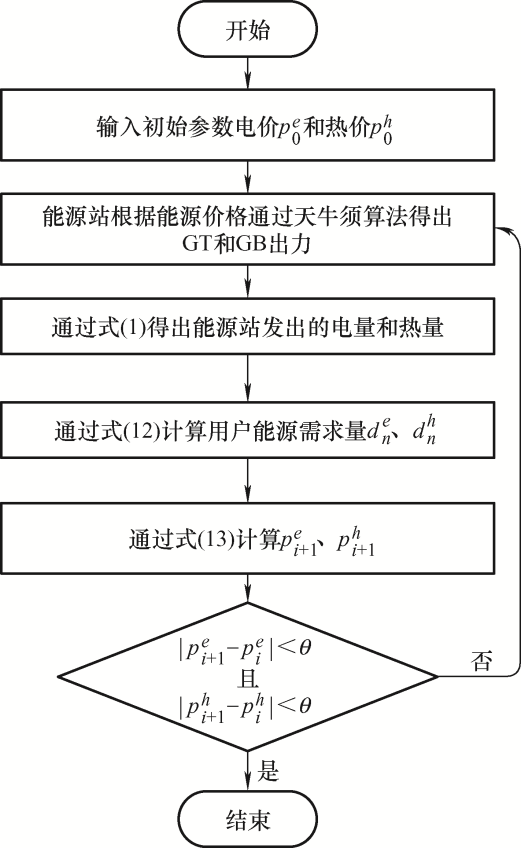
3.2 求解流程图

在本文中由于博弈双方没有内部信息之间的交流，故采取天牛须分布式算法，根据给定电价双方单独计算电、热出力和电、热需求量，计算步骤如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 计算流程图

4 算例分析

考虑到一个分布式能源站将同时为多个用户小区提供能源，为方便计算将分布式能源站和用户的比例设置为1∶2.5，即K取4，N取10组成的综合能源系统，通过算例仿真来分析Stackelberg模型和本文所提分布式算法的可行性。

本文所采取的算例中分布式能源站各设备系数 $η_{G T}^{e}$ 、 $η_{S T}^{e}$ 、 $η_{G T}^{h}$ 、 $η_{G B}^{h}$ 、 $η_{H R}^{h}$ 、 $η_{S T}^{h}$ 、 $η_{G B}^{s}$ 和 $η_{H R}^{s}$ 分别设置为0.35、0.42、0.5、0.7、0.56、0.38、0.1和0.18；各设备处理气体成本系数 $c_{p}^{G T}$ 、 $c_{p}^{G B}$ 、 $c_{p}^{H R}$ 分别取0.34、0.28、0.4。本算例各分布式能源站固定成本参数 $c_{k}$ 、 $f_{k}$ 取18和10；网络损耗系数 $α^{e}$ 、 $α^{h}$ 取0.04和0.06；弃风惩罚系数 $c_{w p}$ 取0.25；误差系数 $θ$ 取10^-6。

为区分用户用能峰谷差异，用户能量需求系数设置如表1所示。

表1 用户电、热需求系数表

	时间		a	b
电	峰	18:00—23:00	10	120
	谷	1:00—5:00	10	80
	平	23:00—1:00	8	80
	平	5:00—18:00	8	80
热	峰	0:00—8:00	5	100
	谷	13:00—20:00	10	120
	平	8:00—13:00	6	90
	平	20:00—24:00	6	90

新窗口打开| 下载CSV

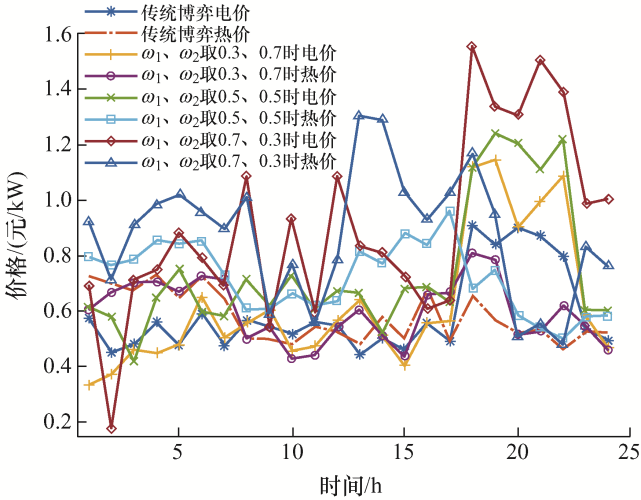
(1) 在未接入新能源情况下，将传统博弈模型与多目标博弈模型相比较，通过调整多目标博弈模型中的权重系数 $ω_{1}$ 、 $ω_{2}$ ，对三个目标函数关系进行分析，结果如表2所示。博弈过程中所对应的电价变化如图3所示。

表2 三个目标函数变化表

博弈模型	$ω_{1}$	$ω_{2}$	净收益 $L^{D E S}$	目标函数 $W_{n}$	用户满意度 $W_{m}$
传统博弈模型	—	—	5 539.9	135.09	0.77
多目标博弈模型	0.3	0.7	7 091.1	121.91	0.82
	0.5	0. 5	8 595.3	107.91	0.85
	0.7	0.3	10 643	86.78	0.90

新窗口打开| 下载CSV

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 传统博弈与多目标博弈能源价格曲线

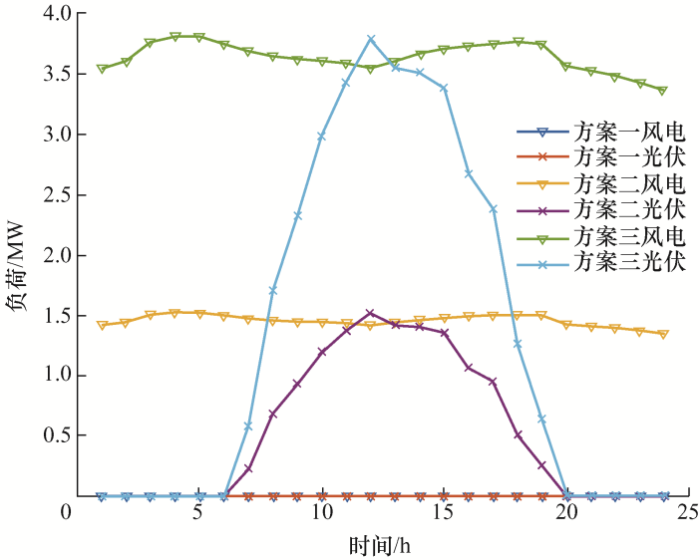
由表2可得，传统博弈模型未考虑用户满意度，用户在与系统的博弈过程中只追求最大获能，忽略用户体验，此时用户满意度较低为0.77，系统获得净收益为5 539.9，用户最大综合获能为135.09；本文在传统博弈模型的基础上考虑用户满意度，当权重系数 $ω_{1}$ 、 $ω_{2}$ 设置为0.3、0.7时，用户满意度得到改善从0.77增加到0.82，系统净收益较传统博弈模型增长28%，而用户最大获能降低9.8%，用户通过牺牲获取最大效能来提高自身满意度，从而使系统净收益提高；结合图3分析可知，相较于传统博弈模型，多目标博弈模型可以通过调整权重系数 $ω_{1}$ 、 $ω_{2}$ 来影响用户满意度，随着需求权重系数 $ω_{1}$ 不断减小， $ω_{2}$ 不断增大，电价曲线向上平移，系统净收益不断增加，用户最大获能不断降低。用户通过牺牲获取综合效能来换取满意度的提升，从而影响系统净收益。

(2) 在上述研究基础上，研究不同程度新能源接入背景下对博弈的影响。在需求量系数 $ω_{1}$ 、 $ω_{2}$ 的取值分别为0.3、0.7时，设计以下几种不同的方案。

方案一：无风电、光伏接入时运行系统。

方案二：40%渗透率风电、光伏接入时运行系统。

方案三：100%渗透率风电、光伏接入时运行系统。

风电与光伏出力如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 三种方案下风电、光伏出力

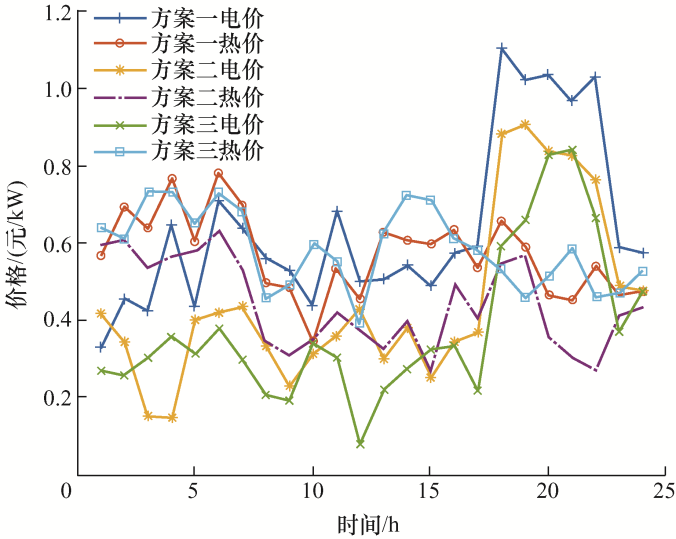
通过仿真可得三种方案下，博弈获取的电、热价格如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 三种方案下博弈得到的电价、热价

由图5分析可知，方案一用户满意度为0.82，在18:00—22:00(用电高峰期)电价最高为1.10元/kW，在1:00—4:00(用电低谷期)电价最低为0.42元/kW，5:00—18:00、21:00—24:00(用电平时期)电价为0.54元/kW，用户最大获能为121.91，系统净收益为7 091.1。由此可知在博弈的过程中分布式能源站会通过提高电价的方式，来削减峰时用户对电能的需求量，以实现削峰填谷的作用；方案二和方案三的满意度分别为0.83、0.85，用户获取最大剩余效能分别为124.98、129.94，系统净收益分别为8 006.3、 9 259.8，其用户电价相对于方案一整体往下平移，是因为有风电和光伏的接入使得分布式能源系统生产电能成本降低，使得电价降低，用户满意度上升，用户获取最大剩余效能和系统净收益增大。在 10:00—15:00方案二、方案三电价出现明显凹陷，此时对应于光伏出力的峰值，大量清洁电能的接入使得电价再次下降，改变了曲线原来的趋势。

观察热价变化曲线，方案一在0:00—8:00(用热高峰期)热价最高为0.78，在13:00—20:00(用热低谷期)热价最低为0.45，在8:00—13:00、20:00—24:00(用热平时期)热价为0.59。由此可知在博弈的过程中分布式能源站会通过提高热价的方式，来削减峰时用户对热能的需求量，以实现对热能的削峰填谷的作用。

5 结论

本文在新能源接入背景下，计及各能量转换设备自身约束的条件，在传统博弈模型的基础上增加对用户满意度的考虑，建立了能源站收益模型和用户获能满意度模型，将能源站作为决策者，用户作为反应者建立Stackelberg主从博弈模型。并验证了所构建模型的有效性，和所提天牛须分布式算法在博弈过程中解决多目标问题的可行性。

算例结果表明：① 相较于传统博弈模型，本文所建立的多目标博弈模型更加注重用户体验，通过对调度的优化，提高用户满意度；② 算例仿真证明，新能源的接入会降低电能成本，从而降低系统电价，提高用户满意度，同时增大用户最大获得效能，提高分布式能源站的净收益；③ 博弈模型在综合能源系统起到了削峰填谷的作用。

本文所提的Stackelberg博弈模型和天牛须分布式算法有助于在保证用户生活质量的前提下，实现交易双方价格策略的制定。但是本文未考虑分布式能源站接入电网时与电网进行信息互换，后期研究中会将电网与分布式能源站相结合探讨更加复杂的博弈问题。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

贾宏杰, 穆云飞, 余晓丹.

对我国综合能源系统发展的思考

[J]. 电力建设, 2015, 36(1):16-25.

DOI:10.3969/j.issn.1000－7229.2015.01.003 [本文引用: 1]

建设完善的社会综合能源系统是低碳经济背景下解决我国社会供能系统安全性低、自愈能力差、设备利用率低下等一系列问题的一种可能解决方案。文章首先给出综合能源系统的基本概念与主要特征，结合世界各国综合能源系统建设的经验与我国能源资源现状，分别从国家、区域和终端这3个层面探讨了我国未来综合能源系统发展中面临的一些问题，并给出了相应的建议。

JIA

Hongjie

, MU

Yunfei

, YU

Xiaodan

Thought about the integrated energy system in China

[J]. Electric Power Construction, 2015, 36(1):16-25.

DOI:10.3969/j.issn.1000－7229.2015.01.003 [本文引用: 1]

<p>Integrated energy system （IES） can provide an effective solution to solve the low security, insufficient self-healing capability, and low utilization rate of energy equipment problems under the background of low-carbon economy, which has a significant potential to support the optimization and adjustment of China’s energy structure. Firstly, the basic concept of IES and its main features are given in detail. Then, considering the valuable IES construction experience around the world and the current status of China’s energy resources, some key issues about China’s IES from the prospective of national level, regional level, and terminal level are discussed. Also, the corresponding suggestions are proposed.</p>

[2]

艾芊, 郝然.

多能互补、集成优化能源系统关键技术及挑战

[J]. 电力系统自动化, 2018, 42(4):2-10,46.