1 引言
电力设备在绝缘逐渐老化过程中会不断发生瞬时性击穿,产生扰动波形,这一系列扰动被称为早期故障。早期故障具有重复性、随机性和瞬时性的特点,前期研究将其刻画成物理本质为电弧故障的瞬时性单相接地[1 ⇓ -3 ] 。早期故障频发使设备的绝缘劣化处遭受进一步损坏,伤害逐渐累积至永久性故障发生,导致停电事故[4 -5 ] 。随着配电网信息化建设,置于站端的扰动波形记录装置能实现早期故障波形的捕获,但同时也记录下大量与其波形特征相似的非早期故障扰动。若能基于扰动波形数据实现对早期故障和其他扰动波形的准确区分,则可以及时感知设备运行状态、指导检修工作安排并消除故障隐患,在一定程度上减少永久性故障导致的停电事故发生[6 ] 。因此,准确识别早期故障对于提高系统供电可靠性具有重要意义。
目前,早期故障识别方法可归纳为基于波形特征[7 ⇓ ⇓ -10 ] 、故障模型[11 ] 和机器学习[12 ⇓ ⇓ -15 ] 三大类。其中,基于波形特征的早期故障识别方法主要利用扰动波形中各电气量的相关变化规律,如文献[7 ]基于电压和电流的各次谐波含量及畸变率对早期故障进行识别;文献[8 ]则将负序电流及故障电流分量的变化规律作为扰动识别判据;文献[9 -10 ]都利用了卡尔曼滤波器计算电压基波分量,并将其与实测值的偏差作为早期故障扰动的特征量。而基于故障模型的早期故障识别方法主要利用早期故障作为电弧故障的物理本质,建立以电弧模型为基础的早期故障仿真模型,通常以扰动波形的电压畸变程度及故障的自清除特性来进行早期故障识别[11 ] 。上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱。
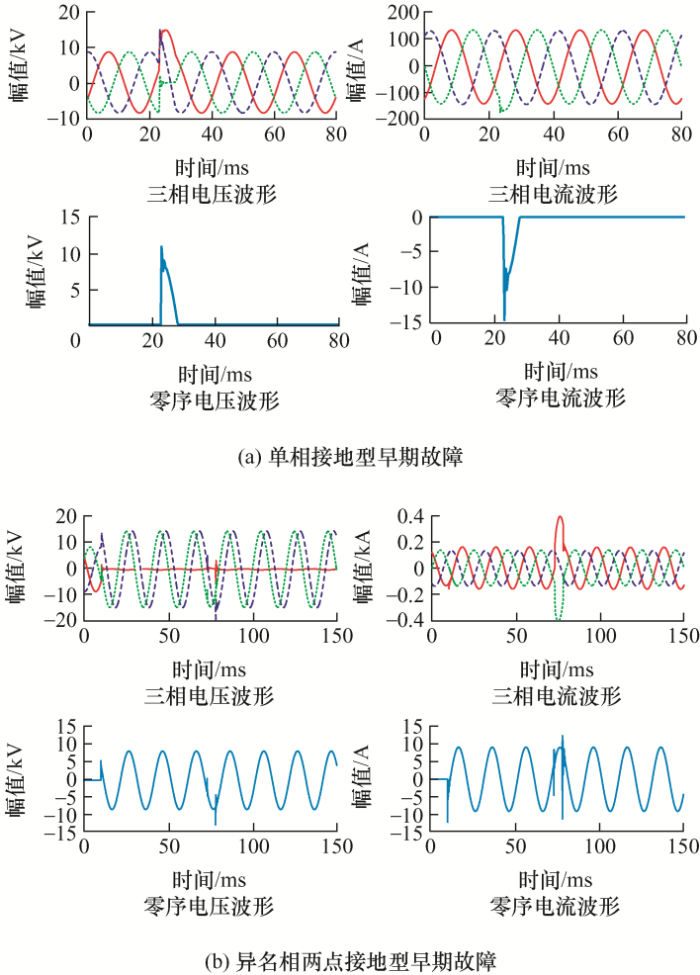
基于机器学习的早期故障识别方法通常依赖于信号分析算法对扰动波形进行处理,获取大量时域或频域的特征信息,在此基础上利用庞大的特征数据对分类器进行训练以构建相应的故障识别模型。例如文献[12 ]利用小波变换算法将扰动波形拆分为不同基元,并基于类人概念学习采用贝叶斯概率学习法挖掘波形基元特征与扰动类型的关联性;文献[13 -14 ]分别采用了小波变换和S变换算法获取大量的扰动波形特征信息,随后将其输入神经网络进行故障模型的训练;文献[15 ]基于快速傅里叶算法将每个窗口波形信号对应频域信息表示为相应字母,因此不同类型扰动波形的字母组合存在较大差异。此类方法基于数据驱动,鲁棒性强但对于扰动波形数据样本的依赖性大,且其特征数据集的维度通常较为庞大。另外,我国中压配电网主要采用小电流接地的方式[16 ] ,早期故障在该类系统中的表现形式分为单相接地型和异名相两点接地型[17 ] ,如图1 所示,而目前的早期故障识别方法主要针对单相接地型。文献[18 ]结合早期故障特性及其扰动波形变化规律,提出了基于复合判据的小电流接地系统早期故障识别方法,能够准确识别单相接地型和异名相两点接地型早期故障,但该算法易受过渡电阻影响,且涉及阈值较多、要求较高,在实际应用中存在一定的局限性。因此,如何解决基于知识驱动方法的适应性不足和基于数据驱动方法特征数据量大的问题,以及充分考虑小电流接地系统早期故障表现形式的多样性,是当前针对我国中压配电网早期故障识别方法研究需要关注的重点。
图1
为解决上述问题,本文提出一种基于最小二乘支持向量机(Least squares support vector machine,LS-SVM)的小电流接地系统早期故障识别方法。在扰动特征提取阶段,同时计及了扰动波形的物理特性和统计特性,充分利用扰动数据特征,并采用最大相关最小冗余方法(Maximum relevance and minimum redundancy,mRMR)进行数据降维并保留强相关特征,构建最优扰动特征集,并基于粒子群算法(Particle swarm optimization,PSO)优化支持向量机的关键参数。经过仿真数据验证和与几种传统识别方法的对比,证明了所提方法的有效性和更高的准确率。
2 扰动特征提取及优化
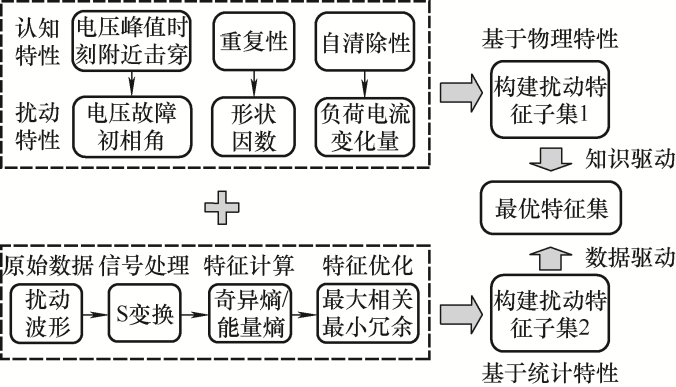
早期故障准确识别的关键在于构建适合的扰动特征集,以此实现早期故障与其他非早期故障波形的可靠区分。考虑到早期故障作为典型小样本事件,具有随机性,实现早期故障与非早期故障波形分类的核心问题在于对扰动特征量的降维选择,以避免数据维数灾难,提高分类模型的适应性。因此,本文分别基于扰动的物理特性和统计特性提取浅层特征集,并进一步采用mRMR法构建最优特征集,在尽量保留扰动强相关特征的同时降低数据维度。最优扰动特征集的构建及其所包含特征如图2 所示。
图2
2.1 初始扰动特征集提取
2.1.1 基于物理特性的特征提取
经前期研究成果可知,早期故障通常发生在电压峰值时刻附近,这是由于此时电压幅值较高而易导致绝缘薄弱点发生击穿。另外,早期故障具有瞬时性和自清除性,在扰动前后其负荷电流不发生改变。基于早期故障物理特性,将电压故障初相角φ U 、负荷电流变化量ΔI load 及故障相电压和电流的波形形状因数F U 和F I 作为扰动特征子集1。其中,形状因数(Form factor)可用来表征扰动波形的实际形状的信息(如波形幅值的突变),因此本文采用形状因数表征早期故障发生时的故障相电压和电流幅值变化程度,故障相电压波形的形状因数F U 的表达式如下所示
(1) F U = U rms U mean = max 1 N half ∑ m = k 1 m + N hal f U 2 ( m ) 1 N d ∑ k 1 k 2 | U ( m ) |
式中,U rms 和U mean 分别表示在扰动期间电压有效值的最大值和平均值;N d 表示扰动期间的总采样点数;N half 为信号的半周期采样点总数;k 1 和k 2 分别表示扰动起止时刻对应的采样点序列数;U 为电压采样信号瞬时值;m 表示采样点序列(m = k 1 , k 1 +1,…, k 2 )。故障相电流的波形形状因数F I 同理可得。另外,若故障相不只一相,则以涉及相别对应形状因数的平均值为最终的特征量。
由此构建的扰动特征子集所含特征量与早期故障的物理特性密切相关。然而,由于故障的不确定性,扰动波形中可能存在大量的隐藏特征信息未被发现,且暂未对其进行基于物理特性的定量刻画,因此基于知识驱动的特征提取思路在当前的研究进展下存在一定局限性。此时,基于数据驱动的特征分析方法则为挖掘隐藏特征信息提供了重要的技术手段。
2.1.2 基于统计特性的特征提取
可变的时频分辨率使S变换具有较好的时频特性和抗噪能力,该类信号处理方式能够提取丰富的时频特征量信息,被广泛应用于电力扰动波形的突变区域分析[19 ] 。对站端扰动电压波形进行S变换并取模处理后,获得一个M ×N 的模时频矩阵S S S A 和奇异熵B 对扰动电压波形各频段上的能量分布特性和信号复杂程度进行刻画[19 ] 。假设模时频矩阵S i 行第j 列个元素表示为sij ,则矩阵S i 和采样时刻j 的条件下的信号能量Eij 可以表示为
(2) E i j = | s i j | 2
在频率为i 条件下对应的所有采样时刻的扰动信号能量之和Ei 以及信号总能量E 可分别表示为
(3) E i = ∑ j = 1 N d E i j
(4) E = ∑ i = 1 M E i
根据矩阵S M 将该矩阵分为低、中、高三个频段,电压扰动波形在不同频段下对应的S变换奇异熵A 可表示为
(5) A f = − ∑ i = M 1 M 2 E i E ln E i E
在计算不同频段的奇异熵时,式(5)中的下标f分别取为low、med、high以对应低、中、高三个频段。在不同频段条件下,M 1 和M 2 分别对应式(6)取值,其中M S 为S M S =采样频率×M ÷采样点数。例如,本文所用扰动数据采样频率为10 kHz,其对应的低、中、高三个频段分别取为0~1 667 Hz、1 668~3 334 Hz、3 335~5 000 Hz。
(6) 低 频 段 : M 1 = 1 M 2 = M S 3 中 频 段 : M 1 = M S 3 + 1 M 2 = 2 M S 3 高 频 段 : M 1 = 2 M S 3 + 1 M 2 = M S
假设低频段的模时频矩阵S low 为一个M low ×N low 矩阵,由奇异值分解理论可知,必然存在一个M low ×r 的矩阵D r ×N low 的矩阵C r ×r 的对角线矩阵R S low 可被分解为
(7) S low = D R C T
对角线矩阵R ri (ri = 1, 2, 3,…, r )为非负数且按降序排列,这些元素即为S low 的奇异值,可表示对应采样时刻及频率条件下的信息量的大小。因此将模时频矩阵低频段的奇异熵B low 表示为
(8) B low = − ∑ i = 1 r ( r i ∑ j = 1 r r j ) ln ( r i ∑ j = 1 r r j )
同理,根据式(8)可分别计算出中频段模时频矩阵S med 和高频段模时频矩阵S high 对应的奇异熵B med 和B high 。
电压扰动波形低、中、高频段对应的S变换奇异熵和S变换能量熵共同组成基于统计特性的扰动波形特征子集2。
2.2 最优扰动特征集构建
基于统计特性构建的扰动波形特征子集2,表征了扰动信号在不同频段上的能量分布情况以及在时频空间中能量分布的复杂程度[19 ] 。对模时频矩阵S
最大相关最小冗余法的核心思想是从已知的特征数据集中寻找与其目标类别有最大相关性且相互之间具有最小冗余性的特征子集,评价标签类别与特征之间的相关性[20 -21 ] 。最大相关最小冗余法能够将扰动特征子集2中具备最大分类能力的最优特征量保留,并将子集中所含的高冗余和不相关信息降低至最小程度,深度挖掘与目标标签相关联的特征信息,提高分类能力[22 ] 。
设两个随机变量a 和b 的概率密度函数p (a )、p (b )和p (a , b ),则可将这两个变量之间的互信息表示为
(9) I ( a , b ) = ∬ p ( a , b ) lg p ( a , b ) p ( a ) p ( b ) d a d b
(10) max D ( X , Y ) = 1 | X | ∑ x i ∈ X I ( x i , Y )
(11) min R ( X ) = 1 | X | 2 ∑ x i , x j ∈ X I ( x i , x j )
式中,|X X Y y 1 , y 2 , y 3 ,…, yn }为类别标签;xi 和xj 分别表示特征集X i 和第j 个特征。根据式(9)可得,两个特征量xi 和xj 之间的互信息为I (xi , xj ),特征量xi 与其对应类别之间的互信息为I (xi ,Y
(12) max ϕ ( D , R ) ϕ = D ( X , Y ) R ( X )
在实际应用场景中,通常采用增量搜索法寻找近似最优特征[23 ] 。特征集X v -1个特征量被确定,该部分特征量组成子集X v -1 ,此时最大相关最小冗余法的目的就是从剩余子集{X X v -1 }中选择第v 个特征量,实现式(12)中ϕ ( · )
(13) m R M R v ( x i ) = max x i ∈ X − X v − 1 I ( x i , Y ) 1 | X | ∑ x j ∈ X v − 1 I ( x i , x j )
3 支持向量机及其优化
3.1 最小二乘支持向量机理论
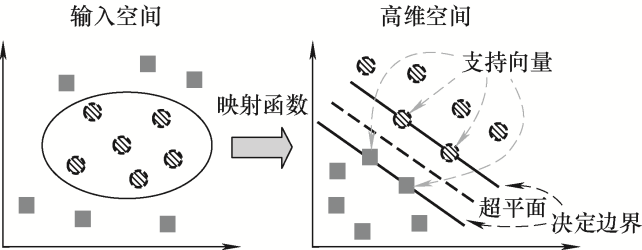
支持向量机(Support vector machine,SVM)以核函数理论为基础,基于映射函数将样本投放至高维空间中以获取最优超平面使样本线性可分,随后又将其反映射回低维空间,实现最终分类[24 ] ,该过程如图3 所示。
图3
LS-SVM则将传统支持向量机模型中的不等式约束改为等式约束[25 ] ,简化了拉格朗日乘子的求解过程,并将误差平方和损失函数作为训练集的经验损失,将二次规划求解问题转化为求解线性方程组,极大提高了计算速度和收敛精度。
对于训练样本集Q ={(xk , yk )|k = 1,2,3,…,n },xk 和yk 分别表示样本及其对应类别,将不同类别样本分类,其目标函数为
(14) min J ( w , ξ ) = 1 2 w T w + γ ∑ k = 1 n ξ k 2
(15) s.t. y k [ w T ψ ( x k ) + h ] − 1 + ξ k = 0
式中,ψ ( x ) w h 为截距;ξ γ 分别为估计偏差和惩罚因子,上式的拉格朗日函数可表示为
(16) L ( w , h , ξ , α ) = J ( w , ξ ) − ∑ k = 1 n α k { w ⋅ ψ ( x ) + h + ξ k − y k }
式中,非负数α w 、 h 、 ξ 、 α
(17) ∂ L ∂ w = 0 ⇒ w = ∑ k = 1 n α k ψ ( x k ) ∂ L ∂ b = 0 ⇒ ∑ k = 1 n α k = 0 ∂ L ∂ ξ k = 0 ⇒ α k = γ ξ k ∂ L ∂ α k = 0 ⇒ w ⋅ ψ ( x ) + h + ξ k + y k = 0
由Mercer条件[26 ] ,存在映射函数ψ ( x ) K ( x , x k )
(18) K ( x k , x l ) = ψ ( x k ) T ψ ( x l )
式中,k , l = 1, 2, 3,…, n 。根据式(16)和式(18)可将基于LS-SVM的分类决策函数表示为
(19) f ( x ) = ∑ k = 1 n α k y i K ( x k , x ) + h = 0
研究表明,支持向量机在径向基函数条件下能够获得较好性能[27 ] ,因此本文选择径向基核函数为LS-SVM的核函数,其表达式如下所示
(20) K ( x , x k ) = exp − | x − x k | 2 σ 2
3.2 基于粒子群算法的参数选择
LS-SVM存在核函数宽度σ 2 和惩罚系数γ 两个变量,当γ 的取值越小,则算法适应性越强,但训练误差也随之增大;而当γ 的取值较大时,算法适应性降低;σ 2 主要影响算法的运行效率[24 ] 。因此需要寻求最优参数组合以满足算法适应性和运算效率的约束。网格搜索法(Grid search)是最常用的参数搜索方法,但该方法的运算时间较长且效率不高[28 ] 。本文选用PSO算法寻找核函数宽度σ 2 和惩罚系数γ 的最优组合。PSO算法将一群初始化粒子经过多次迭代后获取目标函数最优解,在各次迭代过程中,每个粒子基于个体极值pi (该粒子最优解)和全局极值gd (该种群所得最优解)更新自身的位置及速度[29 ] 。第i 个粒子在第k +1次迭代过程中的位置x k + 1 i v k + 1 i
(21) x k + 1 i = x k i + v k + 1 i
(22) v k + 1 i = η v k i + c 1 r 1 ( p i − x k i ) + c 2 r 2 ( g d − x k i )
式中,c 1 和c 2 为学习因子,r 1 和r 2 为[0,1 ]之间的随机值,η 表示加权因子。
根据前期研究经验对PSO算法中初始参数设置情况如表1 所示[30 -31 ] 。
4 早期故障识别算法流程
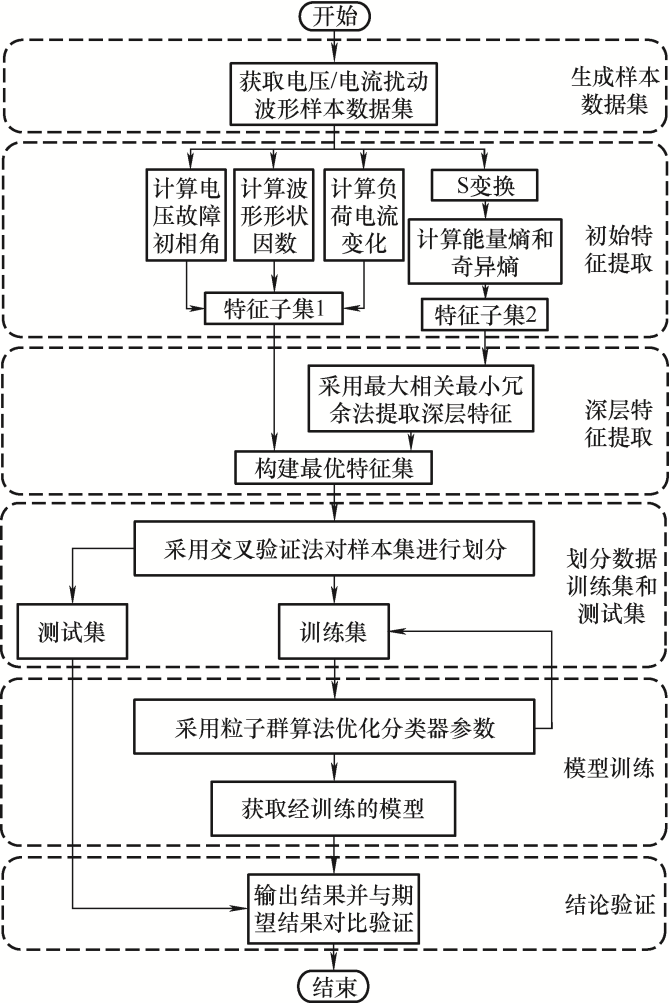
本文提出基于最小二乘支持向量机的适用于小电流接地系统的早期故障识别方法,其具体流程如图4 所示。
图4
(1) 基于PSCAD/EMTDC搭建不同扰动模型,构建配电网早期故障及多种常见扰动波形数据库。
(2) 构建基于物理特性的特征子集1和基于统计特性的特征子集2。其中子集1包含电压故障初相角、故障相电压和电流的波形形状因数以及扰动前后的负荷电流变化量;子集2为电压波形经S变换后不同频段的能量熵和奇异熵。
(3) 利用最大相关最小冗余法对特征子集2进行处理,保留特征集中与扰动波形具有强关联性的特征并消除冗余特征量,降低数据维度,构建最优特征集。
(4) 基于K折交叉验证法划分训练样本集和测试样本集,并算取各样本集对应的最优特征集。
(5) 将训练样本集对应特征集输入LS-SVM以构建扰动分类模型,同时基于粒子群算法进行参数寻优。
(6) 基于训练后得到的分类模型对测试样本集进行验证,利用不同评估指标对算法的性能进行验证,并将该算法与传统扰动识别方法进行对比。
5 算例分析
5.1 样本集构建
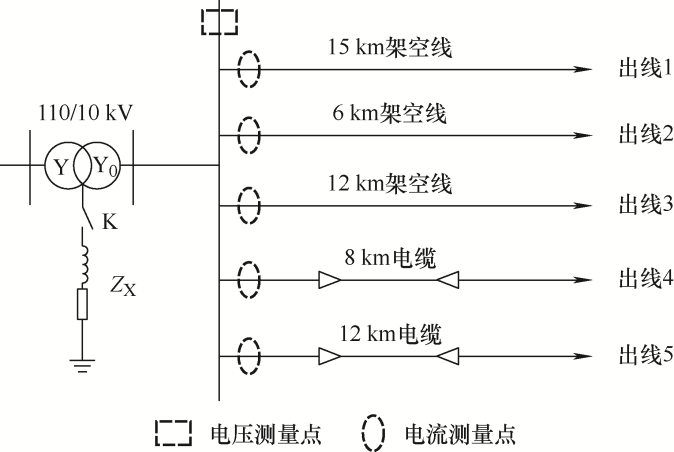
基于PSCAD/EMTDC系统搭建小电流接地配电网仿真模型,其拓扑结构如图5 所示,Z X 表示消弧线圈的阻抗。当开关K闭合时,该系统为中性点经消弧线圈接地,断开时则为中性点不接地。仿真系统中线路模型的参数设置情况如表2 所示。
图5
根据表3 ,采用PSCAD/EMTDC的Multiple Run元件获取不同类型的扰动波形样本数据,包括早期故障、励磁涌流、电容器组投切和恒定阻抗故障的波形样本各360例。
5.2 算法性能分析
5.2.1 算法评价指标
本文基于K折交叉验证法(K-fold cross validation,K-CV)对算法有效性进行分析,即将各类型的扰动波形样本集随机分为K 组,各组的样本数量相等,随后依次使用其中一组作为测试样本集,剩余K -1组则自动归为训练样本集,本文将K 取为5。同时,使用基于混淆矩阵的算法性能度量指标对本文算法性能进行评价[32 ] ,如式(23)~(26)所示。
(1) 算法识别结果和实际类别一致的样本占总样本的比例,即准确率P 1
(23) P 1 = T 1 + T 2 T 1 + T 2 + F 1 + F 2
(2) 算法识别为早期故障且实际类别为早期故障的比例,即精确率P 2
(24) P 2 = T 1 T 1 + F 1
(3) 算法识别且实际类别为早期故障的样本占所有实际类别为早期故障样本的比例,即召回率P 3
(25) P 3 = T 1 T 1 + F 2
(4) 由于实际中需要识别的扰动类型可能存在样本数不平衡的问题,仅靠准确率评估不合理,因此表示精确率P 2 和召回率P 3 的调和均值的指标P 4
(26) 2 P 4 = 1 P 2 + 1 P 3 P 4 = 2 T 1 2 T 1 + P 1 + P 2
式中,T 1 和T 2 分别表示被正确分类的早期故障和非早期故障样本数,F 1 为被误识别为早期故障的非早期故障样本数,F 2 为被误识别为非早期故障的早期故障样本数。
基于K折交叉验证法将各类扰动样本集随机均分为5组并编号,各组依次作为测试样本集,在各次测试中的算法性能评价结果如表4 所示。根据表4 可知,本文所提算法在不同样本集条件下的准确率和精确度均能够高于95%,具备较高的稳健性。
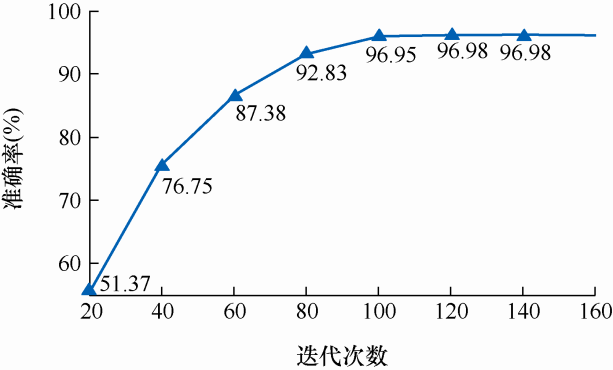
从理论上讲,在寻求最优参数组合时迭代次数越多,最后得到的误差会更小,即识别准确率越高。本文取迭代次数为100,图6 展示了不同迭代次数下算法的识别准确率。可知,当迭代次数小于20次时,准确率较低,而随着迭代次数的增加,准确率上升。当迭代次数达到100时,算法的识别准确率已为96.95%,此后继续增大迭代次数,准确率变化非常小,当迭代次数大于120后,准确率不再上升。
图6
5.2.2 特征及参数选择优点
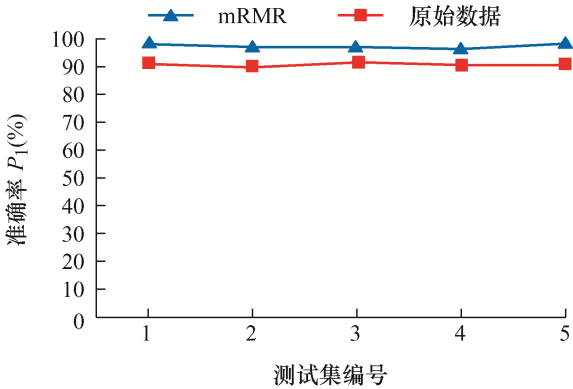
为验证基于mRMR的特征优化法有效性,分别将扰动样本的原始特征集和经mRMR法处理后的最优特征数据集作为分类器的输入。表5 记录了在两种特征集条件下的算法性能评估指标均值及相应的数据处理时间,各次测试结果中的算法性能指标如图7 所示。由表5 和图7 可知,本文采用的扰动最优特征集能够有效降低数据维度并减少冗余特征,减少了数据处理时间且提高了算法准确性。
图7
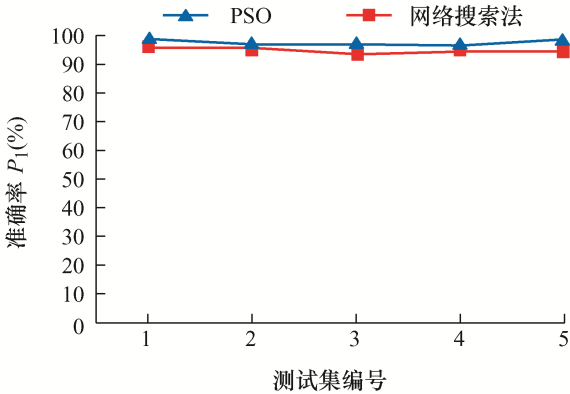
采用PSO算法选择核函数宽度σ 2 和惩罚系数γ 的最优组合,将该方法与常用的网格搜索法进行比较。表6 记录了在两种方法下识别算法的平均评估指标及处理时间。图8 记录了各次测试中上述两种方法对识别算法准确率P 1 的影响。由此可知,在多数的测试案例中,PSO算法与网格搜索法相比具有更高的识别精度且所需的数据处理时间更少。
图8
5.2.3 与其他分类方法比较
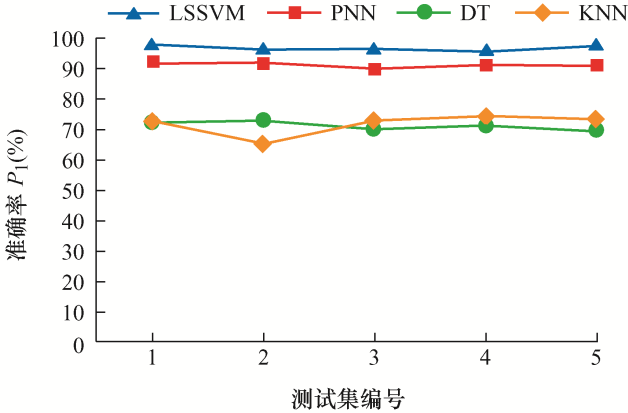
为进一步验证本文算法的有效性,将其与概率神经网络(Probabilistic neural network,PNN)、决策树(Decision tree,DT)和K近邻算法(K-nearest neighbor,KNN)进行比较,识别结果如表7 和图9 所示。
图9
6 结论
本文提出一种基于最小二乘支持向量机的小电流接地系统早期故障识别方法,根据PSCAD/EMTDC系统构建了典型扰动波形数据库,在此基础上对算法性能进行分析并得出以下结论。
(1) 本文结合扰动的物理特性和统计特性提取初始特征集,并采用最大相关最小冗余方法构建最优特征集,消除了冗余信息并降低了数据维度,更加利于分类。
(2) 根据交叉验证法的分析结果,本文算法的准确率和精确度均能够高于95%,具备较高准确性。
(3) 通过与其他传统识别方法的比较,本文所提算法的准确率和运算速度均有所提升。基于仿真波形数据验证了所提早期故障识别算法的有效性,未来需要进一步使用大量实测数据进行验证。
参考文献
View Option
[1]
李宇 , 杨柳林 . 基于卷积神经网络的配电网单相接地故障识别
[J]. 电气工程学报 , 2020 , 15 (3 ):22 -30 .
[本文引用: 2]
LI Yu YANG Liulin Identification of single phase to earth fault in distribution network based on convolution neural network
[J]. Journal of Electrical Engineering , 2020 , 15 (3 ):22 -30 .
[本文引用: 2]
[2]
STRINGER N T KOJOVIC L A Prevention of underground cable splice failures
[J]. IEEE Transactions on Industry Applications , 2001 , 37 (1 ):230 -239 .
DOI:10.1109/28.903154
URL
[本文引用: 1]
[3]
KULKARNI S SANTOSO S SHORT T A Incipient fault location algorithm for underground cables
[J]. IEEE Transactions on Smart Grid , 2014 , 5 (3 ):1165 -1174 .
DOI:10.1109/TSG.2014.2303483
URL
[本文引用: 1]
[4]
SHI S HU Z MA Z et al. Travelling waves-based identification of sub-health condition of feeders in power distribution system
[J]. IET Generation Transmission & Distribution , 2018 , 12 (5 ):1067 -1073 .
DOI:10.1049/gtd2.v12.5
URL
[本文引用: 1]
[5]
JIANG J CHEN R CHEN M et al. Dynamic fault prediction of power transformers based on hidden Markov model of dissolved Gases analysis
[J]. IEEE Transactions on Power Delivery , 2019 , 34 (4 ):1393 -1400 .
DOI:10.1109/TPWRD.61
URL
[本文引用: 1]
[6]
刘亚东 , 丛子涵 , 严英杰 , 等 . 配电设备早期故障检测基本原理、关键技术与发展趋势
[J]. 供用电 , 2020 , 37 (4 ):10 -16 ,32.
[本文引用: 1]
LIU Yadong CONG Zihan YAN Yingjie et al. Basic principles,key technologies and development trends of incipient fault detection for power distribution equipments
[J]. Distribution & Utilization , 2020 , 37 (4 ):10 -16 ,32.
[本文引用: 1]
[7]
戴铭 . 10 kV地下电缆早期故障检测与识别方法探讨 [D]. 成都 : 西南交通大学 , 2015 .
[本文引用: 2]
DAI Ming Discussion methods of incipient fault detection and identification in 10 kV underground cables [D]. Chengdu : Southwest Jiaotong University , 2015 .
[本文引用: 2]
[8]
KASZTENY B VOLOH I JONES C G et al. Detection of incipient faults in underground medium voltage cables
[C]// IEEE Protective Relay Engineers 61st Annual Conference , April 1-3,2008 ,Texas A&M University,College Station,Texas. Piscataway:IEEE, 2008 :349 -366 .
[本文引用: 2]
[9]
SAMET H TAJDINIAN M KHALEGHIAN S et al. A statistical-based criterion for incipient fault detection in underground power cables established on voltage waveform characteristics
[J]. Electric Power Systems Research , 2021 , 197 :107303 .
DOI:10.1016/j.epsr.2021.107303
URL
[本文引用: 2]
[10]
GHANBARI T Kalman filter based incipient fault detection method for underground cables
[J]. IET Generation,Transmission & Distribution , 2015 , 9 (14 ):1988 -1997 .
DOI:10.1049/gtd2.v9.14
URL
[本文引用: 2]
[11]
ZHANG W XIAO X ZHOU K et al. Multi-cycle incipient fault detection and location for medium voltage underground cable
[J]. IEEE Transactions on Power Delivery , 2017 , 32 (3 ):1450 -1459 .
DOI:10.1109/TPWRD.2016.2615886
URL
[本文引用: 2]
[12]
熊思衡 , 刘亚东 , 方健 , 等 . 配电线路早期故障辨识方法
[J]. 高电压技术 , 2020 , 46 (22 ):3970 -3976 .
[本文引用: 2]
XIONG Siheng LIU Yadong FANG Jian et al. Detection method of incipient faults of power system lines
[J]. High Voltage Engineering , 2020 , 46 (22 ):3970 -3976 .
[本文引用: 2]
[13]
汪颖 , 卢宏 , 杨晓梅 , 等 . 堆叠自动编码器与S变换相结合的电缆早期故障识别方法
[J]. 电力自动化设备 , 2018 , 38 (8 ):117 -124 .
[本文引用: 2]
WANG Ying LU Hong YANG Xiaomei et al. Cable incipient fault identification based on stacked autoencoder and S-transform
[J]. Electric Power Automation Equipment , 2018 , 38 (8 ):117 -124 .
[本文引用: 2]
[14]
汪颖 , 孙建风 , 肖先勇 , 等 . 基于优化卷积神经网络的电缆早期故障分类识别
[J]. 电力系统保护与控制 , 2020 , 48 (7 ):10 -18 .
[本文引用: 2]
WANG Ying SUN Jianfeng XIAO Xianyong et al. Cable incipient fault classification and identification based on optimized convolution neural network
[J]. Power System Protection and Control , 2020 , 48 (7 ):10 -18 .
[本文引用: 2]
[15]
WENG Y CUI Q GUO M Transform waveforms into signature vectors for general-purpose incipient fault detection
[J]. IEEE Transactions on Power Delivery , 2022 , 37 (6 ):4559 -4569 .
DOI:10.1109/TPWRD.2022.3151110
URL
[本文引用: 2]
[16]
刘健 , 张小庆 , 张志华 , 等 . 提升小电流接地系统单相接地故障处理能力
[J]. 供用电 , 2021 , 38 (10 ):52 -56 .
[本文引用: 1]
LIU Jian ZHANG Xiaoqing ZHANG Zhihua et al. Solutions to improve the single-phase grounding fault management of neural non-effective grounded systems
[J]. Distribution & Utilization , 2021 , 38 (10 ):52 -56 .
[本文引用: 1]
[17]
楚恬歆 , 张文海 , 瞿科 , 等 . 小电流接地系统接地型早期故障扰动特征分析
[J]. 电力系统保护与控制 , 2021 , 49 (18 ):52 -61 .
[本文引用: 1]
CHU Tianxin ZHANG Wenhai QU Ke et al. Grounded incipient fault analysis in a non-solidly grounding system
[J]. Power System Protection and Control , 2021 , 49 (18 ):52 -61 .
[本文引用: 1]
[18]
楚恬歆 , 张文海 , 瞿科 , 等 . 基于复合判据的小电流接地系统接地型早期故障检测
[J]. 高电压技术 , 2022 , 48 (3 ):1022 -1031 .
[本文引用: 1]
CHU Tianxin ZHANG Wenhai QU Ke et al. The grounded incipient fault detection based on compound criterion in non-solidly grounding system
[J]. High Voltage Engineering , 2022 , 48 (3 ):1022 -1031 .
[本文引用: 1]
[19]
陶维青 , 夏熠 , 陆鼎堃 . S变换熵理论及其在电力系统故障检测中的应用研究
[J]. 合肥工业大学学报 , 2016 , 39 (1 ):40 -45 .
[本文引用: 3]
TAO Weiqing XIA Yi LU Dingkun Study of S-transform entropy theory and its application in fault detection of electric power system
[J]. Journal of Hefei University of Technology , 2016 , 39 (1 ):40 -45 .
[本文引用: 3]
[20]
程玉胜 , 宋帆 , 王一宾 , 等 . 基于专家特征的条件互信息多标记特征选择算法
[J]. 计算机应用 , 2020 , 40 (2 ):503 -509 .
DOI:10.11772/j.issn.1001-9081.2019091626
[本文引用: 1]
特征选择对于分类器的分类精度和泛化性能起重要作用。目前的多标记特征选择算法主要利用最大相关性最小冗余性准则在全部特征集中进行特征选择,没有考虑专家特征,因此多标记特征选择算法的运行时间较长、复杂度较高。实际上,在现实生活中专家依据几个或者多个关键特征就能够直接决定整体的预测方向。如果提取关注这些信息,必将减少特征选择的计算时间,甚至提升分类器性能。基于此,提出一种基于专家特征的条件互信息多标记特征选择算法。首先将专家特征与剩余的特征相联合,再利用条件互信息得出一个与标记集合相关性由强到弱的特征序列,最后通过划分子空间去除冗余性较大的特征。该算法在7个多标记数据集上进行了实验对比,结果表明该算法较其他特征选择算法有一定优势,统计假设检验与稳定性分析进一步证明了所提出算法的有效性和合理性。
CHENG Yusheng SONG Fan WANG Yibin et al. Multi-label feature selection algorithm based on conditional mutual information of expert feature
[J]. Journal of Computer Applications , 2020 , 40 (2 ):503 -509 .
DOI:10.11772/j.issn.1001-9081.2019091626
[本文引用: 1]
Feature selection plays an important role in the classification accuracy and generalization performance of classifiers. The existing multi-label feature selection algorithms mainly use the maximum relevance and minimum redundancy criterion to perform feature selection in all feature sets without considering expert features, therefore, the multi-label feature selection algorithm has the disadvantages of long running time and high complexity. Actually, in real life, experts can directly determine the overall prediction direction based on a few or several key features. Paying attention to and extracting this information will inevitably reduce the calculation time of feature selection and even improve the performance of classifier. Based on this, a multi-label feature selection algorithm based on conditional mutual information of expert feature was proposed. Firstly, the expert features were combined with the remaining features, and then the conditional mutual information was used to obtain a feature sequence of strong to weak relativity with the label set. Finally, the subspaces were divided to remove the redundant features. The experimental comparison was performed to the proposed algorithm on 7 multi-label datasets. Experimental results show that the proposed algorithm has certain advantages over the other feature selection algorithms, and the statistical hypothesis testing and the stability analysis further illustrate the effectiveness and the rationality of the proposed algorithm.
[21]
毛莺池 , 曹海 , 平萍 , 等 . 基于最大联合条件互信息的特征选择
[J]. 计算机应用 , 2019 , 39 (3 ):734 -741 .
DOI:10.11772/j.issn.1001-9081.2018081694
[本文引用: 1]
在高维数据如图像数据、基因数据、文本数据等的分析过程中,当样本存在冗余特征时会大大增加问题分析复杂难度,因此在数据分析前从中剔除冗余特征尤为重要。基于互信息(MI)的特征选择方法能够有效地降低数据维数,提高分析结果精度,但是,现有方法在特征选择过程中评判特征是否冗余的标准单一,无法合理排除冗余特征,最终影响分析结果。为此,提出一种基于最大联合条件互信息的特征选择方法(MCJMI)。MCJMI选择特征时考虑整体联合互信息与条件互信息两个因素,两个因素融合增强特征选择约束。在平均预测精度方面,MCJMI与信息增益(IG)、最小冗余度最大相关性(mRMR)特征选择相比提升了6个百分点;与联合互信息(JMI)、最大化联合互信息(JMIM)相比提升了2个百分点;与LW向前搜索方法(SFS-LW)相比提升了1个百分点。在稳定性方面,MCJMI稳定性达到了0.92,优于JMI、JMIM、SFS-LW方法。实验结果表明MCJMI能够有效地提高特征选择的准确率与稳定性。
MAO Yingchi CAO Hai PING Ping et al. Feature selection based on maximum conditional and joint mutual information
[J]. Journal of Computer Application , 2019 , 39 (3 ):734 -741 .
[本文引用: 1]
[22]
盖晓平 , 王冬青 , 赵喜兰 , 等 . 利用概率统计特性的保护告警信息特征降维方法
[J]. 电网技术 , 2021 , 45 (5 ):2017 -2024 .
[本文引用: 1]
GAI Xiaoping WANG Dongqing ZHAO Xilan et al. Feature reduction method for alarm information protection with probability statistical characteristics
[J]. Power System Technology , 2021 , 45 (5 ):2017 -2024 .
[本文引用: 1]
[23]
李扬 , 顾雪平 . 基于改进最大相关最小冗余判据的暂态稳定评估特征选择
[J]. 中国电机工程学报 , 2013 , 33 (34 ):179 -186 .
[本文引用: 1]
LI Yang GU Xueping Feature selection for transient stability assessment based on improved maximal relevance and minimal redundancy criterion
[J]. Proceedings of the CSEE , 2013 , 33 (34 ):179 -186 .
[本文引用: 1]
[24]
孙志鹏 , 孙志龙 , 魏建 . 基于决策树支持向量机算法的电力变压器故障诊断研究
[J]. 电气工程学报 , 2019 , 14 (4 ):42 -45 .
[本文引用: 2]
SUN Zhipeng SUN Zhilong WEI Jian Research on power transformer fault diagnosis based on decision tree support vector machine
[J]. Journal of Electrical Engineering , 2019 , 14 (4 ):42 -45 .
[本文引用: 2]
[25]
徐世晖 . 基于改进在线最小二乘支持向量机电池故障诊断方法研究 [D]. 哈尔滨 : 哈尔滨理工大学 , 2020 .
[本文引用: 1]
XU Shihui Research on battery fault diagnosis method based on improved online least square support vector machine [D]. Harb in:Harbin University of Science and Technology, 2021 .
[本文引用: 1]
[26]
邓乃扬 , 田英杰 . 数据挖掘中的新方法——支持向量机 [M]. 北京 : 科学出版社 , 2004 .
[本文引用: 1]
DENG Naiyang TIAN Yingjie A new method of data mining:Support vector machines [M]. Beijing : China Science Publishing & Media Ltd. , 2004 .
[本文引用: 1]
[27]
郑含博 , 王伟 , 李晓纲 , 等 . 基于多分类最小二乘支持向量机和改进粒子群优化算法的电力变压器故障诊断方法
[J]. 高电压技术 , 2014 , 40 (11 ):3424 -3429 .
[本文引用: 1]
ZHENG Hanbo WANG Wei LI Xiaogang et al. Fault diagnosis method of power transformers using multi-class LS-SVM and improved PSO
[J]. High Voltage Engineering , 2014 , 40 (11 ):3424 -3429 .
[本文引用: 1]
[28]
LIN S YING K CHEN S et al. Particle swarm optimization for parameter determination and feature selection of support vector machines
[J]. Expert Systems with Applications , 2008 , 35 (4 ):1817 -1824 .
DOI:10.1016/j.eswa.2007.08.088
URL
[本文引用: 1]
[29]
冯茜 , 李擎 , 全威 , 等 . 多目标粒子群优化算法研究综述
[J]. 工程科学学报 , 2021 , 43 (6 ):745 -753 .
[本文引用: 1]
FENG Qian LI Qing QUAN Wei et al. Overview of multiobjective particle swarm optimization algorithm
[J]. Chinese Journal of Engineering , 2021 , 43 (6 ):745 -753 .
[本文引用: 1]
[30]
王文凯 , 邓斌 . 基于DAE-IPSO-SVM的电缆早期故障识别方法
[J]. 国外电子测量技术 , 2021 , 40 (8 ):29 -35 .
[本文引用: 1]
WANG Wenkai DENG Bin Cable incipient fault identification method based on DAE-IPSO-SVM
[J]. Foreign Electronic Measurement Technology , 2021 , 40 (8 ):29 -35 .
[本文引用: 1]
[31]
CHANG G HONG Y LI G A hybrid intelligent approach for classification of incipient faults in transmission network
[J]. IEEE Transactions on Power Delivery , 2019 , 34 (4 ):1785 -1794 .
DOI:10.1109/TPWRD.61
URL
[本文引用: 1]
[32]
杨杏丽 . 分类学习算法的性能度量指标综述
[J]. 计算机科学 , 2021 , 48 (8 ):209 -219 .
DOI:10.11896/jsjkx.200900216
[本文引用: 1]
在机器学习的分类问题研究中,对分类学习算法的正确评价是非常重要的。现实中,许多性能度量指标被从不同的角度提出,文中主要介绍了基于错误率的、基于混淆矩阵的和基于统计显著性检验的三大类性能度量指标,详细地讨论了分类学习算法各性能度量指标的提出背景、意义以及适用范围,分析了各种性能度量之间的差异,提出和分析了各方法中有待进一步研究的问题和方向。进一步,通过实验数据横向(每类度量中各方法之间的类内差异)和纵向(3类度量之间的类间差异)对照了各性能度量指标之间的差异,分析了各性能度量指标在分类算法选择上的一致性。
YANG Xingli Survey of performance measure index of classification learning algorithm
[J]. Computer Science , 2021 , 48 (8 ):209 -219 .
DOI:10.11896/jsjkx.200900216
[本文引用: 1]
In the research of classification task of machine learning,it is important for correctly evaluating the performance of the learning algorithm.In practical application,many performance measure indexes are proposed based on different perspectives.Three kinds of performance measure indexes based on error rate,confusion matrix and statistical test are introduced in this paper.The background,significance and scope of each measure index are discussed.The differences of different methods are analyzed.The future research problems and directions are also put forward and analyzed.Furthermore,the differences of these performance measure indexes are also compared by experimental data in portrait and landscape.The consistency of these performance measure indexes is also analyzed in classification algorithm selection.
基于卷积神经网络的配电网单相接地故障识别
2
2020
... 电力设备在绝缘逐渐老化过程中会不断发生瞬时性击穿,产生扰动波形,这一系列扰动被称为早期故障.早期故障具有重复性、随机性和瞬时性的特点,前期研究将其刻画成物理本质为电弧故障的瞬时性单相接地[1 ⇓ -3 ] .早期故障频发使设备的绝缘劣化处遭受进一步损坏,伤害逐渐累积至永久性故障发生,导致停电事故[4 -5 ] .随着配电网信息化建设,置于站端的扰动波形记录装置能实现早期故障波形的捕获,但同时也记录下大量与其波形特征相似的非早期故障扰动.若能基于扰动波形数据实现对早期故障和其他扰动波形的准确区分,则可以及时感知设备运行状态、指导检修工作安排并消除故障隐患,在一定程度上减少永久性故障导致的停电事故发生[6 ] .因此,准确识别早期故障对于提高系统供电可靠性具有重要意义. ...
... 式中,c 1 和c 2 为学习因子,r 1 和r 2 为[0,1 ]之间的随机值,η 表示加权因子. ...
Identification of single phase to earth fault in distribution network based on convolution neural network
2
2020
... 电力设备在绝缘逐渐老化过程中会不断发生瞬时性击穿,产生扰动波形,这一系列扰动被称为早期故障.早期故障具有重复性、随机性和瞬时性的特点,前期研究将其刻画成物理本质为电弧故障的瞬时性单相接地[1 ⇓ -3 ] .早期故障频发使设备的绝缘劣化处遭受进一步损坏,伤害逐渐累积至永久性故障发生,导致停电事故[4 -5 ] .随着配电网信息化建设,置于站端的扰动波形记录装置能实现早期故障波形的捕获,但同时也记录下大量与其波形特征相似的非早期故障扰动.若能基于扰动波形数据实现对早期故障和其他扰动波形的准确区分,则可以及时感知设备运行状态、指导检修工作安排并消除故障隐患,在一定程度上减少永久性故障导致的停电事故发生[6 ] .因此,准确识别早期故障对于提高系统供电可靠性具有重要意义. ...
... 式中,c 1 和c 2 为学习因子,r 1 和r 2 为[0,1 ]之间的随机值,η 表示加权因子. ...
Prevention of underground cable splice failures
1
2001
... 电力设备在绝缘逐渐老化过程中会不断发生瞬时性击穿,产生扰动波形,这一系列扰动被称为早期故障.早期故障具有重复性、随机性和瞬时性的特点,前期研究将其刻画成物理本质为电弧故障的瞬时性单相接地[1 ⇓ -3 ] .早期故障频发使设备的绝缘劣化处遭受进一步损坏,伤害逐渐累积至永久性故障发生,导致停电事故[4 -5 ] .随着配电网信息化建设,置于站端的扰动波形记录装置能实现早期故障波形的捕获,但同时也记录下大量与其波形特征相似的非早期故障扰动.若能基于扰动波形数据实现对早期故障和其他扰动波形的准确区分,则可以及时感知设备运行状态、指导检修工作安排并消除故障隐患,在一定程度上减少永久性故障导致的停电事故发生[6 ] .因此,准确识别早期故障对于提高系统供电可靠性具有重要意义. ...
Incipient fault location algorithm for underground cables
1
2014
... 电力设备在绝缘逐渐老化过程中会不断发生瞬时性击穿,产生扰动波形,这一系列扰动被称为早期故障.早期故障具有重复性、随机性和瞬时性的特点,前期研究将其刻画成物理本质为电弧故障的瞬时性单相接地[1 ⇓ -3 ] .早期故障频发使设备的绝缘劣化处遭受进一步损坏,伤害逐渐累积至永久性故障发生,导致停电事故[4 -5 ] .随着配电网信息化建设,置于站端的扰动波形记录装置能实现早期故障波形的捕获,但同时也记录下大量与其波形特征相似的非早期故障扰动.若能基于扰动波形数据实现对早期故障和其他扰动波形的准确区分,则可以及时感知设备运行状态、指导检修工作安排并消除故障隐患,在一定程度上减少永久性故障导致的停电事故发生[6 ] .因此,准确识别早期故障对于提高系统供电可靠性具有重要意义. ...
Travelling waves-based identification of sub-health condition of feeders in power distribution system
1
2018
... 电力设备在绝缘逐渐老化过程中会不断发生瞬时性击穿,产生扰动波形,这一系列扰动被称为早期故障.早期故障具有重复性、随机性和瞬时性的特点,前期研究将其刻画成物理本质为电弧故障的瞬时性单相接地[1 ⇓ -3 ] .早期故障频发使设备的绝缘劣化处遭受进一步损坏,伤害逐渐累积至永久性故障发生,导致停电事故[4 -5 ] .随着配电网信息化建设,置于站端的扰动波形记录装置能实现早期故障波形的捕获,但同时也记录下大量与其波形特征相似的非早期故障扰动.若能基于扰动波形数据实现对早期故障和其他扰动波形的准确区分,则可以及时感知设备运行状态、指导检修工作安排并消除故障隐患,在一定程度上减少永久性故障导致的停电事故发生[6 ] .因此,准确识别早期故障对于提高系统供电可靠性具有重要意义. ...
Dynamic fault prediction of power transformers based on hidden Markov model of dissolved Gases analysis
1
2019
... 电力设备在绝缘逐渐老化过程中会不断发生瞬时性击穿,产生扰动波形,这一系列扰动被称为早期故障.早期故障具有重复性、随机性和瞬时性的特点,前期研究将其刻画成物理本质为电弧故障的瞬时性单相接地[1 ⇓ -3 ] .早期故障频发使设备的绝缘劣化处遭受进一步损坏,伤害逐渐累积至永久性故障发生,导致停电事故[4 -5 ] .随着配电网信息化建设,置于站端的扰动波形记录装置能实现早期故障波形的捕获,但同时也记录下大量与其波形特征相似的非早期故障扰动.若能基于扰动波形数据实现对早期故障和其他扰动波形的准确区分,则可以及时感知设备运行状态、指导检修工作安排并消除故障隐患,在一定程度上减少永久性故障导致的停电事故发生[6 ] .因此,准确识别早期故障对于提高系统供电可靠性具有重要意义. ...
配电设备早期故障检测基本原理、关键技术与发展趋势
1
2020
... 电力设备在绝缘逐渐老化过程中会不断发生瞬时性击穿,产生扰动波形,这一系列扰动被称为早期故障.早期故障具有重复性、随机性和瞬时性的特点,前期研究将其刻画成物理本质为电弧故障的瞬时性单相接地[1 ⇓ -3 ] .早期故障频发使设备的绝缘劣化处遭受进一步损坏,伤害逐渐累积至永久性故障发生,导致停电事故[4 -5 ] .随着配电网信息化建设,置于站端的扰动波形记录装置能实现早期故障波形的捕获,但同时也记录下大量与其波形特征相似的非早期故障扰动.若能基于扰动波形数据实现对早期故障和其他扰动波形的准确区分,则可以及时感知设备运行状态、指导检修工作安排并消除故障隐患,在一定程度上减少永久性故障导致的停电事故发生[6 ] .因此,准确识别早期故障对于提高系统供电可靠性具有重要意义. ...
Basic principles,key technologies and development trends of incipient fault detection for power distribution equipments
1
2020
... 电力设备在绝缘逐渐老化过程中会不断发生瞬时性击穿,产生扰动波形,这一系列扰动被称为早期故障.早期故障具有重复性、随机性和瞬时性的特点,前期研究将其刻画成物理本质为电弧故障的瞬时性单相接地[1 ⇓ -3 ] .早期故障频发使设备的绝缘劣化处遭受进一步损坏,伤害逐渐累积至永久性故障发生,导致停电事故[4 -5 ] .随着配电网信息化建设,置于站端的扰动波形记录装置能实现早期故障波形的捕获,但同时也记录下大量与其波形特征相似的非早期故障扰动.若能基于扰动波形数据实现对早期故障和其他扰动波形的准确区分,则可以及时感知设备运行状态、指导检修工作安排并消除故障隐患,在一定程度上减少永久性故障导致的停电事故发生[6 ] .因此,准确识别早期故障对于提高系统供电可靠性具有重要意义. ...
2
2015
... 目前,早期故障识别方法可归纳为基于波形特征[7 ⇓ ⇓ -10 ] 、故障模型[11 ] 和机器学习[12 ⇓ ⇓ -15 ] 三大类.其中,基于波形特征的早期故障识别方法主要利用扰动波形中各电气量的相关变化规律,如文献[7 ]基于电压和电流的各次谐波含量及畸变率对早期故障进行识别;文献[8 ]则将负序电流及故障电流分量的变化规律作为扰动识别判据;文献[9 -10 ]都利用了卡尔曼滤波器计算电压基波分量,并将其与实测值的偏差作为早期故障扰动的特征量.而基于故障模型的早期故障识别方法主要利用早期故障作为电弧故障的物理本质,建立以电弧模型为基础的早期故障仿真模型,通常以扰动波形的电压畸变程度及故障的自清除特性来进行早期故障识别[11 ] .上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱. ...
... 三大类.其中,基于波形特征的早期故障识别方法主要利用扰动波形中各电气量的相关变化规律,如文献[7 ]基于电压和电流的各次谐波含量及畸变率对早期故障进行识别;文献[8 ]则将负序电流及故障电流分量的变化规律作为扰动识别判据;文献[9 -10 ]都利用了卡尔曼滤波器计算电压基波分量,并将其与实测值的偏差作为早期故障扰动的特征量.而基于故障模型的早期故障识别方法主要利用早期故障作为电弧故障的物理本质,建立以电弧模型为基础的早期故障仿真模型,通常以扰动波形的电压畸变程度及故障的自清除特性来进行早期故障识别[11 ] .上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱. ...
2
2015
... 目前,早期故障识别方法可归纳为基于波形特征[7 ⇓ ⇓ -10 ] 、故障模型[11 ] 和机器学习[12 ⇓ ⇓ -15 ] 三大类.其中,基于波形特征的早期故障识别方法主要利用扰动波形中各电气量的相关变化规律,如文献[7 ]基于电压和电流的各次谐波含量及畸变率对早期故障进行识别;文献[8 ]则将负序电流及故障电流分量的变化规律作为扰动识别判据;文献[9 -10 ]都利用了卡尔曼滤波器计算电压基波分量,并将其与实测值的偏差作为早期故障扰动的特征量.而基于故障模型的早期故障识别方法主要利用早期故障作为电弧故障的物理本质,建立以电弧模型为基础的早期故障仿真模型,通常以扰动波形的电压畸变程度及故障的自清除特性来进行早期故障识别[11 ] .上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱. ...
... 三大类.其中,基于波形特征的早期故障识别方法主要利用扰动波形中各电气量的相关变化规律,如文献[7 ]基于电压和电流的各次谐波含量及畸变率对早期故障进行识别;文献[8 ]则将负序电流及故障电流分量的变化规律作为扰动识别判据;文献[9 -10 ]都利用了卡尔曼滤波器计算电压基波分量,并将其与实测值的偏差作为早期故障扰动的特征量.而基于故障模型的早期故障识别方法主要利用早期故障作为电弧故障的物理本质,建立以电弧模型为基础的早期故障仿真模型,通常以扰动波形的电压畸变程度及故障的自清除特性来进行早期故障识别[11 ] .上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱. ...
Detection of incipient faults in underground medium voltage cables
2
2008
... 目前,早期故障识别方法可归纳为基于波形特征[7 ⇓ ⇓ -10 ] 、故障模型[11 ] 和机器学习[12 ⇓ ⇓ -15 ] 三大类.其中,基于波形特征的早期故障识别方法主要利用扰动波形中各电气量的相关变化规律,如文献[7 ]基于电压和电流的各次谐波含量及畸变率对早期故障进行识别;文献[8 ]则将负序电流及故障电流分量的变化规律作为扰动识别判据;文献[9 -10 ]都利用了卡尔曼滤波器计算电压基波分量,并将其与实测值的偏差作为早期故障扰动的特征量.而基于故障模型的早期故障识别方法主要利用早期故障作为电弧故障的物理本质,建立以电弧模型为基础的早期故障仿真模型,通常以扰动波形的电压畸变程度及故障的自清除特性来进行早期故障识别[11 ] .上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱. ...
... ]基于电压和电流的各次谐波含量及畸变率对早期故障进行识别;文献[8 ]则将负序电流及故障电流分量的变化规律作为扰动识别判据;文献[9 -10 ]都利用了卡尔曼滤波器计算电压基波分量,并将其与实测值的偏差作为早期故障扰动的特征量.而基于故障模型的早期故障识别方法主要利用早期故障作为电弧故障的物理本质,建立以电弧模型为基础的早期故障仿真模型,通常以扰动波形的电压畸变程度及故障的自清除特性来进行早期故障识别[11 ] .上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱. ...
A statistical-based criterion for incipient fault detection in underground power cables established on voltage waveform characteristics
2
2021
... 目前,早期故障识别方法可归纳为基于波形特征[7 ⇓ ⇓ -10 ] 、故障模型[11 ] 和机器学习[12 ⇓ ⇓ -15 ] 三大类.其中,基于波形特征的早期故障识别方法主要利用扰动波形中各电气量的相关变化规律,如文献[7 ]基于电压和电流的各次谐波含量及畸变率对早期故障进行识别;文献[8 ]则将负序电流及故障电流分量的变化规律作为扰动识别判据;文献[9 -10 ]都利用了卡尔曼滤波器计算电压基波分量,并将其与实测值的偏差作为早期故障扰动的特征量.而基于故障模型的早期故障识别方法主要利用早期故障作为电弧故障的物理本质,建立以电弧模型为基础的早期故障仿真模型,通常以扰动波形的电压畸变程度及故障的自清除特性来进行早期故障识别[11 ] .上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱. ...
... ]则将负序电流及故障电流分量的变化规律作为扰动识别判据;文献[9 -10 ]都利用了卡尔曼滤波器计算电压基波分量,并将其与实测值的偏差作为早期故障扰动的特征量.而基于故障模型的早期故障识别方法主要利用早期故障作为电弧故障的物理本质,建立以电弧模型为基础的早期故障仿真模型,通常以扰动波形的电压畸变程度及故障的自清除特性来进行早期故障识别[11 ] .上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱. ...
Kalman filter based incipient fault detection method for underground cables
2
2015
... 目前,早期故障识别方法可归纳为基于波形特征[7 ⇓ ⇓ -10 ] 、故障模型[11 ] 和机器学习[12 ⇓ ⇓ -15 ] 三大类.其中,基于波形特征的早期故障识别方法主要利用扰动波形中各电气量的相关变化规律,如文献[7 ]基于电压和电流的各次谐波含量及畸变率对早期故障进行识别;文献[8 ]则将负序电流及故障电流分量的变化规律作为扰动识别判据;文献[9 -10 ]都利用了卡尔曼滤波器计算电压基波分量,并将其与实测值的偏差作为早期故障扰动的特征量.而基于故障模型的早期故障识别方法主要利用早期故障作为电弧故障的物理本质,建立以电弧模型为基础的早期故障仿真模型,通常以扰动波形的电压畸变程度及故障的自清除特性来进行早期故障识别[11 ] .上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱. ...
... -10 ]都利用了卡尔曼滤波器计算电压基波分量,并将其与实测值的偏差作为早期故障扰动的特征量.而基于故障模型的早期故障识别方法主要利用早期故障作为电弧故障的物理本质,建立以电弧模型为基础的早期故障仿真模型,通常以扰动波形的电压畸变程度及故障的自清除特性来进行早期故障识别[11 ] .上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱. ...
Multi-cycle incipient fault detection and location for medium voltage underground cable
2
2017
... 目前,早期故障识别方法可归纳为基于波形特征[7 ⇓ ⇓ -10 ] 、故障模型[11 ] 和机器学习[12 ⇓ ⇓ -15 ] 三大类.其中,基于波形特征的早期故障识别方法主要利用扰动波形中各电气量的相关变化规律,如文献[7 ]基于电压和电流的各次谐波含量及畸变率对早期故障进行识别;文献[8 ]则将负序电流及故障电流分量的变化规律作为扰动识别判据;文献[9 -10 ]都利用了卡尔曼滤波器计算电压基波分量,并将其与实测值的偏差作为早期故障扰动的特征量.而基于故障模型的早期故障识别方法主要利用早期故障作为电弧故障的物理本质,建立以电弧模型为基础的早期故障仿真模型,通常以扰动波形的电压畸变程度及故障的自清除特性来进行早期故障识别[11 ] .上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱. ...
... [11 ].上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱. ...
配电线路早期故障辨识方法
2
2020
... 目前,早期故障识别方法可归纳为基于波形特征[7 ⇓ ⇓ -10 ] 、故障模型[11 ] 和机器学习[12 ⇓ ⇓ -15 ] 三大类.其中,基于波形特征的早期故障识别方法主要利用扰动波形中各电气量的相关变化规律,如文献[7 ]基于电压和电流的各次谐波含量及畸变率对早期故障进行识别;文献[8 ]则将负序电流及故障电流分量的变化规律作为扰动识别判据;文献[9 -10 ]都利用了卡尔曼滤波器计算电压基波分量,并将其与实测值的偏差作为早期故障扰动的特征量.而基于故障模型的早期故障识别方法主要利用早期故障作为电弧故障的物理本质,建立以电弧模型为基础的早期故障仿真模型,通常以扰动波形的电压畸变程度及故障的自清除特性来进行早期故障识别[11 ] .上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱. ...
... 基于机器学习的早期故障识别方法通常依赖于信号分析算法对扰动波形进行处理,获取大量时域或频域的特征信息,在此基础上利用庞大的特征数据对分类器进行训练以构建相应的故障识别模型.例如文献[12 ]利用小波变换算法将扰动波形拆分为不同基元,并基于类人概念学习采用贝叶斯概率学习法挖掘波形基元特征与扰动类型的关联性;文献[13 -14 ]分别采用了小波变换和S变换算法获取大量的扰动波形特征信息,随后将其输入神经网络进行故障模型的训练;文献[15 ]基于快速傅里叶算法将每个窗口波形信号对应频域信息表示为相应字母,因此不同类型扰动波形的字母组合存在较大差异.此类方法基于数据驱动,鲁棒性强但对于扰动波形数据样本的依赖性大,且其特征数据集的维度通常较为庞大.另外,我国中压配电网主要采用小电流接地的方式[16 ] ,早期故障在该类系统中的表现形式分为单相接地型和异名相两点接地型[17 ] ,如图1 所示,而目前的早期故障识别方法主要针对单相接地型.文献[18 ]结合早期故障特性及其扰动波形变化规律,提出了基于复合判据的小电流接地系统早期故障识别方法,能够准确识别单相接地型和异名相两点接地型早期故障,但该算法易受过渡电阻影响,且涉及阈值较多、要求较高,在实际应用中存在一定的局限性.因此,如何解决基于知识驱动方法的适应性不足和基于数据驱动方法特征数据量大的问题,以及充分考虑小电流接地系统早期故障表现形式的多样性,是当前针对我国中压配电网早期故障识别方法研究需要关注的重点. ...
Detection method of incipient faults of power system lines
2
2020
... 目前,早期故障识别方法可归纳为基于波形特征[7 ⇓ ⇓ -10 ] 、故障模型[11 ] 和机器学习[12 ⇓ ⇓ -15 ] 三大类.其中,基于波形特征的早期故障识别方法主要利用扰动波形中各电气量的相关变化规律,如文献[7 ]基于电压和电流的各次谐波含量及畸变率对早期故障进行识别;文献[8 ]则将负序电流及故障电流分量的变化规律作为扰动识别判据;文献[9 -10 ]都利用了卡尔曼滤波器计算电压基波分量,并将其与实测值的偏差作为早期故障扰动的特征量.而基于故障模型的早期故障识别方法主要利用早期故障作为电弧故障的物理本质,建立以电弧模型为基础的早期故障仿真模型,通常以扰动波形的电压畸变程度及故障的自清除特性来进行早期故障识别[11 ] .上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱. ...
... 基于机器学习的早期故障识别方法通常依赖于信号分析算法对扰动波形进行处理,获取大量时域或频域的特征信息,在此基础上利用庞大的特征数据对分类器进行训练以构建相应的故障识别模型.例如文献[12 ]利用小波变换算法将扰动波形拆分为不同基元,并基于类人概念学习采用贝叶斯概率学习法挖掘波形基元特征与扰动类型的关联性;文献[13 -14 ]分别采用了小波变换和S变换算法获取大量的扰动波形特征信息,随后将其输入神经网络进行故障模型的训练;文献[15 ]基于快速傅里叶算法将每个窗口波形信号对应频域信息表示为相应字母,因此不同类型扰动波形的字母组合存在较大差异.此类方法基于数据驱动,鲁棒性强但对于扰动波形数据样本的依赖性大,且其特征数据集的维度通常较为庞大.另外,我国中压配电网主要采用小电流接地的方式[16 ] ,早期故障在该类系统中的表现形式分为单相接地型和异名相两点接地型[17 ] ,如图1 所示,而目前的早期故障识别方法主要针对单相接地型.文献[18 ]结合早期故障特性及其扰动波形变化规律,提出了基于复合判据的小电流接地系统早期故障识别方法,能够准确识别单相接地型和异名相两点接地型早期故障,但该算法易受过渡电阻影响,且涉及阈值较多、要求较高,在实际应用中存在一定的局限性.因此,如何解决基于知识驱动方法的适应性不足和基于数据驱动方法特征数据量大的问题,以及充分考虑小电流接地系统早期故障表现形式的多样性,是当前针对我国中压配电网早期故障识别方法研究需要关注的重点. ...
堆叠自动编码器与S变换相结合的电缆早期故障识别方法
2
2018
... 目前,早期故障识别方法可归纳为基于波形特征[7 ⇓ ⇓ -10 ] 、故障模型[11 ] 和机器学习[12 ⇓ ⇓ -15 ] 三大类.其中,基于波形特征的早期故障识别方法主要利用扰动波形中各电气量的相关变化规律,如文献[7 ]基于电压和电流的各次谐波含量及畸变率对早期故障进行识别;文献[8 ]则将负序电流及故障电流分量的变化规律作为扰动识别判据;文献[9 -10 ]都利用了卡尔曼滤波器计算电压基波分量,并将其与实测值的偏差作为早期故障扰动的特征量.而基于故障模型的早期故障识别方法主要利用早期故障作为电弧故障的物理本质,建立以电弧模型为基础的早期故障仿真模型,通常以扰动波形的电压畸变程度及故障的自清除特性来进行早期故障识别[11 ] .上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱. ...
... 基于机器学习的早期故障识别方法通常依赖于信号分析算法对扰动波形进行处理,获取大量时域或频域的特征信息,在此基础上利用庞大的特征数据对分类器进行训练以构建相应的故障识别模型.例如文献[12 ]利用小波变换算法将扰动波形拆分为不同基元,并基于类人概念学习采用贝叶斯概率学习法挖掘波形基元特征与扰动类型的关联性;文献[13 -14 ]分别采用了小波变换和S变换算法获取大量的扰动波形特征信息,随后将其输入神经网络进行故障模型的训练;文献[15 ]基于快速傅里叶算法将每个窗口波形信号对应频域信息表示为相应字母,因此不同类型扰动波形的字母组合存在较大差异.此类方法基于数据驱动,鲁棒性强但对于扰动波形数据样本的依赖性大,且其特征数据集的维度通常较为庞大.另外,我国中压配电网主要采用小电流接地的方式[16 ] ,早期故障在该类系统中的表现形式分为单相接地型和异名相两点接地型[17 ] ,如图1 所示,而目前的早期故障识别方法主要针对单相接地型.文献[18 ]结合早期故障特性及其扰动波形变化规律,提出了基于复合判据的小电流接地系统早期故障识别方法,能够准确识别单相接地型和异名相两点接地型早期故障,但该算法易受过渡电阻影响,且涉及阈值较多、要求较高,在实际应用中存在一定的局限性.因此,如何解决基于知识驱动方法的适应性不足和基于数据驱动方法特征数据量大的问题,以及充分考虑小电流接地系统早期故障表现形式的多样性,是当前针对我国中压配电网早期故障识别方法研究需要关注的重点. ...
Cable incipient fault identification based on stacked autoencoder and S-transform
2
2018
... 目前,早期故障识别方法可归纳为基于波形特征[7 ⇓ ⇓ -10 ] 、故障模型[11 ] 和机器学习[12 ⇓ ⇓ -15 ] 三大类.其中,基于波形特征的早期故障识别方法主要利用扰动波形中各电气量的相关变化规律,如文献[7 ]基于电压和电流的各次谐波含量及畸变率对早期故障进行识别;文献[8 ]则将负序电流及故障电流分量的变化规律作为扰动识别判据;文献[9 -10 ]都利用了卡尔曼滤波器计算电压基波分量,并将其与实测值的偏差作为早期故障扰动的特征量.而基于故障模型的早期故障识别方法主要利用早期故障作为电弧故障的物理本质,建立以电弧模型为基础的早期故障仿真模型,通常以扰动波形的电压畸变程度及故障的自清除特性来进行早期故障识别[11 ] .上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱. ...
... 基于机器学习的早期故障识别方法通常依赖于信号分析算法对扰动波形进行处理,获取大量时域或频域的特征信息,在此基础上利用庞大的特征数据对分类器进行训练以构建相应的故障识别模型.例如文献[12 ]利用小波变换算法将扰动波形拆分为不同基元,并基于类人概念学习采用贝叶斯概率学习法挖掘波形基元特征与扰动类型的关联性;文献[13 -14 ]分别采用了小波变换和S变换算法获取大量的扰动波形特征信息,随后将其输入神经网络进行故障模型的训练;文献[15 ]基于快速傅里叶算法将每个窗口波形信号对应频域信息表示为相应字母,因此不同类型扰动波形的字母组合存在较大差异.此类方法基于数据驱动,鲁棒性强但对于扰动波形数据样本的依赖性大,且其特征数据集的维度通常较为庞大.另外,我国中压配电网主要采用小电流接地的方式[16 ] ,早期故障在该类系统中的表现形式分为单相接地型和异名相两点接地型[17 ] ,如图1 所示,而目前的早期故障识别方法主要针对单相接地型.文献[18 ]结合早期故障特性及其扰动波形变化规律,提出了基于复合判据的小电流接地系统早期故障识别方法,能够准确识别单相接地型和异名相两点接地型早期故障,但该算法易受过渡电阻影响,且涉及阈值较多、要求较高,在实际应用中存在一定的局限性.因此,如何解决基于知识驱动方法的适应性不足和基于数据驱动方法特征数据量大的问题,以及充分考虑小电流接地系统早期故障表现形式的多样性,是当前针对我国中压配电网早期故障识别方法研究需要关注的重点. ...
基于优化卷积神经网络的电缆早期故障分类识别
2
2020
... 目前,早期故障识别方法可归纳为基于波形特征[7 ⇓ ⇓ -10 ] 、故障模型[11 ] 和机器学习[12 ⇓ ⇓ -15 ] 三大类.其中,基于波形特征的早期故障识别方法主要利用扰动波形中各电气量的相关变化规律,如文献[7 ]基于电压和电流的各次谐波含量及畸变率对早期故障进行识别;文献[8 ]则将负序电流及故障电流分量的变化规律作为扰动识别判据;文献[9 -10 ]都利用了卡尔曼滤波器计算电压基波分量,并将其与实测值的偏差作为早期故障扰动的特征量.而基于故障模型的早期故障识别方法主要利用早期故障作为电弧故障的物理本质,建立以电弧模型为基础的早期故障仿真模型,通常以扰动波形的电压畸变程度及故障的自清除特性来进行早期故障识别[11 ] .上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱. ...
... 基于机器学习的早期故障识别方法通常依赖于信号分析算法对扰动波形进行处理,获取大量时域或频域的特征信息,在此基础上利用庞大的特征数据对分类器进行训练以构建相应的故障识别模型.例如文献[12 ]利用小波变换算法将扰动波形拆分为不同基元,并基于类人概念学习采用贝叶斯概率学习法挖掘波形基元特征与扰动类型的关联性;文献[13 -14 ]分别采用了小波变换和S变换算法获取大量的扰动波形特征信息,随后将其输入神经网络进行故障模型的训练;文献[15 ]基于快速傅里叶算法将每个窗口波形信号对应频域信息表示为相应字母,因此不同类型扰动波形的字母组合存在较大差异.此类方法基于数据驱动,鲁棒性强但对于扰动波形数据样本的依赖性大,且其特征数据集的维度通常较为庞大.另外,我国中压配电网主要采用小电流接地的方式[16 ] ,早期故障在该类系统中的表现形式分为单相接地型和异名相两点接地型[17 ] ,如图1 所示,而目前的早期故障识别方法主要针对单相接地型.文献[18 ]结合早期故障特性及其扰动波形变化规律,提出了基于复合判据的小电流接地系统早期故障识别方法,能够准确识别单相接地型和异名相两点接地型早期故障,但该算法易受过渡电阻影响,且涉及阈值较多、要求较高,在实际应用中存在一定的局限性.因此,如何解决基于知识驱动方法的适应性不足和基于数据驱动方法特征数据量大的问题,以及充分考虑小电流接地系统早期故障表现形式的多样性,是当前针对我国中压配电网早期故障识别方法研究需要关注的重点. ...
Cable incipient fault classification and identification based on optimized convolution neural network
2
2020
... 目前,早期故障识别方法可归纳为基于波形特征[7 ⇓ ⇓ -10 ] 、故障模型[11 ] 和机器学习[12 ⇓ ⇓ -15 ] 三大类.其中,基于波形特征的早期故障识别方法主要利用扰动波形中各电气量的相关变化规律,如文献[7 ]基于电压和电流的各次谐波含量及畸变率对早期故障进行识别;文献[8 ]则将负序电流及故障电流分量的变化规律作为扰动识别判据;文献[9 -10 ]都利用了卡尔曼滤波器计算电压基波分量,并将其与实测值的偏差作为早期故障扰动的特征量.而基于故障模型的早期故障识别方法主要利用早期故障作为电弧故障的物理本质,建立以电弧模型为基础的早期故障仿真模型,通常以扰动波形的电压畸变程度及故障的自清除特性来进行早期故障识别[11 ] .上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱. ...
... 基于机器学习的早期故障识别方法通常依赖于信号分析算法对扰动波形进行处理,获取大量时域或频域的特征信息,在此基础上利用庞大的特征数据对分类器进行训练以构建相应的故障识别模型.例如文献[12 ]利用小波变换算法将扰动波形拆分为不同基元,并基于类人概念学习采用贝叶斯概率学习法挖掘波形基元特征与扰动类型的关联性;文献[13 -14 ]分别采用了小波变换和S变换算法获取大量的扰动波形特征信息,随后将其输入神经网络进行故障模型的训练;文献[15 ]基于快速傅里叶算法将每个窗口波形信号对应频域信息表示为相应字母,因此不同类型扰动波形的字母组合存在较大差异.此类方法基于数据驱动,鲁棒性强但对于扰动波形数据样本的依赖性大,且其特征数据集的维度通常较为庞大.另外,我国中压配电网主要采用小电流接地的方式[16 ] ,早期故障在该类系统中的表现形式分为单相接地型和异名相两点接地型[17 ] ,如图1 所示,而目前的早期故障识别方法主要针对单相接地型.文献[18 ]结合早期故障特性及其扰动波形变化规律,提出了基于复合判据的小电流接地系统早期故障识别方法,能够准确识别单相接地型和异名相两点接地型早期故障,但该算法易受过渡电阻影响,且涉及阈值较多、要求较高,在实际应用中存在一定的局限性.因此,如何解决基于知识驱动方法的适应性不足和基于数据驱动方法特征数据量大的问题,以及充分考虑小电流接地系统早期故障表现形式的多样性,是当前针对我国中压配电网早期故障识别方法研究需要关注的重点. ...
Transform waveforms into signature vectors for general-purpose incipient fault detection
2
2022
... 目前,早期故障识别方法可归纳为基于波形特征[7 ⇓ ⇓ -10 ] 、故障模型[11 ] 和机器学习[12 ⇓ ⇓ -15 ] 三大类.其中,基于波形特征的早期故障识别方法主要利用扰动波形中各电气量的相关变化规律,如文献[7 ]基于电压和电流的各次谐波含量及畸变率对早期故障进行识别;文献[8 ]则将负序电流及故障电流分量的变化规律作为扰动识别判据;文献[9 -10 ]都利用了卡尔曼滤波器计算电压基波分量,并将其与实测值的偏差作为早期故障扰动的特征量.而基于故障模型的早期故障识别方法主要利用早期故障作为电弧故障的物理本质,建立以电弧模型为基础的早期故障仿真模型,通常以扰动波形的电压畸变程度及故障的自清除特性来进行早期故障识别[11 ] .上述两类方法均基于知识驱动,所选择的扰动特征量通常具有较明确的物理意义且判据简单、具有一定的实际应用意义,但其受系统参数、故障参数或电弧特性等随机因素的影响较大,算法适应性较弱. ...
... 基于机器学习的早期故障识别方法通常依赖于信号分析算法对扰动波形进行处理,获取大量时域或频域的特征信息,在此基础上利用庞大的特征数据对分类器进行训练以构建相应的故障识别模型.例如文献[12 ]利用小波变换算法将扰动波形拆分为不同基元,并基于类人概念学习采用贝叶斯概率学习法挖掘波形基元特征与扰动类型的关联性;文献[13 -14 ]分别采用了小波变换和S变换算法获取大量的扰动波形特征信息,随后将其输入神经网络进行故障模型的训练;文献[15 ]基于快速傅里叶算法将每个窗口波形信号对应频域信息表示为相应字母,因此不同类型扰动波形的字母组合存在较大差异.此类方法基于数据驱动,鲁棒性强但对于扰动波形数据样本的依赖性大,且其特征数据集的维度通常较为庞大.另外,我国中压配电网主要采用小电流接地的方式[16 ] ,早期故障在该类系统中的表现形式分为单相接地型和异名相两点接地型[17 ] ,如图1 所示,而目前的早期故障识别方法主要针对单相接地型.文献[18 ]结合早期故障特性及其扰动波形变化规律,提出了基于复合判据的小电流接地系统早期故障识别方法,能够准确识别单相接地型和异名相两点接地型早期故障,但该算法易受过渡电阻影响,且涉及阈值较多、要求较高,在实际应用中存在一定的局限性.因此,如何解决基于知识驱动方法的适应性不足和基于数据驱动方法特征数据量大的问题,以及充分考虑小电流接地系统早期故障表现形式的多样性,是当前针对我国中压配电网早期故障识别方法研究需要关注的重点. ...
提升小电流接地系统单相接地故障处理能力
1
2021
... 基于机器学习的早期故障识别方法通常依赖于信号分析算法对扰动波形进行处理,获取大量时域或频域的特征信息,在此基础上利用庞大的特征数据对分类器进行训练以构建相应的故障识别模型.例如文献[12 ]利用小波变换算法将扰动波形拆分为不同基元,并基于类人概念学习采用贝叶斯概率学习法挖掘波形基元特征与扰动类型的关联性;文献[13 -14 ]分别采用了小波变换和S变换算法获取大量的扰动波形特征信息,随后将其输入神经网络进行故障模型的训练;文献[15 ]基于快速傅里叶算法将每个窗口波形信号对应频域信息表示为相应字母,因此不同类型扰动波形的字母组合存在较大差异.此类方法基于数据驱动,鲁棒性强但对于扰动波形数据样本的依赖性大,且其特征数据集的维度通常较为庞大.另外,我国中压配电网主要采用小电流接地的方式[16 ] ,早期故障在该类系统中的表现形式分为单相接地型和异名相两点接地型[17 ] ,如图1 所示,而目前的早期故障识别方法主要针对单相接地型.文献[18 ]结合早期故障特性及其扰动波形变化规律,提出了基于复合判据的小电流接地系统早期故障识别方法,能够准确识别单相接地型和异名相两点接地型早期故障,但该算法易受过渡电阻影响,且涉及阈值较多、要求较高,在实际应用中存在一定的局限性.因此,如何解决基于知识驱动方法的适应性不足和基于数据驱动方法特征数据量大的问题,以及充分考虑小电流接地系统早期故障表现形式的多样性,是当前针对我国中压配电网早期故障识别方法研究需要关注的重点. ...
Solutions to improve the single-phase grounding fault management of neural non-effective grounded systems
1
2021
... 基于机器学习的早期故障识别方法通常依赖于信号分析算法对扰动波形进行处理,获取大量时域或频域的特征信息,在此基础上利用庞大的特征数据对分类器进行训练以构建相应的故障识别模型.例如文献[12 ]利用小波变换算法将扰动波形拆分为不同基元,并基于类人概念学习采用贝叶斯概率学习法挖掘波形基元特征与扰动类型的关联性;文献[13 -14 ]分别采用了小波变换和S变换算法获取大量的扰动波形特征信息,随后将其输入神经网络进行故障模型的训练;文献[15 ]基于快速傅里叶算法将每个窗口波形信号对应频域信息表示为相应字母,因此不同类型扰动波形的字母组合存在较大差异.此类方法基于数据驱动,鲁棒性强但对于扰动波形数据样本的依赖性大,且其特征数据集的维度通常较为庞大.另外,我国中压配电网主要采用小电流接地的方式[16 ] ,早期故障在该类系统中的表现形式分为单相接地型和异名相两点接地型[17 ] ,如图1 所示,而目前的早期故障识别方法主要针对单相接地型.文献[18 ]结合早期故障特性及其扰动波形变化规律,提出了基于复合判据的小电流接地系统早期故障识别方法,能够准确识别单相接地型和异名相两点接地型早期故障,但该算法易受过渡电阻影响,且涉及阈值较多、要求较高,在实际应用中存在一定的局限性.因此,如何解决基于知识驱动方法的适应性不足和基于数据驱动方法特征数据量大的问题,以及充分考虑小电流接地系统早期故障表现形式的多样性,是当前针对我国中压配电网早期故障识别方法研究需要关注的重点. ...
小电流接地系统接地型早期故障扰动特征分析
1
2021
... 基于机器学习的早期故障识别方法通常依赖于信号分析算法对扰动波形进行处理,获取大量时域或频域的特征信息,在此基础上利用庞大的特征数据对分类器进行训练以构建相应的故障识别模型.例如文献[12 ]利用小波变换算法将扰动波形拆分为不同基元,并基于类人概念学习采用贝叶斯概率学习法挖掘波形基元特征与扰动类型的关联性;文献[13 -14 ]分别采用了小波变换和S变换算法获取大量的扰动波形特征信息,随后将其输入神经网络进行故障模型的训练;文献[15 ]基于快速傅里叶算法将每个窗口波形信号对应频域信息表示为相应字母,因此不同类型扰动波形的字母组合存在较大差异.此类方法基于数据驱动,鲁棒性强但对于扰动波形数据样本的依赖性大,且其特征数据集的维度通常较为庞大.另外,我国中压配电网主要采用小电流接地的方式[16 ] ,早期故障在该类系统中的表现形式分为单相接地型和异名相两点接地型[17 ] ,如图1 所示,而目前的早期故障识别方法主要针对单相接地型.文献[18 ]结合早期故障特性及其扰动波形变化规律,提出了基于复合判据的小电流接地系统早期故障识别方法,能够准确识别单相接地型和异名相两点接地型早期故障,但该算法易受过渡电阻影响,且涉及阈值较多、要求较高,在实际应用中存在一定的局限性.因此,如何解决基于知识驱动方法的适应性不足和基于数据驱动方法特征数据量大的问题,以及充分考虑小电流接地系统早期故障表现形式的多样性,是当前针对我国中压配电网早期故障识别方法研究需要关注的重点. ...
Grounded incipient fault analysis in a non-solidly grounding system
1
2021
... 基于机器学习的早期故障识别方法通常依赖于信号分析算法对扰动波形进行处理,获取大量时域或频域的特征信息,在此基础上利用庞大的特征数据对分类器进行训练以构建相应的故障识别模型.例如文献[12 ]利用小波变换算法将扰动波形拆分为不同基元,并基于类人概念学习采用贝叶斯概率学习法挖掘波形基元特征与扰动类型的关联性;文献[13 -14 ]分别采用了小波变换和S变换算法获取大量的扰动波形特征信息,随后将其输入神经网络进行故障模型的训练;文献[15 ]基于快速傅里叶算法将每个窗口波形信号对应频域信息表示为相应字母,因此不同类型扰动波形的字母组合存在较大差异.此类方法基于数据驱动,鲁棒性强但对于扰动波形数据样本的依赖性大,且其特征数据集的维度通常较为庞大.另外,我国中压配电网主要采用小电流接地的方式[16 ] ,早期故障在该类系统中的表现形式分为单相接地型和异名相两点接地型[17 ] ,如图1 所示,而目前的早期故障识别方法主要针对单相接地型.文献[18 ]结合早期故障特性及其扰动波形变化规律,提出了基于复合判据的小电流接地系统早期故障识别方法,能够准确识别单相接地型和异名相两点接地型早期故障,但该算法易受过渡电阻影响,且涉及阈值较多、要求较高,在实际应用中存在一定的局限性.因此,如何解决基于知识驱动方法的适应性不足和基于数据驱动方法特征数据量大的问题,以及充分考虑小电流接地系统早期故障表现形式的多样性,是当前针对我国中压配电网早期故障识别方法研究需要关注的重点. ...
基于复合判据的小电流接地系统接地型早期故障检测
1
2022
... 基于机器学习的早期故障识别方法通常依赖于信号分析算法对扰动波形进行处理,获取大量时域或频域的特征信息,在此基础上利用庞大的特征数据对分类器进行训练以构建相应的故障识别模型.例如文献[12 ]利用小波变换算法将扰动波形拆分为不同基元,并基于类人概念学习采用贝叶斯概率学习法挖掘波形基元特征与扰动类型的关联性;文献[13 -14 ]分别采用了小波变换和S变换算法获取大量的扰动波形特征信息,随后将其输入神经网络进行故障模型的训练;文献[15 ]基于快速傅里叶算法将每个窗口波形信号对应频域信息表示为相应字母,因此不同类型扰动波形的字母组合存在较大差异.此类方法基于数据驱动,鲁棒性强但对于扰动波形数据样本的依赖性大,且其特征数据集的维度通常较为庞大.另外,我国中压配电网主要采用小电流接地的方式[16 ] ,早期故障在该类系统中的表现形式分为单相接地型和异名相两点接地型[17 ] ,如图1 所示,而目前的早期故障识别方法主要针对单相接地型.文献[18 ]结合早期故障特性及其扰动波形变化规律,提出了基于复合判据的小电流接地系统早期故障识别方法,能够准确识别单相接地型和异名相两点接地型早期故障,但该算法易受过渡电阻影响,且涉及阈值较多、要求较高,在实际应用中存在一定的局限性.因此,如何解决基于知识驱动方法的适应性不足和基于数据驱动方法特征数据量大的问题,以及充分考虑小电流接地系统早期故障表现形式的多样性,是当前针对我国中压配电网早期故障识别方法研究需要关注的重点. ...
The grounded incipient fault detection based on compound criterion in non-solidly grounding system
1
2022
... 基于机器学习的早期故障识别方法通常依赖于信号分析算法对扰动波形进行处理,获取大量时域或频域的特征信息,在此基础上利用庞大的特征数据对分类器进行训练以构建相应的故障识别模型.例如文献[12 ]利用小波变换算法将扰动波形拆分为不同基元,并基于类人概念学习采用贝叶斯概率学习法挖掘波形基元特征与扰动类型的关联性;文献[13 -14 ]分别采用了小波变换和S变换算法获取大量的扰动波形特征信息,随后将其输入神经网络进行故障模型的训练;文献[15 ]基于快速傅里叶算法将每个窗口波形信号对应频域信息表示为相应字母,因此不同类型扰动波形的字母组合存在较大差异.此类方法基于数据驱动,鲁棒性强但对于扰动波形数据样本的依赖性大,且其特征数据集的维度通常较为庞大.另外,我国中压配电网主要采用小电流接地的方式[16 ] ,早期故障在该类系统中的表现形式分为单相接地型和异名相两点接地型[17 ] ,如图1 所示,而目前的早期故障识别方法主要针对单相接地型.文献[18 ]结合早期故障特性及其扰动波形变化规律,提出了基于复合判据的小电流接地系统早期故障识别方法,能够准确识别单相接地型和异名相两点接地型早期故障,但该算法易受过渡电阻影响,且涉及阈值较多、要求较高,在实际应用中存在一定的局限性.因此,如何解决基于知识驱动方法的适应性不足和基于数据驱动方法特征数据量大的问题,以及充分考虑小电流接地系统早期故障表现形式的多样性,是当前针对我国中压配电网早期故障识别方法研究需要关注的重点. ...
S变换熵理论及其在电力系统故障检测中的应用研究
3
2016
... 可变的时频分辨率使S变换具有较好的时频特性和抗噪能力,该类信号处理方式能够提取丰富的时频特征量信息,被广泛应用于电力扰动波形的突变区域分析[19 ] .对站端扰动电压波形进行S变换并取模处理后,获得一个M ×N 的模时频矩阵S S S A 和奇异熵B 对扰动电压波形各频段上的能量分布特性和信号复杂程度进行刻画[19 ] .假设模时频矩阵S i 行第j 列个元素表示为sij ,则矩阵S i 和采样时刻j 的条件下的信号能量Eij 可以表示为 ...
... [19 ].假设模时频矩阵S i 行第j 列个元素表示为sij ,则矩阵S i 和采样时刻j 的条件下的信号能量Eij 可以表示为 ...
... 基于统计特性构建的扰动波形特征子集2,表征了扰动信号在不同频段上的能量分布情况以及在时频空间中能量分布的复杂程度[19 ] .对模时频矩阵S
Study of S-transform entropy theory and its application in fault detection of electric power system
3
2016
... 可变的时频分辨率使S变换具有较好的时频特性和抗噪能力,该类信号处理方式能够提取丰富的时频特征量信息,被广泛应用于电力扰动波形的突变区域分析[19 ] .对站端扰动电压波形进行S变换并取模处理后,获得一个M ×N 的模时频矩阵S S S A 和奇异熵B 对扰动电压波形各频段上的能量分布特性和信号复杂程度进行刻画[19 ] .假设模时频矩阵S i 行第j 列个元素表示为sij ,则矩阵S i 和采样时刻j 的条件下的信号能量Eij 可以表示为 ...
... [19 ].假设模时频矩阵S i 行第j 列个元素表示为sij ,则矩阵S i 和采样时刻j 的条件下的信号能量Eij 可以表示为 ...
... 基于统计特性构建的扰动波形特征子集2,表征了扰动信号在不同频段上的能量分布情况以及在时频空间中能量分布的复杂程度[19 ] .对模时频矩阵S
基于专家特征的条件互信息多标记特征选择算法
1
2020
... 最大相关最小冗余法的核心思想是从已知的特征数据集中寻找与其目标类别有最大相关性且相互之间具有最小冗余性的特征子集,评价标签类别与特征之间的相关性[20 -21 ] .最大相关最小冗余法能够将扰动特征子集2中具备最大分类能力的最优特征量保留,并将子集中所含的高冗余和不相关信息降低至最小程度,深度挖掘与目标标签相关联的特征信息,提高分类能力[22 ] . ...
Multi-label feature selection algorithm based on conditional mutual information of expert feature
1
2020
... 最大相关最小冗余法的核心思想是从已知的特征数据集中寻找与其目标类别有最大相关性且相互之间具有最小冗余性的特征子集,评价标签类别与特征之间的相关性[20 -21 ] .最大相关最小冗余法能够将扰动特征子集2中具备最大分类能力的最优特征量保留,并将子集中所含的高冗余和不相关信息降低至最小程度,深度挖掘与目标标签相关联的特征信息,提高分类能力[22 ] . ...
基于最大联合条件互信息的特征选择
1
2019
... 最大相关最小冗余法的核心思想是从已知的特征数据集中寻找与其目标类别有最大相关性且相互之间具有最小冗余性的特征子集,评价标签类别与特征之间的相关性[20 -21 ] .最大相关最小冗余法能够将扰动特征子集2中具备最大分类能力的最优特征量保留,并将子集中所含的高冗余和不相关信息降低至最小程度,深度挖掘与目标标签相关联的特征信息,提高分类能力[22 ] . ...
Feature selection based on maximum conditional and joint mutual information
1
2019
... 最大相关最小冗余法的核心思想是从已知的特征数据集中寻找与其目标类别有最大相关性且相互之间具有最小冗余性的特征子集,评价标签类别与特征之间的相关性[20 -21 ] .最大相关最小冗余法能够将扰动特征子集2中具备最大分类能力的最优特征量保留,并将子集中所含的高冗余和不相关信息降低至最小程度,深度挖掘与目标标签相关联的特征信息,提高分类能力[22 ] . ...
利用概率统计特性的保护告警信息特征降维方法
1
2021
... 最大相关最小冗余法的核心思想是从已知的特征数据集中寻找与其目标类别有最大相关性且相互之间具有最小冗余性的特征子集,评价标签类别与特征之间的相关性[20 -21 ] .最大相关最小冗余法能够将扰动特征子集2中具备最大分类能力的最优特征量保留,并将子集中所含的高冗余和不相关信息降低至最小程度,深度挖掘与目标标签相关联的特征信息,提高分类能力[22 ] . ...
Feature reduction method for alarm information protection with probability statistical characteristics
1
2021
... 最大相关最小冗余法的核心思想是从已知的特征数据集中寻找与其目标类别有最大相关性且相互之间具有最小冗余性的特征子集,评价标签类别与特征之间的相关性[20 -21 ] .最大相关最小冗余法能够将扰动特征子集2中具备最大分类能力的最优特征量保留,并将子集中所含的高冗余和不相关信息降低至最小程度,深度挖掘与目标标签相关联的特征信息,提高分类能力[22 ] . ...
基于改进最大相关最小冗余判据的暂态稳定评估特征选择
1
2013
... 在实际应用场景中,通常采用增量搜索法寻找近似最优特征[23 ] .特征集X v -1个特征量被确定,该部分特征量组成子集X v -1 ,此时最大相关最小冗余法的目的就是从剩余子集{X X v -1 }中选择第v 个特征量,实现式(12)中 ϕ ( · )
Feature selection for transient stability assessment based on improved maximal relevance and minimal redundancy criterion
1
2013
... 在实际应用场景中,通常采用增量搜索法寻找近似最优特征[23 ] .特征集X v -1个特征量被确定,该部分特征量组成子集X v -1 ,此时最大相关最小冗余法的目的就是从剩余子集{X X v -1 }中选择第v 个特征量,实现式(12)中 ϕ ( · )
基于决策树支持向量机算法的电力变压器故障诊断研究
2
2019
... 支持向量机(Support vector machine,SVM)以核函数理论为基础,基于映射函数将样本投放至高维空间中以获取最优超平面使样本线性可分,随后又将其反映射回低维空间,实现最终分类[24 ] ,该过程如图3 所示. ...
... LS-SVM存在核函数宽度σ 2 和惩罚系数γ 两个变量,当γ 的取值越小,则算法适应性越强,但训练误差也随之增大;而当γ 的取值较大时,算法适应性降低;σ 2 主要影响算法的运行效率[24 ] .因此需要寻求最优参数组合以满足算法适应性和运算效率的约束.网格搜索法(Grid search)是最常用的参数搜索方法,但该方法的运算时间较长且效率不高[28 ] .本文选用PSO算法寻找核函数宽度σ 2 和惩罚系数γ 的最优组合.PSO算法将一群初始化粒子经过多次迭代后获取目标函数最优解,在各次迭代过程中,每个粒子基于个体极值pi (该粒子最优解)和全局极值gd (该种群所得最优解)更新自身的位置及速度[29 ] .第i 个粒子在第k +1次迭代过程中的位置 x k + 1 i v k + 1 i
Research on power transformer fault diagnosis based on decision tree support vector machine
2
2019
... 支持向量机(Support vector machine,SVM)以核函数理论为基础,基于映射函数将样本投放至高维空间中以获取最优超平面使样本线性可分,随后又将其反映射回低维空间,实现最终分类[24 ] ,该过程如图3 所示. ...
... LS-SVM存在核函数宽度σ 2 和惩罚系数γ 两个变量,当γ 的取值越小,则算法适应性越强,但训练误差也随之增大;而当γ 的取值较大时,算法适应性降低;σ 2 主要影响算法的运行效率[24 ] .因此需要寻求最优参数组合以满足算法适应性和运算效率的约束.网格搜索法(Grid search)是最常用的参数搜索方法,但该方法的运算时间较长且效率不高[28 ] .本文选用PSO算法寻找核函数宽度σ 2 和惩罚系数γ 的最优组合.PSO算法将一群初始化粒子经过多次迭代后获取目标函数最优解,在各次迭代过程中,每个粒子基于个体极值pi (该粒子最优解)和全局极值gd (该种群所得最优解)更新自身的位置及速度[29 ] .第i 个粒子在第k +1次迭代过程中的位置 x k + 1 i v k + 1 i
1
2020
... LS-SVM则将传统支持向量机模型中的不等式约束改为等式约束[25 ] ,简化了拉格朗日乘子的求解过程,并将误差平方和损失函数作为训练集的经验损失,将二次规划求解问题转化为求解线性方程组,极大提高了计算速度和收敛精度. ...
1
2021
... LS-SVM则将传统支持向量机模型中的不等式约束改为等式约束[25 ] ,简化了拉格朗日乘子的求解过程,并将误差平方和损失函数作为训练集的经验损失,将二次规划求解问题转化为求解线性方程组,极大提高了计算速度和收敛精度. ...
1
2004
... 由Mercer条件[26 ] ,存在映射函数 ψ ( x ) K ( x , x k )
1
2004
... 由Mercer条件[26 ] ,存在映射函数 ψ ( x ) K ( x , x k )
基于多分类最小二乘支持向量机和改进粒子群优化算法的电力变压器故障诊断方法
1
2014
... 研究表明,支持向量机在径向基函数条件下能够获得较好性能[27 ] ,因此本文选择径向基核函数为LS-SVM的核函数,其表达式如下所示 ...
Fault diagnosis method of power transformers using multi-class LS-SVM and improved PSO
1
2014
... 研究表明,支持向量机在径向基函数条件下能够获得较好性能[27 ] ,因此本文选择径向基核函数为LS-SVM的核函数,其表达式如下所示 ...
Particle swarm optimization for parameter determination and feature selection of support vector machines
1
2008
... LS-SVM存在核函数宽度σ 2 和惩罚系数γ 两个变量,当γ 的取值越小,则算法适应性越强,但训练误差也随之增大;而当γ 的取值较大时,算法适应性降低;σ 2 主要影响算法的运行效率[24 ] .因此需要寻求最优参数组合以满足算法适应性和运算效率的约束.网格搜索法(Grid search)是最常用的参数搜索方法,但该方法的运算时间较长且效率不高[28 ] .本文选用PSO算法寻找核函数宽度σ 2 和惩罚系数γ 的最优组合.PSO算法将一群初始化粒子经过多次迭代后获取目标函数最优解,在各次迭代过程中,每个粒子基于个体极值pi (该粒子最优解)和全局极值gd (该种群所得最优解)更新自身的位置及速度[29 ] .第i 个粒子在第k +1次迭代过程中的位置 x k + 1 i v k + 1 i
多目标粒子群优化算法研究综述
1
2021
... LS-SVM存在核函数宽度σ 2 和惩罚系数γ 两个变量,当γ 的取值越小,则算法适应性越强,但训练误差也随之增大;而当γ 的取值较大时,算法适应性降低;σ 2 主要影响算法的运行效率[24 ] .因此需要寻求最优参数组合以满足算法适应性和运算效率的约束.网格搜索法(Grid search)是最常用的参数搜索方法,但该方法的运算时间较长且效率不高[28 ] .本文选用PSO算法寻找核函数宽度σ 2 和惩罚系数γ 的最优组合.PSO算法将一群初始化粒子经过多次迭代后获取目标函数最优解,在各次迭代过程中,每个粒子基于个体极值pi (该粒子最优解)和全局极值gd (该种群所得最优解)更新自身的位置及速度[29 ] .第i 个粒子在第k +1次迭代过程中的位置 x k + 1 i v k + 1 i
Overview of multiobjective particle swarm optimization algorithm
1
2021
... LS-SVM存在核函数宽度σ 2 和惩罚系数γ 两个变量,当γ 的取值越小,则算法适应性越强,但训练误差也随之增大;而当γ 的取值较大时,算法适应性降低;σ 2 主要影响算法的运行效率[24 ] .因此需要寻求最优参数组合以满足算法适应性和运算效率的约束.网格搜索法(Grid search)是最常用的参数搜索方法,但该方法的运算时间较长且效率不高[28 ] .本文选用PSO算法寻找核函数宽度σ 2 和惩罚系数γ 的最优组合.PSO算法将一群初始化粒子经过多次迭代后获取目标函数最优解,在各次迭代过程中,每个粒子基于个体极值pi (该粒子最优解)和全局极值gd (该种群所得最优解)更新自身的位置及速度[29 ] .第i 个粒子在第k +1次迭代过程中的位置 x k + 1 i v k + 1 i
基于DAE-IPSO-SVM的电缆早期故障识别方法
1
2021
... 根据前期研究经验对PSO算法中初始参数设置情况如表1 所示[30 -31 ] . ...
Cable incipient fault identification method based on DAE-IPSO-SVM
1
2021
... 根据前期研究经验对PSO算法中初始参数设置情况如表1 所示[30 -31 ] . ...
A hybrid intelligent approach for classification of incipient faults in transmission network
1
2019
... 根据前期研究经验对PSO算法中初始参数设置情况如表1 所示[30 -31 ] . ...
分类学习算法的性能度量指标综述
1
2021
... 本文基于K折交叉验证法(K-fold cross validation,K-CV)对算法有效性进行分析,即将各类型的扰动波形样本集随机分为K 组,各组的样本数量相等,随后依次使用其中一组作为测试样本集,剩余K -1组则自动归为训练样本集,本文将K 取为5.同时,使用基于混淆矩阵的算法性能度量指标对本文算法性能进行评价[32 ] ,如式(23)~(26)所示. ...
Survey of performance measure index of classification learning algorithm
1
2021
... 本文基于K折交叉验证法(K-fold cross validation,K-CV)对算法有效性进行分析,即将各类型的扰动波形样本集随机分为K 组,各组的样本数量相等,随后依次使用其中一组作为测试样本集,剩余K -1组则自动归为训练样本集,本文将K 取为5.同时,使用基于混淆矩阵的算法性能度量指标对本文算法性能进行评价[32 ] ,如式(23)~(26)所示. ...