1 引言
近年来,随着不可再生能源的过度开采与消耗,能源紧缺的问题随之而来,同时碳达峰碳中和的目标理念也逐渐被提及,分布式电源(Distributed generation,DG)连入配电网的容量也越来越高。DG具有可再生的显著优势,但其存在的出力随机性也对配电网产生了不利的影响[1 ] 。
配电网是一个呈辐射状结构的网络,功率是从上往下传输的[2 ] 。当大量的分布式电源连入配电网后,这种情况就发生改变,多点分布的功率进入配电网后改变了原有的潮流分布[3 ] ,会造成功率双向流动,电压波动,同时会增加线路损耗。
解决上述问题的重要措施为配电网的无功优化。无功优化是在保证系统安全运行的条件下,通过控制某些变量从而使电压稳定以及网损减少。针对无功优化,现在已经有许多的研究。文献[4 ]以总体网损以及电压波动最小为目标,并以节点电压以及电容器组投切组数为约束建立无功优化模型,用改进的粒子群算法来进行模型的求解,但分布式电源以固定出力来计算,没有考虑其出力的随机性。文献[5 ]考虑了风光出力的波动性对配电网的影响,以全天的网损以及电压偏移最小为目标,建立了兼顾电压安全与配电网经济运行的多目标优化模型。文献[6 ]提出了计及风光相关性的无功优化模型,以斯皮尔曼相关系数把风光出力的相关性表示出来,最后以各设备的出力为自变量,求得兼顾网损和电压偏差最小的多目标优化方案。文献[7 ]对于中压配电网的无功优化提出了同时求解补偿点和补偿量的方法,以年费用最小为目标创立优化模型,在粒子群算法中加入融合裂变的方法,可以避免陷入局部最优解的情况。
本文首先是以基于组合损失函数的BP神经网络来预测短期的风电出力,并建立常用的光伏发电出力随机模型。建立以全天有功网损最小,并将电压越限作为惩罚函数加入到目标函数中,以各无功设备作为自变量,并以系统正常运行为约束条件构造出DG参与的配电网综合无功优化模型,并以改进的粒子群优化算法进行求解,最后以改进的IEEE33系统为例进行仿真,可得出优化后系统网损明显减少,并且电压能稳定在安全范围内,说明了求解算法的可行性以及稳定性。
2 分布式电源预测模型
2.1 基于组合损失函数的BP风电预测模型
(1) ${{P}_{\text{w}}}=\frac{1}{2}C\rho A{{\text{ }\!\!\nu\!\!\text{ }}^{3}}$
式中,P w 为风机功率,kW;C 为电机的功率系数;ρ 为空气密度,kg/m3 ;A 为风轮所转过的面积,m2 ;ν 为当前时刻的风速,m/s。
参考文献[7 ],本文将最小化均方差误差函数与交叉熵损失函数、排序损失函数相结合组成了组合损失函数,以此作为训练目标[8 ] 。将风电场未来一日内间隔为15 min的NWP气象预测数据作为输入,训练样本为过去几日或者十几日的气象数据和风电场实际功率数据[9 ] ,从而得到所需日期的全天风电预测数据曲线。
2.2 光伏发电预测模型
光伏发电主要与光照强度、电池阵列板的面积以及光能转电能的转换效率有关且成正比,公式如下所示
(2) ${{P}_{\text{PV}}}=lA\eta $
式中,P PV 为光伏输出功率,kW;l 为阵列板的面积,m2 ;η 为转换效率。
每天的光照强度变化受到多种因素的影响,比如温度、湿度等,但总体差异不是很大,所以采用标准日的光照强度来进行光伏发电的预测。
2.3 分布式电源无功调节能力分析
2.3.1 光伏发电无功调节能力
随着电力电子器件的发展,通过逆变器连接到配电网的分布式电源也有一定的无功调节能力。当光伏发电通过逆变器连接到配电网时,其无功调节能力与逆变器的稳定运行密切相关。受变频器的最大工作电流以及可逆电压的限制[10 ] ,光伏的有功功率与无功功率的关系为
(3) $P_{\text{PV}}^{2}+Q_{\text{PV}}^{2}\le {{\left( \frac{3}{2}{{U}_{\text{pcc}}}{{I}_{m\text{ax}}} \right)}^{2}}$
(4) $P_{PV}^{2}+{{\left( {{Q}_{\text{PV}}}+\frac{3U_{PCC}^{2}}{2\omega L} \right)}^{2}}\le {{\left( \frac{3{{U}_{\text{dc}}}{{U}_{\text{pcc}}}}{4\omega L} \right)}^{2}}$
式中,P PV 为光伏发电的有功功率;Q PV 为光伏发电的无功功率;U pcc 为逆变器的电网连接点电压;I max 为最大工作电流;U dc 为逆变器的中间直流电压;L 为逆变器的电感;ω 为电网的角频率。
根据式(3)和式(4)可得出光伏无功调节能力的上下限,即
(5) $\left\{\begin{array}{l} Q_{\mathrm{PV} \min }=\max \left(-\sqrt{\frac{9}{4} U_{\mathrm{pcc}}{ }^{2} I_{\max }{ }^{2}-P_{\mathrm{PV}}{ }^{2}},\right. \\ \left.-\sqrt{\left(\frac{3 U_{\mathrm{dc}} U_{\mathrm{pcc}}}{4 \omega L}\right)-P_{\mathrm{PV}}{ }^{2}}-\frac{3 U_{\mathrm{pcc}}{ }^{2}}{2 \omega L}\right) \\ Q_{\mathrm{PV} \max }=\min \left(\sqrt{\frac{9}{4} U_{\mathrm{pcc}}{ }^{2} I_{\max }{ }^{2}-P_{\mathrm{PV}}{ }^{2}}\right. \\ \left.\sqrt{\left(\frac{3 U_{\mathrm{dc}} U_{\mathrm{pcc}}}{4 \omega L}\right)-P_{\mathrm{PV}}{ }^{2}}-\frac{3 U_{\mathrm{pcc}}{ }^{2}}{2 \omega L}\right) \end{array}\right.$
这里为了确保分布式电源的无功调节能力,所以利用DG最低无功功率调节的上限来获得最低可能值,以及DG最高无功功率调节的下限来获得最高可能值[11 ] 。
2.3.2 双馈风力电机无功调节能力
双馈风力电机可以控制并产生无功功率,通过独立控制转子励磁电流来解耦有功和无功功率的控制。其次,无需从电网励磁,而是从转子电路中励磁[12 ] 。由于它是通过逆变器连接到电网中,因此风电的无功调节能力受到逆变器运行的影响。受定子侧与转子侧转换器最大电流的限制,单个风力发电的有功功率与无功功率的关系如下
(6) ${{\left( \frac{{{P}_{\text{w}}}}{1-s} \right)}^{\text{2}}}+{{Q}_{\text{w}}}^{2}\le {{(3{{U}_{\text{S}}}{{I}_{\text{S,max}}})}^{2}}$
(7) ${{\left( \frac{{{P}_{\text{w}}}}{1-s} \right)}^{\text{2}}}+{{\left( {{Q}_{\text{w}}}+3\frac{U_{S}^{2}}{{{X}_{\text{S}}}} \right)}^{2}}\le {{\left( 3\frac{{{X}_{\text{M}}}}{{{X}_{\text{S}}}}{{U}_{\text{S}}}{{I}_{\text{R,max}}} \right)}^{2}}$
式中,P w 是风力发电机的有功输出;Q w 是风力发电机的无功输出;U S 是定子侧电压;I S,max 是定子侧最大电流;I R,max 是转子侧最大电流;X S 是定子侧漏电抗;X M 是励磁电抗;s 是转差率;
同时,风力发电机受到静态稳定极限的影响[13 ] ,公式如下所示
(8) ${{Q}_{\text{w}}}\ge -3{{U}_{\text{S}}}^{2}/{{X}_{\text{S}}}$
根据式(6)~(8)可得出风电无功调节能力的上下限,即
(9) $\left\{ \begin{array}{*{35}{l}} {{Q}_{\text{wmin}}}=-3U_{S}^{2}/{{X}_{\text{S}}} \\ \begin{align} & {{Q}_{\text{wmax}}}=\min \left( \sqrt{{{(3{{U}_{\text{S}}}{{I}_{\text{S,max}}})}^{2}}-{{\left( \frac{{{P}_{\text{w}}}}{1-s} \right)}^{\text{2}}}} \right., \\ & \left. \sqrt{{{\left( 3\frac{{{X}_{\text{M}}}}{{{X}_{\text{S}}}}{{U}_{\text{s}}}{{I}_{\text{R,max}}} \right)}^{2}}-{{\left( \frac{{{P}_{\text{w}}}}{1-s} \right)}^{\text{2}}}}-3\frac{U_{S}^{2}}{{{X}_{\text{S}}}} \right) \\ \end{align} \\ \end{array} \right.$
3 含DG参与的配电网无功优化模型
3.1 目标函数
本文的目标函数为配电网系统全天的网损之和最小,时间间隔为1 h,考虑电网的安全运行,将电压越限作为惩罚函数加入到目标函数中,以配电系统的安全运行为前提,综合考虑系统的经济性,以一天中DG的无功出力、SVC的输出容量以及有载调压变压器的变比为控制变量,建立了含DG无功参与的全天配电网综合无功优化模型。
(10) ${{P}_{\text{loss}}}\text{=}\sum\limits_{t\text{=}1}^{24}{\sum\limits_{i,j\in {{N}_{L}}}{{{G}_{ij}}}}({{U}_{i}}^{2}\text{+}U_{j}^{2}-2{{U}_{i}}{{U}_{j}}\cos {{\theta }_{ij}})$
式中,P loss 为系统的有功网损;N L 为配电网支路数;Gij 、θij 分别为节点i 和节点j 之间的电导和电压相角差;Ui 和Uj 分别为节点i 和节点j 的电压幅值。
(11) $W=\lambda \sum\limits_{t=1}^{24}{\sum\limits_{i=1}^{n}{\Delta }}{{U}_{i}}^{2}$
式中,λ 为惩罚系数;n 为配电网节点数;ΔUi 为越限函数,用公式表达为
(12) $\Delta {{U}_{i}}=\left\{ \begin{array}{*{35}{l}} {{U}_{i}}-{{U}_{i\text{,}\ \text{max}}} & {} & {{U}_{i}}>{{U}_{i\text{,}\ \text{max}}} \\ 0 & {} & {{U}_{i\text{,}\ \text{min}}}\le {{U}_{i}}\le {{U}_{i\text{,}\ \text{max}}} \\ {{U}_{i\text{,}\ \text{min}}}-{{U}_{i}} & {} & {{U}_{i}}<{{U}_{i\text{,min}}} \\ \end{array} \right.$
式中,Ui ,min 、Ui ,max 分别为节点i 电压的最小值和最大值。
(13) $F={{P}_{\text{loss}}}+W$
目标函数第一项的意义为系统的经济性,第二项为系统的安全性,但这两个总体都是求最小值。为了以配电网的安全运行为前提,惩罚函数中的惩罚系数可设置为一个较大的值,相当于给第二项一个较大的权值。
3.2 约束条件
(14) $\left\{ \begin{align} & {{P}_{i}}\text{+}{{P}_{\text{DG}i}}={{P}_{\text{D}i}}+{{U}_{i}}\sum\limits_{j=1}^{{{N}_{\text{L}}}}{{{U}_{j}}({{G}_{ij}}\cos {{\theta }_{ij}}+{{B}_{ij}}\sin {{\theta }_{ij}})} \\ & {{Q}_{i}}\text{+}{{Q}_{\text{DG}i}}+{{Q}_{\text{DS}i}}={{Q}_{\text{D}i}}+{{U}_{i}}\sum\limits_{j=1}^{{{N}_{\text{L}}}}{{{U}_{j}}({{G}_{ij}}\sin {{\theta }_{ij}}-{{B}_{ij}}\cos {{\theta }_{ij}})} \\ \end{align} \right.$
式中,Pi 和Qi 为节点i 输入的有功、无功功率;P DG i Q DG i Q DS i Bij 是节点i 和j 之间的电纳。
(15) $\left\{ \begin{array}{*{35}{l}} {{P}_{\text{DG}i\text{min}}}\le {{P}_{\text{DG}i}}\le {{P}_{\text{DG}i\text{max}}} \\ {{Q}_{\text{DG}i\text{min}}}\le {{Q}_{\text{DG}i}}\le {{Q}_{\text{DG}i\text{max}}} \\ {{Q}_{\text{DS}i\text{min}}}\le {{Q}_{\text{DS}i}}\le {{Q}_{\text{DS}i\text{max}}} \\ {{T}_{\min }}\le T\le {{T}_{\max }} \\ {{N}_{i}}_{\min }\le {{N}_{i}}\le {{N}_{i}}_{\max } \\ {{I}_{ij\min }}\le {{I}_{ij}}\le {{I}_{ij\max }} \\ \end{array} \right.$
式中,T 和T max 、T min 分别为有载调压变压器的档位及其上下限;Ni 和Ni max 、Ni min 分别为有载调压变压器的变换次数及其上下限;Iij 和Iij max 、Iij min 分别为线路电流及其上下限。
4 模型的求解
4.1 改进的粒子群优化算法
粒子群优化算法(Particle swarm optimization, PSO)是模拟鸟群的觅食行为,每个问题的解都相当于搜索空间中的一只鸟,也被称为粒子[14 ] 。所有的粒子都有由目标函数决定的适应值,每个粒子还有一个速度来决定下一次移动的距离和方向。PSO初始为一群随机解,然后进行迭代来求最优解[15 ] ,在每一次迭代中,每个粒子都通过两个极值来更新本身的速度,第一个是粒子自己的最优解,另一个是全局最优解,其具体公式为
(16) $\left\{ \begin{matrix} {{V}_{id\text{,}\ t\text{+1}}}=\omega {{V}_{id\text{,}\ t}}+{{c}_{1}}({{p}_{id}}-{{x}_{id\text{,}\ t}})+{{c}_{2}}({{p}_{gd}}-{{x}_{id\text{,}\ t}}) \\ {{x}_{id\text{,}\ t\text{+1}}}={{x}_{id\text{,}\ t}}+{{V}_{id\text{,}\ t\text{+1}}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.$
式中,Vid , t xid , t t 时刻第i 个粒子中维度为d 的变量的速度和位置;ω 为惯性权重;c 1 、c 2 为学习因子;pid 是第i 个粒子的个体最优值;pgd 是全局最优值。
粒子群算法以简单易实现的优点在数学模型中广泛应用,但同时也有一些缺点,其中最显著的便是易陷入局部最优解,为了防止这种现象,需要对迭代公式中的参数进行修改,从而避免出现局部最优解的现象。
惯性权重ω 代表粒子当前速度对先前速度的记忆能力,本文使用指数递减惯性权重策略[16 ] ,即
(17) $\omega ={{\omega }_{\min }}{{({{\omega }_{\max }}/{{\omega }_{\min }})}^{1/(1+\frac{5T}{{{T}_{\max }}})}}$
式中,ω min 、ω max 分别是惯性权重的最小值和最大值,一般取0.4和0.9;T 和T max 分别是迭代次数和最大迭代次数。
学习因子c 1 和c 2 是调节个体与全局最优值在速度更新中所占的比例[17 ] ,为了提高搜索精度,在初期使得学习因子满足c 1 >c 2 ,而在后期使得学习因子满足c 1 <c 2 。具体公式如下
(18) $\left\{ \begin{matrix} {{c}_{1}}={{c}_{1}}_{\max }+({{c}_{1}}_{\min }-{{c}_{1}}_{\max })\frac{T}{{{T}_{\max }}} \\ {{c}_{2}}={{c}_{2}}_{\min }+({{c}_{2}}_{\max }-{{c}_{2}}_{\min })\frac{T}{{{T}_{\max }}} \\ \end{matrix} \right.$
式中,c 1min =c 2min =0.4,c 1max =c 2max =0.9。
4.2 算法流程
(1) 系统参数的初始化:输入配电网和DG的相关参数,DG和负载的预测值,并计算DG的无功功率调节范围。
(2) 算法的初始化:设置粒子的个数、每个粒子的搜索维度以及最大迭代次数。设置每个粒子变量位置以及速度的上下限。
(4) 通过前推回代法进行24次确定性潮流计算,得出24 h每个节点的电压幅值以及系统的全天有功网损。
(5) 以目标函数进行适应度计算,将每个粒子的适应度与本身个体最优相比较来更新pi ,将全局最优与各个粒子的适应度相比较来更新pg 。
(6) 更新迭代次数,判断是否到达最大迭代次数,若为是,结束循环并输出结果。若为否,继续进行。
(7) 根据式(17)和式(18)更新惯性权重和学习因子,然后根据式(16)更新粒子的速度和位置,重新进入步骤(4)。
5 算例分析
5.1 系统初始化
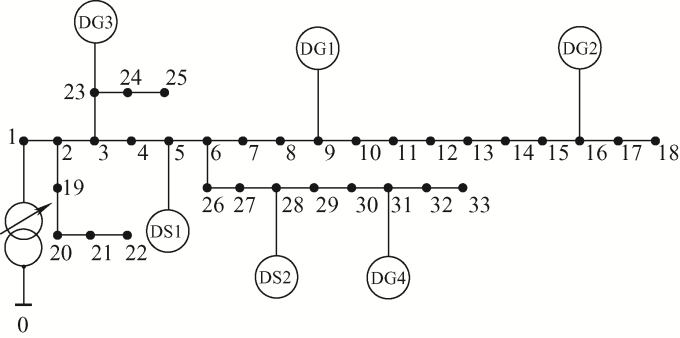
本文采用改进的IEEE33节点系统来进行仿真,其原有的线路参数不变,改进后的系统如图1 所示。在此节点系统中,基准电压为12.66 kV,基准功率为10 MV·A。系统中电压的约束范围为0.95~1.05 p.u.[18 ] 。0号与1号节点安装有载变压调压器,其调节范围为±4×1.25%。在5号和28号节点连接静止无功补偿器,其无功出力范围0~500 kVar。在9号、16号、23号以及31号节点安装DG,包含风力发电以及光伏发电。
图1
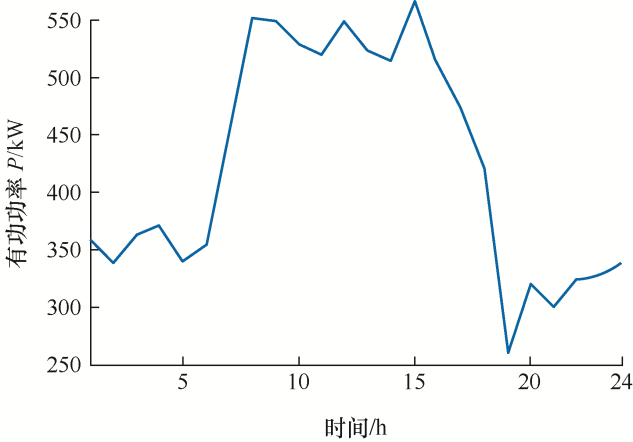
风电机组的有功额定容量为400 kW,无功出力范围为-140~180 kVar。光伏机组的有功额定容量为300 kW,无功出力范围为-100~120 kVar。风力发电的出力情况是以基于组合损失函数的BP函数来预测,使用预测日的NWP数据,经过训练得出最小误差的预测出力曲线,本文采用了层数为5-4-1的BP神经网络结构,其隐含层和输出层的传递函数分别为tansig函数和purelin函数,学习率设置为0.001,联合损失函数的权重系数为1,1,0.001,并以平均绝对误差和均方根误差来反映预测值的误差情况[19 ] ,如表1 所示。光伏发电的出力是以标准日的光照水平得出的预测出力曲线。将两者结合得出DG的有功出力曲线,如图2 所示。
图2
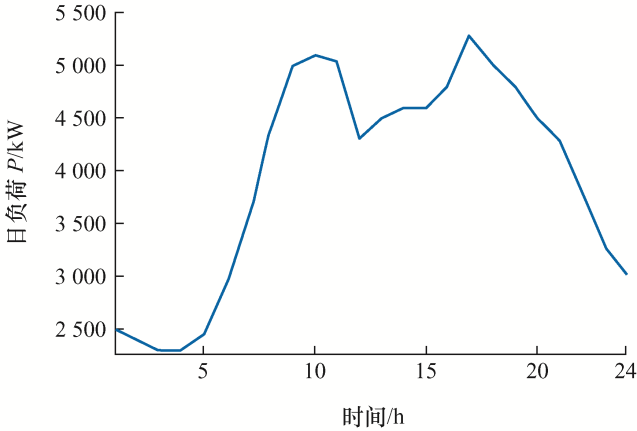
改进的粒子群算法参数设置如下:种群数为40,最大迭代次数为100。某地区的日负荷曲线如图3 所示,并将其以原本系统负荷的占比代入到IEEE33系统中。
图3
5.2 优化结果分析
将日负荷代入系统后,以改进的粒子群算法来进行模型的求解优化,得出全局最优解以及其对应的粒子位置。由于本文考虑了DG的无功出力控制,为了体现模型的控制变量对于网损减少的影响,将未连接DG系统、接入DG未优化的系统和接入DG优化后的系统中的网损值进行对比,如表2 所示。
从表2 可得,当未接入DG时系统的全天总网损为5 648.39 kW。而系统接入DG同时将静止无功补偿器以及有载调压变压器优化后,若未考虑DG的无功出力,系统的总网损为4 582.79 kW,减少了18.9%。如果考虑DG的无功出力并进行优化后,系统的总网损为4 378.25 kW,减少了22.5%。所以当考虑DG的无功出力时,会进一步减少系统的网损值,从而降低配电网系统运行的成本。
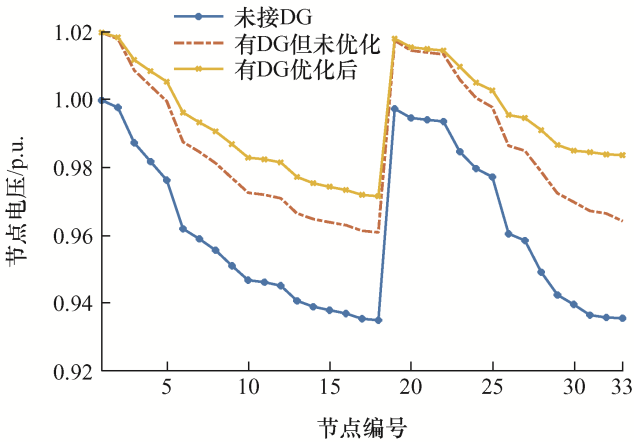
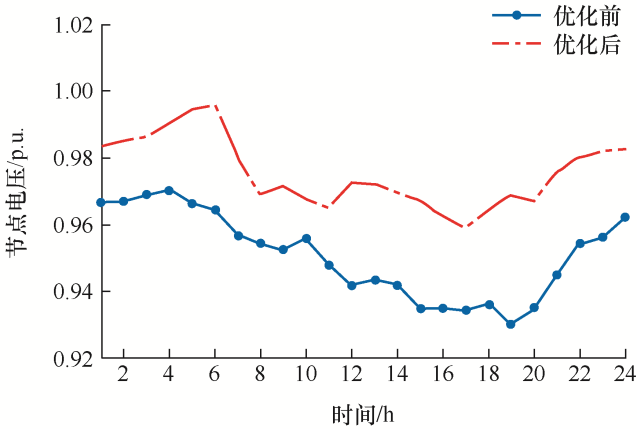
在配电网中,维持电压在安全区间是稳定运行的重要前提,图4 展示了上述三种情况的33节点电压水平,其时间选取为8时。图5 展示了第33节点优化前后的全天电压对比。
图4
图5
由图4 对比可知,当系统不采取优化措施时,较多节点的电压已经低于电压下限,这将不利于配电网的安全运行。当接入DG并且有载调压变压器在最优档位时,所有节点电压都已符合电压安全运行的范围,但有些节点的电压还是存在越下限的风险并且整体的电压波动较大。而当考虑DG的无功出力并优化后,整体的电压波动降低且越下限的风险大大降低。总结上述可得,当考虑DG的无功出力后,可以进一步减少配电网系统的有功网损,从而降低了运行成本,并且减少了系统整体的电压波动,同时提高了节点的电压水平,使其越下限的风险大大降低。
由图5 可以看出,在优化前,33节点在重负荷的情况下电压水平基本都低于电压下限,而在优化之后,33节点的24 h电压都在安全运行的区间之内。可以得出,当考虑DG的无功出力时,可以保证配电网系统节点的全天安全运行。
5.3 算法优化分析
改进的粒子群算法可以有效地避免局部最优的情况,将其与未改进的粒子群作对比,两种算法都在IEEE33系统下进行优化,且系统结构相同。未改进的粒子群算法初始化设置学习因子c 1 =c 2 =2,惯性权重ω =0.5。两种算法分别优化了10次,它们的收敛情况对比如表3 所示。
5.4 静止无功补偿器优点分析
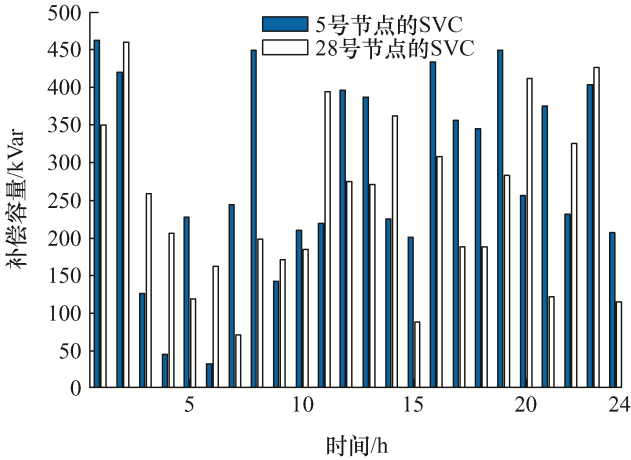
静止无功补偿器是现代技术较成熟的FACTS设备,常用于电力系统的负荷优化以及配电系统优化。它没有采用大容量的电感器以及电容器来生成需要的无功容量,而是采用电力电子器件来实现,这是无功补偿技术的巨大进步,它的动态无功优化与以往的电容器组投切相比更加灵活,并且可以对扰动产生较快的反应[20 ] ,由于其不需要投切的变化,所以运行成本也会更低,图6 为两个静止无功补偿器优化后的24 h补偿容量曲线。
图6
从图6 可以看出,静止无功补偿器的补偿效果比电容组投切更加灵活,并且使用的是电力电子器件,没有改变次数的限制并且运行成本也会减少。
6 结论
本文考虑了DG的无功出力,并得出无功出力的上下限。以改进的BP算法来预测全天的风电出力曲线,综合考虑了配电系统的经济性与安全性,建立了全天配电网无功优化模型,并以改进的粒子群算法来优化此模型,得出以下结论。
(1) 改进的粒子群算法可有效地避免在优化过程中出现局部最优值的情况。
(2) 当考虑DG的无功出力时,可进一步减少系统的有功网损,降低配电系统的运行成本并提高系统的电压水平,系统的整体性能得到了提高。
参考文献
View Option
[1]
柳想 , 王芳禄 . 分布式光伏电源接入对配电网保护的影响
[J]. 农业科技与装备 , 2020 (5 ):37 -39 ,43.
[本文引用: 1]
LIU Xiang WANG Fanglu Influence of distributed photovoltaic power access on distribution network protection
[J]. Agricultural Science & Technology and Equipment , 2020 (5 ):37 -39 ,43.
[本文引用: 1]
[2]
LIU J ZHANG J ZHANG D Effect of distributed generation on power supply reliability of distribution network
[C]// 2015 8th International Conference on Grid and Distributed Computing (GDC),Jeju,Republic of Korea , 2015 :32 -35 .
[本文引用: 1]
[3]
康重庆 , 姚良忠 . 高比例可再生能源电力系统的关键科学问题与理论研究框架
[J]. 电力系统自动化 , 2017 , 44 (9 ):2 -11 .
[本文引用: 1]
KANG Chongqing YAO Liangzhong Key scientific issues and theoretical research framework of high proportion renewable energy power system
[J]. Automation of Electric Power Systems , 2017 , 44 (9 ):2 -11 .
[本文引用: 1]
[4]
鲁裕婷 , 赵天乐 , 都洪基 , 等 . 基于改进粒子群算法的含DG配电网无功优化
[J]. 电力工程技术 , 2018 , 37 (6 ): 69 -74 .
[本文引用: 1]
LU Yuting ZHAO Tianle DU Hongji et al. Reactive power optimization of distribution network with DG based on improved particle swarm optimization algorithm
[J]. Electric Power Engineering Technology , 2018 , 37 (6 ):69 -74 .
[本文引用: 1]
[5]
刘永前 , 王函 , 韩爽 , 等 . 考虑风光出力波动性的实时互补性评价方法
[J]. 电网技术 , 2020 , 44 (9 ):3211 -3220 .
[本文引用: 1]
LIU Yongqian WANG Han HAN Shuang et al. Real time complementarity evaluation method considering the fluctuation of wind and solar output
[J]. Power System Technology , 2020 , 44 (9 ):3211 -3220 .
[本文引用: 1]
[6]
刘梦依 , 邱晓燕 , 张志荣 , 等 . 计及风光出力相关性的配电网多目标无功优化
[J]. 电网技术 , 2020 , 44 (5 ):1892 -1899 .
[本文引用: 1]
LIU Mengyi QIU Xiaoyan ZHANG Zhirong et al. Multi objective reactive power optimization of distribution network considering the correlation between wind and solar output
[J]. Power System Technology , 2020 , 44 (5 ):1892 -1899 .
[本文引用: 1]
[7]
张庭场 , 耿光飞 . 基于改进粒子群算法的中压配电网无功优化
[J]. 电网技术 , 2012 , 36 (2 ):158 -162 .
[本文引用: 3]
ZHANG Tingchang GENG Guangfei Reactive power optimization of medium voltage distribution network based on improved particle swarm optimization
[J]. Power System Technology , 2012 , 36 (2 ):158 -162 .
[本文引用: 3]
[8]
LI M YANG M YU Y et al. Wind power probabilistic forecasting based on wind correction using weather research and forecasting model
[C]// 2020 IEEE 3rd Student Conference on Electrical Machines and Systems (SCEMS),Jinan,China. IEEE , 2020 :19 -624 .
[本文引用: 1]
[9]
刘芳 , 汪震 , 刘睿迪 , 等 . 基于组合损失函数的BP神经网络风力发电短期预测方法
[J]. 浙江大学学报 , 2021 , 55 (3 ):594 -600 .
[本文引用: 1]
LIU Fang WANG Zhen LIU Ruidi et al. BP neural network short-term prediction method of wind power generation based on combined loss function
[J]. Journal of Zhejiang University , 2021 , 55 (3 ):594 -600 .
[本文引用: 1]
[10]
RABIEE A SOROUDI A MOHAMADI-IVATLOO B et al. Corrective voltage control scheme considering demand response and stochastic wind power
[J]. IEEE Transactions on Power Systems , 2014 , 29 (6 ):2965 -2973 .
DOI:10.1109/TPWRS.2014.2316018
URL
[本文引用: 1]
[11]
WU W ZHANG C SU J et al. The design of new high efficiency photovoltaic grid and independent power supply inverter
[C]// 2015 International Conference on Computational Intelligence and Communication Networks (CICN),Jabalpur,India. IEEE , 2015 :1579 -1582 .
[本文引用: 1]
[12]
石晓东 . 风机发电机中电力电子技术的应用
[J]. 中国新技术新产品 , 2020 (16 ):37 -38 .
[本文引用: 1]
SHI Xiaodong Application of power electronic technology in fan generator
[J]. New Technology & New Products of China , 2020 (16 ):37 -38 .
[本文引用: 1]
[13]
HUANG W ZHANG W Research on distributed wind power reactive voltage coordinated control strategy connected to distribution network
[C]// 2021 4th International Conference on Energy,Electrical and Power Engineering (CEEPE),Chongqing,China , 2021 : 529 -534 .
[本文引用: 1]
[14]
赵文芳 , 王京丽 , 尚敏 , 等 . 基于粒子群优化和支持向量机的花粉浓度预测模型
[J]. 计算机应用 , 2019 , 39 (1 ):98 -104 .
DOI:10.11772/j.issn.1001-9081.2018071626
[本文引用: 1]
为了提高花粉浓度预报的准确率,解决现有花粉浓度预报准确率不高的问题,提出了一种基于粒子群优化(PSO)算法和支持向量机(SVM)的花粉浓度预报模型。首先,综合考虑气温、气温日较差、相对湿度、降水量、风力、日照时数等多种气象要素,选择与花粉浓度相关性较强的气象要素构成特征向量;其次,利用特征向量与花粉浓度数据建立SVM预测模型,并使用PSO算法找出最优参数;然后利用最优参数优化花粉浓度预测模型;最后,使用优化后的模型对花粉未来24 h浓度进行预测,并与未优化的SVM、多元线性回归法(MLR)、反向神经网络(BPNN)作对比。此外使用优化后的模型对某市南郊观象台和密云两个站点进行逐日花粉浓度预测。实验结果表明,相比其他预报方法,所提方法能有效提高花粉浓度未来24 h预测精度,并具有较高的泛化能力。
ZHAO Wenfang WANG Jingli SHANG Min et al. Pollen concentration prediction model based on particle swarm optimization and support vector machine
[J]. Journal of Computer Applications , 2019 , 39 (1 ):98 -104 .
DOI:10.11772/j.issn.1001-9081.2018071626
[本文引用: 1]
To improve the accuracy of pollen concentration forecast and resolve low accuracy of current pollen concentration forecast model, a model for daily pollen concentration forecasting based on Particle Swarm Optimization (PSO) algorithm and Support Vector Machine (SVM) was proposed. Firstly, the feature vector extraction was carried out by using correlation analysis technique to select meteorological data with strong correlation with pollen concentration, such as temperature, daily temperature difference, relative humidity, precipitation, wind, sunshine hours. Secondly, an SVM prediction model based on this vector and pollen concentration observation data was established. The PSO algorithm was designed to optimize the parameters in SVM algorithm, and then the optimal parameters were used to construct daily pollen concentration prediction model. Finally, the forecast of pollen concentration in 24 hours in advance was made by using the optimized SVM model. The comparison among the accuracy of the optimized SVM model, Multiple Linear Regression (MLR) model and Back Propagation Neural Network (BPNN) model was performed to evaluate their performances. In addition, the optimized model was also applied for the forecast of pollen concentration in 24 hours in advance at Nanjiao and Miyun meteorological observation stations. The experimental results show that the proposed method performs better than MLR and BPNN methods. Meanwhile, it also provides promising results for forecast of pollen concentration in 24 hours in advance and also has good generalization ability.
[15]
强国栋 , 高锋阳 , 乔垚 , 等 . 基于改进粒子群算法的配电网无功优化
[J]. 电测与仪表 , 2018 , 55 (14 ):21 -26 .
[本文引用: 1]
QIANG Guodong GAO Fengyang QIAO Yao et al. Reactive power optimization of distribution network based on improved particle swarm optimization
[J]. Electrical Measurement and Instrumentation , 2018 , 55 (14 ):21 -26 .
[本文引用: 1]
[16]
李妍 , 马平 , 孙晓 . 基于三点估计法的含分布式电源配电网无功优化
[J]. 广东电力 , 2020 , 33 (7 ):19 -25 .
[本文引用: 1]
LI Yan MA Ping SUN Xiao Reactive power optimization of distribution network with distributed generation based on three-point estimation method
[J]. Guangdong Electric Power , 2020 , 33 (7 ):19 -25 .
[本文引用: 1]
[17]
陶志东 , 顾浩 , 丁晓群 . 基于电压稳定影响的多目标无功优化研究
[J]. 智慧电力 , 2018 , 46 (10 ):63 -70 .
[本文引用: 1]
TAO Zhidong GU Hao DING Xiaoqun Research on multi-objective reactive power optimization based on the influence of voltage stability
[J]. Smart Power , 2018 , 46 (10 ):63 -70 .
[本文引用: 1]
[18]
颜湘武 , 徐韵 , 李若瑾 , 等 . 基于模型预测控制含可再生分布式电源参与调控的配电网多时间尺度无功动态优化
[J]. 电工技术学报 , 2019 , 34 (10 ):2022 -2037 .
[本文引用: 1]
YAN Xiangwu XU Yun LI Ruojin et al. Multi time scale reactive power dynamic optimization of distribution network with renewable distributed generation based on model predictive control
[J]. Transaction of China Electrotechnial Scoiety , 2019 , 34 (10 ):2022 -2037 .
[本文引用: 1]
[19]
CHU Y FEI J HOU S Adaptive global sliding-mode control for dynamic systems using double hidden layer recurrent neural network structure
[J]. IEEE Transactions on Neural Networks and Learning Systems , 2019 , 31 (4 ):1297 -1309 .
DOI:10.1109/TNNLS.5962385
URL
[本文引用: 1]
[20]
康勇 , 林新春 , 潘辰 , 等 . 弱电网下采用SVC与SVG补偿后新能源并网变换器的功率传输特性分析
[J]. 中国电机工程学报 , 2021 , 41 (6 ):2115 -2125 .
[本文引用: 1]
KANG Yong LIN Xinchun PAN Chen et al. Analysis of power transmission characteristics of new energy grid connected converter after SVC and SVG compensation in weak current network
[J]. Proceedings of the CSEE , 2021 , 41 (6 ):2115 -2125 .
[本文引用: 1]
分布式光伏电源接入对配电网保护的影响
1
2020
... 近年来,随着不可再生能源的过度开采与消耗,能源紧缺的问题随之而来,同时碳达峰碳中和的目标理念也逐渐被提及,分布式电源(Distributed generation,DG)连入配电网的容量也越来越高.DG具有可再生的显著优势,但其存在的出力随机性也对配电网产生了不利的影响[1 ] . ...
Influence of distributed photovoltaic power access on distribution network protection
1
2020
... 近年来,随着不可再生能源的过度开采与消耗,能源紧缺的问题随之而来,同时碳达峰碳中和的目标理念也逐渐被提及,分布式电源(Distributed generation,DG)连入配电网的容量也越来越高.DG具有可再生的显著优势,但其存在的出力随机性也对配电网产生了不利的影响[1 ] . ...
Effect of distributed generation on power supply reliability of distribution network
1
2015
... 配电网是一个呈辐射状结构的网络,功率是从上往下传输的[2 ] .当大量的分布式电源连入配电网后,这种情况就发生改变,多点分布的功率进入配电网后改变了原有的潮流分布[3 ] ,会造成功率双向流动,电压波动,同时会增加线路损耗. ...
高比例可再生能源电力系统的关键科学问题与理论研究框架
1
2017
... 配电网是一个呈辐射状结构的网络,功率是从上往下传输的[2 ] .当大量的分布式电源连入配电网后,这种情况就发生改变,多点分布的功率进入配电网后改变了原有的潮流分布[3 ] ,会造成功率双向流动,电压波动,同时会增加线路损耗. ...
Key scientific issues and theoretical research framework of high proportion renewable energy power system
1
2017
... 配电网是一个呈辐射状结构的网络,功率是从上往下传输的[2 ] .当大量的分布式电源连入配电网后,这种情况就发生改变,多点分布的功率进入配电网后改变了原有的潮流分布[3 ] ,会造成功率双向流动,电压波动,同时会增加线路损耗. ...
基于改进粒子群算法的含DG配电网无功优化
1
2018
... 解决上述问题的重要措施为配电网的无功优化.无功优化是在保证系统安全运行的条件下,通过控制某些变量从而使电压稳定以及网损减少.针对无功优化,现在已经有许多的研究.文献[4 ]以总体网损以及电压波动最小为目标,并以节点电压以及电容器组投切组数为约束建立无功优化模型,用改进的粒子群算法来进行模型的求解,但分布式电源以固定出力来计算,没有考虑其出力的随机性.文献[5 ]考虑了风光出力的波动性对配电网的影响,以全天的网损以及电压偏移最小为目标,建立了兼顾电压安全与配电网经济运行的多目标优化模型.文献[6 ]提出了计及风光相关性的无功优化模型,以斯皮尔曼相关系数把风光出力的相关性表示出来,最后以各设备的出力为自变量,求得兼顾网损和电压偏差最小的多目标优化方案.文献[7 ]对于中压配电网的无功优化提出了同时求解补偿点和补偿量的方法,以年费用最小为目标创立优化模型,在粒子群算法中加入融合裂变的方法,可以避免陷入局部最优解的情况. ...
Reactive power optimization of distribution network with DG based on improved particle swarm optimization algorithm
1
2018
... 解决上述问题的重要措施为配电网的无功优化.无功优化是在保证系统安全运行的条件下,通过控制某些变量从而使电压稳定以及网损减少.针对无功优化,现在已经有许多的研究.文献[4 ]以总体网损以及电压波动最小为目标,并以节点电压以及电容器组投切组数为约束建立无功优化模型,用改进的粒子群算法来进行模型的求解,但分布式电源以固定出力来计算,没有考虑其出力的随机性.文献[5 ]考虑了风光出力的波动性对配电网的影响,以全天的网损以及电压偏移最小为目标,建立了兼顾电压安全与配电网经济运行的多目标优化模型.文献[6 ]提出了计及风光相关性的无功优化模型,以斯皮尔曼相关系数把风光出力的相关性表示出来,最后以各设备的出力为自变量,求得兼顾网损和电压偏差最小的多目标优化方案.文献[7 ]对于中压配电网的无功优化提出了同时求解补偿点和补偿量的方法,以年费用最小为目标创立优化模型,在粒子群算法中加入融合裂变的方法,可以避免陷入局部最优解的情况. ...
考虑风光出力波动性的实时互补性评价方法
1
2020
... 解决上述问题的重要措施为配电网的无功优化.无功优化是在保证系统安全运行的条件下,通过控制某些变量从而使电压稳定以及网损减少.针对无功优化,现在已经有许多的研究.文献[4 ]以总体网损以及电压波动最小为目标,并以节点电压以及电容器组投切组数为约束建立无功优化模型,用改进的粒子群算法来进行模型的求解,但分布式电源以固定出力来计算,没有考虑其出力的随机性.文献[5 ]考虑了风光出力的波动性对配电网的影响,以全天的网损以及电压偏移最小为目标,建立了兼顾电压安全与配电网经济运行的多目标优化模型.文献[6 ]提出了计及风光相关性的无功优化模型,以斯皮尔曼相关系数把风光出力的相关性表示出来,最后以各设备的出力为自变量,求得兼顾网损和电压偏差最小的多目标优化方案.文献[7 ]对于中压配电网的无功优化提出了同时求解补偿点和补偿量的方法,以年费用最小为目标创立优化模型,在粒子群算法中加入融合裂变的方法,可以避免陷入局部最优解的情况. ...
Real time complementarity evaluation method considering the fluctuation of wind and solar output
1
2020
... 解决上述问题的重要措施为配电网的无功优化.无功优化是在保证系统安全运行的条件下,通过控制某些变量从而使电压稳定以及网损减少.针对无功优化,现在已经有许多的研究.文献[4 ]以总体网损以及电压波动最小为目标,并以节点电压以及电容器组投切组数为约束建立无功优化模型,用改进的粒子群算法来进行模型的求解,但分布式电源以固定出力来计算,没有考虑其出力的随机性.文献[5 ]考虑了风光出力的波动性对配电网的影响,以全天的网损以及电压偏移最小为目标,建立了兼顾电压安全与配电网经济运行的多目标优化模型.文献[6 ]提出了计及风光相关性的无功优化模型,以斯皮尔曼相关系数把风光出力的相关性表示出来,最后以各设备的出力为自变量,求得兼顾网损和电压偏差最小的多目标优化方案.文献[7 ]对于中压配电网的无功优化提出了同时求解补偿点和补偿量的方法,以年费用最小为目标创立优化模型,在粒子群算法中加入融合裂变的方法,可以避免陷入局部最优解的情况. ...
计及风光出力相关性的配电网多目标无功优化
1
2020
... 解决上述问题的重要措施为配电网的无功优化.无功优化是在保证系统安全运行的条件下,通过控制某些变量从而使电压稳定以及网损减少.针对无功优化,现在已经有许多的研究.文献[4 ]以总体网损以及电压波动最小为目标,并以节点电压以及电容器组投切组数为约束建立无功优化模型,用改进的粒子群算法来进行模型的求解,但分布式电源以固定出力来计算,没有考虑其出力的随机性.文献[5 ]考虑了风光出力的波动性对配电网的影响,以全天的网损以及电压偏移最小为目标,建立了兼顾电压安全与配电网经济运行的多目标优化模型.文献[6 ]提出了计及风光相关性的无功优化模型,以斯皮尔曼相关系数把风光出力的相关性表示出来,最后以各设备的出力为自变量,求得兼顾网损和电压偏差最小的多目标优化方案.文献[7 ]对于中压配电网的无功优化提出了同时求解补偿点和补偿量的方法,以年费用最小为目标创立优化模型,在粒子群算法中加入融合裂变的方法,可以避免陷入局部最优解的情况. ...
Multi objective reactive power optimization of distribution network considering the correlation between wind and solar output
1
2020
... 解决上述问题的重要措施为配电网的无功优化.无功优化是在保证系统安全运行的条件下,通过控制某些变量从而使电压稳定以及网损减少.针对无功优化,现在已经有许多的研究.文献[4 ]以总体网损以及电压波动最小为目标,并以节点电压以及电容器组投切组数为约束建立无功优化模型,用改进的粒子群算法来进行模型的求解,但分布式电源以固定出力来计算,没有考虑其出力的随机性.文献[5 ]考虑了风光出力的波动性对配电网的影响,以全天的网损以及电压偏移最小为目标,建立了兼顾电压安全与配电网经济运行的多目标优化模型.文献[6 ]提出了计及风光相关性的无功优化模型,以斯皮尔曼相关系数把风光出力的相关性表示出来,最后以各设备的出力为自变量,求得兼顾网损和电压偏差最小的多目标优化方案.文献[7 ]对于中压配电网的无功优化提出了同时求解补偿点和补偿量的方法,以年费用最小为目标创立优化模型,在粒子群算法中加入融合裂变的方法,可以避免陷入局部最优解的情况. ...
基于改进粒子群算法的中压配电网无功优化
3
2012
... 解决上述问题的重要措施为配电网的无功优化.无功优化是在保证系统安全运行的条件下,通过控制某些变量从而使电压稳定以及网损减少.针对无功优化,现在已经有许多的研究.文献[4 ]以总体网损以及电压波动最小为目标,并以节点电压以及电容器组投切组数为约束建立无功优化模型,用改进的粒子群算法来进行模型的求解,但分布式电源以固定出力来计算,没有考虑其出力的随机性.文献[5 ]考虑了风光出力的波动性对配电网的影响,以全天的网损以及电压偏移最小为目标,建立了兼顾电压安全与配电网经济运行的多目标优化模型.文献[6 ]提出了计及风光相关性的无功优化模型,以斯皮尔曼相关系数把风光出力的相关性表示出来,最后以各设备的出力为自变量,求得兼顾网损和电压偏差最小的多目标优化方案.文献[7 ]对于中压配电网的无功优化提出了同时求解补偿点和补偿量的方法,以年费用最小为目标创立优化模型,在粒子群算法中加入融合裂变的方法,可以避免陷入局部最优解的情况. ...
... 根据文献[7 ]可知,风机的输出功率为 ...
... 参考文献[7 ],本文将最小化均方差误差函数与交叉熵损失函数、排序损失函数相结合组成了组合损失函数,以此作为训练目标[8 ] .将风电场未来一日内间隔为15 min的NWP气象预测数据作为输入,训练样本为过去几日或者十几日的气象数据和风电场实际功率数据[9 ] ,从而得到所需日期的全天风电预测数据曲线. ...
Reactive power optimization of medium voltage distribution network based on improved particle swarm optimization
3
2012
... 解决上述问题的重要措施为配电网的无功优化.无功优化是在保证系统安全运行的条件下,通过控制某些变量从而使电压稳定以及网损减少.针对无功优化,现在已经有许多的研究.文献[4 ]以总体网损以及电压波动最小为目标,并以节点电压以及电容器组投切组数为约束建立无功优化模型,用改进的粒子群算法来进行模型的求解,但分布式电源以固定出力来计算,没有考虑其出力的随机性.文献[5 ]考虑了风光出力的波动性对配电网的影响,以全天的网损以及电压偏移最小为目标,建立了兼顾电压安全与配电网经济运行的多目标优化模型.文献[6 ]提出了计及风光相关性的无功优化模型,以斯皮尔曼相关系数把风光出力的相关性表示出来,最后以各设备的出力为自变量,求得兼顾网损和电压偏差最小的多目标优化方案.文献[7 ]对于中压配电网的无功优化提出了同时求解补偿点和补偿量的方法,以年费用最小为目标创立优化模型,在粒子群算法中加入融合裂变的方法,可以避免陷入局部最优解的情况. ...
... 根据文献[7 ]可知,风机的输出功率为 ...
... 参考文献[7 ],本文将最小化均方差误差函数与交叉熵损失函数、排序损失函数相结合组成了组合损失函数,以此作为训练目标[8 ] .将风电场未来一日内间隔为15 min的NWP气象预测数据作为输入,训练样本为过去几日或者十几日的气象数据和风电场实际功率数据[9 ] ,从而得到所需日期的全天风电预测数据曲线. ...
Wind power probabilistic forecasting based on wind correction using weather research and forecasting model
1
2020
... 参考文献[7 ],本文将最小化均方差误差函数与交叉熵损失函数、排序损失函数相结合组成了组合损失函数,以此作为训练目标[8 ] .将风电场未来一日内间隔为15 min的NWP气象预测数据作为输入,训练样本为过去几日或者十几日的气象数据和风电场实际功率数据[9 ] ,从而得到所需日期的全天风电预测数据曲线. ...
基于组合损失函数的BP神经网络风力发电短期预测方法
1
2021
... 参考文献[7 ],本文将最小化均方差误差函数与交叉熵损失函数、排序损失函数相结合组成了组合损失函数,以此作为训练目标[8 ] .将风电场未来一日内间隔为15 min的NWP气象预测数据作为输入,训练样本为过去几日或者十几日的气象数据和风电场实际功率数据[9 ] ,从而得到所需日期的全天风电预测数据曲线. ...
BP neural network short-term prediction method of wind power generation based on combined loss function
1
2021
... 参考文献[7 ],本文将最小化均方差误差函数与交叉熵损失函数、排序损失函数相结合组成了组合损失函数,以此作为训练目标[8 ] .将风电场未来一日内间隔为15 min的NWP气象预测数据作为输入,训练样本为过去几日或者十几日的气象数据和风电场实际功率数据[9 ] ,从而得到所需日期的全天风电预测数据曲线. ...
Corrective voltage control scheme considering demand response and stochastic wind power
1
2014
... 随着电力电子器件的发展,通过逆变器连接到配电网的分布式电源也有一定的无功调节能力.当光伏发电通过逆变器连接到配电网时,其无功调节能力与逆变器的稳定运行密切相关.受变频器的最大工作电流以及可逆电压的限制[10 ] ,光伏的有功功率与无功功率的关系为 ...
The design of new high efficiency photovoltaic grid and independent power supply inverter
1
2015
... 这里为了确保分布式电源的无功调节能力,所以利用DG最低无功功率调节的上限来获得最低可能值,以及DG最高无功功率调节的下限来获得最高可能值[11 ] . ...
风机发电机中电力电子技术的应用
1
2020
... 双馈风力电机可以控制并产生无功功率,通过独立控制转子励磁电流来解耦有功和无功功率的控制.其次,无需从电网励磁,而是从转子电路中励磁[12 ] .由于它是通过逆变器连接到电网中,因此风电的无功调节能力受到逆变器运行的影响.受定子侧与转子侧转换器最大电流的限制,单个风力发电的有功功率与无功功率的关系如下 ...
Application of power electronic technology in fan generator
1
2020
... 双馈风力电机可以控制并产生无功功率,通过独立控制转子励磁电流来解耦有功和无功功率的控制.其次,无需从电网励磁,而是从转子电路中励磁[12 ] .由于它是通过逆变器连接到电网中,因此风电的无功调节能力受到逆变器运行的影响.受定子侧与转子侧转换器最大电流的限制,单个风力发电的有功功率与无功功率的关系如下 ...
Research on distributed wind power reactive voltage coordinated control strategy connected to distribution network
1
2021
... 同时,风力发电机受到静态稳定极限的影响[13 ] ,公式如下所示 ...
基于粒子群优化和支持向量机的花粉浓度预测模型
1
2019
... 粒子群优化算法(Particle swarm optimization, PSO)是模拟鸟群的觅食行为,每个问题的解都相当于搜索空间中的一只鸟,也被称为粒子[14 ] .所有的粒子都有由目标函数决定的适应值,每个粒子还有一个速度来决定下一次移动的距离和方向.PSO初始为一群随机解,然后进行迭代来求最优解[15 ] ,在每一次迭代中,每个粒子都通过两个极值来更新本身的速度,第一个是粒子自己的最优解,另一个是全局最优解,其具体公式为 ...
Pollen concentration prediction model based on particle swarm optimization and support vector machine
1
2019
... 粒子群优化算法(Particle swarm optimization, PSO)是模拟鸟群的觅食行为,每个问题的解都相当于搜索空间中的一只鸟,也被称为粒子[14 ] .所有的粒子都有由目标函数决定的适应值,每个粒子还有一个速度来决定下一次移动的距离和方向.PSO初始为一群随机解,然后进行迭代来求最优解[15 ] ,在每一次迭代中,每个粒子都通过两个极值来更新本身的速度,第一个是粒子自己的最优解,另一个是全局最优解,其具体公式为 ...
基于改进粒子群算法的配电网无功优化
1
2018
... 粒子群优化算法(Particle swarm optimization, PSO)是模拟鸟群的觅食行为,每个问题的解都相当于搜索空间中的一只鸟,也被称为粒子[14 ] .所有的粒子都有由目标函数决定的适应值,每个粒子还有一个速度来决定下一次移动的距离和方向.PSO初始为一群随机解,然后进行迭代来求最优解[15 ] ,在每一次迭代中,每个粒子都通过两个极值来更新本身的速度,第一个是粒子自己的最优解,另一个是全局最优解,其具体公式为 ...
Reactive power optimization of distribution network based on improved particle swarm optimization
1
2018
... 粒子群优化算法(Particle swarm optimization, PSO)是模拟鸟群的觅食行为,每个问题的解都相当于搜索空间中的一只鸟,也被称为粒子[14 ] .所有的粒子都有由目标函数决定的适应值,每个粒子还有一个速度来决定下一次移动的距离和方向.PSO初始为一群随机解,然后进行迭代来求最优解[15 ] ,在每一次迭代中,每个粒子都通过两个极值来更新本身的速度,第一个是粒子自己的最优解,另一个是全局最优解,其具体公式为 ...
基于三点估计法的含分布式电源配电网无功优化
1
2020
... 惯性权重ω 代表粒子当前速度对先前速度的记忆能力,本文使用指数递减惯性权重策略[16 ] ,即 ...
Reactive power optimization of distribution network with distributed generation based on three-point estimation method
1
2020
... 惯性权重ω 代表粒子当前速度对先前速度的记忆能力,本文使用指数递减惯性权重策略[16 ] ,即 ...
基于电压稳定影响的多目标无功优化研究
1
2018
... 学习因子c 1 和c 2 是调节个体与全局最优值在速度更新中所占的比例[17 ] ,为了提高搜索精度,在初期使得学习因子满足c 1 >c 2 ,而在后期使得学习因子满足c 1 <c 2 .具体公式如下 ...
Research on multi-objective reactive power optimization based on the influence of voltage stability
1
2018
... 学习因子c 1 和c 2 是调节个体与全局最优值在速度更新中所占的比例[17 ] ,为了提高搜索精度,在初期使得学习因子满足c 1 >c 2 ,而在后期使得学习因子满足c 1 <c 2 .具体公式如下 ...
基于模型预测控制含可再生分布式电源参与调控的配电网多时间尺度无功动态优化
1
2019
... 本文采用改进的IEEE33节点系统来进行仿真,其原有的线路参数不变,改进后的系统如图1 所示.在此节点系统中,基准电压为12.66 kV,基准功率为10 MV·A.系统中电压的约束范围为0.95~1.05 p.u.[18 ] .0号与1号节点安装有载变压调压器,其调节范围为±4×1.25%.在5号和28号节点连接静止无功补偿器,其无功出力范围0~500 kVar.在9号、16号、23号以及31号节点安装DG,包含风力发电以及光伏发电. ...
Multi time scale reactive power dynamic optimization of distribution network with renewable distributed generation based on model predictive control
1
2019
... 本文采用改进的IEEE33节点系统来进行仿真,其原有的线路参数不变,改进后的系统如图1 所示.在此节点系统中,基准电压为12.66 kV,基准功率为10 MV·A.系统中电压的约束范围为0.95~1.05 p.u.[18 ] .0号与1号节点安装有载变压调压器,其调节范围为±4×1.25%.在5号和28号节点连接静止无功补偿器,其无功出力范围0~500 kVar.在9号、16号、23号以及31号节点安装DG,包含风力发电以及光伏发电. ...
Adaptive global sliding-mode control for dynamic systems using double hidden layer recurrent neural network structure
1
2019
... 风电机组的有功额定容量为400 kW,无功出力范围为-140~180 kVar.光伏机组的有功额定容量为300 kW,无功出力范围为-100~120 kVar.风力发电的出力情况是以基于组合损失函数的BP函数来预测,使用预测日的NWP数据,经过训练得出最小误差的预测出力曲线,本文采用了层数为5-4-1的BP神经网络结构,其隐含层和输出层的传递函数分别为tansig函数和purelin函数,学习率设置为0.001,联合损失函数的权重系数为1,1,0.001,并以平均绝对误差和均方根误差来反映预测值的误差情况[19 ] ,如表1 所示.光伏发电的出力是以标准日的光照水平得出的预测出力曲线.将两者结合得出DG的有功出力曲线,如图2 所示. ...
弱电网下采用SVC与SVG补偿后新能源并网变换器的功率传输特性分析
1
2021
... 静止无功补偿器是现代技术较成熟的FACTS设备,常用于电力系统的负荷优化以及配电系统优化.它没有采用大容量的电感器以及电容器来生成需要的无功容量,而是采用电力电子器件来实现,这是无功补偿技术的巨大进步,它的动态无功优化与以往的电容器组投切相比更加灵活,并且可以对扰动产生较快的反应[20 ] ,由于其不需要投切的变化,所以运行成本也会更低,图6 为两个静止无功补偿器优化后的24 h补偿容量曲线. ...
Analysis of power transmission characteristics of new energy grid connected converter after SVC and SVG compensation in weak current network
1
2021
... 静止无功补偿器是现代技术较成熟的FACTS设备,常用于电力系统的负荷优化以及配电系统优化.它没有采用大容量的电感器以及电容器来生成需要的无功容量,而是采用电力电子器件来实现,这是无功补偿技术的巨大进步,它的动态无功优化与以往的电容器组投切相比更加灵活,并且可以对扰动产生较快的反应[20 ] ,由于其不需要投切的变化,所以运行成本也会更低,图6 为两个静止无功补偿器优化后的24 h补偿容量曲线. ...