随着现代社会中超大城市及城市群的形成，电网规模不断扩大，其结构也日趋复杂，所产生的数据也呈现爆炸式增长^[1]。在迅速积累的海量数据中，如何挖掘出与电力系统稳定运行相关联的信息并发挥其价值，是电力系统数据挖掘的关键问题，也是提高电力系统安全稳定性的重要途径。电力系统暂态稳定评估是指在电力系统正常运行时受到某一扰动，模型及时判断系统是否能继续保持稳态。目前，基于相位测量装置的广域测量系统^[2-3]的出现实现了对电力系统实时检测并记录稳态和动态轨迹信息，为电力系统暂态稳定评估提供了大量系统信息，为研究人员从数据挖掘的角度解决这一问题提供了新思路。

按照人工智能方法的发展，暂态稳定评估研究经历了两个阶段：浅层学习模型阶段和深度学习模型阶段。最初的研究者将人工神经网络作为主要的评估模型，在评估方法进一步发展后，暂态稳定评估模型主要包括决策树^[4⇓-6]、支持向量机^{[7⇓⇓⇓-11]}、极限学习机^[12]等浅层学习方法。其中，文献[4]提出一种基于暂态稳定裕度指标的多属性决策树方法。文献[7]提出在安全域概念下基于多支持向量机综合的电力系统暂态稳定评估方法。文献[12]则以传统的基于理论模型的电力系统数值仿真方法为基础，设计出基于极限学习机的评估模型。以上几种机器学习方法均为浅层学习模型，虽然它们都能在一定程度上完成对电力系统暂态的稳定评估，但是都存在浅层学习模型的共同问题，就是对于大电网的高维数据进行分类时模型泛化能力差、训练效率低，并且特征提取时需要依靠专家经验，缺乏科学依据。

近年来，随着深度学习方法的蓬勃发展和数据处理能力的提升，深度学习算法被广泛应用于电力系统暂态稳定评估。目前常用的深度学习方法包括卷积神经网络^[13]、深度置信网络^[14-15]和堆叠自动编码器^[16]等。文献[14]提出了一种基于集成DBN的两阶段暂态稳定评估方法。文献[16]采用一种“预训练-参数微调”两阶段学习方法，提出一种基于堆叠自动编码器的电力系统暂态稳定评估方法。相较于浅层学习模型，深度学习模型通过多层串行的深层架构能够实现基于高维数据的抽象表达与分类，泛化能力也优于浅层模型。然而，深度学习模型的训练需要大量的样本数据，样本数量过少会导致模型最后的拟合程度不足，评估精度不高，但大量的高维数据也可能会出现维数灾难。

在电力系统暂态的过程中，电力系统的物理量(电压、电流、功率、功角等)具有明显的时变特征，电力系统生成的原始数据是一种时间序列数据^[17]。常见的机器学习模型没有挖掘数据中蕴含的时间维度信息，导致时序特征淹没在很多常见特征中，制约了模型评估性能。此外在电力系统中，失稳样本数量要少于暂态稳定样本，存在天然的样本不平衡问题，会使模型在训练过程中具有偏向性，对某一样本的评估更易判定为稳定，在实际电力系统运行过程中，将失稳样本误判为稳定样本会造成重大损失。

针对以上问题，本文提出一种基于邻域粗糙集和改进双向长短期记忆网络的电力系统暂态稳定评估方法。利用邻域粗糙集对原始数据集进行属性约简，得到原始数据的最优特征子集，进一步优化分类模型的评估性能。通过双向长短期记忆网络使分类模型真正实现对暂态过程时序特征的提取，通过注意力机制使模型聚焦于与失稳样本相关的特征，引入焦点损失函数，解决了样本中两类样本数量不平衡的问题，对失稳样本设置更多的关注，减少模型误分类的情况。最后，在新英格兰10机39节点仿真系统中验证了所提方法的准确性和有效性。

基于数据挖掘的电力系统暂态评估方法是以数据为导向的，构建一组与电力系统暂态过程高度关联的原始特征集对模型的评估性能十分重要。根据时间的差异，系统特征可分为静态特征和动态特征。静态特征是指在故障发生前系统的一些潮流量，包括母线电压相角、有功无功功率等。动态特征是故障持续过程中和故障后的一些状态变量或者由其各自组合的组合指标，如转子的角速度、加速度和转子动能、发动机所受冲击等。

在对原始特征集进行选取时，通常要考虑三个原则：系统性、关联性和实效性，即所选特征满足以下特点：① 电力系统的规模大小对原始特征集没有影响，特征不是某一条母线或电机的状态量；② 所选特征量能很好地反映系统的状态，与暂态稳定状态有强关联性；③ 在短时间内，所选的特征量能良好反映系统的稳定性，具有时效性。

根据以上三个原则和参考文献，本文构建了如表1所示的原始特征集，其中t₀、t₁、t₂分别表示故障发生前、故障发生时刻和故障切除时刻。表1中的特征涵盖整个系统暂态过程，充分反映故障对电力系统的冲击影响，所选特征量大多是系统转子、发电机状态和系统物理量的组合指标，构建的特征集不受系统规模影响。其中特征1,2,4,5,13,14,20~22与系统运行水平相关，反映了故障对系统的功率影响；特征6,7,9~12,16~19与转子速度和角速度相关，反映了扰动对转子的影响；特征8,15与转子角度有关，反映系统的同步运行状态。从表1可以看出，构建的特征集可以很好地体现整个电力系统暂态过程，为后续的深度学习分类模型打下良好的基础。

给定实数空间中的有限非空集合，对于U上的任意对象，定义其邻域为信息系统〈U,C,D,f〉，其中U是全部样本的有限集合，称为论域，设有n个对象，则可表示成U=x1,x2,⋯,xn；C为有限个条件属性，设有m个条件属性，表示为C=c1,c2,⋯,cm；D为样本对应的标签属性，也称为决策属性；f为信息函数，f:U×C→D,f(xi,cj)∈Dj。

给定实数空间中的有限非空集合$U=\left\{x_{1}, x_{2}, x_{3}, \mathrm{~L}, x_{n}\right\}$，对于U上的任意对象x_i，定义其邻域为

式中，δ为邻域的阈值，在数据进行标准化以后其数值介于0与1之间；Δ为距离函数。

定义信息系统〈U,C,D,f〉，B⊆A，对于∀xi,xj∈U，令

式中，B满足B=s，当p取不同值时，ΔpB表示的距离含义就不同，本文计算样本之间的距离时p取2，ΔpB为欧式距离。

给定决策系统〈U,C,D,f〉，D将U分成N个等价类，对∀B⊆A，决策D关于特征子集B的下近似为

其中，NB_Xi=xi|δBxi⊆X,xi∈U，δBxi是由特征B和距离度量Δ得到的邻域阈值。决策的下近似也称为决策正域，记为POSBD，决策属性D对条件属性子集B的依赖度定义为

式中，U表示集合U的基数。

对∀B⊆A，属性a∈B，条件属性a对决策属性a的重要度为

基于属性重要度构造一种前向贪心式属性约简算法^[18⇓-20]，该算法以空集为起点，每次计算全部剩余属性的属性重要度，从中选择属性重要度最大的属性加入约简集合，直到剩余属性的重要度为0，即加入任何新的属性，系统依赖度函数的值不再变化为止。相较后向搜索算法，前向搜索算法保证了在有大量冗余特征的样本中将最重要的属性最先提取出来，加入约简集合，既节省了搜索所需的时间，也能去除大量单一分辨能力弱但整体拥有较好分辨能力的特征^[21-22]。属性约简具体过程如下所示。

(1) 对于任意的某个条件属性a，计算它的邻域关系N_a，定义初始空约简集合red。

(2) 对每一个不属于red的条件属性a_i，计算其属性重要度，并取得最大属性重要度的特征a_k。

(3) 如果特征a_k的属性重要度大于0，则将其放入约简集合red，转到第(2)步继续执行，否则输出属性约简集合red。

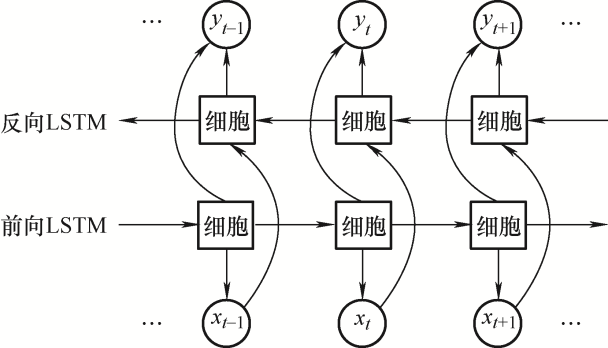
双向长短期记忆网络由连接着同一个输入层的前后两向的长短期记忆网络构成，如图1所示，总输出为两层LSTM的输出之和。

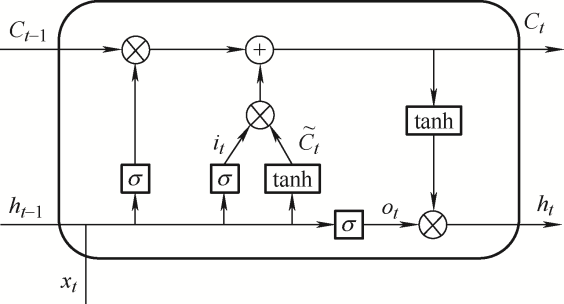
长短期记忆网络是一种时间递归网络，为解决循环神经网络存在梯度消失的问题而提出，通常用于处理间隔和延迟时间较长的时间序列，模型结构如图2所示。长短期记忆网络通过几个不同模块之间的组合判断当前系统信息是否有用，从而决定信息的保存与遗忘，是解决长序列依赖问题的有效手段。长短期记忆网络的结构单元主要包括输入门、遗忘门、输出门以及一个自连接的记忆单元状态值。

其中，输入门决定让多少新信息加入到当前状态，tanh函数决定当前的候选信息Ct˜，再与一个通过sigmoid函数生成的决策向量i_t相乘，得到的结果就确定了候选信息Ct˜有多少内容能加入到单元状态C_t中，计算公式为

遗忘门决定上一时刻的单元状态C_t-1有多少信息能保留到当前时刻的单元状态C_t中，上一时刻的隐藏状态h_t-1与当前时刻的输入x_t作为遗忘门的输入，通过sigmoid函数，得到决策向量f_t，再与上一个时刻的单元状态C_t-1相乘，得到遗忘门的结果，计算公式如下

输出门决定当前细胞的输出和输入到下一个细胞的隐藏状态，上一时刻的隐藏状态h_t-1与当前时刻的输入x_t通过sigmoid函数得到向量o_t，当前单元状态C_t与tanh激活函数生成另一个变量，两者相乘得到当前时刻的隐藏状态h_t，计算表达式为

输入门和遗忘门的结果都作用于细胞状态C_t，细胞状态C_t由上一时刻的单元状态C_t-1与决策向量f_t的乘积加上决策向量i_t与候选信息Ct˜的乘积组成，即

式中，W_i、W_c、W_f、W_o都是各层之间的权重矩阵；b_i、b_c、b_f、b_o是各结构中对应的偏置向量；σ为激活函数sigmoid。

注意力模型最初被用于机器翻译，如今被广泛用于神经网络模型中。传统的编码器-解码器框架在处理数据时，编码器必须将所有输入信息压缩成一个固定的长度，然后将其传给解码器，这可能会导致信息在传递过程中丢失。其次，传统框架无法对结构化输出任务中的输入与输出序列间对齐进行建模。在Seq2Seq任务中，我们期望的输出受输入序列中的某一部分影响较大，但是解码器中缺乏在生成输出时选择性关注相关的输入机制。

注意力模型旨在通过允许解码器访问整个编码的输入序列来解决这些问题，核心思想是在输入序列上引入注意力权重，以优先考虑存在相关信息的位置集，生成下一个输出。网络结构中的注意力模块负责自动学习注意力权重，它可以自动捕获编码器隐藏状态和解码器隐藏状态之间的相关性，注意力权重构建内容向量C，该向量作为输入传递给解码器，在每个解码位置j，内容向量是编码器所有隐藏状态及相应注意力权重的加权和。

为解决数据样本中失稳样本和暂态稳定样本间的不平衡问题，在评估模型中引入焦点损失函数。焦点损失函数是在二值交叉熵损失函数的基础上增加一个常数项α和一个指数项(1−y′)γ进行改进的，如下所示

式中，α是样本数量平衡因子，用来调节正负样本的比重，当α越接近1时，正样本对损失函数的贡献就越大；γ是难易平衡因子，当γ越大时，难分样本对损失函数的贡献越大。焦点损失函数可以同时解决正负、难易样本的分割问题，α和γ参数决定样本的优先级，可根据实际情况调整这两个参数。

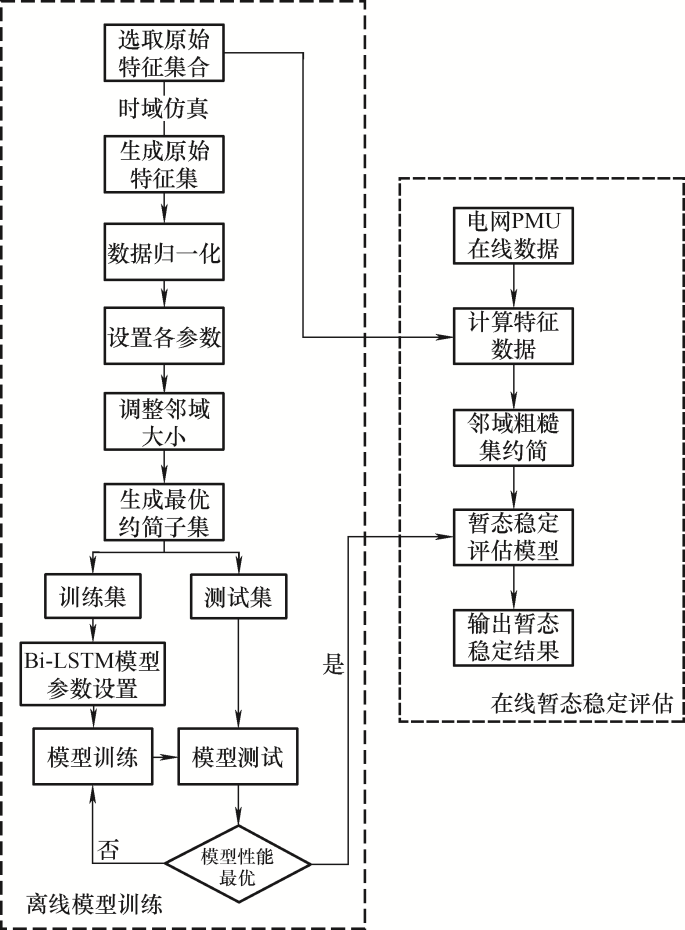
本文设计出一种基于邻域粗糙集和改进Bi-LSTM的电力系统暂态评估模型，流程如图3所示。

在离线训练阶段，首先通过时域仿真模拟系统故障，生成故障样本库，读取各发电机节点仿真数据模拟同步相量测量单位(Phasor measurement unit, PMU)测量过程。在文献[18]中的邻域阈值范围[0,0.2]进行阈值调试，在保证约简结果良好的条件下，将原始数据集中23维的特征降低特征维度，得到不同粒度下的互异约简子集，挑选约简结果的最重要因素是在降低数据维度的前提下约简子集总的重要度接近1，达到与原始数据集近似的效果。在设计深度模型时，将约简后的输入数据集进行十折交叉验证，整个模型主要包括卷积层、Bi-LSTM层、注意力层和输出层，采用Adam优化算法对模型学习率进行自适应调整，使用焦点损失函数替换普通交叉熵函数。为了模型获得更好的泛化能力，使用Dropout策略，并对权值矩阵进行L2范数正则化。

在线暂态稳定评估阶段，读取电网实时同步相量测量单位(PMU)的数据，对数据进行归一化后，将其在邻域粗糙集约简得到的特征子空间进行再表征，再送入训练好的深度学习分类模型中，给出电网暂态稳定状态的预测结果，为电网调度人员作进一步决策提供帮助。

电力系统暂态稳定评估是一个二分类问题，最终判断系统在扰动后是否稳定，通过受扰动后系统各发动机功角的暂态稳定指数(Transient stability index, TSI)，对数据进行标签，表达式为

式中，Δδ_max为仿真时间内任意两台发电机的最大功角差，当Δδ_max小于360°，即TSI大于0，则系统暂态稳定，标签标注为1；当Δδ_max大于360°，即TSI小于0，则系统暂态不稳定，标签标注为0。

对模型进行暂态稳定评估时，误判稳定样本和漏判稳定样本造成损失的严重程度不同。前者将失稳样本误判为稳定，导致电力系统中的故障清除装置不能及时反应，给整个电力系统造成严重破坏，而后者是将稳定样本判定为失稳，使故障清除装置动作，并不会导致太严重的后果。所以考虑到样本类别不平衡和错分代价不同，除了采用常规模型评估使用的准确率ACC之外，还引入漏判率MA、误判率FA和G-mean指标。表2为暂态稳定评估混淆矩阵。各项评估指标的表达式如表3所示。

其中，ACC表示模型对稳定和失稳样本的分类准确度，越高分类效果越好，是评估模型性能好坏的首要关注点；漏判率MA反映模型正确预测负样本纯度的能力，即稳定样本被预测为失稳样本占总稳定样本的比例，MA越小，模型性能越好；误判率FA反映模型正确预测正样本纯度的能力，即失稳样本被预测为稳定样本占总失稳样本的比例，FA越小，模型性能越好；G-mean综合考虑了对稳定样本和失稳样本的评估准确率，G-mean越大，模型对两种类别样本分类的学习效果越平衡，模型评估性能越好。

以新西兰10机39节点为算例在Matlab/Simulink进行时域仿真并根据表1的特征集生成原始数据集，在仿真时考虑全接线系统和N-1、N-2故障运行方式，后两种故障环境为假设系统中任意一条或两条线路、变压器故障失效。以5%为步长，从80%开始，逐渐增加到125%，共设置10个不同负荷水平，调整发电机的发力使潮流收敛。在每种运行方式下，故障位置设在每条输电线路的始段和末端，故障类型设置为三相短路，故障发生时刻为0.1 s，并分别在0.2 s、0.3 s、0.4 s和0.5 s清除故障，仿真时长为5 s。本文通过Matlab/Simulink仿真共生成7 000组样本，其中稳定样本4 818个，失稳样本2 182个，在试验中采用十折交叉验证划分训练集和测试集。

本文模型参数主要是两类，包括邻域粗糙集约简阶段邻域阈值的设定和深度学习算法中的焦点损失函数。

在邻域约简阶段，根据文献[18]设置邻域区间范围为[0,0.3]，以0.01步长设定邻域阈值进行约简，得到若干组互有差异的邻域约简结果，且保证约简过后子集的所有属性重要度之和在0.95以上。不同粒度级别下的邻域约简结果如表4所示。

将不同粒度级别得到的约简子集和23维原始数据集作为IM-Bi-LSTM模型的输入集，在不改变整个深度模型参数的条件下，对模型性能进行评估和分析。评估结果如表5所示。

从表4可以看出，R1粒度级别下的约简子集是最优子集，既保证对特征实现降维，又能得到最佳的评估性能。对比未经约简的原始数据集，在四项评估指标上较其都更为优异。可见，邻域粗糙集摒除原始数据集的冗余特征信息，对于提高分类模型的性能有一定的实际意义。在R3和R4粒度级别下，模型的评估性能要差于原始数据集，这说明不能一味地追求特征集降维，约简后的子集也不能很好地再表征特征集。

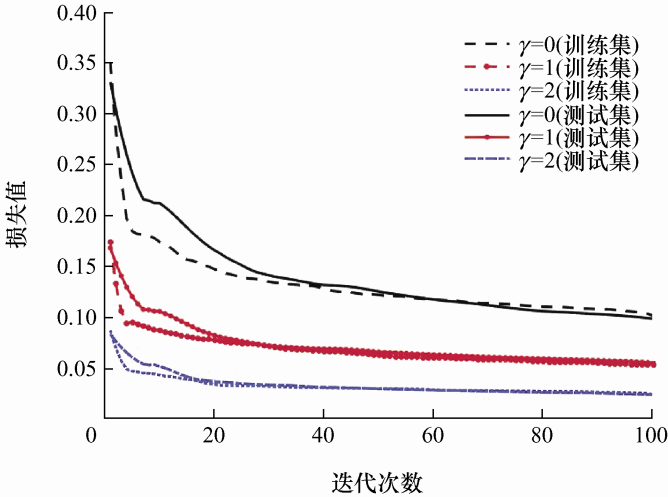
焦点损失函数中有α、γ两个参数，其中α为样本数量平衡因子，表示失稳样本数量与总数据集数量的比值，γ为调试因子指数，表示模型对难易样本的重视程度。当γ取0时，损失函数即为带类别权重的普通二分类交叉熵损失函数。训练过程对比如图4所示。

从图4可以看出，在训练集和测试集上，加入调试因子的焦点损失值比普通交叉熵损失值更小，训练过程更加平稳，说明本文模型采用焦点损失函数提升了模型性能。当γ=2或者1时，训练集和测试集的损失值差距较小，而在迭代10次以后普通交叉熵函数模型的训练集损失与测试集差距较大，说明焦点损失函数能防止模型过拟合。文献[19]中，经过大量数据集验证了当γ=2时，模型训练效果最好。经本文数据验证，γ=2时模型性能最佳，以下讨论中本文模型均采用γ=2作为超参数。

为了验证模型性能，选择常规的机器学习算法进行对比分析，包括SVM、KNN、决策树、卷积神经网络和双向长短期记忆网络，数据集为第5.2节中约简得到的R1粒度级别下的最优约简子集。本文所提IM-Bi-LSTM模型采用Adam学习算法自适应调整学习率，使用L2范数进行正则化，正则化系数设置为0.001，焦点损失函数的α、γ两个参数分别设置为0.3和2。SVM采用高斯核函数，惩罚系数c设置为1。K近邻算法中近邻数K取5，距离度量选择欧式距离，搜索算法选择数据结构中的二叉树。决策树采用CART决策树，最大深度设为10。卷积神经网络设置3层卷积层，训练算法采用梯度下降算法。双向长短期记忆网络的参数与本文使用的IM-Bi-LSTM相同。最终，不同模型的暂态稳定评估结果如表6所示。

从表6可以看出，基于IM-Bi-LSTM的模型在各个评估指标上都优于其他算法模型，不仅有较高的准确率，而且算法对失稳样本的重视使得其对失稳样本的误判明显低于其他分类算法。以决策树为例，本文所提模型在总的准确率上提高了3.74%，而反映模型漏判和误判指标的MA、FA分别降低了2.1%和4.81%，有效降低了漏判和误判带来严重后果的风险。普通Bi-LSTM模型相较于IM-Bi-LSTM模型来说，各项评估结果都稍低，主要原因还是在训练过程中普通模型不能给予与失稳结果关联的特征更多权重，而引入注意力机制提升了模型整体的性能。在所有评估模型中，KNN的评估效果不佳，在评估失稳样本时造成的误判最大。另一方面，选择的浅层模型分类准确率普遍低于深度学习模型，主要原因还是浅层模型自身的学习局限性，不能充分利用特征中的重要信息，在面对非线性映射问题时，浅层模型的泛化能力有限。而本文选择的IM-Bi-LSTM模型除了对失稳样本增加更多权重，还能够对特征信息进行抽象提取，考虑序列的前后因素，挖掘更多隐含在数据中的有用信息，提高模型的性能。

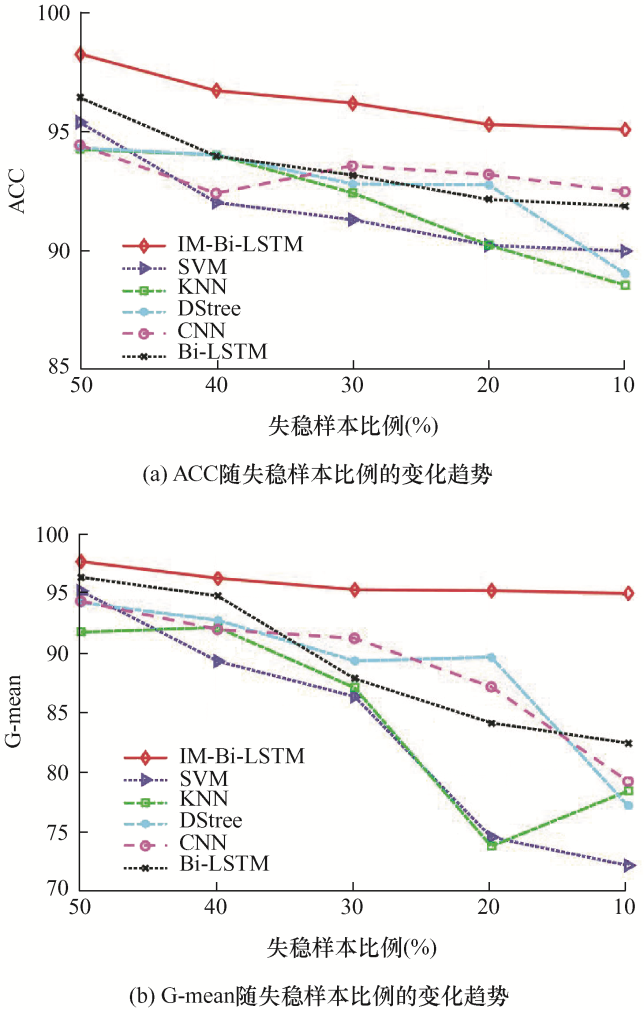
本文通过Matlab/Simulink仿真生成7 000组样本，其中失稳样本所占的比例大约在30%，但是实际电力系统运行产生的数据中失稳样本的数量极少。在模型训练的过程中，往往由于样本间的比例不平衡，导致模型训练不充分，在学习过程中更偏向样本数量较多的类别，对失稳样本的误判和漏判就会增加。为了评估在样本类别不平衡条件下的模型性能，从总样本中抽离暂态稳定样本，生成失稳样本占样本总数量的50%、40%、30%、20%、10%的样本子集，并且在不同的模型算法上进行性能评估，取准确率ACC和G-mean作为本次评估指标，评估结果如图5所示。

从图5可以看出，在稳定样本和失稳样本数量相当时，各个模型的性能都达到最佳，而随着失稳样本数量减少导致的两类样本数量不平衡程度加剧，各类模型的性能也出现不同程度的下降。从准确率ACC指标上看，KNN和决策树模型所受的影响最大，一度降至90%以下，而其他三类模型表现相对稳定。从G-mean指标上来看，各类模型都有下降，不过下降幅度相差较大，IM-Bi-LSTM模型表现最稳定且最优，SVM和KNN下降幅度最大，在各类模型中表现最差。总的来看，IM-Bi-LSTM模型所受影响程度最小，即使失稳样本数量下降到只占总样本数量的10%，ACC和G-mean指标依然有很好的表现，主要原因是本文所提模型引入了注意力机制和焦点损失函数，关注误分类样本进行训练，给予失稳样本更多的分类权重，降低对失稳样本的误分，使模型在样本类别数量不平衡的条件下依然具有较佳的分类性能。

在实际电网中，PMU测量得到的数据往往含有一些噪声，没有仿真数据稳定、标准。为验证模型的抗噪能力，在干净的数据集中加入标准差为0.01的高斯噪声，对比模型的评估性能。不同模型的评估结果如表7所示。

从表7可以看出，本文所提算法模型的评估性能相较于其他算法模型更为优异，与未加噪声时的模型性能几乎没有变化。Bi-LSTM算法在加入噪声后的模型性能与其他机器学习算法相比还是更好，但是CNN算法模型表现不佳，这是由于Bi-LSTM算法与本文的模型一样加入了L2范数正则化和Dropout策略，使模型在保证强大的特征提取能力外还有较好的模型泛化能力，不会轻易过拟合和陷入局部最优。其他三种机器学习算法相较于未加噪声前的评估性能都有所下降，模型的泛化能力较弱，表现不尽如人意。

本文从考虑暂态过程中的样本不平衡和误分类导致严重影响的角度出发，提出一种基于邻域粗糙集和IM-Bi-LSTM的电力系统暂态稳定评估方法。在新西兰10机39节点系统上进行仿真研究，并与其他算法进行对比分析，得到如下结论。

(1) 相较于其他机器学习算法与传统深度学习算法，本文所提模型有效利用了数据集中的时序信息，并引入注意力机制提高了对失稳样本的重视，模型评估性能在各项评估指标上都优于其他算法，更适合用于电力系统的暂态稳定评估。

(2) 使用邻域粗糙集对原始数据集进行属性约简，不但实现了对数据集的降维，而且模型对再表征的约简子集进行学习后，有非常好的评估性能。

(3) 实际暂态稳定问题是一个样本不平衡问题，IM-Bi-LSTM模型通过焦点损失函数，引入权重系数调整模型训练的倾向性，解决了失稳样本与暂态稳定样本间的不平衡问题。

本文考虑了暂态稳定评估过程中样本不平衡问题，未来所提模型与一些样本增强算法结合，训练生成一批特征相似的失稳样本，完善本文所提模型。