一种有源钳位隔离型无桥SEPIC PFC变换器*

doi:10.11985/2023.03.022

一种有源钳位隔离型无桥SEPIC PFC变换器^*

刘入铫^,, 沈霞^,, 陈锐, 向俊君, 王志豪

西南石油大学电气信息学院成都 610500

An Active Clamped Bridgeless Isolated SEPIC PFC Converter

LIU Ruyao^,, SHEN Xia^,, CHEN Rui, XIANG Junjun, WANG Zhihao

School of Electrical Engineering and Information, Southwest Petroleum University, Chengdu 610500

通讯作者: 沈霞，女，1981年生，硕士，副教授。主要研究方向为电力电子技术及其应用。E-mail：shenxia@swpu.edu.cn

收稿日期: 2022-07-8 修回日期: 2023-03-9

基金资助:

* 四川省科技厅资助项目(2019ZHCG0115)

Received: 2022-07-8 Revised: 2023-03-9

作者简介 About authors

刘入铫，男，1995年生，硕士研究生。主要研究方向为功率因数校正技术。E-mail：1538292931@qq.com

摘要

传统隔离型SEPIC功率因数校正(Power factor correction, PFC)变换器的开关管电压应力大，且因输入端整流桥的存在，自身效率难以进一步提升。使用无桥PFC和有源钳位技术对SEPIC PFC变换器进行改进，提出了一种有源钳位隔离型无桥SEPIC PFC变换器，通过使用开关管和快恢复二极管替代整流桥，改善了变换器效率；通过运用有源钳位技术，实现了开关管的软开关，降低了开关管的电压应力，并进一步提高了变换器效率。最后，设计了一台输出功率为70 W的应用于飞机座椅电源的试验样机，仅使用一级变换器就实现了高功率因数、高效率和输入输出的隔离，验证了理论分析的正确性。

关键词： 功率因数校正; SEPIC变换器; 有源钳位; 无桥变换器

Abstract

The voltage stress of the power switch of the traditional isolated SEPIC power factor correction(PFC) converter is large, the efficiency of the traditional isolated SEPIC PFC converter is also limited because of the existence of the input rectifier bridge. An active clamped bridgeless isolated SEPIC PFC converter is proposed by using the bridgeless PFC technology and active clamp technology. Through the elimination of the rectifier bridge, the efficiency of the proposed converter is improved; through the use of active clamping technology, the soft switching of all switches is realized, the voltage stress of the power switch is reduced. Finally, a 70 W experimental prototype for aircraft in-seat power supply is built to achieve high power factor, high efficiency, and isolation between input and output, which verifies the correctness of the theoretical analysis.

Keywords： Power factor correction; SEPIC converter; active clamping; bridgeless converter

PDF (111444KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘入铫, 沈霞, 陈锐, 向俊君, 王志豪. 一种有源钳位隔离型无桥SEPIC PFC变换器^*[J]. 电气工程学报, 2023, 18(3): 206-215 doi:10.11985/2023.03.022

LIU Ruyao, SHEN Xia, CHEN Rui, XIANG Junjun, WANG Zhihao. An Active Clamped Bridgeless Isolated SEPIC PFC Converter[J]. Chinese Journal of Electrical Engineering, 2023, 18(3): 206-215 doi:10.11985/2023.03.022

1 引言

近年来，随着电力电子技术的成熟和电力电子器件性能的提升，电力电子设备已经得到了广泛的应用，为了减少电力电子设备对电网的谐波污染，一些国家和国际学术团体提出并实施了一系列的电流谐波要求和标准^[1⇓⇓-4]。为满足谐波要求和标准，交流输入的电力电子变换器需要采用功率因数校正(Power factor correction, PFC)技术提高用电设备的功率因数，降低电网谐波含量，确保电网安全可靠运行^[5]，因此人们开始广泛研究各种电路拓扑组成的PFC变换器。

相比于Buck、Boost、Buck-Boost等非隔离PFC变换器，隔离型PFC变换器不仅能够实现输入输出隔离，而且通过合理设计，只用一级变换电路就可以实现PFC功能，因此研究人员已经在航空电子设备、车载充电器、通信及计算机设备电源等应用场合开展了隔离型PFC变换器的研究^[6⇓⇓-9]。其中隔离型SEPIC PFC变换器由于具有器件数量少、成本低、输入输出电流连续等优点，得到研究人员的广泛关注^[10-11]。由于变压器漏感带来的电压尖峰，传统隔离型SEPIC PFC变换器开关管的电压应力较大。文献[12-13]所提变换器应用有源钳位技术来降低开关管的电压应力，但是其电路控制复杂。文献[14]提出了一种集成磁结构的隔离有源钳位SEPIC PFC变换器，把输入电感、隔离变压器和二极管钳位电路集成到单个磁结构中，虽然降低了开关管和输出二极管的电压应力，但是该电路系统结构复杂，不易设计与控制；文献[15-16]所提变换器都用了有源钳位技术来抑制电压尖峰，实现了开关管的零电压开通，但是它们的电路控制复杂，成本高；并且文献[14 ⇓-16]均采用了传统整流桥。为进一步提高变换器的整体效率，学者们陆续提出了多种无桥SEPIC PFC拓扑^{[17⇓⇓⇓⇓-22]}，其中文献[22]提出的一种无桥PFC转换器，其输入电感电流交替工作在CCM/DCM模式，以获得高功率因数，提高整体效率，但是该变换器所用元器件数量多，控制复杂。

基于此，本文使用无桥PFC和有源钳位技术对SEPIC PFC变换器进行改进，提出了一种有源钳位隔离型无桥SEPIC PFC变换器。该变换器通过运用有源钳位技术，降低了开关管的电压应力，实现了开关管的软开关，并提高了变换器效率。该变换器采用恒频控制，输入电感电流工作在断续电流模式(Discontinuous conduction mode, DCM)，仅使用单电压环控制就可以实现功率因数校正功能，控制简单。本文详细分析了该变换器的工作原理、输入电感工作在断续模式的条件、中间电容的电压以及功率因数等特性，并设计了一台输出功率为70 W的应用于飞机座椅电源的试验样机验证了理论分析的正确性。

2 电路结构及其工作原理

2.1 电路结构

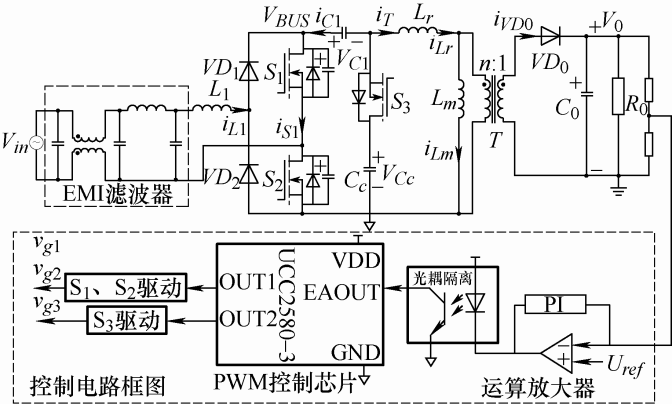
如图1所示为本文提出的有源钳位隔离型无桥SEPIC PFC变换器的整体框图。该变换器的主电路由EMI滤波器，输入电感L₁，二极管VD₁、VD₂，主开关管S₁、S₂，辅助开关管S₃，中间电容C₁，钳位电容C_c，以及隔离变压器T和续流二极管VD₀、输出滤波电容C₀组成；其中隔离变压器的励磁电感为L_m，漏感为L_r，变压器的原副边等效匝比为n。辅助开关管S₃与钳位电容C_c构成有源钳位电路，用以抑制电压尖峰，降低开关管S₁、S₂的电压应力；二极管VD₁、VD₂，主开关管S₁、S₂构成无桥结构代替传统整流桥，进一步提高变换器的转换效率。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 所提变换器电路框图

变换器的控制电路仅由运放、光耦和PWM控制芯片构成；将输出电压分压采样后的信号进行PI调节，再将误差信号通过光耦隔离传递到原边控制芯片UCC2580-3，然后控制芯片UCC2580-3输出一组带死区的互补驱动信号OUT1和OUT2，信号OUT1同步驱动主开关管S₁、S₂，信号OUT2驱动辅助开关管S₃。通过调节两个信号的死区时间来实现开关管S₁、S₂和S₃的ZVS，通过调节漏感L_r和钳位电容C_c的值，让其有足够的谐振深度，从而使能量能完全传递至二次侧^[23]来实现副边续流二极管VD₀的ZCS。由图1可知，所提PFC变换器拓扑仅用一级变换就可以实现AC-DC功能和输入输出隔离，所用元器件数量少，成本低，控制简单。

2.2 工作原理

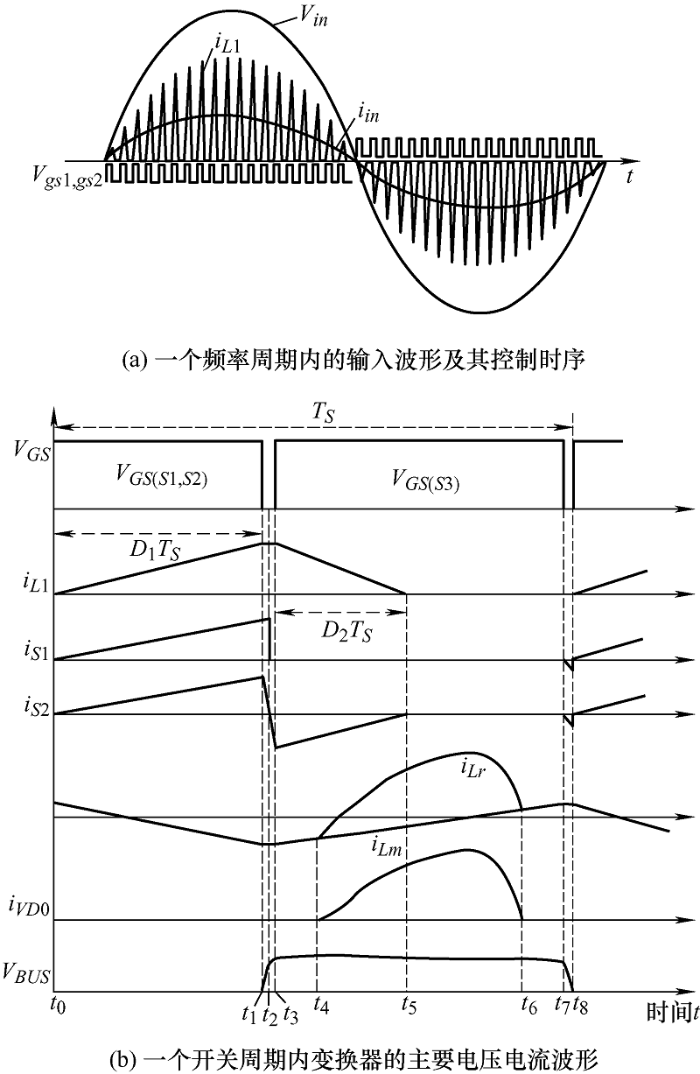
该变换器输入电感L₁的电流工作在DCM模式，如图2a所示。由于电路正负半周原理相同，现以输入电感电流工作在正半周断续导电模式来介绍电路的工作原理。假设输入电压V_in=V_msin(ωt)为理想正弦波，其中V_m为输入电压V_in的峰值，ω为输入电压V_in的角频率。为了便于分析，假设如下：VD_S₁、VD_S₂分别为开关管S₁、S₂的体二极管，C_S₁、C_S₂分别为开关管S₁、S₂的寄生电容，VD_S₃为开关管S₃的体二极管，输出电容C₀足够大；L_m$\gg $L_r，开关管的开关频率f_s远大于输入交流电压频率f_g。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 变换器关键波形

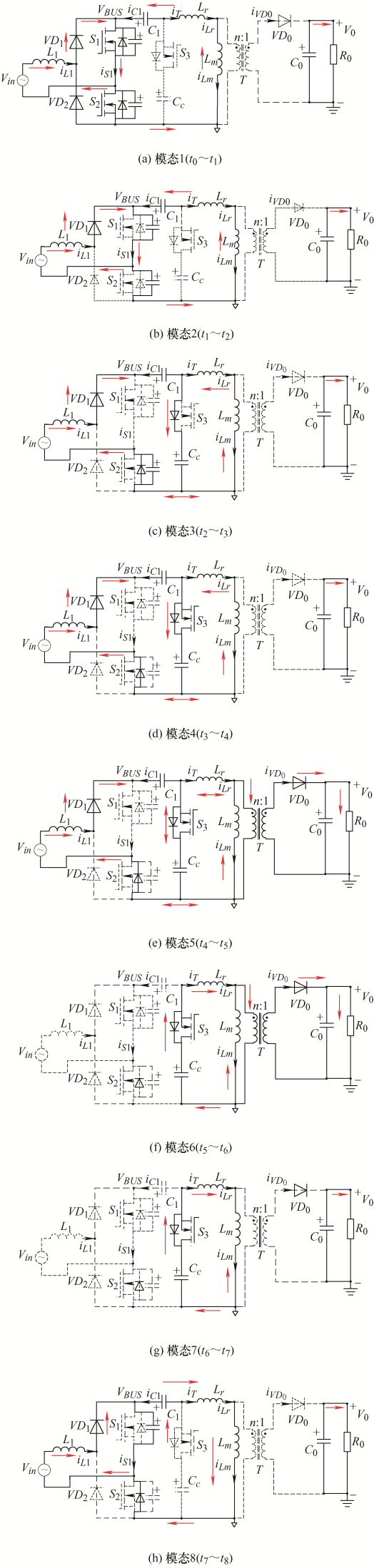
该变换器的关键电压和电流波形如图2所示，图2b对应的工作模态分析如图3所示，相关元器件电流的正方向已在图1中标出。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 输入电压正半周各模态等效电路

模态1(t₀~t₁)：如图3a所示，主开关管S₁、S₂开通，辅助开关管S₃关断，该等效电路有三个回路，其电流流向如图中支路外箭头所示，其中i_s₁=i_L₁+i_c₁。中间电容C₁放电，输入电感L₁和励磁电感L_m及其变压器漏感L_r上的电流均线性变化，均储存能量，且i_Lm=i_Lr=i_T，此时二次侧输出电容C₀释放能量以供给负载，在整个阶段V_BUS电压为零。在这个阶段里，输入电感L₁和励磁电感L_m及其变压器漏感L_r上的电流变化率为

(1)$\frac{\mathrm{d}{{i}_{L1}}(t)}{\mathrm{d}t}=\frac{{{V}_{m}}\sin (\omega t)}{{{L}_{1}}}$

(2)$\frac{\mathrm{d}{{i}_{Lm}}(t)}{\mathrm{d}t}=\frac{\mathrm{d}{{i}_{Lr}}(t)}{\mathrm{d}t}=-\frac{\mathrm{d}{{i}_{C1}}(t)}{\mathrm{d}t}=-\frac{{{V}_{C1}}}{{{L}_{m}}+{{L}_{r}}}$

模态2(t₁~t₂)：如图3b所示，开关管S₁、S₂和S₃均关断，L₁和L_r的电流流向仍然保持模态1的电流流向，均向主开关管S₁、S₂的寄生电容C_S₁和C_S₂充电，i_Lm=i_Lr，V_BUS逐渐上升，输出电容C₀继续向负载供能；当C_S₁和C_S₂充电结束后，进入模态3。

模态3(t₂~t₃)：如图3c所示，由于电感L₁要续流，i_L₁给中间电容C₁充电，给C_S₂放电，同时i_Lr和 i_L₁给钳位电容C_c充电，输出电容C₀继续向负载供能，当C_S₂放电结束后，由S₂的体二极管VD_S₂续流，此时S₂、S₃即可实现ZVS，工作进入模态4。

模态4(t₃~t₄)：如图3d所示，开关管S₃导通，开关管S₂的体二极管VD_S₂续流，i_L₁持续给中间电容C₁和钳位电容C_c充电，同时i_Lr也持续给钳位电容C_c充电，输入电感电流i_L₁和流过磁感L_m和漏感L_r的电流线性减小，且i_Lm=i_Lr。

模态5(t₄~t₅)：如图3e所示，开关管S₁、S₂关断，S₃导通，t=t₄时，i_Lr>i_Lm，此时VD₀开始导通，变压器开始向二次侧传递能量，输出电容C₀储存能量，此时i_L₁和i_Lr继续给钳位电容C_c充电，输入电感电流i_L₁持续线性减小；同时漏感电流i_Lr由负变正，当i_Lm=i_Lr+i_L₁时，钳位电容C_c充电结束，然后开始放电，在整个阶段变压器漏感L_r和钳位电容C_c发生谐振，并向二次侧传递能量。

在t₃~t₅整个阶段，输入电感电流i_L₁均线性减小，其下降斜率为

(3)$\frac{\mathrm{d}{{i}_{L1}}(t)}{\mathrm{d}t}=-\frac{{{V}_{C1}}+n{{V}_{0}}-{{V}_{in}}}{{{L}_{1}}}$

模态6(t₅~t₆)：如图3f所示，此阶段开关管S₁和S₂持续关断，S₃继续导通，当t=t₅时刻，i_L₁线性减小至0，中间电容C₁充电结束，即i_L₁=i_S₂=0；漏感电流i_Lr持续增大，励磁电流i_Lm逐渐减小，当励磁电流i_Lm减小至0时，二次侧电流i_VD₀增加至最大，随后励磁电流i_Lm反向增大，漏感电流i_Lr减小，变压器漏感L_r和钳位电容C_c继续谐振。

在t₄~t₆整个时间段，变压器漏感L_r和钳位电容C_c发生谐振，同时向二次侧传递能量，可以推导出如下表达式

(4)$\begin{matrix} {{V}_{Cc}}(t)=n{{V}_{0}}-(n{{V}_{0}}-{{V}_{Cc}}({{t}_{4}}))\times \\ \cos ({{\omega }_{r}}(t-{{t}_{4}}))-{{i}_{Lr}}({{t}_{4}}){{Z}_{r}}\sin ({{\omega }_{r}}(t-{{t}_{4}})) \\\end{matrix}$

(5)$\begin{matrix} {{i}_{Lr}}(t)=\frac{-n{{V}_{0}}+{{V}_{Cc}}({{t}_{4}})}{{{Z}_{r}}}\sin ({{\omega }_{r}}(t-{{t}_{4}}))+ \\ {{i}_{Lr}}({{t}_{4}})\cos ({{\omega }_{r}}(t-{{t}_{4}}))+{{i}_{Lr}}({{t}_{4}}) \\ \end{matrix}$

(6)${{i}_{Lm}}(t)=\frac{n{{V}_{0}}}{{{L}_{m}}}(t-{{t}_{4}})+{{i}_{Lm}}({{t}_{4}})$

(7)${{i}_{VD0}}(t)=n({{i}_{Lr}}(t)-{{i}_{Lm}}(t))$

式中，${{\omega }_{r}}=\frac{1}{\sqrt{{{C}_{c}}\times {{L}_{r}}}}$，${{Z}_{r}}=\sqrt{\frac{{{L}_{r}}}{{{C}_{c}}}}$。

模态7(t₆~t₇)：如图3g所示，这一阶段开关管S₃继续导通，钳位电容C_c继续放电，i_Lm=i_Lr，并缓慢增大，变压器不再向二次侧传递能量，i_VD₀=0，负载由输出电容C₀供电，二次侧续流二极管D₀零电流关断。

模态8(t₇~t₈)：如图3h所示，在这一阶段，辅助开关管S₃关断，由S₂的体二极管VD_S₂续流构成回路，同时S₁的寄生电容C_S1放电，负载侧输出电容C₀向负载供电，直至t₈时刻，C_S₁放电完毕，V_BUS降为0，开关管S₁即可实现零电压开通，又回到模态1的状态。

3 电路特性分析

3.1 功率因数分析

输入电感电流断续模式下变换器电路稳态工作时，根据电感L₁在一个开关周期内的伏秒平衡可知

(8)${{V}_{m}}\sin (\omega t){{D}_{1}}{{T}_{S}}=({{V}_{C1}}+{{V}_{Cc}}-{{V}_{m}}\sin \omega t){{D}_{2}}{{T}_{S}}$

式中，D₁为主开关管S₁、S₂的占空比；T_S为开关周期；D₂T_S为开关周期内i_L₁从峰值放电为0的时间；n为变压器的原副边变比；ω为输入电压角频率。稳态工作时，漏感L_r两端的平均电压为0，因此钳位电容C_C的电容电压可以表示为

(9)${{V}_{Cc}}=n{{V}_{0}}$

结合式(8)、式(9)，可以得到

(10)${{D}_{2}}=\frac{{{V}_{m}}\sin \omega t}{{{V}_{C1}}+n{{V}_{0}}-{{V}_{m}}\sin \omega t}D{}_{1}$

由式(1)、式(10)可以得到该变换器输入电感L₁在一个开关周期内的平均电流为

(11)${{i}_{L1\_avg}}(t)=\frac{1}{2}\times {{i}_{L1(pk)}}\times ({{D}_{1}}+{{D}_{2}})=\frac{D_{1}^{2}{{V}_{m}}\sin \omega t}{2{{L}_{1}}{{f}_{s}}\left( 1-\frac{{{V}_{m}}\left| \sin \omega t \right|}{{{V}_{C1}}+n{{V}_{0}}} \right)}$

从而，该变换器在一个开关周期内的输入电流平均值i_in(t)可以表示为

(12)${{i}_{in}}(t)=\frac{1}{2}\times {{i}_{L1(pk)}}\times ({{D}_{1}}+{{D}_{2}})=\frac{D_{1}^{2}{{V}_{m}}\sin \omega t}{2{{L}_{1}}{{f}_{s}}\left( 1-\frac{{{V}_{m}}\left| \sin \omega t \right|}{{{V}_{C1}}+n{{V}_{0}}} \right)}$

平均输入功率可以表示为

(13)${{P}_{in}}=\frac{1}{{T}/{2}\;}\int_{0}^{{T}/{2}\;}{{{V}_{in}}(t){{i}_{in}}(t)\mathrm{d}t}\text{=}\frac{D_{1}^{2}V_{m}^{2}}{2\mathrm{ }\!\!\pi\!\!\text{ }{{L}_{1}}{{f}_{s}}}\int_{0}^{\pi }{\frac{{{\sin }^{2}}\omega t}{1-\frac{{{V}_{m}}\left| \sin \omega t \right|}{{{V}_{C1}}+n{{V}_{0}}}}\mathrm{d}\omega t}$

根据功率因数的定义，该变换器的PF可以表示为

(14)$\begin{matrix} PF=\frac{\sqrt{2}{{P}_{in}}}{{{V}_{m}}\times {{I}_{in(rms)}}}= \\ \sqrt{\frac{2}{\mathrm{ }\!\!\pi\!\!\text{ }}}\frac{\int_{0}^{\mathrm{ }\!\!\pi\!\!\text{ }}{\frac{{{\sin }^{2}}\omega t}{1-\frac{{{V}_{m}}}{{{V}_{C1}}+n{{V}_{0}}}\left| \sin \omega t \right|}\mathrm{d}\omega t}}{\sqrt{\int_{0}^{\mathrm{ }\!\!\pi\!\!\text{ }}{{{\left( \frac{\sin \omega t}{1-\frac{{{V}_{m}}}{{{V}_{C1}}+n{{V}_{0}}}\left| \sin \omega t \right|} \right)}^{2}}d\omega t}}} \\ \end{matrix}$

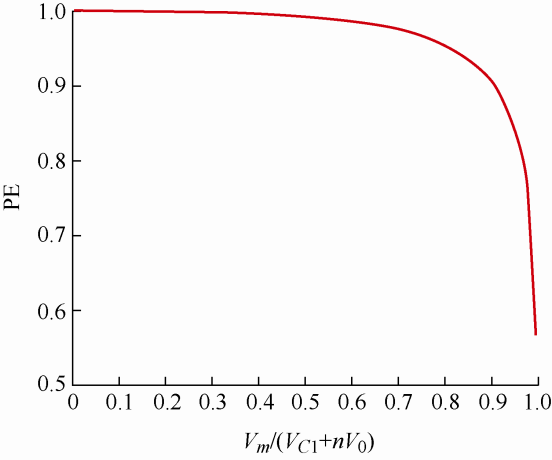
式中，V_m为交流输入电压的峰值；I_in₍_rms₎为输入电流有效值。可以看出该变换器的功率因数PF是关于V_m/(V_C₁+nV₀)的函数，其关系如图4所示，功率因数PF随着V_m/(V_C₁+nV₀)的增大而减小。在低压应用场合，当输入电压、输出电压和变比n确定时，可以通过增大V_C₁来提高功率因数。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 功率因数PF与V_m/(V_C₁+nV₀)的关系曲线

3.2 i_L₁工作在断续模式的条件

假设在最低输入电压下，正弦波波峰输入，确保输入电感电流i_L₁工作在断续模式，则可以在整个范围内工作在断续模式。可以得到

(15)${{i}_{L1,avg}}(t)=\frac{1}{2}\cdot \frac{{{D}^{2}}{{V}_{m}}\sin \omega t}{{{L}_{1}}{{f}_{s}}}\cdot \frac{\frac{1}{D}{{V}_{Cc}}}{\frac{1}{D}{{V}_{Cc}}-{{V}_{m}}\sin \omega t}$

假设$M=\frac{n{{V}_{0}}}{{{V}_{m}}}$，有

(16)${{i}_{L1,avg}}(t)=\frac{1}{2}\cdot \frac{D{{V}_{m}}}{{{L}_{1}}{{f}_{s}}}\cdot \frac{(1+\alpha )M\sin \omega t}{\frac{1}{D}(1+\alpha )M-\sin \omega t}$

根据功率守恒可得

(17)$\begin{matrix} \frac{1}{2\mathrm{ }\!\!\pi\!\!\text{ }}\cdot \frac{D\cdot V_{m}^{2}}{{{L}_{1}}\cdot {{f}_{s}}}\cdot \int_{0}^{\mathrm{ }\!\!\pi\!\!\text{ }}{\frac{(1+\alpha )M{{\sin }^{2}}\omega t}{\frac{1}{D}(1+\alpha )M-\sin \omega t}}\mathrm{d}\omega t= \\ \frac{V_{0}^{2}}{R}=\frac{{{M}^{2}}\cdot V_{m}^{2}}{{{n}^{2}}\cdot R} \\ \end{matrix}$

式中，R为负载；D为占空比；$\alpha =\frac{{{L}_{r}}}{{{L}_{m}}}$，由于${{L}_{m}}\gg {{L}_{r}}$，$\alpha $可忽略不计。令$M=\frac{D}{1-D}$，代入式(17)可得

(18)${{L}_{1}}=\frac{{{n}^{2}}\cdot R\cdot {{(1-D)}^{2}}}{2\mathrm{ }\!\!\pi\!\!\text{ }{{f}_{s}}}\cdot \int_{0}^{\mathrm{ }\!\!\pi\!\!\text{ }}{\frac{\frac{1}{1-D}{{\sin }^{2}}\omega t}{\frac{1}{1-D}-\sin \omega t}}\mathrm{d}\omega t$

因此，只需要确保输入电感取值小于式(18)的计算值，即可保证该变换器在整个范围内工作在断续模式。

3.3 中间电容C₁的平均电压V_C₁的分析

根据上述电路工作模态分析，当开关管S₁、S₂导通时，流经中间电容C₁的电流i_C₁(t)=i_Lm(t)，此时中间电容C₁向励磁电感L_m传递能量，认为中间电容C₁放电时的电压为恒定值V_C₁，则在放电时间D₁T_S时间内，中间电容C₁的平均放电电流为

(19)${{I}_{C1\_out}}=\frac{{{V}_{C1}}{{D}_{1}}{{T}_{S}}}{2{{L}_{m}}}$

所以，在一个开关周期内中间电容C₁释放的功率为

(20)${{P}_{C1\_out}}={{V}_{C1}}{{I}_{C1\_out}}{{D}_{1}}{{T}_{S}}$

当开关管S₁、S₂关断时，流经中间电容C₁的电流i_C₁(t)=i_L₁(t)，此时中间电容吸收能量，认为中间电容C₁充电时的电压为恒定值V_C₁，则在充电时间D₂T_S时间内，中间电容C₁的平均充电电流为

(21)${{I}_{C1\_in}}=\frac{({{V}_{C1}}+n{{V}_{0}}-{{V}_{m}}\left| \sin \omega t \right|)}{2{{L}_{1}}}{{D}_{2}}{{T}_{S}}$

同理，在一个开关周期内中间电容C₁吸收的功率为

(22)${{P}_{C1\_in}}={{V}_{C1}}{{I}_{C1\_in}}{{D}_{2}}{{T}_{S}}$

根据中间电容充放电能量平衡，结合式(11)，可得在半个频率周期内

(23)$\int_{0}^{\mathrm{ }\!\!\pi\!\!\text{ }}{{{P}_{C1\_in}}\mathrm{d}\omega t=\int_{0}^{\mathrm{ }\!\!\pi\!\!\text{ }}{{{P}_{C1\_out}}\mathrm{d}\omega t}}$

结合式(20)、式(22)，整理得到

(24)${{V}_{C1}}=\frac{{{L}_{m}}{{V}_{m}}^{2}}{\mathrm{ }\!\!\pi\!\!\text{ }{{L}_{1}}}\int_{0}^{\mathrm{ }\!\!\pi\!\!\text{ }}{\frac{{{\sin }^{2}}\omega t}{{{V}_{C1}}+n{{V}_{0}}-{{V}_{m}}\left| \sin \omega t \right|}}\mathrm{d}\omega t$

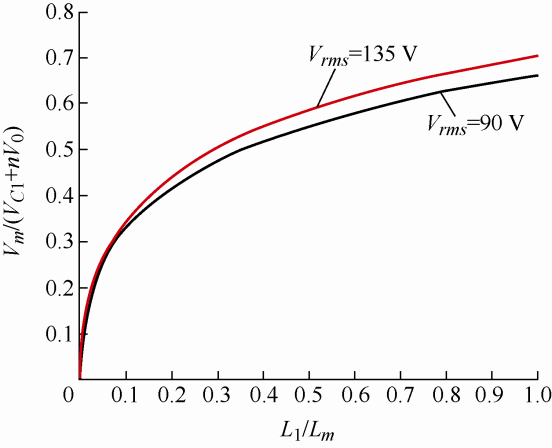
从式(24)可知，中间电容电压V_C₁的大小与变压器匝数比n、输出电压V₀、输入电压峰值V_m以及励磁电感L_m和输入电感L₁的比值相关；当变压器匝数比n和输出电压V₀、输入电压一定时，中间电容电压V_C₁与励磁电感L_m和输入电感L₁的比值呈非线性函数关系，其关系曲线如图5所示。根据图5可得，对于28 V输出，n=3.3时，当输入电压确定时，随着L₁/L_m比值逐渐增大，V_m/(V_C₁+nV₀)的值逐渐增大，中间电容电压V_C₁逐渐减小，因此，可以通过合理设计励磁电感L_m和输入电感L₁的值，来确定中间电容电压V_C₁。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 L₁/L_m与V_m/(V_C₁+nV₀)的关系曲线

4 试验验证

4.1 试验参数

为了验证提出的有源钳位隔离型无桥SEPIC PFC变换器的理论分析的正确性，搭建了一台输出功率为70 W的应用于飞机座椅电源的试验样机，如图6所示。变换器的规格和主要试验参数如表1所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 试验样机图片

表1 变换器规格和主要试验参数

参数	数值(型号)
输入交流电压有效值V_rms/V	90~135
输入交流电压频率f_g/Hz	400
开关频率f_s/kHz	50
输出直流电压V₀/V	28
输出功率P_O/W	70
变压器T变比n_p∶n_s	3.3∶1
输入电感L₁/μH	250
中间电容C₁/μF	1
钳位电容C_c/μF	0.47
励磁电感L_m/μH	300
输出滤波电容C₀/μH	2 000
功率开关管S₁、S₂、S₃型号	FCP11N60F
主二极管VD₁、VD₂型号	FFSP1665A
副边二极管VD₀型号	MBR40250

新窗口打开| 下载CSV

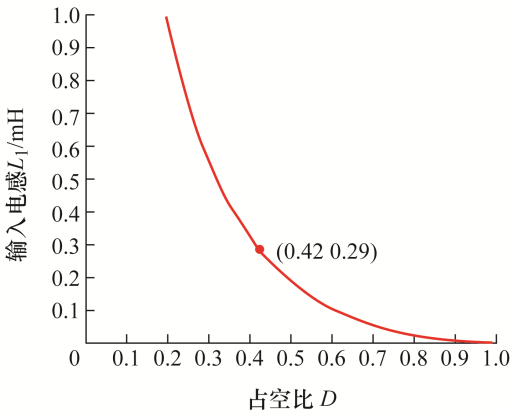
根据式(18)，对于28 V输出，n=3.3时，得出不同占空比D和输入电感L₁的关系，如图7所示。在最低输入电压下，得到占空比D=0.42，对应L₁=290 μH，确保变换器工作在DCM模式，在实际电路中取L₁=250 μH；综合考虑变换器功率因数和中间电容电压V_C₁，结合图4与图5，取L_m=300 μH；同时，由图4和图5折中考虑，可以计算得到中间电容电压在输入电压有效值为90 V、115 V、135 V时的大小分别为153.3 V、197.3 V、225.7 V。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 输入电感L₁与占空比D的关系曲线

4.2 试验结果

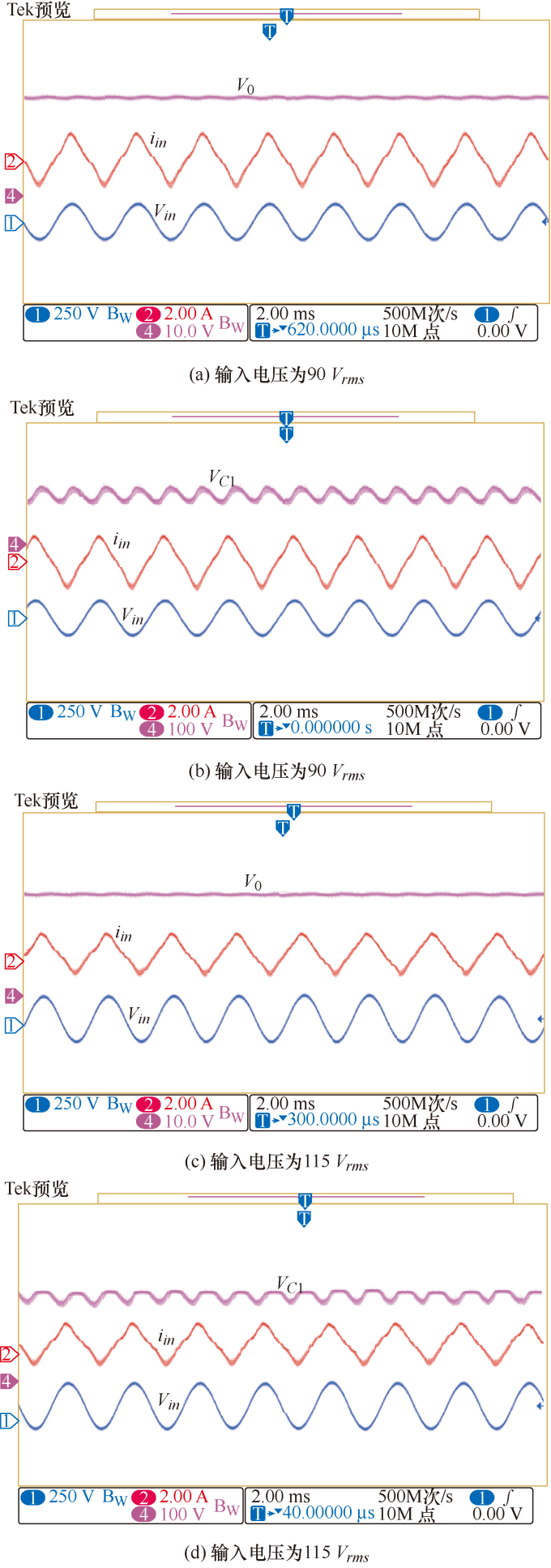
图8为输出电压V₀、输入电压V_in、输入电流i_in和中间电容电压在输入电压有效值为90 V、115 V、135 V时的试验波形。由图8可以看出，不同输入电压下，输入电流波形均能够很好地跟随输入电压波形，输出电压稳定在28 V；由图8b、8d、8f可以看出，交流输入电压有效值为90 V、115 V、135 V时，中间电容电压分别为151 V、200 V和220 V左右；测试结果基本与理论分析一致。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 输出电压、输入电压、输入电流和中间电容电压试验波形

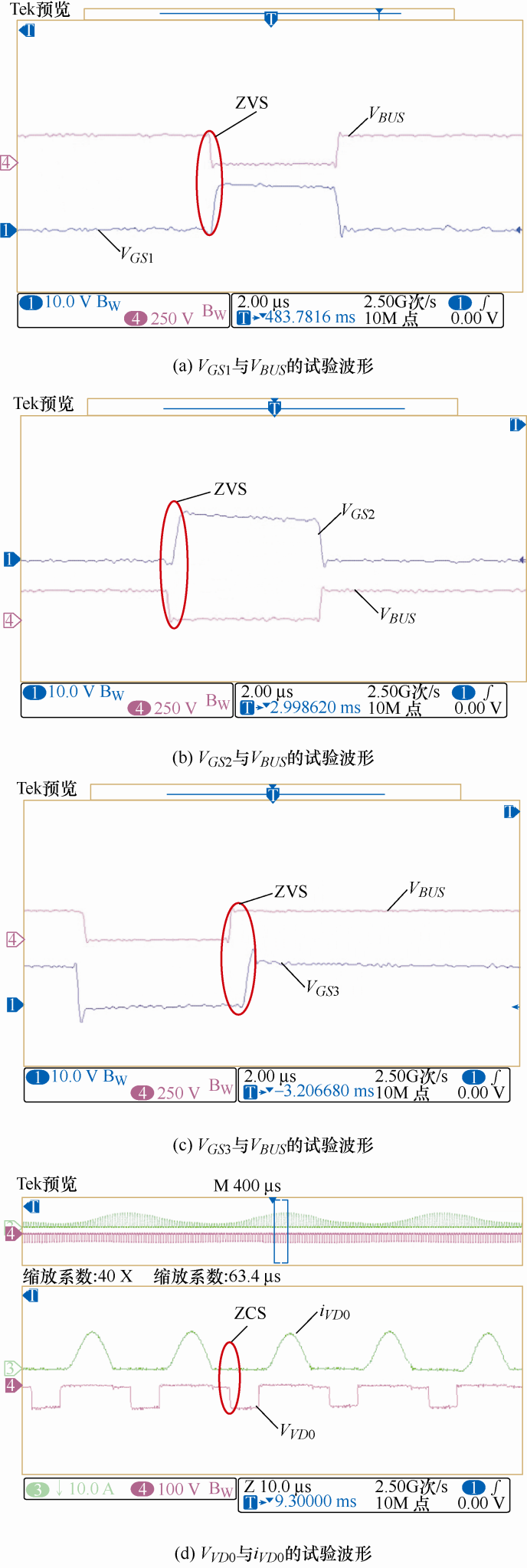
图9a~9c分别为V_rms=115 V时开关管S₁、S₂和S₃的GS端电压V_GS与BUS点对地的电压V_BUS和副边二极管电压V_VD₀和电流i_VD₀的试验波形。从图9a~9c可以看出，有源钳位电路很好地抑制了电压尖峰，降低了开关管的电压应力，开关管S₁、S₂和S₃实现了零电压开通，副边二极管实现了零电流关断。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 V_rms=115 V时开关管S₁、S₂和S₃的GS端电压V_GS与电压V_BUS和副边二极管V_VD₀与i_VD₀试验波形

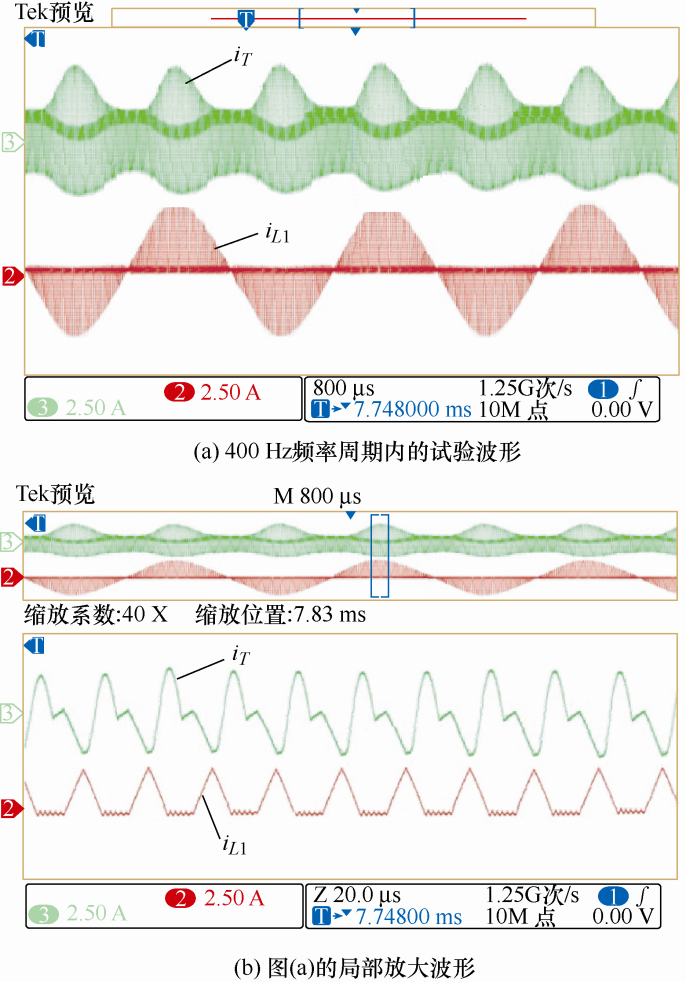
图10所示为V_rms=115 V时输入电感电流i_L₁和流入变压器的电流i_T的试验波形，图10a为基于无桥SEPIC PFC变换电路在400 Hz频率周期内的试验波形，图10b为图10a在输入电压峰值点附近的局部放大波形。从图10可以看出，该变换器的输入电感运行在断续模式，输入电感电流的峰值包络为正弦波，漏感L_r和钳位电容C_c有足够的谐振深度，能使能量完全传递至变压器二次侧，试验波形与理论分析完全一致。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 V_rms=115 V时输入电感电流i_L₁、流入变压器电流i_T的试验波形

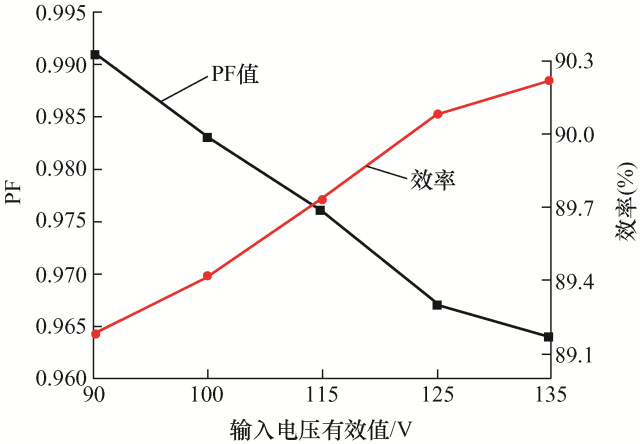
图11为不同输入电压时，所提变换器的PF值和转换效率的测试结果。根据测试结果可得，在90~135 V_rms输入电压范围内，所提变换器的功率因数均大于0.96，效率高达90.22%；由于输入端EMI滤波器中电容的影响，当输入电压较高时，测试的PF值比理论分析结果略低。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 不同输入电压下PF值和转换效率的测试结果

表2为本文所提PFC变换器拓扑与参考文献中部分电路拓扑之间的对比。通过对比分析可知，在单级隔离且不需要能量双向流动的中低压应用场合，尤其对航空电子设备等低输入电压的应用场合，本文所提PFC变换器拓扑在成本、控制单路复杂度和转换效率方面具有一定的优势。

表2 本文拓扑与其他拓扑对比表

方法	主电路结构(复杂度)	输入电压范围/频率	输出电压/V	输出功率/W	开关频率/ kHz	功率器件数量	峰值效率(%)	控制电路复杂度	成本
文献[9]	单级隔离 (一般)	220 V/50 Hz	108	37.8	100	2MOSFET，8二极管	83	一般	中
文献[17]	单级非隔离(一般)	120 V/60 Hz	50	100	100	1MOSFET，5二极管	90.5	复杂	低
文献[20]	多级隔离 (复杂)	90~265 V/50 Hz	12	300	20	9MOSFET，6二极管	85	复杂	高
文献[21]	单级隔离 (一般)	90~130 V/50 Hz	100	80	50	2MOSFET，2二极管	89.5	一般	中
文献[22]	单级隔离 (一般)	110 V/50 Hz	48	150	50	4MOSFET，3二极管	91	一般	中
本文	单级隔离 (一般)	90~135 V/400 Hz	28	70	50	3MOSFET，3二极管	90.22	简单	低

新窗口打开| 下载CSV

5 结论

相较于传统隔离型SEPIC PFC变换器，本文提出的有源钳位隔离型无桥SEPIC PFC变换器具有以下特点。

(1) 使用无桥结构代替了传统PFC变换器中的低频整流桥，并运用了有源钳位技术，实现了开关管的软开关，具有效率高的特点。

(2) 主开关管和辅助开关管采用互补导通的工作方式，系统运行在DCM模式，主电路拓扑控制方式简单，进一步降低了硬件成本。

(3) 尤其适用于中频低压输入的应用场合。

实验室搭建了70 W试验样机，试验结果表明了所提变换器的合理性和可行性；在有效值90~135 V 的交流输入电压下，其功率因数高达0.991，效率高达90.22%，验证了理论分析的正确性。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

LOW

Q W

, SIEK

A single-stage dual-output tri-mode AC-DC regulator or inductively powered application

[J]. IEEE Transactions on Circuits and Systems, 2019, 66(9):3620-3630.

[本文引用: 1]

[2]

经雯荔, 管乐诗, 王懿杰, 等.

高频AC/DC变换器优化控制策略研究

[J]. 电源学报, 2020, 18(5):60-71.

DOI:10.13234/j.issn.2095-2805.2020.5.60 [本文引用: 1]

研究了一种基于GaN HEMT图腾柱软开关无桥PFC电路和LLC谐振电路的高频AC/DC变换器。通过数字控制变换器在临界模式及准方波模式间切换，可实现在全输入范围内零电压开通。闭环控制上应用数字滤波器并基于系统的非线性时变特性研究了补偿方法以实现系统快速响应。同时，为了提升变换器轻载模式下变换效率，采用了自适应多脉冲的突发模式控制方法。为了验证理论合理性和有效性，搭建了输入交流电220 V转输出直流电48 V、额定功率400 W的两级式AC/DC变换器，系统满载时效率为95.2%，同非优化模式相比提升了0.4%；5%轻载条件下，效率为80%，同非优化模式相比提升了42%；当系统输入电压减小为额定电压一半时，系统输出电压响应时间由8.4 ms减小为5.2 ms，响应时间缩减了38%。

JING

Wenli

, GUAN

Yueshi

, WANG

Yijie

, et al.

Research on optimal control strategy for high-frequency AC/DC converter

[J]. Journal of Power Supply, 2020, 18(5):60-71.

DOI:10.13234/j.issn.2095-2805.2020.5.60 [本文引用: 1]

In this paper, a high-frequency AC/DC converter is proposed, which is based on GaN HEMT totem-pole soft-switching bridgeless power factor correction （PFC） circuit and LLC resonant circuit. Through the shifting of a digita-lly controlled converter between the critical mode and quasi-square wave mode, zero-voltage switching can be realized in the full input range. A digital filter is applied to the closed-loop control. In addition, based on the system's non-linear time-varying characteristics, a compensation method is studied to realize the system's fast response. At the same time, a burst-mode control method of adaptive multi-pulse is adopted to improve the converter's conversion efficiency in light-load mode. To verify the validity and effectiveness of the theoretical analysis, a 400 W two-stage converter of 220 V AC to 48 V DC was built, and its efficiency under full load was is 95.2%, which was improved by 0.4% compared with that in the conventional mode. The efficiency under 5% light load was 80%, which was improved by 42% compared with that in the conventional mode. When the input voltage was reduced to half the rated value, the system's output voltage response time was reduced from 8.4 ms to 5.2 ms, i.e., with a decrease of 38%.

[3]

阎铁生, 陶权保, 胡啸天, 等.

基于双路恒流输出单级Cuk PFC变换器的LED驱动电路

[J]. 电机与控制学报, 2020, 24(7):139-146.

[本文引用: 1]

YAN

Tiesheng

, TAO

Quanbao

, HU

Xiaotian

, et al.

LED driving circuit based on single stage Cuk PFC converter with dual constant current outputs

[J]. Electric Machines and Control, 2020, 24(7):139-146.

[本文引用: 1]

[4]

游芳, 甘雪, 魏金成, 等.

新型无桥DCM Pseudo-Boost PFC变换器研究

[J]. 电气工程学报, 2015, 10(11):39-45.

[本文引用: 1]

YOU

Fang

, GAN

Xue

, WEI

Jincheng

, et al.

Research on novel bridgeless DCM Pseudo-Boost PFC converter

[J]. Journal of Electrical Engineering, 2015, 10(11): 39-45.

DOI:10.12677/JEE.2022.101005 URL [本文引用: 1]

[5]

孙百军, 施宏, 邹晓渔.

基于航空电网的Boost PFC变换器设计

[J]. 电力电子技术, 2018, 52(2):90-93.

[本文引用: 1]

SUN

Baijun

, SHI

Hong

, ZOU

Xiaoyu

Design of Boost PFC converter based on aviation power grid

[J]. Power Electronics, 2018, 52(2):90-93.

[本文引用: 1]

[6]

TARZAMNI

, FARHAD

P E

, FARZAD

, et al.

Reliability assessment of conventional isolated PWM DC-DC converters

[J]. IEEE Access, 2021, 9:46191-46200.

DOI:10.1109/ACCESS.2021.3067935 URL [本文引用: 1]

[7]

阎铁生, 李明洪, 陶权保, 等.

DCM-CRM Boost-Flyback单级PFC变换器

[J]. 电力自动化设备, 2019, 39(11):152-158.

[本文引用: 1]

YAN

Tiesheng

, LI

Minghong

, TAO

Quanbao

, et al.

DCM-CRM Boost-Flyback single-stage PFC converter

[J]. Electric Power Automation Equipment, 2019, 39(11):152-158.

[本文引用: 1]

[8]

GOYAL

V K

, SHUKLA

Isolated DC-DC Boost converter for wide input voltage range and wide load range applications

[J]. IEEE Transactions on Industrial Electronics, 2021, 68(10):9527-9539.

DOI:10.1109/TIE.2020.3029479 URL [本文引用: 1]

[9]

章治国, 刘俊良, 郭强, 等.

一种单级隔离型软开关功率因数校正变换器

[J]. 电工技术学报, 2018, 33(14):3222-3230.

[本文引用: 1]

ZHANG

Zhiguo

, LIU

Junliang

, GUO

Qiang

, et al.

A single stage isolated soft switching power factor correction converter

[J]. Transactions of China Electrotechnical Society, 2018, 33(14):3222-3230.

[本文引用: 1]

[10]

TIBOLA

, BARBI

Isolated three-phase high power factor rectifier based on the SEPIC converter operating in discontinuous conduction mode

[J]. IEEE Transactions on Power Electronics, 2013, 28(11):4962-4969.

DOI:10.1109/TPEL.2013.2247775 URL [本文引用: 1]

[11]

LEE

, DO

Isolated SEPIC DC-DC converter with ripple-free input current and lossless snubber

[J]. IEEE Transactions on Industrial Electronics, 2018, 65(2):1254-1262.

DOI:10.1109/TIE.2017.2733440 URL [本文引用: 1]

[12]

LODH

, MAJUMDER

A high gain high efficiency and compact isolated Sepic DC-DC converter

[C]// International Conference on Signal Processing,Communication,Power and Embedded System (SCOPES),Paralakhemundi,India, 2016:1506-1511.

[本文引用: 1]

[13]

ONGARO

, SAGGINI

ZVS isolated active clamp Sepic converter for high power LED applications

[C]// Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), February 5-9,2012,Orlando,FL,USA. IEEE, 2012:957-962.

[本文引用: 1]

[14]

, AYYANAR

Isolated active-clamped SEPIC PFC converter based on SiC devices and integrated magnetics

[C]// IEEE 7th Workshop on Wide Bandgap Power Devices and Applications (WiPDA), October 29-31,2019,Raleigh,NC,USA. IEEE, 2019:151-156.

[本文引用: 2]

[15]

, AYYANAR

Single-phase active-clamped isolated SEPIC PFC converter with partial power processing output stage

[C]// IEEE Applied Power Electronics Conference and Exposition (APEC),New Orleans,LA,USA. IEEE, 2020:1285-1291.

[本文引用: 2]

[16]

, AYYANAR

, MADHURA

, et al.

High-performance active-clamped isolated SEPIC PFC converter with SiC devices and lossless diode clamp

[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(1):567-577.

DOI:10.1109/JESTPE.6245517 URL [本文引用: 2]

[17]

马红波, 郑聪, 余文松, 等.

单开关管无桥SEPIC PFC变换器

[J]. 电力自动化设备, 2014, 34(4):72-77.

[本文引用: 1]

Hongbo

, ZHENG

Cong

, YU

Wensong

, et al.

Single-switch bridgeless SEPIC PFC converter

[J]. Electric Power Automation Equipment, 2014, 34(4):72-77.

[本文引用: 1]

[18]

徐鑫雨, 吴红飞, 贾益行, 等.

基于三端口无桥PFC的两级式隔离型双输出AC-DC变换器

[J]. 中国电机工程学报, 2020, 40(22):7431-7440.

[本文引用: 1]

Xinyu

, WU

Hongfei

, JIA

Yixing

, et al.

Two stage isolated dual output AC-DC converter based on three port bridgeless PFC

[J]. Proceedings of the CSEE, 2020, 40(22):7431-7440.

[本文引用: 1]

[19]

SINGH

, KUSHWAHA

A PFC based EV battery charger using a bridgeless isolated SEPIC converter

[J]. IEEE Transactions on Industry Applications, 2020, 56(1):477-487.

DOI:10.1109/TIA.28 URL [本文引用: 1]

[20]

JHA

, SINGH

Bridgeless SEPIC PFC converter for multistring LED driver

[J]. Journal of the Institution of Engineers (India):Series B, 2018, 99(4):353-367.

DOI:10.1007/s40031-018-0328-6 [本文引用: 1]

[21]

王金平, 胡凡宇, 侯良奎, 等.

一种单级无桥隔离型PFC变换器

[J]. 中国电机工程学报, 2017, 37(24):7276-7283.

[本文引用: 1]

WANG

Jinping

, HU

Fanyu

, HOU

Liangkui

, et al.

A single-stage bridgeless isolated PFC converter

[J]. Proceedings of the CSEE, 2017, 37(24):7276-7283.

[本文引用: 1]

[22]

CHEN

, MO

A bridgeless active-clamp power factor correction isolated SEPIC converter with mixed DCM/CCM operation

[C]// International Future Energy Electronics Conference (IFEEC), November 3-6,2013,Tainan,Taiwan,China. IEEE, 2013:1-6.

[本文引用: 2]

[23]

, QIAN

, TAO

, et al.

Small signal modeling and control loop design of critical conduction mode active clamp flyback converter

[J]. IEEE Transactions on Power Electronics, 2021, 36(6):7250-7263.

DOI:10.1109/TPEL.63 URL [本文引用: 1]

A single-stage dual-output tri-mode AC-DC regulator or inductively powered application

2019

... 近年来，随着电力电子技术的成熟和电力电子器件性能的提升，电力电子设备已经得到了广泛的应用，为了减少电力电子设备对电网的谐波污染，一些国家和国际学术团体提出并实施了一系列的电流谐波要求和标准^[1⇓⇓-4].为满足谐波要求和标准，交流输入的电力电子变换器需要采用功率因数校正(Power factor correction, PFC)技术提高用电设备的功率因数，降低电网谐波含量，确保电网安全可靠运行^[5]，因此人们开始广泛研究各种电路拓扑组成的PFC变换器. ...

高频AC/DC变换器优化控制策略研究

2020

Research on optimal control strategy for high-frequency AC/DC converter

2020

基于双路恒流输出单级Cuk PFC变换器的LED驱动电路

2020

LED driving circuit based on single stage Cuk PFC converter with dual constant current outputs

2020

新型无桥DCM Pseudo-Boost PFC变换器研究

2015

Research on novel bridgeless DCM Pseudo-Boost PFC converter

2015

基于航空电网的Boost PFC变换器设计

2018

Design of Boost PFC converter based on aviation power grid

2018

Reliability assessment of conventional isolated PWM DC-DC converters

2021

... 相比于Buck、Boost、Buck-Boost等非隔离PFC变换器，隔离型PFC变换器不仅能够实现输入输出隔离，而且通过合理设计，只用一级变换电路就可以实现PFC功能，因此研究人员已经在航空电子设备、车载充电器、通信及计算机设备电源等应用场合开展了隔离型PFC变换器的研究^[6⇓⇓-9].其中隔离型SEPIC PFC变换器由于具有器件数量少、成本低、输入输出电流连续等优点，得到研究人员的广泛关注^[10-11].由于变压器漏感带来的电压尖峰，传统隔离型SEPIC PFC变换器开关管的电压应力较大.文献[12-13]所提变换器应用有源钳位技术来降低开关管的电压应力，但是其电路控制复杂.文献[14]提出了一种集成磁结构的隔离有源钳位SEPIC PFC变换器，把输入电感、隔离变压器和二极管钳位电路集成到单个磁结构中，虽然降低了开关管和输出二极管的电压应力，但是该电路系统结构复杂，不易设计与控制；文献[15-16]所提变换器都用了有源钳位技术来抑制电压尖峰，实现了开关管的零电压开通，但是它们的电路控制复杂，成本高；并且文献[14⇓-16]均采用了传统整流桥.为进一步提高变换器的整体效率，学者们陆续提出了多种无桥SEPIC PFC拓扑^{[17⇓⇓⇓⇓-22]}，其中文献[22]提出的一种无桥PFC转换器，其输入电感电流交替工作在CCM/DCM模式，以获得高功率因数，提高整体效率，但是该变换器所用元器件数量多，控制复杂. ...

DCM-CRM Boost-Flyback单级PFC变换器

2019

DCM-CRM Boost-Flyback single-stage PFC converter

2019

Isolated DC-DC Boost converter for wide input voltage range and wide load range applications

2021

一种单级隔离型软开关功率因数校正变换器

2018

A single stage isolated soft switching power factor correction converter

2018

Isolated three-phase high power factor rectifier based on the SEPIC converter operating in discontinuous conduction mode

2013

Isolated SEPIC DC-DC converter with ripple-free input current and lossless snubber

2018

A high gain high efficiency and compact isolated Sepic DC-DC converter

2016

ZVS isolated active clamp Sepic converter for high power LED applications

2012

Isolated active-clamped SEPIC PFC converter based on SiC devices and integrated magnetics

2019

... ]所提变换器都用了有源钳位技术来抑制电压尖峰，实现了开关管的零电压开通，但是它们的电路控制复杂，成本高；并且文献[14⇓-16]均采用了传统整流桥.为进一步提高变换器的整体效率，学者们陆续提出了多种无桥SEPIC PFC拓扑^{[17⇓⇓⇓⇓-22]}，其中文献[22]提出的一种无桥PFC转换器，其输入电感电流交替工作在CCM/DCM模式，以获得高功率因数，提高整体效率，但是该变换器所用元器件数量多，控制复杂. ...

Single-phase active-clamped isolated SEPIC PFC converter with partial power processing output stage

2020

... ⇓-16]均采用了传统整流桥.为进一步提高变换器的整体效率，学者们陆续提出了多种无桥SEPIC PFC拓扑^{[17⇓⇓⇓⇓-22]}，其中文献[22]提出的一种无桥PFC转换器，其输入电感电流交替工作在CCM/DCM模式，以获得高功率因数，提高整体效率，但是该变换器所用元器件数量多，控制复杂. ...

High-performance active-clamped isolated SEPIC PFC converter with SiC devices and lossless diode clamp

2020

... -16]均采用了传统整流桥.为进一步提高变换器的整体效率，学者们陆续提出了多种无桥SEPIC PFC拓扑^{[17⇓⇓⇓⇓-22]}，其中文献[22]提出的一种无桥PFC转换器，其输入电感电流交替工作在CCM/DCM模式，以获得高功率因数，提高整体效率，但是该变换器所用元器件数量多，控制复杂. ...

单开关管无桥SEPIC PFC变换器

2014

Single-switch bridgeless SEPIC PFC converter

2014

基于三端口无桥PFC的两级式隔离型双输出AC-DC变换器

2020

Two stage isolated dual output AC-DC converter based on three port bridgeless PFC

2020

A PFC based EV battery charger using a bridgeless isolated SEPIC converter

2020

Bridgeless SEPIC PFC converter for multistring LED driver

2018

一种单级无桥隔离型PFC变换器

2017

A single-stage bridgeless isolated PFC converter

2017

A bridgeless active-clamp power factor correction isolated SEPIC converter with mixed DCM/CCM operation

2013

... ，其中文献[22]提出的一种无桥PFC转换器，其输入电感电流交替工作在CCM/DCM模式，以获得高功率因数，提高整体效率，但是该变换器所用元器件数量多，控制复杂. ...

Small signal modeling and control loop design of critical conduction mode active clamp flyback converter

2021

... 变换器的控制电路仅由运放、光耦和PWM控制芯片构成；将输出电压分压采样后的信号进行PI调节，再将误差信号通过光耦隔离传递到原边控制芯片UCC2580-3，然后控制芯片UCC2580-3输出一组带死区的互补驱动信号OUT1和OUT2，信号OUT1同步驱动主开关管S₁、S₂，信号OUT2驱动辅助开关管S₃.通过调节两个信号的死区时间来实现开关管S₁、S₂和S₃的ZVS，通过调节漏感L_r和钳位电容C_c的值，让其有足够的谐振深度，从而使能量能完全传递至二次侧^[23]来实现副边续流二极管VD₀的ZCS.由图1可知，所提PFC变换器拓扑仅用一级变换就可以实现AC-DC功能和输入输出隔离，所用元器件数量少，成本低，控制简单. ...

〈

〉