永磁同步电机(Permanent magnet synchronous motor, PMSM)因功率因数高、结构简单、可靠性好等优点，在汽车驱动领域、办公自动化设备以及高精度加工等方面获得了广泛应用。传统直接转矩控制通过滞环控制器和逆变器完成转矩控制，但逆变器的开关频率不高以及滞环控制的不精确性会导致转矩的脉动^[1⇓-3]，这使得永磁同步电机的应用受到了较大限制，因此，转矩脉动的抑制成为了倍受关注的问题。

目前，许多学者主要通过以下控制方法来实现转矩脉动抑制，如PI控制^[4⇓-6]、模糊控制^[7-8]以及滑模控制^[9⇓⇓-12]等。PI控制可以一定程度上降低转矩脉动，但传统PI控制器的参数确定较为复杂，可供选择的参数整定方法较少，且PI控制器对电机参数、转速和负载变化都较为敏感，对电机的工作环境要求较高。为了克服PI参数调节困难和鲁棒性较差的问题，很多学者提出了模糊控制。例如文献[13]设计了一种新型模糊控制器代替PI控制器，一定程度上克服了PI参数调节困难和鲁棒性较差的问题，但模糊规则的建立较为困难，模糊规则制定不合理还可能会导致模糊控制效果变差。针对以上问题，有学者提出了滑模控制策略。滑模控制可在两个方面减小转矩脉动。一方面是通过构造滑模控制器来减小转矩的脉动。文献[14]提出一种双滑模控制方案，通过分别设计磁链和转矩控制器代替滞环控制器实现对PMSM的控制，该方案可以克服传统滞环控制器的脉动，但该滑模控制器以sign函数作为切换函数，又给系统带来了高频抖振。文献[15]提出了基于新型趋近率的滑模控制器，在设计趋近律的过程中，将sign函数替换为sat函数，一定程度上减小了抖阵。然而上述文献中提出的都是整数阶滑模，且仅在滑模的滑动阶段具有鲁棒性，不具备全局鲁棒性，导致趋近阶段的控制效果较差。另一方面是通过构造观测器间接减小脉动。文献[16]设计了电压型定子磁链观测器，由电压型定子磁链观测器表达式可知，定子电阻的变化是导致定子磁链观测不准确的主要原因。在定子电阻可变的场合，电压型定子磁链观测器观测到的磁链幅值有着较大的误差。文献[17]提出了基于电流模型的磁链观测器，但没有考虑电机参数对观测结果的影响。文献[18]提出一种扩展卡尔曼滤波与滑模观测器结合的方法减小系统抖振，但是仍然没有考虑定子电阻变化对结果的影响。

综上所述，本文针对永磁同步电机转矩脉动的问题，提出了一种基于构造分数阶全局滑模控制器和基于Elman神经网络电阻辨识的磁链观测器的PMSM转矩脉动抑制方法。首先，建立了PMSM的数学模型，介绍了分数阶微积分的定义，为了减小抖振且具有全局鲁棒性，设计了以磁链和转矩误差为滑模面的分数阶全局滑模控制器；另外，通过Elman神经网络完成定子电阻辨识，设计了一种考虑定子电阻变化的滑模磁链观测器来改善磁链观测精度，进一步达到抑制转矩脉动的目的。最后，在Matlab/Simulink软件和电机试验台上对本文提出的PMSM转矩抑制方法进行了仿真和试验验证，结果表明，本文所提方法可以明显减少PMSM转矩脉动。

为了便于控制器设计，本文建立两相旋转坐标系下的数学模型，其电压方程可以表示为

式中，${{u}_{d}}$、$\mathop{u}_{\text{q}}$分别为d-q旋转坐标系下的定子电压分量；$\mathop{i}_{\text{d}}$、$\mathop{i}_{\text{q}}$分别为d-q旋转坐标系下的定子电流分量；${{L}_{d}}$、${{L}_{q}}$分别为d-q旋转坐标系下的电感分量；${{\omega }_{\text{e}}}$为电角速度；${{\psi }_{\text{f}}}$为永磁体转子磁链；R为定子电阻。

本文以表贴式PMSM为研究对象，其电感满足${{L}_{\text{d}}}={{L}_{\text{q}}}$，电磁转矩方程可以表示为

式中，${{T}_{e}}$为电磁转矩；$\mathop{p}_{\text{n}}$为PMSM的磁极对数。

磁链方程可表示为

同时有

式中，$\theta $为转矩角；$L$为定子电感。

为了方便后面控制器的设计，分别对$\mathop{T}_{\text{e}}$、${{\psi }_{\text{s}}}$求导。

首先，对式(2)求导，并将式(1)代入可得

其次，由式(3)~(5)可得

式中，$a=-\frac{R}{L}$，$b=\frac{3{{p}_{\text{n}}}{{\psi }_{\text{f}}}}{\mathrm{2}L}$，$c=\frac{\text{3}}{\text{2}L}{{p}_{\text{n}}}{{\psi }_{\text{f}}}{{\omega }_{\text{e}}}\cdot $$(-L{{i}_{d}}-{{\psi }_{\text{f}}})$；${{\psi }_{\text{s}}}$为定子磁链；$m=-\frac{R}{L}$，$n=\frac{R{{\psi }_{\text{f}}}}{L\cos \theta }$，$l=\frac{1}{\cos \theta }$。

自分数阶微积分被提出以来，应用就越来越广泛，同时也越来越受到学者们的关注。它的定义首先从连续函数的整数阶导数开始，然后将整数阶导数推广到任意实数。也就是说整数阶微积分仅仅是分数阶微积分的一种特殊形式。毫无疑问，分数阶微积分相比于整数阶微积分更能准确表达确定系统的数学模型^[19]。并且分数阶系统具有记忆性，可以缓慢传递能量，防止抖振。利用分数阶微积分设计的控制器相比于传统整数阶控制器，具有更好的控制性能^[20-21]。下面介绍分数阶微积分定义及运算性质，为下文分数阶全局滑模控制器的设计提供知识准备。

由于应用范围的不同，分数阶微积分定义的形式主要有G-L型、R-L型和Ca-Puto型三种^[22]。由于Ca-Puto型分数阶微积分定义能很好地应用到现实模型中，运算相对简单，且使得Laplace变换式容易求解，故广泛应用于工程背景下的物理问题中。因此，本文选择Ca-Puto型分数阶微积分的定义形式，并以此为基础设计分数阶全局滑模控制器，其统一定义为

式中，$\mathop{{}_{a}D}_{t}^{\alpha }$为微积分算子；a、t分别为算子的下限和上限；$\alpha $为算子的阶次；n为不小于$\alpha $的最小整数；$\frac{{{\text{d}}^{n}}}{\text{d}{{t}^{n}}}$为整数阶微分。

$\Gamma (\cdot )$为Gamma函数，可表示为

式中，$\mathop{{}_{a}D}_{t}^{\alpha }$的定义为

由式(8)可知，当$n-1\le \alpha \le n$时，$\mathop{{}_{a}D}_{t}^{\alpha }$表示的是区间$[a,t]$上的分数阶微积分；当$\alpha \text{=}n$时，$\mathop{{}_{a}D}_{t}^{\alpha }$表示的是区间$[a,t]$上的整数阶微积分。

分数阶微积分有不同的定义形式，针对本文选择的定义形式，其常见计算性质如式(11)所示，将在下文控制器设计中应用到。

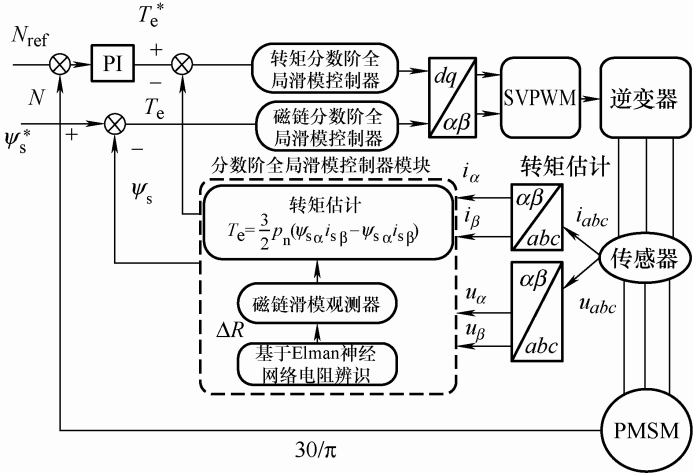
本文直接以磁链误差和转矩误差为控制器的输入，设计了分数阶全局滑模控制器取代传统DTC中的滞环控制器。全局滑模可保证系统的初始状态在滑模面上，故消除了滑模控制的趋近阶段，克服了传统滑模趋近模态不具备鲁棒性的问题，另外，分数阶滑模控制器的设计还能抑制磁链和转矩脉动。基于分数阶全局滑模和磁链观测器的PMSM DTC框图如图1所示。

滑模面是滑模控制器的重要组成部分，已知分数阶控制器具有更好的控制性能。因此，可通过设计分数阶滑模面来抑制磁链和转矩脉动，提高控制性能。本文假设PMSM的转矩误差为${{e}_{\text{T}}}=T_{\text{e}}^{\text{*}}-{{T}_{\text{e}}}$，磁链误差为${{e}_{\text{ }\!\!\psi\!\!\text{ }}}=\psi _{\text{s}}^{\text{*}}-{{\psi }_{\text{s}}}$，其中$T_{\text{e}}^{\text{*}}$、$\psi _{\text{s}}^{\text{*}}$分别为转矩和磁链给定值。

首先，定义分数阶转矩和磁链滑模面为

式中，0和t为分数阶积分的上下限；${{c}_{1}}$、${{c}_{2}}$表示滑模增益。

为了保证初始时刻的状态处于滑模面上，消除滑模控制的趋近模态，使系统的响应在全局都具有鲁棒性，本文在式(12)和式(13)的基础上，设计了转矩和磁链全局滑模面分别为

式中，$f(t)$为待设计函数。$f(t)$是为了保证在初始时刻系统的任意状态都处于滑模面上，即当t=0时可以保证s=0。根据$f(t)$需要满足的条件，可以令$f(t)=\left[ e(0)+{{c}_{1}}{}_{0}D_{t}^{-\alpha }e(t) \right]\exp (-kt)$。

已知直接转矩控制中包括两个滞环控制器和一个PI控制器，本文将传统直接转矩控制中的滞环控制器替换为分数阶全局滑模控制器，以达到减小转矩脉动的目的。

首先，对${{e}_{\text{T}}}$求导并将式(6)代入可得

式中，$\varphi =\dot{T}_{\text{e}}^{\text{*}}-aT_{\text{e}}^{\text{*}}$。

对${{e}_{\text{ }\!\!\psi\!\!\text{ }}}$求导并将式(7)代入可得

式中，$\mu =\dot{\psi }_{\text{s}}^{\text{*}}-m\psi _{\text{s}}^{\text{*}}$。

分别对式(14)和式(15)求导，并结合式(16)和式(17)可得

为了PMSM能获得较好的动态品质，采用等速趋近律

式中，$\operatorname{sgn} (s)$表示符号函数；$\varepsilon >0$。

为了保证系统的稳定性，即满足条件$\dot{V}\le 0$可以设计控制律为

为了消除因引入符号函数而带来的抖振，本文用双曲正切函数$H(x)$来代替符号函数。

可利用李雅普诺夫稳定性判据证明全局滑模控制器的稳定性，构造李雅普诺夫函数为

对李雅普诺夫函数求导可得

因此，当$\varepsilon \tanh (\left| {{s}_{1}} \right|)\ge \left| c \right|$时，${{\dot{V}}_{1}}\le 0$。

同理

因此，当$\varepsilon \tanh (\left| {{s}_{2}} \right|)\ge \left| n \right|$时，${{\dot{V}}_{2}}\le 0$。

根据李雅普诺夫稳定性判据可知，滑模控制器的稳定性条件是构造一个李雅普诺夫函数V，且满足$\dot{V}\le 0$。由以上分析可知当${{\dot{V}}_{1}}\le 0$时，即基于转矩误差设计的分数阶全局滑模控制器满足稳定性条件。同理当$\mathop{{\dot{V}}}_{2}\le 0$时，即基于磁链误差设计的分数阶全局滑模控制器满足稳定性条件。

由PMSM数学模型可知，定子磁链观测精度会直接影响PMSM DTC的控制性能。如果磁链的相位误差过大，则会导致扇区选择错误，输出错误的电压矢量，如果磁链幅值误差过大，会使输出转矩不准确，最终会导致电机直接转矩控制的转矩脉动加剧，不利于电机使用性能的改善。

同时由电机磁链方程式(3)可知，电机定子电阻值变化也会对磁链观测结果产生影响。因此，本文为避免电机定子电阻影响观测精度，利用Elman神经网络算法对电机电阻进行了辨识，然后基于电阻辨识结果，设计了磁链滑模观测器，从而实现定子磁链的精确观测，以达到抑制转矩脉动的目的。

假设三相PMSM为理想电机，选择在两相静止坐标系下建立数学模型，可以得到以${{i}_{s}}$和${{\psi }_{s}}$为状态变量的状态方程

式中，$\mathbf{A}=\left[ \begin{matrix} {{\mathbf{A}}_{11}} & {{\mathbf{A}}_{12}} \\ {{\mathbf{A}}_{21}} & {{\mathbf{A}}_{22}} \\ \end{matrix} \right]$； ${{A}_{11}}=-\frac{R}{L}I+{{\omega }_{e}}J$；${{A}_{12}}=-\frac{{{\omega }_{e}}}{L}J$； ${{A}_{21}}=-RI$；${{A}_{22}}=0$； $x={{\left[ \begin{matrix} {{i}_{s}} & {{\psi }_{s}} \\ \end{matrix} \right]}^{\mathrm{T}}}$；$B={{\left[ \begin{matrix} {{B}_{1}} & {{B}_{2}} \\ \end{matrix} \right]}^{\mathrm{T}}}$； ${{B}_{1}}=\frac{1}{L}I$；${{B}_{2}}=I$； ${{i}_{s}}={{\left[ \begin{matrix} {{i}_{s\alpha }} & {{i}_{s\beta }} \\ \end{matrix} \right]}^{\mathrm{T}}}$； ${{\psi }_{s}}={{\left[ \begin{matrix} {{\psi }_{s\alpha }} & {{\psi }_{s\beta }} \\ \end{matrix} \right]}^{\mathrm{T}}}$；${{u}_{s}}={{\left[ \begin{matrix} {{u}_{s\alpha }} & {{u}_{s\beta }} \\ \end{matrix} \right]}^{\mathrm{T}}}$； ${{i}_{s}}$、${{\psi }_{s}}$、 ${{u}_{s}}$分别表示定子电流、定子磁链和定子电压； $I=\left[ \begin{matrix} 1 & 0 \\ 0 & 1 \\\end{matrix} \right]$；$J=\left[ \begin{matrix} 0 & -1 \\ 1 & 0 \\\end{matrix} \right]$。

在电机运行过程中，电阻会根据运行时间、外界温度、电流和频率的变化而变化，如果依然将电阻当作一个常量，则会严重影响磁链的观测精度。因此，本文设计了基于Elman神经网络电阻辨识的磁链滑模观测器，来进一步提高磁链的观测精度。

基于Elman神经网络电阻辨识的磁链滑模观测器设计思想是：首先，构造以电流和磁链为状态变量的滑模观测器，然后，用Elman神经网络完成电阻的辨识，最后，构造李雅普诺夫函数，证明本文设计观测器的稳定性。

若将电阻当作变量，则可构造如下观测器

式中，$\hat{x}={{\left[ \begin{matrix} {{{\hat{i}}}_{s}} & {{{\hat{\psi }}}_{s}} \\ \end{matrix} \right]}^{\mathrm{T}}}$； ${{\hat{i}}_{s}}$、 ${{\hat{\psi }}_{s}}$为对应状态变量的观测值；$\hat{A}=\left[ \begin{matrix} {{{\hat{A}}}_{11}} & {{A}_{12}} \\ {{{\hat{A}}}_{21}} & {{A}_{22}} \\ \end{matrix} \right]$；${{\hat{A}}_{11}}=-\frac{{\hat{R}}}{L}I+{{\omega }_{e}}J{{\hat{A}}_{21}}$ $=-\hat{R}I$；${{\hat{i}}_{s}}={{\left[ \begin{matrix} {{{\hat{i}}}_{s\alpha }} & {{{\hat{i}}}_{s\beta }} \\ \end{matrix} \right]}^{\mathrm{T} }}$；${{\hat{i}}_{s\alpha }}$、 ${{\hat{i}}_{s\beta }}$为$\alpha \beta $轴的电流观测值；$\hat{R}$为定子电阻观测值；$h={{\left[ \begin{matrix} {{h}_{1}}I & {{h}_{2}}J \\ \end{matrix} \right]}^{\mathrm{T}}}$； ${{h}_{1}}{{h}_{2}}$表示滑模增益。 $s={{\left[ \begin{matrix} {{{\tilde{i}}}_{s\alpha }} & {{{\tilde{i}}}_{s\beta }} \\ \end{matrix} \right]}^{\mathrm{T} }}$； ${{\tilde{i}}_{s\alpha }}$、 ${{\tilde{i}}_{s\beta }}$为电流观测误差。

且${{\tilde{i}}_{s\alpha }}$与${{\tilde{i}}_{s\beta }}$可表示为

将式(27)减去式(28)可得观测误差方程为

式中，$\tilde{x}={{\left[ \begin{matrix} {{{\tilde{i}}}_{s}} & {{{\tilde{\psi }}}_{s}} \\ \end{matrix} \right]}^{\mathrm{T}}}$；${{\tilde{i}}_{s}}$、${{\tilde{\psi }}_{s}}$为对应状态的观测误差； $E=\left[ \begin{matrix} -\frac{\Delta R}{L}I & 0 \\ -\Delta RI & 0 \\ \end{matrix} \right]\hat{x}$；$\Delta R=\hat{R}-R$；${{\tilde{\psi }}_{s}}$的$\alpha \beta $轴分量表达式为

为了消除符号函数引入带来的抖振，用$\tanh (x)$来代替符号函数$\operatorname{sgn}(s)$。接下来用神经网络来辨识出定子电阻的值。

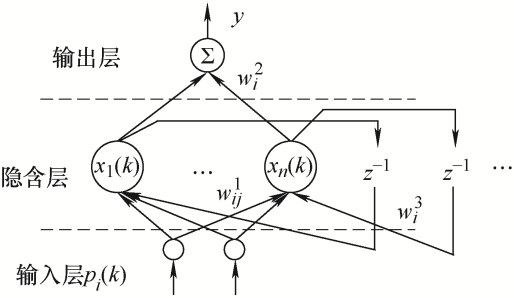
Elman神经网络是一种典型的局部回归网络，可将它看成一个具有局部记忆单元和局部反馈的前向神经网络。Elman神经网络包括输入层、隐含层、承接层和输出层。其中，承接层与每一个隐含层节点都相连接，其作用是将上一时刻的隐含层状态连同当前时刻的输入一起作为隐含层的输入。也就是说，它可从隐含层接收反馈信号，使Elman神经网络对历史数据较为敏感，对系统的动态辨识具有重要意义。Elman神经网络结构如图2所示。

图2中，$w_{ij}^{1}$、$w_{i}^{2}$、$w_{i}^{3}$分别为隐含层、输出层和承接层的权值；${{p}_{i}}(k)$为网络的输入，y为神经网络的输出。

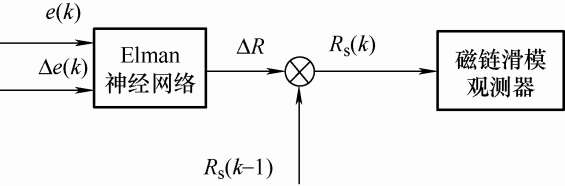
本文以定子电流参考值和定子电流实际值的差$e(k)$以及它们的误差变化$\Delta e(k)$作为Elman神经网络的输入。定子电阻变化为输出。输入输出关系图如图3所示。

其中

式中，$I_{\text{s}}^{\text{*}}$为定子电流的参考值；${{I}_{\text{s}}}$为定子电流的实际值。

同时以电阻变化$\Delta R$为Elman神经网络的输出。由图3可知将神经网络的输出加上电阻上一时刻的值，就可以得到辨识的电阻值，然后将其用于磁链滑模观测器的设计。

为了实现对定子电阻的辨识，以下面的步骤完成对Elman神经网络的训练^[23]。

步骤1：初始化参数：初始权值设为[-1,1]内的随机数。

步骤2：根据仿真获得Elman神经网络的输入输出数据。

步骤3：计算输出层的输出。输出层输出为

式中，$f(\cdot )$表示激活函数，本文取其为tansig函数。

步骤4：计算输出误差。

步骤5：权值更新。其中权值的变化为

对于输出层的权值有

隐含层的权值有

承接层的权值有

如果得到的权值不小于给定的误差，则返回步骤3，直到满足小于给定误差，就可得到训练好的Elman神经网络。然后将神经网络的输出加上上一时刻的电阻值就可以得到辨识后的电阻。即有

以上为Elman电阻辨识的过程。

为了证明定子电流观测滑动模态的存在性，构造李雅普诺夫函数$V=\frac{1}{2}\left[ \begin{matrix} {{{\tilde{i}}}_{\mathrm{s }\!\!\alpha\!\!\text{ }}} & {{{\tilde{i}}}_{\mathrm{s }\!\!\beta\!\!\text{ }}} \\ \end{matrix} \right]\left[ \begin{align} & {{{\tilde{i}}}_{\mathrm{s }\!\!\alpha\!\!\text{ }}} \\ & {{{\tilde{i}}}_{\mathrm{s }\!\!\beta\!\!\text{ }}} \\ \end{align} \right]$。

对$V$求导，并结合式(30)可得

因为${{\tilde{i}}_{\mathrm{s }\!\!\alpha\!\!\text{ }}}\tanh ({{\tilde{i}}_{\mathrm{s }\!\!\alpha\!\!\text{ }}})+{{\tilde{i}}_{\mathrm{s }\!\!\beta\!\!\text{ }}}\tanh ({{\tilde{i}}_{\mathrm{s }\!\!\beta\!\!\text{ }}})>0$，当滑模增益${{h}_{1}}$取较大值时，即可以保证$\dot{V}\le 0$，该观测器具有稳定性。即可以满足${{\tilde{i}}_{\mathrm{s}}}=\frac{\mathrm{d}{{{\tilde{i}}}_{\mathrm{s}}}}{\mathrm{d}t}=0$，为了证明磁链观测滑动模态的存在性，构造李雅普诺夫函数如下

对李雅普诺夫函数求导可得

当${{h}_{1}}={{h}_{2}}\ge \frac{2\left| \Delta R \right|(\left| {{i}_{\mathrm{s }\!\!\beta\!\!\text{ }}} \right|+\left| {{i}_{\mathrm{s }\!\!\alpha\!\!\text{ }}} \right|)}{L[\tanh {{({{{\tilde{i}}}_{\mathrm{s }\!\!\alpha\!\!\text{ }}})}^{2}}+\tanh {{({{{\tilde{i}}}_{\mathrm{s }\!\!\beta\!\!\text{ }}})}^{2}}]}$时满足稳定性条件。

为了进一步验证本文所提方法的有效性，搭建了电机试验台架。试验台架由PMSM、电机试验箱和上位机组成。将Simulink中的仿真模型通过CCS6.2生成可以在DSP中运行的代码，再将代码下载到TMS320F28335之中，然后由逆变器输出信号，完成对PMSM的控制。试验中，利用串联可变电阻来模拟定子电阻的变化。为了获得更好的控制效果选择$\varepsilon =90$、${{c}_{1}}=30$、${{c}_{2}}=33$，本文中PMSM的电机参数与仿真相同，电机试验台架实物如图4所示，电机参数如表1所示。

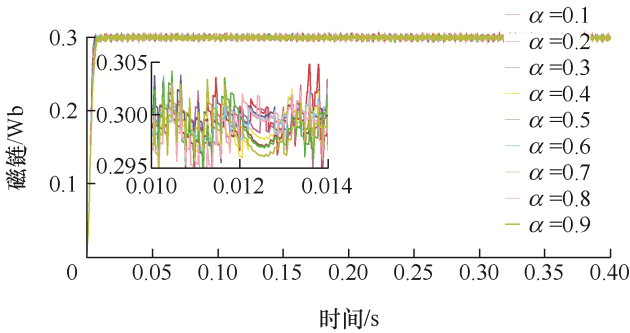
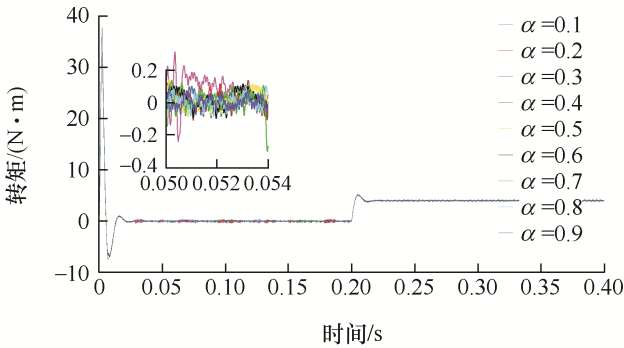
首先，仿真确定分数阶全局滑模控制器的阶次。将分数阶全局滑模控制器的阶次分别选择α=0.1、α=0.2、α=0.3、α=0.4、α=0.5、α=0.6、α=0.7、α=0.8、α=0.9来进行仿真分析。通过仿真得到不同阶次全局滑模控制器控制下的磁链和转矩值，然后确定最优的阶次。为了确保磁链观测效果仅与α的取值有关，设置分数阶全局滑模控制器和磁链观测器的其他参数相同，仿真结果如图5和图6所示。

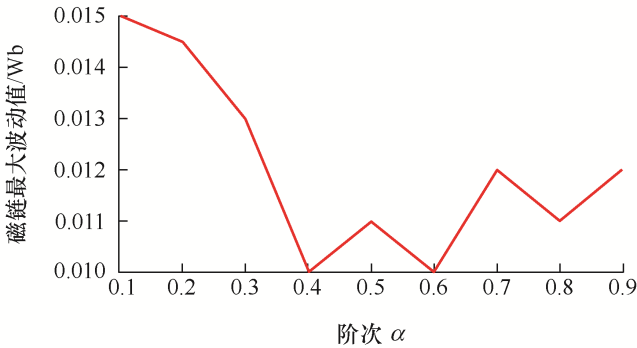
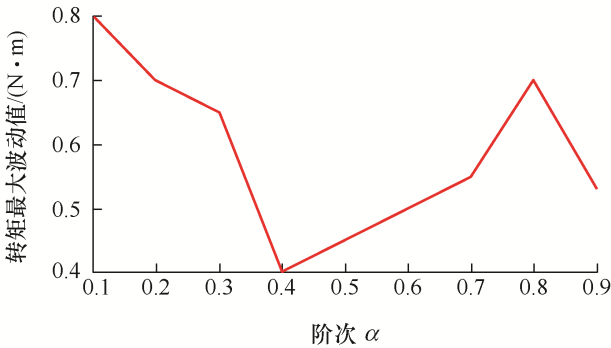
图7和图8分别为不同阶次下分数阶全局滑模控制器的磁链和转矩的最大波动值曲线。

由图7和图8可知，当分数阶阶次为0.4时，磁链和转矩的波动值均较小。因此，本文后续仿真与试验分析中，采用分数阶阶次为0.4的分数阶全局滑模控制器来对PMSM转矩波动抑制进行研究。

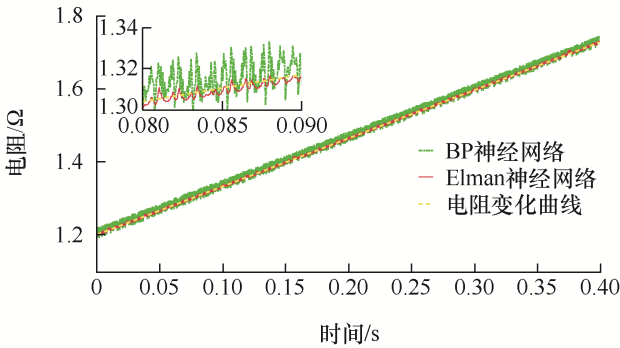
其次，通过仿真分析证明本文所提电阻辨识方法的有效性，并将本文提出的Elman神经网络方法和传统BP神经网络方法进行对比，仿真时设定电阻值由1.2 Ω变化到1.75 Ω，其仿真结果如图9所示。

由图9可知，本文提出的Elman神经网络辨识的电阻值在电阻变化值附近变化，而传统的BP神经网络的电阻辨识值波动较大。因此，仿真结果表明相比于传统BP神经网络，Elman神经网络可以更好地完成定子电阻的辨识。

根据确定的分数阶阶次和本文提出的电阻辨识方法，利用Matlab/Simulink建立如图1所示的基于分数阶全局滑模和磁链观测器的PMSM DTC系统，并生成代码，通过CCS6.2编译后利用仿真器将C代码下载到DSP控制箱中，完成对PMSM的转矩脉动抑制试验。

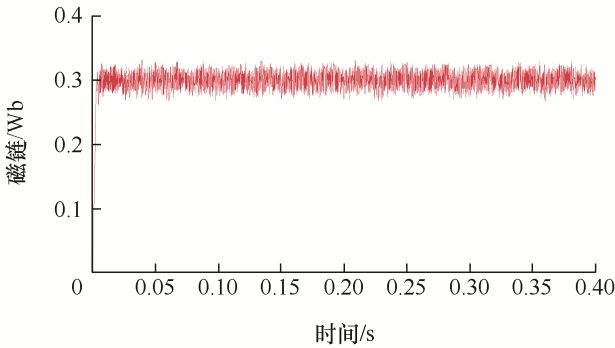
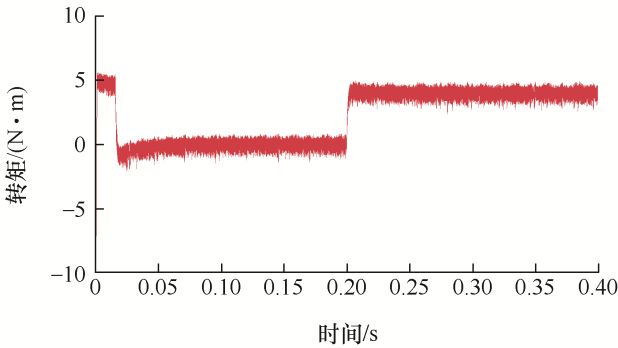
图10和图11为传统DTC中的磁链和转矩图。传统DTC中采用了滞环控制器，由于滞环容差值的存在，导致较大的转矩脉动。由图10可知其磁链观测误差为0.06 Wb左右，对于图11，本文在0.2 s时施加4 N·m的负载转矩。此时转矩脉动范围最大为2 N·m，通过与下面试验的对比可知，采用分数阶全局滑模控制器可以极大减少传统滞环控制中的转矩脉动。

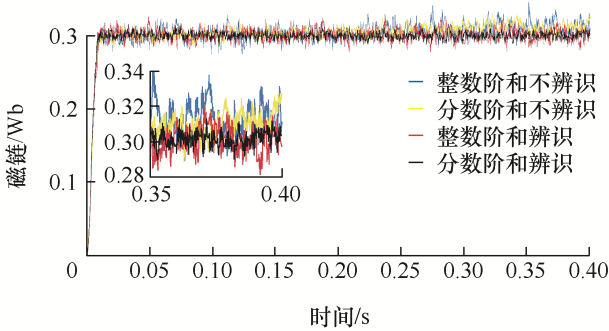
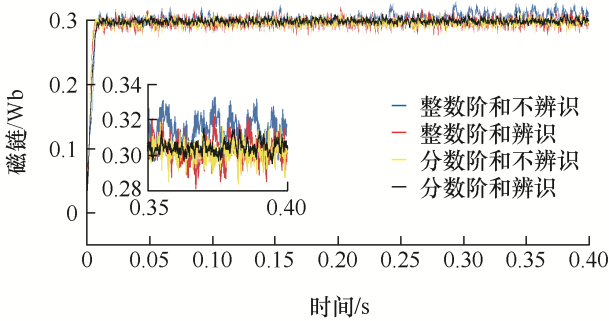
图12和图13分别为基于电阻不辨识磁链滑模观测的整数阶、分数阶全局滑模和基于电阻辨识磁链滑模观测的分数阶、整数阶全局滑模的磁链试验对比结果。其中，图12为给定转速为80 r/min的磁链对比图，由结果可知，基于Elman神经网络电阻辨识磁链滑模观测的分数阶和整数阶全局滑模控制，其磁链脉动范围最大为0.03 Wb和0.04 Wb，其他电阻不辨识磁链观测的分数阶和整数阶全局滑模控制的磁链脉动范围最大分别为0.04 Wb、0.05 Wb。图13为给定转速为800 r/min的磁链对比图，由结果可知，基于Elman神经网络电阻辨识磁链滑模观测的分数阶和整数阶全局滑模控制，其磁链脉动范围最大为0.025 Wb和0.035 Wb，其他电阻不辨识磁链观测的分数阶和整数阶全局滑模控制的磁链脉动范围最大为0.03 Wb、0.04 Wb。因此，试验证明了分数阶全局滑模控制器和基于Elman神经网络电阻辨识的磁链观测器可以有效地降低磁链脉动，同时基于Elman神经网络电阻辨识的磁链观测器在低速工况下对磁链脉动也有较好的抑制效果。

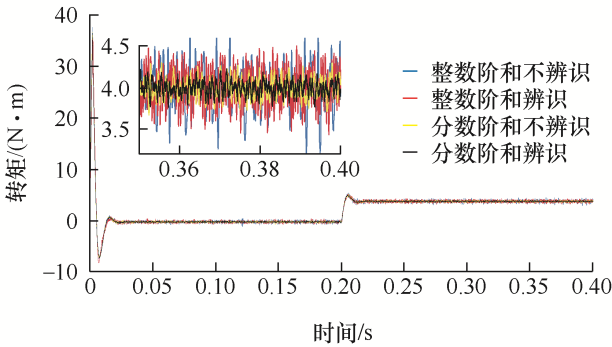
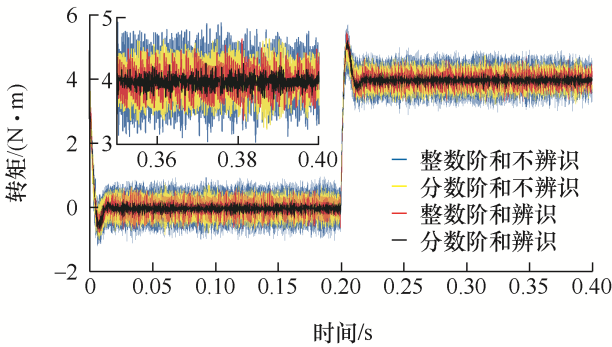
同理，图14和图15为四种方法的转矩试验对比结果。其中，图14为给定转速为800 r/min的转矩对比图，并且在0.2 s时施加4 N·m的负载。由图14可知，基于Elman神经网络电阻辨识磁链滑模观测的分数阶和整数阶全局滑模控制，其转矩脉动范围最大为0.4 N·m和1 N·m，其他电阻不辨识磁链观测的分数阶和整数阶全局滑模控制的转矩脉动范围最大为0.6 N·m、1.2 N·m。图15为给定转速为80 r/min的转矩对比图，并且在0.2 s时施加4 N·m的负载。由图15可知，基于Elman神经网络电阻辨识磁链滑模观测的分数阶和整数阶全局滑模控制，其转矩脉动范围最大为0.6 N·m和1.2 N·m，其他电阻不辨识磁链观测的分数阶和整数阶全局滑模控制的转矩脉动最大为1.2 N·m、1.8 N·m。因此，试验证明了分数阶全局滑模控制器和基于Elman神经网络电阻辨识的磁链观测器可以有效地降低转矩脉动，同时基于Elman神经网络电阻辨识的磁链观测器在低速工况下对转矩脉动有更好的抑制效果。

针对传统DTC的转矩脉动大的问题，本文以PMSM磁链和转矩误差来设计分数阶滑模面，构建分数阶全局滑模控制器代替传统DTC中的滞环控制器。其次，提出了一种基于Elman神经网络电阻辨识的磁链滑模观测器，实现对定子电阻值的精确辨识。最后，构建基于分数阶全局滑模控制和Elman神经网络电阻辨识的磁链观测的PMSM控制系统，并进行了仿真与试验分析，得到如下结论。

(1) 本文提出的分数阶全局滑模控制器可以有效地解决传统滑模控制的抖振问题，并且降低传统DTC的磁链和转矩脉动。

(2) 本文提出的基于Elman神经网络电阻辨识的磁链滑模观测器有更高的观测精度，对定子电阻变化具有鲁棒性，可以有效地降低磁链和转矩脉动，同时在低速工况下，对磁链和转矩的抑制效果更好。

(3) 将两种方法相结合对电机直接转矩控制中转矩脉动抑制具有较好效果。