基于电导增量法的全局最大功率点跟踪算法

doi:10.11985/2023.02.025

基于电导增量法的全局最大功率点跟踪算法

刘祚松^,¹, 王红艳^,¹, 周蒙恩², 钱阳¹

1.南京工程学院电力工程学院南京 210016

2.国华(江苏)风电有限公司东台 224200

Global Maximum Power Point Tracking Algorithm Based on Conductance Increment Method

LIU Zuosong^,¹, WANG Hongyan^,¹, ZHOU Mengen², QIAN Yang¹

1. School of Electric Power Engineering, Nanjing Institute of Technology, Nanjing 210016

2. Guohua (Jiangsu) Wind Power Co., Ltd., Dongtai 224200

通讯作者: 王红艳，女，1972年生，博士，教授。主要研究方向为新能源发电及利用。E-mail：hywang@njit.edu.cn

收稿日期: 2022-08-11 修回日期: 2022-11-28

Received: 2022-08-11 Revised: 2022-11-28

作者简介 About authors

刘祚松，男，1996年生，硕士研究生。主要研究方向为新能源发电及利用。E-mail：1021759658@qq.com

摘要

在部分阴影条件(Partially shaded condition, PSC)下，光伏阵列的功率曲线有多个峰值。传统的跟踪方法只在均匀光照条件(Uniform irradiance condition，UIC)下有效，在PSC情况下则无法追踪到全局峰值(Global peak，GP)。为了在均匀光照条件下和部分阴影条件下均能快速有效地跟踪到GP，提出一种基于变步长电导增量(Incremental conductance，INC)法的GP跟踪算法。该算法主体由四个步骤构成，通过循环执行这四个步骤来寻找全局峰值点。为了提高跟踪精度，所提算法在局部峰值点附近使用一种变步长的INC算法以减小扰动步长。为了减少跟踪时间，算法采用了两种扰动步长，特别是在步骤二和步骤三中通过采用较大的扰动步长，加快了跟踪速度。最后，通过在Matlab构建模型，验证了所提算法的效果。仿真结果表明，该方法比传统的INC全局方法速度更快、精度更大、效率更高。

关键词： 光伏阵列; 电导增量法; 局部阴影; 全局峰值

Abstract

Under the partially shaded condition(PSC), the power curve of the photovoltaic array has multiple peaks. The traditional tracking methods are effective under uniform illumination condition(UIC), but cannot track the global peak(GP) under PSC. In order to track GP quickly and effectively under uniform illumination condition and partially shaded condition, a GP tracking algorithm based on variable step incremental conductance(INC) method is proposed. The main body of the algorithm consists of four steps, which are executed circularly to find the global peak point. In order to improve the tracking accuracy, the algorithm uses an INC algorithm with variable step size to reduce the disturbance step size near the local peak point. In order to reduce the tracking time, the algorithm uses two kinds of perturbation step. Especially in step 2 and step 3, the tracking speed is accelerated by adopting a larger disturbance step size. Finally, the effectiveness of the proposed algorithm is verified by building a model in Matlab. Simulation results show that the proposed method is faster, more accurate and more efficient than the traditional INC global method.

Keywords： PV array; conductance increment method; local shadow; global peak

PDF (467KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

刘祚松, 王红艳, 周蒙恩, 钱阳. 基于电导增量法的全局最大功率点跟踪算法[J]. 电气工程学报, 2023, 18(2): 245-253 doi:10.11985/2023.02.025

LIU Zuosong, WANG Hongyan, ZHOU Mengen, QIAN Yang. Global Maximum Power Point Tracking Algorithm Based on Conductance Increment Method[J]. Chinese Journal of Electrical Engineering, 2023, 18(2): 245-253 doi:10.11985/2023.02.025

1 引言

2020年，我国明确提出“双碳”目标，大规模开发可再生能源，不仅是“双碳”目标实现的重要一环，也是保障我国能源供应的重要手段。近年来，光伏发电以清洁环保、功率可扩展性强、操作和维护简单等优势^[1]得到迅速发展。光伏电池因环境不同，最大功率点(Maximum power point，MPP)会有所差异，而且光伏阵列在均匀光照条件(Uniform irradiance condition, UIC)下其输出特性与单个太阳能电池相似，但在部分阴影条件(Partially shaded condition，PSC)下时，因阵列中模块所受光照不同，其输出特性不再与单个电池呈简单的倍数关系^[2]，因而会影响光伏系统对太阳能的利用效率。

为实现对光能的利用效率最大，学界已提出多种最大功率点跟踪(Maximum power point tracking, MPPT)方法。在UIC下，由于光伏阵列只有一个峰值，传统的MPPT算法，如INC法^[3⇓-5]、扰动观测法^[6⇓-8]可以成功地跟踪到MPP。然而，当其处于PSC条件下时，其功率曲线会有多个峰值^[9]，传统跟踪算法则无法找到全局峰值(Global point, GP)。神经网络^[10]和群体智能优化算法^[11-12]等先进方法在均匀光照条件下和局部阴影条件下都优于传统算法，但与传统算法相比，其架构更复杂，运算量更大。

一些学者为了使传统MPPT方法在PSC下仍能搜寻到MPP，对传统的算法进行相应改进，使之能够准确跟踪PSC下的GP点。文献[13]提出了一种结合INC法和粒子群优化(Particle swarm optimization, PSO)的混合算法，PSO用于快速定位最大功率点的邻域，增量电导法则对该邻域进行二次搜索，以准确地找到最优解。文献[14]通过使用线性方程计算不同峰值间隔的峰值电压，并获得相应的峰值功率，通过比较可以精确地跟踪到GP。文献[15]利用光伏阵列输出电流单调的特性，在进行GP追踪时，用开路电压和短路电流不断刷新电压下限和电流下限，减小了算法的扫描范围和跟踪时间。文献[16]通过分析得出光伏阵列P-U曲线的第k个峰值点约在0.8kU_oc(U_oc为光伏电池的开路电压)处，再用爬山法逐个寻找峰值点，最后通过比较得到GP。文献[17]提出对参数进行优化的算法，先利用环境参数计算出最优电流，通过追踪最优电流，实现对GP的跟踪。文献[18]运用光伏阵列在PSC条件下，峰值点与U_oc和I_sc间的比例关系以及等功率曲线来跟踪GP。文献[19]深入分析了光伏阵列的各个特性，得出I-U曲线中恒流源区域的拐点约在0.7nU_oc(其中n为受同一种光照的模块数)处的特点，运用此特点追踪GP。

评价一个MPPT算法优劣的标准，主要包括跟踪效率、全局最大功率点跟踪能力、对系统参数的依赖性以及跟踪速度(收敛时间)^[20]。上述智能算法大都是为局部阴影下的光伏阵列而设计的，在均匀光照条件下的跟踪性能一般。基于可变步长的INC法，本文提出一种可以实现GP跟踪的算法。该方法不仅可以在UIC条件下，当光照发生变化时迅速追踪到最大功率点，还可以在光伏阵列处于PSC下时，仍能准确地跟踪到GP。在确定GP点的大致位置后，可调节变换器的占空比，使系统运行在GP点左右。

2 光伏系统

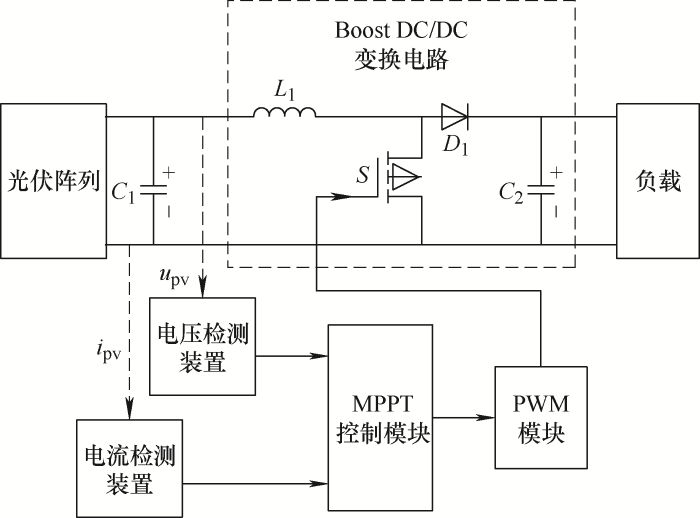
光伏系统的结构如图1所示，主要由光伏阵列、检测装置、DC-DC变换器、MPPT控制模块、PWM模块和负载(阻值为R)构成。在众多DC-DC变换器中，boost变换器因其较高的电压增益和较为简便的构造，在光伏系统中经常使用。当它在连续电流方式下工作时，其输入输出之间的关系如下

(1)

U_{out} = U_{PV} / (1 - D)

(2)

I_{out} = I_{PV} (1 - D)

式中，D为变换器的占空比。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 光伏系统结构

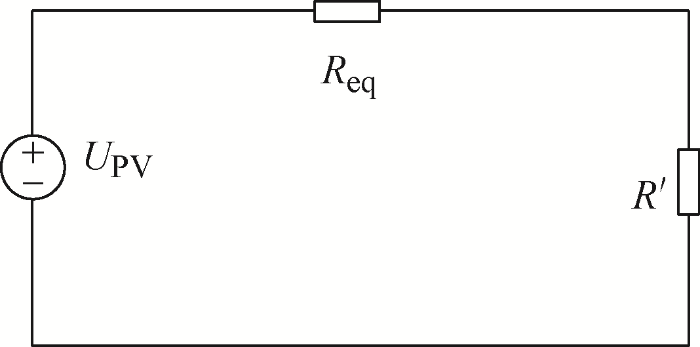
将光伏系统等效为如图2所示的简化电路，其中R_eq为阵列的等效内阻，其值与环境有关：R'为负载R归算到光伏阵列侧的电阻，其值如式(3)所示。由式(3)可知当D越大时，负载电压越小。

(3)

R^{'} = R {(1 - D)}^{2}

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 光伏系统简化电路

由图2可知负载的功率P为

(4)

P = \frac{U_{PV}^{2} R^{'}}{{(R_{eq} + R^{'})}^{2}}

对功率P求关于R'的导数可得

(5)

\frac{d P}{d R^{'}} = \frac{U_{PV}^{2} (R_{eq}^{2} - {R^{'}}^{2})}{{(R_{eq} + R^{'})}^{4}}

由式(5)可知，当R'=R_eq时，此时负载的功率最大，即可调整D的值让R'的值等于R_eq的值，使光伏阵列工作在MPP处。

2.1 单个光伏电池输出特性

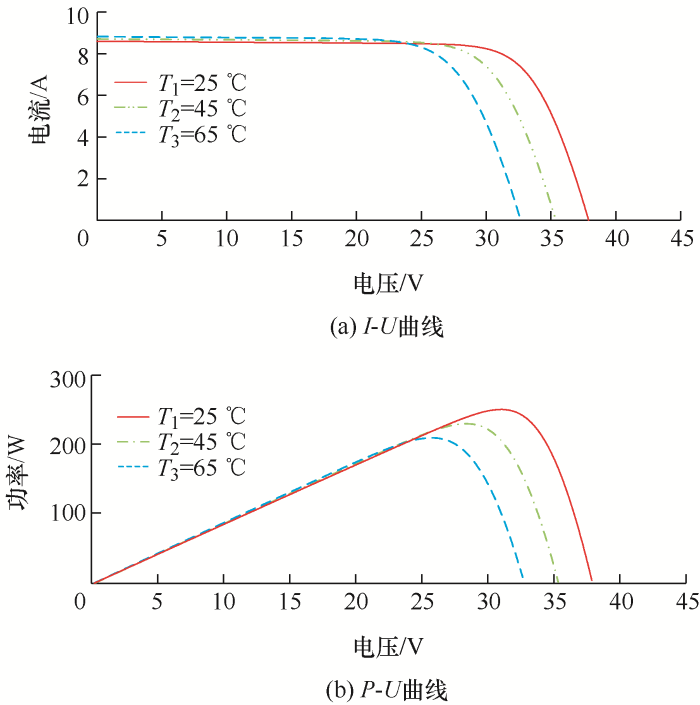
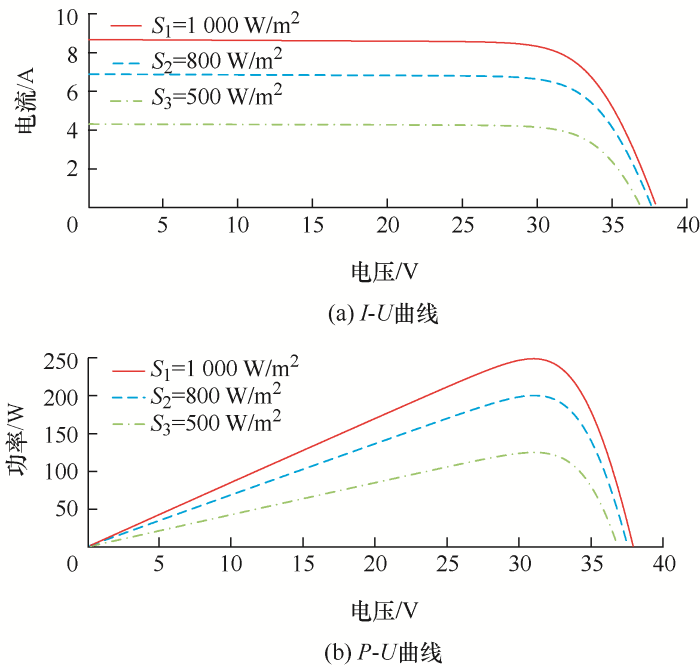
文献[21]中给出了从数学上描述光伏电池I-U特性的基本方程，如式(6)所示。通过采用控制变量法，分析环境因素与光伏电池特性的关系。

(6)

I = I_{ph} - I_{0} \{\exp [\frac{q (U + I R_{s})}{n K T}] - 1\} - (\frac{U + I R_{s}}{R_{sh}})

(1) 保证光伏电池所受的光照(S=1 000 W/m²)一定，温度分别为25 ℃、45 ℃、65 ℃，其输出特性如图3所示，图3a是I-U曲线，图3b是P-U曲线。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 光照强度一定的光伏特性曲线

(2) 保证光伏电池所处的温度(T=25 ℃)一定，光照强度分别为1 000 W/m²、800 W/m²、500 W/m²，其输出特性如图4所示，图4a是I-U曲线，图4b是P-U曲线。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 温度一定的光伏特性曲线

从图3和图4可知，当环境变化时，光伏电池的特性也会随之变化。温度越低，MPP处的电压和功率越大，短路电流几乎不变；光照强度越小，MPP处的电压几乎不变，但功率和短路电流都随之减小。并且验证了文献[16]所提公式，即在不同环境下，光伏电池MPP处的电压小于0.9倍的标准条件下(S=1 000 W/m²，T=25 ℃)的开路电压，如下所示

(7)

U_{mpp} < 0.9 U_{oc_sc}

2.2 PSC下光伏阵列输出特性

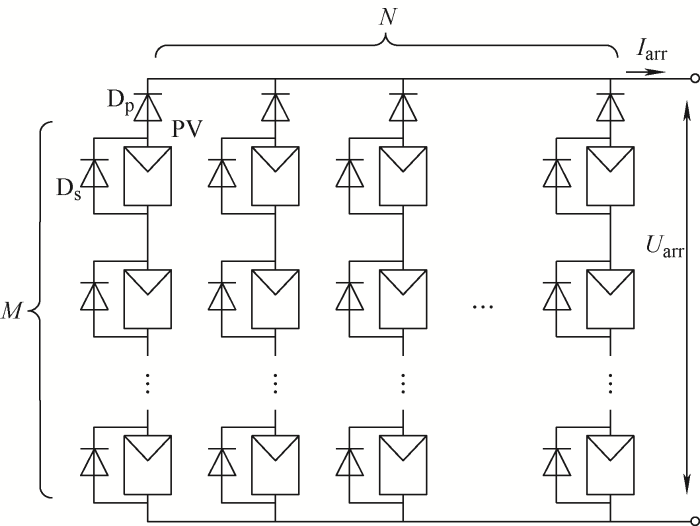
光伏阵列是光伏电池进行一系列的串并联后形成的，其结构如图5所示。其中N表示有N串光伏电池并联，M表示每串有M个光伏电池。当光伏阵列在PSC下时会出现“热区效应”，此时需要二极管D_s将存在“热区效应”的光伏电池短路。在有局部阴影时，各并联支路可能会发生电能倒送，需要在并联支路上串联二极管D_p。在理想情况下，对于M× N个光伏电池构成的阵列，其输出电流和电压为

(8)

I_{arr} = N I

(9)

U_{arr} = M U

式中，U、I分别为单个模块的输出电压、电流。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 光伏阵列的结构

在PSC条件下时，阵列中的光伏电池会受到不同的光照，其功率曲线会有多个峰值。当光伏阵列中有n种光照时，其曲线则会有n个峰值点。若使用传统MPPT方法寻找GP，只会在某个局部峰值点无法跳出，系统无法运行在MPP处，造成光能的浪费。

3 全局最大功率点跟踪算法

3.1 变步长电导增量法

传统的INC法首先在光伏电池的P-U曲线中对功率求导，然后根据求导的结果调整步长，无法找到合适的步长以满足系统运行的要求。文献[3]提出一种步长调节系数用于INC法，当光照强度发生剧烈变化时，此调节系数能以较快的速度响应。步长调节系数为S(k)的绝对值，其中S(k)为

(10)

S (k) = \frac{d P}{d U} / I (k) = 1 + \frac{U (k)}{I (k)} \frac{d I}{d U}

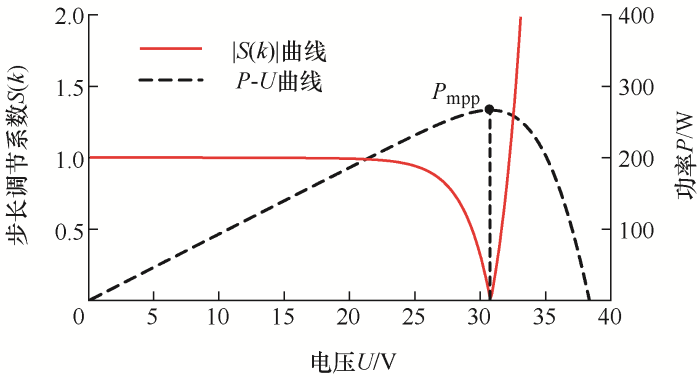
|S(k)|的曲线如图6所示，在恒流源区域内近似为1，在MPP附近时会迅速趋近于0，则占空比的更新关系为

(11)

D (k) = D (k - 1) \pm |S (k)| d

式中，d为扰动定步长。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 |S(k)|曲线和P-U 曲线示意图

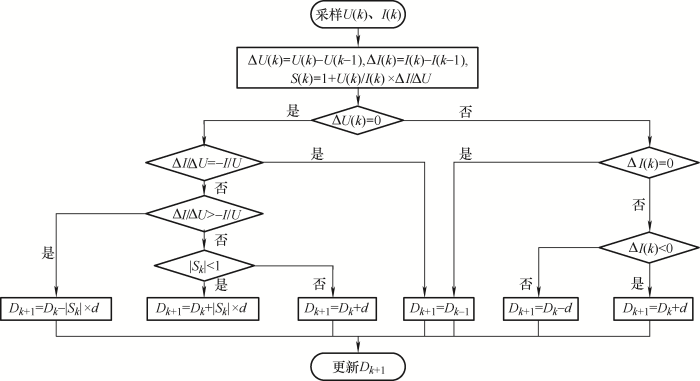
由于在|S(k)|曲线的右侧其值会大于1，为保证算法的收敛性，应规定当|S(k)|>1时，|S(k)|=1。算法在考虑上述因素后，流程图如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 变步长电导增量法流程图

变步长INC法只适用于单峰值的光伏阵列，不能在多峰值中应用，在多峰值的光伏阵列中若用全电压范围内扫描的方式来确定GP，会降低整个系统的效率，不能满足实际要求，因此需要一种在PSC下仍精确、快速的MPPT算法。

为了实现对GP点的跟踪，通过对第3.1节中可变步长INC法进行改进，提出了一种算法。该算法主要包括算法主体、结束条件和重启条件三个部分，算法主体是搜寻GP，它包含4个步骤，通过对这4个步骤的循环执行，就可跟踪到GP。下文将具体讲述该算法的三个部分。

3.2 算法主体

由文献[19]可知，单个光伏电池的功率峰值点处电压大于0.7倍的开路电压，而所提算法是从低压区向高压区进行扫描，为避免低压区峰值的遗漏并加快搜索速度，在算法初始化时，可将系统工作的占空比设为0.85。所提算法的具体步骤如下所示。

步骤一：通过变步长INC法搜寻到局部最大功率点，记录此功率点的功率、电压和占空比，并将其与所记录的最大功率P_m相比较，若比P_m大，则此功率点的功率、电压和占空比分别为新的P_m、U_m和D_m；若比记录的P_m小，则不变。

步骤二：继续增大电压，直到找到P-U曲线上的一个下凹点(此点左侧的dp/du<0，右侧的dp/du>0)，当dp/du首次大于0时，可近似认为此点为下凹点，记录此点的电流为I_ref。

步骤三：用步骤一所得的P_m除以步骤二所得的I_ref，可以得到一个新的参考电压U_ref。此处为加快跟踪速度，会使用较大的扰动步长追踪U_ref。

步骤四：判断P-U曲线在U_ref处功率的导数的正负，当dp/du_ref>0，则重新执行步骤一，寻找下一个局部峰值点；当dp/du_ref<0，则重新执行步骤二，寻找下一个下凹点。

3.3 结束和重启条件

一个完整的GP跟踪算法，不仅要能够找到MPP，还要能够顺利结束算法的搜索和重新启动算法。

3.3.1 结束条件

由式(7)的不等式可知光伏阵列的MPP处电压不会超过0.9U_{oc_arr}(U_{oc_arr}为标准状况下的开路电压)。因此，可通过判断电压是否超过0.9U_{oc_arr}，来决定是否结束算法。为节省搜索时间，有两种途径可以结束算法执行，一种是在整个算法搜寻过程中，将光伏阵列的输出电压与0.9U_{oc_arr}比较，一旦大于0.9U_{oc_arr}就结束算法；另一种是判断算法步骤三所得电压U_ref是否大于0.9U_{oc_arr}，若比0.9U_{oc_arr}大，也应结束算法。

3.3.2 重启条件

本算法是通过改变占空比来调整系统的功率。当找到GP点时，系统的占空比就会工作在GP点所对应的D_m。当外界环境变动时，光伏阵列的特性也会变化，若系统占空比仍是D_m，阵列的输出电压则会上升或下降。可利用这一特性作为算法重启的条件，即当系统占空比为D_m时，若出现式(12)的情况，则系统应当重启算法。

(12)

|U (k) - U (k - 1)| > ε

式中，ε为判断阈值。

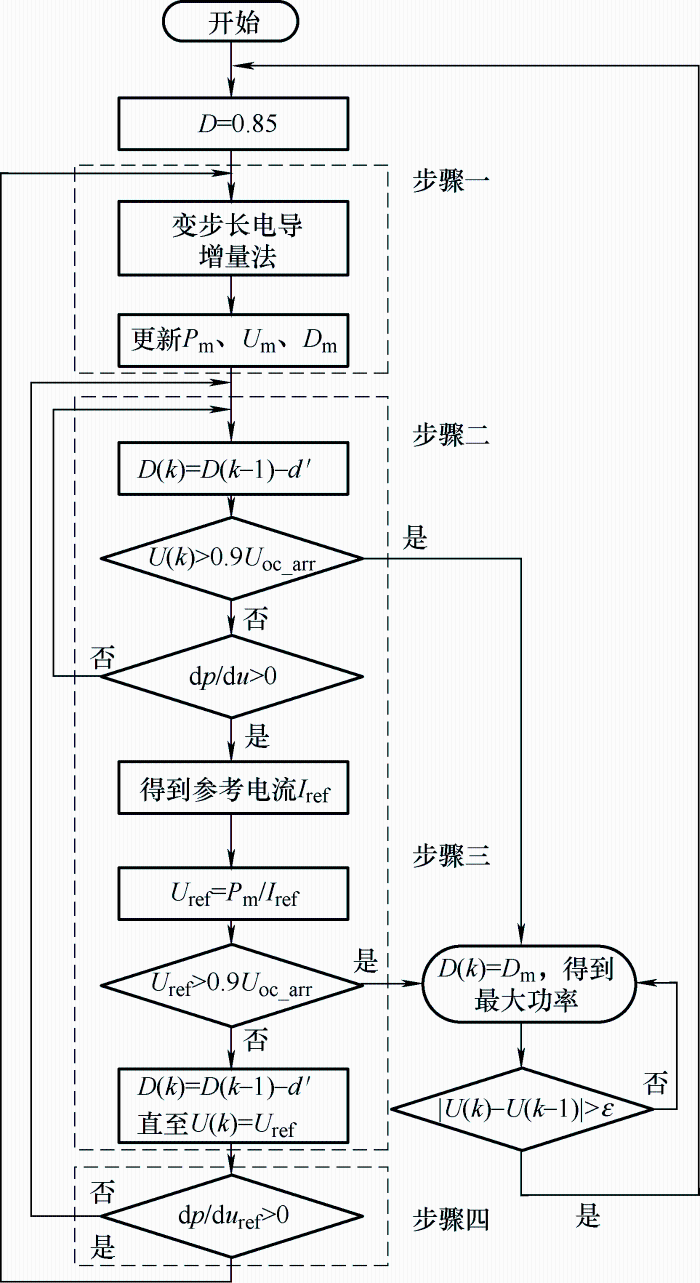
图8是所提算法的完整流程图。其中，P_m为已搜索到的最大功率，U_m和D_m是其对应的电压和占空比。初始化时，将算法的占空比设为0.85，流程图中的d'为算法设定的扰动定步长(其中d<d')。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 算法的完整流程图

3.4 算法实际操作

下面以三个光伏电池串联的光伏阵列为例，对所提算法的实际操作进行详细的论述。

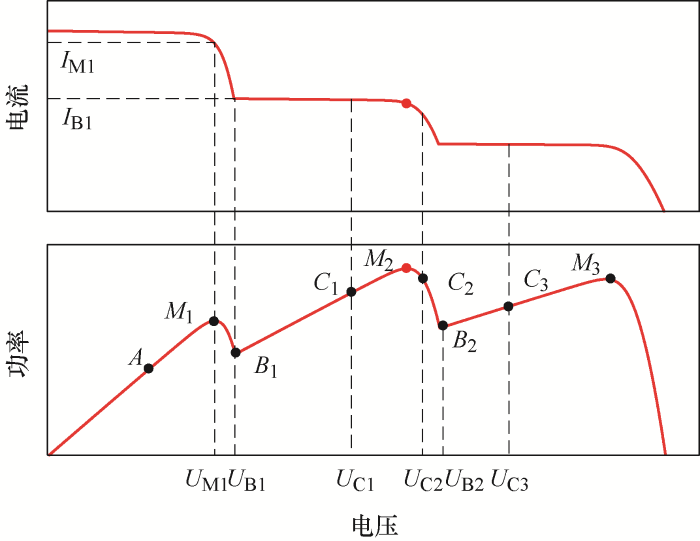
假定三个光伏电池各自受到的光照都不相同，由第2.2节可知，此时的功率曲线会出现三个局部峰值点，设三个峰值点分别为M₁、M₂和M₃。图9是所提算法跟踪的大致过程。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 算法跟踪示意图

算法初始化后，系统先从占空比0.85处(即A点)开始执行，经过步骤一的变步长INC法，算法追踪到局部峰值点M₁点，记录M₁点的功率P_M1和占空比D_M1，此时全局最大功率P_m=P_M1。

接着，执行步骤二，逐渐增加电压，当电压增加到与图9中B₁点电压相同时，刚好符合dp/du>0，此时令I_ref=I_B1。

然后执行步骤三，用功率P_m除以电流I_B1，得到参考电压U_ref。逐渐增大电压，直至追踪至参考电压U_ref。

最后，步骤四是根据P-U曲线在U_ref处功率的导数来决定接下来是执行步骤一或步骤二。但参考电压U_ref的位置有三种可能性，分别如图9所示的C₁、C₂和C₃。

(1) 当U_ref在C₁点时，由于dp/du>0，说明在C₁点后的功率仍会增加，可能会出现大于P_m的功率，所以算法从C₁点继续执行步骤一，利用变步长INC法寻找到局部最大功率点M₂，比较M₂点功率P_M2与P_m的大小，若P_M2>P_m，则令P_m=P_M2，否则P_m不变。之后再通过步骤二寻找另一个下凹点B₂。

(2) 当U_ref在C₂点时，因为I-U曲线是单调递减的曲线，所以在U_B1和U_C2的区间内，I_B1的电流值最大，而P_m=I_B1•U_C2，从中可知在U_B1和U_C2区间内的功率都小于P_m。由于局部最大功率点M₂处于此区间内，所以可以跳过对M₂的搜索，直接执行步骤二寻找另一个下凹点B₂。由C₂点的位置可知，此过程只有当dp/du小于0时才进行。

(3) 当U_ref在C₃点时，点M₂和点B₂都在U_B1和U_C3区间内，由(1)和(2)可知，可以跳过对点M₂和点B₂的搜索，直接从C₃开始搜寻局部最大功率点M₃。

通过对所提算法中四个步骤的循环执行，不断更新搜索到的最大功率，直至阵列的输出电压大于0.9U_{oc_arr}或U_ref大于0.9U_{oc_arr}，才终止算法执行。将光伏阵列的占空比设为算法执行过程中保存的D_m，即可使光伏阵列运行在GP点左右。

4 仿真分析

为了验证所提算法，在Matlab中依据图1建立了各个模块，构建了一个光伏系统。其中阵列是由三个串联光伏电池构成，光伏电池(MX60-245)的规格如表1所示，MPPT控制器中占空比的扰动步长d和d'设为0.1%和0.15%。

表1 标准状况下光伏电池MX60-245的参数

参数	数值
组件开路电压U_oc/V	37.3
组件短路电流I_sc/A	8.62
组件MPP点电压U_m/V	30.5
组件MPP点电流I_m/A	8.03
组件MPP点功率P_m/W	244.915

新窗口打开| 下载CSV

为分析在UIC和PSC情况下所提算法的的追踪效果，将此阵列置于不同光照情况下，具体的光照条件如表2所示。

表2 不同条件下各光伏电池受到的光照度情况 W/m²

不同光照情况	光伏电池1	光伏电池2	光伏电池3
情况a	700	700	700
情况b	1 000	1 000	1 000
情况c	400	400	400
情况d	1 000	300	280
情况e	1 000	700	400
情况f	1 000	700	500

新窗口打开| 下载CSV

4.1 均匀光照下的追踪

图10给出了在均匀光照强度变化时所提算法的仿真结果。在t=0 s时，各光伏电池的光照强度为表2中的情况a，在t=0.5 s时光照强度增加到情况b，然后在t=1 s时光照强度又减小到情况c。从图10可以看出，当光伏阵列在UIC条件下(即P-U曲线为单峰值)能准确跟踪到GP点。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 均匀光照下的追踪结果

表3比较了所提算法与文献[3]中变步长电导增量法在相同情况下的追踪时间，由表3可知，在单峰值的情况下，所提算法的跟踪速度比文献[3]的速度要慢。

表3 均匀光照下追踪时间 s

不同光照情况	所提算法	文献[3]
情况a	0.12	0.08
情况b	0.08	0.06
情况c	0.15	0.12

新窗口打开| 下载CSV

4.2 局部阴影的追踪

本节为验证所提算法在PSC下的跟踪效果，与传统INC全局法(即用INC法在全电压范围内进行扫描)进行了比较，并考虑了不同PSC下的效率，各阴影条件如表2中的情况d、e和f所示，它们代表最大功率点分别位于第一峰值点(M₁)、第二峰值点(M₂)和第三峰值点(M₃)。

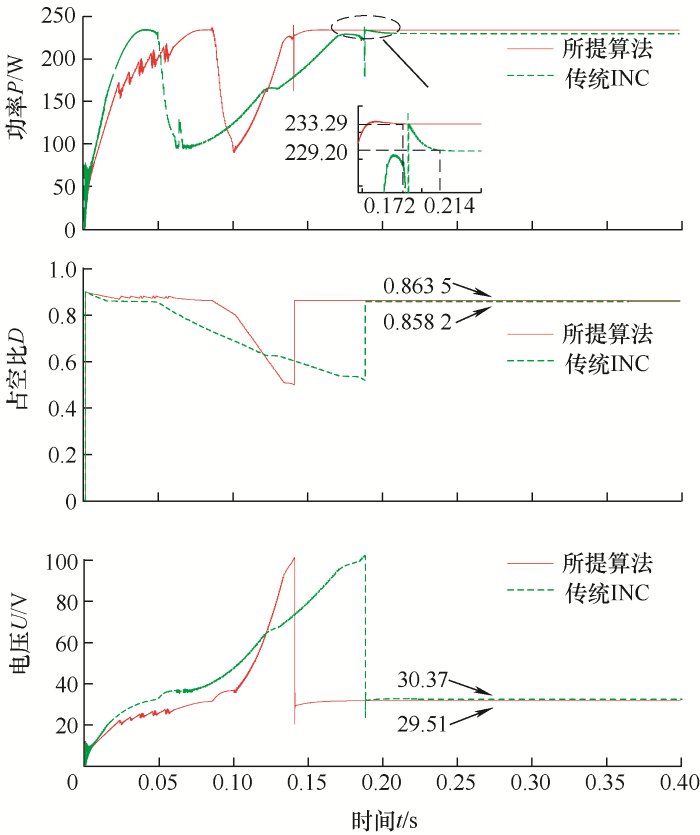
图11显示了光照条件在情况d下的仿真结果，两种算法得到的最大功率点都在M₁点附近。所提算法跟踪到M₁点所花时间为0.172 s，稳定时系统的输出功率为233.29 W。传统的INC所花时间为0.214 s，系统稳定时输出功率为229.20 W。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 最大功率点为M₁点

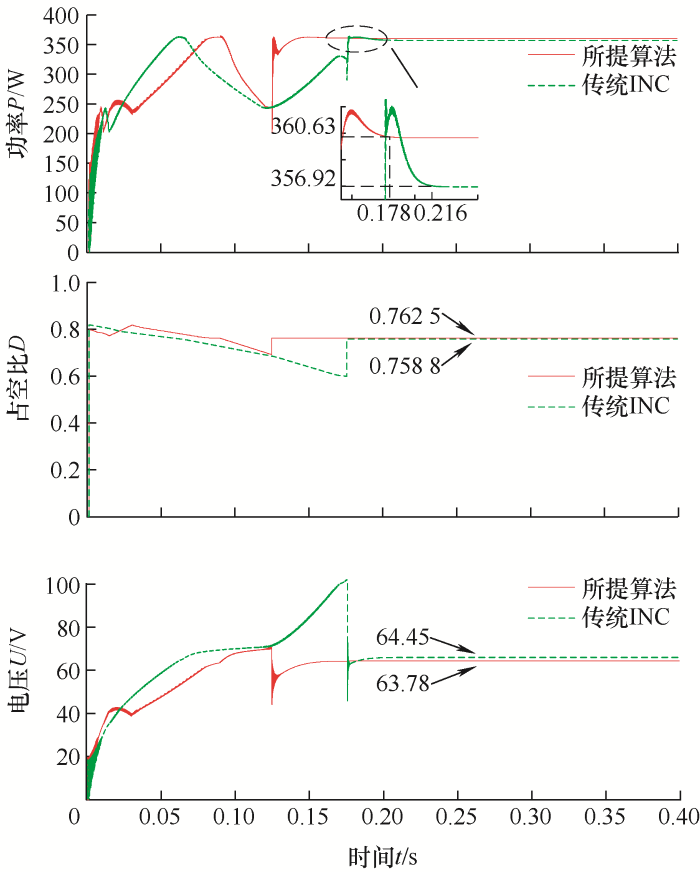
图12显示了光照条件在情况e下的仿真结果。两种算法跟踪到M₂点所花时间分别为0.178 s和0.216 s，稳定时光伏阵列输出功率分别为360.63 W和356.92 W。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 最大功率点为M₂点

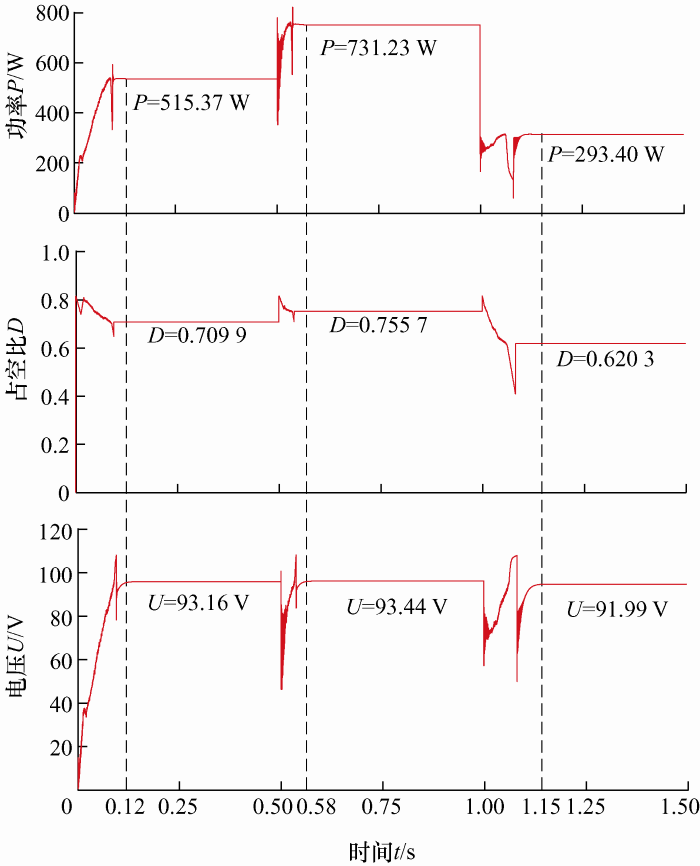
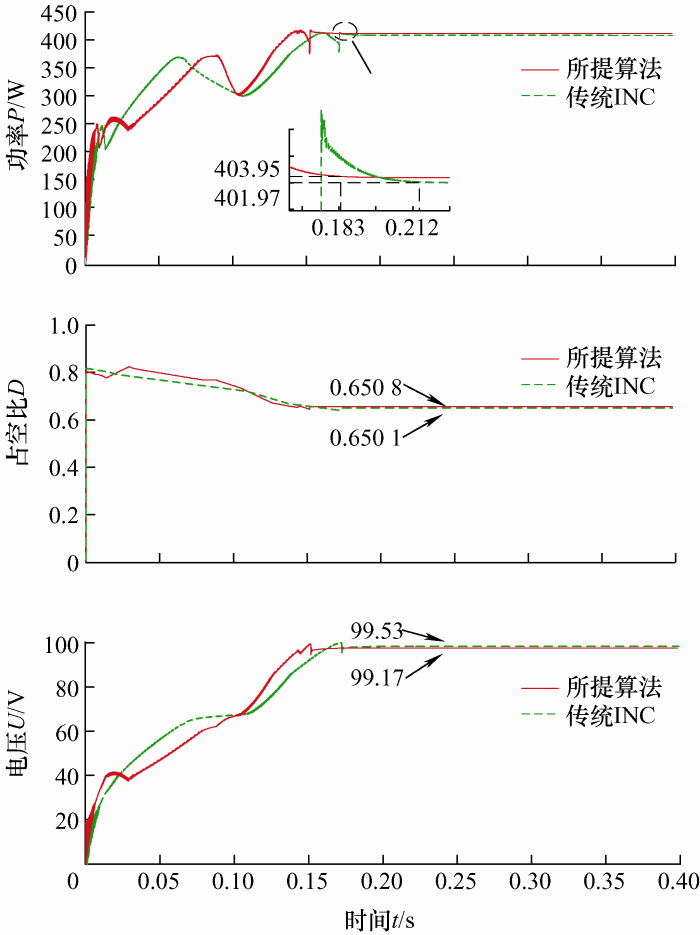
图13显示了光照条件在情况f下的仿真结果。两种算法跟踪到M₃点所花时间分别为0.183 s和0.212 s，稳定时光伏阵列输出功率分别为403.95 W和401.97 W。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 最大功率点为M₃点

4.3 结果分析

在第4.1节中，光伏阵列处于UIC条件下，此时阵列的P-U曲线只有一个峰值。文献[3]算法正适用于此情况，它只需要寻找到这个峰值就可结束算法。所提算法是全局算法，必须达到所设定的结束条件才会终止算法，所以花费时间较文献[3]更长，但文献[3]无法应用于多峰值情况下的光伏阵列。

在第4.2节中，光伏阵列分别处于在三种不同的PSC情况下，传统INC全局搜索法在每种PSC情况下追踪到全局最大功率所用时间相差不大，而所提全局算法由于在步骤二和步骤三中采用了更大的扰动步长d'，可以缩短算法追踪时间，并且通过判断U_ref是否大于0.9U_{oc_arr}，也可以更快结束算法。通过仿真结果可知，所提算法的追踪时间与局部阴影条件有关，即与GP点的位置有关，GP点在M₁点时用时最短，M₂点次之，M₃点用时最长。

由于所提算法在步骤一中使用了变步长的INC法，其跟踪精度也较传统INC全局搜索法更高。两种算法在跟踪效率方面的对比如表4所示。光伏阵列的输出效率用 $η$ 表示

(13)

η = P_{ideal} / P_{real}

式中，P_ideal和P_real分别指光伏阵列在某种光照情况下理论上输出的最大功率和实际输出的功率。从表4可以看出所提算法在三种光照情况下的输出效率较传统INC算法更高，且都在99%以上。

表4 跟踪效率对比

不同光照情况	算法	P_ideal/W	P_real/W	η(%)
情况d	所提算法	233.59	233.29	99.87
情况d	传统INC	233.59	229.20	98.12
情况e	所提算法	362.44	360.63	99.50
情况e	传统INC	362.44	356.92	98.47
情况f	所提算法	406.73	403.95	99.32
情况f	传统INC	406.73	401.91	98.81

新窗口打开| 下载CSV

5 结论

通过对变步长INC法进行改进，本文提出一种适用于光伏阵列全局最大功率点跟踪的算法，整个算法主要通过四个步骤来锁定GP点，在找到GP点后调节变换器的占空比，确保系统工作在GP点附近。所提算法有以下三个特点。

(1) 在硬件电路配置方面与传统MPPT算法一样，无需增加额外的检测装置等硬件电路。

(2) 在跟踪精度方面，当算法搜索到局部峰值点左右时，所提算法使用变步长的方式减小扰动步长，提高了精度。

(3) 在跟踪速度方面，所提算法采用两种扰动步长，特别是在步骤二和步骤三中通过使用较大的扰动步长，减少了跟踪时间。

最后，通过仿真分析了在UIC和PSC条件下所提算法的运行状况。结果表明，与传统的INC法相比，该方法追踪更快、精度更高、效率更高。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

BRITO M A G

, GALOTTO

, SAMPAIO

L P

, et al.

Evaluation of the main MPPT techniques for photovoltaic applications

[J]. IEEE Transactions on Industrial Electronics, 2013, 60(3):1156-1167.

DOI:10.1109/TIE.2012.2198036 URL [本文引用: 1]

[2]

王云平, 阮新波, 李颖.

不均匀光照光伏单元串联电路快速MPPT方法

[J]. 中国电机工程学报, 2015, 35(19):4870-4878.