基于DDPG算法的发电企业报价策略研究

doi:10.11985/2023.02.019

基于DDPG算法的发电企业报价策略研究

马丽莹^,, 魏云冰^,

上海工程技术大学电子电气工程学院上海 201620

Research on Bidding Strategy of Power Generation Enterprise Based on DDPG Algorithm

MA Liying^,, WEI Yunbing^,

School of Electronic and Electrical Engineering, Shanghai University of Engineering Science, Shanghai 201620

收稿日期: 2022-08-31 修回日期: 2022-11-19

Received: 2022-08-31 Revised: 2022-11-19

作者简介 About authors

马丽莹，女，1995年生，硕士研究生。主要研究方向为电力市场中长期交易，电力系统自动化。E-mail：848296323@qq.com

魏云冰，男，1970年生，博士，教授。主要研究方向为电力市场中长期交易，电力系统自动化。E-mail：wei.yunbing@sues.edu.cn

摘要

随着智能代理算法在解决发电企业代理报价策略问题中的优势不断凸显，国内外相关研究层出不穷。由于我国电力市场发展成熟度不够高，目前多数研究采用的是国外电力市场的交易模式，这不符合我国电力市场交易的实际情况，因此提出一种针对国内电力市场中长期集中竞价交易的报价模型。该报价模型建立在深度确定性策略梯度算法(Deep deterministic policy gradient，DDPG)的基础上，提出兼顾社会总效用最大化和发电企业自身收益的报价策略，建立了以市场环境和发电企业自身情况为参考的状态空间，同时还建立了按照统一边际价格出清的市场出清模型。通过仿真算例验证了该模型的可行性，并与Q-Learning算法的结果进行对比，同时也展现了发电企业自身情况对报价模型的市场出清结果和企业收益的影响。

关键词： 电力市场; 报价策略; 强化学习; DDPG算法

Abstract

With the advantages of intelligent agent algorithm in solving the problem of agent quotation strategy in power generation enterprises, there are many relevant researches at domestic and abroad. Due to the immaturity of China’s power market, most of the researches are based on the foreign power market transaction mode, which does not accord with the actual situation of China’s power market transaction, so a medium-long term centralized bidding quotation model is put forward for domestic power market. This quotation model is based on deep deterministic policy gradient(DDPG) algorithm, a quotation strategy is proposed considering the maximization of total social utility and the income of power generation enterprises. The state space is established with the market environment and the situation of the power generation enterprise as the reference, and the market clearing model is established according to the unified marginal price. The feasibility of the model is verified by simulation examples, and the results are compared with those of Q-Learning algorithm. At the same time, the influence of the power generation enterprise’s own situation on the market clearing results of the quotation model and the enterprise income is also shown.

Keywords： Electricity market; quotation strategy; reinforcement learning; DDPG algorithm

PDF (377KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

马丽莹, 魏云冰. 基于DDPG算法的发电企业报价策略研究[J]. 电气工程学报, 2023, 18(2): 192-200 doi:10.11985/2023.02.019

MA Liying, WEI Yunbing. Research on Bidding Strategy of Power Generation Enterprise Based on DDPG Algorithm[J]. Chinese Journal of Electrical Engineering, 2023, 18(2): 192-200 doi:10.11985/2023.02.019

1 引言

随着新一轮电力体制改革的启动，电力市场的建设工作已成为电力市场改革的重点^[1]。发电企业的竞价行为也成为了重要的研究内容之一，在电力市场的长期交易中，采取科学的竞价交易策略，使得市场主体收益最大化对发电企业以及电力市场的发展具有重要的意义^[2]。随着智能代理算法的进一步发展，其在电力系统各类优化问题中的优势也逐渐显现出来。现如今，国内外学者在发电企业报价策略方面关注颇多，并取得了显著的研究成果^[3]。

文献[4]主要阐述了智能代理算法在电力市场仿真方面的应用，总结了众多学者应用智能代理算法解决电力市场问题的实例，由此可以看出在对电力市场方向进行研究时，智能代理技术的应用较为广泛。文献[5]在研究发电企业报价问题时，以英国电力市场情况为例，提出了概念化的模型并结合动态规划方法进行解决。文献[6]提出的发电企业竞价博弈模型建立在对发电企业自身收益考虑的基础上，兼顾了市场上多个主体参与博弈的情况，最终通过强化学习算法多代理技术对相关模型进行求解。文献[7]建立了基于模糊Q学习算法的发电企业报价策略模型，将模糊推理的相关知识与强化学习算法巧妙结合，提出了含有混沌因子的模糊Q学习算法。文献[8]运用Q学习算法解决了日前市场的报价策略问题，通过建立智能的报价方法克服了传统报价策略的缺点，但Q学习算法只适用于低维、离散的状态和动作空间，因此对较为复杂的竞价情况难以适用。文献[9]开发出了基于联邦能源管理委员会批发电力市场规则的电力市场代理仿真系统，并建立强化学习VRE(Value reword environment)算法框架来求解电力市场的竞价博弈行为，但其在报价方法的针对性方面稍显不足，这是由于没有考虑到发电企业所处的状态所导致的。文献[10]将可变学习速率和策略爬山算法相结合，构成多智能体强化学习方法，进而求解针对电力现货市场不同定价机制下建立的发电企业报价双层优化模型，由此进一步验证了强化学习算法在报价决策中的适用性。文献[11]采用多代理仿真方法，建立日前市场出清模型，对发电企业采用单组报价和多组报价时的市场力进行研究，并且定量分析了其对市场主体参与市场的利润影响，对中长期电力市场多代理仿真方法的设计有一定的指导意义。

常见的发电企业报价策略的研究方法大多都需要对市场和竞争对手的报价信息有充足的了解，但实际中这些信息都较难以获取，这将会使得发电企业给出的报价策略不够优化且缺乏有效的应对机制。

鉴于此，本文采用的报价策略模拟多市场的电力交易过程，将发电企业难以获取的外界信息(例如竞争对手的报价、成本以及策略等信息)当作该发电企业所处的外部环境，发电企业在所处的环境中通过策略梯度给出可行的动作，并利用在以往竞价活动中获取的报价经验来指导自身形成一个最优的策略。

本文构建了基于DDPG(Deep deterministic policy gradient，DDPG)算法的发电企业中长期交易模型，以社会总效用最大化为目标，将电力市场环境情况和发电企业自身发电能力等作为算法的状态空间，把发电企业申报的售电价和售电量的系数作为动作空间，按照统一边际出清价格的出清方式建立了中长期电量交易市场集中竞价交易的模型，并采用强化学习DDPG算法进行求解。DDPG算法将Nature DQN(Nature deep Q-learning)、演员-评论家算法(Actor-critic，AC)和确定性策略梯度算法(Deterministic policy gradient，DPG)三种算法结合起来，促进了神经网络更有效地学习，使得DDPG算法的收敛速度大幅加快。

2 电力市场结构

2.1 电力市场交易流程

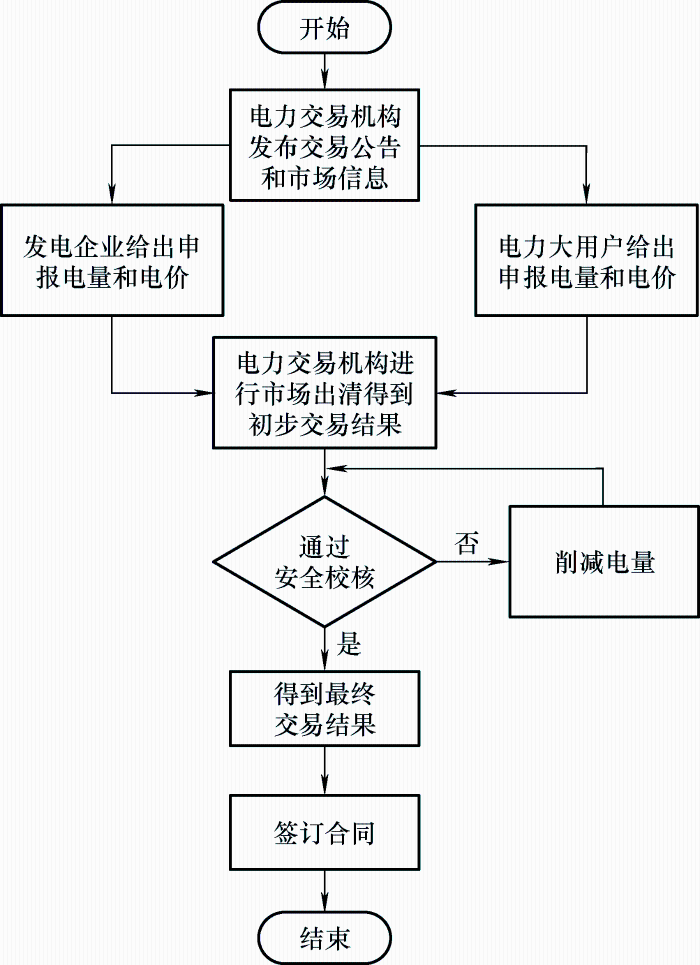
我国电力市场中长期集中撮合交易过程主要是由电力调度交易机构组织买卖双方进行报价，经过高低匹配配对成功后，将匹配结果交由电力调度交易机构进行安全校核，只有当匹配结果经校核通过后才可以正式签订交易合同^[12]。大致分为如下五个步骤。

(1) 组织报价：电力交易机构发布交易公告和市场信息给买卖双方。

(2) 报价决策：买卖双方根据制定好的报价策略提交各自的申报电价和电量。

(3) 报价排序：在不同的交易时段，组织机构将所有卖家的申报电价由低到高排序，买家的排序正好相反，按照申报的电价由高到低的顺序进行排序。

(4) 交易匹配：集中竞价交易的原理是“高低匹配，梯级排队”。

(5) 市场出清：按照统一边际价格出清的机制给出最终的出清价格。

电力市场集中竞价交易的流程如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 电力市场交易流程图

2.2 电力市场出清规则

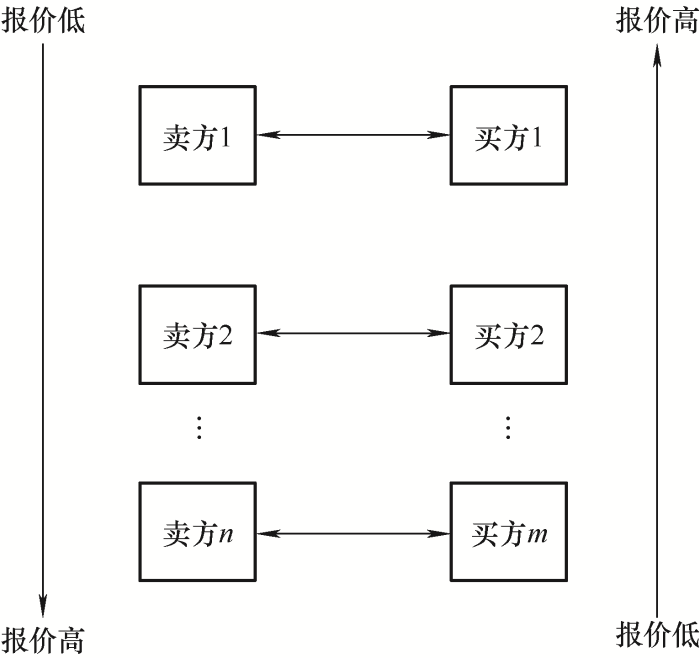
集中撮合交易采用“高低匹配，梯级排队”的方式进行配对，即将卖方的报价由低到高进行排序，买方的报价则由高到低排序，然后优先撮合卖方最低报价的发电企业和买方最高报价的购电方，其次是撮合卖方报价次低的发电企业和买方报价次高的购电方，以此类推进行购售电双方的交易匹配，最后一组实现供给与需求双方平衡时的价格，就是边际成交价格，即市场出清价格，所有匹配成交的购售电双方都将按照边际成交价格进行出清。交易匹配原理如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 市场交易匹配原理图

采用“高低匹配，梯级排队”的原理体现了电力市场的激励相容机制^[13]。将购电报价最高的买方和售电报价最低的卖方优先成交，其次是将购电报价次高的买方和售电报价次低的卖方进行撮合。当发电企业自身的发电效率更高时，其相应的边际成本更低，给出的报价就可以更低，此时反而更容易匹配到购电报价较高的买方，反之，效率更高的购电方由于自身效益更好，给出的购电报价可以更高，则更容易匹配售电报价更低的卖方，这个机制在无形中激励着发电公司自我改革，提高发电效率，降低发电成本，以此来获得更大的利润空间，也激励着用电企业提高自身生产效率，以期在报价时可以压缩购电成本。这就使得在社会资源一定的情况下，发电方可以产生更多的电能，而这些电能优先供给社会效益更大的企业，以此实现社会总效用的最大化。

在经济学中，效用最大化是指在可支配资源有限的条件下，使得用户的需求得到最大限度满足的情况^[14]。在本文中，社会总效用最大化就是在社会发电资源一定的情况下，使得更有效率的发电企业和购电企业优先获得发电和购电的权利，通过市场机制实现资源的最优化配置。

3 DDPG算法

DDPG是一种基于确定性策略梯度的无模型的行为评判算法，可以在连续状态和动作空间中运行^[15]。其所采用的AC框架由两个神经网络组成，一个表示策略函数，另一个表示行动-价值函数。策略函数产生行动并与环境交互，行动-价值函数对行动者的表现进行评价，并指导行动者的后续行动^[16]。DDPG算法同时也体现了DQN算法的思想，每种神经网络都细分为两个。Actor和Critic均有目标网络和现实网络。

在DDPG算法中， $s$ 表示 $t$ 时刻时智能体agent所处的状态； $s^{'}$ 表示 $t + 1$ 时刻时智能体agent所处的状态； $a$ 代表 $t$ 时刻时智能体agent采取的动作； $r$ 表示智能体在状态 $s$ 下采取动作 $a$ 后获得的奖励值； $γ$ 为衰变系数，取值为[0,1]的一个小数。

DDPG算法没有采用基于概率分布选择动作的随机策略，而是进行了简化，采用确定性策略 $μ$ 进行动作选取，选取到最大概率的动作 $a = μ (s | θ^{μ})$ ，其中 $θ^{μ}$ 代表策略网络的参数，其目标函数 $J (θ^{μ})$ 可以定义为^[17]

(1)

J (θ^{μ}) = E_{θ^{μ}} [r_{1} + γ r_{2} + γ^{2} r_{3} + \cdot \cdot \cdot]

确定性策略 $μ$ 选取动作后获得奖励的期望值可以用Q函数来表示

(2)

Q^{μ} (s, a) = E [r + γ Q^{μ} (s^{'}, μ (s^{'}))]

Q网络的参数用 $θ^{Q}$ 来定义，当使用策略 $μ$ 在 $s$ 状态下选择动作时获得期望的回报值可以用 $Q^{μ} (s, μ (s))$ 来表示，对该期望进行求解时，可以采用积分的方式，这是因为动作空间是连续的，因此评判策略 $μ$ 的好坏时可以用式(5)来表示^[18]

(3)

\begin{matrix} J_{β} (μ) = \int_{S} ρ^{β} (s) Q^{μ} (s, μ (s)) d s = \\ E_{S ～ ρ^{β}} [Q^{μ} (s, μ (s))] \end{matrix}

SILVER等^[19]在确定性策略梯度算法中证明了目标函数采用 $μ$ 策略的梯度与Q函数采用 $μ$ 策略的期望梯度是等价的，则有

(4)

\frac{\partial J (θ^{μ})}{\partial θ^{μ}} = E_{S} [\frac{\partial Q (s, a | θ^{Q})}{\partial θ^{μ}}]

Actor网络采用确定性策略 $a = μ (s | θ^{μ})$ ，其梯度为

(5)

\frac{\partial J (θ^{μ})}{\partial θ^{μ}} = E_{S} [\frac{\partial Q (s, a | θ^{Q})}{\partial a} \frac{\partial π (s | θ^{Q})}{\partial θ^{μ}}]

(6)

\begin{matrix} \nabla_{θ} J_{β} (μ_{θ}) = \int_{S} ρ^{β} (s) \nabla_{θ} μ_{θ} (s) Q^{μ} (s, a) |_{a = μ θ} d s = \\ E_{S ～ ρ^{β}} [\nabla_{θ} μ_{θ} (s) Q^{μ} (s, a) |_{a = μ θ}] \end{matrix}

Critic网络上的价值梯度为

(7)

\frac{\partial L (θ^{Q})}{\partial θ^{Q}} = E_{s, a, r, s^{'} ～ D} [T a r g e t Q - Q (s, a | θ^{Q}) \frac{\partial Q (s, a | θ^{Q})}{\partial θ^{Q}}]

(8)

T a r g e t Q = r + γ Q (s^{'}, π (s^{'} | θ^{μ^{'}}) | θ^{Q^{'}})

损失函数采取均方误差损失(Mean squared error，MSE)，网络Q的损耗为

(9)

L (θ^{Q}) = E [(Q {(s, a) - y)}^{2}]

(10)

y = r + γ Q (s^{'}, a^{'})

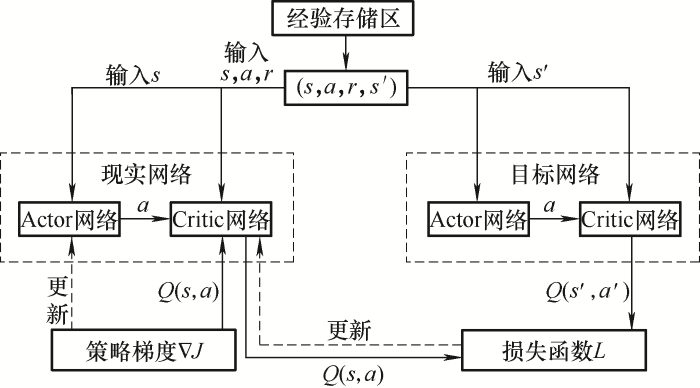
得到两个网络的梯度后，就可以采用梯度下降法进行网络更新。由于采用了DQN的思想，因此在现实网络的基础上增加了一个目标网络，网络结构图如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 DDPG算法网络结构图

4 发电企业报价模型

4.1 发电企业报价的状态空间

强化学习算法有一个较突出的优势就是动作可以和环境交互，以此来获得更好的学习效果。因此，在建立发电企业报价模型的时候需要考虑发电企业所处的市场环境以及自身的发电能力来判断自身在当月市场交易中的市场份额等情况，以便分析当月的报价情况。

在组织月度集中竞价交易之前，电力交易中心会先将当月市场需求电量和发电企业的剩余发电能力等进行信息公开。这使得各个发电企业可以根据公示的信息分析电力市场的环境情况，例如电力市场供需情况等，也可以对自身的市场力和市场份额有一个较为清晰的认知。这两者对于发电企业制定自身的报价策略有着重要影响，因此将发电企业所处的市场环境状态和自身的市场份额两个因素作为发电企业报价策略的状态空间^[20]。

发电企业所处的市场环境状态用市场供需比 $R_{S D}$ 来表示，即为当月各个发电企业全部市场化电量的总和与市场总需求电量的比值。

(11)

R_{S D} = \frac{\sum_{i = 1}^{n} q_{m_{i}}}{q_{D}}

式中， $q_{D}$ 表示月度市场电量需求。

发电企业的市场份额用某发电企业的月度全部市场化电量和当月市场全部供给电量的比值来表示。发电企业的市场份额 $S_{M}$ 表示如下

(12)

S_{M} = \frac{q_{m_{i}}}{\sum_{i = 1}^{n} q_{m_{i}}}

因此，可将状态空间表示为一个二维向量 $s = [R_{S D}, S_{M}]$ ，并将其作为策略网络Actor和评价网络Critic的输入。

4.2 发电企业报价的策略空间

在发电企业经济模型的基础上研究发电企业的报价策略，这就需要了解发电企业的发电成本等情况。假设市场内有 $n$ 家发电企业 $S_{1}, S_{2}, \dots, S_{n}$ ，第 $i$ 家发电企业申报的售电价和售电量分别为 $p_{S_{i}}$ 和 $q_{S_{i}}$ 。

如今参与集中竞价交易的发电企业主要为火力发电企业，火力发电成本模型一般情况下可用发电出力 $P^{'}$ 的二次函数来表示^[21]

(13)

C = a \times {P^{'}}^{2} + b \times P^{'} + c

式中，C为发电企业的总发电成本； $a 、 b 、 c$ 分别为发电成本二次函数的二次项系数、一次项系数和常数项系数。

一般情况下，发电企业按边际成本报价容易获得更多的收益。因此，本文在进行发电企业报价参考成本的选取时考虑用发电企业的边际发电成本来替代，发电企业边际发电成本 $C^{'}$ 为

(14)

C^{'} = 2 a \times P^{'} + b

(15)

P^{'} = P_{E} \times \cos φ

式中， $\cos φ$ 为功率因数，取值0.8； $P_{E}$ 为额定功率。

本文中，通过改变发电企业申报的售电价来变换不同的报价策略，给发电企业的边际成本乘上一个系数因子α，当α高于1时，发电企业报价高于自身边际成本，可以提高发电企业自身收益。由于电力商品是关系国计民生的重要资源，为防止发电企业利用自身市场力谋取暴利，需要对 $α$ 的取值进行限制，因此将α的取值范围设为[1,1.2]。策略申报电价 $p_{S_{i}}$ 为

(16)

p_{S_{i}} = α \times C^{'}

在电力市场集中竞价交易活动中，影响发电企业收益的因素不仅有发电企业申报的售电电价，还包括发电企业申报的售电量。通常情况下，发电企业将把月度全部电量扣除月度全部非市场化电量后剩余的全部市场化电量作为申报的售电量。在现行的市场出清机制下，发电企业可通过适当减少申报的售电量来抬高出清电价，以此获得更高的收益。因此，也可以通过改变发电企业申报的发电量来变换不同的报价策略，给发电企业当月全部市场化电量乘以一个系数因子 $β$ 就可以得到发电企业申报的售电价 $q_{S_{i}}$

(17)

q_{S_{i}} = β \times q_{m_{i}}

式中， $q_{m_{i}}$ 表示第 $i$ 家发电企业当月全部市场化电量， $β$ 的取值范围为[0,1]。

由此，报价模型中策略网络Actor的输出即为策略的动作空间，可表示为一个二维向量 $a = [α, β]$ 。

4.3 发电企业报价策略的奖励

发电企业采取报价策略的目的是使得自身获得更高的收益，这就需要在进行报价策略的选取时给出相应的奖励，激励策略的选取朝着发电企业自身收益增多的方向进行^[22]。本文以发电企业的收益作为奖励，发电企业的收益由发电企业的交易收入和发电成本的差值构成。交易收入即为发电企业在当月交易中的成交电量和当月市场出清电价的乘积。可由式(18)来表示

(18)

I = q_{B_{i}} \times p_{m c}

式中， $I$ 代表发电企业在当月集中竞价交易中的收入； $q_{B_{i}}$ 表示第 $i$ 家发电企业在当月交易中的成交电量； $p_{m c}$ 表示当月市场出清电价。

因此，发电企业在当月集中竞价交易中的收益 $R_{e}$ 可由式(18)和式(13)之差求得

(19)

R_{e} = I - C

由此，报价模型中评价网络Critic的输出即为发电企业在当月集中竞价交易中的收益，即 $r = R_{e}$ 。

4.4 发电企业报价的市场出清模型

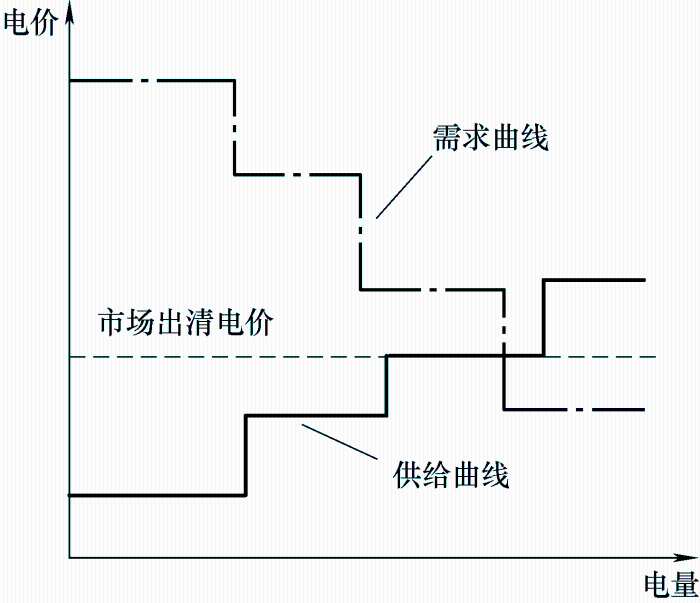
在进行市场出清时，按照“高低匹配，梯级排队”的原理进行配对后，还需要对出清结果进行安全校核，安全校核由电力调度机构进行，只有通过安全校核的出清结果才能作为最终的市场出清结果，若安全校核未能通过则需要削减电量后再进行安全校核，直到安全校核通过后方可出清^[23]。市场出清的原理如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 市场出清原理图

由我国目前电力市场中长期交易现状可知，暂无安全校核未通过的情况出现，因此，本文的市场出清模型中暂不考虑电力网络的物理约束，将市场主体效用最大化作为目标函数。将发电企业申报的售电价由低到高排序，得到交易的供给曲线，将购电方申报的购电价由高到低排序得到需求曲线，这两条曲线的交点即为市场出清电价。

市场出清后，市场主体的社会总效用 $W$ 为购电方电价 $p_{D}$ 与发电企业申报的售电价 $p_{S}$ 之差与当月交易成交电量 $q_{B}$ 的乘积

(20)

W = (p_{D} - p_{S}) \times q_{B}

因此，发电企业报价策略的市场出清模型可定义为

(21)

\max \sum_{i = 1}^{n} W = (p_{D} - p_{S_{i}}) \times q_{B_{i}}

(22)

s.t . \sum_{i = 1}^{n} q_{B_{i}} \leq q_{S_{i}} i = 1, 2, \dots, n

(23)

q_{B_{i}} \geq 0 i = 1, 2, \dots, n

5 电力市场算例仿真

假设某一区域电网内有十家发电企业，相关的技术参数如表1所示。

表1 发电企业技术参数表

发电企业序号	额定容量 $P_{E} /MW$	$a / (\times 10^{- 6})$	$b / (\times 10^{- 3})$	$c$
G1	300	0.088	305	1 150
G2	500	0.057	285	1 280
G3	550	0.054	281	1 340
G4	550	0.058	279	1 300
G5	600	0.052	274	1 420
G6	600	0.048	272	1 400
G7	650	0.050	267	1 480
G8	700	0.046	264	1 550
G9	850	0.045	260	1 650
G10	1 000	0.036	252	1 800

新窗口打开| 下载CSV

该区域某年12个月的月度交易市场电量需求如表2所示。

表2 1—12月月度市场电量需求表

月份	1月	2月	3月	4月	5月	6月
电量需求/ (万 $kW \cdot h$ )	70 794	65 068	85 469	78 059	72 764	85 502
月份	7月	8月	9月	10月	11月	12月
电量需求/ (万 $kW \cdot h$ )	56 407	64 982	71 045	79 004	82 443	76 760

新窗口打开| 下载CSV

把当月集中竞价交易中的电力需求曲线假设为指数是4的幂函数，对市场需求拟合得到需求函数如式(24)所示

(24)

p_{D} = 0.36 - 0.05 \times {(\frac{q_{B}}{Q})}^{4}

(25)

q_{B} = \sum_{i = 1}^{n} q_{B_{i}}

式中， $q_{B}$ 为某月所有发电企业总成交电量； $Q$ 为月度市场电量需求。

当发电企业不采用本文所给的报价策略时，其报价方式是将全部市场化电量都按照边际成本价格进行申报。该区域这十个发电企业一年内各个月份全部市场化电量如表3所示。

表3 十个发电企业的月度市场化电量统计表 10⁴ $kW \cdot h$

发电企业	1月	2月	3月	4月	5月	6月	7月	8月	9月	10月	11月	12月
1	5 170	4 438	5 170	4 920	5 170	4 920	5 170	2 006	4 920	5 170	4 920	5 170
2	8 858	1 882	1 385	8 507	8 858	8 507	8 858	8 858	8 507	8 858	8 507	8 858
3	9 963	8 620	2 543	9 506	9 963	9 506	9 963	9 963	9 506	9 963	9 506	9 963
4	8 091	6 883	8 091	1 979	8 091	7 678	8 091	8 091	7 678	8 091	7 678	8 091
5	6 622	5 549	6 622	6 254	6 622	6 254	6 622	6 622	6 254	6 622	399	6 622
6	8 894	7 577	8 894	8 444	8 894	8 444	4 885	8 894	4 544	8 894	8 444	8 894
7	10 081	8 583	10 081	9 569	10 081	9 569	10 081	10 081	9 569	10 081	9 569	3 711
8	11 255	9 792	11 255	10 758	3 016	10 758	11 255	4 742	10 758	11 255	10 758	11 255
9	15 740	13 672	15 740	15 038	15 740	15 038	15 740	15 740	15 038	2 868	15 038	15 740
10	6 308	10 285	12 276	11 593	12 276	5 816	12 276	12 276	11 593	12 276	11 593	12 276

新窗口打开| 下载CSV

由发电企业的相关技术参数可求得发电企业的边际成本，如表4所示。

表4 十个发电企业边际成本统计表元/( $kW \cdot h$ )

发电企业	1	2	3	4	5
边际成本	0.347 2	0.330 6	0.328 5	0.33	0.323 9
发电企业	6	7	8	9	10
边际成本	0.318 1	0.319	0.315 5	0.321 2	0.309 6

新窗口打开| 下载CSV

5.1 未采取报价策略的情景

本文在Python中利用PyTorch建立DDPG算法的应用框架，同时也建立发电企业市场出清的仿真模型。在未采取文中的报价策略时，发电企业按照上述的申报电量和申报电价情况进行市场出清仿真，得到的收益情况如表5所示。

表5 发电企业不采取策略时年度总收益情况表万元

发电企业	1	2	3	4	5
年度总收益	0	21.78	613.44	200.03	615.19
发电企业	6	7	8	9	10
年度总收益	1 542.82	1 772.81	2 298.16	2 908.35	3 386.92

新窗口打开| 下载CSV

5.2 采取Q-Learning算法的情景

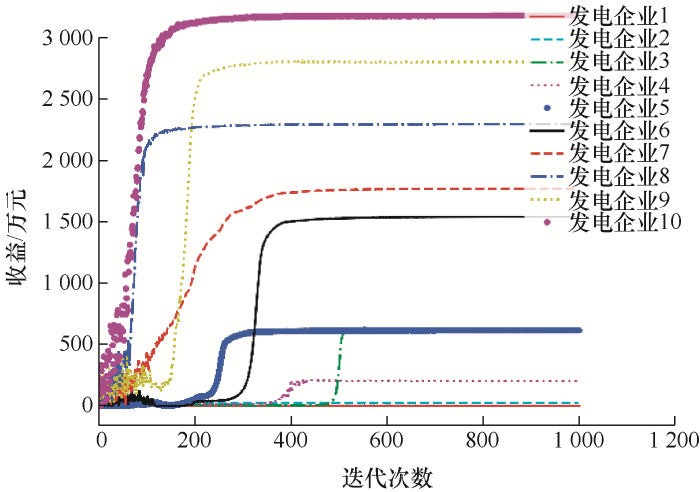
当采用Q-Learning算法进行竞价行为模拟时，发电企业收益迭代过程如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 Q-Learning算法下十个发电企业的收益曲线

5.3 采取DDPG报价策略的情景

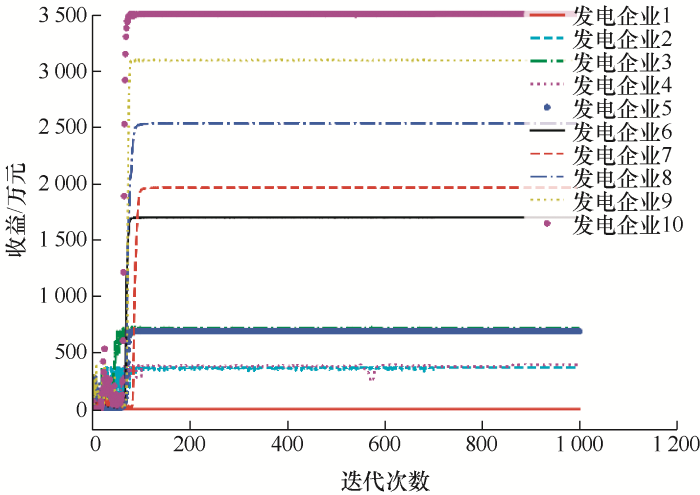
采取基于DDPG算法的报价策略进行仿真试验时的参数设置如下：发电企业总数 $n = 10$ ；衰减率 $γ = 0.9$ ；Actor网络学习率为0.000 1；Critic网络学习率为0.001；仿真次数N=1 000。分别将每一个发电企业作为Agent采用上述的报价策略进行报价。

十个发电企业的报价行为进行1 000次仿真试验后，发电企业的仿真试验迭代过程如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 十个发电企业总收益曲线图

从图5和图6的对比可以看出，该模型实现了发电企业竞价行为的模拟和仿真，并且相较于Q-Learning算法较快收敛到最终结果，相较于未采取DDPG报价策略时一些发电企业的收益有明显的增加，但发电企业的收益增幅不同，这与发电企业的自身发电条件有关。

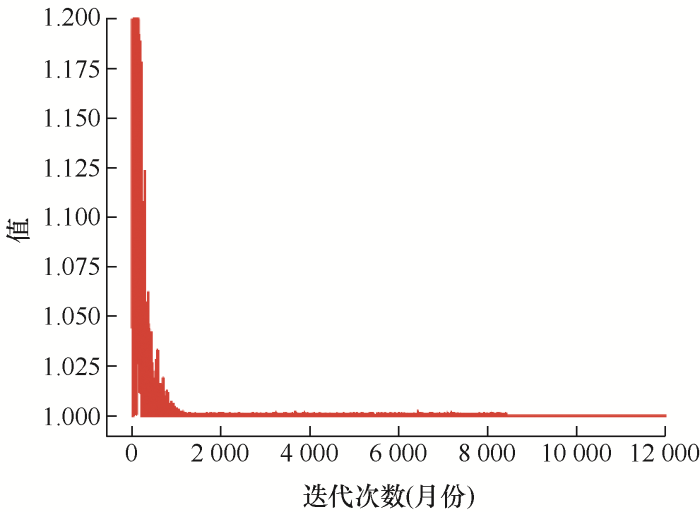
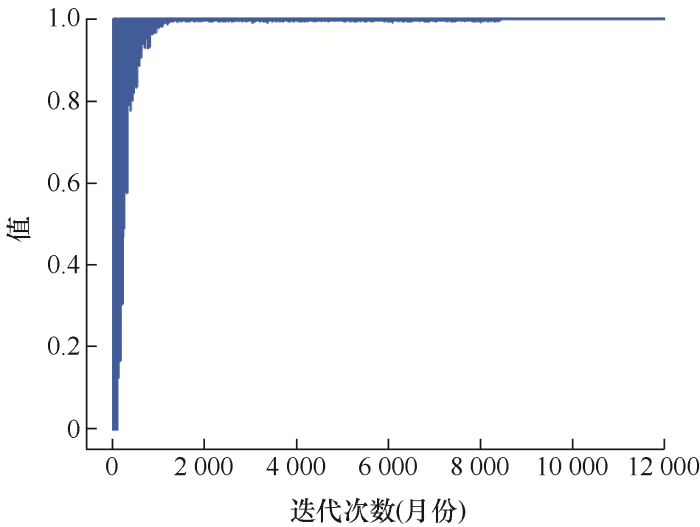
发电企业总收益收敛过程的报价策略可以通过动作空间的系数曲线迭代图来表示，以发电企业2为例，发电企业2作为唯一Agent时的报价策略图如图7和图8所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 发电企业2的 $α$ 系数曲线迭代图

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 发电企业2的 $β$ 系数曲线迭代图

6 结论

本文建立了基于DDPG算法的发电企业报价模型和电力市场出清模型来模拟发电企业的市场出清行为，模型把发电企业在月度交易中申报的售电量和售电报价作为动作空间，将社会效用的最大化作为目标函数，以发电企业的自身收益为奖励，促使发电企业在实现社会效用最大化的同时自身也能获得更多的收益。对发电企业竞争行为的仿真结果进行分析可以得到以下结果。

(1) 仿真结果验证了本文建立的基于DDPG算法的发电企业报价模型和统一边际市场出清模型的可行性，与Q-Learning算法相比，收敛速度更快，且发电企业的收益也有所增加。

(2) 由仿真结果的对比可以看出，当发电企业的实际成本过高时或者过低时，采取报价策略对发电企业的市场出清情况不会造成很大的影响，当发电企业的成本处于市场边际情况时，采取一定的报价策略将对最终收益产生较大的影响。这是因为当发电企业的发电成本过高时，本身就不具备竞价的优势，无论采取何种报价策略都无法使其获得市场收益，例如发电企业1；当发电企业的发电成本较低时，在竞价行为中本身就占有优势，采取一定的报价策略面临的风险较大，采取常规的报价方式较为稳定，例如发电企业10；当发电企业的发电成本处于市场边际情况下，发电企业可通过适度减少申报电量来获取更多的成交机会，以增加自身收益，例如发电企业2。

(3) 本文的仿真算例没有考虑电网的实际约束和输电通道出现阻塞时的情况，这将作为后续的研究方向。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

张紫鹤, 卢继平.

国外电力市场建设对我国新时期电力市场化改革的启示与建议

[J]. 甘肃科技, 2021, 37(6):8-15.

[本文引用: 4]

ZHANG

Zihe

, LU

Jiping

Power market construction in foreign countries:Inspiration and suggestions for China’s power market reform in the new era

[J]. Gansu Science and Technology, 2021, 37(6):8-15.

[本文引用: 4]

[2]

曾嘉志, 赵雄飞, 李静, 等.

用电侧市场放开下的电力市场多主体博弈

[J]. 电力系统自动化, 2017, 41(24):129-136.