基于参数优化的VMD与TEO融合的微电网电能质量检测方法*

doi:10.11985/2023.02.016

基于参数优化的VMD与TEO融合的微电网电能质量检测方法^*

王玉梅^,, 郑义^,

河南理工大学电气工程与自动化学院焦作 454000

Microgrid Power Quality Detection Method Based on Parameter Optimization Fusion of VMD and TEO

WANG Yumei^,, ZHENG Yi^,

School of Electrical Engineering and Automation, Henan Polytechnic University, Jiaozuo 454000

收稿日期: 2021-10-26 修回日期: 2022-02-25

基金资助:

国家自然科学基金资助项目(U1804143)

Received: 2021-10-26 Revised: 2022-02-25

作者简介 About authors

王玉梅，女，1963年生，教授。主要研究方向为供电技术与智能电网。E-mail：1799223255@qq.com

郑义，男，1997年生，硕士研究生。主要研究方向为电能质量检测。E-mail：18839167223@163.com

摘要

针对变分模态分解(Variational mode decomposition，VMD)检测微电网中多类电能质量扰动信号时，其实时性差及多类信号难以统一处理的问题，提出一种参数优化的VMD与Teager能量算子(Teager energy operator，TEO)融合的微电网电能质量扰动检测方法。针对VMD方法参数难确定的问题，利用天牛须搜索(Beetle antennae search，BAS)对VMD方法的最佳参数进行优化搜索。搜索过程以VMD分解后各本征模函数的包络熵极小值与VMD迭代次数的结合作为适应度函数。根据搜索结果设定VMD方法的最佳分解层数K和惩罚因子α，并运用参数优化VMD对扰动信号进行分解。针对扰动信号经分解后本征模函数的筛选问题，以包络熵为指标，选取包络熵较小值的本征模函数进行TEO解调分析，提取扰动信号的特征信息。仿真结果表明，融合算法能实现对微电网电能质量扰动的准确检测，并具有良好的抗噪性。

关键词： 变分模态分解; 天牛须搜索; 电能质量扰动; Teager能量算子; 包络熵; 本征模函数

Abstract

Aiming at the problems of poor real-time performance and difficult unified processing of multiple types of power quality disturbance signals detected by variational mode decomposition(VMD) in microgrid, a power quality disturbance detection method for microgrid based on the combination of parameter optimization VMD and Teager energy operator(TEO) is proposed. Aiming at the problem that the parameters of VMD method are difficult to be determined, the optimal parameters of VMD method are optimized by using beetle antennae search(BAS). In the search process, the combination of the minimum envelope entropy of each intrinsic mode function after VMD decomposition and the number of iterations of VMD is taken as the fitness function. According to the search results, the optimal decomposition layer K and penalty factor α of VMD method are set, and the parameter optimization VMD is used to decompose the disturbance signal. Aiming at the problem of screening intrinsic mode function after disturbance signal decomposition, the intrinsic mode function with smaller envelope entropy is selected to perform TEO demodulation analysis, and the characteristic information of disturbance signal is extracted. The simulation results show that the fusion algorithm can accurately detect the power quality disturbance of microgrid, and has good noise resistance.

Keywords： Variational modal decomposition; beetle antennae search; power quality perturbation; Teager energy operator; envelope entropy; intrinsic mode function

PDF (514KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王玉梅, 郑义. 基于参数优化的VMD与TEO融合的微电网电能质量检测方法^*[J]. 电气工程学报, 2023, 18(2): 164-173 doi:10.11985/2023.02.016

WANG Yumei, ZHENG Yi. Microgrid Power Quality Detection Method Based on Parameter Optimization Fusion of VMD and TEO[J]. Chinese Journal of Electrical Engineering, 2023, 18(2): 164-173 doi:10.11985/2023.02.016

1 引言

以风电、光伏发电为主的微电网，具有间歇性和波动性等特点^[1-2]，容易引起电网电压波动、闪变^[3]，其功率变频器容易产生谐波、三相不平衡等电能质量问题^[4]。为有效治理微电网电能质量问题，重点对微电网易出现的电压闪变、谐波及暂态电压扰动信号进行检测。

在诸多现代信号处理技术中，变分模态分解(Variational mode decomposition，VMD)、小波变换、经验模态分解(Empirical mode decomposition，EMD)^[5-6]及局部均值分解(Local mean decomposition，LMD)^[7]均具有多尺度时频分析的能力。其中VMD具有可预设尺度和自适应的优势，将信号分解转换为约束模型最优解的寻优问题，避免了递归循环分解模式下EMD、LMD易产生模态混叠的问题，并对噪声具有良好的鲁棒性^[8]。文献[9]将VMD与初始化S变换结合应用于混合动力系统的电能质量扰动检测，以判断扰动类型与起止时刻。文献[10]基于VMD与多尺度模糊熵对高压直流输电线路故障时的电流进行分解与筛选，有效实现区内外故障特征识别。VMD虽然对信号处理具有良好优势，但其分解精度很大程度取决于分解参数K与惩罚因子α的取值，而参数预设时往往依赖于人为经验。基于此，文献[11]采用遗传变异粒子群算法优化VMD并应用于滚动轴承故障诊断，在最优 $[K, α]$ 组合下解决了具有较强非平稳性的轴承振动信号的处理问题。文献[12 ⇓⇓-15]分别将果蝇算法、蝗虫优化算法、遗传算法、鲸鱼优化算法应用于参数优化VMD，均取得不错的效果。以上所提优化算法作为元启发式算法，因其较好的灵活性、鲁棒性及避免局部最优的能力而广受欢迎。

上述优化VMD的方法是建立在符合各自信号特点的适应度函数和单一信号参数优化上。而面对快速、多类的电能质量扰动信号检测，需要确保多类信号的统一优化与减少寻优计算量的问题。天牛须搜索算法(Beetle antennae search，BAS)^[16]由于所需参数少，且不需要梯度信息的优势，成为一种解决VMD参数优化的可观选择。与此同时，BAS的时间和空间复杂度低，效率也更高，且跳出局部最优能力更强，收敛速度也更快。文献[17]在风光柴储互补发电系统容量优化配置问题中利用BAS优化非线性规划性能较好的遗传算法(Genetic algorithm，GA)，克服在最优容量配比获取中GA易陷入局部最优的问题。文献[18]在诊断变压器绕组故障中通过BAS优化支持向量机(Support vector machine，SVM)的相关参数，以低计算量解决了SVM分类不准确的问题。

考虑到VMD分解可能存在一定的噪声残留问题，对信号特征提取存在影响，选择噪声鲁棒性强的TEO对信号进行解调，可实现扰动精准定位及特征信息检测。针对以上问题，提出基于BAS优化的VMD与TEO融合的微电网电能质量扰动检测方法。

2 变分模态分解

VMD算法的本质是构造一个受约束的变分模型，通过搜寻所构造的变分模型最优解来自适应分解信号，根据输入信号x(t)自身的频域特性自适应划分出K个具有特定稀疏性的IMF，将每个IMF定义为c_i(t)。因此，第i个IMF可表示如下

(1)

c_{i} (t) = a_{i} (t) \cos [φ_{i} (t)]

式中，a_i(t)为包络函数；相位φ_i(t)为非递减函数，且 ${φ^{'}}_{i} (t) \geq 0$ ，同时a_i(t)和瞬时频率 ${φ^{'}}_{i} (t)$ 的变化曲线稍缓于φ_i(t)。

以所有模态函数估计带宽之和最小为约束条件，确定每个分量对应的中心频率^[8]，以此构造变分模型。表达式如下

(2)

\begin{matrix} \min_{{c_{i}}, {ω_{i}}} = {\sum_{i = 1}^{K} | | η_{t} [(μ (t) + \frac{υ}{π t}) c_{i} (t)] \exp [- j ω_{i} (t)] | |_{2}^{2}} \\ s.t. x (t) = \sum_{i = 1}^{K} c_{i} (t) \end{matrix}

式中，{c_i}、{ω_i}分别为模态分量及对应分量中心频率的集合；η_t为梯度运算； $(μ (t) + \frac{υ}{π t}) c_{i} (t)$ 表示为通过Hilbert变换得到IMF分量c_i(t)的单边频谱。

在求解该模型时需要引入惩罚因子α和拉格朗日乘子λ(t)，将其变换为非约束变分问题并构造如下的增广Lagrange函数，表达式如下

(3)

\begin{matrix} L [{c_{i}}, {ω_{i}}, λ (t)] = \\ α \sum_{i = 1}^{K} | | η_{t} [(μ (t) + \frac{υ}{π t}) \times c_{i} (t)] \exp [- j ω_{i} (t)] | |_{2}^{2} + \\ | | x (t) - \sum_{i = 1}^{K} c_{i} (t) | |_{2}^{2} + 〈λ (t), x (t) - \sum_{i = 1}^{K} c_{i} (t)〉 \end{matrix}

然后运用交替方向乘数法解决上述非约束变分问题，主要思路是通过交替迭代更新 ${\hat{c}}_{i}^{n + 1} (ω)$ 、 $ω_{i}^{n + 1}$ 、 $λ^{n + 1} (ω)$ 来搜寻式(3)的“鞍点”，更新表达式如下

(4)

{\hat{c}}_{i}^{n + 1} (ω) = \frac{\hat{x} (ω) - \sum_{γ < i} {\hat{c}}_{γ}^{n + 1} (ω) - \sum_{γ > i} {\hat{c}}_{γ}^{n} + \frac{λ^{n} (ω)}{2}}{1 + 2 α {(ω - ω_{i})}^{2}}

(5)

ω_{i}^{n + 1} = \frac{\int_{0}^{\infty} ω | {\hat{c}}_{i} (ω) |^{2} d ω}{\int_{0}^{\infty} | {\hat{c}}_{i} (ω) |^{2} d ω}

(6)

λ^{n + 1} (ω) \leftarrow {\hat{λ}}^{n} (ω) + τ [\hat{x} (ω) - \sum_{i = 1}^{K} {\hat{c}}_{i}^{n + 1} (ω)]

式中， ${\hat{c}}_{i}^{n + 1} (ω)$ 表示当前剩余分量 $\hat{x} (ω) - \sum_{γ < i} {\hat{c}}_{γ}^{n + 1} (ω) - \sum_{γ > i} {\hat{c}}_{γ}^{n}$ 的Wiener滤波； $τ$ 为噪声容限。

定义迭代停止条件，如下所示

(7)

\sum_{i = 1}^{K} \frac{| | {\hat{c}}_{i}^{n + 1} - {\hat{c}}_{i}^{n} | |_{2}^{2}}{| | {\hat{c}}_{i}^{n} | |_{2}^{2}} < ε

式中，ε为迭代误差。一旦满足条件，即停止迭代。

3 基于BAS优化的VMD

根据第2节VMD原理的分析，在信号分解之前需要预设参数K、α、τ和ε。τ和ε主要决定迭代次数和误差限度，K和α则对分解精度产生显著影响。K越大分解计算量越大，而越小所能反映的频率分量越少。此外，α越大带宽跨度越大，伴随带宽重叠及过分解问题的出现；而其越小，越容易引起带宽过窄和欠分解问题。因此BAS优化VMD参数的核心思想就是确定K和α的最优组合。

3.1 天牛须搜索算法

BAS寻优策略是根据天牛在空气中捕获猎物或搜寻潜在配偶的味道时，两侧天牛须检测周围气味浓度，然后天牛会沿着检测到气味浓度较高的那根须所指方向前进，如此循环直至到达气味浓度最高的位置结束。

BAS算法数学模型表示的寻优步骤如下所示。

步骤1：天牛在任意位置时，其头部朝向随机，在维度H中，建立头部朝向的随机向量并进行归一化处理，如下所示

(8)

d = \frac{r a n d (H, 1)}{| r a n d (H, 1) |}

式中，rand()为随机函数。

步骤2：天牛左右须位置x_left、x_right可由天牛质心位置x_m和两须间距离b_m表示，如下所示

(9)

\{\begin{cases} x_{l e f t} = x_{m} - b_{m} \cdot d \\ x_{r i g h t} = x_{m} + b_{m} \cdot d \end{cases}

步骤3：构建适应度函数f(x)计算两侧天牛须的气味浓度，即f(x_left)和f(x_right)，为模拟天牛探测机制，构造如下位置迭代更新模型

(10)

x_{m} = x_{m - 1} + ζ_{m} \cdot d \cdot s i g n [f (x_{r i g h t}) - f (x_{l e f t})]

式中，ζ_m为m时刻的搜索步长。

步骤4：搜索步长ζ_m和两须间距离b_m的更新规则如下

(11)

\{\begin{cases} b_{m} = e_{1} \cdot b_{m - 1} + e_{2} \\ ζ_{m} = e_{3} \cdot ζ_{m - 1} \end{cases}

式中，e₁、e₃通常取0.95，e₂取0.01。BAS在达到预设的迭代次数后，其历次迭代的最佳适应度函数值所对应的数据空间位置即为寻优结果。

3.2 BAS适应度函数的确定

包络熵E_p^[19]作为一种评价信号稀疏特性的指标，扰动信号x(t)经VMD分解后，若获得分量中含噪较多，则会掩盖信号中扰动特征，分量信号的稀疏性就较弱，包络熵较大；反之，若各分量中包含规律的扰动特征，其稀疏性就强，包络熵就越小，故在一组 $[K_{0}, α_{0}]$ 的影响下，选择K₀个分量中的最小包络熵作为局部极小熵minE_p，则该熵值对应的分量包含丰富的扰动信息，因此将局部极小熵作为整个搜索过程中适应度函数的一部分，寻找全局最优组合 $[K, α]$ 。文献[11]在K值固定情况下，采用依次增大的α值对同一信号进行VMD分解，观察试验结果发现，合适的α值可以降低VMD的迭代次数，即提高了VMD分解效率，故需要在分解最优时，兼顾算法的高效性，因此在minE_p的基础上，加入迭代次数T，构建适应度函数如下所示

(12)

\min f (x) = \min E_{p} + ρ \cdot T

式中，ρ为适应度函数的量化因子，一般取1/1 000。

4 基于参数优化VMD与TEO的融合算法

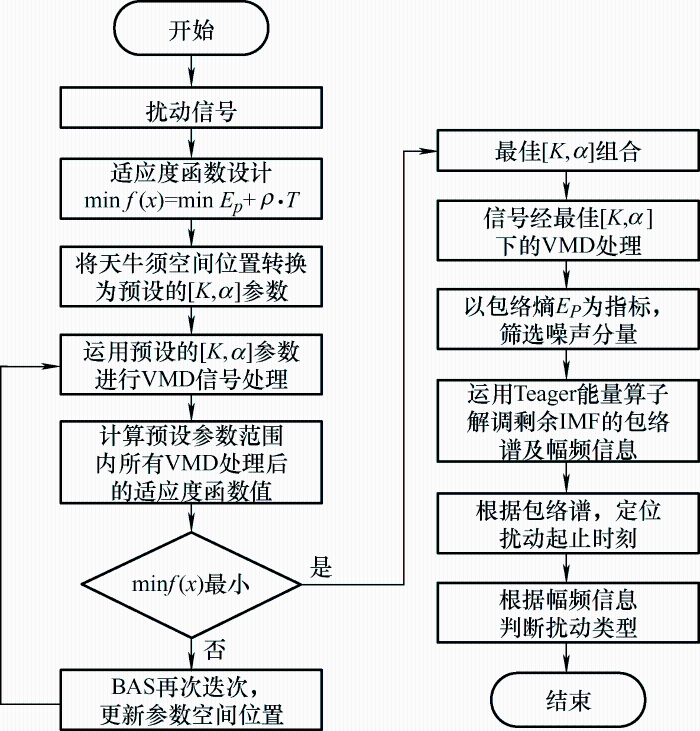
由上文分析可知，VMD分解精度依赖于 $[K, α]$ 参数组合的选取，且VMD是将信号分解为多个具有特定稀疏性的IMF，而包络熵E_p可表明信号稀疏性强弱，对分析包含扰动特征的IMF提供了有效判据。同时合理的α能够降低VMD迭代次数，提高分解效率，因此将包络熵与迭代次数组合作为BAS的适应度函数，能充分量化VMD分解效果。TEO在时间分辨率上比传统Hilbert解调更有优势，且所需样本数据少，具有抑制端点飞翼的优势^[20]。

参数优化VMD多应用于轴承故障诊断领域，相较于电能质量检测领域，两者所测信号均具有不同程度的随机性和冲击性，而参数优化VMD对冲击性较强的轴承故障信号具有良好的检测精度，在电能质量扰动检测领域也具有可观的潜力。同时参数优化VMD与TEO的融合是集各之所长，能达到对微电网电能质量的高精度检测。具体实现步骤流程图如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 融合算法流程图

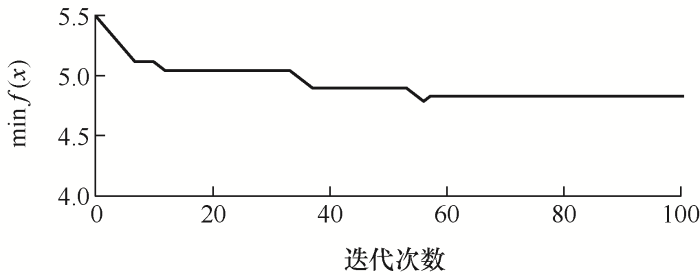
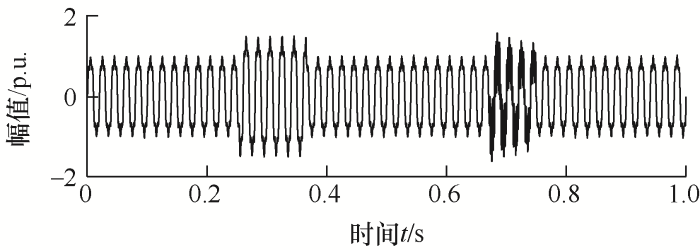
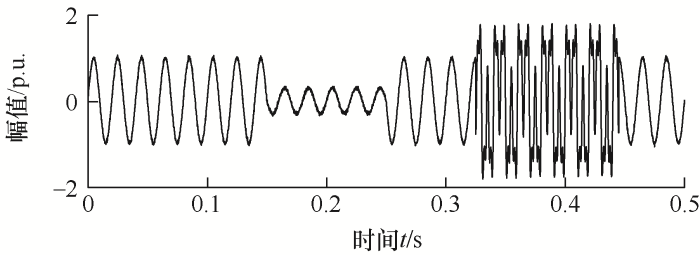
以某地35 kV配电线路发生的一起单相短路故障为例，故障期间短路相电压做归一化处理(本文幅值均为标幺值)。录波装置采样频率为10 kHz，信号时长为0.25 s。

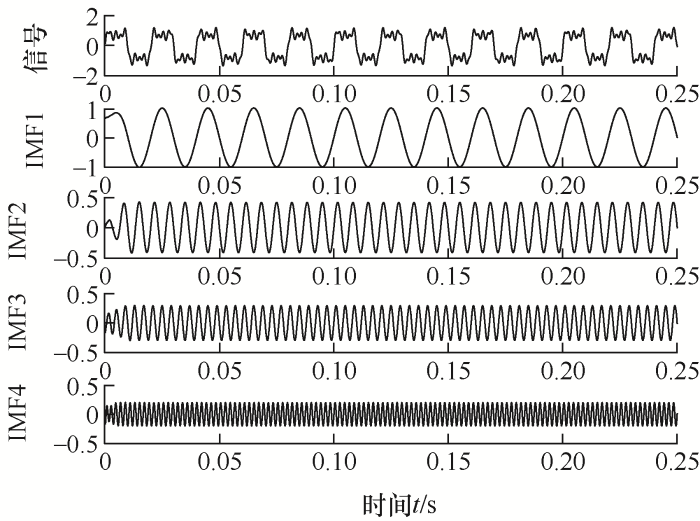
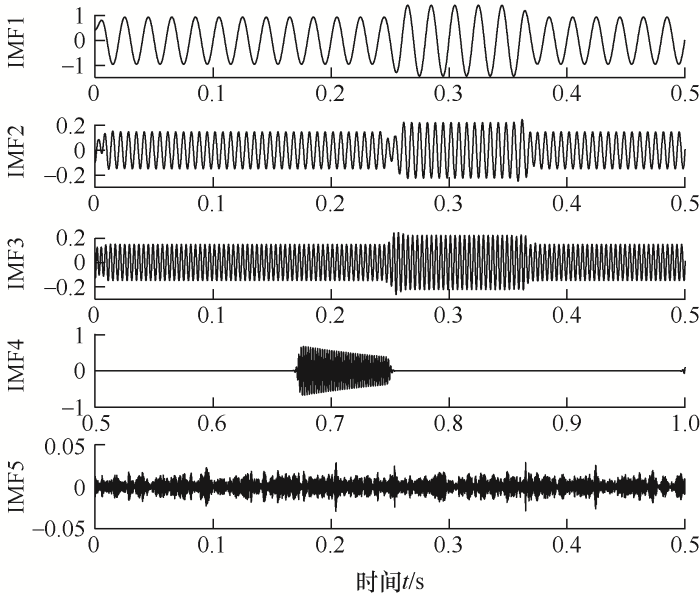
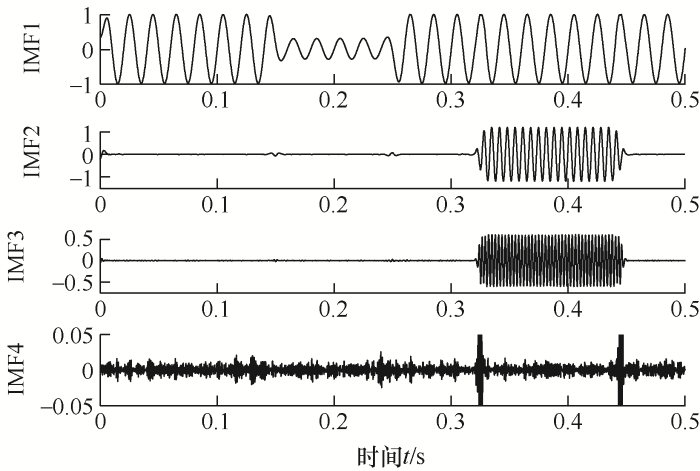
根据文献[11]选取VMD分解中噪声容限τ和迭代误差限度ε，即τ=0，ε=1×10^-7，其中K和α的初值分别设置为2和500。BAS迭代收敛趋势如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 BAS优化收敛曲线

由图2可知，BAS迭代至56次时寻得最优 $[K, α]$ 组合，K=4，α=1 046。分解结果如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 参数优化VMD对故障信号的分解

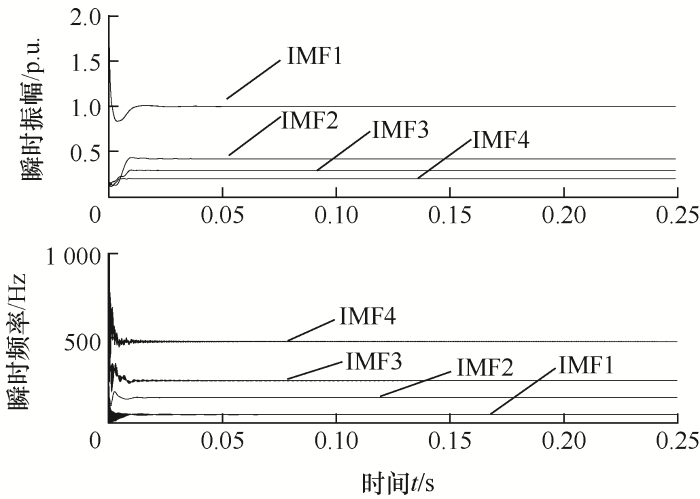
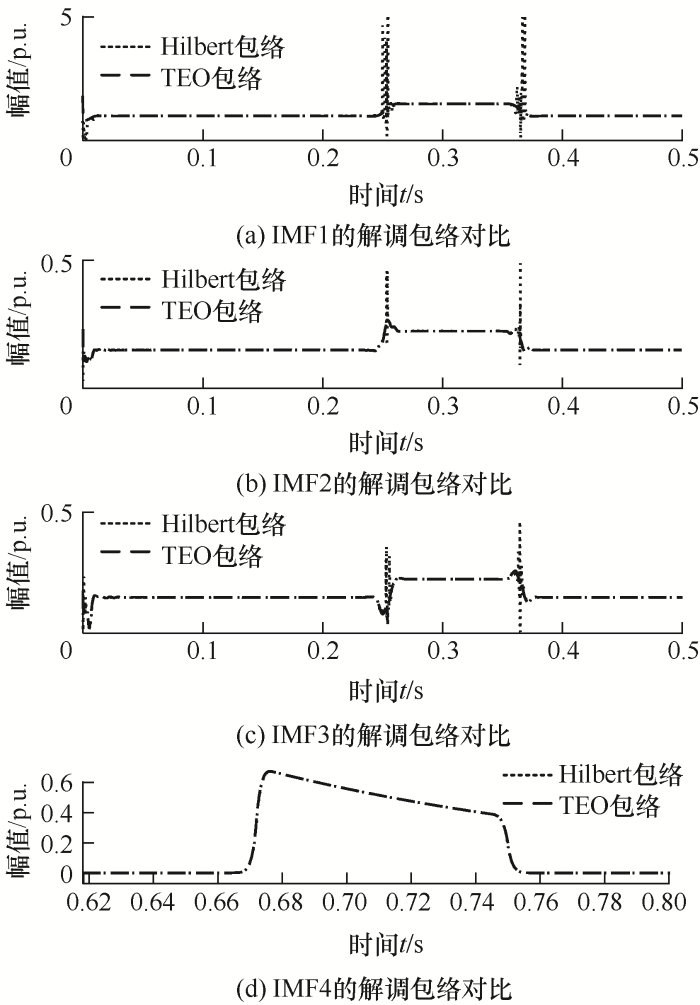
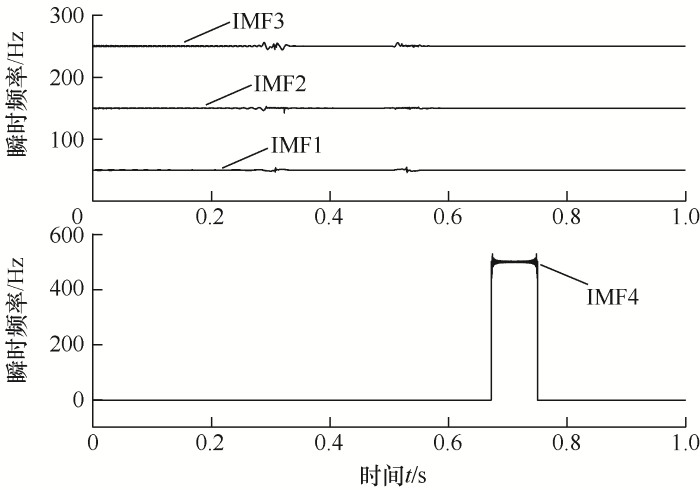
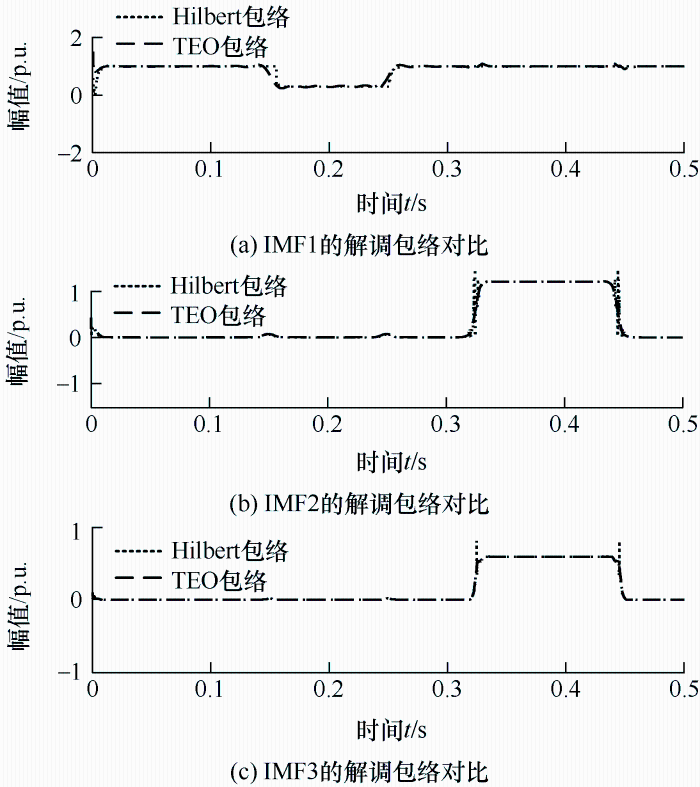
运用TEO对IMF1~IMF4进行瞬时幅-频检测，如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 TEO解调结果

根据图3所示，最佳参数组合 $[K, α]$ 下的VMD分解结果，各个IMF波形光滑，无模态混叠束缚现象。据图4解调结果可知，该故障信号中含基波、三次谐波、五次谐波及480 Hz间谐波，IMFs幅值平稳且频率单一，能准确提取谐波故障特征。

5 电能质量扰动算例仿真

为验证本文方法的有效性，在Matlab仿真环境下生成多种微电网电能质量扰动信号进行仿真测试，设置采样频率为10 kHz。

5.1 单一扰动仿真分析

微电网中单一扰动信号主要包括电压中断、电压暂降、电压脉冲和电压闪变等，本文仿真分析主要针对风电机组启停与切换时、光伏发电与风电自身特性及出现短路故障时所引起的以上几种扰动信号，根据文献[21]中所测单一扰动信号进行仿真分析。

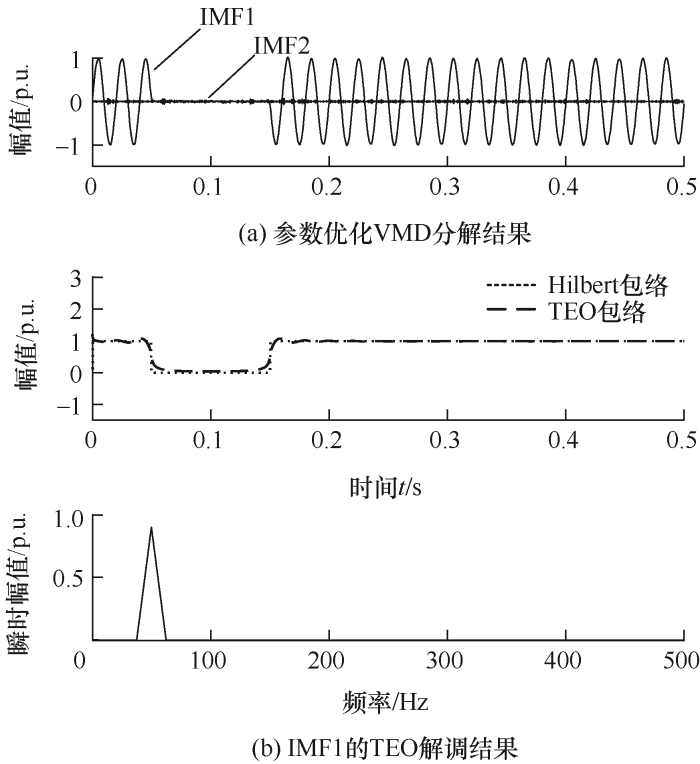
(1) 电压中断扰动模型如下所示

(13)

x_{1} (t) = [1 - r_{1} (σ (t - t_{1}) - σ (t - t_{2}))] \cdot \sin (2 π f_{1} t) + γ_{1} (t)

式中，r₁=0.94，σ(t)为阶跃信号；γ₁(t)是信噪比为20 dB的高斯白噪声；t₁=0.05 s，t₂=0.15 s；f₁=50 Hz。

电压中断过程中频率与幅值波动检测如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 电压中断检测与包络解调结果

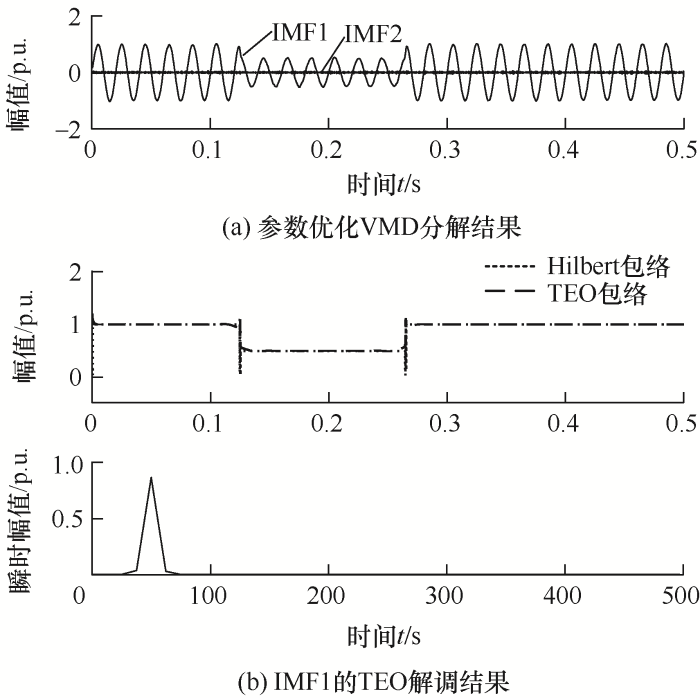
(2) 电压暂降扰动模型如下所示

(14)

x_{2} (t) = [1 - r_{2} (σ (t - t_{3}) - σ (t - t_{4}))] \cdot \sin (2 π f_{1} t) + γ_{1} (t)

式中，r₂=0.5，t₃=0.125 s，t₄=0.265 s。检测结果如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 电压暂降检测与包络解调结果

由图6可知，从0.124 5~0.264 3 s信号幅值减小一半，测出的电压中断起止时间与理论值相近，电压中断的幅值变化也符合扰动信号特征。且验证了在噪声环境下，TEO表现出良好的抗噪性。

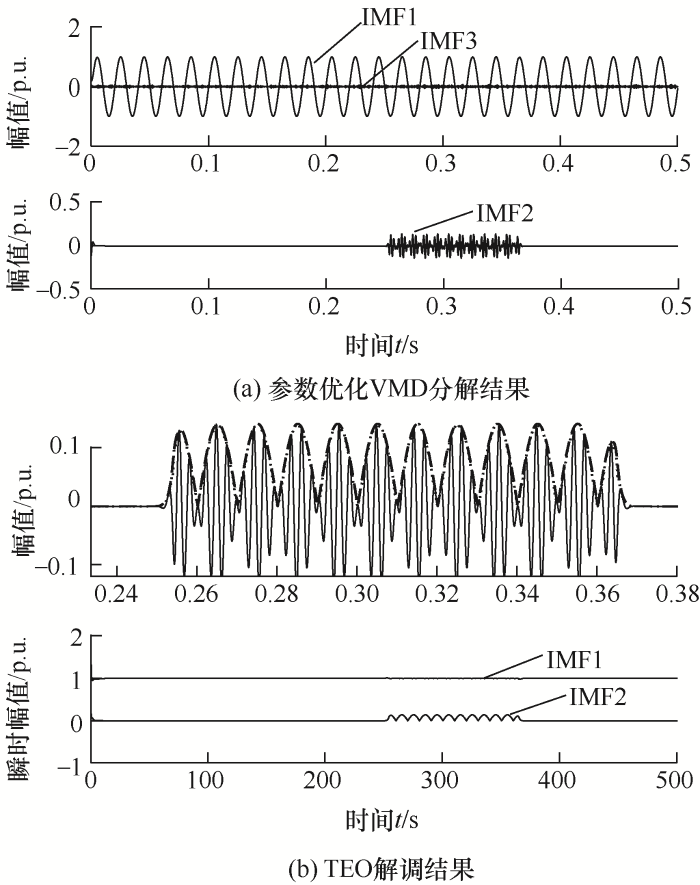
(3) 电压闪变扰动模型如下所示

x_{3} (t) = [1 + r_{3} (σ (t - t_{5}) - σ (t - t_{6}))] \cdot \sin (β \cdot 2 π f_{1} t) \cdot

(15)

\sin (2 π f_{1} t) + γ_{1} (t)

式中，r₃=0.15，t₅=0.254 s，t₆=0.365 s；β=7.5，信号时长为0.5 s，检测结果如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 电压闪变检测与包络解调结果

由图7可知在0.252 1 s时刻电压频率和电压幅值均发生扰动，在0.363 9 s时刻扰动终止，起止时刻误差分别为0.75%、0.30%。

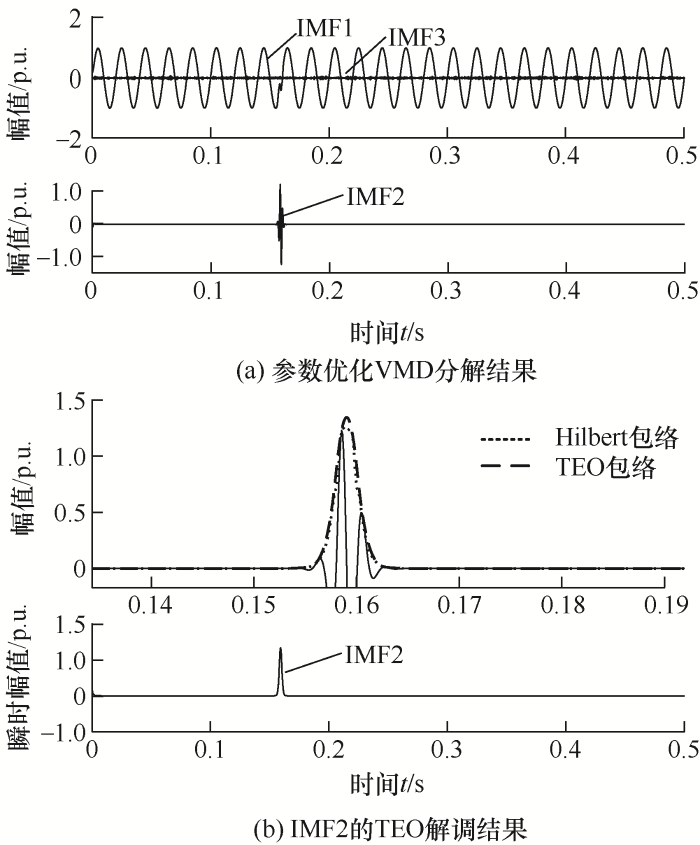
(4) 电压脉冲扰动模型如下所示

(16)

\begin{matrix} x_{4} (t) = \sin (2 π f_{1} t) + r_{4} (σ (t - t_{7}) - σ (t - t_{8})) \cdot \\ \exp (\frac{- t}{t_{y}}) \cdot \sin (20 π f_{1} t) + γ_{1} (t) \end{matrix}

式中，t₇=0.16 s，t₈=0.158 s，r₄=5，t_y=(t₇+t₈)/2；信号时长为0.25 s。检测结果如图8所示。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 电压脉冲检测与包络解调结果

由图8中TEO包络解调可知，IMF2自0.157 2 s到0.160 4 s时刻频率及幅值发生跳变，与理论值相比，检测起止时刻误差仅为0.51%、0.25%，幅值误差为0.50%。

为验证融合算法的检测优势，分别采用融合算法、HHT^[5]和LMD^[7]方法对上述单一扰动信号进行检测，检测结果如表1所示。表1中幅值均为标幺值，HHT、LMD对含噪扰动和过零处的中断扰动无法进行准确分析，参数优化VMD则不受扰动类型及含噪状况的影响，具有更强的适用性，而TEO相较于传统Hilbert变换的时频分析方法，幅值检测及扰动定位准确度也明显更高。

表1 HHT、LMD、参数优化VMD方法下单一扰动检测结果对比

扰动类型	SNR	扰动起始时刻/s				扰动终止时刻/s				扰动幅值/p.u.
		真实值	测量值			真实值	测量值			真实值	测量值
		真实值				真实值	HHT	LMD	VMD-TEO	真实值		HHT	LMD	VMD-TEO	HHT	LMD	VMD-TEO
电压中断	无噪	0.050	0.048 7	0.048 5	0.049 6	0.150	0.148 2	0.148 0	0.149 3	0.94	0.915 8	0.921 3	0.934 4
电压中断	20 dB	0.050	—	—	0.049 5	0.150	—	—	0.149 0	0.94	—	—	0.931 6
电压暂降	无噪	0.125	0.123 8	0.122 9	0.124 6	0.265	0.263 0	0.262 7	0.264 2	0.50	0.488 7	0.492 1	0.497 9
电压暂降	20 dB	0.125	—	—	0.124 5	0.265	—	—	0.264 3	0.50	—	—	0.494 6
电压闪变	无噪	0.254	0.248 2	0.247 3	0.252 8	0.365	0.360 7	0.358 9	0.364 2	0.15	0.132 0	0.134 7	0.146 4
电压闪变	20 dB	0.254	—	—	0.252 1	0.365	—	—	0.363 9	0.15	—	—	0.145 2
电压脉冲	无噪	0.158	0.157 0	0.156 3	0.157 6	0.160	0.1595	0.159 3	0.160 1	1.15	1.102 4	1.112 0	1.144 2
电压脉冲	20 dB	0.158	—	—	0.157 2	0.160	—	—	0.160 4	1.15	—	—	1.143 9

注：“—”表示无法检测，后同。

新窗口打开| 下载CSV

5.2 复合扰动仿真分析

在实际微电网中，故障发生时扰动信号并不是以单一形式出现的，而是多种故障扰动叠加出现的。为进一步验证融合算法检测复合故障扰动的有效性，根据文献[9]构造两种包含多种扰动的故障信号。

5.2.1 含暂态振荡的复合扰动分析

具体数学模型如下

(17)

\begin{matrix} x_{5} (t) = (1 + r_{5} (σ (t - 0.254) - σ (t - 0.365) \cdot (r_{6} \sin (2 π f_{1} t) + \\ r_{7} \sin (6 π f_{1} t) + r_{8} \sin (10 π f_{1} t) + γ_{2} (t) + \\ A \exp [- c (t - 0.672)] [σ (t - 0.672) - σ (t - 0.75)] \sin (20 π f_{1} t) \end{matrix}

式中，r₅=0.5，r₇=r₈=0.15， $r_{6} = \sqrt{1 - r_{7}^{2} - r_{8}^{2}}$ ；A=0.7，c=8； $γ_{2} (t)$ 是信噪比为30 dB高斯白噪声。信号时长为1 s，信号波形如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 含噪扰动波形

VMD分解的最佳 $[K, α]$ 在迭代67次时出现，K=5，α=1 223，分解结果如图10所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 参数优化VMD分解结果

观察图10可知，多类扰动分量被准确分离，IMF5的熵值较大，E_p=8.832 4，判定为噪声分量。经TEO解调IMF1~IMF4，由包络谱可判断出各扰动分量的起止时刻，TEO包络如图11所示。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 TEO包络解调结果

分析图11可知，TEO包络解调相较于Hilbert包络更贴合IMF，在起止时刻无明显飞翼，准确定位各类扰动的起止时刻，并准确获取瞬时幅值信息，再由TEO解调IMF1~IMF4的瞬时频率信息，如图12所示。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 TEO解调的瞬时频率结果

将检测的电压暂降、暂态振荡及谐波分量的特征信息进行整理，如表2所示。

表2 含暂态振荡的复合扰动检测结果

扰动类型	扰动起始时刻/s		扰动终止时刻/s		扰动幅值/p.u.		扰动频率/Hz
扰动类型	理论值	实测值	理论值	实测值	理论值	实测值	理论值	实测值
电压暂降	0.254	0.252 9	0.365	0.366 1	0.50	0.495 2	*	*
暂态振荡	0.672	0.669 3	0.750	0.748 2	0.70	0.701 2	500	499.23
三次谐波	0.254	0.253 1	0.365	0.364 0	0.225	0.224 1	150	150.12
五次谐波	0.254	0.252 3	0.365	0.363 6	0.225	0.223 7	250	249.41

注：“*”表示无需检测，后同。

新窗口打开| 下载CSV

5.2.2 含暂态谐波的复合扰动分析

具体数学模型如下

(18)

\begin{matrix} x_{6} (t) = [1 - 0.7 (σ (t - 0.15) - σ (t - 0.25))] \sin (2 π f_{1} t) + \\ (σ (t - 0.325) - σ (t - 0.445)) (1.2 \sin (6 π f_{1} t) + \\ 0.6 \sin (14 π f_{1} t)) + γ_{2} (t) \end{matrix}

同样将信噪比为30 dB的高斯白噪声加入扰动信号，对其进行检测，含噪扰动波形如图13所示。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 含噪扰动波形

BAS迭代47代搜寻到最佳 $[K, α]$ 组合，其中K=4，α=1 043。VMD分解结果如图14所示。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 参数优化VMD分解结果

据图14可知，参数优化VMD对包含电压暂降与暂态谐波的复合扰动具有高分解精度，经包络熵指标筛选IMFs后，由TEO解调IMF1~IMF3，包络谱如图15所示。

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 TEO包络解调结果

由图15可知，TEO解调包络较Hilbert包络更加平滑，在0.15 s至0.25 s、0.325 s至0.445 s之间有效地检测出电压暂降及三次、七次暂态谐波，定位误差最大仅为0.9 ms，幅值误差小于1.2%。具体数据如表3所示。

表3 含暂态谐波的复合扰动检测结果

扰动类型	扰动起始时刻/s		扰动终止时刻/s		扰动幅值/p.u.		扰动频率/Hz
扰动类型	理论值	实测值	理论值	实测值	理论值	实测值	理论值	实测值
电压暂降	0.150	0.148 2	0.250	0.251 5	0.70	0.692 1	*	*
暂态谐波(3)	0.325	0.319 1	0.445	0.443 2	1.20	1.188 4	150	149.34
暂态谐波(7)	0.325	0.316 0	0.445	0.442 6	0.60	0.594 7	350	351.03

新窗口打开| 下载CSV

6 结论

本文运用BAS对VMD进行参数优化，以克服其参数选取不佳导致分解精度差的缺陷，并利用TEO对扰动分量解调，由试验结果得出以下结论。

(1) 结合包络熵与迭代次数所建立的适应度函数能充分量化VMD的分解效果，可有效作为VMD参数优化的依据。此适应度函数极小值对应的参数组合作为VMD的统一预设参数，有效避免对任一信号的VMD参数单独优化，确保各扰动信号得到较好的分解，极大提高了检测效率。

(2) 利用BAS算法迭代次数少，跳出局部最优快，且所需参数少的优势，能够在短时间内搜索出参数空间内最优的适应度函数值，其寻优策略简单高效，能显著降低计算量。

(3) 对包含扰动特征的IMFs进行TEO解调，结果准确反映了各扰动特征的幅频信息，精确定位扰动起止时刻，体现出良好的适用性。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

汪飞, 全晓庆, 任林涛.

电能质量扰动检测与识别方法研究综述

[J]. 中国电机工程学报, 2021, 41(12):4104-4121.