1 引言
微电网是一种小型的发配电系统,能够实现自我控制、保护和管理,可以并网运行或者孤岛运行[1 -2 ] 。微电网是大电网的延伸拓展,在城市、工业区、商业区等地区有非常高的应用价值。普及微电网的同时也能够让包括新能源在内的微源大规模接入,微电网能够高效地调用各个微源,以此实现对负荷的可靠供给,使传统电网向智能电网过渡。随着用电需求的急剧增加以及光伏风电等清洁能源越来越多的应用,如何完成提高可靠性、提高运营效率、降低成本的任务[3 ] ,这就对微电网运行提出了更高的要求。
此外,电动汽车(Electric vehicle, EV)也已经进入大众的生活,近年来,中国在新能源汽车的研发与推广方面领先全球[4 ] 。随着电动汽车的普及与发展,将能大大缓解我国对石油进口的依赖程度,预计到2025年电动汽车的销量将占总汽车销量的25%。电动汽车本身具有的时空特性所带来的充电不确定性将会使负荷曲线恶化并且增加负荷峰值,这也为微电网稳定运行带来了风险。近年来得到普及的V2G (Vehicle-to-grid)技术,旨在使电动汽车参与到微电网运行调度中,起到缓解电网压力的作用[5 ] 。V2G技术是指在电网负荷高时,将电动汽车电池的电能卖给电网,而当电网负荷低时,则为电动汽车蓄电池充电,从而使车主获得收益,是一种有序的车网互动[6 ] 。电动汽车作为能够移动的储能单元,在调整电网负荷等方面起到积极作用,同时也因其不可预测性而对电网提出了挑战。文献[7 ]通过采用最大模糊满意度将多目标优化问题转化为单目标优化问题,并运用改进遗传算法进行仿真优化。文献[8 ]通过计及分时电价来对微电网中的电动汽车进行优化调度,并采用权重粒子群算法验证方案得到了最优调度策略。文献[9 ]提出一种在原有的NSGA-Ⅲ算法中引入了加速差分进化、Levy搜索策略和对众多复杂约束的处理机制,有效地解决了考虑多约束条件的多目标优化问题。
本文研究在包含光伏风电、柴油发电机、微型燃气轮机、蓄电池和负载的传统微电网系统中计及电动汽车的接入,考虑微电网系统运行成本以及电动汽车充放电成本,然后在NSGA-II算法中引入Levy飞行策略,通过对某地区微电网系统进行仿真求解,验证本文优化方案的可行性。
2 微电网数学模型
2.1 光伏发电
光伏发电的发电量受到光照、温度等因素的影响,当在标准测试环境下(温度为25 ℃,光照强度为1 000 W/m2 ),光伏电池的输出功率模型可近似为
(1) ${{P}_{\text{pv}}}(t)={{P}_{\text{STC}}}\frac{G(t)}{{{G}_{\text{STC}}}}\left[ 1+k\left( T(t)-{{T}_{\text{STC}}} \right) \right]$
式中,${{P}_{\text{STC}}}$ ${{G}_{\text{STC}}}$ G (t )与T (t )分别为测试时的光照强度与表面温度。
2.2 风力发电
风力发电是除水力发电之外最成熟和最有前景的一种发电方式。当风机运行时,只有风速满足大于切入风速且小于切出风速,风机才能正常发电,当风速过小时,则风机不足以运行,而当风速过大时,为防止其内部部件损坏,风机则会停止,此时其输出功率为0。其输出功率与风速的关系可由式(2)表示
(2) ${{P}_{\text{wt}}}=\left\{ \begin{array}{*{35}{l}} \begin{array}{*{35}{l}} \begin{array}{*{35}{l}} {} \\\end{array}0 & \begin{array}{*{35}{l}} {} & {} & {} \\\end{array}\ \ \ v\ <\ {{v}_{\text{in}}} \\\end{array} \\ \begin{matrix} \begin{array}{*{35}{l}} {} \\\end{array}\frac{v-{{v}_{\text{in}}}}{{{\text{v}}_{\text{r}}}-{{v}_{\text{in}}}}{{P}_{\text{r}}} & \ \ {{v}_{\text{in}}}\ <\ v\ <\ {{v}_{\text{r}}} \\\end{matrix} \\ \begin{matrix} \begin{array}{*{35}{l}} {} \\\end{array}{{P}_{\text{r}}} & \begin{matrix} {} & {} \\\end{matrix}\begin{array}{*{35}{l}} \begin{array}{*{35}{l}} {} \\\end{array} \\\end{array}\begin{array}{*{35}{l}} {} \\\end{array}\ \ \ {{v}_{\text{r}}}\ <\ v\ <\ {{v}_{\text{out}}} \\\end{matrix} \\ \begin{matrix} \begin{array}{*{35}{l}} {} \\\end{array}0 & \begin{array}{*{35}{l}} {} & {} & {} \\\end{array}\begin{array}{*{35}{l}} {} \\\end{array}\ {{v}_{\text{out}}}\ <\ v \\\end{matrix} \\\end{array} \right.$
式中,v in 、v out 、v r 分别是风机的切入风速、切出风速以及额定风速;P r 为额定输出功率。
2.3 微型燃气轮机
微型燃气轮机是伴随着分布式供电发展起来的一类小型热力发电机,一般使用天然气为燃料,能耗成本数学模型如式(3)所示
(3) ${{C}_{\text{mt}}}\left( t \right)=\frac{C{{P}_{\text{mt}}}\left( t \right)}{LHV{{\eta }_{\text{mt}}}\left( t \right)}$
式中,C mt (t )为时间t 内的燃料成本;C 为天然气价格,本文取2元/m3 ;P mt (t )为燃气轮机在时间t 内的输出功率;η mt (t )为燃气轮机的效率;天然气低位热值LHV=9.7 kW·h/m3 。
2.4 柴油发电机
柴油发电机能在微电网中起到调峰作用,其数学模型如下
(4) ${{W}_{\text{de}}}=a{{\left( {{P}_{\text{de}}} \right)}^{2}}+b{{P}_{\text{de}}}+c$
式中,${{W}_{\text{de}}}$ P de 为输出功率;a 、b 、c 为燃料成本系数,分别取0.000 85、0.10、5.8。
2.5 蓄电池
蓄电池作为储能设备在微电网中占据了重要地位,当其他出力不足时能够补充需求,当负荷较低时,能够存储多余的电量备用,起到了削峰填谷的作用[10 ] ,荷电状态的数学模型可由式(5)表示
(5) $SO{{C}_{t}}={{S}_{0}}+\frac{\sum\limits_{t=1}^{T}{{{P}_{\text{SB},t}}\Delta t}}{{{S}_{\text{B}}}}$
式中,SOCt ${{P}_{\text{SB},t}}$ t 时段的荷电状态与充放电功率;${{P}_{\text{SB},t}}$ ${{P}_{\text{SB},t}}$ T 为调度周期。
2.6 电动汽车
电动汽车的行驶特性对其日程及充放电时间有较大影响,电动汽车种类用途多样,其中电动家庭汽车具有数量庞大、随机性较大、调度相对困难等特点。通过对美国交通部统计得出的美国家庭汽车出行数据进行拟合,得到了电动汽车的日程概率密度函数如下[11 ]
(6) ${{f}_{\text{d}}}\left( x \right)=\frac{1}{x{{\sigma }_{\text{d}}}\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}\text{exp}\left[ -\frac{{{\left( \text{ln}x-{{\mu }_{\text{d}}} \right)}^{2}}}{2\sigma _{\text{d}}^{\text{2}}} \right]$
(7) ${{f}_{\text{s}}}\left( x \right)=\left\{ \begin{matrix} \begin{matrix} \frac{1}{{{\sigma }_{\text{s}}}\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}\exp \left[ -\frac{{{\left( x+24-{{\mu }_{\text{s}}} \right)}^{2}}}{2\sigma _{\text{s}}^{2}} \right] & 0<x\le {{\mu }_{\text{s}}}-12 \\\end{matrix} \\ \begin{matrix} \frac{1}{{{\sigma }_{\text{s}}}\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}\exp \left[ -\frac{{{\left( x-{{\mu }_{\text{s}}} \right)}^{2}}}{2\sigma _{\text{s}}^{2}} \right] & \begin{matrix} {} & {} \\\end{matrix}{{\mu }_{\text{s}}}-12<x\le 24 \\\end{matrix} \\\end{matrix} \right.$
不考虑电动汽车开始和结束充电时的情况,电动汽车荷电状态设定为0.25~0.9。
3 微电网多目标优化模型及求解算法
3.1 目标函数
当微电网中计及电动汽车的情况下,不光需要考虑微电网本身的运行成本,也要考虑到电动汽车车主的车辆充放电成本,本文以此建立如下数学模型。
3.1.1 微电网运行成本
(8) ${{C}_{t}}=\sum\limits_{t=1}^{24}{\left( {{C}_{\text{ch}}}+{{C}_{\text{dm}}}+{{C}_{\text{fu}}}+{{C}_{\text{grid}}} \right)}$
(9) ${{C}_{\text{ch}}}=\underset{i=1}{\overset{N}{\mathop \sum }}\,\frac{{{C}_{\text{k}}}}{8\ 760\times {{P}_{\text{R}i}}\times {{F}_{\text{C}i}}}\times \frac{d{{\left( \text{1}+d \right)}^{l}}}{{{\left( \text{1+}d \right)}^{l}}-1}$
(10) ${{C}_{\text{dm}}}=\underset{i=1}{\overset{N}{\mathop \sum }}\,{{K}_{\text{M}i}}\times {{P}_{i}}$
(11) ${{C}_{\text{fu}}}={{C}_{\text{de}}}+{{C}_{\text{mt}}}=aP_{\text{de}}^{2}+b{{P}_{\text{de}}}+c+C\frac{1}{LHV}\frac{{{P}_{\text{mt}}}}{{{\eta }_{\text{mt}}}}$
(12) ${{\eta }_{\text{mt}}}=0.075\ 3{{\left( \frac{{{P}_{\text{mt}}}}{65} \right)}^{3}}-0.395{{\left( \frac{{{P}_{\text{mt}}}}{65} \right)}^{2}}+0.417\ 4\frac{{{P}_{\text{mt}}}}{65}+0.106\ 8$
(13) ${{C}_{\text{grid}}}={{C}_{\text{price}\left( t \right)}}{{C}_{\text{grid}\left( t \right)}}$
式中,Ct 为微电网综合运行成本;C ch 、C dm 、C fu 、C grid 、C price 分别为折旧、维护、燃料、交易成本、电价;C k 、P R i F C i d 和l 分别表示折旧率和微电源使用寿命,取d 为0.5。K M i Pi 分别为运行维护费用与微电源i 的发电功率[13 ] 。
3.1.2 电动汽车车主成本
电动汽车车主成本主要是车主给自家汽车充电所需要电费成本减去其将多余的电卖给电网所获得的收益[14 ] 。这样车主通过考虑电价而进行合理充放电就可以达到为电网削峰填谷的效果,其数学模型如下
(14) ${{C}_{\text{ev}}}=\underset{t=1}{\overset{24}{\mathop \sum }}\,\underset{i=1}{\overset{m}{\mathop \sum }}\,\left( {{P}_{\text{EVc},i}}\left( t \right)c\left( t \right)\Delta {{t}_{\text{c},i}}-{{P}_{\text{EVd},i}}\left( t \right)p\left( t \right)\Delta {{t}_{\text{d},i}} \right)$
式中,n 为电动汽车数量;${{P}_{\text{EVc},i}}\left( t \right)$ n 辆电动汽车在t 时间的充电功率,${{P}_{\text{EVd},i}}\left( t \right)$ c (t )、p (t )分别表示t 时间的购电售电价格。
3.2 约束条件
(15) $\underset{i=1}{\overset{N}{\mathop \sum }}\,{{P}_{i}}+{{P}_{\text{grid}}}={{P}_{\text{load}}}+{{P}_{\text{EVload}}}+{{P}_{\text{d}}}$
式中,Pi 代表分布式电源输出功率;N 为分布式电源个数;P grid 为向大电网的购电量;P d 代表蓄电池的充电功率,P load 代表其负荷功率,而P EVload 代表电动汽车的充电功率。
(16) ${{P}_{k\text{,min}}}<{{P}_{k}}<{{P}_{k\text{,max}}}$
式中,${{P}_{k\text{,min}}}$ ${{P}_{k\text{,max}}}$ k 个微源输出的功率下限和上限值。
(17) ${{P}_{\text{grid,min}}}\left( t \right)<{{P}_{\text{grid}}}\left( t \right)<{{P}_{\text{grid,max}}}\left( t \right)$
式中,P grid (t )代表时间为t 时,微电网和大电网之间的交换功率值;P grid,max (t )、P grid,min (t )则代表交换功率的上下限。
(18) $\left\{ \begin{matrix} SO{{C}_{\text{SB,min}}}<SO{{C}_{\text{SB}}}\left( t \right)<SO{{C}_{\text{SB,max}}} \\ SO{{C}_{\text{EV,min}}}<SO{{C}_{\text{EV}}}\left( t \right)<SO{{C}_{\text{EV,max}}} \\\end{matrix} \right.$
式中,SOCSB (t )代表蓄电池所带的电荷量;SOCEV (t )代表电动汽车所带的电荷量;SOCSB,min 、SOCSB,max 分别为蓄电池最小和最大剩余电量;SOCEV,min 、SOCEV,max 分别为电动汽车电池容量的下限与上限[18 ] 。
3.3 基于Levy飞行改进的NSGA-II算法
NSGA-II算法是带精英策略的快速非支配排序遗传算法,是基于遗传算法的多目标优化算法[19 ] ,因其全局收敛性好、通用性高,常用于多目标优化中,但随着其迭代次数的增多,其种群多样性不足的缺点就会显现而容易陷入局部最优。
Levy飞行是以法国数学家保罗•莱维命名,表示步长为有相对较高的概率出现大跨步的随机行走。Levy飞行在智能算法的优化中有了广泛应用,如在鸟群算法中通过使用Mantegna算法表示随机Levy步长,并得到位置更新公式,Levy飞行可以扩大搜索空间[20 ] ,所以通过引入Levy飞行可以提高局部和全局搜索能力,增强种群多样性。Levy飞行位置更新公式如下
(19) $x_{i}^{t+1}=x_{i}^{t}+\alpha \oplus Levy\left( \lambda \right)\ \ \ \ \ \ i=1,2,\cdots,n$
式中,$x_{i}^{t}$ xi 第t 代的位置;α 为步长控制参数;Levy(λ )满足
(20) $Levyu={{t}^{-\lambda }}\ \ \ \ \ 1<\lambda \le 3$
使用Mantegna算法来模拟Levy分布,其步长s 为
(21) $s=\frac{\mu }{{{\left| v \right|}^{\frac{1}{\beta }}}}$
式中,μ 、v 为方向向量,满足正态分布,为$\left\{ \begin{matrix} \mu \ \ \text{N}\left( 0,\sigma _{\mu }^{2} \right) \\v\ \ \text{N}\left( 0,\sigma _{v}^{2} \right) \\\end{matrix} \right.$,标准差表示为
(22) $\left\{ \begin{align} & {{\sigma }_{\mu }}={{\left\{ {\Gamma \left( 1+\beta \right)\sin \left( \frac{\pi \beta }{2} \right)}/{\left( \Gamma \left[ \frac{1+\beta }{2} \right]{{\beta }^{2}}\frac{\left( \beta -1 \right)}{2} \right)}\; \right\}}^{\frac{1}{\beta }}} \\ & {{\sigma }_{v}}=1 \\\end{align} \right.$
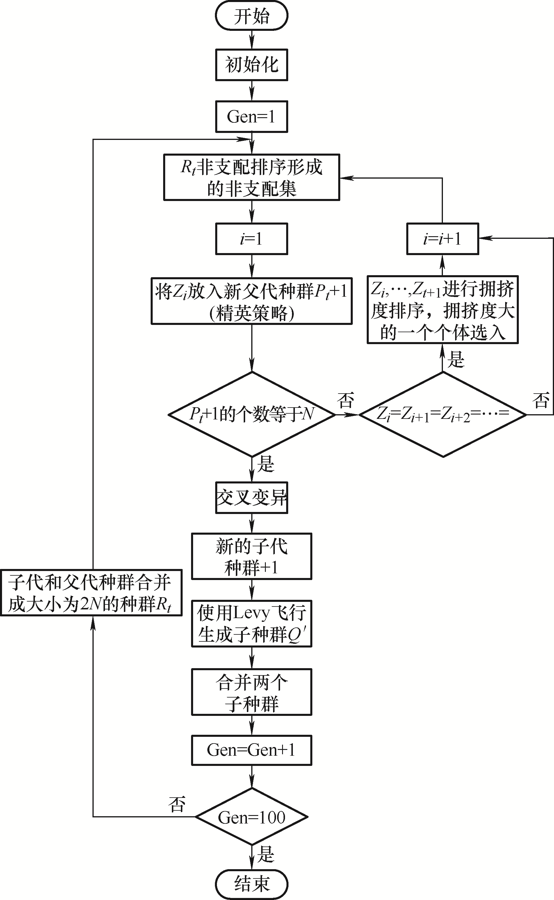
改进NSGA-II算法通过根据Levy飞行特征生成新的子种群,并与传统NSGA-II的子代种群合并,在寻找全局最优解的过程中,以此来增强种群多样性,加强探索能力,最大程度降低陷入局部最优的概率,从而在计算精度与收敛速度上改良标准NSGA-II算法。由于有两个目标函数,没有办法使两个目标函数同时最小,只能求得一组折衷解,使其达到综合最优,其算法流程如下:① 初始化,根据模型输入日负荷以及风光发电等预测参数,然后随机得到规模为N 的初始种群;② 通过遗传算法的选择、交叉、变异三个基本操作得到第一代子代种群,同时通过Levy飞行根据式(19)生成新的子代种群Q' ;③ 合并父代与子代种群;④ 通过目标函数与约束条件对种群进行非支配排序,并计算种群个体拥挤度,保留合适的个体产生新的父代种群;⑤ 当达到最大迭代次数,输出满足约束条件的Pareto最优解集,否则返回步骤②,直到满足输出条件。
图1
4 仿真算例及结果分析
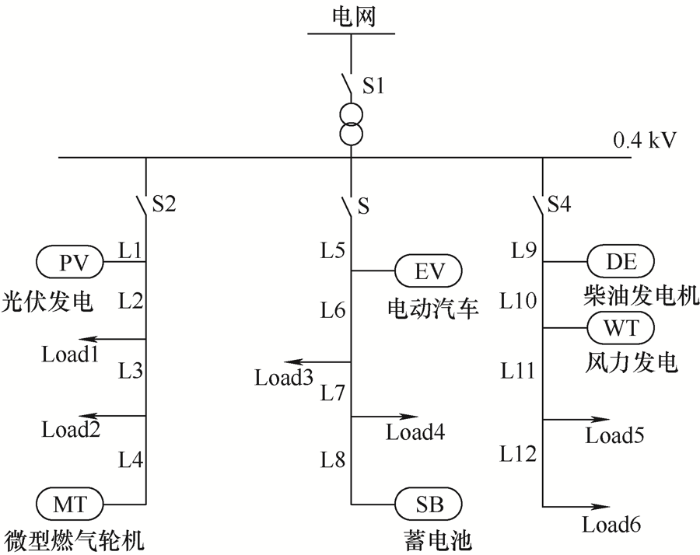
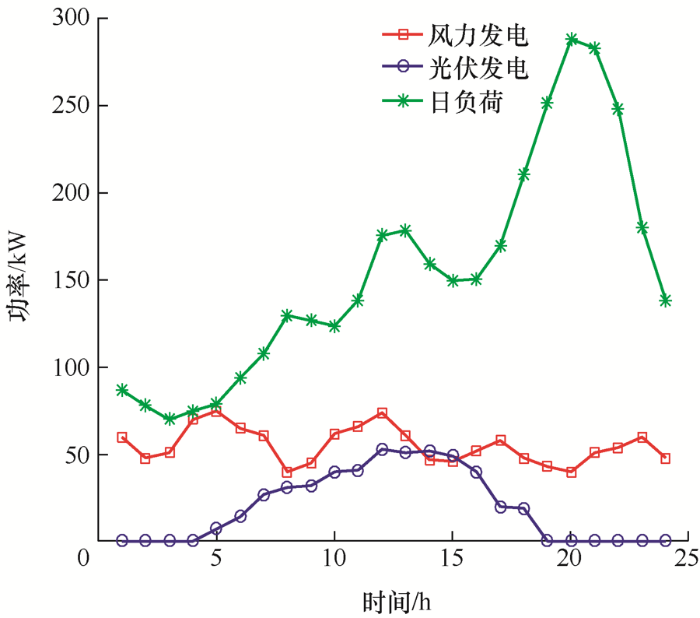
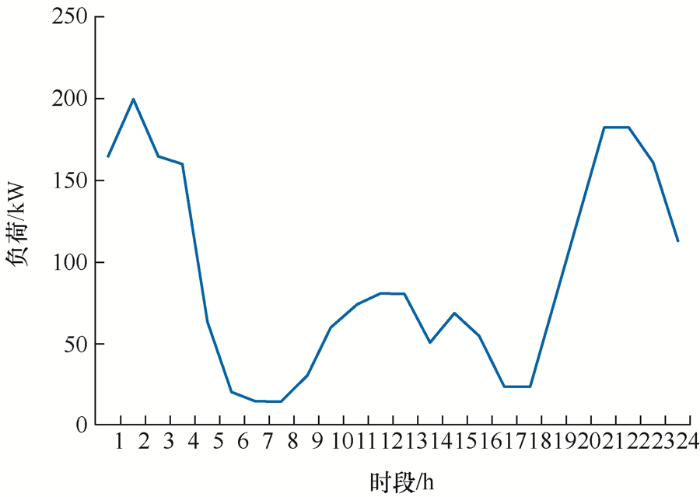
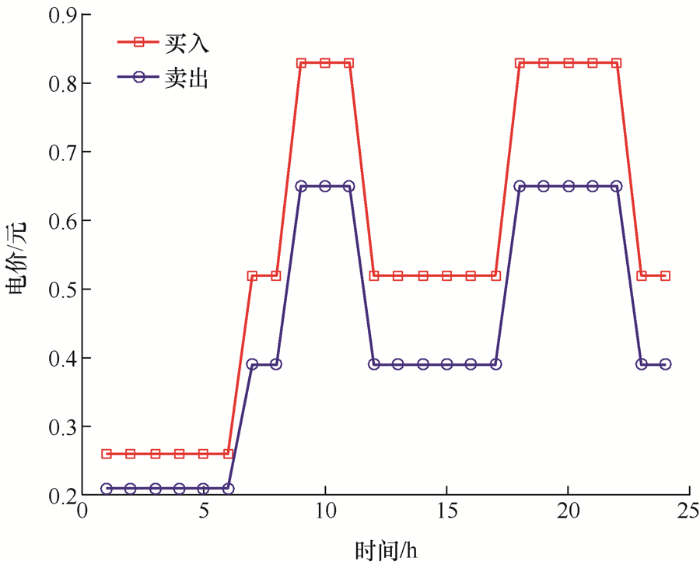
本文选取某地微电网系统进行仿真分析,该系统包括了风力发电、光伏发电以及其他微源发电,并计及了电动汽车,微电网接线如图2 所示,其中L1~12为线路名称,Load1~6为负荷名称。微电网24 h日负荷预测数据以及风光发电的功率如图3 所示。微电网与电网最大交互功率为200 kW,蓄电池容量200 A·h,最大功率40 kW,最大充电功率10 kW,蓄电池荷电状态限制为0.15~0.85。假设微电网中接入的电动汽车数量为70辆,对有序参与充放电的电动汽车用户给予每度电补贴0.43元,对70辆蓄电池SOC范围为0.25~0.9,容量为30 kW·h,充放电功率限值为5 kW的家庭电动汽车充放电负荷情况进行模拟,微电网中有序充放电的电动汽车比例λ =0.5,考虑分时电价的情况下,24 h内电动汽车负荷曲线如图4 所示。表1 为系统中其他各微源的配置参数。
图2
图3
图4
图5
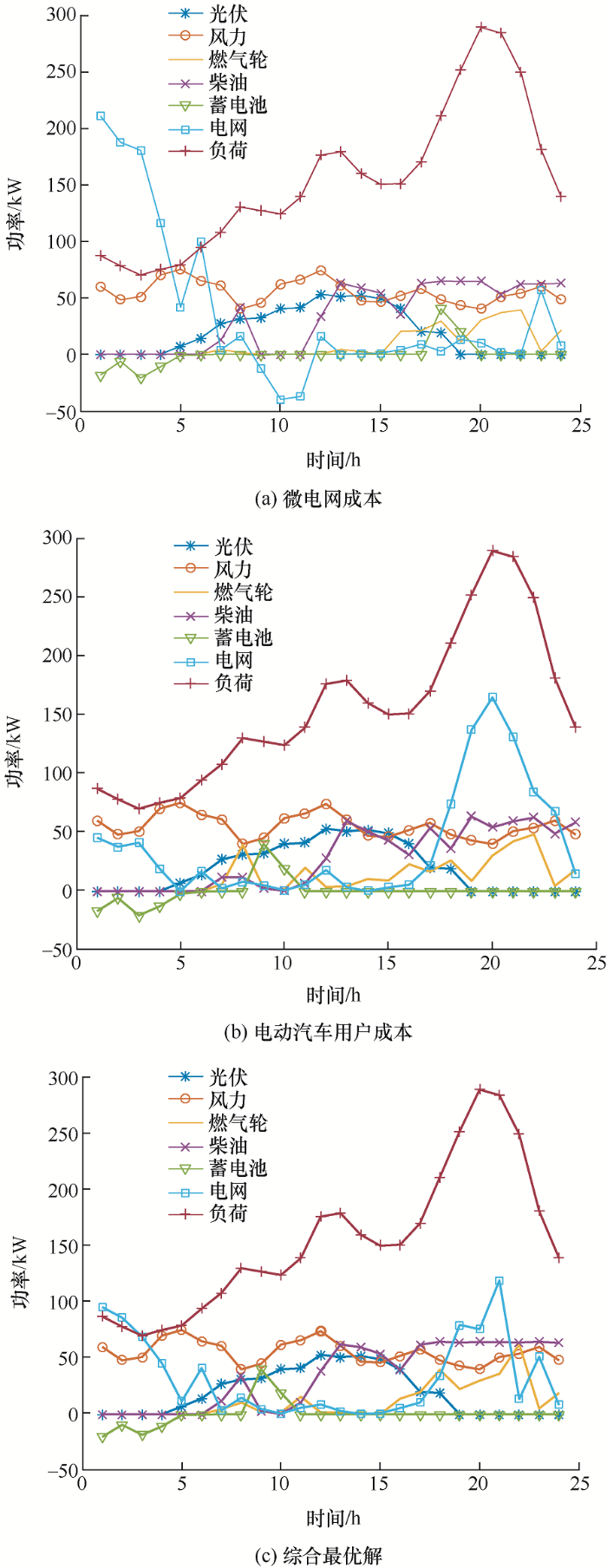
考虑经济成本的情况下,在满足系统负荷需求前提下,风光出力因其无污染低成本,将被优先消耗,其余发电单元根据负荷情况进行出力。为验证基于Levy飞行改进的NSGA-II算法对求解微电网调度优化问题的实际效果,将其与标准NSGA-II算法进行对比,基于Levy飞行改进的NSGA-II算法的求解速度更快,且求得的最优值更小,更加符合综合经济优化的目的,图6 为分别以微电网成本和用户成本以及其目标折衷解为目标优化所得出力结果。
图6
图6
基于Levy改进的NSGA-II算法最优解微源出力
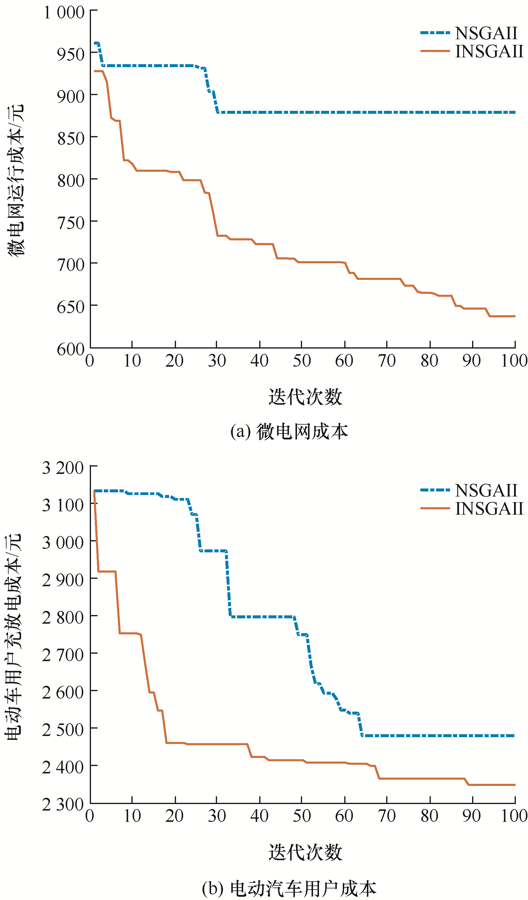
优化后各目标函数与标准算法比较都有不同幅度的下降,由图6 可以看出,各时段燃气轮机,柴油发电机出力结果大体相同;谷时段(1:00—6:00),此时负荷需求较小,燃气轮机、风力发电与购电足以满足负荷,蓄电池对多余电量储存备用;峰时段(18:00—21:00),负荷需求也达到峰值,增加各微源出力的同时若考虑到用户成本则向电网售电来保障用户利益;平时段则会优先使用风光等清洁能源来达到成本最优,当风力光伏力下降时,蓄电池放电来补充负荷需求,以单一目标一优化时,用户成本会明显提高,而当以用户成本为目标时,微电网成本则会相对提高,当对三个目标同时优化时,各目标函数都处于各单一函数值之间,较好地综合两个目标进行优化,微电网最小运行成本及电动汽车用户最小成本的迭代过程如图7 所示。
图7
图7 中图例NSGAII表示标准NSGA-II算法,lNSGAII表示基于Levy飞行改进的NSGA-II算法。电动汽车的有序充放电行为对微电网运行成本与用户充放电成本起到了积极作用,提升了微电网整体经济效益,避免了电动汽车随机性的大规模充电行为而带来的负荷峰值的大大增加。从图7a 可以看出,使用标准NSGA-II算法的微电网运行成本为879.4元,而使用改进后的NSGA-II算法运行成本为637.1元,减少了27.55%,同时,由图7b 可以看出,使用标准NSGA-II算法的用户成本为2 483元,而使用改进的NSGA-II算法后成本为2 352元,用户充放电成本减少了5.28%,因此采用改进的NSGA-II算法不仅求解速度更快,且求得的最优值更小,可以有效地节约成本,更贴合经济优化的目的,给微电网带来更大的收益。
5 结论
本文以微电网运行优化为出发点,在微电网中各微源数学模型的基础上建立了加入电动汽车的数学模型,以微电网综合运营成本与电动汽车用户成本为目标函数,计及功率平衡与微源出力等约束以及电动汽车的有序充放电行为,因电动汽车参与V2G,用户可以在峰谷电价的指导下选择在合适的时间进行充电,使用户成本及微电网的运行成本与稳定性得到明显改善,有效减小峰值负荷,起到了削峰填谷的作用。同时提出了基于Levy飞行的NSGA-II算法,对该模型进行求解,通过引入Levy飞行策略生成新的子种群并与传统NSGA-II的子代种群合并,来增强种群多样性,加强探索能力。结果表明:① 改进后的NSGA-II算法与传统的相比,求解速度更快;② 能够显著降低成本函数,更符合经济优化的目的,体现出了本文算法的优越性与实用性,能够带来更好的经济效益,可以为微电网调度问题提供很好的参考。
参考文献
View Option
[2]
杨新法 , 苏剑 , 吕志鹏 , 等 . 微电网技术综述
[J]. 中国电机工程学报 , 2014 , 34 (1 ):57 -70 .
[本文引用: 1]
YANG Xinfa SU Jian LÜ Zhipeng Overview on micro-grid technology
[J]. Proceedings of the CSEE , 2014 , 34 (1 ):57 -70 .
[本文引用: 1]
[3]
ESPINA E LLANOS J BURGOS-MELLADO C et al . Distributed control strategies for microgrids:An overview
[J]. IEEE Access , 2020 , 8 :193412 -193448 .
DOI:10.1109/Access.6287639
URL
[本文引用: 1]
[4]
崔杨 , 刘柏岩 , 仲悟之 , 等 . 考虑积压惩罚机制的含BSS微网联合系统优化调度策略
[J]. 电网技术 , 2020 , 44 (10 ):3787 -3793 .
[本文引用: 1]
CUI Yang LIU Baiyan ZHONG Wuzhi et al . Optimal scheduling strategy for joint system with micro-grid containing BSS considering overstock punishment mechanism
[J]. Power System Technology , 2020 , 44 (10 ):3787 -3793 .
[本文引用: 1]
[5]
侯慧 , 薛梦雅 , 陈国炎 , 等 . 计及电动汽车充放电的微电网多目标分级经济调度
[J]. 电力系统自动化 , 2019 , 43 (17 ):55 -62 .
[本文引用: 1]
HOU Hui XUE Mengya CHEN Guoyan et al . Multi-objective hierarchical economic dispatching of microgrid including charging and discharging of electric vehicles
[J]. Automation of Electric Power Systems , 2019 , 43 (17 ):55 -62 .
[本文引用: 1]
[6]
刘晓飞 , 张千帆 , 崔淑梅 . 电动汽车V2G技术综述
[J]. 电工技术学报 , 2012 , 27 (2 ):121 -127 .
[本文引用: 1]
LIU Xiaofei ZHANG Qianfan CUI Shumei et al . Review of electric vehicle V2G technology
[J]. Transactions of China Electrotechnical Society , 2012 , 27 (2 ):121 -127 .
[本文引用: 1]
[7]
陈洁 , 杨秀 , 朱兰 , 等 . 微网多目标经济调度优化
[J]. 中国电机工程学报 , 2013 , 33 (19 ):57 -66 .
[本文引用: 1]
CHEN Jie YANG Xiu ZHU Lan et al . Microgrid multi-objective economic dispatch optimization
[J]. Proceedings of the CSEE , 2013 , 33 (19 ):57 -66 .
[本文引用: 1]
[8]
徐从启 , 高瑞林 , 贾桂芝 , 等 . 考虑分时电价电动汽车负荷的微电网优化调度
[J]. 电气工程学报 , 2017 , 12 (11 ):12 -20 .
[本文引用: 1]
XU Congqi GAO Ruilin JIA Guizhi et al . Scheduling of micro-grid considering electrical vehicles of time-of-use tariffs
[J]. Journal of Electrical Engineering , 2017 , 12 (11 ):12 -20 .
[本文引用: 1]
[9]
ZHENG J H WU C Q HUANG J et al . Multi-objective optimization for coordinated day-ahead scheduling problemof integrated electricity-natural gas system with microgrid
[J]. IEEE Access , 2020 , 8 :86788 -86796 .
DOI:10.1109/Access.6287639
URL
[本文引用: 1]
[10]
陈恒安 , 管霖 , 卢操 , 等 . 新能源发电为主电源的独立微网多目标优化调度模型和算法
[J]. 电网技术 , 2020 , 44 (2 ):664 -674 .
[本文引用: 1]
CHEN Hengan GUAN Lin LU Cao et al . Multi-objective optimal dispatch model and its algorithm in isolated microgrid with renewable energy generation as main power supply
[J]. Power System Technology , 2020 , 44 (2 ):664 -674 .
[本文引用: 1]
[11]
张良 , 严正 , 冯冬涵 , 等 . 采用两阶段优化模型的电动汽车充电站内有序充电策略
[J]. 电网技术 , 2014 , 38 (4 ): 967 -973 .
[本文引用: 1]
ZHANG Liang YAN Zheng FENG Donghan et al . Two-stage optimization model based coordinated charging for EV charging station
[J]. Power System Technology , 2014 , 38 (4 ):967 -973 .
[本文引用: 1]
[12]
丁明 , 潘浩 , 张晶晶 . 分布式电源接入交直流混合微电网群优化规划研究
[J]. 太阳能学报 , 2021 , 42 (6 ):54 -62 .
[本文引用: 1]
DING Ming PAN Hao ZHANG Jingjing et al . Research on group optimization planning of AC-DC hybrid microgrid connected by distributed power supply
[J]. Acta Energiae Solaris Sinica , 2021 , 42 (6 ):54 -62 .
[本文引用: 1]
[13]
陈刚 , 杨毅 , 杨晓梅 , 等 . 基于分布式牛顿法的微电网群分布式优化调度方法
[J]. 电力系统自动化 , 2017 , 41 (21 ):156 -162 .
[本文引用: 1]
CHEN Gang YANG Yi YANG Xiaomei et al . Distributed optimization scheduling method for microgrid cluster based on distributed Newton method
[J]. Automation of Electric Power Systems , 2017 , 41 (21 ):156 -162 .
[本文引用: 1]
[14]
AMAMRA S SHI K DINH T Q et al . Optimal day ahead scheduling for plug-in electric vehicles in an industrial microgrid based on V2G system
[C]// 2019 23rd International Conference on Mechatronics Technology (ICMT) , October 23-26,2019 ,San Francisco, USA. IEEE, 2019 :1 -5 .
[本文引用: 1]
[15]
王璟 , 王利利 , 郭勇 , 等 . 计及电动汽车的微电网经济调度方法
[J]. 电力系统保护与控制 , 2016 , 44 (17 ):111 -117 .
[本文引用: 1]
WANG Jing WANG Lili GUO Yong et al . Microgrid economic dispatch method considering electric vehicles
[J]. Power System Protection and Control , 2016 , 44 (17 ):111 -117 .
[本文引用: 1]
[16]
茆美琴 , 徐锐 . 基于分布式控制的孤岛微网经济调度方法
[J]. 电气工程学报 , 2018 , 13 (9 ):8 -13 .
[本文引用: 1]
MAO Meiqin XU Rui Economic dispatch method for islanding microgrids based on distributed control
[J]. Journal of Electrical Engineering , 2018 , 13 (9 ):8 -13 .
[本文引用: 1]
[17]
张志昌 , 吴健 , 骆钊 , 等 . 计及储能运行特性的独立型交直流混合微网优化调度
[J]. 电力系统自动化 , 2018 , 42 (19 ):118 -125 .
[本文引用: 1]
ZHANG Zhichang WU Jian LUO Zhao et al . Optimal scheduling for independent AC/DC hybrid microgrid considering operation charateristics of energy storage
[J]. Automation of Electric Power Systems , 2018 , 42 (19 ):118 -125 .
[本文引用: 1]
[18]
丁宇劼 . 基于可再生能源与储能系统的微电网模型及其优化运行仿真研究
[J]. 电气工程学报 , 2020 , 15 (1 ):36 -40 .
[本文引用: 1]
DING Yujie Microgrid model with renewable energy and energy storage system and its optimal operation simulation
[J]. Journal of Electrical Engineering , 2020 , 15 (1 ):36 -40 .
[本文引用: 1]
[19]
谭碧飞 , 陈皓勇 , 梁子鹏 , 等 . 基于协同NSGA-Ⅱ的微电网随机多目标经济调度
[J]. 高电压技术 , 2019 , 45 (10 ):3130 -3139 .
[本文引用: 1]
TAN Bifei CHEN Haoyong LIANG Zipeng et al . Stochastic multi-objective economic dispatch of micro-grid based on CoNSGA-II
[J]. High Voltage Engineering , 2019 , 45 (10 ):3130 -3139 .
[本文引用: 1]
[20]
张玉 , 卢子广 , 卢泉 , 等 . 基于Levy飞行改进鸟群算法的光伏直流微电网优化配置研究
[J]. 太阳能学报 , 2021 , 42 (5 ):214 -220 .
[本文引用: 1]
ZHANG Yu LU Ziguang LU Quan et al . Research on optimal configuration of photovoltaic DC microgrid based on Levy flight improved bird swarm algorithm
[J]. Acta Energiae Solaris Sinica , 2021 , 42 (5 ):214 -220 .
[本文引用: 1]
Microgrids management
1
2008
... 微电网是一种小型的发配电系统,能够实现自我控制、保护和管理,可以并网运行或者孤岛运行[1 -2 ] .微电网是大电网的延伸拓展,在城市、工业区、商业区等地区有非常高的应用价值.普及微电网的同时也能够让包括新能源在内的微源大规模接入,微电网能够高效地调用各个微源,以此实现对负荷的可靠供给,使传统电网向智能电网过渡.随着用电需求的急剧增加以及光伏风电等清洁能源越来越多的应用,如何完成提高可靠性、提高运营效率、降低成本的任务[3 ] ,这就对微电网运行提出了更高的要求. ...
微电网技术综述
1
2014
... 微电网是一种小型的发配电系统,能够实现自我控制、保护和管理,可以并网运行或者孤岛运行[1 -2 ] .微电网是大电网的延伸拓展,在城市、工业区、商业区等地区有非常高的应用价值.普及微电网的同时也能够让包括新能源在内的微源大规模接入,微电网能够高效地调用各个微源,以此实现对负荷的可靠供给,使传统电网向智能电网过渡.随着用电需求的急剧增加以及光伏风电等清洁能源越来越多的应用,如何完成提高可靠性、提高运营效率、降低成本的任务[3 ] ,这就对微电网运行提出了更高的要求. ...
Overview on micro-grid technology
1
2014
... 微电网是一种小型的发配电系统,能够实现自我控制、保护和管理,可以并网运行或者孤岛运行[1 -2 ] .微电网是大电网的延伸拓展,在城市、工业区、商业区等地区有非常高的应用价值.普及微电网的同时也能够让包括新能源在内的微源大规模接入,微电网能够高效地调用各个微源,以此实现对负荷的可靠供给,使传统电网向智能电网过渡.随着用电需求的急剧增加以及光伏风电等清洁能源越来越多的应用,如何完成提高可靠性、提高运营效率、降低成本的任务[3 ] ,这就对微电网运行提出了更高的要求. ...
Distributed control strategies for microgrids:An overview
1
2020
... 微电网是一种小型的发配电系统,能够实现自我控制、保护和管理,可以并网运行或者孤岛运行[1 -2 ] .微电网是大电网的延伸拓展,在城市、工业区、商业区等地区有非常高的应用价值.普及微电网的同时也能够让包括新能源在内的微源大规模接入,微电网能够高效地调用各个微源,以此实现对负荷的可靠供给,使传统电网向智能电网过渡.随着用电需求的急剧增加以及光伏风电等清洁能源越来越多的应用,如何完成提高可靠性、提高运营效率、降低成本的任务[3 ] ,这就对微电网运行提出了更高的要求. ...
考虑积压惩罚机制的含BSS微网联合系统优化调度策略
1
2020
... 此外,电动汽车(Electric vehicle, EV)也已经进入大众的生活,近年来,中国在新能源汽车的研发与推广方面领先全球[4 ] .随着电动汽车的普及与发展,将能大大缓解我国对石油进口的依赖程度,预计到2025年电动汽车的销量将占总汽车销量的25%.电动汽车本身具有的时空特性所带来的充电不确定性将会使负荷曲线恶化并且增加负荷峰值,这也为微电网稳定运行带来了风险.近年来得到普及的V2G (Vehicle-to-grid)技术,旨在使电动汽车参与到微电网运行调度中,起到缓解电网压力的作用[5 ] .V2G技术是指在电网负荷高时,将电动汽车电池的电能卖给电网,而当电网负荷低时,则为电动汽车蓄电池充电,从而使车主获得收益,是一种有序的车网互动[6 ] .电动汽车作为能够移动的储能单元,在调整电网负荷等方面起到积极作用,同时也因其不可预测性而对电网提出了挑战.文献[7 ]通过采用最大模糊满意度将多目标优化问题转化为单目标优化问题,并运用改进遗传算法进行仿真优化.文献[8 ]通过计及分时电价来对微电网中的电动汽车进行优化调度,并采用权重粒子群算法验证方案得到了最优调度策略.文献[9 ]提出一种在原有的NSGA-Ⅲ算法中引入了加速差分进化、Levy搜索策略和对众多复杂约束的处理机制,有效地解决了考虑多约束条件的多目标优化问题. ...
Optimal scheduling strategy for joint system with micro-grid containing BSS considering overstock punishment mechanism
1
2020
... 此外,电动汽车(Electric vehicle, EV)也已经进入大众的生活,近年来,中国在新能源汽车的研发与推广方面领先全球[4 ] .随着电动汽车的普及与发展,将能大大缓解我国对石油进口的依赖程度,预计到2025年电动汽车的销量将占总汽车销量的25%.电动汽车本身具有的时空特性所带来的充电不确定性将会使负荷曲线恶化并且增加负荷峰值,这也为微电网稳定运行带来了风险.近年来得到普及的V2G (Vehicle-to-grid)技术,旨在使电动汽车参与到微电网运行调度中,起到缓解电网压力的作用[5 ] .V2G技术是指在电网负荷高时,将电动汽车电池的电能卖给电网,而当电网负荷低时,则为电动汽车蓄电池充电,从而使车主获得收益,是一种有序的车网互动[6 ] .电动汽车作为能够移动的储能单元,在调整电网负荷等方面起到积极作用,同时也因其不可预测性而对电网提出了挑战.文献[7 ]通过采用最大模糊满意度将多目标优化问题转化为单目标优化问题,并运用改进遗传算法进行仿真优化.文献[8 ]通过计及分时电价来对微电网中的电动汽车进行优化调度,并采用权重粒子群算法验证方案得到了最优调度策略.文献[9 ]提出一种在原有的NSGA-Ⅲ算法中引入了加速差分进化、Levy搜索策略和对众多复杂约束的处理机制,有效地解决了考虑多约束条件的多目标优化问题. ...
计及电动汽车充放电的微电网多目标分级经济调度
1
2019
... 此外,电动汽车(Electric vehicle, EV)也已经进入大众的生活,近年来,中国在新能源汽车的研发与推广方面领先全球[4 ] .随着电动汽车的普及与发展,将能大大缓解我国对石油进口的依赖程度,预计到2025年电动汽车的销量将占总汽车销量的25%.电动汽车本身具有的时空特性所带来的充电不确定性将会使负荷曲线恶化并且增加负荷峰值,这也为微电网稳定运行带来了风险.近年来得到普及的V2G (Vehicle-to-grid)技术,旨在使电动汽车参与到微电网运行调度中,起到缓解电网压力的作用[5 ] .V2G技术是指在电网负荷高时,将电动汽车电池的电能卖给电网,而当电网负荷低时,则为电动汽车蓄电池充电,从而使车主获得收益,是一种有序的车网互动[6 ] .电动汽车作为能够移动的储能单元,在调整电网负荷等方面起到积极作用,同时也因其不可预测性而对电网提出了挑战.文献[7 ]通过采用最大模糊满意度将多目标优化问题转化为单目标优化问题,并运用改进遗传算法进行仿真优化.文献[8 ]通过计及分时电价来对微电网中的电动汽车进行优化调度,并采用权重粒子群算法验证方案得到了最优调度策略.文献[9 ]提出一种在原有的NSGA-Ⅲ算法中引入了加速差分进化、Levy搜索策略和对众多复杂约束的处理机制,有效地解决了考虑多约束条件的多目标优化问题. ...
Multi-objective hierarchical economic dispatching of microgrid including charging and discharging of electric vehicles
1
2019
... 此外,电动汽车(Electric vehicle, EV)也已经进入大众的生活,近年来,中国在新能源汽车的研发与推广方面领先全球[4 ] .随着电动汽车的普及与发展,将能大大缓解我国对石油进口的依赖程度,预计到2025年电动汽车的销量将占总汽车销量的25%.电动汽车本身具有的时空特性所带来的充电不确定性将会使负荷曲线恶化并且增加负荷峰值,这也为微电网稳定运行带来了风险.近年来得到普及的V2G (Vehicle-to-grid)技术,旨在使电动汽车参与到微电网运行调度中,起到缓解电网压力的作用[5 ] .V2G技术是指在电网负荷高时,将电动汽车电池的电能卖给电网,而当电网负荷低时,则为电动汽车蓄电池充电,从而使车主获得收益,是一种有序的车网互动[6 ] .电动汽车作为能够移动的储能单元,在调整电网负荷等方面起到积极作用,同时也因其不可预测性而对电网提出了挑战.文献[7 ]通过采用最大模糊满意度将多目标优化问题转化为单目标优化问题,并运用改进遗传算法进行仿真优化.文献[8 ]通过计及分时电价来对微电网中的电动汽车进行优化调度,并采用权重粒子群算法验证方案得到了最优调度策略.文献[9 ]提出一种在原有的NSGA-Ⅲ算法中引入了加速差分进化、Levy搜索策略和对众多复杂约束的处理机制,有效地解决了考虑多约束条件的多目标优化问题. ...
电动汽车V2G技术综述
1
2012
... 此外,电动汽车(Electric vehicle, EV)也已经进入大众的生活,近年来,中国在新能源汽车的研发与推广方面领先全球[4 ] .随着电动汽车的普及与发展,将能大大缓解我国对石油进口的依赖程度,预计到2025年电动汽车的销量将占总汽车销量的25%.电动汽车本身具有的时空特性所带来的充电不确定性将会使负荷曲线恶化并且增加负荷峰值,这也为微电网稳定运行带来了风险.近年来得到普及的V2G (Vehicle-to-grid)技术,旨在使电动汽车参与到微电网运行调度中,起到缓解电网压力的作用[5 ] .V2G技术是指在电网负荷高时,将电动汽车电池的电能卖给电网,而当电网负荷低时,则为电动汽车蓄电池充电,从而使车主获得收益,是一种有序的车网互动[6 ] .电动汽车作为能够移动的储能单元,在调整电网负荷等方面起到积极作用,同时也因其不可预测性而对电网提出了挑战.文献[7 ]通过采用最大模糊满意度将多目标优化问题转化为单目标优化问题,并运用改进遗传算法进行仿真优化.文献[8 ]通过计及分时电价来对微电网中的电动汽车进行优化调度,并采用权重粒子群算法验证方案得到了最优调度策略.文献[9 ]提出一种在原有的NSGA-Ⅲ算法中引入了加速差分进化、Levy搜索策略和对众多复杂约束的处理机制,有效地解决了考虑多约束条件的多目标优化问题. ...
Review of electric vehicle V2G technology
1
2012
... 此外,电动汽车(Electric vehicle, EV)也已经进入大众的生活,近年来,中国在新能源汽车的研发与推广方面领先全球[4 ] .随着电动汽车的普及与发展,将能大大缓解我国对石油进口的依赖程度,预计到2025年电动汽车的销量将占总汽车销量的25%.电动汽车本身具有的时空特性所带来的充电不确定性将会使负荷曲线恶化并且增加负荷峰值,这也为微电网稳定运行带来了风险.近年来得到普及的V2G (Vehicle-to-grid)技术,旨在使电动汽车参与到微电网运行调度中,起到缓解电网压力的作用[5 ] .V2G技术是指在电网负荷高时,将电动汽车电池的电能卖给电网,而当电网负荷低时,则为电动汽车蓄电池充电,从而使车主获得收益,是一种有序的车网互动[6 ] .电动汽车作为能够移动的储能单元,在调整电网负荷等方面起到积极作用,同时也因其不可预测性而对电网提出了挑战.文献[7 ]通过采用最大模糊满意度将多目标优化问题转化为单目标优化问题,并运用改进遗传算法进行仿真优化.文献[8 ]通过计及分时电价来对微电网中的电动汽车进行优化调度,并采用权重粒子群算法验证方案得到了最优调度策略.文献[9 ]提出一种在原有的NSGA-Ⅲ算法中引入了加速差分进化、Levy搜索策略和对众多复杂约束的处理机制,有效地解决了考虑多约束条件的多目标优化问题. ...
微网多目标经济调度优化
1
2013
... 此外,电动汽车(Electric vehicle, EV)也已经进入大众的生活,近年来,中国在新能源汽车的研发与推广方面领先全球[4 ] .随着电动汽车的普及与发展,将能大大缓解我国对石油进口的依赖程度,预计到2025年电动汽车的销量将占总汽车销量的25%.电动汽车本身具有的时空特性所带来的充电不确定性将会使负荷曲线恶化并且增加负荷峰值,这也为微电网稳定运行带来了风险.近年来得到普及的V2G (Vehicle-to-grid)技术,旨在使电动汽车参与到微电网运行调度中,起到缓解电网压力的作用[5 ] .V2G技术是指在电网负荷高时,将电动汽车电池的电能卖给电网,而当电网负荷低时,则为电动汽车蓄电池充电,从而使车主获得收益,是一种有序的车网互动[6 ] .电动汽车作为能够移动的储能单元,在调整电网负荷等方面起到积极作用,同时也因其不可预测性而对电网提出了挑战.文献[7 ]通过采用最大模糊满意度将多目标优化问题转化为单目标优化问题,并运用改进遗传算法进行仿真优化.文献[8 ]通过计及分时电价来对微电网中的电动汽车进行优化调度,并采用权重粒子群算法验证方案得到了最优调度策略.文献[9 ]提出一种在原有的NSGA-Ⅲ算法中引入了加速差分进化、Levy搜索策略和对众多复杂约束的处理机制,有效地解决了考虑多约束条件的多目标优化问题. ...
Microgrid multi-objective economic dispatch optimization
1
2013
... 此外,电动汽车(Electric vehicle, EV)也已经进入大众的生活,近年来,中国在新能源汽车的研发与推广方面领先全球[4 ] .随着电动汽车的普及与发展,将能大大缓解我国对石油进口的依赖程度,预计到2025年电动汽车的销量将占总汽车销量的25%.电动汽车本身具有的时空特性所带来的充电不确定性将会使负荷曲线恶化并且增加负荷峰值,这也为微电网稳定运行带来了风险.近年来得到普及的V2G (Vehicle-to-grid)技术,旨在使电动汽车参与到微电网运行调度中,起到缓解电网压力的作用[5 ] .V2G技术是指在电网负荷高时,将电动汽车电池的电能卖给电网,而当电网负荷低时,则为电动汽车蓄电池充电,从而使车主获得收益,是一种有序的车网互动[6 ] .电动汽车作为能够移动的储能单元,在调整电网负荷等方面起到积极作用,同时也因其不可预测性而对电网提出了挑战.文献[7 ]通过采用最大模糊满意度将多目标优化问题转化为单目标优化问题,并运用改进遗传算法进行仿真优化.文献[8 ]通过计及分时电价来对微电网中的电动汽车进行优化调度,并采用权重粒子群算法验证方案得到了最优调度策略.文献[9 ]提出一种在原有的NSGA-Ⅲ算法中引入了加速差分进化、Levy搜索策略和对众多复杂约束的处理机制,有效地解决了考虑多约束条件的多目标优化问题. ...
考虑分时电价电动汽车负荷的微电网优化调度
1
2017
... 此外,电动汽车(Electric vehicle, EV)也已经进入大众的生活,近年来,中国在新能源汽车的研发与推广方面领先全球[4 ] .随着电动汽车的普及与发展,将能大大缓解我国对石油进口的依赖程度,预计到2025年电动汽车的销量将占总汽车销量的25%.电动汽车本身具有的时空特性所带来的充电不确定性将会使负荷曲线恶化并且增加负荷峰值,这也为微电网稳定运行带来了风险.近年来得到普及的V2G (Vehicle-to-grid)技术,旨在使电动汽车参与到微电网运行调度中,起到缓解电网压力的作用[5 ] .V2G技术是指在电网负荷高时,将电动汽车电池的电能卖给电网,而当电网负荷低时,则为电动汽车蓄电池充电,从而使车主获得收益,是一种有序的车网互动[6 ] .电动汽车作为能够移动的储能单元,在调整电网负荷等方面起到积极作用,同时也因其不可预测性而对电网提出了挑战.文献[7 ]通过采用最大模糊满意度将多目标优化问题转化为单目标优化问题,并运用改进遗传算法进行仿真优化.文献[8 ]通过计及分时电价来对微电网中的电动汽车进行优化调度,并采用权重粒子群算法验证方案得到了最优调度策略.文献[9 ]提出一种在原有的NSGA-Ⅲ算法中引入了加速差分进化、Levy搜索策略和对众多复杂约束的处理机制,有效地解决了考虑多约束条件的多目标优化问题. ...
Scheduling of micro-grid considering electrical vehicles of time-of-use tariffs
1
2017
... 此外,电动汽车(Electric vehicle, EV)也已经进入大众的生活,近年来,中国在新能源汽车的研发与推广方面领先全球[4 ] .随着电动汽车的普及与发展,将能大大缓解我国对石油进口的依赖程度,预计到2025年电动汽车的销量将占总汽车销量的25%.电动汽车本身具有的时空特性所带来的充电不确定性将会使负荷曲线恶化并且增加负荷峰值,这也为微电网稳定运行带来了风险.近年来得到普及的V2G (Vehicle-to-grid)技术,旨在使电动汽车参与到微电网运行调度中,起到缓解电网压力的作用[5 ] .V2G技术是指在电网负荷高时,将电动汽车电池的电能卖给电网,而当电网负荷低时,则为电动汽车蓄电池充电,从而使车主获得收益,是一种有序的车网互动[6 ] .电动汽车作为能够移动的储能单元,在调整电网负荷等方面起到积极作用,同时也因其不可预测性而对电网提出了挑战.文献[7 ]通过采用最大模糊满意度将多目标优化问题转化为单目标优化问题,并运用改进遗传算法进行仿真优化.文献[8 ]通过计及分时电价来对微电网中的电动汽车进行优化调度,并采用权重粒子群算法验证方案得到了最优调度策略.文献[9 ]提出一种在原有的NSGA-Ⅲ算法中引入了加速差分进化、Levy搜索策略和对众多复杂约束的处理机制,有效地解决了考虑多约束条件的多目标优化问题. ...
Multi-objective optimization for coordinated day-ahead scheduling problemof integrated electricity-natural gas system with microgrid
1
2020
... 此外,电动汽车(Electric vehicle, EV)也已经进入大众的生活,近年来,中国在新能源汽车的研发与推广方面领先全球[4 ] .随着电动汽车的普及与发展,将能大大缓解我国对石油进口的依赖程度,预计到2025年电动汽车的销量将占总汽车销量的25%.电动汽车本身具有的时空特性所带来的充电不确定性将会使负荷曲线恶化并且增加负荷峰值,这也为微电网稳定运行带来了风险.近年来得到普及的V2G (Vehicle-to-grid)技术,旨在使电动汽车参与到微电网运行调度中,起到缓解电网压力的作用[5 ] .V2G技术是指在电网负荷高时,将电动汽车电池的电能卖给电网,而当电网负荷低时,则为电动汽车蓄电池充电,从而使车主获得收益,是一种有序的车网互动[6 ] .电动汽车作为能够移动的储能单元,在调整电网负荷等方面起到积极作用,同时也因其不可预测性而对电网提出了挑战.文献[7 ]通过采用最大模糊满意度将多目标优化问题转化为单目标优化问题,并运用改进遗传算法进行仿真优化.文献[8 ]通过计及分时电价来对微电网中的电动汽车进行优化调度,并采用权重粒子群算法验证方案得到了最优调度策略.文献[9 ]提出一种在原有的NSGA-Ⅲ算法中引入了加速差分进化、Levy搜索策略和对众多复杂约束的处理机制,有效地解决了考虑多约束条件的多目标优化问题. ...
新能源发电为主电源的独立微网多目标优化调度模型和算法
1
2020
... 蓄电池作为储能设备在微电网中占据了重要地位,当其他出力不足时能够补充需求,当负荷较低时,能够存储多余的电量备用,起到了削峰填谷的作用[10 ] ,荷电状态的数学模型可由式(5)表示 ...
Multi-objective optimal dispatch model and its algorithm in isolated microgrid with renewable energy generation as main power supply
1
2020
... 蓄电池作为储能设备在微电网中占据了重要地位,当其他出力不足时能够补充需求,当负荷较低时,能够存储多余的电量备用,起到了削峰填谷的作用[10 ] ,荷电状态的数学模型可由式(5)表示 ...
采用两阶段优化模型的电动汽车充电站内有序充电策略
1
2014
... 电动汽车的行驶特性对其日程及充放电时间有较大影响,电动汽车种类用途多样,其中电动家庭汽车具有数量庞大、随机性较大、调度相对困难等特点.通过对美国交通部统计得出的美国家庭汽车出行数据进行拟合,得到了电动汽车的日程概率密度函数如下[11 ] ...
Two-stage optimization model based coordinated charging for EV charging station
1
2014
... 电动汽车的行驶特性对其日程及充放电时间有较大影响,电动汽车种类用途多样,其中电动家庭汽车具有数量庞大、随机性较大、调度相对困难等特点.通过对美国交通部统计得出的美国家庭汽车出行数据进行拟合,得到了电动汽车的日程概率密度函数如下[11 ] ...
分布式电源接入交直流混合微电网群优化规划研究
1
2021
... 微电网运行成本可用如下函数表示[12 ] ...
Research on group optimization planning of AC-DC hybrid microgrid connected by distributed power supply
1
2021
... 微电网运行成本可用如下函数表示[12 ] ...
基于分布式牛顿法的微电网群分布式优化调度方法
1
2017
... 式中,Ct 为微电网综合运行成本;C ch 、C dm 、C fu 、C grid 、C price 分别为折旧、维护、燃料、交易成本、电价;C k 、P R i F C i d 和l 分别表示折旧率和微电源使用寿命,取d 为0.5.K M i Pi 分别为运行维护费用与微电源i 的发电功率[13 ] . ...
Distributed optimization scheduling method for microgrid cluster based on distributed Newton method
1
2017
... 式中,Ct 为微电网综合运行成本;C ch 、C dm 、C fu 、C grid 、C price 分别为折旧、维护、燃料、交易成本、电价;C k 、P R i F C i d 和l 分别表示折旧率和微电源使用寿命,取d 为0.5.K M i Pi 分别为运行维护费用与微电源i 的发电功率[13 ] . ...
Optimal day ahead scheduling for plug-in electric vehicles in an industrial microgrid based on V2G system
1
2019
... 电动汽车车主成本主要是车主给自家汽车充电所需要电费成本减去其将多余的电卖给电网所获得的收益[14 ] .这样车主通过考虑电价而进行合理充放电就可以达到为电网削峰填谷的效果,其数学模型如下 ...
Microgrid economic dispatch method considering electric vehicles
1
2016
基于分布式控制的孤岛微网经济调度方法
1
2018
Economic dispatch method for islanding microgrids based on distributed control
1
2018
计及储能运行特性的独立型交直流混合微网优化调度
1
2018
Optimal scheduling for independent AC/DC hybrid microgrid considering operation charateristics of energy storage
1
2018
基于可再生能源与储能系统的微电网模型及其优化运行仿真研究
1
2020
... 式中,SOCSB (t )代表蓄电池所带的电荷量;SOCEV (t )代表电动汽车所带的电荷量;SOCSB,min 、SOCSB,max 分别为蓄电池最小和最大剩余电量;SOCEV,min 、SOCEV,max 分别为电动汽车电池容量的下限与上限[18 ] . ...
Microgrid model with renewable energy and energy storage system and its optimal operation simulation
1
2020
... 式中,SOCSB (t )代表蓄电池所带的电荷量;SOCEV (t )代表电动汽车所带的电荷量;SOCSB,min 、SOCSB,max 分别为蓄电池最小和最大剩余电量;SOCEV,min 、SOCEV,max 分别为电动汽车电池容量的下限与上限[18 ] . ...
基于协同NSGA-Ⅱ的微电网随机多目标经济调度
1
2019
... NSGA-II算法是带精英策略的快速非支配排序遗传算法,是基于遗传算法的多目标优化算法[19 ] ,因其全局收敛性好、通用性高,常用于多目标优化中,但随着其迭代次数的增多,其种群多样性不足的缺点就会显现而容易陷入局部最优. ...
Stochastic multi-objective economic dispatch of micro-grid based on CoNSGA-II
1
2019
... NSGA-II算法是带精英策略的快速非支配排序遗传算法,是基于遗传算法的多目标优化算法[19 ] ,因其全局收敛性好、通用性高,常用于多目标优化中,但随着其迭代次数的增多,其种群多样性不足的缺点就会显现而容易陷入局部最优. ...
基于Levy飞行改进鸟群算法的光伏直流微电网优化配置研究
1
2021
... Levy飞行是以法国数学家保罗•莱维命名,表示步长为有相对较高的概率出现大跨步的随机行走.Levy飞行在智能算法的优化中有了广泛应用,如在鸟群算法中通过使用Mantegna算法表示随机Levy步长,并得到位置更新公式,Levy飞行可以扩大搜索空间[20 ] ,所以通过引入Levy飞行可以提高局部和全局搜索能力,增强种群多样性.Levy飞行位置更新公式如下 ...
Research on optimal configuration of photovoltaic DC microgrid based on Levy flight improved bird swarm algorithm
1
2021
... Levy飞行是以法国数学家保罗•莱维命名,表示步长为有相对较高的概率出现大跨步的随机行走.Levy飞行在智能算法的优化中有了广泛应用,如在鸟群算法中通过使用Mantegna算法表示随机Levy步长,并得到位置更新公式,Levy飞行可以扩大搜索空间[20 ] ,所以通过引入Levy飞行可以提高局部和全局搜索能力,增强种群多样性.Levy飞行位置更新公式如下 ...