1 引言
需求响应(Demand response,DR)的出现改变了以往只针对发电侧资源进行优化调度的局面,从而将需求侧负荷作为一种调度资源来缓解不同时段电力供需不平衡问题。随着需求响应越来越多地参与到综合能源系统调度中,其不确定性对综合能源系统的影响也越来越大[1 ] 。因此,应尽可能地减少需求响应的不确定性,充分发挥负荷侧调度优势。
综合运营商通过价格型和激励型两种激励政策使用户参与系统调度,平抑不确定性能源接入波动带来的影响[2 ] 。但是不同于常规确定性电源的出力响应,用户需求响应的参与程度受诸多因素的影响,在实施过程中可能存在用户违反合同约束、用电行为改变、自身主观疏忽等原因,造成实际的响应程度具有较大的不确定性[3 ] 。文献[4 ]通过建立DR的云模型,验证了不同激励政策下响应波动量的变化特征。因此,考虑需求响应不确定性的调度问题是近年来许多学者越来越关注的问题。
目前,针对综合能源系统中的不确定性问题大多采用模糊机会约束进行处理。文献[5 ]通过将源荷两侧的不确定性问题转化成概率的形式,尽可能地将需求响应不确定量转化成确定的形式,建立模糊随机日前优化调度模型。文献[6 ]考虑源荷两侧的不确定性问题,建立了一种刚性负荷与弹性负荷相结合的多时间尺度互动决策模型。文献[7 ]通过将负荷的种类进行划分,并将一天24 h分成不同的时段,建立了一种负荷响应分段参与的多时间源荷调度策略,充分发挥负荷侧响应潜力。在以上考虑需求响应不确定性的综合能源系统研究中,系统调度模型中功率平衡条件往往基于预测功率,在实际情景发生之前,预测功率往往存在或大或小的误差;或只考虑了需求响应对各备用功率或线路传输容量的影响,没有考虑需求响应不确定性对于调度过程中功率平衡的影响。因此,本文将构造考虑需求响应不确定性和含有负荷预测误差的功率平衡方程,建立计及相关机会规划的综合能源系统优化调度模型,并利用粒子群优化算法[8 ] 对模型进行求解。
2 需求响应不确定性分析
2.1 考虑需求响应不确定性的功率方程
现有考虑需求响应不确定性的综合能源系统研究中,系统的功率平衡约束往往采用预测值[6 -7 ,9 ] 。但是在实际调度过程中,用户的响应率是有波动的。随着综合能源系统中需求响应的应用不断增多,其不确定性是导致综合能源系统不确定性的重要原因[10 ] 。
从另一个方面来看,需求响应是改变用户固有用电习惯,通过减少或推移某时段的用电负荷达到响应电力供应的目的,可以当成一个虚拟出力,因此在功率方程中,系统的电能供应侧计入需求响应削减功率,即
(1) ${{P}_{cc}}(t)+{{P}_{cp}}(t)+{{P}_{es}}(t)+\sum\limits_{i=1}^{n}{{{P}_{dr,i(t)}}}={{P}_{load}}(t)$
式中,Pcc (t )为t 时刻与上级电网的交互功率;Pcp (t )为t 时刻燃气轮机的发电功率;Pes (t )为t 时刻储能装置功率;$\sum\limits_{i=1}^{n}{{{P}_{dr,i(t)}}}$ n 个响应设备t 时刻的预期削减功率之和;Pload (t )为t 时刻负荷预测功率。
随着电力市场改革的不断深入,传统的需求侧管理措施的实施基础发生了改变。综合能源系统的利益主体朝着多元化发展,需求侧能源的管理也逐渐被重视,在综合能源系统中引入需求响应是电力市场发展的必然要求[11 ] 。综合运营商任何调度策略需要时刻满足系统功率平衡约束,因此在考虑需求响应不确定性和负荷的预测误差的综合能源系统中,严格的功率平衡方程为
(2) ${{P}_{cc}}(t)+{{P}_{cp}}(t)+{{P}_{es}}(t)+\sum\limits_{i=1}^{n}{{{P}_{dr,i(t)}}}+{{\partial }^{d}}(t)\text{=}{{P}_{load}}(t)+{{\partial }^{l}}(t)$
式中,${{\partial }^{d}}(t)$ ${{\partial }^{l}}(t)$ t 时刻负荷预测误差。
上述两个功率平衡式中,式(1)忽略预测误差是目前考虑需求响应调度常用的模型,但不能应对需求响应不确定性对于系统功率平衡的影响。式(2)由于含有不确定性变量,无法直接求解[12 ] 。因此,本文在考虑需求响应不确定性和负荷预测误差基础上,利用相关机会规划方法对含有不确定性变量的方程进行建模求解,将等式约束转换为不等式约束,即
(3) $\begin{matrix} |{{P}_{cc}}(t)+{{P}_{cp}}(t)+{{P}_{es}}(t)+\sum\limits_{i=1}^{n}{{{P}_{dr,i(t)}}}+ \\ {{\partial }^{d}}(t)-{{P}_{load}}(t)-{{\partial }^{l}}(t)|\le {{\sigma }_{t}} \\\end{matrix}$
式中,${{\sigma }_{t}}$
式(3)定义了不确定环境下的可行集,其中确定性变量和不确定性变量共同作用下使机会函数以某一概率成立,通过${{\sigma }_{t}}$
(4) $\begin{matrix} \max \Pr \{|{{P}_{cc}}(t)+{{P}_{cp}}(t)+{{P}_{es}}(t)+ \\ \sum\limits_{i=1}^{n}{{{P}_{dr,i(t)}}}+{{\partial }^{d}}(t)-{{P}_{load}}(t)-{{\partial }^{l}}(t)|\le {{\sigma }_{t}}\} \\\end{matrix}$
式中,Pr{·}表示不确定事件的成立的概率。通过调整误差常量${{\sigma }_{t}}$ [13 ] 。其核心思想是使不确定事件的机会函数在不确定环境下成立的可能性最大[14 ] ,从而得到问题的最优解。
2.2 需求响应不确定性分析
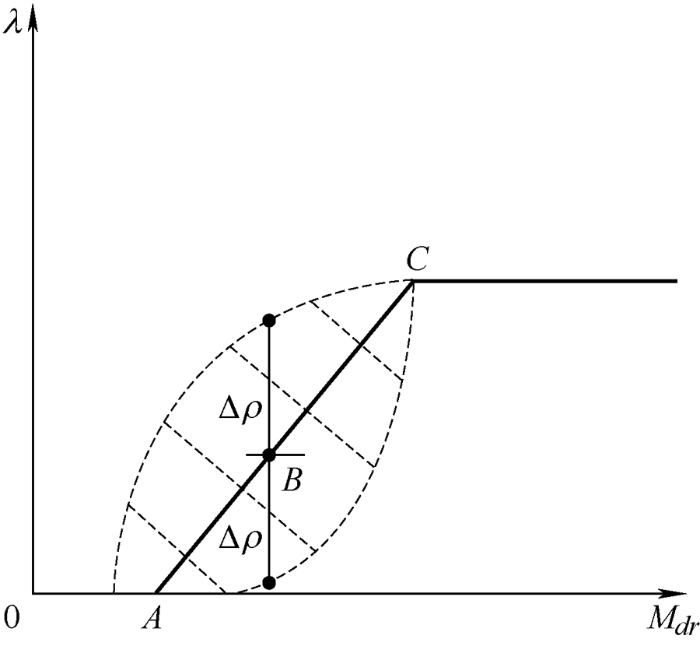
激励水平是影响需求响应波动量的主要因素,用户的响应心理及响应的积极程度很大程度上取决于综合运营商给予的补偿政策。图1 是需求响应量$\lambda $ ρ 与激励水平Mdr 的关系。图1 中实线部分为需求响应的期望值,虚线部分是需求响应不确定性波动量。
图1
可以看出当激励水平在[0, A ]区间时,由于激励水平较低,用户响应意愿几乎为零。在[A , C ]区间随着激励水平的不断增大,用户响应量不断增加。在达到C 点时,用户响应量达到饱和,负荷的响应潜力已被完全挖掘。图1 中的B 点是需求响应波动量Δρ 大小变化的分界点:在[A , B ]区间,随着激励水平Mdr 的增大,响应的波动量也不断增强,在B 点达到最大;随后在[B , C ]区间里,响应波动量随着激励水平的增大而减小,在达到C 点时由于负荷潜力的充分挖掘,响应波动量几乎为零。因此,在保证足够需求响应量和响应波动量随着激励价格的增大而降低的前提下,综合能源系统运营商给予的补偿电价应该在[B , C ]区间内。文献[4 ]通过建立需求响应云模型,验证不同激励价格下经济成本,从而得到了一个最优补偿电价。因此,当确定某一激励政策时,需求响应波动量的上下限也随之确定。
3 基于相关机会规划的IDR调度模型
3.1 目标函数
建立考虑需求响应不确定性的综合能源系统优化调度模型,将式(4)转化为目标函数f 1 ,即
(5) $\begin{matrix} {{f}_{1}}=\max \Pr \{|{{P}_{cc}}(t)+{{P}_{cp}}(t)+{{P}_{es}}(t)+{{\partial }^{d}}(t) \\ \sum\limits_{i=1}^{n}{{{P}_{dr,i(t)}}}-{{P}_{load}}(t)-{{\partial }^{l}}(t)|\le {{\sigma }_{t}}\} \\\end{matrix}$
考虑需求响应的综合能源系统是充分利用可平移或可转移负荷的性质,最终目标是降低经济性成本,其目标函数可用f 2 表示,即
(6) ${{f}_{2}}=\min \sum\limits_{t=1}^{24}{\left[ {{C}_{cp}}(t)+{{C}_{es}}(t)+{{C}_{cc}}(t) \right]}+\sum\limits_{i}^{n}{\sum\limits_{t=1}^{24}{\left[ {{C}_{dr,i(t)}} \right]}}$
式中,Ccp (t )为t 时刻燃气轮机成本;Ces (t )为t 时刻储能装置接受电网调度时需要支付的成本;Ccc (t )为t 时刻的购电成本;Cdr , i ( t ) 是电力需求响应成本,由需求响应协议决定用户的经济补偿。补偿成本的二次函数为
(7) ${{C}_{dr,i(t)}}\text{=}{{a}_{dr,i}}{{P}^{2}}_{dr,i(t)}+{{b}_{dr,i}}{{P}_{dr,i(t)}}$
式中,${{a}_{dr,i}}$ i 个激励型需求响应补偿的二次项系数;${{b}_{dr,i}}$ i 个激励型需求响应补偿的一次项系数[9 ] 。
3.2 约束条件
(8) $\left\{ \begin{align} & P_{cp}^{\min }\le {{P}_{_{mt}}}(t)\le P_{cp}^{\max } \\ & {{P}_{cp}}(t)-{{P}_{_{cp}}}(t-1)\le U_{cp,r}^{{}} \\ & {{P}_{cp}}(t-1)-{{P}_{cp}}(t)\le {{D}_{cp,r}} \\\end{align} \right.$
式中,$P_{cp}^{\max }$ $P_{cp}^{\min }$ $U_{cp,r}^{{}}$ ${{D}_{cp,r}}$
(9) $P_{cp}^{t}=\lambda G_{cp}^{t}$
式中,$P_{cp}^{t}$ t 时刻燃气轮机的发电功率;λ 为燃气轮机的转换效率;$G_{cp}^{t}$ t 时刻燃气的输入功率。
(10) $\left\{ \begin{align} & P_{es}^{\min }\le {{P}_{es}}(t)\le P_{es}^{\max } \\ & SO{{C}_{\min }}\le SOC(t)\le SO{{C}_{\max }} \\\end{align} \right.$
式中,$P_{es}^{\max }$ $P_{es}^{\min }$ max 、SOCm in 分别为储能装置的最大、最小荷电状态[15 ] 。储能装置的模型表达式为
(11) $E_{t}^{s}=(1-{{\eta }_{loss}})E_{t-1}^{s}+r{{\eta }_{es}}P_{t}^{es}$
式中,$E_{t}^{s}$ t 时刻存储的能量;$E_{t-1}^{s}$ t- 1时刻存储的能量;${{\eta }_{loss}}$ $P_{t}^{es}$ t 时刻充放电能量。
(12) $P_{cc}^{\min }\le {{P}_{cc}}(t)\le P_{cc}^{\max }$
式中,$P_{cc}^{\max }$ $P_{cc}^{\min }$
(13) ${{r}_{k1}}{{P}_{dr,i(t)}}\le {{\partial }^{d}}(t)\le {{r}_{k2}}{{P}_{dr,i(t)}}$
式中,${{r}_{k1}}$ ${{r}_{k2}}$
3.3 求解算法
由建模过程可知,上述建立的模型是一个多目标的优化调度模型。本文采用目标规划中序贯算法的求解思路[16 ] ,按照优先级的先后顺序,将多目标规划求解划分为一系列单目标规划,即每次的目标函数只处理一个目标。将此前求解的优先级更高的目标结果作为一个约束条件,可描述为
(14) $\left\{ \begin{align} & \min {{W}_{1}}\sum\limits_{i=1}^{T}{({{\sigma }_{t}}^{\text{+}}+{{\sigma }_{t}}^{-})+{{W}_{2}}\sum\limits_{i=1}^{T}{(d_{2}^{+}+d_{2}^{-})}} \\ & s.t.\ \ {{f}_{1}}+{{\sigma }_{t}}^{\text{+}}-{{\sigma }_{t}}^{-}=f_{1}^{*} \\ & \ \ \ \ \ {{f}_{2}}+d_{2}^{+}-d_{2}^{-}=f_{2}^{*} \\ & \ \ \ \ \ d_{1}^{+},d_{1}^{-},d_{2}^{+},d_{2}^{-}\ge 0 \\\end{align} \right.$
式中,W 1 、W 2 为优先因子,决定多目标优化中各个目标函数所占的权重;$f_{1}^{*}$ $f_{2}^{*}$ $\sigma _{t}^{+}$ $\sigma _{t}^{-}$ $d_{2}^{+}d_{2}^{-}$
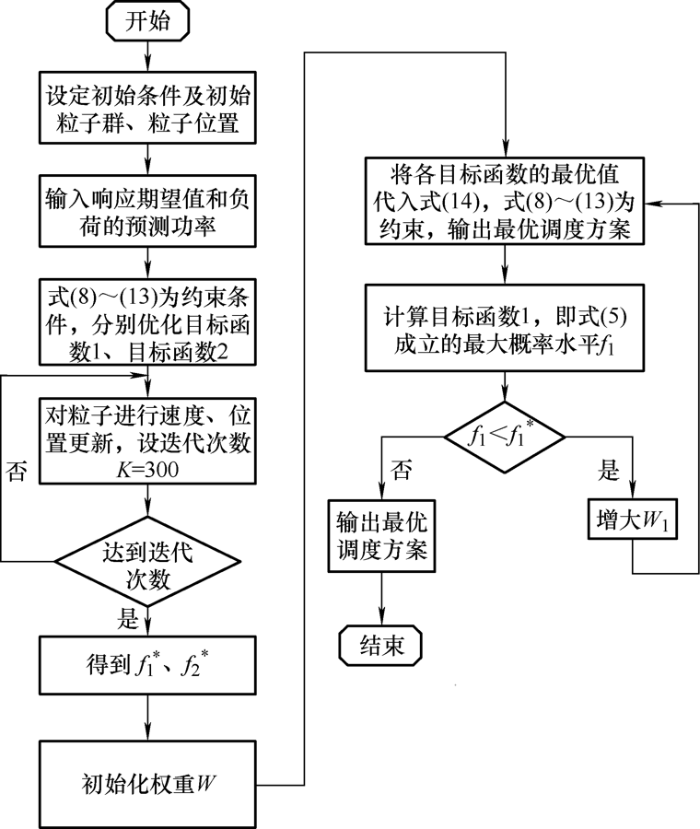
利用粒子群优化算法得到目标函数1、目标函数2的最优解$f_{1}^{*}$ $f_{2}^{*}$ W 1 ,并输出最优的调度方案。图2 为模型求解流程。
图2
4 算例分析
4.1 算例参数
为检验本文所提出模型在综合能源系统调度中的实际效果,选取某社区综合能源系统为仿真算例。调度周期为24 h,以1 h为调度单位。分时能源价格[17 ] 如表1 所示。
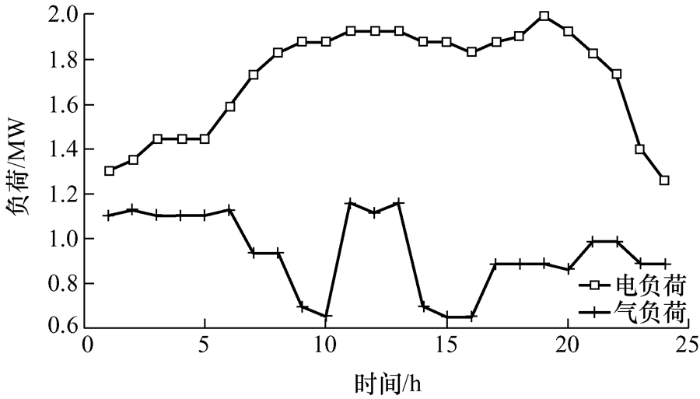
该社区综合能源系统夏季典型日的负荷预测曲线如图3 所示。
图3
图3 所示的电负荷为居民用电负荷,气负荷为燃气轮机的出力用气。该区域白天用电多,夜间用电少,系统的电负荷需求存在明显峰谷现象。为了提升综合运营商经济效益,缓解高峰时段供电紧张的局面,在该社区综合能源系统调度中引入电- 气联合需求响应,实现两种能源互补运行,从而提高能源综合利用效率。
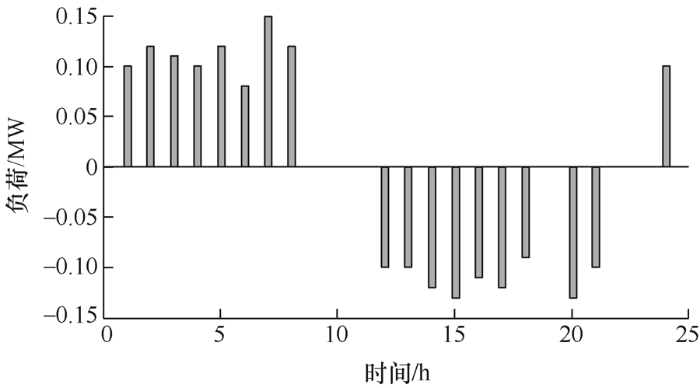
图4 表示各个时段预期需求响应量:在10:00—16:00,18:00—20:00用电高峰段,需求响应量是负荷削减量,在23:00—7:00谷时段,需求响应量是负荷的增加量。
图4
4.2 模型有效性分析
为了验证本文提出模型的合理性,讨论考虑需求响应不确定性和负荷预测误差及相关机会规划方法对综合能源系统运行结果影响,采用以下三种模型进行对比分析,其中模型1、模型2为对比模型,模型3为本文所提模型。三种模型均采用粒子群算法求解。
模型1:忽略需求响应不确定性和负荷预测误差的优化调度模型。
模型2:基于模糊机会约束的考虑需求响应不确定性和负荷预测误差的优化调度模型,置信水平取95%。
模型3:本文提出的模型,基于相关机会规划的考虑需求响应不确定性和负荷预测误差的优化调度模型。
负荷预测误差服从正态分布规律[18 ] ,因此,现有研究中针对负荷预测误差大多采用正态分布来模拟,记为${{\partial }^{l}}$ $N(0,{{\partial }^{2}})$ $\partial $
4.2.1 三种模型仿真结果对比
由表2 可知,模型1的经济成本最高。模型2较模型1相比,经济成本下降0.037万元,模型3与模型1相比,经济成本下降0.189 9万元,这说明在综合能源系统中考虑需求响应不确定性和负荷预测误差可以有效降低经济成本。对比模型3与模型2可知,模型3经济成本下降0.152 9万元,这说明相关机会规划方法相比于模糊机会约束方法求解模型,降低经济成本更为有效。
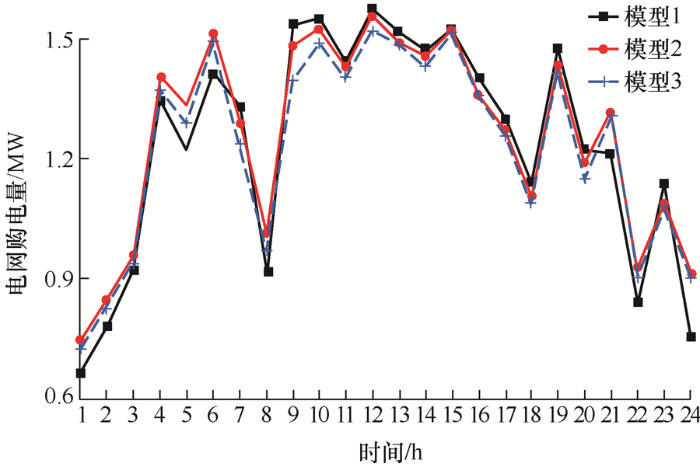
图5 为三种模型各个时段向上级电网的购电量,与模型1相比,模型2、模型3在低谷时段增加了从上级电网的购电量,从而在用电低谷阶段提升能源利用率;在高峰时段降低了从上级电网的购电量,缓解了用电高峰时段供电紧张的局面。另外,模型2为了达到设定的置信水平,各个时段从电网的购电量略大于模型3,以此来满足置信水平,所以模型2的经济成本高于模型3。
图5
4.2.2 模型3的效果分析
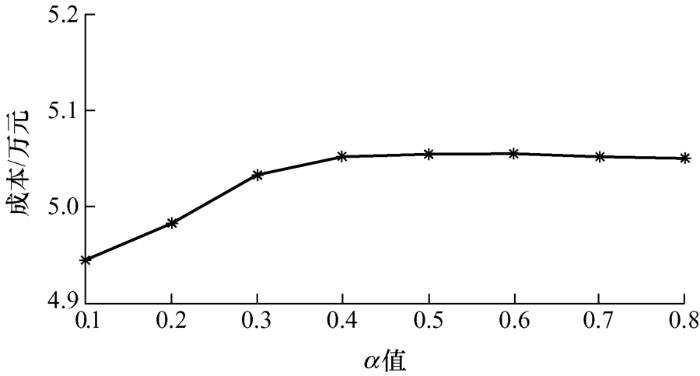
模型3通过相关机会规划方法求解,引入可接受的最小误差α ,即可接受的功率不平衡量,相比于机会约束方法,可以减小系统两端电能的供需偏差,在保证系统稳定运行的同时,降低经济成本。图6 表明随着可接受的功率不平衡量α 的增大,模型3的运行成本随着机会函数成立的概率增大而增大。图6 中当α 在[0.1,0.4]区间取值时,成本会随着α 取值的增加而增大;当α 取值大于0.4时,成本趋于稳定。可以得出α 在0.4左右水平时,机会函数成立的概率接近1。因此,α 在[0.4,0.8]区间随着取值的增大,成本将不再增加。综上,系统运行总成本和机会函数成立的概率水平与功率不平衡量α 有关,因此,调度员可根据实际情况选择合适的功率不平衡量,在风险和利益之间进行权衡,获得最大收益。
图6
5 结论
本文在基于需求响应与综合能源系统联系日益密切的背景下,针对需求响应不确定性和负荷预测误差,建立了考虑需求响应不确定性的综合能源系统优化调度模型,并通过相关算例进行验证,得到了如下结论。
(1) 相关机会规划相对于机会约束处理不确定性问题更加灵活,在得到较高可靠性的同时,降低了常规机组出力,节省了经济成本。
(2) 在同时考虑需求响应不确定性和负荷预测误差的功率平衡模型中,系统的运行成本降低,加强了源荷两侧功率平衡约束的调控能力,提高了综合能源系统运行的灵活性。
参考文献
View Option
[1]
AHMARINEJAD A A multi-objective optimization framework for dynamic planning of energy hub considering integrated demand response program
[J]. Sustainable Cities and Society , 2021 , 74 :103136 .
DOI:10.1016/j.scs.2021.103136
URL
[本文引用: 1]
[2]
孙建军 , 张世泽 , 曾梦迪 , 等 . 考虑分时电价的主动配电网柔性负荷多目标优化控制
[J]. 电工技术学报 , 2018 , 33 (2 ):401 -412 .
[本文引用: 1]
SUN Jianjun ZHANG Shize ZENG Mengdi et al . Multi-objective optimal control for flexible load in active distribution network considering time-of-use tariff
[J]. Transactions of China Electrotechnical Society , 2018 , 33 (2 ):401 -412 .
[本文引用: 1]
[3]
孙宇军 , 李扬 , 王蓓蓓 , 等 . 计及不确定性需求响应的日前调度计划模型
[J]. 电网技术 , 2014 , 38 (10 ):2708 -2714 .
[本文引用: 1]
SUN Yujun LI Yang WANG Beibei et al . A day-ahead scheduling model considering demand response and its uncertainty
[J]. Power System Technology , 2014 , 38 (10 ):2708 -2714 .
[本文引用: 1]
[4]
林俐 , 张玉 . 激励型需求响应参与主动配电网优化调度的不确定性分析
[J]. 华北电力大学学报 , 2020 , 47 (5 ):10 -20 .
[本文引用: 2]
LIN Li ZHANG Yu Uncertainty analysis of incentive demand response participating in optimal scheduling of active distribution networ
[J]. Journal of North China Electric Power University , 2020 , 47 (5 ):10 -20 .
[本文引用: 2]
[5]
李政洁 , 于强 , 龚文杰 , 等 . 计及模糊机会约束的电-气-热能源枢纽多目标优化调度
[J]. 电力系统及其自动化学报 , 2021 , 33 (9 ):49 -56 .
[本文引用: 1]
LI Zhengjie YU Qiang GONG Wenjie et al . Multi-objective optimal operation of electricity-gas-heat energy hub considering fuzzy chance constraint
[J]. Proceedings of the CSU-EPSA , 2021 , 33 (9 ):49 -56 .
[本文引用: 1]
[6]
王子驰 , 雷炳银 , 杨灵艺 , 等 . 考虑电热联合需求响应的区域综合能源系统多目标双层优化调度
[J]. 电力系统及其自动化学报 , 2021 , 33 (7 ):120 -127 .
[本文引用: 2]
WANG Zichi LEI Bingyin YANG Lingyi et al . Multi-objective double-step optimal dispatching of regional integrated energy system considering combined electric and heat demand response
[J]. Proceedings of the CSU-EPSA , 2021 , 33 (7 ):120 -127 .
[本文引用: 2]
[7]
祁江浩 , 李凤婷 , 张高航 . 需求响应分段参与的多时间尺度源荷协调调度策略
[J]. 电力系统保护与控制 , 2021 , 49 (11 ):61 -69 .
[本文引用: 2]
QI Jianghao LI Fengting ZHANG Gaohang Multi-time scale scheduling strategy for source-load coordination considering demand response block participation
[J]. Power System Protection and Control , 2021 , 49 (11 ):61 -69 .
[本文引用: 2]
[8]
SINGH G SINGH A Extension of particle swarm optimization algorithm for solving transportation problem in fuzzy environment
[J]. Applied Soft Computing , 2021 , 110 :107619 .
DOI:10.1016/j.asoc.2021.107619
URL
[本文引用: 1]
[9]
牛文娟 , 李扬 , 王蓓蓓 . 考虑不确定性的需求响应虚拟电厂建模
[J]. 中国电机工程学报 , 2014 , 34 (22 ):3630 -3637 .
[本文引用: 2]
NIU Wenjuan LI Yang WANG Beibei Demand response based virtual power plant modeling considering uncertainty
[J]. Proceedings of the CSEE , 2014 , 34 (22 ):3630 -3637 .
[本文引用: 2]
[10]
VESA A V CIOARA T ANGHEL I et al . Energy flexibility prediction for data center engagement in demand response programs
[J]. Sustainability , 2020 , 12 (4 ):1417 .
DOI:10.3390/su12041417
URL
[本文引用: 1]
[11]
HEYDARI R NIKOUKAR J GANDOMKAR M Optimal operation of virtual power plant with considering the demand response and electric vehicles
[J]. Journal of Electrical Engineering & Technology , 2021 , 16 (5 ):2407 -2419 .
[本文引用: 1]
[12]
HUO Da GU Chenghong GREENWOOD D et al . Chance-constrained optimization for integrated local energy systems operation considering correlated wind generation
[J]. International Journal of Electrical Power & Energy Systems , 2021 , 132 :107153 .
DOI:10.1016/j.ijepes.2021.107153
URL
[本文引用: 1]
[13]
LI Zhiwei JIN Tianran ZHAO Shuqiang et al . Power system day-ahead unit commitment based on chance-constrained dependent chance goal programming
[J]. Energies , 2018 , 11 (7 ):1718 .
DOI:10.3390/en11071718
URL
[本文引用: 1]
[14]
王健鹏 . 相关机会规划的解法及其应用 [D]. 成都 : 西南交通大学 , 2004 .
[本文引用: 1]
WANG Jianpeng The solving method and application of dependent chancce programming [D]. Chengdu : Southwest Jiaotong University , 2004 .
[本文引用: 1]
[15]
朱兰 , 田泽清 , 唐陇军 , 等 . 计及细节层次直接负荷控制的区域综合能源系统多时间尺度优化调度
[J]. 电网技术 , 2021 , 45 (7 ):2763 -2774 .
[本文引用: 1]
ZHU Lan TIAN Zeqing TANG Longjun et al . Multi-time-scale optimal dispatch of regional integrated energy system considering level of detail direct load control
[J]. Power System Technology , 2021 , 45 (7 ):2763 -2774 .
[本文引用: 1]
[16]
PAPAKONSTANTINOU P A Hierarchies for classes of priority algorithms for job scheduling
[J]. Theoretical Computer Science , 2006 , 352 (1-3 ):181 -189 .
DOI:10.1016/j.tcs.2005.10.045
URL
[本文引用: 1]
[17]
李鹏 , 杨莘博 , 李慧璇 , 等 . 计及多能源多需求响应手段的园区综合能源系统优化调度模型
[J]. 电力建设 , 2020 , 41 (5 ):45 -57 .
DOI:10.12204/j.issn.1000-7229.2020.05.006
[本文引用: 1]
清洁能源消纳是影响园区综合能源系统(park integrated energy system, PIES)可持续发展的问题之一,基于此,文章构建了以设计峰谷分时电/热价为依托的综合型价格需求响应模型和以电转气(power to gas, P2G)、电制冷机(electric refrigerator, ER)、电锅炉(electric boiler, EB)为依托的转换型需求响应模型。首先构建了由能源供应中心和能源转换中心构成的耦合冷、热、电、气的园区综合能源系统及其交易策略;其次,在考虑综合型价格和转换型需求响应的基础上,构建了以出力、需求响应前后能量平衡等为约束条件,以系统净收益最大为目标函数的优化调度模型;然后,从经济和环境两方面构建了绩效评估指标;最后,进行了实例分析,验证了所建模型具有提高清洁能源消纳量和系统经济性的作用。
LI Peng YANG Xinbo LI Huixuan et al . Optimal scheduling model of park integrated energy system considering multi energy and multi demand response means
[J]. Electric Power Construction , 2020 , 41 (5 ):45 -57 .
[本文引用: 1]
[18]
周旭 , 包海龙 , 徐凡 , 等 . 计及负荷预测误差的可中断负荷优化管理
[J]. 电力需求侧管理 , 2011 , 13 (2 ):16 -19 ,31.
[本文引用: 1]
ZHOU Xu BAO Hailong XU Fan et al . The interruptible load optimization management considering the load forecast error
[J]. Power Demand Side Management , 2011 , 13 (2 ):16 -19 ,31.
[本文引用: 1]
A multi-objective optimization framework for dynamic planning of energy hub considering integrated demand response program
1
2021
... 需求响应(Demand response,DR)的出现改变了以往只针对发电侧资源进行优化调度的局面,从而将需求侧负荷作为一种调度资源来缓解不同时段电力供需不平衡问题.随着需求响应越来越多地参与到综合能源系统调度中,其不确定性对综合能源系统的影响也越来越大[1 ] .因此,应尽可能地减少需求响应的不确定性,充分发挥负荷侧调度优势. ...
考虑分时电价的主动配电网柔性负荷多目标优化控制
1
2018
... 综合运营商通过价格型和激励型两种激励政策使用户参与系统调度,平抑不确定性能源接入波动带来的影响[2 ] .但是不同于常规确定性电源的出力响应,用户需求响应的参与程度受诸多因素的影响,在实施过程中可能存在用户违反合同约束、用电行为改变、自身主观疏忽等原因,造成实际的响应程度具有较大的不确定性[3 ] .文献[4 ]通过建立DR的云模型,验证了不同激励政策下响应波动量的变化特征.因此,考虑需求响应不确定性的调度问题是近年来许多学者越来越关注的问题. ...
Multi-objective optimal control for flexible load in active distribution network considering time-of-use tariff
1
2018
... 综合运营商通过价格型和激励型两种激励政策使用户参与系统调度,平抑不确定性能源接入波动带来的影响[2 ] .但是不同于常规确定性电源的出力响应,用户需求响应的参与程度受诸多因素的影响,在实施过程中可能存在用户违反合同约束、用电行为改变、自身主观疏忽等原因,造成实际的响应程度具有较大的不确定性[3 ] .文献[4 ]通过建立DR的云模型,验证了不同激励政策下响应波动量的变化特征.因此,考虑需求响应不确定性的调度问题是近年来许多学者越来越关注的问题. ...
计及不确定性需求响应的日前调度计划模型
1
2014
... 综合运营商通过价格型和激励型两种激励政策使用户参与系统调度,平抑不确定性能源接入波动带来的影响[2 ] .但是不同于常规确定性电源的出力响应,用户需求响应的参与程度受诸多因素的影响,在实施过程中可能存在用户违反合同约束、用电行为改变、自身主观疏忽等原因,造成实际的响应程度具有较大的不确定性[3 ] .文献[4 ]通过建立DR的云模型,验证了不同激励政策下响应波动量的变化特征.因此,考虑需求响应不确定性的调度问题是近年来许多学者越来越关注的问题. ...
A day-ahead scheduling model considering demand response and its uncertainty
1
2014
... 综合运营商通过价格型和激励型两种激励政策使用户参与系统调度,平抑不确定性能源接入波动带来的影响[2 ] .但是不同于常规确定性电源的出力响应,用户需求响应的参与程度受诸多因素的影响,在实施过程中可能存在用户违反合同约束、用电行为改变、自身主观疏忽等原因,造成实际的响应程度具有较大的不确定性[3 ] .文献[4 ]通过建立DR的云模型,验证了不同激励政策下响应波动量的变化特征.因此,考虑需求响应不确定性的调度问题是近年来许多学者越来越关注的问题. ...
激励型需求响应参与主动配电网优化调度的不确定性分析
2
2020
... 综合运营商通过价格型和激励型两种激励政策使用户参与系统调度,平抑不确定性能源接入波动带来的影响[2 ] .但是不同于常规确定性电源的出力响应,用户需求响应的参与程度受诸多因素的影响,在实施过程中可能存在用户违反合同约束、用电行为改变、自身主观疏忽等原因,造成实际的响应程度具有较大的不确定性[3 ] .文献[4 ]通过建立DR的云模型,验证了不同激励政策下响应波动量的变化特征.因此,考虑需求响应不确定性的调度问题是近年来许多学者越来越关注的问题. ...
... 可以看出当激励水平在[0, A ]区间时,由于激励水平较低,用户响应意愿几乎为零.在[A , C ]区间随着激励水平的不断增大,用户响应量不断增加.在达到C 点时,用户响应量达到饱和,负荷的响应潜力已被完全挖掘.图1 中的B 点是需求响应波动量Δρ 大小变化的分界点:在[A , B ]区间,随着激励水平Mdr 的增大,响应的波动量也不断增强,在B 点达到最大;随后在[B , C ]区间里,响应波动量随着激励水平的增大而减小,在达到C 点时由于负荷潜力的充分挖掘,响应波动量几乎为零.因此,在保证足够需求响应量和响应波动量随着激励价格的增大而降低的前提下,综合能源系统运营商给予的补偿电价应该在[B , C ]区间内.文献[4 ]通过建立需求响应云模型,验证不同激励价格下经济成本,从而得到了一个最优补偿电价.因此,当确定某一激励政策时,需求响应波动量的上下限也随之确定. ...
Uncertainty analysis of incentive demand response participating in optimal scheduling of active distribution networ
2
2020
... 综合运营商通过价格型和激励型两种激励政策使用户参与系统调度,平抑不确定性能源接入波动带来的影响[2 ] .但是不同于常规确定性电源的出力响应,用户需求响应的参与程度受诸多因素的影响,在实施过程中可能存在用户违反合同约束、用电行为改变、自身主观疏忽等原因,造成实际的响应程度具有较大的不确定性[3 ] .文献[4 ]通过建立DR的云模型,验证了不同激励政策下响应波动量的变化特征.因此,考虑需求响应不确定性的调度问题是近年来许多学者越来越关注的问题. ...
... 可以看出当激励水平在[0, A ]区间时,由于激励水平较低,用户响应意愿几乎为零.在[A , C ]区间随着激励水平的不断增大,用户响应量不断增加.在达到C 点时,用户响应量达到饱和,负荷的响应潜力已被完全挖掘.图1 中的B 点是需求响应波动量Δρ 大小变化的分界点:在[A , B ]区间,随着激励水平Mdr 的增大,响应的波动量也不断增强,在B 点达到最大;随后在[B , C ]区间里,响应波动量随着激励水平的增大而减小,在达到C 点时由于负荷潜力的充分挖掘,响应波动量几乎为零.因此,在保证足够需求响应量和响应波动量随着激励价格的增大而降低的前提下,综合能源系统运营商给予的补偿电价应该在[B , C ]区间内.文献[4 ]通过建立需求响应云模型,验证不同激励价格下经济成本,从而得到了一个最优补偿电价.因此,当确定某一激励政策时,需求响应波动量的上下限也随之确定. ...
计及模糊机会约束的电-气-热能源枢纽多目标优化调度
1
2021
... 目前,针对综合能源系统中的不确定性问题大多采用模糊机会约束进行处理.文献[5 ]通过将源荷两侧的不确定性问题转化成概率的形式,尽可能地将需求响应不确定量转化成确定的形式,建立模糊随机日前优化调度模型.文献[6 ]考虑源荷两侧的不确定性问题,建立了一种刚性负荷与弹性负荷相结合的多时间尺度互动决策模型.文献[7 ]通过将负荷的种类进行划分,并将一天24 h分成不同的时段,建立了一种负荷响应分段参与的多时间源荷调度策略,充分发挥负荷侧响应潜力.在以上考虑需求响应不确定性的综合能源系统研究中,系统调度模型中功率平衡条件往往基于预测功率,在实际情景发生之前,预测功率往往存在或大或小的误差;或只考虑了需求响应对各备用功率或线路传输容量的影响,没有考虑需求响应不确定性对于调度过程中功率平衡的影响.因此,本文将构造考虑需求响应不确定性和含有负荷预测误差的功率平衡方程,建立计及相关机会规划的综合能源系统优化调度模型,并利用粒子群优化算法[8 ] 对模型进行求解. ...
Multi-objective optimal operation of electricity-gas-heat energy hub considering fuzzy chance constraint
1
2021
... 目前,针对综合能源系统中的不确定性问题大多采用模糊机会约束进行处理.文献[5 ]通过将源荷两侧的不确定性问题转化成概率的形式,尽可能地将需求响应不确定量转化成确定的形式,建立模糊随机日前优化调度模型.文献[6 ]考虑源荷两侧的不确定性问题,建立了一种刚性负荷与弹性负荷相结合的多时间尺度互动决策模型.文献[7 ]通过将负荷的种类进行划分,并将一天24 h分成不同的时段,建立了一种负荷响应分段参与的多时间源荷调度策略,充分发挥负荷侧响应潜力.在以上考虑需求响应不确定性的综合能源系统研究中,系统调度模型中功率平衡条件往往基于预测功率,在实际情景发生之前,预测功率往往存在或大或小的误差;或只考虑了需求响应对各备用功率或线路传输容量的影响,没有考虑需求响应不确定性对于调度过程中功率平衡的影响.因此,本文将构造考虑需求响应不确定性和含有负荷预测误差的功率平衡方程,建立计及相关机会规划的综合能源系统优化调度模型,并利用粒子群优化算法[8 ] 对模型进行求解. ...
考虑电热联合需求响应的区域综合能源系统多目标双层优化调度
2
2021
... 目前,针对综合能源系统中的不确定性问题大多采用模糊机会约束进行处理.文献[5 ]通过将源荷两侧的不确定性问题转化成概率的形式,尽可能地将需求响应不确定量转化成确定的形式,建立模糊随机日前优化调度模型.文献[6 ]考虑源荷两侧的不确定性问题,建立了一种刚性负荷与弹性负荷相结合的多时间尺度互动决策模型.文献[7 ]通过将负荷的种类进行划分,并将一天24 h分成不同的时段,建立了一种负荷响应分段参与的多时间源荷调度策略,充分发挥负荷侧响应潜力.在以上考虑需求响应不确定性的综合能源系统研究中,系统调度模型中功率平衡条件往往基于预测功率,在实际情景发生之前,预测功率往往存在或大或小的误差;或只考虑了需求响应对各备用功率或线路传输容量的影响,没有考虑需求响应不确定性对于调度过程中功率平衡的影响.因此,本文将构造考虑需求响应不确定性和含有负荷预测误差的功率平衡方程,建立计及相关机会规划的综合能源系统优化调度模型,并利用粒子群优化算法[8 ] 对模型进行求解. ...
... 现有考虑需求响应不确定性的综合能源系统研究中,系统的功率平衡约束往往采用预测值[6 -7 ,9 ] .但是在实际调度过程中,用户的响应率是有波动的.随着综合能源系统中需求响应的应用不断增多,其不确定性是导致综合能源系统不确定性的重要原因[10 ] . ...
Multi-objective double-step optimal dispatching of regional integrated energy system considering combined electric and heat demand response
2
2021
... 目前,针对综合能源系统中的不确定性问题大多采用模糊机会约束进行处理.文献[5 ]通过将源荷两侧的不确定性问题转化成概率的形式,尽可能地将需求响应不确定量转化成确定的形式,建立模糊随机日前优化调度模型.文献[6 ]考虑源荷两侧的不确定性问题,建立了一种刚性负荷与弹性负荷相结合的多时间尺度互动决策模型.文献[7 ]通过将负荷的种类进行划分,并将一天24 h分成不同的时段,建立了一种负荷响应分段参与的多时间源荷调度策略,充分发挥负荷侧响应潜力.在以上考虑需求响应不确定性的综合能源系统研究中,系统调度模型中功率平衡条件往往基于预测功率,在实际情景发生之前,预测功率往往存在或大或小的误差;或只考虑了需求响应对各备用功率或线路传输容量的影响,没有考虑需求响应不确定性对于调度过程中功率平衡的影响.因此,本文将构造考虑需求响应不确定性和含有负荷预测误差的功率平衡方程,建立计及相关机会规划的综合能源系统优化调度模型,并利用粒子群优化算法[8 ] 对模型进行求解. ...
... 现有考虑需求响应不确定性的综合能源系统研究中,系统的功率平衡约束往往采用预测值[6 -7 ,9 ] .但是在实际调度过程中,用户的响应率是有波动的.随着综合能源系统中需求响应的应用不断增多,其不确定性是导致综合能源系统不确定性的重要原因[10 ] . ...
需求响应分段参与的多时间尺度源荷协调调度策略
2
2021
... 目前,针对综合能源系统中的不确定性问题大多采用模糊机会约束进行处理.文献[5 ]通过将源荷两侧的不确定性问题转化成概率的形式,尽可能地将需求响应不确定量转化成确定的形式,建立模糊随机日前优化调度模型.文献[6 ]考虑源荷两侧的不确定性问题,建立了一种刚性负荷与弹性负荷相结合的多时间尺度互动决策模型.文献[7 ]通过将负荷的种类进行划分,并将一天24 h分成不同的时段,建立了一种负荷响应分段参与的多时间源荷调度策略,充分发挥负荷侧响应潜力.在以上考虑需求响应不确定性的综合能源系统研究中,系统调度模型中功率平衡条件往往基于预测功率,在实际情景发生之前,预测功率往往存在或大或小的误差;或只考虑了需求响应对各备用功率或线路传输容量的影响,没有考虑需求响应不确定性对于调度过程中功率平衡的影响.因此,本文将构造考虑需求响应不确定性和含有负荷预测误差的功率平衡方程,建立计及相关机会规划的综合能源系统优化调度模型,并利用粒子群优化算法[8 ] 对模型进行求解. ...
... 现有考虑需求响应不确定性的综合能源系统研究中,系统的功率平衡约束往往采用预测值[6 -7 ,9 ] .但是在实际调度过程中,用户的响应率是有波动的.随着综合能源系统中需求响应的应用不断增多,其不确定性是导致综合能源系统不确定性的重要原因[10 ] . ...
Multi-time scale scheduling strategy for source-load coordination considering demand response block participation
2
2021
... 目前,针对综合能源系统中的不确定性问题大多采用模糊机会约束进行处理.文献[5 ]通过将源荷两侧的不确定性问题转化成概率的形式,尽可能地将需求响应不确定量转化成确定的形式,建立模糊随机日前优化调度模型.文献[6 ]考虑源荷两侧的不确定性问题,建立了一种刚性负荷与弹性负荷相结合的多时间尺度互动决策模型.文献[7 ]通过将负荷的种类进行划分,并将一天24 h分成不同的时段,建立了一种负荷响应分段参与的多时间源荷调度策略,充分发挥负荷侧响应潜力.在以上考虑需求响应不确定性的综合能源系统研究中,系统调度模型中功率平衡条件往往基于预测功率,在实际情景发生之前,预测功率往往存在或大或小的误差;或只考虑了需求响应对各备用功率或线路传输容量的影响,没有考虑需求响应不确定性对于调度过程中功率平衡的影响.因此,本文将构造考虑需求响应不确定性和含有负荷预测误差的功率平衡方程,建立计及相关机会规划的综合能源系统优化调度模型,并利用粒子群优化算法[8 ] 对模型进行求解. ...
... 现有考虑需求响应不确定性的综合能源系统研究中,系统的功率平衡约束往往采用预测值[6 -7 ,9 ] .但是在实际调度过程中,用户的响应率是有波动的.随着综合能源系统中需求响应的应用不断增多,其不确定性是导致综合能源系统不确定性的重要原因[10 ] . ...
Extension of particle swarm optimization algorithm for solving transportation problem in fuzzy environment
1
2021
... 目前,针对综合能源系统中的不确定性问题大多采用模糊机会约束进行处理.文献[5 ]通过将源荷两侧的不确定性问题转化成概率的形式,尽可能地将需求响应不确定量转化成确定的形式,建立模糊随机日前优化调度模型.文献[6 ]考虑源荷两侧的不确定性问题,建立了一种刚性负荷与弹性负荷相结合的多时间尺度互动决策模型.文献[7 ]通过将负荷的种类进行划分,并将一天24 h分成不同的时段,建立了一种负荷响应分段参与的多时间源荷调度策略,充分发挥负荷侧响应潜力.在以上考虑需求响应不确定性的综合能源系统研究中,系统调度模型中功率平衡条件往往基于预测功率,在实际情景发生之前,预测功率往往存在或大或小的误差;或只考虑了需求响应对各备用功率或线路传输容量的影响,没有考虑需求响应不确定性对于调度过程中功率平衡的影响.因此,本文将构造考虑需求响应不确定性和含有负荷预测误差的功率平衡方程,建立计及相关机会规划的综合能源系统优化调度模型,并利用粒子群优化算法[8 ] 对模型进行求解. ...
考虑不确定性的需求响应虚拟电厂建模
2
2014
... 现有考虑需求响应不确定性的综合能源系统研究中,系统的功率平衡约束往往采用预测值[6 -7 ,9 ] .但是在实际调度过程中,用户的响应率是有波动的.随着综合能源系统中需求响应的应用不断增多,其不确定性是导致综合能源系统不确定性的重要原因[10 ] . ...
... 式中,${{a}_{dr,i}}$ i 个激励型需求响应补偿的二次项系数;${{b}_{dr,i}}$ i 个激励型需求响应补偿的一次项系数[9 ] . ...
Demand response based virtual power plant modeling considering uncertainty
2
2014
... 现有考虑需求响应不确定性的综合能源系统研究中,系统的功率平衡约束往往采用预测值[6 -7 ,9 ] .但是在实际调度过程中,用户的响应率是有波动的.随着综合能源系统中需求响应的应用不断增多,其不确定性是导致综合能源系统不确定性的重要原因[10 ] . ...
... 式中,${{a}_{dr,i}}$ i 个激励型需求响应补偿的二次项系数;${{b}_{dr,i}}$ i 个激励型需求响应补偿的一次项系数[9 ] . ...
Energy flexibility prediction for data center engagement in demand response programs
1
2020
... 现有考虑需求响应不确定性的综合能源系统研究中,系统的功率平衡约束往往采用预测值[6 -7 ,9 ] .但是在实际调度过程中,用户的响应率是有波动的.随着综合能源系统中需求响应的应用不断增多,其不确定性是导致综合能源系统不确定性的重要原因[10 ] . ...
Optimal operation of virtual power plant with considering the demand response and electric vehicles
1
2021
... 随着电力市场改革的不断深入,传统的需求侧管理措施的实施基础发生了改变.综合能源系统的利益主体朝着多元化发展,需求侧能源的管理也逐渐被重视,在综合能源系统中引入需求响应是电力市场发展的必然要求[11 ] .综合运营商任何调度策略需要时刻满足系统功率平衡约束,因此在考虑需求响应不确定性和负荷的预测误差的综合能源系统中,严格的功率平衡方程为 ...
Chance-constrained optimization for integrated local energy systems operation considering correlated wind generation
1
2021
... 上述两个功率平衡式中,式(1)忽略预测误差是目前考虑需求响应调度常用的模型,但不能应对需求响应不确定性对于系统功率平衡的影响.式(2)由于含有不确定性变量,无法直接求解[12 ] .因此,本文在考虑需求响应不确定性和负荷预测误差基础上,利用相关机会规划方法对含有不确定性变量的方程进行建模求解,将等式约束转换为不等式约束,即 ...
Power system day-ahead unit commitment based on chance-constrained dependent chance goal programming
1
2018
... 式中,Pr{·}表示不确定事件的成立的概率.通过调整误差常量${{\sigma }_{t}}$ [13 ] .其核心思想是使不确定事件的机会函数在不确定环境下成立的可能性最大[14 ] ,从而得到问题的最优解. ...
1
2004
... 式中,Pr{·}表示不确定事件的成立的概率.通过调整误差常量${{\sigma }_{t}}$ [13 ] .其核心思想是使不确定事件的机会函数在不确定环境下成立的可能性最大[14 ] ,从而得到问题的最优解. ...
1
2004
... 式中,Pr{·}表示不确定事件的成立的概率.通过调整误差常量${{\sigma }_{t}}$ [13 ] .其核心思想是使不确定事件的机会函数在不确定环境下成立的可能性最大[14 ] ,从而得到问题的最优解. ...
计及细节层次直接负荷控制的区域综合能源系统多时间尺度优化调度
1
2021
... 式中,$P_{es}^{\max }$ $P_{es}^{\min }$ max 、SOCm in 分别为储能装置的最大、最小荷电状态[15 ] .储能装置的模型表达式为 ...
Multi-time-scale optimal dispatch of regional integrated energy system considering level of detail direct load control
1
2021
... 式中,$P_{es}^{\max }$ $P_{es}^{\min }$ max 、SOCm in 分别为储能装置的最大、最小荷电状态[15 ] .储能装置的模型表达式为 ...
Hierarchies for classes of priority algorithms for job scheduling
1
2006
... 由建模过程可知,上述建立的模型是一个多目标的优化调度模型.本文采用目标规划中序贯算法的求解思路[16 ] ,按照优先级的先后顺序,将多目标规划求解划分为一系列单目标规划,即每次的目标函数只处理一个目标.将此前求解的优先级更高的目标结果作为一个约束条件,可描述为 ...
计及多能源多需求响应手段的园区综合能源系统优化调度模型
1
2020
... 为检验本文所提出模型在综合能源系统调度中的实际效果,选取某社区综合能源系统为仿真算例.调度周期为24 h,以1 h为调度单位.分时能源价格[17 ] 如表1 所示. ...
Optimal scheduling model of park integrated energy system considering multi energy and multi demand response means
1
2020
... 为检验本文所提出模型在综合能源系统调度中的实际效果,选取某社区综合能源系统为仿真算例.调度周期为24 h,以1 h为调度单位.分时能源价格[17 ] 如表1 所示. ...
计及负荷预测误差的可中断负荷优化管理
1
2011
... 负荷预测误差服从正态分布规律[18 ] ,因此,现有研究中针对负荷预测误差大多采用正态分布来模拟,记为${{\partial }^{l}}$ $N(0,{{\partial }^{2}})$ $\partial $
The interruptible load optimization management considering the load forecast error
1
2011
... 负荷预测误差服从正态分布规律[18 ] ,因此,现有研究中针对负荷预测误差大多采用正态分布来模拟,记为${{\partial }^{l}}$ $N(0,{{\partial }^{2}})$ $\partial $