1 引言
双斜槽转子感应电机相比于传统的单斜槽转子感应电机具有低振动噪声、大起动力矩、无轴向力等优点[1 -2 ] ,逐渐受到关注并有望作为新型驱动电机应用在新能源电动叉车上[3 ] 。
变频供电时,变频电源的高次时间谐波会在电机内部产生附加损耗,从而引起的温升变化可能对电机的工作性能或驱动系统的安全运行造成威胁。因此对变频供电下双斜槽转子感应电机温升及转子热应力的研究具有一定的迫切性。
目前,国内外对电机温升的计算方法主要包括参数计算法、等效热路法和有限元分析法,其中有限元分析法较为常见。王艳武等[4 ] 对异步电机转子的三维温度场和热应力进行了分析,指出电机温升的高低将直接影响转子热应力的大小。谢颖等[5 ] 采用有限元法对一台小型感应电机进行三维瞬态温度场及转子应力场的计算并指出了普通斜槽转子断条故障的原因。李伟力等[6 ] 采用有限元法对直槽转子感应电机的定转子全域温度场进行了计算,并采用热传导方式等效处理了电机定转子与气隙之间复杂的对流换热过程。丁树业等[7 ] 对变频供电下直槽转子感应电机的传热特性进行了分析,并进一步揭示了变频器参数对电机温升的影响特征。文献[8 ]对变频驱动下的永磁同步电机的温升以及温升应力进行了计算,为该类电机的优化设计提供参考。文献[9 ]考虑变频器供电谐波的影响对不同磁极拓扑结构下的轴向磁通永磁同步电机的传热特性进行了分析,并研究了永磁体分段方式对温度场的影响。
综上所述,针对普通转子感应电机及永磁同步电机的温度场和温度应力场已经有了相当多的研究,但针对变频供电下双斜槽转子感应电机的温升以及转子热应力问题,还尚未有过相关研究。针对以上不足,本文以一台电动叉车用双斜槽转子变频感应电机为例,考虑变频供电下电源时间谐波的影响,采用三维有限元法结合改进的铁耗模型对电机的电磁损耗进行计算。然后将计算得到的损耗施加到温度场模型中作为热源激励,得到了变频供电下双斜槽转子感应电机的温度分布,并搭建试验平台进行机壳温升试验验证温度场分析的正确性。最后以三维温度场计算结果为载荷,耦合仿真得到了变频供电下双斜槽转子的热应力分布情况,为其热优化设计提供重要参考。
2 变频器输出谐波分析
2.1 SPWM原理
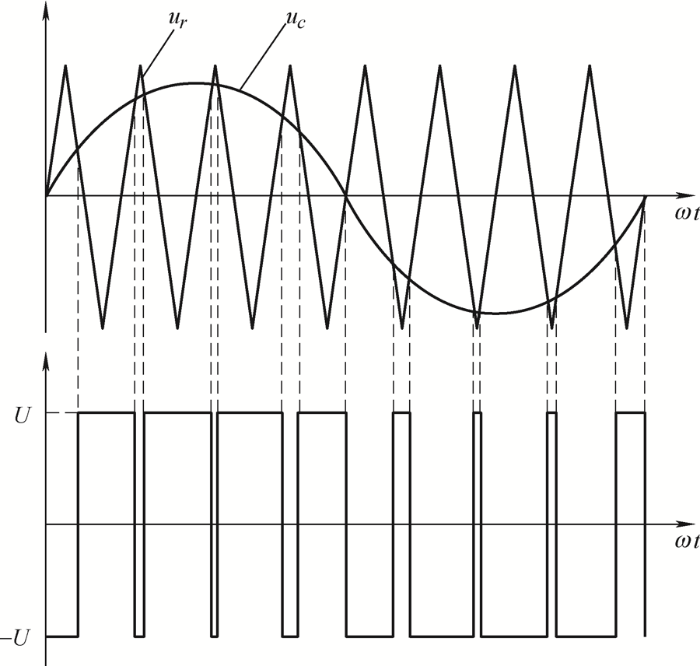
正弦脉冲宽度调制(Sinusoidal pulse width modulation, SPWM)是电机变频调速领域使用最为广泛的调制方式,被广泛应用于各行各业的驱动电路中[10 ] 。其基本原理是将正弦波等效为一系列等幅不等宽的矩形脉冲波,其脉冲宽度一般由正弦调制波和三角载波自然相交而得到。典型的单相双极性SPWM的控制波形如图1 所示。当调制波信号大于载波信号时,输出电压为U ,反之输出电压为-U 。
图1
2.2 SPWM输出电压谐波
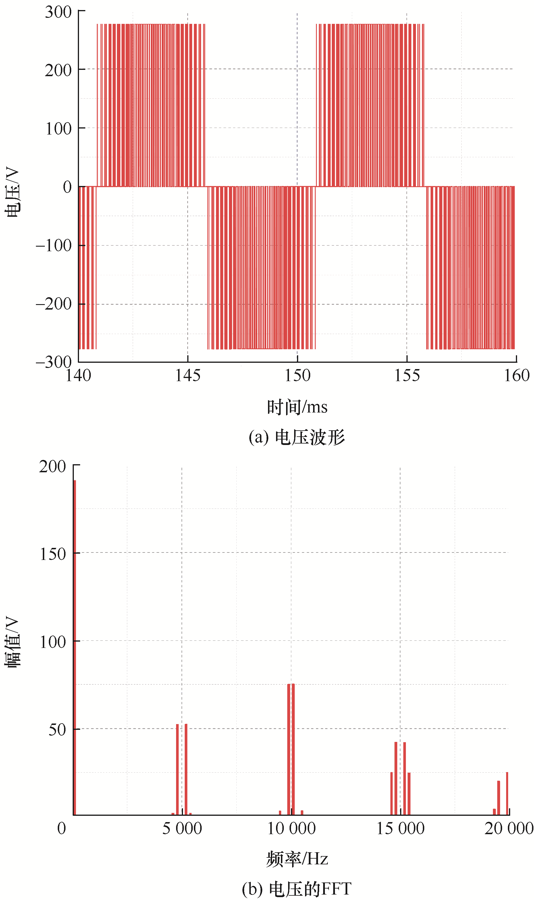
SPWM可以使输出的电压、电流接近正弦波,但由于三角载波对正弦信号波的调制,也产生了和载波有关的谐波分量。以典型的三相SPWM逆变器为例,在Matlab中搭建其仿真电路,所仿真逆变器的载波频率为5 kHz,调制波频率为100 Hz,载波比M =0.8。仿真得到的逆变器输出线电压波形及其FFT如图2 所示。
图2
通过对SPWM电压波的FFT可以看出,输出电压不是标准的正弦波,而是含有大量的谐波成分,且主要的谐波分量集中在开关频率附近。
3 电磁场有限元模型及温升试验平台
3.1 双斜槽转子结构及原理
双斜槽转子结构如图3 所示,双斜槽转子沿着轴向分为两半部分,每半部分相当于一个普通的单斜槽转子。其中两半部分的转子导体部分通过中间环连接,转子铁心部分通过内置硅钢片连接。其基本原理是使上下两半转子反向扭斜,并且交错1/2转子齿距,以抵消轴向力和进一步削弱转子齿谐波,达到降低电机的振动噪声和削弱同步附加转矩的目的。
图3
3.2 三维电磁场有限元模型
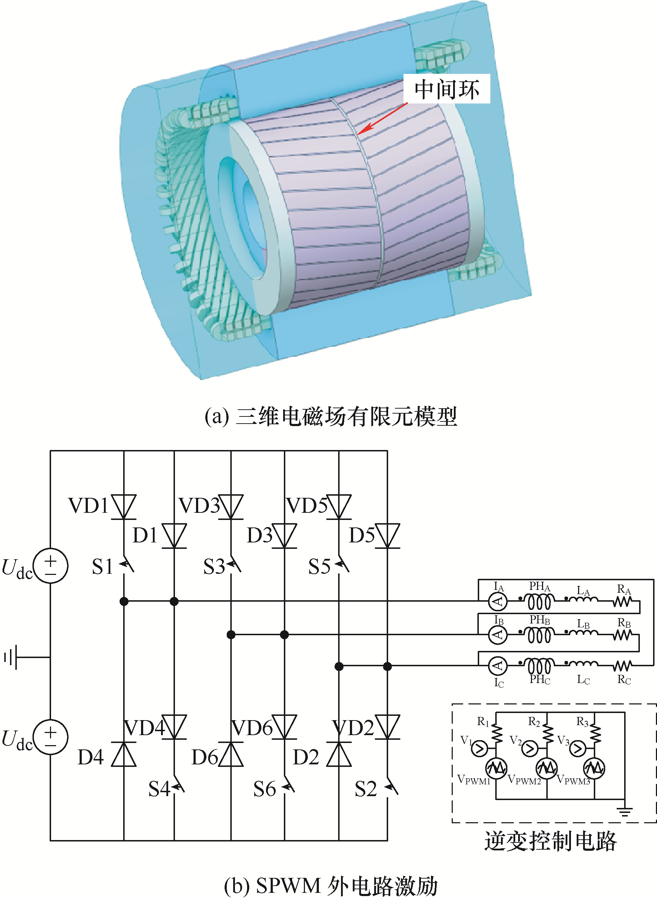
由于双斜槽转子结构的特殊性,使用二维有限元难以准确计算电机的转子侧损耗,因此本文以一台电动叉车用双斜槽转子感应电机为例,建立了电机的三维电磁场有限元模型。样机基本仿真参数如表1 所示。采用Maxwell Circuit插件搭建SPWM外电路对仿真模型施加激励,以模拟电机变频驱动的工况。三维电磁场有限元模型及搭建的SPWM外电路激励如图4 所示。
图4
3.3 电机温升试验平台
为了测试温升性能,搭建了电机的温升试验平台,如图5 所示。双斜槽转子和温度数字显示仪如图6 所示。本文对正弦供电和变频供电两种不同供电方式下电机机壳表面的温升分别进行了测试。试验初始环境温度为18.5 ℃,将温度传感器黏着于机壳表面。由于电机不带有内置风扇,故采用S2短时工作制对电机的温升进行测量,待电机稳定运行至给定输出状态下,每隔10 min对电机机壳表面的温升记录一次,共记录40 min。
图5
图6
4 三维瞬态电磁场损耗计算
电机是机电能量转换的机构,在能量转换的过程中会产生损耗,成为电机温度场计算中的热源。当正弦电源供电时电机内的损耗主要包括定转子基波铜/铝耗、基本铁耗、机械损耗和杂散损耗。当变频供电时,由于高次谐波的存在,电机的内部会产生以下附加损耗[11 ] :① 高次谐波带来的电机附加 定子铜耗;② 高次谐波带来的电机附加铁心损耗;③ 高次谐波及其作用下的集肤效应所带来的附加转子铝耗。这些由电源高次谐波所引入的附加损耗,将会使得电机的温升进一步增加。
4.1 铜耗
当PWM供电时,电机的绕组电流中含有高频的时间谐波分量,产生附加的谐波损耗。采用有限元法计算时可以考虑高频谐波电流的影响,其计算的表达式为[12 ]
(1) ${{p}_{cu}}=\frac{1}{T}\sum\limits_{v}{\int_{0}^{T}{{{R}_{s}}\left( i_{vA}^{2}+i_{vB}^{2}+i_{vC}^{2} \right)\text{d}t}}$
式中,${{R}_{s}}$ ${{i}_{vA}}$ ${{i}_{vB}}$ ${{i}_{vC}}$ T 为基波时间周期。
4.2 铁耗
根据传统Bertotti分立铁耗计算理论,在标准正弦供电条件下,电机的铁耗主要分为磁滞损耗、涡流损耗和附加损耗,其表达式如下[13 ]
(2) $\begin{matrix} {{p}_{Fe}}={{p}_{h}}+{{p}_{c}}+{{p}_{e}}\text{=} \\ {{k}_{h}}f{{B}^{2}}+{{k}_{c}}{{\left( fB \right)}^{2}}+{{k}_{e}}{{\left( fB \right)}^{1.5}} \\\end{matrix}$
式中,${{p}_{h}}$ ${{p}_{c}}$ ${{p}_{e}}$ ${{k}_{h}}$ ${{k}_{c}}$ ${{k}_{e}}$ f 为基波的频率;B 为基波磁通密度的幅值。
对于电机非正弦供电的情况,传统的Bertotti铁耗模型难以准确地计算铁耗,常用方法是对电机铁心内各个节点的磁密波形进行谐波分析,然后分别将各次谐波单独作用下的铁耗进行叠加。但该方法用于三维有限元模型时,其计算过程复杂,计算数量极大。BOGLIETTI等[14 ] 提出了非正弦供电下的铁心损耗可以用正弦基波的磁滞损耗和涡流损耗来表示。基于这一理论,浙江大学WANG等[15 ] 推导出了适合计算变频供电下的电机铁耗计算模型,并通过试验验证了其良好效果,表达式如下
(3) $\left\{\begin{array}{l}p_{F e}=k_{h}^{\prime} f B^{2}+k_{c}^{\prime}(f B)^{2}+k_{e}(f B)^{1.5} \\k_{h}^{\prime}=k_{h} \eta^{2} \\k_{c}^{\prime}=k_{c} \chi^{2} \\\eta=\frac{V_{a v}}{V_{a v, \text { fund }}} \\\chi=\frac{V_{r m s}}{V_{r m s, \text { fund }}}\end{array}\right.$
式中,${k}'_{h}$、${k}'_{c}$分别为改进的磁滞损耗系数和涡流损耗系数;${{V}_{av}}$ ${{V}_{rms}}$ ${{V}_{av,fund}}$ ${{V}_{rms,fund}}$
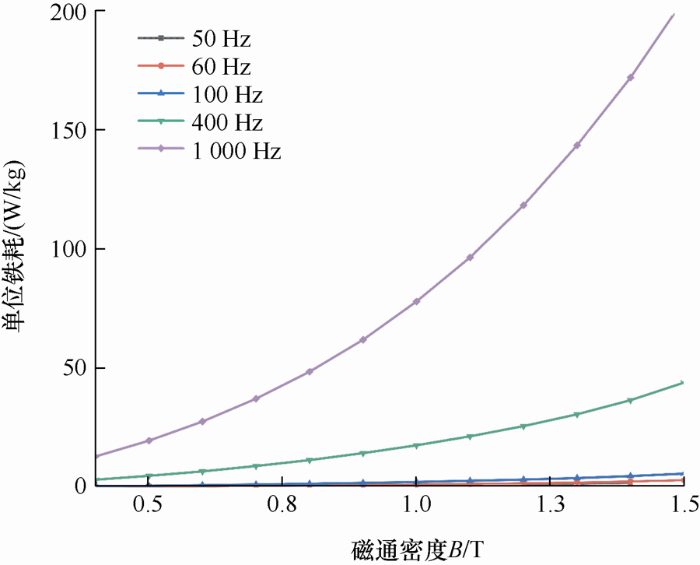
本文样机的定转子铁心所用的硅钢片材料为35W300,硅钢片材料厂家提供的多频率下的铁损曲线如图7 所示。
图7
采用最小二乘法对硅钢片的损耗曲线进行拟合,并结合SPWM输出电压波形谐波的特点,得到硅钢片的各损耗系数如表2 所示。
4.3 铝耗
电机运行时转子导条存在集肤效应,趋于转子外表面的电流密度高。有限元计算变频电机转转子铝耗时,可以考虑谐波成分及集肤效应对损耗的影响,其表达式为[16 ]
(4) ${{p}_{Al}}=\frac{1}{{{\sigma }_{Al}}}\sum\limits_{j=1}^{{{N}_{Al}}}{\left( {{J}^{2}} \right)}{{\Delta }_{Alj}}$
式中,${{\sigma }_{Al}}$ ${{N}_{Al}}$ J 为每个剖分单元中的电流密度;${{\Delta }_{Alj}}$
4.4 机械损耗和杂散损耗
电机的机械损耗主要包括轴承摩擦损耗和通风损耗,难以准确计算其数值大小。由于其在电机总损耗中占比较小,且主要分布在电机轴承上,对电机整体温升影响较小,因此本文不考虑机械损耗的影响。电机的杂散损耗也难以准确计算,一般取额定输出功率的0.5%作为电机的杂散损耗值,表达式如下
(5) ${{p}_{\Delta }}\approx 0.5%{{P}_{N}}$
4.5 电磁场仿真结果
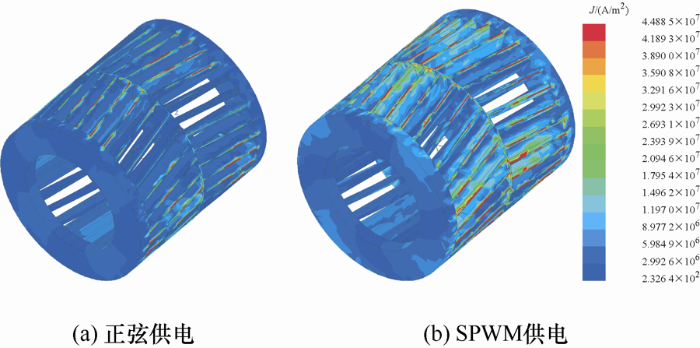
仿真得到相同时刻不同供电方式下的双斜槽转子感应电机转子电流密度分布云图如图8 所示。
图8
可以看到转子导条上存在集肤效应,转子导条表面的电流密度略高。SPWM供电下转子导条表面的电流密度要明显大于正弦供电下的导条表面电流密度。
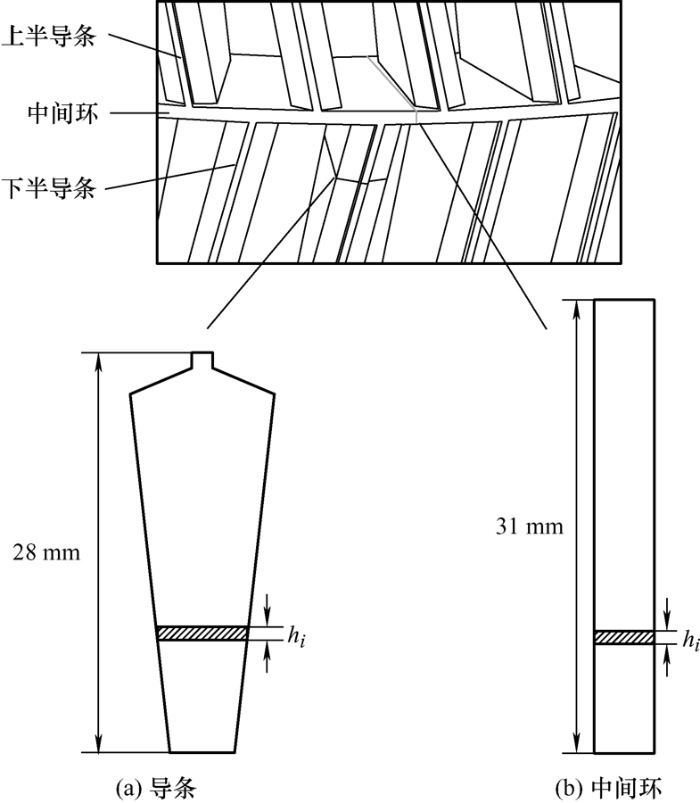
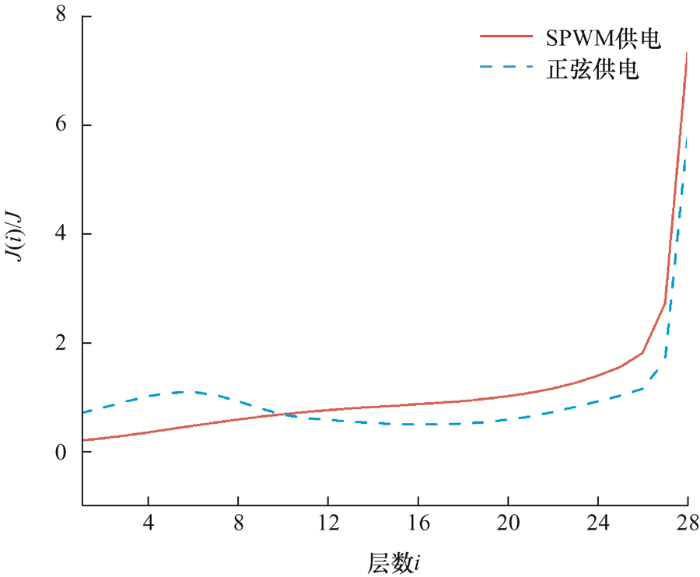
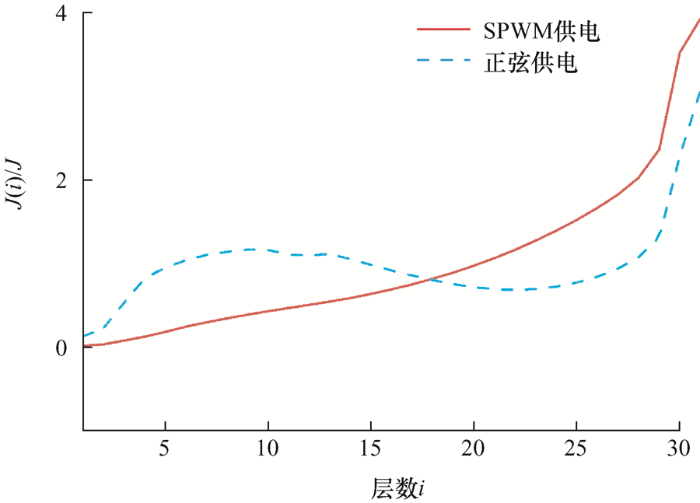
为了进一步观察转子电流密度在导体内部的分布,取转子导条和中间环的剖面图如图9 所示。将电机的转子导条和中间环按径向方向分层,每层的高度hi 为1 mm,导条和中间环在不同层处的平均电流密度变化分别如图10 和图11 所示,J (i )/J 为第i 层平均电流密度与整个剖面平均电流密度的比值。通过观察可以看出,与正弦供电相比,SPWM供电时导体内部的电流密度呈单调递增趋势,导条和中间环上层电流密度增加更加明显,即电流主要集中在导体和中间环的上层,说明SPWM供电下受高次谐波的影响,电机的集肤效应更加严重,这会使得电机的转子铝耗有所增加。
图9
图10
图11
仿真结合计算得到的不同供电方式下电机的损耗如表3 所示。可以看出SPWM供电下电机的各个损耗均有所增加,其中电机的铁耗和转子侧铝耗增加较为明显,分别增加了40.8%和33.3%,电机定子铜耗增加并不明显,仅增加了1.5%。
5 三维瞬态温度场计算
5.1 温度场模型
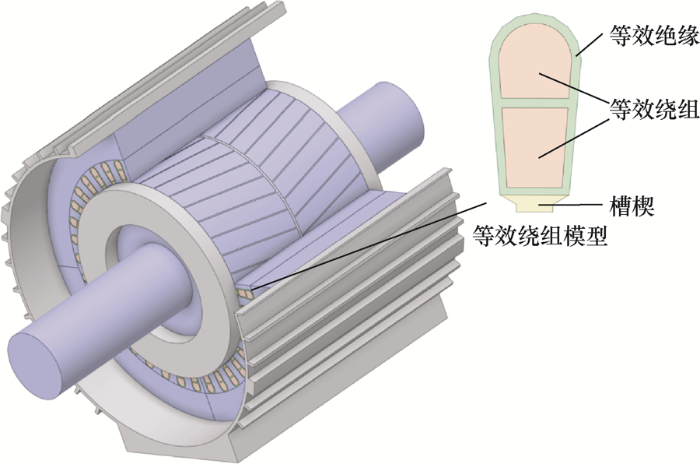
电机三维温度场有限元模型如图12 所示,建模的过程中考虑了机壳、转轴对电机散热的影响。由于电机的绕组为散下线式绕组,绕组端部模型十分复杂,且端部绕组需要浸漆处理,浸漆对端部绝缘模型的建立存在较大影响,因此本文参考文献[5 ]建模时忽略端部绕组,同时参考文献[17 ]建立了等效的定子槽内绕组模型,这种等效能够较好地反映定子槽内的导热情况,其中等效绝缘的导热系数计算公式如下
(6) ${{\lambda }_{eq}}=\frac{\sum\limits_{i=1}^{n}{{{d}_{i}}}}{\sum\limits_{i=1}^{n}{\frac{{{d}_{i}}}{{{\lambda }_{i}}}}}$
式中,${{\lambda }_{eq}}$ n 为绝缘材料的个数;${{\lambda }_{i}}$ ${{d}_{i}}$
图12
5.2 等效导热系数
通过文献[18 ]中电机三维瞬态温度场的数学模型可以看出,电机各部件表面的导热系数和对流换热系数的准确选取在一定程度上决定了电机的温度计算的准确性。在电机旋转的过程中,气隙中的换热过程十分复杂,难以精确计算气隙表面的换热系数。因此本文采用等效气隙导热系数${{\lambda }_{g}}$ [6 ]
(7) $\left\{ \begin{align} & R{{e}_{g}}=\mathrm{ }\!\!\pi\!\!\text{ }{{D}_{2}}g\frac{n}{60\gamma } \\ & R{{e}_{cr}}=41.2\sqrt{\frac{{{D}_{i1}}}{g}} \\\end{align} \right.$
式中,$R{{e}_{g}}$ $R{{e}_{cr}}$ ${{D}_{2}}$ $g$ $n$ $\gamma $
将气隙的雷诺数与临界雷诺数进行比较,当$R{{e}_{g}}<R{{e}_{cr}}$ $R{{e}_{g}}>R{{e}_{cr}}$
(8) $\left\{ \begin{align} & {{\lambda }_{g}}=0.001\ \ 9{{\eta }^{-2.908\ 4}}Re_{g}^{0.461\ 4\ln (3.333\ 61\eta )} \\ & \eta =\frac{{{D}_{2}}}{{{D}_{i1}}} \\\end{align} \right.$
通过计算结合相关工程实践经验得到计算域内各部件的导热系数如表4 所示。
上述各部件均为各向同性导热材料,由于电机定转子铁心的硅钢片叠压制成,其轴向的导热系数与径向导热系数存在较大差异。为了简化分析,将硅钢片以及片间绝缘等效为导热能力为各向异性的整体进行计算,等效后的铁心叠片在径向方向的导热系数近似为硅钢片的导热系数,在轴向方向的等效导热系数计算公式为
(9) $\lambda =\frac{{{l}_{Fe}}+{{l}_{0}}}{\frac{{{l}_{Fe}}}{{{\lambda }_{1}}}+\frac{{{l}_{0}}}{{{\lambda }_{0}}}}=\frac{1}{\frac{{{K}_{Fe}}}{{{\lambda }_{1}}}+\frac{1-{{K}_{Fe}}}{{{\lambda }_{0}}}}$
式中,KFe 为硅钢片叠压系数;lFe 为硅钢片的厚度;l 0 为硅钢片间绝缘的等效厚度;λ 1 为硅钢片的导热系数;λ 0 为绝缘漆的导热系数。
5.3 机壳与铁心的接触热阻
在实际加工过程中,电机定子铁心与机壳之间存在很小的装配间隙。间隙间的主要成分为静止的薄层空气。由于空气的热阻很大,阻碍了电机机壳与定子铁心之间的热量传导,因此不可忽略不计。本文将电机铁心与机壳的接触面施加等效接触热阻以考虑装配间隙的影响,计算公式为
(10) ${{R}_{\delta }}=\frac{{{\delta }_{0}}}{{{\lambda }_{0}}{{A}_{0}}}$
式中,${{A}_{0}}$ ${{\delta }_{0}}$ ${{\lambda }_{0}}$
5.4 温度场仿真结果
在温度场中所施加的激励载荷为损耗密度,即各个发热体的损耗与其体积的比值,计算公式如下
(11) $Q=\frac{{{p}_{loss}}}{V}$
式中,ploss 为发热体的损耗;V 为发热体的体积。
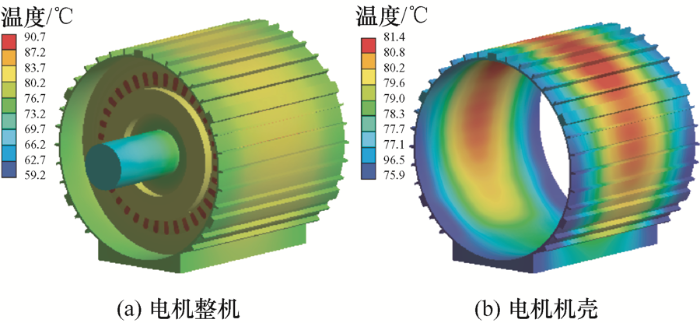
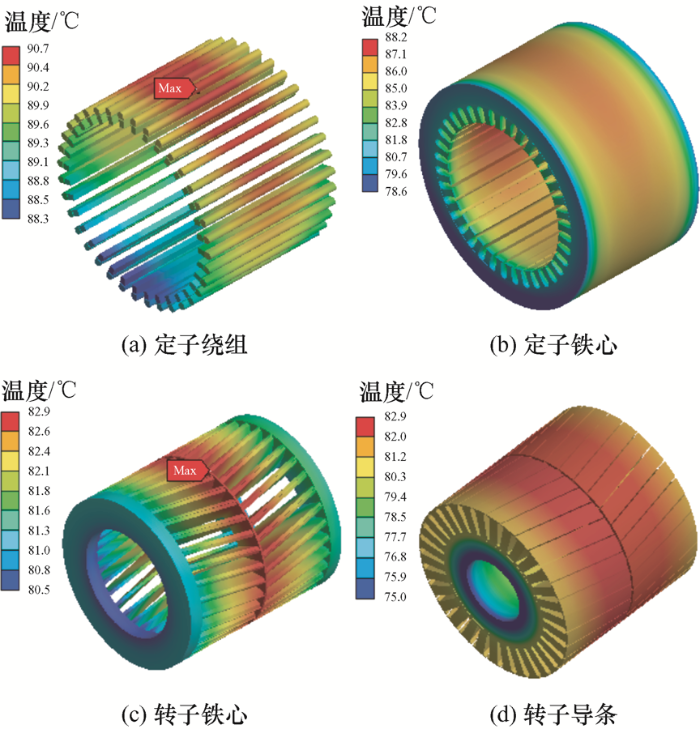
对电机的各个发热部件分别施加对应的损耗密度,其中电机中的杂散损耗各取1/2分别施加于定、转子铁心齿部,并对电机施加相应边界条件,得到电机运行40 min时不同供电方式下电机的温度分布云图如图13 和图14 所示。
图13
图14
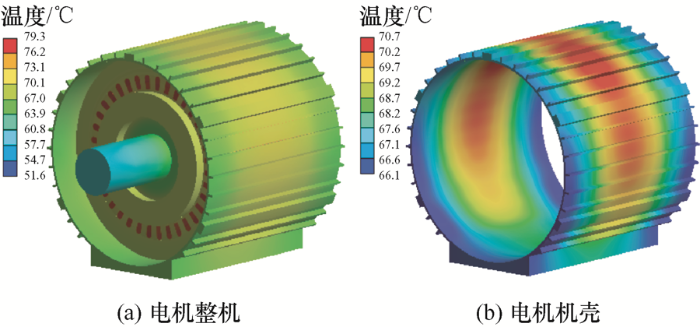
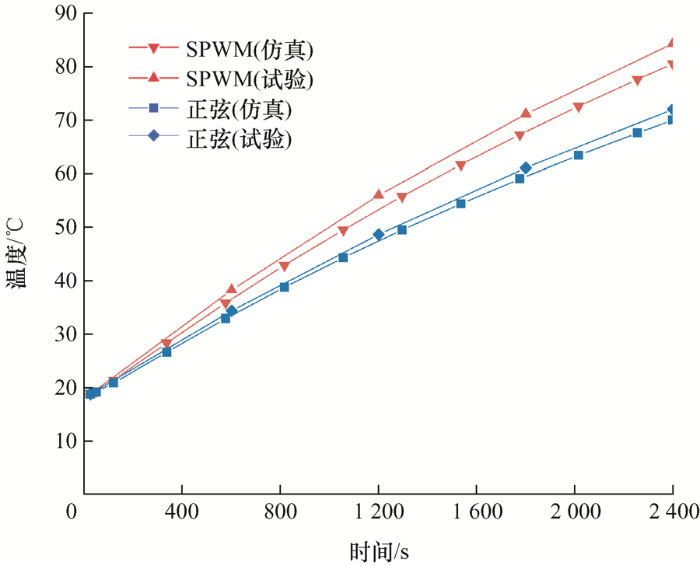
可以看出电机运行至40 min时,不同供电方式下电机机壳温度沿周向的分布并不均匀,由于电机底座处的机壳较厚,导热性能好,故靠近底座处的机壳温度较低。电机整体的温度分布规律大致相同,但对比正弦供电情况,SPWM供电下的电机机壳温度明显升高,其温度的最大值达81.4 ℃,相比正弦供电增加了15.1%。为了验证仿真的准确性,对电机进行机壳温升试验,所得到的不同供电方式下电机机壳温度变化曲线如图15 所示。
图15
通过机壳的温升曲线可以看出,正弦供电和SPWM供电下电机机壳温度的仿真值均要低于试验值,其中正弦供电下温升的最大差值为2.1 ℃,最大误差为2.9%,SPWM供电下温升的最大差值3.8 ℃,误差为4.5%。产生误差的原因可能为没有考虑温度对材料电导率及热导率的影响,且忽略了变频供电谐波对电机内杂散损耗的影响。尽管计算的结果存在误差,但不同供电方式下电机机壳的温度变化基本趋势相同,也在一定程度上验证了仿真方法的合理性。仿真得到的SPWM供电下电机其他各部件40 min时的温度分布如图16 所示。
图16
由图16 可以看出,电机最大温度位于电机定子绕组中部,其温度最大值为90.7 ℃。受绕组传热的影响,电机定子铁心齿部的温度要高于其轭部的温度。电机转子导条和转子铁心的温度均呈现中间高、两端低的趋势,温度的最大值均为82.9 ℃,位于转子中间环表面。电机定子绕组和转子导条的整体温差不大,最大温差仅为2.4 ℃,电机定、转子铁心的温差较大,其中定子铁心的最大温差为9.6 ℃,转子铁心的最大温差为7.9 ℃。
仿真得到不同供电方式下各部件的平均温度如表5 所示。
6 转子热应力计算
感应电机负载运行的过程中,转子会产生较大的温升,使其受热膨胀。由于电机转子各部件材料膨胀系数的不同以及外在结构的约束,会产生较大的热应力,成为电机转子断条与断环故障的重要诱因[19 ] 。双斜槽转子结构具有特殊性,其较薄的中间环结构在热应力的作用下可能存在潜在的中环断裂风险。因此分析双斜槽鼠笼转子热应力的分布情况,可以为双斜槽转子中间环的优化设计提供重要的参考。
以三维瞬态温度场的计算结果为载荷激励,将各个节点单元的温度施加到结构场有限元模型中以求解热载荷作用下的转子应力分布。参考弹性力学相关知识,热应力计算的有限元方程可以表示为[20 ]
(12) $\left\{ \begin{align} & (\sum\limits_{1}^{n}{\int_{V}{{{B}^{\text{T}}}DB\text{d}v}})\centerdot U=\sum\limits_{1}^{n}{\int_{V}{{{B}^{\text{T}}}D{{\varepsilon }_{0}}\text{d}v}} \\ & {{\varepsilon }_{0}}=\Delta T{{\left[ {{\alpha }_{x}},{{\alpha }_{y}},{{\alpha }_{z}},0,0,0 \right]}^{\text{T}}} \\ & \sigma =D\centerdot (\varepsilon -{{\varepsilon }_{0}}) \\ & \varepsilon =B\centerdot U \\\end{align} \right.$
式中,B D U ${{\varepsilon }_{0}}$ $\Delta T$ ${{\alpha }_{x}}$ ${{\alpha }_{y}}$ ${{\alpha }_{z}}$ x 、y 、z 方向上的热膨胀系数;$\varepsilon $ $\sigma $
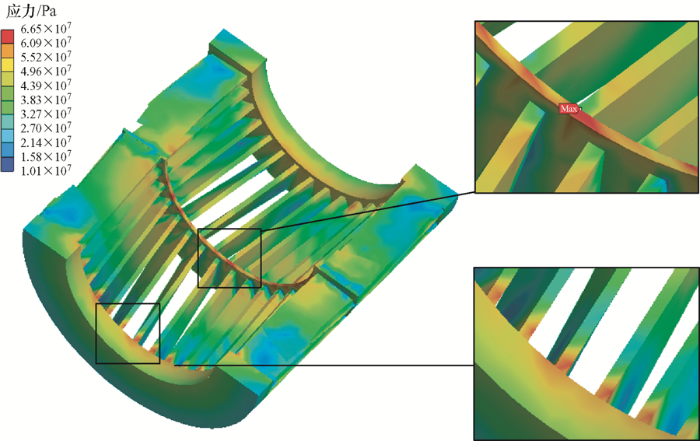
在导条和硅钢片的接触面上施加接触条件,允许两者之间相对滑动,仿真得到SPWM供电下电机转子鼠笼热应力的结果如图17 所示。
图17
可以看出电机转子鼠笼不仅在导条底部与端环的连接处附近存在较大的热应力,在鼠笼导条的中间环处也存在较大的热应力,且热应力的最大值点位于中间环底部一点,最大值为6.65×107 Pa。这说明双斜槽转子感应电机不仅存在导条断裂的风险,中间环受热应力作用也可能会发生断裂,对电机的正常运行产生额外的危害。因此在设计时应该适当增加中间环的厚度或优化中间环的形状以避免这一潜在故障的发生。
7 结论
本文对一台22.5 kW双斜槽转子变频感应电机的温升以及转子热应力进行了分析。采用三维有限元法结合改进的铁耗模型对变频供电下的电磁损耗进行了计算。以损耗为激励,得到了电机温度场分布,并采用顺序耦合的方式得到了电机的转子应力场分布,结合样机温升试验,得出如下结论。
(1) 变频器供电下,受电源高次时间谐波及集肤效应的影响,电机的各项电磁损耗均有所增加,其中电机的铁耗和转子铝耗增加较为明显,分别增加了40.8%和33.3%,定子铜耗增加不明显,仅增加了1.5%。
(2) 短时工作制下,变频供电时电机的机壳温升相比于正弦供电时升高了15.1%,仿真与试验的最大误差为4.5%。电机转子温度的最大值为82.9 ℃,位于转子中间环表面。
(3) 双斜槽转子鼠笼不仅在导条与端环的连接处附近存在较大的热应力,在中间环处也存在较大的热应力,且热应力的最大点出现在中间环底部,最大值为6.65×107 Pa。因此转子中间环会存在潜在的断裂隐患,在设计时应该适当增加中间环厚度或改进中间环结构。
本文研究为双斜槽转子变频感应电机的温升预测,以及转子鼠笼中间环优化设计提供重要参考。
参考文献
View Option
[1]
陈永校 , 诸自强 , 应善成 . 电机噪声的分析和控制 [M]. 杭州 : 浙江大学出版社 ,1987.
[本文引用: 1]
CHEN Yongxiao ZHU Ziqiang YING Shancheng Analysis and control of motor noise [M]. Hangzhou : Zhejiang University Press ,1987.
[本文引用: 1]
[2]
WANG L BAO X DI C et al . Analysis of synchronous parasitic torque in dual skew cage rotor induction motors with equivalent slot number
[J]. IET Electric Power Applications , 2017 , 11 (8 ):1357 -1365 .
DOI:10.1049/elp2.v11.8
URL
[本文引用: 1]
[3]
王春雨 . 电动叉车用双斜槽转子感应电机的振动噪声分析 [D]. 合肥 : 合肥工业大学 , 2018 .
[本文引用: 1]
WANG Chunyu Vibration and noise analysis of induction motor with double skewed slot rotor for electric forklift truck [D]. Hefei : Hefei University of Technology , 2018 .
[本文引用: 1]
[4]
王艳武 , 杨立 , 陈翾 , 等 . 异步电机转子三维温度场及热应力场研究
[J]. 电机与控制学报 , 2010 , 14 (6 ):27 -32 .
[本文引用: 1]
WANG Yanwu YANG Li CHEN Xuan et al . Study on 3D thermal field and thermal stress field of the induction motor rotor
[J]. Electric Machines and Control , 2010 , 14 (6 ):27 -32 .
[本文引用: 1]
[5]
谢颖 , 王泽 , 单雪婷 , 等 . 基于多场量的笼型感应电机三维瞬态磁热固耦合计算分析
[J]. 中国电机工程学报 , 2016 , 36 (11 ):3076 -3084 .
[本文引用: 2]
XIE Ying WANG Ze SHAN Xueting et al . The calculations and analysis of 3D transient magnetic-thermal-solid coupling for squirrel-cage induction motors based on multi fields
[J]. Proceedings of the CSEE , 2016 , 36 (11 ):3076 -3084 .
[本文引用: 2]
[6]
李伟力 , 李守法 , 谢颖 , 等 . 感应电动机定转子全域温度场数值计算及相关因素敏感性分析
[J]. 中国电机工程学报 , 2007 , 27 (24 ):85 -91 .
[本文引用: 2]
LI Weili LI Shoufa XIE Ying et al . Stator-rotor coupled thermal field numerical calculation of induction motors and correlated factors sensitivity analysis
[J]. Proceedings of the CSEE , 2007 , 27 (24 ):85 -91 .
[本文引用: 2]
[7]
丁树业 , 崔广慧 . PWM变频器供电的感应电机传热特性
[J]. 南京航空航天大学学报 , 2016 , 48 (1 ):122 -129 .
[本文引用: 1]
DING Shuye CUI Guanghui Characteristics of heat transfer for induction motor supplied by PWM converter
[J]. Journal of Nanjing University of Aeronautics & Astronautics , 2016 , 48 (1 ):122 -129 .
[本文引用: 1]
[8]
丁树业 , 朱敏 , 江欣 . 永磁同步电机三维全域温度场与温度应力耦合研究
[J]. 电机与控制学报 , 2018 , 22 (1 ):53 -60 ,71.
[本文引用: 1]
DING Shuye ZHU Min JIANG Xin Coupling study of 3D universal temperature field and temperature stress for permanent magnet synchronous motor
[J]. Electric Machines and Control , 2018 , 22 (1 ):53 -60 ,71.
[本文引用: 1]
[9]
曹君慈 , 周柏宇 , 李栋 , 等 . 不同磁极拓扑结构的轴向磁通永磁同步电机传热的研究
[J]. 电机与控制学报 , 2022 , 26 (5 ):26 -36 .
[本文引用: 1]
CAO Junci ZHOU Baiyu LI Dong et al . Heat transfer of axial flux permanent magnet motor with different magnetic pole topologies
[J]. Electric Machines and Control , 2022 , 26 (5 ):26 -36 .
[本文引用: 1]
[10]
宁榕 . SPWM型变频器供电下异步电机电磁噪声
[J]. 电机与控制应用 , 2014 , 41 (7 ):39 -42 .
[本文引用: 1]
NING Rong Electromagnetic noise of induction motor under SPWM inverter power supply
[J]. Electric Machines & Control Application , 2014 , 41 (7 ):39 -42 .
[本文引用: 1]
[11]
赵争鸣 , 袁立强 . 电力电子与电机系统集成分析基础 [M]. 北京 : 机械工业出版社 , 2009 .
[本文引用: 1]
ZHAO Zhengming YUAN Liqiang Integrated analysis of power electronics and motor drive system [M]. Beijing : China Machine Press , 2009 .
[本文引用: 1]
[12]
赵海森 , 刘晓芳 , 罗应立 , 等 . 电压偏差条件下笼型感应电机的损耗特性
[J]. 电机与控制学报 , 2010 , 14 (5 ):13 -19 .
[本文引用: 1]
ZHAO Haisen LIU Xiaofang LUO Yingli et al . Losses characteristics of cage induction motors under voltage deviation conditions
[J]. Electric Machines and Control , 2010 , 14 (5 ):13 -19 .
[本文引用: 1]
[13]
TONG W SUN R LI S et al . Loss and thermal analysis for high speed amorphous metal PMSMs using 3-D electromagnetic-thermal bi-directional coupling
[J]. IEEE Transactions on Energy Conversion , 2021 , 36 (4 ):2839 -2849 .
DOI:10.1109/TEC.2021.3065336
URL
[本文引用: 1]
[14]
BOGLIETTI A CAVAGNINO A IONEL D M et al . A general model to predict the iron losses in PWM inverter-fed induction motors
[J]. IEEE Transactions on Industry Applications , 2010 , 46 (5 ):1882 -1890 .
DOI:10.1109/TIA.2010.2057393
URL
[本文引用: 1]
[15]
WANG Hairong WU Jianhua The calculation of iron losses in inverter-fed induction motors based on time-stepping FEM
[C]// 2013 International Conference on Electrical Machines and Systems (ICEMS) , 2013 :818 -821 .
[本文引用: 1]
[16]
韩力 , 蔡瑞环 , 沈超凡 , 等 .10 MW高速实心转子感应电动机损耗计算与温升分析
[J]. 电机与控制学报 , 2018 , 22 (12 ):44 -53 .
[本文引用: 1]
HAN Li CAI Ruihuan SHEN Chaofan et al . Loss calculation and temperature rise analysis of 10 MW high-speed solid rotor induction motor
[J]. Electric Machines and Control , 2018 , 22 (12 ):44 -53 .
[本文引用: 1]
[17]
谢颖 , 胡圣明 , 陈鹏 , 等 . 永磁同步电机匝间短路故障温度场分析
[J]. 电工技术学报 , 2022 , 37 (2 ):322 -331 .
[本文引用: 1]
XIE Ying HU Shengming CHEN Peng et al . Thermal field analysis on inter-turn short circuit fault of permanent magnet synchronous motor
[J]. Transactions of China Electrotechnical Society , 2022 , 37 (2 ):322 -331 .
[本文引用: 1]
[18]
XIA Y XU Y AI M et al . Temperature calculation of an induction motor in the starting process
[J]. IEEE Transactions on Applied Superconductivity , 2019 , 29 (2 ):1 -4 .
[本文引用: 1]
[19]
谢颖 , 单雪婷 , 郭金鹏 , 等 . 笼型转子导条断裂引发电机各场量变化与故障程度关联性研究
[J]. 中国电机工程学报 , 2017 , 37 (14 ):4222 -4231 .
[本文引用: 1]
XIE Ying SHAN Xueting GUO Jinpeng et al . The relationship study between field changes and faulty condition in squirrel-cage induction motor with broken bars fault
[J]. Proceedings of the CSEE , 2017 , 37 (14 ):4222 -4231 .
[本文引用: 1]
[20]
林巨广 , 赖剑斌 , 路玲 . 车用永磁同步电机转子热结构耦合分析
[J]. 合肥工业大学学报 , 2019 , 42 (2 ):172 -177 ,210.
[本文引用: 1]
LIN Juguang LAI Jianbin LU Ling Thermal-structural coupled analysis of the rotor of vehicle permanent magnet synchronous motor
[J]. Journal of Hefei University of Technology , 2019 , 42 (2 ):172 -177 ,210.
[本文引用: 1]
1
... 双斜槽转子感应电机相比于传统的单斜槽转子感应电机具有低振动噪声、大起动力矩、无轴向力等优点[1 -2 ] ,逐渐受到关注并有望作为新型驱动电机应用在新能源电动叉车上[3 ] . ...
1
... 双斜槽转子感应电机相比于传统的单斜槽转子感应电机具有低振动噪声、大起动力矩、无轴向力等优点[1 -2 ] ,逐渐受到关注并有望作为新型驱动电机应用在新能源电动叉车上[3 ] . ...
Analysis of synchronous parasitic torque in dual skew cage rotor induction motors with equivalent slot number
1
2017
... 双斜槽转子感应电机相比于传统的单斜槽转子感应电机具有低振动噪声、大起动力矩、无轴向力等优点[1 -2 ] ,逐渐受到关注并有望作为新型驱动电机应用在新能源电动叉车上[3 ] . ...
1
2018
... 双斜槽转子感应电机相比于传统的单斜槽转子感应电机具有低振动噪声、大起动力矩、无轴向力等优点[1 -2 ] ,逐渐受到关注并有望作为新型驱动电机应用在新能源电动叉车上[3 ] . ...
1
2018
... 双斜槽转子感应电机相比于传统的单斜槽转子感应电机具有低振动噪声、大起动力矩、无轴向力等优点[1 -2 ] ,逐渐受到关注并有望作为新型驱动电机应用在新能源电动叉车上[3 ] . ...
异步电机转子三维温度场及热应力场研究
1
2010
... 目前,国内外对电机温升的计算方法主要包括参数计算法、等效热路法和有限元分析法,其中有限元分析法较为常见.王艳武等[4 ] 对异步电机转子的三维温度场和热应力进行了分析,指出电机温升的高低将直接影响转子热应力的大小.谢颖等[5 ] 采用有限元法对一台小型感应电机进行三维瞬态温度场及转子应力场的计算并指出了普通斜槽转子断条故障的原因.李伟力等[6 ] 采用有限元法对直槽转子感应电机的定转子全域温度场进行了计算,并采用热传导方式等效处理了电机定转子与气隙之间复杂的对流换热过程.丁树业等[7 ] 对变频供电下直槽转子感应电机的传热特性进行了分析,并进一步揭示了变频器参数对电机温升的影响特征.文献[8 ]对变频驱动下的永磁同步电机的温升以及温升应力进行了计算,为该类电机的优化设计提供参考.文献[9 ]考虑变频器供电谐波的影响对不同磁极拓扑结构下的轴向磁通永磁同步电机的传热特性进行了分析,并研究了永磁体分段方式对温度场的影响. ...
Study on 3D thermal field and thermal stress field of the induction motor rotor
1
2010
... 目前,国内外对电机温升的计算方法主要包括参数计算法、等效热路法和有限元分析法,其中有限元分析法较为常见.王艳武等[4 ] 对异步电机转子的三维温度场和热应力进行了分析,指出电机温升的高低将直接影响转子热应力的大小.谢颖等[5 ] 采用有限元法对一台小型感应电机进行三维瞬态温度场及转子应力场的计算并指出了普通斜槽转子断条故障的原因.李伟力等[6 ] 采用有限元法对直槽转子感应电机的定转子全域温度场进行了计算,并采用热传导方式等效处理了电机定转子与气隙之间复杂的对流换热过程.丁树业等[7 ] 对变频供电下直槽转子感应电机的传热特性进行了分析,并进一步揭示了变频器参数对电机温升的影响特征.文献[8 ]对变频驱动下的永磁同步电机的温升以及温升应力进行了计算,为该类电机的优化设计提供参考.文献[9 ]考虑变频器供电谐波的影响对不同磁极拓扑结构下的轴向磁通永磁同步电机的传热特性进行了分析,并研究了永磁体分段方式对温度场的影响. ...
基于多场量的笼型感应电机三维瞬态磁热固耦合计算分析
2
2016
... 目前,国内外对电机温升的计算方法主要包括参数计算法、等效热路法和有限元分析法,其中有限元分析法较为常见.王艳武等[4 ] 对异步电机转子的三维温度场和热应力进行了分析,指出电机温升的高低将直接影响转子热应力的大小.谢颖等[5 ] 采用有限元法对一台小型感应电机进行三维瞬态温度场及转子应力场的计算并指出了普通斜槽转子断条故障的原因.李伟力等[6 ] 采用有限元法对直槽转子感应电机的定转子全域温度场进行了计算,并采用热传导方式等效处理了电机定转子与气隙之间复杂的对流换热过程.丁树业等[7 ] 对变频供电下直槽转子感应电机的传热特性进行了分析,并进一步揭示了变频器参数对电机温升的影响特征.文献[8 ]对变频驱动下的永磁同步电机的温升以及温升应力进行了计算,为该类电机的优化设计提供参考.文献[9 ]考虑变频器供电谐波的影响对不同磁极拓扑结构下的轴向磁通永磁同步电机的传热特性进行了分析,并研究了永磁体分段方式对温度场的影响. ...
... 电机三维温度场有限元模型如图12 所示,建模的过程中考虑了机壳、转轴对电机散热的影响.由于电机的绕组为散下线式绕组,绕组端部模型十分复杂,且端部绕组需要浸漆处理,浸漆对端部绝缘模型的建立存在较大影响,因此本文参考文献[5 ]建模时忽略端部绕组,同时参考文献[17 ]建立了等效的定子槽内绕组模型,这种等效能够较好地反映定子槽内的导热情况,其中等效绝缘的导热系数计算公式如下 ...
The calculations and analysis of 3D transient magnetic-thermal-solid coupling for squirrel-cage induction motors based on multi fields
2
2016
... 目前,国内外对电机温升的计算方法主要包括参数计算法、等效热路法和有限元分析法,其中有限元分析法较为常见.王艳武等[4 ] 对异步电机转子的三维温度场和热应力进行了分析,指出电机温升的高低将直接影响转子热应力的大小.谢颖等[5 ] 采用有限元法对一台小型感应电机进行三维瞬态温度场及转子应力场的计算并指出了普通斜槽转子断条故障的原因.李伟力等[6 ] 采用有限元法对直槽转子感应电机的定转子全域温度场进行了计算,并采用热传导方式等效处理了电机定转子与气隙之间复杂的对流换热过程.丁树业等[7 ] 对变频供电下直槽转子感应电机的传热特性进行了分析,并进一步揭示了变频器参数对电机温升的影响特征.文献[8 ]对变频驱动下的永磁同步电机的温升以及温升应力进行了计算,为该类电机的优化设计提供参考.文献[9 ]考虑变频器供电谐波的影响对不同磁极拓扑结构下的轴向磁通永磁同步电机的传热特性进行了分析,并研究了永磁体分段方式对温度场的影响. ...
... 电机三维温度场有限元模型如图12 所示,建模的过程中考虑了机壳、转轴对电机散热的影响.由于电机的绕组为散下线式绕组,绕组端部模型十分复杂,且端部绕组需要浸漆处理,浸漆对端部绝缘模型的建立存在较大影响,因此本文参考文献[5 ]建模时忽略端部绕组,同时参考文献[17 ]建立了等效的定子槽内绕组模型,这种等效能够较好地反映定子槽内的导热情况,其中等效绝缘的导热系数计算公式如下 ...
感应电动机定转子全域温度场数值计算及相关因素敏感性分析
2
2007
... 目前,国内外对电机温升的计算方法主要包括参数计算法、等效热路法和有限元分析法,其中有限元分析法较为常见.王艳武等[4 ] 对异步电机转子的三维温度场和热应力进行了分析,指出电机温升的高低将直接影响转子热应力的大小.谢颖等[5 ] 采用有限元法对一台小型感应电机进行三维瞬态温度场及转子应力场的计算并指出了普通斜槽转子断条故障的原因.李伟力等[6 ] 采用有限元法对直槽转子感应电机的定转子全域温度场进行了计算,并采用热传导方式等效处理了电机定转子与气隙之间复杂的对流换热过程.丁树业等[7 ] 对变频供电下直槽转子感应电机的传热特性进行了分析,并进一步揭示了变频器参数对电机温升的影响特征.文献[8 ]对变频驱动下的永磁同步电机的温升以及温升应力进行了计算,为该类电机的优化设计提供参考.文献[9 ]考虑变频器供电谐波的影响对不同磁极拓扑结构下的轴向磁通永磁同步电机的传热特性进行了分析,并研究了永磁体分段方式对温度场的影响. ...
... 通过文献[18 ]中电机三维瞬态温度场的数学模型可以看出,电机各部件表面的导热系数和对流换热系数的准确选取在一定程度上决定了电机的温度计算的准确性.在电机旋转的过程中,气隙中的换热过程十分复杂,难以精确计算气隙表面的换热系数.因此本文采用等效气隙导热系数${{\lambda }_{g}}$ [6 ] ...
Stator-rotor coupled thermal field numerical calculation of induction motors and correlated factors sensitivity analysis
2
2007
... 目前,国内外对电机温升的计算方法主要包括参数计算法、等效热路法和有限元分析法,其中有限元分析法较为常见.王艳武等[4 ] 对异步电机转子的三维温度场和热应力进行了分析,指出电机温升的高低将直接影响转子热应力的大小.谢颖等[5 ] 采用有限元法对一台小型感应电机进行三维瞬态温度场及转子应力场的计算并指出了普通斜槽转子断条故障的原因.李伟力等[6 ] 采用有限元法对直槽转子感应电机的定转子全域温度场进行了计算,并采用热传导方式等效处理了电机定转子与气隙之间复杂的对流换热过程.丁树业等[7 ] 对变频供电下直槽转子感应电机的传热特性进行了分析,并进一步揭示了变频器参数对电机温升的影响特征.文献[8 ]对变频驱动下的永磁同步电机的温升以及温升应力进行了计算,为该类电机的优化设计提供参考.文献[9 ]考虑变频器供电谐波的影响对不同磁极拓扑结构下的轴向磁通永磁同步电机的传热特性进行了分析,并研究了永磁体分段方式对温度场的影响. ...
... 通过文献[18 ]中电机三维瞬态温度场的数学模型可以看出,电机各部件表面的导热系数和对流换热系数的准确选取在一定程度上决定了电机的温度计算的准确性.在电机旋转的过程中,气隙中的换热过程十分复杂,难以精确计算气隙表面的换热系数.因此本文采用等效气隙导热系数${{\lambda }_{g}}$ [6 ] ...
PWM变频器供电的感应电机传热特性
1
2016
... 目前,国内外对电机温升的计算方法主要包括参数计算法、等效热路法和有限元分析法,其中有限元分析法较为常见.王艳武等[4 ] 对异步电机转子的三维温度场和热应力进行了分析,指出电机温升的高低将直接影响转子热应力的大小.谢颖等[5 ] 采用有限元法对一台小型感应电机进行三维瞬态温度场及转子应力场的计算并指出了普通斜槽转子断条故障的原因.李伟力等[6 ] 采用有限元法对直槽转子感应电机的定转子全域温度场进行了计算,并采用热传导方式等效处理了电机定转子与气隙之间复杂的对流换热过程.丁树业等[7 ] 对变频供电下直槽转子感应电机的传热特性进行了分析,并进一步揭示了变频器参数对电机温升的影响特征.文献[8 ]对变频驱动下的永磁同步电机的温升以及温升应力进行了计算,为该类电机的优化设计提供参考.文献[9 ]考虑变频器供电谐波的影响对不同磁极拓扑结构下的轴向磁通永磁同步电机的传热特性进行了分析,并研究了永磁体分段方式对温度场的影响. ...
Characteristics of heat transfer for induction motor supplied by PWM converter
1
2016
... 目前,国内外对电机温升的计算方法主要包括参数计算法、等效热路法和有限元分析法,其中有限元分析法较为常见.王艳武等[4 ] 对异步电机转子的三维温度场和热应力进行了分析,指出电机温升的高低将直接影响转子热应力的大小.谢颖等[5 ] 采用有限元法对一台小型感应电机进行三维瞬态温度场及转子应力场的计算并指出了普通斜槽转子断条故障的原因.李伟力等[6 ] 采用有限元法对直槽转子感应电机的定转子全域温度场进行了计算,并采用热传导方式等效处理了电机定转子与气隙之间复杂的对流换热过程.丁树业等[7 ] 对变频供电下直槽转子感应电机的传热特性进行了分析,并进一步揭示了变频器参数对电机温升的影响特征.文献[8 ]对变频驱动下的永磁同步电机的温升以及温升应力进行了计算,为该类电机的优化设计提供参考.文献[9 ]考虑变频器供电谐波的影响对不同磁极拓扑结构下的轴向磁通永磁同步电机的传热特性进行了分析,并研究了永磁体分段方式对温度场的影响. ...
永磁同步电机三维全域温度场与温度应力耦合研究
1
2018
... 目前,国内外对电机温升的计算方法主要包括参数计算法、等效热路法和有限元分析法,其中有限元分析法较为常见.王艳武等[4 ] 对异步电机转子的三维温度场和热应力进行了分析,指出电机温升的高低将直接影响转子热应力的大小.谢颖等[5 ] 采用有限元法对一台小型感应电机进行三维瞬态温度场及转子应力场的计算并指出了普通斜槽转子断条故障的原因.李伟力等[6 ] 采用有限元法对直槽转子感应电机的定转子全域温度场进行了计算,并采用热传导方式等效处理了电机定转子与气隙之间复杂的对流换热过程.丁树业等[7 ] 对变频供电下直槽转子感应电机的传热特性进行了分析,并进一步揭示了变频器参数对电机温升的影响特征.文献[8 ]对变频驱动下的永磁同步电机的温升以及温升应力进行了计算,为该类电机的优化设计提供参考.文献[9 ]考虑变频器供电谐波的影响对不同磁极拓扑结构下的轴向磁通永磁同步电机的传热特性进行了分析,并研究了永磁体分段方式对温度场的影响. ...
Coupling study of 3D universal temperature field and temperature stress for permanent magnet synchronous motor
1
2018
... 目前,国内外对电机温升的计算方法主要包括参数计算法、等效热路法和有限元分析法,其中有限元分析法较为常见.王艳武等[4 ] 对异步电机转子的三维温度场和热应力进行了分析,指出电机温升的高低将直接影响转子热应力的大小.谢颖等[5 ] 采用有限元法对一台小型感应电机进行三维瞬态温度场及转子应力场的计算并指出了普通斜槽转子断条故障的原因.李伟力等[6 ] 采用有限元法对直槽转子感应电机的定转子全域温度场进行了计算,并采用热传导方式等效处理了电机定转子与气隙之间复杂的对流换热过程.丁树业等[7 ] 对变频供电下直槽转子感应电机的传热特性进行了分析,并进一步揭示了变频器参数对电机温升的影响特征.文献[8 ]对变频驱动下的永磁同步电机的温升以及温升应力进行了计算,为该类电机的优化设计提供参考.文献[9 ]考虑变频器供电谐波的影响对不同磁极拓扑结构下的轴向磁通永磁同步电机的传热特性进行了分析,并研究了永磁体分段方式对温度场的影响. ...
不同磁极拓扑结构的轴向磁通永磁同步电机传热的研究
1
2022
... 目前,国内外对电机温升的计算方法主要包括参数计算法、等效热路法和有限元分析法,其中有限元分析法较为常见.王艳武等[4 ] 对异步电机转子的三维温度场和热应力进行了分析,指出电机温升的高低将直接影响转子热应力的大小.谢颖等[5 ] 采用有限元法对一台小型感应电机进行三维瞬态温度场及转子应力场的计算并指出了普通斜槽转子断条故障的原因.李伟力等[6 ] 采用有限元法对直槽转子感应电机的定转子全域温度场进行了计算,并采用热传导方式等效处理了电机定转子与气隙之间复杂的对流换热过程.丁树业等[7 ] 对变频供电下直槽转子感应电机的传热特性进行了分析,并进一步揭示了变频器参数对电机温升的影响特征.文献[8 ]对变频驱动下的永磁同步电机的温升以及温升应力进行了计算,为该类电机的优化设计提供参考.文献[9 ]考虑变频器供电谐波的影响对不同磁极拓扑结构下的轴向磁通永磁同步电机的传热特性进行了分析,并研究了永磁体分段方式对温度场的影响. ...
Heat transfer of axial flux permanent magnet motor with different magnetic pole topologies
1
2022
... 目前,国内外对电机温升的计算方法主要包括参数计算法、等效热路法和有限元分析法,其中有限元分析法较为常见.王艳武等[4 ] 对异步电机转子的三维温度场和热应力进行了分析,指出电机温升的高低将直接影响转子热应力的大小.谢颖等[5 ] 采用有限元法对一台小型感应电机进行三维瞬态温度场及转子应力场的计算并指出了普通斜槽转子断条故障的原因.李伟力等[6 ] 采用有限元法对直槽转子感应电机的定转子全域温度场进行了计算,并采用热传导方式等效处理了电机定转子与气隙之间复杂的对流换热过程.丁树业等[7 ] 对变频供电下直槽转子感应电机的传热特性进行了分析,并进一步揭示了变频器参数对电机温升的影响特征.文献[8 ]对变频驱动下的永磁同步电机的温升以及温升应力进行了计算,为该类电机的优化设计提供参考.文献[9 ]考虑变频器供电谐波的影响对不同磁极拓扑结构下的轴向磁通永磁同步电机的传热特性进行了分析,并研究了永磁体分段方式对温度场的影响. ...
SPWM型变频器供电下异步电机电磁噪声
1
2014
... 正弦脉冲宽度调制(Sinusoidal pulse width modulation, SPWM)是电机变频调速领域使用最为广泛的调制方式,被广泛应用于各行各业的驱动电路中[10 ] .其基本原理是将正弦波等效为一系列等幅不等宽的矩形脉冲波,其脉冲宽度一般由正弦调制波和三角载波自然相交而得到.典型的单相双极性SPWM的控制波形如图1 所示.当调制波信号大于载波信号时,输出电压为U ,反之输出电压为-U . ...
Electromagnetic noise of induction motor under SPWM inverter power supply
1
2014
... 正弦脉冲宽度调制(Sinusoidal pulse width modulation, SPWM)是电机变频调速领域使用最为广泛的调制方式,被广泛应用于各行各业的驱动电路中[10 ] .其基本原理是将正弦波等效为一系列等幅不等宽的矩形脉冲波,其脉冲宽度一般由正弦调制波和三角载波自然相交而得到.典型的单相双极性SPWM的控制波形如图1 所示.当调制波信号大于载波信号时,输出电压为U ,反之输出电压为-U . ...
1
2009
... 电机是机电能量转换的机构,在能量转换的过程中会产生损耗,成为电机温度场计算中的热源.当正弦电源供电时电机内的损耗主要包括定转子基波铜/铝耗、基本铁耗、机械损耗和杂散损耗.当变频供电时,由于高次谐波的存在,电机的内部会产生以下附加损耗[11 ] :① 高次谐波带来的电机附加 定子铜耗;② 高次谐波带来的电机附加铁心损耗;③ 高次谐波及其作用下的集肤效应所带来的附加转子铝耗.这些由电源高次谐波所引入的附加损耗,将会使得电机的温升进一步增加. ...
1
2009
... 电机是机电能量转换的机构,在能量转换的过程中会产生损耗,成为电机温度场计算中的热源.当正弦电源供电时电机内的损耗主要包括定转子基波铜/铝耗、基本铁耗、机械损耗和杂散损耗.当变频供电时,由于高次谐波的存在,电机的内部会产生以下附加损耗[11 ] :① 高次谐波带来的电机附加 定子铜耗;② 高次谐波带来的电机附加铁心损耗;③ 高次谐波及其作用下的集肤效应所带来的附加转子铝耗.这些由电源高次谐波所引入的附加损耗,将会使得电机的温升进一步增加. ...
电压偏差条件下笼型感应电机的损耗特性
1
2010
... 当PWM供电时,电机的绕组电流中含有高频的时间谐波分量,产生附加的谐波损耗.采用有限元法计算时可以考虑高频谐波电流的影响,其计算的表达式为[12 ] ...
Losses characteristics of cage induction motors under voltage deviation conditions
1
2010
... 当PWM供电时,电机的绕组电流中含有高频的时间谐波分量,产生附加的谐波损耗.采用有限元法计算时可以考虑高频谐波电流的影响,其计算的表达式为[12 ] ...
Loss and thermal analysis for high speed amorphous metal PMSMs using 3-D electromagnetic-thermal bi-directional coupling
1
2021
... 根据传统Bertotti分立铁耗计算理论,在标准正弦供电条件下,电机的铁耗主要分为磁滞损耗、涡流损耗和附加损耗,其表达式如下[13 ] ...
A general model to predict the iron losses in PWM inverter-fed induction motors
1
2010
... 对于电机非正弦供电的情况,传统的Bertotti铁耗模型难以准确地计算铁耗,常用方法是对电机铁心内各个节点的磁密波形进行谐波分析,然后分别将各次谐波单独作用下的铁耗进行叠加.但该方法用于三维有限元模型时,其计算过程复杂,计算数量极大.BOGLIETTI等[14 ] 提出了非正弦供电下的铁心损耗可以用正弦基波的磁滞损耗和涡流损耗来表示.基于这一理论,浙江大学WANG等[15 ] 推导出了适合计算变频供电下的电机铁耗计算模型,并通过试验验证了其良好效果,表达式如下 ...
The calculation of iron losses in inverter-fed induction motors based on time-stepping FEM
1
2013
... 对于电机非正弦供电的情况,传统的Bertotti铁耗模型难以准确地计算铁耗,常用方法是对电机铁心内各个节点的磁密波形进行谐波分析,然后分别将各次谐波单独作用下的铁耗进行叠加.但该方法用于三维有限元模型时,其计算过程复杂,计算数量极大.BOGLIETTI等[14 ] 提出了非正弦供电下的铁心损耗可以用正弦基波的磁滞损耗和涡流损耗来表示.基于这一理论,浙江大学WANG等[15 ] 推导出了适合计算变频供电下的电机铁耗计算模型,并通过试验验证了其良好效果,表达式如下 ...
MW高速实心转子感应电动机损耗计算与温升分析
1
2018
... 电机运行时转子导条存在集肤效应,趋于转子外表面的电流密度高.有限元计算变频电机转转子铝耗时,可以考虑谐波成分及集肤效应对损耗的影响,其表达式为[16 ] ...
Loss calculation and temperature rise analysis of 10 MW high-speed solid rotor induction motor
1
2018
... 电机运行时转子导条存在集肤效应,趋于转子外表面的电流密度高.有限元计算变频电机转转子铝耗时,可以考虑谐波成分及集肤效应对损耗的影响,其表达式为[16 ] ...
永磁同步电机匝间短路故障温度场分析
1
2022
... 电机三维温度场有限元模型如图12 所示,建模的过程中考虑了机壳、转轴对电机散热的影响.由于电机的绕组为散下线式绕组,绕组端部模型十分复杂,且端部绕组需要浸漆处理,浸漆对端部绝缘模型的建立存在较大影响,因此本文参考文献[5 ]建模时忽略端部绕组,同时参考文献[17 ]建立了等效的定子槽内绕组模型,这种等效能够较好地反映定子槽内的导热情况,其中等效绝缘的导热系数计算公式如下 ...
Thermal field analysis on inter-turn short circuit fault of permanent magnet synchronous motor
1
2022
... 电机三维温度场有限元模型如图12 所示,建模的过程中考虑了机壳、转轴对电机散热的影响.由于电机的绕组为散下线式绕组,绕组端部模型十分复杂,且端部绕组需要浸漆处理,浸漆对端部绝缘模型的建立存在较大影响,因此本文参考文献[5 ]建模时忽略端部绕组,同时参考文献[17 ]建立了等效的定子槽内绕组模型,这种等效能够较好地反映定子槽内的导热情况,其中等效绝缘的导热系数计算公式如下 ...
Temperature calculation of an induction motor in the starting process
1
2019
... 通过文献[18 ]中电机三维瞬态温度场的数学模型可以看出,电机各部件表面的导热系数和对流换热系数的准确选取在一定程度上决定了电机的温度计算的准确性.在电机旋转的过程中,气隙中的换热过程十分复杂,难以精确计算气隙表面的换热系数.因此本文采用等效气隙导热系数${{\lambda }_{g}}$ [6 ] ...
笼型转子导条断裂引发电机各场量变化与故障程度关联性研究
1
2017
... 感应电机负载运行的过程中,转子会产生较大的温升,使其受热膨胀.由于电机转子各部件材料膨胀系数的不同以及外在结构的约束,会产生较大的热应力,成为电机转子断条与断环故障的重要诱因[19 ] .双斜槽转子结构具有特殊性,其较薄的中间环结构在热应力的作用下可能存在潜在的中环断裂风险.因此分析双斜槽鼠笼转子热应力的分布情况,可以为双斜槽转子中间环的优化设计提供重要的参考. ...
The relationship study between field changes and faulty condition in squirrel-cage induction motor with broken bars fault
1
2017
... 感应电机负载运行的过程中,转子会产生较大的温升,使其受热膨胀.由于电机转子各部件材料膨胀系数的不同以及外在结构的约束,会产生较大的热应力,成为电机转子断条与断环故障的重要诱因[19 ] .双斜槽转子结构具有特殊性,其较薄的中间环结构在热应力的作用下可能存在潜在的中环断裂风险.因此分析双斜槽鼠笼转子热应力的分布情况,可以为双斜槽转子中间环的优化设计提供重要的参考. ...
车用永磁同步电机转子热结构耦合分析
1
2019
... 以三维瞬态温度场的计算结果为载荷激励,将各个节点单元的温度施加到结构场有限元模型中以求解热载荷作用下的转子应力分布.参考弹性力学相关知识,热应力计算的有限元方程可以表示为[20 ] ...
Thermal-structural coupled analysis of the rotor of vehicle permanent magnet synchronous motor
1
2019
... 以三维瞬态温度场的计算结果为载荷激励,将各个节点单元的温度施加到结构场有限元模型中以求解热载荷作用下的转子应力分布.参考弹性力学相关知识,热应力计算的有限元方程可以表示为[20 ] ...