基于FFT和三次Hermite插值的人体触电判据初探*

doi:10.11985/2023.01.015

基于FFT和三次Hermite插值的人体触电判据初探^*

王欣阳^,, 魏云冰^,, 徐浩^,

上海工程技术大学电子电气工程学院上海 201620

Preliminary Study on the Human Body Electric Shock Criterion Based on FFT and Cubic Hermite Interpolation

WANG Xinyang^,, WEI Yunbing^,, XU Hao^,

School of Electronic and Electrical Engineering, Shanghai University of Engineering Science, Shanghai 201620

通讯作者: 王欣阳，男，1997年生，硕士研究生。主要研究方向为电力系统自动化、智能运检。E-mail：474494759@qq.com

收稿日期: 2021-08-2 修回日期: 2021-09-27

基金资助:

*多状态信息聚合的配电网联网低压智能开关技术研究与应用资助项目. 5211DS190034

Received: 2021-08-2 Revised: 2021-09-27

作者简介 About authors

魏云冰，男，1970年生，博士，教授。主要研究方向为电力系统自动化、智能运检。E-mail：ee_dmegc@263.net

徐浩，男，1996年生，硕士研究生。主要研究方向为电力系统自动化、智能运检。E-mail：948915032@qq.com

摘要

针对当前基于TT系统(电气设备的金属外壳直接接地的保护系统)的低电压配电网输电线路上的剩余电流保护设备无法保证人触电后马上动作的现状，首先搭建活体触电试验平台，通过单相电压有效值220 V、频率50 Hz的电源对猪表皮进行触电试验，并使用控制变量的方法研究触电波形和触电面积、触电湿度以及触电时漏电电流大小之间的关系，得到试验数据；其次，对试验数据进行处理，使用FFT计算触电时刻的谐波畸变率，使用三次Hermite插值算法，绘制触电波形包络线，计算包络线不同时刻的斜率；最后，选择谐波畸变率最小值和合适的斜率，搭建仿真平台，对试验数据拟合得到的人体阻抗进行触电仿真，使用谐波畸变率和波形峰值斜率变化作为剩余电流保护设备触电判断依据，验证了所提判据的可行性。

关键词： TT系统 ; 触电试验 ; 动态阻抗模型 ; 快速傅里叶变换 ; 三次Hermite插值

Abstract

To address the current situation that residual current protection equipment on transmission lines of low-voltage distribution networks based on TT systems(protection systems where the metal enclosures of electrical equipment are directly grounded) cannot guarantee immediate action after human electrocution, firstly, the in vivo electrocution experiment platform is built, and the electrocution experiment is conducted on the pig epidermis through the power supply with single-phase voltage RMS 220 V and frequency 50 Hz, and the relationship between the electrocution waveform and the electrocution area, the electrocution humidity and the leakage current magnitude at the time of electrocution is studied using the method of control variables to obtain the experimental data; secondly, the experimental data are processed, and the harmonic distortion rate at the moment of touching is calculated using FFT, and the touching waveform envelope is plotted using the cubic Hermite interpolation algorithm to calculate the slope of the envelope at different moments. Finally, the minimum value of harmonic distortion rate and suitable slope are selected, and the simulation platform is built to simulate the human body impedance obtained by fitting the experimental data, and the changes of harmonic distortion rate and peak slope of waveform are used as the basis for judging the electrocution of residual current protection equipment. The feasibility of the proposed criterion is verified.

Keywords： TT system ; electric shock test ; dynamic impedance model ; fast Fourier transform ; cubic Hermite interpolation

PDF (681KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王欣阳, 魏云冰, 徐浩. 基于FFT和三次Hermite插值的人体触电判据初探^*. 电气工程学报[J], 2023, 18(1): 133-142 doi:10.11985/2023.01.015

WANG Xinyang, WEI Yunbing, XU Hao. Preliminary Study on the Human Body Electric Shock Criterion Based on FFT and Cubic Hermite Interpolation. Chinese Journal of Electrical Engineering[J], 2023, 18(1): 133-142 doi:10.11985/2023.01.015

1 引言

近年来，人身触电事故在基于TT系统的低压配电网中时有发生，特别是在配电网变压之后到用户的这段线路上，而目前的剩余电流保护断路器仍然停留在传统的工作模式，即通过判断电流是否超过设定的整定值来决定保护器是否动作。对于在用户侧，这个模式是可以使用的，因为漏电电流小，用户家庭中的漏电保护器整定值小，动作时间短，可以有效地保护人身安全，而在传输到用户的这段线路上，由于线损、重复接地、多用户漏电故障叠加等问题，会使漏电电流增大，从而导致漏电保护器的误动。因此，为了防止误动，一般都将整定值提高并增加延迟，以保证网络的正常运作，这就导致如果此线路上发生人身触电事故，输电线上中间保护和总保护不能马上动作，从而造成人员伤亡。

通过对人身触电事故的调查表明，最主要的原因为冒险带电作业和安全防护装置缺失，而安全防护装置缺失就涉及到是否安装剩余电流保护器和剩余电流保护器功能的问题^[1]。而市面上的剩余电流保护器一般具有过载保护、过流保护等基本功能，而不具备识别人体触电的功能。因此，有必要对剩余电流保护器增加人体触电判据功能展开进一步的研究。

剩余电流保护在配电网风险安全管控中是非常重要的一个环节。施工人员在检修或维护配电网输电线路时，剩余电流保护可以有效地保护施工人员的生命安全，保障施工安全，提高配电网工程的施工效率，对社会经济的健康平稳发展带来积极作用^{[2⇓⇓⇓-6]}。

滕松林^[7]提出漏电电流为一个稳定的正弦周期电流，即使有时受气候条件变化的影响而发生变化，也是非常缓慢的，在一二个周期里显示不出来。而人身触电所产生的波形随时间的增加，幅值也在增加，并且在一到三个周期里会有明显的变化。因此利用人体触电电流起始过程的非正弦性，用此信号来控制保护装置的动作机构，从而达到十分理想的触电保护特性。但其仅涉及人体触电特性以及剩余电流保护器进行人体触电识别的理论说明，并未给出详细数值。潘永长等^[8]对触电波形进行谐波研究，对波形进行FFT变换，得到触电时的谐波畸变率相较正常运作时会高很多，通过对剩余电流断路器施加双重判据，从而达到既可以识别到人体触电并及时动作，又可以降低误动的情况。但仅通过判断谐波畸变率和电流整定值来判断人体触电还是会在一定程度上造成误动，非人体触电产生的漏电也会产生谐波，谐波畸变率若超出所设值，保护器可能会造成误动。许冠炜等^[9]通过对现有常见的几种人体阻抗模型进行漏电仿真试验，并发现触电瞬间电流波形发生振荡这一特征，提出可以利用这一特征设计漏电保护器，但未给出详细实现方案。陈航宇等^[10]对福建部分地区低压配电网进行调研，提出当前低压配电网及其剩余电流保护运行所存在的问题，如线路绝缘老化，线路共零、传零，雷击引发跳闸等，并给出相关建议和措施。任龙霞^[11]对国内外活体触电保护现状进行了分析，并说明了研究活体触电识别的意义。

本文从分析触电电流的谐波畸变率和不同时刻波形峰值的角度研究触电判据，进而提出通过谐波畸变率判断触电时刻并将触电波形峰值变化斜率作为人体触电判据，以达到降低人身触电伤亡的目的。

2 算法介绍

2.1 快速傅里叶变换算法

快速傅里叶变换算法(Fast Fourier transform，FFT)将波形转化为频域和时域表达式，进而可以对波形进行分析^[12⇓-14]。

假设电流的时域周期信号为I(t)，则频域上的表达式为

(1)$I\left( \omega \right)=\int_{-\infty }^{+\infty }{i\left( t \right)}\exp (-\text{j}\omega t)dt$

式中，ω为频域变量；i为电流瞬时值；t为时域变量。将式(1)展开，得到电流时域和频域的转化

(2)$\begin{matrix} I\left( t \right)=\frac{{{a}_{0}}}{2}+\sum\limits_{1}^{\infty }{{{a}_{n}}\cos \left( n\omega t \right)}+{{b}_{n}}\sin \left( n\omega t \right) \\ n=1,2,\cdots,20 \\\end{matrix}$

基波幅值为

(3)${{I}_{F}}={{a}_{1}}\cos \left( \text{j}\omega t \right)+{{b}_{1}}\sin \left( \text{j}\omega t \right)$

谐波幅值为

(4)${{H}_{n}}=\sqrt{a_{n}^{2}+b_{n}^{2}}\ \ \ n\ge 2$

式中，a₀为直流分量；n为谐波次数；a_n、b_n为傅里叶系数，如式(5)、(6)所示

(5)${{a}_{n}}=\frac{2}{T}\int_{\ t-T}^{\ t}{I\left( t \right)}\cos \left( n\omega t \right)dt$

(6)${{b}_{n}}=\frac{2}{T}\int_{\ t-T}^{\ t}{I\left( t \right)}\sin \left( n\omega t \right)dt$

总谐波失真率THD为

(7)$THD=\frac{\sqrt{\sum\limits_{2}^{n}{H_{n}^{2}}}}{\sqrt{I_{F}^{2}+\sum\limits_{2}^{n}{H_{n}^{2}}}}$

2.2 三次Hermite插值算法

假设波形函数为f(x)，已知相邻插值节点x₀、x₁，其函数值和导数分别为

(8)$y_i=f\big(\begin{matrix}x_i\end{matrix}\big)\quad m_i=f'\big(x_i\big)\quad i=0,1$

要求的是一次数不超过3的多项式H₃(x)，使满足

(9)${{H}_{3}}\left( {{x}_{i}} \right)={{y}_{i}}\ \ \ {{{H}'}_{3}}\left( {{x}_{i}} \right)={{m}_{i}}\mathop{{}}^{{}}i=0,1$

称H₃(x)为三次Hermite插值多项式^[15⇓-17]。

3 实物试验

3.1 试验平台和试验过程

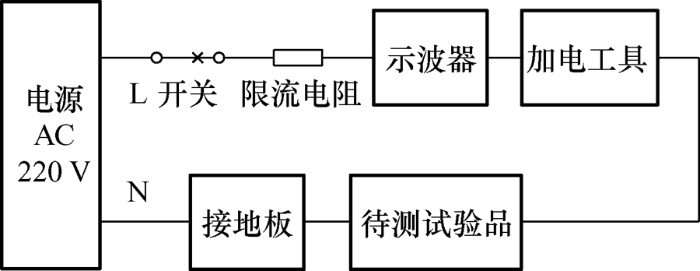
如图1所示，试验平台使用单相电源，电压有效值为220 V，频率50 Hz，接入保护器，保护器引出两根线，一根火线，一根零线。使用电流互感器测量漏电流，将其接入示波器通道1。为了防止试验线路直接短路，因此，火线接限流电阻后，再接示波器通道2探针，零线接待测试试验品的接地板上，测量试验品两端的电压。试验品选用哺乳动物的局部组织，本次试验中选用猪表皮来进行试验。示波器采样频率为10 MHz。实际接线^[18]如图2所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 试验电路图

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 实际接线图

以下试验中使用的猪表皮均来自同一块。为了研究在不同漏电流情况下人体触电电流的波形，选用可使线路中漏电流有效值保持在30 mA、100 mA、300 mA、500 mA的限流电阻。

为了研究不同触电面积下电流的波形，分别选用0.5 cm²、5 cm²、10 cm²的铜片，夹在示波器通道2的探针上，来模拟人手指点触导线，手背接触导线以及手握导线的情况。

为了研究在不同湿度下触电电流的波形，将猪表皮均匀切成三块，以达到最大限度降低试验误差的目的，对三块猪表皮分别进行干燥、半湿润和湿润处理。其中，将一块猪表皮用纸擦干，以手摸上去光滑，手上无水分残留作为干燥处理；将一块猪表皮用纸擦干，用喷壶对其表面进行喷水，水未凝结成大颗水珠，以手摸上去，手上有水分残留作为半湿润处理；将一块猪表皮用纸擦干，用喷壶对其表面进行喷水，以有大颗水珠存在作为湿润处理。用以上三种处理方式来模拟晴天、早晨湿度大以及雨天的情况。

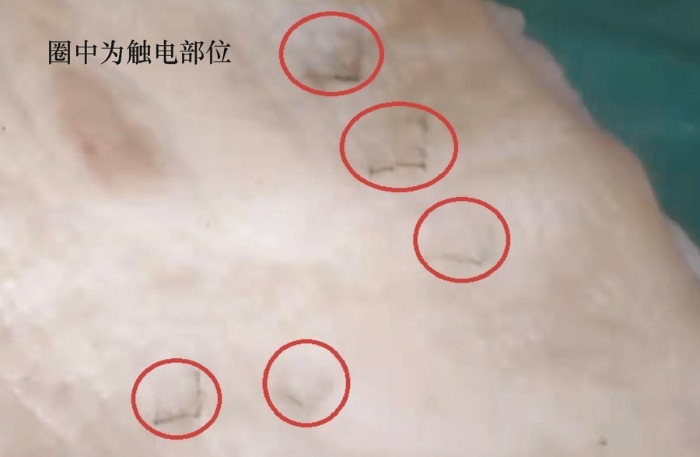
按照上述参数，对三块进行不同湿度处理的猪表皮进行数百次试验。将猪表皮放在接地板上，闭合保护器的开关，用示波器探针上的铜片触碰猪表皮。触电试验后的猪表皮状态如图3所示。观察示波器所示波形，并将其数据导出。最终选取不同参数下共36组数据作为分析依据。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 触电试验后猪表皮状态

3.2 试验数据分析

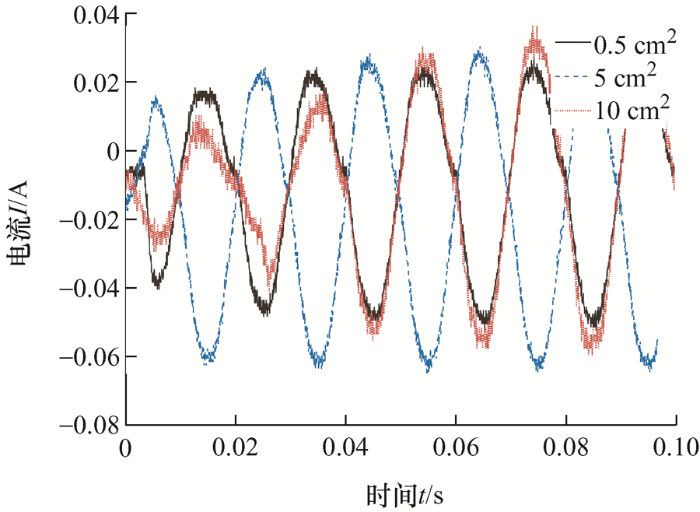
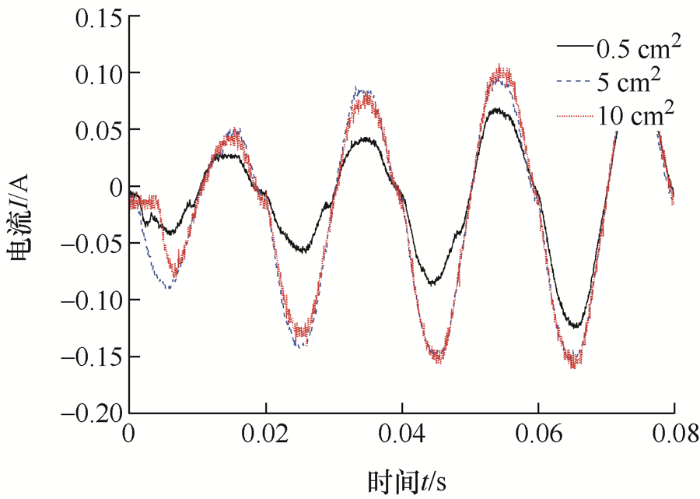
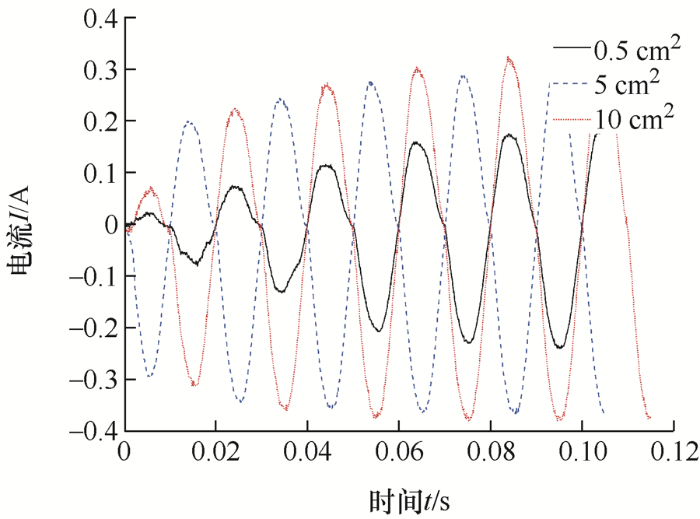
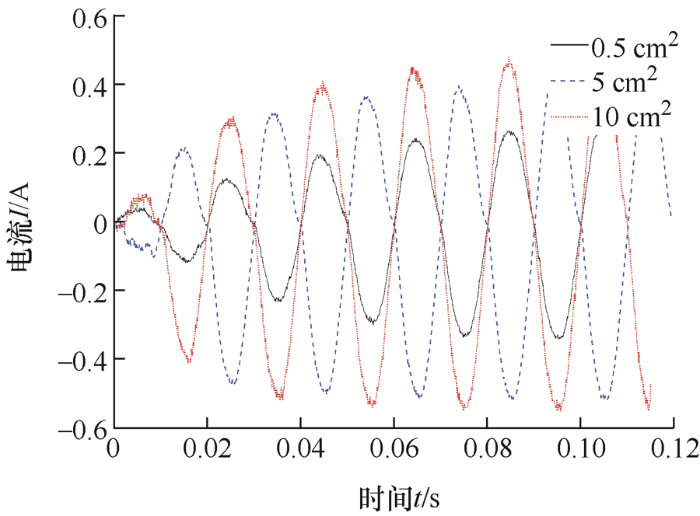
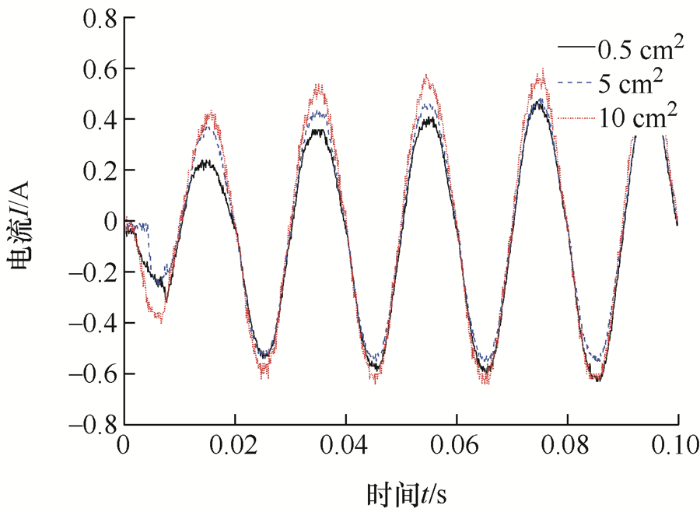
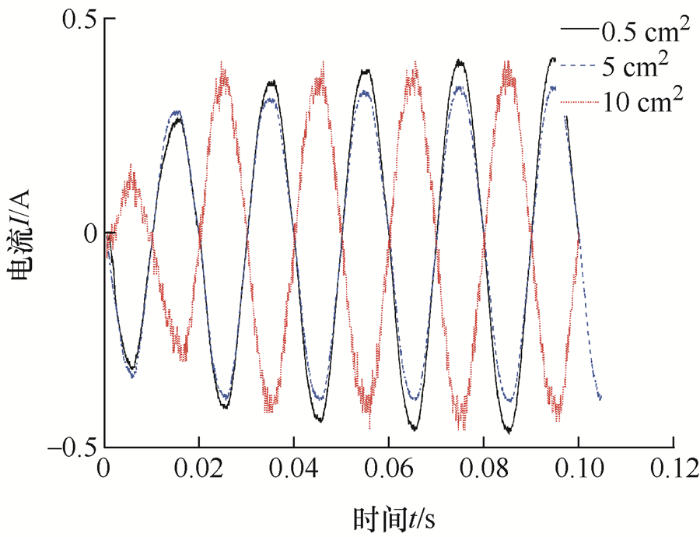
将36组数据进行绘图，截取故障波形。由图4~7可知，在干燥条件下，限制电流30 mA和100 mA的情况下，接触面积的改变不会导致波形大幅度改变，而在限制电流300 mA和500 mA的情况下，接触面积0.5 cm²的波形幅值相较接触面积5 cm²和10 cm²的波形幅值小一倍左右。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 干燥条件、限制电流30 mA

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 干燥条件、限制电流100 mA

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 干燥条件、限制电流300 mA

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 干燥条件、限制电流500 mA

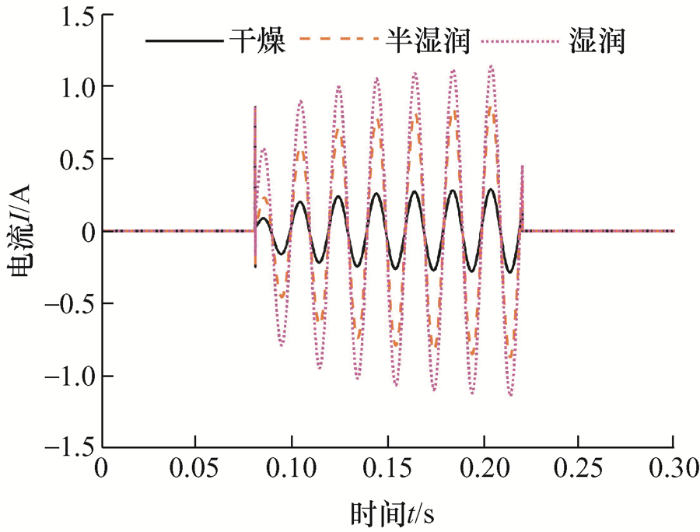
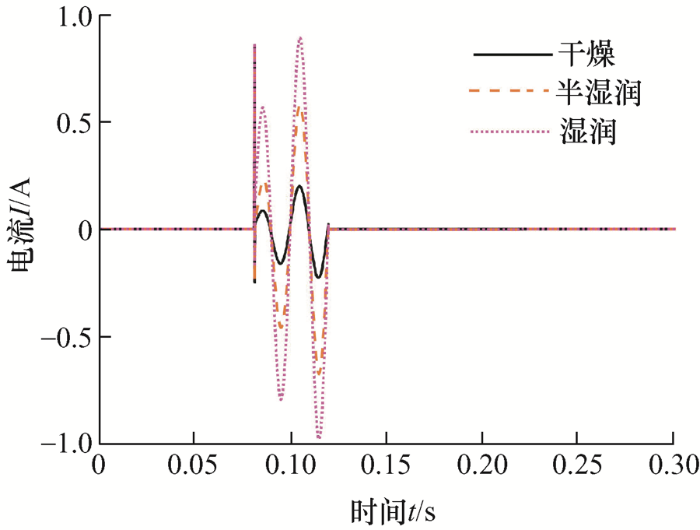
由图8、9可知，在半湿润和湿润条件下，在相同限制电流的情况下，接触面积的改变不会引起波形幅值大幅度改变。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 半湿润条件、限制电流500 mA

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 湿润条件、限制电流300 mA

由图3可以看出，猪表皮触电后，触电部位出现了碳化，表皮被击穿，根据GB/T 13870.1—2008《电流对人和家畜的效应第1部分：通用部分》中所述，皮肤击穿前阻值会比击穿后阻值大1 kΩ左右^[19]。通过观察上述波形，虽然这些波形因为限制电流、湿度和接触面积的不同，幅值都不同，但是都具有相同的特点，即在故障开始后，第二个周波幅值都会比第一个周波幅值大。有些波形在第三个周波幅值上还会比第二个周波幅值大。这就说明了皮肤阻值在触电后是时变的。

3.2.1 试验数据FFT处理

对36组波形计算触电时刻的谐波畸变率，如表1所示。当发生触电时，系统中会产生大量谐波，谐波畸变率都在5%以上，有些甚至超过100%，文献[8]中，潘永长等已经证明谐波畸变率在人体触电时会激增，并提出了一个人体触电判据。因此可以将谐波畸变率检测加入到触电判据中，作为判断人体触电开始的时刻。

表1 干燥、半湿润以及湿润情况下谐波畸变率

限制电流/mA	触电面积/cm²	谐波畸变率(%)
限制电流/mA	触电面积/cm²	干燥情况	半湿润情况	湿润情况
30	0.5	5.49	25.72	83.33
100	0.5	71.52	16.49	15.48
300	0.5	18.97	41.93	49.97
500	0.5	15.07	10.16	68.93
30	5	154.52	43.46	9.81
100	5	14.65	44.26	33.83
300	5	11.25	100.01	75.15
500	5	138.52	39.60	66.10
30	10	30.28	16.66	9.81
100	10	43.67	137.77	93.29
300	10	43.60	44.78	340.09
500	10	51.63	5.75	243.47

新窗口打开| 下载CSV

3.2.2 试验波形包络线分析

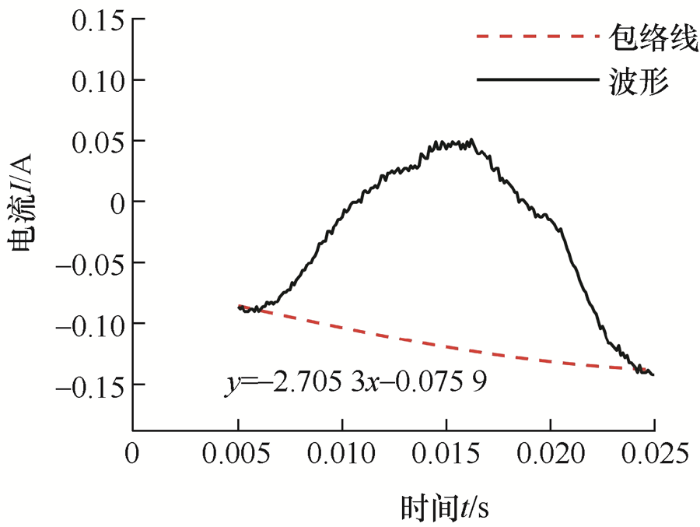
绘制包络线可以直观地看出触电电流变化的规律。对36组触电波形进行绘制包络线，如图10所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 触电波形包络线

从包络线可观察到，触电开始后，电流幅值在不断变大，直至电流幅值几乎没有变化。在触电后前两个周期内，电流幅值变化量较大，因此可以提取相应特征作为触电判据。

根据漏电流大小、触电接触面积以及湿度的不同，人体触电所产生的触电电流大小、各周波幅值间的变化也会不同，因此，选取波峰间斜率可以不受电流大小的影响直观地从数据上分析出各周波幅值间的变化。特征提取第一个周波前半周期峰值和第二个周波前半周期峰值之间的斜率以及第一个周波后半周期峰值和第二个周波后半周期峰值之间的斜率，斜率特征提取如图11所示。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 波形峰值斜率曲线

所有试验数据如表2所示。其中斜率1是第一第二周波前半周期峰值之间的斜率，斜率2是第一第二周波后半周期峰值之间的斜率。

表2 干燥、半湿润以及湿润情况下斜率

限制电流/mA	触电面积/cm²	干燥情况		半湿润情况		湿润情况
限制电流/mA	触电面积/cm²	斜率1	斜率2	斜率1	斜率2	斜率1	斜率2
30	0.5	0.359 6	0.251 6	0.201 0	0.242 5	1.057 2	0.107 8
100	0.5	0.822 4	0.066 5	1.348 3	1.183 2	2.293 1	1.150 0
300	0.5	2.719 1	3.024 2	7.879 3	2.576 9	4.399 4	4.400 8
500	0.5	4.227 9	4.859 3	13.647 5	3.510 7	7.407 5	3.521 4
30	5	0.451 3	0.113 2	0.134 9	0.052 3	0.748 7	0.056 0
100	5	2.705 3	2.075 6	0.949 1	0.566 9	1.424 0	0.303 1
300	5	2.297 6	2.096 4	2.485 9	0.924 1	2.666 2	0.811 4
500	5	5.655 8	1.561 7	9.334 0	3.501 8	10.530 0	0.994 8
30	10	0.650 2	0.328 1	0.650 2	0.075 1	0.748 7	0.013 2
100	10	3.103 5	1.653 2	1.575 0	0.538 1	2.313 9	0.227 3
300	10	7.746 3	2.126 5	8.286 2	6.976 5	11.152 0	6.153 8
500	10	7.087 8	5.018 6	9.457 8	4.604 1	16.395 0	4.920 2

新窗口打开| 下载CSV

表2的试验数据中大部分斜率1都比斜率2大，说明波形的变化随着时间的推移在慢慢变缓，根据这一特征，通过选择合适的斜率可以作为人体触电的判据。

4 触电仿真试验

4.1 试验平台和试验过程

为了还原试验，验证通过谐波畸变率和触电波形峰值斜率变化是否能够保证保护器动作，因此，重新搭建仿真模型。

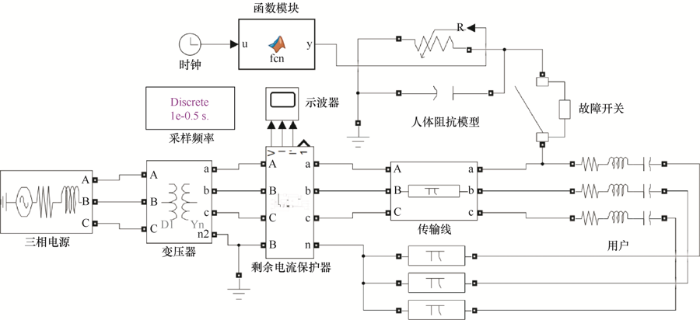
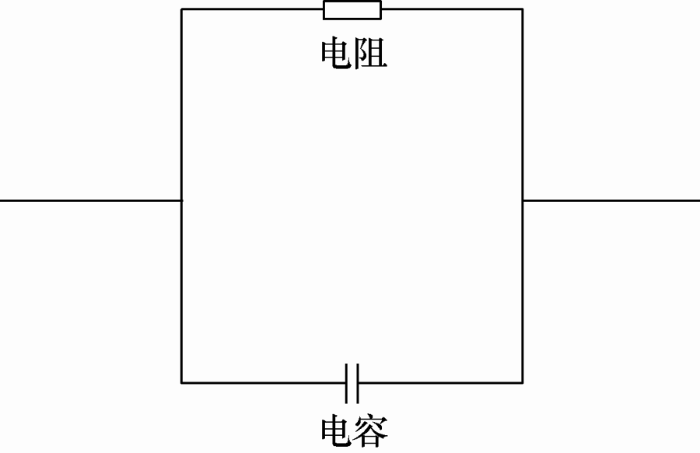
根据台区-线路-用户三层拓扑结构，在Matlab/Simulink中搭建人体触电仿真模型。如图12所示，主电路是一个对称的三相电路，三相电源模拟台区总电源，星形接法，三相线电压10 kV，频率50 Hz，经过变压器降压到三相线电压400 V，之后接保护开关、供电线路以及用户，漏电点在用户负载前。在仿真中，人体阻抗模型仿照UL1563标准人体阻抗网络(图13)，使用可变电阻并联一个小电容。将控制故障的开关和模拟的人体阻抗串联在漏电点处，并且将其直接接地。设置触电开始时刻为t=0.08 s，结束时刻为t=0.22 s，总时长为0.3 s。线路元件详细参数如表3所示。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 仿真模型

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 UL1563标准人体阻抗网络

表3 仿真各模块参数

仿真模块参数	数值
三相电源线电压/V	10 000
三相电源容量/(V·A)	100 000
频率/Hz	50
变压器变比/(一次/二次)	10 000/400
变压器绕线方式	DYn11
线路电阻/(Ω/km)	0.012 73
线路电感/(H/km)	0.933 7×10^-3
线路电容/(F/km)	12.73×10^-9
负载功率/W	30 000
故障开关通断时间/s	0.08~0.22
人体阻抗并联电容/F	2.2×10^-7

新窗口打开| 下载CSV

4.2 人体阻抗模型

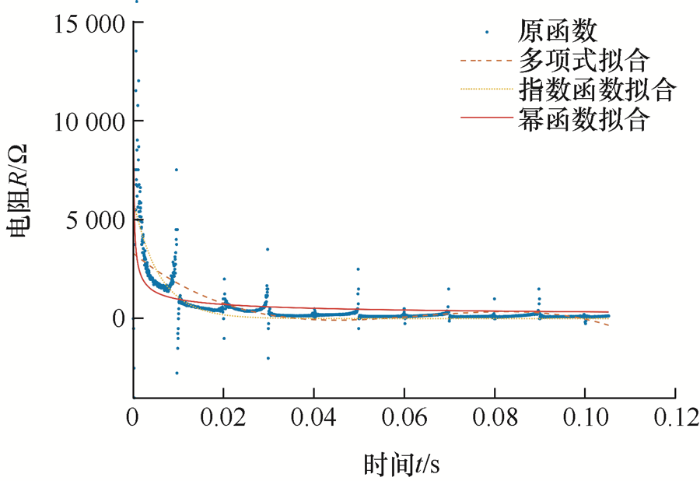
对36组数据进行处理，截取故障数据，对数据进行处理算出阻抗值。使用Matlab函数拟合工具箱对算出的阻抗数据进行处理，试采用多项式拟合、指数函数拟合以及幂函数拟合，如图14所示。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14 函数拟合

幂函数对阻值变化的拟合误差最小，因此对之后的数据均采用幂函数拟合，得到36组不同的函数模型。选取其中干燥情况、半湿润情况以及湿润情况下的典型函数模型各1组，作为仿真试验验证对象。

三组模型函数如下所示。

干燥：$34.99\times {{x}^{-\text{0}\text{.785}\ \text{5}}}+927.3$。

半湿润：$\text{9}\text{.06}\times {{x}^{-\text{0}\text{.869}\ \text{8}}}+307.6$。

湿润：$18.45\times {{x}^{-0.523\ 2}}+221.5$。

触电波形如图15所示。

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15 仿真触电波形

4.3 仿真试验过程

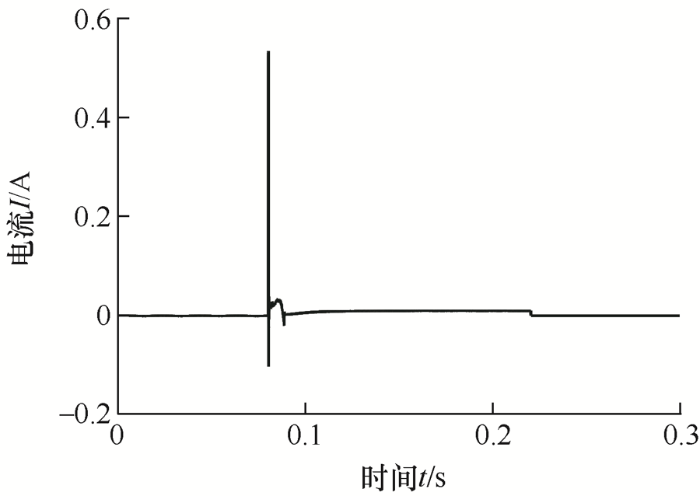
文献[8]给出了通过计算THD是否大于预设值和电流是否大于整定值作为双重触电判据，对此进行复现。仿真波形如图16所示。

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16 加入THD和整定值双重触电判据仿真波形

对于一般的漏电，在漏电电流产生的时刻也会产生谐波，THD值若大于预设值，并且漏电电流大于整定值，那么就有可能造成对触电电流的误判，从而造成误动，如图17所示。

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17 误动情况波形

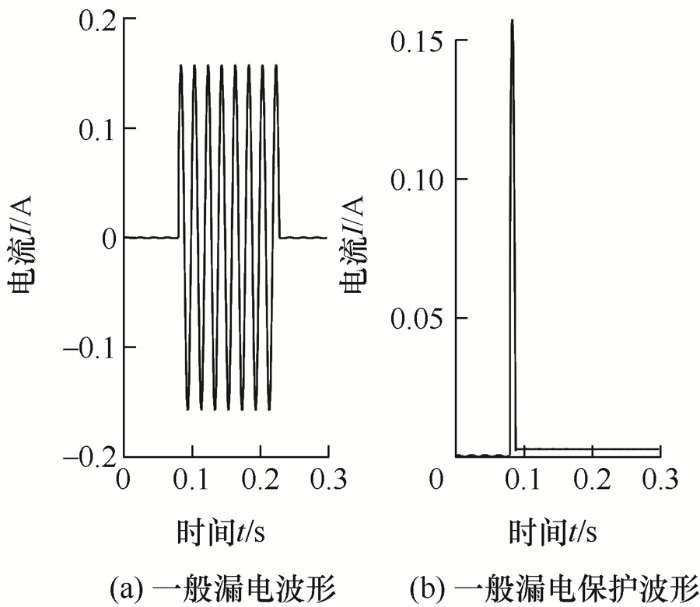
文献[20]中，JD6型漏电保护器通过分离漏电和触电信号，对触电信号各半周波幅值幅度计算来达到保护的目的。将触电信号的一个半波A1的波形储存起来，然后将A1和之后的半波A2进行比较，在10 ms内，其幅度小于设定值(例如80 mA)，则按普通漏电处理，若大于设定值，则继续比较之后的A2和A3，若A2和A3之间变化幅度仍大于设定值(例如80 mA)，且电流大小大于30 mA，则保护器动作。仿真波形如图18所示。

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18 JD6型漏电保护器仿真波形

JD6型漏电保护器虽然能识别触电波形，但仅通过幅值幅度变化判断，灵敏度低，容易造成拒动或误动。

本文设计的剩余电流保护器，使其具有实时计算THD、记录波形、截取波形提取峰值以及计算斜率的功能。对比如表4所示。

表4 判据对比

判据	特点
文献[8]双重触电判据	能够实时计算THD，并通过THD和电流整定值判断人体触电，但会造成误判，导致误动
文献[20]JD6型漏电保护器判据	能够计算各半周波幅值幅度变化大小，并通过幅度大小判断人体触电，但仅通过幅值幅度变化判断，灵敏度低，容易造成拒动或误动
本文判据	能够实时计算THD，判断人体触电开始时刻，并通过计算各周波间的变化来进一步判断是否是人体触电，增加了可靠性和灵敏度

新窗口打开| 下载CSV

剩余电流保护器工作流程如图19所示。

图19

新窗口打开| 下载原图ZIP| 生成PPT

图19 剩余电流保护器保护功能流程图

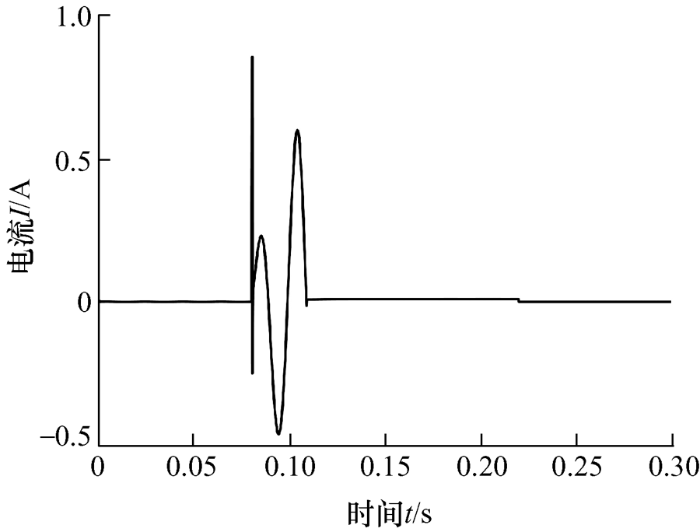
选取表1中谐波畸变率最小值5.49%和表2中波形峰值斜率变化中位数2.490 1、1.053 7，将双重判据代入到仿真试验中的保护器中。对三组典型人体阻抗模型进行触电仿真，仿真波形如图20所示。

图20

新窗口打开| 下载原图ZIP| 生成PPT

图20 仿真波形(接入保护)

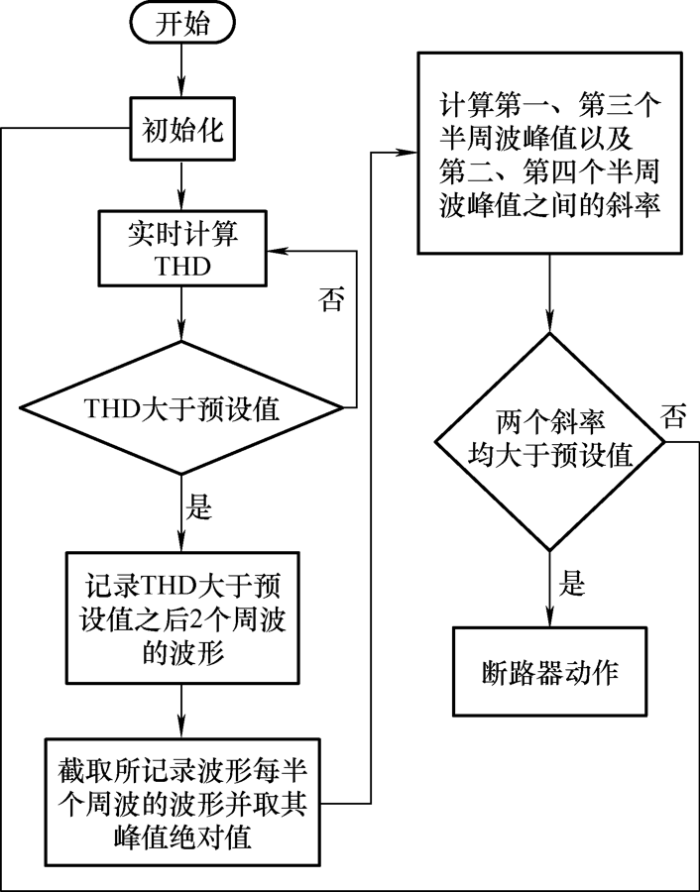
当t=0.08 s开始触电时，检测到谐波畸变率大于所设值，对波形进行每0.01 s的采样，相邻周波之间进行计算，若满足斜率变化条件，断路器在0.12 s左右断开。

5 结论

针对当前基于TT系统的低压配电网中剩余电流保护设备无法正确识别人体触电并及时保护人身安全的问题，本文分析了导致该问题的原因，然后搭建动物组织触电试验平台，对动物表皮进行数百次触电试验，得到触电电流波形并分析其特征。根据特征，提出将检测谐波畸变率和波形峰值变化的斜率纳入保护判据中。为了验证所提保护判据的可行性，又搭建了触电仿真平台，将谐波畸变率和波形峰值变化斜率相结合，作为触电保护的双重判据，并给出判断数值。对三种情况下的典型函数进行仿真试验，得到如下结论。

(1) 触电波形是时变的，即触电后皮肤阻抗随触电时间而变化，时间越长，阻抗越低。

(2) 通过动物表皮触电试验得到三种情况下的典型函数。三个典型函数在仿真试验中均可被保护器识别，保护器均动作。

(3) 保护器动作证明了所提判据，即检测谐波畸变率和波峰峰值变化斜率，可用于漏电保护。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

姚天雨.

基于行为安全理论的生产安全触电事故原因归类和统计研究

[J]. 工业安全与环保, 2021, 47(5):76-79.