电气工程学报, 2023, 18(1): 126-132 doi: 10.11985/2023.01.014

电力系统

LCL型并网逆变器电容电压微分反馈有源阻尼实现技术研究*

王爱华,1, 葛维春1, 李铁1, 崔岱1, 李明明2, 肖华锋,2

1.国网辽宁省电力有限公司 沈阳 110004

2.东南大学电气工程学院 南京 210096

Research on Realization Technology of Active Damping Method with Differential Feedback of Filter Capacitance Voltage for LCL Filter Based Grid-connected Inverters

WANG Aihua,1, GE Weichun1, LI Tie1, CUI Dai1, LI Mingming2, XIAO Huafeng,2

1. State Grid Liaoning Electric Power Supply Co., Ltd., Shenyang 110004

2. School of Electrical Engineering, Southeast University, Nanjing 210096

通讯作者: 肖华锋，男，1981年生，教授。主要研究方向为新能源并网技术。E-mail：xiaohf@seu.edu.cn

收稿日期: 2021-06-28   修回日期: 2022-03-10  

基金资助: *国网辽宁省电力有限公司科技资助项目.  SGLNDK00DWJS2000557

Received: 2021-06-28   Revised: 2022-03-10  

作者简介 About authors

王爱华，男，1971年生，教授级高级工程师。主要研究方向为电力系统及其自动化。E-mail：wangah@163.com

摘要

基于LCL滤波器状态变量反馈实现有源阻尼的方法具有控制灵活、鲁棒性强的优点。在已有方案中，滤波电容电流比例反馈因实现简单得到广泛应用，但滤波电容电流脉动较大，精确检测需要配备高精度电流传感器。理论推导可知对滤波电容电压微分反馈能够实现相同阻尼效果且无需配备高精度传感器，但微分环节易引入高频噪声，影响进网电流质量；另外，现有常规微分实现方法未考虑电容漏电流对LCL滤波器高频段特性的影响。为此，基于滤波电容电流与漏电流矢量关系，提出一种改进型滤波电容电压微分反馈有源阻尼方法，与常规微分相比具有高频噪声抑制能力且不影响LCL滤波器性能。最后，通过试验结果证明了上述优点。

关键词： 有源阻尼 ; LCL滤波器 ; 微分反馈

Abstract

Active damping(AD) methods based on LCL filter state variables feedback have the advantages of flexible control and strong robustness. Among these methods, the filter capacitor current proportional feedback algorithm is widely used because it is easy to implement, but the filter capacitor current has a large pulsation, only high-precision current sensors can accurately measure. The theoretical derivation shows that the differential feedback of the filter capacitor voltage can achieve the same damping effect and does not need to be equipped with a high-precision sensor, but the differential link easily brings high-frequency noise into the control system, which affects the quality of the grid current. Moreover, conventional differential implementation methods do not consider the influence of leakage current of the filter capacitor, which affects the high frequency characteristics of the LCL filter. Therefore, based on the vector relationship between the filter capacitor current and its leakage current, a new differential realization method is proposed, which has high frequency noise suppression capability and does not affect the performance of the LCL filter compared with the conventional differential realization method. Simulation and experimental results prove that the proposed control strategy can achieve satisfactory results in all aspects compared with traditional methods.

Keywords： Active damping ; LCL filter ; derivative feedback

PDF (788KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

王爱华, 葛维春, 李铁, 崔岱, 李明明, 肖华锋. LCL型并网逆变器电容电压微分反馈有源阻尼实现技术研究*. 电气工程学报[J], 2023, 18(1): 126-132 doi:10.11985/2023.01.014

WANG Aihua, GE Weichun, LI Tie, CUI Dai, LI Mingming, XIAO Huafeng. Research on Realization Technology of Active Damping Method with Differential Feedback of Filter Capacitance Voltage for LCL Filter Based Grid-connected Inverters. Chinese Journal of Electrical Engineering[J], 2023, 18(1): 126-132 doi:10.11985/2023.01.014

1 引言

有源阻尼(Activing damping，AD)是抑制LCL滤波器谐振有效方法之一，具有控制灵活、鲁棒性高的优点[1]。其中，滤波电容电流比例反馈 AD(Capacitor current proportional feedback AD，CCPF-AD)由于实现简单得到广泛应用，但电容电流脉动大，难以准确采样，需要配备高精度电流传感器和采样策略[2]。

理想情况下，滤波电容电压微分反馈AD(Capacitor voltage derivative feedback AD，CVDF-AD)能取得与CCPF-AD相同的阻尼效果[3]，而且无需配备高精度传感器，有利于降低系统成本。但微分环节易引入高频噪声，降低进网电流质量，限制了CVDF-AD的应用。为解决该问题，文献[4]提出非理想二阶广义积分、文献[5]提出后向差分+超前校正环节、文献[6]提出负PI控制器等效微分环节，这些方法均能够较好地实现微分功能，但存在以下缺点：① 追求全频段等效微分，导致对高频噪声抑制能力不足，影响进网电流质量，忽略CVDF- AD的本质，即仅需要在谐振频率附近实现微分反馈；② 忽略了电容漏电流的影响，直接对电容电压微分，影响LCL滤波器高频段特性。

为此，本文基于滤波电容电流与漏电流的矢量关系，提出一种既能够消除漏电流影响又对高频噪声具有一定抑制作用的改进型CVDF-AD策略，并且在参数设计时，充分考虑数字控制延迟对阻尼效果的影响。最后通过一台3 kW LCL型并网逆变器验证所提策略的有效性。

2 滤波电容电压微分反馈改进

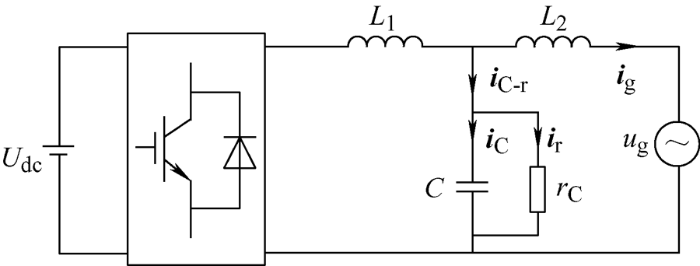
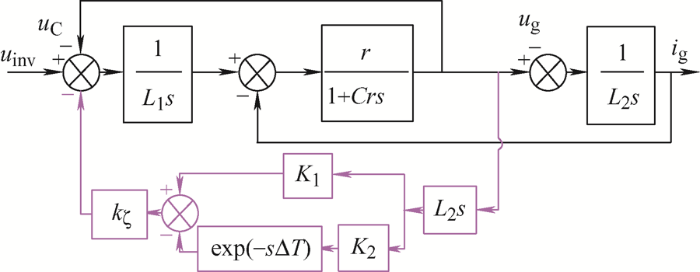
本节以单相LCL型并网逆变器为例，图1给出了系统的电路结构，同时考虑了滤波电容的漏电流。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   LCL型并网逆变器


图1中Udc表示直流侧输入电压，L1、L2分别表示逆变侧、网侧滤波电感，C表示滤波电容，rC表示滤波电容的绝缘电阻，iC表示滤波电容电流，ir表示漏电流，iC-r表示iC与ir矢量和，ig表示进网电流，ug表示电网电压。

2.1 滤波电容电压直接微分反馈性能分析

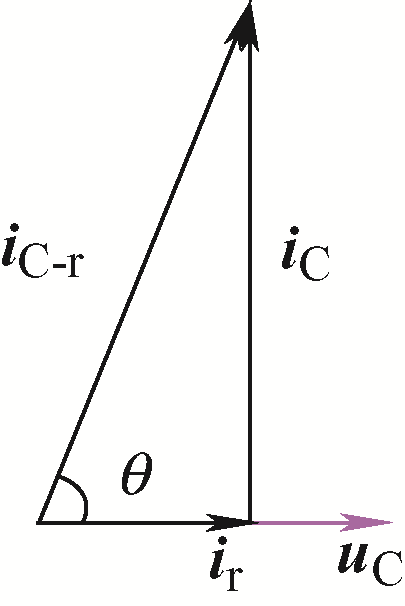
依据图1可绘制出滤波电容支路各个电流之间的矢量关系，如图2所示。不难看出，由于寄生电阻的存在，流过滤波电容支路的总电流超前电容电压的角度θ小于90°。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   iC、ir和iC-r矢量关系


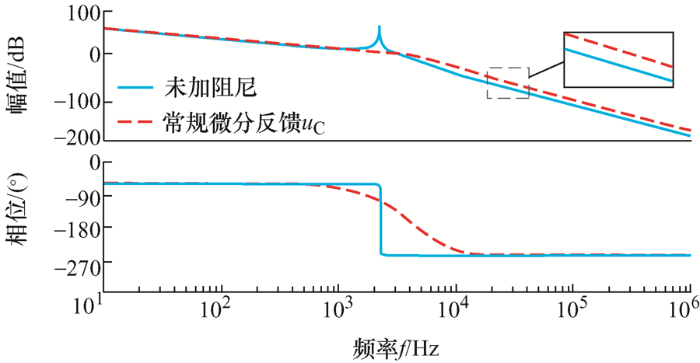
对滤波电容电压微分反馈可认为是先求出滤波电容电流再进行比例反馈；但由于ir的存在，直接对滤波电容电压微分反馈，实际反馈的电流是iC-r，反馈幅值偏大，此时含有CVDF-AD的系统伯德图如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   直接微分反馈uC


可以看出，虽然直接微分反馈uC能够消除LCL滤波器谐振尖峰，但在高频段对信号的增益变大，影响LCL滤波器对高次谐波的抑制能力。

2.2 滤波电容电压直接微分反馈的改进方法

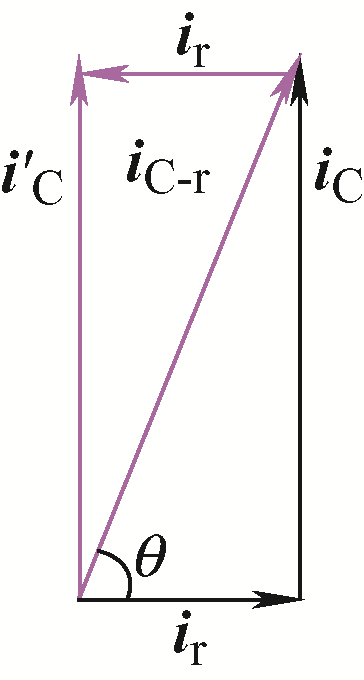
滤波电容电压直接微分反馈，造成LCL滤波器性能下降的根本原因是由于电容漏电流的存在。因此，最直接的方法是依据滤波电容电流、漏电流矢量关系，在对滤波电容电压进行微分反馈时，消除漏电流。图4依据滤波电容电流以及漏电流的矢量关系，给出了消除漏电流影响的方法。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   消除漏电流矢量示意图


可以看出，滤波电容电压直接微分反馈实现AD，实际上与比例反馈iC-r等效，而CVDF-AD原本期望的是比例反馈iC，因此如果在对电容电压进行微分反馈的同时，减去漏电流ir得到i’C，当i’C与iC相等时，即可消除漏电流对LCL滤波器的影响。

依据图4，可以得到i’C期望的表达式为

${{{i}'}_{\text{C}}}=sC{{u}_{\text{C}}}-\frac{1}{{{r}_{\text{C}}}}{{u}_{\text{C}}}$

对式(1)进行离散化，令s=(1-z-1)/ΔT，可得

${{{i}'}_{\text{C}}}=\frac{1}{\Delta T}{{u}_{\text{C}}}-\frac{{{z}^{-1}}}{\Delta T}{{u}_{\text{C}}}-\frac{1}{{{r}_{\text{C}}}}{{u}_{\text{C}}}$

假设当前时刻为第k时刻，z-1uC为前一时刻即第k-1时刻的uC，式(2)可变形为

${{{i}'}_{\text{C}}}=(\frac{1}{\Delta T}-\frac{1}{{{r}_{\text{C}}}}){{u}_{\text{C}}}(k)-\frac{1}{\Delta T}{{u}_{\text{C}}}(k-1)$

式(3)中uC(k-1)可由uC(k)经过适当的延迟得到，如式(4)所示

${{u}_{\text{C}}}(k-1)={{u}_{\text{C}}}(k)\exp {{(-s\Delta T)}^{{}}}$

式中，exp(-sΔT)表示纯延迟环节，代入式(3)可得

${{{i}'}_{\text{C}}}=(\frac{1}{\Delta T}-\frac{1}{{{r}_{\text{C}}}}){{u}_{\text{C}}}(k)-\frac{1}{\Delta T}\exp (-s\Delta T){{u}_{\text{C}}}(k)$

为简化表示，令

$\left\{ \begin{align} & {{K}_{1}}=\frac{1}{\Delta T}-\frac{1}{{{r}_{\text{C}}}} \\ & {{K}_{2}}=\frac{1}{\Delta T} \\\end{align} \right.$

至此，期望的反馈量${{{i}'}_{\text{C}}}$可由图5所示的改进型CVDF-AD环节实现，经过反馈系数kζ后，确保取得最优AD效果。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   包含所提改进型CVDF-AD的系统结构


3 参数设计

根据图5，可以求出系统未含有阻尼支路时，uinv、uC、ug以及ig的关系表达式为

$\left( \left( \left( {{u}_{\text{inv}}}-{{u}_{\text{C}}} \right)\frac{1}{{{L}_{1}}s}-{{i}_{\text{g}}} \right)\frac{r}{1+Crs}-{{u}_{\text{g}}} \right)\frac{1}{{{L}_{2}}s}={{i}_{\text{g}}}$

由于uC=ug+igsL2，代入式(7)可得

$\left( \left( \left( {{u}_{\text{inv}}}-{{i}_{\text{g}}}s{{L}_{2}}-{{u}_{\text{g}}} \right)\frac{1}{{{L}_{1}}s}-{{i}_{\text{g}}} \right)\frac{r}{1+Crs}-{{u}_{\text{g}}} \right)\frac{1}{{{L}_{2}}s}={{i}_{\text{g}}}$

电网电压可视为一个扰动量，根据式(8)可以求出不含阻尼支路时，逆变电压uinv到进网电流ig的表达式为

$G_{\text{uinv }\!\!\_\!\!\text{ 1}}^{\text{ig}}(s)=\frac{1}{{{s}^{3}}{{L}_{1}}{{L}_{2}}C+{{s}^{2}}({{L}_{1}}{{L}_{2}}/{{r}_{1}})+s({{L}_{1}}+{{L}_{2}})}$

因此，系统的特征方程为

$D(s)={{s}^{3}}{{L}_{1}}{{L}_{2}}C+{{s}^{2}}({{L}_{1}}{{L}_{2}}/{{r}_{1}})+s({{L}_{1}}+{{L}_{2}})$

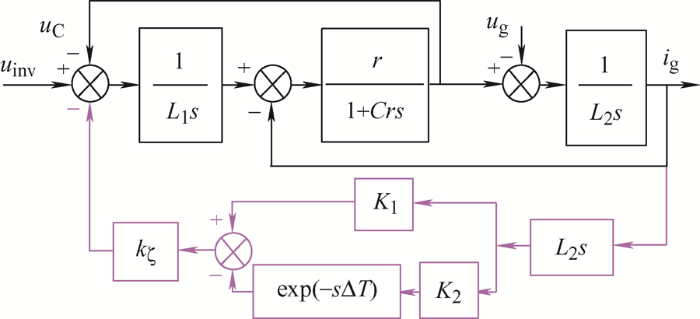
包含所提改进型CVDF-AD时，对图5进行变换，如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   对图5进行等效变换


根据图6，可以求出此时uinv、uC、ug以及ig的关系表达式为

$\left( \left( \left( {{u}_{\text{inv}}}-{{u}_{\text{C}}}-{{i}_{\text{g}}}s{{L}_{2}}({{K}_{1}}-{{K}_{2}}\exp (-s{{T}_{\text{s}}})){{k}_{\text{ }\!\!\zeta\!\!\text{ }}} \right)\frac{1}{{{L}_{1}}s}-{{i}_{\text{g}}} \right)\frac{r}{1+Crs}-{{u}_{\text{g}}} \right)\frac{1}{{{L}_{2}}s}={{i}_{\text{g}}}$

借鉴前面对uC以及ug的处理方法，可以得到含有阻尼支路时，逆变电压uinv到进网电流ig的传递函数为

$G_{\text{uinv }\!\!\_\!\!\text{ 2}}^{\text{ig}}(s)=\frac{1}{D(s)+{{k}_{\text{ }\!\!\zeta\!\!\text{ }}}{{L}_{2}}s({{K}_{\text{1}}}-{{K}_{\text{2}}}\exp (-s\Delta T))}$

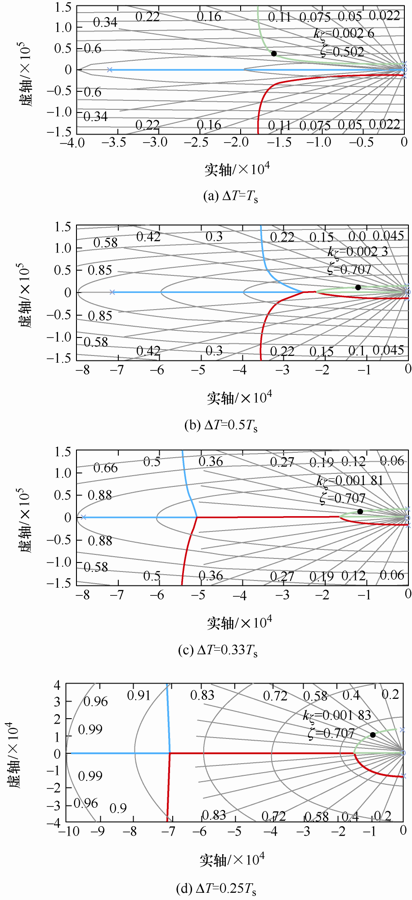
延迟取1个开关周期Ts最便于实现，此时系统根轨迹为如图7a所示，可以看出此时系统无法取得最佳阻尼比。分别将减小ΔT取值至0.5Ts、0.33Ts、0.25Ts，此时系统根轨迹如图7b~7d所示，可以看出此时系统均能够取得最佳阻尼比。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   ΔT取不同值时的系统根轨迹


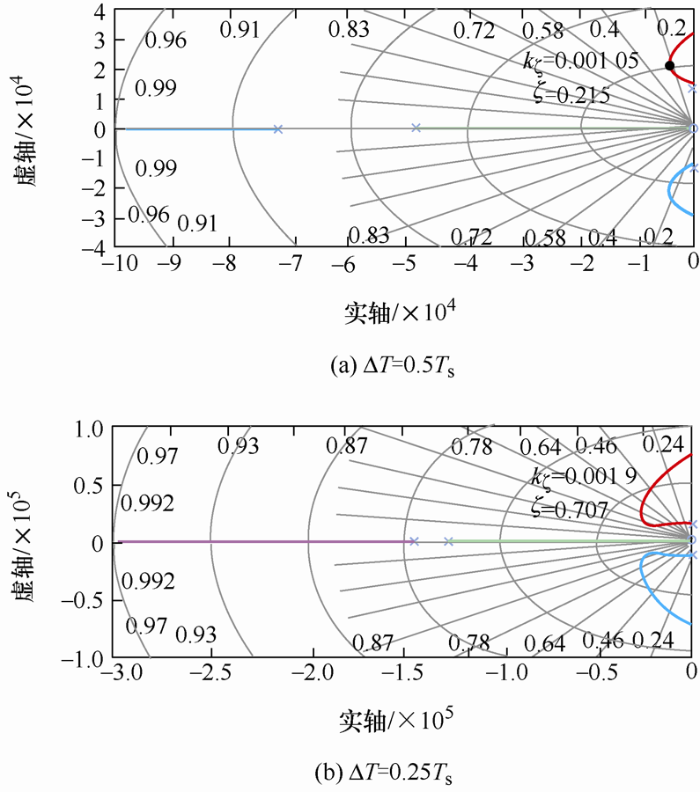
实际系统中存在数字控制延迟，对阻尼效果有影响。文献[7-8]指出数字延迟通常为1.5Ts，考虑数字控制延迟，如果ΔT仍然取0.5Ts，此时系统根轨迹如图8a所示，可以看出，由于数字延迟的存在，系统阻尼比仅为0.342，不满足系统稳定性要求。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   开关频率为18 kHz时，ΔT取不同值时的系统根轨迹


对数字控制延迟造成的影响，通常可以采用两类方法进行解决。第一类是对控制信号进行预测，如串联超前校正环节[9]、插值预测[10]、重复控制预测[11]等；第二类方法是采用即时采样[12-13]、多次采样[14-15]等方法。第一类方法中超前校正、插值预测易放大控制信号中的谐波，而重复控制预测易降低系统的动态特性；第二类方法中即时采样减少的延迟效果并不如多次采样明显，因此本文采用多次采样。经过计算和仿真分析可知，在1个开关周期内进行4次采样，系统能够重新取得最佳阻尼比，根轨迹如图8b所示。

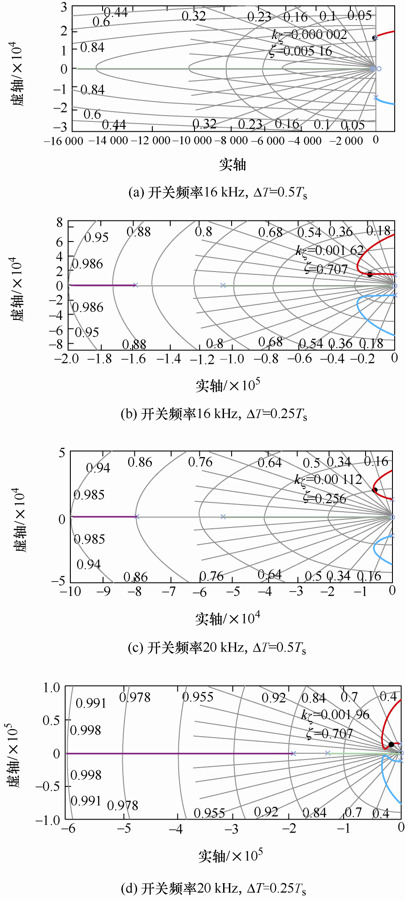
为了验证不同开关频率即不同采样频率下，多次采样的效果，图9分别给出开关频率为16 kHz和20 kHz时系统的根轨迹。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   不同开关频率下，ΔT取不同值时的系统根轨迹


从图8、9可以看出，当开关频率分别为典型的16 kHz、18 kHz和20 kHz时，考虑控制延迟，如果在每次开关周期仅采样2次，那么系统均无法取到最佳阻尼比，随着在单次开关周期内采样次数增加到4次，上述三种开关频率下，系统均能够取得最佳阻尼比。此外，从图9也能够看出，开关频率越低，控制延迟对系统的影响越明显。

采用多次采样且单个开关周期内采样4次时，改进型CVDF-AD环节的参数表达式为

$\left\{ \begin{align} & {{K}_{1}}=\frac{4}{{{T}_{\text{s}}}}-\frac{1}{{{r}_{\text{C}}}} \\ & {{K}_{2}}=\frac{4}{{{T}_{\text{s}}}} \\\end{align} \right.$

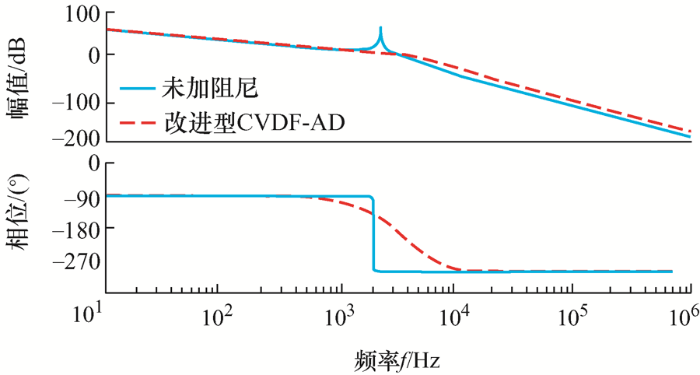
阻尼支路反馈系数kξ可根据系统根轨迹得到。按照上述方法求得所提改进型CVDF-AD策略的参数后，绘制系统伯德图，如图10所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   改进型CVDF-AD对应的系统伯德图


可以看出，采用本文所提的改进型CVDF-AD，不但能够很好地抑制谐振尖峰，而且能够消除漏电流的影响，同时不影响LCL滤波器高频段的性能。

4 试验结果及分析

为验证上述理论分析的正确性，基于一台3 kW LCL型并网逆变器样机进行试验验证，具体参数如表1所示。

表1   并网逆变器参数

参数数值
额定功率S/kW3
直流电压Udc/V360
逆变侧滤波电感L1/mH1.04
滤波电容C/μF10
寄生电阻r/Ω3 000
网侧滤波电感L2/mH1.06
电网/(V/Hz)220/50
开关频率f/kHz18
采样频率fs/kHz72

新窗口打开| 下载CSV


4.1 改进型CVDF-AD有效性验证

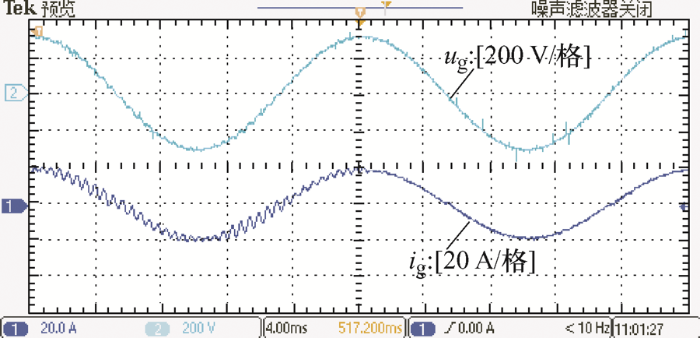
图11为本文提出的改进型CVDF-AD在电流波峰处投切的试验波形，其中ug表示电网电压，ig表示进网电流。可以看出，所提AD策略投切后进网电流谐振被迅速抑制，说明提出的阻尼方法有效。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   提出的AD投切前后进网电流波形


4.2 数字延迟补偿方法验证

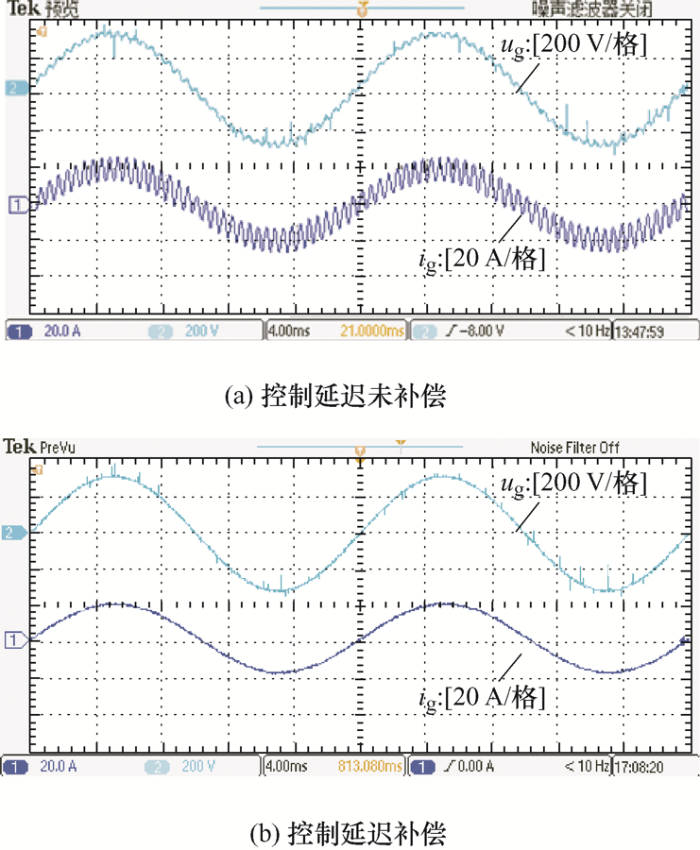
图12a和12b为ΔT分别取1/2Ts和1/4Ts时的电网电压和进网电流波形。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   ΔT取不同值时进网电压和电流波形


可以看出，未考虑数字延迟，阻尼效果受到影响，会导致进网电流振荡；而考虑数字延迟，重新设计改进型CVDF-AD的参数，投切后可有效抑制电流谐振。

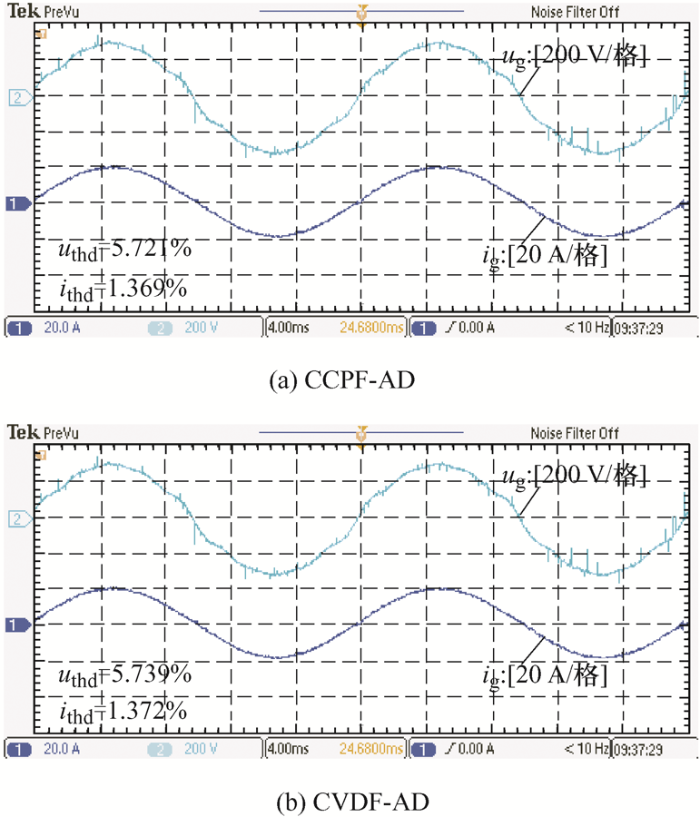
4.3 与常规滤波电容电流比例反馈对比

为验证改进型CVDF-AD能否等效CCPF-AD，试验中利用可编程交流源模拟电网，同时产生低次谐波电压，计算可得电压总谐波失真值(Total harmonic distortion，THD)为5.726%。在该种工况下，两种AD方法的试验结果如图13所示，其中图13a为采用CCPF-AD时对应的波形，图13b为采用CVDF-AD时对应的波形。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13   两种AD方法的性能对比


从图13可以看出，采用CCPF-AD时，进网电流和电网电压THD分别为1.369%和5.721%；采用改进型CVDF-AD时，进网电流和电网电压THD分别为1.372%和5.739%。因此，相比传统的CCPF-AD，本文所提CVDF-AD并未放大高次谐波。

考虑采用CCPF-AD需要配备高精度电流传感器，因此采用本文所提的改进型CVDF-AD能够节省系统成本。

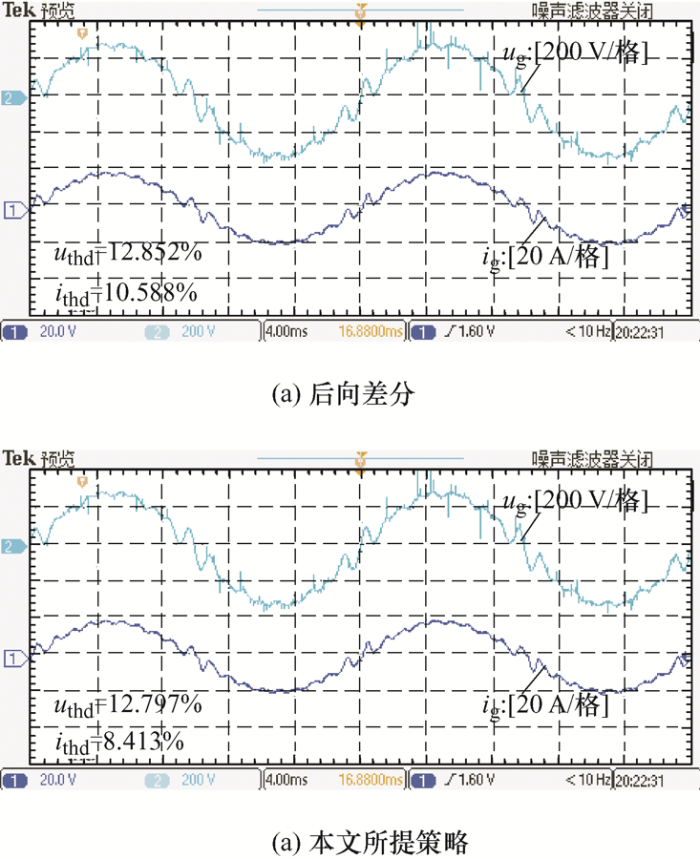
4.4 与常规方法实现CVDF-AD对比

由理论分析可知，采用常规微分实现方法反馈滤波电容电压AD，会降低LCL滤波器对高次谐波的抑制能力，而本文所提改进型CVDF-AD能够避免该缺陷。

利用可编程交流源模拟电网电压，同时产生高次谐波电压，计算可得THD为11.026%。图14为不同CVDF-AD方法对应的进网电流波形对比，其中图14a为常规后向差分实现CVDF-AD对应的进网电流波形，图14b为本文所提方法对应的进网电流波形。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14   不同微分实现方法的性能对比


从图14可以看出，后向差分实现CVDF-AD时进网电流和电网电压THD分别为10.588%和12.852%；采用本文所提改进型CVDF-AD策略时，进网电流和电网电压THD分别为8.413%和12.797%，效果明显优于后向差分法，说明本文所提策略相比传统微分实现方法具有更好的谐波抑制能力。

5 结论

本文提出一种改进型滤波电容电压微分反馈有源阻尼算法，给出了算法的结构和参数设计方法，主要包括以下几点。

(1) 从微分反馈滤波电容电压的数学角度出发，基于滤波电容电流和漏电流矢量关系，建立期望的微分反馈滤波电容电压表达式，并给出实现结构。

(2) 采用多次采样方法降低数字控制延迟对阻尼效果的影响，同时基于系统根轨迹确定反馈系数，确保系统取得优秀阻尼效果。

(3) 试验结果表明所提策略能够取得与滤波电容电流比例反馈相同的阻尼效果，但无需配备高精度电流传感器，而且同传统的微分实现方法相比，能够对电网高次谐波具有较好的抑制作用。

参考文献

CHEN X, ZHANG Y, WANG S, et al.

Impedance-phased dynamic control method for grid-connected inverters in a weak grid

[J]. IEEE Transactions on Power Electronics, 2016, 32(1):274-283.

DOI:10.1109/TPEL.2016.2533563      URL     [本文引用: 1]

XIN Z, WANG X, LOH P C, et al.

Grid-current-feedback control for LCL-filtered grid converters with enhanced stability

[J]. IEEE Transactions on Power Electronics, 2016, 32(4):3216-3228.

DOI:10.1109/TPEL.2016.2580543      URL     [本文引用: 1]

XIN Z, LOH P C, WANG X, et al.

Highly accurate derivatives for LCL-filtered grid converter with capacitor voltage active damping

[J]. IEEE Transactions on Power Electronics, 2015, 31(5):3612-3625.

DOI:10.1109/TPEL.2015.2467313      URL     [本文引用: 1]

HE J, LI Y W, XU D, et al.

Deadbeat weighted average current control with corrective feed-forward compensation for microgrid converters with nonstandard LCL filter

[J]. IEEE Transactions on Power Electronics, 2016, 32(4):2661-2674.

DOI:10.1109/TPEL.2016.2580005      URL     [本文引用: 1]

LI R T H, HO C N M, CHEN E X.

Active virtual ground:Single-phase transformer less grid-connected voltage source inverter topology

[J]. IEEE Transactions on Power Electronics, 2017, 33(2):1335-1346.

DOI:10.1109/TPEL.2017.2690146      URL     [本文引用: 1]

SHEN G, ZHU X, ZHANG J, et al.

A new feedback method for PR current control of LCL-filter-based grid-connected inverter

[J]. IEEE Transactions on Industrial Electronics, 2010, 57(6):2033-2041.

DOI:10.1109/TIE.2010.2040552      URL     [本文引用: 1]

PAN D, RUAN X, WANG X.

Direct realization of digital differentiators in discrete domain for active damping of LCL-type grid-connected inverter

[J]. IEEE Transactions on Power Electronics, 2017, 33(10):8461-8473.

DOI:10.1109/TPEL.63      URL     [本文引用: 1]

LI M, XIAO H, CHENG M.

An adaptive strategy based on repetitive predictive control for improving adaptability of LCL-type grid-connected inverters under weak grid

[J]. IEEE Transactions on Power Electronics, 2022, 37(3):2562-2572.

DOI:10.1109/TPEL.2021.3108878      URL     [本文引用: 1]

MIAO Z, YAO W, LU Z.

Single-cycle-lag compensator-based active damping for digitally controlled LCL/LLCL-type grid-connected inverters

[J]. IEEE Trans. Ind. Electron., 2020, 67(3):1980-1990.

DOI:10.1109/TIE.41      URL     [本文引用: 1]

GUINDON D, SHARK D, ANTONIOU A.

Design methodology for nearly linear-phase recursive digital filters by constrained optimization

[J]. IEEE Trans. Cir & Sys. I Regular Papers, 2010, 57(7):1719-1731.

[本文引用: 1]

EREN S, PAHLEVANINEZHAD M, BAKHSHAI A, et al.

Composite nonlinear feedback control and stability analysis of a grid-connected voltage source inverter with LCL filter

[J]. IEEE Trans. Ind. Electron., 2013, 60(11):5059-5074.

DOI:10.1109/TIE.2012.2225399      URL     [本文引用: 1]

LU M, LU X, DRAGICEIV T.

Graphical evaluation of time-delay compensation techniques for digitally controlled converters

[J]. IEEE Trans. Power Electron., 2017, 33(3):2601-2614.

DOI:10.1109/TPEL.2017.2691062      URL     [本文引用: 1]

YANG D, RUAN X, WU H.

A real-time computation method with dual sampling mode to improve the current control performance of the LCL-type grid-connected inverter

[J]. IEEE Trans. Ind. Electron., 2015, 62(7):4563-4572.

DOI:10.1109/TIE.41      URL     [本文引用: 1]

YAO W, YANG Y, ZHANG X, et al.

Design and analysis of robust active damping for LCL filters using digital notch filters

[J]. IEEE Transactions on Power Electronics, 2017, 32(3):2360-2375.

DOI:10.1109/TPEL.2016.2565598      URL     [本文引用: 1]

HARNEFORS L, YEPES A, VIDAL A, et al.

Passivity-based stabilization of resonant current controllers with consideration of time delay

[J]. IEEE Transactions on Power Electronics, 2014, 29(12):6260-6263.

DOI:10.1109/TPEL.2014.2328669      URL     [本文引用: 1]

/

〈 〉