电气工程学报, 2022, 17(4): 282-288 doi: 10.11985/2022.04.030

电力系统

含分布式光伏的配电网规划设计研究*

宁超,, 杨俊,, 朱咏明,, 刘莎,, 李卫华,

国网新疆电力有限公司昌吉供电公司 昌吉 831100

Research on Distribution Network Planning and Design with Distributed Photovoltaic System

NING Chao,, YANG Jun,, ZHU Yongming,, LIU Sha,, LI Weihua,

Changji Power Supply Company, State Grid Xinjiang Electric Power Co., Ltd., Changji 831100

收稿日期: 2020-12-17   修回日期: 2021-09-31  

基金资助: *国网新疆电力有限公司科技资助项目.  SGXJCJ00KJJS2001417

Received: 2020-12-17   Revised: 2021-09-31  

作者简介 About authors

宁超，男，1972年生，中级工程师。主要研究方向为配电网规划。E-mail：ungyjktv@21cn.com

杨俊，男，1975年生，工程师。主要研究方向为配电网规划。E-mail：ungyj3455ktv@21cn.com

朱咏明，男，1978年生，中级工程师。主要研究方向为配电网规划。E-mail：ung3546666yjktv@21cn.com

刘莎，男，1979年生，高级工程师。主要研究方向为配电网规划。E-mail：ung356yjktv@21cn.com

李卫华，男，1969年生，中级工程师。主要研究方向为配电网规划。E-mail：ung756yjktv@21cn.com

摘要

针对配电网有源设计网络中有源系统的功率消耗严重、电源接入时扰动较大的问题，采用分布式光伏电源作为有源系统，对接入的配电网进行重新规划设计。通过设计光伏电源接入配电网的判定系统，保证分布式光伏接入电网能够更加快速有效；对光伏接入的节点电路进行等效分析，能够精确把控节点位置的运行状态；运用分布式数据信赖域算法对接入系统功率数据限制，保证光伏接入电网时的扰动最小。最后通过试验记录接入节点位置的功率数据，发现接入节点位置的相对偏差不会超过1%，节点40为功率最大接入位置，节点10为最小接入位置；根据试验数据画出谐波扰动对比曲线，发现在P40处达到最大扰动对比；通过Power Factory仿真软件与传统电源接入方法进行仿真对比，发现所提设计规划节点延时时间几乎为零，电源接入过程更加顺畅。从而验证了所提接入规划方案的优越性，证明了该设计方案的可行性。

关键词： 分布式光伏电源 ; 配电网总体设计 ; 节点等效电路 ; 光伏接入方法判定 ; 分布式数据信赖域算法

Abstract

The power consumption of the active system in the active design network of distribution network is serious, and the disturbance of the power supply is large. The distributed photovoltaic power supply is used as the active system to re-design the distribution network. By designing the decision system of photovoltaic power access to the distribution network, the distributed photovoltaic access to the power network can be more quick and effective, and the node circuit of photovoltaic access can be analyzed equivalently to control the operation state of the node position accurately. The distributed data trust region algorithm is used to limit the power data of the access system and ensure the minimum disturbance when the photovoltaic is connected to the power grid. Finally, the power data of the access node position is recorded by experiment, and it is found that the relative deviation of the access node position is less than 1%, the node 40 is the maximum power access position, and the node 10 is the minimum access position. According to the experimental data, the contrast curve of harmonic disturbance is drawn, and it is found that the maximum disturbance contrast is reached at P40. Compared with the traditional power access method by the Power Factory simulation software, it is found that the delay time of the designed node is almost zero, the process of power connection is much smoother. Thus the superiority of the access planning scheme is verified and the feasibility of the design scheme is proved.

Keywords： Distributed photovoltaic power supply ; distribution network design ; node equivalent circuit ; photovoltaic access method determination ; distributed data trust region algorithm

PDF (9910KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

宁超, 杨俊, 朱咏明, 刘莎, 李卫华. 含分布式光伏的配电网规划设计研究*. 电气工程学报[J], 2022, 17(4): 282-288 doi:10.11985/2022.04.030

NING Chao, YANG Jun, ZHU Yongming, LIU Sha, LI Weihua. Research on Distribution Network Planning and Design with Distributed Photovoltaic System. Chinese Journal of Electrical Engineering[J], 2022, 17(4): 282-288 doi:10.11985/2022.04.030

1 引言

为节省能源消耗，光伏发电日渐趋于完善，与此同时，光伏发电配电网也需要不断与时俱进。本文对配电网进行重新规划设计，对接入的分布式光伏进行分析研究。分布式光伏发电概述从基本模式角度出发，可以将其分为输电侧并网以及配电侧并网两种。输电侧并网主要应用于较大规模的发电站，将其中的电能集中并入电网，之后接受电网的统一调配；配电侧并网发电规模小，发电设备产生的电能就近接入配电网，电能会直接被消耗。由此使分布式光伏电源接入配电网更加顺畅，避免造成配电网系统扰动。

通过大量的文献和试验材料，参考多种规划方案，最终提出本文的设计方案。其中文献[1]采用层次分析法对分布式光伏接入方式进行研究，通过控制接入点的谐波振动使配网系统保持稳定。但这种方法对配网本身供能效率并没有显著提升。文献[2]利用粗糙集理论的蚁群算法对现有光伏接入方法进行优化，增加数据处理速度，增强数据采集能力，进而提升配网运行的供能效率。但对于分布式光伏的接入方法比较单一，不能及时调节光伏接入时的谐波振动，容易出现并网振荡故障。文献[3]建立了带约束的3目标优化模型，并设计了基于进化状态评估的自适应多目标粒子群优化算法(AMOPSO/ESE)来求解Pareto最优解集。根据“先粗后精”的决策行为模式提出了由兴趣最优解集和邻域最优解集构成的Pareto前沿来辅助决策过程，但计算处理过程较为复杂，且对系统硬件要求较高。

根据上述方案的规划设计理论中存在的问题，本研究在其基础上对配电网进行设计规划，通过对配电网的总体设计保证系统输电指令的统一调度；利用信赖域算法对分布式光伏数据进行分析处理，保证系统数据合理分配[3]。通过改进，所提设计很好地解决了电网供能效率低、谐波振荡大和抗干扰能力差的问题，具有良好的适用性。

2 配电网总体设计方案

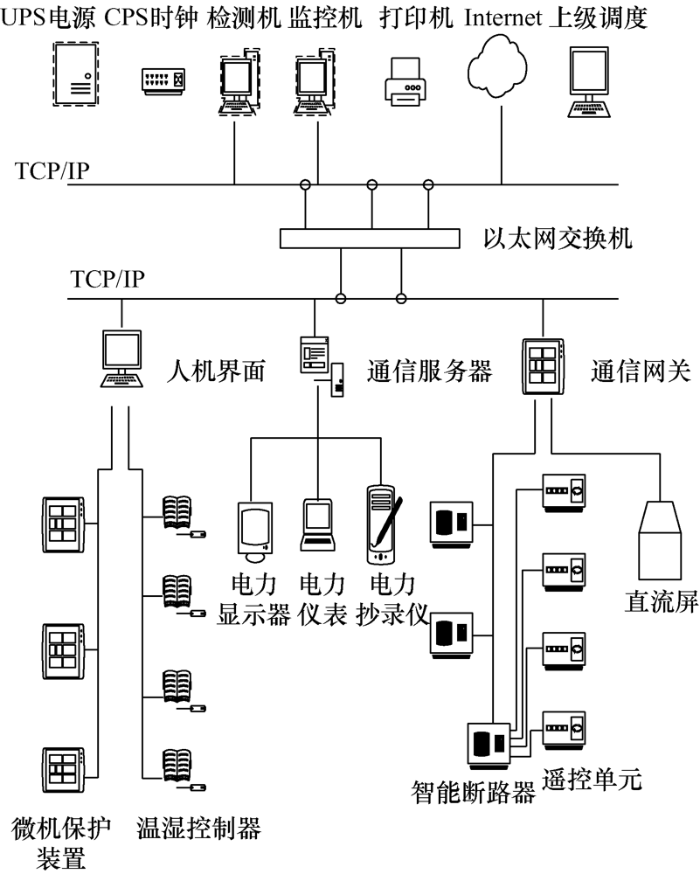
通过实地勘测并参考现有配电网设计系统图，对配电网总体设计进行改进，使配电系统更加匹配分布式光伏的接入，使光伏电源接入时尽可能造成小的扰动[4]。本文设计规划方案如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   冷热电联供系统设计方案


本文设计的总体方案通过TCP/IPZ总线进行供能和数据调度，由上层软件程序进行指令传达，下层设备进行接受指令并执行，上下两层通过以太网交换机综合分配和整理。其中上层指令传达层由UPS电源负责维持系统软件能量消耗，通过CPS时钟设计延时时间，利用检测机和监控机对运行状态进行把控，通过打印机打印报表记录系统运行数据，然后输入到Internet云端网络中，最后进行整体调度规划[5]。下层设备层主要由人机界面、通信服务器和通信网关负责设备运行，人机界面装有微机保护装置和温湿控制器，负责对配电网环境进行把控；通信服务包括信息显示、仪表抄录，职能是记录设备状态；通信网关主要负责电路的保护，由智能断路器、遥控单元和直流屏组成[6]。

3 分布式光伏接入方法判定

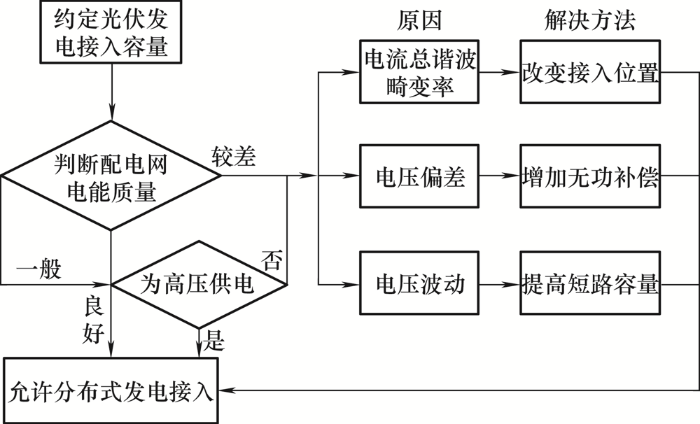
分布式光伏接入在总体设计方案下进行，为保证供电质量需要对接入条件进行判定，符合接入条件才能被允许接入，对符合接入条件的光伏电源给予解决方案，使之能够满足配电网接入需求[7]，光伏接入判定如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   分布式光伏接入判定图


分布式光伏的接入条件判定根据约定的光伏发电接入容量进行综合分析，通过判断接入后配电网的电能质量决定是否接入电网，判定良好可以直接进行接入，判定一般需要进行高压供电，判定较差进入分析阶段。对判定一般的进行高压供电，供电完成可以进行后续接入操作，供电失败需要进入分析阶段[8]。分析阶段主要分析接入时的电流谐波畸变率、电压偏差和电压波动，根据分析出的原因分别给出解决方法，对于电流畸变率较高的需要改变接入位置进行调节；电压偏差较大需要增加无功补偿；电压波动较大的需要提高短路容量。原因排查结束后才能进行后续的接入操作[9]。

4 配电网等效电路

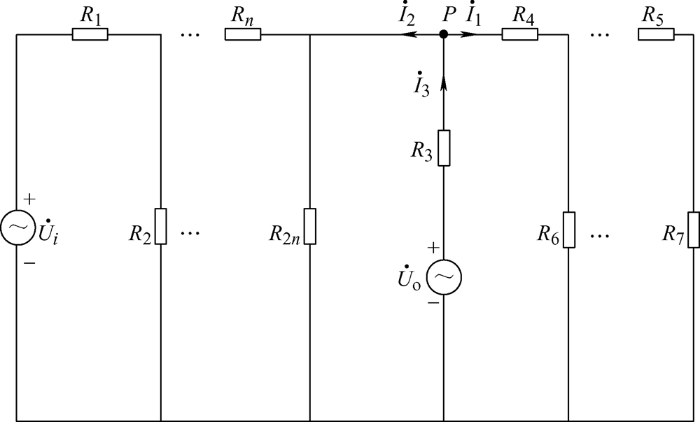
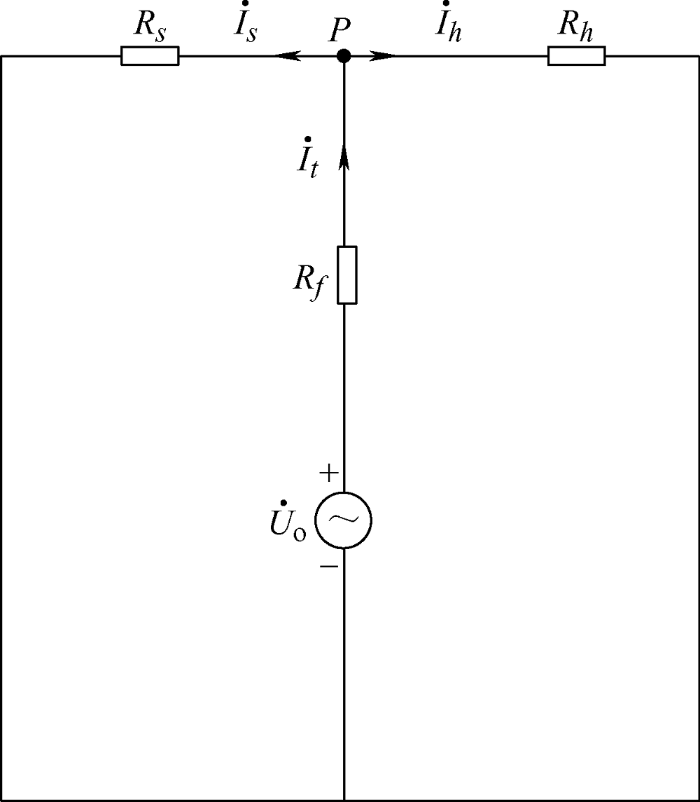
配电网的有源系统接入时往往会造成扰动，对于分布式光伏电源的接入，本文通过分析接入点位置的电路走线，找到最佳接入位置，使配电网扰动达到最小[10]，分布式光伏接入点简要电路图和等效电路图如图3、4所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   接入点简要电路图


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   光伏接入点等效电路图


分布式光伏电源的接入代表配电网系统具有了有源系统，将其进行等效变换得到接入节点的电流为

$\dot{I}=\frac{{{R}_{h}}}{{{R}_{f}}+{{R}_{h}}}{{\dot{I}}_{t}}$

式中，${{R}_{h}}$表示电网侧等效谐波阻抗；${{R}_{f}}$表示接入点等效电阻值；${{\dot{I}}_{t}}$表示输出侧汇合电流值。根据基尔霍夫定律对等效电路图进行分析，多个节点位置的电路阻抗等效为公共节点的总阻值[11]，从而得到整个配电网谐波电压为

${{\dot{U}}_{po}}=\frac{{{R}_{h}}{{R}_{s}}}{{{R}_{s}}+{{R}_{h}}}{{\dot{I}}_{t}}$

假设图3中各接入点位置存在一定的相似性，可以进行合并同化，则式(2)可简化为

${{\dot{U}}_{po}}=\frac{{{R}_{C}}{{R}_{L}}}{\left( n-k \right){{R}_{C}}+{{R}_{L}}/k}{{\dot{I}}_{t}}$

式中，k表示分布式光伏电源接入位置；n表示接入点数量；${{R}_{C}}$表示母线节点线路等效阻抗；${{R}_{L}}$表示负荷间的等效阻抗。根据式(3)进行分析，对分布式光伏电源的接入位置进行简单把控，根据不同的计算结果选择合适的接入点，使接入时对配电网系统的影响达到最小[12⇓⇓-15]。

根据分布式光伏电源接入条件判定方法和等效电路分析，对接入位置更加清晰，使光伏接入配电更易成功，及时避免接入时的扰动影响，使本文设计更加具有信服力[16]。

5 分布式数据信赖域算法

由于本文研究的是有源配电网络，而且接入的电源是分布式光伏电源，因此需要对分布式电力数据进行约束，为更加快速合理处理电网接入过程中的分布式数据，本文采用信赖域算法[17⇓⇓-20]。

根据接入分布式光伏电源采集的数据，对运行状态中的有功和无功功率进行分析得到

$\left\{ \begin{matrix} {{P}_{Li}}={{P}_{0i}}U_{i}^{\alpha }\left[ 1+{{K}_{pfi}}\left( f-{{f}_{0}} \right) \right] \\ {{Q}_{Li}}={{Q}_{0i}}U_{i}^{\beta }\left[ 1+{{K}_{qfi}}\left( f-{{f}_{0}} \right) \right] \\ \end{matrix} \right.$

式中，${{P}_{Li}}$、${{Q}_{Li}}$分别为节点负荷的实际有功、无功功率；${{f}_{\text{0}}}$和$f$分别为设定频率值和实际频率值；${{P}_{\text{0}i}}$、${{Q}_{\text{0}i}}$分别为未接入时的配电网运行的功率数据；$\alpha $为电网接入电源的无功电压增加系数；$\beta $为接入位置的有功增加电压系数；${{K}_{pfi}}$、${{K}_{qfi}}$为负荷的静态频率特性参数。

对电源接入位置进行分析，通过标注接入点位置为PQ，建立方程组，从而更加准确地了解接入点的功率变化。PQ节点功率方程为

$\left\{ \begin{matrix} {{F}_{PpQi}}={{P}_{Gi}}-{{P}_{Li}}-{{P}_{i}}=0 \\ {{F}_{QPQi}}={{Q}_{Gi}}-{{Q}_{Li}}-{{Q}_{i}}=0 \\ \end{matrix}\ \ \ \ \ \ i\in {{S}_{PQ}} \right.$

式中，${{S}_{PQ}}$为PQ节点集合；FPpQi、FQpQi分别为PQ节点的有功、无功功率方程；${{P}_{Gi}}$表示接入点PQ位置的无功输出；${{Q}_{Gi}}$表示有功输出；${{P}_{Li}}$表示光伏接入位置的无功输入；${{Q}_{Li}}$表示光伏有功输入量；${{P}_{i}}$表示节点功率总量；${{Q}_{i}}$表示节点有功总量。若节点上没有DG装置，则${{P}_{Gi}}\text{=0}$、${{Q}_{Gi}}\text{=0}$；若节点上有DG装置，则${{P}_{Gi}}$、${{Q}_{Gi}}$为指定的有功和无功功率输出。则节点注入有功和无功功率为

$\left\{ \begin{matrix} {{P}_{i}}={{U}_{i}}\sum\limits_{j\in i}{{{U}_{j}}\left( {{G}_{ij}}\cos {{\delta }_{ij}}+{{B}_{ij}}\sin {{\delta }_{ij}} \right)} \\ {{Q}_{i}}={{U}_{i}}\sum\limits_{j\in i}{{{U}_{j}}\left( {{G}_{ij}}\cos {{\delta }_{ij}}+{{B}_{ij}}\cos {{\delta }_{ij}} \right)} \\ \end{matrix} \right.$

对式(6)中的接入点位置总功率方程组进行合并，得到分布式光伏接入电网式的总功率变化方程。

${{F}_{PpVi}}={{P}_{Gi}}-{{P}_{Li}}-{{P}_{i}}=0\ \ \ \ \ i\in {{S}_{PV}}$

式中，${{S}_{PV}}$为PV节点集合；FPpVi为PV节点的有功功率方程。下垂节点的功率方程为

$\left\{ \begin{matrix} {{F}_{PDi}}=\frac{1}{{{m}_{Pi}}}\left( {{\omega }_{0}}-\omega \right)-{{P}_{Li}}-{{P}_{i}}=0 \\ {{F}_{QDi}}=\frac{1}{{{n}_{Qi}}}\left( {{U}_{0}}-{{U}_{i}} \right)-{{Q}_{Li}}-{{Q}_{i}}=0 \\ \end{matrix} \right.\ \ \ \ \ \ i\in {{S}_{D}}$

式中，${{S}_{D}}$为下垂节点集合；${{F}_{PDi}}$、${{F}_{QDi}}$分别为下垂节点的有功、无功功率方程。

对下垂节点功率进行限制，限制功率最小值为

$\min f\left( x \right)=\frac{1}{2}F{{\left( x \right)}^{T}}F\left( x \right)\ \ \ \ \ \ x\in {{R}^{n}}$

式中，$f\left( x \right)$表示下垂节点变化规律方程，根据接入点前后功率数据变化得到

$f\left( x \right)=\frac{1}{2}\left( \sum\limits_{i\in {{S}_{PQ}}}{F_{PpQi}^{2}+}\sum\limits_{i\in {{S}_{PQ}}}{F_{QpQi}^{2}+}\sum\limits_{i\in {{S}_{PV}}}{F_{PpVi}^{2}+\sum\limits_{i\in {{S}_{D}}}{F_{PDi}^{2}+}\sum\limits_{i\in {{S}_{D}}}{F_{QDi}^{2}}} \right)$

对下垂节点的限制最小值进行优化，通过限制条件和配电网扰动量进行优化，从而得到优化后的下垂节点最小功率为

$\begin{matrix} \min f\left( {{x}^{k}} \right)+\nabla f{{\left( {{x}^{k}} \right)}^{\mathrm{T}}}{{s}^{k}}+\frac{1}{2}{{\left( {{s}^{k}} \right)}^{\mathrm{T}}}{{\nabla }^{2}}f\left( {{x}^{k}} \right){{s}^{k}} \\ \mathrm{s}.\mathrm{t}.\ \ \ {{\left\| {{s}^{k}} \right\|}_{2}}\le {{\nabla }_{k}}\ \\ \end{matrix}$

式中，${{s}^{k}}\text{=}{{x}_{k+1}}-{{x}_{k}}$；$\nabla f\left( {{x}^{k}} \right)$、${{\nabla }^{\text{2}}}f\left( {{x}^{k}} \right)$分别为f(x)在当前迭代点xk处的梯度向量。

接入点位置的功率方程是否值得信赖，通过判定体系进行判断，对计算出的结果进行判定，即

${{r}_{k}}=\frac{\Delta {{f}_{k}}}{\Delta {{q}_{k}}}=\frac{f\left( {{x}^{k}} \right)-f\left( {{x}^{k}}+{{s}^{k}} \right)}{f\left( {{x}^{k}}-q\left( {{s}^{k}} \right) \right)}$

式中，$\Delta {{f}_{k}}$、$\Delta {{q}_{k}}$分别为f(x)在第k个接入点的前后变化量，对其进行整定

.${{B}_{k+1}}=\left\{ \begin{matrix} {{B}_{k}}-\frac{{{B}_{k}}{{s}^{k}}{{\left( {{s}^{k}} \right)}^{\mathrm{T}}}{{B}_{k}}}{{{\left( {{s}^{k}} \right)}^{\mathrm{T}}}{{B}_{k}}{{s}^{k}}}+\frac{{{y}^{k}}{{\left( {{y}^{k}} \right)}^{\mathrm{T}}}}{{{\left( {{y}^{k}} \right)}^{\mathrm{T}}}{{s}^{k}}}\ \ \ \ \ \ {{r}_{k}}\ge {{\eta }_{1}} \\ {{B}_{k}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{r}_{k}}<{{\eta }_{1}} \\ \end{matrix} \right.$

式中，${{y}^{k}}\text{=}{{g}_{k+1}}-{{g}_{k}}$。设Bk对称正定，则修正可保证Bk+1为对称正定性矩阵，一般设B0为单位矩阵。比较可知，由修正产生Bk+1矩阵比计算矩阵要简单。所以，基于目标函数和其梯度向量的信息构造矩阵的近似矩阵，可保持矩阵的正定性，克服数值上的奇异性。迭代过程中，若${{r}_{k}}$接近于1，则扩大信赖域半径${{\Delta }_{k}}$；若$r_{k}$＞0，但不接近于1，则保持$\Delta{k}$不变；若${{r}_{k}}$接近于0，则缩小$\Delta{k}$，修正如下

${{\Delta }_{k+1}}=\left\{ \begin{matrix} \min \left( {{\gamma }_{2}}{{\Delta }_{k}},{{\Delta }_{\max }} \right)\ \ \ {{r}_{k}}>{{\eta }_{2}} \\ {{\Delta }_{k}}\ \ \ {{\eta }_{1}}\le {{r}_{k}}\le {{\eta }_{2}}\ \ \ \ \ \ \ \ \ \ \\ {{\gamma }_{1}}{{\Delta }_{k}}\ \ \ \ {{r}_{k}}<{{\eta }_{1}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \end{matrix} \right.$

式中，${{\gamma }_{1}}$、${{\gamma }_{2}}$为信赖域半径修正系数，$0<{{\gamma }_{1}}\le 1\le {{\gamma }_{2}}$；${{\eta }_{1}}$、${{\eta }_{2}}$为迭代成功判别系数，$0<{{\eta }_{1}}<1<{{\eta }_{2}}$。

通过修正后的判定条件对电源接入进行数据验证比对，使接入方法更加有效，造成的影响最小，对接入后的配电网系统更加具有信赖性[21]。

6 试验结果与分析

本文研究试验在传统电源接入系统数据的基础上验证，通过试验数据记录，并根据试验结果进行仿真和对比，对接入点进行试验数据记录，根据具体数据分析本研究设计方案的有效性。在试验中有一定的环境要求：处理器CPU的额定功率大于75%，电负荷预测精度大于80%，试验用计算机采用Intel i5以上处理器，应用Power Factory进行模型预测仿真，配电网试验模拟环境如表1所示。

表1   配电网试验模拟环境

试验环境配置参数
配电网系统—
分布式光伏新型光伏接入方法
Intel i78核CPU, 64位处理器, 128 G内存
Power Factory仿真Power Factory 2019

新窗口打开| 下载CSV


本研究在Windows操作系统下，通过模拟配电网运行状态进行数据采集记录，得到分布式光伏接入点的数据测试结果如表2所示。

表2   配电网节点总功率测试数据

光伏接入节点试验数据/kW计算数据/kW相对差值(%)
PQPQΔP
节点103.7853.0913.7503.0900.93
节点205.0464.0335.0004.0350.92
节点3012.6157.42612.5007.4250.92
节点4015.1386.89315.0006.9000.92

新窗口打开| 下载CSV


根据表2数据结果分析，在节点40和节点10分别达到接入电源功率最大和最小值，节点10的有功容量最小，表明节点之间的有功功率分配是基于其有功容量大小，接入点功率越大，证明系统存在频率振荡。由表2可见，节点30发出的无功功率最大，而节点30的无功容量不是最大，表明接入点之间的无功功率分配不是基于其无功容量大小。

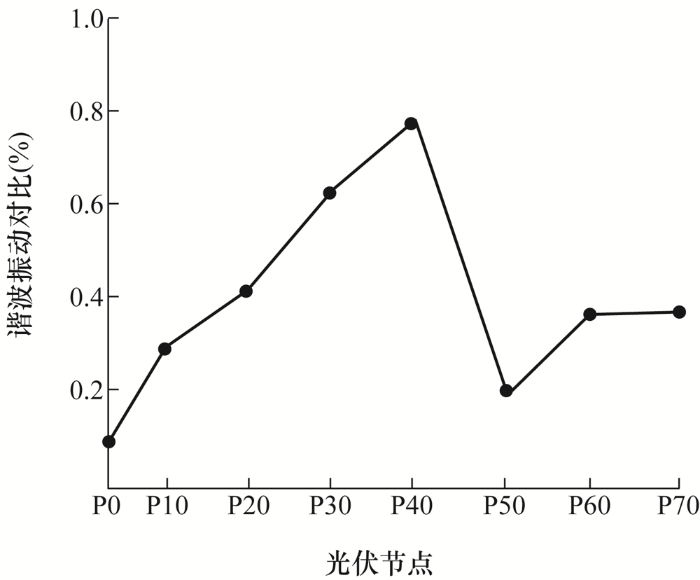
为更清晰直观了解分布式光伏接入配电网的影响，对各接入点进行谐波振动分析，并根据数据画出对比度曲线如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   接入节点谐波振荡对比曲线


分析图5发现从P0~P40谐波振荡一直处于上升状态，表明一直处于干扰状态；在P40~P50节点，谐波振动持续下降，表明本研究接入方法对接入扰动产生作用；P50之后的节点配电网逐渐趋于稳定，表明接入扰动停止。

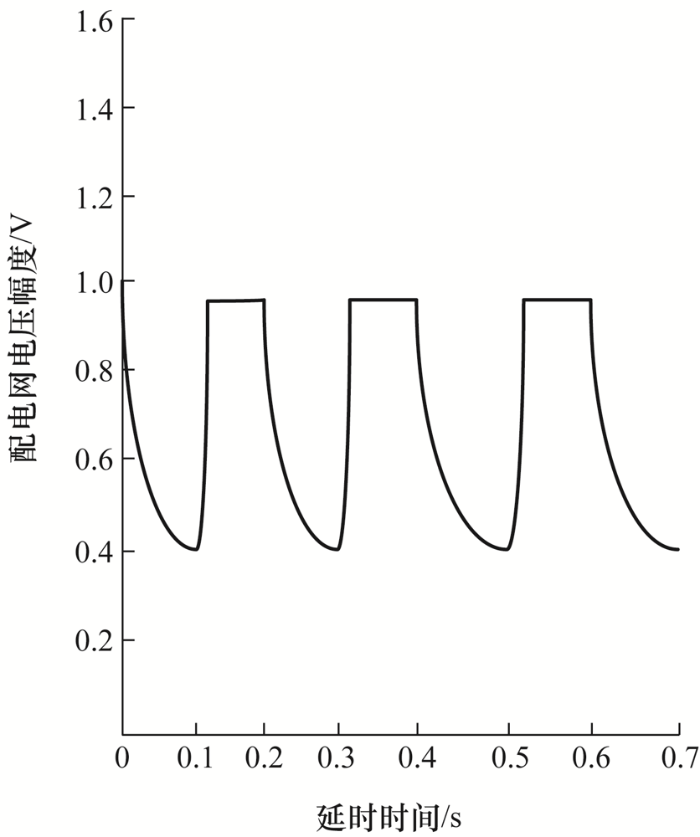
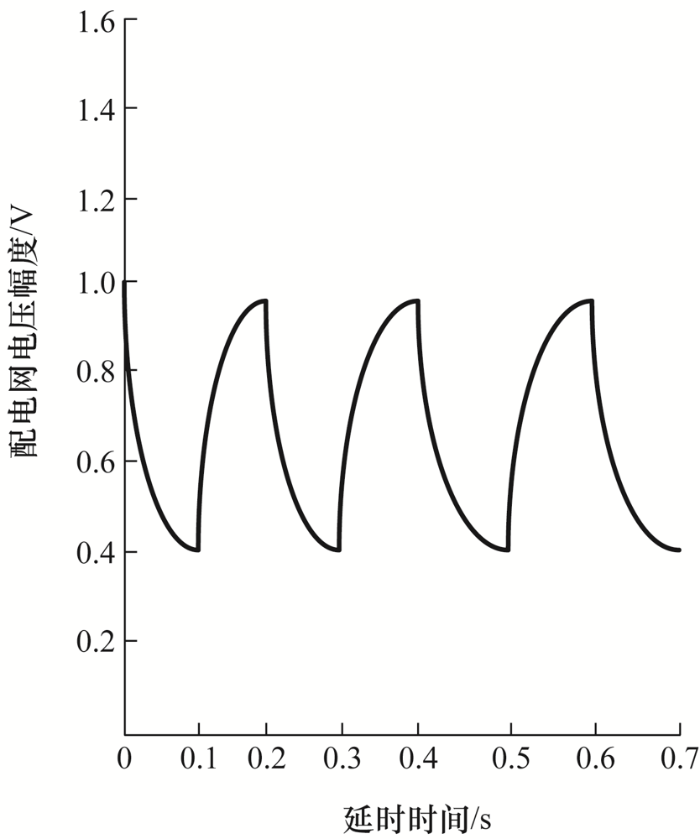
为验证本研究规划的优越性，利用Power Factory仿真软件进行对比验证仿真，与传统电源接入配电网进行对比验证，计算机仿真电压变化幅度对比曲线如图6、7所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   传统电源接入电网电压幅度


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   分布式光伏接入电网电压幅度


通过对比分析发现，传统电源接入配电网会存在一段时间的接入延时，延时时间为0.1 s，而且接入瞬间存在滞留效应，容易对配电网造成冲击；而分布式光伏接入时不存在延时状态，在接入时也没有滞留效应，接入配电网时能够平滑过渡，电压幅度没有显著变化。

综上所述，本文研究的设计方案更加稳定，方法更加有效，能够有效调节节点的振荡谐波，接入瞬间对配电网影响能够达到最小，从而体现出本研究方案在配电网中的实用性。

7 结论

本文对光伏电源在配电网的应用进行规划设计，在有源接入方法的基础上进行创新。

(1) 对整体布局进行设计，设计光伏有源应用方法，使配电网尽可能小地造成扰动。

(2) 分析节点位置的线路，通过电流和等效电阻进行分析，找到最佳光伏接入电网位置。

(3) 利用信赖域算法进行光伏接入节点的功率计算。

(4) 进行试验验证分析，对试验数据进行记录，并给出接入点谐波振荡对比度曲线。

通过以上改进，并与传统有源接入电网方案的电压幅度分析验证，验证了此设计很好地解决了电网供能效率低、谐波振荡大和抗干扰能力差的问题，具有良好的适用性。

但是本研究在试验验证中存在一些硬件上的问题，只能在模拟环境下进行光伏接入，与实际情况存在差距；由于设备问题和人工读取数据容易造成一定的误差等问题仍待解决。

参考文献

苏庭波.

网络中层次化内部威胁态势量化评估方法仿真

[J]. 计算机仿真, 2019(4):265-268.

[本文引用: 1]

SU Tingbo.

Simulation of quantitative assessment method of hierarchical internal threat situation in network

[J]. Computer Simulation, 2019(4):265-268.

[本文引用: 1]

刘江伟, 郭宇, 查珊珊, 等.

基于改进粒子群算法的多工位装配序列规划

[J]. 计算机集成制造系统, 2018, 24(11):2701-2711.

[本文引用: 1]

LIU Jiangwei, GUO Yu, ZHA Shanshan, et al.

Multi-station assembly sequence planning based on improved particle swarm optimization algorithm

[J]. Computer Integrated Manufacturing Systems, 2018, 24(11):2701-2711.

[本文引用: 1]

唐红亮, 吴柏林, 胡旺, 等.

基于粒子群优化的地震应急物资多目标调度算法

[J]. 电子与信息学报, 2020, 42(3):737-745.

[本文引用: 2]

TANG Hongliang, WU Bolin, HU Wang, et al.

Multi-objective scheduling algorithm for earthquake emergency supplies based on particle swarm optimization

[J]. Journal of Electronics & Information Technology, 2020, 42(3):737-745.

[本文引用: 2]

蒙璟, 李训聿, 丁霞燕.

基于改进自适应权重多目标粒子群算法的分布式电源优化配置

[J]. 电力科学与技术学报, 2020, 35(2):55-60,106.

[本文引用: 1]

MENG Jing, LI Xunyu, DING Xiayan.

Optimal allocation of distributed power supply based on improved adaptive weight multi-objective particle swarm optimization algorithm

[J]. Journal of Electric Power Science and Technology, 2020, 35(2):55-60,106.

[本文引用: 1]

VICHAKORN H, THAVATCHAI T, NATTHAPHOB N.

Optimal sizing of photovoltaic distributed generators in a distribution system with consideration of solar radiation and harmonic distortion

[J]. Electrical Power and Energy Systems, 2015(64):646-654.

[本文引用: 1]

肖白, 郭蓓.

配电网规划研究综述与展望

[J]. 电力自动化设备, 2018, 38(12):200-211,217.

[本文引用: 1]

XIAO Bai, GUO Bei.

Review and prospect of distribution network planning

[J]. Electric Power Automation Equipment, 2018, 38(12):200-211,217.

[本文引用: 1]

孙旻, 余愿, 曾伟, 等.

考虑主动管理的配电网分布式光伏并行优化配置

[J]. 电力自动化设备, 2019, 39(3):169-174,181.

[本文引用: 1]

SUN Min, YU Huan, ZENG Wei, et al.

Parallel optimal allocation of distributed PV in distribution network considering active management

[J]. Electric Power Automation Equipment, 2019, 39(3):169-174,181.

[本文引用: 1]

徐全, 袁智勇, 于力, 等.

基于多端SOP的交直流混联配电网多目标运行优化方法

[J]. 电力系统及其自动化学报, 2020, 32(9):42-48,54.

[本文引用: 1]

XU Quan, YUAN Zhiyong, YU Li, et al.

Multi-objective operation optimization method of AC-DC hybrid distribution network based on multi-terminal SOP

[J]. Proceedings of the CSU-EPSA, 2020, 32(9):42-48,54.

[本文引用: 1]

孙惠娟, 刘君, 彭春华.

基于分类概率综合多场景分析的分布式电源多目标规划

[J]. 电力自动化设备, 2018, 38(12):39-45.

[本文引用: 1]

SUN Huijuan, LIU Jun, PENG Chunhua.

Multi-objective DG planning based on classified probability integration multi-scenario analysis

[J]. Electric Power Automation Equipment, 2018, 38(12):39-45.

[本文引用: 1]

侯波.

浅谈分布式光伏发电站功率因数影响及治理

[J]. 百科论坛电子杂志, 2021(3):1959.

[本文引用: 1]

HOU Bo.

Discussion on power factor influence and treatment of distributed photovoltaic power station

[J]. Encyclopedia Forum, 2021(3):1959.

[本文引用: 1]

郑若楠, 李国杰, 韩蓓, 等.

基于加权扩展日特征矩阵的分布式光伏发电日前功率预测

[J]. 电力自动化设备, 2022, 42(2):99-105.

[本文引用: 1]

ZHENG Ruonan, LI Guojie, HAN Bei, et al.

Power forecast of distributed photovoltaic generation day based on weighted extended day feature matrix

[J]. Electric Power Automation Equipment, 2022, 42(2):99-105.

[本文引用: 1]

宋淼, 王克文.

主动配电网中考虑空间与时间相关性的分布式光伏并网规划

[J]. 电力系统保护与控制, 2019, 47(5):106-114.

[本文引用: 1]

SONG Miao, WANG Kewen.

Distributed photovoltaic grid-connection planning considering spatial and temporal correlation in active distribution network

[J]. Power System Protection and Control, 2019, 47(5):106-114.

[本文引用: 1]

赵滨滨, 王莹, 王彬, 等.

基于ARIMA时间序列的分布式光伏系统输出功率预测方法研究

[J]. 可再生能源, 2019, 37(6):820-823.

[本文引用: 1]

ZHAO Binbin, WANG Ying, WANG Bin, et al.

Research on output power prediction method of distributed photovoltaic system based on ARIMA time series

[J]. Renewable Energy, 2019, 37(6):820-823.

[本文引用: 1]

郭宝甫, 舒逸石, 李瑞生, 等.

分布式扶贫光伏智能运维服务系统设计及工程应用

[J]. 电测与仪表, 2019, 56(7):84-88.

[本文引用: 1]

GUO Baofu, SHU Yishi, LI Ruisheng, et al.

Design and engineering application of distributed poverty alleviation photovoltaic intelligent operation and maintenance service system

[J]. Electrical Measurement & Instrumentation, 2019, 56(7):84-88.

[本文引用: 1]

马艳霞, 车彬, 孟旭红, 等.

基于多目标的多阶段主动配电网规划方法分析

[J]. 电网与清洁能源, 2019, 35(10):62-67.

[本文引用: 1]

MA Yanxia, CHE Bin, MENG Xuhong, et al.

Analysis of multi-stage active distribution network planning method based on multi-objective

[J]. Power Grid and Clean Energy, 2019, 35(10):62-67.

[本文引用: 1]

王合建, 王栋, 杨珂.

基于物联网标识技术的分布式光伏数据共享系统技术架构与平台建设

[J]. 电网与清洁能源, 2019, 35(8):69-75.

[本文引用: 1]

WANG Hejian, WANG Dong, YANG Ke.

Technology architecture and platform construction of distributed photovoltaic data sharing system based on Internet of Things identification technology

[J]. Power Grid and Clean Energy, 2019, 35(8):69-75.

[本文引用: 1]

RUIZ F J, HERNANDZ J C, JURADO F.

Voltage unbalance assessment in secondary radial distribution networks with single-phase photo voltaic systems

[J]. Electrical Power and Energy Systems, 2015(64):646-654.

[本文引用: 1]

郑小宇, 季宇, 张颖, 等.

基于模型预测控制的分布式光伏集群协调优化控制

[J]. 电网与清洁能源, 2019, 35(7):66-74.

[本文引用: 1]

ZHENG Xiaoyu, JI Yu, ZHANG Ying, et al.

Distributed photovoltaic cluster coordination and optimization control based on model predictive control

[J]. Power Grid and Clean Energy, 2019, 35(7):66-74.

[本文引用: 1]

LUPANGU C, BANSAL R C.

A review of technical issues on the development of solar photovoltaic systems

[J]. Renewable & Sustainable Energy Reviews, 2017, 73:950-965.

[本文引用: 1]

唐雪晨, 王文锦, 卢国波, 等.

基于人工鱼群算法的多目标分布式光伏电源规划

[J]. 电网与清洁能源, 2019, 35(1):84-90.

[本文引用: 1]

TANG Xuechen, WANG Wenjin, LU Guobo, et al.

Multi-objective distributed photovoltaic power supply planning based on artificial fish swarm algorithm

[J]. Power Grid and Clean Energy, 2019, 35(1):84-90.

[本文引用: 1]

李沐珂, 张靠社.

计及分布式光伏发电的分时电价模型研究

[J]. 电网与清洁能源, 2018, 34(4):74-78.

[本文引用: 1]

LI Muke, ZHANG Kaoshe.

Study on TOU pricing model for distributed photovoltaic power generation

[J]. Power Grid and Clean Energy, 2018, 34(4):74-78.

[本文引用: 1]

/

〈 〉