1 引言
风电的功率输出具有强随机性、可预测性差的特点。因此,需要额外安排一定容量的旋转备用以响应风电场发电功率的随机波动,维持电力系统的功率平衡与稳定[1 ] 。
电力系统备用可以分为一次备用(也称瞬时备用)、二次备用(也称快速备用)和三次备用(也称长期备用)[2 ] ,分别应用于实现不同时间尺度的有功调度控制。其中,系统级有功调度主要关注的是二次备用和三次备用。大规模风电的接入使得系统的等效负荷功率波动更加频繁,对系统多级备用的时间响应特性和协调提出了更高的要求[3 -4 ] 。针对这一特点,文献[5 ]提出以不同响应时间的多级备用协调来解决大规模风电接入后系统运行备用新问题。其中,滚动调度环节在当天开停机计划已知的情况下,通过最新的扩展短期负荷及风电预测结果滚动修正机组的日前计划,使得发电机出力与系统的实际发电需求逐渐逼近,在日前计划与实时计划之间起承上启下的重要作用。该环节的备用对应于传统的三次备用,其主要功能除了应对系统负荷和风电预测误差外,还要应对系统中的突发事件(如发电机或线路故障等),因此,合理的滚动环节备用容量对保证系统的安全运行具有重要意义。
同时,受风资源分布等因素的限制,我国风电场的建设呈现出大规模开发集中并网的特点,但由于风电场往往位于电网的末端,电网结构薄弱且负荷小,使得相关输电断面的负载加重、断面潮流波动剧烈[6 ] ,而不合理的系统分区备用会进一步恶化这种情况。传统的备用分配决策模型中较少考虑备用分区平衡问题,由此可能加大重载断面的受电端失负荷风险,危及系统的安全性[7 ] 。因此,需要研究更合理的系统备用与分区备用决策方法及其与发电计划的配合方案。
针对大规模风电并网系统,本文研究了基于失负荷期望的系统备用风险决策模型,分析了失负荷期望与备用需求的关系。同时研究了基于失负荷期望的备用分区分配策略,以系统一定失负荷期望下的分区失负荷风险最小作为分配原则,并采用模糊优化方法进行多目标优化建模。该决策模型弥补了传统基于概率的备用决策方法[8 ] 对失负荷量考虑不足的缺陷,同时与基于风险的备用决策模型相比,方法更直观,可操作性较强。
由于备用容量与发电计划耦合约束的复杂性,本文采用粒子群算法求解模型。最后,以IEEE 24节点系统为算例系统,对本文所提算法进行了验证。
2 滚动备用分区分配策略
2.1 备用分区分配模型
针对大规模风电传输造成的重载断面受电端备用不足的问题,合理的备用分区分配结果在保证最小弃风的前提下,一方面使得火电机组的发电成本最小,另一方面使得不同分区之间的运行风险水平差异最小。因此,需要定义如下的分区备用分布均衡度指标
(1) ${{I}_{t}}=\sum\limits_{j=1}^{n}{||{{r}_{jt}}-\overline{{{r}_{t}}}||_{2}^{2}}$
式中,${{r}_{jt}}=\frac{E{{G}_{jt}}}{{{D}_{jt}}}$为分区j 的期望失负荷率,$E{{G}_{jt}}$为第j 分区第t 时段的失负荷期望;${{D}_{jt}}$为第j 分区t 时段的负荷水平;n 为所有分区的数目;$\overline{{{r}_{t}}}$为分区期望失负荷率序列的均值。可见,${{I}_{t}}$根据分区的运行安全水平决定合理的备用分布,其取值越小则每个分区的期望失负荷率越相近,系统的备用分布越均匀;反之亦然。本文称${{I}_{t}}$为期望失负荷率偏差指标。
据此,考虑运行安全的滚动调度环节发电备用容量分区分配问题可以表示为如下的多目标优化问题
(2) $\left\{ \begin{align} & {{f}_{1}}=\sum\limits_{j\in {{G}_{wind}}}{\sum\limits_{t={{t}_{0}}+1}^{T}{{{\lambda }_{j}}|p_{jt}^{f}-p_{jt}^{w}}}| \\ & {{f}_{2}}=\sum\limits_{i=1}^{N}{\sum\limits_{t={{t}_{0}}+1}^{T}{({{a}_{i}}{{p}_{it}}^{2}+{{b}_{i}}{{p}_{it}}+{{c}_{i}})}} \\ & {{f}_{3}}=\sum\limits_{t={{t}_{0}}+1}^{T}{}I_{t}^{{}} \\ \end{align} \right.$
式中,${{f}_{1}}$代表电网运行过程中的最小弃风要求,${{f}_{2}}$为常规机组的煤耗成本,$p_{jt}^{f}$代表风电场的预测出力值,${{a}_{i}}{{b}_{i}}{{c}_{i}}$分别为第i 台发电机的煤耗系数;${{\lambda }_{j}}$为风电机组弃风成本因子;当${{\lambda }_{j}}$与${{b}_{i}}$为同一数量级且取值为正时,即可实现最小弃风的目的。f 3 以多时段的分区备用分布均衡度指标衡量系统的运行风险大小。
(3) ${{E}_{t}}\le {{E}_{thresh}}$
式中,${{E}_{t}}$为系统在第t 时刻的失负荷期望;${{E}_{thresh}}$为限定的失负荷期望阈值。
(4) $\sum\limits_{i=1}^{N}{p_{it}^{{}}}+\sum\limits_{j\in {{G}_{\text{wind}}}}{p_{jt}^{{}}}=D_{t}^{{}}$
式中,$D_{t}^{{}}$为第t 时段的系统负荷预测值。
(5) $\underline{{{p}_{i}}}\le {{p}_{it}}\le \overline{{{p}_{i}}}$
(6) $0\le p_{jt}^{w}\le p_{jt}^{up}\ j\in {{G}_{wind}}$
式中,$\overline{{{p}_{i}}}$ 、$\underline{{{p}_{i}}}$分别代表常规机组出力的上下限,$p_{jt}^{up}$代表风电场预测出力区间上限。
(7) ${{p}_{i,t-1}}-\Delta p{{d}_{i}}{{T}_{15}}\le {{p}_{it}}\le {{p}_{i,t-1}}+\Delta p{{u}_{i}}{{T}_{15}}$
式中,$\Delta p{{d}_{i}}$、$\Delta p{{u}_{i}}$分别表示机组$i$向上及向下的爬坡率。
$R_{it}^{u}=\min (\Delta p{{u}_{i}}{{T}_{10}},\overline{{{p}_{i}}}-{{p}_{it}})$
$R_{it}^{d}=\min (\Delta p{{d}_{i}}{{T}_{10}},{{p}_{it}}-\underline{{{p}_{i}}})$
$R_{t}^{u}=\sum\limits_{i\ne W}{R_{it}^{u}}$
$R_{t}^{d}=\sum\limits_{i\ne W}{R_{it}^{d}}$
式中,$R_{t}^{u}$、$R_{t}^{d}$分别代表第t 时段的系统上下旋备容量,$R_{it}^{u}$、$R_{it}^{d}$分别为第i 台机组第t 时段提供的上下旋备容量。
(8) $\underline{T{{L}_{lt}}}\le \sum\limits_{i=1}^{N}{({{k}_{li}}{{p}_{it}})}+\sum\limits_{j\in {{G}_{wind}}}^{{}}{({{k}_{lj}}{{p}_{jt}})}\le \overline{T{{L}_{lt}}}\ \ \ l=1,\cdots,L$
式中,$l$、$L$分别为断面编号和总断面数,${{k}_{li}}$为第i 台机组对第$l$断面的灵敏度[9 ] ,$\overline{T{{L}_{lt}}}$、$\underline{T{{L}_{lt}}}$分别为断面的上下限。
为便于求解,本文采用如下的模糊优化方法将该多目标优化模型转化为单目标模型求解。
2.2 基于模糊优化方法的备用分区分配模型
模糊优化方法通过引入目标隶属度函数,可以把多目标优化问题转换成单目标优化问题。该方法能较好地反映各个目标最优解和多目标满意解之间的相互关系,考虑不同性质、相互矛盾的多个目标的满意程度,得到使各个目标都尽可能最优的折中解[10 ⇓ -12 ] 。
为实现最小弃风的目的,对于风电机组建立如下所示的隶属度函数
${{\mu }_{1}}=\exp \left( -{{\left( \frac{{{p}^{w}}-{{p}^{f}}}{\sigma } \right)}^{2}} \right)$
式中,${{p}^{w}}$为风电场出力,${{p}^{f}}$为风电场预测出力,$\sigma $为风电预测误差标准差。
为体现调度人员对经济性与安全性的偏好,对系统经济性及安全性分别采用如下的二次隶属度评估函数
$\left\{ \begin{align} & {{\mu }_{2}}={{\alpha }_{1}}f_{1}^{2}+{{\beta }_{1}}{{f}_{1}}+{{\gamma }_{1}} \\ & {{\mu }_{3}}={{\alpha }_{2}}f_{2}^{2}+{{\beta }_{2}}{{f}_{2}}+{{\gamma }_{2}} \\ \end{align} \right.$
式中,${{\mu }_{2}}$是经济性目标对应的隶属度函数,${{\mu }_{3}}$是安全性目标对应的隶属度函数。
由${{\mu }_{i}}({{f}_{i,\min }})=1$,${{\mu }_{i}}({{f}_{i,\max }})=0$可得二次隶属度函数的系数值
$\begin{matrix} {{\alpha }_{i}}=\frac{2{{k}_{i}}}{{{({{f}_{i,\min }}-{{f}_{i,\max }})}^{2}}} \\ {{\beta }_{i}}=\frac{1}{{{f}_{i,\min }}-{{f}_{i,\max }}}-{{\alpha }_{i}}({{f}_{i,\min }}+{{f}_{i,\max }}) \\ {{\gamma }_{i}}=\frac{-{{f}_{i,\max }}}{{{f}_{i,\min }}-{{f}_{i,\max }}}+{{\alpha }_{i}}{{f}_{i,\min }}{{f}_{i,\max }} \\ \end{matrix}$
式中,${{f}_{i,\max }}$、${{f}_{i,\min }}$分别代表常规机组运行成本或备用均衡度指标的最大值及最小值。
在定义以上隶属度函数的基础上,原优化问题可以变换为如下形式
(9) $\left\{ \begin{align} & \max \lambda \\ & s.t.{{\mu }_{1}}=\exp \left( -{{\left( \frac{{{p}^{w}}-{{p}^{f}}}{\sigma } \right)}^{2}} \right)\ge \lambda \\ & {{\mu }_{2}}={{\alpha }_{1}}f_{1}^{2}+{{\beta }_{1}}{{f}_{1}}+{{\gamma }_{1}}\ge \lambda \\ & {{\mu }_{3}}={{\alpha }_{2}}f_{2}^{2}+{{\beta }_{2}}{{f}_{2}}+{{\gamma }_{2}}\ge \lambda \\ & 0\le \lambda \le 1 \\ & (3)(8) \\ \end{align} \right.$
3 失负荷期望与发电备用容量
从式(9)可以看出,备用分区分配模型的核心之一是计算系统失负荷期望。因此,需要考虑大规模风电接入的系统失负荷期望指标的计算形式。
大规模风电接入后,传统火电机组出力的确定性与风电机组出力的随机性同时存在,使得系统具有随机-确定相耦合的性质,系统的失负荷期望受风电及负荷随机预测误差的影响成为随机变量。忽略两重及以上的多重故障,导致系统的发电备用不足的情形可分为两种:① 风电预测误差和负荷预测误差造成的不平衡量高于系统的正常备用容量;② 一台发电机发生停运事故,同时由于风电预测误差与负荷预测误差使得发电负荷的不平衡量高于此时的备用水平。下面对这两种情形分别进行讨论。
首先,考虑到风电预测结果与负荷预测结果的独立性,系统总的等值负荷预测误差为$\sigma (t)=\sqrt{{{\sigma }_{1}}^{2}(t)+{{\sigma }_{2}}^{2}(t)}$。其中,假定风电及负荷的预测误差分别服从均值为0,标准差为${{\sigma }_{2}}(t)$、${{\sigma }_{1}}(t)$的正态分布[13 ] 。
(1) 假设预测误差变量为x ,这种情况下的失负荷期望为
(10) $\begin{matrix} {{E}_{1t}}=\prod\limits_{i=1}^{G}{(1-FO{{R}_{i,t}})}\int_{{{R}_{t}}}^{\infty }{(x-{{R}_{t}})f(x)dx=} \\ {{\sigma }_{t}}\prod\limits_{i=1}^{G}{(1-FO{{R}_{i,t}})}\int_{{{R}_{t}}}^{\infty }{(\frac{x}{{{\sigma }_{t}}}-\frac{{{R}_{t}}}{{{\sigma }_{t}}})\frac{1}{\sqrt{2\pi }}\exp \left( -\frac{1}{2}{{\left( \frac{x}{{{\sigma }_{t}}} \right)}^{2}} \right)d(\frac{x}{{{\sigma }_{t}}})} \\ \end{matrix}$
式中,$FO{{R}_{i,t}}$为第i 台发电机在第t 时段的强迫停运率;${{R}_{t}}$为系统在第t 时段的备用需求容量;$f(x)$为考虑风电预测误差与负荷预测误差后的等值负荷预测误差的概率密度函数;${{\sigma }_{t}}$为等值负荷预测误差的标准差。
$FOR(t)=\frac{\lambda }{\lambda +\mu }+\frac{\exp \left( -(\lambda +\mu )t \right)}{\lambda +\mu }[\mu U(0)-\lambda A(0)]$
式中,$\lambda $代表发电机的故障率;μ 代表发电机故障的修复率;A (0)和U (0)代表发电机在t =0时的运行状态,若发电机投入,则A (0)=1,U (0)=0,否则相反。可以看出,当$t\to \infty $时,FOR (t )$\to \lambda /(\lambda +\mu )$,此时为发电机的稳态强迫停运率。该模型考虑了发电机运行状况随时间的变化,能够给出发电机在未来短期时间内的停运概率。
令y =$\frac{x}{{{\sigma }_{t}}}$,则变量y 服从标准正态分布,式(10)可简化如下
(11) $\begin{matrix} {{E}_{1t}}={{\sigma }_{t}}\prod\limits_{i=1}^{G}{(1-FO{{R}_{i,t}})}\int_{\frac{{{R}_{t}}}{{{\sigma }_{t}}}}^{\infty }{(y-\frac{{{R}_{t}}}{{{\sigma }_{t}}})\frac{1}{\sqrt{2\pi }}\times } \\ \exp \left( -\frac{1}{2}{{y}^{2}} \right)dy= \\ \prod\limits_{i=1}^{G}{(1-FO{{R}_{i,t}})}\left( \frac{{{\sigma }_{t}}}{\sqrt{2\pi }}\exp \left( -\frac{1}{2}{{(\frac{{{R}_{t}}}{{{\sigma }_{t}}})}^{2}} \right)-{{R}_{t}}Q(\frac{{{R}_{t}}}{{{\sigma }_{t}}}) \right) \\ \end{matrix}$
$Q(X)=\int_{X}^{\infty }{\frac{1}{\sqrt{2\pi }}\exp (-0.5{{x}^{2}})dx}$
(2) 一台发电机发生停运事故情况下的失负荷期望为
(12) $\begin{matrix} {{E}_{2t}}=\sum\limits_{i=1}^{G}{\left[ FO{{R}_{i,t}}\times \prod\limits_{\begin{smallmatrix} j=1 \\ j\ne i \end{smallmatrix}}^{G}{(1-FO{{R}_{j,t}})}\times \int_{{{R}_{t}}-{{P}_{i,t}}-{{R}_{i,t}}}^{\infty }{(x-{{R}_{t}}+{{P}_{i,t}}+{{R}_{i,t}})f(x)dx} \right]}= \\ \sum\limits_{i=1}^{G}{(}FO{{R}_{i,t}}\times \prod\limits_{\begin{smallmatrix} j=1 \\ j\ne i \end{smallmatrix}}^{G}{(1-FO{{R}_{j,t}})}\times \left( \frac{{{\sigma }_{t}}}{\sqrt{2\pi }}\exp \left( -\frac{1}{2}{{(\frac{{{R}_{t}}-{{P}_{i,t}}-{{R}_{i,t}}}{{{\sigma }_{t}}})}^{2}} \right)-({{R}_{t}}-{{P}_{i,t}}-{{R}_{i,t}})Q(\frac{{{R}_{t}}-{{P}_{i,t}}-{{R}_{i,t}}}{{{\sigma }_{t}}})) \right) \\ \end{matrix}$
风电功率的不确定性具有随时间增加而不断增大的特点,对于较短的时间范畴,所需的备用较小;对于较长的时间范畴,所需的备用随之增加。为了保证系统总成本最小,需要在机组发电成本与由于备用不足导致的期望失负荷损失两者之间权衡备用的最优值[15 -16 ] 。按照上面分析得出的表达式,当给定系统的失负荷期望时,即可获得系统相应的备用水平。
由于备用与发电计划之间相互耦合的复杂性,使得约束条件包含复杂的非线性关系,常规的数学优化类算法难以适用。因此,本文采用粒子群算法[17 -18 ] 进行求解。
4 仿真结果分析
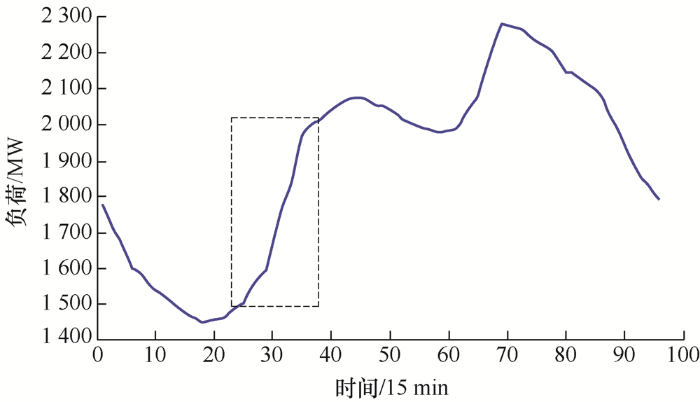
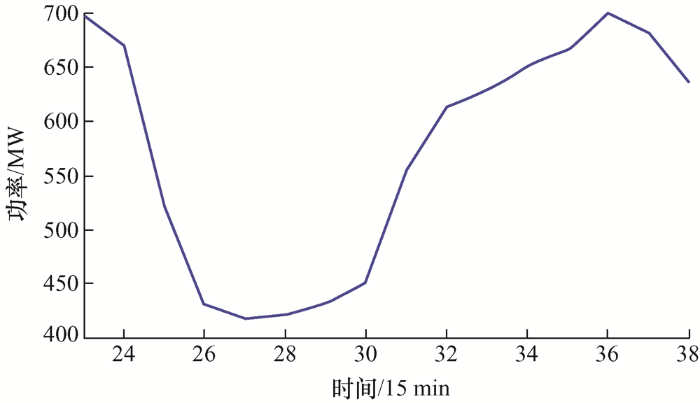
采用IEEE 24节点系统[19 -20 ] 作为研究对象,选取第14号机组为700 MW的风电场。假设风电预测误差标准差为$(0.044+0.006t)p_{t}^{w}$,其中,$p_{t}^{w}$为预测时段的风电出力值;负荷预测误差标准差为2%。设第i 台常规发电机组的故障率为0.005- 0.004 5i /13。系统负荷预测及风电出力预测结果分别如图1 及图2 所示,选取滚动时间窗为负荷快速爬坡阶段的第23~38阶段,如图1 中虚线框所示。
图1
图2
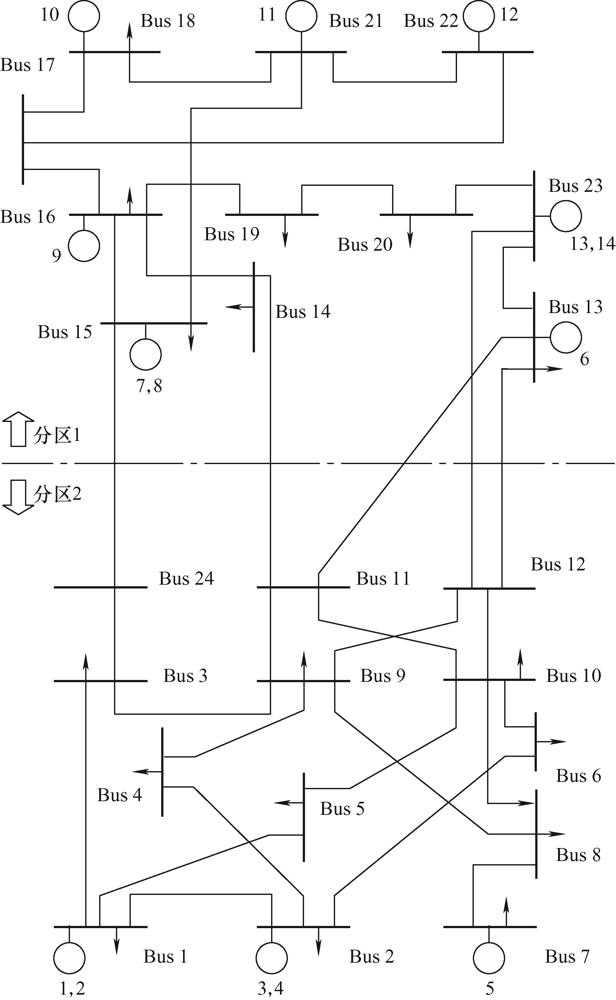
按图3 所示将IEEE 24节点系统划分为南北两个分区。其中,分区2的发电装机容量只占整个系统的20%,负荷需求却占47%。因此,正常运行状态下,断面潮流呈现由北向南供电的态势。
图3
设定失负荷期望的阈值为250 MW,断面传输容量为600 MW,对算例结果分析如下。
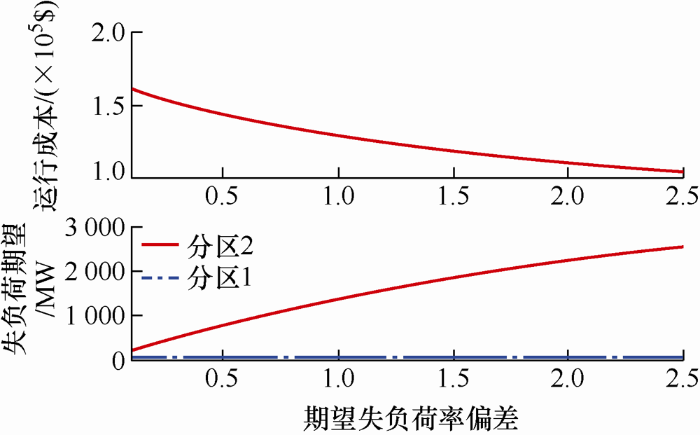
(1) 期望失负荷率偏差指标的影响。图4 给出了系统常规机组运行成本及分区失负荷期望随期望失负荷率偏差指标的变化趋势。可以看出,随着期望失负荷率偏差指标的增大,常规机组的运行成本逐渐降低。同时,随着期望失负荷率偏差的减小,分区的期望失负荷水平趋于一致,表明期望失负荷率偏差指标对于均衡系统运行风险的有效性。
图4
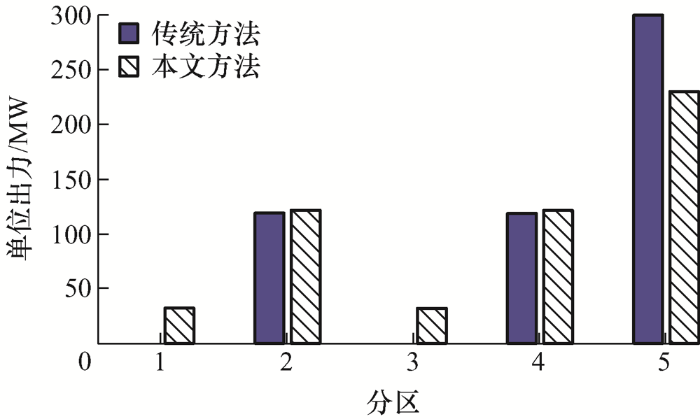
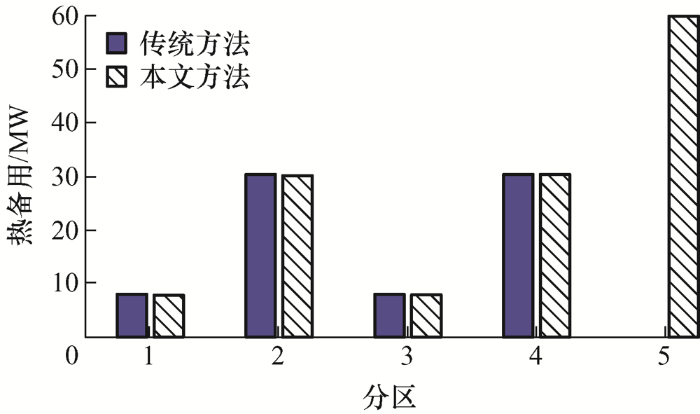
选择优化过程的第38时段,当${{I}_{\max }}$取值为0.5时,分区2发电机出力及备用优化结果分别如图5 及图6 所示。
图5
图6
由图5 、6 可见,备用分区分配模型通过适当降低经济性较好的#5发电机出力,提升经济性较差的#1、#3发电机出力,达到提升分区2的备用水平、降低运行风险的目的。因此,考虑分区备用分配的结果能够使得重载断面的受电端预留更多的备用容量以应对可能的负荷波动或发电机出力故障。
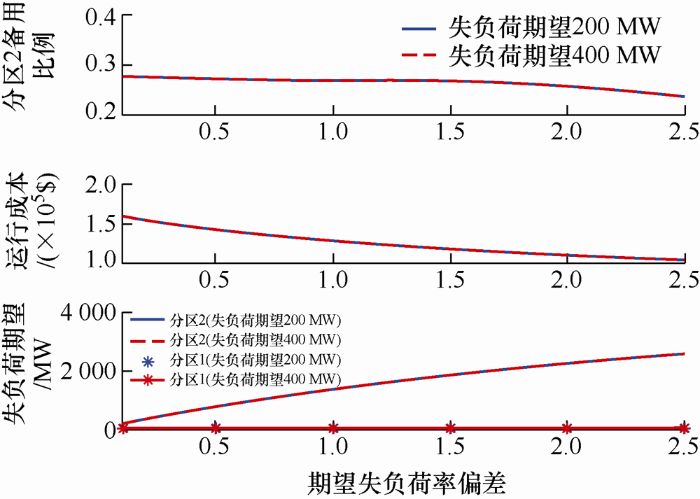
(2) 系统失负荷期望的影响效果。保持其他量不变,在系统失负荷失望阈值分别为400 MW及200 MW时的优化结果如图7 所示。
图7
由图7 可见,在断面重载情况下,相同的期望失负荷率偏差指标下的失负荷期望大小对优化结果的灵敏度不大,而通过调整期望失负荷率的大小可以显著改善系统的安全水平。
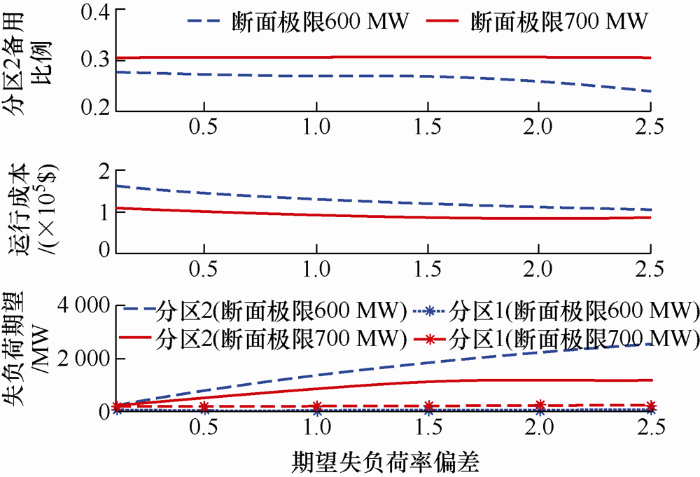
(3) 分区联络断面极限的影响结果。保持失负荷期望为250 MW不变,在不同联络断面极限时的优化结果如图8 所示。
图8
由图8 可见,随着联络断面传输极限的增大,系统成本降低,在供电端子系统失负荷期望基本不变的情况下,受电端子系统的上旋备用比例提高,失负荷期望显著降低。表明此时联络线容量对系统的安全性及经济性具有较高的灵敏度,应通过一定措施提高断面的传输极限,改善系统的运行状况。
(1) 在一定的系统运行风险水平下,期望失负荷率偏差指标能够反映系统备用分布的均匀程度,随着期望失负荷率指标的减小,系统的运行成本升高,重载断面受电端旋备增加。
(2) 在断面重载情况下,分区整体备用水平的提升是通过调整分区内快慢机组的出力,使得快速机组提前降低出力预留备用而满足机组提前增加出力来实现的。
(3) 在断面重载情况下,相同期望失负荷率偏差指标下的系统失负荷期望对运行成本及分区备用比例的灵敏度不大,而分区联络断面极限对系统运行的安全与经济性具有较高的灵敏度。
模糊优化方法能较好地考虑不同性质、相互矛盾的多个目标的满意程度,得到安全性与经济性协调优化的折中解。
5 结论
本文研究了大规模风电并网对系统运行备用的影响,提出了基于失负荷期望的备用风险决策模型,分析了系统失负荷期望与备用需求的关系。考虑到大规模风电集中并网使得断面重载造成受电端备用不足的问题,提出基于模糊优化策略的最小弃风、发电成本和分区期望失负荷率均衡的多目标协调决策方法。针对模型表达形式的复杂性,采用粒子群算法进行求解。在IEEE 24节点系统上的算例结果证明了本文方法的合理性。
参考文献
View Option
[1]
邓恩思 . 大型风电场运行的特点及并网运行的问题
[J]. 能源研究与利用 , 2010 , 4 :8 -11 .
[本文引用: 1]
DENG Ensi . A research on operation characteristics of large grid-connected wind farm
[J]. Energy Research & Utilization , 2010 , 4 :8 -11 .
[本文引用: 1]
[2]
ACKERMANN T . Wind power in power systems [M]. Chichester : John Wiley & Sons Ltd. , 2005 .
[本文引用: 1]
[3]
TUOHY A MEIBOM P DENNY E , et al . Unit commitment for systems with significant wind penetration
[J]. IEEE Trans. Power Syst ., 2009 , 24 (2 ):592 -601 .
DOI:10.1109/TPWRS.2009.2016470
URL
[本文引用: 1]
[4]
ILIC M D XIE L JOO J Y . Efficient coordination of wind power and price-responsive demand-part I:Theoretical foundations
[J]. IEEE Trans. Power Syst ., 2009 , 26 (4 ):1875 -1884 .
DOI:10.1109/TPWRS.2011.2129542
URL
[本文引用: 1]
[5]
张国强 , 吴文传 , 张伯明 . 考虑风电接入的有功运行备用协调优化
[J]. 电力系统自动化 , 2011 , 35 (12 ):15 -19 .
[本文引用: 1]
ZHANG Guoqiang WU Wenchuan ZHANG Boming . Optimization of operation reserve coordination considering wind power integration
[J]. Automation of Electric Power Systems , 2011 , 35 (12 ):15 -19 .
[本文引用: 1]
[6]
MIN Liang STEPHEN T L ZHANG Pei , et al . Short-term probabilistic transmission congestion forecasting
[C]// 2008 Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies(DRPT2008),April 6-9,Nanjing,China, IEEE , 2008 :764 -770 .
[本文引用: 1]
[7]
CHEN C L LEE T Y . Impact analysis of transmission capacity constraints on wind power penetration and production cost in generation dispatch
[C]// International Conference on Intelligent Systems Applications to Power Systems,November 5-8,2007. Toki Messe,Niigata,Japan. IEEE , 2007 :1 -6 .
[本文引用: 1]
[8]
DOHERTY R O’MALLEY M . A new approach to quantify reserve demand in systems with significant installed wind capacity
[J]. IEEE Trans. on Power Systems , 2005 , 20 (2 ):587 -595 .
DOI:10.1109/TPWRS.2005.846206
URL
[本文引用: 1]
[10]
LIANG R H LIAO J H . A fuzzy-optimization approach for generation scheduling with wind and solar energy systems
[J]. IEEE Trans. on Power Systems , 2007 , 22 (4 ):1665 -1674 .
DOI:10.1109/TPWRS.2007.907527
URL
[本文引用: 1]
[11]
VENKATESH B SADASIVAM G KHAN M A . A new optimal reactive power scheduling method for loss minimization and voltage stability margin maximization using successive multi-objective fuzzy LP technique
[J]. IEEE Trans. on Power Systems , 2000 , 15 (2 ):844 -851 .
DOI:10.1109/59.867183
URL
[本文引用: 1]
[12]
VENKATESH B YU P GOOI H B , et al . Fuzzy MILP unit commitment incorporating wind generators
[J]. IEEE Trans. on Power Systems , 2008 , 23 (4 ):1738 -1746 .
DOI:10.1109/TPWRS.2008.2004724
URL
[本文引用: 1]
[13]
FABBRI A GOMEZ T ROMAN S , et al . Assessment of the cost associated with wind generation prediction errors in a liberalized electricity market
[J]. IEEE Trans. on Power Systems , 2005 , 20 (3 ):1440 -1446 .
DOI:10.1109/TPWRS.2005.852148
URL
[本文引用: 1]
[14]
BILLINTON R GHAJAR R . Evaluation of the marginal outage costs of generating systems for the purposes of spot pricing
[J]. IEEE Transactions on Power Systems , 1994 , 9 (1 ):68 -75 .
DOI:10.1109/59.317556
URL
[本文引用: 1]
[15]
刘海涛 , 孙元章 , 程林 , 等 . 计及多状态元件模型的系统状态快速排序技术
[J]. 电力系统自动化 , 2008 , 32 (1 ):16 -21 .
[本文引用: 1]
LIU Haitao SUN Yuanzhang CHENG Lin , et al . Fast sorting technique considering multi-state component models
[J]. Automation of Electric Power Systems , 2008 , 32 (1 ):16 -21 .
[本文引用: 1]
[16]
ORTEGA-VAZQUEZ M A KIRSCHEN D S . Security provision in systems with large penetration of wind power generation
[C]// IEEE Power and Energy Society General Meeting,July 25-29,2010. Minneapolis,MN. USA. IEEE , 2010 :1 -8 .
[本文引用: 1]
[17]
KENNEDY J EBERHART R . Particle swarm optimization
[C]// IEEE Proceedings of the International Conference on Neural Networks. Nov. 27-Dec. 1,Perth,Australia. IEEE , 1995 :1942 -1948 .
[本文引用: 1]
[18]
KENNEDY J EBERHART R . Swarm intelligence [M]. San Francisco : Morgan Kaufmann Publishers , 2001 .
[本文引用: 1]
[19]
WANG S J SHAHIDEHPOUR S M KIRSCHEN D S , et al . Short-term generation scheduling with transmission and environmental constraints using an augmented lagrangian relaxation
[J]. IEEE Trans. Power Syst ., 1995 , 10 (3 ):1294 -1301 .
DOI:10.1109/59.466524
URL
[本文引用: 1]
[20]
ALBRECHT P F . IEEE reliability test system:A report prepared by the reliability test system task force of the application of probability methods subcommittee
[J]. IEEE Trans. Power Apparatus and Syst ., 1979 , 98 (6 ):2047 -2054 .
[本文引用: 1]
大型风电场运行的特点及并网运行的问题
1
2010
... 风电的功率输出具有强随机性、可预测性差的特点.因此,需要额外安排一定容量的旋转备用以响应风电场发电功率的随机波动,维持电力系统的功率平衡与稳定[1 ] . ...
A research on operation characteristics of large grid-connected wind farm
1
2010
... 风电的功率输出具有强随机性、可预测性差的特点.因此,需要额外安排一定容量的旋转备用以响应风电场发电功率的随机波动,维持电力系统的功率平衡与稳定[1 ] . ...
1
2005
... 电力系统备用可以分为一次备用(也称瞬时备用)、二次备用(也称快速备用)和三次备用(也称长期备用)[2 ] ,分别应用于实现不同时间尺度的有功调度控制.其中,系统级有功调度主要关注的是二次备用和三次备用.大规模风电的接入使得系统的等效负荷功率波动更加频繁,对系统多级备用的时间响应特性和协调提出了更高的要求[3 -4 ] .针对这一特点,文献[5 ]提出以不同响应时间的多级备用协调来解决大规模风电接入后系统运行备用新问题.其中,滚动调度环节在当天开停机计划已知的情况下,通过最新的扩展短期负荷及风电预测结果滚动修正机组的日前计划,使得发电机出力与系统的实际发电需求逐渐逼近,在日前计划与实时计划之间起承上启下的重要作用.该环节的备用对应于传统的三次备用,其主要功能除了应对系统负荷和风电预测误差外,还要应对系统中的突发事件(如发电机或线路故障等),因此,合理的滚动环节备用容量对保证系统的安全运行具有重要意义. ...
Unit commitment for systems with significant wind penetration
1
2009
... 电力系统备用可以分为一次备用(也称瞬时备用)、二次备用(也称快速备用)和三次备用(也称长期备用)[2 ] ,分别应用于实现不同时间尺度的有功调度控制.其中,系统级有功调度主要关注的是二次备用和三次备用.大规模风电的接入使得系统的等效负荷功率波动更加频繁,对系统多级备用的时间响应特性和协调提出了更高的要求[3 -4 ] .针对这一特点,文献[5 ]提出以不同响应时间的多级备用协调来解决大规模风电接入后系统运行备用新问题.其中,滚动调度环节在当天开停机计划已知的情况下,通过最新的扩展短期负荷及风电预测结果滚动修正机组的日前计划,使得发电机出力与系统的实际发电需求逐渐逼近,在日前计划与实时计划之间起承上启下的重要作用.该环节的备用对应于传统的三次备用,其主要功能除了应对系统负荷和风电预测误差外,还要应对系统中的突发事件(如发电机或线路故障等),因此,合理的滚动环节备用容量对保证系统的安全运行具有重要意义. ...
Efficient coordination of wind power and price-responsive demand-part I:Theoretical foundations
1
2009
... 电力系统备用可以分为一次备用(也称瞬时备用)、二次备用(也称快速备用)和三次备用(也称长期备用)[2 ] ,分别应用于实现不同时间尺度的有功调度控制.其中,系统级有功调度主要关注的是二次备用和三次备用.大规模风电的接入使得系统的等效负荷功率波动更加频繁,对系统多级备用的时间响应特性和协调提出了更高的要求[3 -4 ] .针对这一特点,文献[5 ]提出以不同响应时间的多级备用协调来解决大规模风电接入后系统运行备用新问题.其中,滚动调度环节在当天开停机计划已知的情况下,通过最新的扩展短期负荷及风电预测结果滚动修正机组的日前计划,使得发电机出力与系统的实际发电需求逐渐逼近,在日前计划与实时计划之间起承上启下的重要作用.该环节的备用对应于传统的三次备用,其主要功能除了应对系统负荷和风电预测误差外,还要应对系统中的突发事件(如发电机或线路故障等),因此,合理的滚动环节备用容量对保证系统的安全运行具有重要意义. ...
考虑风电接入的有功运行备用协调优化
1
2011
... 电力系统备用可以分为一次备用(也称瞬时备用)、二次备用(也称快速备用)和三次备用(也称长期备用)[2 ] ,分别应用于实现不同时间尺度的有功调度控制.其中,系统级有功调度主要关注的是二次备用和三次备用.大规模风电的接入使得系统的等效负荷功率波动更加频繁,对系统多级备用的时间响应特性和协调提出了更高的要求[3 -4 ] .针对这一特点,文献[5 ]提出以不同响应时间的多级备用协调来解决大规模风电接入后系统运行备用新问题.其中,滚动调度环节在当天开停机计划已知的情况下,通过最新的扩展短期负荷及风电预测结果滚动修正机组的日前计划,使得发电机出力与系统的实际发电需求逐渐逼近,在日前计划与实时计划之间起承上启下的重要作用.该环节的备用对应于传统的三次备用,其主要功能除了应对系统负荷和风电预测误差外,还要应对系统中的突发事件(如发电机或线路故障等),因此,合理的滚动环节备用容量对保证系统的安全运行具有重要意义. ...
Optimization of operation reserve coordination considering wind power integration
1
2011
... 电力系统备用可以分为一次备用(也称瞬时备用)、二次备用(也称快速备用)和三次备用(也称长期备用)[2 ] ,分别应用于实现不同时间尺度的有功调度控制.其中,系统级有功调度主要关注的是二次备用和三次备用.大规模风电的接入使得系统的等效负荷功率波动更加频繁,对系统多级备用的时间响应特性和协调提出了更高的要求[3 -4 ] .针对这一特点,文献[5 ]提出以不同响应时间的多级备用协调来解决大规模风电接入后系统运行备用新问题.其中,滚动调度环节在当天开停机计划已知的情况下,通过最新的扩展短期负荷及风电预测结果滚动修正机组的日前计划,使得发电机出力与系统的实际发电需求逐渐逼近,在日前计划与实时计划之间起承上启下的重要作用.该环节的备用对应于传统的三次备用,其主要功能除了应对系统负荷和风电预测误差外,还要应对系统中的突发事件(如发电机或线路故障等),因此,合理的滚动环节备用容量对保证系统的安全运行具有重要意义. ...
Short-term probabilistic transmission congestion forecasting
1
2008
... 同时,受风资源分布等因素的限制,我国风电场的建设呈现出大规模开发集中并网的特点,但由于风电场往往位于电网的末端,电网结构薄弱且负荷小,使得相关输电断面的负载加重、断面潮流波动剧烈[6 ] ,而不合理的系统分区备用会进一步恶化这种情况.传统的备用分配决策模型中较少考虑备用分区平衡问题,由此可能加大重载断面的受电端失负荷风险,危及系统的安全性[7 ] .因此,需要研究更合理的系统备用与分区备用决策方法及其与发电计划的配合方案. ...
Impact analysis of transmission capacity constraints on wind power penetration and production cost in generation dispatch
1
2007
... 同时,受风资源分布等因素的限制,我国风电场的建设呈现出大规模开发集中并网的特点,但由于风电场往往位于电网的末端,电网结构薄弱且负荷小,使得相关输电断面的负载加重、断面潮流波动剧烈[6 ] ,而不合理的系统分区备用会进一步恶化这种情况.传统的备用分配决策模型中较少考虑备用分区平衡问题,由此可能加大重载断面的受电端失负荷风险,危及系统的安全性[7 ] .因此,需要研究更合理的系统备用与分区备用决策方法及其与发电计划的配合方案. ...
A new approach to quantify reserve demand in systems with significant installed wind capacity
1
2005
... 针对大规模风电并网系统,本文研究了基于失负荷期望的系统备用风险决策模型,分析了失负荷期望与备用需求的关系.同时研究了基于失负荷期望的备用分区分配策略,以系统一定失负荷期望下的分区失负荷风险最小作为分配原则,并采用模糊优化方法进行多目标优化建模.该决策模型弥补了传统基于概率的备用决策方法[8 ] 对失负荷量考虑不足的缺陷,同时与基于风险的备用决策模型相比,方法更直观,可操作性较强. ...
A systematic analytical method for quasi-steady-state sensitivity
1
2002
... 式中,$l$、$L$分别为断面编号和总断面数,${{k}_{li}}$为第i 台机组对第$l$断面的灵敏度[9 ] ,$\overline{T{{L}_{lt}}}$、$\underline{T{{L}_{lt}}}$分别为断面的上下限. ...
A fuzzy-optimization approach for generation scheduling with wind and solar energy systems
1
2007
... 模糊优化方法通过引入目标隶属度函数,可以把多目标优化问题转换成单目标优化问题.该方法能较好地反映各个目标最优解和多目标满意解之间的相互关系,考虑不同性质、相互矛盾的多个目标的满意程度,得到使各个目标都尽可能最优的折中解[10 ⇓ -12 ] . ...
A new optimal reactive power scheduling method for loss minimization and voltage stability margin maximization using successive multi-objective fuzzy LP technique
1
2000
... 模糊优化方法通过引入目标隶属度函数,可以把多目标优化问题转换成单目标优化问题.该方法能较好地反映各个目标最优解和多目标满意解之间的相互关系,考虑不同性质、相互矛盾的多个目标的满意程度,得到使各个目标都尽可能最优的折中解[10 ⇓ -12 ] . ...
Fuzzy MILP unit commitment incorporating wind generators
1
2008
... 模糊优化方法通过引入目标隶属度函数,可以把多目标优化问题转换成单目标优化问题.该方法能较好地反映各个目标最优解和多目标满意解之间的相互关系,考虑不同性质、相互矛盾的多个目标的满意程度,得到使各个目标都尽可能最优的折中解[10 ⇓ -12 ] . ...
Assessment of the cost associated with wind generation prediction errors in a liberalized electricity market
1
2005
... 首先,考虑到风电预测结果与负荷预测结果的独立性,系统总的等值负荷预测误差为$\sigma (t)=\sqrt{{{\sigma }_{1}}^{2}(t)+{{\sigma }_{2}}^{2}(t)}$.其中,假定风电及负荷的预测误差分别服从均值为0,标准差为${{\sigma }_{2}}(t)$、${{\sigma }_{1}}(t)$的正态分布[13 ] . ...
Evaluation of the marginal outage costs of generating systems for the purposes of spot pricing
1
1994
... 发电机组在未来时段t 的瞬态强迫停运率为[14 ] ...
计及多状态元件模型的系统状态快速排序技术
1
2008
... 风电功率的不确定性具有随时间增加而不断增大的特点,对于较短的时间范畴,所需的备用较小;对于较长的时间范畴,所需的备用随之增加.为了保证系统总成本最小,需要在机组发电成本与由于备用不足导致的期望失负荷损失两者之间权衡备用的最优值[15 -16 ] .按照上面分析得出的表达式,当给定系统的失负荷期望时,即可获得系统相应的备用水平. ...
Fast sorting technique considering multi-state component models
1
2008
... 风电功率的不确定性具有随时间增加而不断增大的特点,对于较短的时间范畴,所需的备用较小;对于较长的时间范畴,所需的备用随之增加.为了保证系统总成本最小,需要在机组发电成本与由于备用不足导致的期望失负荷损失两者之间权衡备用的最优值[15 -16 ] .按照上面分析得出的表达式,当给定系统的失负荷期望时,即可获得系统相应的备用水平. ...
Security provision in systems with large penetration of wind power generation
1
2010
... 风电功率的不确定性具有随时间增加而不断增大的特点,对于较短的时间范畴,所需的备用较小;对于较长的时间范畴,所需的备用随之增加.为了保证系统总成本最小,需要在机组发电成本与由于备用不足导致的期望失负荷损失两者之间权衡备用的最优值[15 -16 ] .按照上面分析得出的表达式,当给定系统的失负荷期望时,即可获得系统相应的备用水平. ...
Particle swarm optimization
1
1995
... 由于备用与发电计划之间相互耦合的复杂性,使得约束条件包含复杂的非线性关系,常规的数学优化类算法难以适用.因此,本文采用粒子群算法[17 -18 ] 进行求解. ...
1
2001
... 由于备用与发电计划之间相互耦合的复杂性,使得约束条件包含复杂的非线性关系,常规的数学优化类算法难以适用.因此,本文采用粒子群算法[17 -18 ] 进行求解. ...
Short-term generation scheduling with transmission and environmental constraints using an augmented lagrangian relaxation
1
1995
... 采用IEEE 24节点系统[19 -20 ] 作为研究对象,选取第14号机组为700 MW的风电场.假设风电预测误差标准差为$(0.044+0.006t)p_{t}^{w}$,其中,$p_{t}^{w}$为预测时段的风电出力值;负荷预测误差标准差为2%.设第i 台常规发电机组的故障率为0.005- 0.004 5i /13.系统负荷预测及风电出力预测结果分别如图1 及图2 所示,选取滚动时间窗为负荷快速爬坡阶段的第23~38阶段,如图1 中虚线框所示. ...
IEEE reliability test system:A report prepared by the reliability test system task force of the application of probability methods subcommittee
1
1979
... 采用IEEE 24节点系统[19 -20 ] 作为研究对象,选取第14号机组为700 MW的风电场.假设风电预测误差标准差为$(0.044+0.006t)p_{t}^{w}$,其中,$p_{t}^{w}$为预测时段的风电出力值;负荷预测误差标准差为2%.设第i 台常规发电机组的故障率为0.005- 0.004 5i /13.系统负荷预测及风电出力预测结果分别如图1 及图2 所示,选取滚动时间窗为负荷快速爬坡阶段的第23~38阶段,如图1 中虚线框所示. ...