1 引言
随着人们对环境问题和社会可持续发展问题的日益重视,可再生能源发电得到了迅速发展,装机容量也逐年增加[1 ] 。电力电子设备是可再生能源发电的重要组成部分。然而,电网系统的电能质量正遭受着由于大量电力电子设备接入而造成的谐波污染[2 ] 。对于并网逆变系统,并网电流电能质量至关重要[3 ] ,通常用总谐波畸变率(Total harmonic distortion, THD)值的大小来衡量[4 -5 ] 。在IEEE 1547—2018[6 ] 文件中给出了THD的衡量标准,要求注入电网电流的THD小于5%,以避免对其他接入电网的设备造成不良影响。为了提升并网逆变器的并网电流电能质量,国内外学者们对注入电网电流的谐波抑制进行了大量的研究工作。
从频率选择角度,并网电流谐波抑制方法可以划分为两类,即非选择频率谐波抑制方法和选择频率谐波抑制方法。在谐波抑制过程中对系统中存在的所有次谐波都进行抑制,不指定抑制某次谐波的方法称为非选择频率谐波抑制方法。根据谐波抑制过程中是否需要对谐波进行提取,该方法又可分成两个分支,一种是基于重复控制[7 ] 的抑制方式,另一种是基于谐波提取[8 ] 的抑制方式。重复控制具有高稳态精度和良好的抗干扰能力,文献[9 ]针对电网频率波动导致重复控制的谐振频率偏离实际电网的频率进而影响系统谐波抑制能力的问题,提出一种基于有限脉冲响应滤波器的频率自适应复合重复控制方案,可以有效地抑制电网谐波并确保并网逆变器输出高质量的并网电流,但存在动态响应速度较慢的问题。有学者提出将重复控制与其他控制器结合,提高了系统的动态响应速度。文献[10 ]提出了一种适用于微电网有源电力滤波器中的反向传播BP神经网络递推积分重复控制策略,在降低电流畸变率的同时提高了系统的动态响应速度和补偿精度。但此方法所建立的BP神经网络模型需要进行多次训练学习调整权重才能获得较高的跟踪精度,模型结构复杂,计算量较大。
基于谐波提取的并网电流谐波抑制方式就是运用所设计的谐波检测方法将电网电压中的谐波都提取出来,然后在并网控制回路中输入幅值大小相等、方向相反的波形,以此来抵消并网后产生的谐波,达到谐波抑制的效果。文献[11 ]采用的是一种将光伏并网、无功补偿及谐波抑制柔性结合的统一控制方案,引入并优化了FBD(Fryze Buchholz Dpenbrock)算法。与传统瞬时无功功率理论相比,省去了复杂的坐标变换运算,无需锁相环及相关电路,节约了硬件成本,在提高了系统检测精度及动态响应能力的同时又改善了电能质量。文献[12 ]针对单相LCL滤波器双闭环控制系统建立了数学模型,应用频域法和齐格勒-尼科尔斯法(Ziegler-Nichols method)对系统进行稳定性分析,并初步整定了内外环参数,具有较好的鲁棒性和并网谐波抑制能力。文献[13 ]采用虚拟同步发电机控制策略来控制逆变器,利用级联广义积分器构建谐波电流分离网络对基波和谐波电流进行分离,再结合虚拟阻抗构建基波感性虚拟阻抗以改善功率均分特性,构建谐波阻容性可变虚拟阻抗以改变系统输出阻抗并补偿谐波电压,采用多谐振电压控制器对基波和谐波指令电压进行零误差跟踪,改善了输出电压的谐波抑制效果。但该方法增大了控制器的计算负担,且多谐振控制参数较多,不易整定。
与上述不指定抑制某次谐波的谐波抑制方法相比较,目前一些典型的控制方法如鲁棒模型预测重复控制(Robust model predictive control,RMPC)[14 ] 、鲁棒重复控制(Robust repetitive control,R-RC)[15 ] 、广义并行重复控制(General parallel structure repetitive control,GPS-RC)[16 ] 、线性相位超前补偿重复控制(Linear phase lead compensation multirate repetitive control,LPLCM-RC)[17 ] 、最优选择频率重复控制(Optimal selective harmonic repetitive control,OSH-RC)[18 ] 和选择奇次谐波控制(Selective odd-order harmonic repetitive control,SOH-RC)[19 ] 等,可以针对系统中产生的各次谐波进行抑制。此种方式的优势在于抑制效果精确,抽离出的各次谐波都能进行效果显著的抑制[20 ] 。此种方式的缺点是实际应用较困难,涉及大量并行运算,对控制器的要求较高。
综上所述,当电网由于外部扰动发生频率突变时,选择频率谐波抑制的控制效果易受电网频率波动的影响。相比较而言,非选择频率谐波抑制方法在谐波提取与抑制的时候无需针对电网的频率改变而做出特殊处理,因此在此种方式下,电网频率波动不会影响其控制效果。本文从单相并网逆变器控制结构出发,在分析传统控制方法不足的基础上,提出了新型电压型并网电流谐波抑制策略,该策略是基于能量成型控制方法实现的,对并网电流进行了有效抑制,并在实验室搭建的试验平台上进行了验证。
2 传统电压型控制并网电流谐波抑制方法
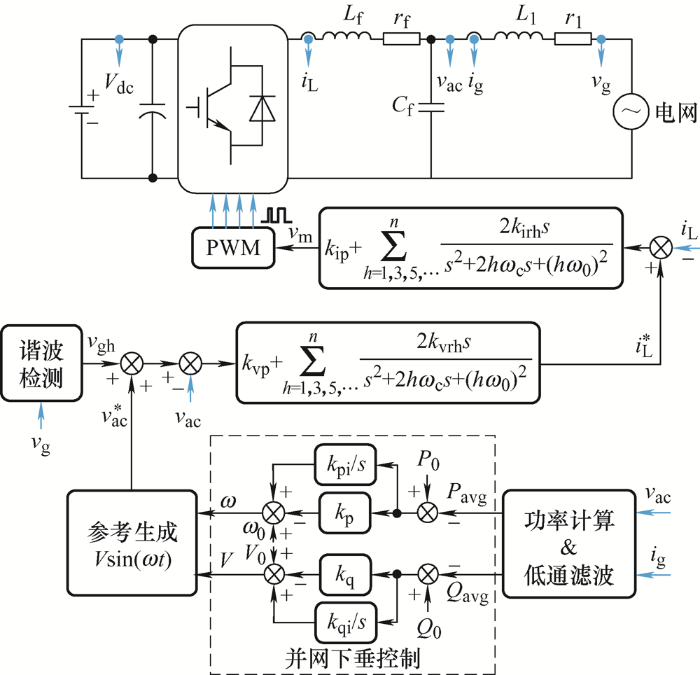
图1 是基于带通滤波器的电压型控制逆变器并网电流谐波抑制控制策略框图,与传统电流型并网控制相对比,该电压型并网控制有两处明显改进。
图1
图1
基于带通滤波器的下垂控制逆变器并网电流谐波抑制方法结构框图
(1) 使用带通滤波器提取电网电压中的背景谐波,为逆变器输出提供参考谐波电压v gh 、v gh 的生成方式如下
(1) ${{v}_{\text{g}\mathrm{h}}}={{v}_{\text{g}}}-\frac{\beta s}{{{s}^{2}}+\beta s+\omega _{\text{g}}^{2}}{{v}_{\text{g}}}$
式中,β 和ω g 分别为二阶带通滤波器的通带带宽和电网电压的基波频率。
(2) 采用比例准多谐振控制(Proportional multi- quasi-resonant,P-q MR)对不同阶次谐波产生抑制作用,同时可以更好地适应电网频率的波动。
仿真和试验结果证明,采用图1 所示并网电流谐波抑制方法的逆变器可以获得较好的谐波抑制效果,但在实际应用过程中仍存在以下问题。
(1) 若要对更多阶次谐波起到抑制作用,则需要按照谐波阶次匹配多谐振控制器,这样会导致系统控制器的并行运算增加,对控制器的性能提出了更高的要求。
(2) 若要对各次谐波均产生较好的抑制效果,则需要对所有阶次谐振控制器参数进行精确调试,由于缺乏完备的参数调试方法,实际应用中极大增加了调试难度,不利于拓展。
3 基于能量成型控制的电压型逆变器并网电流谐波抑制方法
本文基于下垂控制和能量成型控制理论,设计了新型电压型并网逆变器并网电流谐波抑制方法,以解决传统多比例谐振控制方法控制参数多、调试困难的问题。
3.1 端口受控Hamiltonian系统
考虑一个单输入单输出系统,其状态空间模型可以表示为
(2) $\left\{ \begin{align} & \frac{dx}{dt}=f(x,u) \\ & \ \ y=h(x) \\ \end{align} \right.$
式中,$x\in X\subset {{\mathbb{R}}^{n}}$、$u\in U\subset \mathbb{R}$和$y\in Y\subset \mathbb{R}$分别为状态变量、控制输入和系统输出,函数f (·,·)和h (·)分别满足f (·,·):$X\times U\to {{\mathbb{R}}^{n}}$,h (·):$X\to \mathbb{R}$且它们均在开连通集X 中足够平滑。
那么,式(2)可以表示为如下所示的典型端口受控Hamiltonian(Port-controlled Hamiltonian,PCH)系统形式
(3) $\left\{ \begin{align} & \frac{dx}{dt}=(J-R)\frac{\partial H(x)}{\partial x}+Gu \\ & y={{G}^{\mathrm{T}}}\frac{\partial H(x)}{\partial x} \\ \end{align} \right.\ \ $
式中,x =[x 1 , x 2 , …, xn ]T 代表由被控系统定义的状态变量,J R H (x )代表Hamiltonian函数且满足H (x )=x T Dx /2(D =D T >0),G
假设系统(3)的参考输入为x ,且$x\in X\subset {{\mathbb{R}}^{n}}$,若取$u={{u}_{\text{d}}}\in U\subset \mathbb{R}$,那么
(4) $\frac{dx}{dt}=(J-R)\frac{\partial H(x)}{\partial x}+G{{u}_{\text{d}}}$
存在两个各不相同的信号x (t )和x d (t )可以使式(3)成立,此时可以定义新的变量e =x d -x ,即误差变量,将信号x (t )和x d (t )分别代入式(4)并作差,化简可以得到系统参考误差动态方程
(5) $\frac{de}{dt}=\frac{d}{dt}\left( {{x}_{\text{d}}}-x \right)=(J-R)\frac{\partial H(e)}{\partial e}$
式(5)中的H (e )是选定的Lyapunov函数,那么对H (e )求解一阶时间微分
(6) $\frac{dH(e)}{dt}=\frac{1}{2}\left[ {{{\dot{e}}}^{\mathrm{T}}}\frac{\partial H(e)}{\partial e}+{{\left( \frac{\partial H(e)}{\partial e} \right)}^{\mathrm{T}}}\dot{e} \right]=-{{e}^{\mathrm{T}}}{{D}^{\mathrm{T}}}RDe$
式(6)中dH (e )/dt ≤0恒成立,满足Lyapunov渐进稳定定理,即$\underset{t\to \infty }{\mathop{\lim }}\,\parallel {{x}_{\text{d}}}(t)-x(t)\parallel =0$。
3.2 能量成型控制
若被控系统可以转化为PCH系统,则式(7)作为能量成型控制器的目标函数
(7) $\frac{dx}{dt}=({{J}_{\text{d}}}-{{R}_{\text{d}}})\frac{\partial {{H}_{\text{d}}}(x)}{\partial x}$
(8) $(J-R)\frac{\partial H(x)}{\partial x}+Gu=\left( {{J}_{\text{d}}}-{{R}_{\text{d}}} \right)\frac{\partial {{H}_{\text{d}}}(x)}{\partial x}$
因此,式(8)可以用来求解能量成型控制器的输入量u 。
3.3 逆变器电压型并网能量成型控制器设计
根据图1 所示系统结构,可以得到单相并网逆变器动态方程
(9) $\left\{ \begin{align} & {{L}_{\text{f}}}\frac{d{{i}_{\text{L}}}}{dt}=\mu {{V}_{\text{dc}}}-{{v}_{ac}}-{{i}_{\text{L}}}{{r}_{\text{f}}} \\ & {{C}_{\text{f}}}\frac{d{{v}_{\mathrm{ac}}}}{dt}={{i}_{\text{L}}}-{{i}_{\text{g}}} \\ & {{L}_{\text{l}}}\frac{d{{i}_{\text{g}}}}{dt}={{v}_{\text{ac}}}-{{v}_{\text{g}}}-{{i}_{\text{g}}}{{r}_{\text{l}}} \\ \end{align} \right.$
式中,V dc 代表逆变器等效输入源电压,v ac 和i L 分别代表滤波电容电压和逆变器侧输出电流,L f 和r f 分别代表逆变器输出滤波器滤波电感的电感值和等效电阻,i g 和v g 分别代表逆变器注入并网点处的电流和并网点处的电压,C f 代表逆变器输出滤波电容的容值,L l 和r l 分别代表等效线路电感及对应的寄生电阻。
定义PCH系统状态变量x =[x 1 , x 2 , x 3 ]T =[L f i L , C f v ac , L l i g ]T ,将其应用至式(9)可以得到单相并网逆变器的PCH系统动态方程
(10) $\frac{dx}{dt}=(J-R)\frac{\partial H(x)}{\partial x}+Gu\left( \mu \right)$
式中,$J=\left( \begin{matrix} 0 & -1 & 0 \\ 1 & 0 & -1 \\ 0 & 1 & 0 \\\end{matrix} \right)$,$R=diag\left[ {{r}_{\text{f}}},0,{{r}_{1}} \right]$,$G=\left( \begin{matrix} {{V}_{\mathrm{dc}}} & 0 \\ 0 & 0 \\ 0 & -1 \\ \end{matrix} \right)$,$u\left( \mu \right)\text{=}\left( \begin{matrix} \mu \\ {{v}_{\text{g}}} \\\end{matrix} \right)$,$\frac{\partial H(x)}{\partial x}={{D}^{-1}}x,$ $D=diag\left[ {{L}_{\text{f}}},{{C}_{\text{f}}},{{L}_{1}} \right]$。
定义系统期望的端口互联矩阵J d 和阻尼匹配矩阵R d 为
(11) $\left\{ \begin{align} & {{J}_{\text{d}}}=J+{{J}_{\text{a}}}=-J_{\text{d}}^{\mathrm{T}} \\ & {{R}_{\text{d}}}=R+{{R}_{\text{a}}}=R_{\text{d}}^{\mathrm{T}}>0 \\ \end{align} \right.$
J a 为向PCH系统注入的互联结构矩阵,R a 为注入的阻尼匹配矩阵,其形式如下
(12) $\left\{ \begin{align} & {{J}_{\text{a}}}=\left[ \begin{matrix} 0 & {{J}_{12}} & {{J}_{13}} \\ -{{J}_{12}} & 0 & {{J}_{23}} \\ -{{J}_{13}} & -{{J}_{23}} & 0 \\ \end{matrix} \right] \\ & {{R}_{\text{a}}}=\left[ \begin{matrix} {{R}_{1}} & {} & {} \\ {} & {{R}_{2}} & {} \\ {} & {} & {{R}_{3}} \\ \end{matrix} \right] \\ \end{align} \right.$
式中,J mn (m /n =1, 2, 3)∈$\mathbb{R}$为待设计的互联矩阵参数且J mn ≥0,R i i =1, 2, 3)∈$\mathbb{R}$为被控系统可调节的阻尼匹配矩阵参数且满足R i
定义并网逆变器的目标能量函数H d (x )采用如下形式
(13) ${{H}_{\text{d}}}(x)=\frac{1}{2}{{\left( x-{{x}_{0}} \right)}^{T}}{{D}^{-1}}\left( x-{{x}_{0}} \right)$
式中,∂H d (x )/∂x =D -1 (x -x 0 ),状态变量的平衡点为x 0 =[x 10 , x 20 , x 30 ]T =[L f i L0 , C f v ac0 , L l i g0 ]T 。
联立式(8)、式(10)和式(12)可以得到以下平衡方程
(14) $Gu(\mu )=\left( {{J}_{\text{a}}}-{{R}_{\text{a}}} \right){{D}^{-1}}\left( x-{{x}_{0}} \right)-(J-R){{D}^{-1}}{{x}_{0}}$
因此,可以根据式(14)推导出单相并网逆变器的调制波控制输入μ 的表达式
(15) $\mu =\frac{1}{{{V}_{\text{dc}}}}\left( -\frac{{{R}_{1}}}{{{L}_{\text{f}}}}{{x}_{\text{le}}}+\frac{{{J}_{12}}}{{{C}_{\text{f}}}}{{x}_{2\text{e}}}+\frac{{{J}_{13}}}{{{L}_{\text{l}}}}{{x}_{3\text{e}}}+\frac{{{r}_{\text{f}}}}{{{L}_{\text{f}}}}{{x}_{10}}+\frac{1}{{{C}_{\text{f}}}}{{x}_{20}} \right)$
式中,xn e 为系统状态变量xn 的偏差且满足xn e =xn -xn 0 (n =1, 2, 3)。
此外,被控系统式(14)中还可以列写出另外两个等式关系
(16) $\left\{ \begin{matrix} -\frac{{{J}_{12}}}{{{L}_{\text{f}}}}{{x}_{1\text{e}}}-\frac{{{R}_{2}}}{{{C}_{\text{f}}}}{{x}_{2\text{e}}}+\frac{{{J}_{23}}}{{{L}_{1}}}{{x}_{3\text{e}}}-\frac{1}{{{L}_{\text{f}}}}{{x}_{10}}+\frac{1}{{{L}_{1}}}{{x}_{30}}=0\ \ \ \ \ \\ -\frac{{{J}_{13}}}{{{L}_{\text{f}}}}{{x}_{1\text{e}}}-\frac{{{J}_{23}}}{{{C}_{\text{f}}}}{{x}_{2\text{e}}}-\frac{{{R}_{3}}}{{{L}_{1}}}{{x}_{3\text{e}}}-\frac{1}{{{C}_{\text{f}}}}{{x}_{20}}+\frac{{{r}_{1}}}{{{L}_{1}}}{{x}_{30}}=-{{v}_{\text{g}}} \\ \end{matrix} \right.$
本文的一个重要目标就是要减少控制参数,因此将端口互联矩阵参数J 12 、J 13 和J 23 全部设为零,式(16)中的待定参数R 2 和R 3 均可以用已知参数表达
(17) ${{R}_{2}}=\frac{{{C}_{\text{f}}}}{{{x}_{2\text{e}}}}\left( -\frac{1}{{{L}_{\text{f}}}}{{x}_{10}}+\frac{1}{{{L}_{1}}}{{x}_{30}} \right)$
(18) ${{R}_{3}}=\frac{{{L}_{1}}}{{{x}_{3\text{e}}}}\left( -\frac{1}{{{C}_{\text{f}}}}{{x}_{20}}+\frac{{{r}_{1}}}{{{L}_{1}}}{{x}_{30}}+{{v}_{\text{g}}} \right)$
(19) $\begin{matrix} \mu =\frac{1}{{{V}_{\text{dc}}}}\left( -\frac{{{R}_{1}}}{{{L}_{\text{f}}}}{{x}_{1\text{e}}}+\frac{{{r}_{\text{f}}}}{{{L}_{\text{f}}}}{{x}_{10}}+\frac{1}{{{C}_{\text{f}}}}{{x}_{20}} \right)= \\ \frac{1}{{{V}_{\text{dc}}}}\left[ \left( {{R}_{1}}+{{r}_{\text{f}}} \right){{i}_{\text{L}0}}-{{R}_{1}}{{i}_{\text{L}}}+{{v}_{\text{ac}0}} \right] \\ \end{matrix}$
当并网逆变器运行进入目标平衡点时,此时的系统状态变量x =[L f i L0 , C f v ac0 , L l i g0 ]T 仍能使系统的状态方程成立,即
(20) $\left\{ \begin{align} & {{C}_{\text{f}}}\frac{d{{v}_{\text{ac0}}}}{dt}={{i}_{\text{L0}}}-{{i}_{\text{g0}}} \\ & {{L}_{1}}\frac{d{{i}_{\text{g0}}}}{dt}={{v}_{\text{ac0}}}-{{v}_{\text{g}}}-{{i}_{\text{g0}}}{{r}_{1}} \\ \end{align} \right.$
式(20)中的电容电压平衡值v ac0 由下垂控制器输出,那么并网电流i g 的平衡值i g0 可以被直接求解,进而可以得到电感电流i L 的平衡值i L0 。平衡值i g0 和i L0 的表达式如下
(21) $\left\{ \begin{align} & {{i}_{\text{g}0}}=\frac{1}{s{{L}_{1}}+{{r}_{1}}}\left( {{v}_{\text{ac}0}}-{{v}_{\text{g}}} \right) \\ & {{i}_{\text{L}0}}={{C}_{\text{f}}}\frac{\mathrm{d}{{v}_{\text{ac}0}}}{\mathrm{d}t}+{{i}_{\text{g}0}} \\ \end{align} \right.$
为了方便本文提出的能量成型控制器的数字实现,式(21)中的1/(sL 1 +r 1 )可以视为低通滤波器,它与式(20)中的电容电压平衡值v ac0 的一阶时间微分均可用前向Euler公式进行离散化实现。
根据式(19)和式(21),可以得到本文提出的下垂控制并网逆变器能量成型并网电流谐波抑制方法的整体控制框图如图2 所示。
图2
图2
下垂控制并网逆变器能量成型并网电流谐波抑制方法
首先,采样获得逆变器的输出电压v ac 及并网电流i g ,应用功率计算公式可以得到逆变器瞬时功率P ac 和Q ac 。然后应用一阶低通滤波器滤除功率中的高频分量得到逆变器输出平均有功P avg 和无功Q avg 。将上述平均功率送入并网下垂控制模块计算得到逆变器输出电压基波参考量v acf 并与谐波提取模块获取的电网电压谐波量线性叠加形成电容电压平衡值v ac0 。最后,应用本文提出的并网逆变器能量成型控制器控制系统并网。与图1 所示的传统并网逆变器谐波抑制方法相对比,本文提出的能量成型控制方法具有以下三点优势。
(1) 并网逆变器内环控制器结构简单,易于数字化实现。
(2) 并网逆变器内环控制器仅含有一个控制参数且物理意义明确,极大降低了调试难度。
(3) 本文所提出的能量成型控制器对系统参数一定范围内的扰动具有鲁棒性。
3.4 稳定性分析
使用本文所提出的能量成型控制器式(19),被控系统可以自动收敛至目标能量系统式(7),而此时的能量函数H d (x )应具备如下特征
(22) $\frac{\partial {{H}_{\text{d}}}(x)}{\partial x}={{D}^{-1}}\left( x-{{x}_{0}} \right)$
当系统进入目标稳态时,系统状态满足x =x 0 ,因此可以得到能量函数H d (x )为零且其在x 0 处的一阶偏导数也为零,这就表明目标系统在稳态时所具有的能量完全耗尽,因而可以证明系统稳定。
当系统未达到目标稳态时,由于系统状态x 不满足x =x 0 ,因此能量函数H d (x )对时间的一阶偏导数为
(23) $\frac{\partial {{H}_{\text{d}}}(x)}{\partial t}={{\left[ \frac{\partial {{H}_{\text{d}}}(x)}{\partial x} \right]}^{\mathrm{T}}}\frac{\partial x}{\partial t}$
(24) $\frac{\partial {{H}_{\text{d}}}(x)}{\partial t}={{\left[ \frac{\partial {{H}_{\text{d}}}(x)}{\partial x} \right]}^{\mathrm{T}}}\left( {{J}_{\text{d}}}-{{R}_{\text{d}}} \right)\frac{\partial {{H}_{\text{d}}}(x)}{\partial x}$
(25) ${{\left[ \frac{\partial {{H}_{\text{d}}}(x)}{\partial x} \right]}^{\mathrm{T}}}{{J}_{\text{d}}}\left( x \right)\frac{\partial {{H}_{\text{d}}}(x)}{\partial x}=0$
(26) $\frac{\partial {{H}_{\text{d}}}(x)}{\partial t}=-{{\left[ \frac{\partial {{H}_{\text{d}}}(x)}{\partial x} \right]}^{\mathrm{T}}}{{R}_{\text{d}}}\frac{\partial {{H}_{\text{d}}}(x)}{\partial x}$
由于目标阻尼匹配矩阵R d 非负,因此可以证明目标能量函数H d (x )关于系统状态变量的一阶偏导数∂H d (x )/∂x 恒小于等于零。∂H d (x )/∂x ≤0恒成立满足李雅普诺夫渐进稳定定理,因此可以证明本文提出的控制方法在系统目标稳态工作点附近可以达到渐进稳定。
4 试验验证
4.1 无谐波电网试验
本文所使用的无谐波电网是由Chroma公司的Model 61500型号交流源设定生成的,对本文所提出的并网电流谐波抑制控制方法进行理想电网工况试验验证,其试验结果如图3 所示。从图3 中可以看出,并网逆变器在本文提出的并网电流谐波抑制方法控制作用下,可以实现单位功率因数并网(其中有功功率P ac 可达到最大值960 W,无功功率Q ac 维持恒定值0 Var)。在此期间,逆变器为本地负载提供450 W有功功率,并将多余的510 W有功功率并入电网。由于电网电压v g 中无谐波,本文提出的线性离散Kalman滤波谐波提取环节输出的电网电压谐波v gh 约为零。因此,能量成型控制器中的输出电压参考量仅为下垂环输出值v acf 。经过测算,并网电流i g 幅值约为3.3 A,不存在明显谐波畸变且总谐波畸变率约为0.68%。试验波形证明,本文提出的电压型并网逆变器并网电流谐波抑制方法可以有效抑制自身谐波输出以提升并网电流的电能质量。
图3
图3
基于能量成型控制的电压型并网电流谐波抑制策略无谐波电网试验结果
4.2 谐波电网试验
为了验证本文提出的电压型并网电流谐波抑制方法对并网电流谐波的抑制作用,将并网逆变器通过隔离变压器接入实际市电电网,试验结果如图4 所示。从图4 可以看出,本文提出的基于谐波提取的补偿控制方法未启动时(在点划线处t 1 时刻前),并网逆变器仍可实现单位功率因数有功功率960 W并网,但受市电中背景谐波的影响,并网电流i g 波形畸变严重,其测算后的总谐波畸变率约为7.95%,严重超出IEEE1547—2018标准中所要求的5%上限。当基于谐波提取的补偿控制方法启动后(t 1 时刻),并网电流i g 的波形正弦度迅速变好并趋向理想正弦,可以看出其波形电能质量得到显著改善,此时的总谐波畸变率经过测算可降低至1.67%,符合逆变器并网要求。基于传统下垂控制的多比例谐振控制方法与本文所提方法在谐波抑制性能方面的对比结果如表1 所示。
图4
图4
基于能量成型控制的电压型并网电流谐波抑制策略扰动电网暂态试验结果
试验波形证明,本文提出的电压型并网逆变器谐波抑制方法不仅能够实现对参考电压信号的快速跟踪,还能有效降低电网电压背景谐波对并网电流电能质量的影响。
5 结论
本文探究了基于下垂控制的并网逆变器传统并网电流谐波抑制方法存在的缺陷,提出了基于谐波提取补偿的新型电压型控制并网逆变器并网电流谐波抑制策略,以克服多比例谐振控制方法结构复杂、调节参数多且参数整定困难的问题。使用无谐波电网和有谐波电网双工况对本文所提控制方法进行了试验验证,进一步证明了所提控制方法的有效性和可行性。
参考文献
View Option
[1]
闫涵 , 吕建国 , 丁金勇 , 等 . 非理想电网下NPC三电平逆变器多目标模型预测控制方法研究
[J]. 电气工程学报 , 2019 , 14 (3 ):23 -32 .
[本文引用: 1]
YAN Han LÜ Jianguo DING Jinyong , et al . Research on the multi-target grid-connected control method of NPC three-level inverter based on model prediction under non-ideal grid conditions
[J]. Journal of Electrical Engineering , 2019 , 14 (3 ):23 -32 .
[本文引用: 1]
[2]
陈姝慧 , 王红梅 , 陈新 . 基于电网电压前馈的三相LCL并网逆变器电流控制方法研究
[J]. 电气工程学报 , 2016 , 11 (1 ):24 -31 .
[本文引用: 1]
CHEN Shuhui WANG Hongmei CHEN Xin . Research on current control scheme based on grid voltage feedforward for three-phase LCL-type grid-connected inverters
[J]. Journal of Electrical Engineering , 2016 , 11 (1 ):24 -31 .
[本文引用: 1]
[3]
茅靖 , 方健美 . 低压配电系统谐波抑制及治理设计方法
[J]. 电气技术 , 2017 (11 ):128 -132 .
[本文引用: 1]
MAO Jing FANG Jianmei . Discussion on harmonic suppression and control design method of low voltage distribution system
[J]. Electrical Engineering , 2017 (11 ):128 -132 .
[本文引用: 1]
[4]
杭丽君 , 李宾 , 黄龙 , 等 . 一种可再生能源并网逆变器的多谐振PR电流控制技术
[J]. 中国电机工程学报 , 2012 , 32 (12 ):51 -58 .
[本文引用: 1]
HANG Lijun LI Bin HUANG Long , et al . A multi-resonant PR current controller for grid-connected inverters in renewable energy systems
[J]. Proceedings of the CSEE , 2012 , 32 (12 ):51 -58 .
[本文引用: 1]
[5]
ZHOU L M ZHOU X P CHEN Y D , et al . Inverter-current-feedback resonance-suppression method for LCL-type DG system to reduce resonance-frequency offset and grid-inductance effect
[J]. IEEE Transactions on Industrial Electronics , 2018 , 65 (9 ):7036 -7048 .
DOI:10.1109/TIE.2018.2795556
URL
[本文引用: 1]
[6]
IEEE Std 1547—2018 . IEEE standard for interconnection and interoperability of distributed energy resources with associated electric power systems interfaces
[S]. IEEE , 2018 .
[本文引用: 1]
[7]
李翠艳 , 张东纯 , 庄显义 . 重复控制综述
[J]. 电机与控制学报 , 2005 , 9 (1 ):37 -44 .
[本文引用: 1]
LI Cuiyan ZHANG Dongchun ZHUANG Xianyi . Review of repetitive control
[J]. Electric Machines and Control , 2005 , 9 (1 ):37 -44 .
[本文引用: 1]
[8]
叶忠明 , 董伯藩 , 钱照明 . 谐波电流的提取方法比较
[J]. 电力系统自动化 , 1997 (12 ):21 -24 .
[本文引用: 1]
YE Zhongming DONG Bofan QIAN Zhaoming . Comparison of extraction methods of harmonic current
[J]. Automation of Electric Power Systems , 1997 (12 ):21 -24 .
[本文引用: 1]
[9]
李伟锋 , 陆小辉 , 陈赛男 , 等 . 新型频率自适应复合重复控制及并网逆变器应用
[J]. 电力系统保护与控制 , 2020 , 48 (6 ):10 -17 .
[本文引用: 1]
LI Weifeng LU Xiaohui CHEN Sainan , et al . Improved frequency adaptive compound RC scheme for grid-connected inverter
[J]. Power System Protection and Control , 2020 , 48 (6 ):10 -17 .
[本文引用: 1]
[10]
李鑫 , 孟亨 , 杨桢 , 等 . 基于BP神经网络递推积分PI-重复控制在微电网APF中的研究
[J]. 电力系统保护与控制 , 2019 , 47 (6 ):132 -140 .
[本文引用: 1]
LI Xin MENG Heng YANG Zhen , et al . Research on recursive integral PI-repetitive control based on BP neural network in micro-grid APF
[J]. Power System Protection and Control , 2019 , 47 (6 ):132 -140 .
[本文引用: 1]
[11]
焦明曦 , 李强 , 张旭 . 基于优化FBD法的分布式光伏并网及电能质量调节的统一控制
[J]. 电气技术 , 2017 (2 ):106 -110 ,116.
[本文引用: 1]
JIAO Mingxi LI Qiang ZHANG Xu . Unified control strategy for grid-connected photovoltaic system with electric energy quality adjustment based on improved FBD method
[J]. Electrical Engineering , 2017 (2 ):106 -110 ,116.
[本文引用: 1]
[12]
王佐勋 , 李亚洲 , 李国庆 . 基于遗传算法的LCL型逆变器双闭环参数设计
[J]. 电力系统保护与控制 , 2018 , 46 (22 ):1 -7 .
[本文引用: 1]
WANG Zuoxun LI Yazhou LI Guoqing . Parameters optimization of double closed-loop for LCL-type inverter based on genetic algorithm
[J]. Power System Protection and Control , 2018 , 46 (22 ):1 -7 .
[本文引用: 1]
[13]
许柳 , 吕智林 , 孟泽晨 , 等 . 非线性负载下的多变流器谐波电压补偿控制策略
[J]. 电力系统保护与控制 , 2019 , 47 (7 ):1 -11 .
[本文引用: 1]
XU Liu LÜ Zhilin MENG Zechen , et al . Multi-converter harmonic voltage compensation control strategy under nonlinear loads
[J]. Power System Protection and Control , 2019 , 47 (7 ):1 -11 .
[本文引用: 1]
[14]
LIU Y CHENG S M NING B W , et al . Robust model predictive control with simplified repetitive control for electrical machine drives
[J]. IEEE Transactions on Power Electronics , 2019 , 34 (5 ):4524 -4535 .
DOI:10.1109/TPEL.2018.2857837
URL
[本文引用: 1]
[15]
PANDOVE G SINGH M . Robust repetitive control design for a three-phase four wire shunt active power filter
[J]. IEEE Transactions on Industrial Informatics , 2019 , 15 (5 ):2810 -2818 .
DOI:10.1109/TII.2018.2875035
URL
[本文引用: 1]
[16]
LU W Z ZHOU K L WANG D W , et al . A general parallel structure repetitive control scheme for multiphase DC-AC PWM converters
[J]. IEEE Transactions on Power Electronics , 2013 , 28 (8 ):3980 -3987 .
DOI:10.1109/TPEL.2012.2229395
URL
[本文引用: 1]
[17]
LIU Z C ZHANG B ZHOU K L . Universal fractional-order design of linear phase lead compensation multirate repetitive control for PWM inverters
[J]. IEEE Transactions on Industrial Electronics , 2017 , 64 (9 ):7132 -7140 .
DOI:10.1109/TIE.2017.2686348
URL
[本文引用: 1]
[18]
ZHOU K L YAHG Y H BLAABJERG F , et al . Optimal selective harmonic control for power harmonics mitigation
[J]. IEEE Transactions on Industrial Electronics , 2015 , 62 (2 ):1220 -1230 .
DOI:10.1109/TIE.2014.2336629
URL
[本文引用: 1]
[19]
LIU Z C ZHANG B ZHOU K L , et al . Virtual variable sampling discrete fourier transform based selective odd-order harmonic repetitive control of DC/AC converters
[J]. IEEE Transactions on Power Electronics , 2018 , 33 (7 ):6444 -6452 .
DOI:10.1109/TPEL.2017.2764020
URL
[本文引用: 1]
[20]
宫金武 , 查晓明 , 陈佰锋 . 一种快速重复控制策略在APF中的实现和分析
[J]. 电工技术学报 , 2011 , 26 (10 ):110 -117 .
[本文引用: 1]
GONG Jinwu ZHA Xiaoming CHEN Baifeng . Analysis and realization of a fast repetitive controller in active power filter system
[J]. Transactions of China Electrotechnical Society , 2011 , 26 (10 ):110 -117 .
[本文引用: 1]
非理想电网下NPC三电平逆变器多目标模型预测控制方法研究
1
2019
... 随着人们对环境问题和社会可持续发展问题的日益重视,可再生能源发电得到了迅速发展,装机容量也逐年增加[1 ] .电力电子设备是可再生能源发电的重要组成部分.然而,电网系统的电能质量正遭受着由于大量电力电子设备接入而造成的谐波污染[2 ] .对于并网逆变系统,并网电流电能质量至关重要[3 ] ,通常用总谐波畸变率(Total harmonic distortion, THD)值的大小来衡量[4 -5 ] .在IEEE 1547—2018[6 ] 文件中给出了THD的衡量标准,要求注入电网电流的THD小于5%,以避免对其他接入电网的设备造成不良影响.为了提升并网逆变器的并网电流电能质量,国内外学者们对注入电网电流的谐波抑制进行了大量的研究工作. ...
Research on the multi-target grid-connected control method of NPC three-level inverter based on model prediction under non-ideal grid conditions
1
2019
... 随着人们对环境问题和社会可持续发展问题的日益重视,可再生能源发电得到了迅速发展,装机容量也逐年增加[1 ] .电力电子设备是可再生能源发电的重要组成部分.然而,电网系统的电能质量正遭受着由于大量电力电子设备接入而造成的谐波污染[2 ] .对于并网逆变系统,并网电流电能质量至关重要[3 ] ,通常用总谐波畸变率(Total harmonic distortion, THD)值的大小来衡量[4 -5 ] .在IEEE 1547—2018[6 ] 文件中给出了THD的衡量标准,要求注入电网电流的THD小于5%,以避免对其他接入电网的设备造成不良影响.为了提升并网逆变器的并网电流电能质量,国内外学者们对注入电网电流的谐波抑制进行了大量的研究工作. ...
基于电网电压前馈的三相LCL并网逆变器电流控制方法研究
1
2016
... 随着人们对环境问题和社会可持续发展问题的日益重视,可再生能源发电得到了迅速发展,装机容量也逐年增加[1 ] .电力电子设备是可再生能源发电的重要组成部分.然而,电网系统的电能质量正遭受着由于大量电力电子设备接入而造成的谐波污染[2 ] .对于并网逆变系统,并网电流电能质量至关重要[3 ] ,通常用总谐波畸变率(Total harmonic distortion, THD)值的大小来衡量[4 -5 ] .在IEEE 1547—2018[6 ] 文件中给出了THD的衡量标准,要求注入电网电流的THD小于5%,以避免对其他接入电网的设备造成不良影响.为了提升并网逆变器的并网电流电能质量,国内外学者们对注入电网电流的谐波抑制进行了大量的研究工作. ...
Research on current control scheme based on grid voltage feedforward for three-phase LCL-type grid-connected inverters
1
2016
... 随着人们对环境问题和社会可持续发展问题的日益重视,可再生能源发电得到了迅速发展,装机容量也逐年增加[1 ] .电力电子设备是可再生能源发电的重要组成部分.然而,电网系统的电能质量正遭受着由于大量电力电子设备接入而造成的谐波污染[2 ] .对于并网逆变系统,并网电流电能质量至关重要[3 ] ,通常用总谐波畸变率(Total harmonic distortion, THD)值的大小来衡量[4 -5 ] .在IEEE 1547—2018[6 ] 文件中给出了THD的衡量标准,要求注入电网电流的THD小于5%,以避免对其他接入电网的设备造成不良影响.为了提升并网逆变器的并网电流电能质量,国内外学者们对注入电网电流的谐波抑制进行了大量的研究工作. ...
低压配电系统谐波抑制及治理设计方法
1
2017
... 随着人们对环境问题和社会可持续发展问题的日益重视,可再生能源发电得到了迅速发展,装机容量也逐年增加[1 ] .电力电子设备是可再生能源发电的重要组成部分.然而,电网系统的电能质量正遭受着由于大量电力电子设备接入而造成的谐波污染[2 ] .对于并网逆变系统,并网电流电能质量至关重要[3 ] ,通常用总谐波畸变率(Total harmonic distortion, THD)值的大小来衡量[4 -5 ] .在IEEE 1547—2018[6 ] 文件中给出了THD的衡量标准,要求注入电网电流的THD小于5%,以避免对其他接入电网的设备造成不良影响.为了提升并网逆变器的并网电流电能质量,国内外学者们对注入电网电流的谐波抑制进行了大量的研究工作. ...
Discussion on harmonic suppression and control design method of low voltage distribution system
1
2017
... 随着人们对环境问题和社会可持续发展问题的日益重视,可再生能源发电得到了迅速发展,装机容量也逐年增加[1 ] .电力电子设备是可再生能源发电的重要组成部分.然而,电网系统的电能质量正遭受着由于大量电力电子设备接入而造成的谐波污染[2 ] .对于并网逆变系统,并网电流电能质量至关重要[3 ] ,通常用总谐波畸变率(Total harmonic distortion, THD)值的大小来衡量[4 -5 ] .在IEEE 1547—2018[6 ] 文件中给出了THD的衡量标准,要求注入电网电流的THD小于5%,以避免对其他接入电网的设备造成不良影响.为了提升并网逆变器的并网电流电能质量,国内外学者们对注入电网电流的谐波抑制进行了大量的研究工作. ...
一种可再生能源并网逆变器的多谐振PR电流控制技术
1
2012
... 随着人们对环境问题和社会可持续发展问题的日益重视,可再生能源发电得到了迅速发展,装机容量也逐年增加[1 ] .电力电子设备是可再生能源发电的重要组成部分.然而,电网系统的电能质量正遭受着由于大量电力电子设备接入而造成的谐波污染[2 ] .对于并网逆变系统,并网电流电能质量至关重要[3 ] ,通常用总谐波畸变率(Total harmonic distortion, THD)值的大小来衡量[4 -5 ] .在IEEE 1547—2018[6 ] 文件中给出了THD的衡量标准,要求注入电网电流的THD小于5%,以避免对其他接入电网的设备造成不良影响.为了提升并网逆变器的并网电流电能质量,国内外学者们对注入电网电流的谐波抑制进行了大量的研究工作. ...
A multi-resonant PR current controller for grid-connected inverters in renewable energy systems
1
2012
... 随着人们对环境问题和社会可持续发展问题的日益重视,可再生能源发电得到了迅速发展,装机容量也逐年增加[1 ] .电力电子设备是可再生能源发电的重要组成部分.然而,电网系统的电能质量正遭受着由于大量电力电子设备接入而造成的谐波污染[2 ] .对于并网逆变系统,并网电流电能质量至关重要[3 ] ,通常用总谐波畸变率(Total harmonic distortion, THD)值的大小来衡量[4 -5 ] .在IEEE 1547—2018[6 ] 文件中给出了THD的衡量标准,要求注入电网电流的THD小于5%,以避免对其他接入电网的设备造成不良影响.为了提升并网逆变器的并网电流电能质量,国内外学者们对注入电网电流的谐波抑制进行了大量的研究工作. ...
Inverter-current-feedback resonance-suppression method for LCL-type DG system to reduce resonance-frequency offset and grid-inductance effect
1
2018
... 随着人们对环境问题和社会可持续发展问题的日益重视,可再生能源发电得到了迅速发展,装机容量也逐年增加[1 ] .电力电子设备是可再生能源发电的重要组成部分.然而,电网系统的电能质量正遭受着由于大量电力电子设备接入而造成的谐波污染[2 ] .对于并网逆变系统,并网电流电能质量至关重要[3 ] ,通常用总谐波畸变率(Total harmonic distortion, THD)值的大小来衡量[4 -5 ] .在IEEE 1547—2018[6 ] 文件中给出了THD的衡量标准,要求注入电网电流的THD小于5%,以避免对其他接入电网的设备造成不良影响.为了提升并网逆变器的并网电流电能质量,国内外学者们对注入电网电流的谐波抑制进行了大量的研究工作. ...
IEEE standard for interconnection and interoperability of distributed energy resources with associated electric power systems interfaces
1
2018
... 随着人们对环境问题和社会可持续发展问题的日益重视,可再生能源发电得到了迅速发展,装机容量也逐年增加[1 ] .电力电子设备是可再生能源发电的重要组成部分.然而,电网系统的电能质量正遭受着由于大量电力电子设备接入而造成的谐波污染[2 ] .对于并网逆变系统,并网电流电能质量至关重要[3 ] ,通常用总谐波畸变率(Total harmonic distortion, THD)值的大小来衡量[4 -5 ] .在IEEE 1547—2018[6 ] 文件中给出了THD的衡量标准,要求注入电网电流的THD小于5%,以避免对其他接入电网的设备造成不良影响.为了提升并网逆变器的并网电流电能质量,国内外学者们对注入电网电流的谐波抑制进行了大量的研究工作. ...
重复控制综述
1
2005
... 从频率选择角度,并网电流谐波抑制方法可以划分为两类,即非选择频率谐波抑制方法和选择频率谐波抑制方法.在谐波抑制过程中对系统中存在的所有次谐波都进行抑制,不指定抑制某次谐波的方法称为非选择频率谐波抑制方法.根据谐波抑制过程中是否需要对谐波进行提取,该方法又可分成两个分支,一种是基于重复控制[7 ] 的抑制方式,另一种是基于谐波提取[8 ] 的抑制方式.重复控制具有高稳态精度和良好的抗干扰能力,文献[9 ]针对电网频率波动导致重复控制的谐振频率偏离实际电网的频率进而影响系统谐波抑制能力的问题,提出一种基于有限脉冲响应滤波器的频率自适应复合重复控制方案,可以有效地抑制电网谐波并确保并网逆变器输出高质量的并网电流,但存在动态响应速度较慢的问题.有学者提出将重复控制与其他控制器结合,提高了系统的动态响应速度.文献[10 ]提出了一种适用于微电网有源电力滤波器中的反向传播BP神经网络递推积分重复控制策略,在降低电流畸变率的同时提高了系统的动态响应速度和补偿精度.但此方法所建立的BP神经网络模型需要进行多次训练学习调整权重才能获得较高的跟踪精度,模型结构复杂,计算量较大. ...
Review of repetitive control
1
2005
... 从频率选择角度,并网电流谐波抑制方法可以划分为两类,即非选择频率谐波抑制方法和选择频率谐波抑制方法.在谐波抑制过程中对系统中存在的所有次谐波都进行抑制,不指定抑制某次谐波的方法称为非选择频率谐波抑制方法.根据谐波抑制过程中是否需要对谐波进行提取,该方法又可分成两个分支,一种是基于重复控制[7 ] 的抑制方式,另一种是基于谐波提取[8 ] 的抑制方式.重复控制具有高稳态精度和良好的抗干扰能力,文献[9 ]针对电网频率波动导致重复控制的谐振频率偏离实际电网的频率进而影响系统谐波抑制能力的问题,提出一种基于有限脉冲响应滤波器的频率自适应复合重复控制方案,可以有效地抑制电网谐波并确保并网逆变器输出高质量的并网电流,但存在动态响应速度较慢的问题.有学者提出将重复控制与其他控制器结合,提高了系统的动态响应速度.文献[10 ]提出了一种适用于微电网有源电力滤波器中的反向传播BP神经网络递推积分重复控制策略,在降低电流畸变率的同时提高了系统的动态响应速度和补偿精度.但此方法所建立的BP神经网络模型需要进行多次训练学习调整权重才能获得较高的跟踪精度,模型结构复杂,计算量较大. ...
谐波电流的提取方法比较
1
1997
... 从频率选择角度,并网电流谐波抑制方法可以划分为两类,即非选择频率谐波抑制方法和选择频率谐波抑制方法.在谐波抑制过程中对系统中存在的所有次谐波都进行抑制,不指定抑制某次谐波的方法称为非选择频率谐波抑制方法.根据谐波抑制过程中是否需要对谐波进行提取,该方法又可分成两个分支,一种是基于重复控制[7 ] 的抑制方式,另一种是基于谐波提取[8 ] 的抑制方式.重复控制具有高稳态精度和良好的抗干扰能力,文献[9 ]针对电网频率波动导致重复控制的谐振频率偏离实际电网的频率进而影响系统谐波抑制能力的问题,提出一种基于有限脉冲响应滤波器的频率自适应复合重复控制方案,可以有效地抑制电网谐波并确保并网逆变器输出高质量的并网电流,但存在动态响应速度较慢的问题.有学者提出将重复控制与其他控制器结合,提高了系统的动态响应速度.文献[10 ]提出了一种适用于微电网有源电力滤波器中的反向传播BP神经网络递推积分重复控制策略,在降低电流畸变率的同时提高了系统的动态响应速度和补偿精度.但此方法所建立的BP神经网络模型需要进行多次训练学习调整权重才能获得较高的跟踪精度,模型结构复杂,计算量较大. ...
Comparison of extraction methods of harmonic current
1
1997
... 从频率选择角度,并网电流谐波抑制方法可以划分为两类,即非选择频率谐波抑制方法和选择频率谐波抑制方法.在谐波抑制过程中对系统中存在的所有次谐波都进行抑制,不指定抑制某次谐波的方法称为非选择频率谐波抑制方法.根据谐波抑制过程中是否需要对谐波进行提取,该方法又可分成两个分支,一种是基于重复控制[7 ] 的抑制方式,另一种是基于谐波提取[8 ] 的抑制方式.重复控制具有高稳态精度和良好的抗干扰能力,文献[9 ]针对电网频率波动导致重复控制的谐振频率偏离实际电网的频率进而影响系统谐波抑制能力的问题,提出一种基于有限脉冲响应滤波器的频率自适应复合重复控制方案,可以有效地抑制电网谐波并确保并网逆变器输出高质量的并网电流,但存在动态响应速度较慢的问题.有学者提出将重复控制与其他控制器结合,提高了系统的动态响应速度.文献[10 ]提出了一种适用于微电网有源电力滤波器中的反向传播BP神经网络递推积分重复控制策略,在降低电流畸变率的同时提高了系统的动态响应速度和补偿精度.但此方法所建立的BP神经网络模型需要进行多次训练学习调整权重才能获得较高的跟踪精度,模型结构复杂,计算量较大. ...
新型频率自适应复合重复控制及并网逆变器应用
1
2020
... 从频率选择角度,并网电流谐波抑制方法可以划分为两类,即非选择频率谐波抑制方法和选择频率谐波抑制方法.在谐波抑制过程中对系统中存在的所有次谐波都进行抑制,不指定抑制某次谐波的方法称为非选择频率谐波抑制方法.根据谐波抑制过程中是否需要对谐波进行提取,该方法又可分成两个分支,一种是基于重复控制[7 ] 的抑制方式,另一种是基于谐波提取[8 ] 的抑制方式.重复控制具有高稳态精度和良好的抗干扰能力,文献[9 ]针对电网频率波动导致重复控制的谐振频率偏离实际电网的频率进而影响系统谐波抑制能力的问题,提出一种基于有限脉冲响应滤波器的频率自适应复合重复控制方案,可以有效地抑制电网谐波并确保并网逆变器输出高质量的并网电流,但存在动态响应速度较慢的问题.有学者提出将重复控制与其他控制器结合,提高了系统的动态响应速度.文献[10 ]提出了一种适用于微电网有源电力滤波器中的反向传播BP神经网络递推积分重复控制策略,在降低电流畸变率的同时提高了系统的动态响应速度和补偿精度.但此方法所建立的BP神经网络模型需要进行多次训练学习调整权重才能获得较高的跟踪精度,模型结构复杂,计算量较大. ...
Improved frequency adaptive compound RC scheme for grid-connected inverter
1
2020
... 从频率选择角度,并网电流谐波抑制方法可以划分为两类,即非选择频率谐波抑制方法和选择频率谐波抑制方法.在谐波抑制过程中对系统中存在的所有次谐波都进行抑制,不指定抑制某次谐波的方法称为非选择频率谐波抑制方法.根据谐波抑制过程中是否需要对谐波进行提取,该方法又可分成两个分支,一种是基于重复控制[7 ] 的抑制方式,另一种是基于谐波提取[8 ] 的抑制方式.重复控制具有高稳态精度和良好的抗干扰能力,文献[9 ]针对电网频率波动导致重复控制的谐振频率偏离实际电网的频率进而影响系统谐波抑制能力的问题,提出一种基于有限脉冲响应滤波器的频率自适应复合重复控制方案,可以有效地抑制电网谐波并确保并网逆变器输出高质量的并网电流,但存在动态响应速度较慢的问题.有学者提出将重复控制与其他控制器结合,提高了系统的动态响应速度.文献[10 ]提出了一种适用于微电网有源电力滤波器中的反向传播BP神经网络递推积分重复控制策略,在降低电流畸变率的同时提高了系统的动态响应速度和补偿精度.但此方法所建立的BP神经网络模型需要进行多次训练学习调整权重才能获得较高的跟踪精度,模型结构复杂,计算量较大. ...
基于BP神经网络递推积分PI-重复控制在微电网APF中的研究
1
2019
... 从频率选择角度,并网电流谐波抑制方法可以划分为两类,即非选择频率谐波抑制方法和选择频率谐波抑制方法.在谐波抑制过程中对系统中存在的所有次谐波都进行抑制,不指定抑制某次谐波的方法称为非选择频率谐波抑制方法.根据谐波抑制过程中是否需要对谐波进行提取,该方法又可分成两个分支,一种是基于重复控制[7 ] 的抑制方式,另一种是基于谐波提取[8 ] 的抑制方式.重复控制具有高稳态精度和良好的抗干扰能力,文献[9 ]针对电网频率波动导致重复控制的谐振频率偏离实际电网的频率进而影响系统谐波抑制能力的问题,提出一种基于有限脉冲响应滤波器的频率自适应复合重复控制方案,可以有效地抑制电网谐波并确保并网逆变器输出高质量的并网电流,但存在动态响应速度较慢的问题.有学者提出将重复控制与其他控制器结合,提高了系统的动态响应速度.文献[10 ]提出了一种适用于微电网有源电力滤波器中的反向传播BP神经网络递推积分重复控制策略,在降低电流畸变率的同时提高了系统的动态响应速度和补偿精度.但此方法所建立的BP神经网络模型需要进行多次训练学习调整权重才能获得较高的跟踪精度,模型结构复杂,计算量较大. ...
Research on recursive integral PI-repetitive control based on BP neural network in micro-grid APF
1
2019
... 从频率选择角度,并网电流谐波抑制方法可以划分为两类,即非选择频率谐波抑制方法和选择频率谐波抑制方法.在谐波抑制过程中对系统中存在的所有次谐波都进行抑制,不指定抑制某次谐波的方法称为非选择频率谐波抑制方法.根据谐波抑制过程中是否需要对谐波进行提取,该方法又可分成两个分支,一种是基于重复控制[7 ] 的抑制方式,另一种是基于谐波提取[8 ] 的抑制方式.重复控制具有高稳态精度和良好的抗干扰能力,文献[9 ]针对电网频率波动导致重复控制的谐振频率偏离实际电网的频率进而影响系统谐波抑制能力的问题,提出一种基于有限脉冲响应滤波器的频率自适应复合重复控制方案,可以有效地抑制电网谐波并确保并网逆变器输出高质量的并网电流,但存在动态响应速度较慢的问题.有学者提出将重复控制与其他控制器结合,提高了系统的动态响应速度.文献[10 ]提出了一种适用于微电网有源电力滤波器中的反向传播BP神经网络递推积分重复控制策略,在降低电流畸变率的同时提高了系统的动态响应速度和补偿精度.但此方法所建立的BP神经网络模型需要进行多次训练学习调整权重才能获得较高的跟踪精度,模型结构复杂,计算量较大. ...
基于优化FBD法的分布式光伏并网及电能质量调节的统一控制
1
2017
... 基于谐波提取的并网电流谐波抑制方式就是运用所设计的谐波检测方法将电网电压中的谐波都提取出来,然后在并网控制回路中输入幅值大小相等、方向相反的波形,以此来抵消并网后产生的谐波,达到谐波抑制的效果.文献[11 ]采用的是一种将光伏并网、无功补偿及谐波抑制柔性结合的统一控制方案,引入并优化了FBD(Fryze Buchholz Dpenbrock)算法.与传统瞬时无功功率理论相比,省去了复杂的坐标变换运算,无需锁相环及相关电路,节约了硬件成本,在提高了系统检测精度及动态响应能力的同时又改善了电能质量.文献[12 ]针对单相LCL滤波器双闭环控制系统建立了数学模型,应用频域法和齐格勒-尼科尔斯法(Ziegler-Nichols method)对系统进行稳定性分析,并初步整定了内外环参数,具有较好的鲁棒性和并网谐波抑制能力.文献[13 ]采用虚拟同步发电机控制策略来控制逆变器,利用级联广义积分器构建谐波电流分离网络对基波和谐波电流进行分离,再结合虚拟阻抗构建基波感性虚拟阻抗以改善功率均分特性,构建谐波阻容性可变虚拟阻抗以改变系统输出阻抗并补偿谐波电压,采用多谐振电压控制器对基波和谐波指令电压进行零误差跟踪,改善了输出电压的谐波抑制效果.但该方法增大了控制器的计算负担,且多谐振控制参数较多,不易整定. ...
Unified control strategy for grid-connected photovoltaic system with electric energy quality adjustment based on improved FBD method
1
2017
... 基于谐波提取的并网电流谐波抑制方式就是运用所设计的谐波检测方法将电网电压中的谐波都提取出来,然后在并网控制回路中输入幅值大小相等、方向相反的波形,以此来抵消并网后产生的谐波,达到谐波抑制的效果.文献[11 ]采用的是一种将光伏并网、无功补偿及谐波抑制柔性结合的统一控制方案,引入并优化了FBD(Fryze Buchholz Dpenbrock)算法.与传统瞬时无功功率理论相比,省去了复杂的坐标变换运算,无需锁相环及相关电路,节约了硬件成本,在提高了系统检测精度及动态响应能力的同时又改善了电能质量.文献[12 ]针对单相LCL滤波器双闭环控制系统建立了数学模型,应用频域法和齐格勒-尼科尔斯法(Ziegler-Nichols method)对系统进行稳定性分析,并初步整定了内外环参数,具有较好的鲁棒性和并网谐波抑制能力.文献[13 ]采用虚拟同步发电机控制策略来控制逆变器,利用级联广义积分器构建谐波电流分离网络对基波和谐波电流进行分离,再结合虚拟阻抗构建基波感性虚拟阻抗以改善功率均分特性,构建谐波阻容性可变虚拟阻抗以改变系统输出阻抗并补偿谐波电压,采用多谐振电压控制器对基波和谐波指令电压进行零误差跟踪,改善了输出电压的谐波抑制效果.但该方法增大了控制器的计算负担,且多谐振控制参数较多,不易整定. ...
基于遗传算法的LCL型逆变器双闭环参数设计
1
2018
... 基于谐波提取的并网电流谐波抑制方式就是运用所设计的谐波检测方法将电网电压中的谐波都提取出来,然后在并网控制回路中输入幅值大小相等、方向相反的波形,以此来抵消并网后产生的谐波,达到谐波抑制的效果.文献[11 ]采用的是一种将光伏并网、无功补偿及谐波抑制柔性结合的统一控制方案,引入并优化了FBD(Fryze Buchholz Dpenbrock)算法.与传统瞬时无功功率理论相比,省去了复杂的坐标变换运算,无需锁相环及相关电路,节约了硬件成本,在提高了系统检测精度及动态响应能力的同时又改善了电能质量.文献[12 ]针对单相LCL滤波器双闭环控制系统建立了数学模型,应用频域法和齐格勒-尼科尔斯法(Ziegler-Nichols method)对系统进行稳定性分析,并初步整定了内外环参数,具有较好的鲁棒性和并网谐波抑制能力.文献[13 ]采用虚拟同步发电机控制策略来控制逆变器,利用级联广义积分器构建谐波电流分离网络对基波和谐波电流进行分离,再结合虚拟阻抗构建基波感性虚拟阻抗以改善功率均分特性,构建谐波阻容性可变虚拟阻抗以改变系统输出阻抗并补偿谐波电压,采用多谐振电压控制器对基波和谐波指令电压进行零误差跟踪,改善了输出电压的谐波抑制效果.但该方法增大了控制器的计算负担,且多谐振控制参数较多,不易整定. ...
Parameters optimization of double closed-loop for LCL-type inverter based on genetic algorithm
1
2018
... 基于谐波提取的并网电流谐波抑制方式就是运用所设计的谐波检测方法将电网电压中的谐波都提取出来,然后在并网控制回路中输入幅值大小相等、方向相反的波形,以此来抵消并网后产生的谐波,达到谐波抑制的效果.文献[11 ]采用的是一种将光伏并网、无功补偿及谐波抑制柔性结合的统一控制方案,引入并优化了FBD(Fryze Buchholz Dpenbrock)算法.与传统瞬时无功功率理论相比,省去了复杂的坐标变换运算,无需锁相环及相关电路,节约了硬件成本,在提高了系统检测精度及动态响应能力的同时又改善了电能质量.文献[12 ]针对单相LCL滤波器双闭环控制系统建立了数学模型,应用频域法和齐格勒-尼科尔斯法(Ziegler-Nichols method)对系统进行稳定性分析,并初步整定了内外环参数,具有较好的鲁棒性和并网谐波抑制能力.文献[13 ]采用虚拟同步发电机控制策略来控制逆变器,利用级联广义积分器构建谐波电流分离网络对基波和谐波电流进行分离,再结合虚拟阻抗构建基波感性虚拟阻抗以改善功率均分特性,构建谐波阻容性可变虚拟阻抗以改变系统输出阻抗并补偿谐波电压,采用多谐振电压控制器对基波和谐波指令电压进行零误差跟踪,改善了输出电压的谐波抑制效果.但该方法增大了控制器的计算负担,且多谐振控制参数较多,不易整定. ...
非线性负载下的多变流器谐波电压补偿控制策略
1
2019
... 基于谐波提取的并网电流谐波抑制方式就是运用所设计的谐波检测方法将电网电压中的谐波都提取出来,然后在并网控制回路中输入幅值大小相等、方向相反的波形,以此来抵消并网后产生的谐波,达到谐波抑制的效果.文献[11 ]采用的是一种将光伏并网、无功补偿及谐波抑制柔性结合的统一控制方案,引入并优化了FBD(Fryze Buchholz Dpenbrock)算法.与传统瞬时无功功率理论相比,省去了复杂的坐标变换运算,无需锁相环及相关电路,节约了硬件成本,在提高了系统检测精度及动态响应能力的同时又改善了电能质量.文献[12 ]针对单相LCL滤波器双闭环控制系统建立了数学模型,应用频域法和齐格勒-尼科尔斯法(Ziegler-Nichols method)对系统进行稳定性分析,并初步整定了内外环参数,具有较好的鲁棒性和并网谐波抑制能力.文献[13 ]采用虚拟同步发电机控制策略来控制逆变器,利用级联广义积分器构建谐波电流分离网络对基波和谐波电流进行分离,再结合虚拟阻抗构建基波感性虚拟阻抗以改善功率均分特性,构建谐波阻容性可变虚拟阻抗以改变系统输出阻抗并补偿谐波电压,采用多谐振电压控制器对基波和谐波指令电压进行零误差跟踪,改善了输出电压的谐波抑制效果.但该方法增大了控制器的计算负担,且多谐振控制参数较多,不易整定. ...
Multi-converter harmonic voltage compensation control strategy under nonlinear loads
1
2019
... 基于谐波提取的并网电流谐波抑制方式就是运用所设计的谐波检测方法将电网电压中的谐波都提取出来,然后在并网控制回路中输入幅值大小相等、方向相反的波形,以此来抵消并网后产生的谐波,达到谐波抑制的效果.文献[11 ]采用的是一种将光伏并网、无功补偿及谐波抑制柔性结合的统一控制方案,引入并优化了FBD(Fryze Buchholz Dpenbrock)算法.与传统瞬时无功功率理论相比,省去了复杂的坐标变换运算,无需锁相环及相关电路,节约了硬件成本,在提高了系统检测精度及动态响应能力的同时又改善了电能质量.文献[12 ]针对单相LCL滤波器双闭环控制系统建立了数学模型,应用频域法和齐格勒-尼科尔斯法(Ziegler-Nichols method)对系统进行稳定性分析,并初步整定了内外环参数,具有较好的鲁棒性和并网谐波抑制能力.文献[13 ]采用虚拟同步发电机控制策略来控制逆变器,利用级联广义积分器构建谐波电流分离网络对基波和谐波电流进行分离,再结合虚拟阻抗构建基波感性虚拟阻抗以改善功率均分特性,构建谐波阻容性可变虚拟阻抗以改变系统输出阻抗并补偿谐波电压,采用多谐振电压控制器对基波和谐波指令电压进行零误差跟踪,改善了输出电压的谐波抑制效果.但该方法增大了控制器的计算负担,且多谐振控制参数较多,不易整定. ...
Robust model predictive control with simplified repetitive control for electrical machine drives
1
2019
... 与上述不指定抑制某次谐波的谐波抑制方法相比较,目前一些典型的控制方法如鲁棒模型预测重复控制(Robust model predictive control,RMPC)[14 ] 、鲁棒重复控制(Robust repetitive control,R-RC)[15 ] 、广义并行重复控制(General parallel structure repetitive control,GPS-RC)[16 ] 、线性相位超前补偿重复控制(Linear phase lead compensation multirate repetitive control,LPLCM-RC)[17 ] 、最优选择频率重复控制(Optimal selective harmonic repetitive control,OSH-RC)[18 ] 和选择奇次谐波控制(Selective odd-order harmonic repetitive control,SOH-RC)[19 ] 等,可以针对系统中产生的各次谐波进行抑制.此种方式的优势在于抑制效果精确,抽离出的各次谐波都能进行效果显著的抑制[20 ] .此种方式的缺点是实际应用较困难,涉及大量并行运算,对控制器的要求较高. ...
Robust repetitive control design for a three-phase four wire shunt active power filter
1
2019
... 与上述不指定抑制某次谐波的谐波抑制方法相比较,目前一些典型的控制方法如鲁棒模型预测重复控制(Robust model predictive control,RMPC)[14 ] 、鲁棒重复控制(Robust repetitive control,R-RC)[15 ] 、广义并行重复控制(General parallel structure repetitive control,GPS-RC)[16 ] 、线性相位超前补偿重复控制(Linear phase lead compensation multirate repetitive control,LPLCM-RC)[17 ] 、最优选择频率重复控制(Optimal selective harmonic repetitive control,OSH-RC)[18 ] 和选择奇次谐波控制(Selective odd-order harmonic repetitive control,SOH-RC)[19 ] 等,可以针对系统中产生的各次谐波进行抑制.此种方式的优势在于抑制效果精确,抽离出的各次谐波都能进行效果显著的抑制[20 ] .此种方式的缺点是实际应用较困难,涉及大量并行运算,对控制器的要求较高. ...
A general parallel structure repetitive control scheme for multiphase DC-AC PWM converters
1
2013
... 与上述不指定抑制某次谐波的谐波抑制方法相比较,目前一些典型的控制方法如鲁棒模型预测重复控制(Robust model predictive control,RMPC)[14 ] 、鲁棒重复控制(Robust repetitive control,R-RC)[15 ] 、广义并行重复控制(General parallel structure repetitive control,GPS-RC)[16 ] 、线性相位超前补偿重复控制(Linear phase lead compensation multirate repetitive control,LPLCM-RC)[17 ] 、最优选择频率重复控制(Optimal selective harmonic repetitive control,OSH-RC)[18 ] 和选择奇次谐波控制(Selective odd-order harmonic repetitive control,SOH-RC)[19 ] 等,可以针对系统中产生的各次谐波进行抑制.此种方式的优势在于抑制效果精确,抽离出的各次谐波都能进行效果显著的抑制[20 ] .此种方式的缺点是实际应用较困难,涉及大量并行运算,对控制器的要求较高. ...
Universal fractional-order design of linear phase lead compensation multirate repetitive control for PWM inverters
1
2017
... 与上述不指定抑制某次谐波的谐波抑制方法相比较,目前一些典型的控制方法如鲁棒模型预测重复控制(Robust model predictive control,RMPC)[14 ] 、鲁棒重复控制(Robust repetitive control,R-RC)[15 ] 、广义并行重复控制(General parallel structure repetitive control,GPS-RC)[16 ] 、线性相位超前补偿重复控制(Linear phase lead compensation multirate repetitive control,LPLCM-RC)[17 ] 、最优选择频率重复控制(Optimal selective harmonic repetitive control,OSH-RC)[18 ] 和选择奇次谐波控制(Selective odd-order harmonic repetitive control,SOH-RC)[19 ] 等,可以针对系统中产生的各次谐波进行抑制.此种方式的优势在于抑制效果精确,抽离出的各次谐波都能进行效果显著的抑制[20 ] .此种方式的缺点是实际应用较困难,涉及大量并行运算,对控制器的要求较高. ...
Optimal selective harmonic control for power harmonics mitigation
1
2015
... 与上述不指定抑制某次谐波的谐波抑制方法相比较,目前一些典型的控制方法如鲁棒模型预测重复控制(Robust model predictive control,RMPC)[14 ] 、鲁棒重复控制(Robust repetitive control,R-RC)[15 ] 、广义并行重复控制(General parallel structure repetitive control,GPS-RC)[16 ] 、线性相位超前补偿重复控制(Linear phase lead compensation multirate repetitive control,LPLCM-RC)[17 ] 、最优选择频率重复控制(Optimal selective harmonic repetitive control,OSH-RC)[18 ] 和选择奇次谐波控制(Selective odd-order harmonic repetitive control,SOH-RC)[19 ] 等,可以针对系统中产生的各次谐波进行抑制.此种方式的优势在于抑制效果精确,抽离出的各次谐波都能进行效果显著的抑制[20 ] .此种方式的缺点是实际应用较困难,涉及大量并行运算,对控制器的要求较高. ...
Virtual variable sampling discrete fourier transform based selective odd-order harmonic repetitive control of DC/AC converters
1
2018
... 与上述不指定抑制某次谐波的谐波抑制方法相比较,目前一些典型的控制方法如鲁棒模型预测重复控制(Robust model predictive control,RMPC)[14 ] 、鲁棒重复控制(Robust repetitive control,R-RC)[15 ] 、广义并行重复控制(General parallel structure repetitive control,GPS-RC)[16 ] 、线性相位超前补偿重复控制(Linear phase lead compensation multirate repetitive control,LPLCM-RC)[17 ] 、最优选择频率重复控制(Optimal selective harmonic repetitive control,OSH-RC)[18 ] 和选择奇次谐波控制(Selective odd-order harmonic repetitive control,SOH-RC)[19 ] 等,可以针对系统中产生的各次谐波进行抑制.此种方式的优势在于抑制效果精确,抽离出的各次谐波都能进行效果显著的抑制[20 ] .此种方式的缺点是实际应用较困难,涉及大量并行运算,对控制器的要求较高. ...
一种快速重复控制策略在APF中的实现和分析
1
2011
... 与上述不指定抑制某次谐波的谐波抑制方法相比较,目前一些典型的控制方法如鲁棒模型预测重复控制(Robust model predictive control,RMPC)[14 ] 、鲁棒重复控制(Robust repetitive control,R-RC)[15 ] 、广义并行重复控制(General parallel structure repetitive control,GPS-RC)[16 ] 、线性相位超前补偿重复控制(Linear phase lead compensation multirate repetitive control,LPLCM-RC)[17 ] 、最优选择频率重复控制(Optimal selective harmonic repetitive control,OSH-RC)[18 ] 和选择奇次谐波控制(Selective odd-order harmonic repetitive control,SOH-RC)[19 ] 等,可以针对系统中产生的各次谐波进行抑制.此种方式的优势在于抑制效果精确,抽离出的各次谐波都能进行效果显著的抑制[20 ] .此种方式的缺点是实际应用较困难,涉及大量并行运算,对控制器的要求较高. ...
Analysis and realization of a fast repetitive controller in active power filter system
1
2011
... 与上述不指定抑制某次谐波的谐波抑制方法相比较,目前一些典型的控制方法如鲁棒模型预测重复控制(Robust model predictive control,RMPC)[14 ] 、鲁棒重复控制(Robust repetitive control,R-RC)[15 ] 、广义并行重复控制(General parallel structure repetitive control,GPS-RC)[16 ] 、线性相位超前补偿重复控制(Linear phase lead compensation multirate repetitive control,LPLCM-RC)[17 ] 、最优选择频率重复控制(Optimal selective harmonic repetitive control,OSH-RC)[18 ] 和选择奇次谐波控制(Selective odd-order harmonic repetitive control,SOH-RC)[19 ] 等,可以针对系统中产生的各次谐波进行抑制.此种方式的优势在于抑制效果精确,抽离出的各次谐波都能进行效果显著的抑制[20 ] .此种方式的缺点是实际应用较困难,涉及大量并行运算,对控制器的要求较高. ...