1 引言
磁控形状记忆合金(Magnetic shape memory alloy,MSMA)是近几十年被国内外关注较多的智能材料[1 ⇓ -3 ] ,具有磁场诱导应变大、疲劳寿命长等优点[4 -5 ] 。基于这些特性,MSMA逐渐被人们关注,特别是在传感器和执行器方面,是最理想的材料之一,所以MSMA具有成为新一代传感器核心元件的良好潜力。然而,基于MSMA的传感器的输入与输出之间存在非线性的现象。很多国内外的学者对其进行了研究,有些学者主要进行建模研究,由于特定材料的限制,增加了其数学建模的难度。有些学者未考虑系统的内部结构和材料的物理性质,着重关注输入和输出之间的关系,并采用参数识别方法识别模型参数[6 -7 ] 。其中,Preisach模型是用相对简单的数学方法,对输入与输出之间的非线性问题进行概述,得到了比较广泛的应用,但是在参数优化方面存在不足。文献[8 ]介绍了一种参数线性化的KP模型,但是算法的复杂性偏高,相对不易于推导。
本文通过对MSMA传感器的工作原理和磁路进行研究,结合电磁学理论,推导出数学模型。由于传感器输入与输出之间为非线性关系,所以对辨识算法进行改进,考虑到切比雪夫函数曲线在线性和非线性之间有着良好的过渡性,故利用切比雪夫函数的特性,结合粒子群算法,对权重进行非线性调整。并对算法的学习因子、最大速度和目标函数进行改进,从而提高算法的全局优化能力,加快算法的收敛速度,最后对模型的未知参数进行辨识。
2 MSMA传感器数学模型
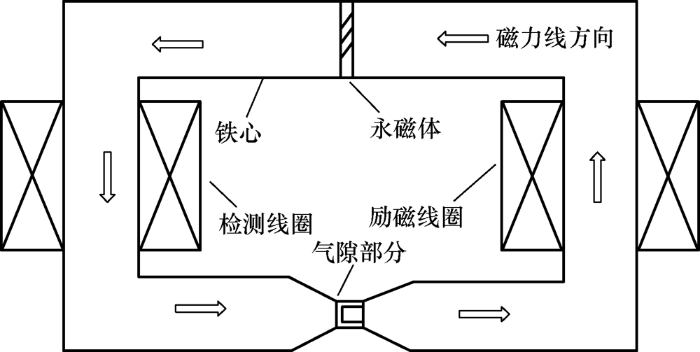
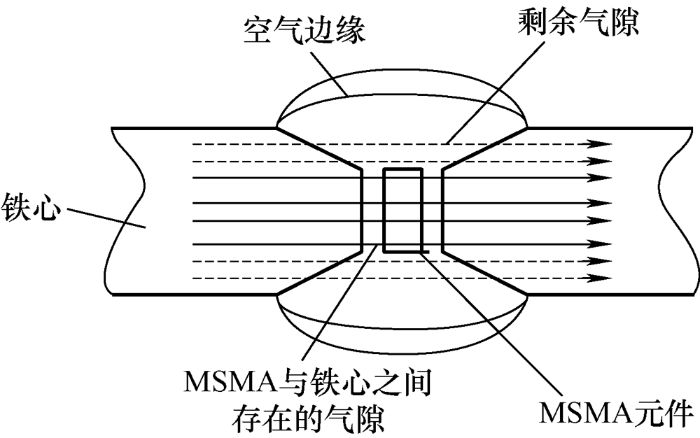
MSMA传感器的模型结构如图1 所示,磁控形状记忆合金传感器是由铁心、气隙、永磁体、励磁线圈、检测线圈、MSMA元件等组成[9 ] 。
图1
图2
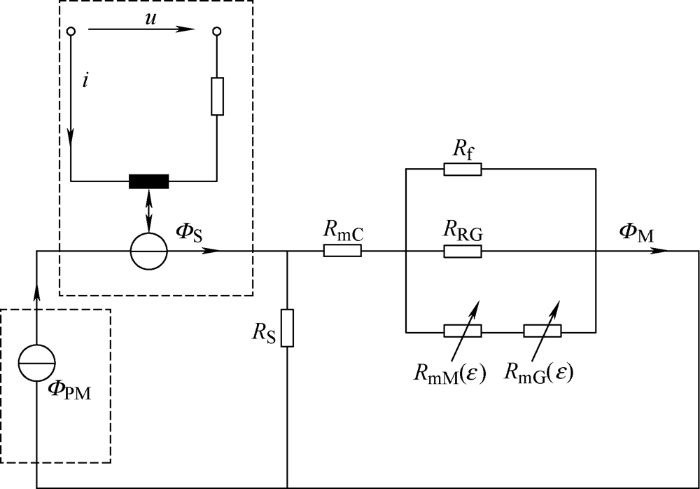
从磁控形状记忆合金的逆特性和磁路定律出发,结合相关的气隙分布,在一定输入条件下,建立MSMA传感器感应电压u 的数学模型[10 ] ,传感器的磁路模型如图3 所示[11 ] 。
图3
由相关的磁路定律,可以得出感应线圈的磁通${{}_{\text{M}}}$为
(1) ${{}_{\text{M}}}\text{=}\frac{{{}_{\text{S}}}{{R}_{\text{S}}}}{{{R}_{\text{S}}}+{{R}_{\text{mC}}}+\frac{[{{R}_{\text{mG}}}(\varepsilon )+{{R}_{\text{mM}}}(\varepsilon )]{{R}_{\text{R}}}_{\text{G}}{{R}_{\text{f}}}}{[{{R}_{\text{mG}}}(\varepsilon )+{{R}_{\text{mM}}}(\varepsilon )]({{R}_{\text{RG}}}+{{R}_{\text{f}}})+{{R}_{\text{RG}}}{{R}_{\text{f}}}}}$
式中,${{}_{\text{S}}}$为励磁线圈产生的磁通,${{R}_{\text{S}}}$为永磁体磁阻,${{R}_{\text{R}}}_{\text{G}}$为剩余气隙磁阻,${{R}_{\text{mM}}}(\varepsilon )$为所选MSMA元件的磁阻,${{R}_{\text{f}}}$为空气边缘磁阻,${{R}_{\text{mC}}}$为所选铁心部件的磁阻,${{R}_{\text{mG}}}(\varepsilon )$为气隙磁阻。其中,${{R}_{\text{mC}}}$、${{R}_{\text{f}}}$、${{R}_{\text{R}}}_{\text{G}}$和${{R}_{\text{S}}}$的计算公式分别为
(2) ${{R}_{\text{mC}}}=\frac{{{l}_{\text{mC}}}}{{{A}_{\text{mC}}}{{\mu }_{\text{mC}}}}$
(3) ${{R}_{\text{f}}}=\frac{1}{0.264{{\mu }_{0}}{{A}_{\text{mC}}}}$
(4) ${{R}_{\text{RG}}}=\frac{{{l}_{\text{gap}}}}{{{\mu }_{0}}({{A}_{\text{mC}}}-{{A}_{\text{MSMA}}})}$
(5) ${{R}_{\text{s}}}=\frac{{{l}_{\text{s}}}}{\frac{{{B}_{\text{r}}}}{{{H}_{\text{c}}}}{{A}_{\text{s}}}}$
气隙的磁阻${{R}_{\text{mG}}}(\varepsilon )$和MSMA元件磁阻${{R}_{\text{mM}}}(\varepsilon )$二者与元件形变量$\varepsilon $呈线性关系,磁通${{}_{\text{M}}}$的表达式可以简化为
(6) ${{}_{\text{M}}}={{B}_{\text{M}}}\frac{{{K}_{2}}+{{K}_{1}}\varepsilon }{{{K}_{3}}+\varepsilon }$
式中,B M 为直流线圈和永磁体叠加作用下的合成磁场,参数K 1 、K 2 、K 3 可由式(7)计算得出
(7) $\left\{ \begin{align} & {{K}_{1}}=\frac{{{R}_{\text{s}}}({{R}_{\text{RG}}}+{{R}_{\text{f}}})}{({{R}_{\text{s}}}+{{R}_{\text{mC}}})({{R}_{\text{RG}}}+{{R}_{\text{f}}})+{{R}_{\text{RG}}}{{R}_{\text{f}}}} \\ & {{K}_{2}}=\frac{{{R}_{\text{s}}}{{R}_{\text{RG}}}{{R}_{\text{f}}}}{({{R}_{\text{s}}}+{{R}_{\text{mC}}})({{R}_{\text{RG}}}+{{R}_{\text{f}}})+{{R}_{\text{RG}}}{{R}_{\text{f}}}} \\ & {{K}_{3}}=\frac{({{R}_{\text{s}}}+{{R}_{\text{mC}}}){{R}_{\text{RG}}}{{R}_{\text{f}}}}{({{R}_{\text{s}}}+{{R}_{\text{mC}}})({{R}_{\text{RG}}}+{{R}_{\text{f}}})+{{R}_{\text{RG}}}{{R}_{\text{f}}}} \\ \end{align} \right.$
在外力和磁场共同工作时,应变量$\varepsilon $为
(8) $\varepsilon ={{K}_{4}}{{B}_{M}}+{{K}_{5}}{{\sigma }_{0}}+{{K}_{6}}+{{K}_{7}}\sigma $
式中,${{K}_{4}}$~${{K}_{7}}$ 为需要辨识的未知参数,${{\sigma }_{0}}$为给传感器加载的预压力,数值为0.15 N。$\sigma $为MSMA元件所受应力。
(9) $u=N\frac{\mathrm{d}{{}_{\text{M}}}}{\mathrm{d}t}=V\frac{N}{{{L}_{\text{MSMA}}}}\frac{\mathrm{d}{{}_{\text{M}}}}{\mathrm{d}\varepsilon }=\frac{N}{{{L}_{\text{MSMA}}}}\frac{\mathrm{d}{{}_{\text{M}}}}{\mathrm{d}\varepsilon }\frac{\mathrm{d}\varepsilon }{\mathrm{d}t}$
式中,$N$为传感器检测线圈的安匝数,$V$为元件的变形速率。
(10) $F={{F}_{\text{M}}}\sin \omega t=\sigma {{S}_{\text{MSMA}}}$
式中,S MSMA 是MSMA元件的受力面积,F M 为给传感器加载的激振力幅值,$\omega $为频率。感应电压u 为
(11) $u=N\frac{{{K}_{7}}({{K}_{1}}{{K}_{3}}-{{K}_{2}}){{B}_{\mathrm{M}}}{{F}_{\mathrm{M}}}\cos \omega t}{{{V}_{\mathrm{MSMA}}}\left( \frac{{{K}_{1}}{{F}_{\mathrm{M}}}\sin \omega t}{{{S}_{\mathrm{MSMA}}}}+{{K}_{4}}{{B}_{\mathrm{M}}}+{{K}_{5}}+{{K}_{6}}+{{K}_{3}} \right)}$
传感器数学模型的部分参数如表1 所示,可得系数K 1 、K 2 、K 3 的数值,未知系数K 4 、K 5 、K 6 、K 7 则由智能算法进行识别。磁场B M 、幅值F M 和频率$\omega $为传感器输入参数,感应电压u 为传感器输出参数。
3 改进的粒子群算法
对粒子群算法在权重、最大速度、经验因子和目标函数等四个方面进行改进,提高算法对模型未知参数的识别精度。
3.1 粒子群算法
近年来,粒子群算法因其独特的表现引起人们的广泛关注,是对鸟类群体行为的一种模型描述[12 ⇓ -14 ] ,可以用于系统识别和控制。它的原理是每个粒子调整其运动,使其朝着自身最佳位置和整个群体所获得的全局最佳位置移动[15 ] 。粒子i 在d 维搜索空间中的位置表示为X i =X id (i =1,2,…,m ),速度为v i =v id (i =1,2,…,m )。
(12) $v_{\text{id}}^{k+1}=\omega v_{\text{id}}^{k}+{{c}_{1}}{{r}_{1}}({{p}_{\text{id}}}-X_{\text{id}}^{k})+{{c}_{2}}{{r}_{2}}({{p}_{\text{gd}}}-X_{\text{di}}^{k})$
(13) $X_{\text{id}}^{k+1}=X_{\text{id}}^{k}+v_{\text{id}}^{k+1}$
式中,$\omega $为权重;c 1 和c 2 为经验因子;r 1 和r 2 为随机数,取值范围在0和1之间;p id 和p gd 分别为粒子自身最佳位置和整体最佳位置;k 为迭代数。
3.2 算法改进
基本粒子群优化算法中的惯性权重$\omega $和经验因子c 均为定值,对于经验因子c ,它与全局最优解也有关,也体现着粒子群经验的积累程度。在开始阶段,粒子需要个体学习能力,所以个体学习系数c 1 变大,才能加速粒子的更新,更快地锁定最佳位置,c 1 的值固定为2。当进行到后期时,群体学习能力尤为重要,群学习因子c 2 的值增加,算法不仅可以在局部范围内找到最优解,提高算法的精度,而且更能体现群体智能优化算法的优越性,学习因子c 2 调整策略为
(14) ${{c}_{2}}=0.8+\frac{t}{T}$
式中,t 为当前的更新次数,T 为设置的最大更新次数。
权重$\omega $可以调节群体寻找最优解的能力。$\omega $变大时,可以提高种群的全局搜索性,局部的搜索能力便随之降低[16 ] ;$\omega $变小时,可以加强种群局部的搜索能力,全局的搜索能力便随之降低。鉴于切比雪夫函数曲线在线性与非线性之间有着良好的过渡性[17 ] ,对权重进行非线性调整,并且引入了调节系数G ,通过改变系数的大小来控制最大惯性权重的值,有利于粒子群在初始时用较大的权重进行全局大范围的搜索,而在最后时用较小的权重进行局部小范围的搜索,权重$\omega $为
(15) $\omega =\frac{0.55}{\sqrt{1+{{\left( \frac{Gt}{T} \right)}^{9}}}}+0.4$
为了保证算法的收敛性,设置动态最大速度${{V}_{\max }}$来调节粒子的运动步长,如果最大速度${{v}_{\text{max}}}$设定值过大,会使粒子错过最优种群的搜索范围,搜索精度会降低。若最大速度的值过小,会使粒子大范围地搜索,最终的收敛性会受到影响。为了提高算法的稳定性,所以引入最大速度动态调整策略[18 ] ,在迭代次数不断增加的同时,粒子的最大速度会非线性减小。另外,设置最小速度${{v}_{\text{min}}}$来降低粒子初始速度大于粒子收敛速度的可能性,则V max 的计算公式为
(16) ${{V}_{\max }}\text{=}\frac{{{v}_{\text{max}}}}{\sqrt{\text{1+}{{\left( \frac{\text{3}t}{T} \right)}^{\text{6}}}}}\text{+}{{v}_{\text{min}}}$
在建立目标函数时,由于在采集试验数据时可能会存在误差,所以在传感器实际输出值与模型输出值差的平方和前面乘上一个可变常数,取值范围在0和1之间,来减小模型误差[19 ] 。传感器模型是一个非线性模型,同时辨识的未知参数有4个,模型的精度会受到影响,加一个规则化项f ,来提高模型的精度,规则化项f 为
(17) $f({{\omega }_{\text{j}}},k)=\frac{{{\gamma }^{2}}}{{{\omega }_{\text{j}}}+\gamma k}$
(18) $J=\min \sum\limits_{i\text{=1}}^{N}{\frac{1}{N}}\left[ {{\omega }_{\text{j}}}{{\left( {{y}_{\text{1}}}-{{y}_{\text{2}}} \right)}^{\text{2}}}\text{+}\frac{{{\gamma }^{\text{2}}}}{{{\omega }_{\text{j}}}\text{+}\gamma k} \right]$
式中,y 1 为实际值,y 2 为模型的输出值,${{\omega }_{\text{j}}}$的取值范围在0和1之间,γ 的值设置为1.2,k 的值设置为1,N 为试验数据样本的数量。
3.3 算法步骤
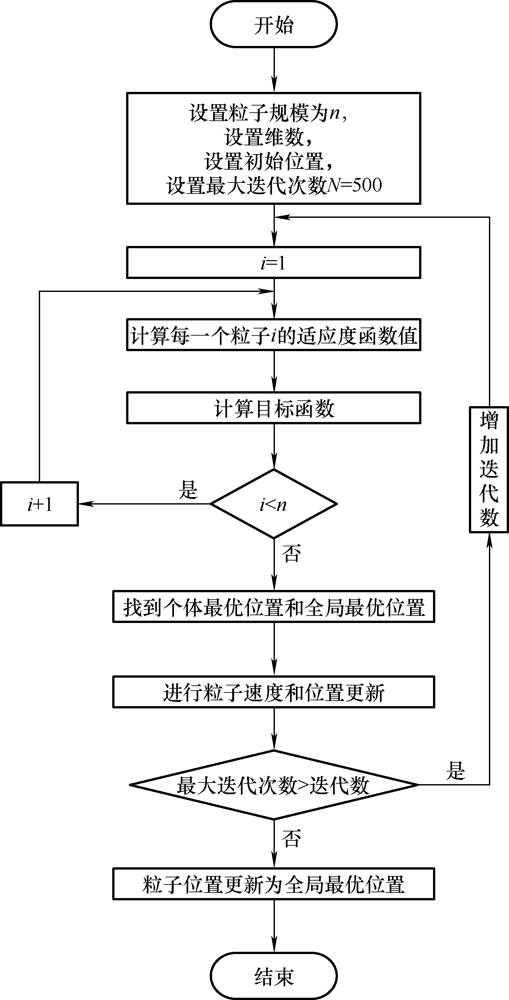
改进PSO算法的流程如图4 所示,初始化粒子的各个参数,计算每个粒子的目标函数。通过比较,找出目标函数值最小的粒子,其余粒子均向其位置移动,直至满足最大迭代数,模型的未知参数得到其最优解,算法结束。
图4
4 参数辨识结果与验证
采集试验数据,为传感器模型的参数辨识提供数据集。用基本粒子群算法和改进粒子群算法分别对传感器模型的未知参数进行识别,得到传感器的模型Ⅰ和模型Ⅱ,在输入相同的前提下,验证模型精度。
4.1 试验数据采集
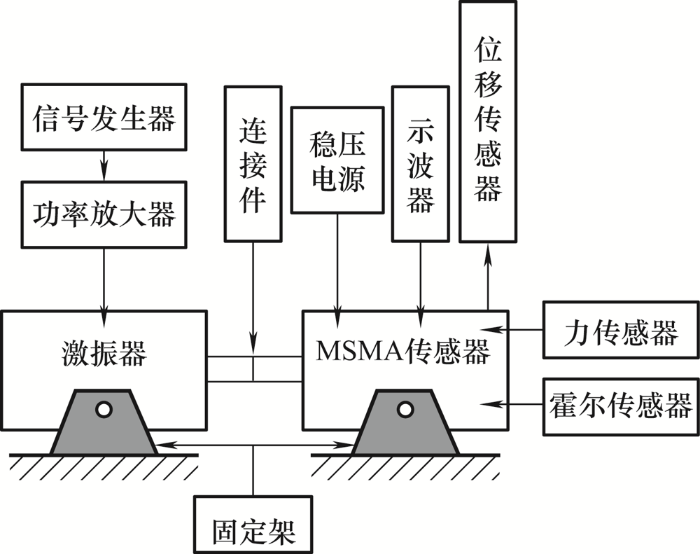
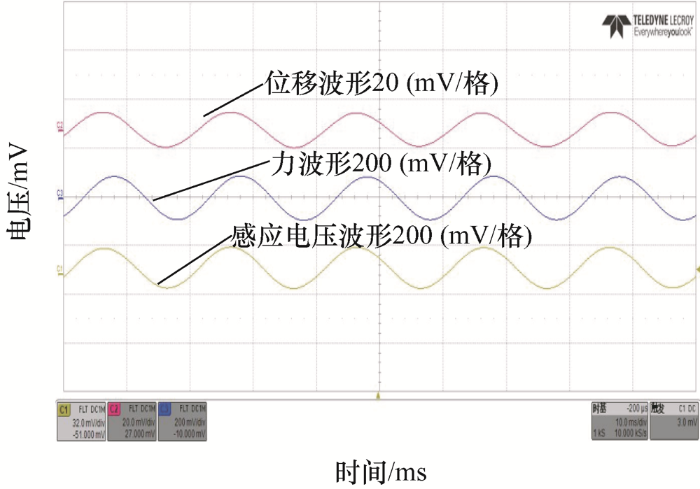
MSMA传感器的试验装置如图5 [20 ] 所示,由激振器、MSMA传感器和力传感器等设备组成。设定激振器的频率为180 Hz、激振力为0.24 N,磁场为0.35 T,从图6 可以看出感应峰峰值为128 mV。通过改变不同的输入,进行多组试验,将试验数据记录下来,为后面传感器数学模型的参数辨识提供数据集。
图5
图6
4.2 参数辨识
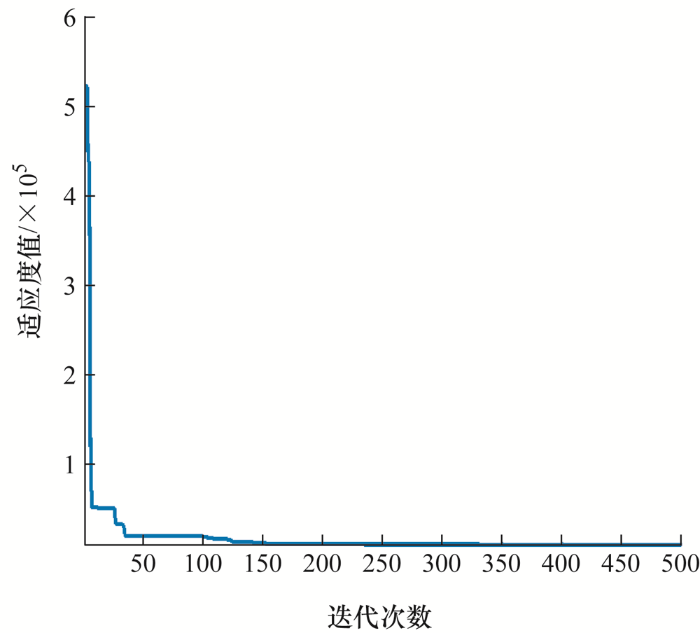
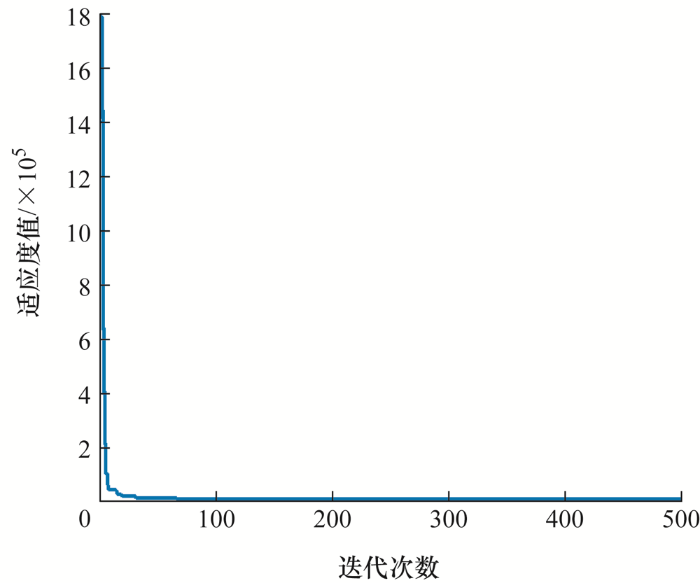
参数辨识就是将收集的试验输出值和模型输出值,经过目标函数的计算,将算出的值作为适应度值输入到算法中,算法将模型中的未知参数不断地进行优化,直至适应度函数取得最小值或者达到算法的终止条件,输出未知参数。经过PSO算法,得到的迭代曲线如图7 所示。可以看出,在更新35次后,算法陷入局部最优解中,在更新约105次跳出,并在更新约120次后,适应度值接近于0。经过改进PSO算法,得到的迭代曲线如图8 所示,相对于PSO算法,收敛速率更快,在更新约71次后,适应度值已经接近于0。当迭代完成后,得到各参数值,表2 为两种算法对未知参数的识别结果。
图7
图8
对表2 中的参数值进行分析,可以看出两种算法辨识得到的磁阻系数K 1 、K 2 、K 3 值一致,验证了优化算法应用于本模型的准确性。K 4 ~K 7 是MSMA传感器感应电压模型的待辨识参数值,与传感器的输出电压有关。
4.3 数学模型验证
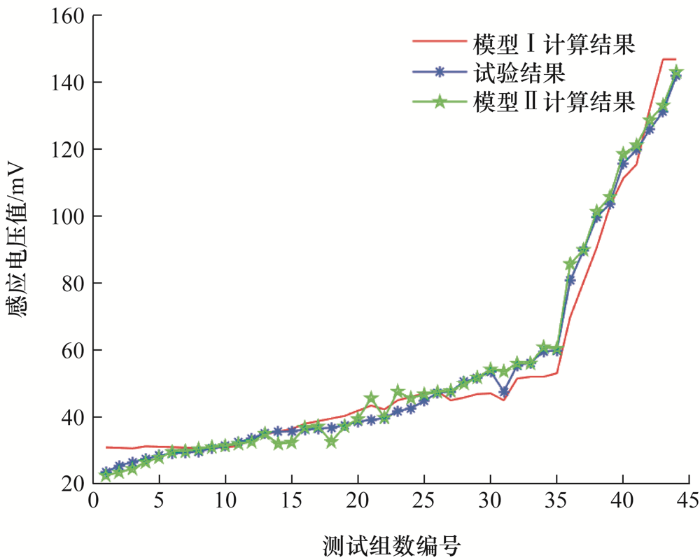
用基本粒子群算法和改进算法分别对传感模型进行参数辨识,将识别出的未知参数值代入式(6),得到传感器的模型Ⅰ和模型Ⅱ。在输入激振力幅值为0.31 N和磁场为325 mT的试验条件下,改变激振力频率,得到传感器输出的感应电压值。选取频率在60~240 Hz范围内的44组试验结果作为模型验证,在输入参数相同的条件下,将实际的感应电压输出值与模型计算得出的电压值进行比较,对比曲线如图9 所示,得出模型Ⅰ的平均误差率为7.68%,模型Ⅱ的输出值与试验值比较接近,且相对误差率约为4.73%,结果表明,模型Ⅱ相对准确。
图9
5 结论
本文主要对MSMA传感器进行建模研究,然后利用PSO算法和改进的PSO算法分别对模型的未知参数进行识别,最后将实际输出值与模型计算值对比。结果表明,在将算法的权重进行非线性调整后,可以比较准确地识别传感器数学模型的参数,计算值与试验值的平均误差率为4.37%,相比于PSO算法误差率减少了2.95%。最大速度和经验因子的改进也有效地提高了算法的全局优化能力,加快了算法的收敛速度,为MSMA传感器的研究提供了理论基础。
为获取更为准确的感应电压模型,需要研究预压力对感应电压的影响规律;改进后的PSO算法应用于感应电压模型时,跳出局部最优解的能力有待提高。
参考文献
View Option
[1]
郭子扬 . MSMA传感器结构优化研究与仿真平台的搭建 [D]. 沈阳 : 沈阳理工大学 , 2020 .
[本文引用: 1]
GUO Ziyang . MSMA sensor structure optimization research and simulation platform,construction [D]. Shenyang : Shenyang Ligong University , 2020 .
[本文引用: 1]
[2]
NGOUALA B LIU Fang XU Jia , et al . Nonlinear dynamic characteristics and optimal control of MSMA actuator subjected to harmonic magnetic field and stochastic excitation
[J]. International Journal of Applied Electromagnetics and Mechanics , 2020 , 64 (1-4 ):1523 -1529 .
DOI:10.3233/JAE-209473
URL
[本文引用: 1]
[3]
WEI Pan RUI Xu YU Yewei , et al . Hysteresis modeling for magnetic shape memory alloy actuator via Pi-Sigma neural network with backlash-like operator
[J]. Acta Physica Polonica A , 2020 , 137 (5 ):634 -636 .
DOI:10.12693/APhysPolA.137.634
URL
[本文引用: 1]
[4]
ZHU Jiachen TAN Changlong ZHAO Wenbin , et al . The crystallization kinetics of Ni-Mn-Ga magnetic shape memory alloy thin films
[J]. Journal of Electronic Materials , 2019 , 48 (4 ):2137 -2143 .
DOI:10.1007/s11664-019-06987-0
[本文引用: 1]
The crystallization mechanism of Ni-Mn-Ga thin films and the reason for the difference of crystallization temperatures of Ni-Mn-based magnetic shape memory alloys (MSMAs) are unknown. Here, the crystallization kinetics of Ni53Mn28Ga19 magnetic shape memory alloy thin films have been determined by non-isothermal and isothermal differential scanning calorimetry (DSC). The reason for the difference of crystallization temperatures of Ni-Mn-based MSMAs was studied by the first-principles methods. The crystal structure of annealed Ni53Mn28Ga19 thin films are 7M martensite. In non-isothermal DSC, crystallization peak temperatures are 588.2K, 593.7K, 601.3K, 604.6K and 608.2K at different heating rates. The apparent activation energy calculated by Kissinger's method is 148.3kJ/mol. For isothermal crystallization, the Avrami exponent of Ni53Mn28Ga19 thin films is approximately 1.6. The local Avrami exponents n(x) which range from 1.1 to 2.8 imply that the crystallization mechanism of Ni53Mn28Ga19 thin films changes from one-dimensional diffusion-controlled growth to two-dimensional and three-dimensional diffusion-controlled growth. Moreover, it is found that crystallization peak temperatures of Ni-Mn-based MSMAs increase with their increasing vacancy formation energy with Ni vacancy.
[5]
段晶晶 . 磁控形状记忆合金力-磁-热耦合行为及控制策略的研究 [D]. 武汉 : 武汉科技大学 , 2015 .
[本文引用: 1]
DUAN Jingjing . Magnetic controlled shape memory alloy power-magnetic-thermal coupling behavior and control strategy research [D]. Wuhan : Wuhan University of Science and Technology , 2015 .
[本文引用: 1]
[6]
ZHAO Qiang LI Changwei . Two-stage multi-swarm particle swarm optimizer for unconstrained and constrained global optimization
[J]. IEEE Access , 2020 , 8 (8 ):124905 -124927 .
DOI:10.1109/ACCESS.2020.3007743
URL
[本文引用: 1]
[7]
WEBB G V LAGOUDAS D C KURDILA A J . Hysteresis modeling of SMA actuators for control applications
[J]. Journal of Intelligent Material Systems & Structures , 1998 , 9 (6 ):432 -448 .
[本文引用: 1]
[8]
涂福泉 , 吕杰 , 庄羽航 , 等 . 基于HFLANN的MSMA传感器动态模型参数识别
[J]. 自动化与仪表 , 2017 , 32 (1 ):21 -23 .
[本文引用: 1]
TU Fuquan LÜ Jie ZHUANG Yuhang , et al . MSMA sensor dynamic model parameter identification based on HFLANN
[J]. Automation & Instrumentation , 2017 , 32 (1 ):21 -23 .
[本文引用: 1]
[9]
高琳 . 磁控形状记忆合金传感器结构设计与实验研究 [D]. 沈阳 : 沈阳理工大学 , 2017 .
[本文引用: 1]
GAO Lin . Structure design and experimental research of magnetron shape memory alloy sensor [D]. Shenyang : Shenyang Ligong University , 2017 .
[本文引用: 1]
[10]
鲁军 , 苏超峰 . 磁控形状记忆合金传感器优化设计
[J]. 电气工程学报 , 2018 , 13 (12 ):1 -6 .
[本文引用: 1]
LU Jun SU Chaofeng . Optimal design of magnetron shape memory alloy sensor
[J]. Journal of Electrical Engineering , 2018 , 13 (12 ):1 -6 .
[本文引用: 1]
[11]
鲁军 , 杨宽 , 王凤翔 . 磁控形状记忆合金振动传感器模型及实验特性
[J]. 电机与控制学报 , 2014 , 18 (3 ):20 -24 .
[本文引用: 1]
LU Jun YANG Kuan WANG Fengxiang . Model and experimental characteristics of magnetron shape memory alloy vibration sensor
[J]. Journal of Electrical Machines and Control , 2014 , 18 (3 ):20 -24 .
[本文引用: 1]
[12]
YANG Xiaoping CHEN Xueying XIA Riting , et al . Wireless sensor network congestion control based on standard particle swarm optimization and single neuron PID
[J]. Sensors , 2018 , 18 (4 ):1265 .
DOI:10.3390/s18041265
URL
[本文引用: 1]
[13]
ZHANG Huizhen LIU Fan MA Liang , et al . A hybrid heuristic based on a particle swarm algorithm to solve the capacitated location-routing problem with fuzzy demands
[J]. IEEE Access , 2020 , 8 (8 ):153671 -153691 .
DOI:10.1109/ACCESS.2020.3018490
URL
[本文引用: 1]
[14]
GABBAR H A ABDUSSAMI M R ADHAM M I . Optimal planning of nuclear-renewable micro-hybrid energy system by particle swarm optimization
[J]. IEEE Access , 2020 , 8 (8 ):189 -206 .
[本文引用: 1]
[15]
LI Zicheng XIONG Xuan WANG Houneng , et al . Prandtl-Ishlinskii model identification strategy based on an improved particle
[C]// 2020 5th International Conference on Control,Robotics and Cybernetics,October 16-18,Wuhan,China. IEEE , 2020 :61 -15 .
[本文引用: 1]
[16]
YANG Chen LIU Yancheng WANG Chuan , et al . Shipboard power system restoration using S-curve inertia weight particle swarm optimization
[J]. Applied Mechanics and Materials , 2013 , 2755 (433-435 ):1226 -1229 .
[本文引用: 1]
[17]
AL-SHAIKHI A A KHAN A H AL-AWAMI A T , et al . A hybrid particle swarm optimization technique for adaptive equalization
[J]. Arabian Journal for Science and Engineering , 2019 , 44 (3 ):2177 -2184 .
DOI:10.1007/s13369-018-3387-8
URL
[本文引用: 1]
[18]
华勇 , 王双园 , 白国振 , 等 . 基于惯性权值非线性递减的改进粒子群算法
[J]. 重庆工商大学学报 , 2021 , 38 (2 ):1 -9 .
[本文引用: 1]
HUA Yong WANG Shuangyuan BAI Guozhen , et al . An improved particle swarm optimization algorithm based on nonlinear decreasing inertial weights
[J]. Journal of Chongqing Technology and Business University , 2021 , 38 (2 ):1 -9 .
[本文引用: 1]
[19]
马欣 , 闫莉 . 粒子释放与速度动态变化的改进粒子群算法
[J]. 电子技术与软件工程 , 2021 (2 ):153 -155 .
[本文引用: 1]
MA Xin YAN Li . Improved particle swarm algorithm for particle release and dynamic change of velocity
[J]. Electronic Technology and Software Engineering , 2021 (2 ):153 -155 .
[本文引用: 1]
[20]
鲁军 , 李园君 , 常强 . MSMA传感器的优化设计及试验特性研究
[J]. 电气工程学报 , 2021 , 16 (1 ):42 -47 .
[本文引用: 1]
LU Jun LI Yuanjun CHANG Qiang . Optimal design and experimental characteristics of MSMA sensor
[J]. Journal of Electrical Engineering , 2021 , 16 (1 ):42 -47 .
[本文引用: 1]
1
2020
... 磁控形状记忆合金(Magnetic shape memory alloy,MSMA)是近几十年被国内外关注较多的智能材料[1 ⇓ -3 ] ,具有磁场诱导应变大、疲劳寿命长等优点[4 -5 ] .基于这些特性,MSMA逐渐被人们关注,特别是在传感器和执行器方面,是最理想的材料之一,所以MSMA具有成为新一代传感器核心元件的良好潜力.然而,基于MSMA的传感器的输入与输出之间存在非线性的现象.很多国内外的学者对其进行了研究,有些学者主要进行建模研究,由于特定材料的限制,增加了其数学建模的难度.有些学者未考虑系统的内部结构和材料的物理性质,着重关注输入和输出之间的关系,并采用参数识别方法识别模型参数[6 -7 ] .其中,Preisach模型是用相对简单的数学方法,对输入与输出之间的非线性问题进行概述,得到了比较广泛的应用,但是在参数优化方面存在不足.文献[8 ]介绍了一种参数线性化的KP模型,但是算法的复杂性偏高,相对不易于推导. ...
1
2020
... 磁控形状记忆合金(Magnetic shape memory alloy,MSMA)是近几十年被国内外关注较多的智能材料[1 ⇓ -3 ] ,具有磁场诱导应变大、疲劳寿命长等优点[4 -5 ] .基于这些特性,MSMA逐渐被人们关注,特别是在传感器和执行器方面,是最理想的材料之一,所以MSMA具有成为新一代传感器核心元件的良好潜力.然而,基于MSMA的传感器的输入与输出之间存在非线性的现象.很多国内外的学者对其进行了研究,有些学者主要进行建模研究,由于特定材料的限制,增加了其数学建模的难度.有些学者未考虑系统的内部结构和材料的物理性质,着重关注输入和输出之间的关系,并采用参数识别方法识别模型参数[6 -7 ] .其中,Preisach模型是用相对简单的数学方法,对输入与输出之间的非线性问题进行概述,得到了比较广泛的应用,但是在参数优化方面存在不足.文献[8 ]介绍了一种参数线性化的KP模型,但是算法的复杂性偏高,相对不易于推导. ...
Nonlinear dynamic characteristics and optimal control of MSMA actuator subjected to harmonic magnetic field and stochastic excitation
1
2020
... 磁控形状记忆合金(Magnetic shape memory alloy,MSMA)是近几十年被国内外关注较多的智能材料[1 ⇓ -3 ] ,具有磁场诱导应变大、疲劳寿命长等优点[4 -5 ] .基于这些特性,MSMA逐渐被人们关注,特别是在传感器和执行器方面,是最理想的材料之一,所以MSMA具有成为新一代传感器核心元件的良好潜力.然而,基于MSMA的传感器的输入与输出之间存在非线性的现象.很多国内外的学者对其进行了研究,有些学者主要进行建模研究,由于特定材料的限制,增加了其数学建模的难度.有些学者未考虑系统的内部结构和材料的物理性质,着重关注输入和输出之间的关系,并采用参数识别方法识别模型参数[6 -7 ] .其中,Preisach模型是用相对简单的数学方法,对输入与输出之间的非线性问题进行概述,得到了比较广泛的应用,但是在参数优化方面存在不足.文献[8 ]介绍了一种参数线性化的KP模型,但是算法的复杂性偏高,相对不易于推导. ...
Hysteresis modeling for magnetic shape memory alloy actuator via Pi-Sigma neural network with backlash-like operator
1
2020
... 磁控形状记忆合金(Magnetic shape memory alloy,MSMA)是近几十年被国内外关注较多的智能材料[1 ⇓ -3 ] ,具有磁场诱导应变大、疲劳寿命长等优点[4 -5 ] .基于这些特性,MSMA逐渐被人们关注,特别是在传感器和执行器方面,是最理想的材料之一,所以MSMA具有成为新一代传感器核心元件的良好潜力.然而,基于MSMA的传感器的输入与输出之间存在非线性的现象.很多国内外的学者对其进行了研究,有些学者主要进行建模研究,由于特定材料的限制,增加了其数学建模的难度.有些学者未考虑系统的内部结构和材料的物理性质,着重关注输入和输出之间的关系,并采用参数识别方法识别模型参数[6 -7 ] .其中,Preisach模型是用相对简单的数学方法,对输入与输出之间的非线性问题进行概述,得到了比较广泛的应用,但是在参数优化方面存在不足.文献[8 ]介绍了一种参数线性化的KP模型,但是算法的复杂性偏高,相对不易于推导. ...
The crystallization kinetics of Ni-Mn-Ga magnetic shape memory alloy thin films
1
2019
... 磁控形状记忆合金(Magnetic shape memory alloy,MSMA)是近几十年被国内外关注较多的智能材料[1 ⇓ -3 ] ,具有磁场诱导应变大、疲劳寿命长等优点[4 -5 ] .基于这些特性,MSMA逐渐被人们关注,特别是在传感器和执行器方面,是最理想的材料之一,所以MSMA具有成为新一代传感器核心元件的良好潜力.然而,基于MSMA的传感器的输入与输出之间存在非线性的现象.很多国内外的学者对其进行了研究,有些学者主要进行建模研究,由于特定材料的限制,增加了其数学建模的难度.有些学者未考虑系统的内部结构和材料的物理性质,着重关注输入和输出之间的关系,并采用参数识别方法识别模型参数[6 -7 ] .其中,Preisach模型是用相对简单的数学方法,对输入与输出之间的非线性问题进行概述,得到了比较广泛的应用,但是在参数优化方面存在不足.文献[8 ]介绍了一种参数线性化的KP模型,但是算法的复杂性偏高,相对不易于推导. ...
1
2015
... 磁控形状记忆合金(Magnetic shape memory alloy,MSMA)是近几十年被国内外关注较多的智能材料[1 ⇓ -3 ] ,具有磁场诱导应变大、疲劳寿命长等优点[4 -5 ] .基于这些特性,MSMA逐渐被人们关注,特别是在传感器和执行器方面,是最理想的材料之一,所以MSMA具有成为新一代传感器核心元件的良好潜力.然而,基于MSMA的传感器的输入与输出之间存在非线性的现象.很多国内外的学者对其进行了研究,有些学者主要进行建模研究,由于特定材料的限制,增加了其数学建模的难度.有些学者未考虑系统的内部结构和材料的物理性质,着重关注输入和输出之间的关系,并采用参数识别方法识别模型参数[6 -7 ] .其中,Preisach模型是用相对简单的数学方法,对输入与输出之间的非线性问题进行概述,得到了比较广泛的应用,但是在参数优化方面存在不足.文献[8 ]介绍了一种参数线性化的KP模型,但是算法的复杂性偏高,相对不易于推导. ...
1
2015
... 磁控形状记忆合金(Magnetic shape memory alloy,MSMA)是近几十年被国内外关注较多的智能材料[1 ⇓ -3 ] ,具有磁场诱导应变大、疲劳寿命长等优点[4 -5 ] .基于这些特性,MSMA逐渐被人们关注,特别是在传感器和执行器方面,是最理想的材料之一,所以MSMA具有成为新一代传感器核心元件的良好潜力.然而,基于MSMA的传感器的输入与输出之间存在非线性的现象.很多国内外的学者对其进行了研究,有些学者主要进行建模研究,由于特定材料的限制,增加了其数学建模的难度.有些学者未考虑系统的内部结构和材料的物理性质,着重关注输入和输出之间的关系,并采用参数识别方法识别模型参数[6 -7 ] .其中,Preisach模型是用相对简单的数学方法,对输入与输出之间的非线性问题进行概述,得到了比较广泛的应用,但是在参数优化方面存在不足.文献[8 ]介绍了一种参数线性化的KP模型,但是算法的复杂性偏高,相对不易于推导. ...
Two-stage multi-swarm particle swarm optimizer for unconstrained and constrained global optimization
1
2020
... 磁控形状记忆合金(Magnetic shape memory alloy,MSMA)是近几十年被国内外关注较多的智能材料[1 ⇓ -3 ] ,具有磁场诱导应变大、疲劳寿命长等优点[4 -5 ] .基于这些特性,MSMA逐渐被人们关注,特别是在传感器和执行器方面,是最理想的材料之一,所以MSMA具有成为新一代传感器核心元件的良好潜力.然而,基于MSMA的传感器的输入与输出之间存在非线性的现象.很多国内外的学者对其进行了研究,有些学者主要进行建模研究,由于特定材料的限制,增加了其数学建模的难度.有些学者未考虑系统的内部结构和材料的物理性质,着重关注输入和输出之间的关系,并采用参数识别方法识别模型参数[6 -7 ] .其中,Preisach模型是用相对简单的数学方法,对输入与输出之间的非线性问题进行概述,得到了比较广泛的应用,但是在参数优化方面存在不足.文献[8 ]介绍了一种参数线性化的KP模型,但是算法的复杂性偏高,相对不易于推导. ...
Hysteresis modeling of SMA actuators for control applications
1
1998
... 磁控形状记忆合金(Magnetic shape memory alloy,MSMA)是近几十年被国内外关注较多的智能材料[1 ⇓ -3 ] ,具有磁场诱导应变大、疲劳寿命长等优点[4 -5 ] .基于这些特性,MSMA逐渐被人们关注,特别是在传感器和执行器方面,是最理想的材料之一,所以MSMA具有成为新一代传感器核心元件的良好潜力.然而,基于MSMA的传感器的输入与输出之间存在非线性的现象.很多国内外的学者对其进行了研究,有些学者主要进行建模研究,由于特定材料的限制,增加了其数学建模的难度.有些学者未考虑系统的内部结构和材料的物理性质,着重关注输入和输出之间的关系,并采用参数识别方法识别模型参数[6 -7 ] .其中,Preisach模型是用相对简单的数学方法,对输入与输出之间的非线性问题进行概述,得到了比较广泛的应用,但是在参数优化方面存在不足.文献[8 ]介绍了一种参数线性化的KP模型,但是算法的复杂性偏高,相对不易于推导. ...
基于HFLANN的MSMA传感器动态模型参数识别
1
2017
... 磁控形状记忆合金(Magnetic shape memory alloy,MSMA)是近几十年被国内外关注较多的智能材料[1 ⇓ -3 ] ,具有磁场诱导应变大、疲劳寿命长等优点[4 -5 ] .基于这些特性,MSMA逐渐被人们关注,特别是在传感器和执行器方面,是最理想的材料之一,所以MSMA具有成为新一代传感器核心元件的良好潜力.然而,基于MSMA的传感器的输入与输出之间存在非线性的现象.很多国内外的学者对其进行了研究,有些学者主要进行建模研究,由于特定材料的限制,增加了其数学建模的难度.有些学者未考虑系统的内部结构和材料的物理性质,着重关注输入和输出之间的关系,并采用参数识别方法识别模型参数[6 -7 ] .其中,Preisach模型是用相对简单的数学方法,对输入与输出之间的非线性问题进行概述,得到了比较广泛的应用,但是在参数优化方面存在不足.文献[8 ]介绍了一种参数线性化的KP模型,但是算法的复杂性偏高,相对不易于推导. ...
MSMA sensor dynamic model parameter identification based on HFLANN
1
2017
... 磁控形状记忆合金(Magnetic shape memory alloy,MSMA)是近几十年被国内外关注较多的智能材料[1 ⇓ -3 ] ,具有磁场诱导应变大、疲劳寿命长等优点[4 -5 ] .基于这些特性,MSMA逐渐被人们关注,特别是在传感器和执行器方面,是最理想的材料之一,所以MSMA具有成为新一代传感器核心元件的良好潜力.然而,基于MSMA的传感器的输入与输出之间存在非线性的现象.很多国内外的学者对其进行了研究,有些学者主要进行建模研究,由于特定材料的限制,增加了其数学建模的难度.有些学者未考虑系统的内部结构和材料的物理性质,着重关注输入和输出之间的关系,并采用参数识别方法识别模型参数[6 -7 ] .其中,Preisach模型是用相对简单的数学方法,对输入与输出之间的非线性问题进行概述,得到了比较广泛的应用,但是在参数优化方面存在不足.文献[8 ]介绍了一种参数线性化的KP模型,但是算法的复杂性偏高,相对不易于推导. ...
1
2017
... MSMA传感器的模型结构如图1 所示,磁控形状记忆合金传感器是由铁心、气隙、永磁体、励磁线圈、检测线圈、MSMA元件等组成[9 ] . ...
1
2017
... MSMA传感器的模型结构如图1 所示,磁控形状记忆合金传感器是由铁心、气隙、永磁体、励磁线圈、检测线圈、MSMA元件等组成[9 ] . ...
磁控形状记忆合金传感器优化设计
1
2018
... 从磁控形状记忆合金的逆特性和磁路定律出发,结合相关的气隙分布,在一定输入条件下,建立MSMA传感器感应电压u 的数学模型[10 ] ,传感器的磁路模型如图3 所示[11 ] . ...
Optimal design of magnetron shape memory alloy sensor
1
2018
... 从磁控形状记忆合金的逆特性和磁路定律出发,结合相关的气隙分布,在一定输入条件下,建立MSMA传感器感应电压u 的数学模型[10 ] ,传感器的磁路模型如图3 所示[11 ] . ...
磁控形状记忆合金振动传感器模型及实验特性
1
2014
... 从磁控形状记忆合金的逆特性和磁路定律出发,结合相关的气隙分布,在一定输入条件下,建立MSMA传感器感应电压u 的数学模型[10 ] ,传感器的磁路模型如图3 所示[11 ] . ...
Model and experimental characteristics of magnetron shape memory alloy vibration sensor
1
2014
... 从磁控形状记忆合金的逆特性和磁路定律出发,结合相关的气隙分布,在一定输入条件下,建立MSMA传感器感应电压u 的数学模型[10 ] ,传感器的磁路模型如图3 所示[11 ] . ...
Wireless sensor network congestion control based on standard particle swarm optimization and single neuron PID
1
2018
... 近年来,粒子群算法因其独特的表现引起人们的广泛关注,是对鸟类群体行为的一种模型描述[12 ⇓ -14 ] ,可以用于系统识别和控制.它的原理是每个粒子调整其运动,使其朝着自身最佳位置和整个群体所获得的全局最佳位置移动[15 ] .粒子i 在d 维搜索空间中的位置表示为X i =X id (i =1,2,…,m ),速度为v i =v id (i =1,2,…,m ). ...
A hybrid heuristic based on a particle swarm algorithm to solve the capacitated location-routing problem with fuzzy demands
1
2020
... 近年来,粒子群算法因其独特的表现引起人们的广泛关注,是对鸟类群体行为的一种模型描述[12 ⇓ -14 ] ,可以用于系统识别和控制.它的原理是每个粒子调整其运动,使其朝着自身最佳位置和整个群体所获得的全局最佳位置移动[15 ] .粒子i 在d 维搜索空间中的位置表示为X i =X id (i =1,2,…,m ),速度为v i =v id (i =1,2,…,m ). ...
Optimal planning of nuclear-renewable micro-hybrid energy system by particle swarm optimization
1
2020
... 近年来,粒子群算法因其独特的表现引起人们的广泛关注,是对鸟类群体行为的一种模型描述[12 ⇓ -14 ] ,可以用于系统识别和控制.它的原理是每个粒子调整其运动,使其朝着自身最佳位置和整个群体所获得的全局最佳位置移动[15 ] .粒子i 在d 维搜索空间中的位置表示为X i =X id (i =1,2,…,m ),速度为v i =v id (i =1,2,…,m ). ...
Prandtl-Ishlinskii model identification strategy based on an improved particle
1
2020
... 近年来,粒子群算法因其独特的表现引起人们的广泛关注,是对鸟类群体行为的一种模型描述[12 ⇓ -14 ] ,可以用于系统识别和控制.它的原理是每个粒子调整其运动,使其朝着自身最佳位置和整个群体所获得的全局最佳位置移动[15 ] .粒子i 在d 维搜索空间中的位置表示为X i =X id (i =1,2,…,m ),速度为v i =v id (i =1,2,…,m ). ...
Shipboard power system restoration using S-curve inertia weight particle swarm optimization
1
2013
... 权重$\omega $可以调节群体寻找最优解的能力.$\omega $变大时,可以提高种群的全局搜索性,局部的搜索能力便随之降低[16 ] ;$\omega $变小时,可以加强种群局部的搜索能力,全局的搜索能力便随之降低.鉴于切比雪夫函数曲线在线性与非线性之间有着良好的过渡性[17 ] ,对权重进行非线性调整,并且引入了调节系数G ,通过改变系数的大小来控制最大惯性权重的值,有利于粒子群在初始时用较大的权重进行全局大范围的搜索,而在最后时用较小的权重进行局部小范围的搜索,权重$\omega $为 ...
A hybrid particle swarm optimization technique for adaptive equalization
1
2019
... 权重$\omega $可以调节群体寻找最优解的能力.$\omega $变大时,可以提高种群的全局搜索性,局部的搜索能力便随之降低[16 ] ;$\omega $变小时,可以加强种群局部的搜索能力,全局的搜索能力便随之降低.鉴于切比雪夫函数曲线在线性与非线性之间有着良好的过渡性[17 ] ,对权重进行非线性调整,并且引入了调节系数G ,通过改变系数的大小来控制最大惯性权重的值,有利于粒子群在初始时用较大的权重进行全局大范围的搜索,而在最后时用较小的权重进行局部小范围的搜索,权重$\omega $为 ...
基于惯性权值非线性递减的改进粒子群算法
1
2021
... 为了保证算法的收敛性,设置动态最大速度${{V}_{\max }}$来调节粒子的运动步长,如果最大速度${{v}_{\text{max}}}$设定值过大,会使粒子错过最优种群的搜索范围,搜索精度会降低.若最大速度的值过小,会使粒子大范围地搜索,最终的收敛性会受到影响.为了提高算法的稳定性,所以引入最大速度动态调整策略[18 ] ,在迭代次数不断增加的同时,粒子的最大速度会非线性减小.另外,设置最小速度${{v}_{\text{min}}}$来降低粒子初始速度大于粒子收敛速度的可能性,则V max 的计算公式为 ...
An improved particle swarm optimization algorithm based on nonlinear decreasing inertial weights
1
2021
... 为了保证算法的收敛性,设置动态最大速度${{V}_{\max }}$来调节粒子的运动步长,如果最大速度${{v}_{\text{max}}}$设定值过大,会使粒子错过最优种群的搜索范围,搜索精度会降低.若最大速度的值过小,会使粒子大范围地搜索,最终的收敛性会受到影响.为了提高算法的稳定性,所以引入最大速度动态调整策略[18 ] ,在迭代次数不断增加的同时,粒子的最大速度会非线性减小.另外,设置最小速度${{v}_{\text{min}}}$来降低粒子初始速度大于粒子收敛速度的可能性,则V max 的计算公式为 ...
粒子释放与速度动态变化的改进粒子群算法
1
2021
... 在建立目标函数时,由于在采集试验数据时可能会存在误差,所以在传感器实际输出值与模型输出值差的平方和前面乘上一个可变常数,取值范围在0和1之间,来减小模型误差[19 ] .传感器模型是一个非线性模型,同时辨识的未知参数有4个,模型的精度会受到影响,加一个规则化项f ,来提高模型的精度,规则化项f 为 ...
Improved particle swarm algorithm for particle release and dynamic change of velocity
1
2021
... 在建立目标函数时,由于在采集试验数据时可能会存在误差,所以在传感器实际输出值与模型输出值差的平方和前面乘上一个可变常数,取值范围在0和1之间,来减小模型误差[19 ] .传感器模型是一个非线性模型,同时辨识的未知参数有4个,模型的精度会受到影响,加一个规则化项f ,来提高模型的精度,规则化项f 为 ...
MSMA传感器的优化设计及试验特性研究
1
2021
... MSMA传感器的试验装置如图5 [20 ] 所示,由激振器、MSMA传感器和力传感器等设备组成.设定激振器的频率为180 Hz、激振力为0.24 N,磁场为0.35 T,从图6 可以看出感应峰峰值为128 mV.通过改变不同的输入,进行多组试验,将试验数据记录下来,为后面传感器数学模型的参数辨识提供数据集. ...
Optimal design and experimental characteristics of MSMA sensor
1
2021
... MSMA传感器的试验装置如图5 [20 ] 所示,由激振器、MSMA传感器和力传感器等设备组成.设定激振器的频率为180 Hz、激振力为0.24 N,磁场为0.35 T,从图6 可以看出感应峰峰值为128 mV.通过改变不同的输入,进行多组试验,将试验数据记录下来,为后面传感器数学模型的参数辨识提供数据集. ...