双边LCL无线供电系统恒流参数设计及特性研究*

doi:10.11985/2022.04.020

双边LCL无线供电系统恒流参数设计及特性研究^*

王玮^,¹, 鲍光婕², 孟涛², 谭林林^,²

1.东南大学国家级电工电子实验教学示范中心南京 211100

2.东南大学电气工程学院南京 210096

Constant Current Parameter Design and Characteristic Research of Bilateral LCL Wireless Power Transmission System

WANG Wei^,¹, BAO Guangjie², MENG Tao², TAN Linlin^,²

1. Electrical and Electronic Experiment Center, Southeast University, Nanjing 211100

2. School of Electric Engineering, Southeast University, Nanjing 210096

通讯作者: 王玮，女，1989年生，硕士，工程师。主要研究方向为电力电子技术、电工学。E-mail：827132943@qq.com

收稿日期: 2022-07-12 修回日期: 2022-10-20

基金资助:

*国家自然科学基金资助项目. 51877036

Received: 2022-07-12 Revised: 2022-10-20

作者简介 About authors

谭林林，男，1986年生，博士，副教授。主要研究方向为无线电能传输技术。E-mail：tanlinlin@seu.edu.cn

摘要

双边LCL补偿方式是无线电能传输系统的最常见的补偿方式，是当前该领域的研究热点。但随着运行条件的变化，系统参数、负载的变动，导致其恒流特性会发生改变，给实际的应用及控制带来了不少困难。从实际参数和影响特性等角度出发，对LCL补偿网络型系统恒流输出特性的影响因素进行了详细研究，建立了双边LCL补偿网络的实际电路参数模型，给出了系统恒流输出设计的负载参数约束条件，分析了损耗参数对系统的影响，提出了一种考虑元器件损耗参数的双边LCL补偿网络型无线供电系统设计方案。仿真与试验结果证明了该方案的有效性，系统输出电流波动率达到了预设的不高于10%的设计需求，同时对高次谐波具有良好的滤除效果，与理论设计一致。

关键词： 无线电能传输 ; LCL补偿网络 ; 恒流输出特性 ; 谐波

Abstract

Bilateral LCL compensation method is the most common compensation method for wireless power transmission systems, and is a research hotspot in this field. However, with the change of operating conditions, the constant current characteristics vary with the system parameters and loads, which brings many difficulties to practical application and control. From the perspective of actual parameters and influence characteristics, the influencing factors of the constant current output characteristics of the LCL compensation network system are studied in detail. The actual circuit parameter model of the bilateral LCL compensation network is established, and the load parameter constraints for the constant current output design of the system are given. The influence of loss parameters on the system is analyzed as well. Considering the loss parameters of components, a design scheme of bilateral LCL compensation network wireless power supply system is proposed. The simulation and experimental results prove the effectiveness of the scheme. The system output current fluctuation rate reaches the preset design requirement of no more than 10%, and has a good filtering effect on high-order harmonics, which is consistent with the theoretical design.

Keywords： Wireless power transmission system ; LCL compensation network ; constant current output characteristics ; harmonic

PDF (25569KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王玮, 鲍光婕, 孟涛, 谭林林. 双边LCL无线供电系统恒流参数设计及特性研究^*. 电气工程学报[J], 2022, 17(4): 203-210 doi:10.11985/2022.04.020

WANG Wei, BAO Guangjie, MENG Tao, TAN Linlin. Constant Current Parameter Design and Characteristic Research of Bilateral LCL Wireless Power Transmission System. Chinese Journal of Electrical Engineering[J], 2022, 17(4): 203-210 doi:10.11985/2022.04.020

1 引言

无线电能传输技术在电子产品、电动汽车、智能家居以及生物医疗等领域的应用越来越广泛^[1⇓⇓-4]。在无线供电系统中，往往会根据不同场合的应用需求，选取不同的补偿网络，以实现不同的输出特性。目前较为简单的补偿网络根据电感、电容元件的串并联形式可简单分为SS、SP、PS、PP四种，结构简单且易实现，但简单的补偿网络存在抗偏移能力较弱，易受耦合系数、谐振频率以及负载的影响，开关器件上的电压电流应力大^[5-6]等问题。因此，由电感、电容元件组成的复合谐振网络应用越来越多，常见的有LCL型、CLC型、LCC型以及LLC型^[7⇓⇓-10]。

LCL型补偿网络应用在无线电能传输系统发射端时，发射线圈中电流呈现恒流特性，同时当系统发射端和接收端均采用LCL网络且收发距离一定时，发射线圈的电流基本不受接收端负载影响，该特性对恒流有需求的场合具有重要的意义，极大地减少了对系统控制的要求。尤其在单发射、多负载的场合，可实现当有负载有效接入或退出，不影响对其他负载的有效供电^[11⇓-13]。

目前学者们已经对LCL补偿网络进行了大量的研究，如文献[14]研究了采用LCL谐振网络的系统存在软开关频率点的参数约束条件，并分析了系统变负载时的频率特性。文献[15]针对双边LCL电路设计了一种变补偿参数的WPT系统，通过投切接收端电感可实现系统由恒流输出向恒压输出的平滑转换。文献[16]分析了LCL谐振网络的恒流特性，并讨论了非谐振点品质因数的改变对恒流输出特性及谐振元器件上的电压电流应力的影响。文献[17]推导了双边LCL补偿网络中的双谐振点特性，提出了次谐振点概念，并对比分析了系统运行在固有谐振点和次谐振点时的逆变器输出特性以及系统输出功率和效率。文献[18]针对LCL补偿网络提出一种改进的参数调整方法，降低了线圈损耗和二极管损耗，高次谐波抑制能力更好，并解决了整流器二极管输入电流不连续的问题。文献[19]分析了LCL谐振补偿网络恒流输出和恒压输出的原理，并提出一种通过切入/切出电容使LCL谐振网络从恒流输出模式向恒压输出模式平滑过渡的方法。文献[20]对双边LCL在互感降低和副边短路的特殊工况下进行了性能分析，得出在特殊工况下，LCL拓扑的鲁棒性较好。

通过调研不难发现，LCL补偿网络在简化电路模型(不考虑内阻参数、参数漂移等)中恒流输出特性具有稳定性，但在实际运行过程中负载电流并不是恒定值，随着负载电阻值的升高，其负载电流会出现随之下降的现象，也就是说，该网络的恒流特性与负载大小存在很大关系。因此，本文从实际运行参数着手，对双边LCL模型进行建模研究，旨在探索影响输出恒流特性稳定性的影响因素，寻求不借助控制手段，达到一定的恒流输出的目的，降低系统设计的成本，提高系统设计的效率，为对电池恒流充电、LED驱动等需要恒流充电系统的设计提供理论指导。

此外，由于发射端的输入电压由逆变器产生，多为方波输出，会造成谐振网络中存在多次谐波的情况，本文还研究了高次谐波对双边LCL输出特性的影响，验证了系统具备较强的低通滤波性。

2 双边LCL补偿网络系统建模与分析

2.1 损耗因素与模型

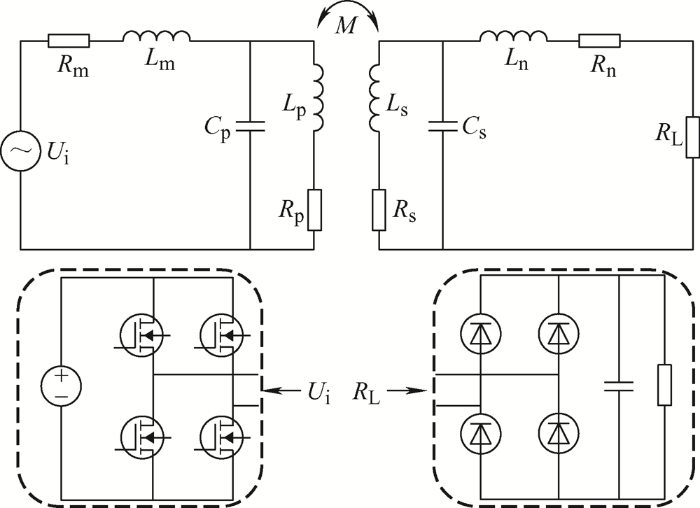
由于电感、电容元器件均非理想元器件，因此在双边LCL结构中，对系统参数影响最大的因素为损耗参数。由于理想元器件下的系统特性已被广泛研究，所以本文主要考虑元器件损耗参数，损耗参数以内阻的形式进行等效，试验中发现影响最大的损耗参数主要为电感和电源等带来的，因此，考虑损耗参数后，双边LCL补偿的无线供电系统等效电路如图1所示。图1中，U_i为逆变电路输出的高频交流电压，L_m、C_p、L_p构成发射端的LCL网络，R_m为电感L_m的等效损耗，L_p是发射线圈的电感，R_p为发射线圈的等效损耗。L_s、C_s、L_n构成接收端的LCL网络，R_n为电感L_n的内阻，L_s是接收线圈的电感，R_s为接收线圈的内阻。R_L为包含整流电路和实际负载的等效折算负载。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 双边LCL补偿网络无线电能传输系统示意图

2.2 双边LCL补偿网络的建模与分析

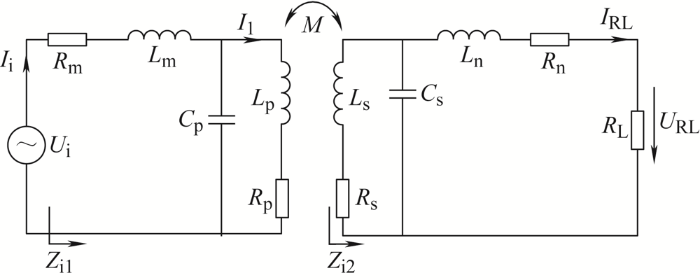
如图2所示，I_i为电源的输入电流，I₁为流过发射线圈L_p的电流，I_RL为流过负载R_L的电流，Z_i1为发射端的等效输入阻抗，Z_i2为接收端的等效输入阻抗。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 双边LCL补偿网络的等效电路

由文献[17]可知，双边LCL除固有谐振点之外，还存在一个与负载参数无关的次谐振点，次谐振点频率大于固有谐振点频率，且该频率点具有更高的输出功率。但在正常负载条件下，系统在固有谐振点处的效率要远大于次谐振点的效率，因此本文对次谐振点情况不做考虑，只分析固有谐振点下双边LCL的工作原理。

当双边LCL电路工作在谐振点时，系统谐振角频率满足$\omega ={{\omega }_{0}}={1}/{\sqrt{{{L}_{\text{m}}}{{C}_{\text{p}}}}}\;={1}/{\sqrt{{{L}_{\text{s}}}{{C}_{\text{s}}}}}\;$，且有L_m=L_p，L_s=L_n，因此不难得到

(1)${{X}_{\text{p}}}=\omega {{L}_{\text{m}}}=\omega {{L}_{\text{p}}}=\frac{1}{\omega {{C}_{\text{p}}}}$

(2)${{X}_{\text{s}}}=\omega {{L}_{\text{s}}}=\omega {{L}_{\text{n}}}=\frac{1}{\omega {{C}_{\text{s}}}}$

式中，X_p表示发射线圈感抗，X_s表示接收端线圈感抗，两者分别由收发线圈的自感参数和谐振频率决定，在给定收发线圈后，相互独立。

由图2可以得出接收端折算到发射端的折算阻抗Z_r表达式为

(3)${{Z}_{\text{r}}}=\frac{{{\omega }^{2}}{{M}^{2}}}{{{Z}_{\text{i2}}}}$

式中，${{Z}_{\text{i2}}}={{R}_{\text{s}}}+\frac{{{L}_{\text{s}}}}{\left( {{R}_{\text{n}}}+{{R}_{\text{L}}} \right){{C}_{\text{s}}}}$，系统的输入阻抗Z_i1为

(4)${{Z}_{\text{i1}}}={{R}_{\text{m}}}+\frac{{{L}_{\text{m}}}}{{{C}_{\text{p}}}({{R}_{\text{p}}}+{{Z}_{r}})}$

进一步地，流过发射线圈L_p的电流为

(5)${{\overset{\bullet }{\mathop{I}}\,}_{1}}=\frac{{{\overset{\bullet }{\mathop{U}}\,}_{\text{i}}}}{\text{j}\omega \left[ {{R}_{\text{m}}}{{C}_{\text{p}}}\left( {{R}_{\text{p}}}+{{Z}_{\text{r}}} \right)+{{L}_{\text{m}}} \right]}$

负载R_L上的负载电流为

(6)${{\overset{\bullet }{\mathop{I}}\,}_{\text{RL}}}=\frac{{{\overset{\bullet }{\mathop{U}}\,}_{\text{i2}}}}{\text{j}\omega \left[ {{R}_{\text{s}}}{{C}_{\text{s}}}\left( {{R}_{\text{n}}}+{{R}_{\text{L}}} \right)+{{L}_{\text{s}}} \right]}=\delta \cdot \frac{M{{\overset{\bullet }{\mathop{U}}\,}_{i}}}{\text{j}\omega {{L}_{\text{m}}}{{L}_{\text{s}}}}$

在式(6)中，引入损耗系数δ，其中δ为

(7)$\delta =\frac{{{L}_{\text{m}}}{{L}_{\text{s}}}}{\left[ {{R}_{\text{m}}}{{C}_{\text{p}}}({{R}_{\text{p}}}+{{Z}_{\text{r}}})+{{L}_{\text{m}}} \right]\left[ {{R}_{\text{s}}}{{C}_{\text{s}}}({{R}_{\text{n}}}+{{R}_{\text{L}}})+{{L}_{\text{s}}} \right]}$

不难发现，当忽略系统中电感的内阻时，即R_m=R_s=R_p=R_n=0时，$\delta =1$，负载R_L上的负载电流表达式为

(8)${{\overset{\bullet }{\mathop{I}}\,}_{\text{RL}}}=\frac{M{{\overset{\bullet }{\mathop{U}}\,}_{i}}}{\text{j}\omega {{L}_{\text{m}}}{{L}_{\text{s}}}}$

此时，负载电流I_RL与负载大小无关，在其电源输出电压、收发线圈互感、自感不变的情况下，系统能够实现理论上的恒流输出。

实际的R_m、R_s、R_p、R_n等参数不可能为零，即使在特定的工况下，该四个参数不发生改变，那么δ值依然与负载有关，因此，在考虑电感电容的感值和容值不发生偏移的情况下，实际上的负载电流是受补偿电感内阻、收发线圈的内阻、负载等因素影响，对外表现的恒流特性与理论值有很大的偏差。

在系统设计时，通常会要求系统输出满足一定的恒流特性，因此存在

(9)$\xi \le \delta \le 1$

式中，ξ为允许输出电流的下限系数，即在输出电流的有效波动范围内，存在电阻的合理区间为

(10)${{R}_{\text{L}}}\le \frac{\left( 1-\xi \right){{L}_{\text{m}}}{{L}_{\text{s}}}-\xi {{R}_{\text{m}}}{{C}_{\text{p}}}{{L}_{\text{s}}}\left( {{R}_{\text{p}}}+{{Z}_{\text{r}}} \right)}{\xi \left[ {{R}_{\text{m}}}{{C}_{\text{p}}}\left( {{R}_{\text{p}}}+{{Z}_{\text{r}}} \right)+{{L}_{\text{m}}} \right]{{R}_{\text{s}}}{{C}_{\text{s}}}}-{{R}_{\text{n}}}$

3 双边LCL补偿网络的系统特性分析

3.1 损耗参数对系统的影响分析

由第2节分析可知，影响双边LCL系统恒流输出的因素主要包括补偿电感L_m和L_n的内阻R_m和R_n、收发线圈L_p和L_s的内阻R_p和R_s、负载R_L等因素。为了更好地研究不同因素的作用效果，下面对常用的收发线圈对称设计的系统进行分析，收发线圈的绕制方式和线径一致，即L_p=L_s，R_p=R_s=R，则存在L_m=L_n，R_m=R_n。引入损耗增益比k，使得

(11)$k=\frac{R\text{m}}{R\text{p}}=\frac{R\text{n}}{R\text{s}}$

则

(12)$\delta =\frac{{{L}_{\text{m}}}{{L}_{\text{s}}}}{\left[ kR{{C}_{\text{p}}}\left( {{R}^{2}}+{{\omega }^{2}}{{M}^{2}} \right)+{{L}_{\text{m}}}R \right]{{C}_{\text{s}}}\left( kR+{{R}_{\text{L}}} \right)+k{{R}^{2}}{{C}_{\text{p}}}{{L}_{\text{s}}}+{{L}_{\text{m}}}{{L}_{\text{s}}}}$

因此，k值不同对δ的影响亦不同，由式(12)不难发现，在线圈内阻固定的情况下，k和R越小，δ值越大，对输出电流的影响越大，但通过观察公式发现，R的幂次比k高，且R因子的关联项也更多，所以R值的变化对δ值的影响更大，即相对于补偿电感的内阻，发射线圈与接收线圈的内阻对电流的恒流特性影响较大，因此在设计过程中应尽量避免发射线圈和接收线圈产生过高的损耗，同时发射线圈和接收线圈过高的内部损耗，也会造成系统效率的降低。

3.2 双边LCL补偿网络的谐波特性分析

以上模型给出了系统恒流设计的约束条件，在实际应用中，该设计思路可满足对恒流输出有一定要求的系统需求。实际上，发射端的输入电压源是由逆变电路产生的方波，经傅里叶级数分解成基波与各奇次谐波的代数和，而前文的理论推导都是以基波作为输入电压进行计算，并未考虑高次谐波的情况，以实际电压波形为例，输入电压u_i的表达式如式(13)所示，其中U₁为基波电压幅值，ω为系统工作的谐振角频率。

(13)${{u}_{\text{i}}}={{U}_{1}}\left( \sin \omega t+\frac{1}{3}\sin 3\omega t+\frac{1}{5}\sin 5\omega t+\cdots \right)$

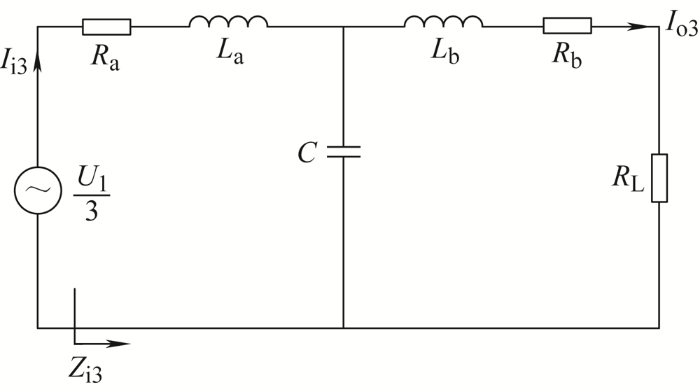
本文以三次谐波为例研究高次谐波对输出电流的影响。图3以单边LCL网络为例，分析基波电压和三次谐波电压在同一回路中的特性参数。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 输入电压为三次谐波时的单边LCL网络

由于LCL电路处于谐振状态满足$\omega _{0}^{2}$CL_a=1，并且L_b=L_a，当电源为三次谐波电压时，输入阻抗Z_i₃表达式为

(14)$\begin{matrix} {{Z}_{\text{i3}}}={{R}_{\text{a}}}+\frac{{{R}_{\text{b}}}+{{R}_{\text{L}}}}{64+9\omega _{0}^{2}{{C}^{2}}{{\left( {{R}_{\text{b}}}+{{R}_{\text{L}}} \right)}^{2}}}\text{+j3}{{\omega }_{0}}{{L}_{\text{a}}}- \\ \text{j}\frac{\text{24}\omega {{L}_{\text{a}}}+\text{3}{{\omega }_{0}}C{{\left( {{R}_{\text{b}}}+{{R}_{\text{L}}} \right)}^{2}}}{64+9\omega _{0}^{2}{{C}^{2}}{{\left( {{R}_{\text{b}}}+{{R}_{\text{L}}} \right)}^{2}}} \\ \end{matrix}$

系统中R_L取值一般远大于线圈内阻，此处忽略R_a、R_b，对式(14)进行简化如式(15)所示

(15)${{Z}_{\text{i3}}}=\frac{{{R}_{\text{L}}}}{64+9\omega _{0}^{2}{{C}^{2}}{{R}_{\text{L}}}^{2}}\text{+j}\frac{168{{\omega }_{0}}{{L}_{\text{a}}}+\text{24}{{\omega }_{0}}C{{R}_{\text{L}}}^{2}}{64+9\omega _{0}^{2}{{C}^{2}}{{R}_{\text{L}}}^{2}}$

流过负载的谐波电流I_o3为

(16)${{I}_{\text{o3}}}=\frac{{{U}_{\text{1}}}}{\left| 3{{Z}_{\text{i3}}}\left( -8+\text{j}3{{\omega }_{0}}C{{R}_{\text{L}}} \right) \right|}$

当电源为基波电压时，负载基波电流I_o1为

(17)${{I}_{\text{o}}}_{1}=\frac{{{U}_{1}}}{{{\omega }_{0}}{{L}_{\text{a}}}}$

引入负载系数

(18)$\beta ={{\omega }_{0}}C{{R}_{\text{L}}}=\frac{{{R}_{\text{L}}}}{{{\omega }_{0}}{{L}_{\text{a}}}}$

将基波电流I_o1与三次谐波电流I_o3的比值记为λ，则

(19)$\lambda =\frac{\left| {{I}_{\text{o1}}} \right|}{\left| {{I}_{\text{o3}}} \right|}=\frac{3\cdot \sqrt{{{\left( 512\beta +72{{\beta }^{3}} \right)}^{2}}+{{\left( 189{{\beta }^{2}}+1\ \ 344 \right)}^{2}}}}{64+9{{\beta }^{2}}}$

根据式(19)可知，λ与β、R_L成正相关。当R_L→0时，λ=63，系统对三次谐波具有高效的滤除作用，同理三次以上谐波的滤除效果更佳，LCL系统具备较强的低通滤波性。由文献[17]可知在小负载段，虽然负载侧电流的三次谐波含量较少，但逆变器输出的电流谐波较高，因此系统一般不易设计在小负载段运行。

4 仿真与试验研究

为了验证以上分析的正确性，本节搭建双边LCL无线充电系统仿真模型具体参数如表1所示。

表1 系统元件参数

参数	数值
基波输入电压U_i/V	80
系统工作频率f/kHz	85
发射线圈自感L_p/μH	33.61
接收线圈自感L_s/μH	33.62
发射端补偿电感L_m/μH	33.60
接收端补偿电感L_n/μH	33.62
发射端补偿电容C_p/nF	104.34
接收端补偿电容C_s/nF	104.34
互感M/μH	4.55

新窗口打开| 下载CSV

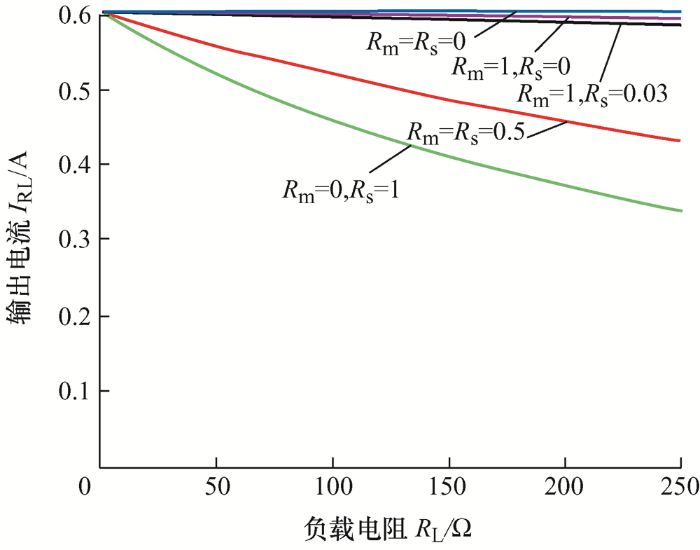
系统的输入电压为80 V有效值的方波电压，谐振频率为85 kHz，设负载电阻R_L的可变化范围为0~250 Ω，因为收发线圈的匝数和绕制方法相同，则R_p=R_s，由于对称性补偿电感也存在R_m=R_n，在仿真模型中，当R_m与R_s取值不同时，得到如图4所示的不同内阻下的输出电流曲线。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 不同寄生参数下输出电流I_RL随负载电阻R_L波动曲线

从图4中不难发现，在R_m=R_s=0 Ω时，输出电流始终处于恒定状态，与负载的变化无关，和电流值理论值0.6 A相同。随着补偿电感内阻的增加，电流开始随负载的增长呈下降趋势。同时在极端情况下，R_m=1 Ω，R_s=0 Ω时，即k趋于无穷大时，在R_L=250 Ω处输出电流下降了1.56%；而R_m=0 Ω，R_s=1 Ω，即k=0时，在R_L=250 Ω处输出电流下降了43.75%，仿真表明损耗增益比k对系统的影响较大，在相同负载下，收发线圈的损耗参数是输出电流波动下降的主要影响因素，与理论分析一致。

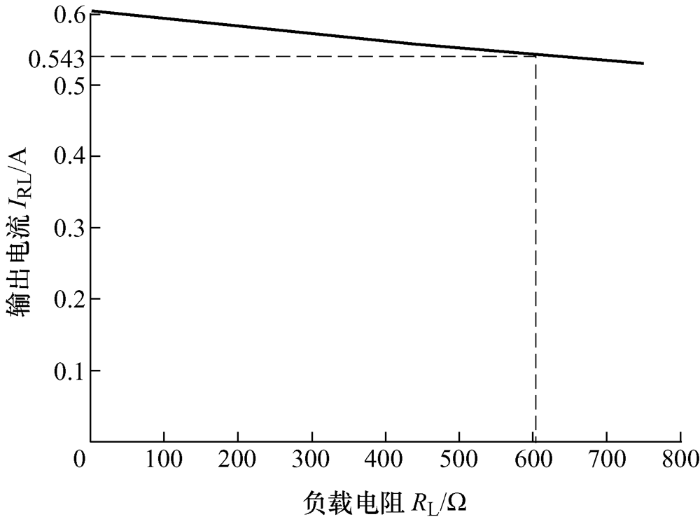
在实际情况中，用于传输能量的收发线圈通常由线径更大，电阻率更低的高频利兹线绕制，而为了减小体积，补偿电感通常为体积更小的磁心骨架绕制而成，故常有R_m>R_p，R_n>R_s。设R_m=R_n=0.5 Ω，R_p=R_s=0.05 Ω，其他参数不变，要求电流的波动率不低于10%，根据理论计算可得到，电阻R_L在I_RL波动10%以内的区间值为0~606 Ω。通过仿真得到上述设置参数下的输出电流曲线如图5所示，通过图5可知，在R_L=606 Ω处I_RL为0.543 A，电流下降至89.5%，与理论设定值90%，仅有0.5%的误差，验证了理论分析的准确性。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 输出电流随负载变化曲线

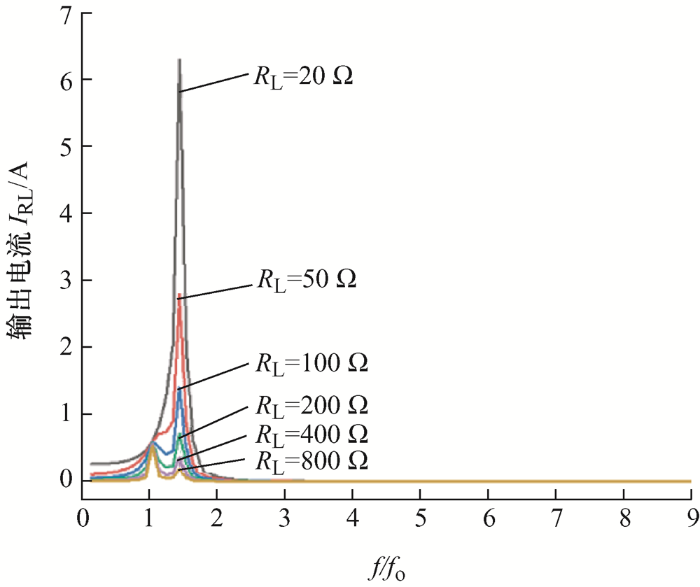
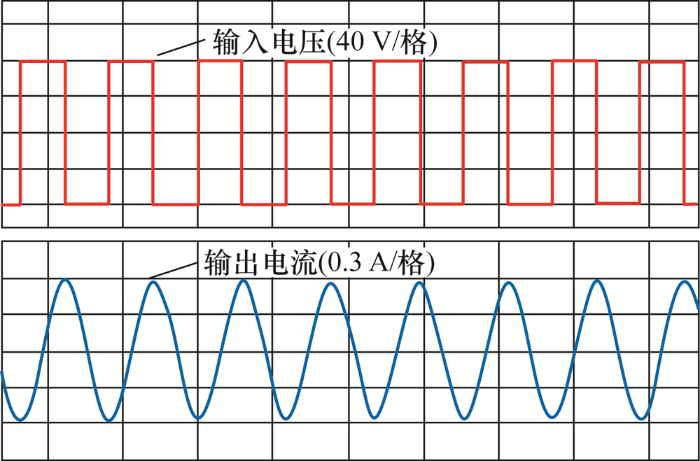
同时，给定系统的输入为方波输入，改变负载电阻的变化范围，系统输出电流的幅频特性曲线如图6所示，系统的输入电压和负载上的电流曲线如图7所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 输出电流I_RL幅频特性曲线

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 系统输入电压与输出电流波形

由图6、图7可以看出，I_RL在固有谐振频率点(f/f₀=1)处电流恒定，为理论值0.6 A。系统存在固有谐振点和次谐振点两个谐振点，当系统工作在次谐振点时虽然可以获得更大的输出功率，但输出电流无法恒定，因此为实现恒流输出，系统需要工作在固有谐振点处。输出电流呈现较好的正弦特性这与前文的理论分析一致，说明系统对高次谐波具有良好的滤波效果。

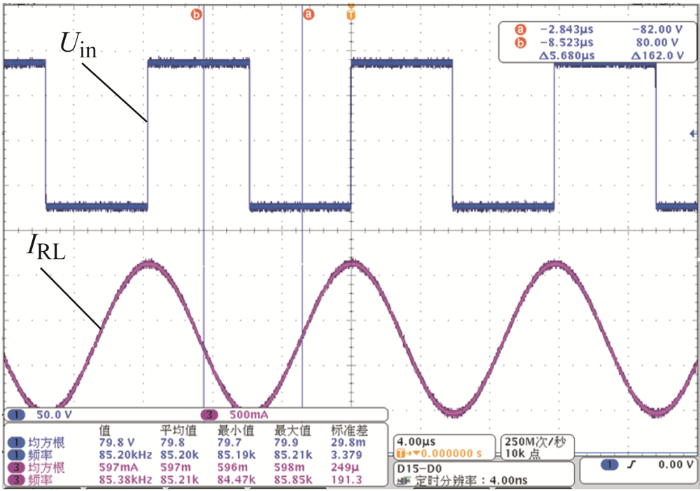
为进一步从试验上验证本文的设计思路，搭建的试验平台如图8所示。负载端采用电子负载等效R_L。图9给出了系统工作在谐振条件下，逆变电源的输出电压U_in和负载电流I_RL的波形。系统工作频率为80.2 kHz，输入电压波形为标准方波，其幅值为79.2 V，输出电流波形为完整的正弦波，其相位与输入电压相位相差90°，系统达到了设计的谐振状态。从输出负载电流波形不难看出，系统已经有效滤除了三次及以上的谐波，与理论分析一致。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 系统试验平台

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 输入电压与输出电流波形(R_L=20 Ω)

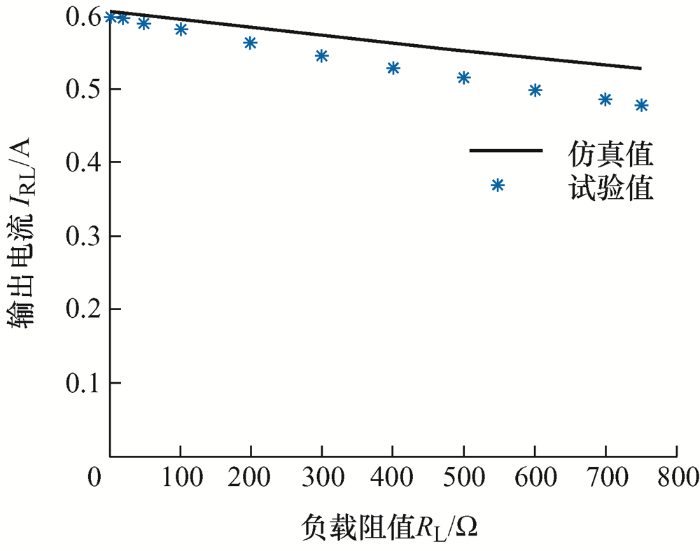
同时，改变电子负载阻值，使得接入系统的等效负载范围为0~750 Ω，读取系统输出电流I_RL的有效值，结果如图10所示。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 I_RL随负载阻值变化曲线

由图10可知，当R_L=20 Ω时，输出电流I_RL=0.597 A，与理论值(0.603 7 A)相差1.1%，当R_L=600 Ω，I_RL=0.498 A与理论值(0.542 A)相差8.1%，基本与理论设计吻合，而试验与理论值相差的主要原因在于高频电流存在集肤效应，导致线圈的实际内阻高出理论值，I_RL的试验值会低于理论值，且随着负载阻值增加，差距更加明显。

综上所述，由于补偿网络和收发线圈的损耗存在，使得双边LCL系统在变负载范围内，不再体现出较好的恒流性，因此在不同需求背景下，应需要综合考虑各参数的合理配置。

5 结论

本文在已有的双边LCL补偿网络型无线供电系统设计中，针对恒流输出受负载变化的影响，探究了影响其恒流特性的影响因素，给出了双边LCL系统设计时的恒流约束条件，提出了一种兼顾元器件参数的系统设计思路，结论如下所述。

(1) 双边LCL补偿拓扑在谐振条件下可以实现恒流输出的前提是尽可能减小收发线圈和补偿电感的损耗内阻，即采用高频特性好、电导率高的材料制作电感，同时收发线圈的损耗等效阻抗对恒流特性的影响较补偿电感大，在实际中应尽量提高收发线圈的品质因数，不仅可以提升输出端恒流特性的能力，还可以获得更高的转换效率。

(2) 负载输出电流在不同工作频率下存在多极值点问题，但仅在固有谐振频率下具有恒流特性，系统应避免在固有谐振点外的其他谐振点运行。

(3) 在输出电流的有效波动范围内，存在负载电阻的合理区间使得双边LCL系统工作在恒流模式。在逆变器输出方波的激励下，系统对三次及以上的谐波具有高效的滤除效果。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

张剑韬, 朱春波, 陈清泉.

应用于无尾家电的非接触式无线能量传输技术

[J]. 电工技术学报, 2014, 29(9):33-37.