1 引言
随着社会的快速发展和科学技术的进步,能源和环境挑战已成为近几十年来全球的热门话题。人们一直在积极寻找石油资源的替代品,尤其是锂电池[1 ⇓ -3 ] 。锂离子电池作为一种储能元件,由于其高能量密度和较长的循环寿命,已经被广泛应用于生产和日常生活中[4 ⇓ -6 ] 。锂离子电池管理系统最重要的组成部分是准确估计锂电池的健康状态。电池健康状态(State of health, SOH)的估计越精确,锂离子电池的安全可靠运行就越有保障,因此对锂离子电池进行准确的状态估计对于实际应用至关重要[7 ] 。锂离子电池的SOH定义按照不同的电池参数有不同的定义方法[8 -9 ] ,本文使用的健康特征参数包括电池容量和能量,计算公式如下所示
(1) $\mathrm{SO}{{\mathrm{H}}_{\mathrm{capacity}}}=\frac{{{C}_{\text{cur}}}}{{{C}_{\text{nom}}}}\times 100%$
(2) $SO{{H}_{\mathrm{energy}}}=\frac{{{E}_{\text{cur}}}}{{{E}_{\text{nom}}}}\times 100%$
式中,${{C}_{\text{cur}}}$和${{C}_{\text{nom}}}$分别是电池的当前容量和标称容量,${{E}_{\text{cur}}}$和${{E}_{\text{nom}}}$分别是电池的当前能量和标称能量[10 ] ,锂离子电池容量C 和能量E 计算公式如下所示
(3) $C=\int_{{{t}_{0}}}^{{{t}_{1}}}{I\left( t \right)}\mathrm{d}t$
(4) $E=\int_{{{t}_{0}}}^{{{t}_{1}}}{V\left( t \right)I\left( t \right)}\mathrm{d}t$
式中,${{t}_{0}}$和${{t}_{1}}$是电池放电的开始和结束时刻,$V\left( t \right)$是随时间变化的电池端电压,$I\left( t \right)$是放电电流。
目前绝大多数SOH估计算法仅针对电池放电容量序列进行跟踪,在动态工况、宽温度范围内的适用性较差,且无法提供更为全面的电池性能衰退程度评估结果。SOH估计方法包括基于模型的方法、数据驱动方法、混合方法[11 ] 。基于等效电路模型的方法运用广泛,FANG等[12 ] 提出了一种基于自回归等效电路模型的电池健康状态估计方法,可实现SOH的在线估计,但此等效电路模型缺乏物理和化学意义,在实际电动汽车运行环境下预测效果较差。数据驱动方法的一个主要问题是对电池退化的建模是基于恒定放电速率和恒定环境温度下采集的数据[13 ] ,在实践中,电池是在吸收了许多不确定性的变化的运行条件下运行的,这些不确定性将使这些模型表现不佳[14 ] 。混合方法往往有更高的精度,对不同工况的SOH估计的适应性也较好[15 ] ,XU等[16 ] 采用等效电路模型描述电池动力学,递归最小二乘在线识别模型参数,无气味卡尔曼滤波器估计电池状态,提出了一个极简的电化学模型来描述电池内部锂含量的分布,并将SOH与锂的不可逆损耗导致的容量衰减联系起来,SOH估计平均误差在2%左右。电化学模型充分考虑了电池中实际的电化学反应过程,包括固相扩散过程、液相扩散和迁移过程等,但经典的伪二维(Pseudo two-dimensional,P2D)
模型往往比较复杂,计算成本较高,可以对P2D模型进行简化,结合数据驱动的智能算法,根据不同工况和环境确定电化学模型的中的参数,对电池SOH进行准确的在线评估。
本文以简化电化学模型为基础,融合灰色预测算法(Metabolism grey algorithm,MGA),以容量和能量为电池健康表征参数进行电池健康状态评估研究,分别采用两种方法进行SOH估计:一是直接利用MGA对电池容量和能量进行预测;二是先采用MGA对简化电化学-老化模型(Simplified electrochemical model,SEM)参数进行预测,将预测后的参数值代入到模型当中,拟合电池端电压曲线,再通过式(3)、(4)求出电池的预测容量和能量。针对两种健康表征参数衰退速度、估计精度等问题,对容量和能量SOH估计结果各取加权系数,提出基于数据-模型混合驱动的锂离子电池健康状态的综合评估方法,实现电池健康状态的准确估计。
本文创新点如下所述:参考弱极化过程的Tafel方程,建立起副反应极化过电势关于充放电电流的定量描述关系式,建立了简化电化学-老化模型,结合简化电化学-老化模型和灰色预测算法,提出基于数据-模型驱动的锂离子SOH估计方法。通过加速老化试验得到不同工况下基于数据-模型驱动的SOH的估计结果平均误差均小于3%,实现锂离子电池SOH的准确估计。
2 简化电化学-老化模型及老化试验
2.1 简化电化学模型
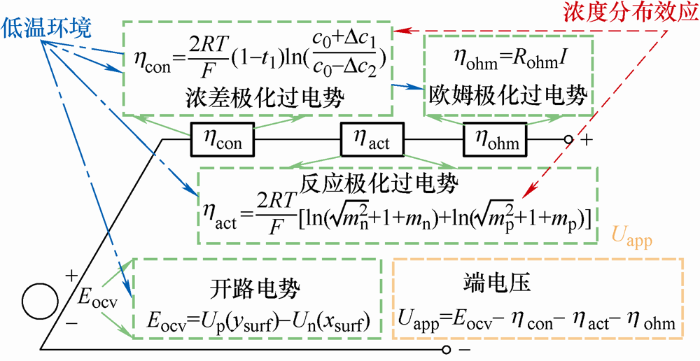
简化电化学模型是由单粒子模型改进而来。单粒子模型仅考虑电池内活性锂离子在电池固相材料上扩散过程,缺少了对活性锂离子在电解液中扩散过程及电势影响的描述,因而导致仿真精度较低。简化电化学模型考虑了活性锂离子液相扩散的影响,并将一系列用于描述电池内部扩散过程的偏微分方程简化为代数方程,提高了模型的计算效率和仿真精度。简化电化学模型基本框架如图1 所示[17 -18 ] 。
图1
表1 给出了简化电化学模型的基本描述。模型中使用参数以及变量分别列于表2 和表3 当中。
简化电化学模型聚焦于电池端电压的实时响应,而电池端电压受到活性锂离子在固-液相中扩散作用影响,因此模型对电池内部的扩散过程以及受其影响的电势分布也进行了描述。
其中,正负电极表面锂离子浓度分数y surf 、x surf 定义式为
(5) ${{y}_{\mathrm{surf}}}=\frac{{{c}_{\mathrm{surf},\mathrm{p}}}}{{{c}_{\max,\mathrm{p}}}}$
(6) ${{x}_{\mathrm{surf}}}=\frac{{{c}_{\mathrm{surf},\mathrm{n}}}}{{{c}_{\max,\mathrm{n}}}}$
电池在满充状态时的正负极嵌锂率,称之为正负极初始嵌锂率y 0 、x 0 。充放电期间,嵌锂率的变化范围称之为嵌锂率的动态变化范围D y 、D x ,其与正负极容量之间的关系有
(7) ${{D}_{\text{y}}}=\frac{{{Q}_{\text{all}}}}{{{Q}_{\text{p}}}}$
(8) ${{D}_{\text{x}}}=\frac{{{Q}_{\text{all}}}}{{{Q}_{\text{n}}}}$
(9) $\begin{matrix} E={{U}_{\text{p}}}({{y}_{\text{surf}}})-{{U}_{\text{n}}}({{x}_{\text{surf}}})= \\ {{U}_{\text{p}}}\left( {{y}_{0}}+\frac{\int_{0}^{t}{I\left( t \right)}\text{d}t}{{{Q}_{\text{p}}}} \right)-{{U}_{\text{n}}}\left( {{x}_{0}}-\frac{\int_{0}^{t}{I\left( t \right)}\text{d}t}{{{Q}_{\text{n}}}} \right) \\ \end{matrix}$
理想电动势是电池内部扩散效应与极化现象都为零时的电池端电压。当流经电极的电流不为零时,电池内部就会产生极化效应,端电压也会发生改变。
(10) $\begin{matrix} {{U}_{\mathrm{OCV}}}\left( t \right)={{U}_{\mathrm{p}}}\left( {{y}_{\text{surf}}} \right)-{{U}_{n}}\left( {{x}_{\text{surf}}} \right)-{{\eta }_{\text{con}}}\left( t \right)- \\ {{\eta }_{\text{act}}}\left( t \right)-{{\eta }_{\text{ohm}}}\left( t \right) \\ \end{matrix}$
2.2 简化电化学-老化模型搭建
电池是一个复杂的化学系统,在电池使用的过程中,除了主要的化学反应之外,也会出现一些副反应,像SEI膜增厚、活性材料损失等,这些副反应会导致副反应极化过电势的产生,从而导致电池性能的衰退。参考弱极化过程的Tafel方程建立副反应极化过电势关于充放电电流的数值计算关系,如下所示
(11) ${{\eta }_{\mathrm{s}}}(t)=\frac{2RT}{F}\ln (\beta I(t))$
式中,${{\eta }_{\mathrm{s}}}$为副反应极化过电势,R 为气体常量,T 为温度,F 为法拉第常数,$\beta $为副反应极化系数,$I(t)$为充放电电流。
(12) $\begin{matrix} {{U}_{\mathrm{OCV}}}\left( t \right)={{U}_{\mathrm{p}}}\left( {{y}_{\text{surf}}} \right)-{{U}_{\mathrm{n}}}\left( {{x}_{\text{surf}}} \right)-{{\eta }_{\text{con}}}\left( t \right)- \\ {{\eta }_{\text{act}}}\left( t \right)-{{\eta }_{\text{ohm}}}\left( t \right)-{{\eta }_{\mathrm{s}}}(t) \\ \end{matrix}$
2.3 试验设计与模型验证
为了获取第2.1节中SEM的相关参数以及验证模型精度,本节设计了不同工况下的电池加速老化对比试验。这也为后续进行电池健康状态估计研究以及电池剩余使用寿命预测研究提供了数据基础。
2.3.1 老化试验设计
本文的电池老化试验使用了由德力普电池科技有限公司制造的26650型锂离子电池,其标称容量为5 A·h,负极材料为石墨,正极材料为LiNi1/3 Co1/3 Mn1/3 O2 。电池的充放电截止电压分别为4.2 V和2.5 V。
电池加速老化试验使用了深圳新威尔电子有限公司的BTS-5V-20A电池充放电测试仪,在室温条件下对电池进行循环老化试验,试验仪器如图2 所示。
图2
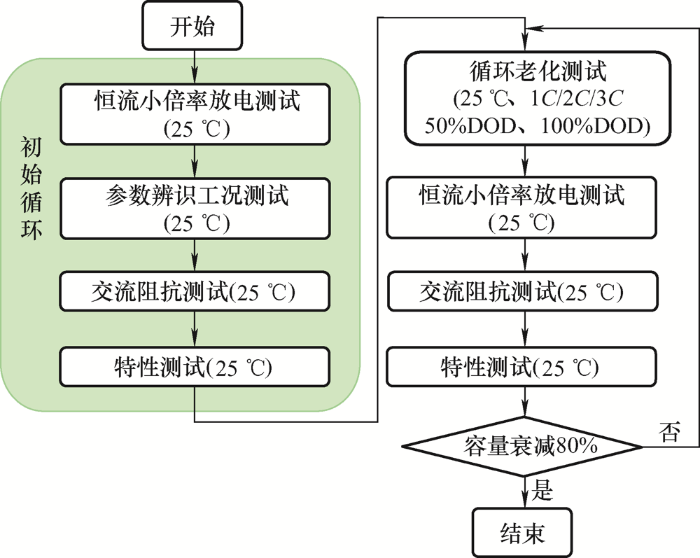
试验主要分为五个工步,分别为小倍率放电工步、参数辨识工步、特性测试工步、阻抗测试工步以及老化循环工步,电池老化试验流程图3 所示。
图3
在每个老化循环中,使用0.5C 倍率恒流充电至电池充电截止电压4.2 V,然后恒压充电至电流降为0.05C 以下。充电过程结束后静置5 min,电池以1C 、2C 恒流放电至电池放电截止电压2.5 V,再静置5 min后,进入下一个循环,每个老化循环工步重复上述过程20次。当电池容量衰退到80%时可认为电池寿命结束[19 ] ,结束电池老化试验。
试验设置了三组不同工况的电池试验,每组电池有两节电池,试验中各个电池的具体老化工况如表4 所示。
2.3.2 简化电化学-老化模型验证
(1) 简化电化学-老化模型开路电压获取。首先要获取模型的开路电压曲线。电流不为零的情况下,电池内部就会产生极化过电势,导致所测电池端电压的试验获得的电压值小于实际电池开路电压。因此为了尽可能地减小极化过电势的影响,在试验中通常采取非常小电流的放电,以使电池端电压的测量值尽量接近电池开路电势。通常,获取电池开路电势时的放电电流要小于1/20C ,此时电池极化过电势很小,可以忽略不计,为了进步一提高模型精度,本试验中采取0.02C 小电流方式,得到了德力普电池的开路电势曲线。通过拟合开路电势曲线,进而得到基本过程中的相关参数。具体步骤如下。
步骤2:设定基本参数x 0 、y 0 、D x 、D y ;并根据式(13)和式(14)求得x surf 、y surf
(13) ${{x}_{\text{surf}}}={{x}_{0}}+{{D}_{\text{x}}}(1-\mathrm{SOC})$
${{E}_{\text{fitted}}}={{U}_{\text{p}}}_{,\text{fitted}}-{{U}_{\text{n}}}$
(14) ${{y}_{\text{surf}}}={{y}_{0}}+{{D}_{\text{y}}}(1-\mathrm{SOC})$
(15) ${{U}_{\text{n}}}=F\left( {{x}_{\text{surf}}} \right)$
(16) ${{U}_{\text{p}}}={{U}_{\text{n}}}+E$
步骤4:利用最小二乘的法拟合正极电势曲线,获得U p ,fitted ;并重构开路电势曲线E fitted 。
(17) ${{E}_{\text{fitted}}}={{U}_{\text{p}}}_{,\text{fitted}}-{{U}_{\text{n}}}$
校正后的德力普锂离子电池正负电极电势函数表达式分别为
(18) $\begin{matrix} {{U}_{p}}({{y}_{\mathrm{surf}}})=1.517\ 1+3\ 072\ 557.523\ 0\times \mathrm{tan}h[({{y}_{\mathrm{surf}}}-0.4)/9\ 781\ 604.41]- \\ 0.114\times \mathrm{tan}h[({{y}_{\mathrm{surf}}}-0.54)/0.14]-2.001\ 5\times \mathrm{tan}h[({{y}_{\mathrm{surf}}}-0.781\ 4)/1.18]+ \\ 1.433\times \mathrm{tan}h[({{y}_{\mathrm{surf}}}-0.44)/1.03]+1.429\ 9\times \mathrm{tan}h[({{y}_{\mathrm{surf}}}-0.643\ 4h)/0.32]- \\ 1.712\times \mathrm{tan}h[({{y}_{\mathrm{surf}}}-0.92)/1.10]-0.630\ 0\times \mathrm{exp}[134.8\times ({{y}_{\mathrm{surf}}}-0.99)]- \\ 0.723\times \mathrm{tan}h[({{y}_{\mathrm{surf}}}-0.83)/2.61]-0.676\ 9\times \mathrm{tan}h[({{y}_{\mathrm{surf}}}-0.954)/2.46]+ \\ 1.505\ 6\times \mathrm{exp}\{-{{[({{y}_{\mathrm{surf}}}-0.992\ 7)/58\ 683.77]}^{2}}\}+0.305\times \{-3.04\times \mathrm{tan}h[({{y}_{\mathrm{surf}}}-0.7)/0.35]-0.55\} \\ \end{matrix}$
(19) $\begin{matrix} {{U}_{n}}({{x}_{\mathrm{surf}}})=0.119\ 444-0.051\ 26\times \mathrm{tan}h[({{x}_{\mathrm{surf}}}-0.983\ 2)/0.029\ 08]- \\ 0.001\ 3\times \mathrm{tan}h[({{x}_{\mathrm{surf}}}-0.755)/0.05]-0.018\ 4\times \mathrm{tan}h[({{x}_{\mathrm{surf}}}-0.5)/0.041]- \\ 0.066\times \mathrm{tan}h[({{x}_{\mathrm{surf}}}-0.135)/0.069]+0.013\times \mathrm{tan}h[({{x}_{\mathrm{surf}}}-0.093)/0.02]+ \\ 1.061\times \mathrm{exp}(-70.23\times {{x}_{\mathrm{surf}}})+0.007\ 48\times \mathrm{tan}h[({{x}_{\mathrm{surf}}}-0.069\ 49)/0.010\ 59]+ \\ 0.004\ 16\times \mathrm{tan}h[({{x}_{\mathrm{surf}}}-0.11)/0.011]-0.021\ 1\times \mathrm{tan}h[({{x}_{\mathrm{surf}}}-0.042)/0.009\ 5]- \\ 0.053\times \mathrm{exp}\{-{{[({{x}_{\mathrm{surf}}}-0.012)/0.005\ 7]}^{2}}\} \\ \end{matrix}$
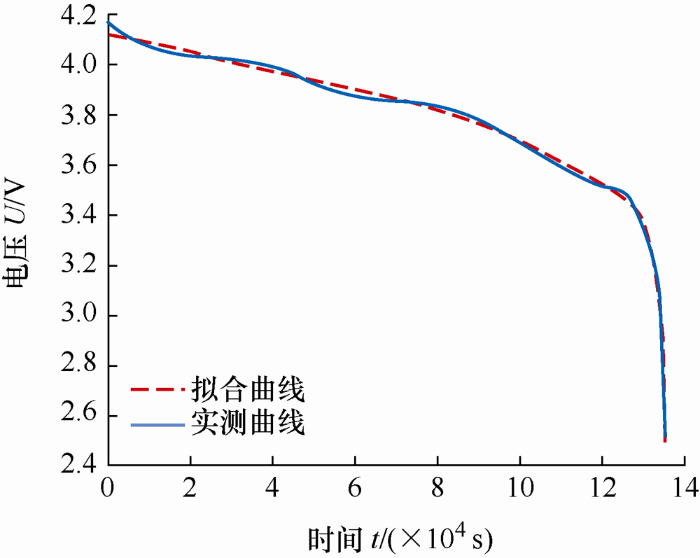
开路电压拟合图像如图4 所示,平均拟合误差为0.014 2 V,精度较高,达到进行后续研究的要求。SEM其余参数均可以通过施加特定工况测试,并结合基本过程参数计算得出。
图4
(2) 简化电化学-老化模型参数辨识。简化电化学-老化模型中需要辨识的参数有12个,分别是c 0 、x 0 、y 0 、Q n 、Q p 、R ohm 、P act 、P con 、τ p 、τ n 、τ e 和P act_s 。其中初始电解液浓度c 0 可以通过咨询生产商获得,本文中c 0 取值为1 000。
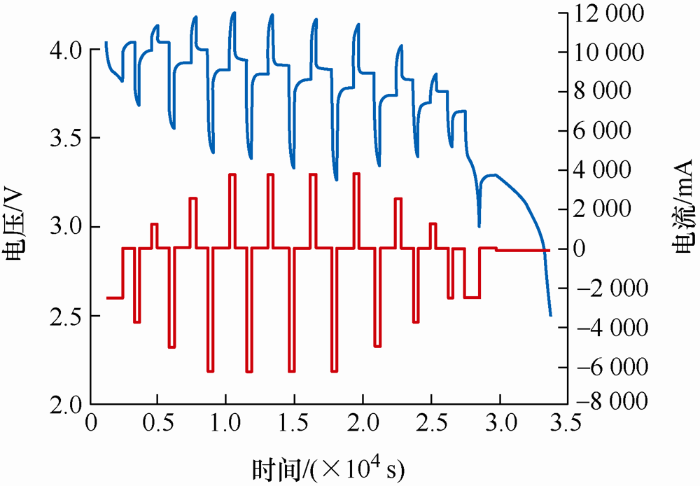
其他11个模型参数通过激励-响应的方法[15 ] 进行辨识。具体参数辨识工况的电流激励以及端电压响应如图5 所示。
图5
(3) 简化电化学-老化模型精度验证。为了分析SEM在不同工况下的适用情况,需要对模型的精度进行验证。将辨识出的模型参数具体值代入到SEM中,拟合电池恒流放电条件下的端电压曲线,并提取不同工况下电池恒流放电至截止电压的端电压数据,通过对比拟合曲线与实测电池端电压曲线重合度,验证所建模型的精度。
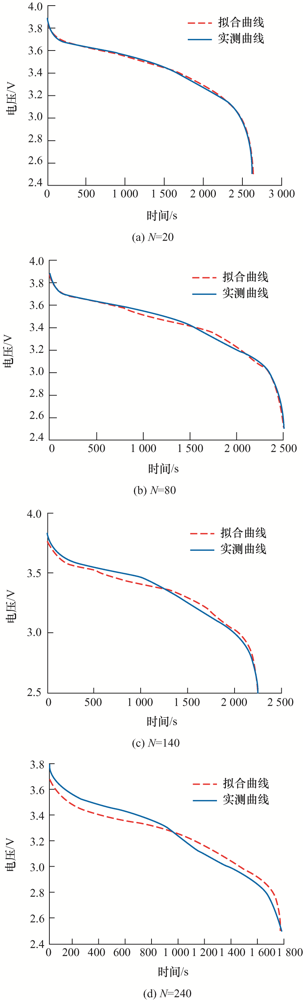
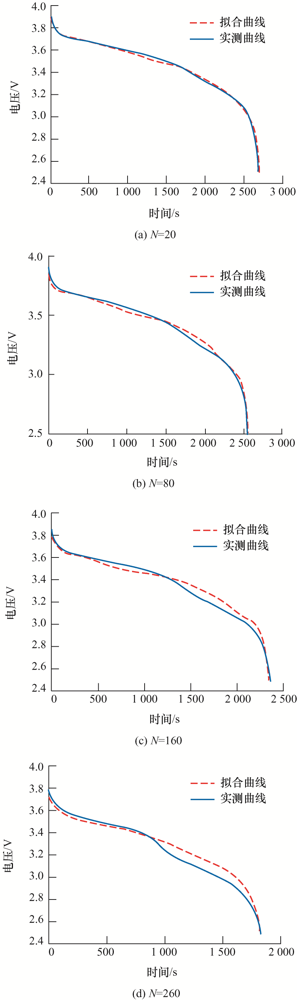
不同工况下、不同循环次数的端电压拟合曲线与实测曲线的仿真图像如图6 、7 所示,误差如表5 所示。
图6
图7
从以上不同工况、不同充放电循环阶段的电池端电压仿真曲线来看,简化电化学-老化模型在电池全寿命周期中都展现出良好的拟合效果,在电池全寿命周期前期的仿真误差在0.01 V左右;随着电池老化程度的加深,电池老化后期拟精度相对降低,但仿真误差仍在0.06 V以内,可满足后期进行电池SOH估计的要求。
3 基于数据驱动和数据-模型混合驱动的健康状态估计
3.1 基于数据驱动的健康状态估计原理
电池容量和能量衰退过程受多种应力条件耦合的影响,很难建立一个涵盖所有应力条件的模型去定量描述电池衰退过程,但是电池容量的衰退趋势是非常明确的,像这种“黑过程,白结果”的系统,我们称之为灰色系统,可以利用灰色理论进行处理。
灰色预测算法通过累加或者累减的方式,将一个看起来不具有规律性的数据序列转换成一个规律性相对突出的序列,尽可能地挖掘数据序列的变化信息,最后实现对未来数据的准确预测。新陈代谢灰色预测是灰色理论中重要思想之一,新陈代谢灰色预测算法是指在预测的过程中,输入最新数据的同时去除最久的数据,保持数据长度不变的情况下,快速跟踪数据波动,提高预测精度。
新陈代谢灰色预测算法MGA具体的建立过程如下[20 ] 。
(20) $\frac{\mathrm{d}X}{\mathrm{d}t}+aX=b$
初始数据序列${{X}^{(0)}}=\left( {{x}^{(0)}}(1),{{x}^{(0)}}(2),\cdot \cdot \cdot,{{x}^{(0)}}(n) \right)$,序列${{X}^{(1)}}=\left( {{x}^{(1)}}(1),{{x}^{(1)}}(2),\cdot \cdot \cdot,{{x}^{(1)}}(n) \right)$是由${{X}^{(0)}}$经一次累加生成得到的,其序列组成元素可通过式(11)计算得到
(21) ${{x}^{(1)}}(k)=\sum\limits_{i=1}^{k}{{{x}^{(0)}}(k)}\ \ \ \ \ \begin{matrix} {} \\ \end{matrix}k=1,2,\cdots,n$
设序列${{Z}^{(1)}}=\left( {{z}^{(1)}}(1),{{z}^{(1)}}(2),\cdot \cdot \cdot,{{z}^{(1)}}(n) \right)$,其序列元素计算公式如下
(22) ${{z}^{(1)}}(k)=\frac{1}{2}\left[ {{x}^{\left( 1 \right)}}\left( k \right)+{{x}^{\left( 1 \right)}}\left( k-1 \right) \right]\ \ \ k=1,2,\cdot \cdot \cdot,n$
(23) ${{x}^{\left( 0 \right)}}\left( k \right)+a{{z}^{\left( 1 \right)}}\left( k \right)=b$
若要对模型进行求解,首先要求解a 和b ,可以用$\hat{a}={{[a,b]}^{\text{T}}}$来表示。令
$B=\left[ \begin{matrix} -{{z}^{(1)}}(2) & 1 \\ -{{z}^{(1)}}(3) & 1 \\ \vdots & \vdots \\ -{{z}^{(1)}}(n) & 1 \\\end{matrix} \right]$ $Y=\left[ \begin{matrix} {{x}^{(0)}}(2) \\ {{x}^{(0)}}(3) \\ \vdots \\ {{x}^{(0)}}(n) \\ \end{matrix} \right]$
根据最小二乘法原理,可以得到参数$\hat{a}$的估计值如下
(24) $\hat{a}={{\left[ a,b \right]}^{\mathrm{T}}}={{\left( {{B}^{\mathrm{T}}}B \right)}^{-1}}{{B}^{\mathrm{T}}}Y$
(25) ${{x}^{\left( 1 \right)}}\left( t \right)=\left( {{x}^{\left( 1 \right)}}-\frac{b}{a} \right)\exp (-at)+\frac{b}{a}$
由于X (1) 序列是初始序列X (0) 经过一次累加后的结果,因此要对X (1) 序列进行还原,得到
(26) ${{\hat{x}}^{(0)}}(k+1)=(1-{{e}^{a}})({{x}^{(0)}}(1)-\frac{b}{a})\exp (-ak)\ \ \ \ k=1,2,\cdots,n$
(27) ${{\widehat{X}}^{(0)}}=\left( {{{\hat{x}}}^{(0)}}(1),{{{\hat{x}}}^{(0)}}(2),\cdot \cdot \cdot,{{{\hat{x}}}^{(0)}}(n) \right)$
MGA进行预测时,会不断地添加新的预测值,并删去最老的数据,在保持数据长度不变的条件下,实现新陈代谢,直到完成预测目标。
3.2 基于数据-模型混合的健康状态估计原理
基于数据-模型混合驱动的健康估计利用第2节中所建简化电化学-老化模型(SEM),将不同循环次数下辨识出的正负极初始嵌锂率x 0 、y 0 ,正负极嵌锂率动态变化范围Dx 、Dy ,正负极容量Qp 、Qn ,电池总容量Q 等相关模型参数经灰色预测算法预测后,代入SEM中,利用参数预测结果对电池端电压进行仿真,并通过式(3)、(4)计算电池预测容量和能量,实现电池健康状态估计。
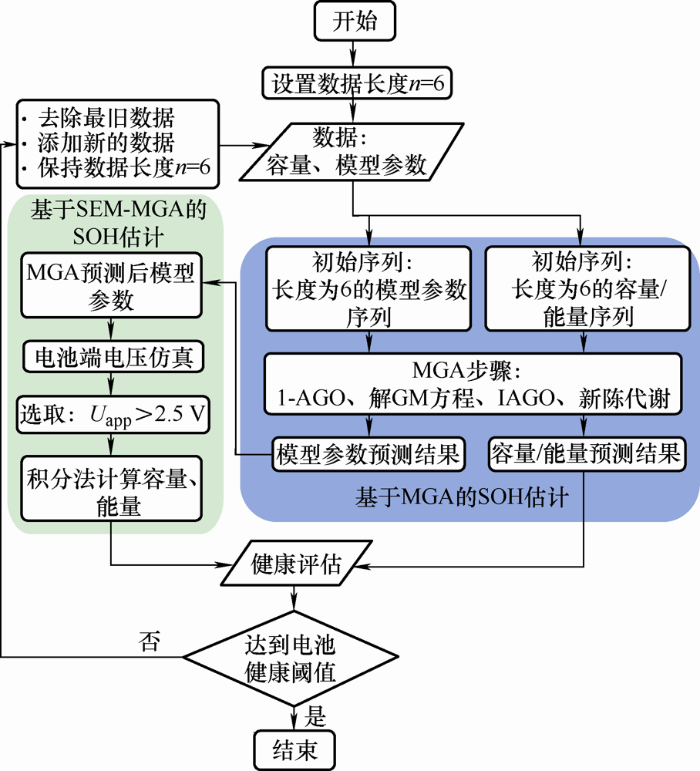
基于数据驱动和数据-模型混合驱动的SOH估计具体步骤如图8 所示。
图8
图8
基于SEM-MGA和MGA的SOH估计流程图
图8 中输入的数据有电池容量数据、能量数据,及不同循环下的SEM模型参数。基于MGA的SOH估计法通过选取初始长度为6的原始电池容量、能量序列,经过一次累加迭代操作,解灰色方程等过程求得电池预测容量和预测能量;基于SEM-MGA的SOH估计法选取与MGA估计法长度相同的初始模型参数序列,模型参数经MGA预测后,代入到SEM中,对电池端电压进行仿真,截取仿真电压曲线至放电截止电压2.5 V,并利用积分法求得电池预测容量,实现电池健康状态估计。判断电池健康状态是否达到阈值,未达到阈值,则通过添加一个新数据,去除最旧的历史数据,重复上述步骤,直至电池健康阈值。
3.3 以容量为表征参数的健康状态估计
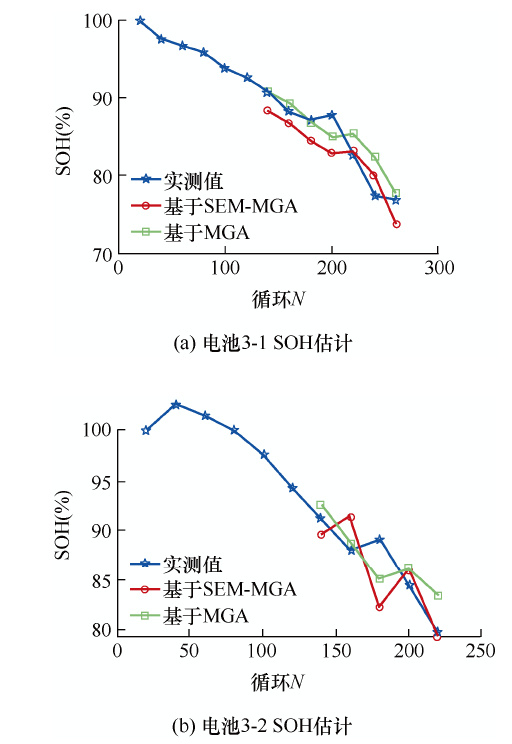
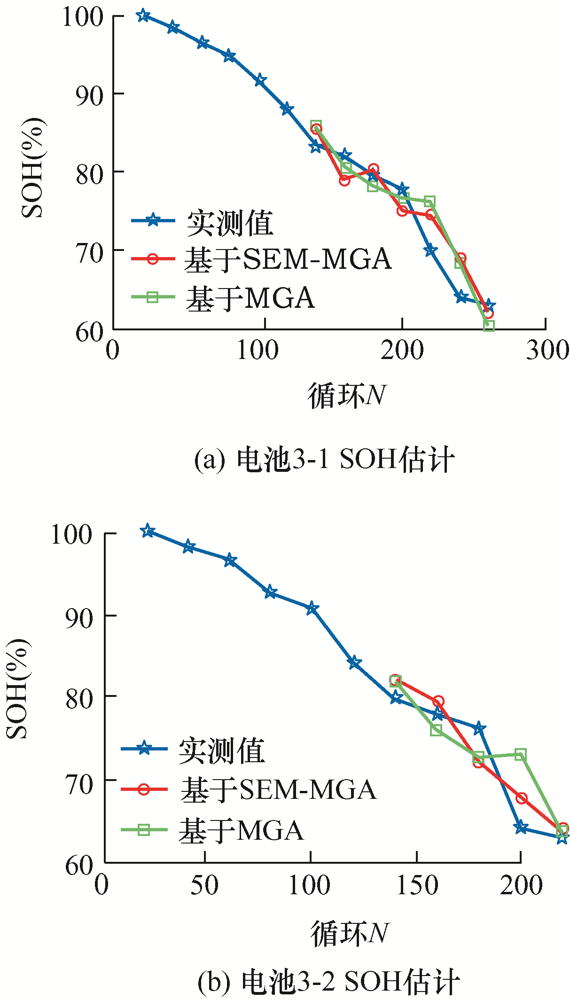
结合老化试验辨识出的电池容量及模型参数数据,选取初始长度n =6的初始数据序列进行电池健康状态估计,得到不同工况下基于MGA和SEM-MGA两种方法的电池容量SOH估计图,如图9 ~11 所示,预测平均误差如表6 所示。
图9
图9
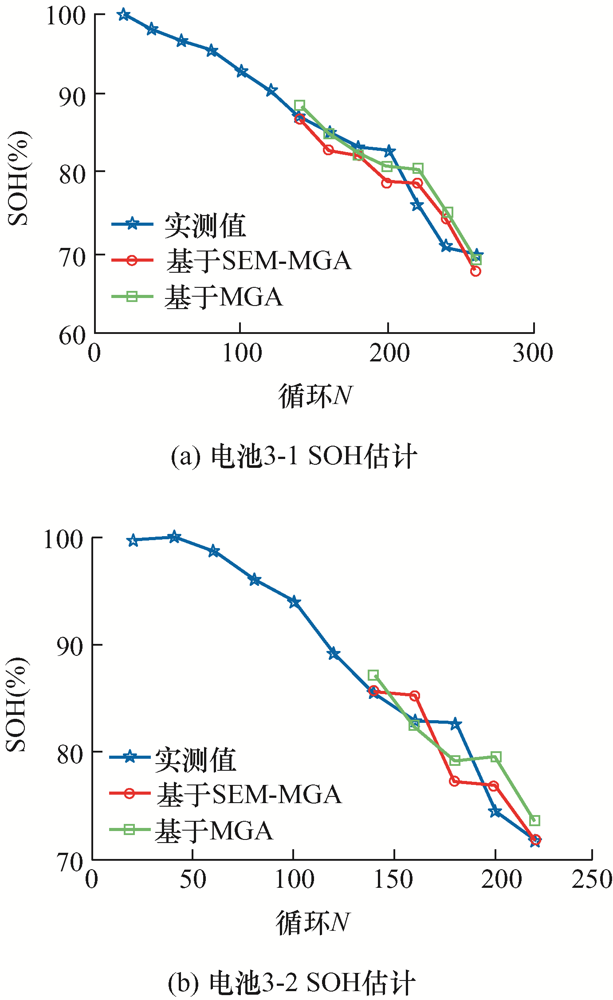
电池3-1、3-2(1C /100%DOD)容量SOH估计
图10
图10
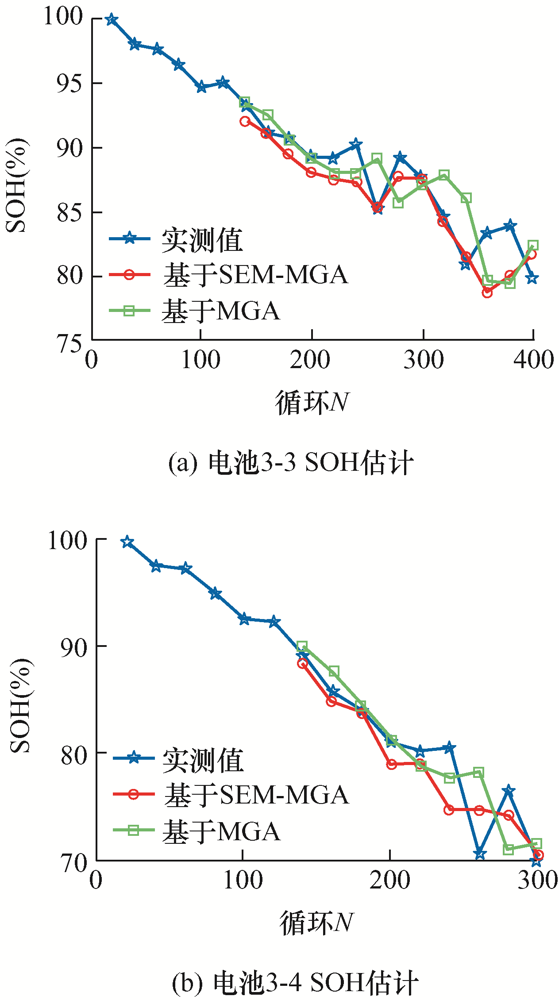
电池3-3、3-4(1C /50%DOD)容量SOH估计
图11
图11
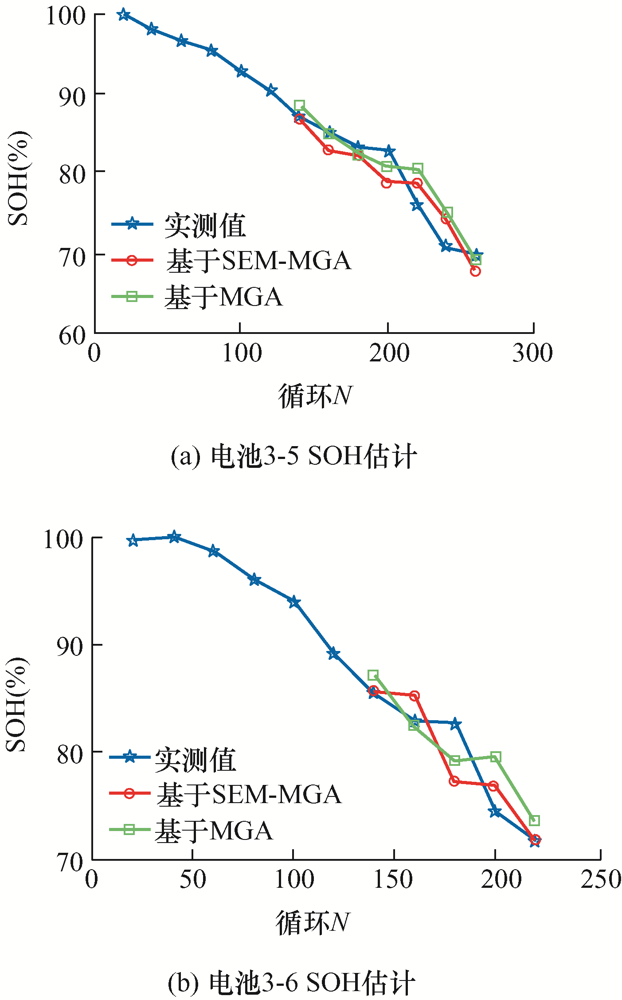
电池3-5、3-6 (2C /100%DOD)容量SOH估计
从图9 ~11 可以看出,以容量为表征参数的健康状态估计呈现以下特点。
(1) 估计精度高。在电池全寿命周期内,基于MGA的容量健康状态估计方法精度略高于基于SEM的容量健康状态估计方法,但精度略低的SEM方法除了电池3-3之外,其余电池的平均误差也都在3%以内。
(2) 估计结果有一定的滞后性。从图9 、10 可以看出,对于数据波动较为剧烈的数据段,如电池3-3的220到400循环和电池3-4的220到300循环,基于SEM和基于MGA的方法跟踪效果都有一定的滞后性。
3.4 以能量为表征参数的健康状态估计
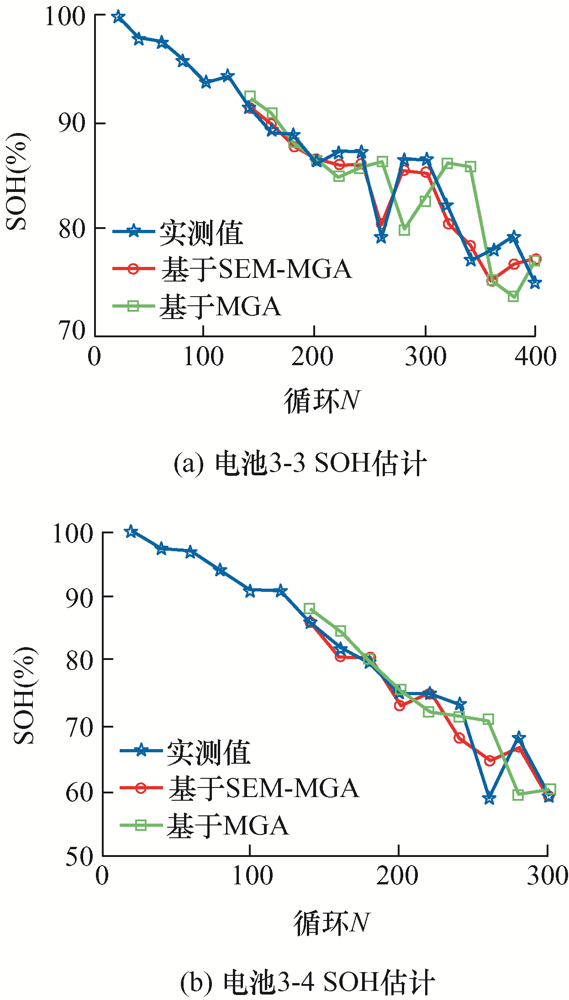
结合老化试验辨识出的电池能量及模型参数数据,选取初始长度n =6的初始数据序列进行电池健康状态估计,得到不同工况下基于MGA和SEM两种方法的电池能量SOH估计图,如图12 ~14 所示,预测平均误差如表7 所示。
图12
图12
电池3-1、3-2(1C /100%DOD)能量SOH估计
图13
图13
电池3-3、3-4(1C /50%DOD)能量SOH估计
图14
图14
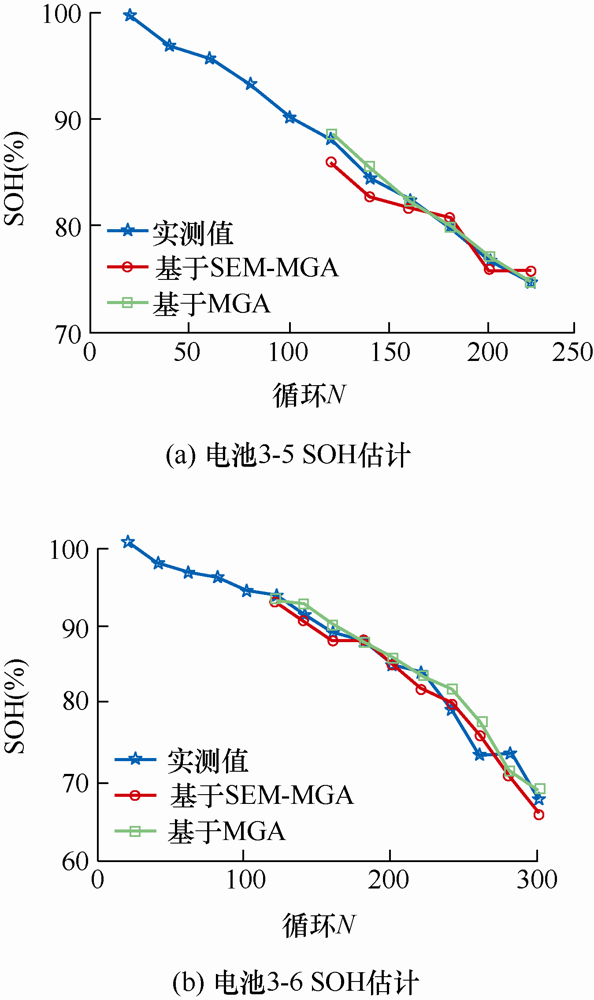
电池3-5、3-6(2C /100%DOD)能量SOH估计
从图12 ~14 来看,以能量为表征参数的健康状态估计呈现以下特点。
(1) 估计精度相比以容量为表征参数的健康状态估计结果略低。不管是基于MGA的方法还是基于SEM的方法,估计精度都略有下降,这是因为电池能量相比于电池容量衰减更快,当电池容量衰减到80%时,电池能量已经衰减到60%左右,绝对误差相同的情况下,能量为表征参数的健康状态估计结果相对误差偏低。
(2) 具有一定的抗噪声干扰能力。从图13 可以看到,对于数据波动较为剧烈的数据段,SEM估计法和MGA估计法也可以实现有效估计,典型的如图13 中电池3-3的240到400循环和电池3-4的220到300循环,基于SEM方法的抗干扰能力很强,可以实现电池健康状态的准确估计。
总的来说,容量和能量都是表示电池健康状态的重要表征参数,但二者衰减的速度有所差异,而且以容量为表征参数的电池健康状态估计方法估计精度较高,但估计结果有一定的滞后性;以能量为表征参数的电池健康状态估计方法估计精度略低,但抗噪声干扰能力强,目前以容量损失定义的健康状态更为常用,但从式(3)来看容量的计算只和电压截止点相关,缺少电池的端电压信息,能量参数和容量参数包含部分相同信息,但不可完全互相取代,所以单独以一种电池健康特征参数作为SOH的估计结果难以准确全面地反映电池真实健康状态,因此,考虑对以容量和能量为表征参数的SOH估计结果各取加权系数。
3.5 以容量和能量混合表征的健康状态估计
本节基于灰色预测模型和简化电化学-老化模型对电池容量、能量健康状态的预测结果,为综合两种预测结果的衰减速度和优缺点,实现电池健康状态的综合准确估计,考虑对以容量和能量为表征参数的SOH估计结果各取加权系数,加权系数各为0.5,综合锂离子电池SOH计算公式如下
(28) $\mathrm{SOH}=0.5\mathrm{SO}{{\mathrm{H}}_{\text{energy}}}+0.5\mathrm{SO}{{\mathrm{H}}_{\mathrm{capacity}}}$
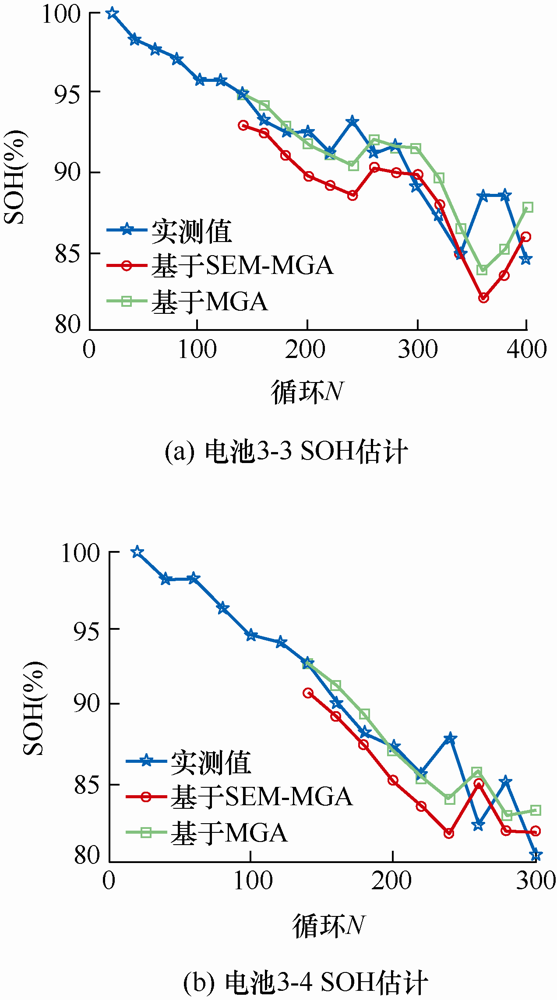
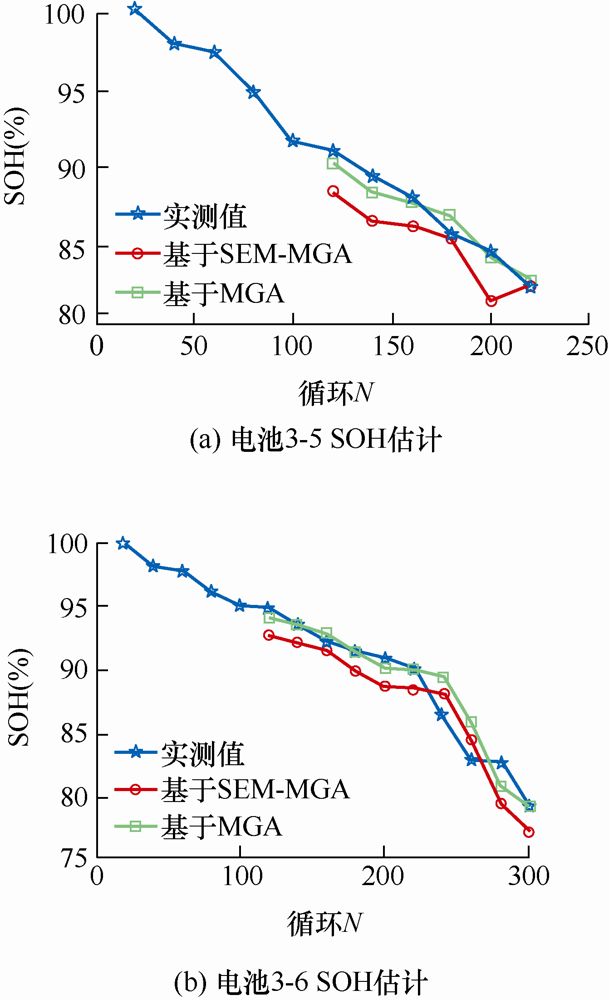
不同工况下基于MGA和SEM-MGA两种方法的电池综合SOH估计图,如图15 ~17 所示,预测平均误差如表8 所示。
图15
图15
电池3-1、3-2(1C /100%DOD)综合SOH估计
图16
图16
电池3-3、3-4(1C /50%DOD)综合SOH估计
图17
图17
电池3-5、3-6(2C /100%DOD)综合SOH估计
从图15 ~17 来看,基于MGA的综合健康状态估计结果精度不稳定。在电池全寿命周期内,基于MGA的SOH估计方法完全基于数据驱动,依赖历史数据质量,在电池健康特征数据线性变化时可以取得较好的估计精度,比如电池3-5,MGA估计精度达到0.047%,当电池健康特征数据波动较大时,估计精度降低,如电池3-4,MGA估计精度为3.401%。
基于SEM-MGA的综合健康状态估计结果适用性强。无论在电池容量线性变化时或者是非线性变化时,都取得了较好的估计精度。不同工况下,预测精度上下浮动的范围为1.421%,也证明了该方法的适用性,可以对不同工作条件下的电池进行精确的SOH评估。
总的来说,基于MGA的SOH估计方法完全基于数据驱动,在利用MGA进行电池健康估计时,由于需要拟合灰色方程的系数,已知数据个数不能少于4个;未考虑电池内部的电池性能衰退机理,仅以容量作为健康表征建立电池健康预警机制,相对而言,是比较片面的。当历史数据量太少或数据变化规律不明显时,基于MGA的SOH估计方法的效果也有待验证。基于SEM-MGA的SOH估计方法,所需要进行预测的参数比MGA较多,需要耗费较多的计算资源,但此方法融合了基于模型方法和数据驱动方法的优点,实现锂离子电池内部老化机理与智能算法相结合,不仅可以对电池的综合健康状态实现准确的估计,还可以基于此方法对锂离子电池的性能衰退过程与失效机制进行分析。
4 结论
本文基于新陈代谢灰色预测算法、简化电化学-老化学模型对不同工况下的电池SOH进行估计。首先分别介绍了基于MGA和SEM的SOH估计方法原理,在此基础上,结合试验数据实现电池SOH估计仿真试验。通过分析SOH估计仿真结果,得出如下结论。
(1) 以容量为表征参数的电池健康状态估计结果衰退较慢、精度较高,但估计结果有一定的滞后性;以能量为表征参数的电池健康状态估计结果衰退较快、精度略低,但抗噪声干扰能力较强,将容量和能量加权后共同作为电池健康状态的表征参数,合理评估SOH的衰退情况,实现电池健康状态的综合评价。
(2) 基于MGA的纯数据驱动SOH估计法精度波动较大,在使用时,需要完整的电池曲线来获取预测所需的容量数据,这在实际应用时难以实现;而且这种方法无法反映电池内部的老化机理。
(3) 基于SEM-MGA的混合驱动SOH估计方法适用性强,无论在电池容量线性变化时或者是非线性变化时都取得了较好的估计精度,又可以通过模型参数的变化反映电池内部老化机制,实现锂离子电池内部老化机理与智能算法相结合,有助于建立更加可靠有效的电池SOH评估系统。
参考文献
View Option
[1]
XIONG R CHEN H WANG C , et al . Towards a smarter hybrid energy storage system based on battery and ultracapacitor:A critical review on topology and energy management
[J]. Journal of Cleaner Production , 2018 (202 ):1228 -1240 .
[本文引用: 1]
[2]
XIONG R YU Q SHEN W , et al . A sensor fault diagnosis method for a lithium-ion battery pack in electric vehicles
[J]. IEEE Transaction on Power Electronics , 2019 (8993 ):1 -11 .
[本文引用: 1]
[3]
张博钊 , 苟斌 , 徐燕璋 . 循环使用与储存条件对石墨/ LiCoO2 电池寿命的影响分析
[J]. 电气工程学报 , 2022 , 17 (2 ):38 -48 .
[本文引用: 1]
ZHANG Bozhao GOU Bin XU Yanzhang . Effect analysis of recycling and storage conditions on graphite/LiCoO2 battery life
[J]. Journal of Electrical Engineering , 2022 , 17 (2 ):38 -48 .
[本文引用: 1]
[4]
LIU K LI Y HU X , et al . Widanage,Gaussian process regression with automatic relevance determination kernel for calendar aging prediction of lithium-ion batteries
[J]. IEEE Trans. Ind. Informatics , 2019 (16 ):3767 -3777 .
[本文引用: 1]
[5]
FENG Y XUE C HAN Q L , et al . Robust estimation for state-of-charge and state-of-health of lithium-ion batteries using integral-type terminal sliding-mode observers
[J]. IEEE Trans. Ind. Electron ., 2019 (67 ):4013 -4023 .
[本文引用: 1]
[6]
杜海忠 , 骆滔 , 宋浩谊 , 等 . 基于电压平衡的锂电池主动均衡电路及策略
[J]. 电气工程学报 , 2021 , 16 (3 ):145 -151 .
[本文引用: 1]
DU Haizhong LUO Tao SONG Haoyi , et al . Active balancing circuit and strategy of Li-ion battery based on voltage balance
[J]. Journal of Electrical Engineering , 2021 , 16 (3 ):145 -151 .
[本文引用: 1]
[7]
JIANG Y ZHANG J XIA L , et al . State of health estimation for lithium-ion battery using empirical degradation and error compensation models
[J]. IEEE Access , 2020 (8 ):123858 -123868 .
[本文引用: 1]
[8]
HU X FENG F LIU K . State estimation for advanced battery management:Key challenges and future trends
[J]. Renew. Sust. Energ. Rev ., 2019 (114 ):109 -124 .
[本文引用: 1]
[9]
张朝龙 , 赵筛筛 , 何怡刚 . 基于信息熵与PSO-LSTM的锂电池组健康状态估计方法
[J]. 机械工程学报 , 2022 , 58 (10 ):180 -190 .
DOI:10.3901/JME.2022.10.180
[本文引用: 1]
针对目前锂电池组健康状态估计方法的不足,提出一种基于信息熵与粒子群算法(Particle swarm optimization, PSO)优化长短时记忆神经网络(Long short-term memory neural network, LSTM)的锂电池组健康状态估计方法。基于锂电池组恒流-恒压充电阶段锂电池组内各单体端电压的信息熵和平均温度信息,应用PSO-LSTM方法提取锂电池组电压熵、平均温度和锂电池组健康状态之间的映射关系,从而建立锂电池组健康状态估计模型。应用试验室测量的锂电池组老化数据对提出的方法进行测试。测试结果表明,该方法能够准确估计锂电池组的健康状态,平均估计误差在1%以内。同时,为验证提出的方法可推广至锂电池单体,利用美国航天航空局测得的锂电池加速老化数据再次测试,平均估计误差在0.7%以内。并针对锂电池组与锂电池单体设计对比试验,进一步验证提出的方法具有良好的估计性能。
ZHANG Chaolong ZHAO Shaishai HE Yigang . State-of-health estimate for lithium-ion battery using information entropy and PSO-LSTM
[J]. Journal of Mechanical Engineering , 2022 , 58 (10 ):180 -190 .
DOI:10.3901/JME.2022.10.180
[本文引用: 1]
In order to address the shortcoming of the existing lithium-ion battery pack state of health(SOH) estimation methods, a SOH estimation approach for lithium-ion battery pack using information entropy and particle swarm optimization(PSO) to optimize the long short-term memory(LSTM) neural network is proposed. The data of the information entropy and the average temperature of each cell terminal voltage in the lithium-ion battery pack during the constant current-constant voltage charging stage are utilized to extract the mapping relationship between the voltage entropy, average temperature, and SOH of the lithium-ion battery pack using PSO-LSTM, and then establish the lithium-ion battery pack SOH estimation model. The measured aging data of lithium-ion battery pack in the laboratory are employed to verify the validity of the presented method. The results show that the developed approach can accurately estimate the SOH of the lithium-ion battery pack with the average estimation error within 1%. Meanwhile, in order to verify the proposed method can be extended to lithium-ion batteries, the accelerated aging data of lithium-ion batteries measured by National Aeronautics and Space Administration(NASA) to test again with the average estimation error within 0.7%. The compared experiment is designed for the battery pack and cells, which further demonstrates that the suggested method offers a favorable estimation performance.
[10]
GOU B XU Y FENG X . An ensemble learning-based data-driven method for online state-of-health estimation of lithium-ion batteries
[J]. IEEE Trans. Transp. Electrif ., 2020 (2 ):422 -436 .
[本文引用: 1]
[11]
TANG X ZOU C YAO K , et al . A fast estimation algorithm for lithium-ion battery state of health
[J]. Journal of Power Sources , 2018 (396 ):453 -458 .
[本文引用: 1]
[12]
FANG Liu CHEN Shao SU Weixing . Online joint estimator of key states for battery based on a new equivalent circuit model
[J]. Journal of Energy Storage , 2022 (52 ):780 -795 .
[本文引用: 1]
[13]
SONG Y LIU D LIAO H , et al . A hybrid statistical data-driven method for on-line joint state estimation of lithium-ion batteries
[J]. Applied Energy , 2020 (261 ):114 -127 .
[本文引用: 1]
[14]
TIAN Huixin QIN Pengliang LI Kun . A review of the state of health for lithium-ion batteries:Research status and suggestions
[J]. Journal of Cleaner Production , 2020 (261 ):813 -840 .
[本文引用: 1]
[15]
LIU J WANG W MA F , et al . A data-model-fusion prognostic framework for dynamic system state forecasting
[J]. Engineering Applications of Artificial Intelligence , 2012 (25 ):814 -823 .
[本文引用: 2]
[16]
XU Zhicheng WANG Jun . Co-estimating the state of charge and health of lithium batteries through combining a minimalist electrochemical model and an equivalent circuit model
[J]. Enengy , 2022 (240 ):281 -295 .
[本文引用: 1]
[17]
罗伟林 . 锂离子电池电化学模型简化及参数估计 [D]. 哈尔滨 : 哈尔滨工业大学 , 2014 .
[本文引用: 1]
LUO Weilin . Simplification of electrochemical model and parameter estimation of lithium-ion battery [D]. Harbin : Harbin Institute of Technology , 2014 .
[本文引用: 1]
[18]
李俊夫 . 锂离子电池解耦合简化第一原理模型及SOC估计 [D]. 哈尔滨 : 哈尔滨工业大学 , 2018 .
[本文引用: 1]
LI Junfu . Simplified first-principle model and SOC estimation for lithium-ion battery decoupling [D]. Harbin : Harbin Institute of Technology , 2018 .
[本文引用: 1]
[19]
LI Junfu WANG Dafang . Aging modes analysis and physical parameter identification based on a simplified electrochemical model for lithium-ion batteries
[J]. Journal of Energy Storage , 2020 (3 ):538 -550 .
[本文引用: 1]
[20]
CHEN L LIN W LI J , et al . Prediction of lithium-ion battery capacity with metabolic grey model
[J]. Energy , 2016 (106 ):662 -672 .
[本文引用: 1]
Towards a smarter hybrid energy storage system based on battery and ultracapacitor:A critical review on topology and energy management
1
2018
... 随着社会的快速发展和科学技术的进步,能源和环境挑战已成为近几十年来全球的热门话题.人们一直在积极寻找石油资源的替代品,尤其是锂电池[1 ⇓ -3 ] .锂离子电池作为一种储能元件,由于其高能量密度和较长的循环寿命,已经被广泛应用于生产和日常生活中[4 ⇓ -6 ] .锂离子电池管理系统最重要的组成部分是准确估计锂电池的健康状态.电池健康状态(State of health, SOH)的估计越精确,锂离子电池的安全可靠运行就越有保障,因此对锂离子电池进行准确的状态估计对于实际应用至关重要[7 ] .锂离子电池的SOH定义按照不同的电池参数有不同的定义方法[8 -9 ] ,本文使用的健康特征参数包括电池容量和能量,计算公式如下所示 ...
A sensor fault diagnosis method for a lithium-ion battery pack in electric vehicles
1
2019
... 随着社会的快速发展和科学技术的进步,能源和环境挑战已成为近几十年来全球的热门话题.人们一直在积极寻找石油资源的替代品,尤其是锂电池[1 ⇓ -3 ] .锂离子电池作为一种储能元件,由于其高能量密度和较长的循环寿命,已经被广泛应用于生产和日常生活中[4 ⇓ -6 ] .锂离子电池管理系统最重要的组成部分是准确估计锂电池的健康状态.电池健康状态(State of health, SOH)的估计越精确,锂离子电池的安全可靠运行就越有保障,因此对锂离子电池进行准确的状态估计对于实际应用至关重要[7 ] .锂离子电池的SOH定义按照不同的电池参数有不同的定义方法[8 -9 ] ,本文使用的健康特征参数包括电池容量和能量,计算公式如下所示 ...
循环使用与储存条件对石墨/ LiCoO2 电池寿命的影响分析
1
2022
... 随着社会的快速发展和科学技术的进步,能源和环境挑战已成为近几十年来全球的热门话题.人们一直在积极寻找石油资源的替代品,尤其是锂电池[1 ⇓ -3 ] .锂离子电池作为一种储能元件,由于其高能量密度和较长的循环寿命,已经被广泛应用于生产和日常生活中[4 ⇓ -6 ] .锂离子电池管理系统最重要的组成部分是准确估计锂电池的健康状态.电池健康状态(State of health, SOH)的估计越精确,锂离子电池的安全可靠运行就越有保障,因此对锂离子电池进行准确的状态估计对于实际应用至关重要[7 ] .锂离子电池的SOH定义按照不同的电池参数有不同的定义方法[8 -9 ] ,本文使用的健康特征参数包括电池容量和能量,计算公式如下所示 ...
Effect analysis of recycling and storage conditions on graphite/LiCoO2 battery life
1
2022
... 随着社会的快速发展和科学技术的进步,能源和环境挑战已成为近几十年来全球的热门话题.人们一直在积极寻找石油资源的替代品,尤其是锂电池[1 ⇓ -3 ] .锂离子电池作为一种储能元件,由于其高能量密度和较长的循环寿命,已经被广泛应用于生产和日常生活中[4 ⇓ -6 ] .锂离子电池管理系统最重要的组成部分是准确估计锂电池的健康状态.电池健康状态(State of health, SOH)的估计越精确,锂离子电池的安全可靠运行就越有保障,因此对锂离子电池进行准确的状态估计对于实际应用至关重要[7 ] .锂离子电池的SOH定义按照不同的电池参数有不同的定义方法[8 -9 ] ,本文使用的健康特征参数包括电池容量和能量,计算公式如下所示 ...
Widanage,Gaussian process regression with automatic relevance determination kernel for calendar aging prediction of lithium-ion batteries
1
2019
... 随着社会的快速发展和科学技术的进步,能源和环境挑战已成为近几十年来全球的热门话题.人们一直在积极寻找石油资源的替代品,尤其是锂电池[1 ⇓ -3 ] .锂离子电池作为一种储能元件,由于其高能量密度和较长的循环寿命,已经被广泛应用于生产和日常生活中[4 ⇓ -6 ] .锂离子电池管理系统最重要的组成部分是准确估计锂电池的健康状态.电池健康状态(State of health, SOH)的估计越精确,锂离子电池的安全可靠运行就越有保障,因此对锂离子电池进行准确的状态估计对于实际应用至关重要[7 ] .锂离子电池的SOH定义按照不同的电池参数有不同的定义方法[8 -9 ] ,本文使用的健康特征参数包括电池容量和能量,计算公式如下所示 ...
Robust estimation for state-of-charge and state-of-health of lithium-ion batteries using integral-type terminal sliding-mode observers
1
2019
... 随着社会的快速发展和科学技术的进步,能源和环境挑战已成为近几十年来全球的热门话题.人们一直在积极寻找石油资源的替代品,尤其是锂电池[1 ⇓ -3 ] .锂离子电池作为一种储能元件,由于其高能量密度和较长的循环寿命,已经被广泛应用于生产和日常生活中[4 ⇓ -6 ] .锂离子电池管理系统最重要的组成部分是准确估计锂电池的健康状态.电池健康状态(State of health, SOH)的估计越精确,锂离子电池的安全可靠运行就越有保障,因此对锂离子电池进行准确的状态估计对于实际应用至关重要[7 ] .锂离子电池的SOH定义按照不同的电池参数有不同的定义方法[8 -9 ] ,本文使用的健康特征参数包括电池容量和能量,计算公式如下所示 ...
基于电压平衡的锂电池主动均衡电路及策略
1
2021
... 随着社会的快速发展和科学技术的进步,能源和环境挑战已成为近几十年来全球的热门话题.人们一直在积极寻找石油资源的替代品,尤其是锂电池[1 ⇓ -3 ] .锂离子电池作为一种储能元件,由于其高能量密度和较长的循环寿命,已经被广泛应用于生产和日常生活中[4 ⇓ -6 ] .锂离子电池管理系统最重要的组成部分是准确估计锂电池的健康状态.电池健康状态(State of health, SOH)的估计越精确,锂离子电池的安全可靠运行就越有保障,因此对锂离子电池进行准确的状态估计对于实际应用至关重要[7 ] .锂离子电池的SOH定义按照不同的电池参数有不同的定义方法[8 -9 ] ,本文使用的健康特征参数包括电池容量和能量,计算公式如下所示 ...
Active balancing circuit and strategy of Li-ion battery based on voltage balance
1
2021
... 随着社会的快速发展和科学技术的进步,能源和环境挑战已成为近几十年来全球的热门话题.人们一直在积极寻找石油资源的替代品,尤其是锂电池[1 ⇓ -3 ] .锂离子电池作为一种储能元件,由于其高能量密度和较长的循环寿命,已经被广泛应用于生产和日常生活中[4 ⇓ -6 ] .锂离子电池管理系统最重要的组成部分是准确估计锂电池的健康状态.电池健康状态(State of health, SOH)的估计越精确,锂离子电池的安全可靠运行就越有保障,因此对锂离子电池进行准确的状态估计对于实际应用至关重要[7 ] .锂离子电池的SOH定义按照不同的电池参数有不同的定义方法[8 -9 ] ,本文使用的健康特征参数包括电池容量和能量,计算公式如下所示 ...
State of health estimation for lithium-ion battery using empirical degradation and error compensation models
1
2020
... 随着社会的快速发展和科学技术的进步,能源和环境挑战已成为近几十年来全球的热门话题.人们一直在积极寻找石油资源的替代品,尤其是锂电池[1 ⇓ -3 ] .锂离子电池作为一种储能元件,由于其高能量密度和较长的循环寿命,已经被广泛应用于生产和日常生活中[4 ⇓ -6 ] .锂离子电池管理系统最重要的组成部分是准确估计锂电池的健康状态.电池健康状态(State of health, SOH)的估计越精确,锂离子电池的安全可靠运行就越有保障,因此对锂离子电池进行准确的状态估计对于实际应用至关重要[7 ] .锂离子电池的SOH定义按照不同的电池参数有不同的定义方法[8 -9 ] ,本文使用的健康特征参数包括电池容量和能量,计算公式如下所示 ...
State estimation for advanced battery management:Key challenges and future trends
1
2019
... 随着社会的快速发展和科学技术的进步,能源和环境挑战已成为近几十年来全球的热门话题.人们一直在积极寻找石油资源的替代品,尤其是锂电池[1 ⇓ -3 ] .锂离子电池作为一种储能元件,由于其高能量密度和较长的循环寿命,已经被广泛应用于生产和日常生活中[4 ⇓ -6 ] .锂离子电池管理系统最重要的组成部分是准确估计锂电池的健康状态.电池健康状态(State of health, SOH)的估计越精确,锂离子电池的安全可靠运行就越有保障,因此对锂离子电池进行准确的状态估计对于实际应用至关重要[7 ] .锂离子电池的SOH定义按照不同的电池参数有不同的定义方法[8 -9 ] ,本文使用的健康特征参数包括电池容量和能量,计算公式如下所示 ...
基于信息熵与PSO-LSTM的锂电池组健康状态估计方法
1
2022
... 随着社会的快速发展和科学技术的进步,能源和环境挑战已成为近几十年来全球的热门话题.人们一直在积极寻找石油资源的替代品,尤其是锂电池[1 ⇓ -3 ] .锂离子电池作为一种储能元件,由于其高能量密度和较长的循环寿命,已经被广泛应用于生产和日常生活中[4 ⇓ -6 ] .锂离子电池管理系统最重要的组成部分是准确估计锂电池的健康状态.电池健康状态(State of health, SOH)的估计越精确,锂离子电池的安全可靠运行就越有保障,因此对锂离子电池进行准确的状态估计对于实际应用至关重要[7 ] .锂离子电池的SOH定义按照不同的电池参数有不同的定义方法[8 -9 ] ,本文使用的健康特征参数包括电池容量和能量,计算公式如下所示 ...
State-of-health estimate for lithium-ion battery using information entropy and PSO-LSTM
1
2022
... 随着社会的快速发展和科学技术的进步,能源和环境挑战已成为近几十年来全球的热门话题.人们一直在积极寻找石油资源的替代品,尤其是锂电池[1 ⇓ -3 ] .锂离子电池作为一种储能元件,由于其高能量密度和较长的循环寿命,已经被广泛应用于生产和日常生活中[4 ⇓ -6 ] .锂离子电池管理系统最重要的组成部分是准确估计锂电池的健康状态.电池健康状态(State of health, SOH)的估计越精确,锂离子电池的安全可靠运行就越有保障,因此对锂离子电池进行准确的状态估计对于实际应用至关重要[7 ] .锂离子电池的SOH定义按照不同的电池参数有不同的定义方法[8 -9 ] ,本文使用的健康特征参数包括电池容量和能量,计算公式如下所示 ...
An ensemble learning-based data-driven method for online state-of-health estimation of lithium-ion batteries
1
2020
... 式中,${{C}_{\text{cur}}}$和${{C}_{\text{nom}}}$分别是电池的当前容量和标称容量,${{E}_{\text{cur}}}$和${{E}_{\text{nom}}}$分别是电池的当前能量和标称能量[10 ] ,锂离子电池容量C 和能量E 计算公式如下所示 ...
A fast estimation algorithm for lithium-ion battery state of health
1
2018
... 目前绝大多数SOH估计算法仅针对电池放电容量序列进行跟踪,在动态工况、宽温度范围内的适用性较差,且无法提供更为全面的电池性能衰退程度评估结果.SOH估计方法包括基于模型的方法、数据驱动方法、混合方法[11 ] .基于等效电路模型的方法运用广泛,FANG等[12 ] 提出了一种基于自回归等效电路模型的电池健康状态估计方法,可实现SOH的在线估计,但此等效电路模型缺乏物理和化学意义,在实际电动汽车运行环境下预测效果较差.数据驱动方法的一个主要问题是对电池退化的建模是基于恒定放电速率和恒定环境温度下采集的数据[13 ] ,在实践中,电池是在吸收了许多不确定性的变化的运行条件下运行的,这些不确定性将使这些模型表现不佳[14 ] .混合方法往往有更高的精度,对不同工况的SOH估计的适应性也较好[15 ] ,XU等[16 ] 采用等效电路模型描述电池动力学,递归最小二乘在线识别模型参数,无气味卡尔曼滤波器估计电池状态,提出了一个极简的电化学模型来描述电池内部锂含量的分布,并将SOH与锂的不可逆损耗导致的容量衰减联系起来,SOH估计平均误差在2%左右.电化学模型充分考虑了电池中实际的电化学反应过程,包括固相扩散过程、液相扩散和迁移过程等,但经典的伪二维(Pseudo two-dimensional,P2D) ...
Online joint estimator of key states for battery based on a new equivalent circuit model
1
2022
... 目前绝大多数SOH估计算法仅针对电池放电容量序列进行跟踪,在动态工况、宽温度范围内的适用性较差,且无法提供更为全面的电池性能衰退程度评估结果.SOH估计方法包括基于模型的方法、数据驱动方法、混合方法[11 ] .基于等效电路模型的方法运用广泛,FANG等[12 ] 提出了一种基于自回归等效电路模型的电池健康状态估计方法,可实现SOH的在线估计,但此等效电路模型缺乏物理和化学意义,在实际电动汽车运行环境下预测效果较差.数据驱动方法的一个主要问题是对电池退化的建模是基于恒定放电速率和恒定环境温度下采集的数据[13 ] ,在实践中,电池是在吸收了许多不确定性的变化的运行条件下运行的,这些不确定性将使这些模型表现不佳[14 ] .混合方法往往有更高的精度,对不同工况的SOH估计的适应性也较好[15 ] ,XU等[16 ] 采用等效电路模型描述电池动力学,递归最小二乘在线识别模型参数,无气味卡尔曼滤波器估计电池状态,提出了一个极简的电化学模型来描述电池内部锂含量的分布,并将SOH与锂的不可逆损耗导致的容量衰减联系起来,SOH估计平均误差在2%左右.电化学模型充分考虑了电池中实际的电化学反应过程,包括固相扩散过程、液相扩散和迁移过程等,但经典的伪二维(Pseudo two-dimensional,P2D) ...
A hybrid statistical data-driven method for on-line joint state estimation of lithium-ion batteries
1
2020
... 目前绝大多数SOH估计算法仅针对电池放电容量序列进行跟踪,在动态工况、宽温度范围内的适用性较差,且无法提供更为全面的电池性能衰退程度评估结果.SOH估计方法包括基于模型的方法、数据驱动方法、混合方法[11 ] .基于等效电路模型的方法运用广泛,FANG等[12 ] 提出了一种基于自回归等效电路模型的电池健康状态估计方法,可实现SOH的在线估计,但此等效电路模型缺乏物理和化学意义,在实际电动汽车运行环境下预测效果较差.数据驱动方法的一个主要问题是对电池退化的建模是基于恒定放电速率和恒定环境温度下采集的数据[13 ] ,在实践中,电池是在吸收了许多不确定性的变化的运行条件下运行的,这些不确定性将使这些模型表现不佳[14 ] .混合方法往往有更高的精度,对不同工况的SOH估计的适应性也较好[15 ] ,XU等[16 ] 采用等效电路模型描述电池动力学,递归最小二乘在线识别模型参数,无气味卡尔曼滤波器估计电池状态,提出了一个极简的电化学模型来描述电池内部锂含量的分布,并将SOH与锂的不可逆损耗导致的容量衰减联系起来,SOH估计平均误差在2%左右.电化学模型充分考虑了电池中实际的电化学反应过程,包括固相扩散过程、液相扩散和迁移过程等,但经典的伪二维(Pseudo two-dimensional,P2D) ...
A review of the state of health for lithium-ion batteries:Research status and suggestions
1
2020
... 目前绝大多数SOH估计算法仅针对电池放电容量序列进行跟踪,在动态工况、宽温度范围内的适用性较差,且无法提供更为全面的电池性能衰退程度评估结果.SOH估计方法包括基于模型的方法、数据驱动方法、混合方法[11 ] .基于等效电路模型的方法运用广泛,FANG等[12 ] 提出了一种基于自回归等效电路模型的电池健康状态估计方法,可实现SOH的在线估计,但此等效电路模型缺乏物理和化学意义,在实际电动汽车运行环境下预测效果较差.数据驱动方法的一个主要问题是对电池退化的建模是基于恒定放电速率和恒定环境温度下采集的数据[13 ] ,在实践中,电池是在吸收了许多不确定性的变化的运行条件下运行的,这些不确定性将使这些模型表现不佳[14 ] .混合方法往往有更高的精度,对不同工况的SOH估计的适应性也较好[15 ] ,XU等[16 ] 采用等效电路模型描述电池动力学,递归最小二乘在线识别模型参数,无气味卡尔曼滤波器估计电池状态,提出了一个极简的电化学模型来描述电池内部锂含量的分布,并将SOH与锂的不可逆损耗导致的容量衰减联系起来,SOH估计平均误差在2%左右.电化学模型充分考虑了电池中实际的电化学反应过程,包括固相扩散过程、液相扩散和迁移过程等,但经典的伪二维(Pseudo two-dimensional,P2D) ...
A data-model-fusion prognostic framework for dynamic system state forecasting
2
2012
... 目前绝大多数SOH估计算法仅针对电池放电容量序列进行跟踪,在动态工况、宽温度范围内的适用性较差,且无法提供更为全面的电池性能衰退程度评估结果.SOH估计方法包括基于模型的方法、数据驱动方法、混合方法[11 ] .基于等效电路模型的方法运用广泛,FANG等[12 ] 提出了一种基于自回归等效电路模型的电池健康状态估计方法,可实现SOH的在线估计,但此等效电路模型缺乏物理和化学意义,在实际电动汽车运行环境下预测效果较差.数据驱动方法的一个主要问题是对电池退化的建模是基于恒定放电速率和恒定环境温度下采集的数据[13 ] ,在实践中,电池是在吸收了许多不确定性的变化的运行条件下运行的,这些不确定性将使这些模型表现不佳[14 ] .混合方法往往有更高的精度,对不同工况的SOH估计的适应性也较好[15 ] ,XU等[16 ] 采用等效电路模型描述电池动力学,递归最小二乘在线识别模型参数,无气味卡尔曼滤波器估计电池状态,提出了一个极简的电化学模型来描述电池内部锂含量的分布,并将SOH与锂的不可逆损耗导致的容量衰减联系起来,SOH估计平均误差在2%左右.电化学模型充分考虑了电池中实际的电化学反应过程,包括固相扩散过程、液相扩散和迁移过程等,但经典的伪二维(Pseudo two-dimensional,P2D) ...
... 其他11个模型参数通过激励-响应的方法[15 ] 进行辨识.具体参数辨识工况的电流激励以及端电压响应如图5 所示. ...
Co-estimating the state of charge and health of lithium batteries through combining a minimalist electrochemical model and an equivalent circuit model
1
2022
... 目前绝大多数SOH估计算法仅针对电池放电容量序列进行跟踪,在动态工况、宽温度范围内的适用性较差,且无法提供更为全面的电池性能衰退程度评估结果.SOH估计方法包括基于模型的方法、数据驱动方法、混合方法[11 ] .基于等效电路模型的方法运用广泛,FANG等[12 ] 提出了一种基于自回归等效电路模型的电池健康状态估计方法,可实现SOH的在线估计,但此等效电路模型缺乏物理和化学意义,在实际电动汽车运行环境下预测效果较差.数据驱动方法的一个主要问题是对电池退化的建模是基于恒定放电速率和恒定环境温度下采集的数据[13 ] ,在实践中,电池是在吸收了许多不确定性的变化的运行条件下运行的,这些不确定性将使这些模型表现不佳[14 ] .混合方法往往有更高的精度,对不同工况的SOH估计的适应性也较好[15 ] ,XU等[16 ] 采用等效电路模型描述电池动力学,递归最小二乘在线识别模型参数,无气味卡尔曼滤波器估计电池状态,提出了一个极简的电化学模型来描述电池内部锂含量的分布,并将SOH与锂的不可逆损耗导致的容量衰减联系起来,SOH估计平均误差在2%左右.电化学模型充分考虑了电池中实际的电化学反应过程,包括固相扩散过程、液相扩散和迁移过程等,但经典的伪二维(Pseudo two-dimensional,P2D) ...
1
2014
... 简化电化学模型是由单粒子模型改进而来.单粒子模型仅考虑电池内活性锂离子在电池固相材料上扩散过程,缺少了对活性锂离子在电解液中扩散过程及电势影响的描述,因而导致仿真精度较低.简化电化学模型考虑了活性锂离子液相扩散的影响,并将一系列用于描述电池内部扩散过程的偏微分方程简化为代数方程,提高了模型的计算效率和仿真精度.简化电化学模型基本框架如图1 所示[17 -18 ] . ...
1
2014
... 简化电化学模型是由单粒子模型改进而来.单粒子模型仅考虑电池内活性锂离子在电池固相材料上扩散过程,缺少了对活性锂离子在电解液中扩散过程及电势影响的描述,因而导致仿真精度较低.简化电化学模型考虑了活性锂离子液相扩散的影响,并将一系列用于描述电池内部扩散过程的偏微分方程简化为代数方程,提高了模型的计算效率和仿真精度.简化电化学模型基本框架如图1 所示[17 -18 ] . ...
1
2018
... 简化电化学模型是由单粒子模型改进而来.单粒子模型仅考虑电池内活性锂离子在电池固相材料上扩散过程,缺少了对活性锂离子在电解液中扩散过程及电势影响的描述,因而导致仿真精度较低.简化电化学模型考虑了活性锂离子液相扩散的影响,并将一系列用于描述电池内部扩散过程的偏微分方程简化为代数方程,提高了模型的计算效率和仿真精度.简化电化学模型基本框架如图1 所示[17 -18 ] . ...
1
2018
... 简化电化学模型是由单粒子模型改进而来.单粒子模型仅考虑电池内活性锂离子在电池固相材料上扩散过程,缺少了对活性锂离子在电解液中扩散过程及电势影响的描述,因而导致仿真精度较低.简化电化学模型考虑了活性锂离子液相扩散的影响,并将一系列用于描述电池内部扩散过程的偏微分方程简化为代数方程,提高了模型的计算效率和仿真精度.简化电化学模型基本框架如图1 所示[17 -18 ] . ...
Aging modes analysis and physical parameter identification based on a simplified electrochemical model for lithium-ion batteries
1
2020
... 在每个老化循环中,使用0.5C 倍率恒流充电至电池充电截止电压4.2 V,然后恒压充电至电流降为0.05C 以下.充电过程结束后静置5 min,电池以1C 、2C 恒流放电至电池放电截止电压2.5 V,再静置5 min后,进入下一个循环,每个老化循环工步重复上述过程20次.当电池容量衰退到80%时可认为电池寿命结束[19 ] ,结束电池老化试验. ...
Prediction of lithium-ion battery capacity with metabolic grey model
1
2016
... 新陈代谢灰色预测算法MGA具体的建立过程如下[20 ] . ...