电气工程学报, 2022, 17(4): 193-202 doi: 10.11985/2022.04.019

电力电子与电力传动

一种改进型同步整流正激变换器研究*

胡经纬,1, 王久和,2, 曲秋莳,1

1.北京交通运输职业学院城市轨道交通学院 北京 100096

2.北京信息科技大学自动化学院 北京 100192

Research on an Improved Synchronous Rectification Forward Converter

HU Jingwei,1, WANG Jiuhe,2, QU Qiushi,1

1. School of Urban Rail Transportation, Beijing Vocational Transportation College, Beijing 100096

2. School of Automation, Beijing Information Science and Technology University, Beijing 100192

通讯作者: 曲秋莳，女，1987年生，硕士，副教授。主要研究方向为电能变换器非线性控制。E-mail：qsq1007@163.com

收稿日期: 2022-01-21   修回日期: 2022-04-1  

基金资助: *国家自然科学基金.  51777012
北京市自然科学基金-市委联合.  KZ201911232045

Received: 2022-01-21   Revised: 2022-04-1  

作者简介 About authors

胡经纬，男，1990年生，硕士，讲师。主要研究方向为带恒功率负载的电能变换器的控制。E-mail：827794655@qq.com

王久和，男，1959年生，博士，教授，博士研究生导师。主要研究方向为电能变换控制、电能质量控制及微电网等。E-mail：wjhyhrwm@163.com

摘要

针对传统同步整流正激变换器效率较低、不适用于宽输入电压场合以及共态导通等问题，提出了一种改进型同步整流正激变换器。改进后的同步整流正激变换器利用辅助绕组两端电压驱动MOSFET管，该变换器效率较高，适用于宽输入电压场合，能够很好地解决共态导通问题。分析了改进型同步整流正激变换器的工作原理、工作模态，建立了改进型同步整流正激变换器的EL(Euler-lagrange, EL)模型，基于无源控制理论，采用阻尼注入方法设计了改进型同步整流正激变换器的无源控制器。无源控制器可使改进后的同步整流正激变换器具有良好的动、静态性能和对负载变化的鲁棒性。仿真及试验结果表明该变换器及其无源控制器是可行的。

关键词： 同步整流 ; 正激变换器 ; 无源控制 ; 阻尼注入

Abstract

Aiming at poor efficiency, inapplicable for wide input voltage occasion and direct conduction under traditional synchronous rectification forward converter, an improved synchronous rectification forward converter is proposed. The MOSFET of the improved converter is driven by both ends voltage of auxiliary winding. This converter has high efficiency, applicable for wide input voltage occasion and can solve the problem of direct conduction. The operating principle and the operating mode of the improved synchronous rectification forward converter are analyzed. The Euler-lagrange(EL) model of the synchronous rectification forward converter is established. Based on passivity based control theory, a passivity based controller of the improved synchronous rectification forward converter is designed by damping injection method. Good dynamic and static performance and robustness to load change of the improved synchronous rectification forward converter is achieved through the passivity-based controller. The simulation and experimental results show that the converter and its passivity based controller are feasible.

Keywords： Synchronous rectification ; forward converter ; passivity based control ; damping injecting

PDF (48313KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

胡经纬, 王久和, 曲秋莳. 一种改进型同步整流正激变换器研究*. 电气工程学报[J], 2022, 17(4): 193-202 doi:10.11985/2022.04.019

HU Jingwei, WANG Jiuhe, QU Qiushi. Research on an Improved Synchronous Rectification Forward Converter. Chinese Journal of Electrical Engineering[J], 2022, 17(4): 193-202 doi:10.11985/2022.04.019

1 引言

正激变换器因其结构简单、性能优良、工作可靠等优点，在光伏系统、中高压并网发电等领域获得了广泛应用[1]。对于正激变换器来说，整流及续流二极管的正向压降产生的功率损耗限制了变换器效率的提高，因此，采用通态电阻极低的功率MOSFET管替代整流及续流二极管，就能降低变换器损耗，进而提高变换器效率[2]。

针对需求，国内外学者致力于研究同步整流驱动控制技术，以期获得可靠的拓扑结构。文献[3]提出了一种自驱式同步整流电路，通过变压器副边为整流管及续流管提供驱动电压，但是该拓扑结构副边绕组电压较高，因而易造成功率器件高电压应力，且存在较大的共态导通问题。应用专门的同步整流驱动芯片进行驱动是较常见的方案[4]，这一类方案结构简单，但成本较高，同时由于芯片本身参数限制，较难应用于高压输出场合，可延展性较差。文献[5]采用电流型驱动电路对同步整流电路进行驱动，该电路驱动信号由次级电流所决定，缺点在于需要增加额外的电流互感器，这势必会增加变换器的体积与成本。

为克服上述变换器的缺点和不足，在现有同步整流正激变换器的基础上，本文提出一种改进型同步整流正激变换器，改进后的同步整流正激变换器无需驱动芯片，利用辅助绕组两端电压驱动副边整流管及续流管。该变换器只需要改变辅助绕组的匝数，就可以有效地驱动不同阈值电压的MOSFET管，适应性强；功率器件所承受的电压应力较低；副边整流管及续流管可快速通断，器件功率损耗较小，可以解决驱动死区和共态导通的问题。

在拓扑结构一定的情况下，变换器的性能主要由控制策略决定，国内外现有较为成熟的控制策略有模糊PID控制[6-7]、滑模变结构控制[8]、自抗扰控制[9]等。模糊PID控制的优点是原理简单、适用性强，缺点是控制精度较低，抗干扰能力较差。滑模变结构控制策略的优势在于能够克服系统的不确定性，具有较强的鲁棒性，缺点是存在抖振问题。自抗扰控制策略对外部扰动具有强抗扰能力，但是当模型阶次较高时，计算量大，控制周期长，实时性差。为克服上述控制策略的缺点和不足，本文构建改进型同步整流正激变换器的EL模型，采用阻尼注入方法[10-11]设计了改进型同步整流正激变换器的无源控制器。仿真及试验结果表明改进后的变换器性能良好、工作可靠，所设计的无源控制器可使改进后的变换器获得良好的动、静态性能和对负载变化的鲁棒性。

2 改进型同步整流正激变换器

2.1 传统同步整流正激变换器

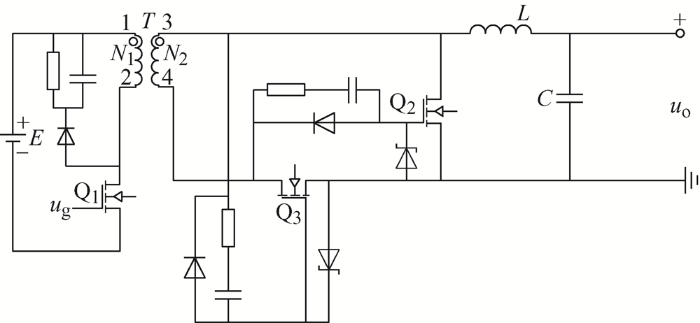
传统的同步整流正激变换器种类众多，图1所示变换器应用最为广泛。该变换器采用电压型自驱动式同步整流技术，副边整流管及续流管驱动信号直接由变压器副边绕组提供，不需要其他电路结构，成本低廉，结构简单。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   传统同步整流正激变换器结构


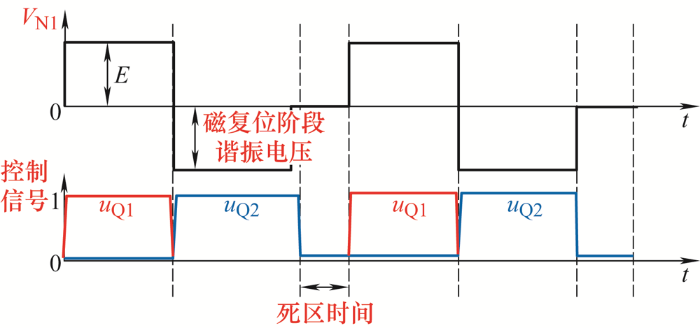
当原边开关管Q1导通时，副边整流管Q3导通，副边续流管Q2关断，当原边开关管Q1关断时，副边整流管Q3关断，副边续流管Q2导通。副边续流管的驱动电压取决于变压器原边的复位电压，而原边的复位电压由变压器激磁电感和Q1漏源极之间的极间电容谐振而来。传统同步整流正激变换器工作波形如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   传统同步整流正激变换器工作波形


图2中，VN1为变压器原边波形，uQ1为Q1控制信号，uQ2为Q2控制信号，经过分析，传统同步整流正激变换器有3个不足。

(1) 变压器磁复位之后，Q2无驱动信号，负载电流转移到Q2体二极管中，由于Q2的体二极管存在相对较高的压降，故降低了变换器的效率，变换器效率严重依赖变压器磁心复位方式[12-13]。

(2) 不适合宽输入电压场合，当输入电压过高时，Q3驱动信号很容易超过Q3的上限电压，当输入电压过低时，Q3驱动信号又不足以驱动Q3导通，同时，变压器原边的复位电压易造成Q2栅极承受较高的电压应力。

(3) Q1关断，Q2导通时刻，Q3无法保证立即关断，变换器存在较大的共态导通隐患。

2.2 拓扑结构

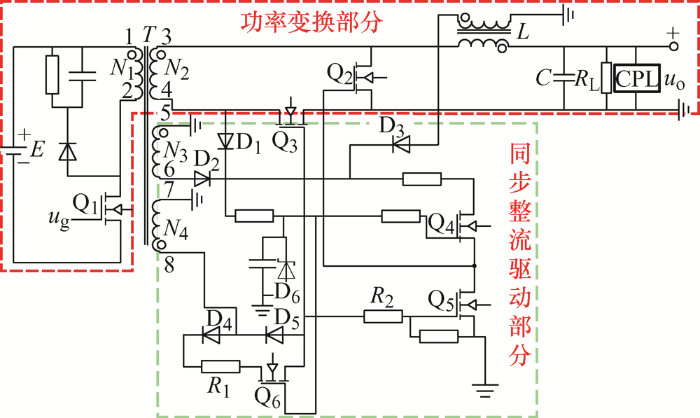
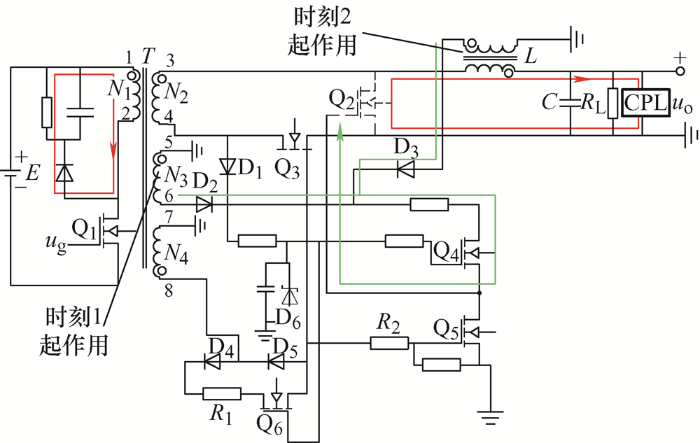
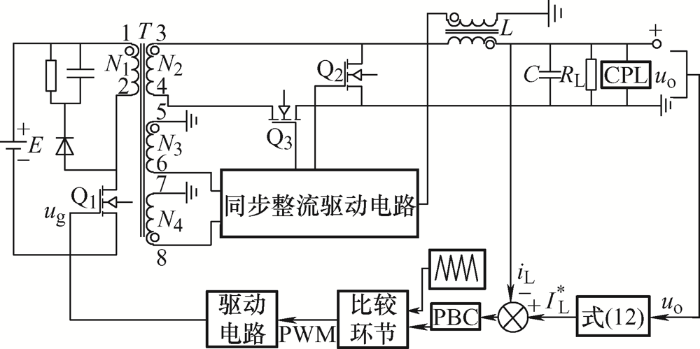
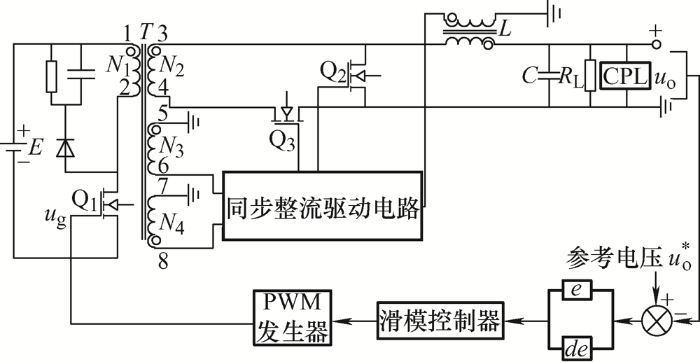
改进后同步整流正激变换器的电路如图3所示，由功率变换部分及同步整流驱动部分组成。功率变换部分由变压器T、原边开关管Q1(MOSFET管)、副边续流管Q2(MOSFET管)、副边整流管Q3(MOSFET管)、滤波电感L、滤波电容C组成，E为供电电源，R1为Q6限流电阻，R2为Q5限流电阻，RL为负载电阻，CPL(Constant power load)为恒功率负载。同步整流驱动部分由半导体器件D1~D5(高频开关二极管)、D6(稳压二极管)、Q4~Q6(MOSFET管)及部分电阻电容组成，同时，滤波电感L磁心上绕制感应线圈为Q2提供驱动电压。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   改进型同步整流正激变换器结构


在系统运行期间负载功率基本保持不变的这一类负载称为恒功率负载(CPL)。在一些应用场合中，电能变换器有时需要通过级联方式方能满足实际需求，而后级变换器通常具有近似的恒功率特性，因此，设计改进型同步整流正激变换器时要考虑在带恒功率负载(CPL)情况下的系统稳定性。

2.3 工作原理

改进型同步整流正激变换器有两个工作模态。能量的存储与传递在工作模态1及工作模态2两个模态下进行。

2.3.1 工作模态1

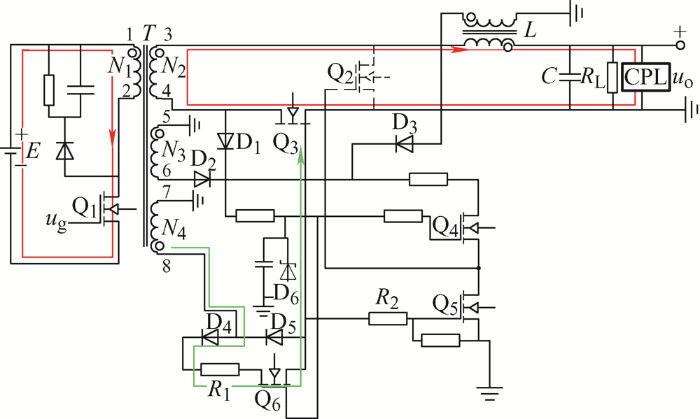
工作模态1如图4所示。Q1的控制信号ug=1时，Q1导通，Q2关断，Q3导通。电源E通过变压器T向滤波电感L、滤波电容C及负载供电，变压器T磁储能增加，此时变压器T的1、3、5、8端极性为正，滤波电感L储能为下一工作模态放电做准备。Q6因稳压二极管D6的稳定电压而保持长通。变压器T的8端通过D4及Q6为副边整流管Q3提供驱动电压[14]。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   改进型同步整流正激变换器工作模态1


在工作模态1，Q5因变压器T的N4绕组而导通，副边续流管Q2栅源极的极间电容通过Q5而迅速放电，保证Q2迅速关断，防止变换器副边短路。

2.3.2 工作模态2

工作模态2如图5所示。Q1的控制信号ug=0时，Q1关断，Q2导通，Q3关断，滤波电感L及滤波电容C向负载供电，变压器T通过旁路电阻、二极管及电容进行RCD磁复位，此时变压器T的2、4、6、7端极性为正。当Q1刚关断时，变压器T的N3绕组电压建立较快，变压器T的6端通过D2及Q4为副边续流管Q2提供驱动电压(时刻1)，当变压器内磁能进一步减少时，滤波电感L通过D3及Q4为Q2提供驱动电压(时刻2)，此时，滤波电感L起反激变换器变压器的作用[15]。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   改进型同步整流正激变换器工作模态2


在工作模态2，因变压器7端为正且与GND相连，故副边整流管Q3栅源极的极间电容通过D5及变压器T的N4绕组迅速放电，Q3栅源极电压因被拉到负电压而迅速关断，防止变换器副边短路。同理，Q5关断保证Q4源极为高电平，以此为Q2的导通提供条件。

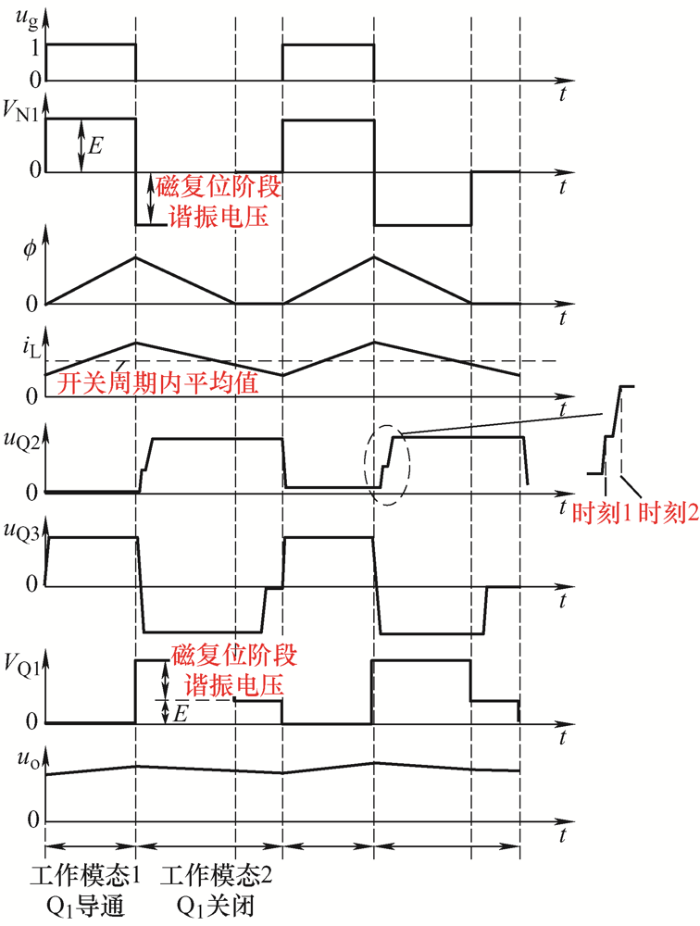
改进的同步整流正激变换器因变压器自身快速反应的特性，保证副边整流管及续流管可快速开通及关断，在最大程度提高效率的前提下，防止副边共态导通情况的发生。改进型同步整流正激变换器工作波形如图6所示。图6中，VN1为变压器原边电压，Φ为变压器磁通量，iL为滤波电感电流值，uQ2为Q2控制信号，uQ3为Q3控制信号，VQ1为Q1漏源极之间电压，uo为输出电压。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   改进型同步整流正激变换器工作电压


特别注意的是，当Q1占空比大于0.5时，需要调整变压器N3及N4绕组匝数以提升Q2和Q3的驱动能力。同理，当输入电压过低时，也要注意变压器N3及N4绕组匝数以保证Q2和Q3的栅极电压不会太低[16]。

3 性能比较

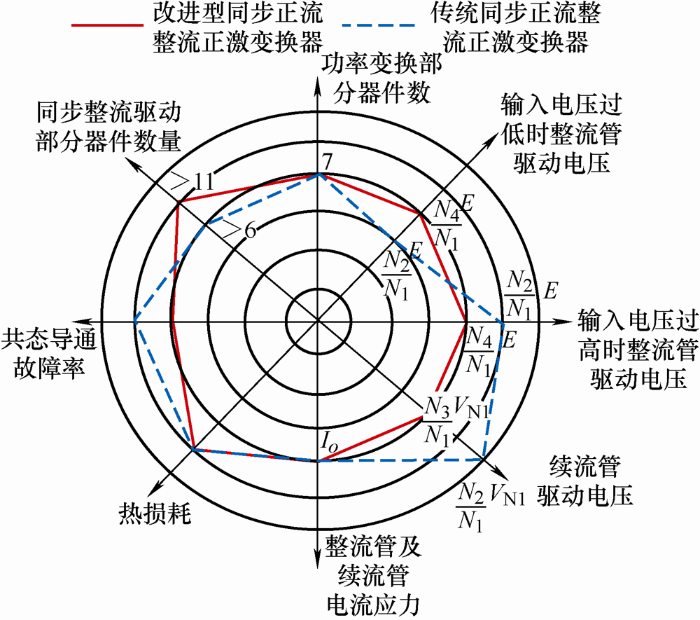
传统同步整流正激变换器同改进型同步整流正激变换器器件的电流电压应力、器件数量及热损耗等指标比较如表1及图7所示。

表1   性能指标

参数传统型改进型
输入电压EE
负载电流IoIo
变压器
原边电压		VN1VN1
续流管
驱动电压		VN1N2/N1VN1N3/N1
整流管
驱动电压		EN2/N1EN4/N1
续流管栅极电容放电路径Q2栅极直接至副边GNDQ2栅极直接至副边GND
整流管栅极电容放电路径Q3栅极直接至副边GNDQ3栅极经变压器N4绕组后至副边GND
主要发热器件变压器T、滤波电感L、原边开关管Q1、副边续流管Q2、副边整流管Q3变压器T、滤波电感L、原边开关管Q1、副边续流管Q2、副边整流管Q3

注：副边GND与输出负端为等电位。

新窗口打开| 下载CSV


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   性能指标综合比较1


在续流管导通，整流管关断时刻，改进型同步整流正激变换器整流管Q3栅极电容经变压器N4绕组向副边GND放电，在此时刻，变压器N4绕组7端电压为正，8端电压为负，N4绕组两端电压可加速Q3栅极电容的放电过程，因而Q3立即关断，而传统变换器无辅助绕组加速放电，故在此时刻，改进型同步整流正激变换器共态导通故障率较低。两种变换器功率变换部分相同，主要发热器件类型及数量一致，故两种变换器热损耗基本相同。

因传统同步整流正激变换器N2绕组匝数受限于输出电压的限制而不能变化，故传统同步整流正激变换器副边整流管驱动电压无法灵活设计，整流管较难灵活选型。而改进型同步整流正激变换器N4绕组匝数可灵活设计，整流管选型较灵活。

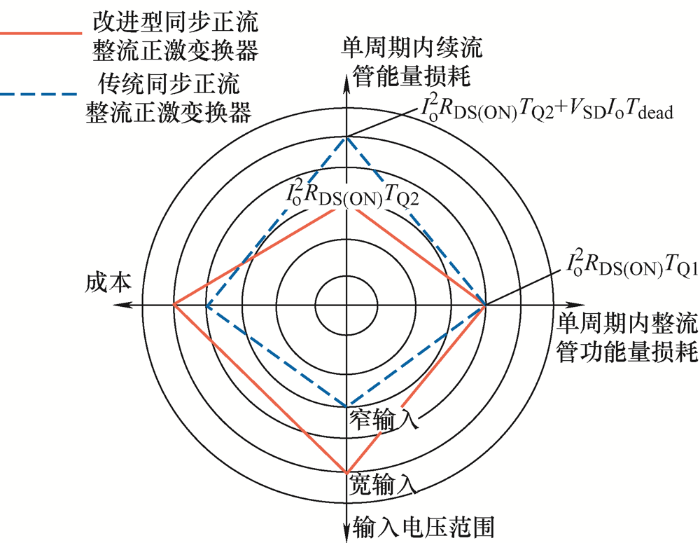
传统同步整流正激变换器同改进型同步整流正激变换器成本、输入电压范围及器件功率损耗等性能指标比较如图8所示。图8中，RDS(ON)为整流管及续流管漏源极导通电阻，TQ2为副边续流管导通时间，TQ1为原边开关管及副边整流管导通时间，VSD为副边续流管体二极管压降，Tdead为死区时间。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   性能指标综合比较2


由图8可知，因改进型同步整流正激变换器副边驱动电压采用单独绕组进行驱动，故适用于宽输入电压场合，同时，续流管功率损耗较低，故改进型同步整流正激变换器整体效率高于传统同步整流正激变换器。改进型与传统型功率变换部分结构一致，新增的辅助元器件属于小功率器件，故成本较低，改进型同步整流正激变换器整机成本略高于传统同步整流正激变换器。

4 改进型同步整流正激变换器数学模型及无源控制器

4.1 改进型同步整流正激变换器数学模型

iL为通过滤波电感L的电流，uC为滤波电容C的两端电压，输出电压为uo，RL为变换器负载，CPL为恒功率负载，设恒功率负载功率为P。设

$\left\{ \begin{matrix} {{x}_{1}}\text{=}{{i}_{\text{L}}}(t){{\text{}}_{T}}=\frac{1}{{{T}_{\text{S}}}}\int_{t}^{t+{{T}_{s}}}{{{i}_{\text{L}}}(\tau )\text{d}\tau }\ \ \\ {{x}_{2}}\text{=}{{u}_{\text{C}}}(t){{\text{}}_{T}}=\frac{1}{{{T}_{\text{S}}}}\int_{t}^{t+{{T}_{s}}}{{{u}_{\text{C}}}(\tau )\text{d}\tau \ } \\ \end{matrix} \right.$

则x1、x2分别代表iL、uC在一个开关周期TS内的平均值，根据图1可得变换器的数学模型为

$\left\{ \begin{matrix} L\frac{\text{d}{{x}_{\text{1}}}}{\text{d}t}+{{x}_{2}}={{u}_{\mathrm{g}}}\frac{{{N}_{2}}}{{{N}_{1}}}E \\ C\frac{\text{d}{{x}_{\text{2}}}}{\text{d}t}+\frac{{{x}_{2}}}{R}+\frac{P}{{{x}_{2}}}={{x}_{1}} \\ \end{matrix} \right.$

式中，ug为原边开关管Q1的开关信号；N2E/N1为当Q1闭合时变压器绕组N2两端电压；P为恒功率负载功率。

4.2 改进型同步整流正激变换器EL模型

把数学模型式(2)变为矩阵形式

$M\dot{x}+Jx+Rx=u$
$\begin{array}{c} \boldsymbol{J}=\left(\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array}\right) \quad \boldsymbol{u}=\left(\begin{array}{c} u_{\mathrm{g}} \frac{N_{2}}{N_{1}} E \\ 0 \end{array}\right) \quad \boldsymbol{M}=\left(\begin{array}{cc} L & 0 \\ 0 & C \end{array}\right) \\ \boldsymbol{R}=\left(\begin{array}{cc} 0 & 0 \\ 0 & \frac{1}{R_{\mathrm{L}}}+\frac{P}{u_{\mathrm{C}}^{2}} \end{array}\right) \quad \boldsymbol{x}=\left(\begin{array}{l} x_{1} \\ x_{2} \end{array}\right) \end{array}$

由于$J=-{{J}^{\text{T}}}$为反对称矩阵形式，则式(3)为改进型同步整流正激变换器的EL模型。

4.3 无源控制器设计

设${{x}_{e}}=x-{{x}^{*}}$，${{x}^{*}}$为电感电流或电容电压的期望值。则由式(3)可得[17-18]

$M{{\dot{x}}_{\mathrm{e}}}+J{{x}_{\mathrm{e}}}+R{{x}_{\mathrm{e}}}=u-M{{\dot{x}}^{*}}-J{{x}^{*}}-R{{x}^{*}}$

取误差能量函数

$V=\frac{1}{2}x_{\mathrm{e}}^{\text{T}}M{{x}_{\mathrm{e}}}$

为加快能量耗散，需要注入阻尼${{R}_{a}}$。由式(4)可得

$M{{\dot{x}}_{\mathrm{e}}}=u-M{{\dot{x}}^{*}}-J{{x}^{*}}-R{{x}^{*}}-J{{x}_{\mathrm{e}}}-\left( {{R}_{\mathrm{d}}}-{{R}_{\mathrm{a}}} \right){{x}_{\mathrm{e}}}$

式中，${{R}_{\mathrm{d}}}=R\text{+}{{R}_{\mathrm{a}}}$，阻尼矩阵为${{R}_{\mathrm{a}}}=\left( \begin{matrix} {{r}_{\mathrm{a}}} & 0 \\ 0 & \frac{1}{{{r}_{\mathrm{a}}}} \\ \end{matrix} \right)$，ra为可设定的正常数。根据式(6)可得无源控制器

$u=M{{\dot{x}}^{*}}+J{{x}^{*}}+R{{x}^{*}}-{{R}_{\mathrm{a}}}{{x}_{\mathrm{e}}}$

无源控制器式(7)能使$\dot{V}=-x_{\mathrm{e}}^{\mathrm{T}}{{R}_{\mathrm{d}}}{{x}_{\mathrm{e}}}<0$，则$V$为能够收敛到0的函数，则有xe收敛到0，达到控制目的[19]。由于x*为恒定值，则有$M{{\dot{x}}^{*}}=0$，无源控制器可简化为

$u=J{{x}^{*}}+R{{x}^{*}}-{{R}_{\mathrm{a}}}{{x}_{\mathrm{e}}}$

由式(8)可得

$\begin{matrix} \left( \begin{matrix} {{u}_{\mathrm{g}}}\frac{{{N}_{2}}}{{{N}_{1}}}E \\ 0 \\ \end{matrix} \right)=\left( \begin{matrix} 0 & 1 \\ -1 & 0 \\ \end{matrix} \right)\left( \begin{matrix} x_{1}^{*} \\ x_{2}^{*} \\ \end{matrix} \right)+\left( \begin{matrix} 0 & 0 \\ 0 & \frac{1}{{{R}_{\text{L}}}}+\frac{P}{u_{\text{C}}^{2}} \\ \end{matrix} \right)\left( \begin{matrix} x_{1}^{*} \\ x_{2}^{*} \\ \end{matrix} \right)- \\ \left( \begin{matrix} {{r}_{\mathrm{a}}} & 0 \\ 0 & \frac{1}{{{r}_{\mathrm{a}}}} \\ \end{matrix} \right)\left( \begin{matrix} {{x}_{1}}-x_{1}^{*} \\ {{x}_{2}}-x_{2}^{*} \\ \end{matrix} \right) \\ \end{matrix}$

式中，$x_{1}^{*}$为滤波电感L的电流期望值；$x_{2}^{*}$为滤波电容C的电压期望值。即可得到

$\left\{ \begin{matrix} {{u}_{\mathrm{g}}}\frac{{{N}_{2}}}{{{N}_{1}}}E=x_{2}^{*}-{{r}_{\mathrm{a}}}({{x}_{1}}-x_{1}^{*})\begin{matrix} {} & {} & {} \\ \end{matrix} \\ -x_{1}^{*}+(\frac{1}{{{R}_{\text{L}}}}+\frac{P}{u_{\text{C}}^{2}})x_{2}^{*}-\frac{1}{{{r}_{\mathrm{a}}}}({{x}_{2}}-x_{2}^{*})\text{=}0 \\ \end{matrix} \right.$

经研究分析，由式(10)可得Q1的控制信号

${{u}_{\mathrm{g}}}=\frac{\left( x_{2}^{*}-{{r}_{\mathrm{a}}}({{x}_{1}}-x_{1}^{*}) \right){{N}_{1}}}{{{N}_{2}}\times E}$

由式(10)可得滤波电感电流IL的计算公式

${{I}_{\text{L}}}=x_{1}^{*}=(\frac{1}{{{R}_{\text{L}}}}+\frac{P}{u_{\text{C}}^{2}})x_{2}^{*}-\frac{1}{{{r}_{\mathrm{a}}}}({{x}_{2}}-x_{2}^{*})$

改进型同步整流正激变换器无源控制框图如图9所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

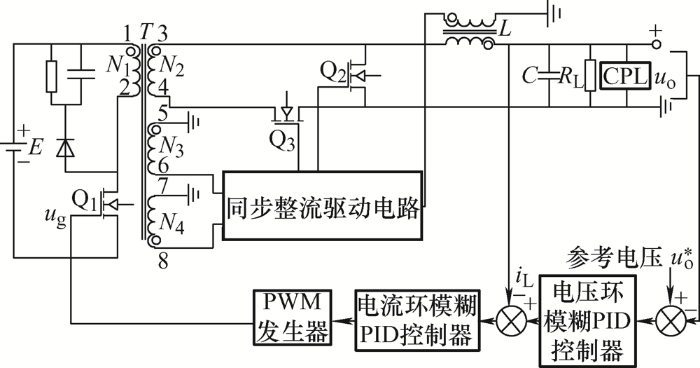
图9   改进型同步整流正激变换器带CPL无源控制框图


5 仿真研究

5.1 参数选择

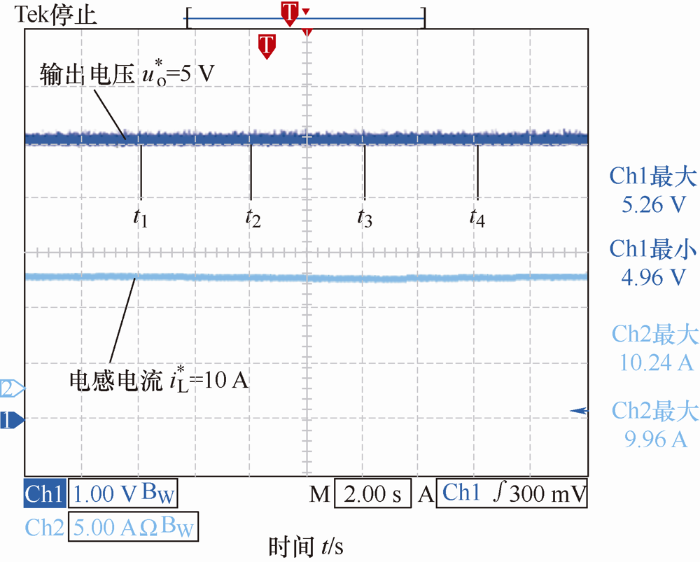
对改进的同步整流正激变换器进行仿真研究，参数选取如下：变压器T原边感量30 μH，变压器变比${{{N}_{1}}}/{{{N}_{2}}}\;={5}/{2}\;$，L=10 μH，C=300 μF，RL=1 Ω，E=28 V，恒功率负载功率P=25 W，变换器PWM开关频率为fs=250 kHz，阻尼注入ra参数选取12，输出电压期望值${{u}_{\mathrm{o}}}={{u}_{\text{C}}}=x_{2}^{*}=5\ \text{V}$。则根据式(12)可得系统达到稳态时的电感电流$x_{1}^{*}=i_{\text{L}}^{\text{*}}\text{=}10\ \text{A}$。

5.2 仿真结果

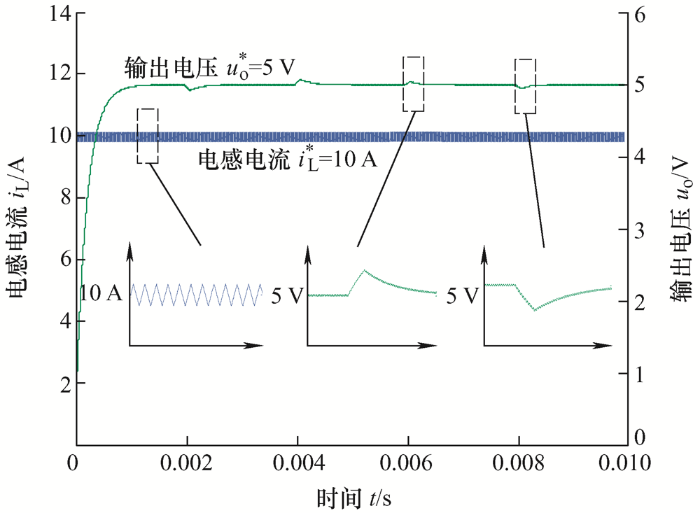
图10为电源电压变化时系统的动态响应过程，仿真时间0.01 s。在0.002 s时，电源电压降至10 V，在0.004 s时，电源电压恢复至28 V，在0.006 s时，电源电压升至36 V，在0.008 s时，电源电压恢复至28 V。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   输入电压变化时系统动态响应


由图10可知，改进型同步整流正激变换器可迅速收敛于期望值，系统全局稳定，无奇异点，变换器拥有较好的电压调整率。

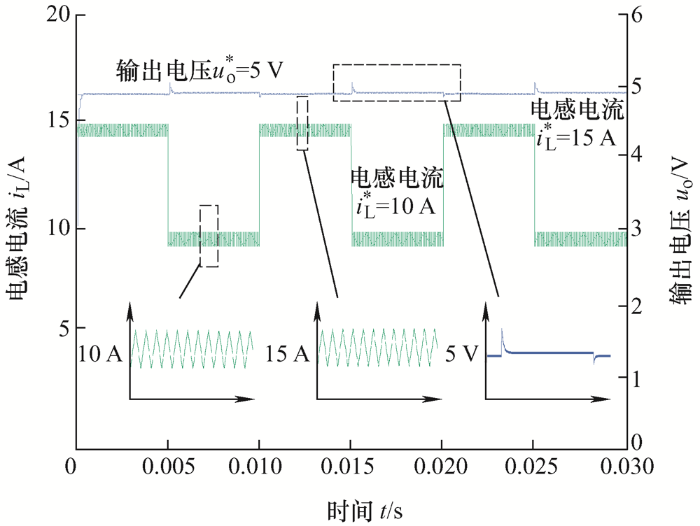
将仿真计算时间改为0.03 s，电阻负载以100 Hz频率在1 Ω至0.5 Ω之间做动态变化，恒功率负载不变，仿真结果如图11所示。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   负载变化时系统动态响应


通过图11仿真结果可以看出，当电阻负载动态变化时，改进型同步整流正激变换器依然能迅速收敛于期望值，系统全局稳定，有良好的负载调整率。

为进一步分析变换器无源控制器的优劣性，设计变换器的模糊PID控制器及滑模变结构控制器，并将两种控制器的控制效果与无源控制器进行仿真对比[20-21]。

模糊PID控制策略是将模糊控制算法与经典PID控制算法相结合，该策略原理简单，适应性强，控制框图如图12所示。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   改进的同步整流正激变换器带CPL模糊PID控制框图


滑模变结构控制的原理是控制器的控制率随着被控对象的变化而变化，使得系统能够按照事先预定的状态轨迹进行小幅度、高频率的上下运动，控制框图如图13所示。

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13   改进的同步整流正激变换器带CPL滑模变结构控制图


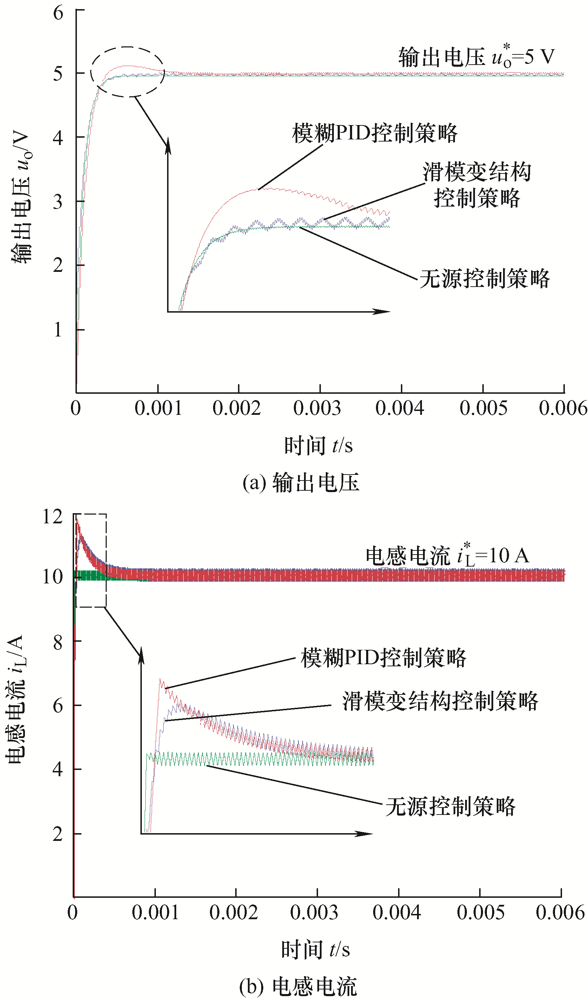
在没有任何扰动的情况下，三种控制策略的启动过程如图14所示，仿真时间为0.006 s。由图14可知，三种控制策略均可使改进型同步整流正激变换器快速收敛于期望值，模糊PID控制在变换器达到稳态前，存在超调问题。滑模变结构控制无超调问题，但是变换器输出电压存在振荡现象，在这种情况下，变换器严重依赖输出滤波电路，合适的输出滤波电路可以解决振荡现象，反之经滤波电感电容作用后振荡现象有可能加剧，基于无源控制策略的变换器可快速收敛于期望值。

图14

新窗口打开| 下载原图ZIP| 生成PPT

图14   三种控制策略下启动波形对比


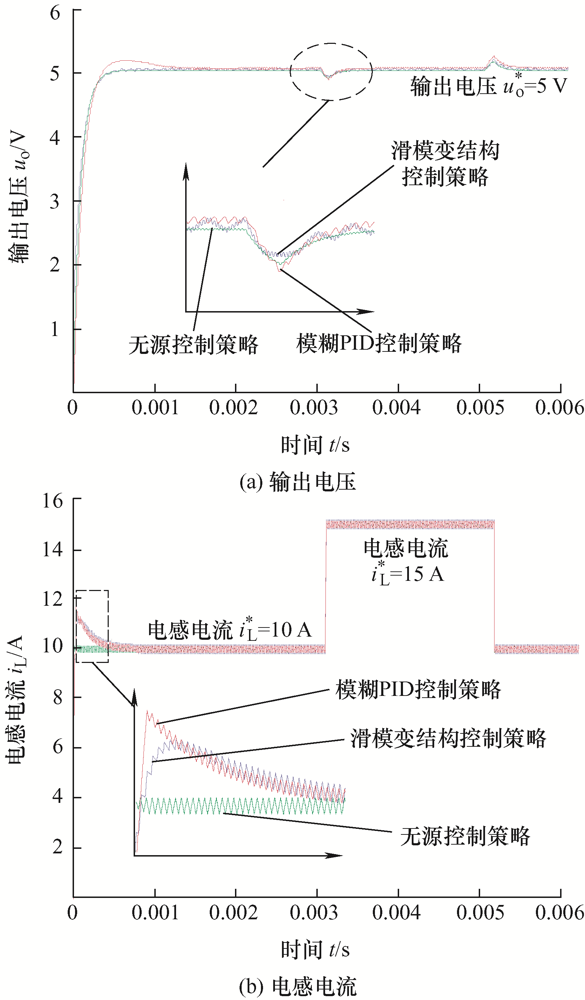
为验证三种控制策略的鲁棒性，在0.003 s时将电阻负载由1 Ω变为0.5 Ω，在0.005 s时将电阻负载由0.5 Ω变为1 Ω，仿真结果如图15所示。

图15

新窗口打开| 下载原图ZIP| 生成PPT

图15   负载变化时三种控制策略动态响应


由图15可知，在负载变化时，三种控制策略均可快速收敛于期望值，相比之下，模糊PID控制策略存在一定的超调问题。

6 试验研究

为验证本文所提出的拓扑结构，研制一台原理样机，并搭建试验系统，试验系统装置如图16所示。

图16

新窗口打开| 下载原图ZIP| 生成PPT

图16   试验系统装置


样机选用器件参数如表2所示，变压器T磁材不开气隙，原边感量30 μH，滤波电感L磁材开气隙，感量10 μH，滤波电容C的容值为300 μF。

表2   样机主要技术参数

参数数值/型号备注
输入电压/V10~36—
输出电压/V5—
开关频率/kHz250—
恒功率负载/W25—
电阻负载/Ω1—
原边开关管Q1SI4190DYVISHAY公司
副边续流管Q2IRF7842IR公司
副边整流管Q3IRF7842IR公司
半导体器件D1~D5BAS21HNXP公司
半导体器件Q4~Q62N7002EVISHAY公司

新窗口打开| 下载CSV


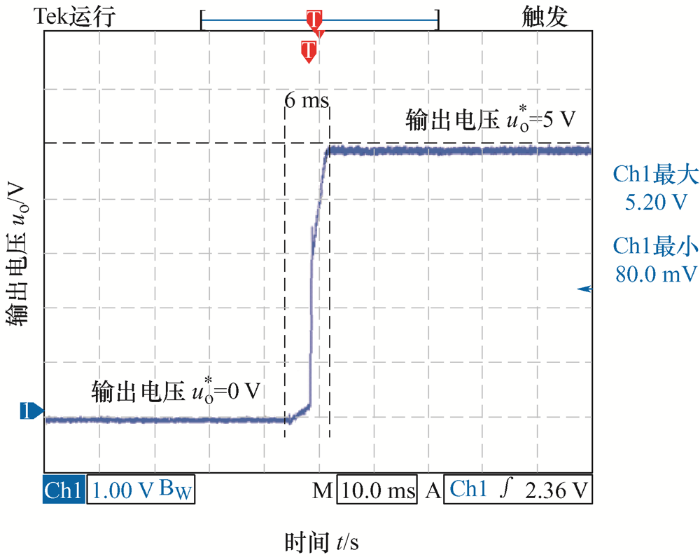
试验样机启动波形如图17所示，改进型同步整流正激变换器可行，输出电压在启动时无超调，无源控制器可迅速跟踪给定值。

图17

新窗口打开| 下载原图ZIP| 生成PPT

图17   试验样机启动波形


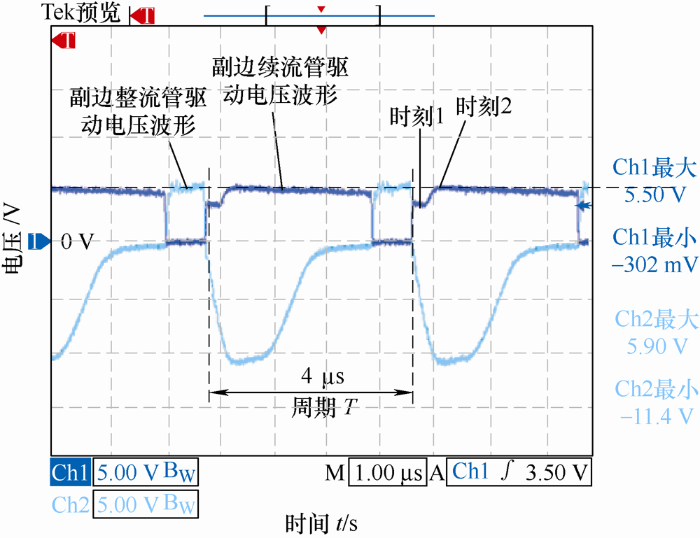
图18为副边整流管及续流管驱动电压波形。由图18可知同步整流驱动信号死区时间极短且无共态导通现象发生，时刻1由变压器绕组N3提供驱动电压，时刻2由滤波电感L提供驱动电压，同步整流驱动部分工作可靠稳定。

图18

新窗口打开| 下载原图ZIP| 生成PPT

图18   副边整流管及续流管驱动电压波形


图19为电源电压变化时系统的动态响应过程，在t1时刻，电源电压降至10 V，在t2时刻，电源电压恢复至28 V，在t3时刻，电源电压升至36 V，在t4时刻，电源电压恢复至28 V。由图19可知，系统闭环响应迅速，输入电压动态变化对电压输出无影响，无源控制器可使改进型同步整流正激变换器获得良好的动、静态性能，改进型同步整流正激变换器有良好的电压调整率。

图19

新窗口打开| 下载原图ZIP| 生成PPT

图19   输入电压变化时系统动态响应


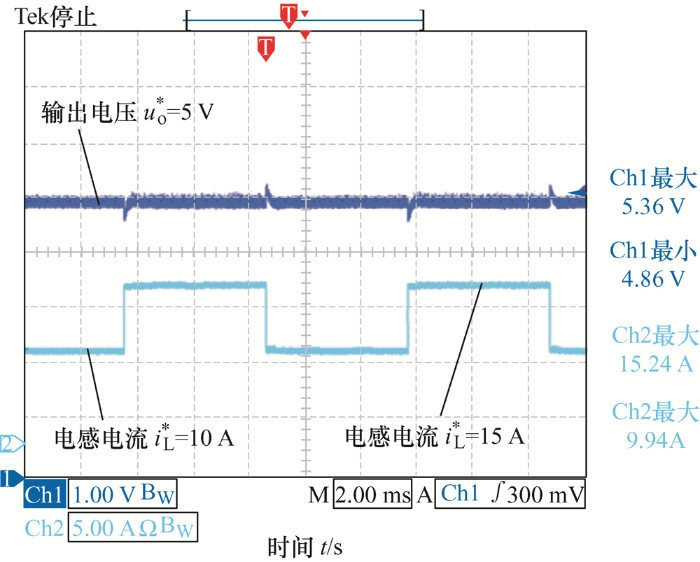
电阻负载以100 Hz频率在1 Ω至0.5 Ω之间做动态变化，恒功率负载不变，试验结果如图20所示，系统闭环响应迅速，改进型同步整流正激变换器有良好的负载调整率，改进后的同步整流正激变换器完全符合下一级用电设备的要求。

图20

新窗口打开| 下载原图ZIP| 生成PPT

图20   负载变化时系统动态响应


改进型同步整流正激变换器在不同输入电压下的电特性如表3所示。

表3   样机电特性

参数输入电压条件/V
102836
输入空载电流/mA90.753.462.7
输入满载电流/A5.596 81.978 01.529 8
输出空载电压/V5.016 05.016 05.019 7
输出满载电压/V4.994 14.994 25.001 1
效率(%)89.23190.17490.809
电压调整率/mV7.0
负载调整率/mV21.80
输出电压纹波(满载)/mV646658

新窗口打开| 下载CSV


由表3可知，试验样机效率达90%。需要指出，试验样机功率较小且功能较全，含输入输出滤波电路及保护电路。如果只考虑变换器本体部分的转换效率或增大样机功率，效率会高于实测值。新型同步整流正激变换器有良好的电源调整率及负载调整率，纹波电压较低，性能优良，工作可靠。

7 结论

本文提出了一种改进型同步整流正激变换器，所提出的变换器利用辅助绕组两端电压驱动MOSFET管，设计了改进型同步整流正激变换器的无源控制器，通过仿真及试验对改进型同步整流正激变换器及其无源控制器的有效性进行了验证，得出如下结论。

(1) 本文提出的拓扑结构工作可靠，利用辅助绕组实现副边整流管及续流管快速通断，具有良好的电压调整率和负载调整率；与传统同步整流正激变换器相比，功率器件所承受的电压应力较低；副边整流管及续流管可快速通断，器件利用率高，可以解决驱动死区和共态导通的问题。

(2) 所设计的无源控制器可快速跟踪与期望输出电压相对应的期望电流，可使改进型同步整流正激变换器获得良好的动、静态性能和对负载变化的鲁棒性。与模糊PID控制器和滑模变结构控制器的控制效果相比，变换器输出电压在无源控制器的控制下无超调问题，无振荡问题。

参考文献

李龙春, 嵇保健, 洪峰, 等.

1500V三电平正激变换器

[J]. 电工技术学报, 2018, 33(9):2044-2054.

[本文引用: 1]

LI Longchun, JI Baojian, HONG Feng, et al.

1500V three-level forward converter

[J]. Transactions of China Electrotechnical Society, 2018, 33(9):2044-2054.

[本文引用: 1]

HOANG N K, LEE S, WOO Y J.

A zero current detector with low negative inductor current using forced freewheel switch operation in synchronous DC-DC converter

[C]// 2014 IEEE Fifth International Conference on Communications and Electronics (ICCE). IEEE, 2014:318-322.

[本文引用: 1]

李佳晨, 彭祥宇, 吕征宇.

一种新型自驱动同步整流电路

[J]. 电力电子技术, 2018, 52(1):67-69.

[本文引用: 1]

LI Jiachen, PENG Xiangyu, LÜ Zhengyu.

A new self-driven synchronous rectification circuit

[J]. Power Electronics, 2018, 52(1):67-69.

[本文引用: 1]

黄莹. PFM模式同步整流DC-DC升压转换器芯片的设计[D]. 南京: 南京邮电大学, 2019.

[本文引用: 1]

HUANG Ying. Design of synchronous rectification DC-DC boost converter in PFM mode[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2019.

[本文引用: 1]

陈增禄, 杨欢, 方日, 等.

同步整流自适应电流驱动技术

[J]. 电力电子技术, 2018, 52(4):69-72.

[本文引用: 1]

CHEN Zenglu, YANG Huan, FANG Ri, et al.

Research on adaptive current self-driven circuit of synchronous rectification

[J]. Power Electronics, 2018, 52(4):69-72.

[本文引用: 1]

张博彦, 齐铂金, 周阳.

基于模糊PID算法的半桥DC/DC控制器的优化设计

[J]. 电力电子技术, 2018, 52(9):74-77.

[本文引用: 1]

ZHANG Boyan, QI Bojin, ZHOU Yang.

Optimal design of half-bridge DC/DC controller based on fuzzy PID algorithm

[J]. Power Electronics, 2018, 52(9):74-77.

[本文引用: 1]

梁光耀, 杜贵平, 刘源俊.

宽工作范围LLC谐振变换器模糊PID控制策略

[J]. 电源学报, 2020, 18(2):138-144.

[本文引用: 1]

LIANG Guangyao, DU Guiping, LIU Yuanjun.

Fuzzy PID control strategy for LLC resonant converter with wide operating range

[J]. Journal of Power Supply, 2020, 18(2):138-144.

[本文引用: 1]

陆翔, 谢运祥, 桂存兵, 等.

基于无源性与滑模变结构控制相结合的VIENNA整流器控制策略

[J]. 电力自动化设备, 2014, 34(10):110-115.

[本文引用: 1]

LU Xiang, XIE Yunxiang, GUI Cunbing, et al.

VIENNA rectifier control strategy based on passivity control and sliding mode variable structure control

[J]. Electric Power Automation Equipment, 2014, 34(10):110-115.

[本文引用: 1]

王孝洪, 吴丰, HOANG T T G, 等.

线性自抗扰控制在全桥DC-DC变换器中的应用

[J]. 控制理论与应用, 2018, 35(11):1610-1616.

[本文引用: 1]

WANG Xiaohong, WU Feng, HOANG T T G, et al.

Application of linear active disturbance rejection control in full-bridge DC-DC converters

[J]. Control Theory & Applications, 2018, 35(11):1610-1616.

[本文引用: 1]

胡经纬, 王久和, 唐骐.

基于EL模型的Cuk变换器无源控制器

[J]. 北京信息科技大学学报, 2013, 28(5):67-71.

[本文引用: 1]

HU Jingwei, WANG Jiuhe, TANG Qi.

Passivity based controller of Cuk converter based on EL model

[J]. Journal of Beijing Information Science and Technology University, 2013, 28(5):67-71.

[本文引用: 1]

崔健, 王久和.

基于最优阻尼注入的Buck变换器无源控制研究

[J]. 电气工程学报, 2018, 13(6):7-13.

[本文引用: 1]

CUI Jian, WANG Jiuhe.

Study of passivity-based control of Buck converter based on optimal damping injection

[J]. Journal of Electrical Engineering, 2018, 13(6):7-13.

[本文引用: 1]

李洪珠, 范茏茏.

双管正激变换器多种导磁材料电磁集成

[J]. 电气工程学报, 2022, 17(1):148-155.

[本文引用: 1]

LI Hongzhu, FAN Longlong.

Dual-tube forward converter with electromagnetic integration of various magnetic materials

[J]. Journal of Electrical Engineering, 2022, 17(1):148-155.

[本文引用: 1]

刘树林, 张海亮, 王航杰, 等.

抑制输出能量倒灌的二次侧自复位正激变换器的能量传输过程分析

[J]. 电工技术学报, 2020, 35(增刊2):477-483.

[本文引用: 1]

LIU Shulin, ZHANG Hailiang, WANG Hangjie, et al.

A new forward converter with self-magnetically reset on the secondary side

[J]. Transactions of China Electrotechnical Society, 2020, 35(Suppl. 2):477-483.

[本文引用: 1]

王志强. 精通开关电源设计[M]. 北京: 人民邮电出版社, 2013.

[本文引用: 1]

WANG Zhiqiang. Proficient in switching power supply design[M]. Beijing: The People’s Posts and Telecommunications Press, 2013.

[本文引用: 1]

YAO J, ZHENG K, ABRAMOVITZ A.

Dynamic analysis of the switched inductor buck converter

[C]// Annual Conference of the IEEE Industrial Electronics Society, 2019, 1:1721-1725.

[本文引用: 1]

丁志刚, 汪世平, 周华良.

一种新型外驱动同步整流电路

[J]. 电力系统自动化, 2012, 36(3):97-100.

[本文引用: 1]

DING Zhigang, WANG Shiping, ZHOU Hualiang.

A novel out-driving synchronous rectifier circuit

[J]. Automation of Electric Power Systems, 2012, 36(3):97-100.

[本文引用: 1]

胡经纬, 王久和, 唐骐.

一种新型高增益Cuk变换器研究

[J]. 电工技术学报, 2014, 29(增刊1):337-344.

[本文引用: 1]

HU Jingwei, WANG Jiuhe, TANG Qi.

Research on a new type of high gain Cuk converter

[J]. Transactions of China Electrotechnical Society, 2014, 29(Suppl. 1):337-344.

[本文引用: 1]

王振业, 王久和, 张梦壕.

多变换器系统无源控制策略研究

[J]. 电气工程学报, 2022, 17(1):63-70.

[本文引用: 1]

WANG Zhenye, WANG Jiuhe, ZHANG Menghao.

Research on passivity-based control strategy of multi-converter system

[J]. Journal of Electrical Engineering, 2022, 17(1):63-70.

[本文引用: 1]

GU Yunjie, LI Wuhua, HE Xiangning.

Passivity-based control of DC microgrid for self-disciplined stabilization

[J]. IEEE Transactions on Power System, 2015, 30(5):2623-2632.

DOI:10.1109/TPWRS.2014.2360300      URL     [本文引用: 1]

周痛快, 宾洋, 罗文广, 等.

Buck变换器的模糊PI控制研究

[J]. 广西科技大学学报, 2021, 32(3):74-79.

[本文引用: 1]

ZHOU Tongkuai, LUO Wenguang, et al.

Research on fuzzy PI control of Buck converter

[J]. Journal of Guangxi University of Science and Technology, 2021, 32(3):74-79.

[本文引用: 1]

孙文静. Buck型DC-DC变换器的滑模控制研究[D]. 北京: 北京交通大学, 2015.

[本文引用: 1]

SUN Wenjing. Research on sliding mode control for DC-DC Buck converter[D]. Beijing: Beijing Jiaotong University, 2015.

[本文引用: 1]

/

〈 〉