1 引言
飞轮电池是一种利用高速旋转的飞轮存储能量的机电一体化产品,具有能量密度高、使用寿命长、充放电性能强、无污染且环境友好等独特优点[1 ⇓ ⇓ -4 ] ,在不间断电源、电动汽车、轨道交通、卫星和航天器等领域具有巨大的潜在应用前景[5 -6 ] 。飞轮电机是飞轮电池能量转换的核心部件,决定了飞轮系统的运行效率和可靠性等。常见的飞轮电机主要包括:感应电机、开关磁阻电机、同步磁阻电机和永磁无刷直流电机等。开关磁阻电机转子无永磁体和绕组,具有结构简单坚固、可靠性高、容错能力强、在高速和恶劣环境下运行性能好等优点,非常适合飞轮电池应用[7 ] 。然而高速运行下,开关磁阻电机传统轴承支撑存在摩擦磨损,导致飞轮电池效率低、自放电严重等问题。磁悬浮开关磁阻电机充分利用开关磁阻电机的高速性能和磁悬浮技术,有效实现转子自悬浮,具有高速无摩擦磨损等优点,将其引入飞轮形成磁悬浮飞轮电机(Bearingless flywheel machine, BFM),可以简化结构、降低损耗,提高临界转速、运行效率和可靠性[8 ] 。轴向永磁BFM(Axial permanent magnet BFM, APM-BFM)进一步通过轴向分相和永磁偏置设计,可实现超低功耗四自由度悬浮,是飞轮电池悬浮运行与能量变换的理想选择之一[9 ] 。
飞轮电池多运行于大功率快速充放电状态,由于APM-BFM具有较高的功率密度,并且采用内定子结构,内嵌式集中绕组散热面积较小,热负荷密度大,导致电机运行时温升问题突出。电机温升是电机性能的重要指标,过高的温度会影响飞轮电池的运行性能、可靠性和使用寿命。因此,在设计APM-BFM过程中对其温度场的分析计算尤为重要,分析计算电机温度场,需要准确计算电机内各部分损耗。APM-BFM损耗主要包括定子绕组铜损、定转子铁心损耗以及电机在高速运转下与空气摩擦产生的机械损耗,而APM-BFM内部磁场是非正弦性、高度非线性,这使得APM-BFM损耗计算成为难点问题。
目前,国内外常用计算电机温升的方法有简化公式法[10 ] 、等效热路法[11 ] 、等效热网络法[12 ] 和有限元法[13 -14 ] 。其中简化公式法计算方法简易,但存在较大误差;等效热路法可求解电机各部分平均温度,但无法得到电机准确的温度分布;等效热网络法依据热传导定律中热对流、温度和热阻三者关系,依照电路中KVL与KCL原理,近似做出等效热网络图,分析各部分的温度[15 ] 。有限元法将温度场计算模型剖分为细小的单元体,通过对每一个细小单元体求解计算再逼近整体解,该方法计算准确、应用广泛、适用性强。
本文以一台APM-BFM为例,进行损耗计算与温度场分析,利用有限元法分析计算不同转速下电机损耗,并采用磁-热双向耦合有限元法分析计算APM-BFM各部分温升情况,为电机散热优化设计和高效应用提供了参考。
2 电机结构及工作原理
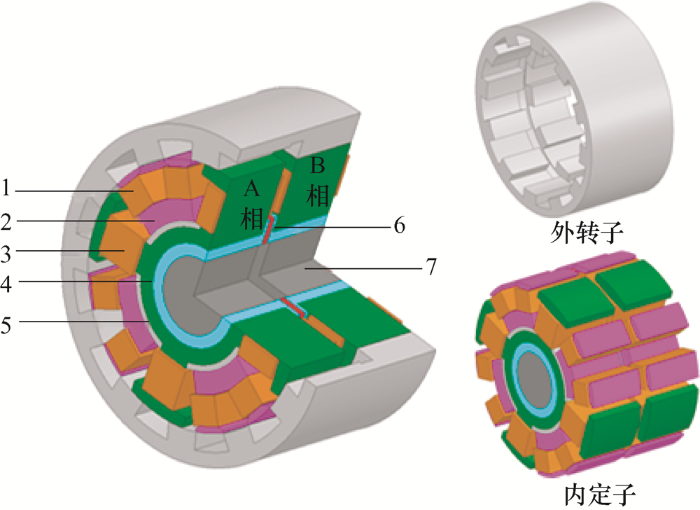
APM-BFM拓扑结构图如图1 所示,该电机采用外转子结构,沿轴向分A、B两相。电机主要由外转子,A、B两相定子铁心,A、B两相定子绕组以及轴向充磁永磁体组成。
图1
图1
APM-BFM结构及组成
1—转矩绕组 2—转矩极 3—悬浮绕组 4—悬浮极5—隔磁体 6—永磁体 7—转轴
如图1 所示,每相外转子铁心内侧沿着周向均匀分布12个等宽转子极,并且A、B两相相差15°。每相定子铁心周向分布8个窄齿转矩极和4个宽齿悬浮极,分别提供电机转矩与悬浮力。转矩极齿宽小于悬浮极齿宽,与转子极齿宽相等,悬浮极齿宽等于转子齿极距,因此无论转子处于任何位置,转子极与悬浮极重叠面积恒定不变,悬浮绕组电感恒定不变,结合定子铁心A、B两相之间的轴向充磁永磁体(提供轴向偏执磁通),从而悬浮极对外转子不会产生切向力,只提供径向悬浮力,而不产生转矩。同时转矩极与悬浮极之间增加非导磁材料制造的隔磁体,通过隔磁体实现转矩磁路与悬浮磁路的独立,在结构上实现了磁路解耦。
3 APM-BFM损耗计算
3.1 APM-BFM损耗计算模型
(1) 定子绕组铜损。电机绕组通入电流,由于绕组存在电阻,产生焦耳热量,即电机铜损。根据欧姆定律,绕组铜损算式为
(1) ${{P}_{\text{Cu}}}=qI_{\text{rms}}^{\text{2}}{{R}_{\text{p}}}$
(2) ${{R}_{\text{p}}}=\frac{234.5+{{\theta }_{t}}}{234.5+75}{{R}_{k75}}$
式中,$q$代表相数;R p 代表相绕组的电阻值;${{\theta }_{t}}$代表计算温度;${{R}_{k75}}$代表75 ℃绕组电阻;I rms 代表相绕组电流的有效值,其表达式为
(3) ${{I}_{\text{rms}}}=\sqrt{\frac{{{N}_{\text{r}}}}{2\mathrm{ }\!\!\pi\!\!\text{ }}\int_{{{\theta }_{1}}}^{{{\theta }_{2}}}{{{i}^{2}}(\theta )\mathrm{d}\theta }}$
式中,${{N}_{\text{r}}}$代表开关磁阻电机的转子齿极数;$\theta $代表转子转过的角度;$i(\theta )$代表相绕组电流的瞬时值;${{\theta }_{1}}$代表开关管开通角度;${{\theta }_{2}}$代表相绕组续流结束时对应的转子角度。
(2) 铁心损耗。开关磁阻电机磁场不是正弦波,且是高度非线性的,相较于传统正弦磁场下电机铁心损耗的求解更加复杂。目前,常见的求解开关磁阻电机铁心损耗的方法是基于Steinmetz方程模型,将电机内非正弦磁通密度波形做傅里叶分解,得到各次谐波下的正弦量进行电机铁心损耗的求解,但是该方法在磁场频率较高的开关磁阻电机中存在拟合误差大、计算不够准确的现象。本文采用改进变系数IEM5模型,以兼顾高频情况下集肤效应对涡流损耗的影响[16 ] 。该方法将铁心损耗模型分为三部分
(4) $\begin{matrix} {{P}_{IEM,h}}={{K}_{adj}}({{B}_{r}}){{k}_{hI}}({{B}_{r}})fB_{r}^{\alpha ({{B}_{r}})}+ \\ {{K}_{adj}}({{B}_{t}}){{k}_{hI}}({{B}_{t}})fB_{t}^{\alpha ({{B}_{t}})} \\ \end{matrix}$
(5) $\begin{aligned} P_{\text {IEM }, e}= & \sum_{k=1}^{K} F_{\text {skin }} k_{\text {eddy }}(k f)^{2}\left\{B_{r, k}^{2}\left[1+k_{a}\left(B_{r, k}\right) B^{\beta\left(B_{r, k}\right) r, k}\right]+\right. \\ & \left.B_{t, k}^{2}\left[1+k_{a}\left(B_{t, k}\right) B^{\beta\left(B_{t, k}\right) t, k}\right]\right\} \end{aligned}$
(6) $\begin{align} & {{P}_{IEM,e\text{x}}}=\sum\limits_{k=1}^{K}{(kf)}1.5[{{k}_{exI}}({{B}_{r,k}},f){{B}^{1.5r,k}}+ \\ & {{k}_{exI}}({{B}_{t,k}},f){{B}^{1.5t,k}}] \\ \end{align}$
式中,${{P}_{IEM,h}}$、${{P}_{IEM,e}}$与${{P}_{IEM,e\text{x}}}$分别为单位质量磁滞损耗、涡流损耗和附加损耗;${{B}_{r}}$和${{B}_{t}}$分别为磁密径向与切向分量;${{B}_{r,k}}$和${{B}_{t,k}}$分别是k 次谐波磁密的径向与切向分量幅值;变系数${{k}_{hI}}(B)$、${{k}_{a}}(B)$、$\alpha (B)$、$\beta (B)$、${{k}_{exI}}(B)$通过多项式拟合得到;${{F}_{skin}}$和${{K}_{adj}}({{B}_{m}})$分别是集肤效应系数和磁滞损耗校正系数,其表达式如下
(7) ${{F}_{skin}}=\frac{3}{D\sqrt{f}}\frac{\sinh (D\sqrt{f})-\sin (D\sqrt{f})}{\cosh (D\sqrt{f})-\cos (D\sqrt{f})}$
(8) ${{K}_{adj}}({{B}_{m}})=1+\frac{0.65}{{{B}_{m}}}\sum\limits_{i=1}^{N}{\Delta {{B}_{i}}}$
式中,$N$为小磁滞回线的个数;$f$为磁感应强度的变化频率;$\Delta {{B}_{i}}$为小磁滞回线磁密峰值与谷值的差值;D 为材料系数,$D=d\sqrt{\mathrm{ }\!\!\pi\!\!\text{ }\mu \sigma }$,d 是硅钢片厚度,$\mu $为材料的平均磁导率,σ 为硅钢材料电导率。
(3) 机械损耗。机械损耗一般由电机轴承摩擦损耗与通风损耗组成,APM-BFM电机转子运行时因无接触可忽略轴承摩擦损耗,主要考虑通风损耗[17 ] 。通风损耗大小取决于电机的转速,且与空气密度、转子内径以及周向叠长相关,其一般表达式如下
(9) ${{P}_{fw}}={{c}_{f}}\mathrm{ }\!\!\pi\!\!\text{ }{{\rho }_{air}}{{\omega }^{3}}{{r}^{4}}l$
式中,${{c}_{f}}$为转子与空气之间摩擦系数;${{\rho }_{air}}$为转子旋转空气密度;$\omega $为转子旋转角速度;$r$为转子内径;$l$为转子轴向叠长。
3.2 APM-BFM损耗有限元分析
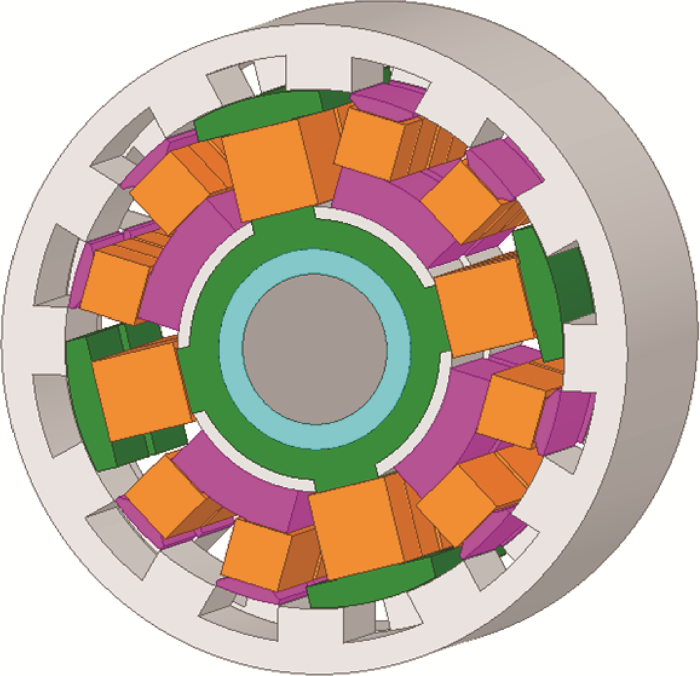
基于有限元电磁特性分析计算APM-BFM不同转速下铁心损耗以及绕组损耗。电机关键结构参数如表1 所示,图2 给出了APM-BFM有限元仿真计算模型。
图2
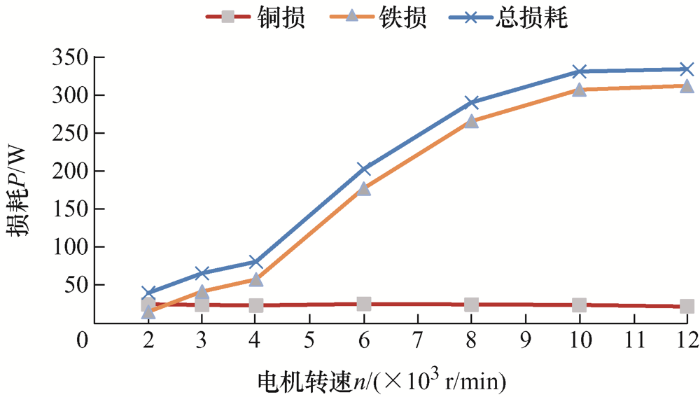
图3 给出了不同转速下APM-BFM损耗变化规律曲线。从图3 可见,APM-BFM铁心损耗随着转速的增加而增加,在4 000 r/min之前电机铁心损耗随着转速增加平缓,4 000 r/min到10 000 r/min之间,APM-BFM铁心损耗随着电机转速的增长迅速增加,10 000 r/min之后电机铁心损耗增长放缓。另外,由图3 可见,APM-BFM绕组铜损随着速度变化基本保持不变。
图3
4 APM-BFM温度场分析
4.1 电机材料属性随温度变化
电机材料温度属性分别通过电导率和磁导率反映出来。电导率与温度可以看成线性关系,电导率与温度之间的斜率称为电导率温度系数[18 ] 。表2 给出几种常见材料的电导率及温度系数。
硅钢片磁导率会存在不规律的波动,磁导率温度系数定义式为
(10) ${{\alpha }_{\mu }}=\frac{{{\mu }_{2}}-{{\mu }_{1}}}{{{\mu }_{1}}({{T}_{2}}-{{T}_{1}})}$
式中,αμ 为磁导率温度系数;μ 1 和μ 2 分别对应T 1 和T 2 温度下的磁导率。
4.2 磁-热双向耦合模型
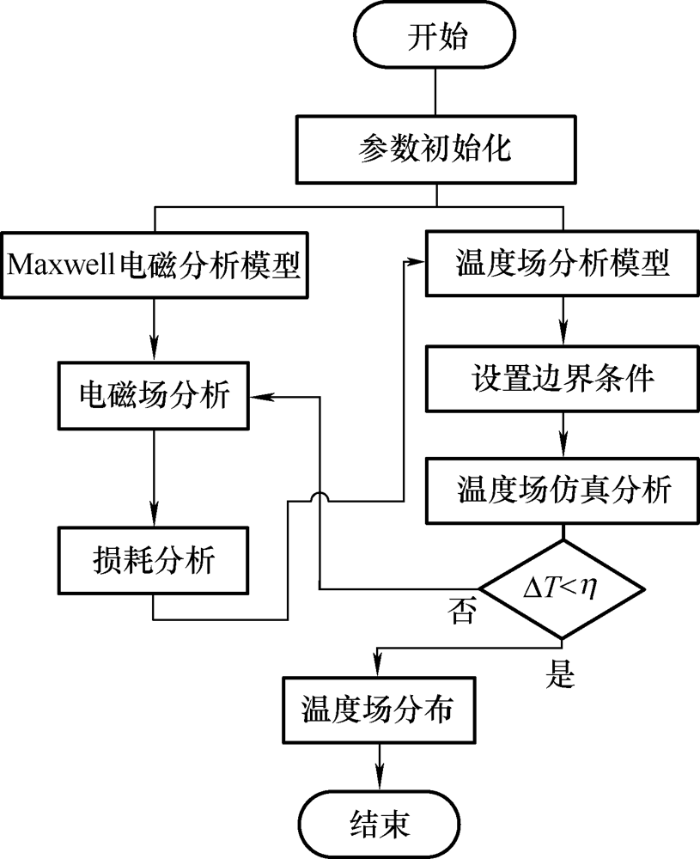
目前对于温度场分析多采用磁-热单向耦合模型,即采用设置默认温度下材料的属性,进行温度场计算,忽略温度对其的影响。磁-热单向耦合模型分析计算模型速度较快[19 ] ,但未考虑材料温度属性,必然会引起计算误差。磁-热双向耦合模型考虑材料温度属性,以材料温度性质为变量,通过稳态温度场仿真得到温升数据作为影响材料性能的参考,传递到电磁仿真中,为温度场计算提供更准确的损耗数据[20 ] ,磁-热双向耦合损耗与温度数据在电磁场与温度场相互交换,经多次迭代达到稳定,即相邻两次数据温度差ΔT 小于设定误差η 。图4 给出了APM-BFM磁-热双向耦合温度计算的流程图。
图4
4.3 磁-热双向耦合有限元仿真
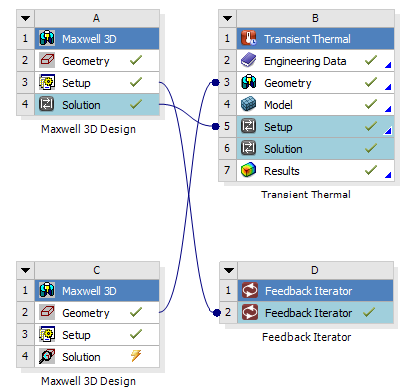
(1) 前处理。基于Workbench仿真平台对APM-BFM进行磁-热双向耦合温度场分析,图5 为APM-BFM磁-热双向耦合温度场分析模型。
图5
表3 给出了温度场分析中APM-BFM材料参数设置,其中气隙传热系数是计算得出的等效散热系数。
(2) APM-BFM对流散热系数。机壳表面散热系数计算公式
(11) ${{h}_{1}}=14(1+0.5\sqrt{\omega })\sqrt[3]{\frac{{{T}_{0}}}{25}}$
(12) ${{h}_{2}}=15+6.5{{V}^{0.7}}$
(13) ${{h}_{3}}=\frac{2\mathrm{N}{{\mathrm{u}}_{r}}{{\lambda }_{\alpha }}}{D}$
(14) $\mathrm{N}{{\mathrm{u}}_{r}}=1.67Re_{r}^{0.385}$
(15) $R{{e}_{r}}=\frac{\mathrm{ }\!\!\pi\!\!\text{ }{{D}^{2}}\text{n}}{120v}$
式中,$\mathrm{N}{{\mathrm{u}}_{r}}$为铁心端部努塞尔数;$\lambda_{\alpha}$为空气导热系数;D为转子铁心外径;Rer 为雷诺系数。
(16) $h_{4}=28\left(1+\omega_{\delta}^{0.5}\right)$
式中,$\omega_{\delta}$为气隙平均风速,一般取$\omega_{\delta} \approx 0.5 u_{2}$;$u_{2}$为转子圆周速度。
将数据代入计算公式,得到各对应对流散热系数如下:h 1 =27.3 W/(m2 ·K),h 2 =179.8 W/(m2 ·K),h 3 =72 W/(m2 ·K),h 4 =188 W/(m2 ·K)。
4.4 磁-热双向耦合仿真结果
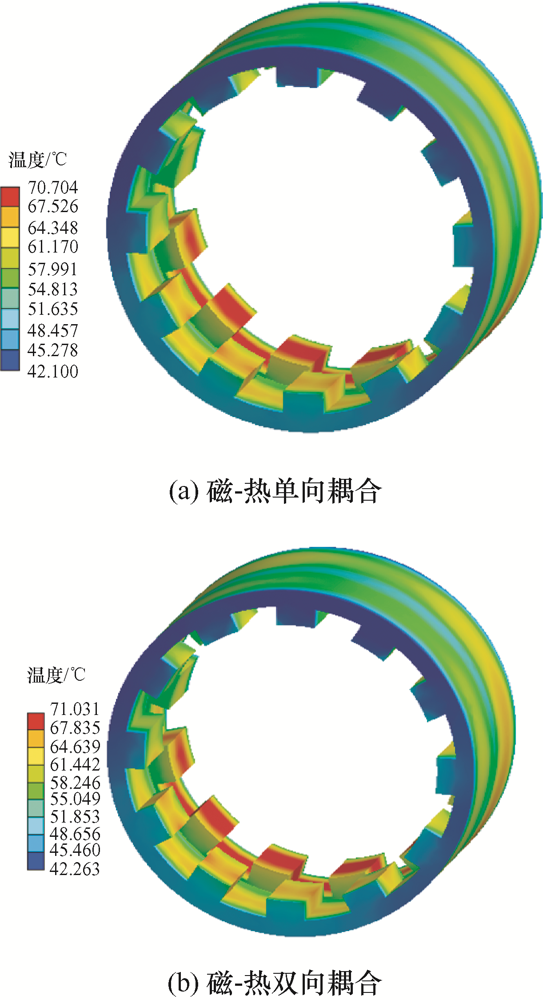
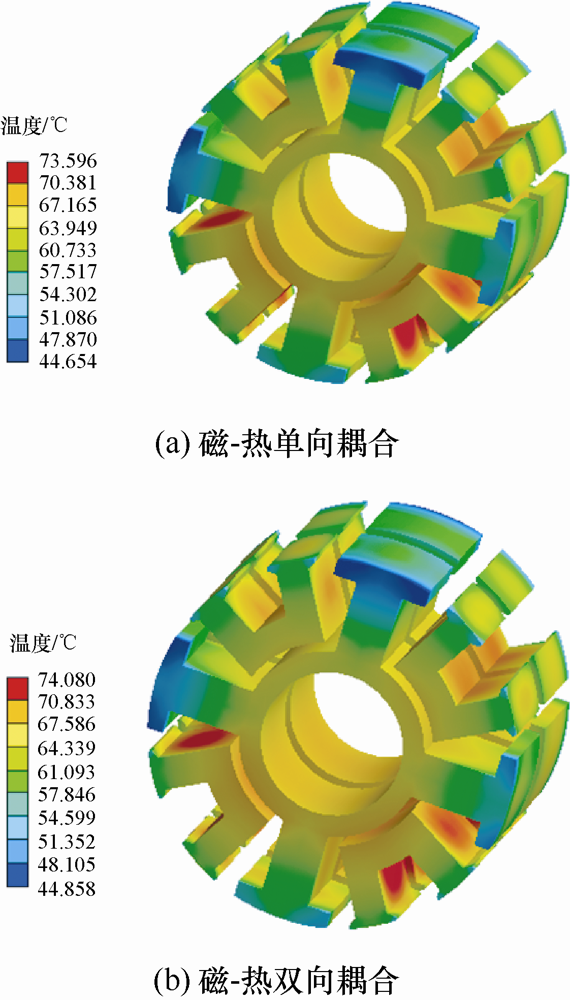
图6 ~8 分别给出了APM-BFM工作在空载转速为12 000 r/min时,电机转子、定子和绕组的温度场分布结果。
图6
图7
图8
由图6 ~8 可见,双向耦合模型与单向耦合模型温度场分布规律趋同,APM-BFM温度最高点都是在绕组部分,达到了73.658 ℃。由图7 可以进一步得出,APM-BFM定子部分两相内侧温度较高,最高温度达到74.08 ℃。主要原因是APM-BFM轴向分相结构,两相内定子内部气息流动性相对较差,影响电机内定子部分的散热。进一步对比APM-BFM温度可见,磁-热双向耦合仿真结果大于磁-热单向耦合仿真结果,尤其是绕组铜损部分,这表明APM-BFM实际温度特性在电磁场与温度场相互影响,证明双向耦合模型能反映电磁场和温度场的互相作用,这说明磁-热双向耦模型在分析电机温度场比磁-热单向耦合模型更为准确。
5 结论
本文以轴向永磁磁悬浮飞轮电机为对象,重点开展电机损耗与温度场研究,得到以下结论。
(1) 轴向永磁磁悬浮飞轮电机内部磁场高度非线性特点,基于改进变系数IEM5铁心损耗求解模型,充分考虑高频下集肤效应对涡流损耗影响,有效提高了电机铁心损耗的分析计算精度。
(2) 考虑电机在运行时电磁场与温度场之间相互影响,采用磁-热双向耦合模型分析计算电机温度场分布,比磁-热单向耦合模型的计算结果更为准确。
(3) 基于磁-热双向耦合模型分析结果,确定轴向永磁磁悬浮飞轮电机内部温升最高点在两相定子内侧,电机定子内侧散热有待提高,为后续电机散热设计与高效应用提供参考。
参考文献
View Option
[1]
ZHU Zhiying ZHU Jin ZHU Hailang , et al . A novel axial split phase bearingless switched reluctance machine for on-board flywheel battery
[J]. IEEE Transactions on Vehicular Technology , 2021 , 70 (4 ):3175 -3186 .
DOI:10.1109/TVT.2021.3065403
URL
[本文引用: 1]
[2]
孙玉坤 , 袁野 , 黄永红 , 等 . 磁悬浮开关磁阻电机及其关键技术发展综述
[J]. 电工技术学报 , 2015 , 30 (22 ):1 -8 .
[本文引用: 1]
SUN Yukun YUAN Ye HUANG Yonghong , et al . Development of the bearingless switched reluctance motor and its key technologies
[J]. Transactions of China Electrotechnical Society , 2015 , 30 (22 ):1 -8 .
[本文引用: 1]
[3]
朱志莹 , 郭旋 , 姜永将 , 等 . 轴向分相永磁式磁悬浮飞轮电机解耦设计与性能分析
[J]. 中国电机工程学报 , 2019 , 39 (24 ):7366 -7374 ,7509.
[本文引用: 1]
ZHU Zhiying GUO Xuan JIANG Yongjiang , et al . Decoupling design and analysis of an axial split phase permanent magnet bearingless flywheel machine
[J]. Proceedings of the CSEE , 2019 , 39 (24 ):7366 -7374 ,7509.
[本文引用: 1]
[4]
周云红 , 孙玉坤 , 王正齐 . 一种双定子磁悬浮开关磁阻飞轮电机控制系统
[J]. 中国电机工程学报 , 2015 , 35 (21 ):5600 -5606 .
[本文引用: 1]
ZHOU Yunhong SUN Yukun WANG Zhengqi . A double-stator bearingless switched reluctance motor drive control system for flywheel energy storage
[J]. Proceedings of the CSEE , 2015 , 35 (21 ):5600 -5606 .
[本文引用: 1]
[5]
赵晗彤 , 张建成 . 基于飞轮储能的独立光伏发电系统的研究
[J]. 电测与仪表 , 2017 , 54 (4 ):34 -38 .
[本文引用: 1]
ZHAO Hantong ZHANG Jiancheng . Research on stand-alone photovoltaic system based on flywheel energy storage system
[J]. Electrical Measurement & Instrumentation , 2017 , 54 (4 ):34 -38 .
[本文引用: 1]
[6]
张维煜 , 杨恒坤 , 朱熀秋 . 电动汽车用飞轮电池关键技术和技术瓶颈分析
[J]. 中国电机工程学报 , 2018 , 38 (18 ):5568 -5581 .
[本文引用: 1]
ZHANG Weiyu YANG Hengkun ZHU Huangqiu . Key technologies and technical bottleneck analysis of flywheel battery systems for electric vehicle
[J]. Proceedings of the CSEE , 2018 , 38 (18 ):5568 -5581 .
[本文引用: 1]
[7]
邓建国 , 蔡亚辉 , 黄守道 , 等 . 压缩机用永磁同步电机无传感器全速度运行策略研究
[J]. 中国机械工程 , 2016 , 27 (6 ):767 -771 ,777.
[本文引用: 1]
DENG Jianguo CAI Yahui HUANG Shoudao , et al . Study on sensorless control strategy of PMSM compressor at full speed range
[J]. Chinese Mechanical Engineering , 2016 , 27 (6 ):767 -771 ,777.
[本文引用: 1]
[8]
ZHU Zhiying ZHU Hailang LI Xinya , et al . Dynamic equivalent magnetic network analysis of an axial PM bearingless flywheel machine
[J]. IEEE Access , 2021 , 9 :32425 -32435 .
DOI:10.1109/ACCESS.2021.3060921
URL
[本文引用: 1]
[9]
ZHU Zhiying WANG Jiabin CHENG Ming . A novel axial split phase bearingless flywheel machine with hybrid-inner-stator permanent magnet-based structure
[J]. IEEE Transactions on Energy Conversion , 2021 , 36 (3 ):1873 -1882 .
DOI:10.1109/TEC.2020.3045143
URL
[本文引用: 1]
[10]
KIM K S LEE B H HONG J P . Improvement of thermal equivalent circuit network and prediction on heat characteristic of motor by calculation of convection heat transfer coefficient
[C]// 2012 Sixth International Conference on Electromagnetic Field Problems and Applications,Dalian,China , 2012 :1 -4 .
[本文引用: 1]
[11]
LI Hongfeng SHEN Yanbo . Thermal analysis of the permanent-magnet spherical motor
[J]. IEEE Transaction on Energy Conversion , 2015 , 30 (3 ):991 -998 .
DOI:10.1109/TEC.2015.2419636
URL
[本文引用: 1]
[12]
ZHU Zhiying ZHANG Wei LI Yibo , et al . Thermal analysis of axial permanent magnet flywheel machine based on equivalent thermal network method
[J]. IEEE Access , 2021 , 9 :33181 -33188 .
DOI:10.1109/ACCESS.2021.3060591
URL
[本文引用: 1]
[13]
ARBAB N WANG Wei LIN Chenjie , et al . Thermal modeling and analysis of a double-stator switched reluctance motor
[J]. IEEE Transactions on Energy Conversion , 2015 , 30 (3 ):1209 -1217 .
DOI:10.1109/TEC.2015.2424400
URL
[本文引用: 1]
[14]
陈美玲 , 石瑶 , 张云 , 等 . 高真空工况下开关磁阻电机温度场分析
[J]. 电测与仪表 , 2020 , 57 (19 ):45 -50 .
[本文引用: 1]
CHEN Meiling SHI Yao ZHANG Yun , et al . Analysis of temperature field of switched reluctance motor under high vacuum conditions
[J]. Electrical Measurement & Instrumentation , 2020 , 57 (19 ):45 -50 .
[本文引用: 1]
[15]
CHEN Hao WANG Kai YAN Wenjun , et al . Temperature analysis of switched reluctance motor based on equivalent heat circuit method
[J]. IEEE Transactions on Applied Superconductivity , 2021 , 31 (8 ):1 -4 .
[本文引用: 1]
[16]
YAN Wenjun CHEN Hao CHEN Lei , et al . Analysis on iron loss of switched reluctance motor under PWM mode
[J]. COMPEL-The International Journal for Computation and Mathematics in Electrical and Electronic Engineering , 2018 , 37 (1 ):448 -464 .
DOI:10.1108/COMPEL-05-2017-0193
URL
[本文引用: 1]
[17]
RAULIN V RADUN A HUSAIN I . Modeling of losses in switched reluctance machines
[J]. IEEE Transactions on Industry Applications , 2004 , 40 (6 ):1560 -1569 .
DOI:10.1109/TIA.2004.836225
URL
[本文引用: 1]
[18]
MO Lihong ZHU Xiaoyong Zhang Tao , et al . Temperature rise calculation of a flux-switching permanent-magnet double-rotor machine using electromagnetic-thermal coupling analysis
[J]. IEEE Transactions on Magnetics , 2018 , 54 (3 ):1 -4 .
[本文引用: 1]
[19]
LIU Guangwei LIU Meiyang ZHANG Yue , et al . High-speed permanent magnet synchronous motor iron loss calculation method considering multi-physics factors
[J]. IEEE Transactions on Industrial Electronics , 2019 , 67 (7 ):5360 -5368 .
DOI:10.1109/TIE.2019.2934075
URL
[本文引用: 1]
[20]
QIANG Yu WANG Xuesong CHENG Yuhu . Electro- magnetic and thermal coupled analysis of can effect of a novel canned switched reluctance machine as a hydraulic pump drive
[J]. International Journal of Applied Electromagnetics and Mechanics , 2017 , 54 (1 ):131 -140 .
DOI:10.3233/JAE-160126
URL
[本文引用: 1]
A novel axial split phase bearingless switched reluctance machine for on-board flywheel battery
1
2021
... 飞轮电池是一种利用高速旋转的飞轮存储能量的机电一体化产品,具有能量密度高、使用寿命长、充放电性能强、无污染且环境友好等独特优点[1 ⇓ ⇓ -4 ] ,在不间断电源、电动汽车、轨道交通、卫星和航天器等领域具有巨大的潜在应用前景[5 -6 ] .飞轮电机是飞轮电池能量转换的核心部件,决定了飞轮系统的运行效率和可靠性等.常见的飞轮电机主要包括:感应电机、开关磁阻电机、同步磁阻电机和永磁无刷直流电机等.开关磁阻电机转子无永磁体和绕组,具有结构简单坚固、可靠性高、容错能力强、在高速和恶劣环境下运行性能好等优点,非常适合飞轮电池应用[7 ] .然而高速运行下,开关磁阻电机传统轴承支撑存在摩擦磨损,导致飞轮电池效率低、自放电严重等问题.磁悬浮开关磁阻电机充分利用开关磁阻电机的高速性能和磁悬浮技术,有效实现转子自悬浮,具有高速无摩擦磨损等优点,将其引入飞轮形成磁悬浮飞轮电机(Bearingless flywheel machine, BFM),可以简化结构、降低损耗,提高临界转速、运行效率和可靠性[8 ] .轴向永磁BFM(Axial permanent magnet BFM, APM-BFM)进一步通过轴向分相和永磁偏置设计,可实现超低功耗四自由度悬浮,是飞轮电池悬浮运行与能量变换的理想选择之一[9 ] . ...
磁悬浮开关磁阻电机及其关键技术发展综述
1
2015
... 飞轮电池是一种利用高速旋转的飞轮存储能量的机电一体化产品,具有能量密度高、使用寿命长、充放电性能强、无污染且环境友好等独特优点[1 ⇓ ⇓ -4 ] ,在不间断电源、电动汽车、轨道交通、卫星和航天器等领域具有巨大的潜在应用前景[5 -6 ] .飞轮电机是飞轮电池能量转换的核心部件,决定了飞轮系统的运行效率和可靠性等.常见的飞轮电机主要包括:感应电机、开关磁阻电机、同步磁阻电机和永磁无刷直流电机等.开关磁阻电机转子无永磁体和绕组,具有结构简单坚固、可靠性高、容错能力强、在高速和恶劣环境下运行性能好等优点,非常适合飞轮电池应用[7 ] .然而高速运行下,开关磁阻电机传统轴承支撑存在摩擦磨损,导致飞轮电池效率低、自放电严重等问题.磁悬浮开关磁阻电机充分利用开关磁阻电机的高速性能和磁悬浮技术,有效实现转子自悬浮,具有高速无摩擦磨损等优点,将其引入飞轮形成磁悬浮飞轮电机(Bearingless flywheel machine, BFM),可以简化结构、降低损耗,提高临界转速、运行效率和可靠性[8 ] .轴向永磁BFM(Axial permanent magnet BFM, APM-BFM)进一步通过轴向分相和永磁偏置设计,可实现超低功耗四自由度悬浮,是飞轮电池悬浮运行与能量变换的理想选择之一[9 ] . ...
Development of the bearingless switched reluctance motor and its key technologies
1
2015
... 飞轮电池是一种利用高速旋转的飞轮存储能量的机电一体化产品,具有能量密度高、使用寿命长、充放电性能强、无污染且环境友好等独特优点[1 ⇓ ⇓ -4 ] ,在不间断电源、电动汽车、轨道交通、卫星和航天器等领域具有巨大的潜在应用前景[5 -6 ] .飞轮电机是飞轮电池能量转换的核心部件,决定了飞轮系统的运行效率和可靠性等.常见的飞轮电机主要包括:感应电机、开关磁阻电机、同步磁阻电机和永磁无刷直流电机等.开关磁阻电机转子无永磁体和绕组,具有结构简单坚固、可靠性高、容错能力强、在高速和恶劣环境下运行性能好等优点,非常适合飞轮电池应用[7 ] .然而高速运行下,开关磁阻电机传统轴承支撑存在摩擦磨损,导致飞轮电池效率低、自放电严重等问题.磁悬浮开关磁阻电机充分利用开关磁阻电机的高速性能和磁悬浮技术,有效实现转子自悬浮,具有高速无摩擦磨损等优点,将其引入飞轮形成磁悬浮飞轮电机(Bearingless flywheel machine, BFM),可以简化结构、降低损耗,提高临界转速、运行效率和可靠性[8 ] .轴向永磁BFM(Axial permanent magnet BFM, APM-BFM)进一步通过轴向分相和永磁偏置设计,可实现超低功耗四自由度悬浮,是飞轮电池悬浮运行与能量变换的理想选择之一[9 ] . ...
轴向分相永磁式磁悬浮飞轮电机解耦设计与性能分析
1
2019
... 飞轮电池是一种利用高速旋转的飞轮存储能量的机电一体化产品,具有能量密度高、使用寿命长、充放电性能强、无污染且环境友好等独特优点[1 ⇓ ⇓ -4 ] ,在不间断电源、电动汽车、轨道交通、卫星和航天器等领域具有巨大的潜在应用前景[5 -6 ] .飞轮电机是飞轮电池能量转换的核心部件,决定了飞轮系统的运行效率和可靠性等.常见的飞轮电机主要包括:感应电机、开关磁阻电机、同步磁阻电机和永磁无刷直流电机等.开关磁阻电机转子无永磁体和绕组,具有结构简单坚固、可靠性高、容错能力强、在高速和恶劣环境下运行性能好等优点,非常适合飞轮电池应用[7 ] .然而高速运行下,开关磁阻电机传统轴承支撑存在摩擦磨损,导致飞轮电池效率低、自放电严重等问题.磁悬浮开关磁阻电机充分利用开关磁阻电机的高速性能和磁悬浮技术,有效实现转子自悬浮,具有高速无摩擦磨损等优点,将其引入飞轮形成磁悬浮飞轮电机(Bearingless flywheel machine, BFM),可以简化结构、降低损耗,提高临界转速、运行效率和可靠性[8 ] .轴向永磁BFM(Axial permanent magnet BFM, APM-BFM)进一步通过轴向分相和永磁偏置设计,可实现超低功耗四自由度悬浮,是飞轮电池悬浮运行与能量变换的理想选择之一[9 ] . ...
Decoupling design and analysis of an axial split phase permanent magnet bearingless flywheel machine
1
2019
... 飞轮电池是一种利用高速旋转的飞轮存储能量的机电一体化产品,具有能量密度高、使用寿命长、充放电性能强、无污染且环境友好等独特优点[1 ⇓ ⇓ -4 ] ,在不间断电源、电动汽车、轨道交通、卫星和航天器等领域具有巨大的潜在应用前景[5 -6 ] .飞轮电机是飞轮电池能量转换的核心部件,决定了飞轮系统的运行效率和可靠性等.常见的飞轮电机主要包括:感应电机、开关磁阻电机、同步磁阻电机和永磁无刷直流电机等.开关磁阻电机转子无永磁体和绕组,具有结构简单坚固、可靠性高、容错能力强、在高速和恶劣环境下运行性能好等优点,非常适合飞轮电池应用[7 ] .然而高速运行下,开关磁阻电机传统轴承支撑存在摩擦磨损,导致飞轮电池效率低、自放电严重等问题.磁悬浮开关磁阻电机充分利用开关磁阻电机的高速性能和磁悬浮技术,有效实现转子自悬浮,具有高速无摩擦磨损等优点,将其引入飞轮形成磁悬浮飞轮电机(Bearingless flywheel machine, BFM),可以简化结构、降低损耗,提高临界转速、运行效率和可靠性[8 ] .轴向永磁BFM(Axial permanent magnet BFM, APM-BFM)进一步通过轴向分相和永磁偏置设计,可实现超低功耗四自由度悬浮,是飞轮电池悬浮运行与能量变换的理想选择之一[9 ] . ...
一种双定子磁悬浮开关磁阻飞轮电机控制系统
1
2015
... 飞轮电池是一种利用高速旋转的飞轮存储能量的机电一体化产品,具有能量密度高、使用寿命长、充放电性能强、无污染且环境友好等独特优点[1 ⇓ ⇓ -4 ] ,在不间断电源、电动汽车、轨道交通、卫星和航天器等领域具有巨大的潜在应用前景[5 -6 ] .飞轮电机是飞轮电池能量转换的核心部件,决定了飞轮系统的运行效率和可靠性等.常见的飞轮电机主要包括:感应电机、开关磁阻电机、同步磁阻电机和永磁无刷直流电机等.开关磁阻电机转子无永磁体和绕组,具有结构简单坚固、可靠性高、容错能力强、在高速和恶劣环境下运行性能好等优点,非常适合飞轮电池应用[7 ] .然而高速运行下,开关磁阻电机传统轴承支撑存在摩擦磨损,导致飞轮电池效率低、自放电严重等问题.磁悬浮开关磁阻电机充分利用开关磁阻电机的高速性能和磁悬浮技术,有效实现转子自悬浮,具有高速无摩擦磨损等优点,将其引入飞轮形成磁悬浮飞轮电机(Bearingless flywheel machine, BFM),可以简化结构、降低损耗,提高临界转速、运行效率和可靠性[8 ] .轴向永磁BFM(Axial permanent magnet BFM, APM-BFM)进一步通过轴向分相和永磁偏置设计,可实现超低功耗四自由度悬浮,是飞轮电池悬浮运行与能量变换的理想选择之一[9 ] . ...
A double-stator bearingless switched reluctance motor drive control system for flywheel energy storage
1
2015
... 飞轮电池是一种利用高速旋转的飞轮存储能量的机电一体化产品,具有能量密度高、使用寿命长、充放电性能强、无污染且环境友好等独特优点[1 ⇓ ⇓ -4 ] ,在不间断电源、电动汽车、轨道交通、卫星和航天器等领域具有巨大的潜在应用前景[5 -6 ] .飞轮电机是飞轮电池能量转换的核心部件,决定了飞轮系统的运行效率和可靠性等.常见的飞轮电机主要包括:感应电机、开关磁阻电机、同步磁阻电机和永磁无刷直流电机等.开关磁阻电机转子无永磁体和绕组,具有结构简单坚固、可靠性高、容错能力强、在高速和恶劣环境下运行性能好等优点,非常适合飞轮电池应用[7 ] .然而高速运行下,开关磁阻电机传统轴承支撑存在摩擦磨损,导致飞轮电池效率低、自放电严重等问题.磁悬浮开关磁阻电机充分利用开关磁阻电机的高速性能和磁悬浮技术,有效实现转子自悬浮,具有高速无摩擦磨损等优点,将其引入飞轮形成磁悬浮飞轮电机(Bearingless flywheel machine, BFM),可以简化结构、降低损耗,提高临界转速、运行效率和可靠性[8 ] .轴向永磁BFM(Axial permanent magnet BFM, APM-BFM)进一步通过轴向分相和永磁偏置设计,可实现超低功耗四自由度悬浮,是飞轮电池悬浮运行与能量变换的理想选择之一[9 ] . ...
基于飞轮储能的独立光伏发电系统的研究
1
2017
... 飞轮电池是一种利用高速旋转的飞轮存储能量的机电一体化产品,具有能量密度高、使用寿命长、充放电性能强、无污染且环境友好等独特优点[1 ⇓ ⇓ -4 ] ,在不间断电源、电动汽车、轨道交通、卫星和航天器等领域具有巨大的潜在应用前景[5 -6 ] .飞轮电机是飞轮电池能量转换的核心部件,决定了飞轮系统的运行效率和可靠性等.常见的飞轮电机主要包括:感应电机、开关磁阻电机、同步磁阻电机和永磁无刷直流电机等.开关磁阻电机转子无永磁体和绕组,具有结构简单坚固、可靠性高、容错能力强、在高速和恶劣环境下运行性能好等优点,非常适合飞轮电池应用[7 ] .然而高速运行下,开关磁阻电机传统轴承支撑存在摩擦磨损,导致飞轮电池效率低、自放电严重等问题.磁悬浮开关磁阻电机充分利用开关磁阻电机的高速性能和磁悬浮技术,有效实现转子自悬浮,具有高速无摩擦磨损等优点,将其引入飞轮形成磁悬浮飞轮电机(Bearingless flywheel machine, BFM),可以简化结构、降低损耗,提高临界转速、运行效率和可靠性[8 ] .轴向永磁BFM(Axial permanent magnet BFM, APM-BFM)进一步通过轴向分相和永磁偏置设计,可实现超低功耗四自由度悬浮,是飞轮电池悬浮运行与能量变换的理想选择之一[9 ] . ...
Research on stand-alone photovoltaic system based on flywheel energy storage system
1
2017
... 飞轮电池是一种利用高速旋转的飞轮存储能量的机电一体化产品,具有能量密度高、使用寿命长、充放电性能强、无污染且环境友好等独特优点[1 ⇓ ⇓ -4 ] ,在不间断电源、电动汽车、轨道交通、卫星和航天器等领域具有巨大的潜在应用前景[5 -6 ] .飞轮电机是飞轮电池能量转换的核心部件,决定了飞轮系统的运行效率和可靠性等.常见的飞轮电机主要包括:感应电机、开关磁阻电机、同步磁阻电机和永磁无刷直流电机等.开关磁阻电机转子无永磁体和绕组,具有结构简单坚固、可靠性高、容错能力强、在高速和恶劣环境下运行性能好等优点,非常适合飞轮电池应用[7 ] .然而高速运行下,开关磁阻电机传统轴承支撑存在摩擦磨损,导致飞轮电池效率低、自放电严重等问题.磁悬浮开关磁阻电机充分利用开关磁阻电机的高速性能和磁悬浮技术,有效实现转子自悬浮,具有高速无摩擦磨损等优点,将其引入飞轮形成磁悬浮飞轮电机(Bearingless flywheel machine, BFM),可以简化结构、降低损耗,提高临界转速、运行效率和可靠性[8 ] .轴向永磁BFM(Axial permanent magnet BFM, APM-BFM)进一步通过轴向分相和永磁偏置设计,可实现超低功耗四自由度悬浮,是飞轮电池悬浮运行与能量变换的理想选择之一[9 ] . ...
电动汽车用飞轮电池关键技术和技术瓶颈分析
1
2018
... 飞轮电池是一种利用高速旋转的飞轮存储能量的机电一体化产品,具有能量密度高、使用寿命长、充放电性能强、无污染且环境友好等独特优点[1 ⇓ ⇓ -4 ] ,在不间断电源、电动汽车、轨道交通、卫星和航天器等领域具有巨大的潜在应用前景[5 -6 ] .飞轮电机是飞轮电池能量转换的核心部件,决定了飞轮系统的运行效率和可靠性等.常见的飞轮电机主要包括:感应电机、开关磁阻电机、同步磁阻电机和永磁无刷直流电机等.开关磁阻电机转子无永磁体和绕组,具有结构简单坚固、可靠性高、容错能力强、在高速和恶劣环境下运行性能好等优点,非常适合飞轮电池应用[7 ] .然而高速运行下,开关磁阻电机传统轴承支撑存在摩擦磨损,导致飞轮电池效率低、自放电严重等问题.磁悬浮开关磁阻电机充分利用开关磁阻电机的高速性能和磁悬浮技术,有效实现转子自悬浮,具有高速无摩擦磨损等优点,将其引入飞轮形成磁悬浮飞轮电机(Bearingless flywheel machine, BFM),可以简化结构、降低损耗,提高临界转速、运行效率和可靠性[8 ] .轴向永磁BFM(Axial permanent magnet BFM, APM-BFM)进一步通过轴向分相和永磁偏置设计,可实现超低功耗四自由度悬浮,是飞轮电池悬浮运行与能量变换的理想选择之一[9 ] . ...
Key technologies and technical bottleneck analysis of flywheel battery systems for electric vehicle
1
2018
... 飞轮电池是一种利用高速旋转的飞轮存储能量的机电一体化产品,具有能量密度高、使用寿命长、充放电性能强、无污染且环境友好等独特优点[1 ⇓ ⇓ -4 ] ,在不间断电源、电动汽车、轨道交通、卫星和航天器等领域具有巨大的潜在应用前景[5 -6 ] .飞轮电机是飞轮电池能量转换的核心部件,决定了飞轮系统的运行效率和可靠性等.常见的飞轮电机主要包括:感应电机、开关磁阻电机、同步磁阻电机和永磁无刷直流电机等.开关磁阻电机转子无永磁体和绕组,具有结构简单坚固、可靠性高、容错能力强、在高速和恶劣环境下运行性能好等优点,非常适合飞轮电池应用[7 ] .然而高速运行下,开关磁阻电机传统轴承支撑存在摩擦磨损,导致飞轮电池效率低、自放电严重等问题.磁悬浮开关磁阻电机充分利用开关磁阻电机的高速性能和磁悬浮技术,有效实现转子自悬浮,具有高速无摩擦磨损等优点,将其引入飞轮形成磁悬浮飞轮电机(Bearingless flywheel machine, BFM),可以简化结构、降低损耗,提高临界转速、运行效率和可靠性[8 ] .轴向永磁BFM(Axial permanent magnet BFM, APM-BFM)进一步通过轴向分相和永磁偏置设计,可实现超低功耗四自由度悬浮,是飞轮电池悬浮运行与能量变换的理想选择之一[9 ] . ...
压缩机用永磁同步电机无传感器全速度运行策略研究
1
2016
... 飞轮电池是一种利用高速旋转的飞轮存储能量的机电一体化产品,具有能量密度高、使用寿命长、充放电性能强、无污染且环境友好等独特优点[1 ⇓ ⇓ -4 ] ,在不间断电源、电动汽车、轨道交通、卫星和航天器等领域具有巨大的潜在应用前景[5 -6 ] .飞轮电机是飞轮电池能量转换的核心部件,决定了飞轮系统的运行效率和可靠性等.常见的飞轮电机主要包括:感应电机、开关磁阻电机、同步磁阻电机和永磁无刷直流电机等.开关磁阻电机转子无永磁体和绕组,具有结构简单坚固、可靠性高、容错能力强、在高速和恶劣环境下运行性能好等优点,非常适合飞轮电池应用[7 ] .然而高速运行下,开关磁阻电机传统轴承支撑存在摩擦磨损,导致飞轮电池效率低、自放电严重等问题.磁悬浮开关磁阻电机充分利用开关磁阻电机的高速性能和磁悬浮技术,有效实现转子自悬浮,具有高速无摩擦磨损等优点,将其引入飞轮形成磁悬浮飞轮电机(Bearingless flywheel machine, BFM),可以简化结构、降低损耗,提高临界转速、运行效率和可靠性[8 ] .轴向永磁BFM(Axial permanent magnet BFM, APM-BFM)进一步通过轴向分相和永磁偏置设计,可实现超低功耗四自由度悬浮,是飞轮电池悬浮运行与能量变换的理想选择之一[9 ] . ...
Study on sensorless control strategy of PMSM compressor at full speed range
1
2016
... 飞轮电池是一种利用高速旋转的飞轮存储能量的机电一体化产品,具有能量密度高、使用寿命长、充放电性能强、无污染且环境友好等独特优点[1 ⇓ ⇓ -4 ] ,在不间断电源、电动汽车、轨道交通、卫星和航天器等领域具有巨大的潜在应用前景[5 -6 ] .飞轮电机是飞轮电池能量转换的核心部件,决定了飞轮系统的运行效率和可靠性等.常见的飞轮电机主要包括:感应电机、开关磁阻电机、同步磁阻电机和永磁无刷直流电机等.开关磁阻电机转子无永磁体和绕组,具有结构简单坚固、可靠性高、容错能力强、在高速和恶劣环境下运行性能好等优点,非常适合飞轮电池应用[7 ] .然而高速运行下,开关磁阻电机传统轴承支撑存在摩擦磨损,导致飞轮电池效率低、自放电严重等问题.磁悬浮开关磁阻电机充分利用开关磁阻电机的高速性能和磁悬浮技术,有效实现转子自悬浮,具有高速无摩擦磨损等优点,将其引入飞轮形成磁悬浮飞轮电机(Bearingless flywheel machine, BFM),可以简化结构、降低损耗,提高临界转速、运行效率和可靠性[8 ] .轴向永磁BFM(Axial permanent magnet BFM, APM-BFM)进一步通过轴向分相和永磁偏置设计,可实现超低功耗四自由度悬浮,是飞轮电池悬浮运行与能量变换的理想选择之一[9 ] . ...
Dynamic equivalent magnetic network analysis of an axial PM bearingless flywheel machine
1
2021
... 飞轮电池是一种利用高速旋转的飞轮存储能量的机电一体化产品,具有能量密度高、使用寿命长、充放电性能强、无污染且环境友好等独特优点[1 ⇓ ⇓ -4 ] ,在不间断电源、电动汽车、轨道交通、卫星和航天器等领域具有巨大的潜在应用前景[5 -6 ] .飞轮电机是飞轮电池能量转换的核心部件,决定了飞轮系统的运行效率和可靠性等.常见的飞轮电机主要包括:感应电机、开关磁阻电机、同步磁阻电机和永磁无刷直流电机等.开关磁阻电机转子无永磁体和绕组,具有结构简单坚固、可靠性高、容错能力强、在高速和恶劣环境下运行性能好等优点,非常适合飞轮电池应用[7 ] .然而高速运行下,开关磁阻电机传统轴承支撑存在摩擦磨损,导致飞轮电池效率低、自放电严重等问题.磁悬浮开关磁阻电机充分利用开关磁阻电机的高速性能和磁悬浮技术,有效实现转子自悬浮,具有高速无摩擦磨损等优点,将其引入飞轮形成磁悬浮飞轮电机(Bearingless flywheel machine, BFM),可以简化结构、降低损耗,提高临界转速、运行效率和可靠性[8 ] .轴向永磁BFM(Axial permanent magnet BFM, APM-BFM)进一步通过轴向分相和永磁偏置设计,可实现超低功耗四自由度悬浮,是飞轮电池悬浮运行与能量变换的理想选择之一[9 ] . ...
A novel axial split phase bearingless flywheel machine with hybrid-inner-stator permanent magnet-based structure
1
2021
... 飞轮电池是一种利用高速旋转的飞轮存储能量的机电一体化产品,具有能量密度高、使用寿命长、充放电性能强、无污染且环境友好等独特优点[1 ⇓ ⇓ -4 ] ,在不间断电源、电动汽车、轨道交通、卫星和航天器等领域具有巨大的潜在应用前景[5 -6 ] .飞轮电机是飞轮电池能量转换的核心部件,决定了飞轮系统的运行效率和可靠性等.常见的飞轮电机主要包括:感应电机、开关磁阻电机、同步磁阻电机和永磁无刷直流电机等.开关磁阻电机转子无永磁体和绕组,具有结构简单坚固、可靠性高、容错能力强、在高速和恶劣环境下运行性能好等优点,非常适合飞轮电池应用[7 ] .然而高速运行下,开关磁阻电机传统轴承支撑存在摩擦磨损,导致飞轮电池效率低、自放电严重等问题.磁悬浮开关磁阻电机充分利用开关磁阻电机的高速性能和磁悬浮技术,有效实现转子自悬浮,具有高速无摩擦磨损等优点,将其引入飞轮形成磁悬浮飞轮电机(Bearingless flywheel machine, BFM),可以简化结构、降低损耗,提高临界转速、运行效率和可靠性[8 ] .轴向永磁BFM(Axial permanent magnet BFM, APM-BFM)进一步通过轴向分相和永磁偏置设计,可实现超低功耗四自由度悬浮,是飞轮电池悬浮运行与能量变换的理想选择之一[9 ] . ...
Improvement of thermal equivalent circuit network and prediction on heat characteristic of motor by calculation of convection heat transfer coefficient
1
2012
... 目前,国内外常用计算电机温升的方法有简化公式法[10 ] 、等效热路法[11 ] 、等效热网络法[12 ] 和有限元法[13 -14 ] .其中简化公式法计算方法简易,但存在较大误差;等效热路法可求解电机各部分平均温度,但无法得到电机准确的温度分布;等效热网络法依据热传导定律中热对流、温度和热阻三者关系,依照电路中KVL与KCL原理,近似做出等效热网络图,分析各部分的温度[15 ] .有限元法将温度场计算模型剖分为细小的单元体,通过对每一个细小单元体求解计算再逼近整体解,该方法计算准确、应用广泛、适用性强. ...
Thermal analysis of the permanent-magnet spherical motor
1
2015
... 目前,国内外常用计算电机温升的方法有简化公式法[10 ] 、等效热路法[11 ] 、等效热网络法[12 ] 和有限元法[13 -14 ] .其中简化公式法计算方法简易,但存在较大误差;等效热路法可求解电机各部分平均温度,但无法得到电机准确的温度分布;等效热网络法依据热传导定律中热对流、温度和热阻三者关系,依照电路中KVL与KCL原理,近似做出等效热网络图,分析各部分的温度[15 ] .有限元法将温度场计算模型剖分为细小的单元体,通过对每一个细小单元体求解计算再逼近整体解,该方法计算准确、应用广泛、适用性强. ...
Thermal analysis of axial permanent magnet flywheel machine based on equivalent thermal network method
1
2021
... 目前,国内外常用计算电机温升的方法有简化公式法[10 ] 、等效热路法[11 ] 、等效热网络法[12 ] 和有限元法[13 -14 ] .其中简化公式法计算方法简易,但存在较大误差;等效热路法可求解电机各部分平均温度,但无法得到电机准确的温度分布;等效热网络法依据热传导定律中热对流、温度和热阻三者关系,依照电路中KVL与KCL原理,近似做出等效热网络图,分析各部分的温度[15 ] .有限元法将温度场计算模型剖分为细小的单元体,通过对每一个细小单元体求解计算再逼近整体解,该方法计算准确、应用广泛、适用性强. ...
Thermal modeling and analysis of a double-stator switched reluctance motor
1
2015
... 目前,国内外常用计算电机温升的方法有简化公式法[10 ] 、等效热路法[11 ] 、等效热网络法[12 ] 和有限元法[13 -14 ] .其中简化公式法计算方法简易,但存在较大误差;等效热路法可求解电机各部分平均温度,但无法得到电机准确的温度分布;等效热网络法依据热传导定律中热对流、温度和热阻三者关系,依照电路中KVL与KCL原理,近似做出等效热网络图,分析各部分的温度[15 ] .有限元法将温度场计算模型剖分为细小的单元体,通过对每一个细小单元体求解计算再逼近整体解,该方法计算准确、应用广泛、适用性强. ...
高真空工况下开关磁阻电机温度场分析
1
2020
... 目前,国内外常用计算电机温升的方法有简化公式法[10 ] 、等效热路法[11 ] 、等效热网络法[12 ] 和有限元法[13 -14 ] .其中简化公式法计算方法简易,但存在较大误差;等效热路法可求解电机各部分平均温度,但无法得到电机准确的温度分布;等效热网络法依据热传导定律中热对流、温度和热阻三者关系,依照电路中KVL与KCL原理,近似做出等效热网络图,分析各部分的温度[15 ] .有限元法将温度场计算模型剖分为细小的单元体,通过对每一个细小单元体求解计算再逼近整体解,该方法计算准确、应用广泛、适用性强. ...
Analysis of temperature field of switched reluctance motor under high vacuum conditions
1
2020
... 目前,国内外常用计算电机温升的方法有简化公式法[10 ] 、等效热路法[11 ] 、等效热网络法[12 ] 和有限元法[13 -14 ] .其中简化公式法计算方法简易,但存在较大误差;等效热路法可求解电机各部分平均温度,但无法得到电机准确的温度分布;等效热网络法依据热传导定律中热对流、温度和热阻三者关系,依照电路中KVL与KCL原理,近似做出等效热网络图,分析各部分的温度[15 ] .有限元法将温度场计算模型剖分为细小的单元体,通过对每一个细小单元体求解计算再逼近整体解,该方法计算准确、应用广泛、适用性强. ...
Temperature analysis of switched reluctance motor based on equivalent heat circuit method
1
2021
... 目前,国内外常用计算电机温升的方法有简化公式法[10 ] 、等效热路法[11 ] 、等效热网络法[12 ] 和有限元法[13 -14 ] .其中简化公式法计算方法简易,但存在较大误差;等效热路法可求解电机各部分平均温度,但无法得到电机准确的温度分布;等效热网络法依据热传导定律中热对流、温度和热阻三者关系,依照电路中KVL与KCL原理,近似做出等效热网络图,分析各部分的温度[15 ] .有限元法将温度场计算模型剖分为细小的单元体,通过对每一个细小单元体求解计算再逼近整体解,该方法计算准确、应用广泛、适用性强. ...
Analysis on iron loss of switched reluctance motor under PWM mode
1
2018
... (2) 铁心损耗.开关磁阻电机磁场不是正弦波,且是高度非线性的,相较于传统正弦磁场下电机铁心损耗的求解更加复杂.目前,常见的求解开关磁阻电机铁心损耗的方法是基于Steinmetz方程模型,将电机内非正弦磁通密度波形做傅里叶分解,得到各次谐波下的正弦量进行电机铁心损耗的求解,但是该方法在磁场频率较高的开关磁阻电机中存在拟合误差大、计算不够准确的现象.本文采用改进变系数IEM5模型,以兼顾高频情况下集肤效应对涡流损耗的影响[16 ] .该方法将铁心损耗模型分为三部分 ...
Modeling of losses in switched reluctance machines
1
2004
... (3) 机械损耗.机械损耗一般由电机轴承摩擦损耗与通风损耗组成,APM-BFM电机转子运行时因无接触可忽略轴承摩擦损耗,主要考虑通风损耗[17 ] .通风损耗大小取决于电机的转速,且与空气密度、转子内径以及周向叠长相关,其一般表达式如下 ...
Temperature rise calculation of a flux-switching permanent-magnet double-rotor machine using electromagnetic-thermal coupling analysis
1
2018
... 电机材料温度属性分别通过电导率和磁导率反映出来.电导率与温度可以看成线性关系,电导率与温度之间的斜率称为电导率温度系数[18 ] .表2 给出几种常见材料的电导率及温度系数. ...
High-speed permanent magnet synchronous motor iron loss calculation method considering multi-physics factors
1
2019
... 目前对于温度场分析多采用磁-热单向耦合模型,即采用设置默认温度下材料的属性,进行温度场计算,忽略温度对其的影响.磁-热单向耦合模型分析计算模型速度较快[19 ] ,但未考虑材料温度属性,必然会引起计算误差.磁-热双向耦合模型考虑材料温度属性,以材料温度性质为变量,通过稳态温度场仿真得到温升数据作为影响材料性能的参考,传递到电磁仿真中,为温度场计算提供更准确的损耗数据[20 ] ,磁-热双向耦合损耗与温度数据在电磁场与温度场相互交换,经多次迭代达到稳定,即相邻两次数据温度差ΔT 小于设定误差η .图4 给出了APM-BFM磁-热双向耦合温度计算的流程图. ...
Electro- magnetic and thermal coupled analysis of can effect of a novel canned switched reluctance machine as a hydraulic pump drive
1
2017
... 目前对于温度场分析多采用磁-热单向耦合模型,即采用设置默认温度下材料的属性,进行温度场计算,忽略温度对其的影响.磁-热单向耦合模型分析计算模型速度较快[19 ] ,但未考虑材料温度属性,必然会引起计算误差.磁-热双向耦合模型考虑材料温度属性,以材料温度性质为变量,通过稳态温度场仿真得到温升数据作为影响材料性能的参考,传递到电磁仿真中,为温度场计算提供更准确的损耗数据[20 ] ,磁-热双向耦合损耗与温度数据在电磁场与温度场相互交换,经多次迭代达到稳定,即相邻两次数据温度差ΔT 小于设定误差η .图4 给出了APM-BFM磁-热双向耦合温度计算的流程图. ...