1 引言
永磁同步电机(Permanent magnet synchronous motor,PMSM)因其具有体积小、功率密度高以及转矩密度高等优点[1 ] ,广泛应用于工业伺服控制、轨道交通以及风力发电等领域[2 ⇓ -4 ] 。准确的转子位置信息是PMSM高效控制的基础[5 ] ,但电机拆装维修、位置传感器故障[6 ] 、驱动控制器更换以及软件数据更新等问题都可能导致转子初始位置信息丢失,进而造成控制系统失效。
采用无位置传感器算法或位置传感器[7 ⇓ -9 ] 是现有获取转子位置信息的两种主要方式。无位置传感器算法通常较复杂,且存在额外损耗、参数敏感等问题[10 ] 。基于高频注入的无位置传感器控制算法通常适用于凸极式永磁同步电机的初始位置判定和中低速运行[11 ] ,而基于反电势的无位置传感器方法对电机参数随磁饱和的变化比较敏感[12 ] 。现有的无位置传感器算法通常无法获取隐极式永磁同步电机的准确位置信息。因此,采用位置传感器仍是获取转子精确位置的主要方式。
其中,增量式编码器以其高精度、高可靠性、高性价比等优势[13 ] ,广泛应用于高精度控制等领域。增量式编码器通过计算脉冲数量来获取位置,无法直接获得转子的绝对位置信息,在使用前通常需要进行零位校正。目前,主要通过定子电流矢量法对增量式编码器进行零位校正[14 ⇓ ⇓ ⇓ -18 ] 。
文献[19 ]中,通过定子电流矢量拖动转子到达零位,进而确定转子初始位置,对编码器信息清零后,通过首个z脉冲信息计算零位偏置角。文献[20 ]中,采用了六种校正模式,将转子分别拖动至六个确定位置,通过任一校正模式的编码器信息与实际转子位置信息间的偏差即可计算零位偏置角。然而,当系统软硬件故障导致零位偏置角出错或丢失时,利用现有方法通常无法实现快速零位校正,恢复系统正常运行。
针对该问题,本文提出了一种基于交轴磁链辨识的永磁同步电机位置传感器零位校正方法,该方法既可用于隐极式电机,也能用于凸极式电机。本文章节安排如下:第2节介绍了零位校正原理与位置误差的影响;第3节介绍了所提的零位校正方法原理与具体实现流程;第4节介绍了试验测试平台构成,并通过试验测试证明了所述方法的可行性与可靠性。试验结果表明,本文提出方法能够实现转子快速定位,进而能对增量式编码器进行零位校正,且启动过程不受转子初始位置误差的影响。
2 基本原理
2.1 增量式编码器零位校正
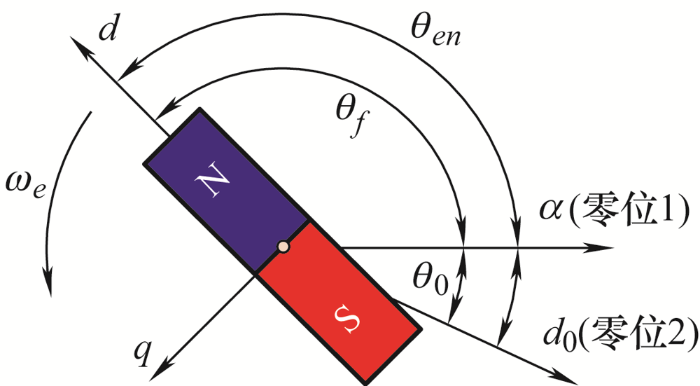
如图1 所示,在静止坐标系下,当转子中心轴d 轴与α 轴重合时,此时转子的电气角度θf 为0°,定义为零位1。
图1
增量式编码器输出信号通常包括两路正交计数脉冲与一路z脉冲。为了防止计数脉冲丢失产生累积误差,转子每旋转一周产生一个z脉冲,对正交脉冲计数清零。定义z脉冲出现时,转子中心轴位置在静止坐标系中的映射为d 0 轴。此时,编码器输出的电气角度θen 为0°,定义为零位2。θen 可以表示为
(1) ${{\theta }_{en}}={{\theta }_{m}}\times {{P}_{n}}$
式中,θm 为编码器输出的机械角度信息;Pn 为极对数。
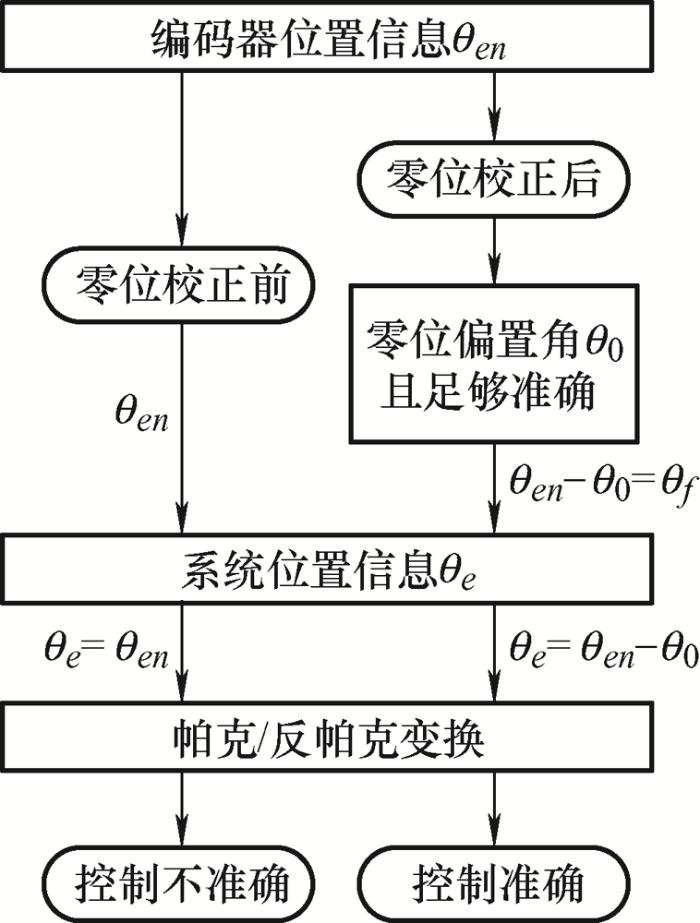
在增量式编码器安装过程中,通常无法将零位1与零位2对齐,这会导致零位偏置角θ 0 的存在。如图2 所示,如果不进行零位校正,则系统位置信息θe 就等于编码器输出角度θen ,实际控制的同步旋转坐标系与转子中心轴不重合,影响控制效果。
图2
只有在编码器输出角度θen 的基础上校正零位偏置角θ 0 ,才能使控制系统通过增量式编码器获得转子绝对位置信息,进而实现正确的坐标变换。当零位校正足够准确时,可以认为校正后的位置信息即为转子真实位置信息,即θe =θen -θ 0 =θf 。
因此,零位校正的目的就是通过获取零位偏置角θ 0 对θen 进行校正,进而获得转子绝对位置信息,实现PMSM的准确高效控制。
2.2 位置误差对直轴电压的影响
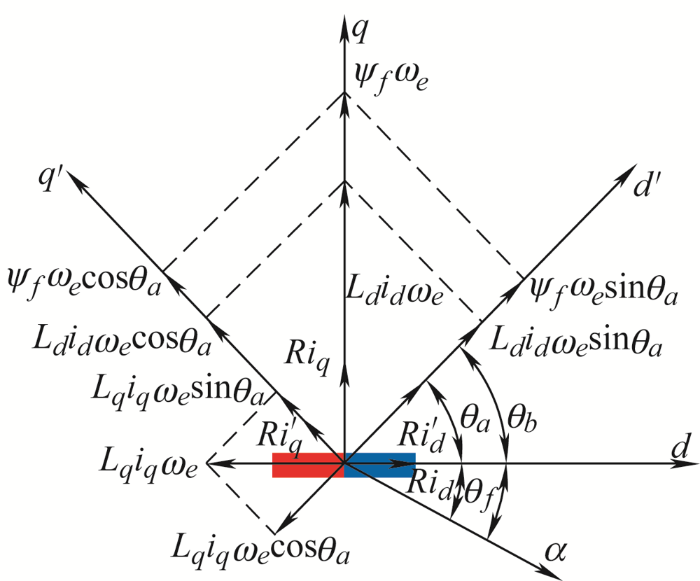
如图3 所示,定义准确零位校正后的同步旋转坐标系为dq ,此时θe =θen -θ0 =θf ,即位置信息准确工况。定义任意位置信息下的同步旋转坐标系为d' q′ ,此时θe =θb ,即位置信息不准确工况。两种工况的同步旋转坐标系间存在位置误差θa 。
图3
(2) $\left\{ \begin{align} & {{u}_{d}}=R{{i}_{d}}-{{L}_{q}}{{i}_{q}}{{\omega }_{e}}=R{{i}_{d}}-{{\psi }_{q}}{{\omega }_{e}} \\ & {{u}_{q}}=R{{i}_{q}}+\left( {{L}_{d}}{{i}_{d}}+{{\psi }_{f}} \right){{\omega }_{e}}=R{{i}_{q}}+{{\psi }_{d}}{{\omega }_{e}} \\ \end{align} \right.$
式中,ud 、uq 为d、q 轴电压;id 、iq 为d、q 轴电流;Ld 、Lq 为d、q 轴电感;ψf 为转子磁链;R 为定子电阻;ωe 为电角速度;ψd 、ψq 为d、q 轴磁链。
(3) $\left\{\begin{array}{l} u_{d}^{\prime}=R i_{d}^{\prime}+L_{d} i_{d} \omega_{e} \sin \theta_{a}- \\ L_{q} i_{q} \omega_{e} \cos \theta_{a}+\psi_{f} \omega_{e} \sin \theta_{a} \\ u_{q}^{\prime}=R i_{q}^{\prime}+L_{d} i_{d} \omega_{e} \cos \theta_{a}+ \\ L_{q} i_{q} \omega_{e} \sin \theta_{a}+\psi_{f} \omega_{e} \cos \theta_{a} \end{array}\right.$
(4) $\left\{\begin{array}{l} i_{d}=i_{d}^{\prime} \cos \theta_{a}-i_{q}^{\prime} \sin \theta_{a} \\ i_{q}=i_{d}^{\prime} \sin \theta_{a}+i_{q}^{\prime} \cos \theta_{a} \end{array}\right.$
(5) $\left\{\begin{array}{l} u_{d}^{\prime}=R i_{d}^{\prime}-\left[L_{q} i_{q}^{\prime} \cos ^{2} \theta_{a}+L_{d} i_{q}^{\prime} \sin ^{2} \theta_{a}-\psi_{f} \sin \theta_{a}-\right. \\ \left.\left(L_{d}-L_{q}\right) i_{d}^{\prime} \sin \theta_{a} \cos \theta_{a}\right] \omega_{e}=R i_{d}^{\prime}-\psi_{q}^{\prime} \omega_{e} \\ u_{q}^{\prime}=R i_{q}^{\prime}+\left[L_{d} i_{d}^{\prime} \cos ^{2} \theta_{a}+L_{q} i_{d}^{\prime} \sin ^{2} \theta_{a}+\psi_{f} \cos \theta_{a}-\right. \\ \left.\left(L_{d}-L_{q}\right) i_{q}^{\prime} \sin \theta_{a} \cos \theta_{a}\right] \omega_{e}=R i_{q}^{\prime}-\psi_{d}^{\prime} \omega_{e} \end{array}\right. $
当id = id ′ = 0,iq = iq ′ 时,由式(2)、式(5)可得到
(6) $\left\{\begin{aligned} u_{d} & =-L_{q} i_{q}^{\prime} \omega_{e}=-\psi_{q} \omega_{e} \\ u_{d}^{\prime} & =-\left[L_{q} i_{q}^{\prime} \cos ^{2} \theta_{a}+L_{d} i_{q}^{\prime} \sin ^{2} \theta_{a}-\psi_{f} \sin \theta_{a}\right] \omega_{e}= \\ & -\psi_{q}^{\prime} \omega_{e} \end{aligned}\right.$
通过式(6)可以看到,此时位置误差θa 的存在导致两坐标系下交轴磁链大小不同,进而导致直轴电压大小不同,在转速相同的情况下,只有当θa =0时,直轴电压才能相等,此时,θb =θf 则为u'd =ud 的充分必要条件。
基于这一结论,当id =i'd =0时,如果已知dq 坐标系下交轴磁链ψq 的变化方程,通过式(6)则可以得到任意转速下的ud ,在任意转子位置信息θb 的控制下,将ud 作为参考值,当u'd =ud 时,则有θb =θf ,即可获得准确的转子位置信息,实现转子定位的目的,对增量式编码器进行零位校正。因此,本文提出了基于交轴磁链辨识的位置传感器零位校正方法。
3 基于交轴磁链辨识的零位校正方法
3.1 交轴磁链辨识方法
(7) $\left\{ \begin{array}{*{35}{l}} {{u}_{d}}\left( k \right)=R{{i}_{d}}\left( k \right)-{{\psi }_{q}}\left( k \right){{\omega }_{e}}\left( k \right) \\ {{u}_{q}}\left( k \right)=R{{i}_{q}}\left( k \right)+{{\psi }_{d}}\left( k \right){{\omega }_{e}}\left( k \right) \\ \end{array} \right.$
式中,k 是系统的离散采样时刻。由于矢量控制系统通常采用脉宽调制技术进行电压输出,难以测量实际电压,所以通常采用参考电压代替。但实际电压通常会受到逆变器非线性因素的影响,因此,式(7)可以表示为
(8) $\left\{ \begin{array}{*{35}{l}} u_{d}^{*}\left( k \right)+{{V}_{dead}}\left( k \right){{D}_{d}}\left( k \right)={{u}_{d}}\left( k \right)= \\ R{{i}_{d}}\left( k \right)-{{\psi }_{q}}\left( k \right){{\omega }_{e}}\left( k \right) \\ u_{q}^{*}\left( k \right)+{{V}_{dead}}\left( k \right){{D}_{q}}\left( k \right)={{u}_{q}}\left( k \right)= \\ R{{i}_{q}}\left( k \right)+{{\psi }_{d}}\left( k \right){{\omega }_{e}}\left( k \right) \\ \end{array} \right.$
式中,Vdead Dd 和Vdead Dq 分别表示逆变器非线性因素引起的dq 轴畸变电压。Vdead 可以表示为[20 ]
(9) ${{V}_{dead}}=\frac{1}{6}\left( \frac{{{T}_{off}}-{{T}_{on}}-{{T}_{d}}}{{{T}_{s}}}{{V}_{dc}}-{{V}_{ce0}}-{{V}_{d0}} \right)$
结合式(9)可知,Vdead 与以下因素有关:开关延时Ton 和Toff 、死区时间Td ,以及IGBT和二极管导通压降Vce 0 和Vd 0 。
Dd 和Dq 与三相电流方向和系统电气角度有关[21 ] ,Dd 和Dq 可以表示为
(10) $\begin{matrix} \left[ \begin{matrix} {{D}_{d}} \\ {{D}_{q}} \\ \end{matrix} \right]=\left[ \begin{matrix} \cos \left( {{\theta }_{e}} \right) \\ \begin{align} & \\ & -\sin \left( {{\theta }_{e}} \right) \\ \end{align} \\ \end{matrix}\begin{matrix} \cos \left( {{\theta }_{e}}-\frac{2\mathrm{ }\!\!\pi\!\!\text{ }}{3} \right) \\ -\sin \left( {{\theta }_{e}}-\frac{2\mathrm{ }\!\!\pi\!\!\text{ }}{3} \right) \\ \end{matrix}\begin{matrix} \cos \left( {{\theta }_{e}}+\frac{2\mathrm{ }\!\!\pi\!\!\text{ }}{3} \right) \\ \sin \left( {{\theta }_{e}}-\frac{\mathrm{ }\!\!\pi\!\!\text{ }}{3} \right) \\ \end{matrix} \right]\times \\ \left[ \begin{matrix} sign\left( {{i}_{a}} \right) \\ sign\left( {{i}_{b}} \right) \\ sign\left( {{i}_{c}} \right) \\ \end{matrix} \right]\times 2 \\ \end{matrix}$
(11) $sign\left( i \right)=\left\{ \begin{array}{*{35}{l}} 1\ \ \ \ \ \ i\ge 0 \\ -1\ \ \ \ i<0 \\ \end{array} \right.$
式(8)是秩数为2的方程组,但包含R 、Vdead 、ψd 、ψq 四个未知变量,无法直接求解得到ψd 或ψq 。因此,文献[22 ]提出了一种永磁同步电机dq 轴磁链辨识的新方法,该方法的辨识模型消除了逆变器非线性因素以及电阻的影响,从而提高了辨识精度。
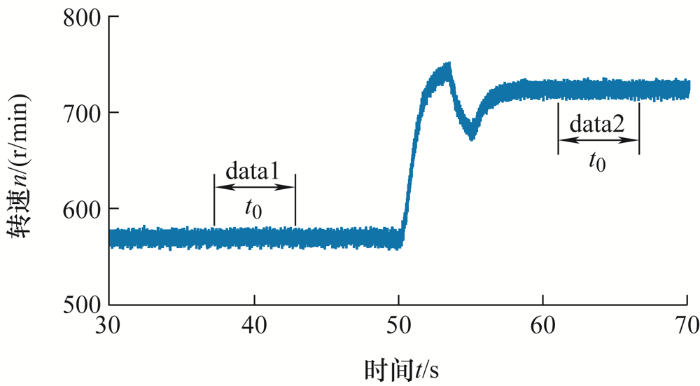
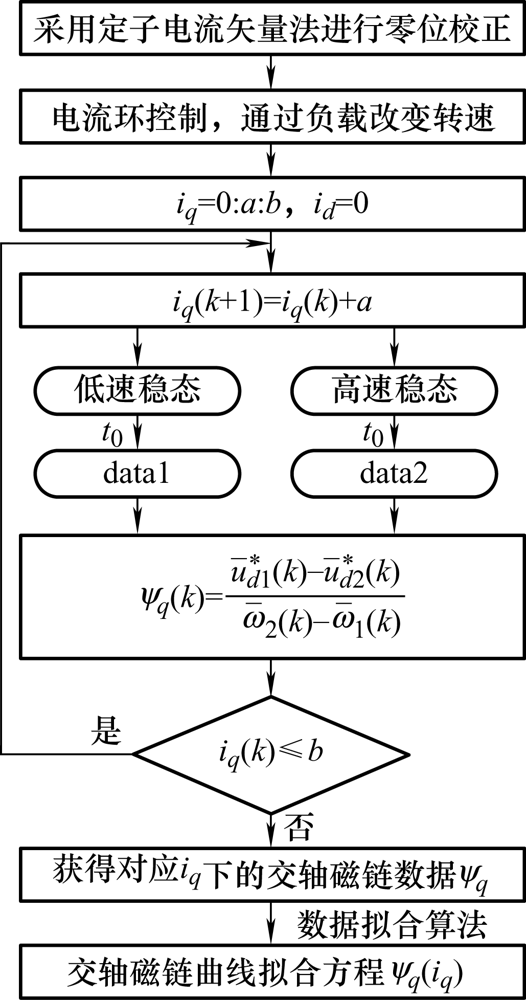
在文献[22 ]中,系统采用电流环控制模式,通过调整负载大小改变电机转速,实现连续变速工况,然后采集两组不同转速下的运行数据,并对基于智能算法的辨识模型进行最小化运算,实现dq 轴磁链的准确辨识。然而,该方法的试验工况和模型求解过程较复杂,因此本文对二者进行了简化,采用的试验工况如图4 所示,将原方法中的连续变速工况改为一次稳态变速工况,进而可以简化辨识模型和求解过程。下文仅对交轴磁链辨识过程进行介绍。
图4
如图4 所示,分别采集并存储两组采样时间同为t 0 ,转速不同的稳态运行数据,称为data1和data2。因此,通过式(8)得到两个离散的d 轴电压方程,可以表示为
(12) $\left\{ \begin{align} & u_{d}^{*}\left( i \right)+{{V}_{dead}}\left( i \right){{D}_{d}}\left( i \right)=R{{i}_{d}}\left( i \right)-{{\psi }_{q}}\left( i \right){{\omega }_{e}}\left( i \right) \\ & u_{d}^{*}\left( j \right)+{{V}_{dead}}\left( j \right){{D}_{d}}\left( k \right)=R{{i}_{d}}\left( j \right)-{{\psi }_{q}}\left( j \right){{\omega }_{e}}\left( j \right) \\ \end{align} \right.$
式中,i 、j 分别为data1、data2的数据下标,且i =j ,将式(12)中两方程相减,可以得到
(13) $\begin{array}{*{35}{l}} \ \ \ \ {{\psi }_{q}}\left( j \right){{\omega }_{e}}\left( j \right)-{{\psi }_{q}}\left( i \right){{\omega }_{e}}\left( i \right)= \\ R\left( {{i}_{d}}\left( j \right)-{{i}_{d}}\left( i \right) \right)+{{V}_{dead}}\left( i \right){{D}_{d}}\left( i \right)- \\ \ \ {{V}_{dead}}\left( j \right){{D}_{d}}\left( j \right)+u_{d}^{*}\left( i \right)-u_{d}^{*}\left( j \right) \\\end{array}$
data1、data2中每一组对应的数据点都满足式(13),因此将式(13)进行求和,可以得到
(14) $\begin{array}{*{35}{l}} \sum\limits_{i=j=1}^{N}{\left( {{\psi }_{q}}\left( j \right){{\omega }_{e}}\left( j \right)-{{\psi }_{q}}\left( i \right){{\omega }_{e}}\left( i \right) \right)=} \\ \begin{matrix} \sum\limits_{i=j=1}^{N}{\left( R\left( {{i}_{d}}\left( j \right)-{{i}_{d}}\left( i \right) \right) \right)+} \\ \sum\limits_{i=j=1}^{N}{\left( {{V}_{dead}}\left( i \right){{D}_{d}}\left( i \right)-\left. {{V}_{dead}}\left( j \right){{D}_{d}}\left( j \right) \right)+ \right.} \\ \end{matrix} \\ \ \ \ \ \ \ \ \ \ \ \ \ \sum\limits_{i=j=1}^{N}{\left( u_{d}^{*}\left( i \right)-u_{d}^{*}\left( j \right) \right)} \\ \end{array}$
式中,N 是data1和data2的数据长度。当采用电流环控制时,ψq 、Vdead 通常被认为是常数[23 ] ,并且通过式(10)可以看到,Dd 仅与电流方向和电气角度有关。因此,可以得到
(15) $\left\{ \begin{align} & \sum\limits_{i=j=1}^{N}{\left( {{i}_{d}}\left( j \right)-{{i}_{d}}\left( i \right) \right)=0} \\ & \sum\limits_{i=j=1}^{N}{{{D}_{d}}\left( i \right)}=\sum\limits_{i=j=1}^{N}{{{D}_{d}}\left( j \right)} \\ & \sum\limits_{i=j=1}^{N}{{{\psi }_{q}}\left( i \right)}=\sum\limits_{i=j=1}^{N}{{{\psi }_{q}}\left( j \right)=N{{\psi }_{q}}} \\ & \sum\limits_{i=j=1}^{N}{{{V}_{dead}}\left( i \right)}=\sum\limits_{i=j=1}^{N}{{{V}_{dead}}\left( j \right)}=N{{V}_{dead}} \\ \end{align} \right.\text{ }\ \ \ \ \text{ }$
因为data1和data2均为稳态运行数据,所以式(14)可以简化为
(16) $\begin{array}{*{35}{l}} {{\psi }_{q}}=\frac{\sum\limits_{i=j=1}^{N}{\left( u_{d}^{*}\left( i \right)-u_{d}^{*}\left( j \right) \right)}}{\sum\limits_{i=j=1}^{N}{\left( {{\omega }_{e}}\left( j \right)-{{\omega }_{e}}\left( i \right) \right)}} \\ \end{array}=\frac{\bar{u}_{d1}^{*}-\bar{u}_{d2}^{*}}{{{{\bar{\omega }}}_{2}}-{{{\bar{\omega }}}_{1}}}$
式中,$\bar{u}_{d1}^{*}$、${{\bar{\omega }}_{1}}$、$\bar{u}_{d2}^{*}$、${{\bar{\omega }}_{2}}$分别为data1、data2的d 轴参考电压平均值和电角速度平均值。因此,可以通过式(16)辨识电机交轴磁链ψq 。
3.2 交轴磁链曲线拟合方程
如图5 所示,通过定子电流矢量法对编码器进行零位校正,此时系统位置信息θe =θen -θ 0 ,采用id = 0控制,设定iq 在0~b 范围内,通过调整步长a 改变iq 大小。采用第3.1节所述方法,辨识不同iq 下的磁链ψq 。采用定子电流矢量法得到的零位偏置角θ 0 足够准确,可以认为校正后的系统位置信息即为转子真实位置信息,此时θe = θen - θ 0 = θf ,进而可以获得准确定位工况下的q 轴磁链曲线拟合方程ψq (iq )。通过该方程,可以得到dq 坐标系下任意大小iq 所对应的ψq 。
图5
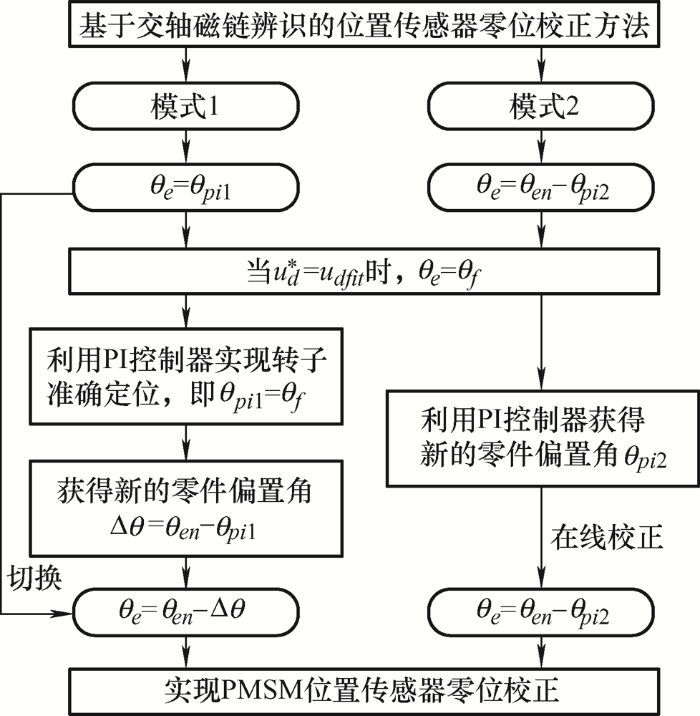
3.3 零位校正方法
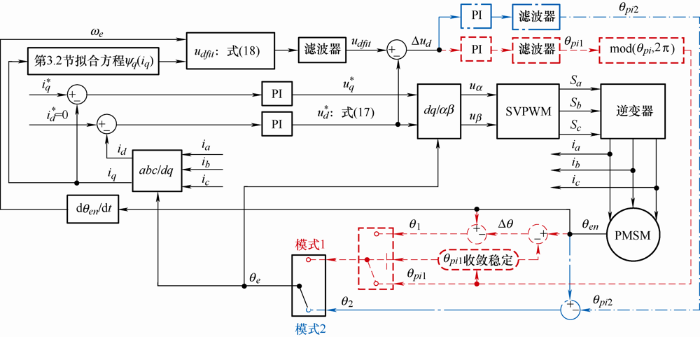
如图6 所示,为提出方法的系统控制框图,该方法采用电流环控制,且令id =0。如第2.2节所述,u′ d =ud 为θb =θf 的充分必要条件,基于这一结论可采用两种控制模式,分别为模式1与模式2,实现基于交轴磁链辨识的增量式编码器零位校正。
图6
在模式1中,将比例积分(PI)控制器的输出变量θpi 1 直接作为系统位置信息,即θe =θpi 1 ;在模式2中,则将PI控制器的输出变量θpi 2 作为编码器位置信息θen 的补偿,并将二者之差作为系统位置信息,即θe =θen -θpi 2 。在收敛过程中,θpi 1 与θpi 2 均大小任意,因此由图3 可知,θe 等价于θb ,此时系统控制的同步旋转坐标系可以表示为d ′ q′
(17) $u_{d}^{*}=-{\psi }'_{q}{{\omega }_{e}}$
同时通过第3.2节所述方法,计算获得图3 中dq 坐标系下的q 轴磁链曲线拟合方程ψq (iq ),同样,由式(6)可以得到
(18) ${{u}_{dfit}}=-{{\psi }_{q}}\left( {{i}_{q}} \right){{\omega }_{e}}$
式中,udfit 为拟合电压,即准确定位工况下的d 轴电压,iq 为q 轴实际电流,ωe 通过增量式编码器获取。将udfit 作为系统d 轴电压$u_{d}^{*}$的参考值,并将$u_{d}^{*}$输入控制系统,与滤波后的udfit 比较,将二者的误差Δud 作为控制量输入到PI控制器,当Δud 减小时,$u_{d}^{*}$逐渐收敛为udfit ,输出量θpi 1 或θpi 2 滤波后参与坐标变换,同时θe 逐渐收敛为θf ,经变换得到的id 、iq 参与udfit 和$u_{d}^{*}$的运算,从而实现闭环反馈控制。
如图7 所示,当系统收敛稳定时,可以得到$u_{d}^{*}$=udfit ,此时在模式1中可以得到θpi 1 =θf ,同时,通过增量式编码器不能获取准确的转子绝对位置信息,因此令Δθ=θen –θpi 1 ,将Δθ 称为偏置角,显然Δθ 即可作为新的零位偏置角,然后切换系统位置信息为θ 1 实现零位校正。在模式2中可以得到θ 2 =θen –θpi 2 =θf ,显然,此时θpi 2 即为新的零位偏置角。因此采用两种模式均可实现增量式编码器的零位校正。
图7
4 试验验证与分析
4.1 试验装置
试验装置如图8 所示,采用Speedgoat快速原型试验平台,主要包括一台三相PMSM,一台直流电机以及相应的控制系统,直流母线电压设定为40 V,采用2 500PPI分辨率的增量式编码器获取转子位置信息,PMSM参数如表1 所示。
图8
4.2 交轴磁链辨识与数据拟合
采用前文所述方法获取PMSM的q 轴磁链曲线拟合方程,具体方法如下:PMSM采用电流环控制模式且id =0,iq 从0递增至3 A,每增加0.5 A采集一组数据。采用直流电机控制转速,对应于每一个iq ,先调整为低转速采集数据data1,然后提高转速采集数据data2,完成一组数据的采集,数据采集时间t 0 为5 s。
需要说明的是,文献[22 ]采用连续变速工况试验,辨识结果不受转速波动影响,数据采集时间仅为1 s。本文采样频率与文献[22 ]相同,为防止速度波动对辨识结果造成影响,数据采集时间增加为5 s。
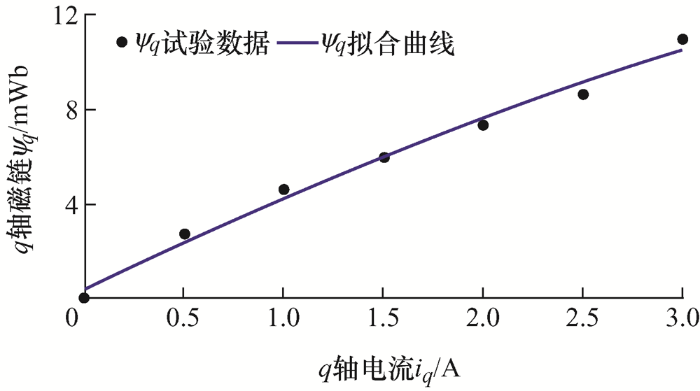
根据采集的稳态运行数据,通过式(16)计算对应iq 下的q 轴磁链ψq ,并使用Matlab中的Curve Fitting Tool进行数据拟合。拟合方程ψq (iq )如式(19)所示,拟合曲线如图9 所示,由图9 可知,数据均匀分布在曲线附近,拟合效果良好。
(19) ${{\psi }_{q}}\left( {{i}_{q}} \right)=-0.027\ 52\times \exp \left( -0.153\ 9\times {{i}_{q}} \right)+0.027\ 8$
图9
4.3 零位校正试验
零位校正试验采用电流环控制模式空载运行,设置iq =1 A,id =0 A。PMSM由静止状态起动,并加速至稳定运行。
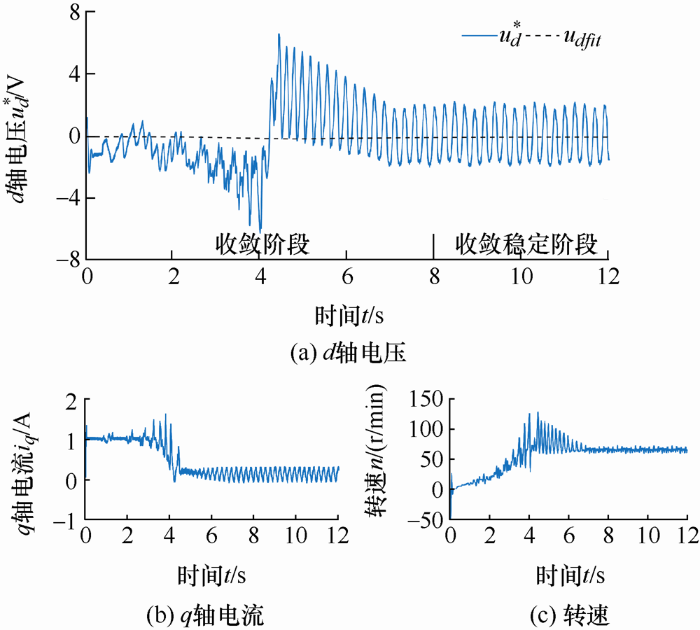
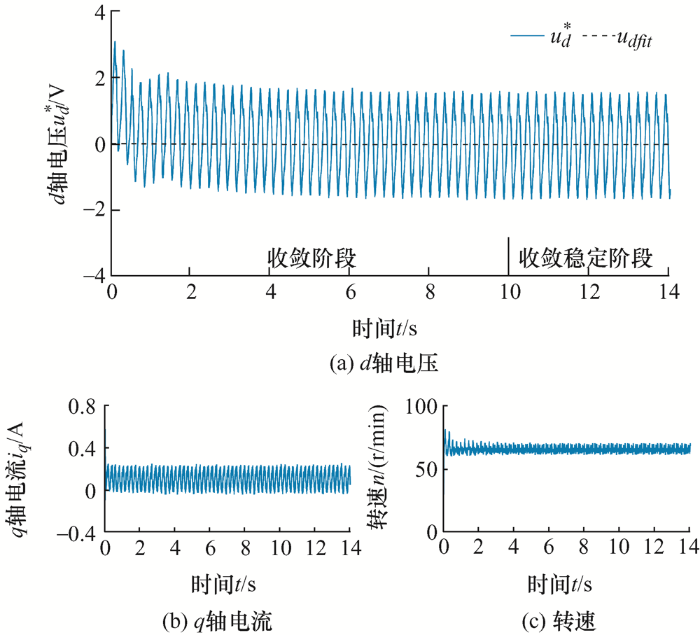
4.3.1 模式1
图10 为采用模式1进行零位校正时的试验波形。由图10 可知,0~8 s为收敛阶段,同时为起动加速阶段,d 轴参考电压$u_{d}^{*}$从0开始波动,逐渐收敛到拟合电压udfit 。在8~12 s,$u_{d}^{*}$围绕udfit 稳定波动,经计算得到平均值$\bar{u}_{d}^{*}$=udfit = –0.028 V,同时电流、转速稳定波动,说明8 s后系统已经收敛到稳定状态。
图10
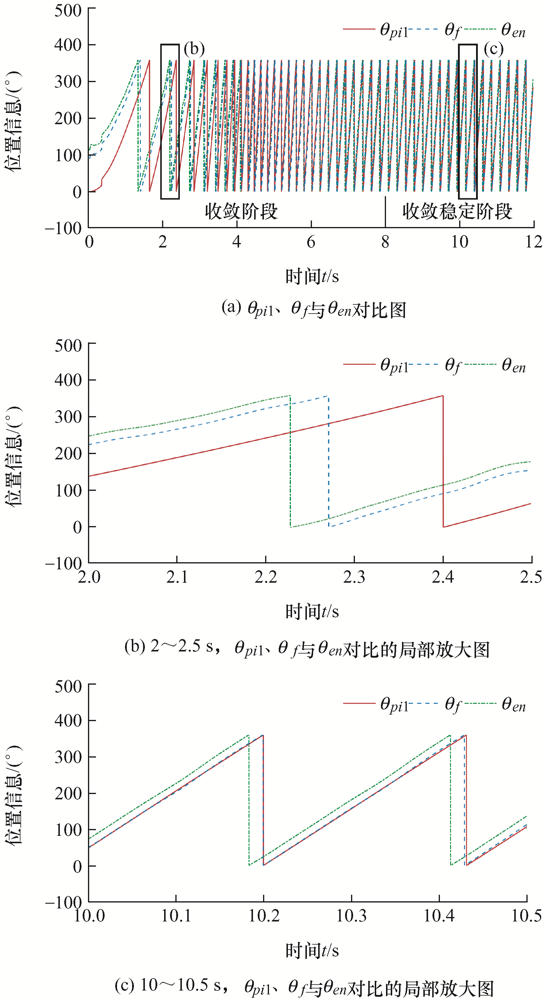
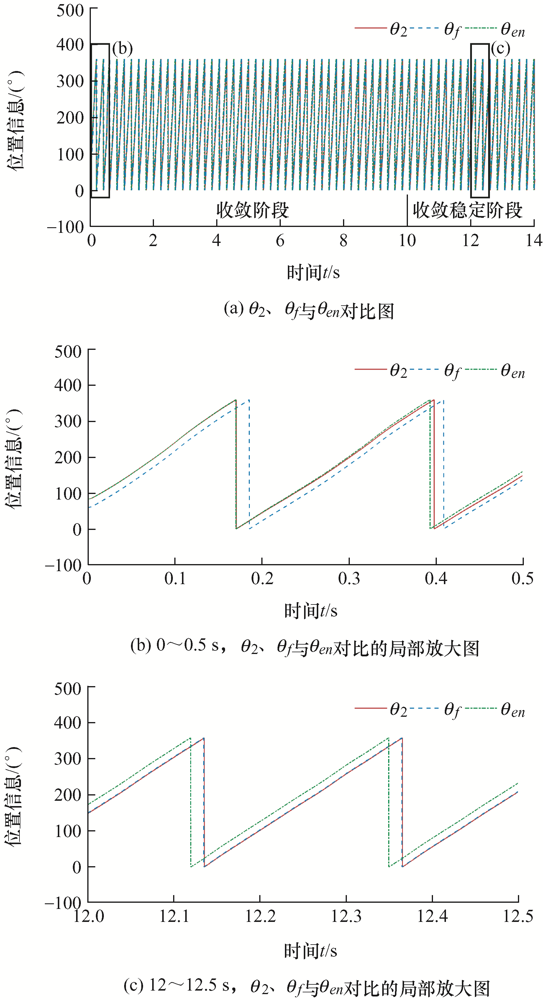
如图11 所示,θf 为采用定子电流矢量法得到的转子真实位置信息,θf = θen - θ 0 ,在图中的表示为θen 与θf 间的稳定偏差。
图11
图11
控制器输出位置信息θpi 1 、转子真实位置信息θf 与编码器输出位置信息θen 对比图,(b)、(c)为(a)的局部放大图
如图11 b所示,在收敛阶段,θpi 1 从0开始变化,且与θf 间存在明显位置偏差,经过8 s逐渐收敛为θf 。如图11 c所示,在收敛稳定阶段,此时θpi 1 与θf 十分接近,θpi 1 与θen 间同样存在稳定偏差,即偏置角Δθ 。
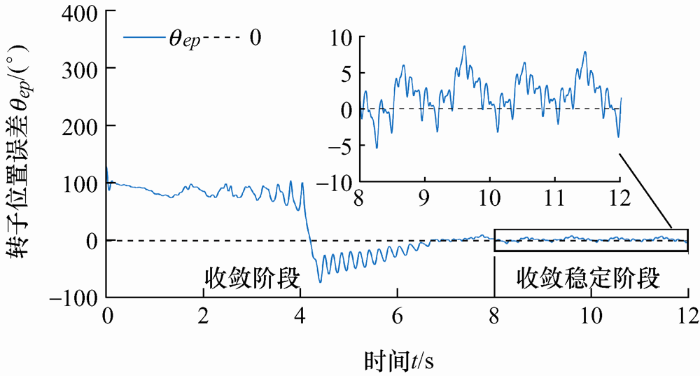
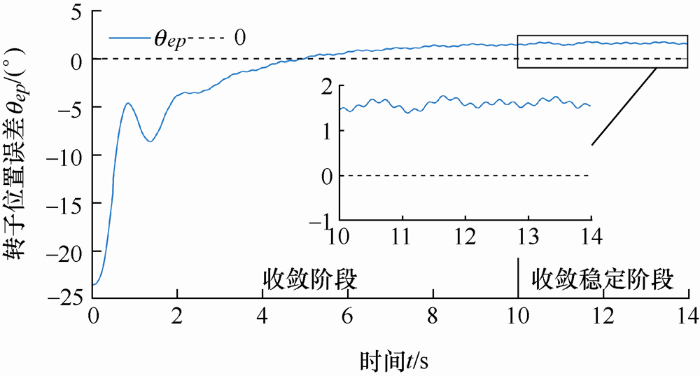
令θep =θf - θe ,其中θep 表示转子位置误差,为系统位置信息θe 与转子真实位置信息θf 间的误差,因此对于模式1有θep =θf - θpi 1 。
如图12 所示,θep 最终收敛在0附近,通过图中局部放大可以看到,θep 在0附近波动,这一波动主要是由转速波动引起,且变化幅值较小,经计算可得,稳定阶段误差均值${{\bar{\theta }}_{ep}}$=1.1°,即机械角度0.275°,这一误差对控制效果的影响很小,可以认为此时θpi 1 完全收敛,通过PI控制器获得了SPMSM的转子真实位置信息,实现了隐极式电机转子定位。
图12
采用θpi 1 作为系统位置信息只能在特定工况下运行,无法适应全部工况,因此,仍需要校正后的编码器信息参与系统控制。在θf 未知的情况下,可以通过模式1获取θpi 1 ,当收敛完成时,θpi 1 与θen 间存在偏置角Δθ ,显然Δθ 即为新的零位偏置角,可以用于校正θen ,从而获取准确的转子位置信息θ 1 ,然后将系统位置信息θe 从θpi 1 切换为θ 1 ,完成模式1的增量式编码器零位校正。为消除转速波动的影响,求取Δθ 的平均值$\overline{\Delta \theta }$作为新的零位偏置角,即θ 1 =θen –$\overline{\Delta \theta }$。
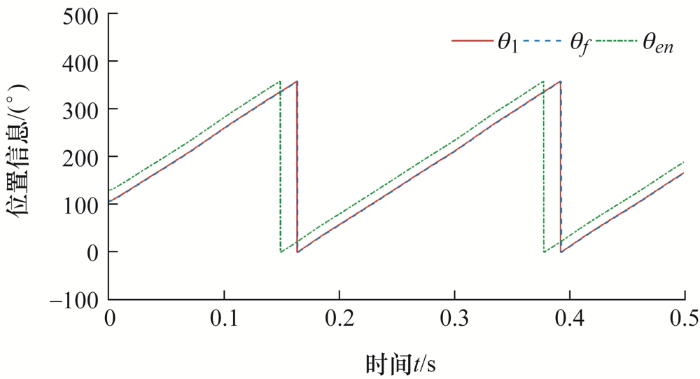
如图13 所示,θ 1 为校正后位置信息,θen 为校正前位置信息,θf 作为位置信息参考,可以看到零位校正前,θen 与θf 间存在稳定位置偏差,零位校正后,θ 1 与θf 几乎完全重合,校正误差即为${{\bar{\theta }}_{ep}}$=1.1°。综上所述,采用模式1可以实现编码器零位校正,且校正效果良好。
图13
图13
模式1校正后位置信息θ 1 、转子真实位置信息θf 与编码器输出位置信息θen 对比图
4.3.2 模式2
图14 为采用模式2零位校正时的试验波形。由图14 可知,0~10 s为系统收敛阶段,相较于模式1,起动加速时间很短,同样d 轴参考电压$u_{d}^{*}$从0开始波动,逐渐收敛到拟合电压udfit 。在10~14 s,$u_{d}^{*}$围绕udfit 稳定波动,经计算得到$\bar{u}_{d}^{*}$=udfit = –0.027 V,同时电流、转速稳定波动,说明10 s后系统已经收敛到稳定状态。
图14
如图15 所示,采用模式2时,θ 2 为校正后位置信息,θ 2 =θen - θpi 2 ,θen 为校正前位置信息,θf 作为位置信息参考。
图15
图15
控制器输出位置信息θpi 2 、转子真实位置信息θf 与编码器输出位置信息θen 对比图,(b)、(c)为(a)的局部放大图
如图15 b所示,在收敛阶段,θpi 2 初始为0,θ 2 与θen 十分接近,且与θf 间存在明显偏差,随着θpi 2 收敛,θ 2 与θen 间产生明显偏差,同时θ 2 逐渐收敛为θf 。如图15 c所示,在收敛稳定阶段,θ 2 与θf 几乎完全重合。
如图16 所示,对于模式2有θep =θf – θ 2 ,θep 最终收敛在0附近,经计算稳定阶段误差均值${{\bar{\theta }}_{ep}}$=1.6°,即机械角度0.4°,且波动幅值仅为0.2°,可以认为此时θ 2 完全收敛。因此,采用模式2可以获取转子真实位置信息,同时也可以实现增量式编码器零位校正,θpi 2 即为新的零位偏置角。
图16
综上所述,当PMSM因为系统软硬件故障,导致原有的零位偏置角θ 0 出错或丢失时,即可采用本方法对增量式编码器进行快速零位校正。采用模式1时,空载运行8 s左右即可获取准确的转子位置信息θpi 1 ,进而求取$\overline{\Delta \theta }$作为新的零位偏置角,从而校正编码器获取准确的转子位置信息θ 1 。采用模式2时,空载运行10 s左右即可获取准确的转子位置信息θ 2 ,θpi 2 即为新的零位偏置角,用于校正编码器信息θen 。两种模式均可实现位置传感器的快速零位校正,试验证明了本方法的可行性。
4.4 任意初始位置误差起动试验
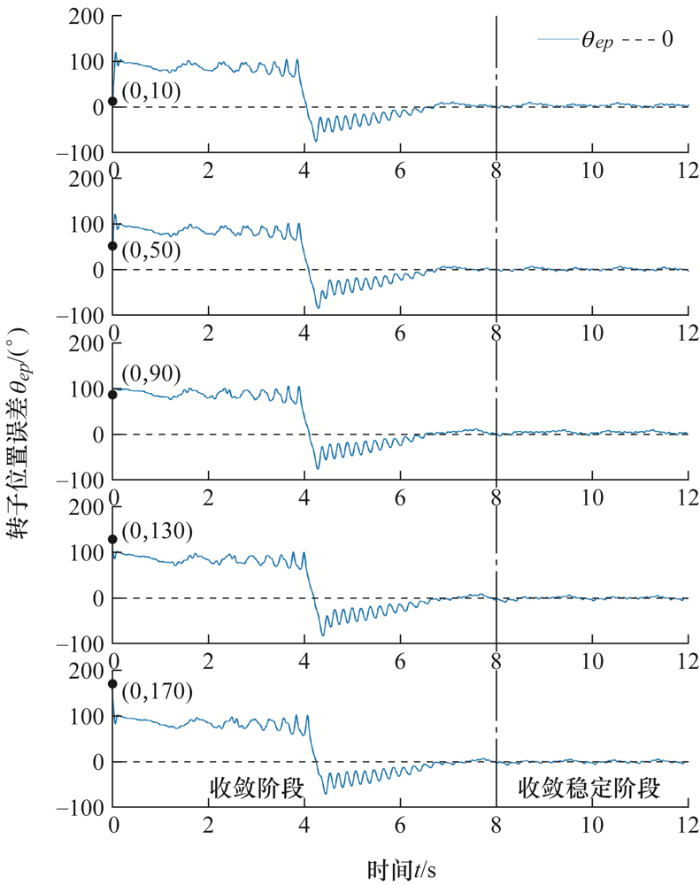
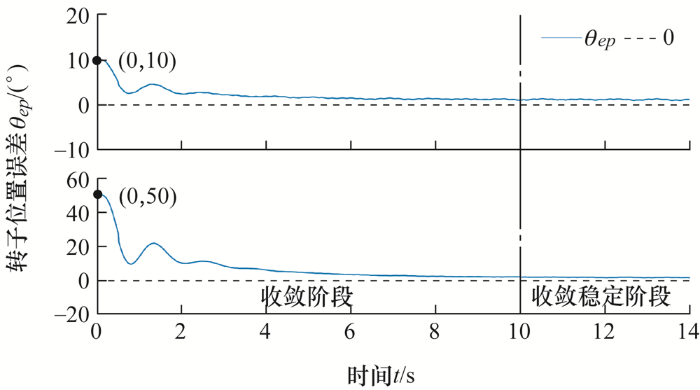
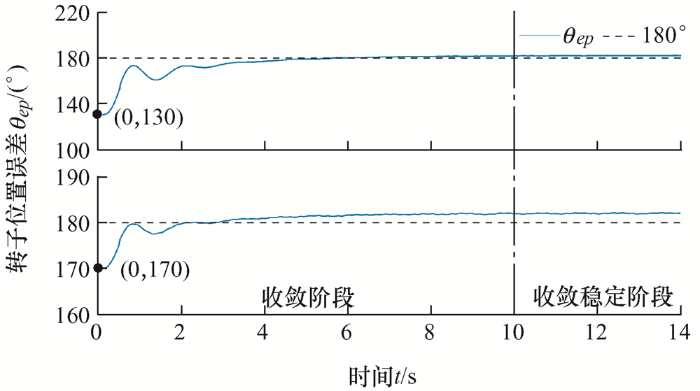
由于PI控制器没有设定初始值,在起动时刻θpi 1 =θpi 2 =0°,但转子初始位置是任意的,则可能存在由于转子初始位置误差太大,导致电机起动受到影响的情况。因此对于两种模式,分别调整转子位置误差θep 为10°、50°、90°、130°和170°进行起动,测试初始位置误差对起动效果的影响。
4.4.1 模式1
如图17 所示,10~14 s时θep 均能收敛到0附近,电机起动及运行不受初始位置误差的影响。
图17
图17
模式1转子位置误差θep ,起动时刻θep 分别为10°、50°、90°、130°和170°
由图17 可知,在起动瞬间,转子位置误差突变到90°左右,这一位置突变主要由iq 引起。在起动时刻,iq 矢量在同步旋转坐标系中的位置为90°,因此在起动瞬间电流将转子牵引至90°附近,造成这一位置突变。这就导致了不同初始位置误差下,θep 变化基本相同,同时也表明即使初始位置误差大于90°,电机仍然能够保持正转。
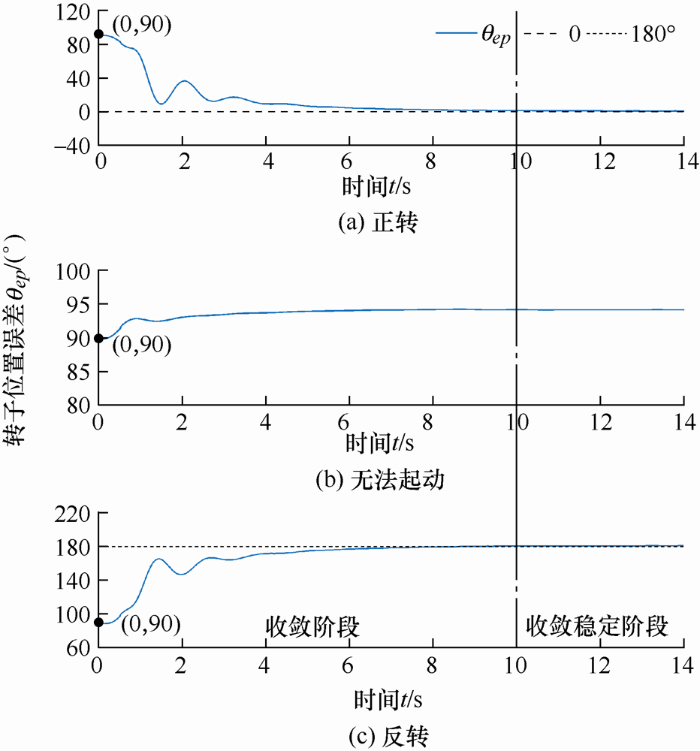
4.4.2 模式2
如图18 所示,当转子初始位置误差分别为10°和50°时,采用模式2均能正常收敛,10~14 s时θep 收敛到0附近,且电机正转。
图18
图18
模式2转子位置误差θep ,起动时刻θep 分别为10°和50°
如图19 所示,当转子初始位置误差分别为130°和170°时,采用模式2均能正常收敛,10~14 s时θep 收敛到180°附近,说明此时转子真实位置信息θf 与系统位置信息θe 相差180°,此时电机反转。
图19
图19
模式2转子位置误差θep ,起动时刻θep 分别为130°和170°
如图20 所示,当转子初始位置误差为90°时,此时iq 与转子同向,导致起动转矩很小,因此出现了以下三种结果:当电机正转时,θep 收敛到0附近;当电机反转时,θep 收敛到180°附近;当电机无法起动时,θep 无法收敛。
图20
图20
模式2转子位置误差θep ,起动时刻θep 为90°
经多次试验,当初始位置误差在79°~103°范围内时,因起动转矩太小,均存在无法起动的可能,因此模式2存在起动死区,转子初始位置误差对起动过程有一定影响。
综上所述,采用本文提出的方法进行零位校正时,当使用模式1时,任意初始位置误差工况下,系统都能够正常起动并稳定收敛,但在起动时刻会存在转子位置突变的现象;当使用模式2时,在较大初始位置误差范围内,系统都能够正常起动并稳定收敛,但当电流矢量与转子间夹角过小,导致起动转矩太小时,存在无法起动的问题。试验验证了本方法的可靠性。
5 结论
在id =0工况下,位置信息相同是直轴电压相等的充分必要条件。利用这一结论,本文通过两种控制模式实现了增量式编码器的快速零位校正。
(1) 对于模式1,无需位置传感器信息,利用控制器即可输出转子准确位置信息,进而可以对编码器进行零位校正。该模式起动不受转子初始位置误差影响,且对电机凸极性没有要求,既可用于凸极式电机,也可用于隐极式电机。
(2) 对于模式2,可以通过控制器直接获取零位偏置角,在线补偿转子位置信息,从而实现编码器零位校正。但该模式存在一定的起动死区,起动过程会受转子初始位置误差影响。
(3) 通过零位校正试验与任意初始位置误差起动试验分别说明了本文提出方法的可行性与可靠性。结果表明,该方法定位效果良好,零位校正速度快、精度高,可靠性高,具有一定的工程应用价值。
参考文献
View Option
[1]
LIU Kan ZHANG Qiao CHEN Jintao , et al . Online multiparameter estimation of nonsalient-pole PM synchronous machines with temperature variation tracking
[J]. IEEE Transactions on Industrial Electronics , 2011 , 58 (5 ):1776 -1788 .
DOI:10.1109/TIE.2010.2054055
URL
[本文引用: 1]
[2]
ZHU Ying CHENG Ming HUA Wei , et al . Sensorless control strategy of electrical variable transmission machines for wind energy conversion systems
[J]. IEEE Transactions on Magnetics , 2013 , 49 (7 ):3383 -3386 .
DOI:10.1109/TMAG.2013.2243904
URL
[本文引用: 1]
[3]
孙凯 , 许镇琳 , 盖廓 , 等 . 基于自抗扰控制器的永磁同步电机位置伺服系统
[J]. 中国电机工程学报 , 2007 (15 ):43 -46 .
[本文引用: 1]
SUN Kai XU Zhenlin GAI Kuo , et al . A novel position controller of PMSM servo system based on active-disturbance rejection controller
[J]. Proceedings of the CSEE , 2007 (15 ):43 -46 .
[本文引用: 1]
[4]
何亚屏 , 文宇良 , 许峻峰 , 等 . 基于多模式SVPWM算法的永磁同步牵引电机弱磁控制策略
[J]. 电工技术学报 , 2012 , 27 (3 ):92 -99 .
[本文引用: 1]
HE Yaping WEN Yuliang XU Junfeng , et al . High-power permanent magnet flux-weakening strategy based on multi-mode SVPWM
[J]. Transactions of China Electrotechnical Society , 2012 , 27 (3 ):92 -99 .
[本文引用: 1]
[5]
RAHMAN K M HITI S . Identification of machine parameters of a synchronous motor
[C]// 38th IAS Annual Meeting on Conference Record of the Industry Applications Conference,UT,USA , 2003 :409 -415 .
[本文引用: 1]
[6]
董亮辉 , 刘景林 . 永磁同步电机位置传感器的故障检测和容错控制
[J]. 西北工业大学学报 , 2016 , 34 (2 ):306 -312 .
[本文引用: 1]
DONG Lianghui LIU Jinglin . Fault detection and fault tolerant control of permanent magnet synchronous motor drives with hall sensors
[J]. Journal of Northwestern Polytechnical University , 2016 , 34 (2 ):306 -312 .
[本文引用: 1]
[7]
张洪帅 , 王平 , 韩邦成 . 基于模糊PI模型参考自适应的高速永磁同步电机转子位置检测
[J]. 中国电机工程学报 , 2014 , 34 (12 ):1889 -1896 .
[本文引用: 1]
ZHANG Hongshuai WANG Ping HAN Bangcheng . Rotor position measurement for high-speed permanent magnet synchronous motors based on fuzzy PI MRAS
[J]. Proceedings of the CSEE , 2014 , 34 (12 ):1889 -1896 .
[本文引用: 1]
[8]
RAJA R SEBASTIAN T WANG M , et al . Effect of position sensor error on the performance of permanent magnet machine drives
[J]. IEEE Transactions on Industry Applications , 2017 , 53 (6 ):5518 -5526 .
DOI:10.1109/TIA.2017.2704898
URL
[本文引用: 1]
[9]
尚喆 , 赵荣祥 , 窦汝振 . 基于自适应滑模观测器的永磁同步电机无位置传感器控制研究
[J]. 中国电机工程学报 , 2007 (3 ):23 -27 .
[本文引用: 1]
SHANG Zhe ZHAO Rongxiang DOU Ruzhen . Research on sensorless control method of PMSM based on an adaptive sliding mode observer
[J]. Proceedings of the CSEE , 2007 (3 ):23 -27 .
[本文引用: 1]
[10]
刘计龙 , 肖飞 , 沈洋 , 等 . 永磁同步电机无位置传感器控制技术研究综述
[J]. 电工技术学报 , 2017 , 32 (16 ):76 -88 .
[本文引用: 1]
LIU Jilong XIAO Fei SHEN Yang , et al . Position-sensorless control technology of permanent-magnet synchronous motor:A review
[J]. Transactions of China Electrotechnical Society , 2017 , 32 (16 ):76 -88 .
[本文引用: 1]
[11]
杨健 , 杨淑英 , 李浩源 , 等 . 基于旋转高频电压注入的永磁同步电机转子初始位置辨识方法
[J]. 电工技术学报 , 2018 , 33 (15 ):3547 -3555 .
[本文引用: 1]
YANG Jian YANG Shuying LI Haoyuan , et al . Initial rotor position estimation for IPMSM based on high frequency rotating voltage injection
[J]. Transactions of China Electrotechnical Society , 2018 , 33 (15 ):3547 -3555 .
[本文引用: 1]
[12]
黄雷 , 赵光宙 , 年珩 . 基于扩展反电势估算的内插式永磁同步电动机无传感器控制
[J]. 中国电机工程学报 , 2007 (9 ):59 -63 .
[本文引用: 1]
HUANG Lei ZHAO Guangzhou NIAN Heng . Sensor- less control of interior permanent magnet synchronous motor by estimation of an extended electromotive force
[J]. Proceedings of the CSEE , 2007 (9 ):59 -63 .
[本文引用: 1]
[13]
ANUCHIN A DIANOV A BRIZ F . Synchronous constant elapsed time speed estimation using incremental encoders
[J]. IEEE/ASME Transactions on Mechatronics , 2019 , 24 (4 ):1893 -1901 .
DOI:10.1109/TMECH.2019.2928950
URL
[本文引用: 1]
[14]
马小勇 . PMSM转子位置复合检测与编码器校正研究 [D]. 郑州 : 郑州大学 , 2017 .
[本文引用: 1]
MA Xiaoyong . Research on rotor position hybrid detection and encodercorrection of permanent magnet synchronous motor [D]. Zhengzhou : Zhengzhou University , 2017 .
[本文引用: 1]
[15]
朱熀秋 , 成秋良 . 无起动绕组永磁同步电机初始定位及起动策略
[J]. 中国电机工程学报 , 2008 (9 ):61 -65 .
[本文引用: 1]
ZHU Huangqiu CHENG Qiuliang . Initial orientation and starting strategy on PMSM without starting windings
[J]. Proceedings of the CSEE , 2008 (9 ):61 -65 .
[本文引用: 1]
[16]
JUNG D H HA I J . An efficient method for identifying the initial position of a PMSM with an incremental encoder
[J]. IEEE Transactions on Industrial Electronics , 1998 , 45 (4 ):682 -685 .
DOI:10.1109/41.704901
URL
[本文引用: 1]
[17]
ZHAO Yifan YAN Fuwu DU Changqing . Fast start-up control method of PMSM based on incremental photoelectric encoder
[C]// I ET International Conference on Information Science and Control Engineering 2012 (ICISCE 2012),Shenzhen,China2012 :1 -4 .
[本文引用: 1]
[18]
胡庆波 , 胡海兵 , 吕征宇 . 全数字伺服系统中电机转子初始定位的方法
[J]. 电力系统及其自动化学报 , 2005 (4 ):7 -10 .
[本文引用: 1]
HU Qingbo HU Haibing LÜ Zhengyu . Method for measuring initial position of motor rotor of a digital servo system
[J]. Proceedings of the CSU-EPSA , 2005 (4 ):7 -10 .
[本文引用: 1]
[19]
王要强 , 马小勇 , 程志平 , 等 . PMSM转子初始位置检测分析及起动策略
[J]. 电力自动化设备 , 2016 , 36 (9 ):156 -161 ,168.
[本文引用: 1]
WANG Yaoqiang MA Xiaoyong CHENG Zhiping , et al . PMSM initial rotor position detection and startup strategy
[J]. Electric Power Automation Equipment , 2016 , 36 (9 ):156 -161 ,168.
[本文引用: 1]
[20]
OH H SONG K CHO K , et al . Initial rotor position detecting algorithm of PM synchronous motor using incremental encoder
[C]// IEEE ECCE Asia Downunder,Melbourne,Australia , 2013 :681 -686 .
[本文引用: 2]
[21]
KIM H W YOUN M J CHO K Y , et al . Nonlinearity estimation and compensation of PWM VSI for PMSM under resistance and flux linkage uncertainty
[J]. IEEE Trans. Control Syst. Technol ., 2006 , 14 (4 ):589 -601 .
DOI:10.1109/TCST.2006.876622
URL
[本文引用: 1]
[22]
LIU Kan FENG Jianghua GUO Shuying , et al . Identification of flux linkage map of permanent magnet synchronous machines under uncertain circuit resistance and inverter neonlinearity
[J]. IEEE Transactions on Industrial Informatics , 2018 , 14 (2 ):556 -568 .
DOI:10.1109/TII.2017.2722470
URL
[本文引用: 4]
[23]
周世超 , 刘侃 , 丁荣军 , 等 . 基于谐波分离的逆变器非线性因素直接提取和补偿方法
[J]. 中国电机工程学报 , 2021 , 41 (22 ):7763 -7771 .
[本文引用: 1]
ZHOU Shichao LIU Kan DING Rongjun , et al . Direct extraction and compensation of inverter nonlinearity based on harmonic separation
[J]. Proceedings of the CSEE , 2021 , 41 (22 ):7763 -7771 .
[本文引用: 1]
Online multiparameter estimation of nonsalient-pole PM synchronous machines with temperature variation tracking
1
2011
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)因其具有体积小、功率密度高以及转矩密度高等优点[1 ] ,广泛应用于工业伺服控制、轨道交通以及风力发电等领域[2 ⇓ -4 ] .准确的转子位置信息是PMSM高效控制的基础[5 ] ,但电机拆装维修、位置传感器故障[6 ] 、驱动控制器更换以及软件数据更新等问题都可能导致转子初始位置信息丢失,进而造成控制系统失效. ...
Sensorless control strategy of electrical variable transmission machines for wind energy conversion systems
1
2013
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)因其具有体积小、功率密度高以及转矩密度高等优点[1 ] ,广泛应用于工业伺服控制、轨道交通以及风力发电等领域[2 ⇓ -4 ] .准确的转子位置信息是PMSM高效控制的基础[5 ] ,但电机拆装维修、位置传感器故障[6 ] 、驱动控制器更换以及软件数据更新等问题都可能导致转子初始位置信息丢失,进而造成控制系统失效. ...
基于自抗扰控制器的永磁同步电机位置伺服系统
1
2007
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)因其具有体积小、功率密度高以及转矩密度高等优点[1 ] ,广泛应用于工业伺服控制、轨道交通以及风力发电等领域[2 ⇓ -4 ] .准确的转子位置信息是PMSM高效控制的基础[5 ] ,但电机拆装维修、位置传感器故障[6 ] 、驱动控制器更换以及软件数据更新等问题都可能导致转子初始位置信息丢失,进而造成控制系统失效. ...
A novel position controller of PMSM servo system based on active-disturbance rejection controller
1
2007
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)因其具有体积小、功率密度高以及转矩密度高等优点[1 ] ,广泛应用于工业伺服控制、轨道交通以及风力发电等领域[2 ⇓ -4 ] .准确的转子位置信息是PMSM高效控制的基础[5 ] ,但电机拆装维修、位置传感器故障[6 ] 、驱动控制器更换以及软件数据更新等问题都可能导致转子初始位置信息丢失,进而造成控制系统失效. ...
基于多模式SVPWM算法的永磁同步牵引电机弱磁控制策略
1
2012
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)因其具有体积小、功率密度高以及转矩密度高等优点[1 ] ,广泛应用于工业伺服控制、轨道交通以及风力发电等领域[2 ⇓ -4 ] .准确的转子位置信息是PMSM高效控制的基础[5 ] ,但电机拆装维修、位置传感器故障[6 ] 、驱动控制器更换以及软件数据更新等问题都可能导致转子初始位置信息丢失,进而造成控制系统失效. ...
High-power permanent magnet flux-weakening strategy based on multi-mode SVPWM
1
2012
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)因其具有体积小、功率密度高以及转矩密度高等优点[1 ] ,广泛应用于工业伺服控制、轨道交通以及风力发电等领域[2 ⇓ -4 ] .准确的转子位置信息是PMSM高效控制的基础[5 ] ,但电机拆装维修、位置传感器故障[6 ] 、驱动控制器更换以及软件数据更新等问题都可能导致转子初始位置信息丢失,进而造成控制系统失效. ...
Identification of machine parameters of a synchronous motor
1
2003
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)因其具有体积小、功率密度高以及转矩密度高等优点[1 ] ,广泛应用于工业伺服控制、轨道交通以及风力发电等领域[2 ⇓ -4 ] .准确的转子位置信息是PMSM高效控制的基础[5 ] ,但电机拆装维修、位置传感器故障[6 ] 、驱动控制器更换以及软件数据更新等问题都可能导致转子初始位置信息丢失,进而造成控制系统失效. ...
永磁同步电机位置传感器的故障检测和容错控制
1
2016
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)因其具有体积小、功率密度高以及转矩密度高等优点[1 ] ,广泛应用于工业伺服控制、轨道交通以及风力发电等领域[2 ⇓ -4 ] .准确的转子位置信息是PMSM高效控制的基础[5 ] ,但电机拆装维修、位置传感器故障[6 ] 、驱动控制器更换以及软件数据更新等问题都可能导致转子初始位置信息丢失,进而造成控制系统失效. ...
Fault detection and fault tolerant control of permanent magnet synchronous motor drives with hall sensors
1
2016
... 永磁同步电机(Permanent magnet synchronous motor,PMSM)因其具有体积小、功率密度高以及转矩密度高等优点[1 ] ,广泛应用于工业伺服控制、轨道交通以及风力发电等领域[2 ⇓ -4 ] .准确的转子位置信息是PMSM高效控制的基础[5 ] ,但电机拆装维修、位置传感器故障[6 ] 、驱动控制器更换以及软件数据更新等问题都可能导致转子初始位置信息丢失,进而造成控制系统失效. ...
基于模糊PI模型参考自适应的高速永磁同步电机转子位置检测
1
2014
... 采用无位置传感器算法或位置传感器[7 ⇓ -9 ] 是现有获取转子位置信息的两种主要方式.无位置传感器算法通常较复杂,且存在额外损耗、参数敏感等问题[10 ] .基于高频注入的无位置传感器控制算法通常适用于凸极式永磁同步电机的初始位置判定和中低速运行[11 ] ,而基于反电势的无位置传感器方法对电机参数随磁饱和的变化比较敏感[12 ] .现有的无位置传感器算法通常无法获取隐极式永磁同步电机的准确位置信息.因此,采用位置传感器仍是获取转子精确位置的主要方式. ...
Rotor position measurement for high-speed permanent magnet synchronous motors based on fuzzy PI MRAS
1
2014
... 采用无位置传感器算法或位置传感器[7 ⇓ -9 ] 是现有获取转子位置信息的两种主要方式.无位置传感器算法通常较复杂,且存在额外损耗、参数敏感等问题[10 ] .基于高频注入的无位置传感器控制算法通常适用于凸极式永磁同步电机的初始位置判定和中低速运行[11 ] ,而基于反电势的无位置传感器方法对电机参数随磁饱和的变化比较敏感[12 ] .现有的无位置传感器算法通常无法获取隐极式永磁同步电机的准确位置信息.因此,采用位置传感器仍是获取转子精确位置的主要方式. ...
Effect of position sensor error on the performance of permanent magnet machine drives
1
2017
... 采用无位置传感器算法或位置传感器[7 ⇓ -9 ] 是现有获取转子位置信息的两种主要方式.无位置传感器算法通常较复杂,且存在额外损耗、参数敏感等问题[10 ] .基于高频注入的无位置传感器控制算法通常适用于凸极式永磁同步电机的初始位置判定和中低速运行[11 ] ,而基于反电势的无位置传感器方法对电机参数随磁饱和的变化比较敏感[12 ] .现有的无位置传感器算法通常无法获取隐极式永磁同步电机的准确位置信息.因此,采用位置传感器仍是获取转子精确位置的主要方式. ...
基于自适应滑模观测器的永磁同步电机无位置传感器控制研究
1
2007
... 采用无位置传感器算法或位置传感器[7 ⇓ -9 ] 是现有获取转子位置信息的两种主要方式.无位置传感器算法通常较复杂,且存在额外损耗、参数敏感等问题[10 ] .基于高频注入的无位置传感器控制算法通常适用于凸极式永磁同步电机的初始位置判定和中低速运行[11 ] ,而基于反电势的无位置传感器方法对电机参数随磁饱和的变化比较敏感[12 ] .现有的无位置传感器算法通常无法获取隐极式永磁同步电机的准确位置信息.因此,采用位置传感器仍是获取转子精确位置的主要方式. ...
Research on sensorless control method of PMSM based on an adaptive sliding mode observer
1
2007
... 采用无位置传感器算法或位置传感器[7 ⇓ -9 ] 是现有获取转子位置信息的两种主要方式.无位置传感器算法通常较复杂,且存在额外损耗、参数敏感等问题[10 ] .基于高频注入的无位置传感器控制算法通常适用于凸极式永磁同步电机的初始位置判定和中低速运行[11 ] ,而基于反电势的无位置传感器方法对电机参数随磁饱和的变化比较敏感[12 ] .现有的无位置传感器算法通常无法获取隐极式永磁同步电机的准确位置信息.因此,采用位置传感器仍是获取转子精确位置的主要方式. ...
永磁同步电机无位置传感器控制技术研究综述
1
2017
... 采用无位置传感器算法或位置传感器[7 ⇓ -9 ] 是现有获取转子位置信息的两种主要方式.无位置传感器算法通常较复杂,且存在额外损耗、参数敏感等问题[10 ] .基于高频注入的无位置传感器控制算法通常适用于凸极式永磁同步电机的初始位置判定和中低速运行[11 ] ,而基于反电势的无位置传感器方法对电机参数随磁饱和的变化比较敏感[12 ] .现有的无位置传感器算法通常无法获取隐极式永磁同步电机的准确位置信息.因此,采用位置传感器仍是获取转子精确位置的主要方式. ...
Position-sensorless control technology of permanent-magnet synchronous motor:A review
1
2017
... 采用无位置传感器算法或位置传感器[7 ⇓ -9 ] 是现有获取转子位置信息的两种主要方式.无位置传感器算法通常较复杂,且存在额外损耗、参数敏感等问题[10 ] .基于高频注入的无位置传感器控制算法通常适用于凸极式永磁同步电机的初始位置判定和中低速运行[11 ] ,而基于反电势的无位置传感器方法对电机参数随磁饱和的变化比较敏感[12 ] .现有的无位置传感器算法通常无法获取隐极式永磁同步电机的准确位置信息.因此,采用位置传感器仍是获取转子精确位置的主要方式. ...
基于旋转高频电压注入的永磁同步电机转子初始位置辨识方法
1
2018
... 采用无位置传感器算法或位置传感器[7 ⇓ -9 ] 是现有获取转子位置信息的两种主要方式.无位置传感器算法通常较复杂,且存在额外损耗、参数敏感等问题[10 ] .基于高频注入的无位置传感器控制算法通常适用于凸极式永磁同步电机的初始位置判定和中低速运行[11 ] ,而基于反电势的无位置传感器方法对电机参数随磁饱和的变化比较敏感[12 ] .现有的无位置传感器算法通常无法获取隐极式永磁同步电机的准确位置信息.因此,采用位置传感器仍是获取转子精确位置的主要方式. ...
Initial rotor position estimation for IPMSM based on high frequency rotating voltage injection
1
2018
... 采用无位置传感器算法或位置传感器[7 ⇓ -9 ] 是现有获取转子位置信息的两种主要方式.无位置传感器算法通常较复杂,且存在额外损耗、参数敏感等问题[10 ] .基于高频注入的无位置传感器控制算法通常适用于凸极式永磁同步电机的初始位置判定和中低速运行[11 ] ,而基于反电势的无位置传感器方法对电机参数随磁饱和的变化比较敏感[12 ] .现有的无位置传感器算法通常无法获取隐极式永磁同步电机的准确位置信息.因此,采用位置传感器仍是获取转子精确位置的主要方式. ...
基于扩展反电势估算的内插式永磁同步电动机无传感器控制
1
2007
... 采用无位置传感器算法或位置传感器[7 ⇓ -9 ] 是现有获取转子位置信息的两种主要方式.无位置传感器算法通常较复杂,且存在额外损耗、参数敏感等问题[10 ] .基于高频注入的无位置传感器控制算法通常适用于凸极式永磁同步电机的初始位置判定和中低速运行[11 ] ,而基于反电势的无位置传感器方法对电机参数随磁饱和的变化比较敏感[12 ] .现有的无位置传感器算法通常无法获取隐极式永磁同步电机的准确位置信息.因此,采用位置传感器仍是获取转子精确位置的主要方式. ...
Sensor- less control of interior permanent magnet synchronous motor by estimation of an extended electromotive force
1
2007
... 采用无位置传感器算法或位置传感器[7 ⇓ -9 ] 是现有获取转子位置信息的两种主要方式.无位置传感器算法通常较复杂,且存在额外损耗、参数敏感等问题[10 ] .基于高频注入的无位置传感器控制算法通常适用于凸极式永磁同步电机的初始位置判定和中低速运行[11 ] ,而基于反电势的无位置传感器方法对电机参数随磁饱和的变化比较敏感[12 ] .现有的无位置传感器算法通常无法获取隐极式永磁同步电机的准确位置信息.因此,采用位置传感器仍是获取转子精确位置的主要方式. ...
Synchronous constant elapsed time speed estimation using incremental encoders
1
2019
... 其中,增量式编码器以其高精度、高可靠性、高性价比等优势[13 ] ,广泛应用于高精度控制等领域.增量式编码器通过计算脉冲数量来获取位置,无法直接获得转子的绝对位置信息,在使用前通常需要进行零位校正.目前,主要通过定子电流矢量法对增量式编码器进行零位校正[14 ⇓ ⇓ ⇓ -18 ] . ...
1
2017
... 其中,增量式编码器以其高精度、高可靠性、高性价比等优势[13 ] ,广泛应用于高精度控制等领域.增量式编码器通过计算脉冲数量来获取位置,无法直接获得转子的绝对位置信息,在使用前通常需要进行零位校正.目前,主要通过定子电流矢量法对增量式编码器进行零位校正[14 ⇓ ⇓ ⇓ -18 ] . ...
1
2017
... 其中,增量式编码器以其高精度、高可靠性、高性价比等优势[13 ] ,广泛应用于高精度控制等领域.增量式编码器通过计算脉冲数量来获取位置,无法直接获得转子的绝对位置信息,在使用前通常需要进行零位校正.目前,主要通过定子电流矢量法对增量式编码器进行零位校正[14 ⇓ ⇓ ⇓ -18 ] . ...
无起动绕组永磁同步电机初始定位及起动策略
1
2008
... 其中,增量式编码器以其高精度、高可靠性、高性价比等优势[13 ] ,广泛应用于高精度控制等领域.增量式编码器通过计算脉冲数量来获取位置,无法直接获得转子的绝对位置信息,在使用前通常需要进行零位校正.目前,主要通过定子电流矢量法对增量式编码器进行零位校正[14 ⇓ ⇓ ⇓ -18 ] . ...
Initial orientation and starting strategy on PMSM without starting windings
1
2008
... 其中,增量式编码器以其高精度、高可靠性、高性价比等优势[13 ] ,广泛应用于高精度控制等领域.增量式编码器通过计算脉冲数量来获取位置,无法直接获得转子的绝对位置信息,在使用前通常需要进行零位校正.目前,主要通过定子电流矢量法对增量式编码器进行零位校正[14 ⇓ ⇓ ⇓ -18 ] . ...
An efficient method for identifying the initial position of a PMSM with an incremental encoder
1
1998
... 其中,增量式编码器以其高精度、高可靠性、高性价比等优势[13 ] ,广泛应用于高精度控制等领域.增量式编码器通过计算脉冲数量来获取位置,无法直接获得转子的绝对位置信息,在使用前通常需要进行零位校正.目前,主要通过定子电流矢量法对增量式编码器进行零位校正[14 ⇓ ⇓ ⇓ -18 ] . ...
Fast start-up control method of PMSM based on incremental photoelectric encoder
1
2012
... 其中,增量式编码器以其高精度、高可靠性、高性价比等优势[13 ] ,广泛应用于高精度控制等领域.增量式编码器通过计算脉冲数量来获取位置,无法直接获得转子的绝对位置信息,在使用前通常需要进行零位校正.目前,主要通过定子电流矢量法对增量式编码器进行零位校正[14 ⇓ ⇓ ⇓ -18 ] . ...
全数字伺服系统中电机转子初始定位的方法
1
2005
... 其中,增量式编码器以其高精度、高可靠性、高性价比等优势[13 ] ,广泛应用于高精度控制等领域.增量式编码器通过计算脉冲数量来获取位置,无法直接获得转子的绝对位置信息,在使用前通常需要进行零位校正.目前,主要通过定子电流矢量法对增量式编码器进行零位校正[14 ⇓ ⇓ ⇓ -18 ] . ...
Method for measuring initial position of motor rotor of a digital servo system
1
2005
... 其中,增量式编码器以其高精度、高可靠性、高性价比等优势[13 ] ,广泛应用于高精度控制等领域.增量式编码器通过计算脉冲数量来获取位置,无法直接获得转子的绝对位置信息,在使用前通常需要进行零位校正.目前,主要通过定子电流矢量法对增量式编码器进行零位校正[14 ⇓ ⇓ ⇓ -18 ] . ...
PMSM转子初始位置检测分析及起动策略
1
2016
... 文献[19 ]中,通过定子电流矢量拖动转子到达零位,进而确定转子初始位置,对编码器信息清零后,通过首个z脉冲信息计算零位偏置角.文献[20 ]中,采用了六种校正模式,将转子分别拖动至六个确定位置,通过任一校正模式的编码器信息与实际转子位置信息间的偏差即可计算零位偏置角.然而,当系统软硬件故障导致零位偏置角出错或丢失时,利用现有方法通常无法实现快速零位校正,恢复系统正常运行. ...
PMSM initial rotor position detection and startup strategy
1
2016
... 文献[19 ]中,通过定子电流矢量拖动转子到达零位,进而确定转子初始位置,对编码器信息清零后,通过首个z脉冲信息计算零位偏置角.文献[20 ]中,采用了六种校正模式,将转子分别拖动至六个确定位置,通过任一校正模式的编码器信息与实际转子位置信息间的偏差即可计算零位偏置角.然而,当系统软硬件故障导致零位偏置角出错或丢失时,利用现有方法通常无法实现快速零位校正,恢复系统正常运行. ...
Initial rotor position detecting algorithm of PM synchronous motor using incremental encoder
2
2013
... 文献[19 ]中,通过定子电流矢量拖动转子到达零位,进而确定转子初始位置,对编码器信息清零后,通过首个z脉冲信息计算零位偏置角.文献[20 ]中,采用了六种校正模式,将转子分别拖动至六个确定位置,通过任一校正模式的编码器信息与实际转子位置信息间的偏差即可计算零位偏置角.然而,当系统软硬件故障导致零位偏置角出错或丢失时,利用现有方法通常无法实现快速零位校正,恢复系统正常运行. ...
... 式中,Vdead Dd 和Vdead Dq 分别表示逆变器非线性因素引起的dq 轴畸变电压.Vdead 可以表示为[20 ] ...
Nonlinearity estimation and compensation of PWM VSI for PMSM under resistance and flux linkage uncertainty
1
2006
... Dd 和Dq 与三相电流方向和系统电气角度有关[21 ] ,Dd 和Dq 可以表示为 ...
Identification of flux linkage map of permanent magnet synchronous machines under uncertain circuit resistance and inverter neonlinearity
4
2018
... 式(8)是秩数为2的方程组,但包含R 、Vdead 、ψd 、ψq 四个未知变量,无法直接求解得到ψd 或ψq .因此,文献[22 ]提出了一种永磁同步电机dq 轴磁链辨识的新方法,该方法的辨识模型消除了逆变器非线性因素以及电阻的影响,从而提高了辨识精度. ...
... 在文献[22 ]中,系统采用电流环控制模式,通过调整负载大小改变电机转速,实现连续变速工况,然后采集两组不同转速下的运行数据,并对基于智能算法的辨识模型进行最小化运算,实现dq 轴磁链的准确辨识.然而,该方法的试验工况和模型求解过程较复杂,因此本文对二者进行了简化,采用的试验工况如图4 所示,将原方法中的连续变速工况改为一次稳态变速工况,进而可以简化辨识模型和求解过程.下文仅对交轴磁链辨识过程进行介绍. ...
... 需要说明的是,文献[22 ]采用连续变速工况试验,辨识结果不受转速波动影响,数据采集时间仅为1 s.本文采样频率与文献[22 ]相同,为防止速度波动对辨识结果造成影响,数据采集时间增加为5 s. ...
... ]采用连续变速工况试验,辨识结果不受转速波动影响,数据采集时间仅为1 s.本文采样频率与文献[22 ]相同,为防止速度波动对辨识结果造成影响,数据采集时间增加为5 s. ...
基于谐波分离的逆变器非线性因素直接提取和补偿方法
1
2021
... 式中,N 是data1和data2的数据长度.当采用电流环控制时,ψq 、Vdead 通常被认为是常数[23 ] ,并且通过式(10)可以看到,Dd 仅与电流方向和电气角度有关.因此,可以得到 ...
Direct extraction and compensation of inverter nonlinearity based on harmonic separation
1
2021
... 式中,N 是data1和data2的数据长度.当采用电流环控制时,ψq 、Vdead 通常被认为是常数[23 ] ,并且通过式(10)可以看到,Dd 仅与电流方向和电气角度有关.因此,可以得到 ...