随着社会的高速发展，对能源的需求也在不断增大^[1]。锂离子电池作为一种清洁、无污染的能源，在智能电网的储能系统和电动汽车领域得到了广泛的应用^[2]。由于单节电池电压较低，所以需要将多个单体电池串联使用才可以满足不同的电压需求^[3]。由于制造工艺、内阻、自放电率、老化和温度存在一些差异，各个电池的能量衰减速率不相同，这会在频繁的充放电过程中加剧电池组的不一致性，导致电池组可用容量下降、电池组使用寿命缩短等问题。为了解决电池组的不一致性，需要对电池组进行均衡^[4-5]。

电池的均衡方式一般可以分为主动均衡和被动均衡，其中主动均衡因为能够最大限度地利用电池组中的能量，成为了目前研究的重点^[6]。主动均衡的方式有很多种^[7]，按照能量的流动方式可以分为分层式均衡拓扑、电池-电池均衡拓扑、电池-电池组均衡拓扑和基于模块的电池组-电池组均衡拓扑。在分层式均衡拓扑中，能量可以从一节单体电池流动到与它相关联的多节单体电池^[8]；在电池-电池均衡拓扑中，能量只能在相邻电池之间流动^[9]；在电池-电池组均衡拓扑中，能量可以从单体电池流动到整个电池组^[10]；在基于模块的电池组-电池组均衡拓扑中，将电池分组构成不同的模块，既可以在模块内实现相邻电池之间能量流动，又可以以模块为单位实现模块间的能量流动^[11]。按照均衡单元的构成可以分为基于电感的均衡^[12]、基于电容的均衡^[13-14]、基于DC-DC变换器^[15-16]的均衡等。其中基于电感的均衡方式具有均衡效率高、拓展性好的优点。

基于电感的均衡方式有很多，都有着各自的特点。文献[17]提出了经典电感法(Classical inductance method, CIM)，利用电感元件的储能特性，将电池组中能量较高的电池中的能量转移到能量较低的电池，达到电池组均衡的目的。它的优点是简单，缺点是只能实现相邻电池之间的能量交换，当SOC偏高的电池和SOC偏低的电池不相邻时，均衡速度会很慢。文献[18]提出了并行架构式均衡(Parallel architecture for battery charge equalization，PAE)，以CIM为基础，在不增加均衡单元的前提下增加了均衡层数，当SOC偏高与SOC偏低的电池相距较远时均衡速度远大于CIM。文献[19]提出了双路交错式均衡(Two-circuit interleaved architecture for battery charge equalization，TIAE)，在CIM的基础上对均衡单元改进，使用双电感均衡单元(Double inductance equalization unit，DIEU)，能够在不增加最大均衡电流的前提下增加均衡电流的有效值，提高均衡速度。文献[20]提出了双路交错并行架构式均衡(Two-circuit interleaved parallel architecture for battery charge equalization，TIPAE)，使用并行架构式的均衡拓扑和双路交错式的均衡单元，既可以加快SOC偏高与SOC偏低的电池相距较远时的均衡速度，又可以提高均衡电流的有效值。本文在双路交错并行架构式均衡拓扑的基础上进行改进，对均衡单元进行分档控制，在不增加电流最大值的前提下使电流一直保持在较高的水平，能够有效地加快均衡速度。首先给出双路交错并行架构式均衡拓扑，在此基础上给出它的改进型拓扑。

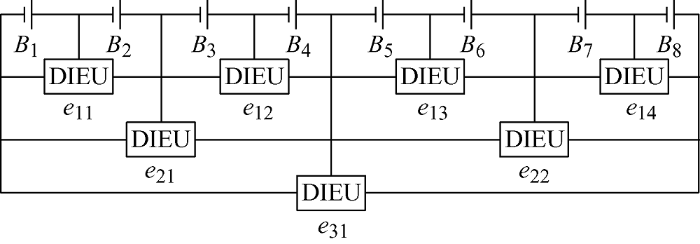
双路交错并行架构式均衡拓扑结构采用了文献[18]中的并行架构式拓扑，均衡单元采用了文献[19]中的双电感均衡单元，为具体说明改进拓扑的结构及工作原理，以8节电池为例，其拓扑图如图1所示。

图1中，B₁~B₈表示电池组中的电池，e₁₁、e₁₂、e₁₃和e₁₄表示第1层的均衡单元，e₂₁和e₂₂表示第2层的均衡单元，e₃₁表示第3层的均衡单元，DIEU表示双电感均衡单元。由图1可知，TIPAE采用了并行架构式的总体框架，实行分层管理，第1层的均衡单元控制2节相邻电池的均衡，第2层的均衡单元控制4节相邻电池的均衡，第3层的均衡单元控制8节电池的均衡。这种分层管理的方法在能量转移路径较远的情况下可以大大提高电池组的均衡速度。假设$n$为电池数量，则它的均衡层数C可按式(1)计算

式中，若$C$为小数，可向上取整。

当电池组中电池节数不是2^C时(比如6节电池)，TIPAE的均衡拓扑如图2所示。

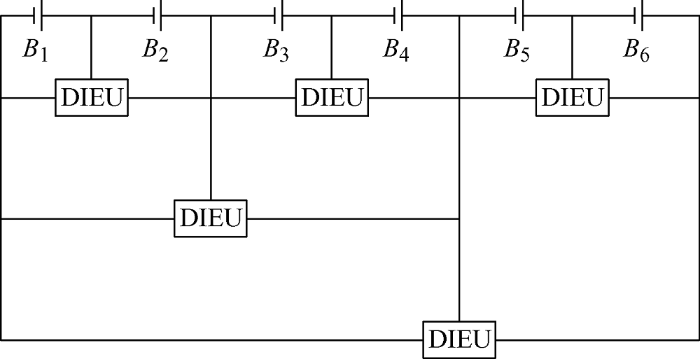
图2中，B₁~B₆表示电池组中的电池，DIEU表示双路交错式均衡单元。由图2可知，当电池组中电池的数量为6时，第1层有3个均衡单元，每个均衡单元控制2节相邻电池的均衡，均衡单元是否开启均衡的判断依据是均衡单元左右两边电池的SOC差值是否超过阈值；第2层有1个均衡单元，控制4节相邻电池的均衡，均衡单元是否开启均衡的判断依据是均衡单元左右两边电池的SOC均值的差值(B₁、B₂的SOC均值与B₃、B₄的SOC均值的差值)是否超过阈值；第3层有1个均衡单元，控制电池组中6节电池的均衡，均衡单元是否开启均衡的判断依据是均衡单元左右两边电池的SOC均值的差值(B₁、B₂、B₃、B₄的SOC均值与B₅、B₆ SOC均值的差值)是否超过阈值。

图1和图2中的DIEU如图3所示。

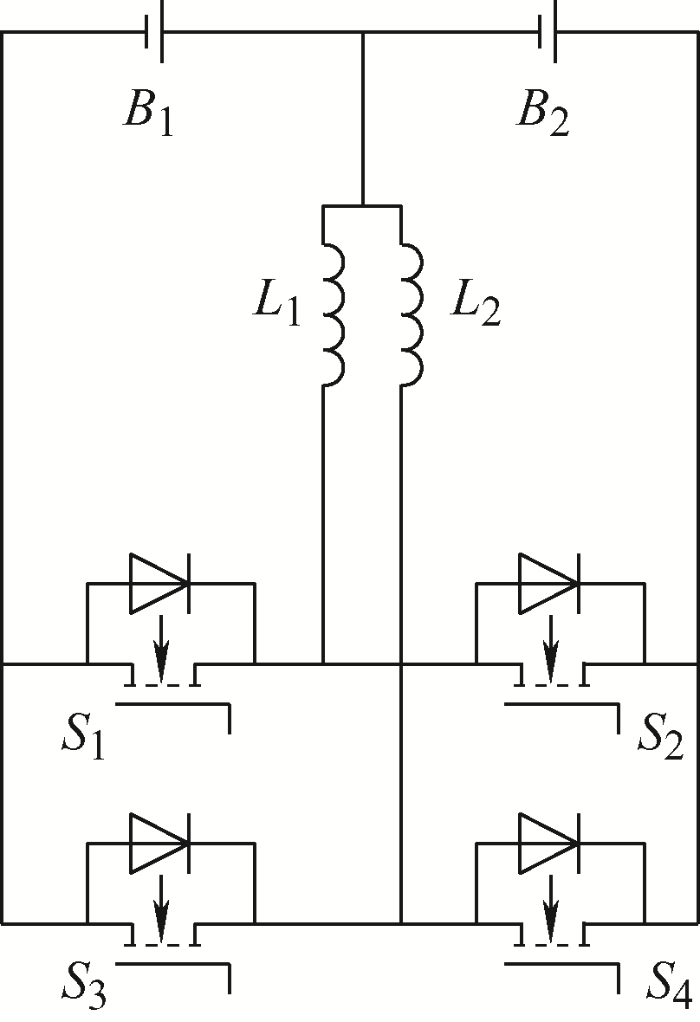
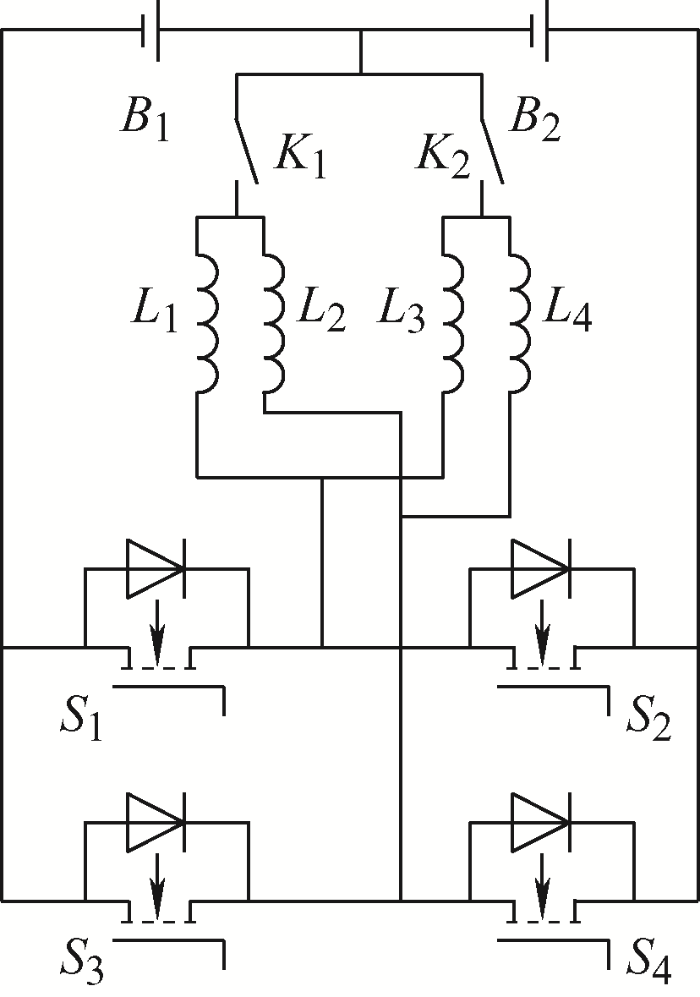
图3中，${{B}_{1}}$和${{B}_{2}}$是需要均衡的电池，${{L}_{1}}$和${{L}_{2}}$是电感，${{S}_{1}}$、${{S}_{2}}$、${{S}_{3}}$和${{S}_{4}}$是MOS管。由图3可知，均衡单元使用了双路交错式的均衡方式。

当${{B}_{1}}$向${{B}_{2}}$充电时，${{S}_{2}}$和${{S}_{4}}$保持断开状态，在${{S}_{1}}$和${{S}_{3}}$中通入PWM波。当通入${{S}_{1}}$的PWM波是高电位时，${{S}_{1}}$闭合，${{B}_{1}}$向电感${{L}_{1}}$充电；通入${{S}_{1}}$的PWM波是低电位时，${{S}_{1}}$断开，电感${{L}_{1}}$通过${{S}_{2}}$中的续流二极管向${{B}_{2}}$充电。当通入${{S}_{3}}$的PWM波是高电位时，${{S}_{3}}$闭合，${{B}_{1}}$向电感${{L}_{2}}$充电，通入${{S}_{3}}$的PWM波是低电位时，${{S}_{3}}$断开，电感${{L}_{2}}$通过${{S}_{4}}$中的续流二极管向${{B}_{2}}$充电。

在DIEU中，与控制${{S}_{1}}$和${{S}_{2}}$的PWM波相比，控制${{S}_{3}}$和${{S}_{4}}$的PWM波滞后了180°。在${{L}_{1}}$充电时，${{L}_{2}}$通过续流二极管转移能量；${{L}_{1}}$通过续流二极管转移能量时，${{L}_{2}}$充电。这样的运行方式使效率提高了一倍，在不增加均衡电流最大值的基础上增加了均衡电流的有效值，进而提高均衡速度。

TIPAE首先对单个均衡单元的工作效率进行了提升，能够在不增大均衡电流最大值的条件下提升均衡速度，还兼顾了均衡电池距离较远时效率低下的问题，对均衡系统的均衡速度和均衡效果都有较大的提升。

使用TIPAE进行均衡存在一个问题：随着均衡的进行均衡电流会减小。由图1可知，B₈最多可以同时受到e₁₄、e₂₂、e₃₁这3个均衡单元的均衡控制，当B₇和B₈的SOC差值低于设定的阈值时，e₁₄停止工作，B₈最多可以同时受到e₂₂和e₃₁这2个均衡单元的均衡控制；当B₅和B₆的SOC均值与B₇和B₈的SOC均值差值低于设定阈值时，e₂₂停止工作，B₈只能受到e₃₁的均衡控制，在均衡单元中各元件参数不变的情况下会导致流过B₈的均衡电流减少。针对这种情况，在TIPAE的基础上，本文提出一种改进型的均衡方案，称为改进型双路交错并行架构式均衡拓扑(Improved two-circuit interleaved parallel architecture for battery charge equalization，IM-TIPAE)。

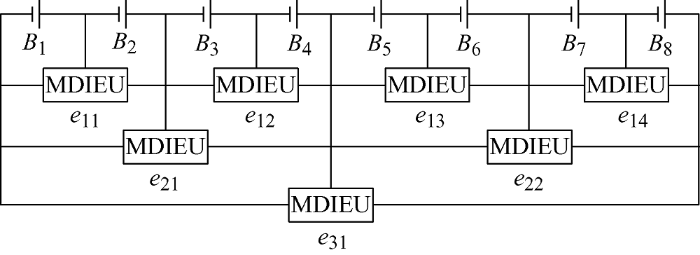
为具体说明改进拓扑的结构及工作原理，以8节电池为例，其拓扑图如图4所示。

图4中，B₁~B₈表示电池组中的电池，e₁₁、e₁₂、e₁₃、e₁₄表示第1层的均衡单元，e₂₁、e₂₂表示第2层的均衡单元，e₃₁表示第3层的均衡单元，MDIEU表示多档位双路交错式均衡单元(Multi-position double inductance equalization unit，MDIEU)。可以看出该方案的总体拓扑没有进行优化，而是对每一个均衡单元进行了优化。这里的多档位具体是指均衡单元中分为高档和低档两种控制方式，当均衡单元实行低档控制时，均衡单元中电感值较高的那组电感接入回路，当均衡单元采用高档控制时，均衡器中电感值较低的那组电感接入回路。

当开始均衡时所有均衡单元都实行低档控制：① e₃₁停止均衡或者e₂₁停止均衡时，e₁₁和e₁₂实行高档控制；② e₃₁停止均衡或者e₂₂停止均衡时，e₁₃和e₁₄实行高档控制；③ e₁₁和e₁₂停止均衡时，e₂₁实行高档控制；④ e₁₃和e₁₄停止均衡时，e₂₂实行高档控制；⑤ e₁₁、e₁₂、e₁₃、e₁₄、e₂₁、e₂₂停止均衡时，e₃₁实行高档控制。

通过多档位控制，可以在不增加均衡电流最大值的前提下，使流过电池的均衡电流保持在较高的水平。

由图4可知，当电池组中电池的数量为2ⁿ时，存在n层MDIEU。TIPAE中各个均衡单元独立运行，互不影响，而IM-TIPAE中任意层的均衡单元的档位会受到其他层均衡单元的影响。MDIEU如图5所示。

图5中，B₁和B₂是需要均衡的电池，L₁和L₂是低档时接入电路的电感，L₃和L₄是高档时接入电路的电感，S₁、S₂、S₃和S₄是MOS管，K₁和K₂是控制档位的开关。由图5可知，MDIEU中有4个电感，分为2组，对应于2个档位，每个档位中的2个电感的电感值相同。MDIEU采用双路交错的形式进行工作，均衡单元中的2个电感均衡电路以电流相位偏移180°的方式工作。IM-TIPAE在拓扑结构上没有改进，所以它的均衡原理与TIPAE一致，不同之处在于MDIEU实行多档位运行。

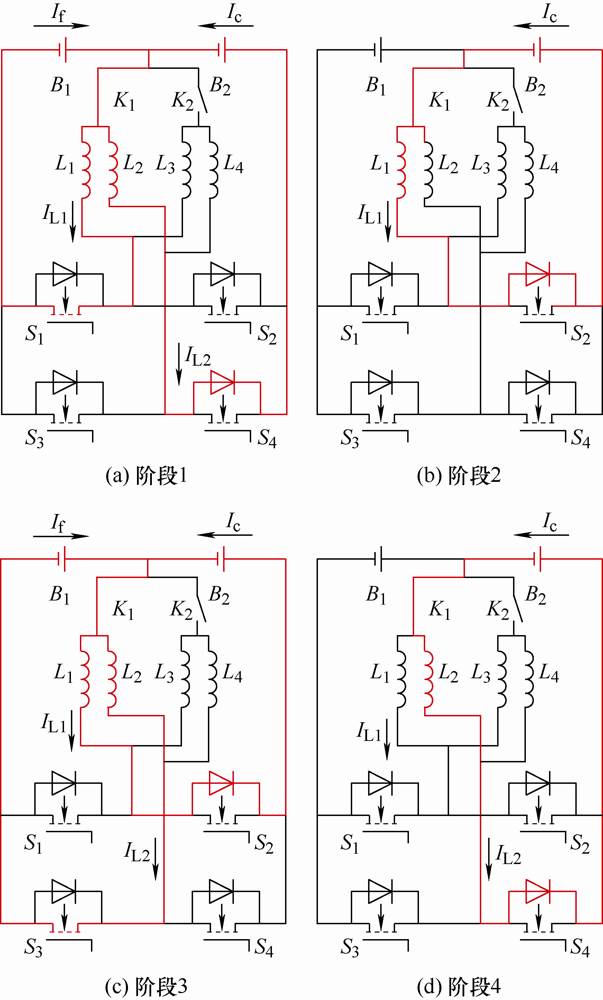
在图5中，以低档控制(即K₁闭合时)时B₁的SOC大于B₂的SOC，且B₁和B₂的SOC的差值超过阈值时为例，分析均衡时的能量流动过程，能量流动过程如图6所示。

图6中，I_f是B₁的释放电流，I_c是B₂的充电电流，I_L1是流过L₁的电流，I_L2是L₂流过的电流。由图6可知，阶段1时B₁向L₁充电，L₂向B₂充电；阶段2时L₁向B₂充电，L₂停止工作；阶段3时L₁向B₂充电，B₁向L₂充电；阶段4时L₂向B₂充电，L₁停止工作。同一时间，每块电池只能向每个均衡单元中的1个电感放电(或者接受1个电感的充电)，所以不会增加均衡电流的最大值。

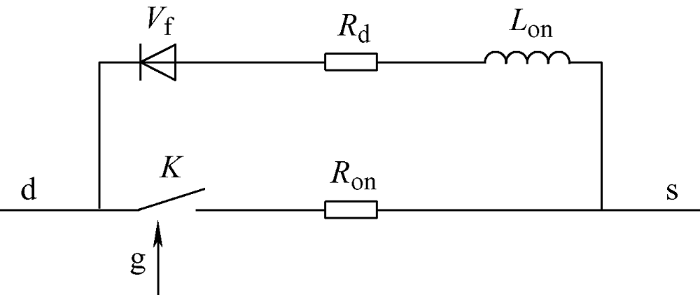
由图3可以看出，均衡单元中含有大量的MOS管，MOS管的结构如图7所示。

图7中R_on是场效应管内阻，L_on是内部二极管电感，R_d是内部二极管电阻，V_f是内部二极管正向电压，g是MOS管的栅极，d是MOS管的漏极，K是开关，s是MOS管的源极。本文仿真采用理想情况下的MOS管，令内部二极管电感L_on的感值为零，在下文的计算中忽略了L_on。

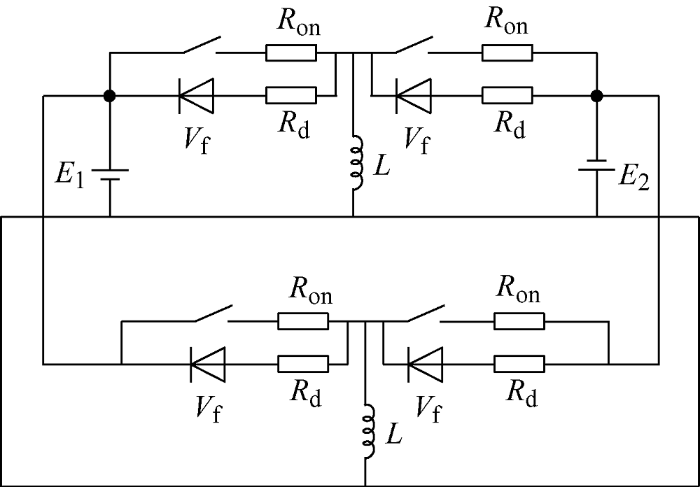
MDIEU是在DIEU的基础上进行改进的，其均衡方式和DIEU一样都是双路交错，所以以图3为例进行均衡电路参数计算。结合图3(DIEU)和图7可以得到由B₁、B₂和e₁₁构成的均衡电路如图8所示。

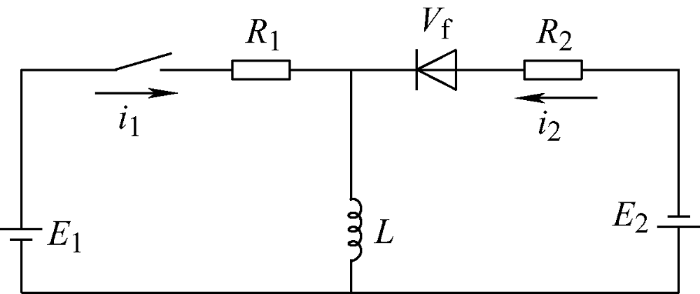
图8中R_on是场效应管内阻，R_d是内部二极管电阻，E₁是电池B₁的电压，E₂是电池B₂的电压，V_f是内部二极管正向电压。由于采用的是双路交错的方式进行均衡，所以由2个电感组成的2条均衡回路原理相同，均衡电流大小相同，唯一的差异是电流相位相差180°。为了分析各个均衡参数，以B₁在一个周期内通过一个电感向B₂充电为例进行分析，在这一个周期T内，均衡开始时开关闭合，B₁的电流流过R_on向电感L充电，经过DT的时间后，开关断开，电感电流通过续流二极管流过R_d向B₂充电，简化过的均衡电路图如图9所示。

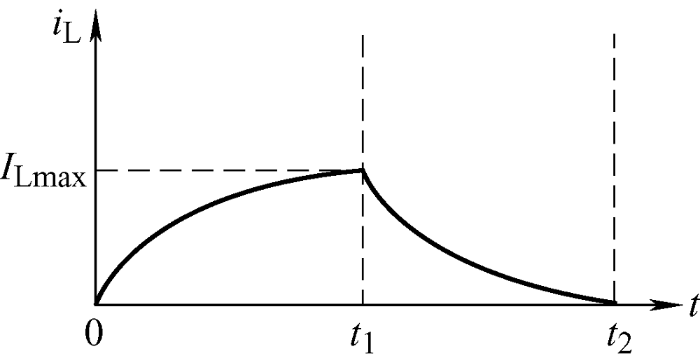
在图9中E₁是释能回路中的电压，i₁是释能回路中的电流，L是电感的感值，R₁是释能回路中的等效电阻，E₂是储能回路中的电压，i₂是储能回路中的电流，R₂是释能回路中的等效电阻，V_f是内部二极管正向电压。在一个周期内，电感电流如图10所示。

为了能够实现双路交错，图10中${{t}_{1}}$为电感充电时间，${{t}_{2}}$为电感完成一次充放电所需要的时间，令${{t}_{1}}=DT$，${{t}_{2}}=0.5T+DT$。在开关${{S}_{1}}$处于开通状态时，即处在0~${{t}_{1}}$时间段内，设电感电流为${{i}_{1}}$，可以列写方程

求得

电感电流${{i}_{1}}\left( 0 \right)$初值为0，代入式(3)可得释能回路电流为

同理，${{t}_{1}}$~${{t}_{2}}$时间段内，列写电路方程，得

解得

将${{i}_{2}}\left( 0.5T+DT \right)=0$代入式(6)可得储能回路的电流为

由于${{i}_{1}}\left( DT \right)={{i}_{2}}\left( DT \right)$，结合式(3)和式(5)可得

本文仿真时有${{R}_{1}}=10{{R}_{2}}$，则由式(8)可得

此时一个周期内电感刚好把储存的电量放完，实际操作中

电感的峰值电流为

在闲置的情况下，在断续工作模式下，不存在电感电流叠加的问题，本文仿真时参数如下：${{R}_{1}}=0.1\ \Omega $，${{R}_{2}}=0.01\ \Omega $，D=30%，T=0.01 s，第一层均衡单元中E_max=4.2 V，第二层均衡单元中E_max=8.4 V，第三层均衡单元中E_max=16.8 V。为了电池的安全，流过电池的最大电流限制在5 A，由拓扑图可知，当电池数量为8时，每节电池最多同时受到3个均衡单元的充电。令每层的均衡器流过的最大电流为1.66 A。

由式(9)可得

代入式(10)可得，对于第一层均衡单元，最小电感为L=7.41 mH，对于第二层均衡单元，最小电感为14.97 mH，对于第三层均衡单元，最小电感为30.09 mH。此处得到的是理论计算值，实际应用中应根据具体情况进行参数修正。

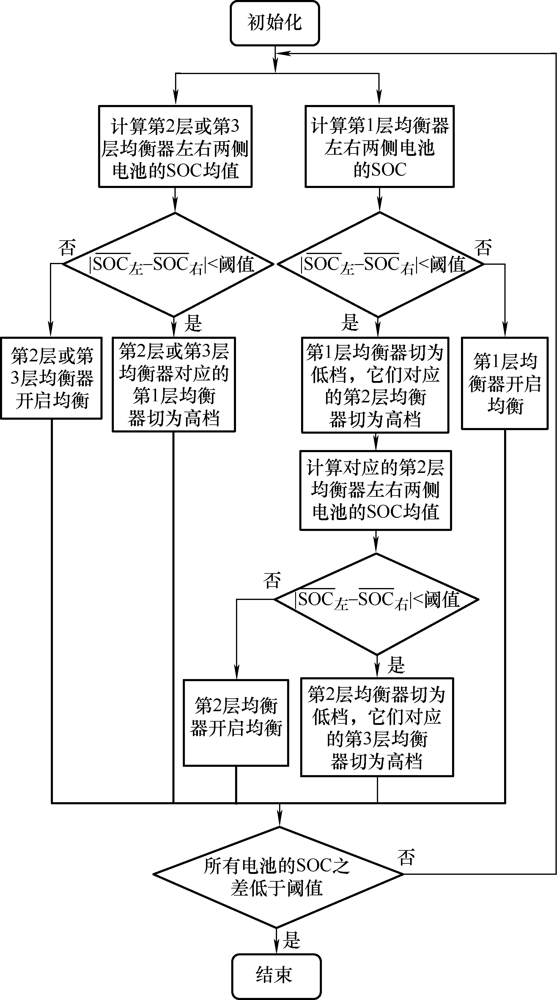
为更进一步说明改进拓扑的均衡控制思路，给出三层均衡单元下IM-TIPAE的均衡控制流程，如图11所示。

首先初始化使所有MDIEU采用低档控制，在均衡过程中根据各个电池的SOC来切换相应MDIEU的档位，e₃₁停止均衡时e₁₁、e₁₂、e₁₃和e₁₄实行高档控制；e₂₁停止均衡时e₁₁和e₁₂实行高档控制；e₂₂停止均衡时e₁₃和e₁₄实行高档控制；e₁₁和e₁₂停止均衡时e₂₁实行高档控制并将e₁₁和e₁₂切为低档；e₁₃和e₁₄停止均衡时e₂₂实行高档控制并将e₁₃和e₁₄切为低档；e₁₁、e₁₂、e₁₃、e₁₄、e₂₁、e₂₂停止均衡时e₃₁实行高档控制，并将e₁₁、e₁₂、e₁₃、e₁₄、e₂₁、e₂₂切为低档，当所有层的MDIEU完成均衡后，电池组完成均衡。

设流过电池的最大均衡电流为I，则每一层MDIEU为低档控制时，流过MDIEU的均衡电流为$\frac{I}{3}$，第1层和第2层的MDIEU为高档控制时，流过MDIEU的均衡电流为$\frac{2}{3}I$，当3层的MDIEU为高档控制时，流过MDIEU的均衡电流为I。每个电池最多可以同时受到3层MDIEU的均衡。以B₈为例解释分档控制不会造成均衡电流超过设定值：B₈最多可以同时受到e₁₄、e₂₂、e₃₁的均衡，流过B₈的最大均衡电流为I，当e₁₄切换为高档控制时，e₂₂和e₃₁至少有一个因为完成了均衡而停止工作，流过B₈的最大均衡电流为$\frac{2I}{3}+\frac{I}{3}=I$；当e₂₂切换为高档控制时，e₁₄因为完成均衡而停止工作，流过B₈的最大均衡电流为$\frac{2I}{3}+\frac{I}{3}=I$；当e₃₁切换为高档控制时，e₁₄、e₂₂都因为完成了均衡而停止工作，流过B₈的最大均衡电流为I。所以经过分档控制，流过电池的最大均衡电流不会超过设定值，但却能使均衡电流保持在较高的水平，进而有效提高均衡速度。

为验证改进型均衡拓扑的有效性，在Simulink中对TIPAE和IM-TIPAE进行建模仿真试验，以8节电池为例进行仿真。电池的仿真参数如表1所示。

仿真模型中PWM的周期T=0.01 s，占空比D=30%。在TIPAE中第一层DIEU中的电感为9 mH，第二层DIEU中的电感为18 mH，第三层DIEU中的电感为36 mH；在IM-TIPAE第一层MDIEU低档时电感为9 mH，高档时电感为4.5 mH，第二层MDIEU低档时电感为18 mH，高档时电感为9 mH，第三层MDIEU低档时电感为低档时电感36 mH，高档时电感为12 mH。各电池的SOC初值条件如表2所示。

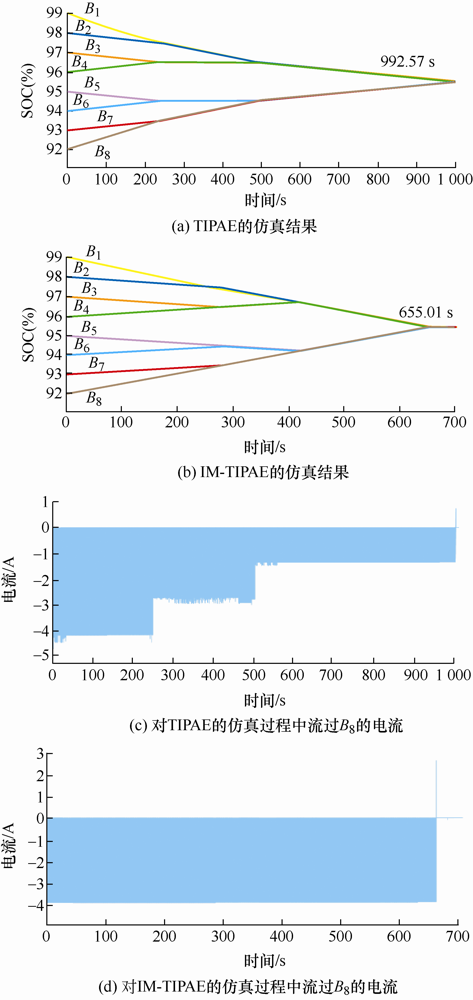
(1) SOC初值条件1下的仿真结果及分析。对电池组在3组SOC初值条件下进行仿真，图12~14为在这3组SOC初值下，使用TIPAE和IM-TIPAE对电池组进行仿真的结果和仿真过程中流过SOC最小的电池的电流图。在SOC初值条件1时进行的仿真结果如图12所示。

由图12a和图12b可以看出，在第一层均衡单元完成均衡之前，TIPAE和IM-TIPAE的均衡速度几乎一致。对于TIPAE，245.39 s时第一层均衡单元完成均衡，均衡速度减慢，497.08 s时第二层均衡单元完成，均衡速度再度减慢。对于IM-TIPAE，第一层均衡单元完成均衡后，第二层均衡单元切为高档，第一层和第二层均衡单元都完成均衡后第三层均衡单元切为高档，所以均衡速度无明显变化。最终TIPAE在992.57 s时完成均衡，IM-TIPAE在655.01 s时完成均衡，在这种均衡条件下，IM-TIPAE比TIPAE节省了34%的时间。

由图12c和图12d可以看出，随着TIPAE均衡的进行，e₁₄完成均衡后流过B₈的均衡电流大约减少了$\frac{1}{3}$，e₂₂完成均衡后流过B₈的均衡电流再度减少，减小至最大均衡电流的$\frac{1}{3}$。随着IM-TIPAE均衡的进行，e₁₃和e₁₄完成均衡后，e₂₂切为高档运行，流过e₂₂的均衡电流增加了1倍，第一层和第二层MDIEU完成均衡后e₃₁切为高档运行，流过e₃₁的均衡电流增加了2倍，所以流过B₈的均衡电流几乎无变化，因此IM-TIPAE的均衡速度大于TIPAE。

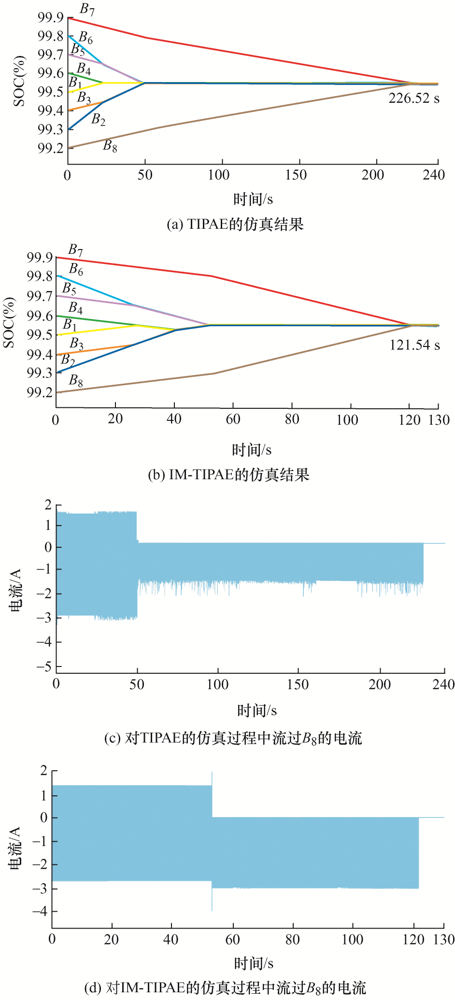
(2) SOC初值条件2下的仿真结果及分析。在SOC初值条件2时的仿真结果如图13所示。

由图13a和图13b可知，在SOC初值条件2下：对于TIPAE，49.32 s时B₁、B₂、B₃、B₄的平均SOC等于B₅、B₆、B₇、B₈的平均SOC，导致e₃₁停止工作，由于B₈通过e₁₄和e₂₂充电，通过e₃₁放电，所以B₈的SOC变化速度加快，49.50 s时B₅和B₆的平均SOC等于B₇和B₈的平均SOC，e₂₂停止工作，B₈的SOC变化速度减慢，和49.32 s前的变化速度几乎一致。对于IM-TIPAE，52.95 s时e₃₁停止工作，e₁₄切为高档，通过e₁₄流过B₈的均衡电流增加了1倍，所以B₈的SOC变化速度加快，52.96 s时e₂₂停止工作，B₈的SOC变化速度减慢，但仍大于52.95 s前的变化速度。最终TIPAE在226.52 s时完成均衡，IM-TIPAE在121.54 s时完成了均衡，在这种条件下IM-TIPAE比TIPAE减少了46%的均衡时间。

由图13c和图13d可知，对于TIPAE，在0~49.32 s时流过B₈的均衡电流有正有负，说明此时B₈既充电又放电，由于B₈通过e₁₄和e₂₂充电，通过e₃₁放电，所以充电电流约是放电电流的2倍，49.32~49.50 s时e₃₁停止工作，流过B₈的电流只有充电电流，49.50~226.52 s时e₂₂也停止工作，只有约1.5 A的充电电流流过B₈。对于IM-TIPAE，在0~52.95 s时流过B₈的均衡电流有正有负，52.95~52.96 s时e₃₁停止工作，e₁₄切为高档运行，这个时间段流过B₈的均衡电流只有充电电流，且充电电流增加了约二分之一，52.96~121.54 s时e₂₂停止工作，此时有约3.2 A的充电电流流过B₈。

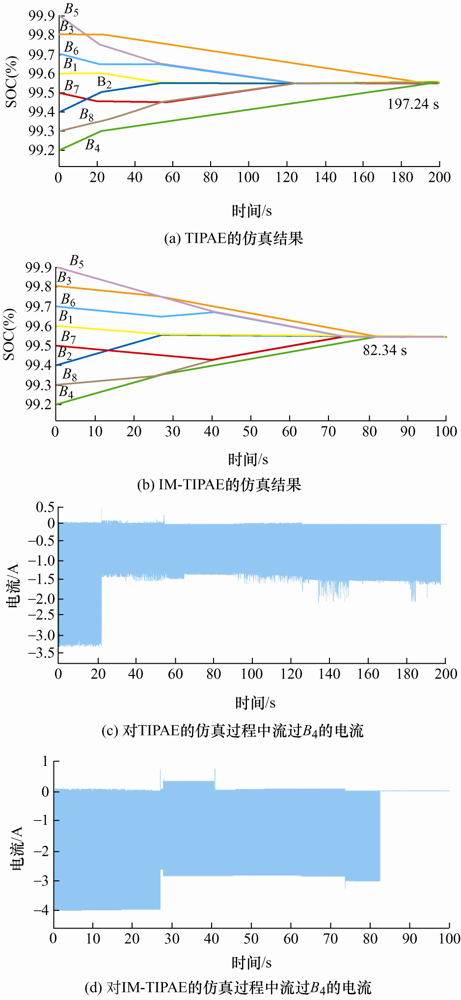
(3) SOC初值条件3下的仿真结果及分析。在SOC初值条件3下的仿真结果如图14所示。

由图14a和图14b可知，在SOC初值条件3下B₁和B₂的平均SOC等于B₃和B₄的平均SOC，所以e₂₁停止工作，e₁₂和e₃₁向B₄充电。在TIPAE中，21.81 s时B₁、B₂、B₃、B₄的平均SOC等于B₅、B₆、B₇、B₈的平均SOC，e₃₁停止工作，只有e₁₂向B₄充电，所以B₄的SOC上升速度下降了约一半。IM-TIPAE中开始均衡时的e₁₂切为高档，流过e₁₂的均衡电流大了1倍，所以开始均衡时IM-TIPAE中B₄的SOC上升速度比TIPAE中B₄的SOC上升速度快，26.84 s时B₁、B₂、B₃、B₄的平均SOC等于B₅、B₆、B₇、B₈的平均SOC，e₃₁停止工作，只有e₁₂向B₄充电，B₄的SOC变化速度下降了约三分之一。最终TIPAE在197.24 s时完成均衡，IM-TIPAE在82.34 s时完成了均衡，在这种条件下IM-TIPAE比TIPAE减少了58%的均衡时间。

由图14c和图14d可知对于TIPAE，在0~21.81 s时流过B₄的均衡电流最大，此时B₄通过e₁₂和e₃₁充电，21.81~197.24 s时e₃₁停止工作，B₄的充电电流减小了约二分之一。对于IM-TIPAE，在0~26.84 s时，e₁₂切为高档运行，26.84~82.34 s时e₃₁也停止工作，B₄的充电电流降低了约三分之一。

在三种SOC初值条件下，两种均衡拓扑的均衡时间如表3所示。可以看出在三种情况下，改进的均衡拓扑的均衡时间都是最短的。

在上述分析的基础上，以8个单体串联构成的电池组为例，表4进一步系统地比较了常见的均衡拓扑和本文列举的均衡拓扑的各类元器件的个数及各性能指标。由表4可以看出，本文提出的IM-TIPAE的优点是均衡速度快，缺点是电路中的电感数量多，电路复杂度高。

电池组的不一致性可能会带来电池组可用容量下降、电池组使用寿命缩短等问题，所以需要进行电池均衡。本文基于TIPAE拓扑结构，提出一种改进的IM-TIPAE均衡拓扑。为验证改进均衡拓扑的有效性，搭建了8节串联电池的仿真模型，分别在三种不同SOC初值情况下进行仿真，试验结果表明如下结论。

(1) 随着均衡的进行，IM-TIPAE中有些均衡单元会切为高档，提高均衡速度。在第一种SOC初值条件下，改进前的均衡拓扑用时992.57 s完成均衡，改进后的均衡拓扑用时655.01 s完成均衡，均衡时间减少了34%。

(2) 在第二种SOC初值条件下，改进前的均衡拓扑用时226.52 s完成均衡，改进后的均衡拓扑用时121.54 s完成均衡，均衡时间减少了46%。

(3) 在第三种SOC初值条件下，改进前的均衡拓扑用时197.24 s完成均衡，改进后的均衡拓扑用时82.34 s完成均衡，均衡时间减少了58%；表明改进后的均衡拓扑可以有效提高均衡速度。

在实际应用中，如果侧重于减少均衡电路的体积，本文提出的均衡拓扑不具备优势；如果侧重于提高均衡速度，本文提出的均衡拓扑有很大的优势。