1 引言
近年来,电力电子技术在高压大功率电能场合得到充足的发展,大功率多单元级联型变换器被广泛应用于储能、机车牵引、船舶直流电力系统、直流输电和直流电网等相关领域,实现高效的电能变换功能。
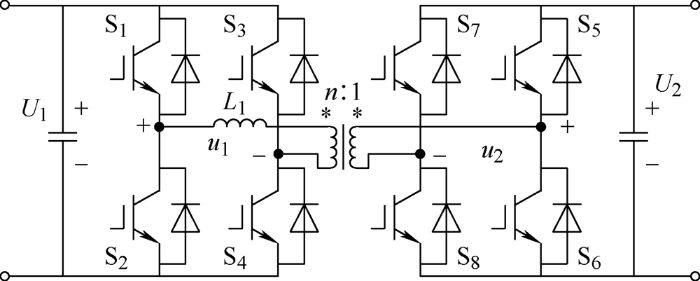
双有源桥变换器是多单元级联型变换器中的重要变流部件。双有源桥变换器的基本拓扑结构(图1 )和工作原理于20世纪90年代被提出[1 ] ,其控制灵活,具有高频电能变换、软开关、电气隔离等优点。
图1
双有源桥变换器有三个调制的自由度:原边桥臂内移相、副边桥臂内移相和原副边桥臂外移相。单移相调制只采用原副边桥臂外移相作为控制变量,是最简单的调制方法。采用这种调制策略,当电压变比和变压器变比不匹配时,高频电流迅速增大,软开关工作区域变窄,变换器导通损耗与开关损耗增加。为解决这个问题,很多文献提出了多自由度移相调制方法。文献[2 ]采用了扩展移相调制,副边不存在内移相,通过控制原边桥臂内移相和原副边桥臂外移相来完成功率的传递。文献[3 ⇓ -5 ]中采用双移相调制,原副边存在内移相且内移相值相同,通过改变原副边外移相值控制功率的传递。三移相调制则采用全部三个调制自由度[6 ⇓ ⇓ ⇓ ⇓ -11 ] ,单移相调制、扩展移相调制和双移相调制都是三移相调制的特殊形式。
为了提升变换器的工作效率,不少文献会结合调制方法对双有源桥变换器的电流、功率情况进行分析。针对双有源桥变换器的电流优化,主要包括最优电流应力调制[8 ,10 ] 、最优电流平均值调制[11 ] 、最优电流RMS值调制[12 ] 。最优电流应力调制将电感电流峰值降为最小,减小了器件的开关损耗与电流应力。最优电流平均值调制能够保证电感电流的平均值最小,从而使IGBT器件的通态损耗降为最低。最优电流RMS调制能够保证电感电流的有效值最小,从而使MOSFET器件的通态损耗降为最低。这些调制方法通常仅针对双有源桥变换器的部分损耗进行优化,未考虑其他部分的损耗。此外,还有文献提出了最小功率回流的调制方法[13 ⇓ -15 ] 。但是回流功率的定义不具备明确的物理意义,无法直接联系常用的无功功率概念。这种建模方法计算量大、过程复杂,随着调制自由度的增多,通过瞬时功率积分计算回流功率的难度加大。文献[16 ]从频域上定义了统一的无功功率,并通过优化调制参数对基波或是一部分无功功率进行优化。但是双有源桥变换器的高频电压和高频电流分别呈方波和梯形波,其中含有大量的谐波分量,因此基于基波的优化方法必然存在误差。
基于以上分析,本文通过对双有源桥变换器的电流时域解析建模,描述其开关器件带来的损耗,结合启发式算法和各工作模态边界约束条件,提出了损耗最小的优化调制策略,并通过实际算例与现有的基于电流的优化调制方法进行了对比,表明了本文提出的最优损耗调制策略算法的有效性。
2 双有源桥变换器的工作模态分析
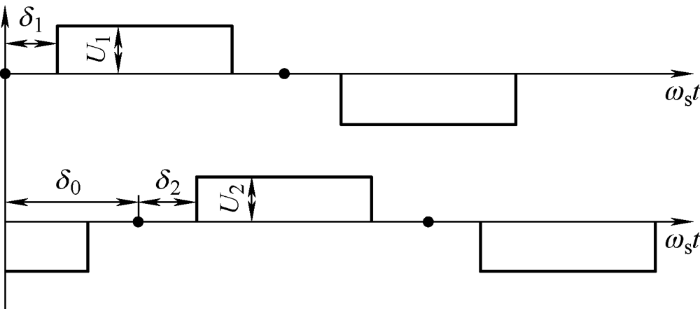
对于一个双有源桥变换器,设开关器件编号为S 1 ~S 8 ,变压器为变比为1∶1的理想变压器,双有源电感为L 1 ,原副边直流电压分别为U 1 和U 2 ,原副边交流电压分别为u 1 和u 2 ,d 为输入输出电压变比。令δ 0 、δ 1 、δ 2 分别代表原副边方波之间的相位差、原边内移相值和副边内移相值,如图2 所示。
图2
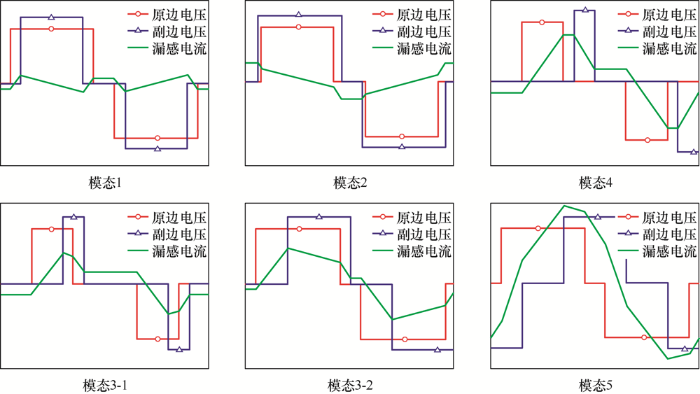
依据不同的调制方式,可以将双有源桥变换器的工作情况分为5种模态,如图3 所示。
图3
$ \delta_{1} \leqslant \delta_{2},\left|\delta_{0}\right| \leqslant \delta_{2}-\delta_{1}$
$ \delta_{1} \geqslant \delta_{2},\left|\delta_{0}\right| \leqslant \delta_{1}-\delta_{2}$
$ \delta_{1}+\delta_{2} \geqslant 0.5, \quad\left|\delta_{1}-\delta_{2}\right| \leqslant\left|\delta_{0}\right| \leqslant 1-\delta_{1}-\delta_{2}$
$ \delta_{1}+\delta_{2} \leqslant 0.5, \quad\left|\delta_{1}-\delta_{2}\right| \leqslant\left|\delta_{0}\right| \leqslant \delta_{1}+\delta_{2}$
$ \delta_{1}+\delta_{2} \geqslant 0.5, \quad 1-\delta_{1}-\delta_{2} \leqslant\left|\delta_{0}\right| \leqslant 0.5$
$ \delta_{1}+\delta_{2} \leqslant 0.5, \quad \delta_{1}+\delta_{2} \leqslant\left|\delta_{0}\right| \leqslant 0.5$
其中,模态4电流大且没有传递功率,带来较大损耗,因此该调制策略是要避免出现的。剩余4种模态下开关时刻的电流值以及积分后得到的电流有效值分别如下所示。
(1) $ \left\{\begin{array}{l}i_{L s}\left(\omega t=\pi-\delta_{1} \pi\right)=\frac{1}{4 f L_{s}}\left(u_{1}\left(1-2 \delta_{1}\right)-u_{2}\left(1-2 \delta_{2}\right)\right) \\i_{L s}\left(\omega t=\pi+\delta_{1} \pi\right)=\frac{1}{4 f L_{s}}\left(u_{1}\left(1-2 \delta_{1}\right)-u_{2}\left(1-2 \delta_{2}\right)\right) \\i_{L s}\left(\omega t=\delta_{0} \pi-\delta_{2} \pi\right)=\frac{1}{4 f L_{s}}\left(u_{2}\left(1-2 \delta_{2}\right)-u_{1}\left(1+2 \delta_{0}-2 \delta_{2}\right)\right) \\i_{L s}\left(\omega t=\delta_{0} \pi+\delta_{2} \pi\right)=\frac{1}{4 f L_{s}}\left(u_{2}\left(1-2 \delta_{2}\right)-u_{1}\left(1-2 \delta_{0}-2 \delta_{2}\right)\right)\end{array}\right.$
(2) $ \begin{aligned}i_{r m s}^{2}=& \frac{\pi^{2} u_{1}^{2}}{12 \omega^{2} L^{2}}\left(1-12 \delta_{1}^{2}+16 \delta_{1}^{3}\right)+\\& \frac{\pi^{2} u_{2}^{2}}{12 \omega^{2} L^{2}}\left(1-12 \delta_{2}^{2}+16 \delta_{2}^{3}\right)-\\& \frac{\pi^{2} u_{1} u_{2}}{6 \omega^{2} L^{2}}\left(1-2 \delta_{1}\right)\left(1+2 \delta_{1}-6 \delta_{0}^{2}-2 \delta_{1}^{2}-6 \delta_{2}^{2}\right)\end{aligned}$
(3) $ \left\{\begin{array}{l}i_{L s}\left(\omega t=\pi-\delta_{1} \pi\right)=\frac{1}{4 f L_{s}}\left(u_{1}\left(1-2 \delta_{1}\right)-u_{2}\left(1-2 \delta_{0}-2 \delta_{1}\right)\right) \\i_{L s}\left(\omega t=\pi+\delta_{1} \pi\right)=\frac{1}{4 f L_{s}}\left(u_{1}\left(1-2 \delta_{1}\right)-u_{2}\left(1+2 \delta_{0}-2 \delta_{1}\right)\right) \\i_{L s}\left(\omega t=\delta_{0} \pi-\delta_{2} \pi\right)=\frac{1}{4 f L_{s}}\left(u_{2}\left(1-2 \delta_{2}\right)-u_{1}\left(1-2 \delta_{1}\right)\right) \\i_{L s}\left(\omega t=\delta_{0} \pi+\delta_{2} \pi\right)=\frac{1}{4 f L_{s}}\left(u_{2}\left(1-2 \delta_{2}\right)-u_{1}\left(1-2 \delta_{1}\right)\right)\end{array}\right.$
(4) $ \begin{aligned}i_{r m s}^{2}=& \frac{\pi^{2} u_{1}^{2}}{12 \omega^{2} L^{2}}\left(1-12 \delta_{1}^{2}+16 \delta_{1}^{3}\right)+\\& \frac{\pi^{2} u_{2}^{2}}{12 \omega^{2} L^{2}}\left(1-12 \delta_{2}^{2}+16 \delta_{2}^{3}\right)-\\& \frac{\pi^{2} u_{1} u_{2}}{6 \omega^{2} L^{2}}\left(1-2 \delta_{2}\right)\left(1+2 \delta_{2}-6 \delta_{0}^{2}-2 \delta_{2}^{2}-6 \delta_{1}^{2}\right)\end{aligned}$
(5) $ \left\{\begin{array}{l}i_{L s}\left(\omega t=\pi-\delta_{1} \pi\right)=\frac{1}{4 f L_{s}}\left(u_{1}\left(1-2 \delta_{1}\right)-u_{2}\left(1-2 \delta_{0}-2 \delta_{1}\right)\right) \\i_{L s}\left(\omega t=\pi+\delta_{1} \pi\right)=\frac{1}{4 f L_{s}}\left(u_{1}\left(1-2 \delta_{1}\right)-u_{2}\left(1-2 \delta_{2}\right)\right) \\i_{L s}\left(\omega t=\delta_{0} \pi-\delta_{2} \pi\right)=\frac{1}{4 f L_{s}}\left(u_{2}\left(1-2 \delta_{2}\right)-u_{1}\left(1-2 \delta_{1}\right)\right) \\i_{L s}\left(\omega t=\delta_{0} \pi+\delta_{2} \pi\right)=\frac{1}{4 f L_{s}}\left(u_{2}\left(1-2 \delta_{2}\right)-u_{1}\left(1-2 \delta_{0}-2 \delta_{2}\right)\right)\end{array}\right.$
(6) $ \begin{aligned}i_{r m s}^{2}=& \frac{\pi^{2} u_{1}^{2}}{12 \omega^{2} L^{2}}\left(1-12 \delta_{1}^{2}+16 \delta_{1}^{3}\right)+\\& \frac{\pi^{2} u_{2}^{2}}{12 \omega^{2} L^{2}}\left(1-12 \delta_{2}^{2}+16 \delta_{2}^{3}\right)-\\& \frac{\pi^{2} u_{1} u_{2}}{3 \omega^{2} L^{2}}\left(\delta_{0}^{3}+3 \delta_{0}^{2}\left(\delta_{1}+\delta_{2}\right)+3 \delta_{0}\left(\delta_{1}-\delta_{2}\right)^{2}+\right) \\&\left.=3 \delta_{0}^{2}-3 \delta_{1}^{2}-3 \delta_{2}^{2}+0.5\right)\end{aligned}$
(7) $ \left\{\begin{array}{l}i_{L s}\left(\omega t=\pi-\delta_{1} \pi\right)=\frac{1}{4 f L_{s}}\left(u_{1}\left(1-2 \delta_{1}\right)-u_{2}\left(1-2 \delta_{0}-2 \delta_{1}\right)\right) \\i_{L s}\left(\omega t=\pi+\delta_{1} \pi\right)=\frac{1}{4 f L_{s}}\left(u_{1}\left(1-2 \delta_{1}\right)-u_{2}\left(1-2 \delta_{0}+2 \delta_{1}\right)\right) \\i_{L s}\left(\omega t=\delta_{0} \pi-\delta_{2} \pi\right)=\frac{1}{4 f L_{s}}\left(u_{2}\left(1-2 \delta_{2}\right)-u_{1}\left(1-2 \delta_{0}+2 \delta_{2}\right)\right) \\i_{L s}\left(\omega t=\delta_{0} \pi+\delta_{2} \pi\right)=\frac{1}{4 f L_{s}}\left(u_{2}\left(1-2 \delta_{2}\right)-u_{1}\left(1-2 \delta_{0}-2 \delta_{2}\right)\right)\end{array}\right.$
(8) $ \begin{aligned}i_{r m s}^{2}=& \frac{\pi^{2} u_{1}^{2}}{12 \omega^{2} L^{2}}\left(1-12 \delta_{1}^{2}+16 \delta_{1}^{3}\right)+\\& \frac{\pi^{2} u_{2}^{2}}{12 \omega^{2} L^{2}}\left(1-12 \delta_{2}^{2}+16 \delta_{2}^{3}\right)-\\& \frac{\pi^{2} u_{1} u_{2}}{6 \omega^{2} L^{2}}\left(1-2 \delta_{0}\right)\left(1+2 \delta_{0}-2 \delta_{0}^{2}-6 \delta_{1}^{2}-6 \delta_{2}^{2}\right)\end{aligned}$
3 双有源桥变换器最优损耗调制方法
3.1 双有源桥损耗模型
推导出电流的波形之后,就可以得到双有源桥变换器的总体损耗,由导通损耗和关断损耗构成。由于MOSFET的导通损耗正比于电流有效值的平方,关断损耗正比于开关频率。总体损耗的模型由式(9)给出
(9) $ P_{\text {loss }}=4 R_{d s(o n)} i_{r m s}^{2}+2 f_{s} E_{o f f}$
式中,Rds ( on ) 是MOSFET导通电阻;Eoff 是开关时刻S 1 ~S 8 的关断损耗能量,可以通过数据手册,根据实际关断电流与工作温度,线性拟合至实际工作点。
将电流波形代入双有源桥变换器的损耗模型,则可以得到损耗关于三个移相比的函数。代入任意调制方法下的移相比,就可以计算出该调制方法下的双有源桥变换器整体损耗。
3.2 双有源桥最优损耗调制
推导变换器的整体损耗模型之后,则可以求解以下优化模型,得到双有源桥变换器最优损耗的调制方法
(10) min Ploss (δ 0 , δ 1 , δ 2 )
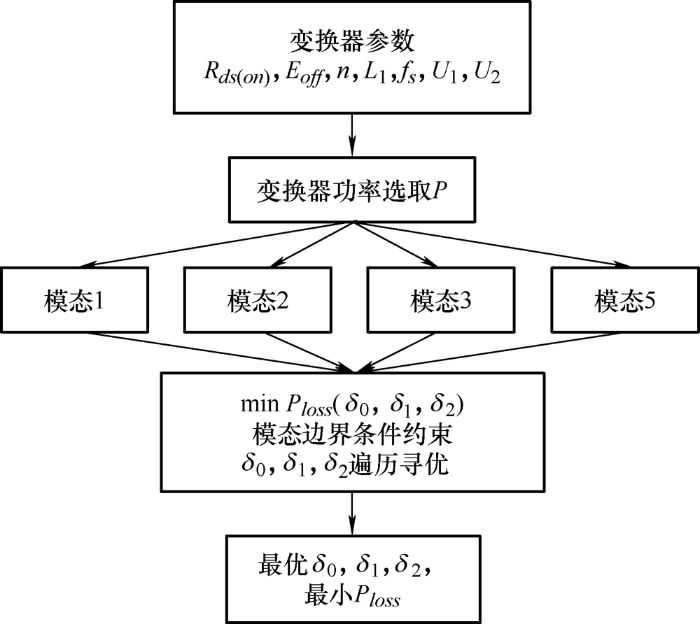
根据式(5)、(6),即双有源桥变换器的总损耗和具体选择器件的参数、MOSFET导通电阻Rds ( on ) 和开关器件关断损耗Eoff 将会影响损耗的大小。这个优化模型的解析表达式难以求解,可以采用暴力搜索或启发式算法如遗传算法、粒子群算法等求解移相比。具体算法流程如图4 所示。
图4
首先确定双有源桥变换器的工作参数,然后依次从小到大选取变换器功率,在不同模态下分别用暴力搜索的方法遍历各工作点损耗,同时利用各模态的边界条件作为限制因素,最终求解得到的最优移相比可以保证双有源桥变换器在给定的工作点、电路参数和开关器件的特性下,取到最小的损耗。
该优化调制策略的构建考虑了不同的器件特性和电路参数,因此适用于所有双有源桥变换器的情况。同时,由于优化目标直接为双有源桥变换器的整体损耗,而非高频电流等中间变量,因此可以确保最小损耗。
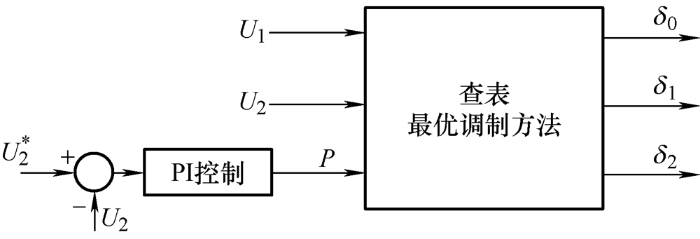
实际使用时,可以通过对输出电压进行积分得到电路的功率指令值,结合当前电路的输入电压与输出电压,即可得到当前工作点信息,通过查表方法可以得到当前工作点下的最优的δ 0 、δ 1 、δ 2 ,如图5 所示。
图5
4 双有源桥变换器最优损耗调制实例
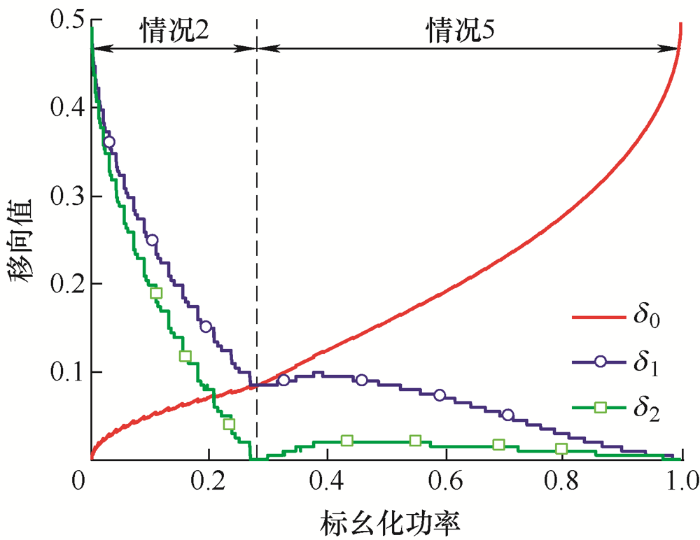
假设双有源桥变换器的所有开关管采用来自Cree的SiC MOSFET C2M0080120D,在d =0.8,开关频率50 kHz的情况下,最优损耗调制下的移相比求解如图6 所示。此时双有源桥变换器的整体损耗主要由导通损耗和关断损耗组成,如图6 在轻载部分的锯齿是因为此时最优损耗调制情况存在于情况2和3的边界附近。
图6
图6
d =0.8,50 kHz下的内外移相比示意图
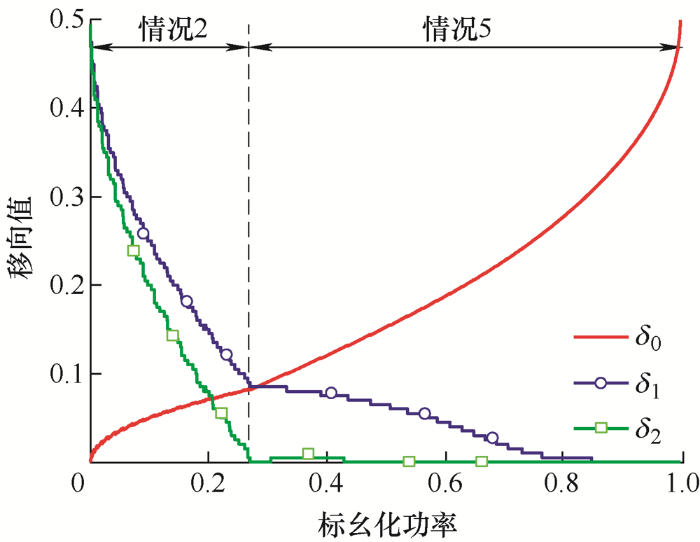
若在同样的参数下,降低开关频率到15 kHz,最优损耗调制下的移相比如图7 所示。此时双有源桥变换器的损耗基本为MOSFET开关管的导通损耗,所以可以近似认为双有源桥变换器最优损耗等于最小的MOSFET导通损耗,即对应最优电流RMS值调制的情况。因此,最优损耗调制得到的移相比也与最优电流RMS调制的结果几乎一致。说明最优电流RMS调制仅为最优损耗调制的一个特例,即假设双有源桥变换器的整体损耗基本为MOSFET导通损耗构成。
图7
图7
d =0.8,15 kHz下的内外移相比示意图
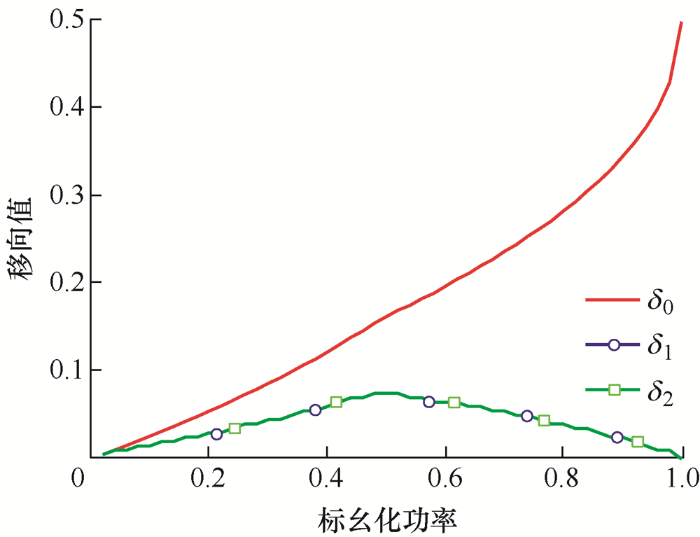
当原副边电压匹配时,即d =1,在开关频率50 kHz的情况下,最优损耗调制的移相比如图8 所示。与其他调制方法显著的不同之处在于,最优的内移相比不为零。通过采用非零的内移相比,原副边各有一个桥臂的开关管会承受更小(近似为原先一半)的关断电流,进一步降低DAB变压器的总损耗。不同于单移相调制下,原边的两个桥臂的开关管都需要承受最大的关断损耗,此时有一个桥臂的开关管承受近似原先一半的关断损耗,副边同理。此时的调制类似于梯形调制,最优损耗调制能通过梯形调制减小关断损耗,取得更高的效率。
图8
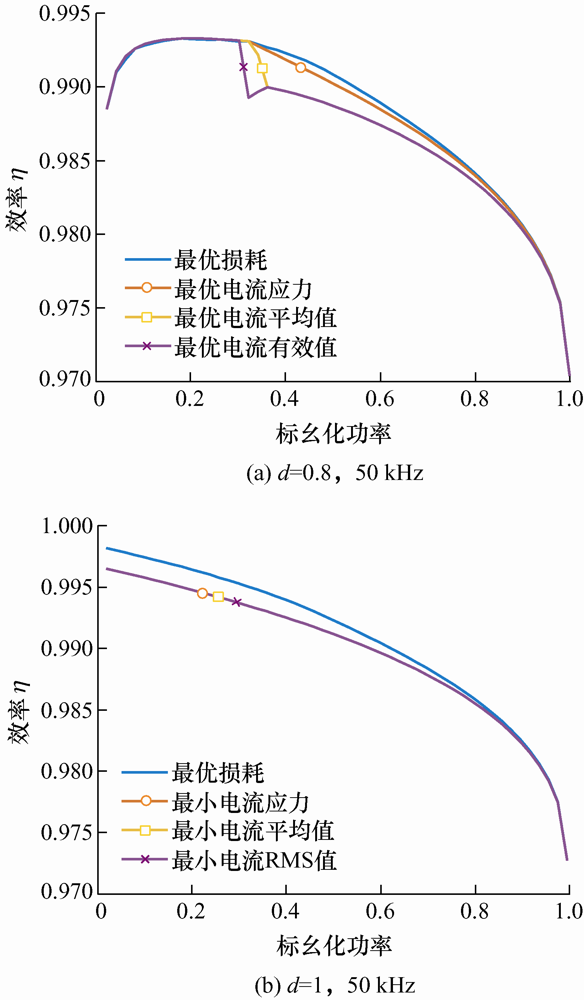
图9 a对比了最优调制策略和现有的几种电流优化调制策略下的效率,此时d =0.8,开关频率为50 kHz。可以看到大约在有功功率小于33%的低功率区,所有的调制方式显示了一样的效率,因为在两端电压不匹配且功率较小的时候,可以通过构造三角形电流波形实现,此时四种调制策略均为效率最优。随着功率增加,上述调制方法无法满足有功功率的需求,在图9 a中约P =0.33处,几种最优调制方式进入不同的工作模式,使用不同的移相比。对比几条效率曲线,本文提出的最优损耗调制,始终能取得最高的效率(即最小的损耗)。随着有功功率逐渐增加到100%,几种调制方法的效率又趋于一致,因为随着负载增加,移相比的调整自由度逐渐减小,几种调制方式的移相比逐渐收敛到唯一可行的移相比。图9 b中,在电压匹配时,即d =1时,最优损耗调制方法在全功率段取得了更高的效率。其他的最优调制方法在电压匹配时均采取最为简单的单移相调制,此时内移相δ 1 和δ 2 均为零,尽管此时可以实现ZVS软开通,关断损耗却并非最小。
图9
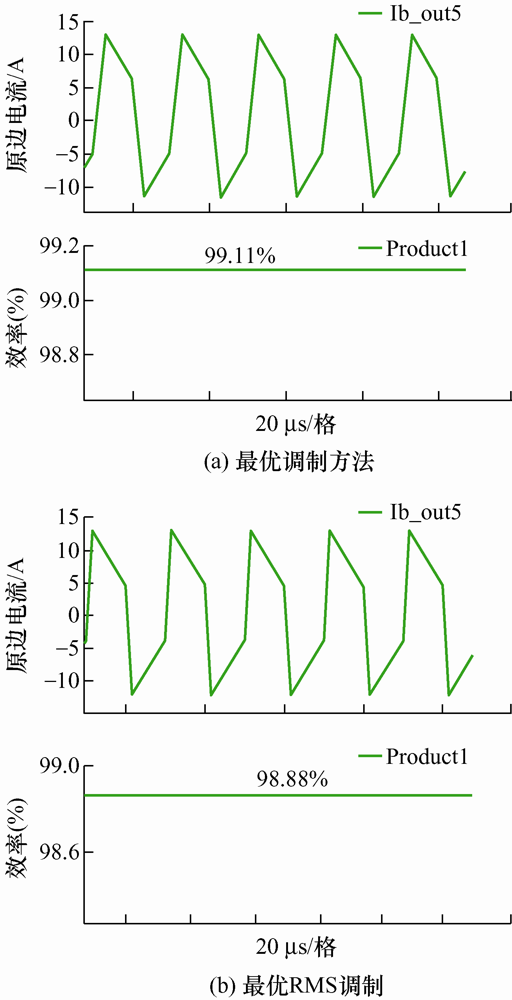
在PLECS中对电压不匹配(d =0.8)的情况进行仿真,选择开关器件C2M0080120D,开关频率50 kHz。对比了P =0.5情况下的最优损耗调制和最优电流有效值的效率,如图10 所示。从图10 可以看出,采用了最优损耗调制的双有源桥变换器效率为99.1%,采用了最优电流有效值调制的双有源桥变换器效率为98.9%,基本与理论计算一致,验证了理论的正确性。
图10
图10
最优损耗调制方法与最优RMS调制方法的仿真效率对比
(1) 当原副边电压不匹配时,在轻载区最优损耗调制与最优电流应力、最优电流平均值和最优电流RMS值调制是一样的。因为在传输功率较低时,可以控制高频电流在半个周期内回到零,实现了所有开关管的零电压开通和关断。
(2) 在中载区,最优损耗调制仍然采用近似三角波调制,以实现小电流关断,这有利于降低关断损耗;在重载区,最优损耗调制会存在较小的副边内移相比,以降低副边的关断电流。然而,最优电流应力调制则载进入中载区之后,退化为扩展移相调制,即副边的内移相角恒为零,这说明了最优电流应力调制只优化了原边开关管的关断损耗,并没有考虑副边的关断损耗。最优损耗调制完整地考虑了DAB变换器的全部损耗,在全功率范围充分利用了三个移相比,实现整体损耗最小。
(3) 当原副边电压匹配时,最优损耗调制引入了非零的内移相比,进一步降低了开关管的关断损耗。
(4) 当双有源桥变换器的导通损耗和关断损耗占比相近时,现有的电流优化调制方法均无法得到最小的变换器损耗,这是因为它们只优化了其中一部分的损耗。最优损耗调制则可以应对这种情况。
5 结论
本文提出了一种最优损耗调制策略,主要分析过程与创新点如下。
(1) 本文对双有源桥变换器的工作模态进行了分析,明确了各模态的工作特性与边界条件,在此基础上构造最优损耗调制方法,通过建立目标函数并结合边界条件求解,可以得到使变换器总损耗(通态损耗与开关损耗之和)最低的最优调制参数δ 0 、δ 1 、δ 2 。
(2) 通过对实例进行分析,同时对比了现有的电流优化调制方法,验证了本文提出的最优损耗调制策略的可行性与正确性。
(3) 相比于目前的电流优化调制方法,本文提出的调制策略能确保在给定电路参数和工作点时,寻找到最佳的移相比,使得总损耗最低,是一种更为通用、损耗最小的调制方法。
参考文献
View Option
[1]
KHERALUWALA M N GASCOIGNE R W DIVAN D M , et al . Performance characterization of a high-power dual active bridge DC-to-DC converter
[J]. IEEE Transactions on Industry Applications , 1992 , 28 (6 ):1294 -1301 .
DOI:10.1109/28.175280
URL
[本文引用: 1]
[2]
ZHAO B SONG Q LIU W , et al . Overview of dual-active-bridge isolated bidirectional DC-DC converter for high-frequency-link power-conversion system
[J]. IEEE Transactions on Power Electronics , 2014 , 29 (8 ):4091 -4106 .
DOI:10.1109/TPEL.2013.2289913
URL
[本文引用: 1]
[3]
HOU N LI Y W . Overview and comparison of modulation and control strategies for a nonresonant single-phase dual-active-bridge DC-DC converter
[J]. IEEE Transactions on Power Electronics , 2020 , 35 (3 ):3148 -3172 .
DOI:10.1109/TPEL.2019.2927930
URL
[本文引用: 1]
[4]
OGGIER G G GARCÍA G O OLIVA A R . Switching control strategy to minimize dual active bridge converter losses
[J]. IEEE Transactions on Power Electronics , 2009 , 24 (7 ):1826 -1838 .
DOI:10.1109/TPEL.2009.2020902
URL
[本文引用: 1]
[5]
OGGIER G G GARCIA G O OLIVA A R . Modulation strategy to operate the dual active bridge DC-DC converter under soft switching in the whole operating range
[J]. IEEE Transactions on Power Electronics , 2011 , 26 (4 ):1228 -1236 .
DOI:10.1109/TPEL.2010.2072966
URL
[本文引用: 1]
[6]
ZHAO B YU Q SUN W . Extended-phase-shift control of isolated bidirectional DC-DC converter for power distribution in microgrid
[J]. IEEE Transactions on Power Electronics , 2012 , 27 (11 ):4667 -4680 .
DOI:10.1109/TPEL.2011.2180928
URL
[本文引用: 1]
[7]
赵彪 , 于庆广 , 孙伟欣 . 双重移相控制的双向全桥DC-DC变换器及其功率回流特性分析
[J]. 中国电机工程学报 , 2012 , 32 (12 ):43 -50 .
[本文引用: 1]
ZHAO Biao YU Qingguang SUN Weixin . Bi-directional full-bridge DC-DC converters with dual-phase-shifting control and its backflow power characteristic analysis
[J]. Proceedings of the CSEE , 2012 , 32 (12 ):43 -50 .
[本文引用: 1]
[8]
ZHAO B SONG Q LIU W , et al . Current-stress-optimized switching strategy of isolated bidirectional DC-DC converter with dual-phase-shift control
[J]. IEEE Transactions on Industrial Electronics , 2013 , 60 (10 ):4458 -4467 .
DOI:10.1109/TIE.2012.2210374
URL
[本文引用: 2]
[9]
王聪 , 沙广林 , 王俊 , 等 . 基于双重移相控制的双有源桥DC-DC变换器的软开关
[J]. 电工技术学报 , 2015 , 30 (12 ):106 -113 .
[本文引用: 1]
WANG Cong SHA Guanglin WANG Jun , et al . The analysis of zero voltage switching dual active bridge DC-DC converters based on dual-phase-shifting control
[J]. Transactions of China Electrotechnical Society , 2015 , 30 (12 ):106 -113 .
[本文引用: 1]
[10]
HUANG J WANG Y LI Z , et al . Unified triple-phase-shift control to minimize current stress and achieve full soft-switching of isolated bidirectional DC-DC converter
[J]. IEEE Transactions on Industrial Electronics , 2016 , 63 (7 ):4169 -4179 .
DOI:10.1109/TIE.2016.2543182
URL
[本文引用: 2]
[11]
KRISMER F KOLAR J W . Closed form solution for minimum conduction loss modulation of DAB converters
[J]. IEEE Transactions on Power Electronics , 2012 , 27 (1 ):174 -188 .
DOI:10.1109/TPEL.2011.2157976
URL
[本文引用: 2]
[12]
TONG A HANG L LI G , et al . Modeling and analysis of a dual-active-bridge-isolated bidirectional DC/DC converter to minimize RMS current with whole operating range
[J]. IEEE Transactions on Power Electronics , 2018 , 33 (6 ):5302 -5316 .
DOI:10.1109/TPEL.2017.2692276
URL
[本文引用: 1]
[13]
侯聂 , 宋文胜 , 王顺亮 . 全桥隔离DC/DC变换器相移控制归一化及其最小回流功率控制
[J]. 中国电机工程学报 , 2016 , 36 (2 ):499 -506 .
[本文引用: 1]
HOU Nie SONG Wensheng WANG Shunliang . Normalization of phase shift control and minimum reflux power control of full-bridge isolated DC/DC converters
[J]. Proceedings of the CSEE , 2016 , 36 (2 ):499 -506 .
[本文引用: 1]
[14]
SHAO S JIANG M YE W , et al . Optimal phase-shift control to minimize reactive power for a dual active bridge DC-DC converter
[J]. IEEE Transactions on Power Electronics , 2019 , 34 (10 ):10193 -10205 .
DOI:10.1109/TPEL.2018.2890292
URL
[本文引用: 1]
[15]
BAI H MI C . Eliminate reactive power and increase system efficiency of isolated bidirectional dual-active- bridge DC-DC converters using novel dual-phase-shift control
[J]. IEEE Transactions on Power Electronics , 2008 , 23 (6 ):2905 -2914 .
DOI:10.1109/TPEL.2008.2005103
URL
[本文引用: 1]
[16]
ZHAO B SONG Q LIU W , et al . Universal high-frequency-link characterization and practical fundamental-optimal strategy for dual-active-bridge DC-DC converter under PWM plus phase-shift control
[J]. IEEE Transactions on Power Electronics , 2015 , 30 (12 ):6488 -6494 .
DOI:10.1109/TPEL.2015.2430934
URL
[本文引用: 1]
Performance characterization of a high-power dual active bridge DC-to-DC converter
1
1992
... 双有源桥变换器是多单元级联型变换器中的重要变流部件.双有源桥变换器的基本拓扑结构(图1 )和工作原理于20世纪90年代被提出[1 ] ,其控制灵活,具有高频电能变换、软开关、电气隔离等优点. ...
Overview of dual-active-bridge isolated bidirectional DC-DC converter for high-frequency-link power-conversion system
1
2014
... 双有源桥变换器有三个调制的自由度:原边桥臂内移相、副边桥臂内移相和原副边桥臂外移相.单移相调制只采用原副边桥臂外移相作为控制变量,是最简单的调制方法.采用这种调制策略,当电压变比和变压器变比不匹配时,高频电流迅速增大,软开关工作区域变窄,变换器导通损耗与开关损耗增加.为解决这个问题,很多文献提出了多自由度移相调制方法.文献[2 ]采用了扩展移相调制,副边不存在内移相,通过控制原边桥臂内移相和原副边桥臂外移相来完成功率的传递.文献[3 ⇓ -5 ]中采用双移相调制,原副边存在内移相且内移相值相同,通过改变原副边外移相值控制功率的传递.三移相调制则采用全部三个调制自由度[6 ⇓ ⇓ ⇓ ⇓ -11 ] ,单移相调制、扩展移相调制和双移相调制都是三移相调制的特殊形式. ...
Overview and comparison of modulation and control strategies for a nonresonant single-phase dual-active-bridge DC-DC converter
1
2020
... 双有源桥变换器有三个调制的自由度:原边桥臂内移相、副边桥臂内移相和原副边桥臂外移相.单移相调制只采用原副边桥臂外移相作为控制变量,是最简单的调制方法.采用这种调制策略,当电压变比和变压器变比不匹配时,高频电流迅速增大,软开关工作区域变窄,变换器导通损耗与开关损耗增加.为解决这个问题,很多文献提出了多自由度移相调制方法.文献[2 ]采用了扩展移相调制,副边不存在内移相,通过控制原边桥臂内移相和原副边桥臂外移相来完成功率的传递.文献[3 ⇓ -5 ]中采用双移相调制,原副边存在内移相且内移相值相同,通过改变原副边外移相值控制功率的传递.三移相调制则采用全部三个调制自由度[6 ⇓ ⇓ ⇓ ⇓ -11 ] ,单移相调制、扩展移相调制和双移相调制都是三移相调制的特殊形式. ...
Switching control strategy to minimize dual active bridge converter losses
1
2009
... 双有源桥变换器有三个调制的自由度:原边桥臂内移相、副边桥臂内移相和原副边桥臂外移相.单移相调制只采用原副边桥臂外移相作为控制变量,是最简单的调制方法.采用这种调制策略,当电压变比和变压器变比不匹配时,高频电流迅速增大,软开关工作区域变窄,变换器导通损耗与开关损耗增加.为解决这个问题,很多文献提出了多自由度移相调制方法.文献[2 ]采用了扩展移相调制,副边不存在内移相,通过控制原边桥臂内移相和原副边桥臂外移相来完成功率的传递.文献[3 ⇓ -5 ]中采用双移相调制,原副边存在内移相且内移相值相同,通过改变原副边外移相值控制功率的传递.三移相调制则采用全部三个调制自由度[6 ⇓ ⇓ ⇓ ⇓ -11 ] ,单移相调制、扩展移相调制和双移相调制都是三移相调制的特殊形式. ...
Modulation strategy to operate the dual active bridge DC-DC converter under soft switching in the whole operating range
1
2011
... 双有源桥变换器有三个调制的自由度:原边桥臂内移相、副边桥臂内移相和原副边桥臂外移相.单移相调制只采用原副边桥臂外移相作为控制变量,是最简单的调制方法.采用这种调制策略,当电压变比和变压器变比不匹配时,高频电流迅速增大,软开关工作区域变窄,变换器导通损耗与开关损耗增加.为解决这个问题,很多文献提出了多自由度移相调制方法.文献[2 ]采用了扩展移相调制,副边不存在内移相,通过控制原边桥臂内移相和原副边桥臂外移相来完成功率的传递.文献[3 ⇓ -5 ]中采用双移相调制,原副边存在内移相且内移相值相同,通过改变原副边外移相值控制功率的传递.三移相调制则采用全部三个调制自由度[6 ⇓ ⇓ ⇓ ⇓ -11 ] ,单移相调制、扩展移相调制和双移相调制都是三移相调制的特殊形式. ...
Extended-phase-shift control of isolated bidirectional DC-DC converter for power distribution in microgrid
1
2012
... 双有源桥变换器有三个调制的自由度:原边桥臂内移相、副边桥臂内移相和原副边桥臂外移相.单移相调制只采用原副边桥臂外移相作为控制变量,是最简单的调制方法.采用这种调制策略,当电压变比和变压器变比不匹配时,高频电流迅速增大,软开关工作区域变窄,变换器导通损耗与开关损耗增加.为解决这个问题,很多文献提出了多自由度移相调制方法.文献[2 ]采用了扩展移相调制,副边不存在内移相,通过控制原边桥臂内移相和原副边桥臂外移相来完成功率的传递.文献[3 ⇓ -5 ]中采用双移相调制,原副边存在内移相且内移相值相同,通过改变原副边外移相值控制功率的传递.三移相调制则采用全部三个调制自由度[6 ⇓ ⇓ ⇓ ⇓ -11 ] ,单移相调制、扩展移相调制和双移相调制都是三移相调制的特殊形式. ...
双重移相控制的双向全桥DC-DC变换器及其功率回流特性分析
1
2012
... 双有源桥变换器有三个调制的自由度:原边桥臂内移相、副边桥臂内移相和原副边桥臂外移相.单移相调制只采用原副边桥臂外移相作为控制变量,是最简单的调制方法.采用这种调制策略,当电压变比和变压器变比不匹配时,高频电流迅速增大,软开关工作区域变窄,变换器导通损耗与开关损耗增加.为解决这个问题,很多文献提出了多自由度移相调制方法.文献[2 ]采用了扩展移相调制,副边不存在内移相,通过控制原边桥臂内移相和原副边桥臂外移相来完成功率的传递.文献[3 ⇓ -5 ]中采用双移相调制,原副边存在内移相且内移相值相同,通过改变原副边外移相值控制功率的传递.三移相调制则采用全部三个调制自由度[6 ⇓ ⇓ ⇓ ⇓ -11 ] ,单移相调制、扩展移相调制和双移相调制都是三移相调制的特殊形式. ...
Bi-directional full-bridge DC-DC converters with dual-phase-shifting control and its backflow power characteristic analysis
1
2012
... 双有源桥变换器有三个调制的自由度:原边桥臂内移相、副边桥臂内移相和原副边桥臂外移相.单移相调制只采用原副边桥臂外移相作为控制变量,是最简单的调制方法.采用这种调制策略,当电压变比和变压器变比不匹配时,高频电流迅速增大,软开关工作区域变窄,变换器导通损耗与开关损耗增加.为解决这个问题,很多文献提出了多自由度移相调制方法.文献[2 ]采用了扩展移相调制,副边不存在内移相,通过控制原边桥臂内移相和原副边桥臂外移相来完成功率的传递.文献[3 ⇓ -5 ]中采用双移相调制,原副边存在内移相且内移相值相同,通过改变原副边外移相值控制功率的传递.三移相调制则采用全部三个调制自由度[6 ⇓ ⇓ ⇓ ⇓ -11 ] ,单移相调制、扩展移相调制和双移相调制都是三移相调制的特殊形式. ...
Current-stress-optimized switching strategy of isolated bidirectional DC-DC converter with dual-phase-shift control
2
2013
... 双有源桥变换器有三个调制的自由度:原边桥臂内移相、副边桥臂内移相和原副边桥臂外移相.单移相调制只采用原副边桥臂外移相作为控制变量,是最简单的调制方法.采用这种调制策略,当电压变比和变压器变比不匹配时,高频电流迅速增大,软开关工作区域变窄,变换器导通损耗与开关损耗增加.为解决这个问题,很多文献提出了多自由度移相调制方法.文献[2 ]采用了扩展移相调制,副边不存在内移相,通过控制原边桥臂内移相和原副边桥臂外移相来完成功率的传递.文献[3 ⇓ -5 ]中采用双移相调制,原副边存在内移相且内移相值相同,通过改变原副边外移相值控制功率的传递.三移相调制则采用全部三个调制自由度[6 ⇓ ⇓ ⇓ ⇓ -11 ] ,单移相调制、扩展移相调制和双移相调制都是三移相调制的特殊形式. ...
... 为了提升变换器的工作效率,不少文献会结合调制方法对双有源桥变换器的电流、功率情况进行分析.针对双有源桥变换器的电流优化,主要包括最优电流应力调制[8 ,10 ] 、最优电流平均值调制[11 ] 、最优电流RMS值调制[12 ] .最优电流应力调制将电感电流峰值降为最小,减小了器件的开关损耗与电流应力.最优电流平均值调制能够保证电感电流的平均值最小,从而使IGBT器件的通态损耗降为最低.最优电流RMS调制能够保证电感电流的有效值最小,从而使MOSFET器件的通态损耗降为最低.这些调制方法通常仅针对双有源桥变换器的部分损耗进行优化,未考虑其他部分的损耗.此外,还有文献提出了最小功率回流的调制方法[13 ⇓ -15 ] .但是回流功率的定义不具备明确的物理意义,无法直接联系常用的无功功率概念.这种建模方法计算量大、过程复杂,随着调制自由度的增多,通过瞬时功率积分计算回流功率的难度加大.文献[16 ]从频域上定义了统一的无功功率,并通过优化调制参数对基波或是一部分无功功率进行优化.但是双有源桥变换器的高频电压和高频电流分别呈方波和梯形波,其中含有大量的谐波分量,因此基于基波的优化方法必然存在误差. ...
基于双重移相控制的双有源桥DC-DC变换器的软开关
1
2015
... 双有源桥变换器有三个调制的自由度:原边桥臂内移相、副边桥臂内移相和原副边桥臂外移相.单移相调制只采用原副边桥臂外移相作为控制变量,是最简单的调制方法.采用这种调制策略,当电压变比和变压器变比不匹配时,高频电流迅速增大,软开关工作区域变窄,变换器导通损耗与开关损耗增加.为解决这个问题,很多文献提出了多自由度移相调制方法.文献[2 ]采用了扩展移相调制,副边不存在内移相,通过控制原边桥臂内移相和原副边桥臂外移相来完成功率的传递.文献[3 ⇓ -5 ]中采用双移相调制,原副边存在内移相且内移相值相同,通过改变原副边外移相值控制功率的传递.三移相调制则采用全部三个调制自由度[6 ⇓ ⇓ ⇓ ⇓ -11 ] ,单移相调制、扩展移相调制和双移相调制都是三移相调制的特殊形式. ...
The analysis of zero voltage switching dual active bridge DC-DC converters based on dual-phase-shifting control
1
2015
... 双有源桥变换器有三个调制的自由度:原边桥臂内移相、副边桥臂内移相和原副边桥臂外移相.单移相调制只采用原副边桥臂外移相作为控制变量,是最简单的调制方法.采用这种调制策略,当电压变比和变压器变比不匹配时,高频电流迅速增大,软开关工作区域变窄,变换器导通损耗与开关损耗增加.为解决这个问题,很多文献提出了多自由度移相调制方法.文献[2 ]采用了扩展移相调制,副边不存在内移相,通过控制原边桥臂内移相和原副边桥臂外移相来完成功率的传递.文献[3 ⇓ -5 ]中采用双移相调制,原副边存在内移相且内移相值相同,通过改变原副边外移相值控制功率的传递.三移相调制则采用全部三个调制自由度[6 ⇓ ⇓ ⇓ ⇓ -11 ] ,单移相调制、扩展移相调制和双移相调制都是三移相调制的特殊形式. ...
Unified triple-phase-shift control to minimize current stress and achieve full soft-switching of isolated bidirectional DC-DC converter
2
2016
... 双有源桥变换器有三个调制的自由度:原边桥臂内移相、副边桥臂内移相和原副边桥臂外移相.单移相调制只采用原副边桥臂外移相作为控制变量,是最简单的调制方法.采用这种调制策略,当电压变比和变压器变比不匹配时,高频电流迅速增大,软开关工作区域变窄,变换器导通损耗与开关损耗增加.为解决这个问题,很多文献提出了多自由度移相调制方法.文献[2 ]采用了扩展移相调制,副边不存在内移相,通过控制原边桥臂内移相和原副边桥臂外移相来完成功率的传递.文献[3 ⇓ -5 ]中采用双移相调制,原副边存在内移相且内移相值相同,通过改变原副边外移相值控制功率的传递.三移相调制则采用全部三个调制自由度[6 ⇓ ⇓ ⇓ ⇓ -11 ] ,单移相调制、扩展移相调制和双移相调制都是三移相调制的特殊形式. ...
... 为了提升变换器的工作效率,不少文献会结合调制方法对双有源桥变换器的电流、功率情况进行分析.针对双有源桥变换器的电流优化,主要包括最优电流应力调制[8 ,10 ] 、最优电流平均值调制[11 ] 、最优电流RMS值调制[12 ] .最优电流应力调制将电感电流峰值降为最小,减小了器件的开关损耗与电流应力.最优电流平均值调制能够保证电感电流的平均值最小,从而使IGBT器件的通态损耗降为最低.最优电流RMS调制能够保证电感电流的有效值最小,从而使MOSFET器件的通态损耗降为最低.这些调制方法通常仅针对双有源桥变换器的部分损耗进行优化,未考虑其他部分的损耗.此外,还有文献提出了最小功率回流的调制方法[13 ⇓ -15 ] .但是回流功率的定义不具备明确的物理意义,无法直接联系常用的无功功率概念.这种建模方法计算量大、过程复杂,随着调制自由度的增多,通过瞬时功率积分计算回流功率的难度加大.文献[16 ]从频域上定义了统一的无功功率,并通过优化调制参数对基波或是一部分无功功率进行优化.但是双有源桥变换器的高频电压和高频电流分别呈方波和梯形波,其中含有大量的谐波分量,因此基于基波的优化方法必然存在误差. ...
Closed form solution for minimum conduction loss modulation of DAB converters
2
2012
... 双有源桥变换器有三个调制的自由度:原边桥臂内移相、副边桥臂内移相和原副边桥臂外移相.单移相调制只采用原副边桥臂外移相作为控制变量,是最简单的调制方法.采用这种调制策略,当电压变比和变压器变比不匹配时,高频电流迅速增大,软开关工作区域变窄,变换器导通损耗与开关损耗增加.为解决这个问题,很多文献提出了多自由度移相调制方法.文献[2 ]采用了扩展移相调制,副边不存在内移相,通过控制原边桥臂内移相和原副边桥臂外移相来完成功率的传递.文献[3 ⇓ -5 ]中采用双移相调制,原副边存在内移相且内移相值相同,通过改变原副边外移相值控制功率的传递.三移相调制则采用全部三个调制自由度[6 ⇓ ⇓ ⇓ ⇓ -11 ] ,单移相调制、扩展移相调制和双移相调制都是三移相调制的特殊形式. ...
... 为了提升变换器的工作效率,不少文献会结合调制方法对双有源桥变换器的电流、功率情况进行分析.针对双有源桥变换器的电流优化,主要包括最优电流应力调制[8 ,10 ] 、最优电流平均值调制[11 ] 、最优电流RMS值调制[12 ] .最优电流应力调制将电感电流峰值降为最小,减小了器件的开关损耗与电流应力.最优电流平均值调制能够保证电感电流的平均值最小,从而使IGBT器件的通态损耗降为最低.最优电流RMS调制能够保证电感电流的有效值最小,从而使MOSFET器件的通态损耗降为最低.这些调制方法通常仅针对双有源桥变换器的部分损耗进行优化,未考虑其他部分的损耗.此外,还有文献提出了最小功率回流的调制方法[13 ⇓ -15 ] .但是回流功率的定义不具备明确的物理意义,无法直接联系常用的无功功率概念.这种建模方法计算量大、过程复杂,随着调制自由度的增多,通过瞬时功率积分计算回流功率的难度加大.文献[16 ]从频域上定义了统一的无功功率,并通过优化调制参数对基波或是一部分无功功率进行优化.但是双有源桥变换器的高频电压和高频电流分别呈方波和梯形波,其中含有大量的谐波分量,因此基于基波的优化方法必然存在误差. ...
Modeling and analysis of a dual-active-bridge-isolated bidirectional DC/DC converter to minimize RMS current with whole operating range
1
2018
... 为了提升变换器的工作效率,不少文献会结合调制方法对双有源桥变换器的电流、功率情况进行分析.针对双有源桥变换器的电流优化,主要包括最优电流应力调制[8 ,10 ] 、最优电流平均值调制[11 ] 、最优电流RMS值调制[12 ] .最优电流应力调制将电感电流峰值降为最小,减小了器件的开关损耗与电流应力.最优电流平均值调制能够保证电感电流的平均值最小,从而使IGBT器件的通态损耗降为最低.最优电流RMS调制能够保证电感电流的有效值最小,从而使MOSFET器件的通态损耗降为最低.这些调制方法通常仅针对双有源桥变换器的部分损耗进行优化,未考虑其他部分的损耗.此外,还有文献提出了最小功率回流的调制方法[13 ⇓ -15 ] .但是回流功率的定义不具备明确的物理意义,无法直接联系常用的无功功率概念.这种建模方法计算量大、过程复杂,随着调制自由度的增多,通过瞬时功率积分计算回流功率的难度加大.文献[16 ]从频域上定义了统一的无功功率,并通过优化调制参数对基波或是一部分无功功率进行优化.但是双有源桥变换器的高频电压和高频电流分别呈方波和梯形波,其中含有大量的谐波分量,因此基于基波的优化方法必然存在误差. ...
全桥隔离DC/DC变换器相移控制归一化及其最小回流功率控制
1
2016
... 为了提升变换器的工作效率,不少文献会结合调制方法对双有源桥变换器的电流、功率情况进行分析.针对双有源桥变换器的电流优化,主要包括最优电流应力调制[8 ,10 ] 、最优电流平均值调制[11 ] 、最优电流RMS值调制[12 ] .最优电流应力调制将电感电流峰值降为最小,减小了器件的开关损耗与电流应力.最优电流平均值调制能够保证电感电流的平均值最小,从而使IGBT器件的通态损耗降为最低.最优电流RMS调制能够保证电感电流的有效值最小,从而使MOSFET器件的通态损耗降为最低.这些调制方法通常仅针对双有源桥变换器的部分损耗进行优化,未考虑其他部分的损耗.此外,还有文献提出了最小功率回流的调制方法[13 ⇓ -15 ] .但是回流功率的定义不具备明确的物理意义,无法直接联系常用的无功功率概念.这种建模方法计算量大、过程复杂,随着调制自由度的增多,通过瞬时功率积分计算回流功率的难度加大.文献[16 ]从频域上定义了统一的无功功率,并通过优化调制参数对基波或是一部分无功功率进行优化.但是双有源桥变换器的高频电压和高频电流分别呈方波和梯形波,其中含有大量的谐波分量,因此基于基波的优化方法必然存在误差. ...
Normalization of phase shift control and minimum reflux power control of full-bridge isolated DC/DC converters
1
2016
... 为了提升变换器的工作效率,不少文献会结合调制方法对双有源桥变换器的电流、功率情况进行分析.针对双有源桥变换器的电流优化,主要包括最优电流应力调制[8 ,10 ] 、最优电流平均值调制[11 ] 、最优电流RMS值调制[12 ] .最优电流应力调制将电感电流峰值降为最小,减小了器件的开关损耗与电流应力.最优电流平均值调制能够保证电感电流的平均值最小,从而使IGBT器件的通态损耗降为最低.最优电流RMS调制能够保证电感电流的有效值最小,从而使MOSFET器件的通态损耗降为最低.这些调制方法通常仅针对双有源桥变换器的部分损耗进行优化,未考虑其他部分的损耗.此外,还有文献提出了最小功率回流的调制方法[13 ⇓ -15 ] .但是回流功率的定义不具备明确的物理意义,无法直接联系常用的无功功率概念.这种建模方法计算量大、过程复杂,随着调制自由度的增多,通过瞬时功率积分计算回流功率的难度加大.文献[16 ]从频域上定义了统一的无功功率,并通过优化调制参数对基波或是一部分无功功率进行优化.但是双有源桥变换器的高频电压和高频电流分别呈方波和梯形波,其中含有大量的谐波分量,因此基于基波的优化方法必然存在误差. ...
Optimal phase-shift control to minimize reactive power for a dual active bridge DC-DC converter
1
2019
... 为了提升变换器的工作效率,不少文献会结合调制方法对双有源桥变换器的电流、功率情况进行分析.针对双有源桥变换器的电流优化,主要包括最优电流应力调制[8 ,10 ] 、最优电流平均值调制[11 ] 、最优电流RMS值调制[12 ] .最优电流应力调制将电感电流峰值降为最小,减小了器件的开关损耗与电流应力.最优电流平均值调制能够保证电感电流的平均值最小,从而使IGBT器件的通态损耗降为最低.最优电流RMS调制能够保证电感电流的有效值最小,从而使MOSFET器件的通态损耗降为最低.这些调制方法通常仅针对双有源桥变换器的部分损耗进行优化,未考虑其他部分的损耗.此外,还有文献提出了最小功率回流的调制方法[13 ⇓ -15 ] .但是回流功率的定义不具备明确的物理意义,无法直接联系常用的无功功率概念.这种建模方法计算量大、过程复杂,随着调制自由度的增多,通过瞬时功率积分计算回流功率的难度加大.文献[16 ]从频域上定义了统一的无功功率,并通过优化调制参数对基波或是一部分无功功率进行优化.但是双有源桥变换器的高频电压和高频电流分别呈方波和梯形波,其中含有大量的谐波分量,因此基于基波的优化方法必然存在误差. ...
Eliminate reactive power and increase system efficiency of isolated bidirectional dual-active- bridge DC-DC converters using novel dual-phase-shift control
1
2008
... 为了提升变换器的工作效率,不少文献会结合调制方法对双有源桥变换器的电流、功率情况进行分析.针对双有源桥变换器的电流优化,主要包括最优电流应力调制[8 ,10 ] 、最优电流平均值调制[11 ] 、最优电流RMS值调制[12 ] .最优电流应力调制将电感电流峰值降为最小,减小了器件的开关损耗与电流应力.最优电流平均值调制能够保证电感电流的平均值最小,从而使IGBT器件的通态损耗降为最低.最优电流RMS调制能够保证电感电流的有效值最小,从而使MOSFET器件的通态损耗降为最低.这些调制方法通常仅针对双有源桥变换器的部分损耗进行优化,未考虑其他部分的损耗.此外,还有文献提出了最小功率回流的调制方法[13 ⇓ -15 ] .但是回流功率的定义不具备明确的物理意义,无法直接联系常用的无功功率概念.这种建模方法计算量大、过程复杂,随着调制自由度的增多,通过瞬时功率积分计算回流功率的难度加大.文献[16 ]从频域上定义了统一的无功功率,并通过优化调制参数对基波或是一部分无功功率进行优化.但是双有源桥变换器的高频电压和高频电流分别呈方波和梯形波,其中含有大量的谐波分量,因此基于基波的优化方法必然存在误差. ...
Universal high-frequency-link characterization and practical fundamental-optimal strategy for dual-active-bridge DC-DC converter under PWM plus phase-shift control
1
2015
... 为了提升变换器的工作效率,不少文献会结合调制方法对双有源桥变换器的电流、功率情况进行分析.针对双有源桥变换器的电流优化,主要包括最优电流应力调制[8 ,10 ] 、最优电流平均值调制[11 ] 、最优电流RMS值调制[12 ] .最优电流应力调制将电感电流峰值降为最小,减小了器件的开关损耗与电流应力.最优电流平均值调制能够保证电感电流的平均值最小,从而使IGBT器件的通态损耗降为最低.最优电流RMS调制能够保证电感电流的有效值最小,从而使MOSFET器件的通态损耗降为最低.这些调制方法通常仅针对双有源桥变换器的部分损耗进行优化,未考虑其他部分的损耗.此外,还有文献提出了最小功率回流的调制方法[13 ⇓ -15 ] .但是回流功率的定义不具备明确的物理意义,无法直接联系常用的无功功率概念.这种建模方法计算量大、过程复杂,随着调制自由度的增多,通过瞬时功率积分计算回流功率的难度加大.文献[16 ]从频域上定义了统一的无功功率,并通过优化调制参数对基波或是一部分无功功率进行优化.但是双有源桥变换器的高频电压和高频电流分别呈方波和梯形波,其中含有大量的谐波分量,因此基于基波的优化方法必然存在误差. ...