MSMA自感知执行器结构优化设计*

doi:10.11985/2022.02.029

MSMA自感知执行器结构优化设计^*

鲁军^,, 季宝爽^,, 贾士杰^,, 张源鑫^,

沈阳理工大学自动化与电气工程学院沈阳 110159

Structural Optimization Design of Self-sensing Actuator Based on MSMA

LU Jun^,, JI Baoshuang^,, JIA Shijie^,, ZHANG Yuanxin^,

School of Automation and Electrical Engineering, Shenyang Ligong University, Shenyang 110159

收稿日期: 2021-10-20 修回日期: 2022-03-1

基金资助:

*国家自然科学基金. 51377110
辽宁省科学技术基金. 20170540774

Received: 2021-10-20 Revised: 2022-03-1

作者简介 About authors

鲁军,男,1965年生,博士,教授。主要研究方向为智能材料与智能控制系统。E-mail： lujunst@126.com

季宝爽,男,1997年生,硕士研究生。主要研究方向为检测技术与自动化装置。E-mail： 2508869312@qq.com

贾士杰,男,1995年生,硕士研究生。主要研究方向为检测技术与自动化装置。E-mail： 1109496413@qq.com

张源鑫,男,1996年生,硕士研究生。主要研究方向为检测技术与自动化装置。E-mail： 361630797@qq.com

摘要

磁控形状记忆合金(Magnetically controlled shape memory alloy,MSMA)是一种新型功能材料,利用其可逆特性研制的自感知执行器,可实现机械力与电磁信号的双向转换。基于理论分析及有限元软件Ansoft Maxwell,以增加气隙磁密,减少励磁功率和磁路漏磁为优化目标,开展了MSMA自感知执行器的气隙宽度、铁心结构、材料等结构参数的优化设计及仿真研究。优化设计后的自感知执行器结构合理,磁场分布均匀,励磁功率显著减小。试验结果表明,自感知执行器输出的感应电压幅值与信号稳定性均得到提高,验证了自感知执行器结构优化设计的正确性与合理性。

关键词： MSMA ; 自感知执行器 ; 优化设计 ; 结构仿真

Abstract

Magnetically controlled shape memory alloy(MSMA) is a new kind of functional material. A self-sensing actuator developed by using its reversible property can realize bidirectional conversion between mechanical force and electromagnetic signal. Based on theoretical analysis and finite element software Ansoft Maxwell, in order to increase the air gap flux density, reduce the excitation power and magnetic circuit leakage as the optimization objectives, the air gap width, core structure, MSMA material selection and other aspects of the optimization design and simulation are studied. The self-sensing actuator with optimized design has more reasonable structure, more uniform magnetic field distribution and better overall performance. The experimental results show that the induced voltage amplitude and signal stability of the self-sensing actuator are improved, which verifies the correctness and rationality of the structure optimization design of the self-sensing actuator.

Keywords： MSMA ; self-sensing actuator ; optimization design ; structure of the simulation

PDF (367KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

鲁军, 季宝爽, 贾士杰, 张源鑫. MSMA自感知执行器结构优化设计^*. 电气工程学报[J], 2022, 17(2): 251-256 doi:10.11985/2022.02.029

LU Jun, JI Baoshuang, JIA Shijie, ZHANG Yuanxin. Structural Optimization Design of Self-sensing Actuator Based on MSMA. Chinese Journal of Electrical Engineering[J], 2022, 17(2): 251-256 doi:10.11985/2022.02.029

1 引言

磁控形状记忆合金是是一种新型的智能材料,兼具形变量大和反应快等特点,同时其可控性较好、能量密度较高、传感特性良好,因此被认为是研制控制器、微驱动器等的首选材料之一。现有文献中,MSMA的研究方向多集中在传感器、驱动器与振动能量采集^[1⇓⇓-4]等方面,且自感知执行器选用的材料多是压电材料和磁致伸缩材料^[5],MSMA自感知执行器研究较少,因此基于MSMA自感知执行器的优化设计等相关研究有较大的实用价值。

本文采用有限元分析软件和理论计算对自感知执行器进行仿真研究,通过磁路结构的设计及参数选取可有效减小励磁功率及放置MSMA材料处的气隙宽度,优化后的自感知执行器性能更加完善。该研究为开展MSMA材料在航空航天、机器人、医疗仪器等领域的应用奠定了技术基础。

2 MSMA自感知执行器优化设计

减小自感知执行器的气隙宽度可显著提高气隙磁通密度并降低励磁功率,铁心结构优化使磁路磁场分布更加均匀合理,MSMA元件处铁心楔形结构可获得良好的聚磁效果,MSMA及永磁材料的选取为设计磁路提供了可靠依据^[6]。

2.1 气隙尺寸及聚磁角度

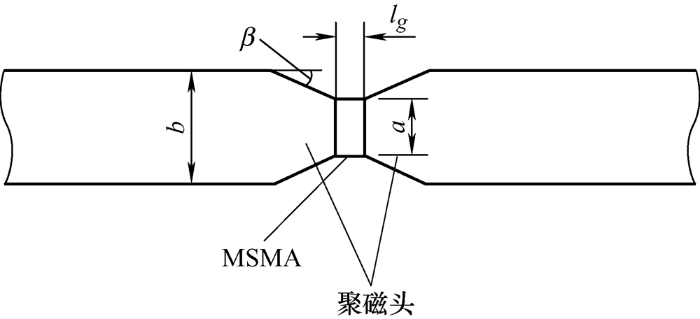
MSMA自感知执行器局部结构如图1所示。中间的气隙l_g即MSMA元件工作气隙,气隙两侧是硅钢片铁心。自感知执行器磁路结构中,气隙的减小会增加相同铁心结构的磁通密度,减小磁路的总磁阻并降低直流励磁功率。根据磁路欧姆定律

(1)$N I=\Phi R=B_{\delta} \frac{l_{\delta}}{\mu_{\delta} \mu_{0}}+B_{m} \frac{l_{m}}{\mu_{m} \mu_{0}}+B_{g} \frac{l_{g}}{\mu_{g} \mu_{0}}$

式中,Φ为磁路的磁通;R为磁路总磁阻;NI为励磁线圈的安匝数;B_δ、B_m、B_g分别为铁心材料、永磁体处、气隙处的磁通密度;l_δ、l_m、l_g为相应宽度;μ_δ、μ_m、μ_g分别为三者的相对磁导率;μ₀为真空磁导率。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 铁心局部结构图

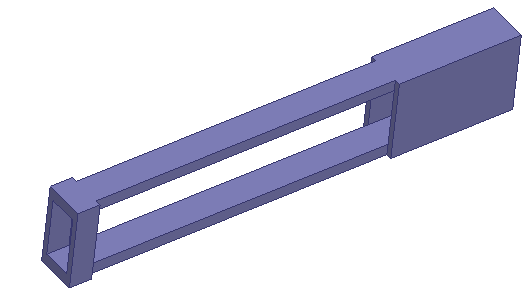
硅钢片铁心材料的磁导率远大于气隙磁导率,其磁阻可以忽略,由式(1)可知,励磁线圈的安匝数不变时,工作气隙宽度越小,气隙磁通密度就越大。合理设计保护MSMA元件的护套可有效减小气隙尺寸,其护套结构设计如图2所示。气隙由3.5 mm减至2.5 mm。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 MSMA护套结构图

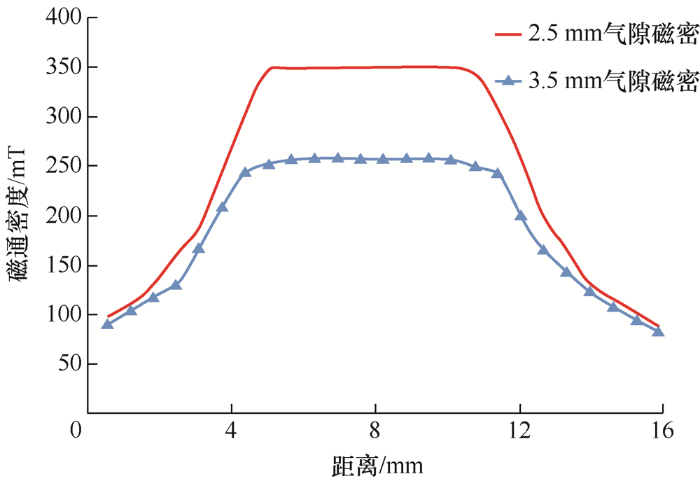
仅选用2块N45永磁体(1.3 mm×16 mm×25 mm)为MSMA元件单独励磁,沿图1气隙中部的垂线做剖面,不同气隙宽度的磁通密度对比如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 不同气隙宽度的磁密对比图

从图3中可以看出,当工作气隙为3.5 mm,气隙处平均磁通密度约为253 mT,当气隙宽度为2.5 mm时,磁通密度可达350 mT,相较于优化前提高了97 mT。

聚磁头斜度ω为^[7]

(2)$\ln \left(\frac{B_{0}}{B}\right)=-0.0297+0.02366 \omega\left(\frac{S}{S_{0}}\right)^{2}$

式中,B为无聚磁效应时的气隙磁通密度;B₀为聚磁后气隙中的磁通密度;S为铁心的横截面积;S₀为聚磁头最小的端面面积。

在励磁电流一定时,铁心聚磁对磁场分布及磁通密度有影响。由图1可得磁路结构聚磁头角度β为

(3)$\beta=\arctan \frac{5 \omega}{b-a}$

通过计算,磁路结构的聚磁头角度为35°时聚磁效果最好。

2.2 铁心结构优化

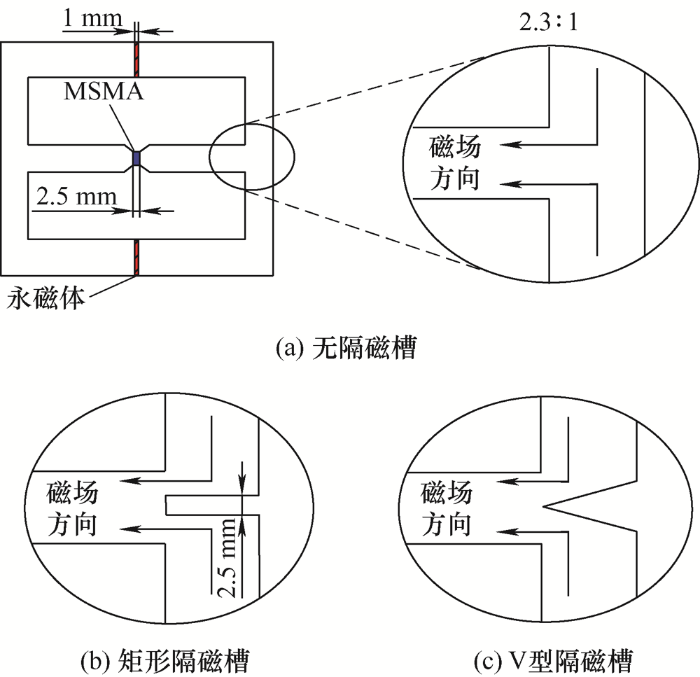
不同隔磁槽形状如图4所示。原自感知执行器结构中,上下磁回路在相交处磁场因方向相反而相互削弱,为了减小该影响,采用隔磁槽来解决该问题。在该处铁心加入空气槽,可增加磁阻,迫使磁通绕过隔磁槽,达到提高铁心磁密的目的^[8⇓-10]。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 隔磁槽方案比较

不同尺寸与形状的隔磁槽对磁通抑制效果是不同的,其他参数保持不变,分别对无隔磁槽、矩形隔磁槽和V型隔磁槽三种结构进行仿真。不同隔磁槽形状下的工作气隙磁密如表1所示。

表1 不同形状隔磁槽的气隙磁密

隔磁槽形状	无隔磁槽	矩形隔磁槽	V型隔磁槽
气隙磁密/mT	350.34	387.15	362.15

新窗口打开| 下载CSV

由表1可知,隔磁槽可减少一定的磁力线抵消,且矩形隔磁槽的隔磁效果最好。根据仿真结果,矩形隔磁槽宽度大于2.5 mm时,气隙磁密趋于稳定,不随隔磁槽宽度增加而增加。因此实际选择隔磁槽的宽度为2.5 mm。

结构优化后的自感知执行器的整体体积减少了20%,同时节省了铁心及永磁体材料。

2.3 材料选取

本文采用新型的磁控形状记忆合金材料,尺寸为2.5 mm×5 mm×25 mm,表2给出了新旧MSMA材料性能的比较。由于新型磁控形状记忆合金的响应速度更快、更利于控制,且相对磁导率较高,使用新型磁控形状记忆合金有利于提高MSMA自感知执行器的性能。

表2 新旧MSMA材料性能参数的比较

特性参数	MSMA	新型MSMA
响应时间/ms	1	0.5
相对磁导率	1.5~40	2~90
抗压强度/MPa	700	750
应变率(%)	6~9.5	6
电阻率/(×10^-8 Ω·m)	80	70
居里温度/℃	103	95

新窗口打开| 下载CSV

永磁体材料选用牌号为N52钕铁硼,材料剩磁B_r为1.43~1.46 T,矫顽力H_c为939 kA/m,最大磁能积(BH)_max为398~413 kJ/m³。

根据电磁第一定律,在回路中的任一节点流入的磁通量之和等于流出的磁通量之和

(4)$\left(\Phi_{m}+\Phi_{m}\right)-\Phi_{g}-\sum_{i=1}^{n} \Phi_{i}=0$

式中,Φ_m为永磁体处的磁通量;Φ_g为气隙处的磁通量;Φ_i为铁心漏磁通。

根据电磁第二定律,围绕封闭的回路一周,永磁体的磁压降等于回路中其他压降之和

(5)$\sum_{i=1}^{n} H_{i} L_{i}+\sum_{i=1}^{n} H_{\Delta i} L_{\Delta i}+H_{g} L_{g}-H_{m} L_{m}=0$

式中,H_iL_i为铁心磁路的压降;H_Δ_iL_Δ_i为磁路漏磁压降;H_gL_g为气隙处磁压降;H_mL_m为永磁体磁压降。

利用永磁体最佳工作点和式(4)、(5)可计算出永磁体宽度为1 mm,横截面积为325 mm²。

2.4 功率计算

MSMA材料在磁场为270~620 mT的范围内,其应变与磁通密度基本呈线性关系,因此励磁线圈需要提供350 mT的磁场方能满足试验要求。场强H约为

(6)$H=\frac{B}{\mu_{0} \mu_{r}}=\frac{0.35}{4 \pi \times 10^{-7} \times 1} \approx 278 \mathrm{kA} / \mathrm{m}$

气隙宽度L_g设为2.5 mm,永磁体宽度L_m为1 mm,永磁体磁导率与空气相同,可近似气隙,则

(7)$N I=H\left(L_{g}+L_{m}\right)$

由于2个永磁体为并联结构,经计算安匝数为835 A,考虑漏磁等影响,在保证试验要求前提下合理地增加线圈匝数,最终确定匝数为900^[11]。

漆包线的选择对电流与线圈的体积均有影响,需要合理选择其线径。漆包线的线径D为

(8)$D=2 \sqrt{\frac{I}{\pi J}}$

式中,电流I取0.8 A;电流密度J取值4 A/mm²,可以计算出励磁线圈的线径D=0.51 mm。

气隙处和永磁体处的磁阻R_m为

(9)$R_{m}=\frac{l}{\mu_{0} \mu_{r} A}$

式中,μ_r为相对磁导率;l为导磁长度;A为磁路材料导磁面积。根据磁路结构,表3给出了优化前后各处磁阻的计算值。优化设计后的结构有较小的磁阻。

表3 结构优化前后磁阻值的比较

磁阻	优化前	优化后
气隙磁阻/(×10⁷ H^-1)	2.23	1.59
永磁体磁阻/(×10⁶ H^-1)	1.30	1.20
总磁阻/(×10⁷ H^-1)	2.36	1.70

新窗口打开| 下载CSV

假设优化前后的结构中产生相同的磁通Φ₀,线圈匝数均为N,优化前、后的励磁线圈电流分别为I_a、I_b。优化前后的磁路总磁阻分别为R_a、R_b,则

(10)$\begin{array}{l}N I_{a}=\Phi_{0} R_{a} \\N I_{b}=\Phi_{0} R_{b}\end{array}$

由于线圈匝数设为相同,线圈电阻R相同,优化前后的励磁功率分别为P_a、P_b,根据P=I²R,功率之比为

(11)$\frac{P_{b}}{P_{a}}=\frac{I_{b}^{2}}{I_{a}^{2}}=\frac{R_{b}^{2}}{R_{a}^{2}} \approx 52 \%$

计算可知,MSMA自感知执行器结构优化设计后的励磁功率比优化前减少48%。

3 MSMA自感知执行器有限元分析

Ansoft Maxwell可以为优化自感知执行器提供仿真环境^[12]。对电磁场的分析与研究是以麦克斯韦方程组为出发点,其积分形式为

(12)$\left\{\begin{array}{l}\oint_{L} \boldsymbol{H} \mathrm{d} \boldsymbol{l}=∯_{S}\left(\boldsymbol{J}+\frac{\partial \boldsymbol{D}}{\partial t}\right) \mathrm{d} \boldsymbol{S} \\\oint_{L} \boldsymbol{E} \mathrm{d} \boldsymbol{l}=-∯_{S}\left(\boldsymbol{J}+\frac{\partial \boldsymbol{B}}{\partial t}\right) \mathrm{d} \boldsymbol{S} \\∯_{S} \boldsymbol{D} \mathrm{d} \boldsymbol{S}=\iiint_{V} \rho \mathrm{d} V \\∯_{S} \boldsymbol{B} \mathrm{d} \boldsymbol{S}=0\end{array}\right.$

式中,D为电通密度; $\frac{\partial D}{\partial t}$为位移电流密度;E为电场强度;ρ为电荷密度;V为闭合曲面S所围成的体积区域。其中电流包括传导电流和位移电流。

对应的微分麦克斯韦方程组为

(13)$\left\{\begin{array}{l}\nabla \times \boldsymbol{H}=\boldsymbol{J}+\frac{\partial \boldsymbol{D}}{\partial t} \\\nabla \times \boldsymbol{E}=-\frac{\partial \boldsymbol{B}}{\partial t} \\\nabla \bullet \boldsymbol{B}=0 \\\nabla \bullet \boldsymbol{D}=\rho\end{array}\right.$

在电磁场计算时,通过定义两个量来把电场和磁场变量分离开来,分别形成独立的磁场或者电场的偏微分方程,以便数值求解。其中两个变量分别是矢量磁势A和标量电势Φ。定义矢量磁势A满足

(14)$\boldsymbol{B}=\nabla \times \boldsymbol{A}$

当利用静磁场求解器仿真求解时,由于静磁场区域中无自由电流和电荷,磁场与电场没有发生直接联系,根据麦克斯韦方程可得

(15)$\left\{\begin{array}{c}\nabla \times \boldsymbol{H}=\boldsymbol{J} \\\nabla \times \boldsymbol{B}=0\end{array}\right.$

将式(6)、(14)代入式(13)可得

(16)$\nabla^{2} \times \boldsymbol{A}=-\mu_{r} \mu_{0} \boldsymbol{J}$

由此静磁场问题转变为磁矢势方程的解,利用有限元法求得磁势的场分布值,经过分析和后处理,可得到静磁场的各种物理量。

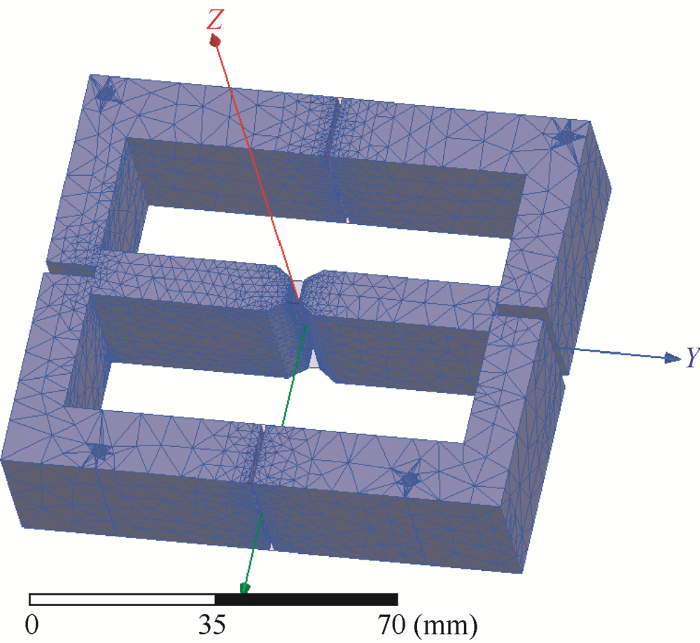
在理论分析的基础上,使用Ansoft Maxwell软件对磁路进行仿真分析^[13⇓-15]。自感知执行器的铁心网格剖分如图5所示。由图5可见,将每个剖分体记为一个计算单元,对于几何尺寸较规则的铁心部分,磁场变化较小,因此剖分单元较大,可设单元长度最大限值为10 mm,单元剖分数量最大限值为2 000;对于气隙和永磁体处,磁导率变化致使磁场的变化幅度较大,因此计算单元较小,可设单元长度最大限值2 mm,单元剖分数量最大限值50 000。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 铁心网格剖分图

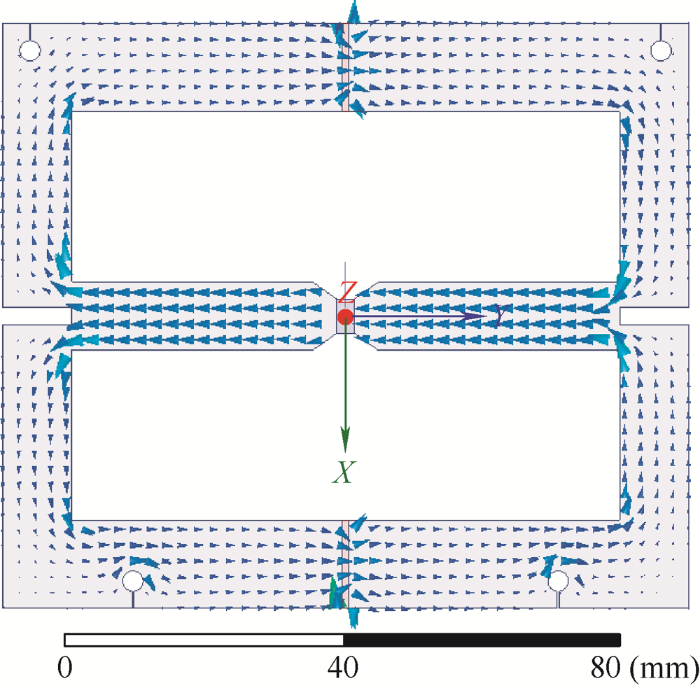
优化后的铁心磁场矢量分布的仿真结果如图6所示。其工作气隙宽度为2.5 mm,永磁体宽度为1 mm,励磁线圈的匝数为900。图6中可见,铁心中的磁力线在隔磁槽处抵消更少,分布更加合理。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 铁心磁场矢量分布剖面图

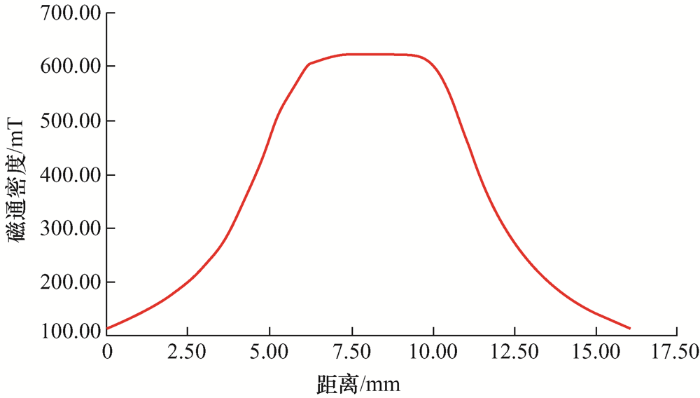
励磁线圈磁动势为900安匝时,放置MSMA元件气隙处的磁通密度剖面图如图7所示,从仿真结果图中可以看出,永磁体与励磁线圈共同励磁时气隙磁通密度可达620 mT。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 励磁线圈上电后气隙磁通密度剖面图

4 试验结果

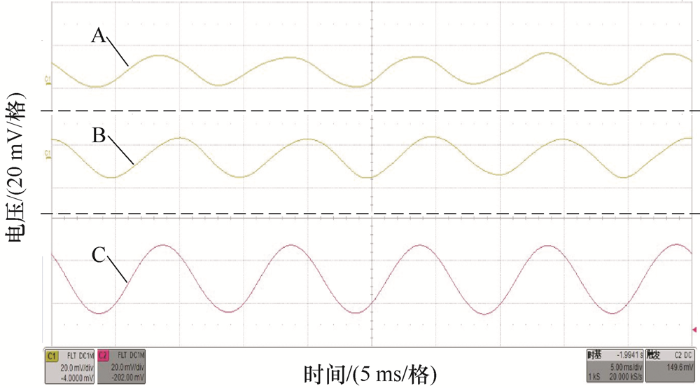
激振器施加频率为100 Hz,幅值为0.2 N的激振力,偏置磁场为300 mT,优化前后自感知执行器输出的感应电压如图8所示。其中波形A为结构优化前的MSMA自感知执行器输出的感应电压波形;波形B为其结构优化后的输出感应电压波形;波形C为采用新型MSMA材料的感应电压波形。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 感应电压输出对比图

通过观察波形A、B可知,MSMA自感知执行器结构优化后的感应电压幅值比优化前提高了27%,观察波形A、C可知,采用新型MSMA材料后输出的感应电压幅值提高了39%,且优化设计后输出的波形更加稳定,励磁功率较小,验证了自感知执行器优化设计的合理性。

根据试验可知,结构优化前后的永磁体均可提供250 mT左右的偏置磁场,但优化后的永磁体体积更小,永磁体磁阻更小,进而所需励磁功率减少。结构优化前后的励磁功率实测数据如表4所示。根据试验所需,励磁线圈励磁时需要使气隙处的磁场达到620 mT。此时通过对励磁电流及线圈电阻的测量,可得优化后的励磁功率减少了47%,试验表明理论计算值与试验值吻合。

表4 结构优化前后励磁功率比较

结构	气隙磁密/ mT	励磁电流/A	线圈电阻/Ω	励磁功率/W
优化前	620	0.98	18.53	17.81
优化后	620	0.79	14.79	9.43

新窗口打开| 下载CSV

5 结论

根据电磁学理论和有限元仿真软件Ansoft Maxwell,分别对MSMA自感知执行器的气隙尺寸、磁路铁心的结构、聚磁头角度、MSMA材料的选取等进行了优化设计,并验证了MSMA自感知执行器结构优化设计的正确性与合理性。

(1) 优化后气隙磁密显著提高,有效地减少了磁路漏磁。

(2) 优化后试验所需励磁功率减少了47%。

(3) 试验结果表明优化后的自感知执行器输出的感应电压幅值提高了39%,且波形更加完善。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

鲁军, 李敏, 王凤翔.

基于MSMA逆特性的振动传感器理论及实验

[J]. 电工技术学报, 2014, 29(5):233-238.