基于GRU神经网络的WGAN短期负荷预测模型*

doi:10.11985/2022.02.019

基于GRU神经网络的WGAN短期负荷预测模型^*

高翱^,¹, 王帅², 韩兴臣², 张智晟^,¹

1.青岛大学电气工程学院青岛 266071

2.国网山东省电力公司青岛供电公司青岛 266001

Short-term Load Forecasting Model of WGAN Based on GRU Neural Network

GAO Ao^,¹, WANG Shuai², HAN Xingchen², ZHANG Zhisheng^,¹

1. College of Electrical Engineering, Qingdao University, Qingdao 266071

2. Qingdao Power Supply Company, State Grid Shandong Electric Power Company, Qingdao 266001

通讯作者: 张智晟,男,1975年生,博士,教授,博士研究生导师。主要研究方向为电力系统短期负荷预测和经济调度。E-mail：slnzzs@126.com

收稿日期: 2021-05-15 修回日期: 2021-09-3

基金资助:

*国家自然科学基金资助项目. 52077108

Received: 2021-05-15 Revised: 2021-09-3

作者简介 About authors

高翱,男,1995年生,硕士研究生。主要研究方向为电力系统短期负荷预测。E-mail： 1061904751@qq.com

摘要

为了提高短期负荷预测模型的精度,提出了一种基于门控循环单元(Gated recurrent unit,GRU)神经网络的Wasserstein生成对抗网络(Wasserstein generative adversarial network,WGAN)短期负荷预测模型。将Wasserstein距离作为生成对抗网络(Generative adversarial network,GAN)的损失函数,与传统GAN相比,可以解决其训练过程中存在的梯度消失、模式崩溃等问题。同时,其生成器和判别器模型采用GRU神经网络,用以解决循环神经网络中存在的梯度问题。通过与GRU神经网络模型、传统GAN模型、采用KL散度作为损失函数且生成器和判别器采用GRU的GAN模型进行对比试验,证明了所提出的新模型具有更好的预测精度和稳定性。

关键词： 短期负荷预测 ; 生成对抗网络 ; Wasserstein距离 ; GRU神经网络 ; 电力系统

Abstract

To improve the accuracy of short-term load forecasting, a short-term load forecasting model of WGAN based on GRU neural network is proposed. The Wasserstein distance is taken as the loss function of GAN, compared with the traditional GAN, it can solve the problems of gradient disappearance and mode collapse in the training process. At the same time, its generator and discriminator model uses GRU neural network to solve the gradient problem in recurrent neural network. Compared with GRU neural network model, traditional GAN model, and GAN model with KL divergence as loss function and GRU as generator and discriminator, it is proved that the new model has better prediction accuracy and stability.

Keywords： Short-term load forecasting ; GAN model ; Wasserstein distance ; GRU neural network ; power system

PDF (410KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

高翱, 王帅, 韩兴臣, 张智晟. 基于GRU神经网络的WGAN短期负荷预测模型^*. 电气工程学报[J], 2022, 17(2): 168-175 doi:10.11985/2022.02.019

GAO Ao, WANG Shuai, HAN Xingchen, ZHANG Zhisheng. Short-term Load Forecasting Model of WGAN Based on GRU Neural Network. Chinese Journal of Electrical Engineering[J], 2022, 17(2): 168-175 doi:10.11985/2022.02.019

1 引言

电力负荷受天气、日期等因素的影响,具有随机性和非线性特征^[1-2],负荷随时间的波动性较大,预测时可能存在误差值较大的现象。随着机器学习和深度学习的不断发展,神经网络、支持向量机、随机森林等方法都能够拟合负荷的特性^[3⇓-5],起到减小预测误差,保证短期负荷预测的精确性和稳定性的作用^[6-7]。

GAN是一种生成式神经网络,其模型由生成器和判别器组成。文献[8]和文献[9]提出了一种基于GRU神经网络的短期负荷预测模型,既提高了预测精度,也兼顾了时效性,但是单一模型结构难以继续提升其预测精度和稳定性。文献[10]提出了一种GAN和深层LSTM结合的短期负荷预测模型,其生成器和判别器模型采用对抗训练方式,有效提升了短期负荷预测的精度,但是GAN模型存在梯度消失和模式崩溃,模型训练较为困难。文献[11]采用Wasserstein距离取代KL散度及JS散度作为GAN的损失函数,有效解决了GAN模型训练中的问题,提高了模型的预测性能。

针对以上研究现状,本文提出了一种基于GRU神经网络的WGAN短期负荷预测模型。WGAN通过将Wasserstein距离作为模型的损失函数,可以解决常规GAN模型训练过程中的梯度消失和模式崩溃等问题。在WGAN模型中采用GRU神经网络可以解决循环神经网络中梯度消失和梯度爆炸的问题^[12-13]。以某地区的负荷数据作为仿真依据,验证了本文模型可有效提高短期负荷预测的精度。

2 基于GRU神经网络的Wasserstein生成对抗网络

2.1 生成对抗网络模型

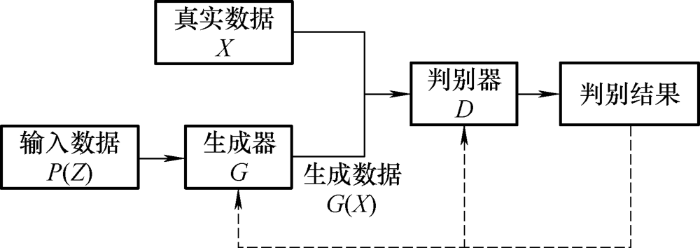
GAN由生成器和判别器组成,生成器用于生成符合真实数据分布的样本数据,判别器对输入的信息进行准确的判断与分类,若判断输入数据为真实数据,则输出为1;若判断输入数据为假数据,则输出为0^[14-15],生成对抗网络模型如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 生成对抗网络模型

GAN的训练分为两个阶段,先训练判别器再训练生成器^[16]。在训练的过程中,两个模型会不断更新自身的参数,使得各自的损失函数和输出误差最小化。

2.2 Wasserstein距离

传统GAN模型采用KL散度或JS散度作为模型的损失函数,存在梯度消失和模式崩溃,导致生成器的生成数据不理想^[17-18]。

Wasserstein距离的含义为两个分布之间的成本最小值^[19],公式如下所述

(1)$ \left\{\begin{array}{l}W\left(P_{r}, P_{g}\right)=\gamma \sim \Pi\left(P_{r}, P_{g}\right) \\E_{(x, y) \sim \gamma}\|x-y\|\end{array}\right.$

式中,P_r表示真实数据分布;P_g表示生成数据分布;W(P_r, P_g)表示P_r和P_g的Wasserstein距离;inf表示取下确界;$ \gamma \sim \prod\left(\begin{array}{ll}P_{r}, & P_{g}\end{array}\right)$为P_r和P_g联合分布的集合;γ代表其中的一个联合分布;x是真实数据,y是生成数据;(x, y)~γ表示(x, y)是来自γ的采样;||x-y||是x和y之间的Wasserstein距离;E_{(x, y) \sim \gamma}\|x-y\|为样本对距离的期望值。

与KL散度和JS散度相比,即使P_r、P_g两个分布之间没有交集,Wasserstein距离仍然可以反映出它们的远近,用公式表示为

(2)$ W\left(P_{r}, \quad P_{g}\right)=|\theta|$

(3)$ K L\left(P_{r} \| P_{g}\right)=\left\{\begin{array}{cc}+\infty & \theta \neq 0 \\0 & \theta=0\end{array}\right.$

(4)$ J S\left(P_{r} \| P_{g}\right)=\left\{\begin{array}{cc}\ln 2 & \theta \neq 0 \\0 & \theta=0\end{array}\right.$

由上述公式可知,当两个分布之间没有交集时,KL散度和JS散度是不连续且突变的。在梯度下降过程中,其导数为0的部分并不能提供梯度,导致生成器的梯度为0,出现梯度消失。而Wasserstein距离是连续可导的,在进行梯度更新时,不会出现梯度消失的现象。

由于直接求解Wasserstein距离的计算非常困难,所以采用其对偶形式。

(5)$ W\left(P_{r}, \quad P_{g}\right)=\frac{1}{K} \sup _{\|f\| L \leqslant K} E_{x \sim p_{r}}[f(x)]-E_{x \sim p_{g}}[f(x)]$

式中,$ \|f\| L \leqslant K$表示函数f(x)满足K-Lipschitz连续条件。

2.3 Wasserstein生成对抗网络

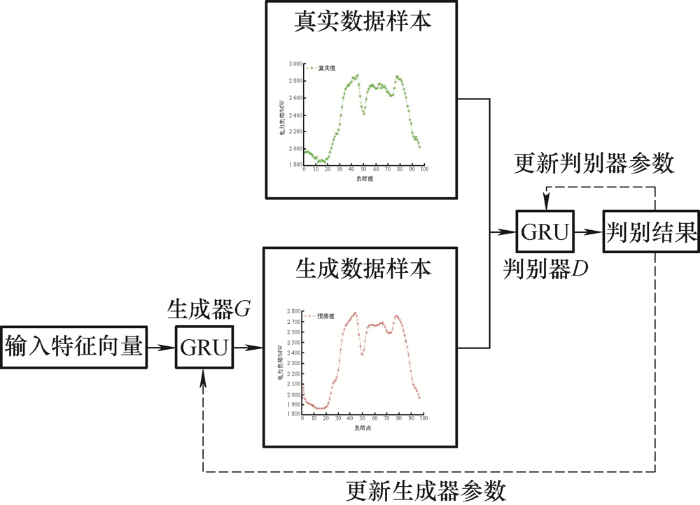
WGAN采用Wasserstein距离判别两个分布间的差距,当两个分布差距较大时,仍然能够保证生成器进行更新,解决了GAN中的训练问题,提升了生成器生成数据的质量,进一步提高了预测精度^[20-21]。本文所采用的WGAN模型如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 WGAN模型

与传统生成对抗网络模型相比,WGAN主要在以下方面进行了改进。

(1) 判别器输出层的sigmoid激活函数不再使用。

(2) 损失函数不再取对数。

(3) 将判别器梯度更新的数值控制在[-c, c] 之间。

(4) 采用随机梯度下降等非基于动量的算法。

WGAN模型中判别器的目标函数为最大化两个分布之间的Wasserstein距离,而生成器目标函数为最小化Wasserstein距离^[22],因而WGAN模型的目标函数可以描述为

(6)$ \begin{array}{l}W\left(P_{\text {data }}, P_{G}\right)=D \in 1-\text { Lipschitz } \\\left\{E_{x \sim p_{\text {data }}}[D(x)]-E_{x \sim P_{G}}[D(x)]\right\}\end{array}$

式中,P_data表示真实数据分布;P_G表示生成数据分布;D∈1-Lipschitz是指判别器要符合1-Lipschitz函数;D(x)表示判别器输出。

WGAN模型多采用全连接神经网络、循环神经网络及卷积神经网络模型,但是全连接神经网络没有考虑前一时刻的输出对当前时刻的影响;循环神经网络训练时难以收敛^[23]。本文生成器和判别器均采用GRU模型,有效解决了循环神经网络中存在的梯度问题。

2.3.1 生成器模型

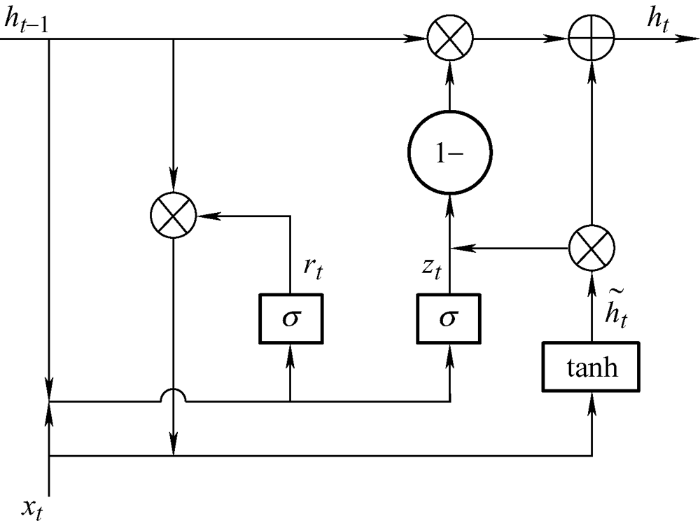
生成器训练的目标是使生成器生成与真实数据几乎一样的数据,本文采用的生成器模型为GRU神经网络,GRU神经网络优化了长短期记忆神经网络的模型结构,在解决循环神经网络训练问题的同时,加快了训练时的收敛速度^[24⇓-26]。其模型结构如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 GRU结构图

图3中x_t表示t时刻的输入;h_t_-₁表示t-1时刻的输出;z_t为更新门;r_t为重置门;$\tilde{h}_{t}$为t时刻隐含层的激活状态;h_t为t时刻的输出。

GRU可由如下公式描述

(7)$ z_{t}=\sigma\left(W_{z} x_{t}+U_{z} h_{t-1}\right)$

(8)$ r_{r}=\sigma\left(W_{r} x_{t}+U_{r} h_{t-1}\right)$

(9)$ \tilde{h}_{t}=\tanh \left(W x_{t}+U\left(r_{t} \odot h_{t-1}\right)\right)$

(10)$h_{t}=\left(1-z_{t}\right) \odot h_{t-1}+z_{t} \odot \tilde{h}_{t}$

(11)$y=\sigma\left(h_{t} W_{y}\right)$

式中,W_z、U_z、W_r、U_r、W、U、W_y为GRU神经网络的权值;y为神经网络的输出。

2.3.2 判别器模型

判别器在训练时,通过不断迭代训练来获取判别器最优权重。判别器训练的目标是使判别器能够准确判断生成数据为假数据。本文采用的判别器模型为GRU神经网络,取消了最后一层的sigmoid激活函数,使判别器的输出不再局限于0~1。本文中生成器和判别器模型的优化算法均采用随机梯度下降算法。

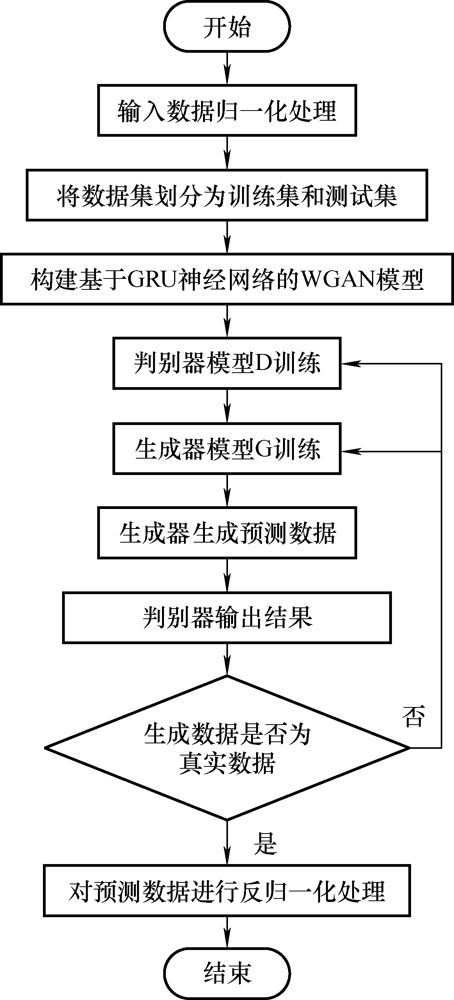
3 基于GRU神经网络的WGAN短期负荷预测模型

WGAN模型在训练时,先训练判别器,再训练生成器。训练的目标是最小化模型中的Wasserstein损失函数。

如要预测第d天的负荷数据,首先,固定生成器参数,将第d天的真实数据和生成数据作为输入,输入到判别器模型中,通过不断地迭代训练,来获取判别器的最优参数。

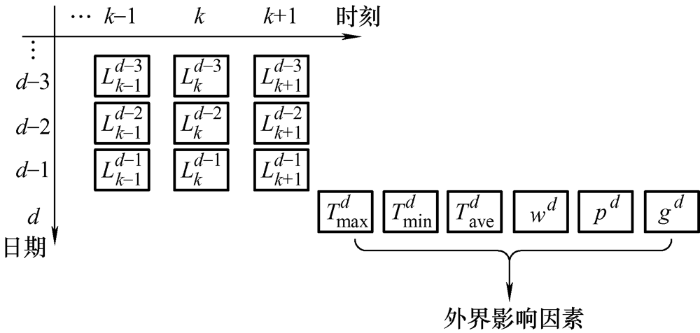
然后,将预测日前三天的t-1时刻、t时刻、t+1时刻的负荷数据(共9维),以及预测日当天的最低气温、最高气温、平均气温、天气因素、降水概率、日类型(共6维)作为生成器的输入向量,将输入向量输入到生成器中,生成器会预测出第d天t时刻的负荷数据。重复此过程便可以得到第d天96个点的负荷预测数据,以此作为生成器的生成数据。生成器的15维输入向量组成如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 生成器输入向量组成

图4中,d表示日期;k表示时间序号,1≤k≤96;L_k^d表示第d天k时刻的负荷;$T_{min}^{d}$、$T_{max}^{d}$、$T_{ave}^{d}$分别表示第d天的最低、最高和平均气温;w^d表示第d天的天气;p^d表示第d天的降水概率; g^d表示第d天的日类型。

其中天气因素的具体含义如下：定义雨、雪天气的影响因子为0,阴天、多云、雾天的天气影响因子为0.5,晴天的天气影响因子为1。日类型因素的具体含义如下：定义工作日的影响因子为1,休息日的影响因子为0.5。

最后,将生成器输出的生成数据和真实数据一起输入到训练好的判别器网络中。若判别器系统判定该组生成样本数据为假数据,将此结果反馈给生成器和判别器,用于指导WGAN模型的重新训练;若判定输入数据为真实数据,则终止训练,输出生成样本数据。

其中Wasserstein算法的程序实现方式如表1 所示。

表1 程序实现

输入	学习率α=0.1;权重裁剪参数c=0.01; 批量值m=64;n=5;w为判别器参数; θ为生成器参数
1	while θ do
2	for t=0,1,…,n do
3	样本$\left\{x^{(i)}\right\}_{i=1}^{m} \sim P_{r}$为真实数据
4	样本$\left\{g\left(z^{(i)}\right)\right\}_{i=1}^{m} \sim P_{g}$为生成数据
5	$\mathrm{d} w \leftarrow \nabla w\left[\frac{1}{m} \sum_{i=1}^{m} f_{w}\left(x^{(i)}\right)-\frac{1}{m} \sum_{i=1}^{m} f_{w}\left(g\left(z^{(i)}\right)\right)\right]$ 计算判别器梯度
6	w←w+a·dw判别器参数梯度更新
7	w←clip(w,-c,c) 将判别器参数梯度更新的数值控制在(-c, c)之间
8	end for
9	$\mathrm{d} \theta \leftarrow-\nabla \theta\left[\frac{1}{m} \sum_{i=1}^{m} f_{w}\left(g\left(z^{(i)}\right)\right)\right]$计算生成器梯度
10	θ←θ-dθ生成器参数梯度更新
11	end while

新窗口打开| 下载CSV

表1中,n的含义为WGAN模型采用交替训练方式,每训练5次判别器后,训练一次生成器。

预测模型流程图如图5所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 预测流程图

4 算例分析

为了使输入数据的量纲统一,消除指标之间的量纲影响,对输入数据采用归一化处理^[27-28]。

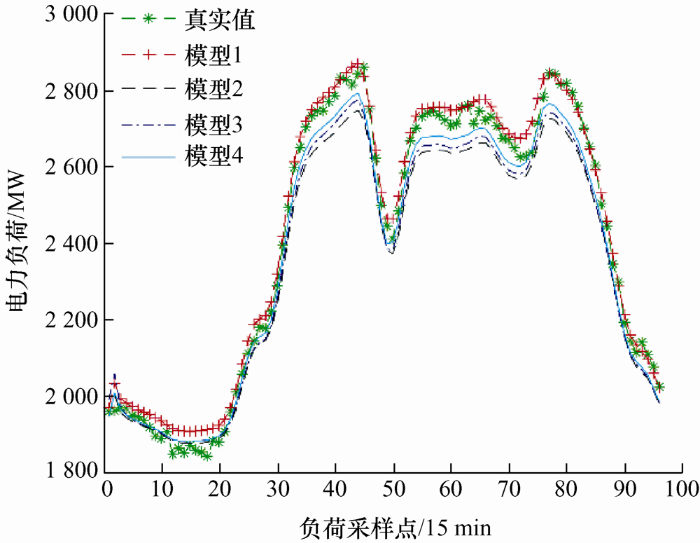
为了验证本文所提出的短期负荷预测模型的有效性,将本文所提出的模型(模型1)与常规GRU神经网络模型(模型2)、传统GAN模型(模型3)、损失函数采用KL散度,生成器和判别器采用GRU神经网络的GAN模型(模型4)进行对比研究分析。以某地区春季的电网负荷数据作为历史负荷,对春季某天的电力负荷进行预测。四种短期负荷预测模型的对比图如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 负荷预测对比图

本文将预测日前10天的电力负荷数据作为训练样本,每15 min取一个负荷点,故训练集共有960个负荷点。4种预测模型的输入向量均为图4所示的15维输入特征向量,在模型训练时,每个负荷点对应一组15维输入向量,故训练模型的历史数据样本容量为960×15维的矩阵。其中模型1和模型4的生成器和判别器的GRU隐含层神经元数目均取8,学习率均取0.1,最大迭代次数为8 000次,训练目标误差取0.000 55。模型2为单一GRU神经网络结构,只有GRU构成的生成器负责生成负荷数据,其损失函数采用KL散度,GRU隐含层神经元数目取8,学习率取0.09,最大迭代次数为5 000次,训练目标误差取0.001。模型3的生成器和判别器均采用全连接神经网络,损失函数采用KL散度,其生成器和判别器的隐含层神经元数目均取8,学习率取0.1,最大迭代次数取8 000次,训练目标误差取0.000 55。

待模型训练完成后,采用对未来多点预报的直接式对预测日的96个负荷点进行电力负荷预测。

采用平均绝对百分比误差E_MAPE、最大相对误差E_max和平均误差ME(也称方均根误差)作为评判模型预测性能优劣的依据。4种预测模型的预测性能如表2所示。由表2可知,模型3与模型2相比,E_MAPE下降了0.31%,E_max下降了1.09%,由此可知,GAN模型的预测性能优于GRU模型,可进一步提高预测精度。模型1与模型3相比,E_MAPE下降了0.69%,E_max下降了0.17%;与模型2相比,E_MAPE下降了1%,E_max下降了1.26%。模型1与模型4相比,E_MAPE下降了0.42%,E_max下降了0.15%,且其训练耗时减少了126s,由此可见,采用Wasserstein距离的GAN短期负荷预测模型可以加快训练的收敛速度,减少模型的训练时间,有效提高了短期负荷预测的精度。故基于GRU神经网络的WGAN模型,不但预测精度较好,而且其预测的日负荷全天误差波动较小,最大误差仅为3.7%。

表2 预测性能对比表

预测模型	E_MAPE(%)	E_max(%)	ME/MW	训练耗时/s
模型1	1.2	3.7	32.67	766
模型2	2.2	4.96	63.27	492
模型3	1.89	3.87	54.69	970
模型4	1.62	3.85	47.76	892

新窗口打开| 下载CSV

为了进一步验证基于GRU神经网络的WGAN模型的稳定性,对该地区春季季节的电网进行连续一周的负荷预测。预测结果如表3所示。

表3 春季季节连续一周预测误差表

星期	模型1
星期	E_MAPE(%)	E_max(%)	ME/MW
周一	1.87	4..03	53.46
周二	1.32	3.75	39.05
周三	1.28	3.76	37.04
周四	1.25	3.63	36.84
周五	1.23	3.74	35.73
周六	2.05	4.2	60.03
周天	2.0	4.17	58.05
平均值	1.57	3.90	45.74

新窗口打开| 下载CSV

由表3数据可知,其休息日误差略大于工作日误差,这是因为工作日的用电情况更加规律,其波动性和随机性较休息日较小。且本模型在春季季节连续一周的误差波动较小,连续一周的平均绝对百分比误差和最大相对误差的平均值为1.57%和3.90%。由此可见,基于GRU神经网络的WGAN的短期负荷预测模型具有较好的稳定性和预测性能,可进一步提高预测精度。

因为在我国大多数地区,影响电力负荷的天气因子在不同的季节是不同的。为了验证基于GRU神经网络的WGAN模型在不同季节的有效性和稳定性,对某地区夏季季节的电网进行了连续一周的负荷预测,预测结果如表4所示。

表4 夏季季节连续一周预测误差表

星期	模型1
星期	E_MAPE(%)	E_max(%)	ME/MW
周一	1.94	3.89	56.81
周二	1.43	3.29	41.29
周三	1.37	3.66	42.53
周四	1.12	3.79	30.16
周五	1.45	3.87	42.64
周六	2.0	4.35	58.67
周日	2.39	4.2	68.15
平均值	1.67	3.86	48.61

新窗口打开| 下载CSV

对比春季季节和夏季季节连续7天的负荷预测结果可知,本文所提出的短期负荷预测模型在某地区的春季和夏季均具有较好的预测性能和稳定性,能够处理天气因子的变化对短期负荷预测的影响。

5 结论

本文提出了一种基于GRU神经网络的WGAN短期负荷预测模型,结合实际算例,主要得到以下结论。

(1) GAN可以通过生成器和判别器的相互博弈训练生成与真实数据高度相似的预测数据样本,WGAN解决了GAN模型梯度消失、模式崩溃等问题。

(2) 其生成器和判别器采用的GRU神经网络模型不仅解决了循环神经网络中的梯度问题,而且可以加快模型的训练速度,从而进一步提升了模型的预测精度。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

郑睿程, 顾洁, 金之俭, 等.

数据驱动与预测误差驱动融合的短期负荷预测输入变量选择方法研究

[J]. 中国电机工程学报, 2020, 40(2):487-500.