电气工程学报, 2022, 17(1): 171-178 doi: 10.11985/2022.01.022

电力系统

基于ADMM的电-气综合能源系统分布式滚动优化调度*

孟丽娜,, 赵兴勇,, 郭珠珠, 王晋华

山西大学电力与建筑学院 太原 030013

Distributed Rolling Optimization Scheduling of Electric Gas Integrated Energy System Based on ADMM

MENG Lina,, ZHAO Xingyong,, GUO Zhuzhu, WANG Jinhua

College of Electric Power and Architecture, Shanxi University, Taiyuan 030013

通讯作者: 孟丽娜,女,1996年生,硕士研究生。主要研究方向为综合能源系统分析与优化运行、分布式能源。E-mail：2869046294@qq.com

收稿日期: 2021-05-7   修回日期: 2021-10-18  

基金资助: *国网山西省电力公司科技资助项目.  SGTYHT/18-JS-206

Received: 2021-05-7   Revised: 2021-10-18  

作者简介 About authors

赵兴勇,男,1965年生,博士,教授,硕士研究生导师。主要研究方向为分布式发电并网、智能电网、微电网等。E-mail： shzhxy@163.com

摘要

电-气综合能源系统优化调度是提高系统经济效益的重要手段,而其优化调度模型复杂、约束条件较多、求解困难,同时负荷及可再生能源预测值存在较大误差。针对这一问题,首先构建集中式优化调度模型,其次采用交替方向乘子算法(Alternative direction multiplier method,ADMM)将集中式优化调度模型转化为两个可以信息交互的子系统,同时将滚动优化方法引入到算法之中,构建分布式滚动优化调度模型。最后通过算例验证了所提方法的可行性及有效性,一定程度上减小了预测误差对系统的影响;对比三种优化模型下系统运行成本,证明分布式滚动优化模型算法收敛性好的同时具有一定的经济效益。

关键词： 电-气综合能源系统 ; 优化调度 ; 集中式优化 ; ADMM ; 分布式滚动优化

Abstract

The optimal dispatch of electricity gas integrated energy system is an important means to improve the economic benefits of the system. However, its optimal dispatch model is complex, with many constraints and difficult to solve. At the same time, there are large errors in the load and renewable energy forecast values. In order to solve this problem, firstly, a centralized optimal scheduling model is constructed. Secondly, ADMM is used to transform the centralized optimal scheduling model into two subsystems that can interact with each other. At the same time, rolling optimization method is introduced into the algorithm to build a distributed rolling optimal scheduling model. Finally, an example is given to verify the feasibility and effectiveness of the proposed method, which reduces the impact of prediction error on the system to a certain extent. By comparing the system operation cost of three optimization models, it shows that the distributed rolling optimization model has good convergence and certain economic benefits.

Keywords： Electricity gas integrated energy system ; optimal scheduling ; centralized optimization ; ADMM ; distributed rolling optimization

PDF (466KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

孟丽娜, 赵兴勇, 郭珠珠, 王晋华. 基于ADMM的电-气综合能源系统分布式滚动优化调度*. 电气工程学报[J], 2022, 17(1): 171-178 doi:10.11985/2022.01.022

MENG Lina, ZHAO Xingyong, GUO Zhuzhu, WANG Jinhua. Distributed Rolling Optimization Scheduling of Electric Gas Integrated Energy System Based on ADMM. Chinese Journal of Electrical Engineering[J], 2022, 17(1): 171-178 doi:10.11985/2022.01.022

1 引言

燃气轮机与电转气技术的发展使得对电、气系统之间进行统一的规划与调度成为了关注焦点[1]。这不但有助于提高电-气互联系统经济效益,提高能源利用率,而且可以缓解系统负荷高峰[2⇓⇓-5]。如果仍以传统的电网与天然气网独立运行模式考虑,将无法保证调度方案经济性及稳定性。

目前关于电-气互联综合能源系统的研究多在建模、优化算法以及规划调度等方面[6⇓-8]。由于电-气互联系统内设备众多、建模复杂、约束条件较多,集中式优化调度模型均为大规模非线性优化问题。同时多时间尺度调度使得模型求解更加复杂,容易出现求解时间长、目标函数不稳定、求解困难等问题、为解决这些问题,适应用于大规模分布式计算和优化问题的交替方向乘子算法(Alternative direction multiplier method,ADMM)获得广泛关注。ADMM算法具有收敛性好、形式简单等优点,更适合应用于电-气互联系统。文献[9-10]采用ADMM分别将电源与电网协同规划框架转换为电源规划决策子问题与电网规划决策子问题,将多个含分布式电源互联微电网转换为独立微电网交互求解,实现了电源与网架分布式协同规划,微电网间分布式优化调度。文献[11]针对电力流与天然气流采用ADMM实现其分布式协同优化。另外,制定调度计划过程中,负荷及风电场等日前预测值会因随机波动,与真实值之间出现偏差。文献[12⇓-14]提出了基于模型预测控制的综合能源系统多时间尺度协调优化调度及动态优化调度。调度结果均基于预测值优化,负荷预测信息可由多种方法得出。文献[15]提出了一种考虑天然气系统优化运行的电力-天然气综合能源系统双层优化调度模型。文献[16]提出了分阶梯加速惩罚因子交替方向乘子法的模型分布式协同求解机制。但是仍未综合考虑关于解决决策变量过多、模型复杂以及预测信息不确定性的问题。

为此,本文提出了基于ADMM的电-气综合能源系统分布式滚动优化调度模型。以预测值下系统运行成本最小为目标函数建立集中式优化调度模型,利用ADMM将集中式优化调度模型转换为分布式调度模型求解。同时将滚动优化引入算法,根据电负荷、气负荷以及风电场等的实时预测值对其日前预测值进行不断调整。最后通过算例说明所提算法的可行性及经济性,两系统之间实现了协同运行。

2 电-气互联综合能源系统建模

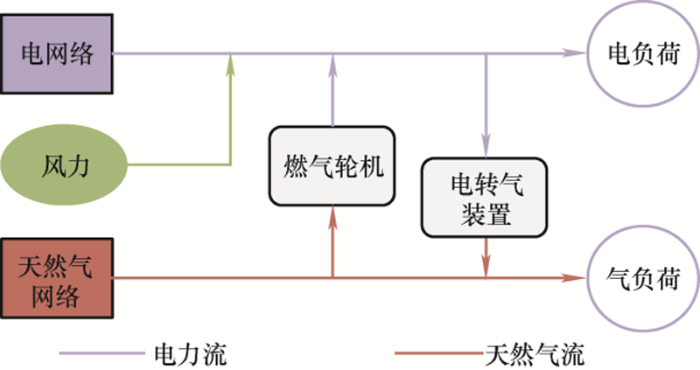
电-气互联系统的结构如图1所示。考虑电网和天然气网两种能源网络,风电场作为可再生能源发电机组接入网络中。通过燃气轮机与电转气装置进行耦合,提高能源利用率以及系统安全可靠性。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   电-气互联系统结构图


2.1 电力系统建模

电力系统模型常以交流潮流分析,包括有功功率和无功功率,存在大量非线性关系,求解复杂。这里建立了线性化最优潮流电网模型,不考虑电网的无功功率和电压,采用直流潮流对电-气互联系统中的电力系统建模。

${{P}_{ij}}=\frac{{{\theta }_{i}}-{{\theta }_{j}}}{{{X}_{ij}}}$

式中,θi、θj分别为i、j节点的相角;Χij为i、j节点之间线路的阻抗;Pij为从i节点流向j节点的功率。

2.2 天然气系统建模

考虑较小时间尺度天然气管道内的压力不随外界因素变化,始终处于稳定状态,管道端任意时刻都满足理想状态下的能量守恒定律。

(1) 天然气管道气流稳态模型

${{f}_{mn}}={{x}_{mn}}{{\delta }_{mn}}\sqrt{{{\delta }_{mn}}\left( \text{ }\!\!\pi\!\!\text{ }_{m}^{2}-\text{ }\!\!\pi\!\!\text{ }_{n}^{2} \right)}$
${{\delta }_{mn}}=\left\{ \begin{align} & 1\ \ \ \ \ \ {{\text{ }\!\!\pi\!\!\text{ }}_{m}}\ge {{\text{ }\!\!\pi\!\!\text{ }}_{n}} \\ & -1\ \ \ \ {{\text{ }\!\!\pi\!\!\text{ }}_{m}}<{{\text{ }\!\!\pi\!\!\text{ }}_{n}} \\ \end{align} \right.$

式中,fmn为管道从节点m到节点n的天然气流量;xmn为管道的传输系数,与管道长度、内径、压力等因素有关;δmn反映了管道内天然气的流动方向;πm、πn分别为管网节点m、n的节点气压。

(2) 天然气管存的稳态模型

$V=\nu \frac{{{T}_{0}}}{{{X}_{0}}}\left( \frac{{{X}_{2}}}{{{Z}_{2}}{{T}_{2}}}-\frac{{{X}_{1}}}{{{Z}_{1}}{{T}_{1}}} \right)$

式中,V为管道末端的储气量;T0为天然气基准状态温度;X0表示天然气基准状态压力;T1、T2分别表示储气前后的天然气平均温度;X1、X2分别表示储气前后的平均压力;Z1、Z2分别表示在X1、X2压力下的压缩因子。

(3) 压缩机的稳态模型

${{f}_{W}}={{f}_{k}}K\left( {{\text{ }\!\!\pi\!\!\text{ }}_{in}}-{{\text{ }\!\!\pi\!\!\text{ }}_{out}} \right)$

式中,fW为压缩机运行消耗的天然气流量;fk为压缩机流入的天然气流量;K为压缩机常数;πin、πout分别为管道输入端与输出端的气压。

2.3 燃气轮机建模

燃气轮机是将天然气转换为电力的能源重要转换装置,为表征其能源转换关系,建立如下模型

${{f}_{GT}}=\alpha +\beta {{P}_{t}}+\nu {{P}_{t}}^{2}$

式中,fGT为燃气轮机消耗的燃气流量;Pt为燃气轮机输出功率;α、β、ν分别为燃气轮机的能耗系数。

2.4 电转气装置建模

电转气装置是将电能通过电解水制成氢气,然后再制造甲烷的过程。它的电能输入可以由电网、风电、燃气轮机等发电装置来提供,调度比较灵活。为表征其能源转换关系,建立如下模型

${{f}_{P\text{2}G}}=\frac{{{P}_{P\text{2}G}}{{\eta }_{P\text{2}G}}}{{{H}_{G}}}$

式中,fP2G为电转气装置输出的天然气流量;PP2G为电转气装置消耗的电功率;${{\eta }_{P\text{2}G}}$为能量转换效率;HG为天然气热值。

3 电-气综合能源系统集中式优化调度模型

3.1 目标函数

从经济角度出发,以预测值下满足系统调度周期内运行成本最小为目标函数。系统调度周期内运行成本包括24 h内电力系统的出力总成本和天然气系统气源产气总成本。

$\begin{matrix} F=\text{min}\left( {{C}_{\text{PF}}}+{{C}_{\text{GF}}} \right)= \\ \min (\sum\limits_{t=1}^{24}{\sum\limits_{i=1}^{n}{\left( {{C}_{Ai}}P_{Gi}^{2}\left( t \right)+{{C}_{Bi}}{{P}_{Gi}}\left( t \right)+{{C}_{Ci}} \right)}}+ \\ \sum\limits_{t=1}^{24}{\sum\limits_{i=1}^{n}{\left( \left. {{C}_{Gi}}{{f}_{Gi}}\left( t \right) \right) \right)}} \\ \end{matrix}$

式中,CPF为电力系统出力总运行成本;CGF为天然气系统气源产气总成本;CAi、CBi、CCi为电力网络中第i台燃煤机组价格参数;PGi(t)为任意时刻第i台燃煤机组出力;CGi为天然气网络中第i个气源价格参数;fGi(t)为任意时刻第i个气源 流量。

3.2 电力系统约束条件

(1) 电力系统功率平衡约束

$\sum\limits_{i=1}^{n}{{{P}_{Gi,t}}}+\sum\limits_{i=1}^{n}{{{P}_{GTi,t}}+\sum\limits_{i=1}^{n}{{{P}_{WTi,t}}=\sum\limits_{i=1}^{n}{{{P}_{P\text{2}Gi,t}}+\sum\limits_{i=1}^{n}{{{P}_{Li,t}}}}}}$

式中,PG、PGT、PWTi分别为燃煤机组出力、燃气轮机出力及风电场出力;PP2G、PL分别为电转气装置耗电量及电负荷。

(2) 燃煤机组、风电场、燃气轮机出力及电转气装置出力约束

$\left\{ \begin{align} & P_{Gi}^{\min }\le {{P}_{Gi,t}}\le P_{Gi}^{\max } \\ & \text{0}\le {{P}_{WTi,t}}\le P_{WTi}^{\max } \\ & P_{GTi}^{\min }\le {{P}_{GTi,t}}\le P_{GTi}^{\max } \\ & \text{0}\le {{P}_{P\text{2}Gi,t}}\le P_{P\text{2}Gi}^{\max } \\ \end{align} \right.$ `

(3) 系统电网直流潮流变量的约束。任一电网节点之间的潮流变量不超过线路最大传输功率值,同时节点电压相位角处于其上下限之间

$\left| {{P}_{ij}} \right|\le {{P}_{F\max }}$
${{\theta }_{\min }}\le {{\theta }_{i,j}}\le {{\theta }_{\max }}$

(4) 机组正负旋转备用出力约束

$\left\{ \begin{align} & \sum\limits_{i=1}^{n}{{{P}_{Gup,i,t}}\ge {{P}_{BAKup,t}}} \\ & \sum\limits_{i=1}^{n}{{{P}_{Gdw\text{,}i,t}}}\ge {{P}_{BAKdw,t}} \\ \end{align} \right.$

式中,PGup,i,t、PGdw,i,t分别为t时刻第i台发电机组正,负旋转备用出力;PBAKup,t、PBAKdw,t分别为t时刻系统所需正、负旋转备用出力。

3.3 天然气网络约束条件

(1) 天然气系统流量平衡约束

${{f}_{G,m,t}}+{{f}_{P2G,m,t}}={{f}_{GT,m,t}}+{{f}_{L,m,t}}$

式中,fG,m,t、fP2G,m,t分别为t时刻m节点气源流量及电转气装置产气量;fGT,m,t、fL,m,t分别为t时刻m节点燃气轮机耗气量以及气负荷流量。

(2) 节点气压及气源流量约束

$\text{ }\!\!\pi\!\!\text{ }_{m}^{\min }\le {{\text{ }\!\!\pi\!\!\text{ }}_{m}}\le \text{ }\!\!\pi\!\!\text{ }_{m}^{\max }$
$f_{Gi}^{\min }\le {{f}_{Gi,t}}\le f_{Gi}^{\max }$

式中,$\pi _{m}^{\max }\pi _{m}^{\min }$为节点气压上下限;$f_{Gi}^{\max }$、$f_{Gi}^{\min }$为第i个气源流量上下限。

(3) 备用容量约束

$\left\{ \begin{align} & \sum\limits_{i=1}^{n}{\left( f_{Gi,t}^{\max }-{{f}_{Gi,t}} \right)\ge {{f}_{BAKup,t}}} \\ & \sum\limits_{i=1}^{n}{\left( {{f}_{Gi,t}}-f_{Gi,t}^{\min } \right)\ge {{f}_{BAKdw,t}}} \\ \end{align} \right.$

4 基于ADMM的电-气综合能源系统分布式滚动优化调度模型及求解

综合能源优化调度研究通常采用集中式优化调度方法,由于模型涉及的决策变量、约束条件较多,这里采用ADMM将集中式模型分解为电力和天然气两个优化子问题,通过耦合元件作为共享变量来实现信息交互并交替迭代求解,同时为了提高调度的准确性将动态滚动优化引起其中,实现协同优化。

4.1 ADMM算法基本原理

ADMM算法具有收敛性好、形式简单等优点,近年来广泛应用于分布式数学优化问题。其优化问题可以统一描述为

$\left\{ \begin{align} & \min f\left( x \right)+g\left( y \right) \\ & \text{s}\text{.t}\text{. }Ax+By=C \\ \end{align} \right.$

式中,f(x)和g(y)为两个优化子问题;A、B、C为变量的约束矩阵。

将耦合约束加入目标函数中,引入新的变量构造出扩增的拉格朗日函数

$\begin{matrix} L\left( x,y,z \right)=f\left( x \right)+g\left( y \right)+z\left( Ax+By-C \right)+ \\ \left( \rho /2 \right)\left\| Ax+By-C \right\|_{2}^{2} \\ \end{matrix}$

式中,z为拉格朗日乘子向量;$\rho $为常数惩罚因子;‖•‖为范数算子。

将原问题中的变量进行拆分,得到迭代子问题函数。任意时刻只有一个子问题处于计算状态,通过交叉换方向来交替优化求解。迭代方程为

$\left\{ \begin{align} & {{x}^{k+1}}=\arg \min L\left( x,{{y}^{k}},{{z}^{k}} \right) \\ & {{y}^{k+1}}=\arg \min L\left( {{x}^{k+1}},y,{{z}^{k}} \right) \\ & {{z}^{k+1}}={{z}^{k}}+\rho \left( A{{x}^{k+1}}+B{{y}^{k+1}}-C \right) \\ \end{align} \right.$

迭代过程中需要通过原始残差和对偶残差来判断算法收敛,则ADMM停止准则为

$\left\| {{r}^{k+1}} \right\|_{2}^{2}\text{=}\left\| A{{x}^{k+1}}+B{{y}^{k+1}}-C \right\|_{2}^{2}\le {{\varepsilon }_{\text{pri}}}$
$\left\| {{s}^{k+1}} \right\|_{2}^{2}=\left\| \rho {{A}^{T}}B\left( {{z}^{k+1}}-{{z}^{k}} \right) \right\|_{\text{2}}^{\text{2}}\le {{\varepsilon }_{\text{dual}}}$

式中,rk+1、sk+1分别为第k+1次迭代计算后的原始残差和对偶残差。

4.2 优化子问题的模型建立

将基于燃气轮机的耦合关系式作为共享变量代入集中式优化调度模型目标函数中得到增广拉格朗日函数,从而将原来的集中式优化模型拆分为两个优化子问题。式(23)为电力系统优化子问题的目标函数,式(24)为天然气网络优化子问题的目标函数。

$\min {{C}_{PF}}+{{\left( {{Z}^{\left( k-1 \right)}} \right)}^{T}}\left( \alpha +\beta {{P}^{\left( k \right)}}_{GT}+\nu {{P}^{2\left( k \right)}}_{GT}-{{f}^{\left( k-1 \right)}}_{GT} \right)+\frac{\rho }{2}\left\| \alpha +\beta {{P}^{\left( k \right)}}_{GT}+\nu {{P}^{2\left( k \right)}}_{GT}-{{f}^{\left( k-1 \right)}}_{GT} \right\|_{2}^{2}$
$\min {{C}_{GF}}+{{\left( {{Z}^{\left( k-1 \right)}} \right)}^{T}}\left( {{f}^{\left( k \right)}}_{GT}-\alpha -\beta {{P}^{\left( k-1 \right)}}_{GT}-\nu {{P}^{2\left( k-1 \right)}}_{GT} \right)+\frac{\rho }{2}\left\| {{f}^{\left( k \right)}}_{GT}-\alpha -\beta {{P}^{\left( k-1 \right)}}_{GT}-\nu {{P}^{2\left( k-1 \right)}}_{GT} \right\|_{2}^{2}$

两个子优化问题需要满足的约束条件与集中式优化调度模型中两系统约束条件相同,此外还需要考虑电转气装置约束。

在对两个优化子问题调度模型的求解过程中,随迭代次数的增加,目标函数及乘子系数不断收敛,其中乘子系数更新表达式见式(25)。原始残差和对偶残差最终均需要小于容忍上限,见式(26)、式(27),则迭代完成。

${{Z}^{\left( k \right)}}={{Z}^{\left( k-\text{1} \right)}}+\rho \left( {{f}^{\left( k \right)}}_{GT}-\alpha -\beta {{P}^{\left( k \right)}}_{GT}-\nu {{P}^{2\left( k \right)}}_{GT} \right)$
$\left\| {{r}^{\left( k \right)}} \right\|_{2}^{2}\text{=}\left\| {{f}^{\left( k \right)}}_{GT}-\alpha -\beta {{P}^{\left( k \right)}}_{GT}-\nu {{P}^{2\left( k \right)}}_{GT} \right\|_{2}^{2}\le {{\varepsilon }_{pri}}$
$\begin{align} & \left\| {{s}^{\left( k \right)}} \right\|_{2}^{2}=\left\| \rho \left[ {{f}^{\left( k \right)}}_{GT}\left( \alpha \text{+}\beta {{P}^{\left( k \right)}}_{GT}\text{+}\nu {{P}^{2\left( k \right)}}_{GT} \right) \right. \right.- \\ & \left. \left. {{f}^{\left( k-\text{1} \right)}}_{GT}\left( \alpha \text{+}\beta {{P}^{\left( k-\text{1} \right)}}_{GT}\text{+}\nu {{P}^{2\left( k-\text{1} \right)}}_{GT} \right) \right] \right\|_{\text{2}}^{\text{2}}\le {{\varepsilon }_{dual}} \\ \end{align}$

4.3 动态滚动优化

由于预测时间尺度较长,日前预测数据随外界因素变化出现较大误差,无法满足系统实际需求,这里采用动态滚动优化方法来使得预测精度更高。

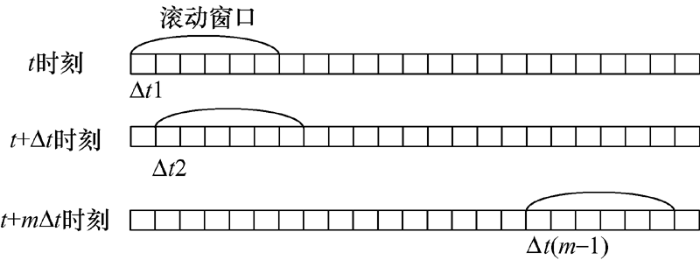
动态滚动优化模型时间窗口如图2所示。t时刻,对滚动时间窗口内预测数据采用ADMM算法求最优解,并只在Δt1内执行该方案。同时将该时刻实时预测数据反馈到日前预测数据模块来修正相关数据。t+Δt时刻,滚动窗口向前移动1个时间间隔Δt,执行此时滚动时间窗口内优化求解,同样在第1个时间间隔Δt2内执行该方案。重复滚动直至完成所有调度。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   动态滚动优化模型时间窗口


4.4 分布式滚动优化调度模型求解流程

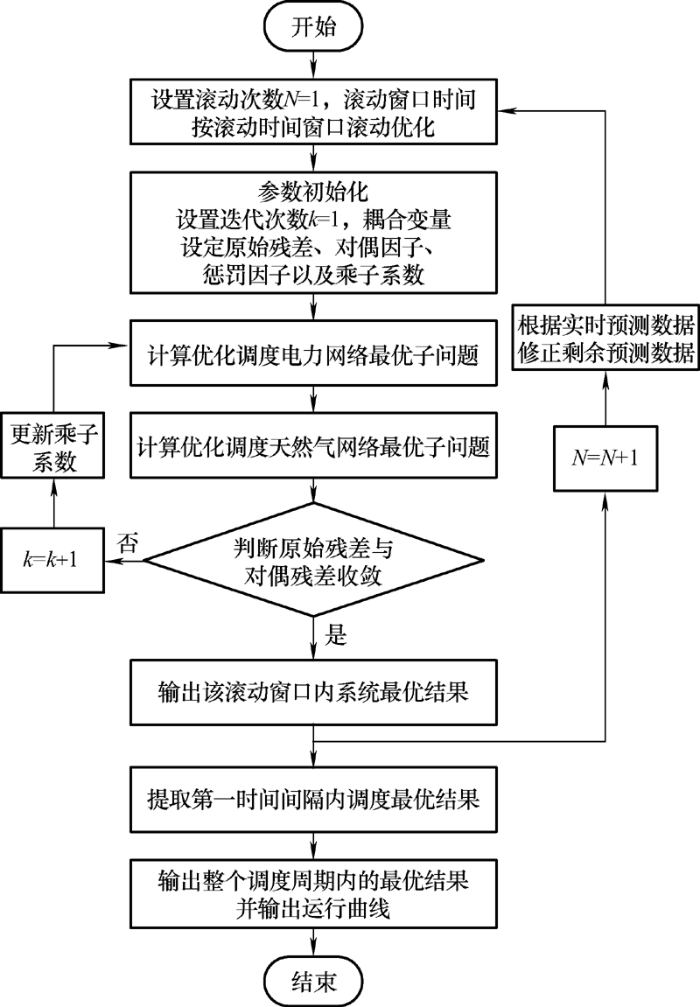
基于ADMM的电-气综合能源系统分布式滚动优化调度模型求解流程如图3所示。针对第一个滚动窗口内预测数据及参数设置,计算电力网络最优子问题,将耦合元件信息传递至天然气网络计算最优子问题,循环迭代直至完成第一个滚动窗口最优调度。随后滚动窗口向前移动,依据更新后窗口内的预测值按上述方法重复求解,最终得到整个调度周期内最佳方案。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   基于ADMM的分布式滚动优化调度算法流程


5 算例分析

5.1 算例系统介绍及参数设置

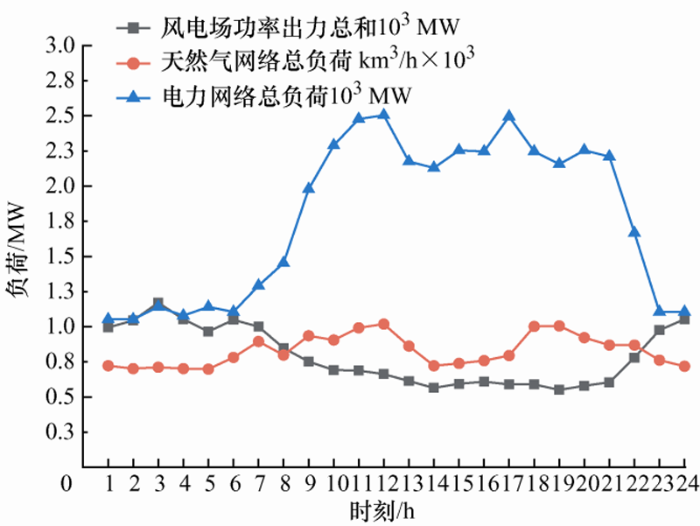
针对上述所提出的模型及算法,采用基于改进的IEEE新英格兰39节点电力网络与比利时20节点天然气网络构成的综合能源系统作为算例进行分析。系统中燃煤机组参数、天然气网络气源参数、燃气轮机参数、电转气装置参数以及其他网络参数详见文献[14]。风电场出力、天然气网络的负荷、电力网络负荷的预测曲线如图4所示。系统调度周期为24 h,时间间隔Δt为1 h,滚动窗口为6 h,初始惩罚因子取10。利用Matlab2018b平台实现ADMM下的优化调度模型编程并调用CPLEX12.8求解器求解上述优化问题。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   负荷和风电场预测曲线


5.2 调度结果与分析

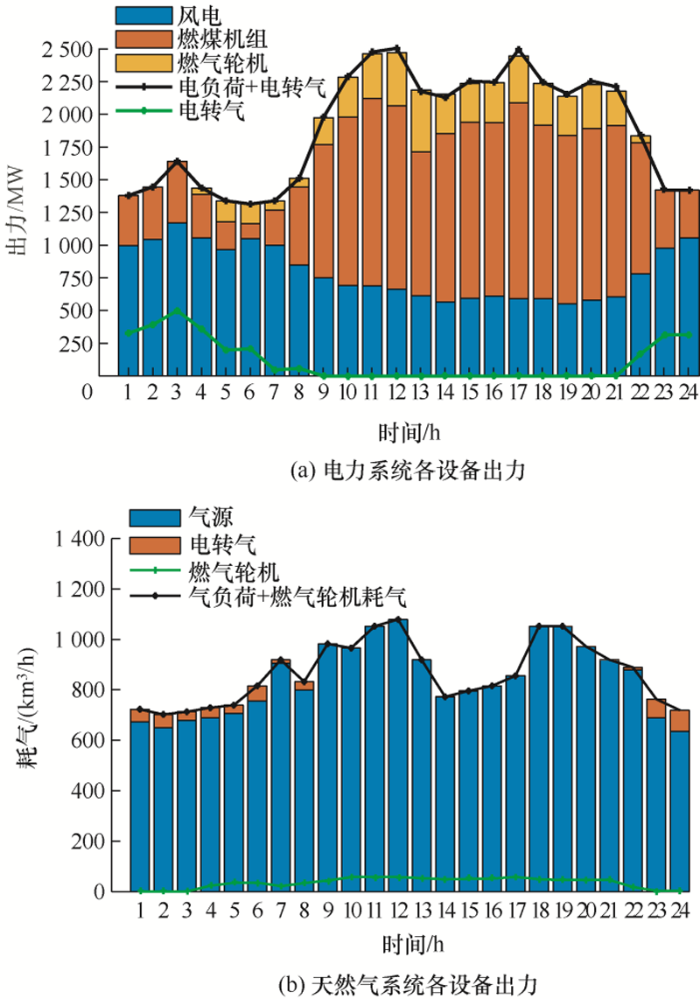
5.2.1 供能设备出力情况

图5a为电力系统中各设备出力结果,前8 h需要满足供应的电负荷相对较低且由于夜间风电场出力较高,大部分电负荷供应主要由风电场承担,电转气装置也在这一时段将风电场产生的富余电力转换为甲烷给天然气负荷供应。这样可以消纳过剩的风电,降低天然气系统燃气成本。此外,由于燃煤机组的燃料价格低于燃气轮机的购气价格,只有当电网出现负荷高峰且仅靠燃煤机组和风电场出力不能满足电负荷的平衡时,燃气轮机才投入运行。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   不同机组/气源出力的调度优化结果


图5b为天然气系统中各设备耗气结果,为满足天然气负荷的平衡,除电转气装置的供应外,需要从外购置天然气。当气负荷处于高峰期时,电负荷同样处于高峰期,由于此时天然气价格低于电力价格,需要从外购置大量天然气,并且一部分天然气投入燃气轮机的运行来满足电负荷的平衡。

模型建立过程中对任意时刻电功率及气流量进行了平衡约束,有效保证了系统安全稳定性。且滚动优化引入使得优化调度结果更符合实际要求,减小了随机波动带来的预测误差,增强了调度准确性。

5.2.2 经济性分析

表1为该算例下电-气综合能源系统采用三种优化调度模型的运行成本。分布式滚动优化模型中电力系统和天然气系统优化运行成本分别为587 706美元和163 072美元,与集中式优化模型相比运行成本节省了0.004 3%,两种方式下运行成本差别很小,验证了该优化算法的可行性。分布式滚动模型调度运行成本要比分布式模型调度运行成本增加0.071%,但与集中式优化调度下相比,运行成本仍有降低,说明构建的经济优化调度可以更好地提高系统运行的经济水平。

表1   不同优化模型下运行成本对比 美元

优化模型电力系统运行成本天然气系统
运行成本		互联系统
运行成本
集中式587 810165 004750 814
分布式587 286162 957750 243
分布式滚动587 706163 072750 778

新窗口打开| 下载CSV


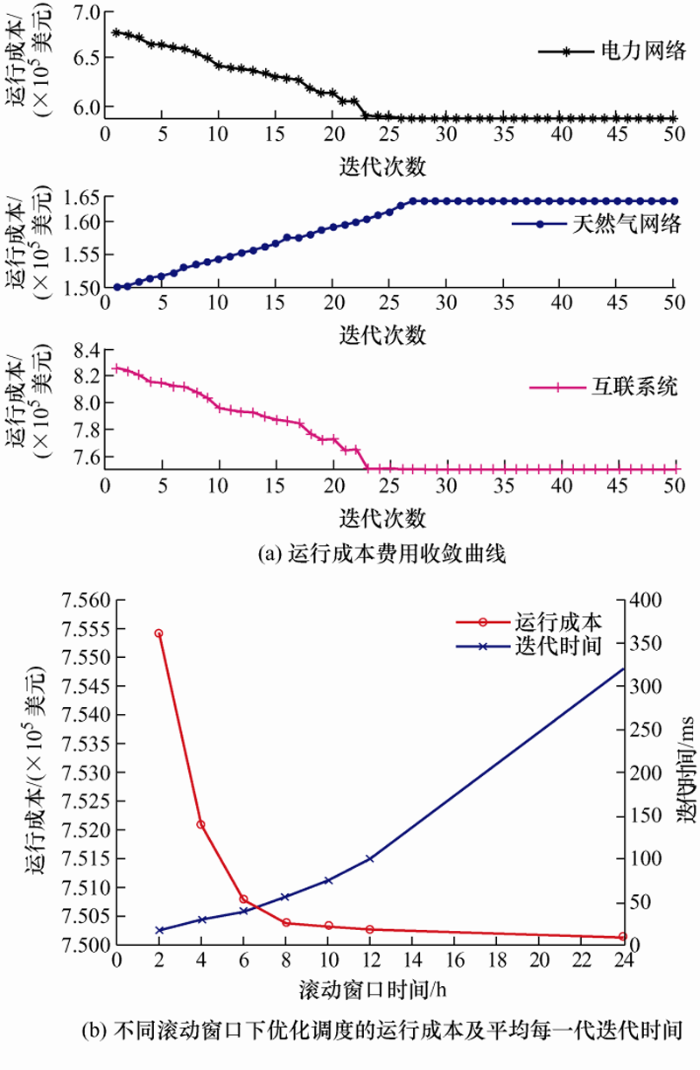
5.2.3 算法性能分析

从图6a可以看出,在27次迭代计算后,两个子网络的运行成本基本趋于稳定,算法收敛性较好,同时滚动窗口为6 h的计算时间为42 s,计算时间较短。迭代开始时,电力网络运行成本较高,这是由于采用ADMM算法计算开始时天然气供应为0,燃气轮机出力小,电力网络的平衡主要有燃煤机组来供应。而此时天然气网络的气源对外购置小,主要依靠电转气装置的产气量来供给气负荷,运行成本低。随着迭代的进行,两系统之间通过协同合作,使运行成本在满足负荷需求的条件下向着最小化的方向进行,最终趋于稳定。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   基于ADMM算法的分布式滚动优化的算法性能分析


从图6b看出,随滚动窗口时长的增加,针对滚动窗口内的预测信息考虑更多,波动较小,整体的调度结果会由此而变得更经济,总运行费用有明显下降趋势。同时窗口内涉及的信息量增多,完成计算所需的平均迭代时间也逐步增长。

6 结论

本文考虑了燃气轮机与电转气装置双向耦合,建立了基于ADMM的电-气综合能源系统的分布式滚动优化调度模型。通过算例分析得到了以下结论。

(1) 采用ADMM的分布式滚动优化调度结果很好地反映了两个系统之间的协同过程,减小了预测误差对系统的影响。

(2) 通过将集中式优化,分布式优化与分布式滚动优化三种调度模型进行对比,表明分布式滚动优化的有效性,更好地提高了系统运行的经济水平。

(3) 对算法性能的分析表明基于ADMM的分布式滚动优化调度在求解过程中具有良好的收敛性,同时滚动窗口时长不同会影响其计算效率,需要根据实际情况选择合适的窗口时长。

参考文献

贾宏杰, 王丹, 徐宪东, 等.

区域综合能源系统若干问题研究

[J]. 电力系统自动化, 2015(7):198-207.

[本文引用: 1]

JIA Hongjie, WANG Dan, XU Xiandong, et al.

Research on some problems of regional integrated energy system

[J]. Automation of Electric Power Systems, 2015(7):198-207.

[本文引用: 1]

卫志农, 张思德, 孙国强, 等.

计及电转气的电–气互联综合能源系统削峰填谷研究

[J]. 中国电机工程学报, 2017, 37(16):4601-4609.

[本文引用: 1]

WEI Zhinong, ZHANG Side, SUN Guoqiang, et al.

Study on peak shaving and valley filling of electricity to gas interconnected integrated energy system

[J]. Proceedings of the CSEE, 2017, 37(16):4601-4609.

[本文引用: 1]

权超, 董晓峰, 姜彤.

基于 CCHP 耦合的电力、天然气区域综合能源系统优化规划

[J]. 电网技术, 2018, 42(8):2456-2466.

[本文引用: 1]

QUAN Chao, DONG Xiaofeng, JIANG Tong.

Optimization planning of power and natural gas regional integrated energy system based on CCHP coupling

[J]. Power System Technology, 2018, 42(8):2456-2466.

[本文引用: 1]

MARTINEZ-MARES A, FUERTE-ESQUIVEL C R.

A untlied gas and power flow analysis in natural gas and electricity coupled networks

[J]. IEEE Transaction on Power Systems, 2012, 27(4):2156-2166.

DOI:10.1109/TPWRS.2012.2191984      URL     [本文引用: 1]

SUN Guoqiang, CHEN Shuang, WEI Zhinong, et al.

Multi-period integrated natural gas and electricpower system probabilistic optimal power flow incorporating power-to-gas units

[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(3):412-423.

DOI:10.1007/s40565-017-0276-1      URL     [本文引用: 1]

李杨, 刘伟佳, 赵俊华, 等.

含电转气的电气-热系统协同调度与消纳风电效益分析

[J]. 电网技术, 2016, 40(12):3680-3688.

[本文引用: 1]

LI Yang, LIU Weijia, ZHAO Junhua, et al.

Analysis on cooperative dispatching and wind power consumption benefit of electric thermal system with electricity to gas

[J]. Power System Technology, 2016, 40(12):3680-3688.

[本文引用: 1]

王伟亮, 王丹, 贾宏杰, 等.

考虑天然气网络状态的电力-天然气区域综合能源系统稳态分析

[J]. 中国电机工程学报, 2017, 37(5):1293-1305.

[本文引用: 1]

WANG Weiliang, WANG Dan, JIA Hongjie, et al.

Steady state analysis of power natural gas regional integrated energy system considering natural gas network state

[J]. Proceedings of the CSEE, 2017, 37(5):1293-1305.

[本文引用: 1]

龚睿. 区域型电气互联综合能源系统运行模式与优化控制算法研究[D]. 南京: 南京理工大学, 2018.

[本文引用: 1]

GONG Rui. Research on operation mode and optimal control algorithm of regional interconnected integrated energy system[D]. Nanjing: Nanjing University of Technology, 2018.

[本文引用: 1]

李婷, 叶希, 唐权, 等.

基于交替方向乘子法的源网协同多适应规划

[J]. 电力建设, 2017, 38(11):105-112.

[本文引用: 1]

LI Ting, YE Xi, TANG Quan, et al.

Source network cooperative multi adaptation planning based on alternating direction multiplier method

[J]. Electric Power Construction, 2017, 38(11):105-112.

[本文引用: 1]

王程, 刘念.

基于交替方向乘子法的互联微电网系统分布式优化调度

[J]. 电网技术, 2016, 40(9):2675-2681.

[本文引用: 1]

WANG Cheng, LIU Nian.

Interconnected microelectronics based on alternating direction multiplier method distributed optimal dispatching of power grid system

[J]. Power System Technology, 2016, 40(9):2675-2681.

[本文引用: 1]

瞿小斌, 文云峰, 叶希, 等.

基于串行和并行ADMM算法的电-气能量流分布式协同优化

[J]. 电力系统自动化, 2017, 41(4):12-19.

[本文引用: 1]

QU Xiaobin, WEN Yunfeng, YE Xi, et al.

Distributed collaborative optimization of power gas energy flow based on serial and parallel ADMM algorithm

[J]. Automation of Electric Power Systems, 2017, 41(4):12-19.

[本文引用: 1]

王成山, 吕超贤, 李鹏, 等.

园区型综合能源系统多时间尺度模型预测优化调度

[J]. 中国电机工程学报, 2019, 39(23):6791-6803,7093.

[本文引用: 1]

WANG Chengshan, LÜ Chaoxian, LI Peng, et al.

Multi time scale model prediction and optimal dispatch of park type integrated energy system

[J]. Proceedings of the CSEE, 2019, 39(23):6791-6803,7093.

[本文引用: 1]

肖浩, 裴玮, 孔力.

基于模型预测控制的微电网多时间尺度协调优化调度

[J]. 电力系统自动化, 2016, 40(18):7-14.

[本文引用: 1]

XIAO Hao, PEI Wei, KONG Li.

Multi time scale coordinated optimal dispatch of microgrid based on model predictive control

[J]. Automation of Electric Power Systems, 2016, 40(18):7-14.

[本文引用: 1]

梅建春, 卫志农, 张勇, 等.

电-气互联综合能源系统多时间尺度动态优化调度

[J]. 电力系统自动化, 2018, 42(13):36-42.

[本文引用: 2]

MEI Jianchun, WEI Zhinong, ZHANG Yong, et al.

Multi time scale dynamic optimal dispatching of power gas interconnected integrated energy system

[J]. Automation of Electric Power Systems, 2018, 42(13):36-42.

[本文引用: 2]

张儒峰, 姜涛, 李国庆, 等.

考虑电转气消纳风电的电-气综合能源系统双层优化调度

[J]. 中国电机工程学报, 2018, 38(19):5668-5678.

[本文引用: 1]

ZHANG Rufeng, JIANG Tao, LI Guoqing, et al.

Double layer optimal scheduling of power gas integrated energy system considering power to gas consumption of wind power

[J]. Proceedings of the CSEE, 2018, 38(19):5668-5678.

[本文引用: 1]

陈泽兴. 电-气互联系统协同运行优化的模型与算法研究[D]. 广州: 华南理工大学, 2019.

[本文引用: 1]

CHEN Zexing. Research on model and algorithm of coordinated operation optimization of power gas interconnected system[D]. Guangzhou: South China University of Technology, 2019.

[本文引用: 1]

/

〈 〉