电气工程学报, 2021, 16(4): 68-77 doi: 10.11985/2021.04.009

特邀专栏：高性能永磁电机驱动与控制

基于模型预测控制算法的永磁同步电机弱磁控制新策略

罗宇,1, 李政1, 桂永麟1, 柯栋梁1, 潘先喜2, 但志敏2, 汪凤翔,1

1.中国科学院海西研究院泉州装备制造研究所 泉州 362200

2.宁德时代新能源科技股份有限公司 宁德 352100

New Strategy of Flux-weakening Control of PMSM Based on Model Predictive Control

LUO Yu,1, LI Zheng1, GUI Yonglin1, KE Dongliang1, PAN Xianxi2, DAN Zhimin2, WANG Fengxiang,1

1. Quanzhou Institute of Equipment Manufacturing, Haixi Institute Chinese Academy of Sciences, Quanzhou 362200

2. Contemporary Amperex Technology Co., Ltd., Ningde 352100

通讯作者: * 汪凤翔,男,1982年生,研究员,博士研究生导师。主要研究方向为电机驱动与电力电子。E-mail：fengxiang.wang@fjirsm.ac.cn

收稿日期: 2021-06-30   修回日期: 2021-08-10  

Received: 2021-06-30   Revised: 2021-08-10  

作者简介 About authors

罗宇,男,1996年生,硕士研究生。主要研究方向为电机拖动及其控制。E-mail： 790192285@qq.com

摘要

针对内嵌式永磁同步电机高速弱磁区域的电压极限椭圆约束及电流参数整定问题,提出一种基于有限集预测电流控制方法和实时电压反馈的混合弱磁控制策略。首先,采用有限集预测电流控制方法在最大转矩电流比和弱磁区域中进行转矩、转速、电流和角度的标定,解决传统复杂电流参数整定问题,提升标定数据的可靠性;其次,在预测电流采样控制方法基础上,结合实时电压反馈,设计弱磁区域的混合弱磁控制策略,避免电流环参数整定的同时,解决电压极限椭圆约束问题和实现高速运行。最后,通过仿真和试验验证了方法的有效性。

关键词： 永磁同步电机 ; 混合弱磁控制 ; 模型预测控制

Abstract

Aiming at the problem of voltage limit ellipse constraint and current parameter tuning in high-speed flux weakening region of interior permanent magnet synchronous motor, a hybrid flux weakening control strategy based on finite set predictive current control method and real-time voltage feedback is proposed. Firstly, the finite-set predictive current control method is used to calibrate the torque, speed, current and angle in the maximum torque current ratio and flux weakening region, which solves the traditional complex current parameter setting problem and improves the reliability of calibration data. Secondly, on the basis of predictive current sampling control method, combined with real-time voltage feedback, a hybrid flux weakening control strategy is designed to avoid the parameter setting of current loop, solve the problem of voltage limit ellipse constraint and realize high-speed operation. Finally, the effectiveness of the proposed method is verified by simulation and experiment.

Keywords： Permanent magnet synchronous motor ; hybrid flux-weakening control ; model predictive control

PDF (4144KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

罗宇, 李政, 桂永麟, 柯栋梁, 潘先喜, 但志敏, 汪凤翔. 基于模型预测控制算法的永磁同步电机弱磁控制新策略. 电气工程学报[J], 2021, 16(4): 68-77 doi:10.11985/2021.04.009

LUO Yu, LI Zheng, GUI Yonglin, KE Dongliang, PAN Xianxi, DAN Zhimin, WANG Fengxiang. New Strategy of Flux-weakening Control of PMSM Based on Model Predictive Control. Journal of Electrical Engineering[J], 2021, 16(4): 68-77 doi:10.11985/2021.04.009

1 引言

永磁同步电机(Permanent magnet synchronous motor, PMSM)因其体积小、结构简单、功率密度大、效率高等优点,成为目前新能源电动汽车驱动系统不可或缺的一部分。由于新能源电动汽车存在多种工况的控制需求,例如快速动态响应、高速稳定性和宽调速范围,永磁同步电机成为当前电动汽车驱动系统研究的热点之一。其中,内嵌式永磁同步电机(Interior permanent magnet synchronous motor, IPMSM)的永磁体位于转子内部,具有机械强度高、气隙磁密度高、可有效利用磁阻转矩等优点,更加适合于电动汽车的应用[1,2]。

电机高速调控的安全性与稳定性是汽车研发的重点。由于永磁体的磁场是固定的,因而转子的磁场无法灵活调节。当电机转速高于额定转速范围时,电机的感生电动势高于供电电压,转速无法继续提升,此时需要进行弱磁控制提高转速范围。近些年,有许多文献对弱磁调控策略进行了详细研究,主要分为前馈弱磁[3,4]、反馈弱磁[5]和混合弱磁[6,7,8]控制。前馈弱磁控制中常用的方法是通过公式计算获取驱动电机所需的d-q坐标轴电流。该方式结构简单,但需要进行复杂的非线性方程组求解,极大地增加了计算的复杂度。其次,求解过程严重依赖电机的参数,因而容易受到外部的干扰。反馈弱磁控制中,常采用电压差反馈的方法对控制环中的d-q坐标轴电流进行动态调节,保证控制系统能够准确跟踪逆变器所能承受的电压极限。该方法虽然不依赖电机的参数,对外部的干扰也具有一定的抵抗能力,但其动态性能相较前馈控制有一定的损失。混合弱磁控制则是前馈弱磁控制和反馈弱磁控制的一种折中方式,这种方法不仅避免了公式计算中复杂的求解过程,同时也能够带来良好的动态响应。因此,在工程应用中,混合弱磁控制方法经常被使用在驱动算法研究之中。文献[9]基于虚拟电阻的单电流调节器弱磁控制策略,对单电流调节器弱磁控制中的弱磁电压依据电流轨迹进行优化设计。文献[10]基于由直轴电流和交轴电流所构成的状态空间,以最大电流曲线、最大磁链曲线和最小磁链转矩比曲线为边界而提出的一种最优弱磁路径。文献[11]提出了利用电压极限椭圆的梯度下降法进行弱磁和电流参考值修正的新方法。

早期对永磁同步电机的研究以磁场定向控制和直接转矩控制为主。随着电子芯片的快速发展,模型预测等新型控制方法得以推广应用。模型预测控制算法具有以下优点：原理简单、鲁棒性好、在线优化能力强、响应速度快、容易处理非线性约束 等[12,13,14,15]。为了提升模型预测控制算法的控制性能,众多学者分别对算法的抗扰动性能[16]、运算速 度[17]、容错能力[18]、权重系数设计[19]等方面进行了进一步探索。

本文提出一种将弱磁控制和预测控制结合的调速策略。该策略将弱磁标定查表法和反电动势电压前馈进行结合用于驱动电机的高速控制应用中。其中,查表法由转矩、转速、电流坐标系组成数据集,而电压差前馈则包含在模型预测控制模块中。虽然需要大量的离线预试验获取到查表的数据,但是这也使得算法更加贴合于实际运行工况,高转速区间更加稳定,抗扰动能力强。查表数据的获取采用数据处理中内插法和遍历思想,内插法的使用大大减少了离线数据点的采集压力,也保证了数据的可靠性。此外,预测电流控制采用有限集的思想,借助最小化预测控制中的成本函数的方式直接得到逆变器所需的开关矢量,取代了传统矢量控制中的调制解调器,简化了整个控制回路的结构。

2 数学模型和控制原理

2.1 内置式永磁同步电机数学模型

IPMSM在d-q旋转坐标系下的电压方程可以表示为

$\left\{ \begin{array}{l}{u_d} = {R_s}{i_d} + {L_d}\frac{{{\rm{d}}{i_d}}}{{{\rm{d}}t}} - {L_q}{i_q}{\omega _e}\\{u_q} = {R_s}{i_q} + {L_q}\frac{{{\rm{d}}{i_q}}}{{{\rm{d}}t}} + {L_d}{i_d}{\omega _e} + {\psi _f}{\omega _e}\end{array} \right.$

式中,ud和uq分别为d-q坐标系下的电压;id、iq分别为d-q坐标轴下的电流;Ld、Lq分别是d-q坐标轴下的定子电感参数;Rs为定子电阻;${\psi _f}$为永磁体磁链;ωe为电角速度。

IPMSM的转矩和机械方程可由以下式子表示

${T_e} = \frac{3}{2}{p_n}[{\psi _f}{i_q} + ({L_d} - {L_q}){i_d}{i_q}]$
${T_e} - {T_l} - B{\omega _m} = J\frac{{{\rm{d}}{\omega _m}}}{{{\rm{d}}t}}$

式中,Te、Tl分别为电磁转矩和负载转矩;pn为永磁体极对数;B和J分别为粘滞系数和转动惯量;ωm为电机的机械角速度。

IPMSM的转速与电角速度、机械角速度的关系如式(4)所示

$\left\{ {\begin{array}{*{20}{c}}{{\omega _e} = {p_n}{\omega _m}}\\{n = \frac{{30}}{\pi }{\omega _m}}\end{array}} \right.$

式中,n为电机的转速。

2.2 弱磁控制模型及约束

在全转速运行范围,驱动电机主要受到两种限制条件：一是逆变器输出电压的限制,二是电机本身最大电流的限制。这两种限制条件表示如下

$\left\{ \begin{array}{l}\sqrt {{{({i_d})}^2} + {{({i_q})}^2}} \le {i_{lim}}\\\sqrt {{{({u_d})}^2} + {{({u_q})}^2}} \le {u_{lim}}\end{array} \right.$

式中,ilim和ulim分别为电机的极限电流和极限反电动势电压;${{{u_{lim}} = {u_{dc}}} \mathord{\left/ {\vphantom {{{u_{lim}} = {u_{dc}}} {\sqrt 3 }}} \right. } {\sqrt 3 }}$,udc为直流母线电压。忽略定子阻值电压降后,反电动势uemf满足以下条件

$\left\{ \begin{array}{l}{u_{emf}} = \left| {{\omega _e}} \right|\sqrt {{{({\psi _f} + {L_d}{i_d})}^2} + {{({L_q}{i_q})}^2}} \\{u_{emf}} \le {u_{lim}}\end{array} \right.$

为进一步分析,将式(6)进一步转换成椭圆方程得

$\frac{{{{\left( {{i_d} + \frac{{{\psi _f}}}{{{L_d}}}} \right)}^2}}}{{{{\left( {\frac{{{u_{lim}}}}{{{L_d}{\omega _e}}}} \right)}^2}}} + \frac{{{{({i_q})}^2}}}{{{{\left( {\frac{{{u_{lim}}}}{{{L_q}{\omega _e}}}} \right)}^2}}} \le \;1$

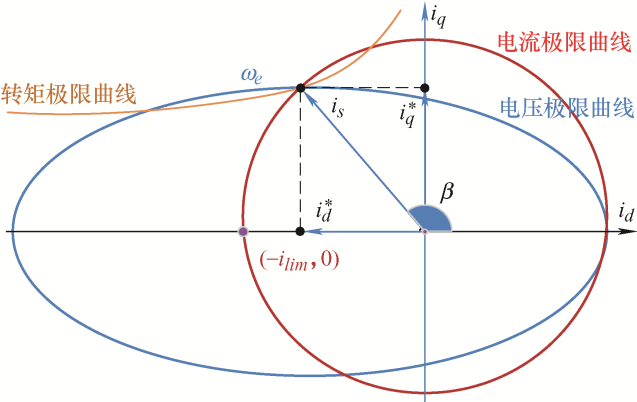
图1为d-q坐标系下电压、电流与转矩的关系。其中最大电流极限圆方程式和最大电压极限椭圆方程均已标明。在电机的动态运行过程中,电流极限圆为静态方程,表示电机的电流极大值。电压极限椭圆为动态椭圆。由式(7)可得,当电机的转速上升时,最大电压不变,电压极限椭圆随之减小,电机转矩随转矩电流曲线对应减小。因此电压极限圆为动态椭圆图形。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   电压、电流、转矩极限曲线示意图


2.3 逆变器模型

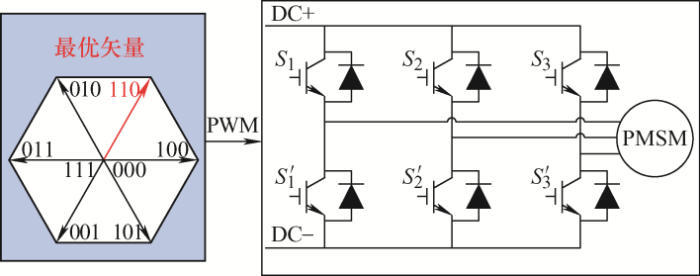
本文应用经典两电平电压源逆变器实现对IPMSM的控制,其原理图如图2所示。由于同一桥臂的上下开关器件不能同时导通,开关矢量共有8种。针对这8种开关矢量,利用式(8)可获得每种开关矢量对应的电压空间矢量。

${u_{out}} = \frac{{2{u_{dc}}}}{3}\left( {{S_1} + \exp \left( {j\frac{2}{3}\pi } \right){S_2} + \exp \left( { - j\frac{2}{3}\pi } \right){S_3}} \right)$

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   有限集矢量与三相两电平拓扑结构


式中,uout为逆变器输出电压;${S_i} = 1$代表第i个开关处于开通状态,${S_i} = 0$则表示处于关断状态。

功率器件开关矢量与逆变器输出电压之间的对应关系如表1所示。

表1   开关矢量与输出电压

S1S2S3unuout
000(0, 0, 1)0
100(1, 0, 0)$\frac{2}{3}{u_{dc}}$
010(0, 1, 0)$\frac{2}{3}{u_{dc}}\exp \left( {j\frac{2}{3}\pi } \right)$
110(1, 1, 0)$\frac{2}{3}{u_{dc}}\exp \left( {j\frac{\pi }{3}} \right)$
001(0, 0, 1)$\frac{2}{3}{u_{dc}}\exp \left( {j\frac{4}{3}\pi } \right)$
101(1, 0, 1)$\frac{2}{3}{u_{dc}}\exp \left( {j\frac{5}{3}\pi } \right)$
011(0, 1, 1)$\frac{2}{3}{u_{dc}}\exp \left( {j\pi } \right)$
111(1, 1, 1)0

新窗口打开| 下载CSV


2.4 传统弱磁控制原理

IPMSM弱磁控制的思想来源于他励直流电动机的调磁控制,当他励直流电动机端电压达到最大电压时,只能通过降低电动机的励磁电流,改变励磁磁通,使得电动机能够运行到更高的转速。对于IPMSM而言,励磁磁动势由转子永磁体产生,无法灵活调节,只能通过调节定子电流增加去磁分量达到弱磁提速的目的。

传统弱磁控制方法为增强d轴去磁电流,设计了前馈弱磁、反馈弱磁等方法,但这些方法大多采用矢量控制作为基本控制回路,因而往往存在多个PI控制器。这些PI控制器的引入会带来参数耦合和复杂调参的问题。此外,在前馈查表法中,其数据标定过程也常会因PI参数设置的原因,导致标定的数据表格存在一定的误差。

3 IPMSM高速运行控制策略

3.1 预测电流控制算法

预测电流控制算法中,输入输出分别为参考电流和下一时刻最优开关矢量。若要获得下一时刻的最优开关矢量,须将式(1)进行转换,得到式(9)

$\left\{ \begin{array}{l}\frac{{{\rm{d}}{i_d}}}{{{\rm{d}}t}} = \frac{1}{{{L_d}}}{u_d} - \frac{{{R_s}}}{{{L_d}}}{i_d} + \frac{{{L_q}}}{{{L_d}}}{i_q}{\omega _e}\\\frac{{{\rm{d}}{i_q}}}{{{\rm{d}}t}} = \frac{1}{{{L_q}}}{u_q} - \frac{{{R_s}}}{{{L_q}}}{i_q} - \frac{{{L_d}}}{{{L_q}}}{i_d}{\omega _e} - \frac{{{\omega _e}{\psi _f}}}{{{L_q}}}\end{array} \right.$

利用欧拉公式对上述微分方程进行离散化,得到下一时刻电流计算表达式

$\left\{ \begin{array}{l}i_d^{k + 1} = (1 - \frac{{{R_s}{T_s}}}{{{L_d}}})i_d^k + {\omega _e}\frac{{{L_q}{T_s}}}{{{L_d}}}i_q^k + \frac{{{T_s}}}{{{L_d}}}{u_d}\\i_q^{k + 1} = - {\omega _e}\frac{{{L_d}{T_s}}}{{{L_q}}}i_d^k + (1 - \frac{{{R_s}{T_s}}}{{{L_q}}})i_q^k + \frac{{{T_s}}}{{{L_q}}}{u_q} - {\omega _e}\frac{{{\psi _f}}}{{{L_q}}}{T_s}\end{array} \right.$

式中,Ts为控制周期;ik d和ik q代表当前第tk时刻电流采样值;ik+1 d和ik+1 q代表下一时刻预测电流值。

根据表1中不同开关矢量与输出电压的对应关系,代入式(10)计算获得不同开关矢量的预测电流后,预测电流控制算法借助成本函数选择出成本值最小的开关矢量。成本函数定义形式一般如下所示

$\left\{ \begin{array}{l}g[{u_n}] = \sqrt {{{(i_d^{k + 1}[n] - i_d^{ref})}^2} + {{(i_q^{k + 1}[n] - i_q^{ref})}^2}} \\{f_{out}} = \min \{ g[{u_n}]\} \;\;\;\;{\rm{ }}n = 0,1, \cdots,7\end{array} \right.$

鉴于控制算法的安全问题,在成本函数中还须加入对总电流$i_s^{k + 1}$的限制条件实现控制过程的过流保护。限流措施定义为

$g[{u_n}] = \left\{ {\begin{array}{*{20}{c}}{g[{u_n}]}&{\;\;\;\;i_s^{k + 1}[n] \le {i_{\lim }}}\\{ + \infty \;\;\;}&{\;\;\;\;\;\;}\end{array}} \right.$

3.2 预测电流控制时序

由于采用的预测电流控制算法中采样周期与此刻计算所得的脉冲发出周期不一致,因而产生动作延时,故在控制算法设计过程中须进行延时补偿。

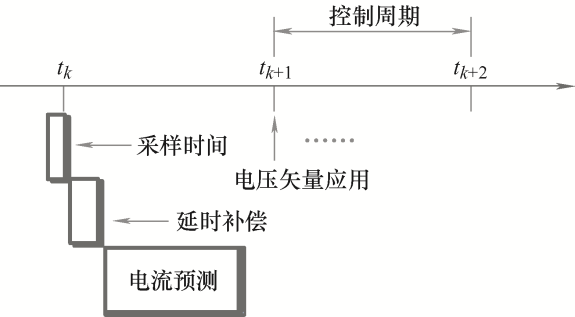
参考MPC的延时补偿方法,本文补偿延时的方案也是考虑计算时间。补偿方法为将采样的电流与tk+1时刻应用的开关状态用于式(10)来估算tk+1时刻的负载电流值,然后将该电流值作为起点开始 进行所有开关状态的预测。其具体控制时序如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   预测电流控制时序


3.3 基于预测电流控制的弱磁标定

查表法因其控制结构简单、计算量较小、鲁棒性强等优点成为工程中应用较为广泛的方法。但是由于在矢量控制中需要同时调节两个PI电流控制器,导致参数设置复杂。预测电流控制不需要复杂的参数设置,本文以MPC作为电流控制环,进行弱磁数据的标定。标定过程为在不同的转速条件下,给定d轴和q轴电流,同时保证反电动势在电压限制之内,记录此时id、iq所形成的磁链、转速和转矩数据,形成转速-转矩-电流的数据集。以下为具体的标定步骤。

(1) 构建预测电流控制为基础的电流环控制算法,利用对拖负载电机拖动驱动电机至一定转速,在额定转速内,通过输入不同的电流is和角度β,观测电流is的输出最大转矩,并记录此时的id、iq。形成额定转速之内的最大转矩电流比数据。

(2) 利用对拖负载电机拖动驱动电机转速至步骤(1)测得最大转矩对应的额定转速以上,通过调整电流is和角度β,使电压在限制电压范围之内,记录不同转速,电流is和角度β对应的最大转矩与此时的id、iq,形成额定转速以上的弱磁范围内数据。

(3) 将采样获取的转矩、转速与对应的电流进行关联,得到原始数据。

(4) 利用数据拟合算法,将该数据集映射到三维坐标系中,得到初步拟合的数据平面。

(5) 观察初步拟合的平面,修正不正确的数据点,并通过遍历算法得到两张最终的数据拟合平面及表格。

通过以上的步骤,可以得到最终的拟合平面及表格。但需要注意的是,以上标定方法中涉及到了各种数据信息的获取,包括最大转矩电流比、转折速度、空载电流和弱磁工作区等。它们的标定过程是渐进的,最终可以被融合到一张数据集中,因此,该表格不但包括了电机运行的全速域信息,而且也能够确保低速至高速之间的稳定切换。

3.4 电压反馈控制

永磁同步电机高速运行时的电压极限约束是弱磁控制的一大难题。常用的方式是利用电压反馈方法,设计一种动态弱磁参数来调节永磁同步电机产生的反电动势。其具体设计如下

$p = \frac{{{u_{dc}}}}{{\sqrt 3 \left| {{\omega _e}} \right|\sqrt {{{({\psi _f} + {L_d}{i_d})}^2} + {{({L_q}{i_q})}^2}} }}$

根据式(13),该参数可以用于调节转矩、转速或d-q轴电流输出,进而达到调节施加在电机两端的电压的目的。另外,由于该动态弱磁参数仅在反电动势超过极限时激活,因而设置一个限幅来适配此种情形,幅值设置为0~1。

3.5 混合弱磁控制策略

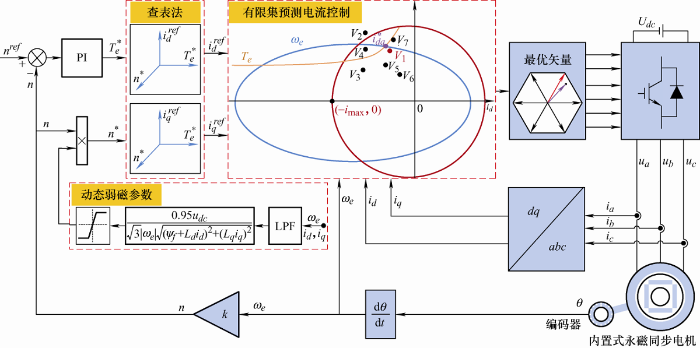
结合以上所述预测电流控制、查表弱磁控制和电压反馈控制,本文提出一种融合三者优势的混合弱磁控制策略,不仅解决了解决传统复杂PI参数调节问题,满足弱磁约束条件,还提高了系统的电流响应性能[20,21,22]。具体控制结构如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   算法整体控制结构


其中,查表弱磁控制根据标定步骤中获得了iref d、iref q与Te、n的关系,具体形式如下

$\left\{ {\begin{array}{*{20}{c}}{f(i_d^{ref},i_q^{ref}) = {T_e}}\\{g(i_d^{ref},i_q^{ref}) = n}\end{array}} \right.$

根据Te、n与iref d、iref q存在唯一对应关系,利用反函数与原函数关系可得

$\left\{ {\begin{array}{*{20}{c}}{(i_d^{ref},i_q^{ref}) = {f^{ - 1}}({T_e})}\\{(i_d^{ref},i_q^{ref}) = {g^{ - 1}}(n)}\end{array}} \right.$

由于采集数据有限,本文利用内插法进行线性插值,获得未标定的数据。内插法定义如下

$\frac{{T_e^{un} - {T_{e1}}}}{{n_{_{}}^{un} - {n_1}}} = \frac{{{T_{e1}} - {T_{e2}}}}{{{n_1} - {n_2}}}$

式中,(Te1, n1)、(Te2, n2)为已知数据,(Tun e, nun )为插入数据。此时,Te、n与iref d、iref q形成完整的映射关系,生成弱磁控制必要的参考电流数据。

预测电流控制则是利用查表法输出的参考电流,选择最优的开关矢量。设计的成本函数如下 所示

$\left\{ \begin{array}{l}g[{u_n}] = \sqrt {{{(i_d^{k + 1}[n] - i_d^{ref})}^2} + 2{{(i_q^{k + 1}[n] - i_q^{ref})}^2}} \\{f_{out}} = \min \{ g[{u_n}]\} \;\;\;\;n = 0,1, \cdots,7\end{array} \right.$

其中,成本函数以iref d、iref q与各预测值之差的平方为参考。除此之外,根据参考文献[21]和试验过程中电流和转矩的响应情况,本文引入了权重系数并发现当(ik+1 q- iref q)2前的系数设置为2时,系统总体的跟踪性能更加优越。

本文设计的电压反馈控制则在式(13)基础之上加入了电压利用率的概念。式(13)中的电压利用率为100%,但在实际运行过程中,如此高的利用率会导致反电动势存在超过限值且电机发生振荡的情况。因此,基于充分利用电压且满足电压约束的思想,设计的动态弱磁参数为

$p = \frac{{0.95{u_{dc}}}}{{\sqrt 3 \left| {{\omega _e}} \right|\sqrt {{{({\psi _f} + {L_d}{i_d})}^2} + {{({L_q}{i_q})}^2}} }}$

4 试验结果

为验证本文提出算法的有效性,本文试验选取一台内置式永磁同步电机来进行试验,试验包含数据标定试验和算法验证试验。数据标定试验采用预测电流控制算法进行数据获取,设计算法验证试验则是观测电机在不同工况下的运行状态,从而得出有效的控制。

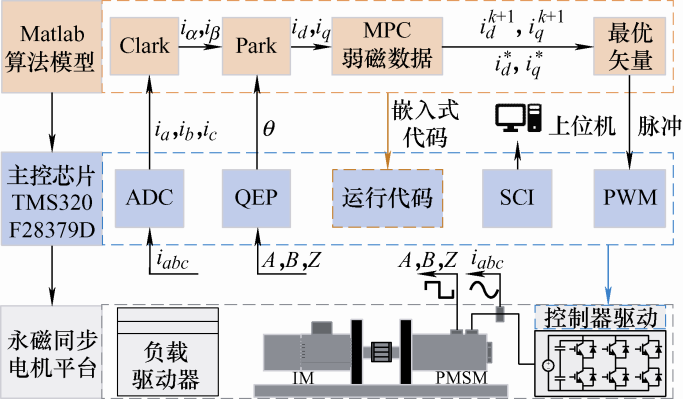
根据策略的控制需求,搭建了一个电机测试平台,其系统结构如图5所示,试验平台如图6所示。主控制器为TMS320F28379D,系统在在DSP中实现算法控制,控制频率为16 kHz。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   系统结构框图


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   电机对拖试验平台


永磁同步电机的参数如表2所示。

表2   内置式永磁同步电机参数

参数数值参数数值
d轴电感Ld/mH10额定转矩Te/(N·m)23
q轴电感Lq/mH14.5额定电压Vn/V380
定子电阻Rs/Ω0.637额定电流In/A9
磁链ψf/Wb0.31额定功率Pn/kW4.8
极对数pn4额定转速nr/(r/min)2 000

新窗口打开| 下载CSV


4.1 数据标定试验

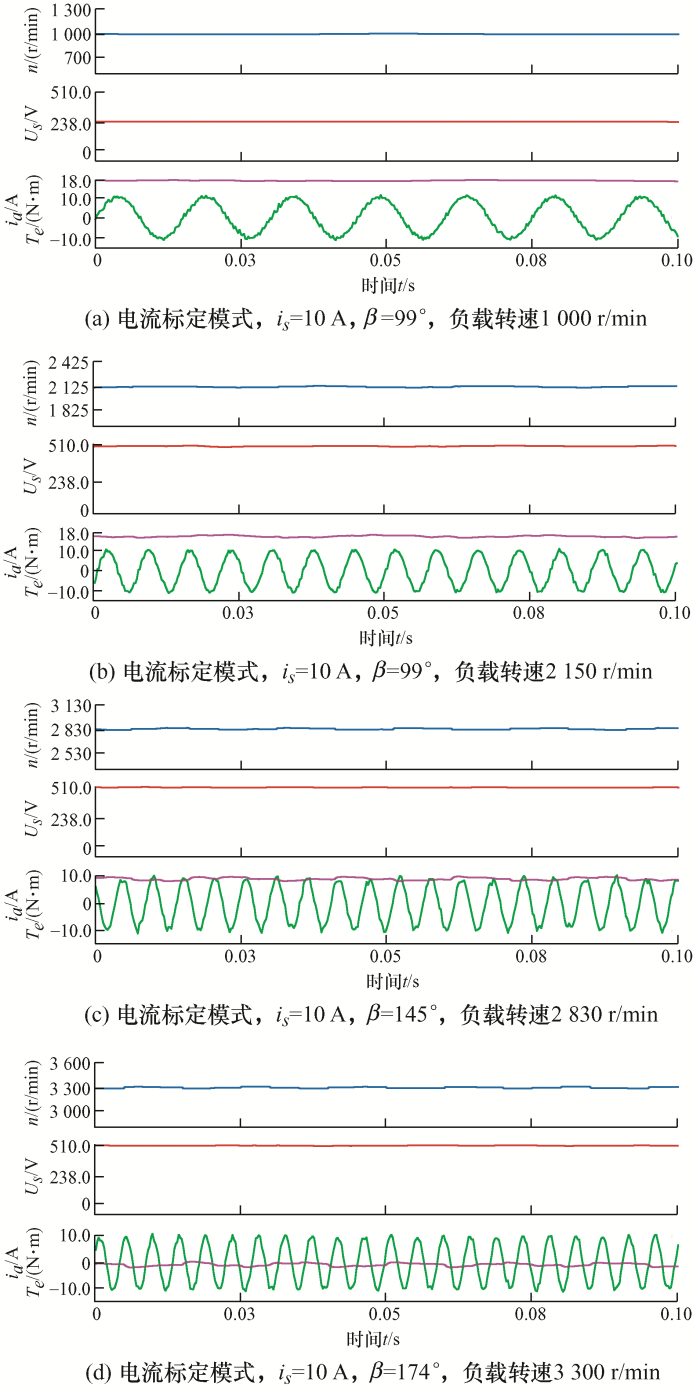
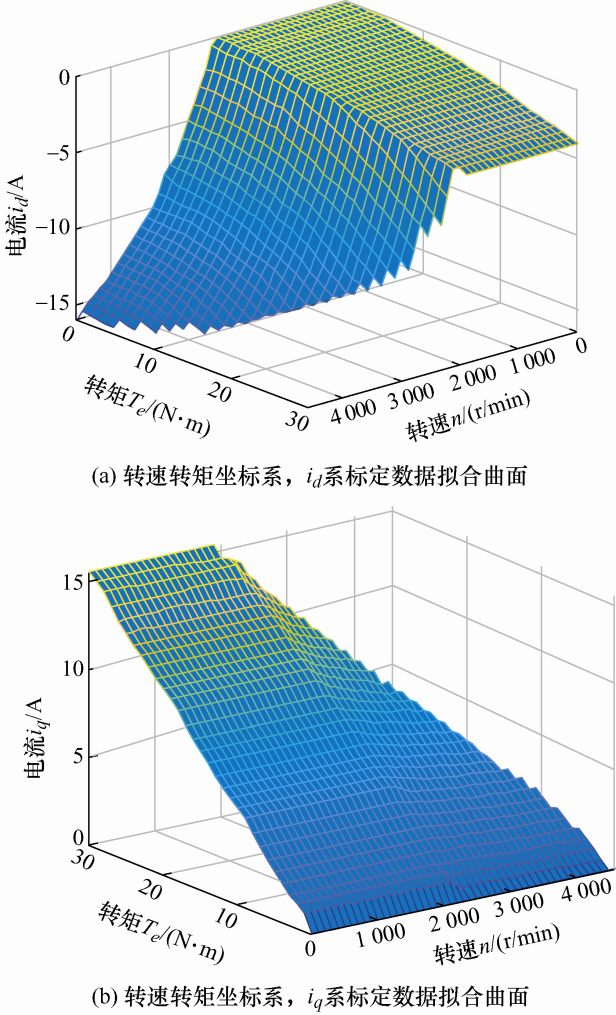
该数据标定试验是所设计算法的先验条件,其核心思想是在最大极限电流圆和最大极限电压椭圆的约束内,找到基速区域和弱磁区域中符合条件最大转矩的数据标定点,即需要找到合理的d-q轴电流指令组合。这种方式基于电机的试验标定数据,实际适应度高、动态响应好。在本文标定试验中,拟采用预测电流控制算法进行测试。试验图(图7)记录了不同工况下被测电机的转速、反电动势、转矩和a相电流。首先进行额定速度区间内MTPA数据的标定,固定一个转速点,其值为额定转速的2/3,然后通过调整不同的电流和角度,得到相应的最大转矩的数据信息。如图7a所示,首先固定转速为1 000 r/min,电流为10 A,通过调整图1中电流矢量is的角度,发现在角度99°时输出转矩最大,此时转子的反电动势约为238 V,转矩为18 N·m。当转速超过额定转速时,如图7b所示,角度固定为99°,通过负载电机提升转速至2 125 r/min,此时数值转换后的反电动势约为510 V,达到电压利用率的约束条件,这也是电机在10 A时的转折速度。若想要继续增大转速,只能通过增大电流,或者增大角度来降低转子的反电动势电压。图7c中,转速约为2 830 r/min,调节电流is与坐标轴的角度β为145°,此时电压为510 V,最大输出转矩为10 N·m。图7d中,转速为3 300 r/min,调节电流is与坐标轴的角度β为174°,此时电压为510 V,最大输出转矩为0,达到is为10 A时的最大弱磁转速。在不同工况下,重复以上步骤,并记录此时的标定数据,可以获取到拟合平面所需要的信息,进而获得全速域下转矩转速与d轴和q轴电流的映射关系。此过程也一一对应于混合弱磁模块设计中前三步标定步骤,后续利用数据拟合及数据遍历成功获得最终所需的平面和算法所需的表格。其中得到的d轴和q轴电流的拟合平面如图8所示,该平面相对而言较为平滑,为MTPA与弱磁的切换提供有效的保障。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   电流数据标定试验


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   标定数据拟合曲面


4.2 设计算法验证试验

4.2.1 稳态运行试验

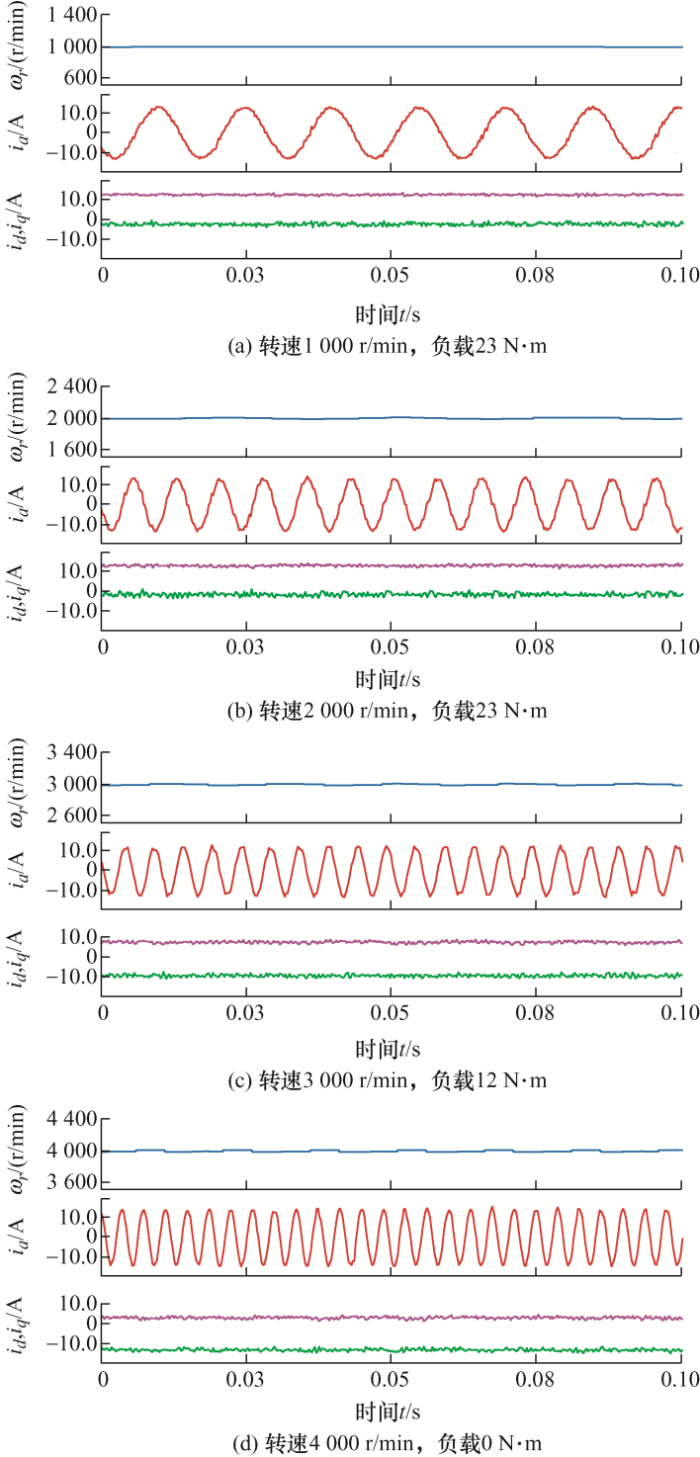
为验证算法在稳态情况下是否具有有效性,如图9所示,分析稳态运行时1 000 r/min、2 000 r/min、3 000 r/min和4 000 r/min工况下的a相电流ia、d-q坐标系下的电流id与iq。结果表明,在给定转速下,电机均能够到达给定的转速与转矩并稳定运行。在相电流方面可以看出,随着给定转速的不断增大,电流的变化频率也随之提高,进而保证电机在两倍额定转速时能够运行稳定。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   转速稳态运行试验


4.2.2 动态运行试验

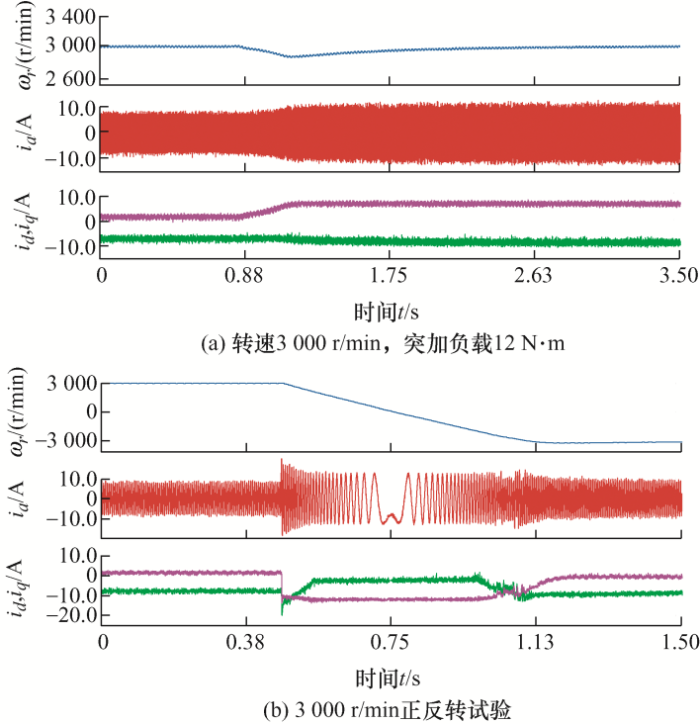
为测试算法动态性能,进行了负载突变和正反转试验。如图10a所示,进行负载突变试验时,驱动电机转速给定为3 000 r/min,初始负载转矩 为0。若突加负载至12 N·m,系统的动态响应十分迅速,约0.8 s时转速到达到稳态。系统的d轴电流主要用于降低电机的反电动势电压,q轴电流的输出主要保证转矩的维持,d轴和q轴的电流均随着转速与转矩的变化快速响应。q轴电流由0 A迅速增大至6.5 A,d轴电流由-8 A减小至-9 A。另一项试验测试了电机正反转的变化状况,如图10b所示,电机的初始转速为3 000 r/min,给定指令为-3 000 r/min,电机实现了由弱磁区域-额定转速区域-弱磁区域的三种状态的变化。此过程不需要复杂的公式计算变化与状态切换,只需要根据数据集即可完成正反弱磁区间转速的快速响应。

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   转速动态运行试验


4.2.3 转矩观测试验

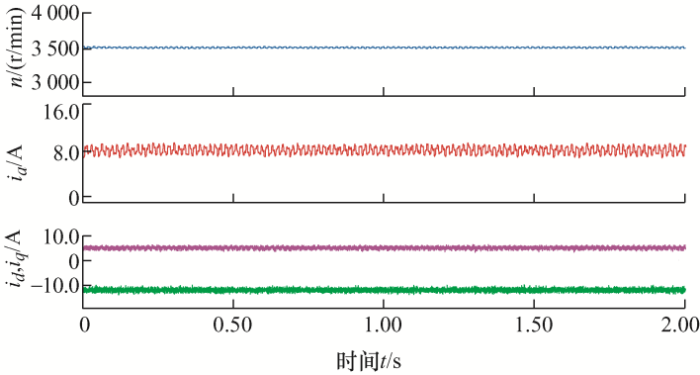
为进一步验证方案在弱磁区域运行时的稳定性,对永磁同步电机输出转矩进行详细研究。如 图11所示,在转速3 500 r/min的工况下,d-q轴电流运行平稳,电机负载转矩Te稳定在8 N·m,转矩脉动较小。这说明所提出的策略能够有效地实现对转矩的精确控制。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   转矩观测试验


4.2.4 MTPA至弱磁控制试验

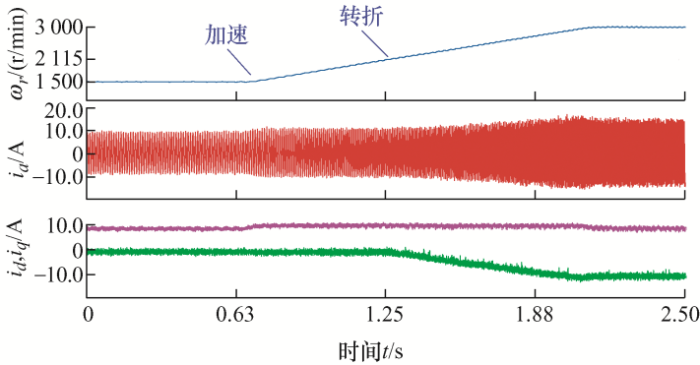
为验证方案能够实现MTPA与弱磁控制之间的稳定切换,对永磁同步电机进行详细的提速研究。将转速从最大转矩电流比区域1 500 r/min加速至弱磁区域3 000 r/min,负载转矩恒定设置为15 N·m,此时负载转矩对应的额定转速的转折速度为2 115 r/min。如图12所示,被测电机能够以良好的速度响应到达给定转速且无超调,这说明所提出的策略能够有效实现电机在MTPA与弱磁控制之间稳定切换。

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12   MTPA至弱磁控制验证试验


以一台IPMSM为试验对象进行上述试验,结果表明所提出的策略具有良好的稳态性能和动态性能,不但针对负载突变具有较强的抗干扰能力和动态响应能力,而且其在同步旋转坐标系下的电流均表现良好,转矩控制稳定且转矩脉动较小。同时,MTPA至弱磁控制的试验结果表明了所提出的算法能够实现电机在MTPA与弱磁之间直接的平滑切换。

5 结论

本文以内置式永磁同步电机的全速域运行为研究对象,提出了一种结合预测控制算法的弱磁策略。该策略具有以下优点。

(1) 针对实现电机宽速域运行这一难题,借助合理的标定试验以及数据拟合方式,整理出两张存有不同工况下电流信息的二维表格。通过控制输出电流确保低高速运行的稳定,同时保证低高速之间的平滑过渡。

(2) 借助模型预测控制与有限集思想的优点,取消调制环节,简化算法控制的整体结构,提高系统的动态响应。

(3) 通过实时反馈的反电动势和合理的动态弱磁参数来调节转速系数,保证系统的稳态和动态控制效果。

参考文献

康劲松, 蒋飞, 钟再敏, 等.

电动汽车用永磁同步电机弱磁控制策略综述

[J]. 电源学报, 2017, 15(1):15-22.

[本文引用: 1]

KANG Jinsong, JIANG Fei, ZHONG Zaimin, et al.

Overviews of flux weakening control schemes with permanent magnet synchronous motor used in electric vehicles

[J]. Journal of Power Supply, 2017, 15(1):15-22.

[本文引用: 1]

杨阳.

基于转矩—转速—电流MAP的车用永磁同步电机矢量控制优化

[D]. 长春:吉林大学, 2018.

[本文引用: 1]

YANG Yang.

Optimization of field control for permanent magnet synchronous motor in electric vehicle based on torque-speed-current MAP

[D]. Changchun:Jilin University, 2018.

[本文引用: 1]

MICHAEL M, JOACHIM B.

Optimum control for interior permanent magnet synchronous motors (IPMSM) in constant torque and flux weakening range

[C]// 2006 12th International Power Electronics and Motion Control Conference,August 30-Stepember 1,2006,Portoroz,Slovenia. Piscataway:IEEE, 2006:282-286.

[本文引用: 1]

ERIC A, RADU I B, PAOLO G, et al.

Experimental identification of the magnetic model of synchronous machines

[J]. IEEE Transactions on Industry Applications, 2013, 49(5):2116-2125.

DOI:10.1109/TIA.2013.2258876      URL     [本文引用: 1]

YONG-CHEOL K, SUNGMIN K, SEUNG-KI S.

Voltage feedback current control scheme for improved transient performance of permanent magnet synchronous machine drives

[J]. IEEE Transactions on Industrial Electronics, 2012, 59(5):3373-3382.

DOI:10.1109/TIE.2011.2173097      URL     [本文引用: 1]

SAVERIO B, SILVERIO B, LUCA P, et al.

Combined speed and current model predictive control with inherent field-weakening features for PMSM drives

[C]// MELECON 2008 - The 14th IEEE Mediterranean Electrotechnical Conference,May 5-7,2008,Ajaccio,France. Piscataway:IEEE, 2008:472-478.

[本文引用: 1]

JINGLIN L, CHAO G, ZEXIU H, et al.

IPMSM model predictive control in flux-weakening operation using an improved algorithm

[J]. IEEE Transactions on Industrial Electronics, 2018, 65(12):9378-9387.

DOI:10.1109/TIE.2018.2818640      URL     [本文引用: 1]

BON-HO B, NITIN P, STEVEN S, et al.

New field weakening technique for high saliency interior permanent magnet motor

[C]// 38th IAS Annual Meeting on Conference Record of the Industry Applications Conference,October 12-16,2003,Salt Lake City,UT,USA. Piscataway:IEEE, 2003:898-905.

[本文引用: 1]

李雪, 迟颂, 刘聪, 等.

基于虚拟电阻的永磁同步电机单电流调节器弱磁控制

[J]. 电工技术学报, 2020, 35(5):1046-1054.

[本文引用: 1]

LI Xue, CHI Song, LIU Cong, et al.

Flux-weakening control with single current regulator of permanent magnet synchronous motor based on virtual resistor

[J]. Transactions of China Electrotechnical Society, 2020, 35(5):1046-1054.

[本文引用: 1]

白玉成, 唐小琦, 吴功平.

内置式永磁同步电机弱磁调速控制

[J]. 电工技术学报, 2011, 26(9):54-59.

[本文引用: 1]

BAI Yucheng, TANG Xiaoqi, WU Gongping, et al.

Speed control of flux weakening on interior permanent magnet synchronous motors

[J]. Transactions of China Electrotechnical Society, 2011, 26(9):54-59.

[本文引用: 1]

盛义发, 喻寿益, 桂卫华, 等.

轨道车辆用永磁同步电机系统弱磁控制策略

[J]. 中国电机工程学报, 2010, 30(9):74-79.

[本文引用: 1]

SHENG Yifa, YU Shouyi, GUI Weihua, et al.

Field weakening operation control strategies of permanent magnet synchronous motor for railway vehicles

[J]. Proceedings of the CSEE, 2010, 30(9):74-79.

[本文引用: 1]

席裕庚, 李德伟, 林姝.

模型预测控制——现状与挑战

[J]. 自动化学报, 2013, 39(3):222-236.

[本文引用: 1]

XI Yugeng, LI Dewei, LIN Shu.

Model predictive control——Status and challenges

[J]. Acta Automatica Sinica, 2013, 39(3):222-236.

[本文引用: 1]

RALPH K, JOSE R, JOSE R E, et al.

High performance speed control methods for electrical machines: An assessment

[C]// 2010 IEEE International Conference on Industrial Technology,March 14-17,2010,Via del Mar,Chile. Piscataway:IEEE, 2010:1793-1799.

[本文引用: 1]

郑泽东, 王奎, 李永东, 等.

采用模型预测控制的交流电机电流控制器

[J]. 电工技术学报, 2013(11):118-123.

[本文引用: 1]

ZHENG Zedong, WANG Kui, LI Yongdong, et al.

Current controller for AC motors using model predictive control

[J]. Transactions of China Electrotechnical Society, 2013(11):118-123.

[本文引用: 1]

FENGXIANG W, SHIHUA L, XUEZHU M, et al.

Model-based predictive direct control strategies for electrical drives:An experimental evaluation of PTC and PCC Methods

[J]. IEEE Transactions on Industrial Informatics, 2015, 11(3):671-681.

DOI:10.1109/TII.2015.2423154      URL     [本文引用: 1]

柯栋梁, 汪凤翔, 李家祥.

基于自适应高增益观测器的永磁同步电机预测电流控制方法

[J]. 中国电机工程学报, 2021, 41(2):728-738.

[本文引用: 1]

KE Dongliang, WANG Fengxiang, LI Jiaxiang.

Predictive current control of permanent magnet synchronous motor based on adaptive high-gain observer

[J]. Proceedings of the CSEE, 2021, 41(2):728-738.

[本文引用: 1]

张永昌, 杨海涛, 魏香龙.

基于快速矢量选择的永磁同步电机模型预测控制

[J]. 电工技术学报, 2016, 31(6):66-73.

[本文引用: 1]

ZHANG Yongchang, YANG Haitao, WEI Xianglong.

Model predictive control of permanent magnet synchronous motors based on fast vector selection

[J]. Transactions of China Electrotechnical Society, 2016, 31(6):66-73.

[本文引用: 1]

张昌凡, 吴公平, 何静, 等.

一种永磁同步电机失磁故障容错预测控制算法

[J]. 电工技术学报, 2017, 32(15):100-110.

[本文引用: 1]

ZHANG Changfan, WU Gongping, HE Jing, et al.

Fault-tolerant predictive control for demagnetization faults in permanent magnet synchronous machine

[J]. Transactions of China Electrotechnical Society, 2017, 32(15):100-110.

[本文引用: 1]

李家祥, 汪凤翔, 柯栋梁, 等.

基于粒子群算法的永磁同步电机模型预测控制权重系数设计

[J]. 电工技术学报, 2021, 36(1):50-59,76.

[本文引用: 1]

LI Jiaxiang, WANG Fengxiang, KE Dongliang, et al.

Weighting factors design of model predictive control for permanent synchronous machine using particle swarm optimization

[J]. Transactions of China Electrotechnical Society, 2021, 36(1):50-59,76.

[本文引用: 1]

王伟华, 肖曦.

永磁同步电机高动态响应电流控制方法研究

[J]. 中国电机工程学报, 2020, 40(10):3328-3336.

[本文引用: 1]

WANG Weihua, XIAO Xi.

An current control method for permanent magnet synchronous motors with high dynamic performancel

[J]. Proceedings of the CSEE, 2020, 40(10):3328-3336.

[本文引用: 1]

SAMIR K, PATRICIO C, RENÉ V, et al.

Model predictive control:A simple and powerful method to control power converters

[J]. IEEE Transactions on Industrial Electronics, 2009, 56(6):1826-1838.

DOI:10.1109/TIE.2008.2008349      URL     [本文引用: 2]

TAKUYA S, SHINJI D.

Improvement of torque control system of PMSM based on model predictive control

[C]// IECON 2011 - 37th Annual Conference of the IEEE Industrial Electronics Society,September 2-6,2013,Lille,France. Piscataway:IEEE, 2013:1-7.

[本文引用: 1]

/

〈 〉