电气工程学报, 2021, 16(4): 33-41 doi: 10.11985/2021.04.005

特邀专栏：高性能永磁电机驱动与控制

内置式永磁同步电机的极宽调制低振噪设计*

马琛,, 吉敬华,, 赵文祥,, 刘童,

江苏大学电气信息工程学院 镇江 212013

Pole Width Modulation-based Low Vibration and Noise Design for Interior Permanent Magnet Synchronous Motor

MA Chen,, JI Jinghua,, ZHAO Wenxiang,, LIU Tong,

School of Electrical and Information Engineering, Jiangsu University, Zhenjiang 212013

收稿日期: 2021-05-27   修回日期: 2021-09-27  

基金资助: * 国家自然科学基金重大资助项目.  51991383

Received: 2021-05-27   Revised: 2021-09-27  

作者简介 About authors

马琛,男,1989年生,硕士研究生。主要研究方向为永磁同步电机振动与噪声。E-mail： 420952047@qq.com

刘童,男,1996年生,博士研究生。主要研究方向为永磁同步电机振动与噪声建模与分析。E-mail： 15052937229@163.com

赵文祥,男,1976年生,教授,博士研究生导师。主要研究方向为电机及其控制。E-mail： zwx@ujs.edu.cn

刘童,男,1996年生,博士研究生。主要研究方向为永磁同步电机振动与噪声建模与分析。E-mail： 15052937229@163.com

摘要

对于整数槽内置式永磁同步电机,槽数阶电磁力是零阶振动的主要来源。为实现电机的低振噪设计,采用极宽调制技术对电机转子进行修型,抑制齿数阶电磁力。首先,推导出72槽12极内置式永磁同步电机激振力的时空分布数学模型,分析72阶电磁力来源。然后,采用极宽调制技术优化72阶电磁力,并确定最终设计方案。最后,建立电机电磁-振动-噪声的多物理场仿真模型,对电机的电磁力、模态特征、振动响应和噪声辐射进行仿真分析。通过对比优化前和优化后电机的零阶振动和噪声,验证所提方法的有效性,为内置式永磁同步电机的低振噪设计提供新的方法。

关键词： 极宽调制 ; 齿数阶电磁力 ; 转子修型 ; 低振噪设计 ; 永磁电机

Abstract

For the integer slot interior permanent magnet synchronous motor (IPMSM), slot number order force is an important source of the zeroth mode vibration. Pole width modulation technology is used to modify the rotor, restrain slot number order force, and realize the low vibration and noise design. Firstly, the mathematical model of the temporal and spatial characteristics of electromagnetic force of the 72-slot/22-pole IPMSM is deduced. Then, the source of 72nd-order electromagnetic force is analyzed. Subsequently, pole width modulation technology is used to optimize the 72nd-order electromagnetic force, and the final optimization scheme is adopted by simulated validated. Finally, the multi-physical simulation model of electromagnetic vibration and noise is established to predict the electromagnetic force, modal characteristics, vibration response and radiation noise of machine are analyzed. Vibration displacement and sound pressure level are compared between the existed and proposed machine. The results verify the effectiveness of the proposed method. A new method for low vibration and noise design for IPMSM is provided.

Keywords： Pole width modulation ; slot number order force ; modal analysis ; low vibration and noise design ; permanent magnet motor

PDF (2720KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

马琛, 吉敬华, 赵文祥, 刘童. 内置式永磁同步电机的极宽调制低振噪设计*. 电气工程学报[J], 2021, 16(4): 33-41 doi:10.11985/2021.04.005

MA Chen, JI Jinghua, ZHAO Wenxiang, LIU Tong. Pole Width Modulation-based Low Vibration and Noise Design for Interior Permanent Magnet Synchronous Motor. Journal of Electrical Engineering[J], 2021, 16(4): 33-41 doi:10.11985/2021.04.005

1 引言

内置式永磁同步电机(Interior permanent magnet synchronous motor,IPMSM)具有宽调速范围、高功率密度、高效率等诸多优点,因此在电动汽车、船舶推进等领域中得到了广泛的应用[1,2]。随着各应用领域的快速发展,对IPMSM的品质性能有了更高的要求。其中,电磁振动噪声已成为评价IPMSM电机性能的重要指标。

IPMSM电机的电磁振动噪声分析主要涉及电磁场、结构模态、振动和声辐射[3]。目前,国内外学者已对电机电磁振动噪声的分析与抑制方法进行了大量研究。文献[4]通过优化转子隔磁桥结构,减少了径向气隙磁密的谐波含量,抑制电磁力谐波幅值来降低电机的振动噪声,但文中未给出选择该优化结构的理论依据。文献[5]提出了一种定子齿偏移结构来削弱幅值较大的径向电磁力,以此来降低电机的振动噪声幅值。文献[6]研究了磁极偏心对电机高频振动噪声的抑制机理,然而未对低频振动噪声进行研究。上述研究中主要是优化电机的电磁拓扑结构,抑制电磁力谐波幅值以及电机的振动噪声。优化电机极弧系数[7]、定子齿宽[8]、磁极偏心距离[9]、定子斜槽等参数,能够有效改善气隙磁场波形的正弦度。因此,本文将基于对关键电磁部件进行修型这一思路对电机的特定阶次电磁力谐波幅值进行抑制,实现对电机的低振动噪声设计。

近些年来有学者对电机驱动控制中的脉宽调制(Pulse width modulation, PWM)波形进行等效处理,并将这一波形应用于转子的优化设计。文献[10]在表贴式电机上采用极宽调制技术对永磁体进行分块设计。通过理论计算确定了整个转子表面分块永磁体的空间位置与磁极的大小,有效地抑制了气隙磁密中的谐波含量。文献[11]研究了内置式永磁同步电机采用极宽调制技术改善气隙磁场正弦波畸变率。但是文中仅对比了空载气隙磁密谐波幅值变化,并未进一步对负载气隙磁密谐波抑制效果进行研究。文献[12]阐述了IPMSM采用极宽调制技术对齿槽转矩、空载反电势谐波含量的影响。上述研究表明极宽调制技术在空载工况对于抑制电机内磁密谐波含量有着一定的效果。在此基础上,本文进一步地研究了极宽调制技术在负载工况对IPMSM的电磁力和振动噪声的抑制作用。需要注意的是,采用该方法实现对电机振动噪声的抑制,首先需要分析对电机振动噪声贡献最大的电磁力的时空特征分布及其来源,进而针对性选取合理的极宽调制修型 方案。

在传统的电机电磁力及振动噪声的研究中,主要是对气隙内最低阶次的电磁力时空特征进行研究分析,忽略了高阶次电磁力对电机振动噪声的影响。然而,近期电磁力调制效应受到了国内外学者的广泛关注。文献[13]研究了阶次大于槽数阶的电磁力对电机低阶次振动噪声的贡献。主要是由于定子齿结构对电磁力的调制效应,从而使高阶电磁力能够引起定子轭部的低阶次、大幅值的振动位移。该文章揭示了对于特定槽极配合的电机,高阶电磁力是引起电机振动的主要因素。文献[14]根据电磁力调制效应,发现电机中槽数阶电磁力能够引起整数槽电机大振幅的零阶振动,同时验证了槽数阶径向力是导致整数槽电机零阶振动的主要因素。电磁力调制理论的研究为IPMSM的低振动噪声设计提供了新的理论依据与设计思路。

本文针对72槽12极V型磁极结构IPMSM进行低振动噪声设计的研究。采用极宽调制技术对转子铁心结构进行修型,抑制IPMSM的72阶电磁力幅值,进而改善IPMSM的振动噪声表现。首先确定IPMSM转子修型的最优方案,接着对比优化前后的72阶电磁力幅值,最后搭建振动噪声仿真模型对比电机的振动响应和声压级,验证极宽调制技术对电机振动噪声抑制的有效性。该方法同样适用于其他槽极配合的IPMSM的低振噪设计。

2 电磁力特征分析

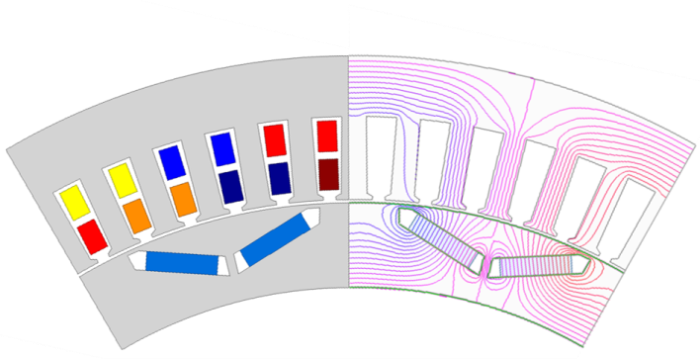
本文以一台72槽12极V型磁极IPMSM为例开展研究。表1给出了该电机的基本尺寸参数及电磁性能,电机的二维有限元模型及其磁力线分布如图1所示。

表1   72槽12极IPMSM基本参数

参数数值
额定功率/kW67
额定转速/(r/min)4 282
额定转矩/(N·m)116
绕组相数6
极数/槽数12/72
定子外径/mm430
定子内径/mm340
转子内径/mm285
气隙长度/mm1
永磁体厚度/mm6
直轴电感/交轴电感/mH3.62/6.38

新窗口打开| 下载CSV


图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   电机二维模型与磁力线分布


2.1 电磁力分析

根据Maxwell应力方程,定子齿表面的径向和切向电磁力密度可以表示为

$\left\{ \begin{array}{l}{F_r} = \frac{1}{{2{\mu _0}}}(B_r^2 - B_\tau ^2)\\{F_\tau } = \frac{1}{{{\mu _0}}}{B_r}{B_\tau }\end{array} \right.$

式中,Fr和Fτ分别为径向和切向电磁力密度;μ0为真空磁导率;Br和Bτ分别为气隙磁通密度的径向和切向分量。

因此,要对电磁力的时空特征进行分析,首先需要对气隙内径向和切向磁密分量进行解析。由于一个磁极下永磁体的几何结构都是左右对称的,同时考虑到磁极的周期性,电机的气隙磁场可以展开为周向坐标θ的傅里叶级数形式。根据傅里叶级数的性质,径向磁密的展开式中将只包含余弦项,而切向磁密将只包含正弦项[15]。

忽略铁心饱和效应,气隙内永磁磁场的径向和切向磁密分别表示为

$\begin{array}{l}{B_{r\_PM}} = \sum\limits_n^\infty {B_{r\_PM}^n\cos \left[ {n(p\theta - \omega t){\rm{ + }}{\beta _0}} \right]} + \\\;\;\sum\limits_n^\infty {\sum\limits_k^\infty {B_{rk\_PM}^n\cos [(np \pm kZ)\theta - n\omega t{\rm{ + }}{\beta _n}]} } \end{array}$
$\begin{array}{l}{B_{\tau \_PM}} = \sum\limits_n^\infty {B_{\tau \_PM}^n\sin \left[ {n(p\theta - \omega t){\rm{ + }}{\beta _0}} \right]} + \\\;\;\sum\limits_n^\infty {\sum\limits_k^\infty {B_{\tau k\_PM}^n\sin [(np \pm kZ)\theta - n\omega t{\rm{ + }}{\beta _n}]} } \end{array}$

式中,Bn r_PM和Bn τ_PM分别为n阶永磁磁密谐波的径向和切向分量幅值;n=2k-1,k=0, 1, 2, …;p为电机极对数;ω为基波角频率;β为磁密相位。

类似地,IPMSM的电枢磁密径向和切向分量表示为[6]

${B_{r\_arm}} = \sum\limits_v^\infty {\sum\limits_k^\infty {{B_\mu }\sin [(\nu {N_t} \pm kZ)\theta - {\omega _1}t + {\theta _1}]}}$
${B_{\tau \_arm}} = \sum\limits_v^\infty {\sum\limits_k^\infty {{B_\mu }\cos [(\nu {N_t} \pm kZ)\theta - {\omega _1}t + {\theta _1}]} }$

式中,对于整数槽双层绕组电机而言,v=12k±1,k=0, 1, 2, …;Nt=GCD(Z, p),GCD为最大公约数;Z为电机槽数;ω1为基波电流角频率;θ1为基波电流相位角。

根据线性叠加原理,气隙中合成磁场的径向和切向分量可由下式得到

$\left\{ \begin{array}{l}{B_r} = {B_{r\_PM}} + {B_{r\_arm}}\\{B_\tau } = {B_{\tau \_PM}} + {B_{\tau \_arm}}\end{array} \right.$

联立上式,将式(6)代入式(1)即可得到径向与切向电磁力密度的解析表达式。

根据式(6)的计算结果,电磁力密度可以按照其来源分为3类：第1类为永磁磁场相互作用产生;第2类为永磁和电枢磁场相互作用产生;第3类为电枢磁场相互作用产生。表2总结了这3类电磁力密度的空间阶次和频率特征,其中fr为电机电频率。

表2   电磁力密度阶次与频率特征

分类阶次频率
第1类(n1+n2)p(n1+n2)fr
(n1-n2)p(n1-n2)fr
(n1+n2)p±kZ(n1+n2)fr
(n1-n2)p±kZ(n1-n2)fr
第2类(n+ν)p±kZ(n+1)fr
(n-ν)p±kZ(n-1)fr
第3类(ν1-ν2)p±kZ0
(ν1+ν2)p±kZ2fr

新窗口打开| 下载CSV


2.2 电磁力调制效应

由于定子齿的调制作用,当电磁力的空间阶次大于定子齿数的一半时,对应的高阶电磁力会引起定子的低阶振动形变[14, 16-17],其具体过程可由式(7)表示[18]

$\left\{ \begin{array}{l}{P_r}{\rm{ = }}{F_r}\cos [(\lambda - a{Z_s}){\theta _z} + i\omega t + \beta ]\\\left| {\left| \lambda \right| - aZ} \right| \le \frac{{{Z_s}}}{2}\end{array} \right.$

式中,Fr为径向电磁力密度幅值;λ和i分别为径向力谐波的空间阶次与时间阶次;Zs为电机总槽数;θz为第Z个定子齿的位置角度;a为非负整数。

根据奈奎斯特-香农采样定理,当λ>Zs/2时,电磁力谐波的空间阶次大于奈奎斯特频率,会发生混叠现象,由定子齿采样后的电磁力的空间阶次会变为(λ-mZ)阶。以72槽12极电机为例,气隙中的72阶电磁力被72个齿调制为零阶电磁力,从而引起定子轭部的零阶振动。

将定子轭部和机壳结构等效为一个圆环,其零阶振动的位移与其他阶次振动位移的比值可以表示为[14]

$\frac{{{Y_{m = 0}}}}{{{Y_{m \ge 2}}}}{\rm{ = }}\frac{1}{{12}} \times {(\frac{{{T_y}}}{{{R_y}}})^2} \times \frac{{{F_r}_{m = 0}}}{{{F_r}_{m \ge 2}}} \times {({m^2} - 1)^2}$

式中,Ty为定子轭部厚度;Ry为定子轭部平均半径。m为径向力的阶次。当m增大时,随着(m2-1)2的值增大,零阶振动位移占整体振动位移的比重就越大。

因此对于72槽12极整数槽电机,72阶径向电磁力引起的零阶振动是电机振动位移的主要分量。表3考虑永磁磁场的作用以及永磁磁场和电枢磁场的作用,分析了72阶径向力来源成分的阶次与频率。

表3   72槽12极电机72阶径向力电磁力来源

永磁磁密阶次n电枢v永磁磁密阶次n
1Nt11Nt13Nt1p11p
p0/060/1072/120/060/10
12/272/1284/1412/272/12
3p12/248/860/1012/248/8
24/484/1496/1624/484/14
5p24/436/648/824/436/6
36/696/16108/1836/696/16
7p36/624/436/636/624/4
48/8108/18120/2048/8108/18
9p48/812/224/448/812/2
60/10120/20132/2260/10120/20
11p60/100/012/260/100/0
72/12132/22144/2472/12132/22

新窗口打开| 下载CSV


3 极宽调制转子修型

3.1 永磁磁密谐波抑制

第2.2节中阐述了72阶电磁力引起零阶振动的原因。本节将重点介绍极宽调制技术对72阶电磁力抑制机理。

根据表3中的分析结果可知,72槽12极IPMSM的72阶径向力主要是由阶次相差60的永磁磁密谐波相互作用产生。由表4可见,6(1p)阶基波永磁磁密和66(11p)阶永磁磁密谐波的贡献最大。

表4   72阶径向力磁场谐波来源

磁场谐波成分径向力幅值/(N/cm2)
(1p, 11Nt)10.6
(1p, 13Nt)17.5
(1p, 11p)9.95
(3p, 9p)0.06
(5p, 7p)0.15
(11p, 1Nt)24.3

新窗口打开| 下载CSV


对IPMSM转子铁心上开槽会改变等效磁导函数的分布,进而影响永磁磁密的谐波次数与幅值。因此,选取合理的开槽方案可以实现对66阶永磁磁密谐波的抑制,达到抑制72阶径向电磁力的目的。

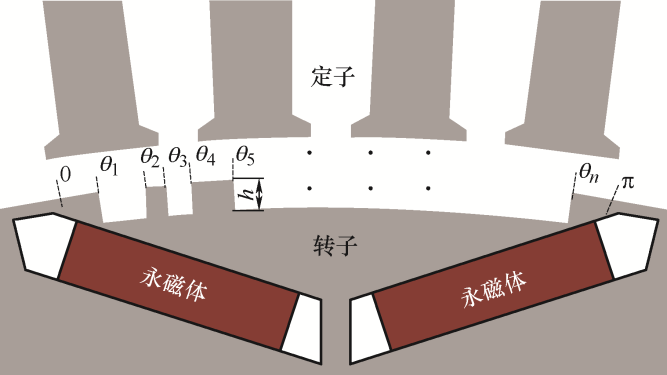
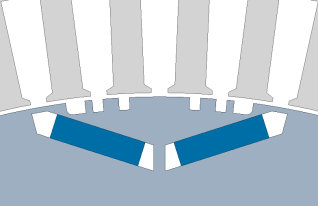
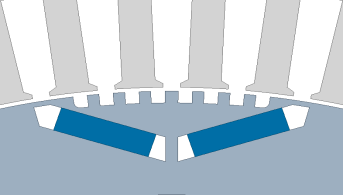
采用极宽调制技术对转子进行修型可以看成是在极轴周围设置对称的沟槽,沟槽的形状根据一组角度θ1,θ2,…,θn和深度h确定,图2所示为一个磁极下的理想结构示意图。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   理想转子结构


根据式(9)和式(10)可以推导出这些沟槽的具体角度[11]。在一个极距[0, π]内,沟槽的角度位置的列向量为A=[θ1, θ2, …, θn]T,其中0<θ1<θ2<…<θn<π。

$P\left( {{A_\infty }} \right){\rm{ = }}{\left[ {{p_1},{p_2}{\rm{,}} \cdots {\rm{,}}\;{p_n}} \right]^T}\;\;\;\;\left( {{A_\infty }} \right) = 0$
$\left\{ \begin{array}{l}{p_1}({A_{\bf{1}}}) = \sum {B(\theta )\sin \theta {\rm{d}}\theta } - \frac{{\pi }}{2}{B_1}\\{p_i}({A_{\bf{2}}}) = \sum {B(\theta )\sin (i\theta ){\rm{d}}\theta } \end{array} \right.$

式中,B(θ)为[0, π]范围内上的磁通密度;B1为磁通密度的基波幅值;i为需要消除的i次永磁谐波磁动势,i=3, 5, 7, …;选取i=11可以抑制66阶永磁磁密的幅值,对应的结构为6槽结构;另外选取i为7、9、15进行对比,分别对应4槽、5槽、8槽结构。使用Matlab编程求解出优化的角度矩阵,选择这四种转子修型方案建立结构模型,如表5所示。

表5   四种极宽调制修型结构

槽结构结构模型
4槽
5槽
6槽
8槽

新窗口打开| 下载CSV


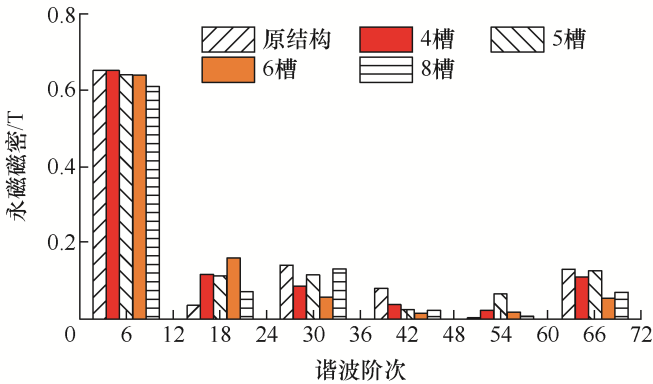
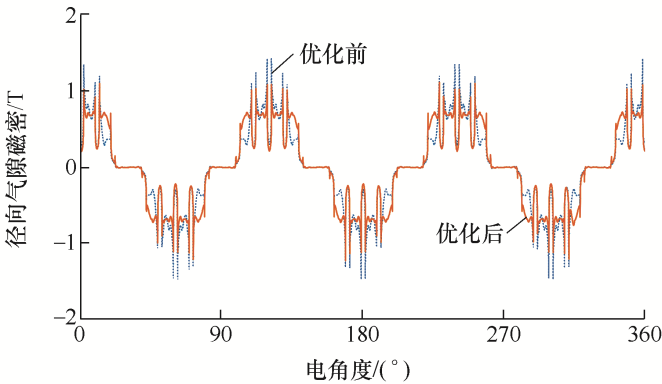
图3为原IPMSM转子结构和四种开槽结构空载永磁磁密谐波分析结果。整体来看,偶数槽数结构抑制谐波的效果好于奇数槽数结构,奇数槽的54阶、66阶谐波幅值明显大于偶数槽。首先对比6阶谐波即永磁基波,4、5、6槽结构对基波磁密的抑制不大而8槽结构对基波的抑制作用太大,其中6槽结构的基波磁密仅下降1.9%。接着比较66阶谐波,由于66阶永磁谐波与基波永磁磁密相互作用产生72阶电磁力,图3中6槽结构的66阶永磁谐波幅值最小,最后选择6槽结构为最终开槽方案。图4为原始结构和6槽结构电机的空载气隙磁密波形对比。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   原结构与四种修型方案永磁磁密谐波对比


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   原始结构与6槽结构空载径向气隙磁密波形


3.2 齿数阶电磁力抑制

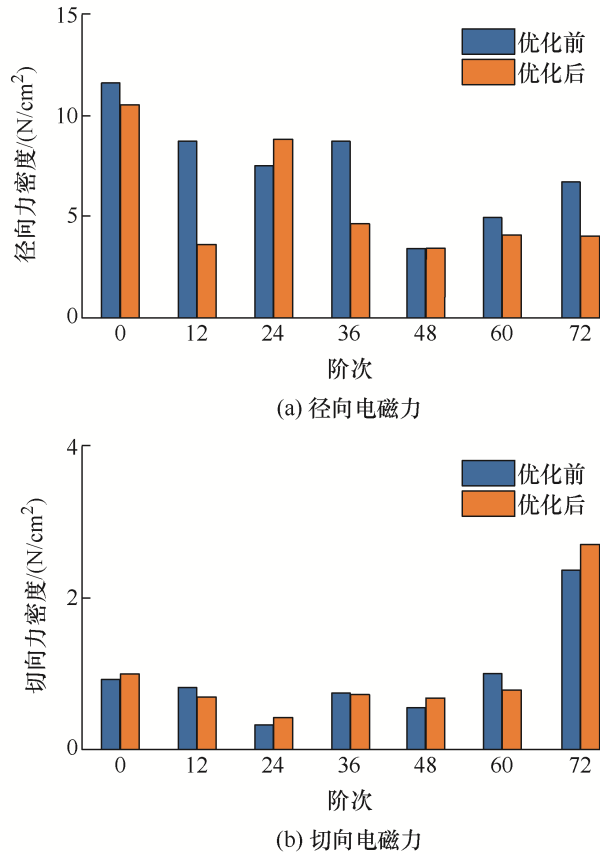
极宽调制转子修型的主要目的是抑制72阶径向电磁力的幅值,图5为优化前后电磁力幅值对比。从图5中可以看出,优化后的径向电磁力幅值整体呈现下降的趋势,只有24阶径向力有所增加,其中72阶径向电磁力降低了40.22%;优化后的0阶、72阶切向电磁力幅值略有上升,其中72阶切向电磁力增加了13.9%。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   优化前后电磁力谐波阶次


根据电磁力密度的传递模型,气隙中的径向和切向电磁力密度可以用一组径向集中力和一组切向集中力进行等效替换[19]。等效后的径向和切向集中力可以表示为

$\left\{ \begin{array}{l}{P_{\rm{r}}} = \int {L{R_s}\left( {{F_r}\cos \alpha + {F_\tau }\sin \alpha } \right)} \;{\rm{d}}\theta \\{P_\tau } = \int {L{R_s}\left( {{F_\tau }\cos \alpha + {F_r}\sin \alpha } \right)} \;{\rm{d}}\theta \\\\\alpha = {\theta _z} - \theta \end{array} \right.$

式中,L为定子有效长度;Rs为定子内径。

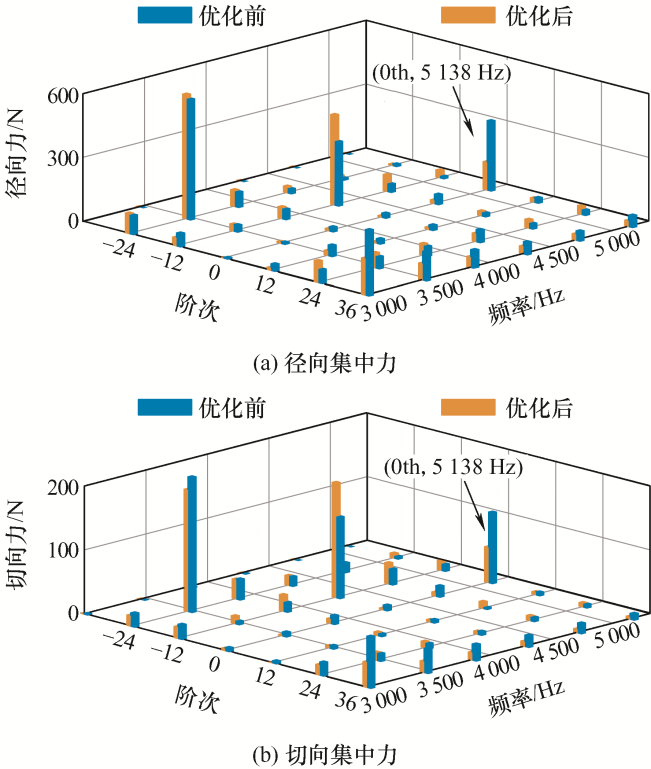
通过式(11)可计算得到等效后的集中力。图6为两种结构的集中力对比。72阶12倍频电磁力被调制为0阶12倍频的集中力,优化后的0阶12倍频径向集中力幅值下降59.8%,切向集中力幅值下降50%。总体而言,6槽结构有效地抑制了72槽12极电机的72阶12倍频电磁力幅值。该方法同样适用于其他槽极配合的整数槽IPMSM的电磁力谐波抑制。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   优化前后集中电磁力对比


3.3 转子应力分析

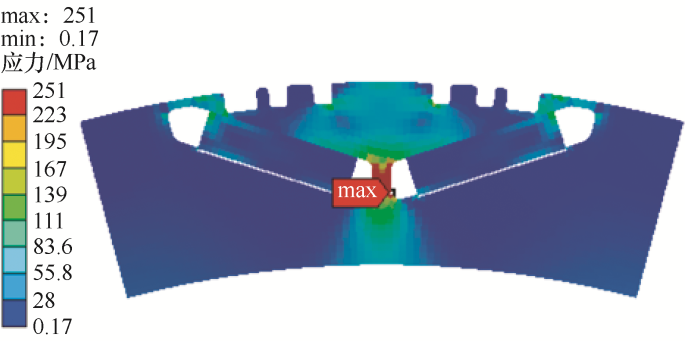
极宽调制转子修型会影响转子铁心的应力分布,一定程度上槽口处的受力会更为集中。为了确保优化后转子的机械强度,利用有限元法对6槽结构转子部件进行强度校核。图7为电机在10 000 r/min工况下转子应力分布图。其中,电机转子材料为硅钢片B35AH230,其屈服强度为400 MPa。从图7可以看出,6槽结构在隔磁桥处受最大应力为251 MPa,槽口处的最大应力为190 MPa,两者都小于其屈服强度400 MPa,因此修型后的转子结构满足机械强度设计要求。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   优化后转子应力分布图


3.4 电磁性能分析

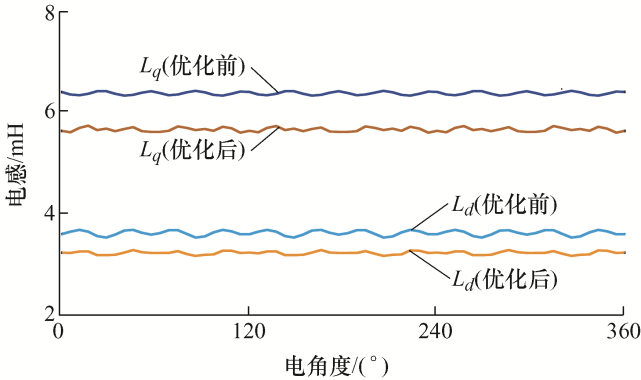
转子表面修型会导致电机d、q轴磁路磁阻的变化,会对磁阻转矩以及弱磁能力产生一定影响。图8为两种结构d、q轴电感变化对比。优化前Ld为3.62 mH,Lq为6.38 mH,凸极率为1.763;优化后Ld为3.22 mH,Lq为5.67 mH,凸极率为1.76。由于两种结构的凸极率基本一致,所以优化前后电机的磁阻转矩和弱磁能力保持不变。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   优化前后交直轴电感曲线


表6为电机负载转矩波对比,在三种工况下,优化后的负载平均转矩比原结构有所降低,在额定工况和弱磁工况优化后的转矩脉动明显增加,在过载工况优化后的转矩脉动小于优化前。转矩脉动的增加会增加电机的横向运动,可以通过提高电机安装刚度来减小电机的横向运动[20]。

表6   负载转矩对比

负载工况结构平均转矩/ (N·m)转矩脉动(%)
额定工况
(4 282 r/min)		优化前11632
优化后11444
弱磁工况
(9 100 r/min)		优化前5244
优化后5065
过载工况
(2 150 r/min)		优化前40539
优化后39433

新窗口打开| 下载CSV


4 分析与验证

4.1 模态分析

电机的结构模态是电机的固有属性,当电磁力的频率和电机结构对应阶次模态的频率相近或一致时,会产生共振。

模态分析主要是分析电机定子侧结构固有振型的阶次与频率。模态分析主要有三种：解析法、有限元法以及模态试验法。本文采用有限元法对电机模态进行仿真分析,有限元法能够同时设置约束条件、正交各项异性材料特征和各部件接触方式等,较为精确地计算出电机定子侧结构的模态振型和频率。表7为电机各部件的材料参数。

表7   材料参数

材料密度/ (kg/m3)泊松比弹性模量/GPa切变模量/GPa
定子铁心8 000uxy=0.3
uyz= uxz=0.27		Ex= Ey=195
Ez =130		Gyz= Gxz=26.5
Gxy=55
机壳7 2000.2811043

新窗口打开| 下载CSV


表8为定子铁心模型和整机模型的有限元模态仿真结果。由表8可以得出机壳的加入会使各阶振型固有频率上升,额定工况下电机的电频率为428.2 Hz,72阶电磁力对应的12倍频的频率为5 138.4 Hz,电机零阶固有频率为11 168 Hz,两者相差较大,因此电机在12倍频处发生共振的可能性较小。

表8   定子铁心和整机模态频率及模态振型

阶次定子铁心结构频率/Hz整机模型频率/Hz
3阶1 0243 795
4阶1 8724 253
5阶2 8905 421
6阶3 9956 992
0阶7 07511 168

新窗口打开| 下载CSV


4.2 振动分析

将电机定子侧结构简化为圆柱壳体,则m阶模态的振动位移可以表示为[17]

${A_m} = \frac{{{P_m}/M}}{{\sqrt {(\omega _m^2 - \omega _r^2) + 4\xi _m^2\omega _m^2\omega _r^2} }}$

式中,Pm为m阶电磁力幅值;M为等效圆柱壳体质量;ωm为m阶模态的固有角频率;ωr为r阶电磁力角频率;ζm为模态阻尼系数,对于中小型电机的经验公式为

${\xi _m} = \frac{1}{{2\pi }}(2.76 \times {10^{ - 5}}{f_m} + 0.062)$

表9为12倍频处机壳表面振动加速度和位移对比。在额定工况(4 282 r/min)、弱磁工况(9 100 r/min)、过载工况(2 150 r/min)和5 893 r/min工作点,6槽结构的振动加速度和位移大小优于原结构。

表9   不同工况下机壳表面12倍频振动加速度和位移

运行工况结构振动加速度/(m/s2)位移/mm
额定工况优化前1.41
优化后0.36
弱磁工况优化前1.23
优化后0.27
过载工况优化前1.83
优化后0.63
运行工况结构振动加速度/(m/s2)位移/mm
5 893 r/min优化前1.62
优化后0.57

新窗口打开| 下载CSV


4.3 噪声分析

用有限长圆柱壳体替代电机机壳得到电机定子的辐射声功率为

$W{\rm{ = }}\frac{1}{2}\rho c{\omega ^2}A_m^2{S_{cl}}$

式中,Scl与电机表面积和定子铁心的模态辐射率相关。根据辐射声功率可以得到声功率级

${L_w}{\rm{ = }}10\lg \frac{W}{{{{10}^{ - 12}}}}$

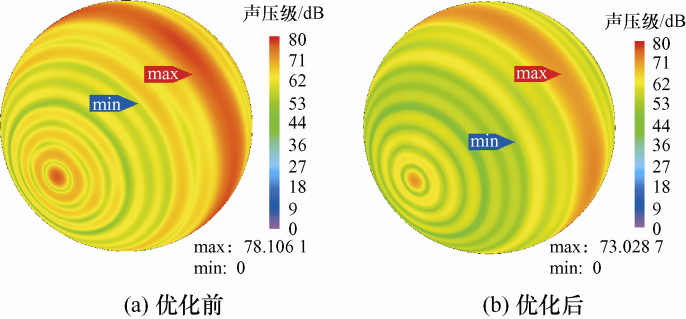
通过JMAG建立两种结构的声学有限元仿真模型,并采用边界元法求解耦合模型的声压级,对额定负载工况下电机辐射的噪声进行预测。图9为1 m球域模型的噪声分布,可以看出其为零阶振动位移所辐射的噪声。两模型的声压级水平(A计权)在12倍频时最高,原结构的声压级为78 dB,极宽调制修型结构的声压级为73 dB,这一结果与振动加速度变化趋势保持一致。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   电机辐射噪声对比


5 结论

(1) 采用极宽调制技术,对72槽12极V型磁极IPMSM的转子铁心表面进行修型,降低了引起电机零阶振动的72阶电磁力波幅值,并通过有限元仿真验证了极宽调制技术降低内置式整数槽永磁同步电机振动噪声的有效性。

(2) 通过仿真对比了空载永磁磁密各阶次谐波幅值,得到偶数槽抑制谐波的效果好于奇数槽,同时开槽数为6时,对72阶电磁力的幅值抑制效果最好。将6槽结构与原结构对比,电机经过优化后其振动加速度及声压级均有大幅度的下降,同时未增加其他对振动噪声贡献大的谐波。

(3) 本文所提出的方法适用于其他槽极配合的整数槽IPMSM的槽数阶电磁力抑制与低振噪设计。

参考文献

HAN Z, LIU J.

Comparative analysis of vibration and noise in IPMSM considering the effect of MTPA control algorithms for electric vehicles

[J]. IEEE Transactions on Power Electronics, 2021, 36(6):6850-6862.

DOI:10.1109/TPEL.63      URL     [本文引用: 1]

AMIN M, AZIZ G A A, DURKIN J, et al.

A robust simplified dynamic observer-based backstepping control of six-phase induction motor for marine vessels applications

[J]. IEEE Transactions on Industrial Electronics, 2020, 56(6):7044-7054.

[本文引用: 1]

MAO Y, ZHAO W, ZHU S, et al.

Vibration investigation of spoke-type PM machine with asymmetric rotor considering modulation effect of stator teeth

[J]. IEEE Transactions on Industrial Electronics, 2021, 68(10):9092-9103.

DOI:10.1109/TIE.2020.3022530      URL     [本文引用: 1]

王晓远, 贺晓钰, 高鹏.

电动汽车用V型磁钢转子永磁电机的电磁振动噪声削弱方法研究

[J]. 中国电机工程学报, 2019, 35(16):4919-4926.

[本文引用: 1]

WANG Xiaoyuan, HE Xiaoyu, GAO Peng.

Research on electromagnetic vibration and noise reduction method of V type magnet rotor permanent magnet motor electric vehicles

[J]. Proceedings of the CSEE, 2019, 35(16):4919-4926.

[本文引用: 1]

谢颖, 李飞, 黎志伟, 等.

内置永磁同步电机减振设计与研究

[J]. 中国电机工程学报, 2017, 37(18):5437-5445.

[本文引用: 1]

XIE Ying, LI Fei, LI Zhiwei, et al.

Optimized design and research of vibration reduction with an interior permanent magnet synchronous motor

[J]. Proceedings of the CSEE, 2017, 37(18):5437-5445.

[本文引用: 1]

LIU T, ZHAO W, JI J, et al.

Effects of eccentric magnet on high-frequency vibroacoustic performance in integral-slot SPM machines

[J]. IEEE Transactions on Energy Conversion, 2021, 36(3):2393-2403.

DOI:10.1109/TEC.2021.3060752      URL     [本文引用: 2]

邢泽智, 王秀和, 赵文良.

基于不同极弧系数组合分段倾斜磁极的表贴式永磁同步电机齿槽转矩削弱措施研究

[J]. 中国电机工程学报, 2021, 41(16):5737-5747.

[本文引用: 1]

XING Zezhi, WANG Xiuhe, ZHAO Wenliang.

Research on reduction methods of cogging torque based on segmented skewing magnetic poles with different combinations of pole-arc coefficients in surface-mounted permanent magnet synchronous motors

[J]. Proceedings of the CSEE, 2021, 41(16):5737-5747.

[本文引用: 1]

WU M, ZHAO W, JI J, et al.

Reduction of tooth harmonic in fractional-slot concentrated-winding permanent-magnet machines using new stator design

[J]. Journal of Magnetics, 2018, 23(2):218-228.

DOI:10.4283/JMAG.2018.23.2.218      URL     [本文引用: 1]

ZHOU M, ZHANG X, ZHAO W, et al.

Influence of magnet shape on the cogging torque of a surface-mounted permanent magnet motor

[J]. Chinese Journal of Electrical Engineering, 2021, 5(4):40-50.

DOI:10.23919/CJEE.7873788      URL     [本文引用: 1]

安跃军, 温宏亮, 安辉, 等.

磁极调制式永磁电机的磁场分析与实验

[J]. 电工技术学报, 2012, 27(11):111-117.

[本文引用: 1]

AN Yuejun, WEN Hongliang, AN Hui, et al.

Magnetic field analysis and experiment of sinusoidal magnetic pole modulation permanent magnet machine

[J]. Transactions of China Electrotechnical Society, 2012, 27(11):111-117.

[本文引用: 1]

CHAITHONGSUK S, TAKORABET N, KREUAWAN S.

Reduction of eddy-current losses in fractional-slot concentrated-winding synchronous PM motors

[J]. IEEE Transactions on Magnetics, 2015, 51(3):8102204.

[本文引用: 2]

王凯, 孙海阳, 张露锋, 等.

永磁同步电机转子磁极优化技术综述

[J]. 中国电机工程学报, 2017, 37(24):7304-7317.

[本文引用: 1]

WANG Kai, SUN Haiyang, ZHANG Lufeng, et al.

An overview of rotor pole optimization techniques for permanent magnet synchronous machines

[J]. Proceedings of the CSEE, 2017, 37(24):7304-7317.

[本文引用: 1]

ZHAO W, ZHU S, JI J, et al.

Analysis and reduction of electromagnetic vibration in fractional-slot concentrated- windings PM machines

[J]. IEEE Transactions on Industrial Electronics, 2021,DOI: 10.1109/TIE. 2021.3071701.

[本文引用: 1]

WANG S, HONG J, SUN Y, et al.

Analysis of zeroth-mode slot frequency vibration of integer slot permanent-magnet synchronous motors

[J]. IEEE Transactions on Industrial Electronics, 2019, 67(4):2954-2964.

DOI:10.1109/TIE.41      URL     [本文引用: 3]

LAN H, ZOU J, XU Y, et al.

Effect of local tangential force on vibration performance in fractional-slot concentrated winding permanent magnet synchronous machines

[J]. IEEE Transactions on Energy Conversion, 2019, 34(2):1082-1093.

DOI:10.1109/TEC.60      URL     [本文引用: 1]

WANG S, HONG J, SUN Y, et al.

Mechanical and magnetic pivot roles of tooth in vibration of electrical machines

[J]. IEEE Transactions on Energy Conversion, 2021, 36(1):139-148.

DOI:10.1109/TEC.60      URL     [本文引用: 1]

LIANG W, LUK P C K, et al.

Analytical study of stator tooth modulation on electromagnetic radial force in permanent magnet synchronous machines

[J]. IEEE Transactions on Industrial Electronics, 2021, 68(12):11731-11739.

DOI:10.1109/TIE.2020.3029462      URL     [本文引用: 2]

ZHU S, ZHAO W, JI J, et al.

Investigation of bread-loaf magnet on vibration performance in FSCW PMSM considering force modulation effect

[J]. IEEE Transactions on Transportation Electrification, 2021, 7(3):1379-1389.

DOI:10.1109/TTE.2020.3035180      URL     [本文引用: 1]

FANG H, LI D, GUO J, et al.

Hybrid model for electromagnetic vibration synjournal of electrical machines considering tooth modulation and tangential effects

[J]. IEEE Transactions on Industrial Electronics, 2021, 68(8):7284-7293.

DOI:10.1109/TIE.2020.3000137      URL     [本文引用: 1]

ZOU J, LAN H, XU Y, et al.

Analysis of global and local force harmonics and their effects on vibration in permanent magnet synchronous machines

[J]. IEEE Transactions on Energy Conversion, 2017, 32(4):1523-1532.

DOI:10.1109/TEC.2017.2720422      URL     [本文引用: 1]

/

〈 〉