电气工程学报, 2021, 16(4): 213-222 doi: 10.11985/2021.04.027

新能源发电与电能存储

考虑混合储能调频死区的自适应下垂控制策略*

方红艳,, 马平,

青岛大学电气工程学院 青岛 266071

Adaptive Droop Control Strategy Considering Frequency Modulation Dead Band of Hybrid Energy Storage

FANG Hongyan,, MA Ping,

College of Electric Engineering, Qingdao University, Qingdao 266071

收稿日期: 2021-05-8   修回日期: 2021-06-18  

基金资助: * 2016年智慧青岛建设工作计划重点资助项目

Received: 2021-05-8   Revised: 2021-06-18  

作者简介 About authors

方红艳,女,1995年生,硕士研究生。主要研究方向为电力系统分析与控制。E-mail： 819962276@qq.com

马平,女,1973年生,博士,副教授。主要研究方向为电力系统分析与控制。E-mail： qdumaping@163.com

摘要

为了优化混合储能参与电网一次调频,提出一种考虑混合储能调频死区的自适应下垂控制策略。采用超级电容和蓄电池组成的混合储能设备,根据各储能元件的特点,为了充分发挥其作用,将混合储能的调频死区设置在火电机组死区内,超级电容的调频死区设置在蓄电池死区内,不仅能提高调频效果,还能有效减少火电机组动作次数;基于Logistic函数,建立储能设备荷电状态(State of charge, SOC)与下垂系数的关系,利用自适应下垂控制策略参与电网一次调频,有效防止储能设备发生过充或过放现象;最后利用Matlab/Simulink进行仿真分析,结果证明该控制策略可以有效提高调频效果,改善频率质量,稳定储能设备荷电状态。

关键词： 混合储能 ; 调频死区 ; 一次调频 ; 自适应下垂控制 ; 荷电状态

Abstract

In order to optimize the hybrid energy storage participating in the primary frequency regulation of power grid, an adaptive droop control strategy considering the dead band of hybrid energy storage is proposed. According to the characteristics of each energy storage element, in order to give full play to its role, the frequency regulation dead zone of the hybrid energy storage is set in the thermal power unit, and the frequency regulation dead zone of the super capacitor is set in the battery, which can not only improve the frequency regulation effect, but also effectively reduce the frequent action of the thermal power unit. Then, based on the Logistic function, the relationship between the state of charge (SOC) of energy storage equipment and the droop coefficient is established, and the adaptive droop control strategy is used to participate in the primary frequency regulation of power grid, to effectively prevent the energy storage equipment from overcharging or discharging; Finally, Matlab/Simulink is used for simulation, and the results show that the proposed control strategy can effectively improve the frequency regulation effect, improve the frequency quality and stabilize the state of charge of energy storage equipment.

Keywords： Hybrid energy storage ; dead band ; primary frequency regulation ; adaptive droop control ; state of charge

PDF (1529KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

方红艳, 马平. 考虑混合储能调频死区的自适应下垂控制策略*. 电气工程学报[J], 2021, 16(4): 213-222 doi:10.11985/2021.04.027

FANG Hongyan, MA Ping. Adaptive Droop Control Strategy Considering Frequency Modulation Dead Band of Hybrid Energy Storage. Journal of Electrical Engineering[J], 2021, 16(4): 213-222 doi:10.11985/2021.04.027

1 引言

近年来,随着可再生能源的开发利用,其发电技术突飞猛进,但所产生的电能具有随机性和波动性,当大规模并入电网时,将对系统频率稳定造成严重影响[1,2]。电网要求发电系统在并网后具有一定的调频能力,因此需要借助调频手段进行频率调整[3]。

目前针对可再生能源发电的调频手段主要有两种,其一是通过对可再生能源自身的控制进行频率调整,虽然能达到一定的调频效果,但该方法调频范围较小,且会产生一定的能量损失[4,5]。其二是通过增加储能设备进行调频,文献[6,7,8,9]在传统调频控制策略的基础上,根据储能设备的荷电状态 (State of charge, SOC)特点对控制策略进行改进,提高储能设备的调频能力,但此改进策略只针对单一的储能设备,无法充分利用各储能的优势。随着对混合储能的深入研究,文献[10,11,12,13,14]采用单一的传统控制策略参与调频,虽然此策略容易实现,但无法达到最优的调频效果。文献[15,16,17]混合储能采用两种控制策略相结合的方式进行调频,虽然能更好地满足调频需要,但实际应用较困难,且其中的控制策略均为传统方式。文献[18,19]根据混合储能的SOC情况进行控制策略的改进,使混合储能得到充分利用,并根据SOC值对下垂系数进行调整,达到更好的调频效果且能延长储能设备的寿命,但SOC与下垂系数间呈线性关系,使储能在SOC临界状态发生过充或过放现象。上述文献均未考虑储能调频死区,文献[20]仅对单一储能的调频死区进行了研究,但对混合储能的调频死区研究少之又少。

综合以上分析,本文采用超级电容和蓄电池组成的混合储能参与一次调频。通过试验研究,设置恰当的混合储能调频死区,充分发挥各自的作用。基于Logistic函数分析SOC对超级电容与蓄电池下垂系数的影响,采用自适应下垂控制策略,在缩小频率偏差的同时,稳定储能设备荷电状态,提高使用寿命。最后对阶跃扰动和连续扰动进行仿真,针对阶跃扰动对调频效果以及频率恶化进行定量分析,针对连续扰动,对调频效果及SOC维持效果进行综合评价,结果表明本文控制策略的有效性。

2 混合储能参与一次调频的仿真模型

目前大部分风机都无法自然响应频率变化,同时水电参与调频的备用容量较小,所以本文不考虑风电和水电的一次调频作用。但风电对电网频率影响较大,本文将风电出力加入到负荷波动中进行 分析。

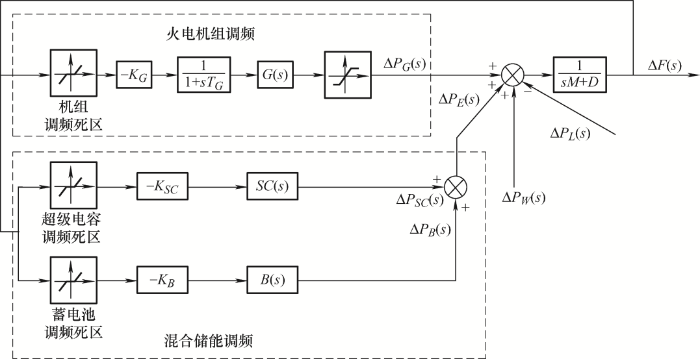
混合储能参与一次调频的仿真模型如图1所示,其中主要包括火电机组调频模型和混合储能调频模型。两种模型均能通过频率反馈通道检测频率的变化,根据频率偏差调整自身出力,后将有功功率增量叠加至有功功率控制环,由图1可得频率变化量与各机组有功功率增量关系的复频域表达式为

$\frac{{\Delta {P_G}(s) + \Delta {P_E}(s) - \Delta {P_L}(s)}}{{(sM + D)}} = \Delta F(s)$

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   混合储能参与一次调频仿真模型


式中,ΔPG(s)表示火电机组有功功率增量;ΔPE(s)表示储能设备有功功率增量;ΔPL(s)表示系统负荷的变化量;ΔF(s)表示电网频率的变化量;M表示电网惯性时间常数;D表示负荷阻尼系数。

调频设备的传递函数方程为

$\left\{ \begin{array}{l}\Delta {P_G}(s) = - \Delta F(s)\frac{{{K_G}}}{{1 + s{T_G}}}G(s)\\\Delta {P_E}(s) = - \Delta F(s)({K_{SC}}SC(s) + {K_B}B(s))\end{array} \right.$

式中,G(s)表示火电机组调速器的传递函数,SC(s)、B(s)分别表示超级电容和蓄电池的传递函数,表达式如下

$\left\{ \begin{array}{l}G(s) = \frac{{1 + s{F_{HP}}{T_{RH}}}}{{(1 + s{T_{CH}})(1 + s{T_{RH}})}}\\SC(s) = \frac{1}{{1 + s{T_{SC}}}}\\B(s) = \frac{1}{{1 + s{T_B}}}\end{array} \right.$

式中,KG、TG分别表示火电机组的单位调节功率系数和转速变换时间;KSC、KB、TSC、TB分别表示超级电容、蓄电池的单位调节功率系数和功率转换时间常数;FHP表示汽轮机再热器增益;TRH表示再热器时间常数;TCH表示汽轮机时间常数。

应用此仿真模型,对混合储能参与一次调频控制策略进行研究,是本文的研究重点。

3 混合储能参与一次调频死区设置及控制策略

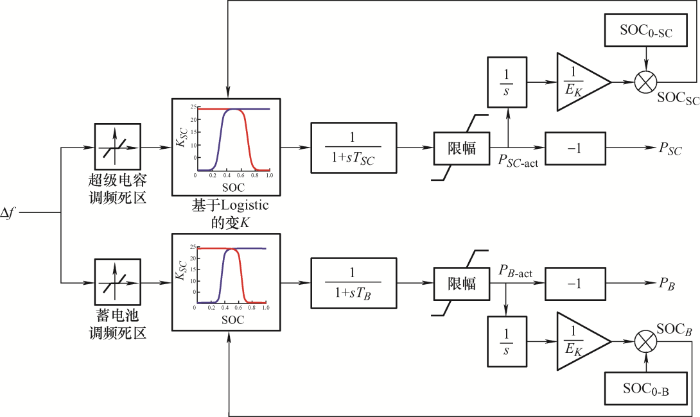
为了使系统在频率波动较小的情况下减少机组响应次数,本文通过对超级电容和蓄电池设置相应的调频死区,并根据储能设备的SOC值采用自适应下垂系数的控制策略,研究混合储能对频率调整的有效性。

3.1 混合储能的调频死区

常规火电机组的一次调频死区一般设置为(50-0.033 Hz, 50+0.033 Hz),为了防止小幅高频扰动造成频率在调频死区边界上下波动,使常规机组频繁进行一次调频,假设将混合储能的调频死区设置在机组死区内。由于超级电容的寿命受充放电次数影响小,且超级电容的响应速度快,假设将超级电容调频死区设置在蓄电池死区内。本文的调频死区用频率偏差表示,各设备的调频死区为机组$\left| {\Delta f_G^d} \right| = 0.033\;\;Hz$,蓄电池$\left| {\Delta f_B^d} \right|$,超级电容$\left| {\Delta f_{SC}^d} \right|$。

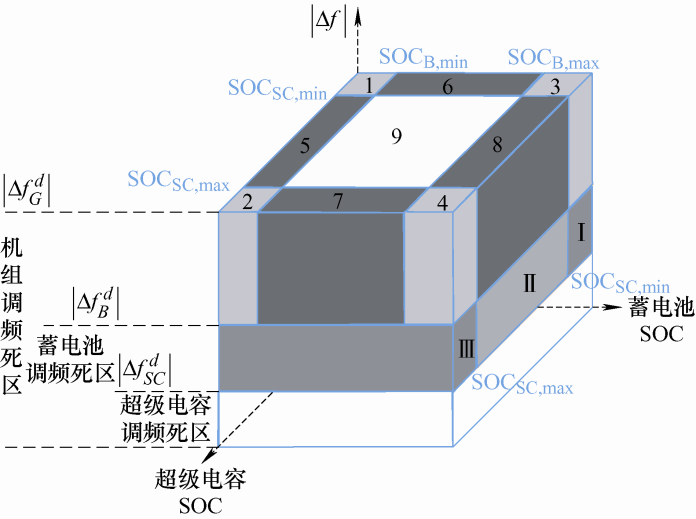
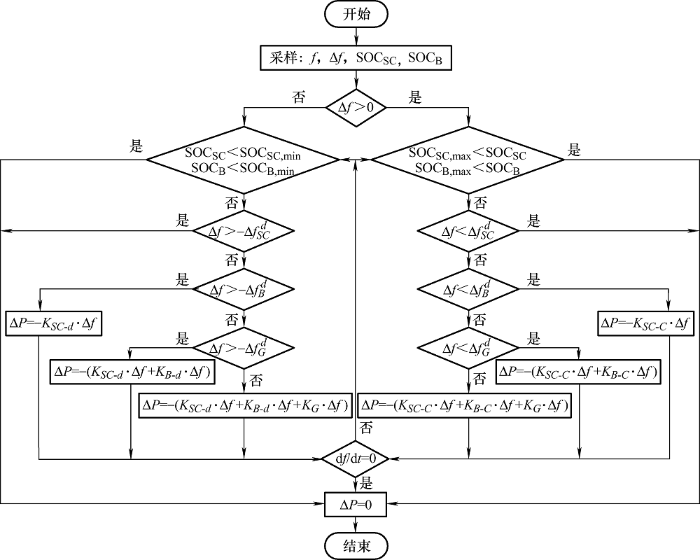
如图2所示,考虑储能的过充及过放问题,分别设置SOCmin及SOCmax,其中蓄电池的SOC阈值为SOCB,min=0.2,SOCB,max=0.8;超级电容的阈值为SOCSC,min=0.1,SOCSC,max=0.9。当储能位于各自的调频死区内时,不参与调频,此时根据自身的情况进行SOC恢复,达到最佳状态,为下一轮调频做好准备。根据储能SOC以及各调频死区的设定,将储能的动作范围进行分区。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   基于调频死区和SOC的储能工作区域


当频率偏差在超级电容调频死区内时即$\left| {\Delta f} \right| < \left| {\Delta f_{SC}^d} \right|$,所有调频设备均不动作,如图2中区域I,此时$\Delta P = 0$。

当频率偏差在超级电容调频死区外,蓄电池调频死区内时即$\left| {\Delta f_{SC}^d} \right| < \left| {\Delta f} \right| < \left| {\Delta f_B^d} \right|$,此时超级电容参与调频,而蓄电池和机组不动作,根据超级电容的SOC情况,将该部分分为三个区域,如图2中I、II、III所示。

$\left\{ \begin{array}{l}I\left( {0 < SO{C_{SC}} < SO{C_{SC,min}}} \right)\\II\left( {SO{C_{SC,min}} < SO{C_{SC}} < SO{C_{SC,max}}} \right)\\III\left( {SO{C_{SC,max}} < SO{C_{SC}} < 1} \right)\end{array} \right.$

此时$\Delta P$的具体情况如下。

当$\Delta f < 0$时,超级电容放电情况为

$\Delta P = \left\{ \begin{array}{l}0{\rm{ }}I\\\Delta {P_{SC}}{\rm{ }}IIIII\end{array} \right.$

当$\Delta f > 0$时,超级电容充电情况为

$\Delta P = \left\{ \begin{array}{l}\Delta {P_{SC}}{\rm{ }}III\\0{\rm{ }}III\end{array} \right.$

当频率偏差在蓄电池调频死区外,机组调频死区内时,即$\left| {\Delta f_B^d} \right| < \left| {\Delta f} \right| < \left| {\Delta f_G^d} \right|$,此时超级电容与蓄电池都参与调频,只有机组不动作,根据超级电容和蓄电池各自的SOC情况,将该部分分为9个区域如图2中区域1~9所示。

$\left\{ \begin{array}{l} 1\left( {0 < SO{C_{SC}} < SO{C_{SC,min}}\;0 < SO{C_B} < SO{C_{B,min}}} \right)\\ 2\left( {0 < SO{C_{SC}} < SO{C_{SC,min}}SO{C_{B,max}} < SO{C_B} < 1} \right)\\ 3\left( {SO{C_{SC,max}} < SO{C_{SC}} < 1\;0 < SO{C_B} < SO{C_{B,min}}} \right)\\ 4\left( {SO{C_{SC,max}} < SO{C_{SC}} < 1SO{C_{B,max}} < SO{C_B} < 1} \right)\\ 5\left( {SO{C_{SC,min}} < SO{C_{SC}} < SO{C_{SC,max}}\;0 < SO{C_B} < SO{C_{B,min}}} \right)\\ 6\left( {SO{C_{SC,min}} < SO{C_{SC}} < SO{C_{SC,max}}SO{C_{B,max}} < SO{C_B} < 1} \right)\\ 7\left( {0 < SO{C_{SC}} < SO{C_{SC,min}}SO{C_{B,min}} < SO{C_B} < SO{C_{B,max}}} \right)\\ 8\left( {SO{C_{SC,max}} < SO{C_{SC}} < 1SO{C_{B,min}} < SO{C_B} < SO{C_{B,max}}} \right)\\ 9\left( {SO{C_{SC,min}} < SO{C_{SC}} < SO{C_{SC,max}}SO{C_{B,min}} < SO{C_B} < SO{C_{B,max}}} \right) \end{array} \right.$

此时$\Delta P$的具体情况如下。

当$\Delta f < 0$时,储能放电情况为

$\;\Delta P = \left\{ \begin{array}{l} 0{\rm{ }}\;\;\;1\\ \Delta {P_B}{\rm{ }}\;\;2\\ \Delta {P_{SC}} \;3\\ \Delta {P_{SC}} + \Delta {P_B} \;\;4\\ \Delta {P_{SC}} \;5\\ \Delta {P_{SC}} + \Delta {P_B} \;\;6\\ \Delta {P_B} \;\;\;7\\ \Delta {P_{SC}} + \Delta {P_B} \;\;8\\ \Delta {P_{SC}} + \Delta {P_B} \;\;9 \end{array} \right.$

当$\Delta f > 0$时,储能充电情况为

$\Delta P = \left\{ \begin{array}{l} \Delta {P_{SC}} + \Delta {P_B}{\rm{ }}1\\ \Delta {P_{SC}}{\rm{ }}\;2\\ \Delta {P_B} 3\\ 0 4\\ \Delta {P_{SC}} + \Delta {P_B} 5\\ \Delta {P_{SC}} 6\\ \Delta {P_{SC}} + \Delta {P_B} 7\\ \Delta {P_B} \;\;8\\ \Delta {P_{SC}} + \Delta {P_B} 9 \end{array} \right.$

当频率偏差在机组调频死区外时,超级电容、蓄电池和机组都参与调频。此时$\Delta P = \Delta {P_G} + \Delta {P_{SC}} + \Delta {P_B}$,其中超级电容与蓄电池的充放电情况与区域1~9相同。本文未对此类情况进行详细研究。

3.2 混合储能的自适应下垂系数

虚拟下垂控制是储能参与调频的经典控制策略,为了实现对储能的保护,对储能的下垂系数进行修正,根据储能元件的SOC情况改变下垂系数K,这种方法称为自适应下垂控制,本文采用此方法对储能进行出力控制。

本文中储能设备的单位调节功率与SOC的关系基于Logistic函数,此函数初始阶段大致呈指数增长,随着逐渐饱和,增加速度减慢,到一定程度后停止增长,并稳定在某一值。其表达式为

$K(t) = \frac{{{K_{\max }}{P_0}\exp \left( {nt} \right)}}{{{K_{\max }} + {P_0}(\exp \left( {nt} \right) - 1)}}$

式中,${K_{\max }}$为终值,本文取24;${P_0}$、n均为曲线的自适应因子。

基于Logistic函数储能设备的单位调节功率与SOC的关系表达式如下。

当$\Delta f > 0$时,储能设备充电的单位调节功率

${K_c} = \left\{ \begin{array}{l} {K_{\max }}{\rm{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 < {\rm{SOC < SO}}{{\rm{C}}_{\min }}{\rm{ }}\\ \frac{{{K_{\max }}{P_0}\exp \left( {\frac{{n(SO{C_{\max }} - SOC)}}{{0.4}}} \right)}}{{{K_{\max }} + {P_0}(\exp \left( {\frac{{n(SO{C_{\max }} - SOC)}}{{0.4}}} \right) - 1)}}\;\;\;\;\;\;\;\;\;\;{\rm{SO}}{{\rm{C}}_{\min }} < {\rm{SOC}} < {\rm{SO}}{{\rm{C}}_{\max }}\\ 0{\rm{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{SO}}{{\rm{C}}_{\max }} < {\rm{SOC}} < 1 \end{array} \right.$

当$\Delta f < 0$时,储能设备放电的单位调节功率

${K_d} = \left\{ \begin{array}{l} {\rm{0 }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 < {\rm{SOC < SO}}{{\rm{C}}_{\min }}{\rm{ }}\\ \frac{{{K_{\max }}{P_0}\exp \left( {\frac{{n(SOC - SO{C_{\min }})}}{{0.4}}} \right)}}{{{K_{\max }} + {P_0}(\exp \left( {\frac{{n(SOC - SO{C_{\min }})}}{{0.4}}} \right) - 1)}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{SO}}{{\rm{C}}_{\min }} < {\rm{SOC}} < {\rm{SO}}{{\rm{C}}_{\max }}\\ {K_{\max }}{\rm{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{SO}}{{\rm{C}}_{\max }} < {\rm{SOC}} < 1 \end{array} \right.$

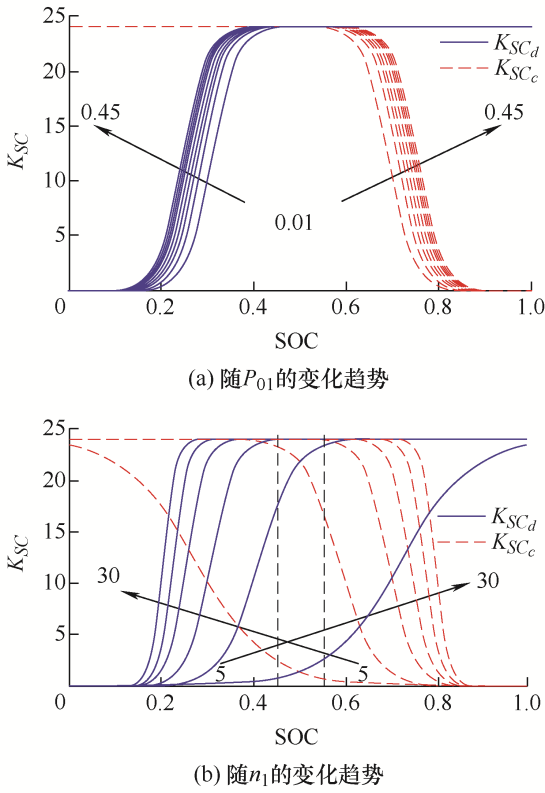
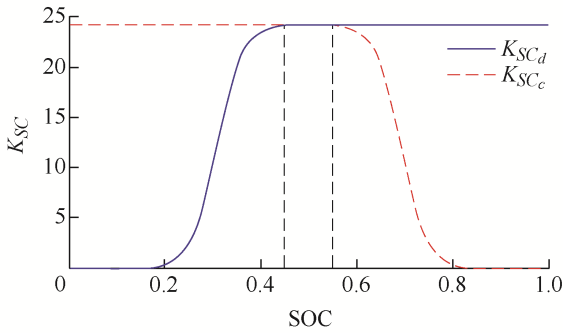
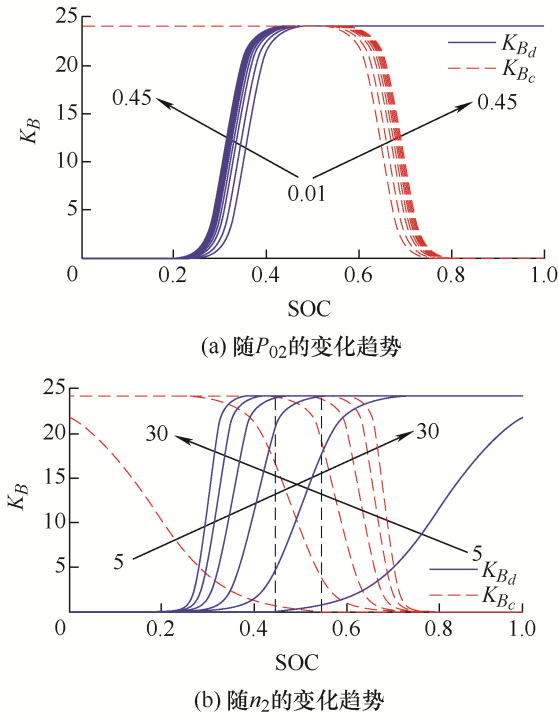
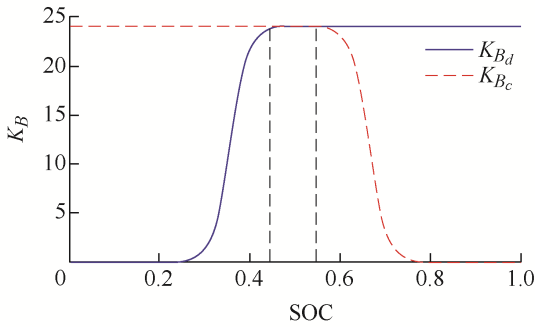
超级电容充放电的单位调节功率分别为${K_{SC - c}}$、${K_{SC - d}}$,其中$SO{C_{\max }} = 0.9$,$SO{C_{\min }} = 0.1$。为了区别超级电容与蓄电池的自适应因子,此处用${P_{01}}$、${n_1}$表示${K_{SC}}$-SOC曲线的自适应因子,选取方法为控制变量法：当n1不变时,P01从0.01增大到0.45(图3a),随着P01的增大,SOCmin对应的${K_{S{C_d}}}$减小,SOCmax对应的${K_{S{C_c}}}$增大,为了防止超级电容发生过充和过放现象,此处P01取值为0.01。当P01不变时,n1从5增大到30(图3b),随着n1的增大,KSC对SOC的变化越来越敏感,为了使超级电容在SOC良好条件下(0.45~0.55)能得到充分利用,此处n1取值为15。当P01=0.01,n1=15时,超级电容单位调节功率与SOC的关系如图4所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   KSC-SOC曲线随P01、n1变化趋势


图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   P01=0.01,n1=15时KSC-SOC的关系


蓄电池充放电的单位调节功率分别为${K_{B{\rm{ - }}c}}$、${K_{B{\rm{ - }}d}}$,其中$SO{C_{\max }} = 0.8$,$SO{C_{\min }} = 0.2$。${P_{02}}$、${n_2}$表示${K_B}{\rm{ - }}SOC$曲线的自适应因子,其选取方法与原则和超级电容相同,此处不再赘述(图5)。此时P02的取值为0.01,n2的取值为20。当P02=0.01,n2=20时蓄电池单位调节功率与SOC的关系如 图6所示。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   KB-SOC曲线随P02、n2的变化趋势


图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   P02=0.01,n2=20时KB-SOC的关系


采用此方法进行下垂系数的确定,不但算法简单,而且容易实现,同时可以有效地预防储能设备在SOC临界阈值发生过充过放。

综合上文的分析,混合储能控制部分如图7所示,本文提出的混合储能参与调频控制策略流程图如图8所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   混合储能控制方法


图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   混合储能控制策略流程图


4 仿真分析

基于Matlab/Simulink平台进行仿真,为了能更好地反映出混合储能参与一次调频的优势,且不需要考虑经济性,将储能设备的功率和容量设置较大,超级电容1 MW/0.6 MW·h,蓄电池0.1 MW/1 MW·h。仿真过程中各参数设置如表1所示。

表1   仿真参数设置

仿真参数仿真取值仿真参数仿真取值
KG25M10
TG0.3D2
FHP0.5TSC0.2
TRH10TB0.3
TCH0.3

新窗口打开| 下载CSV


4.1 混合储能调频死区设置仿真分析

为合理设置混合储能调频死区,对超级电容和蓄电池的死区设置进行分析研究。4.1.1 调频评价指标针对连续负荷扰动,评价指标为频率偏差的方均根值($RM{S_f}$)和SOC偏差的方均根值($RM{S_{SOC}}$,超级电容与蓄电池表达式相同),两者分别反映调频 效果和SOC保持效果,表达式如下

$RM{S_f} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {\Delta {f_i}^2} }$
$RM{S_{SOC}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{(SO{C_i} - SO{C_0})}^2}} }$

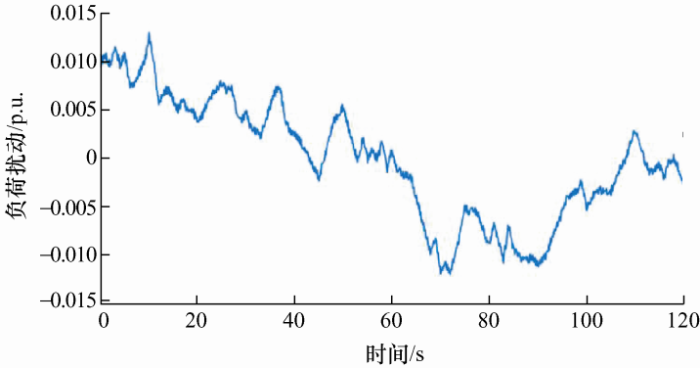
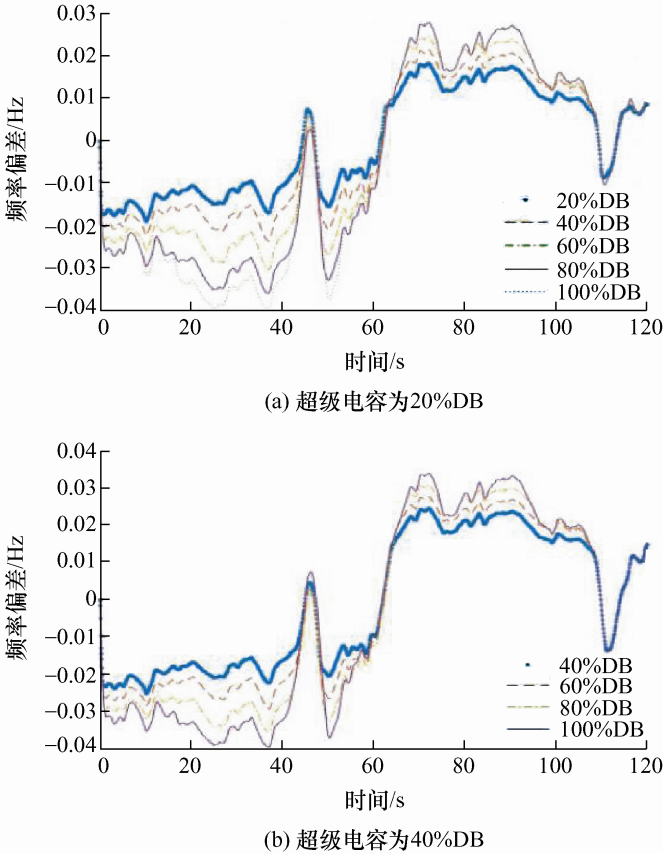
式中,$\Delta {f_i}$和$SO{C_i}$分别表示采样点i的频率偏差和SOC;$SO{C_0}$为0.5;N为总采样点个数。$RM{S_f}$和$RM{S_{SOC}}$这两个指标值越小,表示系统频率偏离标准频率程度越低,SOC偏离SOC0程度越低,说明调频效果和SOC保持效果越好。4.1.2 2 min连续负荷扰动仿真分析为验证混合储能不同调频死区设置对调频效果的影响,选择本文提出的自适应下垂控制策略进行一次调频,并分别设置超级电容与蓄电池的调频死区,具体设置如下。当超级电容调频死区为火电机组死区的20%(简称超级电容为20%DB)时,蓄电池死区设置为火电机组的20%、40%、60%、80%、100%(分别简称为20%DB、40%DB、60%DB、80%DB、100%DB);其余几种死区设置与此类似。在混合储能参与电网一次调频的模型中,加入图9所示的连续负荷扰动,对应的频率偏差曲线如图10a~10e所示,调频评价指标如 表2所示。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9   2 min连续负荷扰动变化曲线


图10

新窗口打开| 下载原图ZIP| 生成PPT

图10   混合储能不同调频死区下的频率偏差曲线


表2   混合储能不同调频死区组合下调频评价指标

调频死区$RM{S_f}$$RM{S_{SOC{\rm{ - }}SC}}$$RM{S_{SOC{\rm{ - }}B}}$火电机组出力时间
比例(%)		$\left| {\Delta {P_G}} \right|$/p.u.
超级电容蓄电池
20%DB20%DB0.012 00.135 10.088 900
40%DB0.015 50.166 40.070 500
60%DB0.019 10.186 90.061 900
80%DB0.022 60.197 60.050 647.990.005 7
100%DB0.023 80.204 20.026 258.840.032 6
40%DB40%DB0.017 70.131 60.085 100
60%DB0.021 00.162 80.062 300
80%DB0.024 60.184 30.050 347.390.003 9
100%DB0.026 90.194 90.026 460.910.032 8
60%DB60%DB0.023 20.126 00.080 100
80%DB0.026 70.159 20.054 089.930.002 9
100%DB0.028 90.176 00.025 091.660.051 9
80%DB80%DB0.028 70.114 30.071 098.730.026 7
100%DB0.030 50.147 90.028 798.940.088 7
100%DB100%DB0.032 20.070 10.047 799.360.158 5

新窗口打开| 下载CSV


由图10可知,当超级电容的死区一定时,蓄电池的调频死区设置的越小,频率偏差越小,调频效果越好。同时两者的调频死区差距越大,频率偏差越大。当负荷扰动变化较小时,各调频死区间频率偏差较小,该特点在扰动为0附近尤其明显,这证明当负荷扰动较小时,调频死区的设置对频率调整效果不明显。当蓄电池的调频死区相同时,随着超级电容调频死区的增大,频率偏差在增大,且随着蓄电池调频死区的增大,偏差越大。

分析表2数据可知,当蓄电池的调频死区小于等于60%DB时,火电机组不出力,此时主要由混合储能进行调频,对储能设备的容量配置要求较高,经济性较差。当超级电容死区一定时,随着蓄电池调频死区的增大,超级电容的SOC偏差增大,蓄电池的SOC偏差减小,表明在负荷扰动的过程中,两者的调频死区差距越大,超级电容需要调频的范围增加,出力也随之增加,导致其SOC偏差加大。此时,由于超级电容优先放电使频率偏差减小,同时火电机组也参与一部分调频,所以蓄电池出力较少,SOC偏差较小。超级电容先于蓄电池动作,将频率调整到蓄电池死区内,减少蓄电池的充放电次数,可延长其使用寿命。当储能设备调频死区与火电机组相同时,火电机组的出力时间比例明显高于其他调频死区,均为50%以上,所以应将混合储能各自的调频死区设置在火电机组死区内,此时,储能设备先于火电机组出力,将火电机组调频死区附近的频率调节至机组死区内,可以有效地减少机组出力时间,仿真数据支持第3.1节中所提假设。在设置混合储能调频死区时,死区不宜过大,否则增加火电机组出力的同时也无法弥补其频率响应较慢的缺陷,混合储能调频失去意义;死区也不宜过小,小幅度的高频负荷波动会被电力系统的机械惯性环节与滤波器所吸收,储能不需要平抑这类扰动,避免影响储能设备的运行经济性。

综上所述,结合超级电容动作速度快以及充放电次数对寿命影响小的优点,将超级电容调频死区设置得适当小于蓄电池的调频死区。由于火电机组死区附近小幅度的高频随机波动,使得机组频繁动作,影响运行稳定性,提高运行成本,储能设备的调频死区应适当小于火电机组的调频死区。所以,本文选取超级电容的调频死区为40%DB,蓄电池的调频死区为80%DB,此调频死区的组合在频率偏差满足要求的同时,能使混合储能的SOC偏差较小,且火电机组出力时间较短,出力较小。

4.2 混合储能参与一次调频控制策略仿真分析

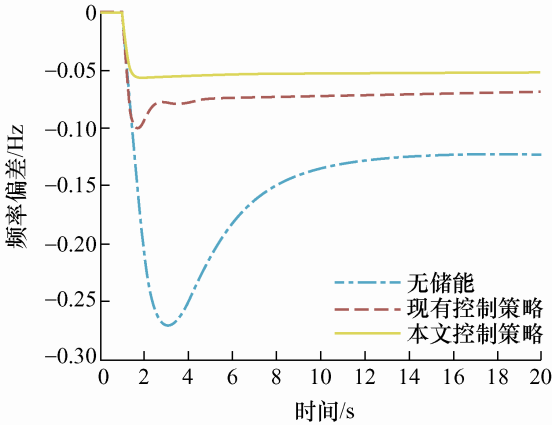
针对本文提出的控制策略(简称混合储能变K),设置如下场景。在混合储能与火电机组参与一次调频的仿真模型中(混合储能的调频死区设置同第3.1节的结论),加入0.05 p.u.的阶跃负荷扰动,将本文所提控制策略与无储能、现有控制策略进行对比,对应的频率偏差曲线如图11所示。根据图11可得扰动后的最大频率偏差$\Delta {f_m}$、最大频率偏差时刻${t_m}$、频率变化时间$\Delta {t_m}$和频率恶化速率${v_m}$,各数据如 表3所示,其中$\Delta {f_m}$值越小,表明调频效果越显著;${v_m}$越小,表明电网频率维持能力越强,即电网频率稳定性越好。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11   0.05 p.u.阶跃扰动下频率偏差曲线


表3   阶跃扰动下对应调频指标

调频方法Δf/Hztm/sΔt/s$\left| {{v_m}} \right|$/(Hz/s)
无储能-0.269 53.0182.0180.133 5
现有策略-0.101 51.7210.7210.140 7
本文策略-0.057 21.9070.9070.063 1

新窗口打开| 下载CSV


在0.05 p.u.阶跃扰动下,由图11及表3可以看出,本文控制策略最大频率偏差值小于无储能和现有控制策略,最终达到的稳态频率偏差比另外两种控制策略小,且在调频过程中,本文控制策略的频率偏差值变化较平滑,所以本文的调频效果优于另外两种。比较达到最大频率偏差值的时刻,本文的控制策略比无储能的时刻早,但比现有控制策略晚,这是因为本文控制策略的下垂系数需要根据储能的SOC情况进行系数调整,此过程需要消耗一定的时间,但达到频率偏差稳定值的时间早于现有控制策略。比较频率恶化速率发现本文控制策略比另外两种小,说明本文控制策略维持电网频率能力较强。综上所述,本文控制策略对阶跃扰动引起的频率变化有较好的调频效果以及较强的维持电网频率的能力。

5 结论

本文提出一种考虑混合储能调频死区的自适应下垂控制策略,结论如下。

(1) 当超级电容调频死区为(49.986 8 Hz,50.013 2 Hz),蓄电池调频死区为(49.973 6 Hz,50.026 4 Hz)时,能够有效减少火电机组参与调频的时间以及出力大小,同时能使超级电容及蓄电池的SOC更加稳定,提高运行经济性。

(2) 该控制策略充分体现了超级电容和蓄电池各自的优点,并充分发挥了混合储能参与电网调频的作用。考虑混合储能SOC约束,采用基于Logistic函数的自适应下垂控制,有效提高了调频效果。

本文工作为今后进一步深入研究混合储能参与电网调频奠定基础,储能调频死区与储能的类型密切相关,本文只是选取了较为常见的超级电容与蓄电池的组合,因此在混合储能调频死区设定方面,其与火电机组旋转备用容量间的关系仍有很大的研究价值;混合储能高昂的成本阻碍其大规模参与电网调频,所以根据实际情况进行混合储能优化配置也将是今后的研究工作之一。

参考文献

LI J, MA Y, MU G, et al.

Optimal configuration of energy storage system coordinating wind turbine to participate power system primary frequency regulation

[J]. Energies, 2018, 11(6):1396.

DOI:10.3390/en11061396      URL     [本文引用: 1]

LIU J, YAO W, WEN J, et al.

Impact of power grid strength and PLL parameters on stability of grid-connected DFIG wind farm

[J]. IEEE Transactions on Sustainable Energy, 2020, 11(1):545-557.

DOI:10.1109/TSTE.5165391      URL     [本文引用: 1]

乔左江, 杜欣慧, 薛晴.

大规模风电参与系统调频研究综述

[J]. 电测与仪表:1-13[2021-12-17]. http://kns.cnki.net/kcms/detail/23.1202.TH.20210105.1040.004.html .

URL     [本文引用: 1]

QIAO Zuojiang, DU Xinhui, XUE Qing.

Review of large scale wind power participating in system frequency regulation

[J]. Electrical Measurement & Instrumentation. 电测与仪表:1-13[2021-12-17]. http://kns.cnki.net/kcms/detail/23.1202.TH.20210105.1040.004.html .

URL     [本文引用: 1]

吉静, 郝丽丽, 王昊昊, 等.

风电机组参与一次调频的自适应控制方法

[J]. 电力电容器与无功补偿, 2020, 41(6):174-179.

[本文引用: 1]

JI Jing, HAO Lili, WANG Haohao, et al.

Adaptive control method for wind turbines participating in primary frequency regulation

[J]. Power Capacitor & Reactive Power Compensation, 2020, 41(6):174-179.

[本文引用: 1]

李天宁.

考虑电动汽车移动储能的电力系统一次调频控制研究

[D]. 镇江:江苏大学, 2017.

[本文引用: 1]

LI Tianning.

Study on primary frequency regulation control of power system considering mobile energy storage by electric vehicles

[D]. Zhenjiang:Jiangsu University, 2017.

[本文引用: 1]

吴启帆, 宋新立, 张静冉, 等.

电池储能参与电网一次调频的自适应综合控制策略研究

[J]. 电网技术, 2020, 44(10):3829-3836.

[本文引用: 1]

WU Qifan, SONG Xinli, ZHANG Jingran, et al.

Study on self-adaptation comprehensive strategy of battery energy storage in primary frequency regulation of power grid

[J]. Power System Technology, 2020, 44(10):3829-3836.

[本文引用: 1]

李军徽, 侯涛, 穆钢, 等.

基于权重因子和荷电状态恢复的储能系统参与一次调频策略

[J]. 电力系统自动化, 2020, 44(19):63-72.

[本文引用: 1]

LI Junhui, HOU Tao, MU Gang, et al.

Primary frequency regulationstrategy with energy storage system based on weight factors andstate of charge recovery

[J]. Automation of Electric Systems, 2020, 44(19):63-72.

[本文引用: 1]

李军徽, 高卓, 应鸿, 等.

基于动态下垂系数与SOC基点的储能一次调频控制策略

[J]. 电力系统保护与控制, 2021, 49(5):1-10.

[本文引用: 1]

LI Junhui, GAO Zhuo, YING Hong, et al.

Primary frequency regulation control strategy of energy storage based on dynamic droop coefficient and SOC reference

[J]. Power System Protection and Control, 2021, 49(5):1-10.

[本文引用: 1]

吴青峰, 孙孝峰, 王雅楠, 等.

基于分布式下垂控制的微电网分布式储能系统SOC平衡策略

[J]. 电工技术学报, 2018, 33(6):1247-1256.

[本文引用: 1]

WU Qingfeng, SUN Xiaofeng, WANG Yanan, et al.

A distributed control strategy for SOC balancing of distributed energy storage systems in microgrid

[J]. Transactions of China Eloectrotechnical Society, 2018, 33(6):1247-1256.

[本文引用: 1]

高松, 王嘉琛, 李德鑫, 等.

一种混合储能参与电网一次调频的充放电策略

[J]. 供用电, 2020, 37(2):14-20,40.

[本文引用: 1]

GAO Song, WANG Jiachen, LI Dexin, et al.

A charging and discharging strategy of hybrid energy storage system in primary frequency modulation

[J]. Distribution & Utilization, 2020, 37(2):14-20,40.

[本文引用: 1]

金强, 杨卫红, 王涛, 等.

考虑混合储能调频需求的独立微电网投资优化

[J]. 电力科学与技术学报, 2021, 36(1):52-62.

[本文引用: 1]

JIN Qiang, YANG Weihong, WANG Tao, et al.

Research on investment optimtzation of standalone microgrid considering frequency modulation with hybrid energy storage

[J]. Journal of Electric Power Science and Technology, 2021, 36(1):52-62.

[本文引用: 1]

郭潇潇, 李岚, 吴雷, 等.

基于下垂控制的微电网混合储能系统调频策略

[J]. 电力电容器与无功补偿, 2021, 42(2):176-182.

[本文引用: 1]

GUO Xiaoxiao, LI Lan, WU Lei, et al.

Frequency modulation strategy of hybrid energy storage system of microgrid based on droop control

[J]. Power Capacitor & Reactive Power Compensation, 2021, 42(2):176-182.

[本文引用: 1]

刘旭峰, 张继红, 吴振奎.

一种混合储能微电网中对频率的下垂控制方法

[J]. 电气自动化, 2018, 40(6):17-19,48.

[本文引用: 1]

LIU Xufeng, ZHANG Jihong, WU Zhenkui.

Frequency droop control method in the hybrid energy storage microgrid

[J]. Electrical Automation, 2018, 40(6):17-19,48.

[本文引用: 1]

董京, 宋华辉, 王磊, 等.

基于混合储能的虚拟惯量控制技术研究

[J]. 电工技术, 2021(5):48-49.

[本文引用: 1]

DONG Jing, SONG Huahui, WANG Lei, et al.

Research on virtual inertia control technology based on hybrid energy storage system

[J]. Electric Engineering, 2021(5):48-49.

[本文引用: 1]

张茜.

蓄电池和超级电容混合储能系统控制策略研究

[J]. 电气应用, 2018(1):20-23.

[本文引用: 1]

ZHANG Qian.

Research on control strategy of battery and supercapacitor hybrid energy storage system

[J]. Electrotechnical Application, 2018(1):20-23.

[本文引用: 1]

褚鑫.

混合储能系统参与风电并网一次调频的研究

[D]. 上海:上海电机学院, 2019.

[本文引用: 1]

CHU Xin.

Study on wind power grid-connected primary frequency modulation with hybrid energy storage system

[D]. Shanghai:Shanghai Dianji University, 2019.

[本文引用: 1]

王明扬.

基于储能风电场一次调频的研究

[D]. 沈阳:沈阳工程学院, 2019.

[本文引用: 1]

WANG Mingyang.

Research on primary frequency regulation of wind farm based on energy storage

[D]. Shenyang:Shenyang Institute of Engineering, 2019.

[本文引用: 1]

张仰维.

基于动态变系数的混合储能系统频率控制方法

[J]. 电子设计工程, 2020, 28(5):27-30.

[本文引用: 1]

ZHANG Yangwei.

Frequency control method of hybrid energy storage system based on dynamic variable coefficient

[J]. Electronic Design Engineering, 2020, 28(5):27-30.

[本文引用: 1]

任萱, 李桐歌, 马骏毅, 等.

考虑荷电状态的光伏微电网混合储能容量优化配置

[J/OL]. 电测与仪表:1-8[2021-12-17]. http://kns.cnki.net/kcms/detail/23.1202.TH.20210419.1341.008.html .

URL     [本文引用: 1]

REN Xuan, LI Tongge, MA Junyi, et al.

Optimal allocation of hybrid energy storage capacity in PV micro-grid considering SOC

[J/OL]. Electrical Measurement & Instrumentation:1-8[2021-12-17]. http://kns.cnki.net/kcms/detail/23.1202.TH.20210419.1341.008.html .

URL     [本文引用: 1]

马智慧, 李欣然, 谭庄熙, 等.

考虑储能调频死区的一次调频控制方法

[J]. 电工技术学报, 2019, 34(10):2102-2115.

[本文引用: 1]

MA Zhihui, LI Xinran, TAN Zhuangxi, et al.

Integrated control of primary frequency regulation considering dead band of energy storage

[J]. Transactions of China Electrotechnical Society, 2019, 34(10):2102-2115.

[本文引用: 1]

/

〈 〉