电气工程学报, 2021, 16(4): 196-204 doi: 10.11985/2021.04.025

新能源发电与电能存储

柔性直流系统的交流侧故障穿越优化控制策略*

夏天,1,2, 夏向阳,1,3, 刘代飞1,2, 刘远3, 易海淦3

1.长沙理工大学可再生能源电力技术湖南省重点实验室 长沙 410114

2.长沙理工大学能源与动力工程学院 长沙 410114

3.长沙理工大学电气与信息工程学院 长沙 410114

AC-side Fault Crossing Optimization Control Strategy for VSC-HVDC

XIA Tian,1,2, XIA Xiangyang,1,3, LIU Daifei1,2, LIU Yuan3, YI Haigan3

1. Hunan Key Laboratory of Renewable Energy Power Technology, Changsha University of Science & Technology, Changsha 410114

2. College of Energy and Power Engineering, Changsha University of Science & Technology, Changsha 410114

3. School of Electrical and Information Engineering, Changsha University of Science & Technology, Changsha 410114

通讯作者: * 夏向阳,男,1968年生,博士,教授,博士研究生导师。主要研究方向为柔性直流输电控制和储能安全控制。E-mail：307351045@qq.com

收稿日期: 2021-09-18   修回日期: 2021-11-17  

基金资助: * 国家自然科学基金.  51977014
湖南省自然科学基金.  2020JJ6054

Received: 2021-09-18   Revised: 2021-11-17  

作者简介 About authors

夏天,男,1993年生,硕士研究生。主要研究方向为新能源发电并网控制技术。E-mail： 86255540@qq.com

摘要

基于模块化多电平换流器(Modular multilevel converter, MMC)的柔性直流输电在大规模的风电并网中具有广阔的发展前景,针对风电接入下交流侧故障时MMC的故障穿越能力进行研究,提出一种基于功率预测控制的交流侧故障穿越控制方法,通过新型瞬时功率理论建立功率预测控制模型及环流预测控制模型,并以上下桥臂插入子模块数为控制变量,相比于传统的功率控制理论,无需计算功率补偿项,能够实现有功及无功功率的同步控制,采用的分层预测控制模型,无需引入权重因子,控制系统结构简单、计算量小,最后通过Matlab/Simulink仿真平台建立仿真模型,仿真结果表明所提控制策略能够实现稳态及网压不平衡故障情况下的有效控制。

关键词： 模块化多电平换流器 ; 风电接入 ; 模型预测控制 ; 交流侧故障穿越

Abstract

Flexible HVDC transmission based on modular multi-level converter (MMC) has broad prospects for development in large-scale wind power grid-connected. The fault-crossing capability of MMC in AC side fault under wind power access is studied, a fault-crossing control method for AC side based on predictive direct power control is proposed. A predictive power model and a circulating current predictive control model are established through a new instantaneous power theory. Compared with the traditional power control theory, the insertion of sub-modules into the lower arm is a control variable, which can realize the synchronous control of reactive power and active power without calculating the power compensation term. The hierarchical predictive control model is adopted without introducing the weight factor. The control structure is simple and accurate. Finally, the simulation model is established through the simulation platform of Matlab/Simulink. The simulation results show that the proposed model can achieve the synchronous control of reactive power and active power without calculating the power compensation term. The control strategy can achieve effective control in the case of steady state and unbalanced network voltage.

Keywords： Modular multi-level converter ; wind power access ; model predictive control ; AC side fault crossing

PDF (2266KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

夏天, 夏向阳, 刘代飞, 刘远, 易海淦. 柔性直流系统的交流侧故障穿越优化控制策略*. 电气工程学报[J], 2021, 16(4): 196-204 doi:10.11985/2021.04.025

XIA Tian, XIA Xiangyang, LIU Daifei, LIU Yuan, YI Haigan. AC-side Fault Crossing Optimization Control Strategy for VSC-HVDC. Journal of Electrical Engineering[J], 2021, 16(4): 196-204 doi:10.11985/2021.04.025

1 引言

高压直流输电在大规模风电并网中的应用受到大量关注,其中基于模块化多电平换流器(Modular multilevel converter, MMC)的柔性直流输电技术由于其显著优势在风电并网中受到广泛的应用[1]。MMC在网压平衡状态下的控制策略相对成熟,但是在不平衡网压情况下,MMC运行会对系统稳定运行造成危害,确保直流侧功率的稳定安全输送至关重要[2,3,4]。

针对上述问题,国内外学者展开了研究工作,文献[5]设计了双矢量电流控制策略,旨在消除负序电流及有功功率波动,但是直流电压波动较大;文献[6,7]提出了一种直接功率控制策略,但没有针对模块化多电平换流器进一步分析;文献[8,9]提出了基于模块化多电平换流器的直接功率控制策略,但控制器设计较为复杂,控制性能易受影响。

基于上述控制方法的不足,模型预测控制是一种合适的可选方案,该控制策略善于处理多输入多输出系统,适用于模型的多目标优化。文献[10]提出了一种基于模型预测的环流控制策略,但未发挥出模型预测控制多目标协同控制的优越性。综上所述,文章提出一种基于新型瞬时功率的预测直接功率控制策略,无需计算功率补偿项,能够实现对于有功和无功功率二倍频波动的同步抑制,确保网压不平衡下功率输送的稳定。根据MMC-HVDC的离散时间数学模型,建立了新型瞬时功率预测模型及环流控制预测模型,采用的分层预测控制模型,无需引入权重系数,所提控制策略在电网电压对称、不对称情况下都具有良好的控制效果,最后通过仿真验证了所提方法的有效性。

2 MMC数学模型建立

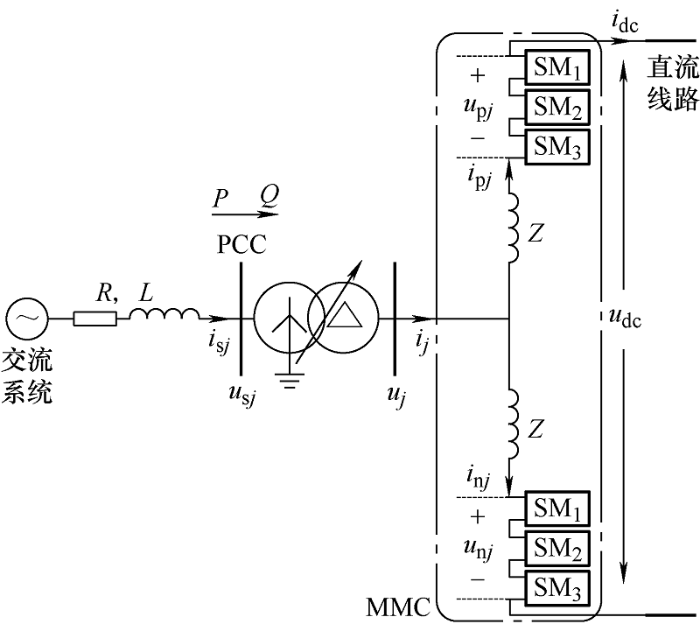
模块化多电平换流器(MMC)结构是由许多的子模块级联而成,MMC有三个相单元,共6个桥臂,每个桥臂上有N个子模块,正常工作状态下,每相上下桥臂总共投入子模块数为N,图1为MMC-HVDC整流侧示意图,交流侧电压和电流表示为uj、ij,桥臂上串联的电抗为Z=r+jl,直流侧电压为udc,upj、ulj分别为子模块上下桥臂电压,ipj、ilj分别为子模块上下桥臂电流,其中j=a,b,c。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   MMC-HVDC系统整流侧示意图


忽略MMC损耗,其桥臂电流表示如下

$\left\{ \begin{array}{l}{i_{{\rm{p}}j}} = 0.5{i_j} + {i_{{\rm{dif}}}}\\{i_{lj}} = - 0.5{i_j} + {i_{{\rm{dif}}}}\end{array} \right.$
$i_{{\rm{dif}}\_j}^{} = \frac{{{i_{{\rm{p}}j}} + {i_{{\rm{l}}j}}}}{2}$

式中,idif为换流器的j相内部环流,包含j相直流母线电流分量idcj和j相交流环流分量icirj。

定义上下桥臂电压共模分量和差模分量为udif、usum,可得

${\rm{ }}{u_{{\rm{dif}}}} = {u_{{\rm{l}}j}} - {u_{{\rm{p}}j}}$
${\rm{ }}{u_{{\rm{sum}}}} = {u_{{\rm{l}}j}} + {u_{{\rm{p}}j}}$

由此可求得MMC的j相动态数学表达式

$\frac{{{U_{{\rm{dc}}}}}}{2} - l\frac{{{\rm{d}}{i_{{\rm{P}}j}}}}{{{\rm{d}}t}} - {u_{{\rm{p}}j}} - r{i_j} - R{i_j} - L\frac{{{\rm{d}}{i_j}}}{{{\rm{d}}t}} = {u_j}$
$ - \frac{{{U_{{\rm{dc}}}}}}{2} + l\frac{{{\rm{d}}{i_{{\rm{l}}j}}}}{{{\rm{d}}t}} + {u_{{\rm{l}}j}} + r{i_{{\rm{l}}j}} - R{i_j} - L\frac{{{\rm{d}}{i_j}}}{{{\rm{d}}t}} = {u_j}$

式中,交流侧电压为uj,直流侧电压为Udc,其中R、L分别表示交流侧电阻和电感,桥臂上电感为l,示桥臂电阻为r。

将式(5)、(6)分别相加和相减求得MMC内外部动态特性方程如下

${u_{{\rm{sum}}}} = l\frac{{d{i_j}}}{{dt}} + r{i_j} + 2R{i_j} + 2L\frac{{d{i_j}}}{{dt}} + 2{u_j}$
${U_{{\rm{dc}}}} - {u_{{\rm{dif}}}} = 2l\frac{{d{i_{{\rm{dif}}\_j}}}}{{dt}} + 2r{i_{{\rm{dif}}\_j}}$

MMC各桥臂电压可由插入的子模块电容电压之和表示如下

$\left\{ \begin{array}{l}u_{{\rm{p}}j}^{} = {n_{{\rm{p}}j}}\frac{{U_{{\rm{cp}}j}^\sum }}{N}\\u_{{\rm{l}}j}^{} = {n_{{\rm{l}}j}}\frac{{U_{{\rm{cl}}j}^\sum }}{N}\end{array} \right.$

式中,$U_{{\rm{cp}}j}^\sum$、$U_{{\rm{cl}}j}^\sum$分别为MMC上下桥臂所有子模块电容电压之和,ucpj、uclj分别为上下桥臂中处于开通状态的子模块电容的和,npj、nlj为处于开通状态的子模块个数。

3 网压不对称故障下的功率预测控制模型

由瞬时功率理论的定义可知[11],传统瞬时功率表达式如下

$P = 1.5{\mathop{\rm Re}\nolimits} (u\dot i)$
$Q = 1.5{\mathop{\rm Im}\nolimits} (u\dot i)$

式中,“·表示共轭。

基于传统瞬时功率理论建立的模型在计算时 需要引入功率补偿项,因而文章引入新型瞬时功 率[12],定义如下

$P = 1.5{\mathop{\rm Re}\nolimits} (u\dot i)$
$Q_{}^{{\rm{nov}}} = 1.5{\mathop{\rm Re}\nolimits} ({u^{{\rm{nov}}}}\dot i)$

式中,unov和u存在正交关系,前者滞后于后者90°。

当电网处于不对称故障状态下时,由对称分解理论,可将三相系统,分解为正序、负序及零序,换流器一般情况下都采用$Y/\Delta$接线,因而忽略零序分量的影响[13],电压和电流如下所示

$u = {u^ + } + {u^ - } = {U^ + }\exp \left[ {j\left( {{\omega _0}t + \theta _i^ + } \right)} \right] + {U^ - }\exp \left[ { - j({\omega _0}t + \theta _i^ - )} \right]$
$i = {i^ + } + {i^ - } = {I^ + }\exp \left[ {j({\omega _0}t + \theta _i^ + )} \right] + {I^ - }\exp \left[ { - j({\omega _0}t + \theta _i^ - )} \right]$

式中,“+”“-”分别为正序和负序分量,ω0为基波角频率,电压及电流初相角由u、i表示。

${u^{{\rm{nov}}}} = u\exp \left( { - {{j\pi } \mathord{\left/ {\vphantom {{j\pi } 2}} \right. } 2}} \right) = - j{u^ + } + j{u^ - }$

结合以上分析,将式(14)、(15)和(16)分别代入传统瞬时功率表达式及新型瞬时功率表达式 (式(10)~(13))中,可分别求得其在不对称电网状态下的表达式

$S = P + jQ = {S_0} + S_2^ + + S_2^ -$
${S^{{\rm{nov}}}} = P + j{Q^{{\rm{nov}}}} = S_0^{{\rm{nov}}} + S_2^{{\rm{nov}} + }$

式中,S0、$S_2^ +$、$S_2^ -$分别为传统瞬时功率定义下的平均分量、二倍频正序分量和二倍频负序分量,$S_0^{{\rm{nov}}}$、$S_2^{{\rm{nov}}}$分别为新型瞬时功率定义下平均分量、二倍频正序分量。

电网电压不平衡时,换流器根据不同的控制目标选择理想的控制方式,如平衡交流三相电流,可通过抑制交流侧负序电流实现;为抑制功率波动,需要令式(17)、(18)中二倍频分量等于0,从而能够有效消除直流侧有功及无功功率波动。

在传统瞬时功率定义下,电网电压不对称时,无法实现对于有功及无功功率波动的同步抑制,同时会在电网侧引入电流谐波分量,导致交流侧电流不平衡,对于换流器正常运行造成严重影响,为了使得交流侧电流平衡,需要在原有功率指令的基础上叠加功率补偿项,为了得到新的参考值,需要分别从电压及电流中分离得到负序电压和正序电流,增加了系统设计时的难度[14,15,16]。

在新型瞬时功率定义下,当交流侧发生故障,能够实现对于有功及无功薄波动的同步抑制,不会在电网侧产生电流谐波分量,无需添加额外的功率补偿项,无需对正序电流及负序电压进行分离,因此文章控制方法采用在新型瞬时功率定义下进行设计。

由式(14)将电压u对时间t进行求导

$\frac{{du}}{{dt}} = j{\omega _0}{u^ + } - j{\omega _0}{u^ - } = - {\omega _0}{u^{{\rm{nov}}}}$

同样可将unov对时间t进行求导

$\frac{{d{u^{{\rm{nov}}}}}}{{dt}} = j{\omega _0}{u^ + } - j{\omega _0}{u^ - } = {\omega _0}u$

由式(14)~(16)将P、Qnov对时间t进行求导,同时联立式(12)、(13)可得

$\begin{array}{l} frac{{dP}}{{dt}} = 1.5{\mathop{\rm Re}\nolimits} (\frac{{du}}{{dt}}\dot i + \frac{{d\dot i}}{{dt}}u) = - \frac{{r + 2R}}{{l + 2L}}P{\rm{ + }}\\ \frac{3}{{l + 2L}}|u{|^2} - {\omega _0}{Q^{{\rm{nov}}}} - \frac{3}{{l + 2L}}{\mathop{\rm Re}\nolimits} (u\dot u_{{\rm{dif}}}^{}) \end{array}$
$\begin{array}{c} \frac{{d{Q^{{\rm{nov}}}}}}{{dt}} = 1.5{\mathop{\rm Re}\nolimits} (\frac{{d{u^{{\rm{nov}}}}}}{{dt}}\dot i + \frac{{d\dot i}}{{dt}}{u^{{\rm{nov}}}}) = - \frac{{r + 2R}}{{l + 2L}}{Q^{{\rm{nov}}}}{\rm{ + }}\\ {\omega _0}P + \frac{3}{{l + 2L}}{\mathop{\rm Re}\nolimits} [{u^{{\rm{nov}}}}(\dot u - {{\dot u}_{{\rm{dif}}}})] \end{array}$

将以上新型瞬时功率表达转换到αβ坐标系表示,由

${x_{\partial \beta }} = \sqrt {\frac{2}{3}} \left( {{x_a} + {x_b}\exp \left( {j\frac{{2\pi }}{3}} \right) + {x_c}\exp \left( { - j\frac{{2\pi }}{3}} \right)} \right)$

得到如下新型瞬时功率模型

$\begin{array}{l}\frac{{dP}}{{dt}} = - \frac{{r + 2R}}{{l + 2L}}P + \frac{2}{{l + 2L}}|{u_{\partial \beta }}{|^2} - \\\;\;{\omega _0}{Q^{{\rm{nov}}}} - \frac{1}{{l + 2L}}{\mathop{\rm Re}\nolimits} ({u_{\partial \beta }}\mathop {{{\dot u}_{{\rm{dif}}\_\partial \beta }}}\limits^{} )\end{array}$
$\begin{array}{l}\frac{{d{Q^{{\rm{nov}}}}}}{{dt}} = - \frac{{r + 2R}}{{l + 2L}}{Q^{{\rm{nov}}}} + {\omega _0}P + \\\frac{1}{{l + 2L}}{\mathop{\rm Re}\nolimits} [u_{\partial \beta }^{{\rm{nov}}}(2{{\dot u}_{\partial \beta }} - \mathop {{{\dot u}_{{\rm{dif}}\_\partial \beta }}}\limits^{} )]\end{array}$

将P、Qnov基于前向欧拉公式进行离散化展开

$\begin{array}{c}P(t + {T_s}) = P(t) + {T_s}[\frac{2}{{l + 2L}}|{u_{\partial \beta }}{|^2} - \\ {\omega _0}{Q^{{\rm{nov}}}} - \frac{1}{{l + 2L}}{\mathop{\rm Re}\nolimits} ({u_{\partial \beta }}{\rm{ }}{{\dot u}_{{\rm{dif}}\_\partial \beta }})] \end{array}$
$\begin{array}{c}{Q^{{\rm{nov}}}}(t + {T_s}) = {Q^{{\rm{nov}}}}(t) + {T_s}[ - \frac{{r + 2R}}{{l + 2L}}{Q^{{\rm{nov}}}}(t) + \\{\omega _0}P(t) + \frac{1}{{l + 2L}}{\mathop{\rm Re}\nolimits} (2\dot u_{\partial \beta }^{}(t) - \dot u_{{\rm{dif}}\_\partial \beta }^{}(t))u_{\partial \beta }^{{\rm{nov}}}(t)]\end{array}$

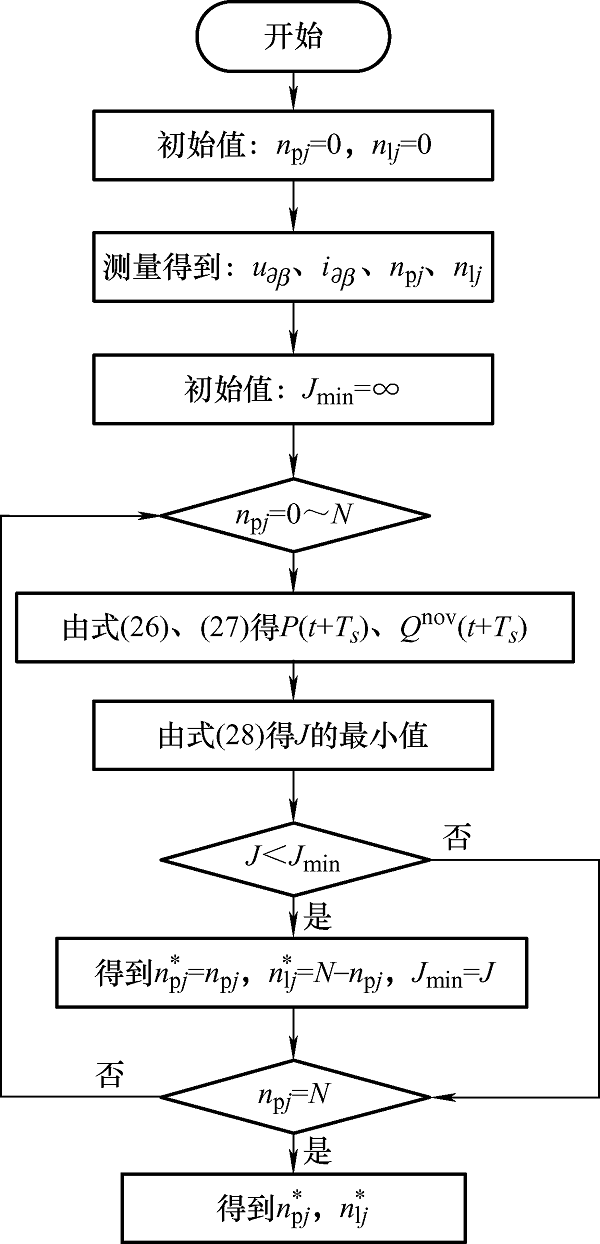
为了使有功功率P及无功功率Qnov能够准确跟踪其参考值,分别以预测有功、无功功率与其相应参考值之差的绝对值之和构建价值函数,对所有可能的上下桥臂插入子模块数npj、nlj组合进行选优,使得价值函数最小化,其最优桥臂子模块插入数npj、nlj求解流程图如图2所示,并将得到的npj、nlj最优解n* pj、n* lj用于环流控制阶段,其价值函数表达式如下

$J = |p(t + {T_s}) - {p^{{\rm{ref}}}}| + |{Q^{{\rm{nov}}}}(t + {T_s}) - {Q^{{\rm{ref}}}}|$

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   预测有功及无功控制流程


4 基于模型预测的相间环流控制

状态变量和输入变量定义如下

$x = {i_{{\rm{dif}}\_j}}$
${\rm{ }}u = {u_{{\rm{sum}}\_j}}$

则由式(8)能够求得如下MMC系统数序模型的离散化状态方程

$\begin{array}{c} {i_{{\rm{dif}}\_j}}(t + {T_s}) = [{u_{{\rm{dc}}}} - u_{{\rm{sum}}\_j}^{}(t + {T_s})]\frac{{{T_s}}}{{2l}} + \\ i_{{\rm{dif}}\_j}^{}(t + {T_s})(1 - \frac{{{T_s}r}}{{2l}}) \end{array}$

式中,预测的时间间隔为Ts,通过预测t+Ts时刻上下桥臂投入的子模块电压及t时刻的环流idif_j(t)能够得到t+Ts时刻的环流idif_j(t+Ts)。

由式(4)、(9)可得,桥臂电压共模分量的值是由预测直接功率控制阶段得到的最优桥臂子模块插入数$n_{pj}^ *$、$n_{lj}^ *$所决定的,由式(7)可得,通过对上下桥臂插入子模块数同时进行加减,不会对交流侧电压$n_{lj}^ *$造成影响,即所提的环流控制环节不会对先前建立的有功及无功功率控制造成不利影响,同时能够有效实现环流抑制。

$n_{{\rm{p}}j}^{{\rm{ref}}} = n_{{\rm{p}}j}^ * + \Delta n$
$n_{{\rm{l}}j}^{{\rm{ref}}} = n_{{\rm{l}}j}^ * + \Delta n$

为了获得理想的环流抑制效果,应使环流越小越好,很大程度上能够减小子模块电容电压纹波及逆变器损耗,同时考虑对于直流侧电压的稳定性的影响,尽可能使每相上下桥臂多投入或者少投入的子模块数量少些,上下桥臂投入子模块数量之和在N附近波动[17],∆n的值为-1、0、1,无论每个阶段子模块数量是多少,总的迭代次数为2~3次预测。

结合式(9)、(32)和(33),式(31)可改写为如下表达式

$\begin{array}{c}i_{{\rm{dif}}\_j}^{}(t + {T_s}) = [{u_{{\rm{dc}}}} - u_{{\rm{sum}}\_j}^{{\rm{ref}}}(t + {T_s})]\frac{{{T_s}}}{{2l}} + \\i_{{\rm{dif}}\_j}^{}(t)(1 - \frac{{{T_s}r}}{{2l}})\end{array}$

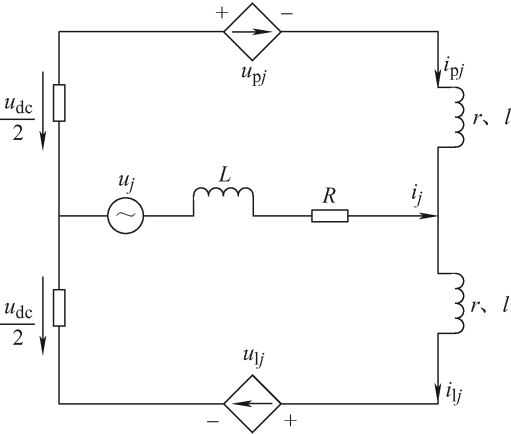
桥臂内部环流包含有直流分量和交流分量,抑制环流的交流分量,能够降低系统损耗,减小相应开关器件的电流应力,一般将各相桥臂环流参考值设定为直流母线电流的三分之一,此设置适用于理想的情况下[18],当电网电压突发不平衡故障时,为了实现对于三相环流的准确控制,结合图3所示单相等效电路,由交直流侧功率平衡原理可求解其环流参考值。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   j相简化电路


由上述分析分别求得MMC直流侧、交流侧 功率

$P_{{\rm{dc}}}^{} = - \frac{{{u_{{\rm{dc}}}}}}{2}{i_{{\rm{p}}j}} - \frac{{{u_{{\rm{dc}}}}}}{2}{i_{{\rm{l}}j}} = - \frac{{i_{{\rm{p}}j}^{} + {i_{{\rm{l}}j}}}}{2}{u_{{\rm{dc}}}} = - {i_{{\rm{dif}}\_j}}{u_{{\rm{dc}}}}$
${P_{{\rm{ac}}}} = \frac{1}{2}{U_j}{I_j}\cos ({\varphi _2} - {\varphi _1}) - \frac{1}{2}I_j^2R$

式中,Uj、Ij、${\varphi _2}$、${\varphi _1}$分别为电网侧交流电压和电流的幅值及初始相位角。

MMC内部有功损耗为

${P_{{\rm{loss}}j}} = 2i_{{\rm{dif\_}}j}^2r$

根据功率守恒原理,MMC交流侧输入有功功率等于直流侧输出有功功率及MMC内部损耗之和

${P_{{\rm{ac}}}} = {P_{{\rm{dc}}}} + {P_{{\rm{loss}}j}}$

联立式(35)~(38)可求得环流参考值如下

$i_{{\rm{dif}}\_j}^ * = \frac{{{u_{{\rm{dc}}}} - \sqrt {u_{{\rm{dc}}}^2 + 4{R_0}[I_j^2R - {E_j}{I_j}\cos ({\varphi _2} - {\varphi _1})]} }}{{4{R_0}}}$

由于MMC各相桥臂等效电阻r很小,其内部有功损耗Plossj相比于直流侧和交流侧功率的值来 说非常小,因此忽略其影响,得到环流参考近似值为

$i_{{\rm{dif}}\_j}^ * \approx \frac{{{P_{{\rm{ac}}}}}}{{{u_{{\rm{dc}}}}}} = \frac{{{U_j}{I_j}\cos ({\varphi _2} - {\varphi _1}) - I_j^2R}}{{2{u_{{\rm{dc}}}}}}$

网侧电流电压信号由采样环节获得,通过采样结果计算其幅值。综合上述分析可得到基于模型预测控制的环流抑制目标函数

${J_{{\rm{dif}}}} = \;|i_{{\rm{dif}}\_j}^ * - i_{{\rm{dif}}\_j}^{}(t + {T_s})|$

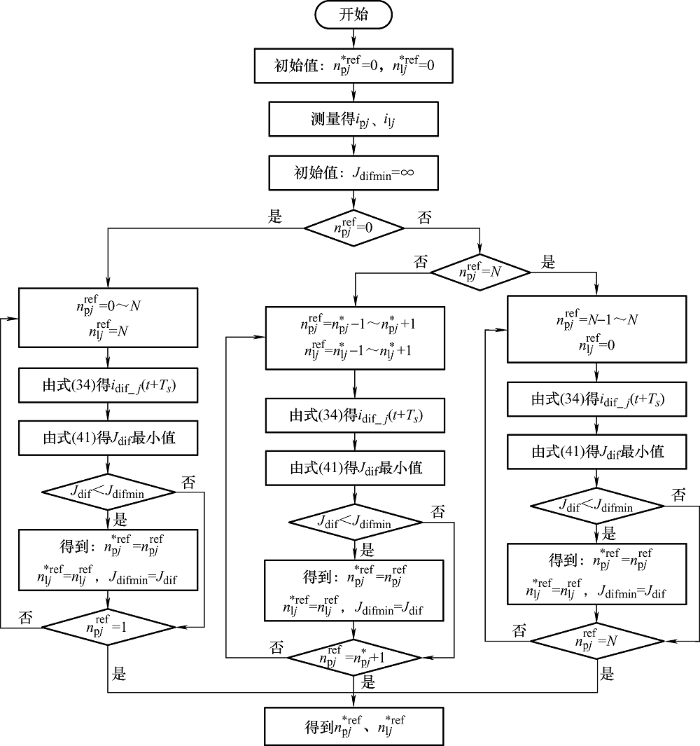
通过对环流计算值与给定值之间的误差进行计算,使得其目标函数值最小时,求得实际最优的上下桥臂子模块插入数目$n_{{\rm{p}}j}^{ * ref}$、$n_{{\rm{l}}j}^{ * ref}$,其具体的实施过程如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   环流预测控制流程框图


图4中Jdifmin是当前目标(代价)函数的最小值,当计算得到的Jdif小于Jdifmin时,则对开关状态和Jdifmin进行更新,若Jdif大于Jdifmin,则重复Jdif计算,直至遍历所有的开关状态,得到目标函数最小值Jdifmin为全局最小值,输出对应子模块开通数目组合。

4.1 子模块电容电压平衡

由上述基于模型预测的环流抑制阶段得到最优上下桥臂子模块投入数目$n_{{\rm{p}}j}^{ * ref}$、$n_{{\rm{l}}j}^{ * ref}$,且能够实现上下桥臂投入子模块数目实时的更新,最后,电压平衡过程结合了子模块排序方法,得到了相应开关的脉冲触发信号。子模块电容电压平衡过程通过加入调制和电容电压平衡算法以固定开关频率,提高了电网电压不平衡情况下MMC换流器的稳态性能。

4.2 MMC整体控制框架

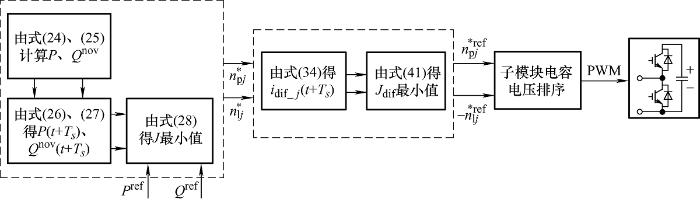
图5为MMC整体控制框图,首先是基于新型瞬时功率的功率预测控制,通过控制有功和无功功 率跟踪其参考值,当电网处于平衡状态时,可以实现交流侧电流的平衡及有功、无功功率的稳定控制,当电网突发电压不平衡故障时,所提功率预测控制策略,有效地实现了交流侧电流的平衡及有功和无功功率的恒定输送。其次,由功率预测控制阶段得到上下桥臂子模块电容电压插入数n* pj、$n_{{\rm{l}}j}^ *$用于环流控制阶段,通过控制上下桥臂插入子模块数之和在N附近微量变化,同时建立相间环流目标函数,求得最优上下桥臂子模块插入数目$n_{pj}^{ * ref}$、$n_{{\rm{l}}j}^{ * ref}$,并将其用于电容电压平衡控制阶段,最后,经过子模块排序算法得到开关脉冲触发信号。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   MMC整体控制框图


5 仿真验证

为了验证文章所提控制策略的有效性,在Matlab/Simulink仿真平台上搭建了仿真模型,风电场采用等效模型代替,MMC采用半桥型的子模块拓扑结构,其系统结构如图6所示,表1为系统仿真平台的参数。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   双端MMC-HVDC系统仿真模型结构图


表1   仿真平台主要参数

名称数值
交流系统额定电压/kV400
交流系统电感/mH72.8
系统额定频率/Hz50
系统额定有功功率/MW220
整流端变压器额定电压/kV400/66(Yg/Y)
整流端变压器额定功率/(MV·A)220
变压器漏抗(%)5
逆变端变压器额定电压/kV66/18(Yg/Y)
整流端变压器额定功率/(MV·A)220
桥臂阻抗0.03 Ω+0.15 H
系统电抗/H0.015
系统电阻/Ω0.1
稳态直流电压/kV135
子模块额定电容/mF10.48
子模块额定电容电压/kV2.7

新窗口打开| 下载CSV


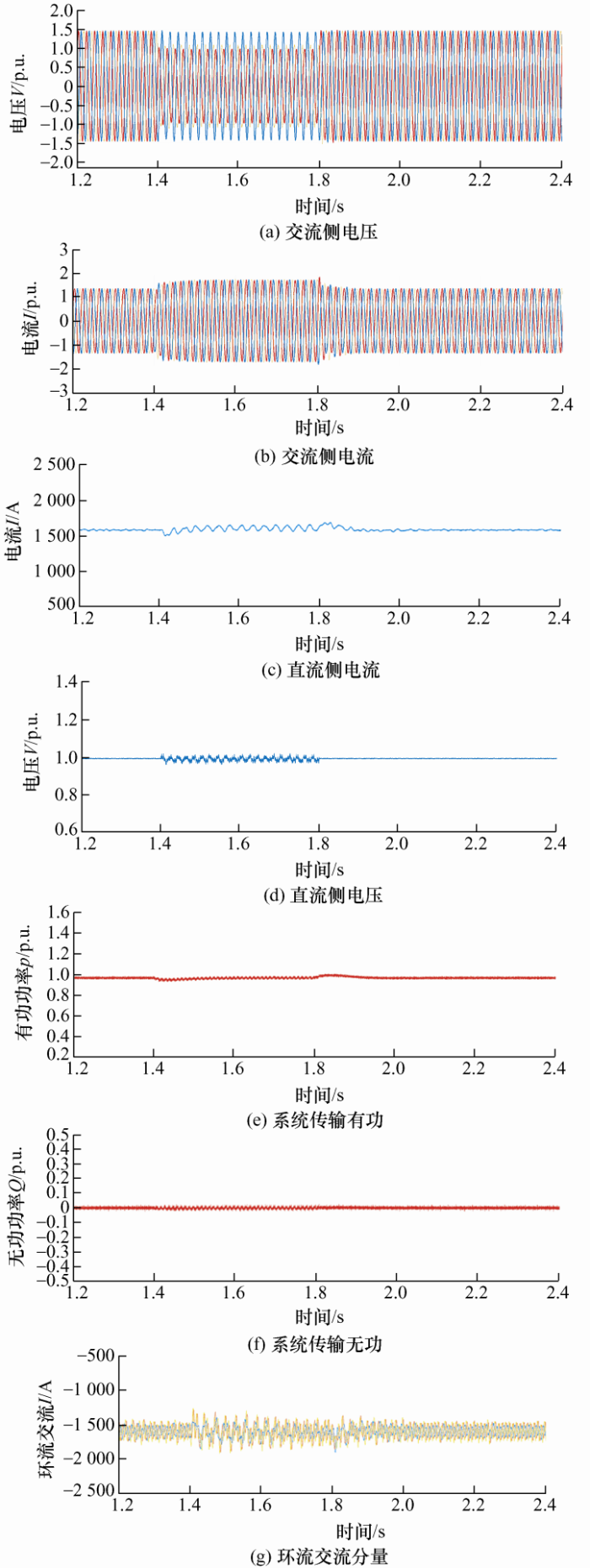
在变压器高压测设置了相应故障,此时交流侧电压波形如图7a所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   仿真结果(文章所提方法)


图7所示为交流侧故障时的仿真结果,图7a~7g分别为交流侧电压、交流侧电流、直流侧电流、直流侧电压、系统传输有功功率、新型无功功率、三相环流交流分量。

在1.4 s时刻,交流侧电压突发不平衡故障,如图7e、7f所示,即使在电网电压不平衡状态下,实际的有功功率及无功功率均能够精确地跟踪其参考值,同时有功及无功功率中都不含有二倍频波动量,由此可知采用文章所提的功率预测控制策略,能够同时实现有功和无功二倍频波动的有效抑制,有效验证了其在网压不平衡状态下控制器的良好控制效果。

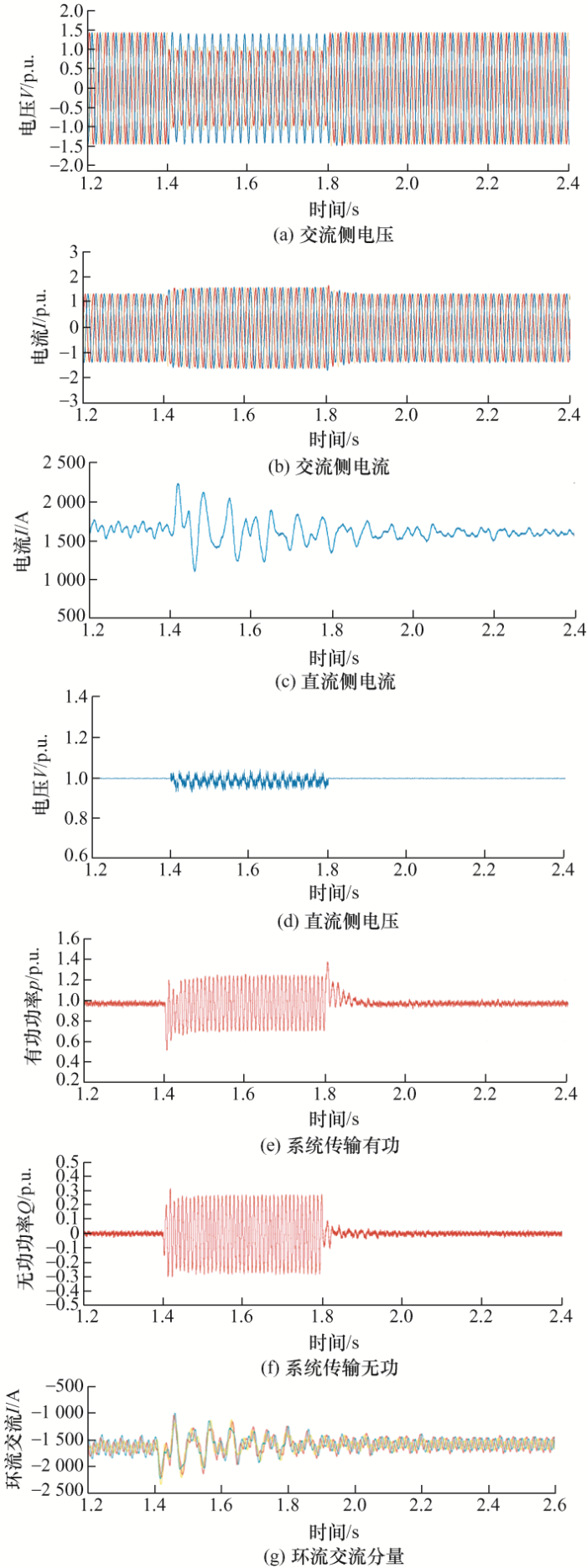
传统直接抑制负序电流的交流侧故障穿越方法仿真结果分别如图8所示,图8a~8g分别为交流侧电压、交流侧电流、直流侧电流、直流侧电压、系统传输有功功率、新型无功功率、三相环流交流分量,相比于文章所提预测直接功率控制策略,1.4 s时,电网电压不对称,其输送实际有功和无功功率如图8e、8f所示,因二倍频波动分量的存在有功和无功都具有较大的波动,如图8g所示,其三相环流交流分量波动明显,传统方法通过控制抑制故障下的负序分量实现交流侧电流的平衡,但是故障状态下环流中依然存在二倍频负序和零序分量,如图8c所示,当这些分量流入直流侧会使得直流电流产生很大波动,而文章所提方法能够更好地实现三相环流及直流母线电流控制,表明了其优越性能。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   仿真结果(直接抑制负序电流)


6 结论

基于新型瞬时功率理论的研究,文章提出一种风电接入下的柔直交流侧故障穿越控制策略,经过上述分析得出如下结论。文章基于新型瞬时功率理论建立了预测功率模型,所提控制策略无需计算功率补偿项,能够实现对于有功和无功功率二倍频波动的同步抑制,确保网压不平衡下功率输送的稳定。建立的功率预测模型及环流预测模型,采用分层控制策略,相比于传统的MPC控制方法,无需引入权重系数,控制系统结构简单,计算量小,所提控制策略在电网电压平衡、不对称情况下都具有良好的控制效果。在Matlab/Simulink上建立了风电并网柔直等效仿真模型,对比了常用方法与文章所提方法在交流侧故障状态下的控制效果,验证了文章所提预测功率直接控制策略在风电接入下柔直交流侧故障穿越的优越性能。

参考文献

李琦, 宋强, 刘文华, 等.

基于柔性直流输电的风电场并网故障穿越协调控制策略

[J]. 电网技术, 2014, 38(7):1739-1745.

[本文引用: 1]

LI Qi, SONG Qiang, LIU Wenhua, et al.

A coordinated control strategy for fault ride-through of wind farm integration based on VSC-HVDC

[J]. Power System Technology, 2014, 38(7):1739-1745.

[本文引用: 1]

TAYLOR C W, MITTELSTADT W A, LEE T N, et al.

Single-pole switching for stability and reliability

[J]. IEEE Transactions on Power Systems, 1986, 1(2):25-36.

[本文引用: 1]

SHI Xiaojie, WANG Zhiqiang, LIU Bo, et al.

Steady-state modeling of modular multilevel converter under unbalanced grid conditions

[J]. IEEE Transactions on Power Electronics, 2017, 32(9):7306-7324.

DOI:10.1109/TPEL.63      URL     [本文引用: 1]

GUAN Minyuan, XU Zheng.

Modeling and control of a modular multilevel converter-based HVDC system under unbalanced grid conditions

[J]. IEEE Transactions on Power Electronics, 2012, 27(12):4858-4867.

DOI:10.1109/TPEL.2012.2192752      URL     [本文引用: 1]

年珩, 程鹏.

电网电压不平衡时 PWM 整流器的谐振直接功率控制策略

[J]. 电工技术学报, 2013, 28(11):86-94.

[本文引用: 1]

NIAN Heng, CHENG Peng.

Resonant based direct power control strategy for PWM rectifier under unbalanced grid voltage condition

[J]. Transactions of China Electrotechnical Society, 2013, 28(11):86-94.

[本文引用: 1]

年珩, 沈永波, 宋亦鹏.

不平衡及谐波电网电压下并网逆变器的直接功率控制策略

[J]. 电网技术, 2014, 38(6):1452-1458.

[本文引用: 1]

NIAN Heng, SHEN Yongbo, SONG Yipeng.

Direct power control strategy of grid connected inverter under unbalanced and harmonic grid voltage

[J]. Power System Technology, 2014(6):1452-1458.

[本文引用: 1]

SHANG Lei, HU Jiabing.

Sliding-mode-based direct power system control of grid-connected wind-turbine-driven doubly fed induction generators under unbalanced grid voltage conditions

[J]. IEEE Transactions on Energy Conversion, 2012, 27(2):362-373.

DOI:10.1109/TEC.2011.2180389      URL     [本文引用: 1]

HU Jiefeng, ZHU Jianguo, DORRELL D G.

Model predictive direct power,control of doubly-fed induction generators under unbalanced grid voltage conditions in wind energy applications

[J]. IET Renewable Power Generation, 2014, 8(6):687-695.

DOI:10.1049/rpg2.v8.6      URL     [本文引用: 1]

辛业春, 王威儒, 李国庆, 等.

基于桥臂电流直接控制的模块化多电平换流器控制策略

[J]. 电力自动化设备, 2018, 38(10):115-120.

[本文引用: 1]

XIN Yechun, WANG Weiru, LI Guoqing, et al.

Control strategy of modular multilevel converter based on arm current direct control

[J]. Electric Power Automation Equipment, 2018, 38(10):115-120.

[本文引用: 1]

郭鹏, 何志兴, 罗安, 等.

基于多步模型预测控制的模块化多电平换流器环流控制策略

[J]. 电力系统自动化, 2017, 41(16):137-143,157.

[本文引用: 1]

GUO Peng, HE Zhixing, LUO An, et al.

Control strategy of circulating current for modular multilevel converters based on multistep model predictive control

[J]. Automation of Electric Power Systems, 2017, 41(16):137-143,157.

[本文引用: 1]

AKAGI H, KANAZAWA Y, NABAE A.

Instantaneous reactive power compensators comprising switching devices without energy storage components

[J]. IEEE Transactions on Industry Applications, 1984, IA- 20(3):625-630.

[本文引用: 1]

ZHANG Yongchang, QU Changqi.

Model predictive direct power control of PWM rectifiers under unbalanced network conditions

[J]. IEEE Transactions on Industrial Electronics, 2015, 62(7):4011-4022.

DOI:10.1109/TIE.2014.2387796      URL     [本文引用: 1]

梁营玉, 张涛, 刘建政, 等.

不平衡电网电压下模块化多电平换流器的环流抑制策略

[J]. 电工技术学报, 2016, 31(9):120-128.

[本文引用: 1]

LIANG Yingyu, ZHANG Tao, LIU Jianzheng, et al.

A circulating current suppressing method for modular multilevel converter under unbalanced grid voltage

[J]. Transactions of China Electrotechnical Society, 2016, 31(9):120-128.

[本文引用: 1]

RODRIGUEZ P, LUNA A, CANDELA I, et al.

Grid synchronization of power converters using multiple second order generalized integrators

[C]// 34th Annual Conference of IEEE Industrial Electronics, 2008:755-760.

[本文引用: 1]

蔡洁.

模块化多电平柔性直流输电交流侧故障穿越与控制策略研究

[D]. 长沙:长沙理工大学, 2018.

[本文引用: 1]

CAI Jie.

Research on fault pass-through and control strategy in AC side of modular multilevel high voltage direct current transmission system

[D]. Changsha:Changsha University of Science & Technology, 2018.

[本文引用: 1]

刘普, 王跃, 丛武龙, 等.

模块化多电平换流器优化模型预测控制策略研究

[J]. 中国电机工程学报, 2014, 34(36):6380-6388.

[本文引用: 1]

LIU Pu, WANG Yue, CONG Wulong, et al.

Researches on optimized model predictive control for modular multilevel converters

[J]. Proceedings of the CSEE, 2014, 34(36):6380-6388.

[本文引用: 1]

BEN-BRAHIM L, GASTLI A, TRABELSI M, et al.

Modular multilevel converter circulating current reduction using model predictive control

[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6):3857-3866.

DOI:10.1109/TIE.2016.2519320      URL     [本文引用: 1]

周月宾, 江道灼, 郭捷, 等.

模块化多电平换流器子模块电容电压波动与内部环流分析

[J]. 中国电机工程学报, 2012, 32(24):8-14.

[本文引用: 1]

ZHOU Yuebin, JIANG Daozhuo, GUO Jie, et al.

Analysis of sub-module capacitor voltage ripples and circulating currents in modular multilevel converters

[J]. Proceedings of the CSEE, 2012, 32(24):8-14.

[本文引用: 1]

/

〈 〉