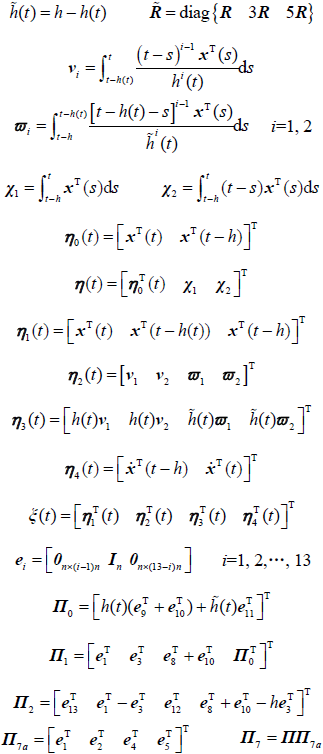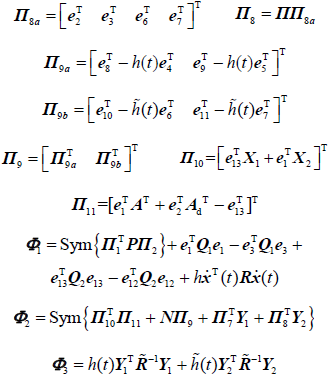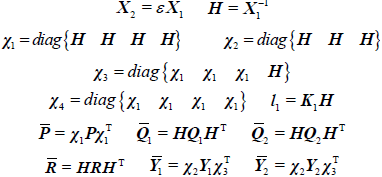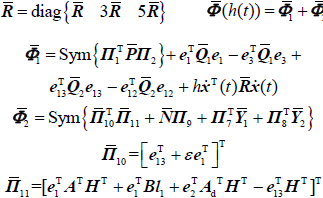1 引言
随着智能电网发展,现代电力系统更加趋向于多互联,大规模方向发展,因此仅依赖传统的区域信号控制方法将无法满足系统对性能的要求。近些年,随着同步相量测量装置技术,全球定位系统技术和现代电力通信技术的广域测量系统的应用,使得将本地电力系统信息同步采样并传送至远程控制中心成为可能,这就可以通过广域控制器对电力系统进行协调控制[1 ] 。但是,电网广域监测系统(Wide area measurement system, WAMS)的应用将电力系统变成了一个时滞系统,各类广域控制信道中难免存在时滞,直接影响到电力系统的稳定性。因此,研究电力系统所能承受的时滞稳定裕度是很有意义的。此外,为了保证电力系统稳定运行,研究电力系统时滞镇定器的设计也具有非常重要的意义。
目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] 。通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度。文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统。文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] 。二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] 。文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差。文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题。文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器。
文章基于常时滞电力系统模型基础上,建立了时变时滞(即时滞不确定)电力系统模型,构建新的增广LK泛函,应用文献[21 ]中Bessel-Legendre不等式估计该泛函的导数,以改善时变时滞电力系统的最大时滞上界。再应用参数调整法[22 ] 进行时变时滞电力系统鲁棒镇定控制器设计,通过典型二阶时滞系统和单机无穷大电力系统进行实例验证、模型仿真,证明了文章方法的实用性和优越性。
2 系统模型
在进行时滞电力系统稳定性分析时,通常建立简单的系统模型,达到对系统基本性能和概念的理解。本文主要从单机无穷大系统着手研究,以此为基础,从而可以分析更加复杂的大型网络系统。
单机无穷大系统模型主要由一个发电机组(原动机、发电机以及励磁系统等)、变压器、输电线路以及理想化的无穷大母线端构成。单机无穷大系统简化模型见图1 。
图1
本节主要讨论三阶矩阵模型的单机无穷大电力系统,常用的模型方程如下
(1) $\dot \delta = {\omega _B}\omega$
(2) $\dot \omega = \frac{1}{M}\left( {{P_{m}} - {P_{G}} - D\omega } \right)$
(3) $\dot E_q^{'} = \frac{1}{{{{T'}_{do}}}}\left( {{E_{fd}} - E_q^{'} - ({x_d} - {{x'}_q}){I_d}} \right)$
${\omega _B} = 2\pi {f_0} {P_G} = \frac{{{{E}_q}{V_o}\sin \delta }}{{{x_e} + {{x'}_d}}} {I_d} = \frac{{{{E}_q} - {V_0}\cos \delta }}{{{x_e} + x_d^{'}}}$
式中,$\delta$表示功角;$\omega$表示角速度;${\omega _B}$表示额定角速度;f 0 表示基准频率;M 表示惯性时间常数;${P_m}$表示输出的机械功率;PG 表示输出的电磁功率;D 表示阻尼系数;${\dot E_q}$表示q 轴电抗后暂态电势;${T_{do}}$表示发电机的d 轴开路时间常数;${E_{fd}}$表示励磁系统的输出电势;${x_d}$表示发电机的d 轴稳态电抗;$x_d^{'}$表示发电机的d 轴暂态电抗;Id 表示d 轴的电流;${V_0}$表示无穷大母线的端电压;xe 表示线路的阻抗。
(4) ${V_G} = \frac{{\sqrt {{{({{{x'}}_d} + {{x}_e}{{E}_q}\cos {\delta })}^2} + {{({{x}_e}{{E}_q}\sin \delta )}^2}} }}{{{{x}_e} + {{{x'}}_d}}}$
假定系统的稳定平衡点为$\left( {{\delta _0},{\kern 1pt} {\kern 1pt} {\omega _0},{\kern 1pt} {\kern 1pt} E_{q0}^{'},{\kern 1pt} {\kern 1pt} {E_{fd0}}} \right)$,将式(1)~(4)描述的非线性模型在平衡点处作线性化处理。经推导,得到下述线性系统
(5) $\left[ {\begin{array}{*{20}{c}} {\Delta \dot \delta }\\ {\Delta \dot \omega }\\ {\Delta \dot E_q^{'}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0&{{{\bf{\omega }}_B}}&0\\ { - \frac{{{K_1}}}{M}}&{ - \frac{D}{M}}&{ - \frac{{{K_2}}}{M}}\\ { - \frac{{{K_3}}}{{T_{d0}^{'}}}}&0&{ - \frac{{{K_4}}}{{T_{d0}^{'}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\Delta \delta }\\ {\Delta \omega }\\ {\Delta E_q^{'}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {\frac{1}{{T_{d0}^{'}}}} \end{array}} \right]\Delta {E_{fd}}$
${K_1} = \frac{{E_{q0}^{'}{V_s}\cos {\delta _0}}}{{{x_e} + x_d^{'}}} {K_2} = \frac{{{V_0}\sin {\delta _0}}}{{{{\bf{x}}_e} + {\bf{x'}}_d^{'}}} \\ {K_3} = \frac{{{{\bf{x}}_d} - {\bf{x'}}_d^{'}}}{{{{\bf{x}}_e} + {\bf{x'}}_d^{'}}}{V_0}\sin {\delta _0} {K_4} = \frac{{{{\bf{x}}_e} + {{\bf{x}}_d}}}{{{{\bf{x}}_e} + {\bf{x'}}_d^{'}}}$
文章讨论基于自动电压调节励磁控制系统的时滞相关鲁棒性,假定在机组电压测量时存在时滞,得到下列状态方程
(6) ${\dot E_{fd}} = - \frac{{{K_A}}}{{{{\bf{T}}_A}}}({{\bf{V}}_G}(t - h) - {{\bf{V}}_{ref}}) - \frac{1}{{{{\bf{T}}_A}}}({{\bf{E}}_{fd}} - {{\bf{E}}_{fd0}})$
式中,KA 表示控制增益;TA 表示时间常数;h 表示时滞参数;Vref 表示机端电压的参考值;${E_{fd0}}$表示励磁控制的输出参考值。
结合系统模型式(5)和状态方程式(6),在平衡点$\left( {{{\bf{\delta }}_0},{\kern 1pt} {\kern 1pt} {{\bf{\omega }}_0},{\kern 1pt} {\kern 1pt} {\bf{E}}_{q0}^{'},{\kern 1pt} {\kern 1pt} {{\bf{E}}_{fd0}}} \right)$处进行线性化处理,经过计算推导得到含时滞的线性电力系统模型
(7) $\dot x(t) = Ax(t) + {A_1}x(t - h)\;\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} t > 0$
其中,${\bf{x}}(t) = {\left[ {\begin{array}{*{20}{c}}{\Delta {\bf{\delta }}}&{\Delta {\bf{\omega }}}&{\Delta {\bf{E}}_q^{'}}&{\Delta {{\bf{E}}_{fd}}}\end{array}} \right]^T}$
$A = \left[ {\begin{array}{*{20}{c}} 0&{{{\bf{\omega }}_B}}&0&0\\ { - \frac{{{K_1}}}{{\bf{M}}}}&{ - \frac{{\bf{D}}}{{\bf{M}}}}&{ - \frac{{{K_2}}}{{\bf{M}}}}&0\\ { - \frac{{{K_3}}}{{{\bf{T'}}_{d0}^{'}}}}&0&{ - \frac{{{K_4}}}{{{\bf{T'}}_{d0}^{'}}}}&0\\ 0&0&0&{ - \frac{1}{{{{\bf{T}}_A}}}} \end{array}} \right]$
${A_1} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0\\ { - \frac{{{K_5}{{\bf{K}}_A}}}{{{{\bf{T}}_A}}}}&0&{ - \frac{{{K_6}{{\bf{K}}_A}}}{{{{\bf{T}}_A}}}}&0 \end{array}} \right] {K_5} = \frac{{ - {{\bf{x}}_e}{\bf{x'}}_d^{'}{\bf{E}}_{q0}^{'}\sin {{\bf{\delta }}_0}}}{{\left( {{{\bf{x}}_e} + {\bf{x'}}_d^{'}} \right)\sqrt {{{\left( {{{\bf{x}}_q}{{\bf{V}}_0}\sin {{\bf{\delta }}_0}} \right)}^2} + {{\left( {{{\bf{x}}_e}{\bf{E}}_{q0}^{'} + {\bf{x'}}_d^{'}{{\bf{V}}_0}\cos {{\bf{\delta }}_0}} \right)}^2}} }}$
${K_6} = \frac{{{{\bf{x}}_e}{\bf{x'}}_d^{'}{\bf{E}}_{q0}^{'}\cos {{\bf{\delta }}_0} + {\bf{x}}_e^2{\bf{E}}_{q0}^{'}}}{{\left( {{{\bf{x}}_e} + {\bf{x'}}_d^{'}} \right)\sqrt {{{\left( {{{\bf{x}}_q}{{\bf{V}}_0}\sin {{\bf{\delta }}_0}} \right)}^2} + {{\left( {{{\bf{x}}_e}{\bf{E}}_{q0}^{'} + {\bf{x'}}_d^{'}{{\bf{V}}_0}\cos {{\bf{\delta }}_0}} \right)}^2}} }}$
文章讨论的电力系统模型是基于式(6)的自动电压调节励磁控制系统的时滞电力系统模型,不同的是模型的时滞类型为时变时滞,且时滞变化量未知(即$\dot h(t)$未知),式(6)转变为
(8) ${\dot E_{fd}} = - \frac{{{K_A}}}{{{T_A}}}({V_G}(t - h(t)) - {V_{ref}}) - \frac{1}{{{T_A}}}({E_{fd}} - {E_{fd0}})$
(9) $\dot x(t) = Ax(t) + {A_1}x(t - h(t))\;\;\;\;t > 0$
式中,$0h(t)h$为时滞变量,$h$为时滞稳定裕度。
(10) $u\left( t \right) = {K_1}x(t) + {K_2}x(t - h\left( t \right))$
式中,${K_1}$、${K_2}$表示待解的反馈控制器增益矩阵。
3 稳定判据
引理1[21 ] :定义$\omega$是在区间[a , b ]→Rn
(11) $ - \int_a^b {{{\dot \omega }^T}(s)Z\dot \omega (s){\rm{d}}s} \le {\varsigma ^T}\left[ {Sym\left\{ {{\Pi ^T}M} \right\} + (b - a){M^T}\tilde ZM} \right]\varsigma$
$\tilde Z = diag\left\{ {Z{\kern 1pt},{\kern 1pt} {\kern 1pt} {\kern 1pt} 3Z{\kern 1pt},{\kern 1pt} {\kern 1pt} {\kern 1pt} 5Z} \right\} \varsigma = {\left[ {\begin{array}{*{20}{c}}{\omega (b)}&{\omega (b)}&{{\gamma _1}}&{{\gamma _2}}\end{array}} \right]^T}$
${\gamma _1} = \int_a^b {\frac{{\omega (s)}}{{b - a}}} ds {\gamma _2} = \int_a^b {\frac{{(b - s)\omega (s)}}{{{{(b - a)}^2}}}} ds \Pi = \left[ {\begin{array}{*{20}{c}}I&{ - I}&0&0\\I&I&{ - 2I}&0\\I&{ - I}&{ - 6I}&{12I}\end{array}} \right]$
基于Bessel-Legendre不等式并结合自由权矩阵方法,得到时变时滞电力系统的稳定判据如下。
定理1:存在实对称矩阵$\bar P$ ($\Phi$${R^{4n \times 4n}}$)>0,${\bar Q_1}$ ($\Phi$${R^{n \times n}}$)>0,${\bar Q_2}$ ($\Phi$${R^{n \times n}}$)>0,$\bar R$ ($\Phi$${R^{n \times n}}$)>0,适当维数任意矩阵${\bar Y_1}$、${\bar Y_2}$、$H$、${l_1}$、$\bar N$,任意标量$\varepsilon$,对于条件$0 \le h(t) \le h$,如果不等式组(23)、(24)成立,则系统式(22)稳定。
(12) $\left[ {\begin{array}{*{20}{c}}{\Phi (0)}&{hY_2^T}\\*&{ - h\tilde R}\end{array}} \right]0$
(13) $\left[ {\begin{array}{*{20}{c}}{\Phi (h)}&{hY_1^T}\\*&{ - h\tilde R}\end{array}} \right]0$
式中,$\Phi (h(t)) = {\Phi _1} + {\Phi _2}$。
证明:根据Lyapunov稳定理论,构建新的增广型LK泛函如下
(14) $\begin{array}{c}V({x_t}) = {\eta ^T}(t)P\eta (t) + \int_{t - h}^t {x({\kern 1pt} s){Q_1}x({\kern 1pt} s)ds + } \\ \int_{t - h}^t {\dot x({\kern 1pt} s){Q_2}\dot x({\kern 1pt} s)ds + } \int_{ - h}^0 {\int_{t + \theta }^t {{{\dot x}^T}(s)R\dot x(s)dsd\theta } } \end{array}$
当P >0,Q 1 >0,Q 2 >0,R >0时,则函数正定,即$V({x_t})0$。对$V({x_t})$求导可得
(15) $\dot V({x_t}) = {\xi ^T}(t){\Phi _1}\xi (t) - \int_{t - h}^t {{{\dot x}^T}(s)R\dot x(s)ds}$
(16) $ - \int_{t - h}^t {{{\dot x}^T}(s)} R\dot x(s){\rm{d}}s = - \int_{t - h(t)}^t {{{\dot x}^T}(s)R\dot x(s){\rm{d}}s} {\dot x^T}(s)R\dot x(s){\rm{d}}s - \int_{t - h(t)}^t {{{\dot x}^T}(s)R\dot x(s){\rm{d}}s}$
(17) $\begin{array}{c} - \int_{t - h(t)}^t {{{\dot x}^T}(s)R\dot x(s)} \le {\xi ^T}(t) \times \\\left( {Sym\left\{ {\Pi _7^T{Y_1}} \right\} + h(t)Y_1^T{{\tilde R}^{ - 1}}{Y_1}} \right)\xi (t)\end{array}$
(18) $\begin{array}{c} - \int_{t - h}^{t - h(t)} {{{\dot x}^T}(s)R\dot x(s){\rm{d}}s} \le {\xi ^T}(t) \times \\ \left( {Sym\left\{ {\Pi _8^T{Y_2}} \right\} + \tilde h(t)Y_2^T{{\tilde R}^{ - 1}}{Y_2}} \right)\xi (t) \end{array}$
(19) $2{\xi ^T}(t)N{\Pi _9}\xi (t) = 0$
考虑到适当维数任意矩阵Xi (i =1, 2, 3),有以下等式成立
(20) $\begin{array}{c}2\left[ { - \dot x(t) + Ax(t) + {A_1}{x^T}(t - h(t))} \right] \times \\ \left[ {{{\dot x}^T}(t){X_1} + {x^T}(t){X_2}} \right] = 0\end{array}$
(21) $\dot V({x_t}) \le {\xi ^T}(t)\left( {{\Phi _1} + {\Phi _2} + {\Phi _3}} \right)\xi (t)$
应用Schur补定理,式(21)等价于式(12)、(13)。因此,如果式(12)、(13)成立,则有$\dot V(t)0$,根据Lyapunov稳定理论,系统(式(9))稳定,证毕。
4 控制器设计
4.1 无记忆反馈控制器设计
若${K_2}$是零向量,则式(10)表示无记忆控制器。在控制器式(10)的作用下,式(9)转变为
(22) $\dot x(t) = \left( {A + B{K_1}} \right)x(t) + {A_1}x(t - h(t))\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} t > 0$
此时,将不等式(12)、(13)中A 替换成$A + B{K_1}$,定义
$\bar N = {\chi _3}N\chi _1^T$,在式(12)、(13)分别左乘和右乘${\chi _4}$,可得如下判据。
定理2:存在实对称矩阵$\bar P$ (${R^{4n \times 4n}}$)>0,${\bar Q_1}$ (${R^{n \times n}}$)>0,${\bar Q_2}$ (${R^{n \times n}}$)>0,$\bar R$ (${R^{n \times n}}$)>0,适当维数任意矩阵${\bar Y_1}$、${\bar Y_2}$、$H$、${l_1}$、$\bar N$,任意标量$\varepsilon$,对于条件$0 \le h(t) \le h$,如果不等式组(23)、(24)成立,则系统式(22)稳定。
(23) $\left[ {\begin{array}{*{20}{c}}{\bar \Phi (0)}&{h\bar Y_2^T}\\*&{ - h\tilde \bar R}\end{array}} \right]0$
(24) $\left[ {\begin{array}{*{20}{c}}{\bar \Phi (h)}&{h\bar Y_1^T}\\*&{ - h\tilde \bar R}\end{array}} \right]0$
4.2 有记忆反馈控制器设计
若${K_2}$是非零向量,则式(10)表示有记忆控制器。在控制器式(10)的作用下,式(9)转变为
(25) $\dot x(t) = \left( {A + B{K_1}} \right)x(t) + \left( {{A_1} + B{K_2}} \right)x(t - h(t))\;\;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} t > 0$
此时,将不等式(12)、(13)中A 替换成$A + B{K_1}$,${A_1}$替换成$A + B{K_2}$,定义:${l_2} = {K_2}H$,在式(12)、(13)分别左乘和右乘${\chi _4}$,可得如下判据。
定理3:存在实对称矩阵$\bar P$ ( ${R^{4n \times 4n}}$)>0,${\bar Q_1}$ (${R^{n \times n}}$)>0,${\bar Q_2}$ (${R^{n \times n}}$)>0,$\bar R$ (${R^{n \times n}}$)>0,适当维数任意矩阵${\bar Y_1}$、${\bar Y_2}$、$H$、${l_1}$、${l_2}$、$\bar N$,任意标量$\varepsilon$,对于条件$0 \le h(t) \le h$,如果不等式组 式(26)、(27)成立,则系统(式(25))稳定。
(26) $\left[ {\begin{array}{*{20}{c}}{\bar \bar \Phi (0)}&{h\bar Y_2^T}\\*&{ - h\tilde \bar R}\end{array}} \right]0$
(27) $\left[ {\begin{array}{*{20}{c}}{\bar \bar \Phi (h)}&{h\bar Y_1^T}\\*&{ - h\tilde \bar R}\end{array}} \right]0$
$\bar \bar \Phi (h(t)) = {\bar \Phi _1} + {\bar \bar \Phi _2}$
${\bar \Phi _2} = Sym\left\{ {\bar \Pi _{10}^T{{\bar \bar \Pi }_{11}} + \bar N{\Pi _9} + \Pi _7^T{{\bar Y}_1} + \Pi _8^T{{\bar Y}_2}} \right\}$
${\bar \bar \Pi _{11}}{\rm{ = [}}e_1^T{A^T}{H^T} + e_1^TB{l_1} + e_2^T{A_d}^T{H^T} + e_2^TB{l_2} - e_{13}^T{H^T}{]^T}$
5 算例分析
使用二阶系统和单机无穷大系统为例,考虑$\varepsilon = 1$的情况下无记忆控制器和有记忆控制器作用下的系统情况。
5.1 典型二阶系统
$A = \left[ {\begin{array}{*{20}{c}} 0&0\\ 0&1 \end{array}} \right]\;\;\;\;\;{A_1} = \left[ {\begin{array}{*{20}{c}} { - 2}&{ - 0.5}\\ 0&{ - 1} \end{array}} \right]\;\;\;\;\;B{\rm{ = }}\left[ {\begin{array}{*{20}{c}} 0\\ 1 \end{array}} \right]$
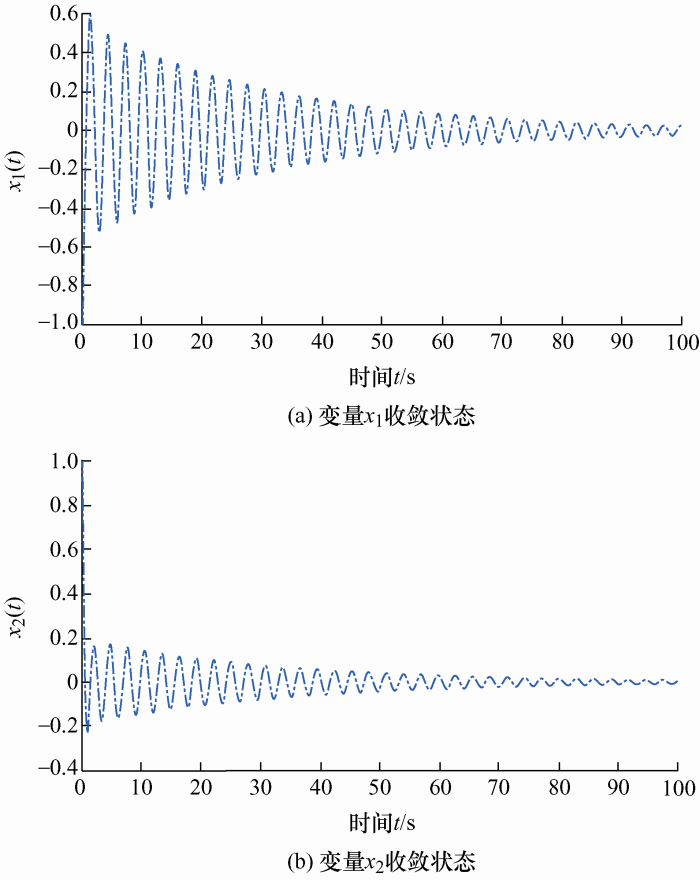
若使用无记忆状态反馈控制器镇定时,所得时滞稳定裕度为h =0.691 6 s,此时控制器的反馈增益[K 1 ]= [0.598 8-2.208 3],图2 为该系统状态变量响应曲线。
图2
图2
无记忆控制器下的状态变量x 1 和x 2 的响应(h =0.691 6 s)
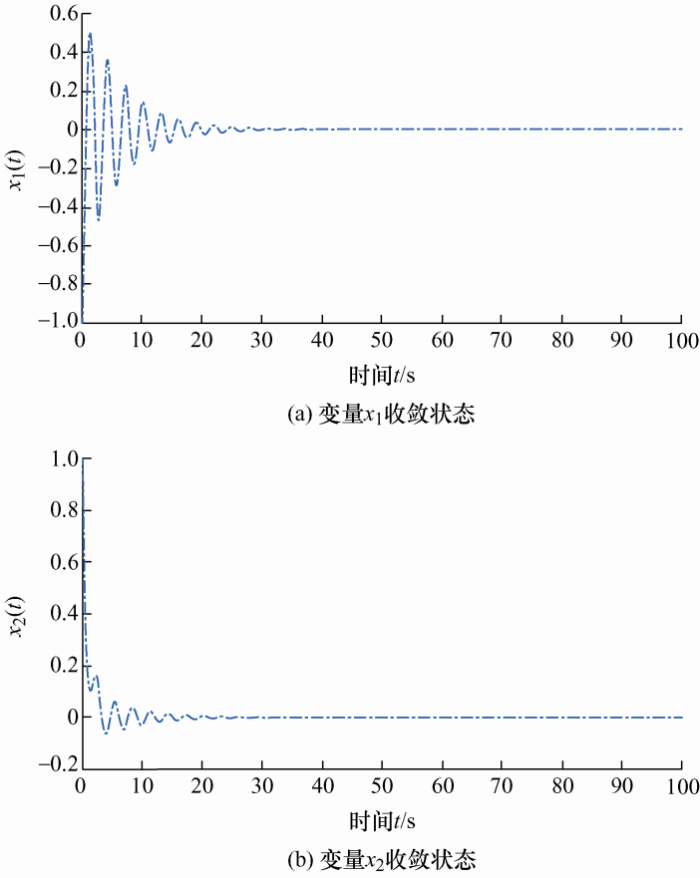
若使用有记忆状态反馈控制器镇定时,所得时滞稳定裕度为h =0.691 6 s,此时控制器的反馈增益如下,此时的状态变量响应曲线如图3 所示。
$\left[ {\begin{array}{*{20}{c}}{{K_1}}\\{{K_2}}\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}0&{ - 2.423\;1}\\{0.500\;0}&{1.328\;3}\end{array}} \right]$
图3
图3
有记忆控制器下的状态变量x 1 和x 2 的响应(h =0.691 6 s)
通过对比文献[23 ]获得的时滞上界h =0.656 9 s,体现出所提方法有一定的优越性。虽然无记忆控制器和有记忆控制器求得的最大时滞上界相同,但是可以从图2 、3 中看出,有记忆反馈控制器在收敛速度上明显优于无记忆控制器。
5.2 单机无穷大系统
考虑单机无穷大系统时,参照文献[23 ],系统矩阵参数A 、A 1 和B 分别为
$A = \left[ {\begin{array}{*{20}{c}}0&{376.991\;1}&0&0\\{ - 0.096\;3}&{ - 0.700\;0}&{ - 0.080\;1}&0\\{ - 0.048\;0}&0&{ - 0.166\;7}&{0.100\;0}\\0&0&0&{ - 1.000\;0}\end{array}} \right] {A_1} = \left[ {\begin{array}{*{20}{c}}0&0&0&0\\0&0&0&0\\0&0&0&0\\{38.018\;7}&0&{ - 95.256\;0}&0\end{array}} \right] B = \left[ {\begin{array}{*{20}{c}}0\\0\\0\\1\end{array}} \right]$
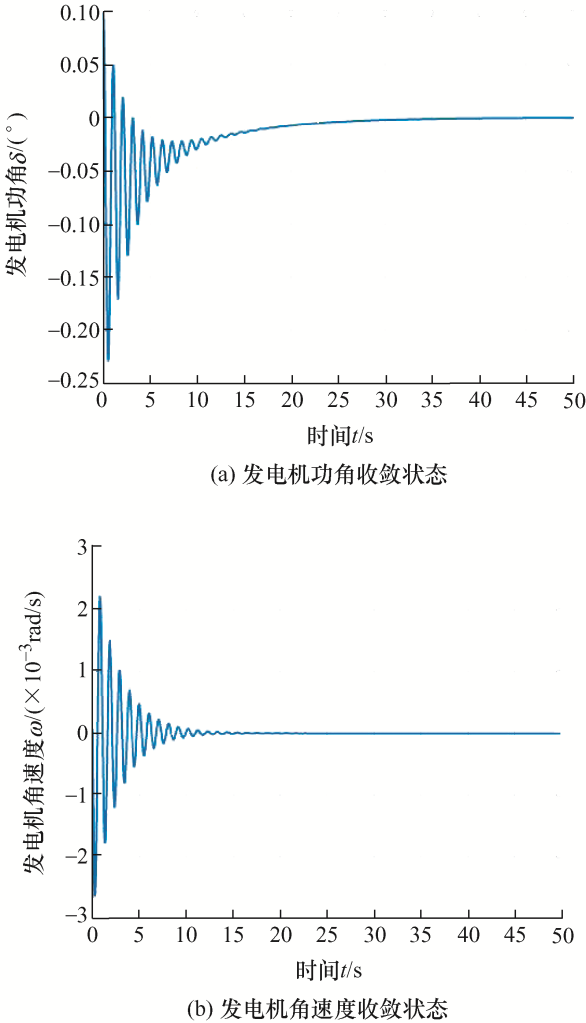
若使用无记忆状态反馈控制器镇定时,所得时滞稳定裕度为h =0.143 2 s,此时控制器的反馈增益$\left[ {{K_1}} \right] = {10^7} \times \left[ {\begin{array}{*{20}{c}}{ - 0.112\;6}&{0.003\;3}&{0.001\;5}&{ - 1.367\;3}\end{array}} \right]\;\;$图4 为该系统状态变量响应曲线。
图4
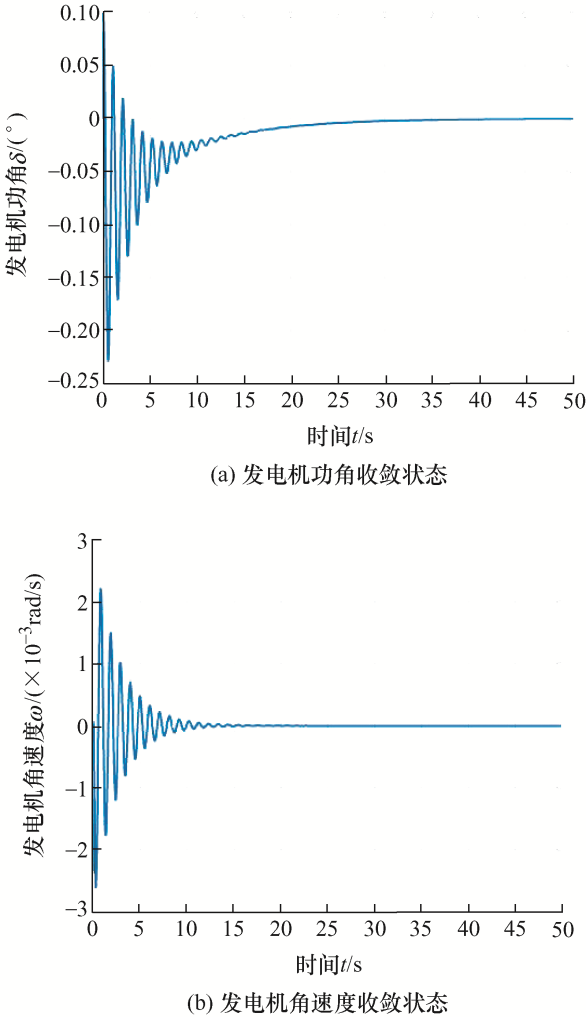
若使用有记忆状态反馈控制器镇定时,所得时滞稳定裕度为h =0.143 2 s,此时控制器的反馈增益如下,此时的状态变量响应曲线如图5 所示。
$\left[ {\begin{array}{*{20}{c}}{{K_1}}\\{{K_2}}\end{array}} \right] = {10^6} \times \left[ {\begin{array}{*{20}{c}}{ - 0.754\;2}&{0.021\;8}&{0.010\;3}&{ - 9.158\;3}\\{ - 0.000\;4}&0&0&{ - 1.605\;1}\end{array}} \right]$
图5
通过对比文献[23 ]的时滞上界h =0.140 7 s,体现出所提方法有一定的优越性。
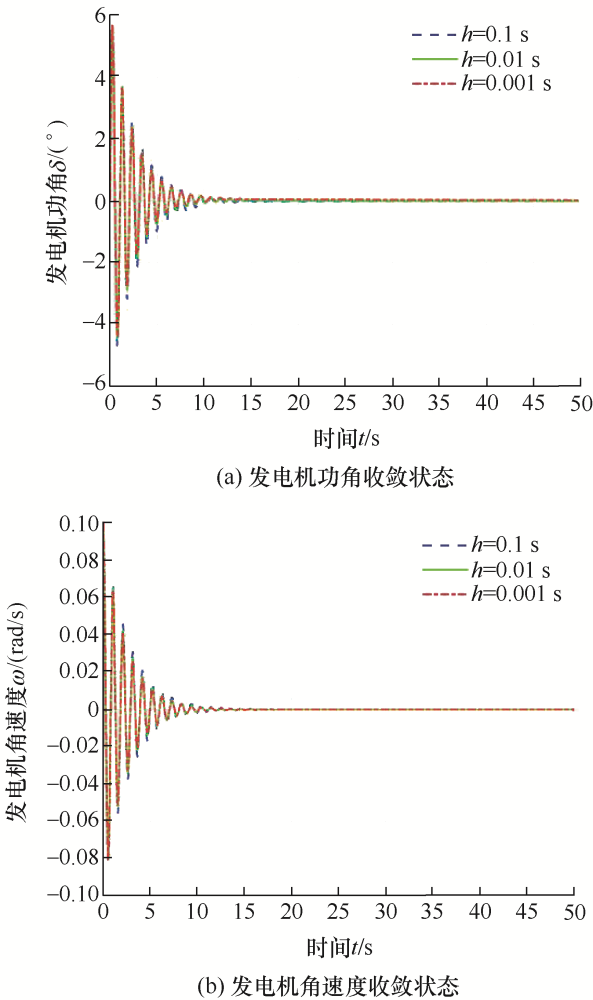
当h 取0.1 s/0.01 s/0.001 s时,在无记忆控制器作用下,求得控制器增益参数见表1 ,单机无穷大系统的仿真结果如图6 所示。
图6
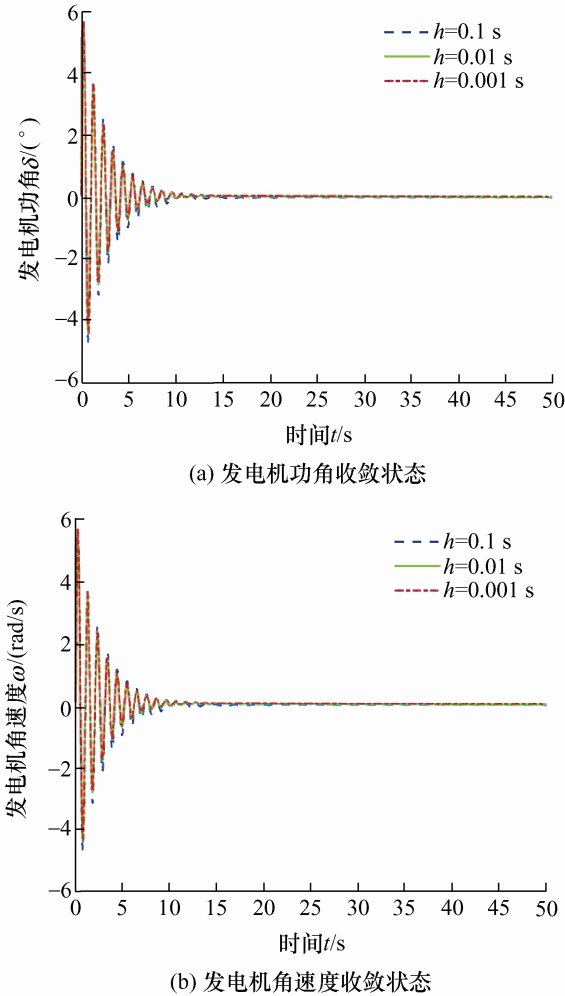
当h 取0.1 s/0.01 s/0.001 s时,在有记忆控制器作用下,求得控制器增益参数见表2 ,单机无穷大系统的仿真结果如图7 所示。
图7
由图6 、7 可知,在单机无穷大系统中,无论是记忆状态反馈控制器还是有记忆状态反馈控制器,在不同时滞中的镇定控制效果差异不大。
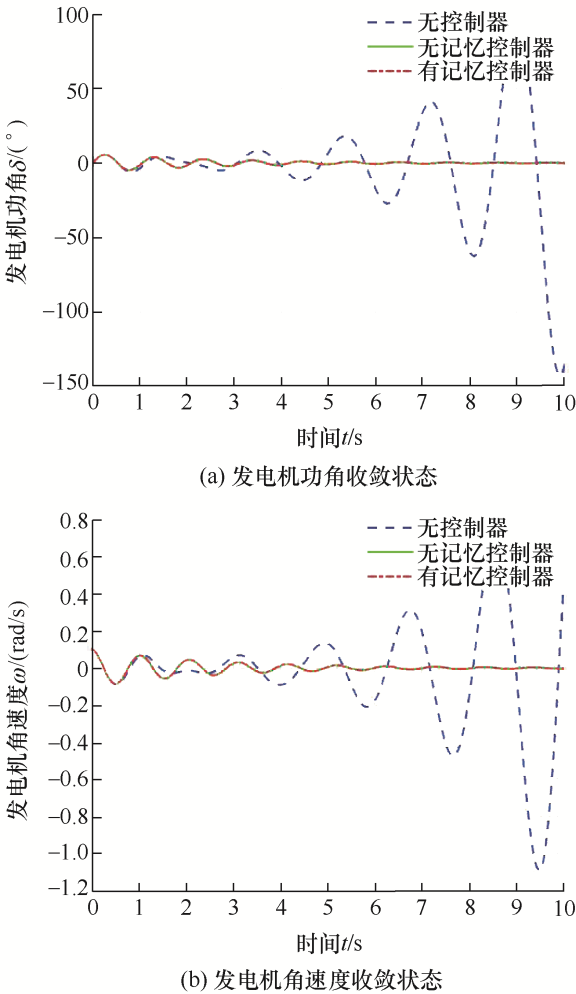
由图8 可知,在h =0.143 2 s时,有记忆状态反馈控制器和无记忆状态反馈控制器对系统镇定控制作用几乎相同;但是没有控制器作用时,单机无穷大系统是不稳定的。
图8
6 结论
(1) 建立了时变时滞(即时滞不确定)电力系统模型,考虑时滞情况比较全面。
(2) 通过构建合适的增广Lyapunov泛函,应用Bessel-Legendre不等式处理泛函导数中的积分项,大大提高了时变时滞电力系统的时滞上界。
(3) 再应用参数调整法进行时变时滞电力系统无记忆和有记忆鲁棒镇定控制器设计,通过分析和比较,两种实例验证、模型仿真证明了文章方法的优越性和实用性。
参考文献
View Option
[1]
MEESSINA A R . Inter-area oscillations in power systems
[M]. New York:Springer , 2009 .
[本文引用: 1]
[2]
ZHANG X M HAN Q L . State estimation for static neural networks with time-varying delays based on an improved reciprocally convex inequality
[J]. IEEE Trans. Neural Netw. Learn Syst ., 2018 , 29 (4 ):1376 -1381 .
DOI:10.1109/TNNLS.2017.2661862
URL
[本文引用: 1]
[3]
贾宏杰 , 谢星星 , 余晓丹 . 考虑时滞影响的电力系统小扰动稳定域
[J]. 电力系统自动化 , 2006 , 30 (21 ):1 -5 .
[本文引用: 1]
JIA Hongjie XIE Xingxing YU Xiaodan . Power system small signal stability region with time delay considered
[J]. Automation of Electric Power Systems , 2006 , 30 (21 ):1 -5 .
[本文引用: 1]
[4]
贾宏杰 , 陈建华 , 余晓丹 . 时滞环节对电力系统小扰动稳定性的影响
[J]. 电力系统自动化 , 2006 , 30 (5 ):5 -8,17 .
[本文引用: 1]
JIA Hongjie CHEN Jianhua YU Xiaodan . Impact of time delay on power system small signal stability
[J]. Automation of Electric Power Systems , 2006 , 30 (5 ):5 -8,17 .
[本文引用: 1]
[5]
贾宏杰 , 尚蕊 , 张宝贵 . 电力系统时滞稳定裕度求解方法
[J]. 电力系统自动化 , 2007 , 31 (2 ):5 -11 .
[本文引用: 2]
JIA Hongjie SHANG Rui ZHANG Baogui . Computation of delay stability margin of electric power systems
[J]. Automation of Electric Power Systems , 2007 , 31 (2 ):5 -11 .
[本文引用: 2]
[6]
贾宏杰 , 安海云 , 余晓丹 . 电力系统改进时滞依赖型稳定判据
[J]. 电力系统自动化 , 2008 , 32 (19 ):15 -19 .
[本文引用: 2]
JIA Hongjie AN Haiyun YU Xiaodan . An improved delay-dependent stability criteria for power system with multiple time delays
[J]. Automation of Electric Power Systems , 2008 , 32 (19 ):15 -19 .
[本文引用: 2]
[8]
WU M HE Y SHE J H . New delay-dependent stability criteria and stabilizing method for neutral systems
[J]. IEEE Trans. on Automatic Control , 2004 , 49 (12 ):2266 -2271 .
DOI:10.1109/TAC.2004.838484
URL
[本文引用: 1]
[10]
贾宏杰 , 安海云 , 余晓丹 . 电力系统时滞依赖型鲁棒稳定判据及其应用
[J]. 电力系统自动化 , 2010 , 34 (3 ):6 -11 .
[本文引用: 1]
JIA Hongjie AN Haiyun YU Xiaodan . A delay-dependent robust stability criterion for power system amd its application
[J]. Automation of Electric Power Systems , 2010 , 34 (3 ):6 -11 .
[本文引用: 1]
[11]
董朝宇 , 贾宏杰 , 姜懿郎 . 含积分二次型的电力系统改进时滞稳定判据
[J]. 电力系统自动化 , 2015 , 39 (24 ):35 -40 .
[本文引用: 1]
DONG Chaoyu JIA Hongjie JIANG Yilang . Time-delay stability criteria for power system with integral quadratic from
[J]. Automation of Electric Power Systems , 2015 , 39 (24 ):35 -40 .
[本文引用: 1]
[12]
李晓萌 , 贾宏杰 . 电力系统改进时滞依赖型鲁棒稳定判据
[J]. 电力系统及其自动化学报 , 2018 , 30 (4 ):114 -120 .
[本文引用: 1]
LI Xiaomeng JIA Hongjie . Improved time-delay- dependent robust stability criteria for power system
[J]. Proceedings of the CSU-EPSA , 2018 , 30 (4 ):114 -120 .
[本文引用: 1]
[13]
李宁 , 孙永辉 , 卫志农 , 等 . 基于Wirtinger不等式的电力系统延时依赖稳定判据
[J]. 电力系统自动化 , 2017 , 41 (2 ):108 -113 .
[本文引用: 1]
LI Ning SUN Yonghui WEI Zhinong , et al . Delay-dependent stability criteria for power system based on Wirtingers intergral inequality
[J]. Automation of Electric Power Systems , 2017 , 41 (2 ):108 -113 .
[本文引用: 1]
[14]
孙永辉 , 李宁 , 卫志农 , 等 . 多时滞不确定电力系统的改进时滞依赖鲁棒稳定判据
[J]. 电力系统自动化 , 2017 , 41 (16 ):117 -122 .
[本文引用: 1]
SUN Yonghui LI Ning WEI Zhinong , et al . Improved robust delay-dependent stability crriteria for power systems with multiple time delays and uncertain parameters
[J]. Automation of Electric Power Systems , 2017 , 41 (16 ):117 -122 .
[本文引用: 1]
[15]
孙勇 , 李志民 , 于继来 . 基于最小熵H∞ 控制的降阶电力系统稳定器设计
[J]. 吉林大学学报 , 2010 , 40 (2 ):523 -528 .
[本文引用: 1]
SUN Yong LI Zhiming YU Jilai . Design of reduced-order power system stabilizer based on minimum entropy H∞ theory
[J]. Journal of Jilin Unversity , 2010 , 40 (2 ):523 -528 .
[本文引用: 1]
[16]
石颉 , 王成山 . 基于线性矩阵不等式理论的广域电力系统状态反馈控制器设计
[J]. 电网技术 , 2008 , 32 (6 ):36 -41 .
[本文引用: 1]
SHI Jie WANG Chengshan . Design of state feedback controller for wide-area power system based on linear matrix inequalities theory
[J]. Power System Technology , 2008 , 32 (6 ):36 -41 .
[本文引用: 1]
[17]
俞立 . 鲁棒控制:线性矩阵不等式处理方法 [M]. 北京 : 清华大学出版社 , 2002 .
[本文引用: 1]
YU Li . Robust control:Linear matrix inequality approach [M]. Beijing : Tsinghua University Press , 2002 .
[本文引用: 1]
[18]
QI J JIANG Q Y WANG G Z , et al . Wide-area time-delay robust damping control for power system
[J]. European Trans. on Electrical Power , 2009 , 19 (7 ):899 -910 .
DOI:10.1002/etep.v19:7
URL
[本文引用: 1]
[19]
袁金鹏 , 王秀明 , 姜志国 . 基于LMI的电力系统广域附加阻尼控制
[J]. 东北电力大学学报 , 2009 (4 ):50 -54 .
[本文引用: 1]
YUAN Jinpeng WANG Xiuming JIANG Zhiguo . Design of additional damped controller using LMI in power system
[J]. Journal of Northeast Electric Power University , 2009 (4 ):50 -54 .
[本文引用: 1]
[20]
SOLIMAN A H ELSHAFEI A L BENDARY F , et al . LMI static output-feedback design of fuzzy power system stabilizers
[J]. Expert Systems with Applications , 2009 , 36 (3 ):6817 -6825 .
DOI:10.1016/j.eswa.2008.08.018
URL
[本文引用: 1]
[21]
ZHANG X M HAN Q L SEURET A , et al . Overview of recent advances in stability of liner systems with time-varying delay
[J]. IET Control Theory and Applications , 2019 , 13 (1 ):1 -16 .
DOI:10.1049/cth2.v13.1
URL
[本文引用: 2]
[22]
BOYD S GHAOUI L FERON E , et al . Linear matrix inequalities in system and control theory
[M]. Philadelphia:SIAM , 1994 .
[本文引用: 1]
[23]
王真 . 广域测量时变时滞电力系统稳定性分析与控制
[D]. 株洲:湖南工业大学 , 2019 .
[本文引用: 3]
WANG Zhen . Wide-area measurement of time-varying delay power system stability analysis and control
[D]. Zhuzhou:Hunan University of Technology , 2019 .
[本文引用: 3]
Inter-area oscillations in power systems
1
2009
... 随着智能电网发展,现代电力系统更加趋向于多互联,大规模方向发展,因此仅依赖传统的区域信号控制方法将无法满足系统对性能的要求.近些年,随着同步相量测量装置技术,全球定位系统技术和现代电力通信技术的广域测量系统的应用,使得将本地电力系统信息同步采样并传送至远程控制中心成为可能,这就可以通过广域控制器对电力系统进行协调控制[1 ] .但是,电网广域监测系统(Wide area measurement system, WAMS)的应用将电力系统变成了一个时滞系统,各类广域控制信道中难免存在时滞,直接影响到电力系统的稳定性.因此,研究电力系统所能承受的时滞稳定裕度是很有意义的.此外,为了保证电力系统稳定运行,研究电力系统时滞镇定器的设计也具有非常重要的意义. ...
State estimation for static neural networks with time-varying delays based on an improved reciprocally convex inequality
1
2018
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
考虑时滞影响的电力系统小扰动稳定域
1
2006
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
考虑时滞影响的电力系统小扰动稳定域
1
2006
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
时滞环节对电力系统小扰动稳定性的影响
1
2006
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
时滞环节对电力系统小扰动稳定性的影响
1
2006
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
电力系统时滞稳定裕度求解方法
2
2007
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
... ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
电力系统时滞稳定裕度求解方法
2
2007
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
... ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
电力系统改进时滞依赖型稳定判据
2
2008
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
... -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
电力系统改进时滞依赖型稳定判据
2
2008
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
... -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
New results on stability analysis for systems with discrete distributed delay
1
2015
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
New delay-dependent stability criteria and stabilizing method for neutral systems
1
2004
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
Stability and robust stability for systems with a time-varying delay
1
2007
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
电力系统时滞依赖型鲁棒稳定判据及其应用
1
2010
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
电力系统时滞依赖型鲁棒稳定判据及其应用
1
2010
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
含积分二次型的电力系统改进时滞稳定判据
1
2015
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
含积分二次型的电力系统改进时滞稳定判据
1
2015
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
电力系统改进时滞依赖型鲁棒稳定判据
1
2018
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
电力系统改进时滞依赖型鲁棒稳定判据
1
2018
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
基于Wirtinger不等式的电力系统延时依赖稳定判据
1
2017
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
基于Wirtinger不等式的电力系统延时依赖稳定判据
1
2017
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
多时滞不确定电力系统的改进时滞依赖鲁棒稳定判据
1
2017
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
多时滞不确定电力系统的改进时滞依赖鲁棒稳定判据
1
2017
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
基于最小熵H∞ 控制的降阶电力系统稳定器设计
1
2010
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
基于最小熵H∞ 控制的降阶电力系统稳定器设计
1
2010
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
基于线性矩阵不等式理论的广域电力系统状态反馈控制器设计
1
2008
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
基于线性矩阵不等式理论的广域电力系统状态反馈控制器设计
1
2008
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
1
2002
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
1
2002
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
Wide-area time-delay robust damping control for power system
1
2009
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
基于LMI的电力系统广域附加阻尼控制
1
2009
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
基于LMI的电力系统广域附加阻尼控制
1
2009
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
LMI static output-feedback design of fuzzy power system stabilizers
1
2009
... 目前,时滞系统的研究方法通常是基于Lyapunov直接法的时域法[2 ,3 ,4 ,5 ,6 ] .通过构造Lyapunov泛函,借助Lyapunov稳定性理论,得出系统的稳定判据,最后借助线性矩阵不等式技术求解得出系统的时滞稳定裕度.文献[7 ]提出新的积分不等式处理方式,有效地降低了结果的保守性;文献[8 ]引入自由权矩阵来降低双时滞系统判据的保守性;文献[9 ]利用Wirtinger不等式对泛函的导数中一次积分项进行有效放缩;文献[5 -6 , 10 ]主要研究电力系统单时滞系统的情况;文献[11 ,12 ]中的试验结果具有较大的保守性;文献[13 ]采用“时滞分割”思想降低试验结果的保守性;文献[14 ]将Wirtinger不等式引入双时滞系统.文献[15 ]采用H ∞ 控制理论进行控制器的设计,但是由于权函数选取没有规律性,这种方法就受到了一定的限制[16 ] .二十世纪九十年代开始,线性矩阵不等式技术迅速发展[17 ] .文献[18 ]通过Pade多项式方法,逼近时滞超越项,再使用线性矩阵不等式方法,得到了一种广域控制器设计方法,但是该方法属于近似方法,难免存在误差.文献[19 ]利用线性矩阵不等式方法,把励磁控制器参数的设计问题转变为求解确保一个闭环系统稳定运行的合适参数问题.文献[20 ]根据数学推算得到的时滞稳定判据,设计反馈控制器. ...
Overview of recent advances in stability of liner systems with time-varying delay
2
2019
... 文章基于常时滞电力系统模型基础上,建立了时变时滞(即时滞不确定)电力系统模型,构建新的增广LK泛函,应用文献[21 ]中Bessel-Legendre不等式估计该泛函的导数,以改善时变时滞电力系统的最大时滞上界.再应用参数调整法[22 ] 进行时变时滞电力系统鲁棒镇定控制器设计,通过典型二阶时滞系统和单机无穷大电力系统进行实例验证、模型仿真,证明了文章方法的实用性和优越性. ...
... 引理1[21 ] :定义$\omega$是在区间[a , b ]→Rn
Linear matrix inequalities in system and control theory
1
1994
... 文章基于常时滞电力系统模型基础上,建立了时变时滞(即时滞不确定)电力系统模型,构建新的增广LK泛函,应用文献[21 ]中Bessel-Legendre不等式估计该泛函的导数,以改善时变时滞电力系统的最大时滞上界.再应用参数调整法[22 ] 进行时变时滞电力系统鲁棒镇定控制器设计,通过典型二阶时滞系统和单机无穷大电力系统进行实例验证、模型仿真,证明了文章方法的实用性和优越性. ...
广域测量时变时滞电力系统稳定性分析与控制
3
2019
... 通过对比文献[23 ]获得的时滞上界h =0.656 9 s,体现出所提方法有一定的优越性.虽然无记忆控制器和有记忆控制器求得的最大时滞上界相同,但是可以从图2 、3 中看出,有记忆反馈控制器在收敛速度上明显优于无记忆控制器. ...
... 考虑单机无穷大系统时,参照文献[23 ],系统矩阵参数A 、A 1 和B 分别为 ...
... 通过对比文献[23 ]的时滞上界h =0.140 7 s,体现出所提方法有一定的优越性. ...
广域测量时变时滞电力系统稳定性分析与控制
3
2019
... 通过对比文献[23 ]获得的时滞上界h =0.656 9 s,体现出所提方法有一定的优越性.虽然无记忆控制器和有记忆控制器求得的最大时滞上界相同,但是可以从图2 、3 中看出,有记忆反馈控制器在收敛速度上明显优于无记忆控制器. ...
... 考虑单机无穷大系统时,参照文献[23 ],系统矩阵参数A 、A 1 和B 分别为 ...
... 通过对比文献[23 ]的时滞上界h =0.140 7 s,体现出所提方法有一定的优越性. ...