电气工程学报, 2021, 16(4): 101-107 doi: 10.11985/2021.04.013

特邀专栏：高性能永磁电机驱动与控制

基于转子电流模型参考自适应的双馈电机无位置传感器预测功率控制

张晟铵,1, 张永昌,2, 焦健,3, 蒋涛,2

1.北方工业大学电力电子与电气传动北京市工程研究中心 北京 100144

2.华北电力大学电气与电子工程学院 北京 102206

3.北京交通大学电气工程学院 北京 100044

Position Sensorless Predictive Power Control of Doubly-fed Induction Generator Based on Rotor Current Model Reference Adaptive System

ZHANG Shengan,1, ZHANG Yongchang,2, JIAO Jian,3, JIANG Tao,2

1. Power Electronics and Motor Drive Engineering Research Center of Beijing, North China University of Technology, Beijing 100144

2. School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206

3. School of Electrical Engineering, Beijing Jiaotong University, Beijing 100044

通讯作者: * 张永昌,男,1982年生,博士,教授,博士研究生导师。主要研究方向为电力电子与电机控制。E-mail：zyc@ncut.edu.cn

收稿日期: 2021-03-25   修回日期: 2021-05-25  

Received: 2021-03-25   Revised: 2021-05-25  

作者简介 About authors

张晟铵,男,1995年生,硕士研究生。主要研究方向为双馈电机预测控制。E-mail： zsa15531679188@163.com

焦健,男,1993年生,博士研究生。主要研究方向为双馈电机预测控制。E-mail： 79157937@qq.com

蒋涛,男,1995年生,博士研究生。主要研究方向为双馈电机预测控制。E-mail： jiangtao1130@qq.com

摘要

双馈电机以其变流器功率小、有功无功控制灵活、能量双向流动等优点在风力发电系统中得到了广泛应用。现有的矢量控制需要对多个PI系数进行整定,还需要安装位置传感器来获得转子位置和转速,在增大电机体积和成本的同时降低了系统的可靠性。为此,提出一种无需PI整定和安装位置传感器的新型解决方案。首先,在解析推导定子侧复功率微分的基础上,基于功率无差拍控制的思想直接计算得到转子侧的电压参考值,无需任何控制器整定工作。其次,通过比较实测转子电流和基于定子磁链电流模型的估计转子电流,构造了基于转子电流模型参考自适应的位置估计方法,从而实现了无位置传感器控制。试验结果表明,所提出的方法在次同步、超同步和功率阶跃等各种工况下都能够较好地跟踪实际位置和转速,并且具有优异的稳态性能和快速的动态响应,为双馈电机风力发电系统提供了一种低成本、高性能、易于应用的解决方案。

关键词： 双馈电机 ; 位置观测器 ; 无差拍预测控制

Abstract

Doubly-fed induction generators have been widely used in wind power generation systems due to their low converter power, flexible active and reactive power control, and two way flow of energy. The existing vector control needs to tune multiple PI coefficients, and additionally needs to install a position sensor to obtain the rotor position and speed, which increases the volume and cost of the generator while reducing the reliability of the system. Therefore, a new solution that does not require PI setting and installation of position sensors is proposed. First, on the basis of analytically deriving the complex power differential on the stator side, the voltage reference value on the rotor side is directly calculated based on the idea of power deadbeat control without any controller setting work. Secondly, by comparing the measured rotor current with the estimated rotor current based on the stator flux current model, a position estimation method based on the rotor current model reference adaptive is constructed, thereby realizing the position sensorless control. The experimental results show that the method proposed can track the actual position and speed well under various working conditions such as sub-synchronization, super-synchronization and power step, and has excellent steady-state performance and fast dynamic response and provides the doubly-fed wind power generation system provides a low-cost, high-performance, and easy-to-apply solution.

Keywords： Doubly-fed induction generator ; position observer ; deadbeat predictive control

PDF (2721KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

张晟铵, 张永昌, 焦健, 蒋涛. 基于转子电流模型参考自适应的双馈电机无位置传感器预测功率控制. 电气工程学报[J], 2021, 16(4): 101-107 doi:10.11985/2021.04.013

ZHANG Shengan, ZHANG Yongchang, JIAO Jian, JIANG Tao. Position Sensorless Predictive Power Control of Doubly-fed Induction Generator Based on Rotor Current Model Reference Adaptive System. Journal of Electrical Engineering[J], 2021, 16(4): 101-107 doi:10.11985/2021.04.013

1 引言

随着硬件处理器的飞速发展,模型预测控制(Model predictive control, MPC)[1]以其原理简单、多变量控制和易于处理非线性约束等优点,吸引了众多电力电子领域学者进行深层次的研究。相比于其他高性能控制策略,如矢量控制(Vector control, VC)和直接功率控制(Direct power control, DPC)[2,3],MPC作为一种新兴的控制策略具有很多优点。与VC相比,MPC无需使用电流环调节器及相应的参数整定,可以直接根据所选电压矢量产生驱动脉冲而无需脉宽调制策略,容易处理多变量和非线性约束,具有结构简单、动态响应快、无需参数整定等优点。与DPC相比,由于MPC采用了最小化误差求解策略,在矢量选择方面可以更加精确、有效,具有稳态性能好、控制简单灵活等优点。此外,MPC可以适用于各种类型的电机,在电机数学模型被正确建立的基础上,与控制器的设计相结合,就可以应用于各种交流电机电气传动系统中。

早期的双馈电机无位置控制方法主要基于开环无位置传感器方法,转子位置直接通过比较采样得到的转子电流和估计出的转子电流得到[4]。由于这种方法是开环估计,所以没有考虑反馈的误差,也没有办法确定估计的误差是否在减小,导致其不适用于实际应用场合。后来,有一些基于闭环误差反馈校正的角度/转速估计方法被应用于双馈电机控制系统中,并取得了比较好的控制效果。首先,基于模型参考自适应系统(Model reference adaptive system, MRAS)的方法[5,6,7]被提出。这种方法通过对参考模型和适应模型的比较得到转速和转子角度信息,结果比较准确。此外,有基于锁相环(Phase locked loop, PLL)的无位置传感器方法[8,9,10]被应用于双馈电机中。这种基于PLL的位置估计方法与基于MRAS的位置估计器方法类似,其中基于PLL的位置估计方法调节估计矢量和参考矢量之间的相位为零。

对于基于双馈电机的风力发电控制系统,如果电机参数出现变化,控制算法的性能将较大程度地变差。无差拍预测控制(Deadbeat predictive control, DBPC)作为一种原理清晰简洁的预测控制,依靠系统精准的数学模型,根据当前时刻采样值,直接计算得到所需控制量[11,12]。文献[13]中提出一种双馈电机无位置传感器并网运行的直接功率控制方法。通过分析作用矢量和对定子侧功率的作用效果之间的关系,估计出转子磁链矢量所在扇区,综合考虑转子磁链矢量所在的扇区位置和上一时刻作用的转子电压矢量得到的定子侧功率变化效果,直接选出当前时刻需要作用的转子电压矢量。这种方法可以在无位置传感器状态下稳定运行。另有一种速度自适应降阶观测器[14]被应用于双馈电机的速度估计中。这种方法与双馈电机矢量控制相结合,运行效果良好,可以较为准确地估计出转子位置信息和角度信息,但是由于矢量控制不仅需要调节一些参数,比如比例积分(Proportional-integral, PI)参数,还需要在三种不同坐标系之间切换以及使用锁相环,因此所包含的复杂解耦过程和坐标变换会造成比较大的计算量,导致动态响应速度比较慢。

基于无差拍预测控制的思想,本文通过推导双馈电机定子侧复功率微分式,得到转子侧电压的参考值,利用空间矢量调制(Space vector modulation, SVM)获得开关信号并作用于两电平逆变器,避免了传统矢量控制中复杂的PI系数整定过程,减少了计算量,提升了动态响应速度。将转子电流的估计值与实际值的比较值经过PI控制器,准确获得转子位置信息,实现了无位置传感器控制。试验结果证明了该方法在不同工况下运行的有效性。

2 双馈电机数学模型

双馈电机的各变量在转子坐标系下用复矢量表示的数学模型如下所示

$\left\{ \begin{array}{l}{u_s} = {R_s}{i_s} + \frac{{{\rm{d}}{\psi _s}}}{{dt}} + j{\omega _r}{\psi _s}\\{u_r} = {R_r}{i_r} + \frac{{{\rm{d}}{\psi _r}}}{{dt}}\\{\psi _s} = {L_s}{i_s} + {L_m}{i_r}\\{\psi _r} = {L_r}{i_r} + {L_m}{i_s}\end{array} \right.$

式中,${u_s}$、${u_r}$、${i_s}$、${i_r}$、${\psi _s}$、${\psi _r}$分别表示为定子电压、转子电压、定子电流、转子电流、定子磁链和转子磁链;${R_s}$、${R_r}$、${L_s}$、${L_r}$和${L_m}$分别表示为定子电阻、转子电阻、定子电感、转子电感和互感;${\omega _r}$为转子电角速度。

根据瞬时功率定义,以静止坐标系下的定转子变量表示功率为例,定转子功率可以分别表示为

$\left\{ \begin{array}{l}{P_s} = \frac{3}{2}{R_e}\left( {i_s^* \cdot {u_s}} \right)\\{Q_s} = \frac{3}{2}{I_m}\left( {i_s^* \cdot {u_s}} \right)\\{P_r} = \frac{3}{2}{R_e}\left( {i_r^* \cdot {u_r}} \right)\\{Q_r} = \frac{3}{2}{I_m}\left( {i_r^* \cdot {u_r}} \right)\end{array} \right.$

式中,上标*表示取共轭。${P_s}$、${Q_s}$、${P_r}$、${Q_r}$分别表示定子侧有功功率、定子侧无功功率、转子侧有功功率和转子侧无功功率。${R_e}$和${I_m}$分别表示取实部和虚部。

3 无差拍预测功率控制

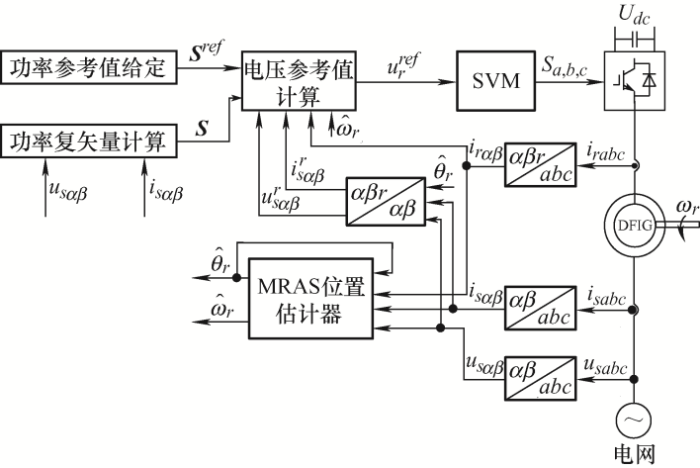
基于模型参考自适应系统(MRAS)位置观测器的无差拍预测控制整体控制框图如图1所示。整个控制系统包括MRAS位置估计部分和转子电压参考值计算两个部分,最终得到的转子电压参考值则利用空间矢量调制(SVM)方法进行合成。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   基于MRAS位置估计器的无差拍预测控制框图


根据双馈电机数学模型式(1),定子电流和转子电流可以用定子磁链和转子磁链表示出来,其公式如下

$\left\{ \begin{array}{l}{i_s} = \lambda \left( {{L_r}{\psi _s} - {L_m}{\psi _r}} \right)\\{i_r} = \lambda \left( {{L_s}{\psi _r} - {L_m}{\psi _s}} \right)\end{array} \right.$

式中,λ=1/(LsLr–$L_m^2$)。

根据式(2),双馈电机定子侧复功率S可以表 示为

$S = {P_s} + j{Q_s} = \frac{3}{2}\left( {i_s^* \cdot {u_s}} \right)$

对式(4)关于时间t求导,复功率的导数可以具体表示为

$\frac{{{\rm{d}}S}}{{{\rm{d}}t}} = 1.5\left( {i_s^*\frac{{{\rm{d}}{u_s}}}{{{\rm{d}}t}} + {u_s}\frac{{{\rm{d}}i_s^*}}{{{\rm{d}}t}}} \right)$

根据式(1)和式(3)可将复功率的导数具体化为

$\begin{array}{c}\frac{{{\rm{d}}S}}{{{\rm{d}}t}} = 1.5\left( {i_s^*\frac{{{\rm{d}}{u_s}}}{{{\rm{d}}t}} + {u_s}\frac{{{\rm{d}}i_s^*}}{{{\rm{d}}t}}} \right) = \\1.5\left( {i_s^*j{\omega _1}{u_s} + {u_s}\frac{{{\rm{d}}i_s^*}}{{{\rm{d}}t}}} \right) = - \left( {\lambda {L_r}{R_s} - j{\omega _{s1}}} \right)S + \\1.5\left( {\lambda {L_r}{{\left| {{u_s}} \right|}^2}} \right. - \left. {\lambda {L_m}\left( {u_r^* - {R_r}i_r^*} \right){u_s} + j\lambda {L_r}{\omega _r}{u_s}\psi _s^*} \right)\end{array}$

式中,${\omega _{s1}} = {\omega _1} - {\omega _r}$表示转差频率;${\omega _1}$表示定子电角速度。

无差拍预测控制方法目的在于使下一时刻定子侧复功率实际值${S^{k + 1}}$与预先给定的复功率参考值${S^{ref}}$相等,本文中利用“k”表示当前时刻,利用上标“k+1”表示下一时刻。基于这个原理,利用一阶欧拉离散的方法可以离散化式(6),结果为

$\begin{array}{c}\frac{{{S^{ref}} - {S^k}}}{{{T_{sc}}}} = - \left( {\lambda {L_r}{R_s} - j\left( {{\omega _1} - \widehat \omega _r^k} \right)} \right){S^k} + \\1.5\lambda \left[ {{L_r}{{\left| {u_s^k} \right|}^2} - {L_m}u_s^k{{\left( {\left( {u_r^k} \right)} \right.}^{\rm{*}}} - \left. {{R_r}{{\left( {i_r^k} \right)}^{\rm{*}}}} \right) + j{L_r}\widehat \omega _r^ku_s^k{{\left( {\psi _s^k} \right)}^{\rm{*}}}} \right]\end{array}$

式中,${T_{sc}}$表示控制周期;转子电角速度$\omega _r^k$用估计出的转子电角速度$\widehat \omega _r^k$代替。

求解式(7),所需要的转子电压矢量可以表示为

$\begin{array}{c}{u^{ref}} = \frac{1}{{1.5\lambda {L_m}{T_{sc}}}}{\left( {\frac{{{S^k} - {S^{ref}}}}{{u_s^k}}} \right)^*} + \\\frac{{{L_r}}}{{{L_m}}}u_s^k - \frac{{j{L_r}\widehat \omega _r^k}}{{{L_m}}}\psi _s^k + {R_r}i_r^k - \frac{{\lambda {L_r}{R_s} + j\omega _{s1}^k}}{{\lambda {L_m}}}i_s^k\end{array}$

4 基于转子电流的模型参考自适应无位置传感器方法

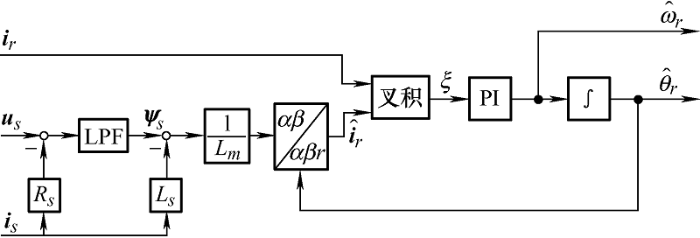
基于转子电流的模型参考自适应系统(MRAS)位置观测器如图2所示。这种观测器具有一系列优点：转子电流可通过采样方便地获得,原理过程较为简单。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   基于转子电流的模型参考自适应位置观测器


根据观测器控制框图2所示,在定子参考坐标系下,首先利用一种改进的磁链积分器[15]求得定子磁链${\psi _s}$

${\psi _s} = \frac{{{u_s} - {R_s}{i_s}}}{{s + {\omega _c}}} \cdot (1 - j{\lambda _1}sgn({\omega _e}))$

式中,${\omega _e}$为定子磁链的同步频率,${\omega _c} = {\lambda _1}{\omega _e}$,其中λ1为取值0.1~0.5之间的常数,本文选值为0.1。

在定子坐标系下,根据双馈电机数学模型,由定转子电流可以计算出定子磁链

${\psi _s} = {L_s}{i_s} + {L_m}{i_r}\exp \left( {j{\theta _r}} \right)$

式中,${\psi _s}$、${i_s}$处在定子坐标系,${i_r}$处在转子坐标系。

通过式(10)可以推导出由定子磁链和定子电流表示出的转子电流,具体表示为

${i_r} = \frac{{{\psi _s} - {L_s}{i_s}}}{{{L_m}}}\exp \left( { - j{\theta _r}} \right)$

将式(11)中的转子电角速度${\theta _r}$用估计的转子电角速度${\theta _r}$进行替换,可以得到估计出的转子电流为

${\hat i_r} = \frac{{{\psi _s} - {L_s}{i_s}}}{{{L_m}}}\exp \left( { - j{{\hat \theta }_r}} \right)$

根据Popov超稳定性理论可以对位置观测器误差的动态稳定性进行分析,并对转速进行估计[16]。

利用直接采样得到的转子电流${i_r}$和估计出的转子电流${\hat i_r}$可以得到二者的叉积

$\xi = {\widehat i_{r\alpha }}{i_{r\beta }} - {i_{r\alpha }}{\widehat i_{r\beta }}$

将叉积$\xi$经过PI控制器可以得到估计出的转子电角速度${\hat \omega _r}$,转子电角速度通过积分得到估计出的转子位置${\hat \theta _r}$,所估计出的转子位置反馈回式(12)参与估计转子电流的计算。

5 试验结果

5.1 试验平台

本文采用dSPACE公司MicroLabBox作为虚拟控制器,永磁-双馈电机对拖机组来模拟实际风力发电系统中的风机和发电机。整个试验平台如图3所示。图3a为系统的控制器部分,主要包括调试计算机、虚拟控制器(MicroLabBox)、电网模拟器(Chroma,Regenerative Grid Simulator,Model 61860)、双向直流电源(EA-PSB 9360-80)、采样和主电路以及示波器(Tektronix,MDO3034)。图3b为双馈-永磁对拖机组,采用1.5 kW绕线式异步电机 模拟双馈发电机,采用2.2 kW永磁同步电机模拟 风机。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   试验平台


系统运行时,首先由模拟风机带动发电机运转到系统能够正常工作的转速范围,然后通过调试计算机向虚拟控制器下达同步指令,待定子侧电压与电网电压幅值、频率、相位完全相同进行并网,然后整个系统就能够根据给定的功率参考以及相应的电机运转状态自动调节发电机转子侧的电压,实现变速恒频发电运行模式。

5.2 稳态试验结果

本文提出的基于转子电流的模型参考自适应位置观测器在双馈电机无差拍预测控制中的有效性,可以通过如下试验波形加以验证。试验参数如表1所示。采样频率为10 kHz。

表1   电机与系统参数

系统参数数值
电网电压ug/V150
额定功率Ps/W1 500
额定频率fs/Hz50
极对数p3
定子电阻Rs/Ω4.57
定子漏感Lσs/mH10.83
转子电阻Rr/Ω3.228
转子漏感Lσr/mH10.83
互感Lm/mH214.57
定转子匝比k3.36
直流母线电压Udc/V100

新窗口打开| 下载CSV


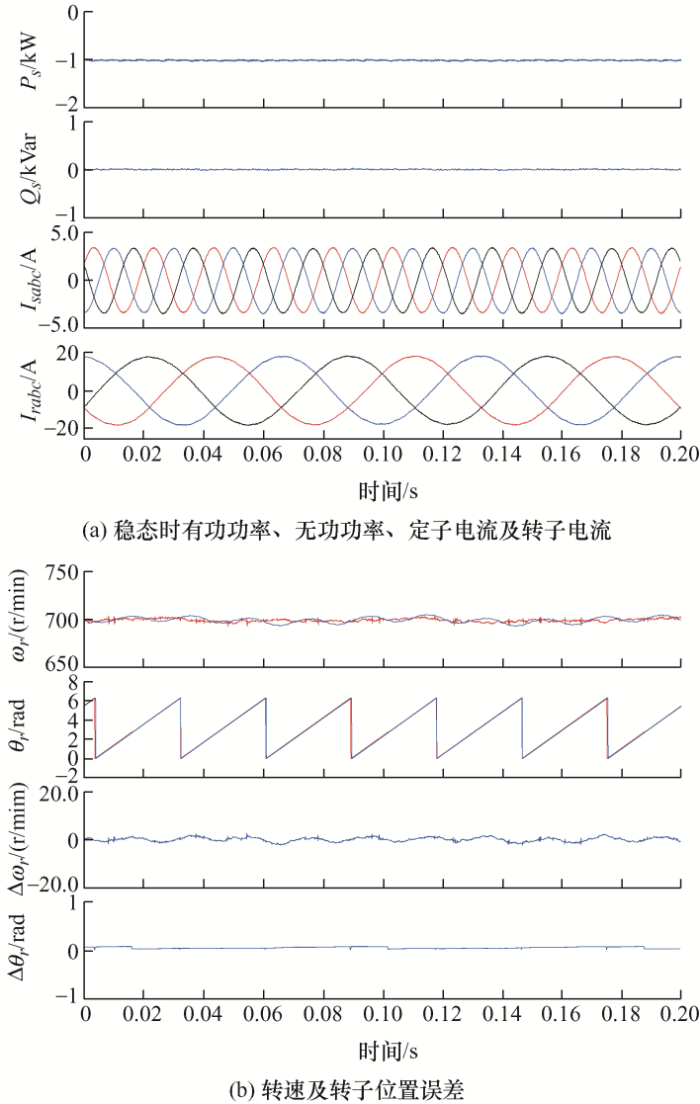
稳态试验波形图如图4所示,电机转速稳定在700 r/min。给定的定子侧有功功率参考值为-1 000 W,无功功率参考值为0 Var。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   双馈电机转速为700 r/min时基于RCMO的DBPC方法试验波形


图4a的四个通道分别表示的是定子侧有功功率实际值Ps、无功功率实际值Qs、定子电流Isabc和转子电流Irabc。可以看出定子侧的功率实际值紧紧跟踪给定的参考值,定转子电流控制效果较好。

图4b的四个通道分别表示电机转速ωr、转子位置θr、转速估计值与转速实际值之间的误差Δωr、估计转子位置和实际转子位置之间的误差Δθr。在转速通道中,两条线分别为电机转速实际值ωr和电机转速估计值${\hat \omega _r}$;类似地,在转子位置通道中,两条线分别是编码器给出的转子位置的实际值θr和RCMO转子位置的估计值${\hat \theta _r}$。

可以看出,估计的转速以及转子位置与电机实际的转速和转子位置非常一致,几乎重合。从转速误差和转子位置误差也可以看出,两种误差都几乎为零,这表示在稳态过程中,这种无位置传感器的算法能够非常准确地估计出转速和转子位置。

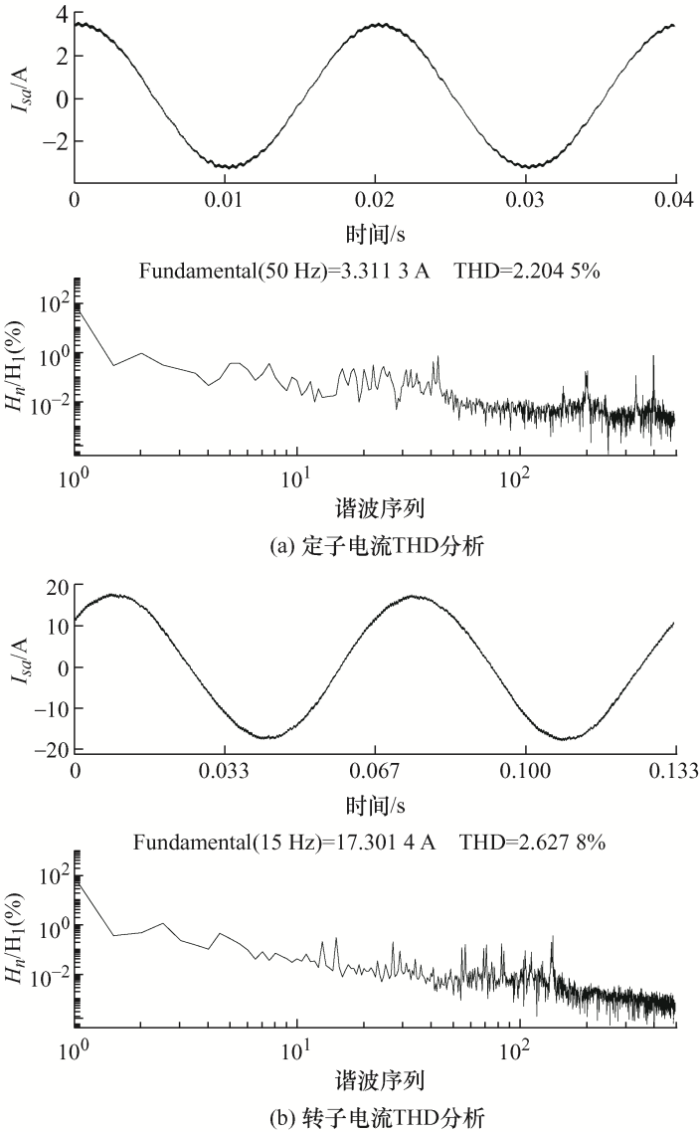
图5给出了稳态时定转子电流的THD分析图,其中定子电流的THD为2.20%,转子电流的THD为2.63%,表明当使用这种无位置传感器方法后,无差拍功率控制依然可以取得非常好的控制效果。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   双馈电机转速为700 r/min时基于RCMO的DBPC方法的定转子电流THD分析


5.3 动态试验结果

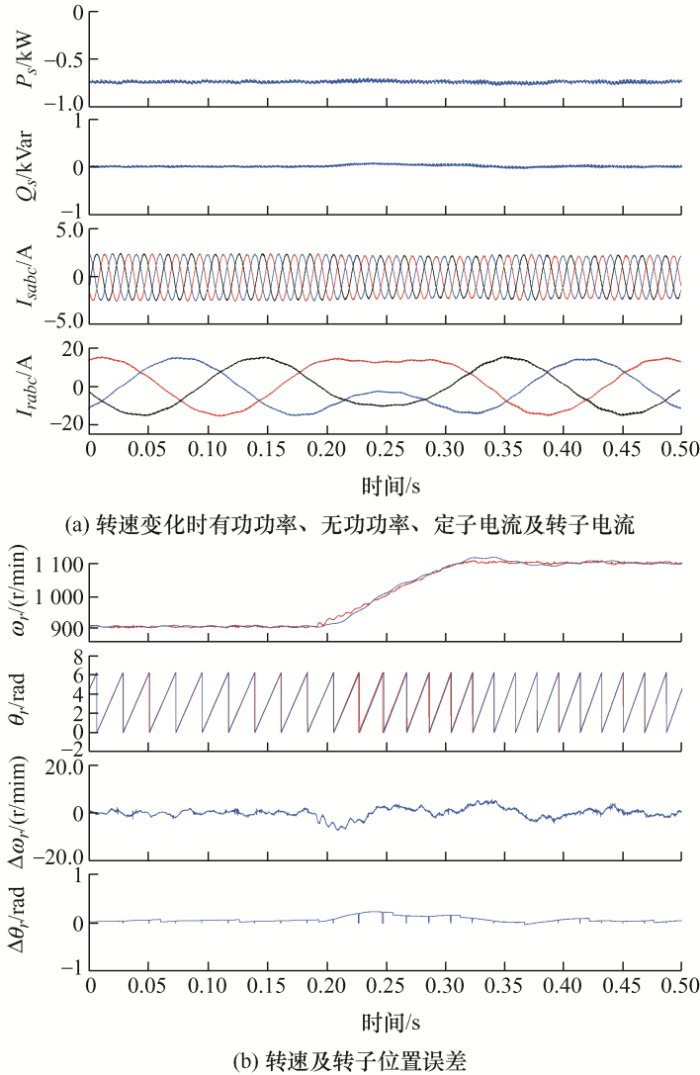
图6给出了电机从次同步状态到超同步状态变化时的动态试验波形。电机的同步速为1 000 r/min,电机的初始转速是900 r/min,随后逐渐变化至1 100 r/min。给定的定子侧有功功率参考值为-750 W,无功功率参考值为0 Var。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   基于RCMO的DBPC方法的转速变化波形


从图6a可以看出,当电机从次同步速变化至超同步速时,定子侧功率的跟踪效果较好,定转子电流控制效果也比较稳定。

从图6b可以看出,当电机转速变化时,转速估计值与转速实际值非常接近,估计的转子位置与实际的转子位置之间的误差几乎为零。

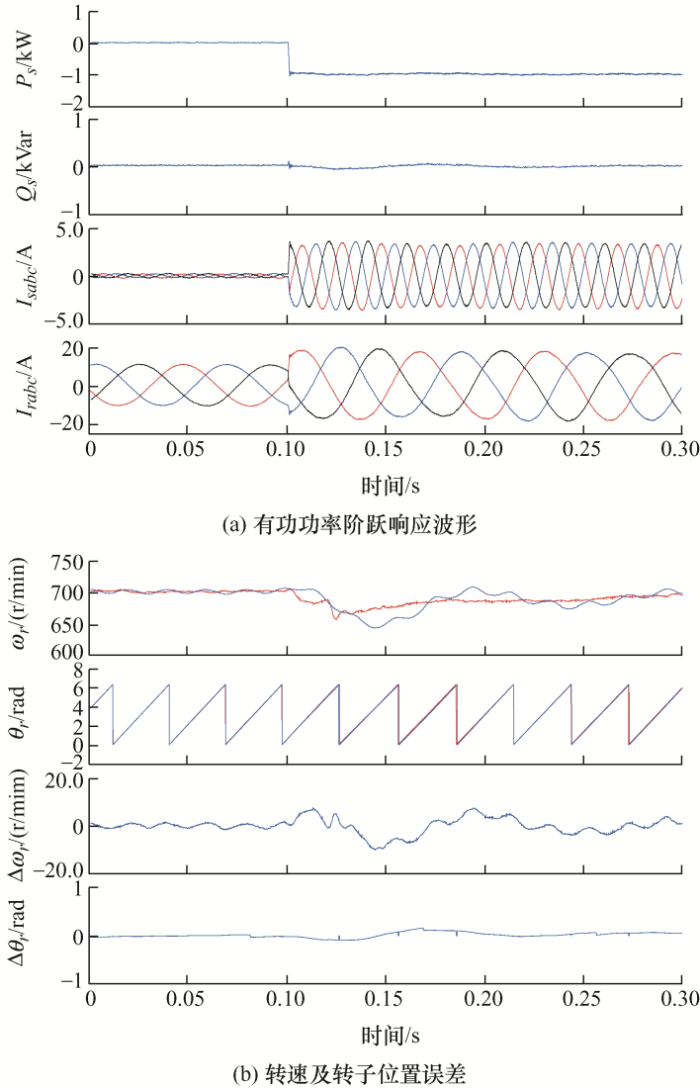
图7所示为转速稳定时,定子侧有功功率发生阶跃变化时的动态试验波形。此时电机转速实际值为700 r/min,初始给定的定子侧有功功率参考值为0 W,无功功率参考值为0 Var。在0.1 s时,有功功率的参考值阶跃至-1 000 W。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   双馈电机转速为700 r/min时基于RCMO的DBPC方法的有功功率阶跃试验波形


从图7a可以看出,当有功功率的参考值发生阶跃变化时,尽管系统的有功功率和无功功率存在小范围的波动,但很快可以恢复到稳定状态。

从图7b可以看出,当有功功率发生阶跃时,尽管转子位置实际值有一个小的跌落,但是这种RCMO位置观测器依然能够很好地估计出转子位置,估计的转子位置与实际的转子位置几乎完全一致,误差几乎为零,这说明转子位置估计较为准确。

6 结论

(1) 针对传统基于矢量控制的双馈电机控制存在的参数整定复杂和依赖位置传感器等问题,本文首先通过功率无差拍预测控制的方法直接计算出所需参考值,避免了传统矢量控制中求取参考值时PI参数的复杂整定过程,实现了实际值准确跟踪参考值的目标。

(2) 通过基于转子电流的模型参考自适应系统(MRAS)位置观测器方法,解决了位置传感器在外界干扰时可能出现反馈的转子角度信息不准确,维护成本高以及系统稳定性降低等一系列问题,并且可以在不同工况下准确获得转子位置信息。

(3) 试验结果验证了该方法在稳态和动态时可以获取准确的转子位置,并取得高效、稳定的控制效果。

参考文献

WANG X, SUN D.

Three-vector-based low-complexity model predictive direct power control strategy for doubly fed induction generators

[J]. IEEE Transactions on Power Electronics, 2017, 32(1):773-782.

DOI:10.1109/TPEL.2016.2532387      URL     [本文引用: 1]

JACOMINI R V, SGUAREZI FILHO A J.

Finite control set applied to the direct power control of a DFIG operating under voltage sags

[J]. IEEE Transactions on Sustainable Energy, 2019, 10(2):952-960.

DOI:10.1109/TSTE.5165391      URL     [本文引用: 1]

ZHANG Y, JIAO J, XU D.

Direct power control of doubly fed induction generator using extended power theory under unbalanced network

[J]. IEEE Transactions on Power Electronics, 2019, 34(12):12024-12037.

DOI:10.1109/TPEL.63      URL     [本文引用: 1]

KRZEMINSKI Z.

Sensorless multiscalar control of double fed machine for wind power generators

[C]// Proceedings of the Power Conversion Conference-Osaka 2002, 2002, 1(1):334-339.

[本文引用: 1]

TOUAITI B, AZZA H B, JEMLI M.

A MRAS observer for sensorless control of wind-driven doubly fed induction generator in remote areas

[C]// 2016 17th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA),Sousse,Tunisia, 2016:526-531.

[本文引用: 1]

IWANSKI G, SZYPULSKI M, LUSZCZYK T, et al.

Cross and dot product based MRAS observer of the rotor position of doubly fed induction machine

[C]// Proceedings of 2014 Ninth International Conference on Ecological Vehicles and Renewable Energies (EVER), 2014:1-5.

[本文引用: 1]

LU L, AVILA N F, CHU C, et al.

Model reference adaptive back-electromotive-force estimators for sensorless control of grid-connected DFIGs

[J]. IEEE Transactions on Industry Applications, 2018, 54(2):1701-1711.

DOI:10.1109/TIA.28      URL     [本文引用: 1]

MBUKANI M W K, GULE N.

PLL-based sliding mode observer estimators for sensorless control of rotor-tied DFIG systems

[J]. IEEE Transactions on Industry Applications, 2019, 55(6):5960-5970.

DOI:10.1109/TIA.28      URL     [本文引用: 1]

PUCHALAPALLI S, SINGH B.

A novel control scheme for wind turbine driven DFIG interfaced to utility grid

[J]. IEEE Transactions on Industry Applications, 2020, 56(3):2925-2937.

DOI:10.1109/TIA.28      URL     [本文引用: 1]

MARQUES G D, PIRES V F, SOUSA S, et al.

A DFIG sensorless rotor-position detector based on a hysteresis controller

[J]. IEEE Transactions on Energy Conversion, 2011, 26(1):9-17.

DOI:10.1109/TEC.2010.2070507      URL     [本文引用: 1]

陈燕东, 罗安, 彭自强, 等.

光伏并网发电与无功补偿的鲁棒预测控制

[J]. 电工技术学报, 2013, 28(11):239-246,253.

[本文引用: 1]

CHEN Yandong, LUO An, PENG Ziqiang, et al.

Robust predictive control strategy for photovoltaic grid-connected generation and reactive power compensation

[J]. Transactions of China Electrotechnical Society, 2013, 28(11):239-246,253.

[本文引用: 1]

孙丹, 方扬, 孙士涛, 等.

双馈异步风力发电机无差拍直接功率控制及延时补偿

[J]. 电工技术学报, 2013, 28(11):70-77.

[本文引用: 1]

SUN Dan, FANG Yang, SUN Shitao, et al.

Dead-beat direct power control of doubly fed induction generators with delay compensation

[J]. Transactions of China Electrotechnical Society, 2013, 28(11):70-77.

[本文引用: 1]

DATTA R, RANGANATHAN V T.

Direct power control of grid-connected wound rotor induction machine without rotor position sensors

[J]. IEEE Transactions on Power Electronics, 2001, 16(3):390-399.

DOI:10.1109/TPEL.63      URL     [本文引用: 1]

YANG S, AJJARAPU V.

A speed-adaptive reduced-order observer for sensorless vector control of doubly fed induction generator-based variable-speed wind turbines

[J]. IEEE Transactions on Energy Conversion, 2010, 25(3):891-900.

DOI:10.1109/TEC.2009.2032589      URL     [本文引用: 1]

ZHANG Y, ZHU J, XU W, et al.

A simple method to reduce torque ripple in direct torque-controlled permanent-magnet synchronous motor by using vectors with variable amplitude and angle

[J]. IEEE Transactions on Industrial Electronics, 2011, 58(7):2848-2859.

DOI:10.1109/TIE.2010.2076413      URL     [本文引用: 1]

杨俊华, 吕惠子, 吴捷, 等.

基于波波夫超稳定性的无刷双馈电机直接转矩控制

[J]. 中国电机工程学报, 2009, 29(15):107-113.

[本文引用: 1]

YANG Junhua, LÜ Huizi, WU Jie, et al.

Direct torque control strategy for brushless doubly-fed machines based on Popov hyperstability theory

[J]. Proceedings of the CSEE, 2009, 29(15):107-113.

[本文引用: 1]

/

〈 〉