电气工程学报, 2021, 16(3): 33-39 doi: 10.11985/2021.03.005

电力电子与电力传动

一种具有大降压比的新型DC-DC变换器*

万文轩,1, 刘纲,1, 尹力,1, 傅萌,2

1.国网湖北省电力有限公司武汉供电公司 武汉 430000

2.东南大学电气工程学院 南京 210096

A Novel DC-DC Converter with High Step-down Ratio

WAN Wenxuan,1, LIU Gang,1, YIN Li,1, FU Meng,2

1. Wuhan Power Supply Company of State Grid Hubei Power Company, Wuhan 430000

2. School of Electrical Engineering, Southeast University, Nanjing 210096

收稿日期: 2020-10-21   修回日期: 2020-11-26  

基金资助: * 国家重点研发计划资助项目.  2020YFF0426410

Received: 2020-10-21   Revised: 2020-11-26  

作者简介 About authors

万文轩,男,1970年生,工程师。主要研究方向为用电信息采集,分布式电源等。E-mail： wanwx1@126.com

刘纲,男,1977年生,工程师。主要研究方向为电力营销,分布式电源等。E-mail： shifuggyy@163.com

尹力,女,1989年生,硕士,工程师。主要研究方向为用电信息采集,分布式电源等。E-mail： gyqfcgp@126.com

傅萌,女,1983年生,博士。主要研究方向为微网协同技术、综合能源优化等。E-mail： tianshanfeiniao1@126.com

摘要

在一定占空比下,研究一种具有更大降压比和低开关电压应力的新型DC-DC变换器。该变换器由低侧开关型降压单元和开关电感型降压单元级联而成。其中,低侧开关型降压单元在拓扑上等同于主控开关位于低侧的Buck电路;开关电感型降压单元则由两个二极管与两个电感以X型方式连接而成。用两套低侧开关型降压单元相互堆叠以及配置两个主控开关的方式来大幅降低开关器件的电压应力。在对该变换器的工作模态与稳态特性进行分析的基础上,使用SIMPLIS对理论分析进行仿真验证。调试了一台功率为500 W的硬件样机,试验结果表明该变换器具备降压比大、开关器件电压应力低、输入电流连续的特点。

关键词： DC-DC变换器 ; 大降压比 ; 低电压应力 ; 级联架构 ; SIMPLIS仿真

Abstract

At certain duty cycle, a novel DC-DC converter with larger step-down ratio and low voltage stress of switching devices is studied. The proposed converter consists of a low-side switch type step-down unit cascading with switched inductor step-down unit. Topologically, the low-side switch type step-down unit is equivalent to Buck converter with main switch located on low side. As for the switched inductor step-down unit, it is organized as X-shape connection by two diodes and two inductors. Thanks to stacking two sets of low-side switch type units and configuring two main control switches in the circuit, voltage stress of switching devices are dramatically reduced. Based on the analysis of operation modes and steady-state performance of the converter, SIMPLIS is used to do simulation in order to verify theoretical analysis. A 500 W hardware prototype with 94.1% peak efficiency is built and tested with results demonstrating that the proposed buck converter features large step-down ratio, low voltage stress of switching devices, continuous input current.

Keywords： DC-DC converter ; large step-down ratio ; low voltage stress ; cascaded architecture ; SIMPLIS simulation

PDF (4686KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

万文轩, 刘纲, 尹力, 傅萌. 一种具有大降压比的新型DC-DC变换器*. 电气工程学报[J], 2021, 16(3): 33-39 doi:10.11985/2021.03.005

WAN Wenxuan, LIU Gang, YIN Li, FU Meng. A Novel DC-DC Converter with High Step-down Ratio. Journal of Electrical Engineering[J], 2021, 16(3): 33-39 doi:10.11985/2021.03.005

1 引言

随着电子电气技术的飞速发展以及可再生能源的广泛应用,高压母线与低压负载之间的压差愈发加大。例如数据中心电源架构中母线电压逐渐向400 V发展,而目前主流的先进芯片组供电电压则低于1 V,降压比达1∶400[1]。在户用光伏储能应用中,面板阵列输出电压与电池组电压之间的降压比通常也低于1∶10[2]。为了适配母线与负载之间的大压差,通常需要使用高性能、大降压比的降压转换器。

一种方案是使用经典的Buck变换器直接降压,但此时通常工作在极小占空比,导致变换效率、器件应力、电磁干扰都非常恶劣[3,4]。其次,可以考虑加入高频变压器进行降压,但同时也增加了体积和控制复杂度,且变压器漏感会导致额外的损耗和器件应力[5,6,7]。另一种方法是将多级Buck电路级联,尽管开关器件的应力有所改善,但是整体电路的效率较低,且电路元件众多,控制复杂[8,9,10]。此外,所谓的二次Buck变换器是在传统Buck电路的输入侧加入一级低侧开关型降压单元,从而实现较大的降压比,但是主控开关的电压应力高[11,12,13]。文 献[14-15]研究了基于耦合电感的Buck变换器,通过引入匝比这个变量来改变电压增益以实现较大的降压比,然而主控开关的电压应力为输入电压与部分线圈感应电压之和,加上漏感所致尖峰电压的存在,应力依旧较高。为了吸收漏感导致的尖峰电压,文献[16]研究了基于耦合电感的二次Buck变换器,其中的低侧开关型降压单元同时起到无损钳位的作用,但是主控开关电压应力大的问题依然存在。文献[17,18]探讨了基于开关电感网络的Buck变换器,这种变换器同样具有较大的降压比,但主控开关的电压应力也较高。基于开关电容单元的DC-DC变换器具有较大的降压比,但是随着单元数目的增加,器件数量和电路复杂度都随之增加,且该变换器通常应用于小功率或微功率场合[19,20]。

额定耐压越高的功率开关器件通常具有更大的通态电阻或通态压降、更严重的反向恢复。本文研究一种具有大降压比、低开关电压应力的DC-DC变换器,将低侧开关型Buck电路与开关电感型Buck电路的特性相结合,从而获得极大的降压比。同时,对二者结合后的电路做相应改进,添加一套低侧开关型Buck电路和一个主控开关,以降低开关器件的电压应力。另外,输入侧电感的存在使得输入电流得以连续,降低了对输入滤波电容值的 要求。

2 电路结构与工作模态

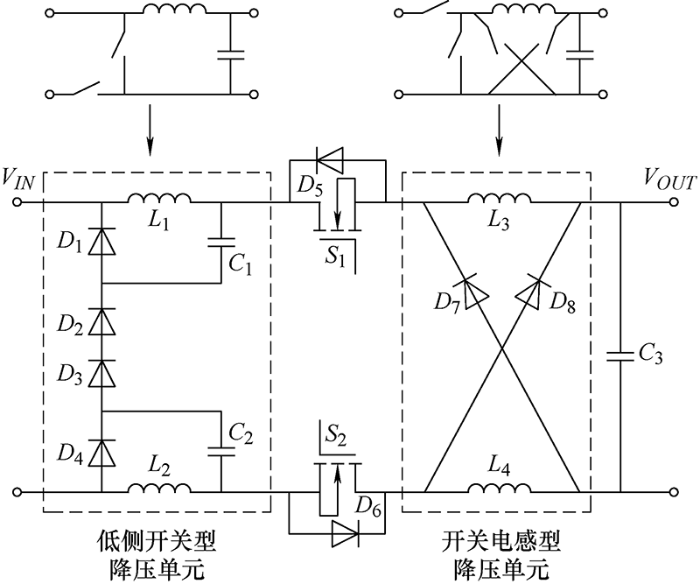
基于低侧开关型降压单元和开关电感型降压单元的新型大降压比DC-DC变换器电路结构如图1所示,同时分别给出了拓扑意义下两者的结构,以便理解本文所探讨的DC-DC变换器的拓扑演变过程。${D_1}$、${D_2}$、${L_1}$、${C_1}$组成一组低侧开关降压单元;${D_3}$、${D_4}$、${L_2}$、${C_2}$组成另一组低侧开关降压单元。${S_1}$、${S_1}$为两个主控开关,${D_5}$、${D_6}$为寄生体二极管。开关电感型降压单元则由${D_77}$、${D_8}$、${L_3}$、${L_4}$组成,其中两个二极管在空间交叉,并无电气连接。在电感电流连续状态下,开关器件组${S_1}$、${S_2}$、${D_2}$、${D_3}$以一定的频率和占空比进行工作;开关器件组${D_1}$、${D_4}$、${D_7}$、${D_8}$则以互补的形式进行工作,完成一个开关周期的功率变换。两个低侧开关型降压单元先将输入电压${V_{IN}}$降压成电容电压${V_{C2}}$、${V_{C1}}$,两个电容串联后作为后级的输入电压源,接着由开关电感型降压单元进一步降压。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   新型DC-DC变换器的拓扑


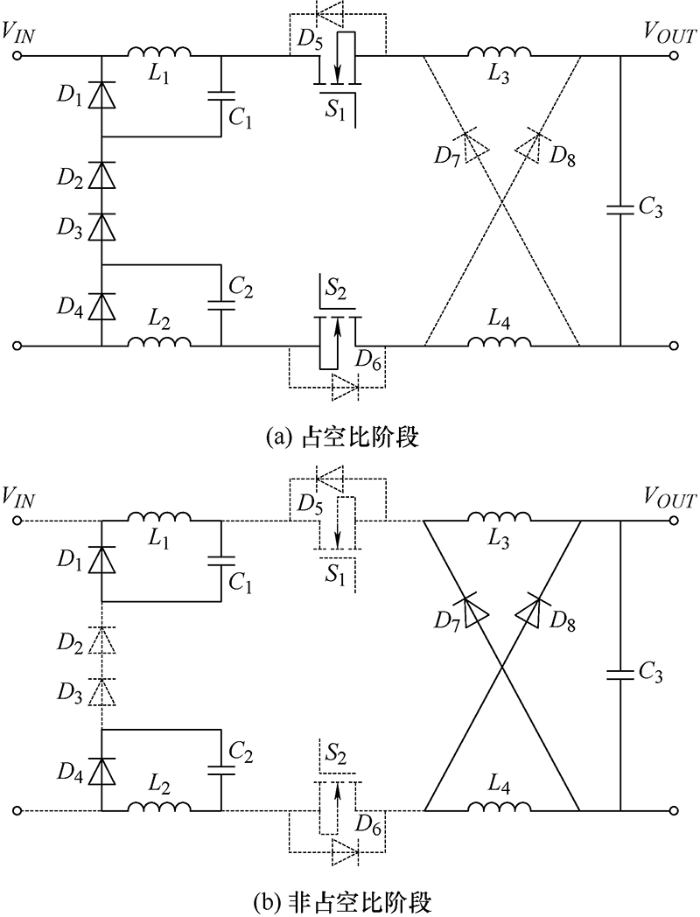
在电感电流连续状态下,该新型DC-DC变换器的两种工作模态如图2所示。当${S_1}$、${S_2}$导通时,${D_2}$、${D_3}$也导通,${D_1}$、${D_4}$、${D_7}$、${D_8}$由于承受反向电压均关断。${L_1}$、${L_2}$、${L_3}$、${L_4}$两端承受正向电压,因此它们的电流均线性上升,此时变化器状态如图2a所示。占空比阶段结束后,${S_1}$、${S_2}$、${D_2}$、${D_3}$均关断,由于电感续流的本质需求,${D_1}$、${D_4}$、${D_7}$、${D_8}$开始导通。${L_1}$、${L_2}$、${L_3}$、${L_4}$由于承受反向电压,它们的电流均开始线性下降。${L_1}$、${L_2}$中储存的能量分别转移到${C_1}$、${C_2}$。${L_3}$、${L_4}$也由之前的串联变为并联,同时将储存的能量提供给负载。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   新型DC-DC变换器的工作模态


3 稳态分析

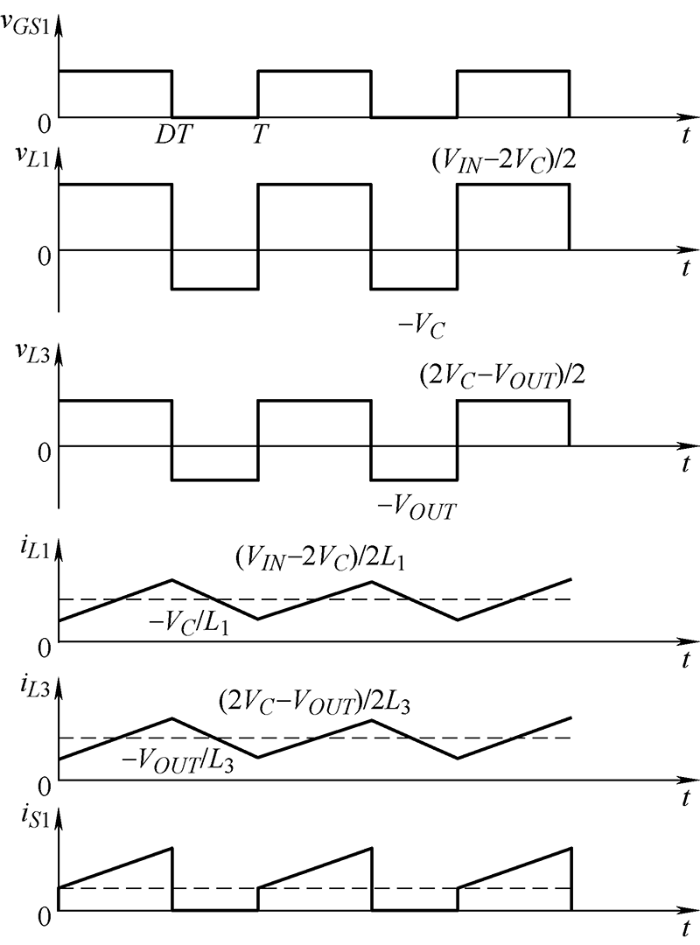
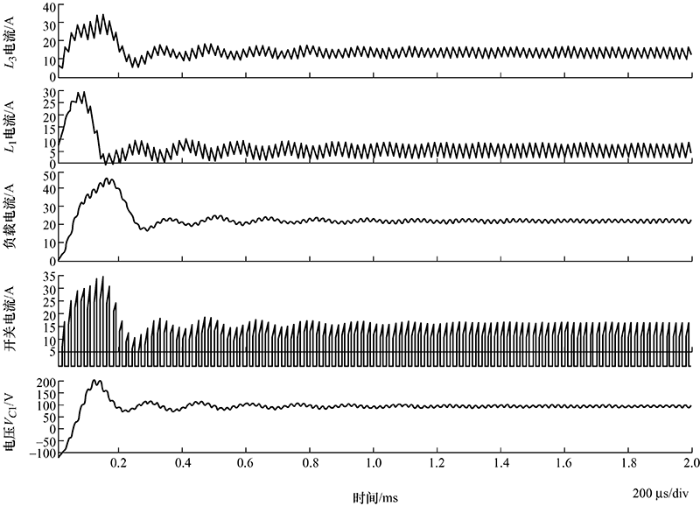
对变换器的稳态工作情况进行分析有助于了解其本质和外特性,对后续的实际电路设计具有十分重要的指导意义。同样假设电感电流处于连续状态,基于转换器工作在电感电流连续模式的假设,该新型DC-DC变换器的主要电量波形如图3所示。${v_{GS1}}$、${i_{S1}}$分别为S1、S2的门极驱动脉冲和电流波形;${v_{L1}}$、${i_{L1}}$分别为L1、L2的电压、电流波形;${v_{L3}}$、${i_{L3}}$分别为L3、L4的电压、电流波形。由于稳态时C1、C2电压相同,因此都用VC表示。另外,D为稳态时的占空比,T为开关周期。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   主要电量的稳态波形


考虑到L1、L2的工况一致,L3、L4的工况一致,因此只需要根据L1、L3的伏秒平衡关系来推导变换器的相关特性。L1、L3的伏秒平衡方程分别如式(1)、(2)所示,其中${V_{IN}}$、${V_{OUT}}$分别为输入电压和输出电压。以${V_C}$作为中间变量对式(1)、(2)进行整理可得变换器的增益$M$如式(3)所示

$\frac{{{V_{IN}} - 2{V_C}}}{2} \cdot DT = {V_C} \cdot (1 - D)T$
$\frac{{2{V_C} - {V_{OUT}}}}{2} \cdot DT = {V_{OUT}} \cdot (1 - D)T$
$M = \frac{{{V_{OUT}}}}{{{V_{IN}}}} = \frac{{{D^2}}}{{2 - D}}$

根据电感的电气特性${u_L} = L \cdot {\text{d}}{i_L}/{\text{d}}t$以及图3中${L_1}$、${L_3}$电流波形中的上升斜率和下降斜率,可以得出它们各自的电流纹波峰峰值,分别如式(4)和式(5)所示

$\Delta {i_{L1}} = \frac{{({D^2} - 3D + 2){V_{OUT}}T}}{{2D{L_1}}}$
$\Delta {i_{L3}} = \frac{{(1 - D){V_{OUT}}T}}{{{L_3}}}$

针对一定的负载电流${I_{OUT}}$,当电感L3、L4处于临界导通状态时,记此时电感L3、L4的电流为${I_{OC}}$在$\Delta {i_{L3}}$半与临界电流${I_{OC}}$相等,根据式(5)可以推导出保持电感L3电流不断续的感量如式(6)所示。假设变换效率为100%,根据功率守恒,推导出电感L1、L2的电流平均值与电感L3、L4电流平均值的关系如式(7)所示。最后,将式(7)代入式(6)得到电感L1电流保持不断续的条件如式(8)所示。

${L_3} \geqslant \frac{{(1 - D){V_{OUT}}T}}{{2{I_{OC}}}}$
${I_{L1}} = \frac{{D{I_{L3}}}}{{2 - D}} = \frac{{D{I_{OUT}}}}{{2 - D}}$
${L_1} \geqslant \frac{{({D^2} - 3D + 2){V_{OUT}}T}}{{2D{I_{OC}}}}$

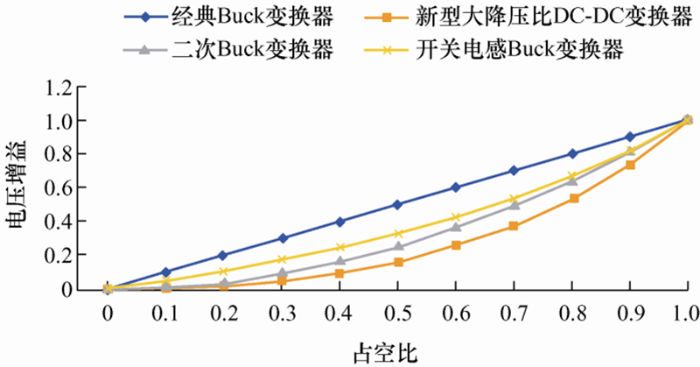
为直观比较该新型DC-DC变换器的电压增益与其他三种Buck变换器的电压增益,绘制了如图4所示的增益曲线对比。对于耦合电感二次Buck变换器和开关电容变换器而言,其电压增益和开关应力受到诸如匝比、电容单元数量等实际设计参数影响,不便于直接进行比较。图4中的增益曲线从上至下依次属于经典Buck变换器、开关电感Buck变换器、二次Buck变换器和新型大降压比DC-DC变换器,前三种Buck变换器的电压增益${M_1}$、${M_3$分别如式(9)、(10)、(11)所示。在这四种Buck变换器中,在相同占空比情况下,新型DC-DC变换器具有最强的降压能力。当占空比同为0.5~0.8时,新型DC-DC变换器的降压比优势较为明显,而当占空比接近0或者1时,优势逐渐减小。

${M_1} = D$
${M_2} = \frac{D}{{2 - D}}$
${M_3} = {D^2}$

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   新型DC-DC变换器与其他Buck型转换器的电压增益对比


由于采用了两套低侧开关型降压单元和两个主控开关,因此本文探讨的新型DC-DC变换器具有较低的开关器件电压应力。表1给出了变换器电路中主要器件的电压应力情况,并以输入电压为基底进行归一化处理。

表1   主要器件的电压应力

器件名称电压应力(归一化)
D1~D41/2
D7、D8D/(2–D)
S1、S2(2+D)/(4–2D)
C1、C2D/2
C3D2/(2–D)

新窗口打开| 下载CSV


以主控开关为例,表2对比了相同工况下,前文提到的四种Buck变换器中主控开关的电压应力情况。假定工况如下：输入电压${V_{IN}}$为450 V,占空比D为0.5。从对比结果可以得出结论,新型DC-DC变换器在降压能力和主控开关电压应力方面具有明显优势。

表2   主控开关电压应力比较

拓扑指标
输出电压/V电压应力/V
经典Buck变换器225450
二次Buck变换器113675
开关电感Buck变换器150600
新型DC-DC变换器75375

新窗口打开| 下载CSV


表3给出了四种Buck变换器功率元件数量的对比结果。尽管新型DC-DC变换器具有最多的元件数量,但是多数元件的额定耐压都大幅降低,从而具有更好的电气特性和更低的成本。另外,随着半导体技术和小型化器件的不断发展,更高功率密度的开关器件和更小尺寸的无源器件得到越来越多的应用。因此,较多的元件数量并不会对新型DC-DC变换器的功率密度和成本带来显著的影响。

表3   四种Buck变换器功率元件数量对比

拓扑有源开关无源开关电容电感
经典Buck1111
二次Buck1322
开关电感Buck1211
新型DC-DC2634

新窗口打开| 下载CSV


4 试验验证

为了验证理论分析的正确性,首先在软件工具SIMPLIS中建立新型DC-DC变换器的电路模型,对24 V额定电压,容量为30 A·h的电池组进行充电,主要参数如表4所示。电感${L_3}$、${L_4}$的电流纹波系数取值25%。电容${C_1}$和${C_3}$的最小值分别如式(12)和式(13)所示[21,22]。$\Delta {V_{C1}}$和$\Delta {V_{C3}}$分别为电容电压纹波峰峰值,取各自稳态值的2%。转换器的占空比为0.4。

${C_1},{C_2} \geqslant \frac{{(1 - D){V_{OUT}}{T^2}}}{{8\Delta {V_{C1}}D{L_1}}}$
${C_3} \geqslant \frac{{(1 - D){V_{OUT}}{T^2}}}{{8\Delta {V_{C3}}{L_3}}}$

表4   主要仿真参数

参数数值
输入电压/V450
输出电压/V24
开关频率/kHz50
电容C1、C2/μF6.8
电容C3/μF47
电感L1、L2/μH208
电感L3、L4/μH54
满载功率/W500
输出电压纹波系数(%)2
输出电流纹波系数(%)25

新窗口打开| 下载CSV


图5给出了新型DC-DC变换器仿真试验中的主要波形,从上至下依次为电感${L_3}$的电流波形、电感${L_1}$的电流波形、输出充电电流波形、主控开关${S_1}$电流波形和电容${C_1}$电压波形。将各个波形的稳态值与表3的相关参数代入前文的计算公式进行验证,结果完全吻合。仿真试验的结果验证了理论分析的正确性和有效性。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   新型DC-DC变换器仿真波形


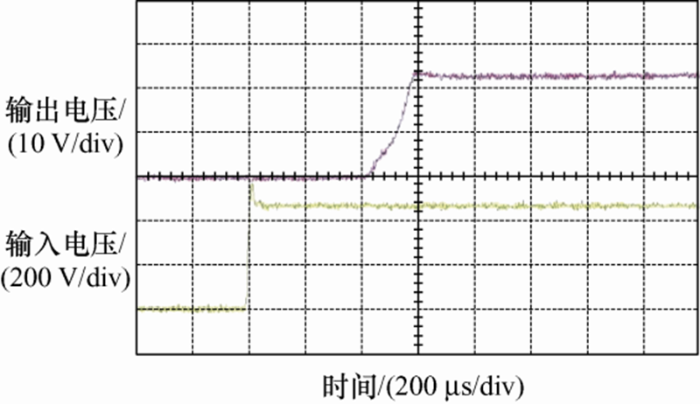
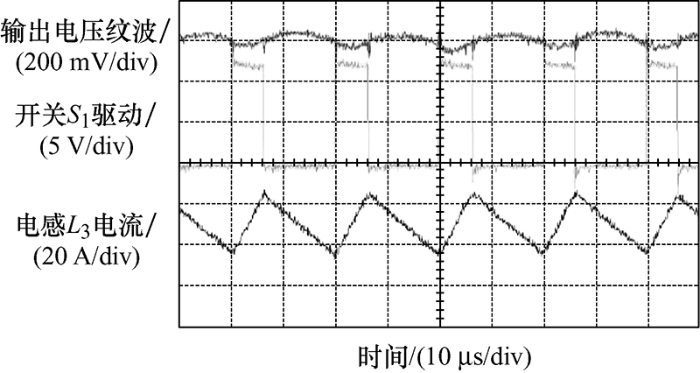
基于一台功率为500 W的电池充电器样机,对新型DC-DC变换器进行了硬件试验和相关测试。开关频率为50 kHz,输入电压为450 V,输出电压为24 V。主控开关S1、S2采用ST公司的STB50N65DM6,该器件基于快恢复体二极管工艺,能够有效减少反向恢复时间和损耗。二极管D1、D2、D3、D4选择ST公司的STPSC4H065碳化硅二极管。二极管D7、D8选取ST公司的STPS40M120C肖特基二极管。图6给出了变换器软起动的过程,数字控制芯片检测到输入电压存在一段时间后开始执行软启动程序。图7给出了部分试验波形,从上到下依次为交流耦合下的输出电压纹波,主控开关${S_1}$的门极驱动以及电感${L_3}$的电流。硬件样机的持续稳定工作进一步验证了前文理论分析与仿真试验的正确性。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   变换器软起动过程


图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   输出电压纹波、S1驱动、L3电流


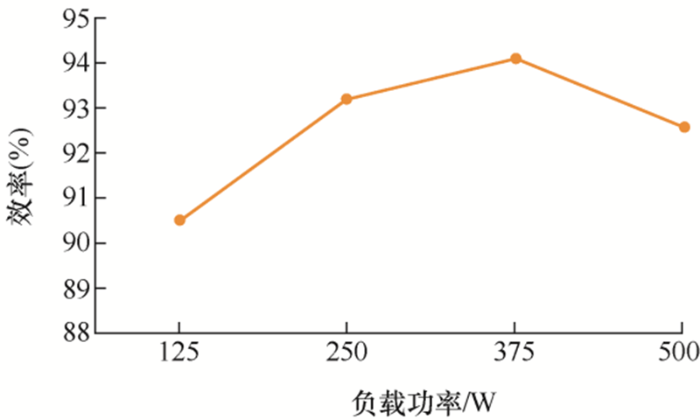
初步测试了试验样机在25%负载、50%负载、75%负载和100%负载下的效率,并绘制成曲线如图8所示。峰值效率出现在75%负载左右,约为94.1%。由于损耗分析、器件优化选型和电路板优化布局等工作尚未开展,因此目前变换器的效率相对不高。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8   新型DC-DC变换器的效率曲线


5 结论

(1) 提出并分析了一种具有大降压比和低开关电压应力的新型DC-DC变换器。在电感电流连续的情况下,进行了变换器工作模态与稳态特征的理论分析。

(2) 通过软件工具SIMPLIS对理论分析进行了仿真验证,仿真结果与推导结果完全吻合。

(3) 设计和调试了功率为500 W,峰值效率为94.1%的硬件样机,测试结果表明该新型DC-DC变换器具有降压比大、开关器件电压应力低、输入电流连续以及变换效率较高的特点。

(4) 由于本文的主要工作在于验证电路原理和可行性,尚未对变换器进行各方面的优化设计,因此变换效率相对不高。未来的主要工作将集中在器件优化选型、电路板优化布局等方面,以期得到更高的效率。

参考文献

张文利, 斯利, 刘芳.

高压直流智能母线在数据中心的应用

[J]. 智能建筑与智慧城市, 2016(2):67-68.

[本文引用: 1]

ZHANG Wenli, SI Li, LIU Fang.

The application of HVDC intelligent bus in data center

[J]. Intelligent Building & Smart City, 2016(2):67-68.

[本文引用: 1]

阎晓金.

独立光伏发电混合储能系统功率转换控制研究

[J]. 可再生能源, 2020(10):1368-1374.

[本文引用: 1]

YAN Xiaojin.

Research on power control for hybrid energy storage of photovoltaic generation system

[J]. Renewable Energy Resources, 2020(10):1368-1374.

[本文引用: 1]

黄硕, 王久和.

基于自抗扰控制的Buck变换器无源控制研究

[J]. 电气工程学报, 2020, 15(1):71-75.

[本文引用: 1]

HUANG Shuo, WANG Jiuhe.

Research on passivity-based control of buck converter based on active disturbance rejection control

[J]. Journal of Electrical Engineering, 2020, 15(1):71-75.

[本文引用: 1]

荣德生, 陈淑涵, 李洪珠, 等.

磁集成Buck变换器在超级电容充电系统中的建模

[J]. 电工电能新技术, 2015, 34(5):13-17.

[本文引用: 1]

RONG Desheng, CHEN Shuhan, LI Hongzhu, et al.

Modeling of magnetic integration buck converter with supercapacitors charging system

[J]. Advanced Technology of Electrical Engineering and Energy, 2015, 34(5):13-17.

[本文引用: 1]

IQBAL Z, NASIR U, RASHEED M, et al.

A comparative analysis of synchronous buck,isolated buck and buck converter

[C]// IEEE International Conference on Environment and Electrical Engineering, 2015:43-47.

[本文引用: 1]

高帅, 张兴, 赵文广, 等.

双有源桥DC-DC变换器最小回流功率控制策略

[J]. 电气工程学报, 2019, 14(2):24-29.

[本文引用: 1]

GAO Shuai, ZHANG Xing, ZHAO Wenguang, et al.

Minimum reactive power control strategy for dual active bridge DC-DC converter

[J]. Journal of Electrical Engineering, 2019, 14(2):24-29.

[本文引用: 1]

宋华江.

半桥式双向DC-DC变换器的优化控制研究

[J]. 电子设计工程, 2019, 27(24):57-60.

[本文引用: 1]

SONG Huajiang.

Research and optimal control for half-bridge bidirectional DC-DC converter

[J]. Electronic Design Engineering, 2019, 27(24):57-60.

[本文引用: 1]

杜韦静, 张军明, 钱照明.

Buck变流器级联系统直流母线电压补偿控制策略

[J]. 电工技术学报, 2015(1):135-142.

[本文引用: 1]

DU Weijing, ZHANG Junming, QIAN Zhaoming.

Compensation methodology for DC bus voltage of cascaded system formed by Buck converters

[J]. Transactions of China Electrotechnical Society, 2015(1):135-142.

[本文引用: 1]

LEONG K, DEBOY G, KRISCHAN K, et al.

A single stage 54 V to 1.8 V multi-phase cascaded buck voltage regulator module

[C]// IEEE Applied Power Electronics Conference and Exposition, 2015:1966-1973.

[本文引用: 1]

马佳睿, 穆琳.

Buck变换器级联系统直流母线电压稳定控制策略研究

[J]. 舰船电子工程, 2019, 39(1):164-168.

[本文引用: 1]

MA Jiarui, MU Lin.

Research on DC bus voltage stability control strategy of buck converter cascade system

[J]. Ship Electronic Engineering, 2019, 39(1):164-168.

[本文引用: 1]

王涛, 巫旺, 牛明哲, 等.

二次型Buck变换器的分析与设计

[J]. 电源学报, 2017, 15(1):146-152.

[本文引用: 1]

WANG Tao, WU Wang, NIU Mingzhe, et al.

Analysis and design of quadratic Buck converter

[J]. Journal of Power Supply, 2017, 15(1):146-152.

[本文引用: 1]

陆治国, 田海涛, 汪渊.

一种新型的交错并联二次型Buck变换器

[J]. 电力电子技术, 2014(2):19-23.

[本文引用: 1]

LU Zhiguo, TIAN Haitao, WANG Yuan.

A new interleaved quadratic Buck converter

[J]. Power Electronics, 2014(2):19-23.

[本文引用: 1]

卢志飞, 杨平, 刘雪山.

单开关二次型DCM Buck变换器

[J]. 电工技术学报, 2011(S1):71-76.

[本文引用: 1]

LU Zhifei, YANG Ping, LIU Xueshan.

Single-switch quadratic DCM Buck converter

[J]. Transactions of China Electrotechnical Society, 2011(S1):71-76.

[本文引用: 1]

CHADHA A, AYACHIT A, SAINI D, et al.

Steady-state analysis of PWM tapped-inductor DC-DC converter in CCM

[C]// IEEE Texas Power and Energy Conference, 2018:97-82.

SAINI D, CHADHA A, AYACHIT A, et al.

Duty cycle and input-to-output voltage transfer functions of tapped-inductor buck DC-DC converter

[C]// IEEE International Symposium on Circuits and Systems, 2018:113-117.

YAO K, YE M, XU M, et al.

Tapped-inductor buck converter for high-step-down DC-DC conversion

[J]. IEEE Transactions on Power Electronics, 2005, 20(4):775-780.

DOI:10.1109/TPEL.2005.850920      URL     [本文引用: 1]

YAO J, ZHENG K, ABRAMOVITZ A.

Dynamic analysis of the switched inductor buck converter

[C]// Annual Conference of the IEEE Industrial Electronics Society, 2019, 1:1721-1725.

[本文引用: 1]

荣德生, 杨干兴, 胡举爽, 等.

具有开关电感单元的电感磁集成Buck变换器

[J]. 电源学报, 2018(3):23-27.

[本文引用: 1]

RONG Desheng, YANG Ganxing, HU Jushuang, et al.

Inductive integrated Buck converter with switched-inductor units

[J]. Journal of Power Supply, 2018(3):23-27.

[本文引用: 1]

MAKSIMOVIC D, DHAR S.

Switched-capacitor DC-DC converters for low-power on-chip applications

[C]// IEEE Power Electronics Specialists Conference, 1999, 1:54-59.

[本文引用: 1]

SEEMAN M, SANDERS S, RABAEY J.

An ultra-low-power management IC for wireless sensor nodes

[C]// IEEE Custom Integrated Circuits Conference, 2007:567-570.

[本文引用: 1]

AYACHIT A, KAZIMIERCZUK M.

Steady-state analysis of PWM quadratic buck converter in CCM

[C]// IEEE International Midwest Symposium on Circuits and Systems, 2013:49-52.

[本文引用: 1]

AYACHIT A, KAZIMIERCZUK M.

Power losses and efficiency analysis of the quadratic buck converter in CCM

[C]// IEEE International Midwest Symposium on Circuits and Systems, 2014:463-466.

[本文引用: 1]

/

〈 〉