电气工程学报, 2021, 16(3): 123-129 doi: 10.11985/2021.03.017

电力系统

基于小波包与回声状态网的风电功率预测

李忠,

内蒙古自治区气象服务中心 呼和浩特 010000

Wind Power Forecasting Based on Wavelet Packet and Echo State Network

LI Zhong,

Inner Mongolia Meteoroloical Service, Hohhot 010000

收稿日期: 2021-03-4   修回日期: 2021-06-20  

Received: 2021-03-4   Revised: 2021-06-20  

作者简介 About authors

李忠,男,1969年生,硕士,高级工程师。主要从事能源气象研究。E-mail： 13848138555@139.com

摘要

为提高风电并网的稳定性、安全性,风电功率预测的准确性研究具有重要意义,提出一种基于小波包与回声状态网的风电功率预测方法,并给出了具体的应用步骤。通过小波包分解方法将历史的风速、风向、温度、湿度等气象因素以及输出功率数据进行分解,能够准确地反映历史数据的规律性;应用回声状态网对各个分解信号进行建模和预测,提高了建模的速度和准确性;最后,将各个分解信号的预测结果进行合成得到风电功率的预测值。

关键词： 风电功率预测 ; 小波包 ; 回声状态网 ; 分解信号

Abstract

In order to improve the stability and security of wind power integration, the accuracy of wind power prediction is of great significance. The method of wind power forecasting based on the wavelet packet and echo state network is proposed, and the specific application steps are given. Firstly, the historical data of meteorological factors such as wind speed, wind direction, temperature, humidity and wind power is decomposed by wavelet packet decomposition, which can accurately reflect the regularity of historical data. Secondly, the echo state network is applied to model and predict each decomposed signal, which improves the speed and accuracy of modeling. Finally, the prediction results of each decomposed signal are synthesized to obtain the predicted value of wind power.

Keywords： Wind power prediction ; wavelet packet ; echo state network ; each decomposed signal

PDF (4649KB) 元数据 多维度评价 相关文章 导出 EndNote| Ris| Bibtex  收藏本文

本文引用格式

李忠. 基于小波包与回声状态网的风电功率预测. 电气工程学报[J], 2021, 16(3): 123-129 doi:10.11985/2021.03.017

LI Zhong. Wind Power Forecasting Based on Wavelet Packet and Echo State Network. Journal of Electrical Engineering[J], 2021, 16(3): 123-129 doi:10.11985/2021.03.017

1 引言

随着全球经济的快速发展,现有的化石资源已经不能满足人们的生产生活要求,同时化石能源带来的生态环境污染也是亟需解决的问题,因此,大力发展可再生能源变得尤为重要。风电作为一种清洁能源,可以替代化石燃料的使用,减少温室气体的排放,有效地缓解能源危机。

近年来,全球的风电装机容量大幅度增长,然而风力发电的波动性、不确定性给电网和能源系统的经济、稳定和安全运行带来了巨大的挑战,因此,准确地对风电功率进行预测十分必要。目前,常用的风电功率预测方法有统计学习方法、物理方法[1]以及空间相关性方法[2,3]。统计学习方法主要是根据历史的风电数据来建立气象因素与风电功率的学习模型,然后再根据实时的数据与数值天气预报代入到模型中进行预测,其中较为常用的方法有人工神经网络(Artificial neural networks,ANN)方法[4]、时间序列法[5]、支持向量机(Support vector machine,SVM)[6]等。物理方法则不考虑历史风电数据,通过求解热力动力学方程组来预测未来天气的变化和风电功率[7,8]。空间相关性方法是根据各个风机的位置、尾流效应等的空间相关性来推测关联风机的风电功率[2,3]。对比以上方法,统计学习方法由于应用较为简便、计算速度快等优点而被广泛应用。

为了提高预测的准确性,通常选用混合模型来进行风电功率建模,先对历史的风电数据等进行信号分解,再采用统计方法对分解后的序列数据分别进行建模,重构后获得风电功率预测模型,最后将未来数值天气预报数据代入模型进行风电功率预测。常用的分解方法有小波分解(Wavelet decomposition,WP)[9]、小波包分解(Wavelet packet decomposition,WPD)[10]、经验模态分解(Empirical mode decomposition,EMD)[11]和快速集合经验模态分解(Fast ensemble empirical mode decomposition,FEEMD)[12]。文献[13,14]采用一种小波变换与BP神经网络建立风电功率预测模型,该方法在传统的BP神经网络中融合小波变化提高了神经网络的收敛速度和抗干扰能力,但文中只是与传统的BP神经网络进行了误差对比分析,忽略了BP神经网络算法与其他方法的对比,不能很好地说明该方法的优势;文献[15]基于小波分解和改进粒子群算法优化神经网络进行风电功率的建模,并与小波-BP神经网络方法进行了对比,说明了该方法的收敛性能较好;文献[16]为了解决粒子群算法容易陷入局部最优解的缺点,提出了基于小波包分解和带扰动的粒子群训练算法对Elman神经网络进行优化,建立风电功率预测模型,并与传统的Elman神经网络进行对比,说明了该方法的正确性和有效性。

以上方法都在传统的机器学习算法基础上引入小波分解等理论对原始风电数据进行处理,更好地反映数据的规律性,提高模型的预测精度。但是针对于支持向量机、前向神经网络等算法存在的过拟合、计算量大等缺点却无法避免。近年来,回声状态网络(Echo state network,ESN)[17,18]逐渐成为神经网络领域的研究热点,ESN具有良好的非线性函数逼近的能力,可以更好地解决局部最小问题,在全局最优性、稳定性等方面都有很大的优势,同时,该方法以储备池作为信息处理的媒介,生成过程与训练过程相互独立,且只训练储备池到输出层的权值,具有训练算法简单、计算效率高等优点。

小波包分解相较于小波分解信号更为精细,克服了小波分解高频部分存在的时频率分辨率低和时间分辨率高的问题[19],本文采用小波包分解对原始的气象数据和输出功率数据进行处理;同时,考虑到回声状态网络的简单、稳定性高、效率高等优势,对分解后的各个分量建立预测模型,最终得到合成后的风电功率预测结果。

2 小波包分解基本原理

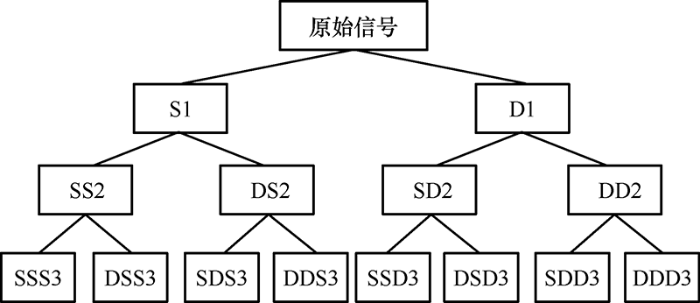
小波包分解可以称为最佳子带树结构,即利用多次迭代的小波转换分析输入信号的细节部分[8]。小波包分解是在小波变化的基础上,在每一级信号分解时,不但对低频子带进行进一步的分解,而且对高频子带进行进一步分解,最后通过最小化一个代价函数,计算出最优的信号分解路径,并以此分解路径对原始信号进行分解。因此,小波包分解信号更为精细,克服了小波分解高频部分存在的时频率分辨率低和时间分辨率高的问题。

假设小波函数$\psi \left( x \right)$和尺度函数$\phi \left( x \right)$,并且令其为

$\left\{ \begin{array}{l}{\psi _{\rm{0}}}\left( x \right) = \phi \left( x \right)\\{\psi _{\rm{1}}}\left( x \right) = \psi \left( x \right)\end{array} \right.$
$\left\{ \begin{array}{l}{\phi _{2l}}\left( x \right) = \sum\limits_{k = - \infty }^{ + \infty } {{h_k}{\phi _l}} \left( {2x - k} \right)\\{\psi _{{\rm{2}}l{\rm{ - 1}}}}\left( x \right) = \sum\limits_{k = - \infty }^{ + \infty } {{g_k}{\phi _l}} \left( {2x - k} \right)\end{array} \right.$

那么,定义的函数$\left\{ {{\psi _n}} \right\}$称为关于尺度函数$\phi \left( x \right)$的小波包。

小波包分解的低通、高通滤波器组条件下的计算公式如式(3)所示[20]

$\left\{ \begin{array}{l}d_j^{2n}\left[ k \right] = \sum\limits_{l \in Z} {{h_{l - 2k}}d_{j + 1}^n\left[ l \right]} \\d_j^{2n + 1}\left[ k \right] = \sum\limits_{l \in Z} {{g_{l - 2k}}d_{j + 1}^n\left[ l \right]} \end{array} \right.$

式中,$d_j^{2n}\left[ k \right]$、$d_j^{2n + 1}\left[ k \right]$分别为小波包第k层内(j,n)的节点系数;${h_{l - 2k}}$、${g_{l - 2k}}$分别为小波包分解后的低通、高通滤波器组;$d_{j + 1}^n\left[ l \right]$为小波包第l层内(i+1,n)处的节点系数。

小波包重构的表达式为

$d_{j + 1}^n\left[ k \right] = \sum\limits_{l \in Z} {{h_{k - 2l}}d_j^{2n}} \left[ l \right] + \sum\limits_{l \in Z} {{g_{k - 2l}}d_j^{2n}} \left[ l \right]$

式中,$d_{j + 1}^n\left[ k \right]$为重构节点系数;${h_{l - 2k}}$、${g_{l - 2k}}$分别为重构后的低通、高通滤波器组;$d_{j + 1}^n\left[ l \right]$为重构节点系数。

根据小波包分解和重构的定义,可以得到三层小波包分解的示意图,如图1所示。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1   小波包分解图


3 回声状态网基本原理

3.1 回声状态网基本原理

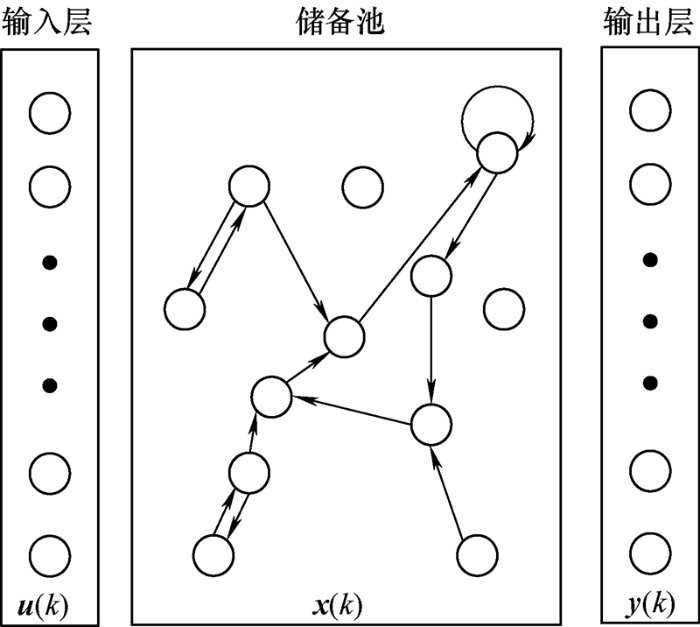
回声状态网络是最初由JAEGER[21]提出来的一种新型递归互联神经网络,主要是为了解决循环神经网络(Recurrent neural network,RNN)中训练过程复杂、计算效率低的问题。ESN主要由输入层、储备池、输出层组成,输入信号u(t)通过权值矩阵Win连接到储备池,储备池即传统神经网络的隐含层,但其内部的网络结构以及连接权值Wres在训练过程中不会发生变化,且采用线性方法得到的输出权值Wout即可保证较好的网络预测性能。

典型网络结构如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2   ESN结构图


假设ESN输入神经元个数为L,输出神经元个数为M,储备池内部神经元个数为N,则输入向量u(k)、输出向量y(k)、内部状态向量x(k)在k时刻可用式(5)表示

$\left\{ \begin{array}{l}{\bf{u}}\left( k \right) = {\left[ {{u_1}\left( k \right),{u_2}\left( k \right), \cdots,{u_L}\left( k \right)} \right]^T}\\{\bf{y}}\left( k \right) = {\left[ {{y_1}\left( k \right),{y_2}\left( k \right), \cdots,{y_M}\left( k \right)} \right]^T}\\{\bf{x}}\left( k \right) = {\left[ {{x_1}\left( k \right),{x_2}\left( k \right), \cdots,{x_N}\left( k \right)} \right]^T}\end{array} \right.$

ESN储备池中内部向量以及输出向量的更新如下所示

${\bf{x}}\left( {k + 1} \right) = f\left( {{{\bf{W}}^{{\text{res}}}}x\left( k \right) + {{\bf{W}}^{{\text{in}}}}u\left( k \right) + {{\bf{W}}^{{\text{fb}}}}y\left( k \right)} \right)$
${\bf{y}}\left( {k + 1} \right) = {f_{{\text{out}}}}\left( {{{\bf{W}}^{{\text{out}}}}\left[ {x\left( {k + 1} \right),u\left( {k + 1} \right),y\left( k \right)} \right]} \right)$

式中,Wres、Win、Wfb分别为N$\times$N储备池内部权重矩阵,N$\times$L为输入权重矩阵,N$\times$M为反馈权重矩阵;f=[f1, f2,$\cdots$, fN]为储备池神经元的激励函数;fout为输出神经元的激励函数。

3.2 回声状态网模型训练

在训练回声状态网时,主要包括如下两个步 骤[18]。

步骤一：采样阶段。假设输入训练样本的个数为n,给定初始状态,令内部状态向量$x\left( n \right) = 0$,输入样本$u\left( n \right)$经过内部权重矩阵Win到储备池中,并根据式(6)、(7)来计算内部状态向量x(n)和输出向量y(n)。

为了对接下来计算输出权值提供数据,将m时刻到p时刻的内部状态向量$\left( {{x_{\text{1}}}\left( m \right),{x_{\text{2}}}\left( {m + 1} \right), \cdots,{x_N}\left( p \right)} \right)$,以及输出向量$\left( {{y_{\text{1}}}\left( m \right),{y_{\text{2}}}\left( {m + 1} \right), \cdots,{y_L}\left( p \right)} \right)$,并分别构成矩阵$B\left( {p - m + 1,N} \right)$、$T\left( {p - m + 1,L} \right)$。

步骤二：权值计算。考虑到$x\left( n \right)$和实际输出$\tilde y\left( n \right)$为线性关系,因此,应用式(8)将实际输出$\tilde y\left( n \right)$和期望输出$y\left( n \right)$逼近来计算权值。

$y\left( n \right) \approx \sum\limits_{i = 1}^K {w_i^{{\text{out}}}{u_i}\left( n \right) + } \sum\limits_{i = K + 1}^{K + N} {w_i^{{\text{out}}}{x_{i - K}}\left( n \right)}$

同时,在计算权值时必须要保证均方误差最小,故采用如下的方程来进行计算

$\eqalign{ & \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{min}}\frac{1}{{p - m + 1}} = \cr & {\sum\limits_{n = m}^p {\left( {y\left( n \right) - \sum\limits_{i = 1}^K {w_i^{{\text{out}}}{u_i}\left( n \right) + } \sum\limits_{i = K + 1}^{K + N} {w_i^{{\text{out}}}{x_{i - K}}\left( n \right)} } \right)} ^2} \cr}$

求解如上的公式,即计算公式${W^{{\text{out}}}} = {B^{ - 1}}T$。

4 基于小波包-回声状态网的风电功率预测方法

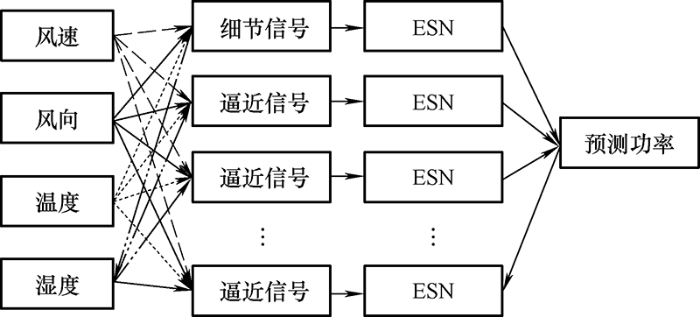
基于小波包分解和回声状态网的风电功率预测方法的具体实施步骤如图3所示。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3   风电功率预测流程图


步骤一：数据预处理。对历史的风速、风向、温度、湿度气象数据以及输出功率数据进行预处理,即对于缺失数据进行补充、对异常数据进行剔除等处理。

步骤二：小波包分解。将处理后的历史数据作为训练数据进行小波包分解,将风速、风向、温度、湿度和实际输出功率数据分解为细节信号和多个逼近信号。

步骤三：以风速、风向、温度、湿度和输出功率五部分数据的相同频段的为一组,即将其分为多组作为ESN的输入信号,训练不同结构的ESN 模型。

步骤四：以上三个步骤可获得ESN模型,之后输入预测数据,将待预测日的风速、风向、温度和湿度作为ESN模型的输入进行预测,对各子序列的预测结果进行重构,获得最终的功率预测数据。

5 算例分析

本文以某风电场为例,选取该风电场2019年1月风速、风向、温度、湿度以及输出功率等数据,采样频率为15 min,并将其分为两个子集。子集1选取1月1日至30日的风速数据进行小波包分解用以证明小波包分解算法的有效性,并训练ESN模型,共计2 880个样本数据;子集2选取1月31日的数据进行风电功率预测,用以说明本文提出的基于回声状态网的风电功率预测方法的准确性。为了进一步说明本文方法的优越性,对小波包-BP神经网络法、小波-支持向量机法以及本文方法的风电功率预测结果进行对比分析。

5.1 小波包分解应用

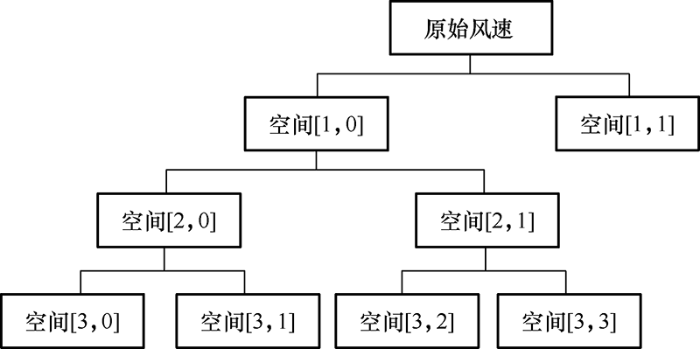
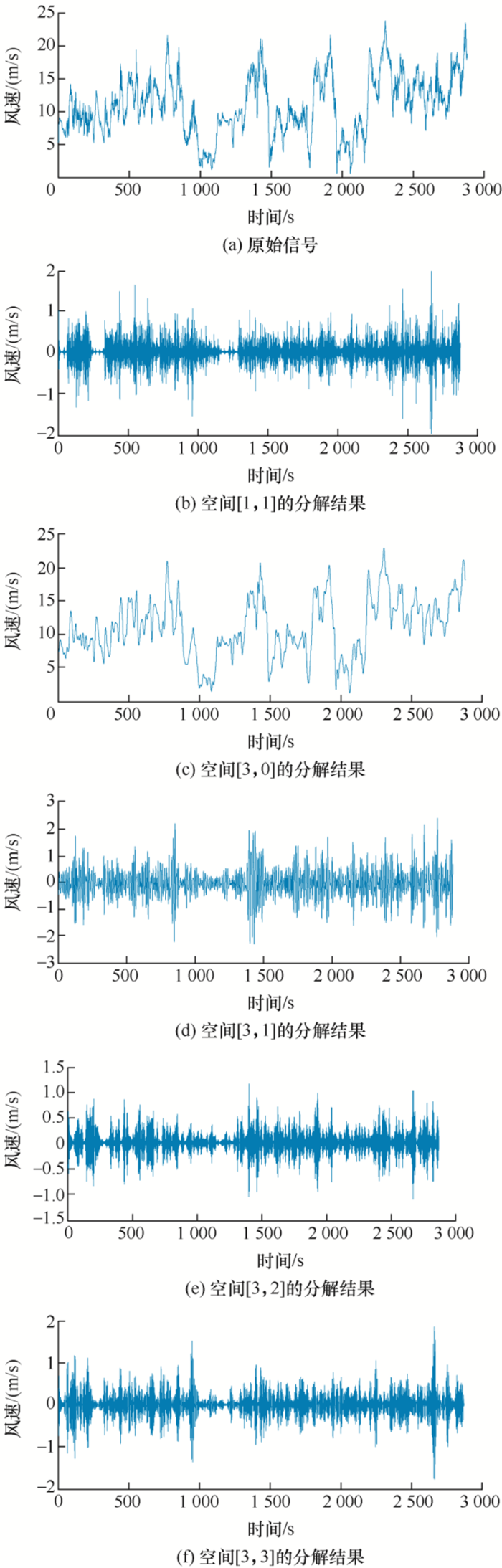
首先,对子集1的2 880个原始风速样本数据进行小波包分解,并给出最优小波包分解树,如 图4所示。其中空间[1,1]、[3,0]、[3,1]、[3,2]、[3,3]分别对应一种频段。经小波包分解和重构后,波形如图5所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4   风速数据最优小波包分解树


图5

新窗口打开| 下载原图ZIP| 生成PPT

图5   不同频段下的风速波形


5.2 基于回声状态网的风电功率预测

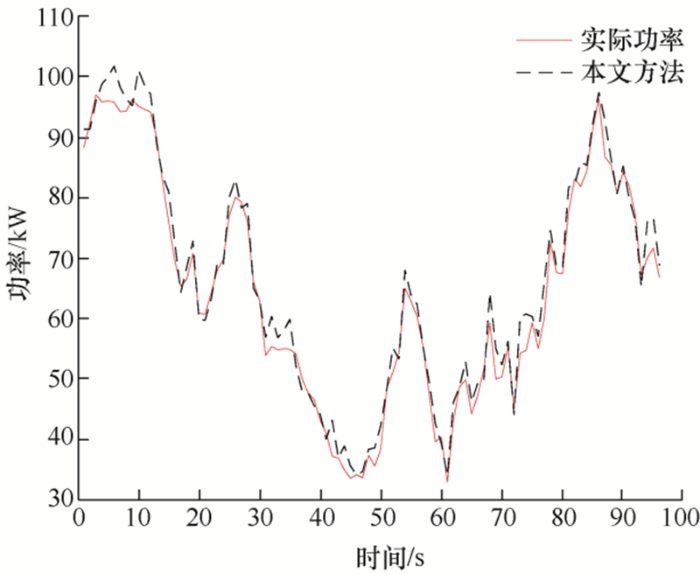
应用小波包-回声状态网方法进行风电功率预测,为了说明本文方法的有效性,将预测值与实测值对比,如图6所示。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6   本文方法与实际功率对比图


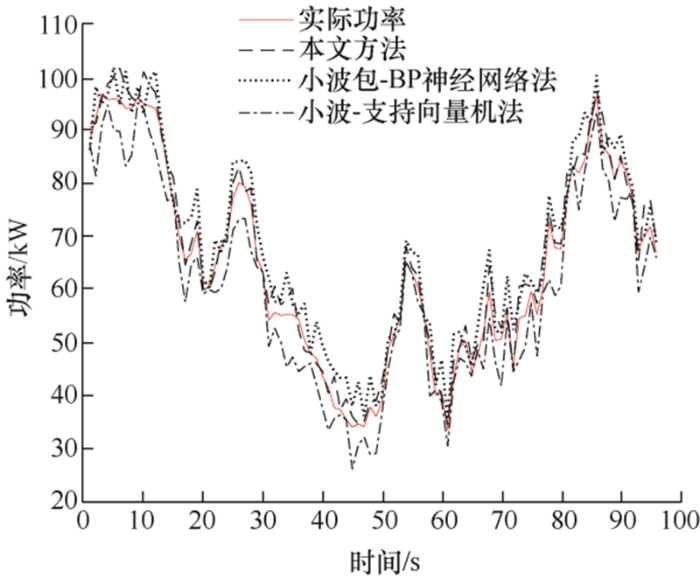
从图6中可以看出,采用本文方法获得的功率预测结果与实际功率较为接近,可以达到较好的预测效果,为了进一步说明本文方法的优越性,分别采用小波包-BP神经网络模型、小波-支持向量机模型以及本文模型进行功率预测,并与实测数据进行对比,如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7   不同预测模型预测结果对比图


从图7中可以看出几种功率预测方法与实际的功率趋势大致相同,本文方法与实际功率更为接近;为了进一步分析本文方法的有效性、预测的准确性以及计算效率,下面对以上三种方法进行误差分析和运行时间对比。选定平均绝对误差(MAE)、均方根误差(RMSE)、平均误差(ME)为预测模型准确性的评价指标,具体计算公式如下所示[20,21],误差结果对比如表1所示;运行时间对比如表2所示。

$MAE = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {{{\tilde P}_i} - {P_i}} \right|}$
$RMSE = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{{\tilde P}_i} - {P_i}} \right)}^2}} }$
$ME = \frac{1}{N}\sum\limits_{i = 1}^N {\left( {{P_i} - {{\tilde P}_i}} \right)}$

表1   不同预测方法的误差分析对比

预测方法MAE/kWRMSE/kWME/kW
小波包-ESM2.312.881.73
小波包-BP
神经网络		3.864.673.57
小波-支持
向量机		4.495.454.38

新窗口打开| 下载CSV


表2   不同预测方法的运行时间对比

预测方法小波包-ESM小波包-BP神经网络小波-支持
向量机
运行时间t/s1.706.163.87

新窗口打开| 下载CSV


式中,${\tilde P_i}$为风电输出功率的预测值,${P_i}$为风电输出功率的实际值,N为样本数量。

从表1中可知,本文方法获得的平均误差、平均绝对误差和均方根误差较小,说明本文方法预测精度略高于小波包-BP神经网络法和小波-支持向量机法,能够正确地反映实际的风电功率;从表2中可以看出,回声状态网络在训练时仅需要确定隐含层到输出层的连接权重,网络结构和其他连接权重保持不变,与神经网络方法、支持向量机方法相比,大大减少了运行时间,提高了计算效率。

6 结论

为了提高风电功率的预测准确性,本文提出一种基于小波包分解和回声状态网的风电功率短期预测模型,最终可得到如下结论。

(1) 小波包分解克服了小波分解高频部分存在的时频率分辨率低和时间分辨率高的问题;采用小波包对风电场数值天气预报数据和输出功率数据进行分解和重构,提升了样本数据的质量,提高了预测准确性;

(2) 利用回声状态网络的简单、稳定性高、效率高等优势,通过回升状态网络对分解后的各个频段的分量建立预测模型;并将本文方法与小波-BP神经网络预测方法、小波-PSO预测方法以及小波-支持向量机预测方法进行了误差对比分析,说明了文中方法的预测精度较高,可以有效预测风电功率。

参考文献

钱政, 裴岩, 曹利宵, 等.

风电功率预测方法综述

[J]. 高电压技术, 2016, 42(4):1047-1060.

[本文引用: 1]

QIAN Zheng, PEI Yan, CAO Lixiao, et al.

Review of wind power forecasting method

[J]. High Voltage Engineering, 2016, 42(4):1047-1060.

[本文引用: 1]

AHMED A, KHALID M.

A review on the selected applications of forecasting models in renewable power systems

[J]. Renewable and Sustainable Energy Reviews, 2019(100):9-21.

[本文引用: 2]

YANG Bo, ZHONG Linen, WANG Jingbo, et al.

State-of-the-art one-stop handbook on wind forecasting technologies:An overview of classifications,methodologies,and analysis

[J]. Journal of Cleaner Production, 2021(283):124628.

[本文引用: 2]

KARINIOTAKIS G N, STAVRAKAKIS G S, NOGARET E F.

Wind power forecasting using advanced neural networks models

[J]. IEEE Transactions on Energy Conversion, 1996, 11(4):762-767.

DOI:10.1109/60.556376      URL     [本文引用: 1]

王丽婕, 厉虹, 方市彬.

基于人工鱼群优化算法的支持向量机短期风电功率预测模型

[J]. 电气工程学报, 2016, 11(10):7-12.

[本文引用: 1]

WANG Lijie, LI Hong, FANG Shibin.

A short-term wind electric power prediction model of support vector machine based on artificial fish population optimization algorithm

[J]. Journal of Electrical Engineering, 2016, 11(10):7-12.

[本文引用: 1]

MOHANDES M A, HALAWAN T O, REHMAN S, et al.

Support vector machines for wind speed prediction

[J]. Renewable Energy, 2004, 29(6):939-947.

DOI:10.1016/j.renene.2003.11.009      URL     [本文引用: 1]

FOLEY A M, LEAHY P G, MARVUGLIA A, et al.

Current methods and advances in forecasting of wind power generation

[J]. Renewable Energy, 2012, 37(1):1-8.

DOI:10.1016/j.renene.2011.05.033      URL     [本文引用: 1]

LOUKA P, GALANIS G, SIEBERT N, et al.

Improvements in wind speed forecasts for wind power prediction purposes using Kalman filtering

[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2008, 96(12):2348-2362.

[本文引用: 2]

INGRID D. 小波十讲[M]. 北京: 国防工业出版社, 2004.

[本文引用: 1]

INGRID D. Ten lectures on wavelets[M]. Beijing: National Defense Industry Press, 2004.

[本文引用: 1]

韩晓娟, 陈跃燕, 张浩, 等.

基于小波包分解的混合储能技术在平抑风电场功率波动中的应用

[J]. 中国电机工程学报, 2013, 33(19):8-13.

[本文引用: 1]

HAN Xiaojuan, CHEN Yueyan, ZHANG Hao, et al.

Application of hybrid energy storage technology based on wavelet packet decomposition in smoothing the fluctuation of wind power

[J]. Proceedings of the CSEE, 2013, 33(19):8-13.

[本文引用: 1]

RUIZ-AGUILAR J J, TURIAS I, GONZALEZ-ENRIQ UE J, et al.

A permutation entropy-based EMD-ANN forecasting ensemble approach for wind speed prediction

[J]. Neural Computing and Applications, 2021, 33(7):2369-2391.

DOI:10.1007/s00521-020-05141-w      URL     [本文引用: 1]

LIU Hui, TIAN Hongqi, LI Yanfei.

Comparison of new hybrid FEEMD-MLP,FEEMD-ANFIS,wavelet packet-MLP and wavelet packet-ANFIS for wind speed predictions

[J]. Energy Conversion and Management, 2015, 89,1-11.

DOI:10.1016/j.enconman.2014.09.060      URL     [本文引用: 1]

马晓博.

基于小波变换和BP神经网络的短期风电功率预测

[J]. 电力科学与技术学报, 2015, 30(2):92-97.

[本文引用: 1]

MA Xiaobo.

Short-term wind power prediction based on wavelet analysis and BP neural network

[J]. Journal of Electric Power Science and Technology, 2015, 30(2):92-97.

[本文引用: 1]

肖迁, 李文华, 李志刚, 等.

基于改进的小波-BP神经网络的风速和风电功率预测

[J]. 电力系统保护与控制, 2014, 42(15):80-86.

[本文引用: 1]

XIAO Qian, LI Wenhua, LI Zhigang, et al.

Wind speed and power prediction based on improved wavelet-BP neural network

[J]. Power System Protection and Control, 2014, 42(15):80-86.

[本文引用: 1]

叶小岭, 刘波, 邓华, 等.

基于小波分析和PSO优化神经网络的短期风电功率预测

[J]. 可再生能源, 2014, 32(10):1486-1492.

[本文引用: 1]

YE Xiaoling, LIU Bo, DENG Hua, et al.

Short-term wind power prediction based on wavelet analysis and PSO optimized neural network

[J]. Renewable Energy Resources, 2014, 32(10):1486-1492.

[本文引用: 1]

叶瑞丽, 郭志忠, 刘瑞叶, 等.

基于小波包分解和改进Elman神经网络的风电场风速和风电功率预测

[J]. 电工技术学报, 2017, 32(21):103-111.

[本文引用: 1]

YE Ruili, GUO Zhizhong, LIU Ruiye, et al.

Wind speed and wind power forecasting method based on wavelet packet decomposition and improved Elman neural network

[J]. Transactions of China Electrotechnical Society, 2017, 32(21):103-111.

[本文引用: 1]

曹青.

并网型光伏发电短期功率预测与优化配置研究

[D]. 合肥:安徽工程大学, 2019.

[本文引用: 1]

CAO Qing.

Study on short-term power prediction and optimal configuration of grid-connected photovoltaic power generation

[D]. Hefei:Anhui Polytechnic University, 2019.

[本文引用: 1]

杨德全.

基于神经网络的光伏发电系统发电功率预测

[D]. 北京:华北电力大学, 2014.

[本文引用: 2]

YANG Dequan.

Generation forecasting for photovoltaic system based on artificial neural networks

[D]. Beijing:North China Electric Power University, 2014.

[本文引用: 2]

LIU H, TIAN H Q, LI Y F.

Four wind speed multi-step forecasting models using extreme learning machines and signal decomposing algorithms

[J]. Energy Conversion & Management, 2015, 100(16):16-22.

[本文引用: 1]

杨茂, 杨宇.

基于小波包与LSSVM的短期光伏输出功率预测研究

[J]. 可再生能源, 2019, 37(11):1595-1602.

[本文引用: 2]

YANG Mao, YANG Yu.

Short-term photovoltaic output power prediction based on wavelet packet and LSSVM

[J]. Renewable Energy Resources, 2019, 37(11):1595-1602.

[本文引用: 2]

JAEGER H.

The “Echo State” approach to analyze and training recurrent neural networks

[R]. Technical Report 148,GMD-Frauhofer Institute for Autonomous Intelligent Systems, 2001.

[本文引用: 2]

/

〈 〉