1 引言
低速大转矩永磁同步电机具有损耗小、功率密度大、动态性能好等优点[1 ,2 ,3 ] ,但也存在永磁材料用料多、空间利用率低的问题,而本文介绍的永磁/磁阻复合转子双定子同步电机由于存在磁阻侧提供磁阻转矩,可以提高电机的内部空间利用率,进而可以节省永磁材料的使用。本文针对的电机常用于煤矿运输行业,工况复杂,电机运行过程中不允许存在较大的转速超调,且负载突变是影响电机转速超调的重要因素,如果不能对负载扰动进行抑制,会严重影响电机在复杂工况下的性能。
目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] 。这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] 。比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] 。基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整。基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] 。
本文针对永磁/磁阻复合转子双定子同步电机设计一种新型滑模变结构速度控制器和一种新型的负载扰动观测器,将负载扰动观测器的扰动转矩与新型滑模观测器输出的电磁转矩信号叠加在一起,构成一种新型的复合滑模控制器对速度调节,解决传统PI调节器算法参考转矩电流信号估算不准确、存在积分饱和的问题。
2 新型永磁/磁阻复合转子双定子同步电机的转矩解耦控制
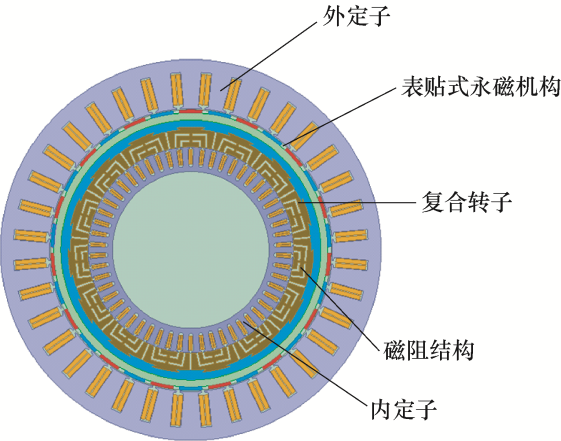
新型永磁/磁阻复合转子双定子同步电机采用双定子单转子结构,转子外侧采用表贴式永磁结构,转子内侧采用磁阻结构,内外结构用隔磁环隔开,当电机运行时,转子外侧结构通过表面装有的永磁体以产生电磁转矩,而转子内侧结构通过d 、q 轴磁阻存在差异,扭曲磁力线以产生磁阻转矩,电机的结构如图1 所示。
图1
永磁/磁阻复合转子双定子同步电机设计时,内外电机的电磁功率配比为1∶4,由式(1)可得电磁功率配比即为内外电机电磁转矩比。
(1) ${{P}_{\text{e}}}={{T}_{\text{e}}}n$
式中,P e 为电机的电磁功率;T e 为电机的电磁转矩;n 为电机转速。
(2) $\frac{{{P}_{\text{e}1}}}{{{P}_{\text{e}2}}}=\frac{{{T}_{\text{e}1}}}{{{T}_{\text{e}2}}}=\frac{1}{4}$
由于内电机采用最大转矩电流比控制方法,即i d =i q 。内电机的磁阻转矩方程可以写成式(3)的形式
(3) ${{T}_{\text{e}1}}={{p}_{1}}({{L}_{\text{d}1}}-{{L}_{\text{q}1}}){{i}_{\text{q}1}}^{2}$
式中,p 1 为内电机结构的极对数;L d1 、L q1 分别为内电机的d、q 轴电感;i q1 为内电机的q 轴电流。
外电机采用i d =0控制方式,外电机的电磁转矩方程如式(4)所示
(4) ${{T}_{\text{e}2}}={{p}_{2}}{{\psi }_{f}}{{i}_{\text{q}2}}$
式中,p 2 为外电机的极对数;L q2 为外电机的q 轴电感;ψf 为外转子生成的转子磁链;i q2 为外电机的q 轴电流。
(5) $\frac{{{T}_{\text{e}1}}}{{{T}_{\text{e}2}}}=\frac{{{p}_{1}}({{L}_{\text{d1}}}-{{L}_{\text{q1}}})i_{\text{q}1}^{2}}{{{p}_{2}}{{\psi }_{f}}{{i}_{\text{q}2}}}=\frac{1}{4}$
理想状态下,ψf 、L d1 、L q1 、L q2 不随温度改变而变化,设$i_{\text{q}}^{*}$为转矩电流给定值,引入K Te1 和K Te2 作为电机的转矩解耦系数,推导可得
(6) $\frac{{{T}_{\text{e}1}}}{{{T}_{\text{e}2}}}=\frac{{{K}_{\text{Te}1}}{{p}_{1}}({{L}_{\text{d}1}}-{{L}_{\text{q}1}})i_{\text{q}}^{*2}}{{{K}_{\text{Te}2}}{{p}_{2}}{{\psi }_{f}}i_{\text{q}}^{*}}=\frac{1}{4}$
(7) ${{K}_{\text{Te}1}}+{{K}_{\text{Te}2}}=1$
(8) $\frac{{{p}_{1}}({{L}_{\text{d}1}}-{{L}_{\text{q}1}}){{K}_{\text{Te}1}}}{{{p}_{1}}{{\psi }_{f}}(1-{{K}_{\text{Te}1}})}i_{\text{q}}^{*}=\frac{1}{4}$
(9) ${{K}_{\text{Te}1}}=\frac{\frac{1}{4}\frac{{{p}_{2}}{{\psi }_{f}}}{{{p}_{1}}({{L}_{\text{d}1}}-{{L}_{\text{d}2}})}}{\frac{1}{4}\frac{{{p}_{2}}{{\psi }_{f}}}{{{p}_{1}}({{L}_{\text{d}1}}-{{L}_{\text{d}2}})}+i_{\text{q}}^{*}}$
(10) ${{K}_{\text{Te}2}}=1-{{K}_{\text{Te}1}}$
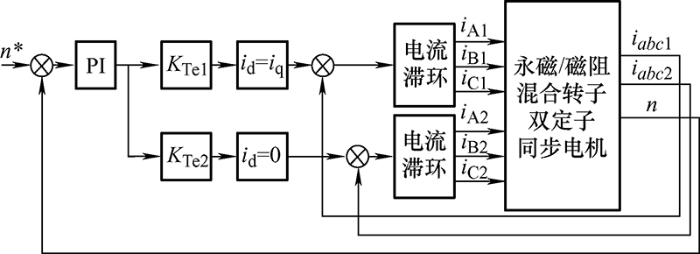
通过K Te1 和K Te2 将内外电机的转矩电流进行解耦,内外电机的参考转矩电流分别作为两套变频器的参考输入,经过两个变频器得到i A1 、i B1 、i C1 和i A2 、i B2 、i C2 ,并将两组三相电流输入到内外电机,实现内外电机的转矩解耦控制[16 ] 。其控制框图如图2 所示。
图2
3 复合滑模速度控制器的设计
(11) $J\frac{\text{d}\Omega }{\text{d}t}=\frac{3}{2}{{p}_{1}}({{L}_{\text{d}1}}-{{L}_{\text{q}1}}){{i}_{\text{d}1}}{{i}_{\text{q}1}}+\frac{3}{2}{{p}_{2}}{{\psi }_{f}}{{i}_{\text{q}1}}-{{T}_{\text{L}}}$
式中,J 为复合转子的转动惯量;T L 为电机的负载转矩;Ω 为电机机械角速度。
(12) $\left\{ \begin{matrix} {{x}_{1}}={{\Omega }^{*}}-\Omega \\ {{x}_{2}}={{{\dot{x}}}_{1}}=-\dot{\Omega } \\ \end{matrix} \right.$
(13) $\left\{ \begin{matrix} {{{\dot{x}}}_{1}}={{x}_{2}}=\frac{1}{J}({{T}_{\text{L}}}-\frac{3{{p}_{1}}({{L}_{\text{d}1}}-{{L}_{\text{q}1}}){{i}_{\text{d}1}}{{i}_{\text{q}1}}}{2}-\frac{3{{p}_{2}}{{\psi }_{f}}{{i}_{\text{q}2}}}{2} \\ {{{\dot{x}}}_{2}}=-\ddot{\Omega }=-\frac{3{{p}_{1}}({{L}_{\text{d}1}}-{{L}_{\text{q}1}}){{i}_{\text{d}1}}{{i}_{\text{q}1}}}{2J}-\frac{3{{p}_{2}}{{\psi }_{f}}{{i}_{\text{q}2}}}{2J}\ \ \ \ \ \ \\ \end{matrix} \right.$
由于磁阻电机采用i d =i q 控制方法,即i d1 =i q1 ,可重写上述方程
(14) $\left\{ \begin{matrix} {{{\dot{x}}}_{1}}={{x}_{2}}=\frac{1}{J}({{T}_{\text{L}}}-\frac{3{{p}_{1}}({{L}_{\text{d}1}}-{{L}_{\text{q}1}})i_{\text{q}1}^{2}}{2}-\frac{3{{p}_{2}}{{\psi }_{f}}{{i}_{\text{q}2}}}{2} \\ {{{\dot{x}}}_{2}}=-\ddot{\Omega }=-\frac{3{{p}_{1}}({{L}_{\text{d}1}}-{{L}_{\text{q}1}})i_{\text{q}1}^{2}}{2J}-\frac{3{{p}_{2}}{{\psi }_{f}}{{i}_{\text{q}2}}}{2J}\ \ \ \ \ \ \\ \end{matrix} \right.$
(15) $\frac{{{T}_{\text{e}1}}}{{{T}_{\text{e}2}}}=\frac{{{p}_{1}}({{L}_{\text{d}1}}-{{L}_{\text{q}1}})i_{\text{q}1}^{2}}{{{p}_{2}}{{\psi }_{f}}{{i}_{\text{q}2}}}=\frac{1}{4}$
(16) $\frac{i_{\text{q}1}^{2}}{{{i}_{\text{q}2}}}=\frac{{{p}_{1}}{{\psi }_{f}}{{i}_{\text{q}2}}}{4{{p}_{1}}({{L}_{\text{d}1}}-{{L}_{\text{q}1}})}$
(17) $i_{\text{q}1}^{2}=\frac{{{p}_{2}}{{\psi }_{f}}}{4{{p}_{1}}({{L}_{\text{d}1}}-{{L}_{\text{q}1}})}\times {{i}_{\text{q}2}}$
(18) $\left[ \begin{matrix} {{{\dot{x}}}_{1}} \\ {{{\dot{x}}}_{2}} \\ \end{matrix} \right]=\left[ \begin{matrix} 0 & 1 \\ 0 & 0 \\ \end{matrix} \right]\left[ \begin{matrix} {{x}_{1}} \\ {{x}_{2}} \\ \end{matrix} \right]+\left[ \begin{matrix} 0 \\ -D \\ \end{matrix} \right]i{{_{q}^{*}}_{2}}$
(19) $D=\frac{3{{p}_{1}}\left( {{L}_{\text{d}1}}-{{L}_{\text{q1}}} \right)}{2J}\times \frac{{{p}_{2}}{{\varphi }_{f}}}{4{{p}_{1}}\left( {{L}_{\text{d}1}}-{{L}_{\text{q1}}} \right)}+\frac{3{{p}_{2}}{{\varphi }_{f}}}{2J}$
(20) $s=c{{x}_{1}}+{{x}_{2}}$
(21) $\dot{s}=c{{\dot{x}}_{1}}+{{\dot{x}}_{2}}=c{{x}_{2}}+{{\dot{x}}_{2}}=c{{x}_{2}}+Di_{\text{q2}}^{\text{*}}$
为保证电机具有较好的动态性能,采用指数趋近律,为防止开关函数引起的抖动,采用双曲正弦函数代替符号函数。
(22) $i_{\text{q}1}^{*}=\frac{1}{D}\int_{\ 0}^{\ t}{[c{{x}_{2}}+\varepsilon \tan sig(s)+qs]\text{d}\tau }$
根据$i_{q}^{*}=i_{q1}^{*}+i_{q2}^{*}$和式(17)可求出给定电流
(23) $i_{\text{q}}^{*}=\frac{5}{4}i_{\text{q}1}^{*}$
式(23)计算给定电流过程中,在计算参考转矩电流时过于理想化,在实际过程中计算的参考转矩电流并不是很精确,内外电机电流控制器转矩电流参考值比值会在式(17)的计算结果上下波动,导致$i_{\text{q}1}^{*}$计算结果不精确,间接导致$i_{\text{q}}^{*}$的计算结果也会有误差,在起动过程中会造成一定的转速超调,在负载扰动时也会对转速有一定的影响,因此采用负载扰动观测器作为反馈调节,构成复合滑模结构,将多余的转矩电流量看成外部转矩扰动信号,对滑模速度控制器输出的转矩信号进行调节再转换成参考转矩电流。从而达到更快更精确的起动,转速的超调也会更小。
根据传统的龙伯格观测器原理,电机的运动方程可以写为
(24) $\left\{ \begin{align} & \frac{\text{d}\overset{\wedge }{\mathop{\Omega }}\,}{\text{d}t}=-\frac{B}{J}\Omega -\frac{1}{J}\overset{\wedge }{\mathop{{{T}_{\text{L}}}}}\,+\frac{1}{J}{{T}_{\text{e}1}}+\frac{1}{J}{{T}_{\text{e}2}}+\frac{{{K}_{1}}}{J}(\Omega -\overset{\wedge }{\mathop{\Omega }}\,) \\ & \frac{\text{d}\overset{\wedge }{\mathop{{{T}_{\text{L}}}}}\,}{\text{d}t}={{K}_{2}}(\Omega -\overset{\wedge }{\mathop{\Omega }}\,)+{{K}_{3}}\frac{\text{d(}\Omega -\overset{\wedge }{\mathop{\Omega }}\,)}{\text{d}t} \\ \end{align} \right.$
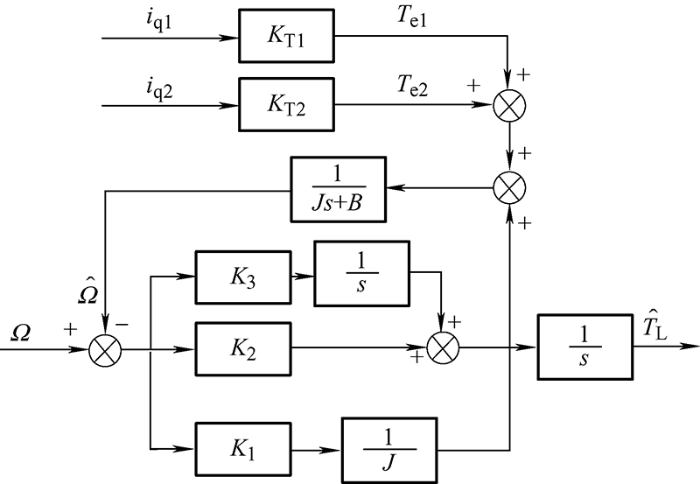
将电机转矩电流i q1 和i q2 作为观测器的输入变量,以转子转速Ω 作为观测器的输出变量,将观测转速$\overset{\wedge }{\mathop{\Omega }}\,$、扰动转矩$\overset{\wedge }{\mathop{{{T}_{\text{L}}}}}\,$作为观测器的状态变量,构成降阶的龙伯格观测器,其控制框图如图3 所示。
图3
本文根据降阶龙伯格观测器与内模控制原理,对负载扰动观测器进行设计。传统的龙伯格观测器对扰动转矩$\overset{\wedge }{\mathop{{{T}_{\text{L}}}}}\,$的输出,采用比例形式输出,为抑制扰动转矩输出存在阶跃响应,采用比例积分的形式输出,可以削弱负载转矩突变对电机转速的影响。
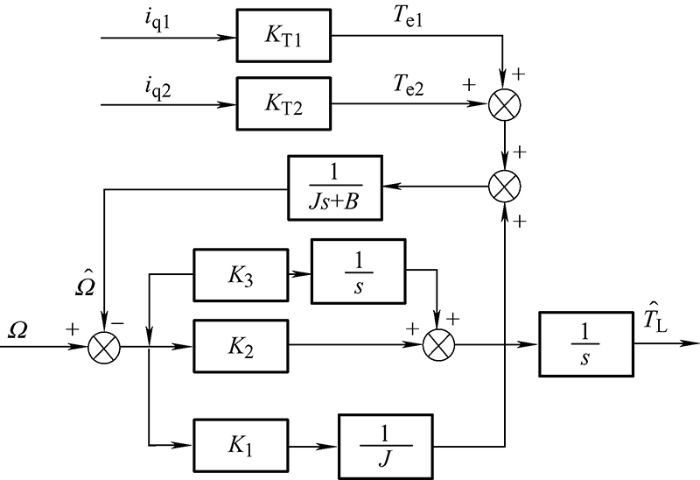
本文提出一种基于内模原理的负载扰动观测器状态方程如式(25)所示
(25) $\left\{ \begin{align} & \frac{\text{d}\overset{\wedge }{\mathop{\Omega }}\,}{\text{d}t}=-\frac{B}{J}\Omega -\frac{1}{J}\overset{\wedge }{\mathop{{{T}_{\text{L}}}}}\,+\frac{1}{J}{{T}_{\text{e}1}}+\frac{1}{J}{{T}_{\text{e}2}}+\frac{{{K}_{1}}}{J}(\Omega -\overset{\wedge }{\mathop{\Omega }}\,) \\ & \frac{\text{d}\overset{\wedge }{\mathop{{{T}_{\text{L}}}}}\,}{\text{d}t}={{K}_{2}}(\Omega -\overset{\wedge }{\mathop{\Omega }}\,)+{{K}_{3}}\frac{\text{d(}\Omega -\overset{\wedge }{\mathop{\Omega }}\,)}{\text{d}t} \\ \end{align} \right.$
图4
负载扰动观测器与滑模控制器构成一种复合结构,将负载扰动观测器的扰动转矩信号与滑模观测器输出的电磁转矩信号叠加在一起,输出较为精确的电磁转矩输出量,再通过计算得到较为精确的参考转矩电流。这种方法不但在起动过程中响应速度加快,超调减小,系统稳态时间短,而且在负载突变时也可以达到较为理想的效果。
4 仿真结果分析
利用Matlab/Simulink仿真平台搭建永磁/磁阻复合转子双定子同步电机转矩解耦控制系统,并在此基础上搭建上述设计的复合滑模速度控制策略和传统的PI速度控制策略,验证本文提出的复合滑模控制器的可行性和优越性。
永磁/磁阻复合转子双定子同步电机仿真参数:外定子绕组电阻R s1 = 1.833 Ω,外电机d 轴电感L d1 = 0.174 H,q 轴电感L q1 =0.174 H,永磁磁链ψf = 1.573 6 Wb,p 1 =15,内定子绕组电R s2 = 1.57 Ω,内电机d 轴电感L d2 = 0.268 H,q 轴电感L q2 = 0.026 5 H,p 2 =5,转子转动惯量12 kg•m2 。
搭建基于转矩解耦控制的传统PI速度控制策略和基于转矩解耦控制的复合滑模控制策略。设置电机的参考转速为90 r/min,起动时的负载转矩为3 500 N•m,在0.6 s突变负载为4 500 N•m,在1 s负载突变为4 000 N•m。
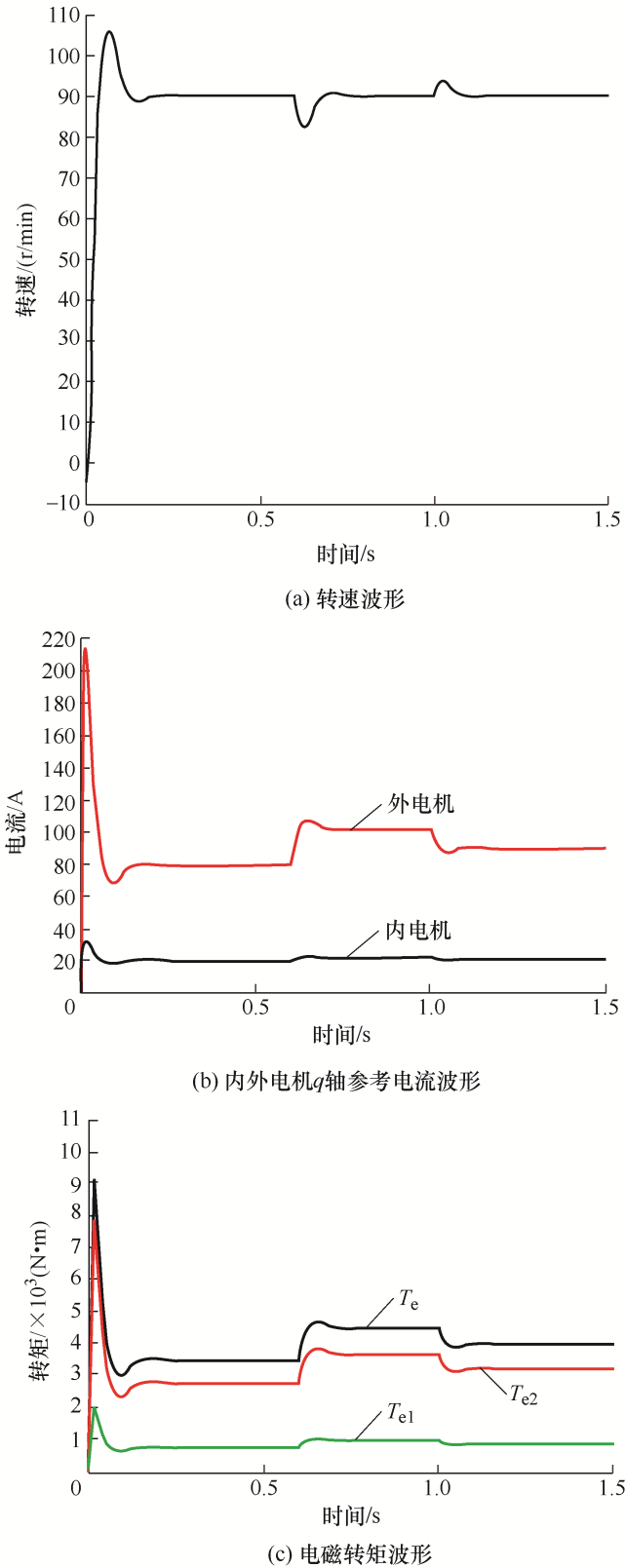
图5 为基于转矩解耦控制的传统PI速度控制策略的转速波形、参考电流波形及电磁转矩波形,速度环P 值为2,I 值为80。
图5
图5
基于转矩解耦控制的传统PI速度控制策略的仿真波形
由图5 可以看出,当负载为3 500 N•m时,内外电机转矩分配比约为2 800∶700,当负载为4 500 N•m时,内外电机转矩分配比约为3 600∶900,当负载为4 000 N•m时,内外电机转矩分配比约为 3 200∶800,验证了转矩解耦控制的正确性。在电机带3 500 N•m负载起动时,电机转速超调量约为15 r/min,系统稳态时间约为0.2 s,当负载从3 500 N•m突变到4 500 N•m的时候,转速超调约为8 r/min,当负载从4 500 N•m突变到4 000 N•m时,转速超调约为4 r/min,在负载突变的情况下,传统PI的速度受负载扰动的影响较大。
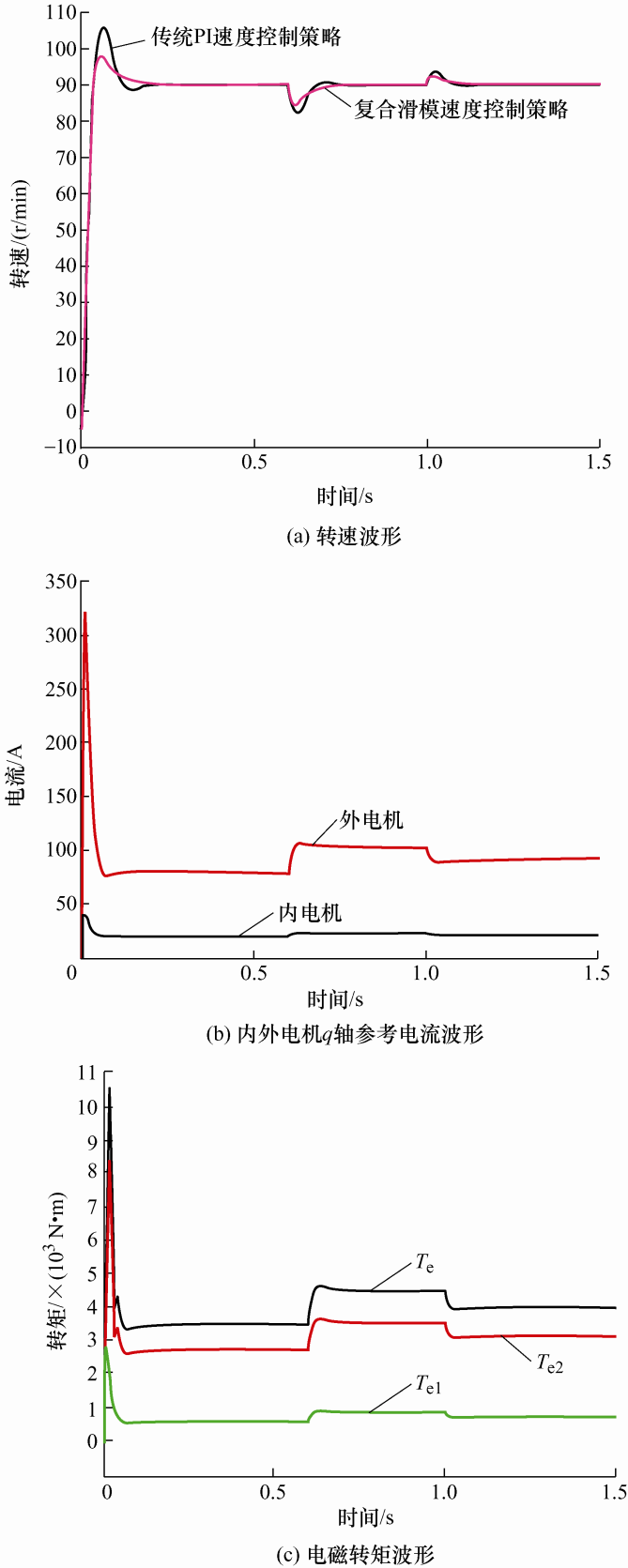
图6 为基于转矩解耦控制的复合滑模速度控制策略的转速波形及电磁转矩波形,滑模控制器参数c =20,ɛ =200,q =100,负载扰动观测器参数K 1 =14,K 2 = -0.000 1,K 3 = -0.08。
图6
图6
基于转矩解耦控制的复合滑模速度控制策略的仿真波形
由图6 可以看出,复合滑模速度控制策略在电机起动时,超调量、响应速度及趋于稳定的时间都有较大的优化,在电机带3 500 N•m负载起动时,电机转速超调量约为7 r/min时,系统稳定时间约为0.15 s,在电机起动时,复合滑模速度控制策略对转速超调有一定的抑制作用并且响应速度较传统PI速度控制器快。在负载突变时从3 500 N•m突变到4 500 N•m的时候,转速超调约为5 r/min,当负载从4 500 N•m突变到4 000 N•m时,转速超调约为2.5 r/min,在负载突变时,能够快速恢复且对电机转速超调有一定的抑制作用。
5 结论
(1) 本文针对永磁/磁阻复合转子双定子同步电机提出单速度环进行控制。
(2) 针对抗负载扰动提出改进,设计单个滑模速度控制器测算内外电机所需电流,针对电流计算存在误差,设计负载扰动观测器进行反馈调节,提高电流的计算精度。
通过q 轴电流的分配实现转矩解耦控制,从而达到内外电机的转矩分配控制。本文所提方法在电机起动过程中的响应速度较快,且超调量较小。当存在负载扰动时,能够减小转速超调,且能够快速跟踪给定转速。
参考文献
View Option
[1]
陈嘉龙 . 基于新型扰动观测器的永磁同步电机复合滑模控制
[D]. 镇江:江苏大学 , 2019 .
[本文引用: 2]
CHEN Jialong . Compound sliding mode control of permanent magnet synchronous motor based on a new type of disturbance observer
[D]. Zhenjiang:Jiangsu University , 2019 .
[本文引用: 2]
[2]
纪秉男 . 低速大转矩永磁同步电机速度控制策略研究
[D]. 天津:天津大学 , 2015 .
[本文引用: 2]
JI Bingnan . Research on the speed control strategy of low-speed and large-torque permanent magnet synchronous motors
[D]. Tianjin:Tianjin University , 2015 .
[本文引用: 2]
[3]
韩京清 . 从PID技术到“自抗扰控制”技术
[J]. 控制工程 , 2002 (3 ):13 -18 .
[本文引用: 2]
HAN Jingqing . From PID technology to“auto disturbance rejection control”technology
[J]. Control Engineering , 2002 (3 ):13 -18 .
[本文引用: 2]
[4]
杨雄 , 张凤阁 , 王秀平 . 轨道交通用初级永磁型直线电机电磁特性分析
[J]. 电气工程学报 , 2018 , 13 (5 ):1 -7 .
[本文引用: 1]
YANG Xiong ZHANG Fengge WANG Xiuping . Electromagnetic characteristics analysis of primary permanent magnet linear motor for rail transit
[J]. Journal of Electrical Engineering , 2018 , 13 (5 ):1 -7 .
[本文引用: 1]
[5]
冯桂宏 , 黄赫 , 刘祥炎 . 永磁同步电机直接转矩控制的研究与优化
[J]. 电气工程学报 , 2018 , 13 (9 ):1 -7 .
[本文引用: 1]
FENG Guihong HUANG He LIU Xiangyan . Research and improvement of permanent magnet synchronous motor direct torque control
[J]. Journal of Electrical Engineering , 2018 , 13 (9 ):1 -7 .
[本文引用: 1]
[6]
杨志豪 , 杨梦雪 , 王思诺 , 等 . 定子斜槽对永磁同步电动机性能的影响
[J]. 电气工程学报 , 2019 , 14 (3 ):97 -102 .
[本文引用: 1]
YANG Zhihao YANG Mengxue WANG Sinuo , et al . Effect of stator skewed slot on performance of permanent magnet synchronous motor
[J]. Journal of Electrical Engineering , 2019 , 14 (3 ):97 -102 .
[本文引用: 1]
[7]
陈垒 , 吴长江 , 鲍晓华 . 负载特性对不均匀气隙结构异步起动永磁同步电机退磁的影响
[J]. 电气工程学报 , 2018 , 13 (1 ):1 -8 .
[本文引用: 1]
CHEN Lei WU Changjiang BAO Xiaohua . Influence of load characteristics on the demagnetization of LSPMSM with non-uniform air gap structure
[J]. Journal of Electrical Engineering , 2018 , 13 (1 ):1 -8 .
[本文引用: 1]
[8]
胡土雄 , 胡弼 , 王伟 , 等 . 高密度永磁同步电机永磁体失磁特征量分析
[J]. 电气工程学报 , 2019 , 14 (2 ):121 -126 .
[本文引用: 1]
HU Tuxiong HU Bi WANG Wei , et al . Analysis of demagnetization characteristics of permanent magnets in high density permanent magnet synchronous motor
[J]. Journal of Electrical Engineering , 2019 , 14 (2 ):121 -126 .
[本文引用: 1]
[9]
张苏英 , 王跃龙 , 刘慧贤 , 等 . 基于新型趋近律的永磁同步电机滑模速度控制
[J]. 微特电机 , 2020 , 48 (4 ):50 -54,63 .
[本文引用: 1]
ZHANG Suying WANG Yuelong LIU Huixian , et al . Permanent magnet synchronous motor sliding mode speed control based on a new approaching law
[J]. Micro Special Motor , 2020 , 48 (4 ):50 -54,63 .
[本文引用: 1]
[10]
侯孝涵 , 杨兴华 , 杨喜军 , 等 . 基于新型趋近律的PMSM反馈线性化滑模控制
[J]. 微电机 , 2019 , 52 (12 ):45 -48 .
[本文引用: 1]
HOU Xiaohan YANG Xinghua YANG Xijun , et al . PMSM feedback linearization sliding mode control based on a new reaching law
[J]. Micromotor , 2019 , 52 (12 ):45 -48 .
[本文引用: 1]
[11]
韩凯伟 , 王艳 , 纪志成 . 一种直线感应电机的新型积分滑模控制器的设计与仿真
[J]. 系统仿真学报 , 2020 , 32 (11 ):2146 -2154 .
[本文引用: 1]
HAN Kaiwei WANG Yan JI Zhicheng . Design and simulation of a new integral sliding mode controller for linear induction motor
[J]. Journal of System Simulation , 2020 , 32 (11 ):2146 -2154 .
[本文引用: 1]
[12]
ZHANG Xiaoguang SUN Lizhi ZHAO Ke , et al . Nonlinear speed control for PMSM system using sliding-mode control and disturbance compensation technique
[J]. IEEE Transactions on Power Electronics , 2013 , 28 (3 ):1358 -1365 .
DOI:10.1109/TPEL.2012.2206610
URL
[本文引用: 1]
[13]
XIN Ping BAI Jing . SMC with disturbance observer for high performance PMSM
[C]// International Conference on Mechatronic Science,Electric Engineering and Computer,Jilin,China , 2011 :986 -989 .
[本文引用: 1]
[14]
李歌航 . 基于扰动观测器的永磁同步电机预测电流控制研究
[J]. 机电信息 , 2019 (3 ):30 -31 .
[本文引用: 1]
LI Gehang . Research on predictive current control of permanent magnet synchronous motor based on disturbance observer
[J]. Electromechanical Information , 2019 (3 ):30 -31 .
[本文引用: 1]
[15]
孙静 , 刘旭东 . 基于无差拍预测控制和扰动观测器的永磁同步电机电流控制
[J]. 电机与控制应用 , 2017 , 44 (10 ):25 -29,35 .
[本文引用: 1]
SUN Jing LIU Xudong . Current control of permanent magnet synchronous motor based on deadbeat predictive control and disturbance observer
[J]. Motors and Control Applications , 2017 , 44 (10 ):25 -29,35 .
[本文引用: 1]
[16]
金石 , 刘金星 , 宋顺千 . 一种新型混合转子双定子同步电机的转矩解耦矢量控制
[J]. 大电机技术 , 2020 (1 ):1 -5 .
[本文引用: 1]
JIN Shi LIU Jinxing SONG Shunqian . Torque decoupling vector control of novel hybrid rotor double stator synchronous motor
[J]. Large Electric Machine and Hydraulic Turbine , 2020 (1 ):1 -5 .
[本文引用: 1]
基于新型扰动观测器的永磁同步电机复合滑模控制
2
2019
... 低速大转矩永磁同步电机具有损耗小、功率密度大、动态性能好等优点[1 ,2 ,3 ] ,但也存在永磁材料用料多、空间利用率低的问题,而本文介绍的永磁/磁阻复合转子双定子同步电机由于存在磁阻侧提供磁阻转矩,可以提高电机的内部空间利用率,进而可以节省永磁材料的使用.本文针对的电机常用于煤矿运输行业,工况复杂,电机运行过程中不允许存在较大的转速超调,且负载突变是影响电机转速超调的重要因素,如果不能对负载扰动进行抑制,会严重影响电机在复杂工况下的性能. ...
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
基于新型扰动观测器的永磁同步电机复合滑模控制
2
2019
... 低速大转矩永磁同步电机具有损耗小、功率密度大、动态性能好等优点[1 ,2 ,3 ] ,但也存在永磁材料用料多、空间利用率低的问题,而本文介绍的永磁/磁阻复合转子双定子同步电机由于存在磁阻侧提供磁阻转矩,可以提高电机的内部空间利用率,进而可以节省永磁材料的使用.本文针对的电机常用于煤矿运输行业,工况复杂,电机运行过程中不允许存在较大的转速超调,且负载突变是影响电机转速超调的重要因素,如果不能对负载扰动进行抑制,会严重影响电机在复杂工况下的性能. ...
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
低速大转矩永磁同步电机速度控制策略研究
2
2015
... 低速大转矩永磁同步电机具有损耗小、功率密度大、动态性能好等优点[1 ,2 ,3 ] ,但也存在永磁材料用料多、空间利用率低的问题,而本文介绍的永磁/磁阻复合转子双定子同步电机由于存在磁阻侧提供磁阻转矩,可以提高电机的内部空间利用率,进而可以节省永磁材料的使用.本文针对的电机常用于煤矿运输行业,工况复杂,电机运行过程中不允许存在较大的转速超调,且负载突变是影响电机转速超调的重要因素,如果不能对负载扰动进行抑制,会严重影响电机在复杂工况下的性能. ...
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
低速大转矩永磁同步电机速度控制策略研究
2
2015
... 低速大转矩永磁同步电机具有损耗小、功率密度大、动态性能好等优点[1 ,2 ,3 ] ,但也存在永磁材料用料多、空间利用率低的问题,而本文介绍的永磁/磁阻复合转子双定子同步电机由于存在磁阻侧提供磁阻转矩,可以提高电机的内部空间利用率,进而可以节省永磁材料的使用.本文针对的电机常用于煤矿运输行业,工况复杂,电机运行过程中不允许存在较大的转速超调,且负载突变是影响电机转速超调的重要因素,如果不能对负载扰动进行抑制,会严重影响电机在复杂工况下的性能. ...
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
从PID技术到“自抗扰控制”技术
2
2002
... 低速大转矩永磁同步电机具有损耗小、功率密度大、动态性能好等优点[1 ,2 ,3 ] ,但也存在永磁材料用料多、空间利用率低的问题,而本文介绍的永磁/磁阻复合转子双定子同步电机由于存在磁阻侧提供磁阻转矩,可以提高电机的内部空间利用率,进而可以节省永磁材料的使用.本文针对的电机常用于煤矿运输行业,工况复杂,电机运行过程中不允许存在较大的转速超调,且负载突变是影响电机转速超调的重要因素,如果不能对负载扰动进行抑制,会严重影响电机在复杂工况下的性能. ...
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
从PID技术到“自抗扰控制”技术
2
2002
... 低速大转矩永磁同步电机具有损耗小、功率密度大、动态性能好等优点[1 ,2 ,3 ] ,但也存在永磁材料用料多、空间利用率低的问题,而本文介绍的永磁/磁阻复合转子双定子同步电机由于存在磁阻侧提供磁阻转矩,可以提高电机的内部空间利用率,进而可以节省永磁材料的使用.本文针对的电机常用于煤矿运输行业,工况复杂,电机运行过程中不允许存在较大的转速超调,且负载突变是影响电机转速超调的重要因素,如果不能对负载扰动进行抑制,会严重影响电机在复杂工况下的性能. ...
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
轨道交通用初级永磁型直线电机电磁特性分析
1
2018
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
轨道交通用初级永磁型直线电机电磁特性分析
1
2018
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
永磁同步电机直接转矩控制的研究与优化
1
2018
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
永磁同步电机直接转矩控制的研究与优化
1
2018
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
定子斜槽对永磁同步电动机性能的影响
1
2019
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
定子斜槽对永磁同步电动机性能的影响
1
2019
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
负载特性对不均匀气隙结构异步起动永磁同步电机退磁的影响
1
2018
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
负载特性对不均匀气隙结构异步起动永磁同步电机退磁的影响
1
2018
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
高密度永磁同步电机永磁体失磁特征量分析
1
2019
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
高密度永磁同步电机永磁体失磁特征量分析
1
2019
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
基于新型趋近律的永磁同步电机滑模速度控制
1
2020
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
基于新型趋近律的永磁同步电机滑模速度控制
1
2020
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
基于新型趋近律的PMSM反馈线性化滑模控制
1
2019
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
基于新型趋近律的PMSM反馈线性化滑模控制
1
2019
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
一种直线感应电机的新型积分滑模控制器的设计与仿真
1
2020
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
一种直线感应电机的新型积分滑模控制器的设计与仿真
1
2020
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
Nonlinear speed control for PMSM system using sliding-mode control and disturbance compensation technique
1
2013
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
SMC with disturbance observer for high performance PMSM
1
2011
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
基于扰动观测器的永磁同步电机预测电流控制研究
1
2019
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
基于扰动观测器的永磁同步电机预测电流控制研究
1
2019
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
基于无差拍预测控制和扰动观测器的永磁同步电机电流控制
1
2017
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
基于无差拍预测控制和扰动观测器的永磁同步电机电流控制
1
2017
... 目前,国内外学者针对电机的调速系统进行了许多控制策略的研究[4 ,5 ,6 ,7 ,8 ] .这些控制策略大致分为三类:基于经典控制理论的控制策略、基于现代控制理论的控制策略以及基于智能控制理论的控制策略[1 ] .比例积分控制物理概念明晰且易于工程实现,但是在设计控制器参数时一般需要折中考虑跟随性能和抗扰性能,虽然能够满足大多数电机控制系统的要求,但在高性能控制系统应用时存在一定的局限 性[2 ] .基于智能控制理论的控制策略不依赖电机模型,当电机参数发生变化时,控制效果不会受到太大的影响,但智能控制算法较为繁琐,需要一定的计算时间,当负载转矩出现突变时,不能及时做出调整.基于现代控制理论的控制策略具有控制精度高、鲁棒性强且对转速超调的抑制效果较好等优点,例如:自抗扰控制[3 ] 、滑模变结构控制[9 ,10 ,11 ,12 ,13 ] 、电流预测控制[14 ,15 ] . ...
一种新型混合转子双定子同步电机的转矩解耦矢量控制
1
2020
... 通过K Te1 和K Te2 将内外电机的转矩电流进行解耦,内外电机的参考转矩电流分别作为两套变频器的参考输入,经过两个变频器得到i A1 、i B1 、i C1 和i A2 、i B2 、i C2 ,并将两组三相电流输入到内外电机,实现内外电机的转矩解耦控制[16 ] .其控制框图如图2 所示. ...
一种新型混合转子双定子同步电机的转矩解耦矢量控制
1
2020
... 通过K Te1 和K Te2 将内外电机的转矩电流进行解耦,内外电机的参考转矩电流分别作为两套变频器的参考输入,经过两个变频器得到i A1 、i B1 、i C1 和i A2 、i B2 、i C2 ,并将两组三相电流输入到内外电机,实现内外电机的转矩解耦控制[16 ] .其控制框图如图2 所示. ...