1 引言
随着我国能源互联网的建设和能源系统的转型,薄膜电容器因其微/纳秒级的充电速度,优异的耐压和柔韧性能在柔直输电工程、脉冲功率技术、电动汽车等领域发挥重要作用。发展高储能密度、低成本以及安全可靠的薄膜介质材料已成为国内外研究的热点[1,2]。聚丙烯由于其自身化学结构特点,具备优良的化学稳定性和电气绝缘性,作为热塑性树脂的代表,同时具有良好的可加工性,是薄膜电容器中常用的介质材料[3,4]。然而当介质实际运行在高压直流电场下时,电荷从电极注入介质内部并受电场力驱动输运和积累能量,当载流子能量达到阈值时引发击穿,造成材料永久性破坏。材料的击穿强度是影响介质薄膜电容器储能密度的一个关键参数,是制约储能技术发展的重要因素。因此开展对介电材料击穿强度的研究很有必要。
但是当电介质内部载流子输运与能量积累过程发生波动时,直流击穿强度分布如何变化,是否符合击穿威布尔分布,以及描述载流子输运过程的参数,例如迁移率、注入势垒、陷阱能级等对威布尔分布的作用规律尚不明确。本文分析了载流子输运和能量积累造成绝缘电介质击穿的物理过程,仿真研究了不同电荷输运随机变量波动时击穿强度的威布尔分布特性,得到了电荷输运参数方差与威布尔分布的关系,阐释了电荷输运随机变量通过调控载流子输运与能量积累改变击穿威布尔分布特性的作用机理。
2 电介质直流击穿过程
式中,Vappl为外施电压,V;kramp是升压速率,V· s-1。
图1
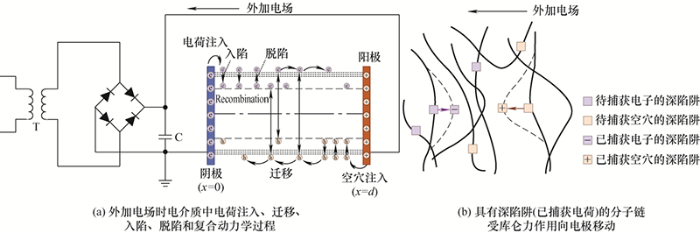
在外加电场作用下,电极通过肖特基热发射向介质内部注入电荷[14],场助热发射电荷对应的注入电流密度与温度、电场、注入势垒、试图逃逸频率等有关。
式中,jin(e)(t)和jin(h)(t)分别为阴极和阳极的注入电流密度,A·m-2;vATE为试图逃逸频率,s-1;NC和NV分别为导带和价带状态密度;F(0,t)和F(d,t)分别为阴极和阳极处电场;ϕin(e)和ϕin(h)分别为介质与阴极和阳极间的注入势垒,eV;kB为玻尔兹曼常数;f为电场下降系数,由库仑半径rc、电场强度F和温度T决定,表达式为f=eFrc/kBT,库仑半径rc公式为rc=e2/4πε0εrkBT,ε0εr是材料介电常数;参数$\psi $可被表示为$\psi $(f) =f-1+f-1/2 -f-1(1+2f1/2)1/2,$\psi $与电场强度F相关。
式中,jc(e)和jc(h)分别为电子和空穴传导电流密度,A·m-2;nf(e)和nf(h)分别为自由电子和自由空穴密度,m-3;μ0(e)和μ0(h)分别为电子和空穴的迁移率,m2·V-1·s-1。
根据能带理论,物理缺陷(例如构像不规则)会在介质导带或价带附近形成局域态能级,即浅陷阱;而化学缺陷(例如极性基团)会在费米能级附近形成局域态能级,即深陷阱[17]。迁移过程中的载流子会受到极性基团陷阱的强库仑力作用,当库仑力足够大时,载流子有概率被陷阱捕获,载流子能量转移到原子或分子上,造成能量耗散,有利于提高击穿强度。当陷阱中电荷能量超过陷阱势垒时,可通过热激发过程脱陷,继续在介质内部迁移;而当陷阱电荷能量不足以跃过陷阱势垒时,会形成稳定的空间电荷,使电场发生畸变,且介质内最大局部场强随着空间电荷的积聚而增强。介质中电子与空穴相遇时会发生复合,本模型假设存在三对电荷复合,即自由电子/自由空穴、自由电子/陷阱空穴和陷阱电子/自由空穴,且正负电荷复合会导致电荷湮灭,不产生第三类中性电荷。电荷遵守通量平衡方程组(即电荷守恒方程和泊松方程)[10, 18]。
电荷和电场关系满足泊松方程
式中,方程边界条件φ(0)=0 V,φ(d,t)=Vappl(t)。e为元电荷量,C。
式中,λ为分子链位移,m;μmol为分子链迁移率,m2·V-1·s-1;τmol为分子链弛豫时间常数,s,等于电荷在陷阱中的停留时间,与陷阱能级和温度等相关,即τmol=τ0exp(ET/kBT)。
介质中的载流子会在库仑力作用下分子链运动导致扩张的自由体积中被电场持续加速、能量积累,载流子能量取决于局部电场和局部自由体积长度,即w=eFλ,当载流子积累的能量超过一定阈值(陷阱能级)时,载流子会持续定向迁移并触发击穿,击穿引发方式有多种可能:载流子迁移在局部形成的大电流和大焦耳热可能引发局部放电导致击穿;高能载流子也可能发生剧烈碰撞电离产生大量电子从而引发雪崩击穿;此外,载流子也有概率碰撞介质分子造成化学键断裂进而发生击穿。
3 电荷输运参数的提取
根据以上对电介质直流击穿过程的分析,发现载流子输运和能量积累是导致电介质在外施电场作用下发生击穿的关键过程。从载流子输运和能量积累造成击穿的过程中可提炼出六个电荷输运特征参数:试图逃逸频率、电荷注入势垒、载流子迁移率、陷阱能级、陷阱密度和陷阱捕获概率。
在外施强电场作用下,电极与电介质界面上的电荷通过肖特基热发射越过注入势垒到达导带,为介质提供大量载流子,载流子受到电场力作用定向迁移形成电流。而试图逃逸频率降低或注入势垒提高会使得电极电荷不易越过势垒注入介质,从而减小了迁移载流子和电流密度,电阻率提高,同时,载流子密度减小也会降低介质体内空间电荷积聚量,使得空间电荷引起的电场畸变减弱,最终表现为击穿场强的提高。介质中载流子迁移率的降低会减小电流密度进而提高体电阻率,提升击穿性能。
陷阱能级、陷阱密度或陷阱捕获概率增大时可增强介质体内陷阱捕获效应,载流子定向迁移过程受到阻碍,介质内部载流子迁移率和局部电流密度降低,体电阻率升高;同时,电荷被陷阱捕获后积聚在电极附近形成同极性空间电荷,根据泊松方程,这大大削弱了电极/界面处的等效电场,电荷注入过程受到抑制,介质内空间电荷积聚和电场畸变减弱,击穿场强提高;此外,陷阱捕获电荷的过程中载流子能量耗散,电场畸变的减弱也会减慢载流子能量积累过程,有利于击穿性能的提升。三个因素共同作用使得增大陷阱能级、陷阱密度或陷阱捕获概率时直流击穿强度提升。
模型中电荷输运参数的变化会改变电荷输运和分子链位移与自由体积扩张特性,调控输载流子输运与能量积累过程并进而影响击穿强度。
4 基于CTMD模型的载流子输运与能量积累调制直流击穿威布尔分布仿真
4.1 仿真参数与数值方法
高斯分布是建模仿真中的常用模型,可以用来模拟电荷输运变量的波动行为。将提炼出的六个电荷输运参数设置成期望值(来源于聚丙烯的TSDC、介电谱、电位衰减等试验结果)如表1所示,服从高斯分布的50维向量作为随机变量,输运随机变量方差非零时可仿真载流子输运以及分子链位移和自由体积扩张过程的波动,进而调控载流子能量积累与耗散过程。基于CTMD模型通过Matlab采取高阶精度间断伽辽金法和有限元法数值求解自洽方程组式(1)~(7),可计算得到一组(50个)具有分散性的击穿强度。
表1 CTMD模型仿真中的参数设置
| 参数 | 期望值 |
|---|---|
| 温度T/℃ | 33 |
| 样品厚度d/mm | 100 |
| 升压速率kramp/(V/s) | 2 000 |
| 相对介电常数εr | 2.3(1 MHz) |
| 陷阱能级ET/eV | 0.86 |
| 陷阱密度NT/m-3 | 1.0×1021 |
| 陷阱捕获概率Ptr/s-1 | 0.085 |
| 试图逃逸频率vATE/s-1 | 1.727×108 |
| 注入势垒ϕin/eV | 0.86 |
| 载流子迁移率μ0/(m2·V-1·s-1) | 1.0×10-13 |
4.2 击穿过程的仿真结果与讨论
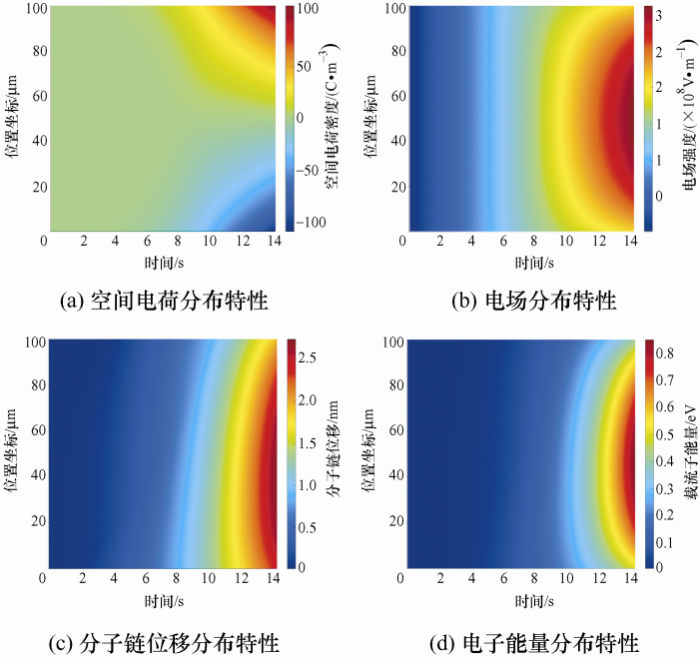
采用CTMD模型仿真载流子输运与能量积累过程,当各随机变量方差为0时得到从加压到击穿的过程中,介质电压在斜坡电压源作用下以设定斜率升高时,介质内部空间电荷、电场强度、分子链位移、载流子能量分布随加压时间的演变特性,如图2所示。
图2
在前6 s时间内,外加场强未达到电荷注入的临界电场,电荷注入不明显,而当6 s后,外加电场达到一定值,电荷注入量明显增多,注入电荷被陷阱捕获形成同极性空间电荷积聚在电极附近,载流子难以向介质内部迁移,如图2a所示,随着加压时间增加,电极附近空间电荷积聚量持续增大,电介质在6 s、10 s和14 s时阴极附近电荷空间电荷密度分别为-5.32 C·m-3、-37.49 C·m-3和-107.61 C·m-3,随着空间电荷分布逐渐向介质体内发展,在介质中部正、负电荷相遇并相互中和,此处空间电荷积聚较少,因此从电极附近向介质内部空间电荷积聚逐渐减少,14 s时阴极、介质中间和阳极处空间电荷密度分别为-107.61 C·m-3、-0.04 C·m-3和107.04 C·m-3。图2b为电场分布图,前6 s内,介质内部各处电场分布均匀,这是因为初始阶段无明显的空间电荷积聚使电场畸变[24],随着时间或外施电压增大,电场持续增大,6 s、10 s和14 s时介质体内最大电场分别为120.02 kV·mm-1、212.18 kV·mm-1和310.58 kV·mm-1。当外施电压较大时,发现电场分布明显畸变,从电极/介质边界到介质内部场强增大,这与空间电荷的积聚密切相关。根据泊松方程,电极附近的同极性空间电荷会建立反向电场(与外施电场反向)从而减小该处等效电场[7],相反介质内部电场在叠加空间电荷建立的同向电场作用后持续增强,14 s时阴极、介质中间和阳极处的电场强度分别为208.16 kV·mm-1、310.58 kV·mm-1和209.20 kV·mm-1。图2c为分子链位移分布图,当介质中陷阱捕获电荷时,与极性基团相连接的分子链因捕获电荷受到电场力作用而发生定向位移,根据分子链动力学公式(7),当只保留右边第一项,不考虑第二项分子链弛豫时间常数对分子链运动影响时,式(7)简化为dλ/dt=μmolF,若忽略空间电荷积聚导致的电场畸变效应,即F=krampt,并考虑初始条件λ(t=0)=0,可得λ=(krampμmol/2d)t2,分子链位移与时间的平方成正比,6 s、10 s和14 s时局部最大分子链位移分别为0.49 nm、1.33 nm和2.71 nm。若考虑电场畸变,从电极/介质边界到介质内部分子链位移逐渐增大,与电场分布规律一致,14 s时阴极、介质中间和阳极处的分子链位移分别为2.39 nm、2.68 nm和1.92 nm。图2d为载流子能量分布图,分子链的定向运动会扩张局部自由体积,假设自由体积长度等于分子链位移,载流子在扩张的自由体积中被电场持续加速、能量增大,其能量与局部电场和分子链位移有关,即w=eFλ,6 s、10 s和14 s时介质局部最大载流子能量积累分别为0.06 eV、0.27 eV和0.83 eV。且载流子能量分布不均,局部场强较大处载流子积聚能量更多,14 s时阴极、介质中间和阳极处的载流子能量积累分别为0.50 eV、0.83 eV和0.40 eV。12~14.1 s时间内(临近击穿),空间电荷积聚引发严重的电场畸变,介质内局部电场增强、局部自由体积扩张剧烈,导致此处载流子积累能量急剧增大,直至在14.1 s时载流子能量积累超过陷阱能级,载流子将在介质内部自由迁移不被陷阱捕获,局部电流密度和局部温度激增,同时运动过程中的载流子也可能碰撞高分子材料晶格而触发剧烈的碰撞电离或使得高分子化学键断裂,导致击穿。
4.3 威布尔分布的仿真结果与讨论
单独调节每个电荷输运随机变量的方差,得到一组击穿强度计算结果并用威布尔分布拟合。威布尔分布是一种基于弱点理论广泛应用于寿命诊断和可靠性分析的方法,双参数威布尔分布被广泛用于介质电击穿性能分析,其表达式为
式中,α为特征击穿强度(累计概率为63.2%),kV·mm-1;β为形状分布参数,表征击穿场强分散程度,β与分散程度成负相关。将一系列击穿电压从小到大排列,用i=1, 2, $\cdots $,n编号,Ross函数Pi=(i-0.44)/(n+0.25)表示第i个击穿电压对应概率;n为样品个数。
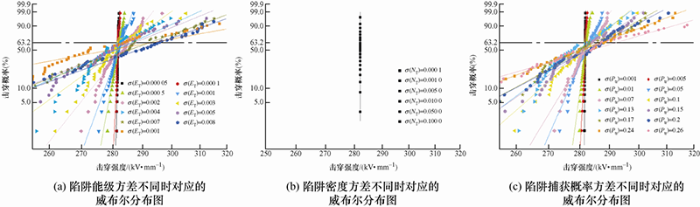
图3为与陷阱特性相关的三个电荷输运随机变量方差不同时得到的击穿强度计算结果威布尔分布图,σ为高斯分布标准差,图3a中当陷阱能级的σ分别为0.000 1、0.001、0.003、0.005和0.01时,威布尔形状分布参数分别为214.54、117.22、30.82、17.34和7.74。图3b中陷阱密度的σ从0.000 1递增到0.1,发现得到的击穿强度始终为定值,不符合威布尔分布。图3c中当陷阱捕获概率的σ分别为0.001、0.01、0.05、0.1、0.15、0.2、0.24、0.26时,形状分布参数分别为3 987.51、313.72、96.66、37.54、29.09、22.46、16.33、12.55。结果表明,基于本模型,陷阱能级或陷阱捕获概率为符合高斯分布的随机变量时,得到的击穿强度服从威布尔分布,且改变随机变量方差可调制威布尔分布特性,具体地,方差增大时击穿数据分散性增大,从而形状分布参数减小。而陷阱密度为符合高斯分布的随机变量时,得到的击穿强度一定,这是因为本模型中假设电荷捕获概率为定值0.085 s-1,肖特基电荷捕获模型认为捕获概率表达式为:Ptr=vScNT,其中v为电子运动速度、Sc为陷阱捕获面积,NT为陷阱密度[20, 25],陷阱密度的波动可改变捕获概率进而影响击穿强度,但本文模型未考虑陷阱密度对捕获概率的影响,导致击穿强度计算结果不具有分散性。
图3
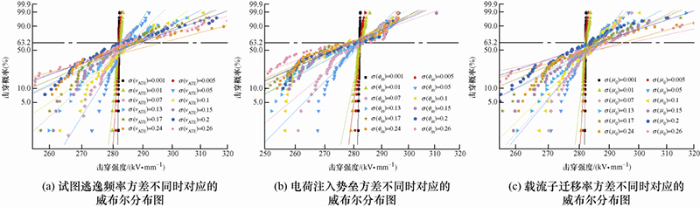
图4为试图逃逸频率、注入势垒和载流子迁移率三个电荷输运随机变量方差不同时得到的威布尔分布图,图4a中当试图逃逸频率的σ分别为0.001、0.01、0.05、0.1、0.15、0.17、0.2、0.26时,威布尔形状分布参数分别为2 896.81、391.90、68.85、28.45、19.85、17.99、15.36、13.89,图4b中当注入势垒的σ分别为0.001、0.01、0.05、0.1、0.15、0.2、0.24、0.26时,形状分布参数分别为1 698.01、193.75、39.77、23.50、18.60、17.09、16.95、13.96,图4c中当载流子迁移率的σ分别为0.001、0.01、0.05、0.1、0.15、0.17、0.2、0.26时,形状分布参数分别为3 779.03、372.30、50.85、42.07、21.05、17.84、14.21、9.22。结果表明,基于本模型,试图逃逸频率、注入势垒或载流子迁移率为符合高斯分布的随机变量时,得到的击穿强度服从威布尔分布,且形状分布参数随输运随机变量方差的增大而减小,改变随机变量方差可调制威布尔分布特性。
图4
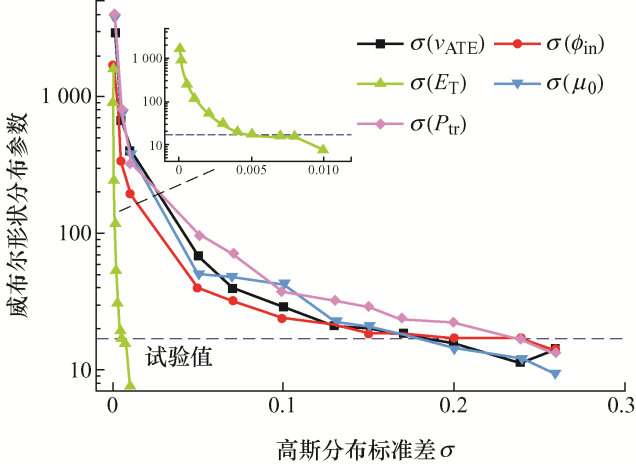
通过计算机控制电压击穿测试仪(HJC-100kV,华阳仪器有限公司,扬州,中国),使用直径25 mm的球球铜电极进行直流击穿试验(33 ℃),得到聚丙烯直流击穿威布尔分布的特征击穿强度为281.5 kV·mm-1,形状分布参数为17.0。根据图3和图4,本模型中陷阱能级、陷阱捕获概率、试图逃逸频率、注入势垒和迁移率五个电荷输运参数会引起威布尔分布变化,对比仿真结果与试验结果,建立威布尔形状分布参数与以上五个输运随机变量方差的关系,如图5所示。显然变化曲线呈现下降趋势,形状分布参数随着方差的增加而减小。这是因为输运随机变量方差的增大会增强载流子输运和能量积累过程的波动,提高击穿数据分散性,从而减小形状分布参数。
图5
对比各曲线变化趋势,发现形状分布参数随陷阱能级方差增大而减小的速率最快,说明威布尔分布对陷阱能级方差变化的敏感度最强,强于其他电荷输运参数。试图逃逸频率、迁移率、注入势垒和捕获概率四个参数的曲线下降趋势类似,在σ较小(0<σ<0.05)时,形状分布参数随着σ的增大而大幅下降,当σ增大到0.05时下降趋于平缓,几何效应参数逐渐趋向于试验值,当σ>0.26时,击穿数据分散性过大,在实际应用中不具有参考价值。
当威布尔形状分布参数与试验结果一致时,陷阱能级、试图逃逸频率、迁移率、注入势垒、捕获概率对应的-σ依次增大,分别为0.005、0.17、0.17、0.24、0.24。说明基于此模型,威布尔分布对陷阱能级的依赖性最强,对试图逃逸频率和迁移率的依赖性较弱,对注入势垒和陷阱捕获概率的依赖性最弱。
陷阱能级增大会增加电荷在陷阱中的弛豫时间,即τmol=τ0exp(ET/kBT),从而增强陷阱捕获效应,击穿强度提高。根据式(2)可得,试图逃逸频率或注入势垒都与电极注入电流有关,会影响击穿强度,但试图逃逸频率是注入电流密度的线性系数项,而注入势垒与1/kBT相乘后是注入电流密度的负指数项,这可能是二者对威布尔分布影响相异的原因。捕获概率为式(4)中Ptr,发现其对电荷脱陷入陷的影响受到系数1-qt/qeNT的作用,陷阱密度NT越大时,1-qt/qeNT越大,捕获概率波动对介质电荷输运和能量积累过程的影响越明显,对威布尔分布的调制作用越强。在本模型NT为1.0×1021 m-3的条件下,捕获概率对威布尔分布的影响比较弱。迁移率在电荷迁移和复合过程中作为前置系数对威布尔分布产生影响,见式(3)和式(5)。
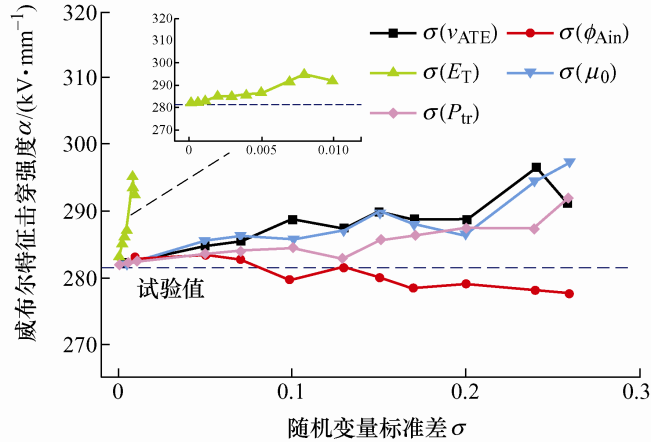
建立威布尔特征击穿强度与五个输运随机变量方差的关系,如图6所示。结果表明,随着方差的增大,特征击穿强度由于仿真数据的随机性而略有波动,但其最小值277.6 kV·mm-1、最大值297.2 kV·mm-1始终稳定在试验值281.5 kV·mm-1附近,误差小于5.6%。说明利用本模型进行直流威布尔仿真可以有效模拟击穿过程,得到较准确的特征击穿强度。
图6
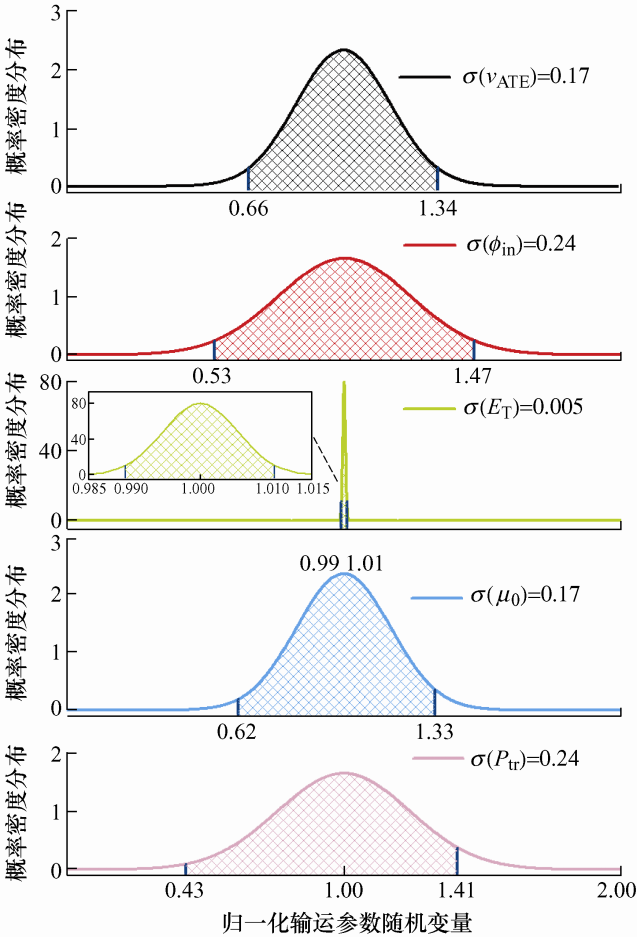
图7
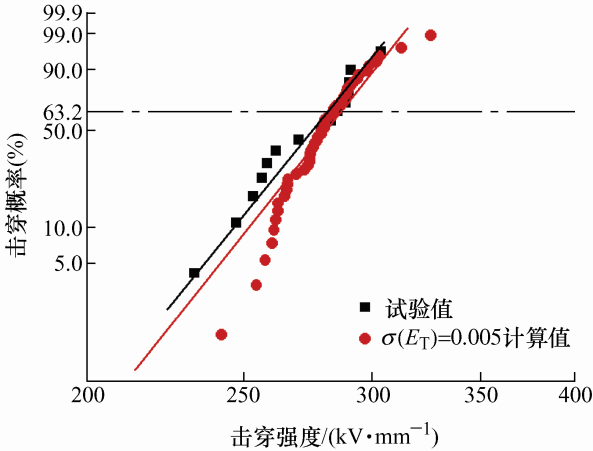
图8
5 结论
本文研究了电介质体内电荷输运随机变量通过调控载流子输运与能量积累改变击穿威布尔分布特性的作用机理,得到的主要结论如下。
(1) 阐释了电介质直流击穿机理,外施强电场作用下,电极/绝缘电介质界面注入的电荷在电场力驱动下输运并积累能量,形成泄漏电流,积聚空间电荷、畸变电场,最终导致绝缘电介质发生击穿。载流子输运与能量积累为造成电介质击穿的关键物理过程,从中提取出六个特征参数:电荷注入势垒、试图逃逸频率、载流子迁移率、陷阱能级、陷阱密度和陷阱捕获概率。
(2) 将六个电荷输运参数设置为符合高斯分布的随机变量时,可基于CTMD模型仿真载流子输运与能量积累过程中的波动,当电荷注入势垒、试图逃逸频率、载流子迁移率、陷阱能级和陷阱捕获概率方差非零时的击穿强度计算结果服从威布尔分布,陷阱密度在方差非零时得到的击穿强度计算结果为定值,不具有随机性,因为本模型未考虑陷阱密度变化对捕获概率的影响。建立了威布尔特征击穿强度与形状分布参数随不同电荷输运随机变量方差的变化关系,随着方差的增大,特征击穿强度基本稳定在试验值附近,形状分布参数由于击穿数据分散性增大而下降。
(3) 对比了各输运参数方差与威布尔分布的关系。陷阱能级、试图逃逸频率、载流子迁移率、注入势垒和陷阱捕获概率的方差分别为2.50×10-5、2.89×10-2、2.89×10-2、5.76×10-2、5.76×10-2时得到的威布尔形状分布参数与试验结果一致。说明威布尔分布对陷阱能级的依赖性较强,对试图逃逸频率和迁移率的依赖性较弱,对注入势垒和陷阱捕获概率的依赖性最弱。
参考文献
Review of polymer-based nanodielectric exploration and film scale-up for advanced capacitors
[J].DOI:10.1002/adfm.v30.18 URL [本文引用: 1]
Interfacial coupling effect in organic/inorganic nanocomposites with high energy density
[J].DOI:10.1002/adma.v30.17 URL [本文引用: 1]
Improvement of space charge suppression of polypropylene for potential application in HVDC cables
[J].DOI:10.1109/TDEI.2016.7556511 URL [本文引用: 1]
Thermoplastic isotactic polypropylene/ethylene-octene polyolefin copolymer nanocomposite for recyclable HVDC cable insulation
[J].DOI:10.1109/TDEI.2017.006208 URL [本文引用: 1]
Proposal of a multi-core model for polymer nanocomposite dielectrics
[J].DOI:10.1109/TDEI.2005.1511092 URL [本文引用: 1]
空间电荷在聚合物老化和击穿过程中的作用
[J].
The effect of space charge in polymer aging and breakdown
[J].
固体电介质空间电荷研究进展
[J].
Review of research on space charge in solid dielectrics
[J].
聚乙烯与聚丙烯中空间电荷注入特性的比较
[J].
Comparison of space charge injection behaviors between polythene and polypropylene
[J].
温度梯度效应对油纸绝缘材料空间电荷分布特性的影响
[J].
Effect of temperature gradient on space charge distribution in oil impregnated papers
[J].
Modelling of dielectric breakdown through charge dynamics for polymer nanocomposites
[J].DOI:10.1109/TDEI.2016.006051 URL [本文引用: 2]
Numerical simulation on molecular displacement and DC breakdown of LDPE
[J].DOI:10.1109/TDEI.2015.005402 URL [本文引用: 3]
Thickness-dependent DC electrical breakdown of polyimide modulated by charge transport and molecular displacement
[J].DOI:10.3390/polym10091012 URL [本文引用: 1]
Carrier transport and molecular displacement modulated DC electrical breakdown of polypropylene nanocomposites
[J].DOI:10.3390/polym10111207 URL [本文引用: 1]
Charge injection and recombination at the metal-organic interface
[J].DOI:10.1016/S0009-2614(98)01277-9 URL [本文引用: 1]
Numerical analysis of space charge accumulation and conduction properties in LDPE nanodielectrics
[J].DOI:10.1109/TDEI.2015.7116341 URL [本文引用: 2]
Origin of thickness dependent DC electrical breakdown in dielectrics
[J].DOI:10.1063/1.4721809 URL [本文引用: 2]
Understanding the conduction and breakdown properties of polyethylene nanodielectrics:Effect of deep traps
[J].DOI:10.1109/TDEI.2015.004823 URL [本文引用: 1]
聚合物介质材料电荷捕获输运特性和机理的研究
[D].
Investigation into charge trapping transport properties and mechanisms in polymeric insulating materials
[D].
Electron-hole recombination in disordered organic semiconductors:Validity of the Langevin formula
[J].DOI:10.1103/PhysRevB.80.235202 URL [本文引用: 1]
Statistics of the recombinations of holes and electrons
[J].DOI:10.1103/PhysRev.87.835 URL [本文引用: 2]
Trap-assisted recombination in disordered organic semiconductors
[J].DOI:10.1103/PhysRevLett.107.256805 URL [本文引用: 1]
Absorption and conduction currents in polymers:A unified model
[J].DOI:10.1088/0022-3727/23/2/011 URL [本文引用: 1]
Charge generation,charge transport,and residual charge in the electrospinning of polymers:A review of issues and complications
[J].DOI:10.1063/1.3682464 URL [本文引用: 1]
Polyethylene/silica nanocomposites:Absorption current and the interpretation of SCLC
[J].DOI:10.1088/0022-3727/49/29/295305 URL [本文引用: 1]
Nonequilibrium steady-state statistics and associated effects for insulators and semiconductors containing an arbitraty distribution of traps
[J].DOI:10.1103/PhysRevB.4.502 URL [本文引用: 1]