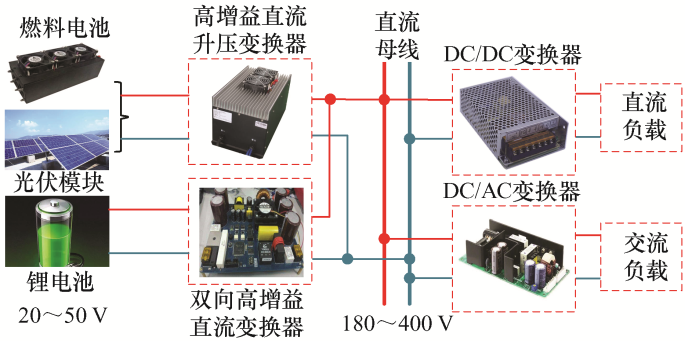
随着人们对能源需求的急剧增长,一次能源短缺和环境污染问题日益突出,开发可再生清洁能源已成为人类实现可持续发展的必然抉择^[1,2,3]。其中,氢能与太阳能因其无地域限制、储量丰富、无污染的特点在全球范围内得到了广泛的关注与重视。但燃料电池和光伏属于低压直流电源,一般输出电压范围在20~50 V,远低于并网逆变、氢电动车等应用场合中较高的直流母线电压。因此,如图1所示,在燃料电池和光伏系统后级设计高增益DC/DC变换器作为接口电路至关重要^[4,5,6]。

隔离型直流变换器具有天然的高升压比特性,文献[7]中提出一种高增益隔离式双开关谐振开关电容变换器,通过调节变压器匝比可轻易实现高电压传输比。但隔离型结构存在设计相对复杂、效率低、成本高等缺点^[8,9],且若不能妥善处理变压器漏感问题会导致开关管上产生严重的电压尖峰^[10]。

相比之下,非隔离型升压变换器由于结构简单、成本低、效率高等特点,在新能源领域中得到了广泛的关注。传统Boost变换器当占空比趋近于1时,理论上可实现无穷大电压增益,但电感与功率器件存在寄生电阻,变换器实际电压增益往往小于5,并且过高的占空比致使二极管导通时间很短,将加剧二极管反向恢复和EMI问题^[11]。在非隔离型变换器中采用耦合电感结构,可显著提高电压增益,但耦合电感本质与变压器相同,为防止开关管上产生电压尖峰和提升系统效率,往往需要新增钳位电路^[12,13]。文献[14]中研究了一种磁集成LCL倍压单元高增益变换器,通过磁集成技术可减小变换器体积并改善电感电流纹波,但这也增加了变换器设计的复杂度。文献[15]则基于级联结构实现了高电压增益,但两级变换结构会降低系统的能量转换效率,同时增加稳定性设计的难度^[16]。文献[17]无需电感器件,通过构建开关电容网络可直接抬升输出电压,有利于减小变换器体积,提高功率密度,但存在升压比受制于电路结构、难以控制等缺点。文献[18]中提出一种四相浮地并联高增益变换器,其具有良好的容错特性,但变换器电压增益提升有限,仅为传统Boost变换器电压增益的$1\text{+D}$倍。文献[19]中通过在浮地并联结构后级增加二极管开关单元进一步提升了电压增益,但该拓扑中部分开关管和二极管的电压应力没有改善,仍等于甚至大于输出电压,且变换器中两个开关管的占空比之和不能大于1,对控制要求较高。文献[20]则尝试将浮地并联结构与一种由两个二极管和两个电容构成的升压单元结合,取得了良好的效果,但对开关器件承受的电流应力改善有限。

在电力电子变换器控制方面,PI(Proportional integral)控制算法因其简单、易设计的特点得到了广泛应用。然而,通过变换器交流小信号模型所设计的PI参数当变换器工作点发生变化时往往难以继续保持较好的动态性能^[21]。模型预测控制则由于具有动态响应快、可避免调节系统参数等优点在DC/DC变换器领域也吸引了广大学者的研究。但Boost变换器为非最小相位系统,在直接电压控制中往往需要较长的预测步数,这将大大增加控制系统计算量^[22]。相比之下,滑模控制是根据控制律做变结构切换控制,这种运动与系统参数和扰动无关,因此具备对外部干扰和系统参数变化不敏感的优点,且容易实现。但传统滑模控制相对阶为1,存在高频切换动作所引起的抖振^[23]。故有必要将滑模函数转移到更高阶,保障系统鲁棒性的同时实现抖振抑制。

针对上述问题,本文在浮地并联变换器的基础上结合开关电容单元,提出一种无耦合电感的新型非隔离高增益变换器。该变换器不仅具备高电压增益的特点,同时具有开关管和二极管低电压应力、低电流应力的优点;此外引入的开关电容单元还使变换器同侧电感电流具备自动均流能力,而多电感并联结构则有利于提升变换器功率等级。文章在第2节中详细分析了所提变换器的拓扑与工作原理;并在第3节中主要讨论了变换器的稳态性能;此外,针对此变换器在第4节中设计了相应的鲁棒控制策略;最后,在第5节和第6节中分别给出相关仿真与试验结果和结论。

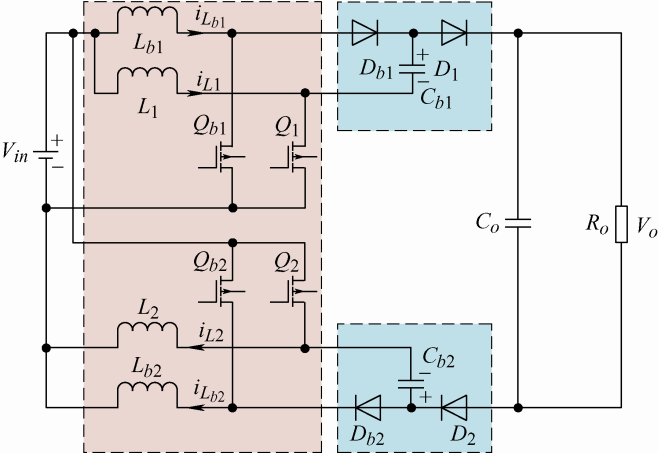
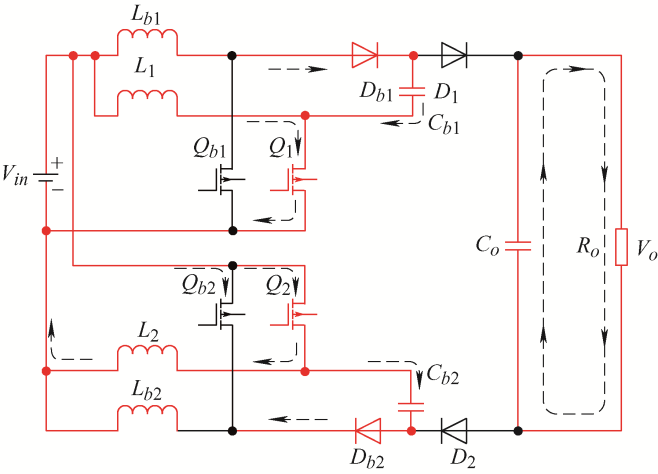
本文提出的新型高增益变换器拓扑如图2所示,${{\text{V}}_{\text{in}}}$和${{\text{V}}_{o}}$分别代表变换器输入和输出电压,${{\text{C}}_{o}}$和${{\text{R}}_{o}}$分别为输出电容与负载电阻。变换器主电路上下对称,输入与输出端不共地,新增开关电容单元如上、下两个小方框中所示,其在变换器单侧电感并联结构的支路各增加一个开关电容${{\text{C}}_{\text{b}\mathrm{1}}}$和${{\text{C}}_{\text{b}\mathrm{2}}}$,并移动二极管${{\text{D}}_{\mathrm{1}}}$和${{\text{D}}_{\mathrm{2}}}$位置构成,二极管${{\text{D}}_{\mathrm{1}}}、 {{\text{D}}_{b1}}$与${{\text{D}}_{\mathrm{2}}}、 {{\text{D}}_{b2}}$方向不同分别形成正向开关电容单元与反向开关电容单元。电感${{\text{L}}_{\mathrm{1}}}、 {{\text{L}}_{b1}}$和${{\text{L}}_{\mathrm{2}}}、 {{\text{L}}_{b2}}$则构成四相浮地并联结构,当开关管${{Q}_{1}}$与${{Q}_{2}}$、${{Q}_{\text{b}1}}$与${{Q}_{\text{b}2}}$保持同时导通,${{Q}_{1}}$与${{Q}_{\text{b}1}}$、${{Q}_{2}}$与${{Q}_{\text{b}2}}$相互交错180°导通时可实现电感的并联充电串联放电,从而获得高升压比。

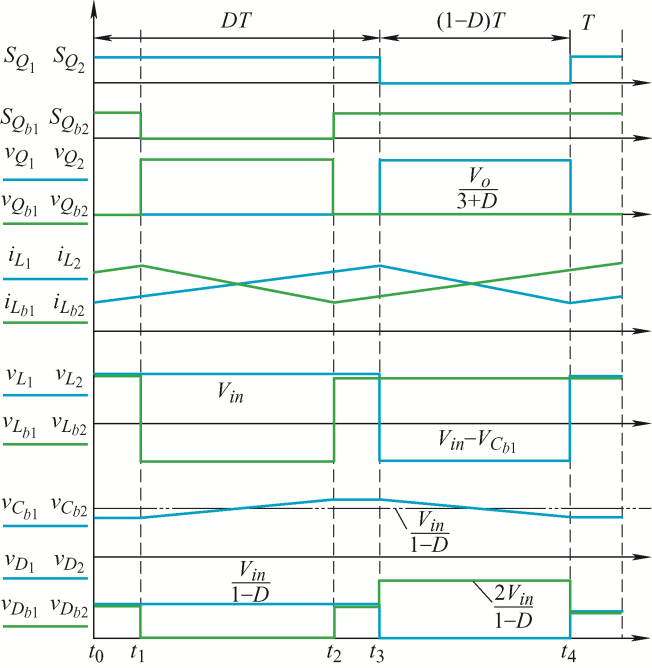
为便于工作原理分析,作出如下假设：① 所有器件均为理想器件;② 变换器工作在稳定状态,电感电流连续,且为获得高电压增益,主要讨论开关管占空比$D$大于0.5的情况;③ ${{\text{C}}_{\text{o}}}$电容值足够大,可忽略输出电压纹波。提出的变换器在一个开关周期内共有4种工作模态,其对应的主要波形如图3所示,其中${{S}_{{{Q}_{1}}}}、 {{S}_{{{Q}_{2}}}}、 {{S}_{{{Q}_{\text{b}1}}}}、 {{S}_{{{Q}_{\text{b}2}}}}$表示对应开关的驱动信号。

工作模态1(t₀~t₁)：由图4所示,此时开关管${{Q}_{1}}、 {{Q}_{2}}、 {{Q}_{\text{b}1}}、 {{Q}_{\text{b}2}}$均处于导通状态,${{\text{D}}_{1}}、 {{\text{D}}_{2}}、 {{\text{D}}_{\text{b}1}}、 {{\text{D}}_{\text{b}2}}$关断;电感${{L}_{1}}、 {{L}_{2}}、 {{L}_{\text{b}1}}、 {{L}_{\text{b}2}}$与输入源${{V}_{\text{in}}}$并联,对电感持续充电,对应电感电流以恒定的斜率线性增加;电容${{C}_{\text{b}1}}、 {{C}_{\text{b}2}}$电压则保持不变。其状态方程为

工作模态2(t₁~t₂)：该模态工作等效电路如图5所示,此时开关管${{Q}_{1}}、 {{Q}_{2}}$仍然导通,而${{Q}_{\text{b}1}}、 {{Q}_{\text{b}2}}$关断,二极管${{\text{D}}_{\text{b}1}}、 {{\text{D}}_{\text{b}2}}$正向导通,${{\text{D}}_{1}}、 {{\text{D}}_{2}}$反向截止;输入源对电感${{L}_{1}}、 {{L}_{2}}$继续并联充电,${{i}_{{{L}_{1}}}}、 {{i}_{{{L}_{2}}}}$线性增加,而电感${{L}_{\text{b}1}}、 {{L}_{\text{b}2}}$分别与开关电容${{C}_{\text{b}1}}、 {{C}_{\text{b}2}}$串联,释放能量对电容进行充电,电感电流${{i}_{{{L}_{\text{b}1}}}}、 {{i}_{{{L}_{\text{b}2}}}}$下降,电容电压${{\text{v}}_{{{c}_{\text{b}1}}}}、 {{\text{v}}_{{{c}_{\text{b}2}}}}$线性上升。

工作模态3(t₂~t₃)：该模态工作原理与等效电路同工作模态1相同。

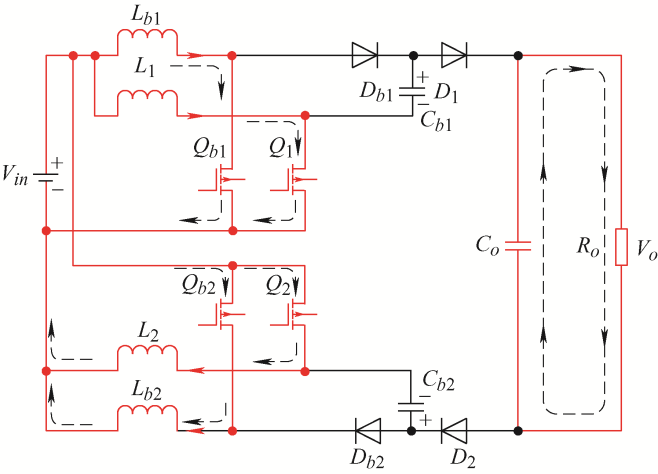
工作模式4(t₃~t₄)：在此模态中开关管${{Q}_{\text{b}1}}、 {{Q}_{\text{b}2}}$导通,${{Q}_{1}}、 {{Q}_{2}}$关断,而二极管${{\text{D}}_{1}}、 {{\text{D}}_{2}}$正向导通,${{\text{D}}_{\text{b}1}}、 {{\text{D}}_{\text{b}2}}$截止;电感${{L}_{1}}、 {{L}_{2}}$与开关电容${{C}_{\text{b}1}}、 {{C}_{\text{b}2}}$串联,均释放能量向负载供电,对应电感电流${{i}_{{{L}_{\mathrm{1}}}}}、 {{i}_{{{L}_{\mathrm{2}}}}}$和开关电容电压${{\text{v}}_{{{C}_{\text{b}\mathrm{1}}}}}、 {{\text{v}}_{{{C}_{\text{b}2}}}}$线性减小,而输入源${{V}_{\text{in}}}$对电感${{L}_{\text{b}1}}、 {{L}_{\text{b}2}}$继续充电,此阶段等效电路如图6所示,状态方程为

通过上述工作原理分析,得到变换器不同工作模态下的状态方程(1)~(5),进一步根据一个开关周期内电感${{L}_{1}}、 {{L}_{2}}、 {{L}_{\text{b}1}}、 {{L}_{\text{b}2}}$的伏秒平衡原则有

联立式(6)~(8)推得电压增益与开关电容电压为

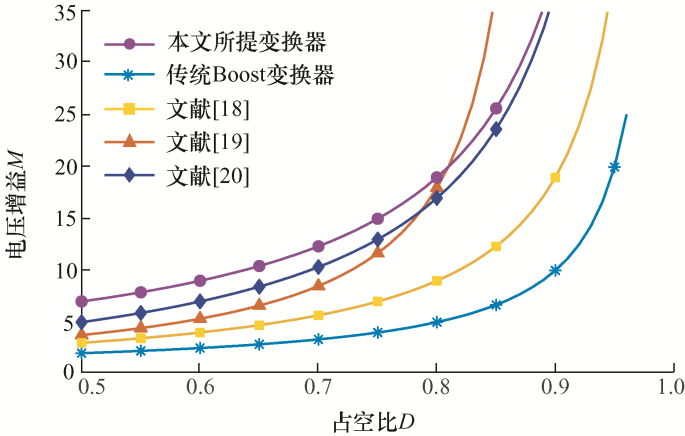
由式(9)可知,所提出的新型高增益变换器电压增益为传统Boost变换器电压增益的$3\text{+}D$倍。图7为本文变换器与文献[18,19,20]中变换器电压增益的对比曲线,文献[19]变换器电压增益曲线是其占空比${{D}_{2}}$等于0.1时随${{D}_{1}}$变化的曲线,可看出本文所提变换器电压增益特性与传统Boost变换器相比大幅提升,相比于文献[18,19,20]中的高增益变换器也具有一定的优势。

根据变换器工作原理分析可知,二极管与开关管的电压应力被开关电容电压钳位,将式(9)中已知的开关电容电压换算为与输出电压的关系,则有

开关电容${{C}_{\text{b}1}}、 {{C}_{\text{b}2}}$的电压在${{{V}_{\text{o}}}}/{\left( 3+D \right)}\;$上下波动,电压波动大小与开关电容容值关系如下所示

式中,$\Delta {{V}_{{{c}_{\text{b}}}}}$表示开关电容在一个开关周期内充放电的电压波动。

进一步,结合变换器主要工作波形分析可推得开关管与二极管承受的最大电压应力为

可看出二极管${{D}_{1}}、 {{D}_{2}}$和开关管${{Q}_{1}}、 {{Q}_{2}}、 {{Q}_{\text{b}1}}、 {{Q}_{\text{b}2}}$最大电压应力等于开关电容电压,为输出电压的$1/\left( 3\text{+}D \right)$;而二极管${{D}_{\text{b}1}}、 {{D}_{\text{b}2}}$最大电压应力是开关电容电压的二倍,但仍约为输出电压的一半。相比于传统Boost变换器,变换器开关器件电压应力大幅减小,有助于选择低额定电压的器件以减小器件的导通损耗,并提高整体工作效率与降低系统成本,使变换器适用于低压输入高压输出的场合。

根据能量守恒定律,可得输入平均电流${{\text{I}}_{\text{in}}}$与输出平均电流${{\text{I}}_{\text{o}}}$关系为

设各电感电流平均值分别为${{\text{I}}_{{{\text{L}}_{1}}}}、 {{\text{I}}_{{{\text{L}}_{2}}}}、 {{\text{I}}_{{{\text{L}}_{\text{b}1}}}}、 {{\text{I}}_{{{\text{L}}_{\text{b}2}}}}$,根据变换器中电容的安秒平衡推得电感电流如下

通过工作模态分析,在一个开关周期内,开关管${{Q}_{1}}、 {{Q}_{2}}$在模态1和模态3中流过的电流分别为${{\text{I}}_{{{\text{L}}_{1}}}}、 {{\text{I}}_{{{\text{L}}_{2}}}}$,持续时间为$\left( 2D-1 \right)T$,在模态2中流过的电流分别为${{\text{I}}_{{{\text{L}}_{1}}}}\text{+}{{\text{I}}_{{{\text{L}}_{\text{b}1}}}}、 {{\text{I}}_{{{\text{L}}_{2}}}}\text{+}{{\text{I}}_{{{\text{L}}_{\text{b}2}}}}$,持续时间为$\left( 1-D \right)T$;而开关${{Q}_{\text{b}1}}、 {{Q}_{\text{b}2}}$在模态1、模态3以及模态4中有流过电流,分别为${{\text{I}}_{{{\text{L}}_{\text{b}1}}}}、 {{\text{I}}_{{{\text{L}}_{\text{b}2}}}}$,持续时间为$DT$,因此可得各开关管的电流平均值为

同理可推得,各二极管的电流平均值如下

从式(17)~(19)可看出,开关器件的电流平均值均远小于总输入电流,有助于降低开关器件的导通损耗。

从工作原理分析,结合图3可知,在一个开关周期$T$内有4种工作模式,其中模式1和3中开关电容${{C}_{\text{b}1}}、 {{C}_{\text{b}2}}$不进行充放电,电压保持不变;模式2中电感${{L}_{\text{b}1}}、 {{L}_{\text{b}2}}$对${{C}_{\text{b}1}}、 {{C}_{\text{b}2}}$充电,充电电流为${{i}_{{{L}_{\text{b}1}}}}、 {{i}_{{{L}_{\text{b}2}}}}$;模式4中${{C}_{\text{b}1}}、 {{C}_{\text{b}2}}$释放能量,放电电流为${{i}_{{{L}_{1}}}}、 {{i}_{{{L}_{2}}}}$;且充电时间与放电时间均为$\left( 1-D \right)T$,根据开关电容的安秒平衡原则有

从式(20)可知,当开关管${{Q}_{1}}$与${{Q}_{\text{b}1}}$、${{Q}_{2}}$与${{Q}_{\text{b}2}}$导通时间相同时,其各自对应的电感电流之间具备自动均流特性。

根据上述分析,表1给出所提变换器与传统Boost变换器、文献[18,19,20]变换器的主要特性对比。可看出所提出的变换器在$D\text{=}0.7$时,计算理想电压增益可达12.33,而此时开关管${{Q}_{1}}、 {{Q}_{2}}、 {{Q}_{\text{b}1}}、 {{Q}_{\text{b}2}}$和二极管${{D}_{1}}、 {{D}_{2}}$电压应力仅为输出电压的0.27倍,二极管${{D}_{\text{b}1}}、 {{D}_{\text{b}2}}$电压应力也只为输出电压的0.54倍,与传统Boost变换器、文献[18,19,20]等非隔离高增益变换器相比,所提变换器在电压增益、开关器件电压应力特性上均有所改进。

开关变换器作为一种强非线性系统,采用传统线性PI控制,当变换器元件参数和工作点变化时会使控制器性能下降。为提高变换器系统的动态性能,针对所提变换器设计一种基于ST(Super-twisting)的二阶滑模控制算法,其控制律仅与控制变量有关,且可实现定频控制。因此设计相对简单,既保持了传统滑模强鲁棒性的优点,通过将控制率转移至更高阶的滑模面,也减弱了滑模控制的抖振现象,实现输入电压和输出负载扰动时变换器的平稳电压输出。

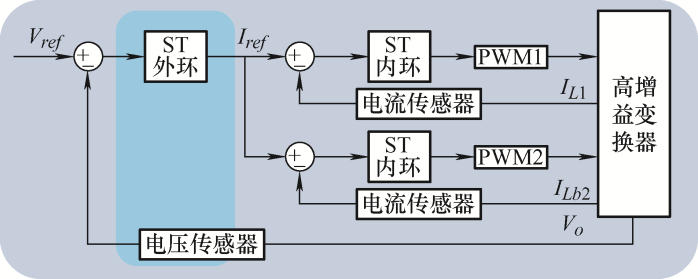
针对所提变换器,具体控制算法如图8所示,采用双闭环结构,内环为电流环,外环为电压环。ST算法的内环控制滑模面选取为$S={{i}_{L}}-{{I}_{Lref}}$,内环参考电流值由电压外环给出。电流内环滑模控制率$u$由两部分构成,第一部分是关于滑模面的函数,第二部分是滑模面在时间上的积分。

式中,$\lambda $和$\alpha $为需要设计的控制器参数;sgn为符号函数。

为稳定母线电压,ST外环控制滑模面选取以输出电压反馈值与给定参考电压值的差作为滑模面,即${{S}_{o}}={{V}_{o}}-{{V}_{ref}}$,对应电流外环滑模控制率${{u}_{o}}$为

此外由于变换器同侧两路电感电流具有自动均流能力,如图8所示,上下路只各采一路电流信号。PWM1与PWM2信号相互移相180°使开关管${{Q}_{1}}、 {{Q}_{2}}$与${{Q}_{\text{b}1}}、 {{Q}_{\text{b}2}}$分别交错控制,其中开关管${{Q}_{1}}、 {{Q}_{2}}$使用PWM1信号控制,开关管${{Q}_{\text{b}1}}、 {{Q}_{\text{b}2}}$使用PWM2信号控制。算法收敛性详细证明可根据文献[24]推得,本文不再赘述。

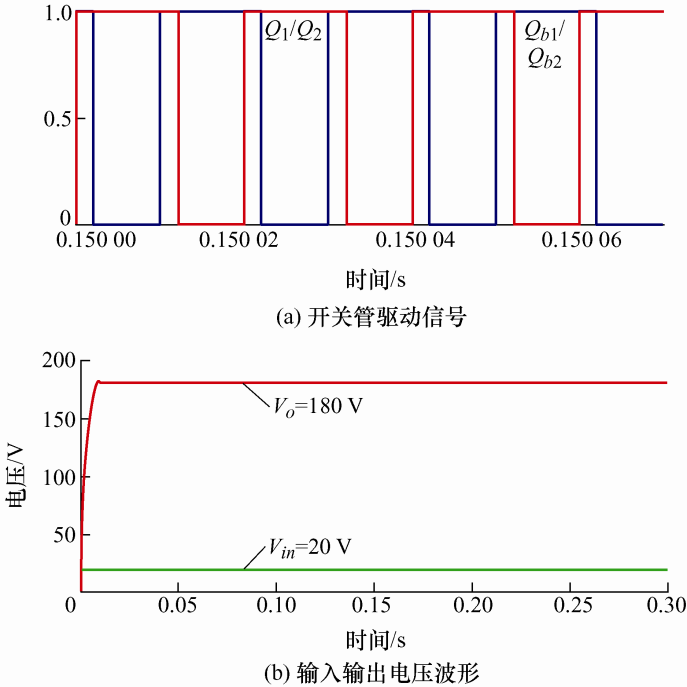
为验证变换器理论分析的正确性,在Matlab/Simulink中搭建了所提变换器的仿真电路模型,并相应制作了一个200 W变换器样机进行了试验验证。试验参数设计见表2。

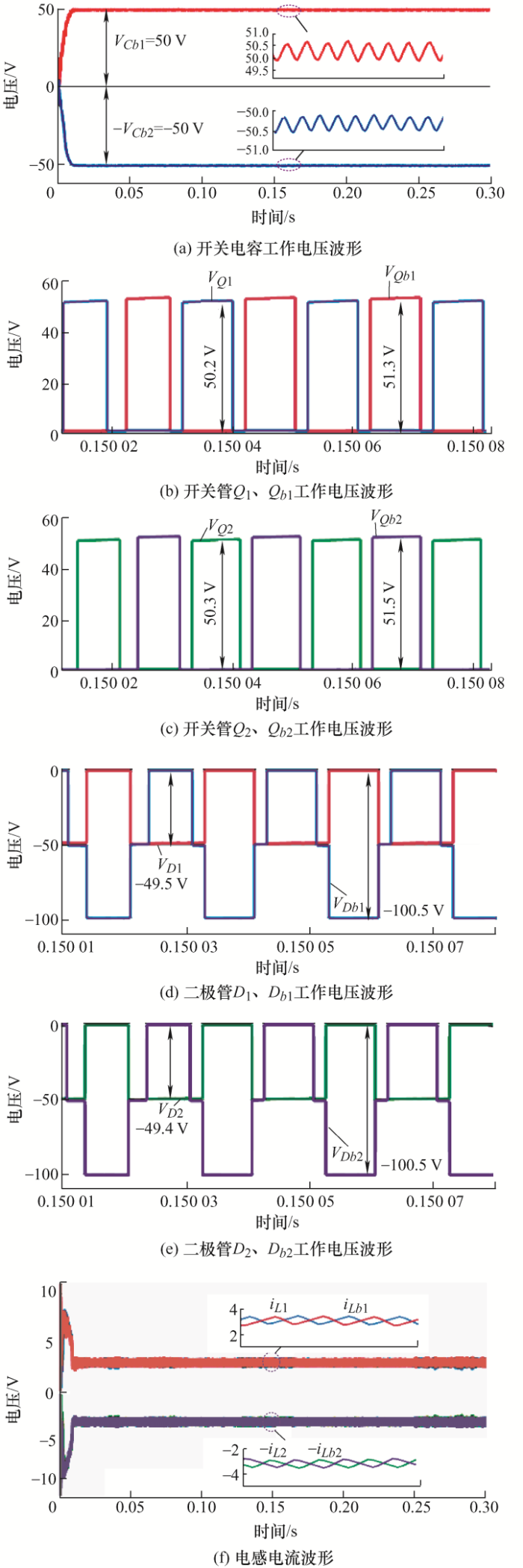
变换器仿真稳态工作波形如图9所示,图9a为开关管的驱动信号,图9b为变换器满载工作时的输入输出电压波形,当占空比稳定在0.6左右时,变换器将20 V输入电压升到180 V,电压增益为9倍,避免了极限占空比的出现。此时开关电容电压如图10a所示,电压稳定在50 V并小幅波动,与理论分析的工作波形一致,且符合${{V}_{in}}/\left( 1-D \right)\text{=}{{50}_{{}}}\text{V}$的理论计算值。

开关管与二极管工作仿真电压波形如图10b~10e所示,从波形可知开关管${{Q}_{1}}、 {{Q}_{2}}、 {{Q}_{\text{b}1}}、 {{Q}_{\text{b}2}}$和二极管${{D}_{1}}、 {{D}_{2}}$承受的最大电压应力约为50 V,等于开关电容电压,远低于180 V输出电压;二极管${{D}_{\text{b}1}}、 {{D}_{\text{b}2}}$承受的最大电压应力等于2倍的开关电容电压,约为100 V,但其电压应力仍小于输出电压,仿真结果与理论计算值一致,这验证了变换器的低开关器件电压应力特性。图10f为电感${{L}_{1}}、 {{L}_{\text{b}1}}、 {{L}_{2}}、 {{L}_{\text{b}2}}$的电流波形,可看出同侧两路电感电流相互交错180°且由于电容的自动均流能力两电感电流保持一致。

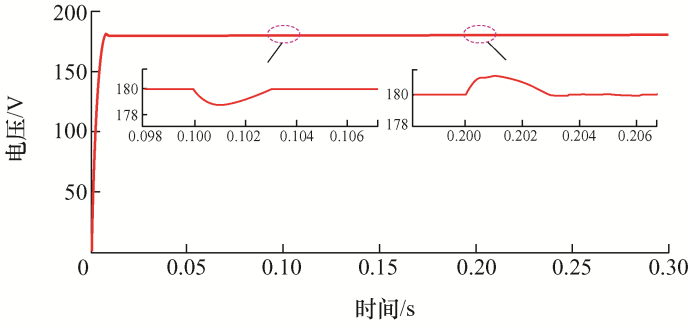
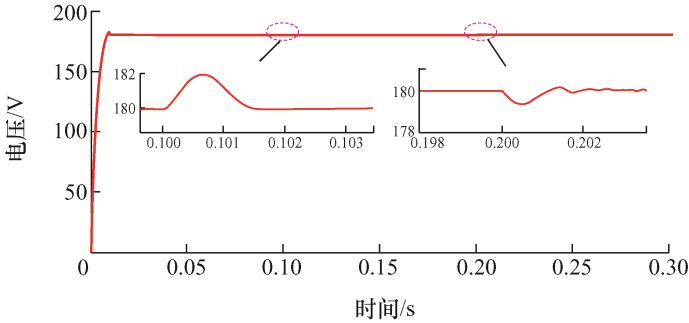
图11为施加负载扰动时的输出电压波形,负载电阻在0.1 s处由162 Ω突变为108 Ω,即输出功率从200 W跳变成300 W,从仿真波形可看出输出电压跌落仅为1.25 V,恢复时间为2.8 ms;在0.2 s处负载电阻则从108 Ω跳变回162 Ω,输出电压超调为1.2 V,调节时间也约为2.8 ms,具有良好的抗负载扰动能力。图12为施加输入电压扰动时的输出电压波形,输入电压在0.1 s处从20 V突升到25 V,此时调节时间仅为1.5 ms,电压超调为2.2 V;在0.2 s处输入电压从25 V跳变回20 V,此时调节时间为2 ms,电压超调只有0.6 V,结果表明系统具有良好的动态性能,验证了ST控制的强鲁棒性和快速性。

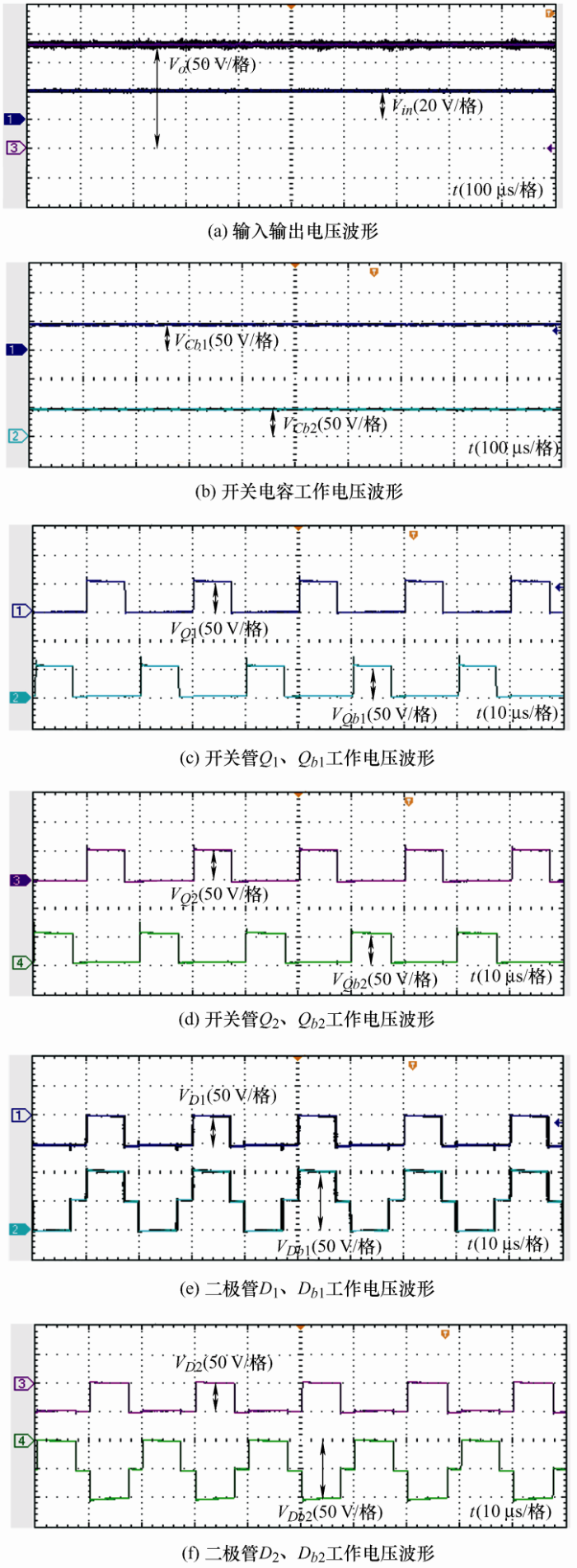
为进一步验证理论分析的正确性,与仿真参数一致,制作了一台200 W变换器样机,试验波形如图13所示。从试验波形可知,与仿真结果相同,当变换器工作在20 V输入、180 V输出时,开关电容电压、开关管${{Q}_{1}}、 {{Q}_{2}}、 {{Q}_{\text{b}1}}、 {{Q}_{\text{b}2}}$电压应力、二极管${{D}_{1}}、 {{D}_{2}}$电压应力均约为50 V,二极管${{D}_{\text{b}1}}、 {{D}_{\text{b}2}}$承受的最大电压应力则为100 V。综上,仿真与试验结果表明所提出的基于开关电容倍压单元的新型浮地并联高增益变换器拓扑具有可行性。

通过浮地并联结构与开关电容单元结合,本文提出一种新型高增益DC/DC变换器,并针对其设计了ST控制策略,通过对其理论分析与试验验证,结果表明所提变换器具有如下特点。

(1) 无需耦合电感和变压器,变换器就具有高电压增益特性,适用于燃料电池、光伏等低压输入、高压输出的应用场合。

(2) 开关器件承受的电压应力与电流应力显著降低,有利于选择低耐压高性能开关器件,提高系统效率。

(3) 对于多并联电感结构,开关电容单周期内的充放电安秒平衡使同侧电感电流具有自动均流能力,可减少电流传感器的使用。

(4) 设计的ST控制算法使变换器具有良好的动态性能,可应对大负载扰动和电源扰动。